A New General Correlation for the Influence Parameter in Density Gradient Theory and Peng–Robinson Equation of State for n-Alkanes
Abstract
1. Introduction
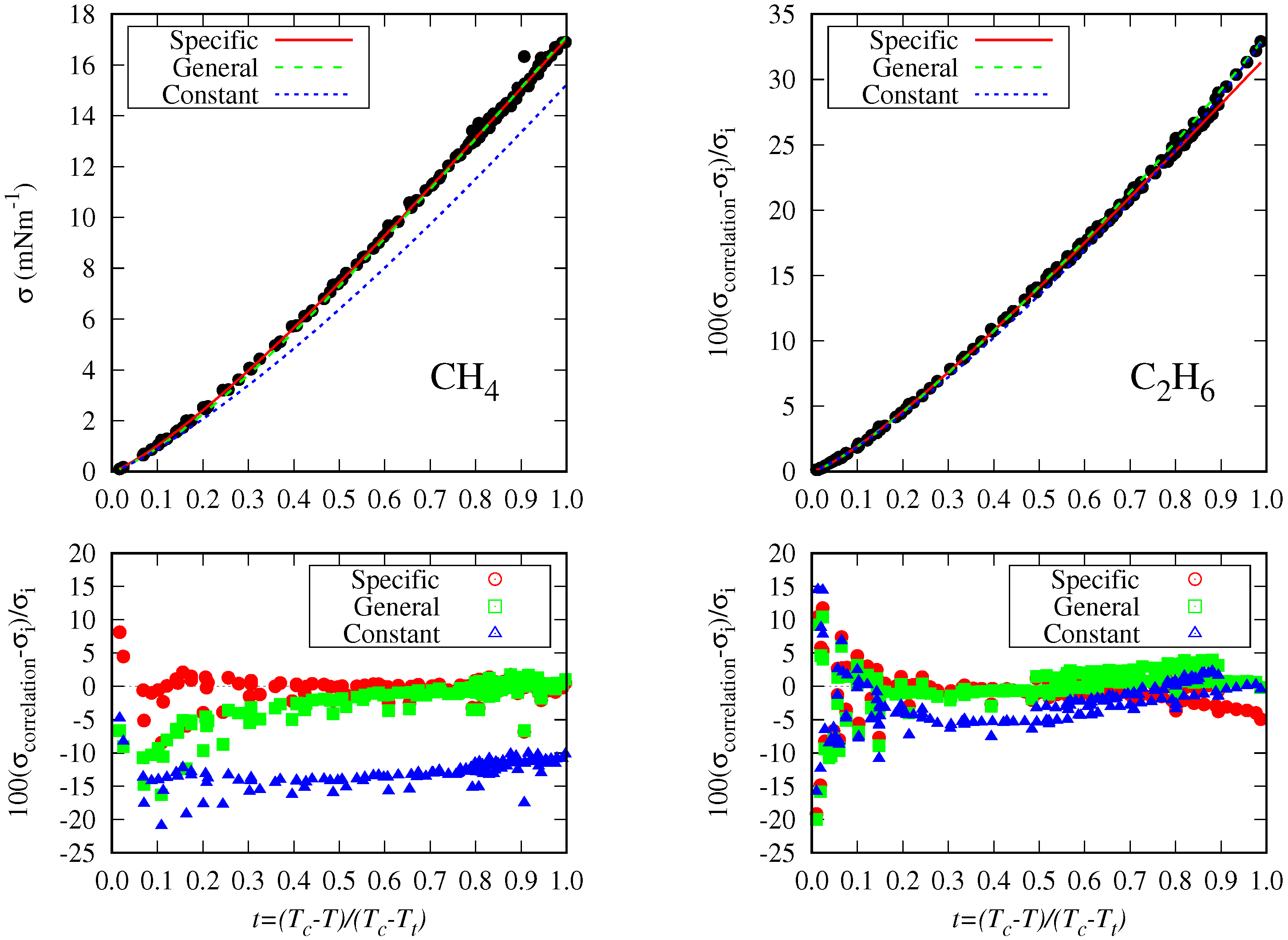
2. Density Gradient Theory and Peng–Robinson Equation of State
- (i)
- (ii)
- The fluid properties of the saturated single phases (vapor and liquid) are obtained from an EoS, so no other data sources or analytical expressions are necessary.
- (iii)
- The theory allows the calculation of the surface or interfacial tension, density profiles and their thickness, the surface enthalpy and entropy, and some other properties for the adsorption processes [80].
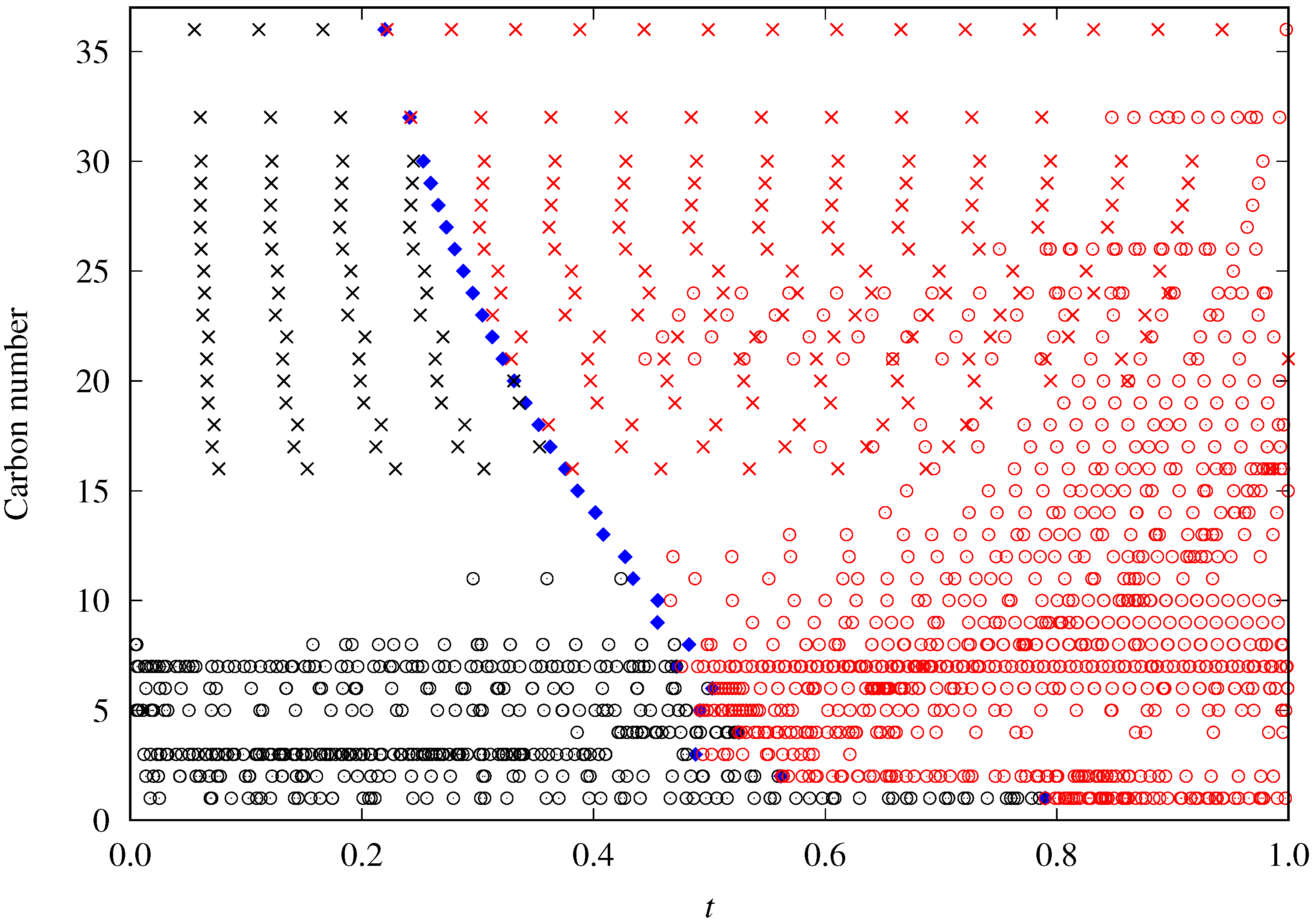
3. Sources of Data
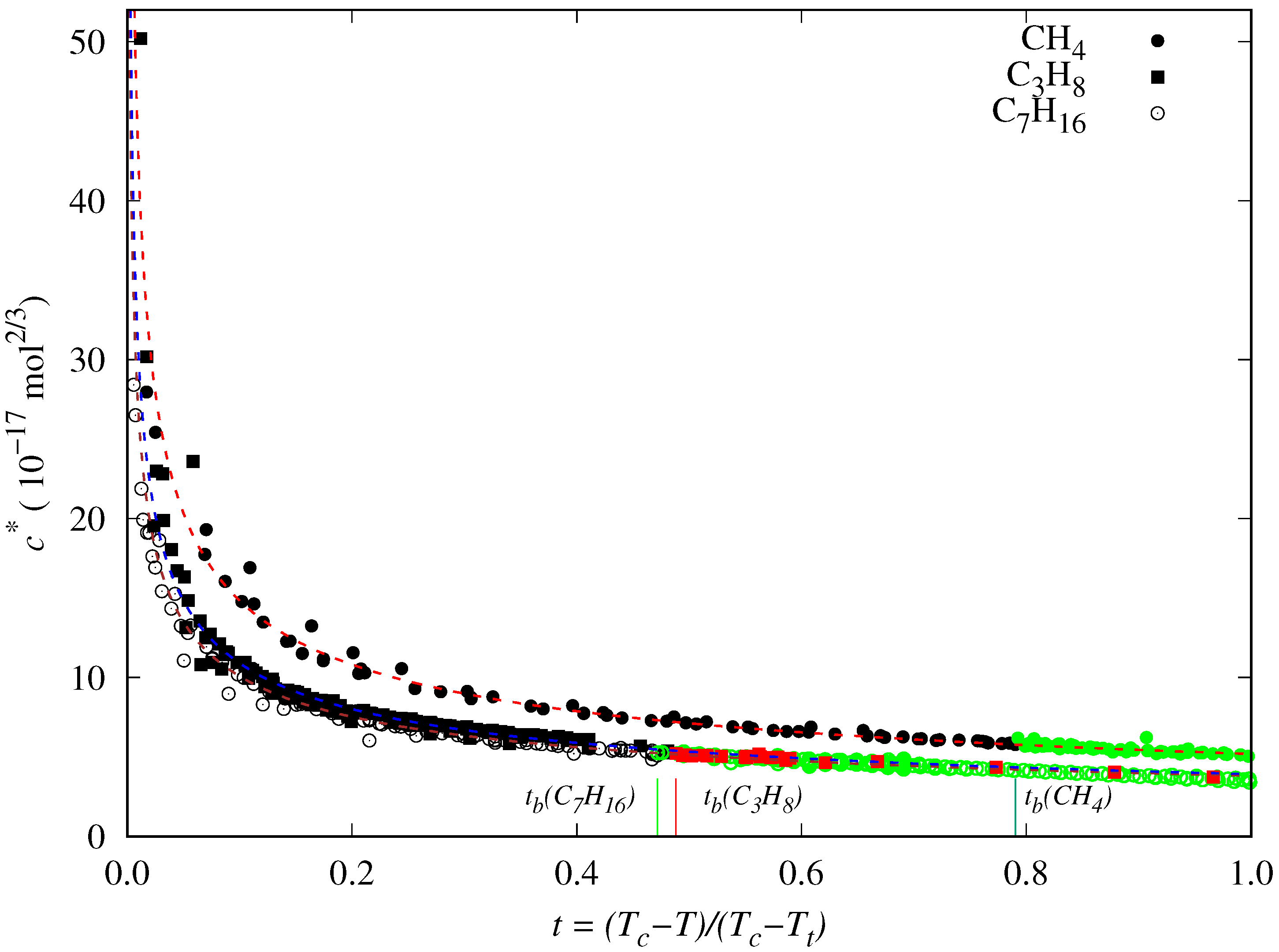
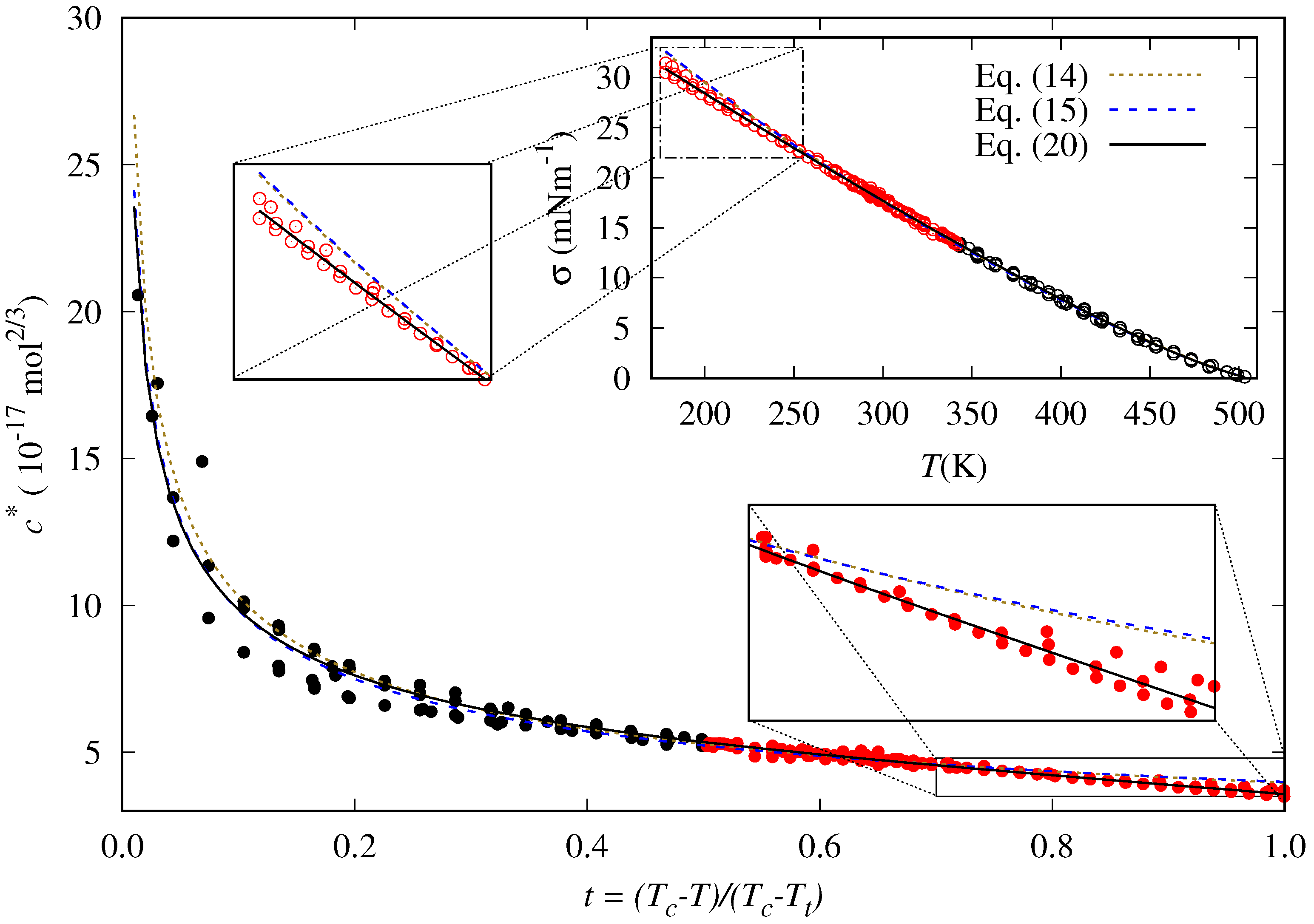
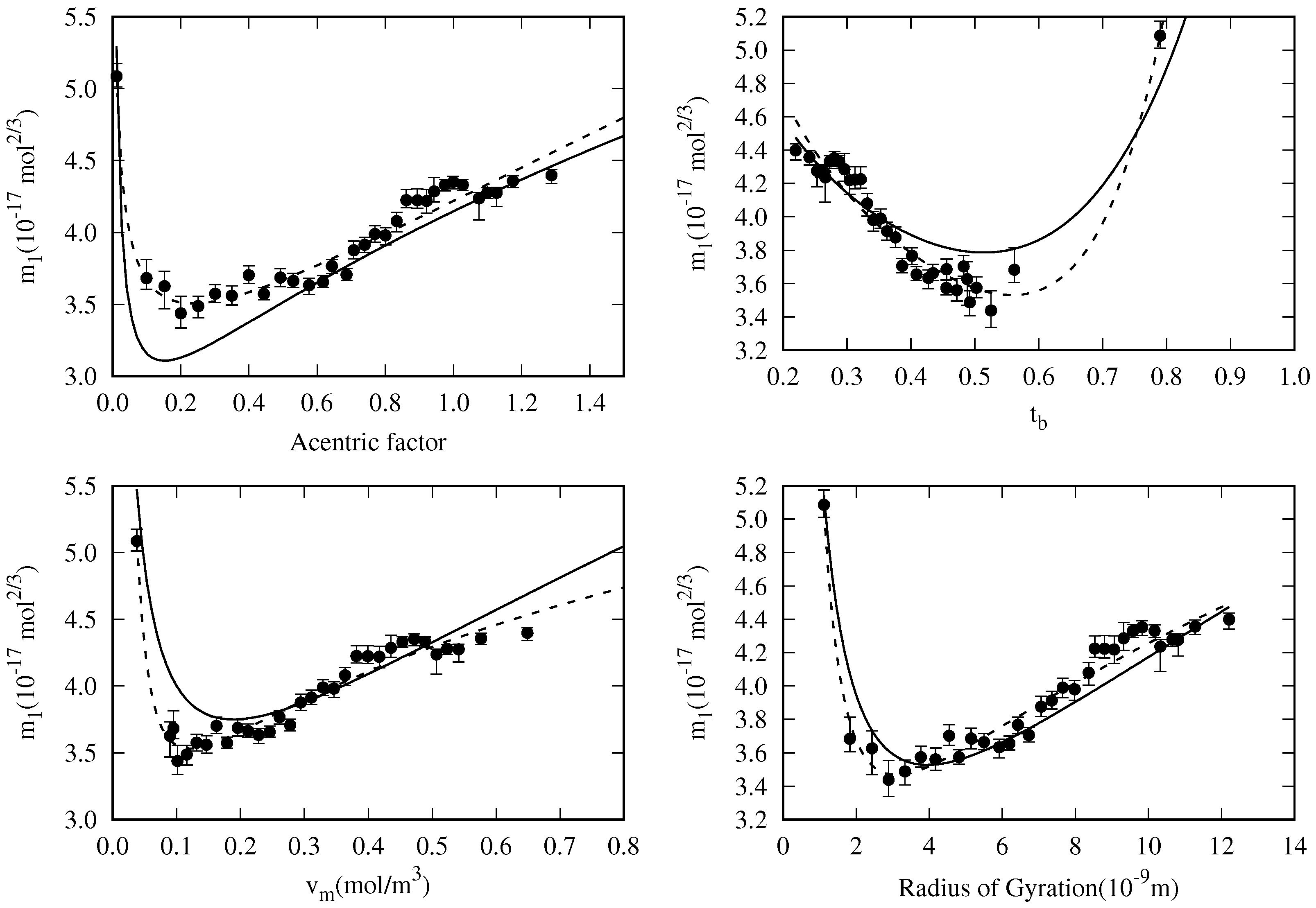
4. New Correlation for the Reduced Influence Parameter
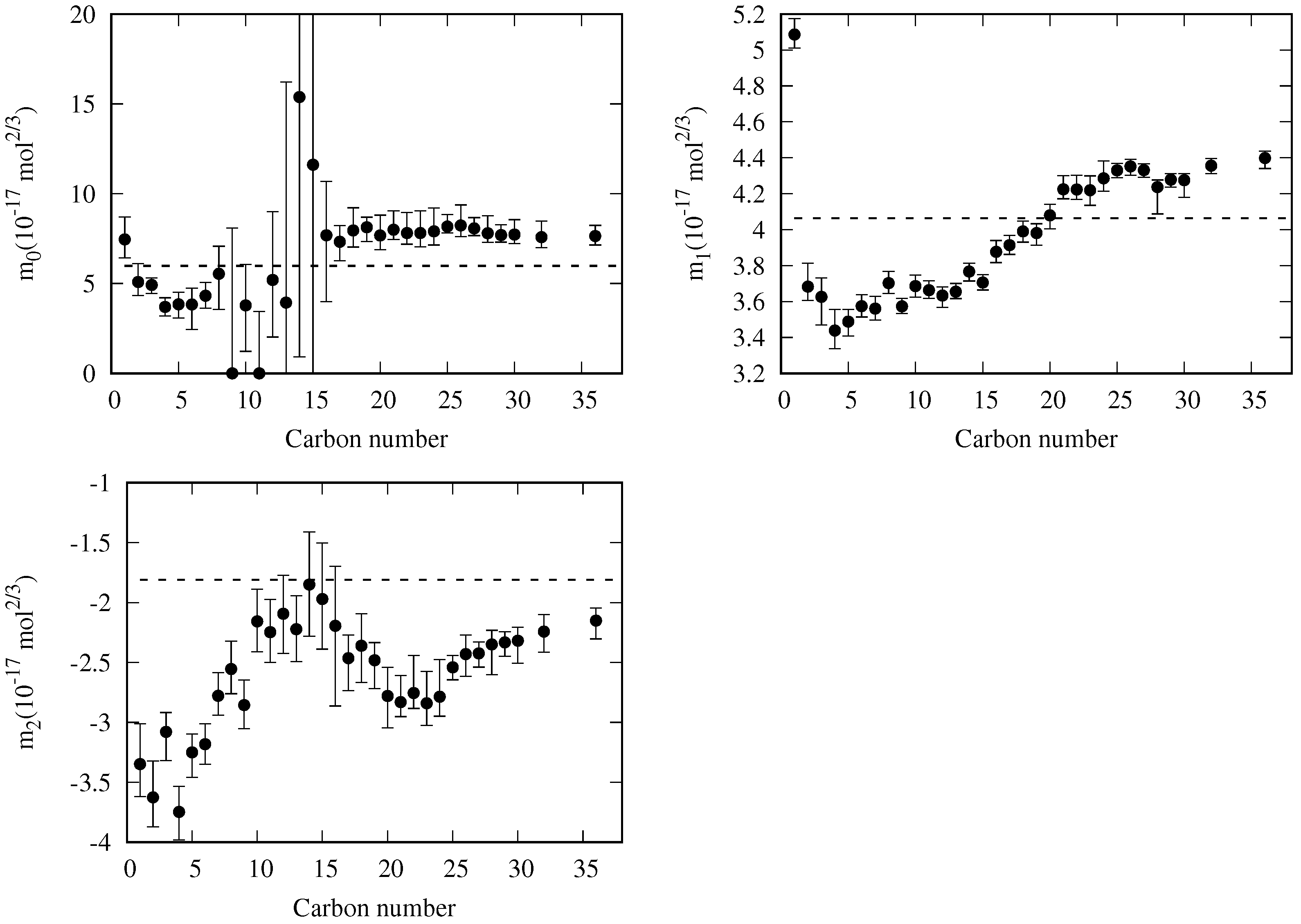
- decreases almost linearly in the range [], so it could be fitted to a linear expression:where is the slope and is the value of the reduced influence parameter at the triple point temperature.
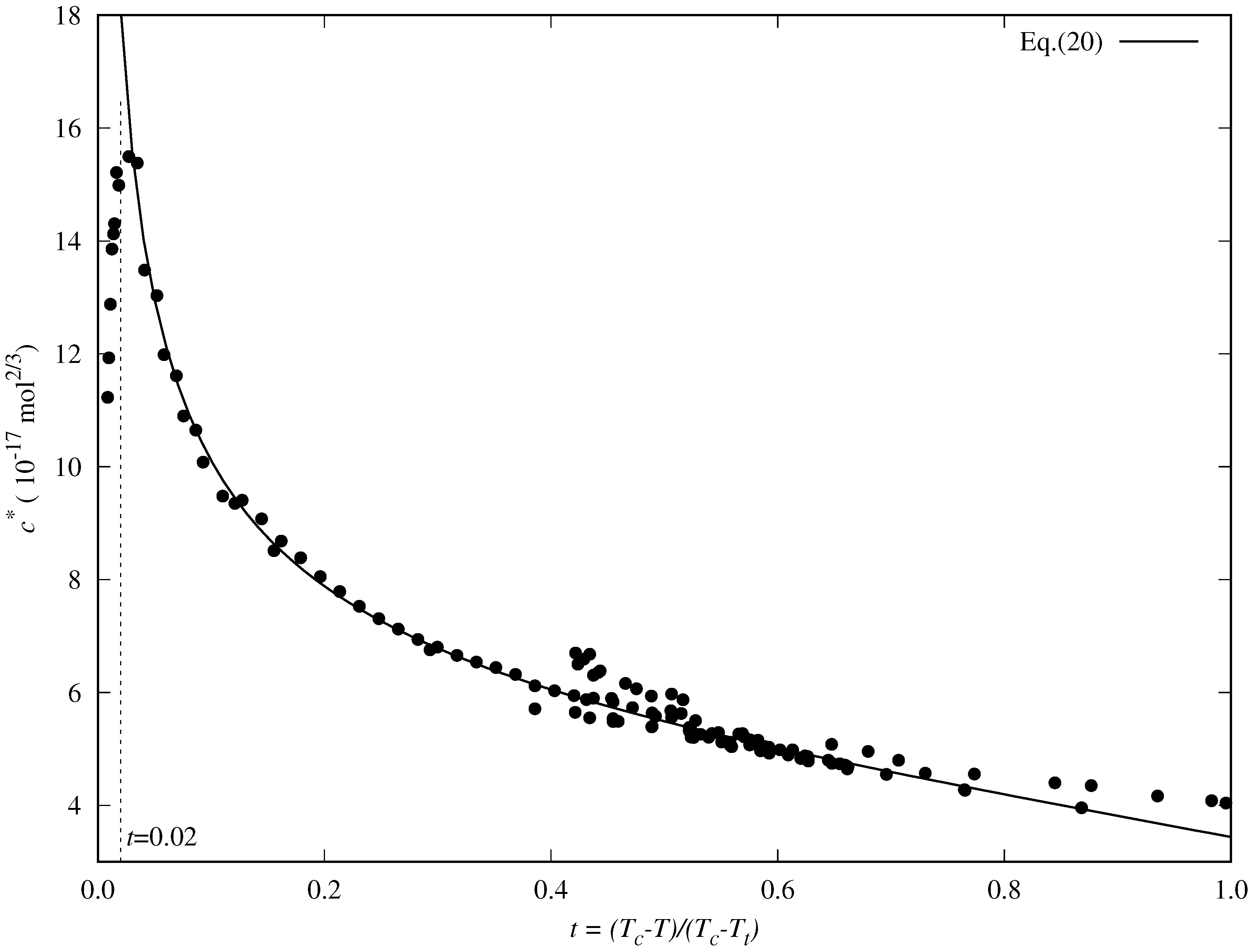
- Near the critical point (), tends to infinity. To reproduce this behavior, an analytical expression such as the one proposed by Zuo and Stenby [70] has to be used:
5. Results and Discussion
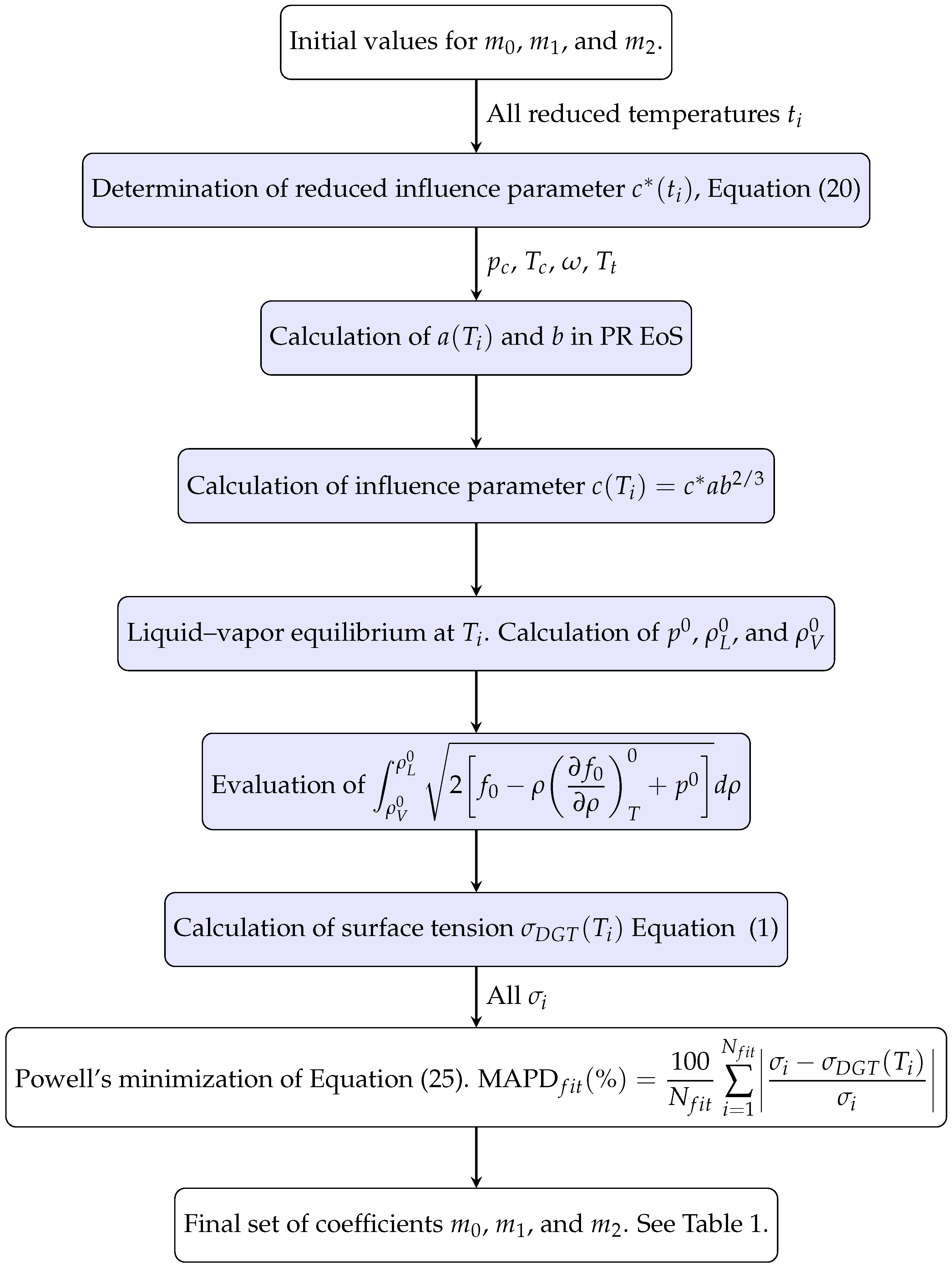
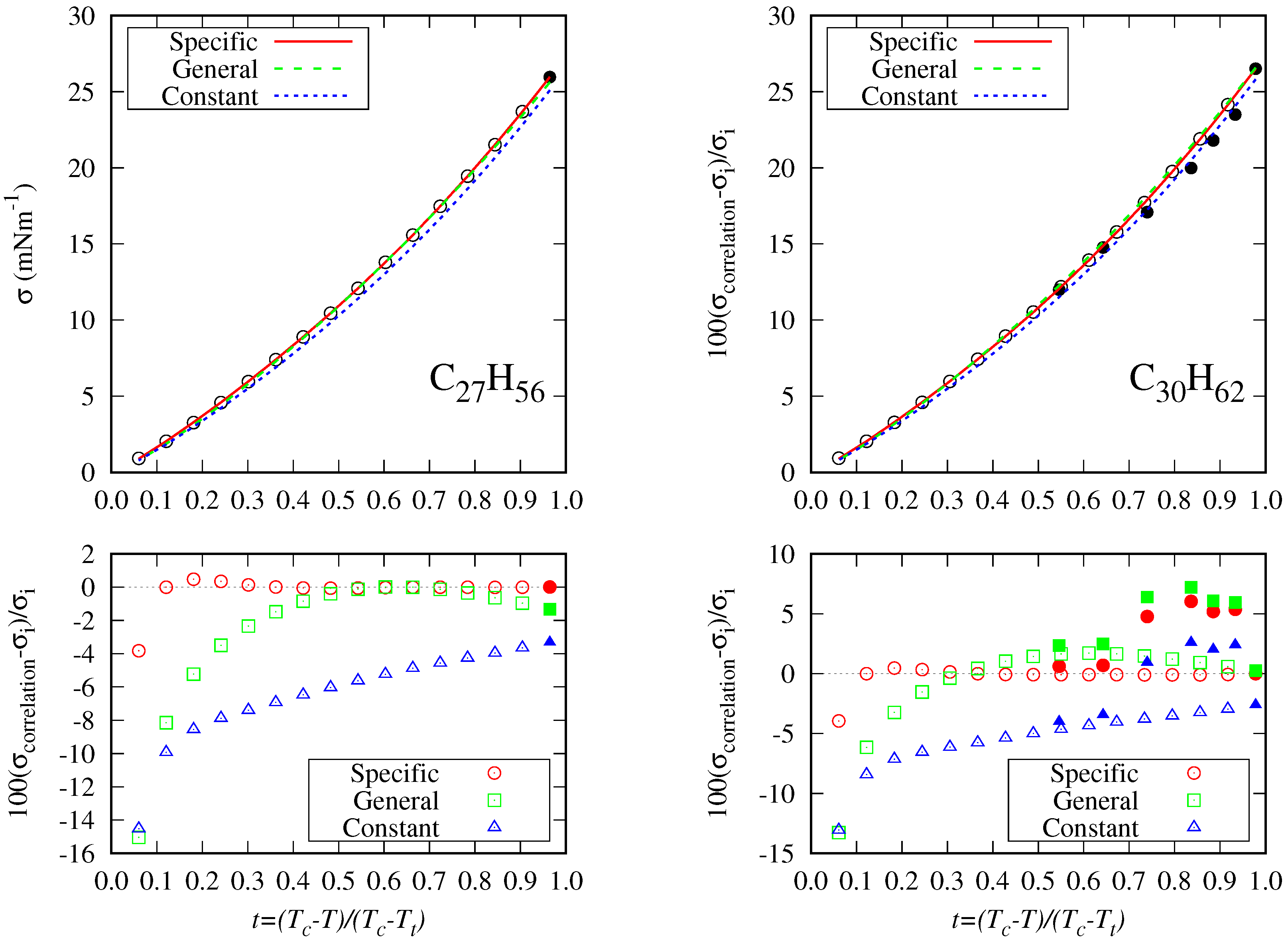
5.1. Adjustable Coefficients for the Specific Correlation
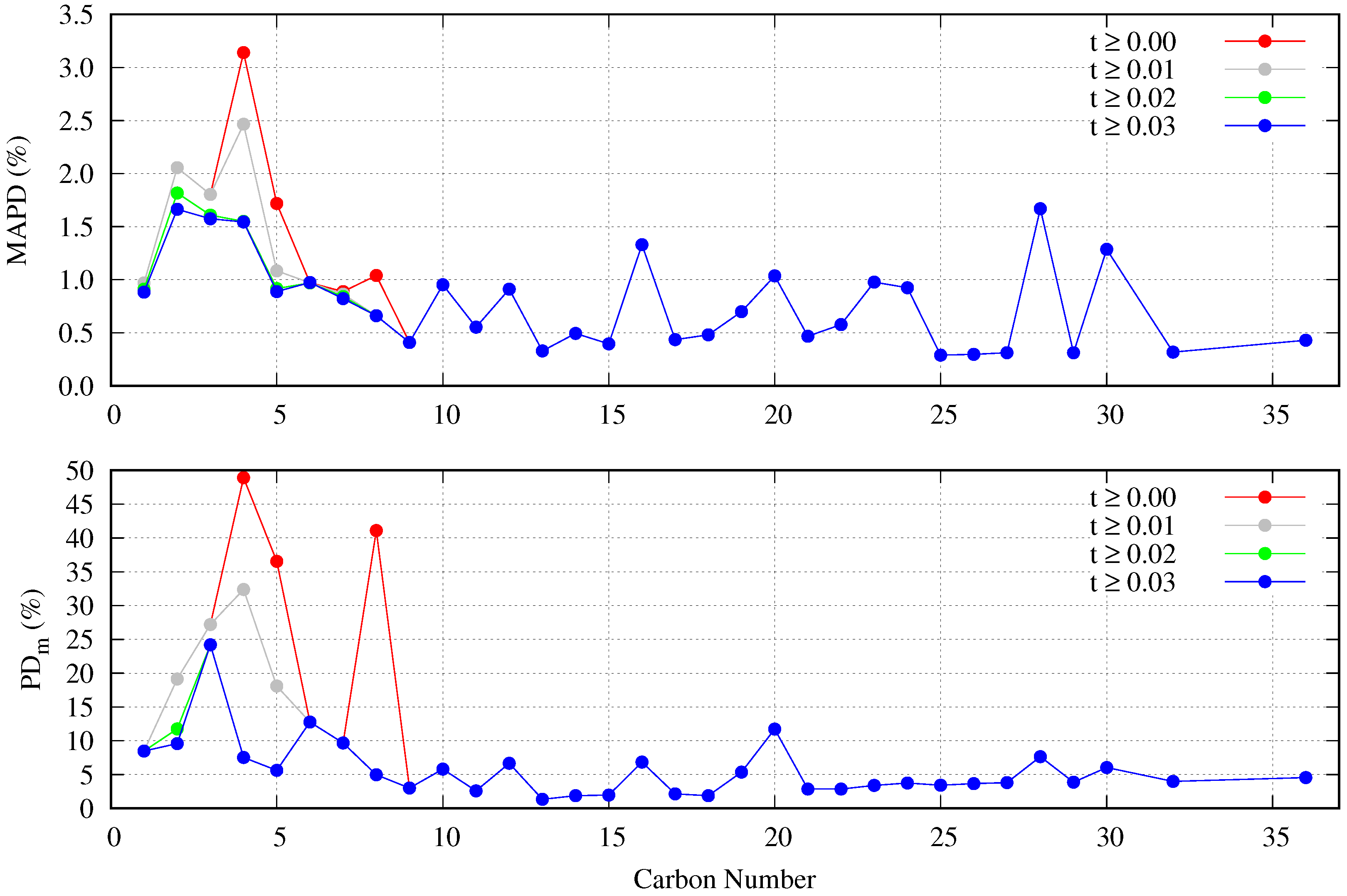
5.2. Accuracy of the Proposed Specific Model
5.3. General Correlation
- The DIPPR data predicted using Sugden’s correlation will not be considered in the new global correlation, and only data in the range will be considered in the coefficient determination of the global correlation. The number of available data and fitting data for each fluid are compiled in Table 2.
- There are some fluids (see Figure 1) for which a considerable number of fitting data are available (i.e., n-heptane and n-hexane with 357 and 269 data, respectively), whereas in other cases the number of data is one (n-hexatriacontane and others). To have a suitable general correlation not biased by the data availability, the adjustable coefficients will be obtained by minimizing the overall mean absolute percentage deviation (OMAPDfit), defined as:where MAPDfit,k is the mean absolute percentage deviation of the fluid k, defined in Equation (25), but taking from Table 2, and with the number of fluids (32 in these cases). Thus, the coefficients of the general correlation will be determined with data, with a weighing scheme depending on the fitting data of each fluid.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adamson, A.; Gast, A. Physical Chemistry of Surfaces; Interscience Publishers’: New York, NY, USA, 1967; Volume 150. [Google Scholar]
- Myers, D. Surfaces, Interfaces, and Colloids: Principles and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Liu, H. Science and Engineering of Droplets: Fundamentals and Applications; Noyes Publications: Norwich, NY, USA, 2000. [Google Scholar]
- Hartland, S. Surface and Interfacial Tension: Measurement, Theory and Applications; Marcel Dekker: New City, NY, USA, 2004. [Google Scholar]
- Schramm, L.L. Emulsions, Foams, and Suspensions: Fundamentals and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Neumann, A.W.; David, R.; Zuo, Y. Applied Surface Thermodynamics; CRC Press: Boca Raton, FL, USA, 2010; Volume 151. [Google Scholar]
- Ashgrid, N. Handbook of Atomization and Sprays. Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Aleiferis, P.G.; van Romunde, Z. An analysis of spray development with iso-octane, n-pentane, gasoline, ethanol and n-butanol from a multi-hole injector under hot fuel conditions. Fuel 2013, 105, 143–168. [Google Scholar] [CrossRef]
- Ejim, C.; Fleck, B.; Amirfazli, A. Analytical study for atomization of biodiesels and their blends in a typical injector: Surface tension and viscosity effects. Fuel 2007, 86, 1534–1544. [Google Scholar] [CrossRef]
- Seneviratne, K.N.; Hughes, T.J.; Johns, M.L.; Marsh, K.N.; May, E.F. Surface tension and critical point measurements of methane+ propane mixtures. J. Chem. Thermodyn. 2017, 111, 173–184. [Google Scholar] [CrossRef]
- West, Z.J.; Yamada, T.; Bruening, C.R.; Cook, R.L.; Mueller, S.S.; Shafer, L.M.; DeWitt, M.J.; Zabarnick, S. Investigation of water interactions with petroleum-derived and synthetic aviation turbine fuels. Energy Fuels 2018, 32, 1166–1178. [Google Scholar] [CrossRef]
- Ameli, F.; Hemmati-Sarapardeh, A.; Schaffie, M.; Husein, M.M.; Shamshirband, S. Modeling interfacial tension in N2/n-alkane systems using corresponding state theory: Application to gas injection processes. Fuel 2018, 222, 779–791. [Google Scholar] [CrossRef]
- Ahmad, W.; Vakilinejad, A.; Aman, Z.M.; Vakili-Nezhaad, G.R. Thermophysical study of binary systems of tert-amyl methyl ether with n-hexane and m-xylene. J. Chem. Eng. Data 2019, 64, 459–470. [Google Scholar] [CrossRef]
- Chaparro, G.; Cartes, M.; Mejía, A. Vapor–liquid equilibrium at 94 kPa and surface tension at 298.15 K for hexane+ ethanol+ cyclopentyl methyl ether mixture. Fuel 2020, 279, 118415. [Google Scholar] [CrossRef]
- Luning Prak, D.J.; Cowart, J.S.; Trulove, P.C. Density, viscosity, speed of sound, bulk modulus, and surface tension of binary mixtures of n-heptane+ 2, 2, 4-trimethylpentane at (293.15 to 338.15) K and 0.1 MPa. J. Chem. Eng. Data 2014, 59, 3842–3851. [Google Scholar] [CrossRef]
- Luning Prak, D.J.; Luning Prak, P.J.; Cowart, J.S.; Trulove, P.C. Densities and viscosities at 293.15–373.15 K, speeds of sound and bulk moduli at 293.15–333.15 K, surface tensions, and flash points of binary mixtures of n-hexadecane and alkylbenzenes at 0.1 MPa. J. Chem. Eng. Data 2017, 62, 1673–1688. [Google Scholar] [CrossRef]
- Luning Prak, D.J.; Mungan, A.L.; Cowart, J.S.; Trulove, P.C. Densities, viscosities, speeds of sound, bulk moduli, surface tensions, and flash points of binary mixtures of ethylcyclohexane or methylcyclohexane with n-dodecane or n-hexadecane at 0.1 MPa. J. Chem. Eng. Data 2018, 63, 1642–1656. [Google Scholar] [CrossRef]
- Luning Prak, D.J.; Fries, J.M.; Gober, R.T.; Vozka, P.; Kilaz, G.; Johnson, T.R.; Graft, S.L.; Trulove, P.C.; Cowart, J.S. Densities, viscosities, speeds of sound, bulk moduli, surface tensions, and flash points of quaternary mixtures of n-dodecane (1), n-butylcyclohexane (2), n-butylbenzene (3), and 2, 2, 4, 4, 6, 8, 8-heptamethylnonane (4) at 0.1 MPa as potential surrogate mixtures for military jet fuel, JP-5. J. Chem. Eng. Data 2019, 64, 1725–1745. [Google Scholar]
- Luning Prak, D.J.; Cowart, J.S.; Simms, G.R. Physical Properties of Binary Mixtures of n-Dodecane and Various Ten-Carbon Aromatic Compounds (2-Methyl-1-phenylpropane, 2-Methyl-2-phenylpropane, 2-Phenylbutane, and 1, 3-Diethylbenzene): Densities, Viscosities, Speeds of Sound, Bulk Moduli, Surface Tensions, and Flash Points at T = (293.15–333.15) K and 0.1 MPa. J. Chem. Eng. Data 2020, 65, 3941–3954. [Google Scholar]
- Mejía, A.; Cartes, M.; Chaparro, G. Isobaric vapor–liquid equilibrium and isothermal surface tension for hexane+ cyclopentyl methyl ether binary mixture: Experimental determinations and theoretical predictions. Fluid Phase Equilibria 2020, 520, 112654. [Google Scholar] [CrossRef]
- Klein, T.; Lenahan, F.D.; Kerscher, M.; Rausch, M.H.; Economou, I.G.; Koller, T.M.; Fröba, A.P. Characterization of long linear and branched alkanes and alcohols for temperatures up to 573.15 K by surface light scattering and molecular Dynamics Simulations. J. Phys. Chem. B 2020, 124, 4146–4163. [Google Scholar] [CrossRef]
- Prak, D.J.L.; Trulove, P.C.; Cowart, J.S. Density, viscosity, speed of sound, surface tension, and flash point of binary mixtures of n-hexadecane and 2, 2, 4, 4, 6, 8, 8-heptamethylnonane and of algal-based hydrotreated renewable diesel. J. Chem. Eng. Data 2013, 58, 920–926. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhao, G.; Zhang, X.; Yin, J.; Ma, S. Experimental investigation and correlations of thermophysical properties for bio-aviation kerosene surrogate containing n-decane with ethyl decanoate and ethyl dodecanoate. J. Chem. Thermodyn. 2020, 150, 106201. [Google Scholar] [CrossRef]
- Shardt, N.; Wang, Y.; Jin, Z.; Elliott, J. Surface tension as a function of temperature and composition for a broad range of mixtures. Chem. Eng. Sci. 2021, 230, 116095. [Google Scholar] [CrossRef]
- Massarweh, O.; Abushaikha, A.S. The use of surfactants in enhanced oil recovery: A review of recent advances. Energy Rep. 2020, 6, 3150–3178. [Google Scholar] [CrossRef]
- Mejía, A.; Segura, H.; Wisniak, J.; Polishuk, I. Association and molecular chain length effects on interfacial behavior. Phys. Chem. Liq. 2006, 44, 45–59. [Google Scholar] [CrossRef]
- Oliveira, M.; Marrucho, I.; Coutinho, J.; Queimada, A. Surface tension of chain molecules through a combination of the gradient theory with the CPA EoS. Fluid Phase Equilibria 2008, 267, 83–91. [Google Scholar] [CrossRef]
- Chalbaud, C.; Robin, M.; Lombard, J.; Martin, F.; Egermann, P.; Bertin, H. Interfacial tension measurements and wettability evaluation for geological CO2 storage. Adv. Water Resour. 2009, 32, 98–109. [Google Scholar] [CrossRef]
- Mejia, A.; Cartes, M.; Segura, H.; Müller, E. Use of equations of state and coarse grained simulations to complement experiments: Describing the interfacial properties of carbon dioxide+ decane and carbon dioxide+ eicosane mixtures. J. Chem. Eng. Data 2014, 59, 2928–2941. [Google Scholar] [CrossRef]
- Cui, J.; Bi, S.; Fröba, A.P.; Wu, J. Viscosity and interfacial tension of n-heptane with dissolved carbon dioxide by surface light scattering (SLS). J. Chem. Thermodyn. 2021, 152, 106266. [Google Scholar] [CrossRef]
- Vijande, J.; Pineiro, M.; García, J.; Valencia, J.; Legido, J. Density and surface tension variation with temperature for heptane+ 1-alkanol. J. Chem. Eng. Data 2006, 51, 1778–1782. [Google Scholar] [CrossRef]
- Estrada-Baltazar, A.; López-Lázaro, J.d.l.S.; Iglesias-Silva, G.; Barajas-Fernández, J. Density and surface tension of binary mixture of 1-nonanol+ n-octane,+ n-nonane, and+ n-decane from (293.15 to 323.15) K at P = 0.1 MPa. J. Chem. Thermodyn. 2020, 150, 106225. [Google Scholar] [CrossRef]
- Farzi, N.; Yazdanshenas, Z. Surface tension prediction of n-alkanes by a modified Peng-Robinson equation of state using the Density Functional Theory. Phys. Chem. Res. 2017, 5, 569–583. [Google Scholar]
- Sastri, S.; Rao, K. A simple method to predict surface tension of organic liquids. Chem. Eng. J. Biochem. Eng. J. 1995, 59, 181–186. [Google Scholar] [CrossRef]
- Zuo, Y.X.; Stenby, E. Corresponding-states and parachor models for the calculation of interfacial tensions. Can. J. Chem. Eng. 1997, 75, 1130–1137. [Google Scholar] [CrossRef]
- Romero-Martinez, A.; Trejo, A. Surface tension of pure hydrocarbons. Int. J. Thermophys. 1998, 19, 1605–1614. [Google Scholar] [CrossRef]
- Miqueu, C.; Broseta, D.; Satherley, J.; Mendiboure, B.; Lachaise, J.; Graciaa, A. An extended scaled equation for the temperature dependence of the surface tension of pure compounds inferred from an analysis of experimental data. Fluid Phase Equilibria 2000, 172, 169–182. [Google Scholar] [CrossRef]
- Knotts, T.; Wilding, W.; Oscarson, J.; Rowley, R. Use of the DIPPR database for development of QSPR correlations: Surface tension. J. Chem. Eng. Data 2001, 46, 1007–1012. [Google Scholar] [CrossRef]
- Queimada, A.; Marrucho, I.M.; Coutinho, J. Surface tension of pure heavy n-alkanes: A corresponding states approach. Fluid Phase Equilibria 2001, 183, 229–238. [Google Scholar] [CrossRef]
- Queimada, A.J.; Silva, F.A.; Caço, A.I.; Marrucho, I.M.; Coutinho, J.A. Measurement and modeling of surface tensions of asymmetric systems: Heptane, eicosane, docosane, tetracosane and their mixtures. Fluid Phase Equilibria 2003, 214, 211–221. [Google Scholar] [CrossRef]
- Queimada, A.J.; Marrucho, I.M.; Stenby, E.H.; Coutinho, J.A. Generalized relation between surface tension and viscosity: A study on pure and mixed n-alkanes. Fluid Phase Equilibria 2004, 222, 161–168. [Google Scholar] [CrossRef]
- Queimada, A.; Miqueu, C.; Marrucho, I.; Kontogeorgis, G.; Coutinho, J. Modeling vapor–liquid interfaces with the gradient theory in combination with the CPA equation of state. Fluid Phase Equilibria 2005, 228, 479–485. [Google Scholar] [CrossRef]
- Delgado, E.; Diaz, G. A molecular structure based model for predicting surface tension of organic compounds. SAR QSAR Environ. Res. 2006, 17, 483–496. [Google Scholar] [CrossRef]
- Pazuki, G.; Nikookar, M.; Sahranavard, L. Prediction of surface tension of pure hydrocarbons by an artificial neural network system. Pet. Sci. Technol. 2011, 29, 2384–2396. [Google Scholar] [CrossRef]
- Gharagheizi, F.; Eslamimanesh, A.; Mohammadi, A.H.; Richon, D. Use of artificial neural network-group contribution method to determine surface tension of pure compounds. J. Chem. Eng. Data 2011, 56, 2587–2601. [Google Scholar] [CrossRef]
- Gharagheizi, F.; Eslamimanesh, A.; Tirandazi, B.; Mohammadi, A.H.; Richon, D. Handling a very large data set for determination of surface tension of chemical compounds using quantitative structure–property relationship strategy. Chem. Eng. Sci. 2011, 66, 4991–5023. [Google Scholar] [CrossRef]
- Gharagheizi, F.; Eslamimanesh, A.; Sattari, M.; Mohammadi, A.; Richon, D. Development of corresponding states model for estimation of the surface tension of chemical compounds. AIChE J. 2013, 59, 613–621. [Google Scholar] [CrossRef]
- Roosta, A.; Setoodeh, P.; Jahanmiri, A. Artificial neural network modeling of surface tension for pure organic compounds. Ind. Eng. Chem. Res. 2012, 51, 561–566. [Google Scholar] [CrossRef]
- Mulero, A.; Parra, M.; Cachadiña, I. The Somayajulu correlation for the surface tension revisited. Fluid Phase Equilibria 2013, 339, 81–88. [Google Scholar] [CrossRef]
- Aleem, W.; Mellon, N.; Sufian, S.; Mutalib, M.; Subbarao, D. A model for the estimation of surface tension of pure hydrocarbon liquids. Pet. Sci. Technol. 2015, 33, 1908–1915. [Google Scholar] [CrossRef]
- Randová, A.; Bartovská, L. Group contribution method: Surface tension of linear and branched alkanes. Fluid Phase Equilibria 2016, 429, 166–176. [Google Scholar] [CrossRef]
- Zhang, C.; Yi, H.; Tian, J. Lielmezs–Herrick correlation for the temperature-dependent surface tension of hydrocarbons. Int. J. Mod. Phys. B 2016, 30, 1650154. [Google Scholar] [CrossRef]
- Farzi, R.; Esmaeilzadeh, F. Prediction of surface tension of pure hydrocarbons using Esmaeilzadeh-Roshanfekr equation of state and group contribution method. Fluid Phase Equilibria 2016, 427, 353–361. [Google Scholar] [CrossRef]
- Aleem, W.; Mellon, N. New relation between viscosity and surface tension for pure hydrocarbon liquids. Pet. Sci. Technol. 2017, 35, 338–344. [Google Scholar] [CrossRef]
- Lashkarbolooki, M.; Bayat, M. Prediction of surface tension of liquid normal alkanes, 1-alkenes and cycloalkane using neural network. Chem. Eng. Res. Des. 2018, 137, 154–163. [Google Scholar] [CrossRef]
- Yaws, C.L.; Gabbula, C. Yaws’ Handbook of Thermodynamic and Physical Properties of Chemical Compounds; Knovel: New York, NY, USA, 2003. [Google Scholar]
- Singh, J.; Errington, J. Calculation of phase coexistence properties and surface tensions of n-alkanes with grand-canonical transition-matrix Monte Carlo simulation and finite-size scaling. J. Phys. Chem. B 2006, 110, 1369–1376. [Google Scholar] [CrossRef]
- Müller, E.A.; Mejia, A. Comparison of united-atom potentials for the simulation of vapor–liquid equilibria and interfacial properties of long-chain n-alkanes up to n-C100. J. Phys. Chem. B 2011, 115, 12822–12834. [Google Scholar] [CrossRef]
- Mejía, A.; Herdes, C.; Müller, E. Force fields for coarse-grained molecular simulations from a corresponding states correlation. Ind. Eng. Chem. Res. 2014, 53, 4131–4141. [Google Scholar] [CrossRef]
- Garrido, J.M.; Cartes, M.; Mejía, A. Coarse-grained theoretical modeling and molecular simulations of nitrogen+ n-alkanes:(n-pentane, n-hexane, n-heptane, n-octane). J. Supercrit. Fluids 2017, 129, 83–90. [Google Scholar] [CrossRef]
- Mulero, A.; Cachadiña, I.; Bautista, D. Recommended correlations for the surface tension of n-alkanes. J. Phys. Chem. Ref. Data 2021, 50, 023104. [Google Scholar] [CrossRef]
- Breure, B.; Peters, C. Modeling of the surface tension of pure components and mixtures using the density gradient theory combined with a theoretically derived influence parameter correlation. Fluid Phase Equilibria 2012, 334, 189–196. [Google Scholar] [CrossRef]
- Chaparro, G.; Mejía, A. Phasepy: A Python based framework for fluid phase equilibria and interfacial properties computation. J. Comput. Chem. 2020, 41, 2504–2526. [Google Scholar] [CrossRef]
- Fu, D.; Li, X.S.; Yan, S.; Liao, T. Investigation of critical properties and surface tensions for n-alkanes by perturbed-chain statistical associating fluid theory combined with density-gradient theory and renormalization-group theory. Ind. Eng. Chem. Res. 2006, 45, 8199–8206. [Google Scholar] [CrossRef]
- Garrido, J.; Mejía, A.; Piñeiro, M.; Blas, F.; Müller, E. Interfacial tensions of industrial fluids from a molecular-based square gradient theory. AIChE J. 2016, 62, 1781–1794. [Google Scholar] [CrossRef]
- Maghari, A.; Najafi, M. On the calculation of surface tensions of n-alkanes using the modified SAFT-BACK-DFT approach. J. Solut. Chem. 2010, 39, 31–41. [Google Scholar] [CrossRef]
- Mohsen-Nia, M.; Rasa, H.; Naghibi, S. Experimental and theoretical study of surface tension of n-pentane, n-heptane, and some of their mixtures at different temperatures. J. Chem. Thermodyn. 2010, 42, 110–113. [Google Scholar] [CrossRef]
- Mohsen-Nia, M. Measurement and modelling of surface tensions of systems containing n-hexadecane, n-heptane and n-pentane. Phys. Chem. Liq. 2011, 49, 608–614. [Google Scholar] [CrossRef]
- Müller, E.; Mejía, A. Interfacial properties of selected binary mixtures containing n-alkanes. Fluid Phase Equilibria 2009, 282, 68–81. [Google Scholar] [CrossRef]
- Zuo, Y.X.; Stenby, E. Calculation of interfacial tensions with gradient theory. Fluid Phase Equilibria 1997, 132, 139–158. [Google Scholar] [CrossRef]
- Miqueu, C.; Mendiboure, B.; Graciaa, A.; Lachaise, J. Modelling of the surface tension of pure components with the gradient theory of fluid interfaces: A simple and accurate expression for the influence parameters. Fluid Phase Equilibria 2003, 207, 225–246. [Google Scholar] [CrossRef]
- Cachadiña, I.; Hernández, A.; Mulero, Á. Surface tension of esters. Temperature dependence of the influence parameter in density gradient theory with Peng-Robinson equation of state. Case Stud. Therm. Eng. 2022, 36, 102193. [Google Scholar] [CrossRef]
- Sengers, J.; Sengers, J. Thermodynamic behavior of fluids near the critical point. Annu. Rev. Phys. Chem. 1986, 37, 189–222. [Google Scholar] [CrossRef]
- Brovchenko, I.; Oleinikova, A. Interfacial and Confined Water; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Peng, D.Y.; Robinson, D. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Robinson, D.; Peng, D. The characterization of the heptanes and heavier fractions. In Gas Processors Association Report; Research Report RR-28; Gas Processors Association: Edmonton, AB, Canada, 1978; pp. 1–36. [Google Scholar]
- Cahn, J.; Hilliard, J. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Carey, B.; Scriven, L.; Davis, H. Semiempirical theory of surface tensions of pure normal alkanes and alcohols. AIChE J. 1978, 24, 1076–1080. [Google Scholar] [CrossRef]
- Oliveira, M.; Coutinho, J.; Queimada, A. Surface tensions of esters from a combination of the gradient theory with the CPA EoS. Fluid Phase Equilibria 2011, 303, 56–61. [Google Scholar] [CrossRef]
- Hernández, A. Interfacial behavior prediction of alcohol+ glycerol mixtures using gradient theory. Chem. Phys. 2020, 534, 110747. [Google Scholar] [CrossRef]
- Hernández, A.; Khosharay, S. Investigation on the Surface Tension and Viscosity of (dimethylsulfoxide+alcohol) Mixtures by Using Gradient Theory and Eyring’s Rate Theory. Int. J. Thermophys. 2020, 41, 1–22. [Google Scholar] [CrossRef]
- Hernández, A.; Zabala, D. Modeling of the Interfacial Behavior of Carbon Dioxide+ Methyl Myristate, Carbon Dioxide+ Palmitate, and Carbon Dioxide+ Methyl Myristate+ Methyl Palmitate Mixtures Using CPA-EOS and Gradient Theory. Int. J. Thermophys. 2021, 42, 1–21. [Google Scholar] [CrossRef]
- Biglar, F.; Hernández, A.; Khosharay, S. Modeling of the Interfacial Behavior of CO2 + H2O and H2S + H2O with CPA EOS and Gradient Theory. Int. J. Thermophys. 2021, 42, 1–19. [Google Scholar] [CrossRef]
- Yang, A.; Fleming III, P.; Gibbs, J. Molecular theory of surface tension. J. Chem. Phys. 1976, 64, 3732–3747. [Google Scholar] [CrossRef]
- Liang, X.; Michelsen, M.; Kontogeorgis, G. A density gradient theory based method for surface tension calculations. Fluid Phase Equilibria 2016, 428, 153–163. [Google Scholar] [CrossRef]
- Garrido, J.; Polishuk, I. Toward development of a universal CP-PC-SAFT-based modeling framework for predicting thermophysical properties at reservoir conditions: Inclusion of surface tensions. Ind. Eng. Chem. Res. 2018, 57, 8819–8831. [Google Scholar] [CrossRef]
- Chow, Y.; Eriksen, D.; Galindo, A.; Haslam, A.; Jackson, G.; Maitland, G.; Trusler, J. Interfacial tensions of systems comprising water, carbon dioxide and diluent gases at high pressures: Experimental measurements and modelling with SAFT-VR Mie and square-gradient theory. Fluid Phase Equilibria 2016, 407, 159–176. [Google Scholar] [CrossRef]
- Cornelisse, P.; Peters, C.; de Swaan Arons, J. Application of the Peng-Robinson equation of state to calculate interfacial tensions and profiles at vapour-liquid interfaces. Fluid Phase Equilibria 1993, 82, 119–129. [Google Scholar] [CrossRef]
- Larsen, P.; Maribo-Mogensen, B.; Kontogeorgis, G. A collocation method for surface tension calculations with the density gradient theory. Fluid Phase Equilibria 2016, 408, 170–179. [Google Scholar] [CrossRef]
- Pérez-López, J.; González-Ortiz, L.; Leiva, M.; Puig, J. Estimation of surface tension of pure fluids using the gradient theory. AIChE J. 1992, 38, 753–760. [Google Scholar] [CrossRef]
- Zuo, Y.X.; Stenby, E. A linear gradient theory model for calculating interfacial tensions of mixtures. J. Colloid Interface Sci. 1996, 182, 126–132. [Google Scholar] [CrossRef]
- Mejía, A.; Segura, H.; Wisniak, J.; Polishuk, I. Correlation and prediction of interface tension for fluid mixtures: An approach based on cubic equations of state with the Wong-Sandler mixing rule. J. Phase Equilibria Diffus. 2005, 26, 215–224. [Google Scholar] [CrossRef]
- Mejía, A.; Segura, H.; Vega, L.; Wisniak, J. Simultaneous prediction of interfacial tension and phase equilibria in binary mixtures: An approach based on cubic equations of state with improved mixing rules. Fluid Phase Equilibria 2005, 227, 225–238. [Google Scholar] [CrossRef]
- Oliveira, M.; Freitas, S.; Llovell, F.; Vega, L.; Coutinho, J.A. Development of simple and transferable molecular models for biodiesel production with the soft-SAFT equation of state. Chem. Eng. Res. Des. 2014, 92, 2898–2911. [Google Scholar] [CrossRef]
- Haarmann, N.; Reinhardt, A.; Danzer, A.; Sadowski, G.; Enders, S. Modeling of Interfacial Tensions of Long-Chain Molecules and Related Mixtures Using Perturbed Chain-Statistical Associating Fluid Theory and the Density Gradient Theory. J. Chem. Eng. Data 2019, 65, 1005–1018. [Google Scholar] [CrossRef]
- Avaullee, L.; Trassy, L.; Neau, E.; Jaubert, J.N. Thermodynamic modeling for petroleum fluids I. Equation of state and group contribution for the estimation of thermodynamic parameters of heavy hydrocarbons. Fluid Phase Equilibria 1997, 139, 155–170. [Google Scholar] [CrossRef]
- Lopez-Echeverry, J.; Reif-Acherman, S.; Araujo-Lopez, E. Peng-Robinson equation of state: 40 years through cubics. Fluid Phase Equilibria 2017, 447, 39–71. [Google Scholar] [CrossRef]
- Jaubert, J.N.; Mutelet, F. VLE predictions with the Peng–Robinson equation of state and temperature dependent kij calculated through a group contribution method. Fluid Phase Equilibria 2004, 224, 285–304. [Google Scholar] [CrossRef]
- Mulero, A.; Cachadiña, I.; Parra, M. Recommended correlations for the surface tension of common fluids. J. Phys. Chem. Ref. Data 2012, 41, 043105. [Google Scholar] [CrossRef]
- Mulero, A.; Cachadiña, I. Recommended correlations for the surface tension of several fluids included in the REFPROP program. J. Phys. Chem. Ref. Data 2014, 43, 023104. [Google Scholar] [CrossRef]
- Mulero, A.; Cachadiña, I.; Sanjuán, E. Recommended correlations for the surface tension of aliphatic, carboxylic, and polyfunctional organic acids. J. Phys. Chem. Ref. Data 2016, 45, 033105. [Google Scholar] [CrossRef]
- Mulero, A.; Cachadiña, I.; Vegas, A. Recommended correlations for the surface tension of 80 esters. J. Phys. Chem. Ref. Data 2021, 50, 033106. [Google Scholar] [CrossRef]
- Mulero, A.; Cachadiña, I.; Vegas, A. Recommended correlations for the surface tension of aromatic, polyfunctional and glyceride esters. J. Phys. Chem. Ref. Data 2022, 51, 023102. [Google Scholar] [CrossRef]
- Rowley, R.; Wilding, W.; Oscarson, J.; Knotts, T.; Giles, N. DIPPR®Data Compilation of Pure Chemical Properties; AIChE: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- DETHERM, Thermophysical Properties of Pure Substances & Mixtures. DECHEMA, Gesellschaft für Chemische Techink und Biotechnologie e.V. 2018. Available online: https://dechema.de/en/detherm.html (accessed on 24 October 2024).
- Wohlfarth, C.; Wohlfarth, B. Surface Tension of Pure Liquids and Binary Liquid Mixtures; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Wohlfarth, C. Surface Tension of Pure Liquids and Binary Liquid Mixtures, Supplement to IV/16; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Wohlfarth, C.; Lechner, M. Surface Tension of Pure Liquids and Binary Liquid Mixtures: Supplement to Volume IV/24; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Sugden, S., VI. The variation of surface tension with temperature and some related functions. J. Chem. Soc. Trans. 1924, 125, 32–41. [Google Scholar] [CrossRef]
- Cornelisse, P. The Gradient Theory Applied, Simultaneous Modelling of Interfacial Tension and Phase Behaviour. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 1997. [Google Scholar]
- Soreide, I. Improved Phase Behavior Predictions of Petroleum Reservoir Fluids from a Cubic Equation of State. Ph.D. Thesis, Sharif University of Technology, Tehran, Iran, 1989. [Google Scholar]
- Press, W.; Teukolsky, S.; Vetterling, W.; Flannery, B. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Poling, B.; Prausnitz, J.; O’Connell, J. The Properties of Gases and Liquids; McGraw-Hill: New York, NY, USA, 2001; Volume 5. [Google Scholar]
- Di Nicola, G.; Pierantozzi, M. A new scaled equation to calculate the surface tension of ketones. J. Therm. Anal. Calorim. 2014, 116, 129–134. [Google Scholar] [CrossRef]
- Di Nicola, G.; Coccia, G.; Pierantozzi, M. Surface tension of silanes: A new equation. Fluid Phase Equilibria 2016, 418, 88–93. [Google Scholar] [CrossRef]
- Di Nicola, G.; Coccia, G.; Pierantozzi, M. A new equation for the surface tension of carboxylic acids. Fluid Phase Equilibria 2016, 417, 229–236. [Google Scholar] [CrossRef]
- Di Nicola, G.; Coccia, G.; Malvagi, L.; Pierantozzi, M. New equation for the liquid viscosity of silanes. J. Thermophys. Heat Transf. 2017, 31, 832–840. [Google Scholar] [CrossRef]


| CN | Fluid | MAPD | MD | PDm | |||||
|---|---|---|---|---|---|---|---|---|---|
| mol2/3) | mol2/3) | mol2/3) | (%) | (%) | (%) | ||||
| 1 | methane | 7.5(12+) | 5.086(88+) | −3.35(34+) | 127/126 | 0.97 | −0.28 | 8.5 | 0.11 |
| 2 | ethane | 5.1(10+) | 3.68(13+) | −3.63(31+) | 163/160 | 2.06 | −0.77 | 19.2 | 0.01 |
| 3 | propane | 4.92(48−) | 3.63(16−) | −3.08(24−) | 193/191 | 1.80 | 0.04 | 27.2 | 0.01 |
| 4 | n-butane | 3.70(51+) | 3.44(12+) | −3.75(23−) | 126/118 | 3.14 | 1.17 | 48.9 | 0.01 |
| 5 | n-pentane | 3.84(76−) | 3.488(80−) | −3.25(21−) | 149/143 | 1.72 | 1.03 | 36.5 | 0.01 |
| 6 | n-hexane | 3.8(14−) | 3.574(64+) | −3.18(17+) | 270/269 | 0.97 | 0.18 | 12.8 | 0.07 |
| 7 | n-heptane | 4.32(74+) | 3.560(68+) | −2.78(20+) | 363/357 | 0.89 | 0.09 | 9.7 | 0.22 |
| 8 | n-octane | 5.5(20−) | 3.702(65+) | −2.55(23+) | 196/194 | 1.04 | 0.43 | 41.1 | 0.01 |
| 9 | n-nonane | 0.0(81+) | 3.573(44+) | −2.86(21+) | 78 | 0.41 | 0.07 | 3.0 | 0.80 |
| 10 | n-decane | 3.8(26−) | 3.686(62−) | −2.16(27+) | 149 | 0.95 | −0.08 | 5.8 | 0.68 |
| 11 | n-undecane | 0.0(34+) | 3.663(53+) | −2.25(27+) | 60 | 0.55 | 0.05 | 2.6 | 0.49 |
| 12 | n-dodecane | 5.2(38+) | 3.633(65−) | −2.09(33−) | 100 | 0.91 | 0.30 | 6.7 | 0.91 |
| 13 | n-tridecane | 4(12+) | 3.655(45+) | −2.22(28+) | 48 | 0.33 | −0.02 | 1.3 | 0.69 |
| 14 | n-tetradecane | 15(14−) | 3.767(53−) | −1.85(44+) | 49 | 0.49 | 0.07 | 1.9 | 0.97 |
| 15 | n-pentadecane | 12(44+) | 3.705(44+) | −1.97(47+) | 40 | 0.40 | −0.01 | 2.0 | 0.67 |
| 16 | n-hexadecane | 7.7(37−) | 3.876(64+) | −2.19(67−) | 127 | 1.33 | 0.12 | 6.8 | 0.40 |
| 17 | n-heptadecane | 7.3(11−) | 3.914(54+) | −2.46(27−) | 44 | 0.44 | 0.08 | 2.1 | 0.78 |
| 18 | n-octadecane | 8.0(13+) | 3.990(59−) | −2.36(30−) | 39 | 0.48 | 0.05 | 1.9 | 0.79 |
| 19 | n-nonadecane | 8.13(79−) | 3.981(67−) | −2.48(24−) | 23 | 0.70 | 0.02 | 5.4 | 0.34 |
| 20 | n-eicosane | 7.7(11+) | 4.079(75−) | −2.78(26−) | 38 | 1.04 | −0.10 | 11.7 | 0.33 |
| 21 | n-heneicosane | 8.0(10+) | 4.225(76+) | −2.83(22+) | 28 | 0.47 | −0.18 | 2.8 | 0.07 |
| 22 | n-docosane | 7.8(12+) | 4.223(78+) | −2.75(31+) | 32 | 0.58 | −0.28 | 2.9 | 0.07 |
| 23 | n-tricosane | 7.8(12+) | 4.219(84−) | −2.84(27+) | 36 | 0.98 | 0.12 | 3.4 | 0.06 |
| 24 | n-tetracosane | 7.9(13+) | 4.286(96+) | −2.79(31+) | 36 | 0.93 | −0.11 | 3.8 | 0.98 |
| 25 | n-pentacosane | 8.17(67+) | 4.330(40−) | −2.54(10−) | 15 | 0.29 | −0.21 | 3.4 | 0.06 |
| 26 | n-hexacosane | 8.2(11+) | 4.352(49−) | −2.43(19−) | 31 | 0.30 | −0.04 | 3.7 | 0.06 |
| 27 | n-heptacosane | 8.07(60+) | 4.331(41−) | −2.42(12−) | 16 | 0.31 | −0.19 | 3.8 | 0.06 |
| 28 | n-octacosane | 7.80(97+) | 4.24(15−) | −2.35(25−) | 24 | 1.67 | 1.26 | 7.7 | 0.78 |
| 29 | n-nonacosane | 7.70(58+) | 4.278(42−) | −2.33(12−) | 16 | 0.31 | −0.18 | 3.9 | 0.06 |
| 30 | n-triacontane | 7.72(83+) | 4.276(95−) | −2.32(19−) | 22 | 1.29 | 0.86 | 6.0 | 0.84 |
| 32 | n-dotriacontane | 7.58(90+) | 4.356(45−) | −2.24(17−) | 25 | 0.32 | −0.09 | 4.0 | 0.06 |
| 36 | n-hexatriacontane | 7.65(58+) | 4.399(58−) | −2.15(15−) | 18 | 0.43 | −0.13 | 4.6 | 0.06 |
| Overall mean absolute percentage deviation (defined in Equation (30)) | 0.79 | ||||||||
| CN | MAPD/MAPDfit | MD/MDfit | PDm/PDmfit | ||
|---|---|---|---|---|---|
| (%) | (%) | (%) | |||
| 1 | 127/126 | 12.99/13.05 | −12.99/−13.05 | 20.95/20.95 | 0.11/0.11 |
| 2 | 163/160 | 3.48/3.28 | −2.33/−2.29 | 15.80/14.41 | 0.01/0.02 |
| 3 | 193/191 | 2.14/2.00 | −0.49/−0.34 | 22.59/22.10 | 0.01/0.06 |
| 4 | 126/118 | 5.42/2.59 | 2.35/−0.70 | 75.48/15.04 | 0.01/0.03 |
| 5 | 149/143 | 3.53/2.06 | 3.00/1.51 | 62.01/17.12 | 0.01/0.02 |
| 6 | 270/269 | 1.82/1.76 | 1.20/1.14 | 17.35/16.20 | 0.01/0.04 |
| 7 | 363/357 | 2.94/2.71 | 2.90/2.68 | 20.39/17.97 | 0.01/0.05 |
| 8 | 196/194 | 2.41/2.00 | 2.17/1.76 | 45.07/5.72 | 0.01/1.00 |
| 9 | 78 | 3.52 | 3.52 | 6.93 | 0.99 |
| 10 | 149 | 3.80 | 3.74 | 9.71 | 0.12 |
| 11 | 60 | 4.36 | 4.36 | 10.43 | 0.30 |
| 12 | 100 | 4.98 | 4.98 | 12.18 | 0.91 |
| 13 | 48 | 4.30 | 4.30 | 5.86 | 0.99 |
| 14 | 49 | 3.60 | 3.39 | 5.72 | 0.97 |
| 15 | 40 | 4.19 | 4.19 | 5.37 | 0.95 |
| 16 | 127/117 | 2.40/2.31 | 1.52/1.90 | 7.31/7.17 | 0.08/1.00 |
| 17 | 44/34 | 1.56/1.06 | −0.13/0.80 | 7.16/2.15 | 0.07/0.78 |
| 18 | 39/29 | 1.57/0.55 | −0.92/0.34 | 9.37/1.40 | 0.07/1.00 |
| 19 | 23/12 | 2.85/1.20 | −2.49/−0.51 | 10.41/10.20 | 0.07/0.34 |
| 20 | 38/25 | 2.89/1.43 | −2.78/−1.26 | 17.69/17.69 | 0.33/0.33 |
| 21 | 28/14 | 5.86/4.78 | −5.86/−4.78 | 14.00/7.35 | 0.07/0.49 |
| 22 | 32/19 | 5.16/4.05 | −5.16/−4.05 | 13.18/6.99 | 0.07/0.54 |
| 23 | 36/22 | 5.05/3.74 | −5.05/−3.74 | 13.93/6.97 | 0.06/0.52 |
| 24 | 36/22 | 5.60/4.43 | −5.56/−4.36 | 14.37/7.22 | 0.06/0.61 |
| 25 | 15/ 1 | 6.92/3.48 | −6.92/−3.48 | 14.70/3.48 | 0.06/0.95 |
| 26 | 31/19 | 5.40/3.96 | −5.40/−3.96 | 14.97/4.45 | 0.06/0.81 |
| 27 | 16/ 1 | 6.45/3.32 | −6.45/−3.32 | 14.52/3.32 | 0.06/0.96 |
| 28 | 24/ 9 | 4.42/2.57 | −3.35/0.29 | 13.13/4.23 | 0.06/0.78 |
| 29 | 16/ 1 | 5.41/2.60 | −5.41/−2.60 | 12.95/2.60 | 0.06/0.97 |
| 30 | 22/ 7 | 4.64/2.57 | −3.91/−0.30 | 13.07/4.01 | 0.06/0.55 |
| 32 | 25/12 | 4.92/3.64 | −4.92/−3.64 | 12.61/4.23 | 0.06/0.85 |
| 36 | 18/ 1 | 5.67/3.48 | −5.67/−3.48 | 13.36/3.48 | 0.06/1.00 |
| - | 2681/2427 | 75.48/22.10 | |||
| OMAPD/ | OMD/ | ||||
| OMAPDfit | OMDfit | ||||
| 32 | 4.38/3.35 | −1.38/−0.53 |
| Name | Symbol | Units | |
|---|---|---|---|
| 0 | No dependency (constant) | - | - |
| 1 | Critical pressure | Pa | |
| 2 | Critical temperature | K | |
| 3 | Acentric factor | - | |
| 4 | Critical compressibility factor | - | |
| 5 | Critical volume | L mol−1 | |
| 6 | Melting temperature | K | |
| 7 | Triple point temperature | K | |
| 8 | Normal boiling point temperature | K | |
| 9 | Logarithmic ratio between and | - | |
| 10 | Liquid molar volume at 298.15 K and 101,325 Pa | L mol−1 | |
| 11 | Radius of gyration | RG | m |
| 12 | Dipole moment | Cm | |
| 13 | Molar weight | kg kmol−1 | |
| 14 | Reduced triple point temperature | - | |
| 15 | Reduced normal boiling temperature | - | |
| 16 | Pseudo compressibility factor | ) | - |
| 17 | Reduced boiling temperature | - |
| Adjustable Coefficients | RG | |||||
|---|---|---|---|---|---|---|
| () | 5.01227 | 4.91156 | 5.37325 | 6.48294 | 4.99955 | |
| () | 4.40431 | 1.09159 | 0.662073 | 3.03929 | 0.625431 | |
| 0.885059 | 0.53364 | 0.595946 | 0.254804 | 0.452929 | ||
| () | 1.08825 | 2.68771 | 4.84453 | 5.0875 | 3.52179 | |
| 0.519495 | 0.401163 | 0.542305 | 4.98139 | 0.405698 | ||
| () | −2.92951 | −2.6442 | −2.05972 | −2.20715 | −3.45186 | |
| Statistical figures for the fitting set | ||||||
| OMAPDfit (%) | 1.78 | 1.94 | 1.99 | 2.16 | 2.18 | |
| MDfit (%) | 0.04 | −0.02 | −0.13 | 0.16 | 0.24 | |
| PDmfit (%) | 23.93 | 24.37 | 23.76 | 21.44 | 24.35 | |
| Statistical figures for the whole set | ||||||
| OMAPD (%) | 2.26 | 2.52 | 2.78 | 2.68 | 2.57 | |
| MD (%) | −0.45 | −0.79 | −1.20 | −0.37 | 0.11 | |
| PDm (%) | 65.02 | 63.50 | 68.36 | 81.76 | 64.95 | |
| CN | MAPD/MAPDfit | MD/MDfit | PDm/PDmfit | ||
|---|---|---|---|---|---|
| (%) | (%) | (%) | |||
| 1 | 127/126 | 2.49/2.45 | −2.20/−2.16 | 16.28/16.28 | 0.11/0.11 |
| 2 | 163/160 | 2.58/2.35 | 0.09/0.25 | 20.01/10.71 | 0.01/0.04 |
| 3 | 193/191 | 1.84/1.65 | 0.27/0.48 | 26.76/23.93 | 0.01/0.06 |
| 4 | 126/118 | 4.54/2.19 | 1.53/−1.02 | 65.02/10.03 | 0.01/0.03 |
| 5 | 149/143 | 2.42/1.25 | 1.75/0.54 | 51.44/11.26 | 0.01/0.02 |
| 6 | 270/269 | 1.72/1.69 | −0.37/−0.41 | 12.64/12.64 | 0.07/0.07 |
| 7 | 363/357 | 1.36/1.22 | 0.96/0.81 | 13.96/13.96 | 0.05/0.05 |
| 8 | 196/194 | 1.40/1.08 | −0.34/−0.68 | 35.68/4.47 | 0.01/0.19 |
| 9 | 78 | 0.54 | 0.38 | 3.76 | 0.54 |
| 10 | 149 | 1.55 | 0.97 | 8.52 | 0.12 |
| 11 | 60 | 1.77 | 1.77 | 11.63 | 0.30 |
| 12 | 100 | 2.37 | 2.34 | 7.96 | 0.91 |
| 13 | 48 | 1.66 | 1.66 | 4.26 | 0.69 |
| 14 | 49 | 0.96 | 0.61 | 3.76 | 0.72 |
| 15 | 40 | 1.67 | 1.67 | 4.58 | 0.74 |
| 16 | 127/117 | 1.77/1.73 | −0.24/−0.09 | 8.64/7.67 | 0.08/0.46 |
| 17 | 44/34 | 1.15/0.84 | −0.68/−0.39 | 8.56/2.20 | 0.07/0.78 |
| 18 | 39/29 | 1.50/1.08 | −1.24/−0.74 | 10.54/2.65 | 0.07/0.99 |
| 19 | 23/12 | 2.06/1.44 | −1.54/−0.64 | 11.62/7.08 | 0.07/0.34 |
| 20 | 38/25 | 2.48/1.97 | −2.18/−1.52 | 14.55/14.55 | 0.33/0.33 |
| 21 | 28/14 | 3.80/2.81 | −3.80/−2.81 | 14.97/3.63 | 0.07/0.49 |
| 22 | 32/19 | 3.15/2.48 | −3.15/−2.48 | 13.98/3.32 | 0.07/0.63 |
| 23 | 36/22 | 2.79/1.90 | −2.53/−1.47 | 14.82/3.23 | 0.06/0.64 |
| 24 | 36/22 | 3.02/2.20 | −2.92/−2.04 | 15.08/3.94 | 0.06/0.80 |
| 25 | 15/ 1 | 3.64/2.25 | −3.64/−2.25 | 15.32/2.25 | 0.06/0.95 |
| 26 | 31/19 | 2.32/1.39 | −2.31/−1.36 | 15.59/2.09 | 0.06/0.93 |
| 27 | 16/ 1 | 2.53/1.31 | −2.53/−1.31 | 15.04/1.31 | 0.06/0.96 |
| 28 | 24/ 9 | 3.33/4.91 | 1.05/4.91 | 13.58/8.81 | 0.06/0.78 |
| 29 | 16/ 1 | 2.22/0.07 | −0.92/0.07 | 13.24/0.07 | 0.06/0.97 |
| 30 | 22/ 7 | 3.07/4.39 | 0.83/4.39 | 13.29/7.22 | 0.06/0.84 |
| 32 | 25/12 | 1.64/0.55 | −0.11/0.55 | 12.66/0.97 | 0.06/0.87 |
| 36 | 18/ 1 | 2.88/1.30 | 0.45/1.30 | 13.31/1.30 | 0.06/1.00 |
| Overall | 2681/2427 | 65.02/23.93 | |||
| OMAPD/ | OMD/ | ||||
| OMAPDfit | OMDfit | ||||
| 32 | 2.26/1.78 | −0.45/0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cachadiña, I.; Hernández, A.; Mulero, Á. A New General Correlation for the Influence Parameter in Density Gradient Theory and Peng–Robinson Equation of State for n-Alkanes. Molecules 2024, 29, 5643. https://doi.org/10.3390/molecules29235643
Cachadiña I, Hernández A, Mulero Á. A New General Correlation for the Influence Parameter in Density Gradient Theory and Peng–Robinson Equation of State for n-Alkanes. Molecules. 2024; 29(23):5643. https://doi.org/10.3390/molecules29235643
Chicago/Turabian StyleCachadiña, Isidro, Ariel Hernández, and Ángel Mulero. 2024. "A New General Correlation for the Influence Parameter in Density Gradient Theory and Peng–Robinson Equation of State for n-Alkanes" Molecules 29, no. 23: 5643. https://doi.org/10.3390/molecules29235643
APA StyleCachadiña, I., Hernández, A., & Mulero, Á. (2024). A New General Correlation for the Influence Parameter in Density Gradient Theory and Peng–Robinson Equation of State for n-Alkanes. Molecules, 29(23), 5643. https://doi.org/10.3390/molecules29235643







