The Thermodynamic and Kinetic Properties of the dA-rU DNA-RNA Hybrid Base Pair Investigated via Molecular Dynamics Simulations
Abstract
1. Introduction
2. Results and Discussion
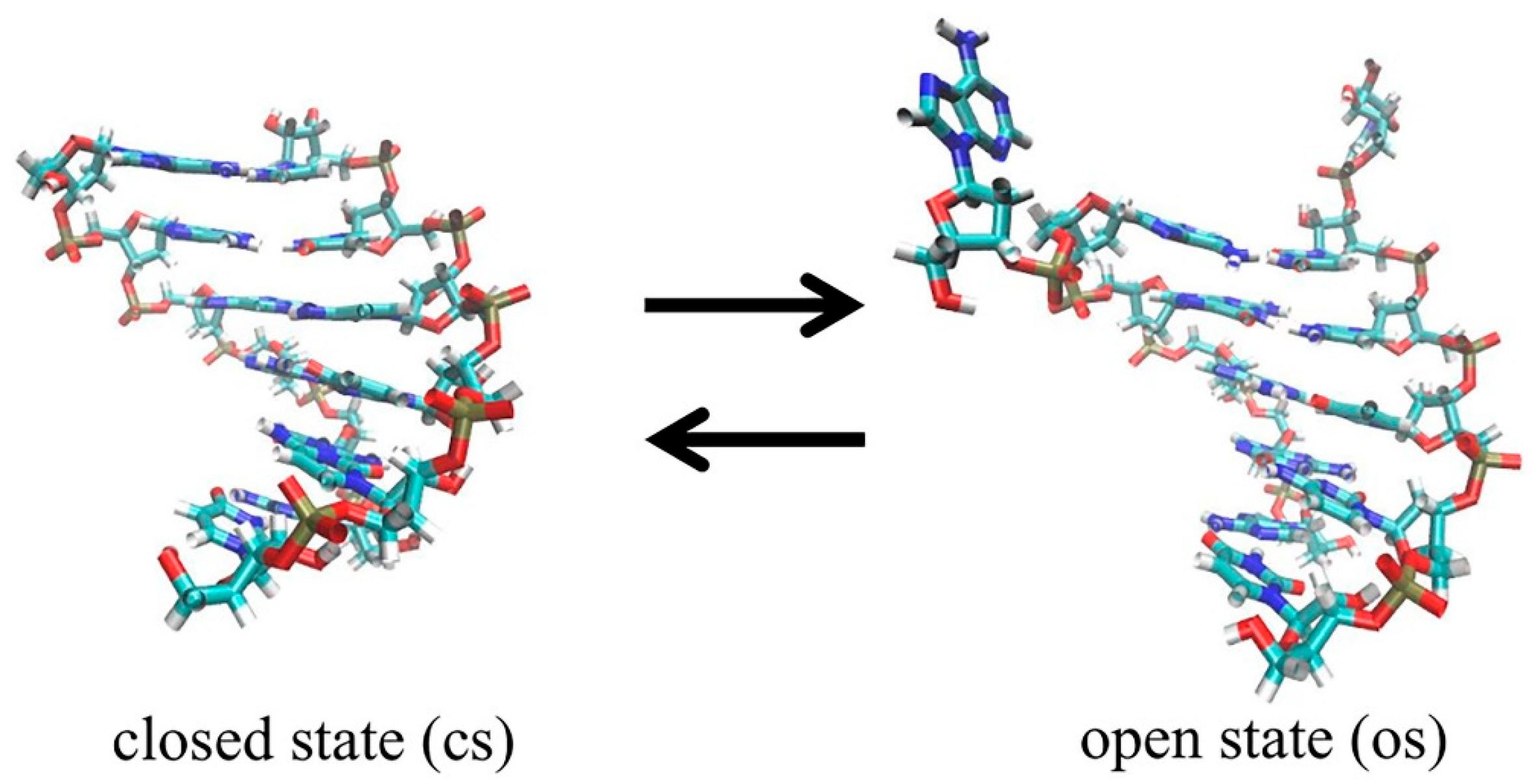
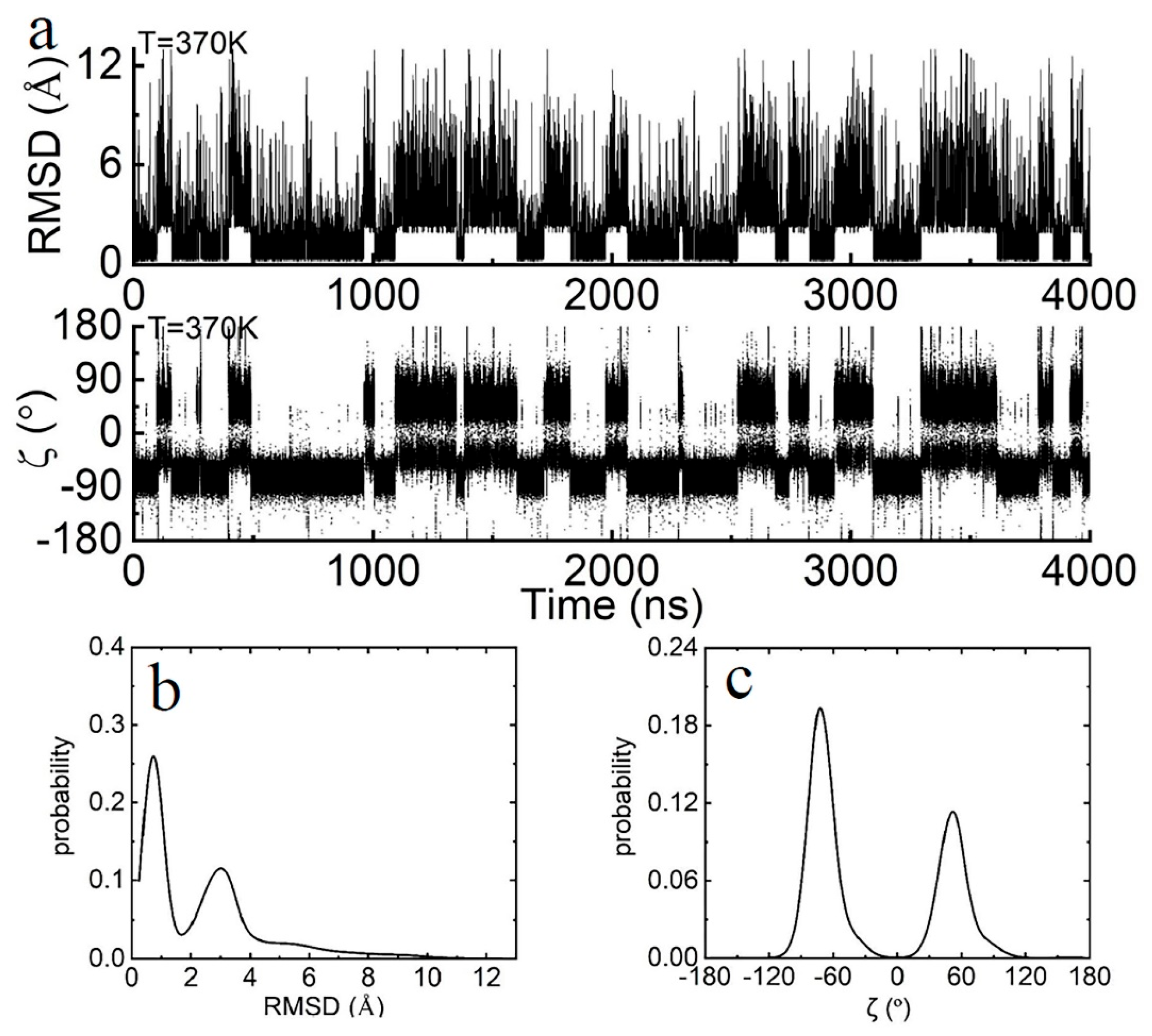
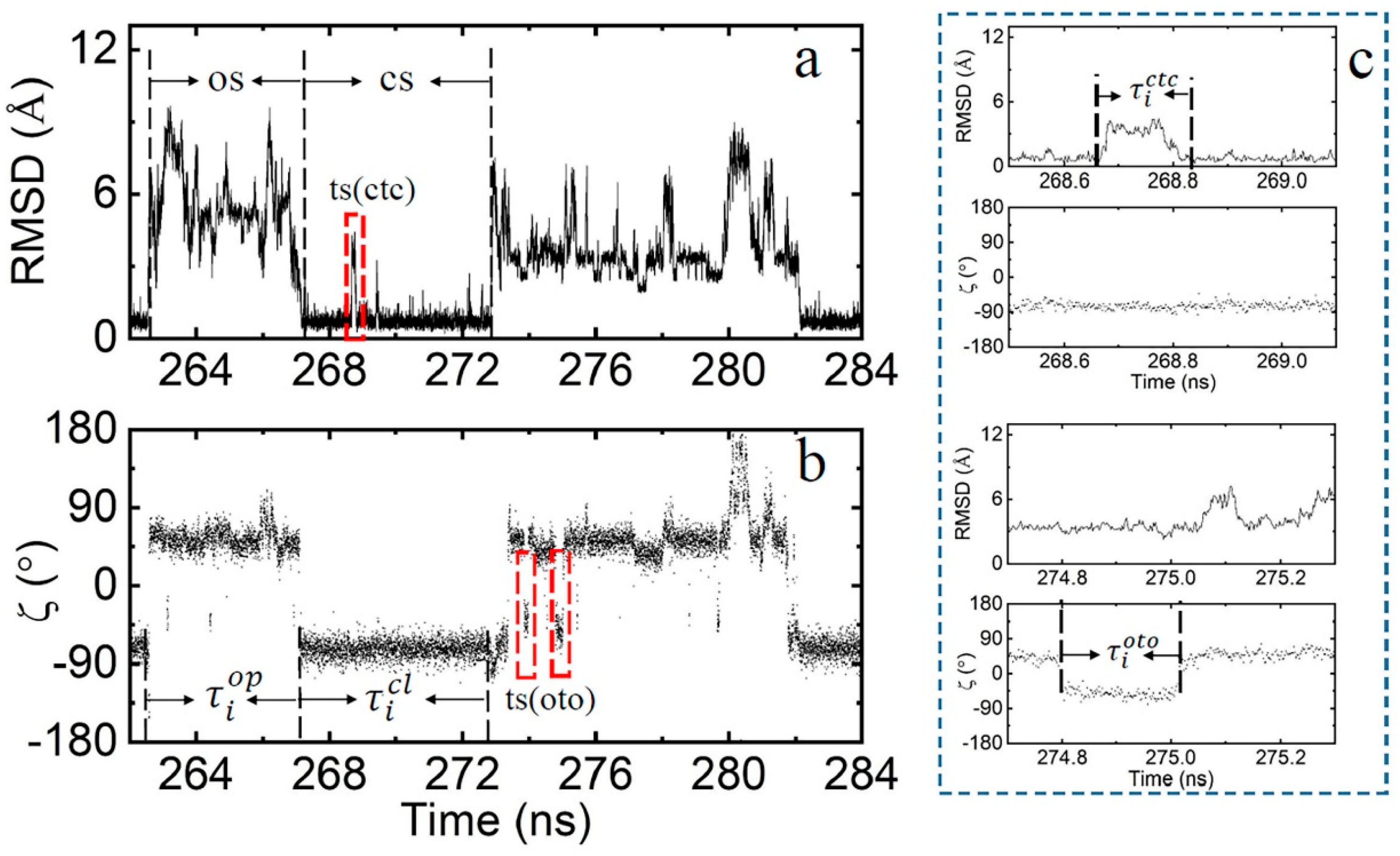
2.1. Definition of Closed State (cs), Open State (os), and Transition State (ts)
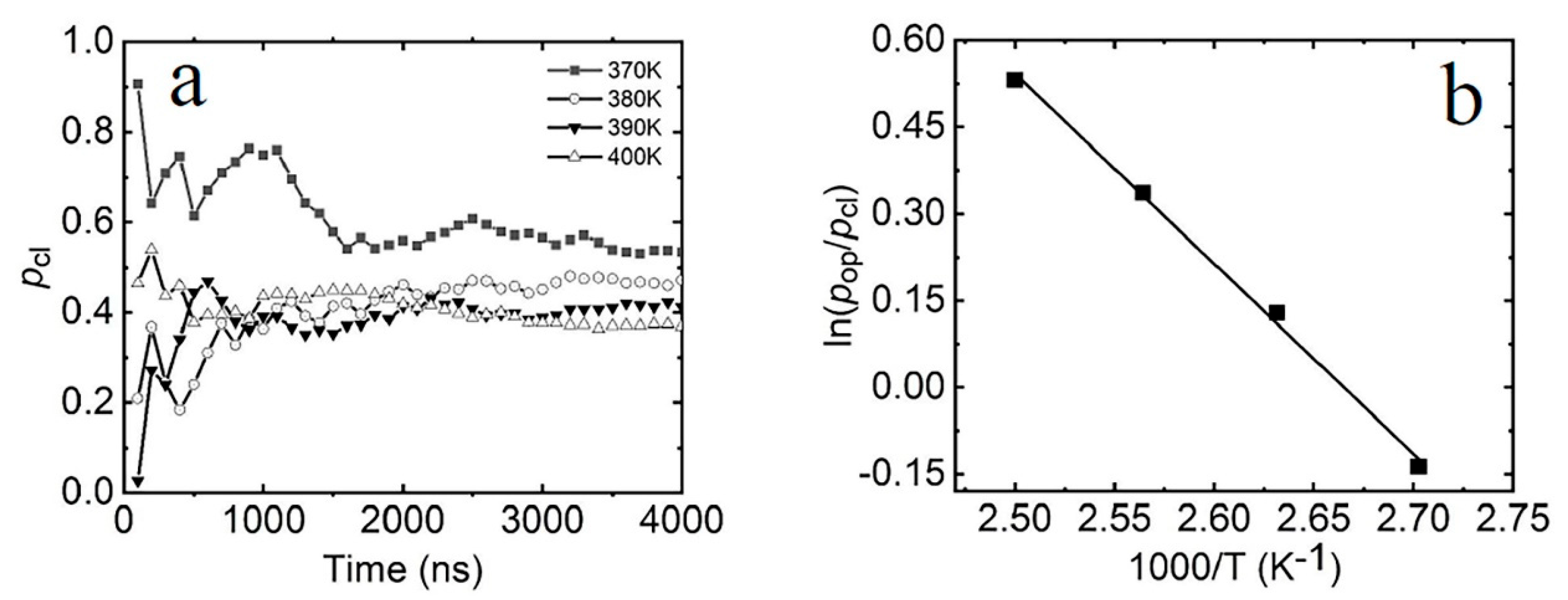
2.2. Thermodynamic Properties of the Terminal dA-rU Base Pair
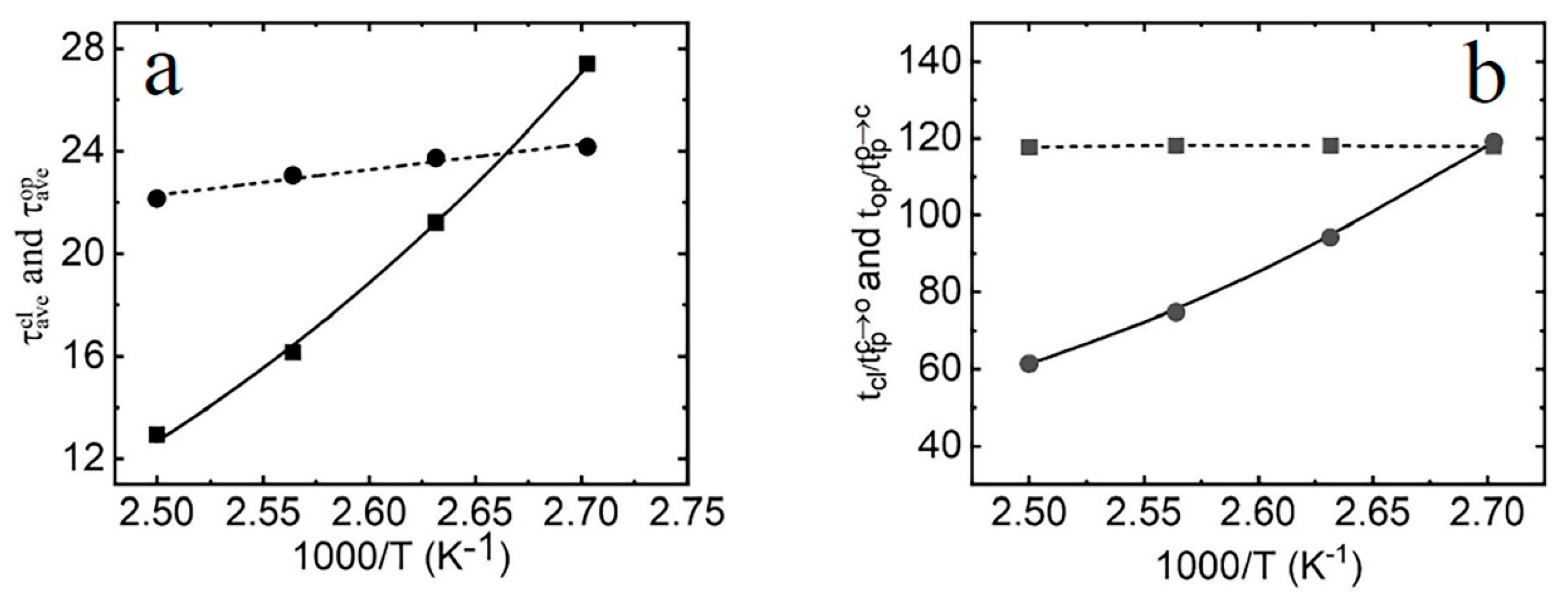
2.3. The Kinetic Mechanism of the Terminal dA-rU Base Pair
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ogawa, T.; Okazaki, T. Discontinuous DNA replication. Annu. Rev. Biochem. 1980, 49, 421. [Google Scholar]
- Temin, H. Reverse transcription in the eukaryotic genome: Retroviruses, pararetroviruses, retrotransposons, and retrotranscripts. Mol. Biol. Evol. 1985, 2, 455–468. [Google Scholar]
- Thidathip, W.; Piroon, J.; Keong, K.C.; Vladimir, K. Quantitative model of R-loop forming structures reveals a novel level of RNA-DNA interactome complexity. Nucleic Acids Res. 2012, 40, e16. [Google Scholar]
- Aguilera, A.; García-Muse, T. R loops: From transcription byproducts to threats to genome stability. Mol. Cell. 2012, 46, 115–124. [Google Scholar] [CrossRef]
- Grunseich, C.; Wang, I.X.; Watts, J.A.; Burdick, J.T.; Guber, R.D.; Zhu, Z.; Bruzel, A.; Lanman, T.; Chen, K.; Schindler, A.B. Senataxin mutation reveals how R-loops promote transcription by blocking DNA methylation at gene promoters. Mol. Cell. 2018, 69, 426–437. [Google Scholar]
- Lin, R.; Zhong, X.; Zhou, Y.; Geng, H.; Hu, Q.; Huang, Z.; Hu, J.; Fu, X.-D.; Chen, L.; Chen, J.-Y. R-loopBase: A knowledgebase for genome-wide R-loop formation and regulation. Nucleic Acids Res. 2022, 50, D303–D315. [Google Scholar] [CrossRef]
- Niehrs, C.; Luke, B. Regulatory R-loops as facilitators of gene expression and genome stability. Nat. Rev. Mol. Cell Biol. 2020, 21, 167–178. [Google Scholar]
- Plosky, B.S. The good and bad of RNA: DNA hybrids in double-strand break repair. Mol. Cell. 2016, 64, 643–644. [Google Scholar]
- Stoy, H.; Zwicky, K.; Kuster, D.; Lang, K.S.; Krietsch, J.; Crossley, M.P.; Schmid, J.A.; Cimprich, K.A.; Merrikh, H.; Lopes, M. Direct visualization of transcription-replication conflicts reveals post-replicative DNA: RNA hybrids. Nat. Struct. Mol. Biol. 2023, 30, 348–359. [Google Scholar] [CrossRef]
- Mojumdar, A.; Granger, C.; Cobb, J. Dna2 nuclease resolves RNA: DNA hybrids at double-strand breaks. bioRxiv 2024, 23, 609401. [Google Scholar]
- Nowotny, M.; Gaidamakov, S.A.; Crouch, R.J.; Yang, W. Crystal structures of RNase H bound to an RNA/DNA hybrid: Substrate specificity and metal-dependent catalysis. Cell 2005, 121, 1005–1016. [Google Scholar] [CrossRef]
- Wu, H.; Lima, W.F.; Zhang, H.; Fan, A.; Sun, H.; Crooke, S.T. Determination of the role of the human RNase H1 in the pharmacology of DNA-like antisense drugs. J. Biol. Chem. 2004, 279, 17181–17189. [Google Scholar]
- Groh, M.; Gromak, N. Out of balance: R-loops in human disease. PLoS Genet. 2014, 10, e1004630. [Google Scholar] [CrossRef]
- Haeusler, A.R.; Donnelly, C.J.; Rothstein, J.D. The expanding biology of the C9orf72 nucleotide repeat expansion in neurodegenerative disease. Nat. Rev. Neurosci. 2016, 17, 383–395. [Google Scholar] [CrossRef]
- Perego, M.G.; Taiana, M.; Bresolin, N.; Comi, G.P.; Corti, S. R-loops in motor neuron diseases. Mol. Neurobiol. 2019, 56, 2579–2589. [Google Scholar]
- Richard, P.; Manley, J.L. R loops and links to human disease. J. Mol. Biol. 2017, 429, 3168–3180. [Google Scholar]
- Schmidt, M.H.; Pearson, C.E. Disease-associated repeat instability and mismatch repair. DNA Repair. 2016, 38, 117–126. [Google Scholar] [CrossRef]
- Jinek, M.; Chylinski, K.; Fonfara, I.; Hauer, M.; Doudna, J.A.; Charpentier, E. A programmable dual-RNA–guided DNA endonuclease in adaptive bacterial immunity. Science 2012, 337, 816–821. [Google Scholar]
- Sander, J.D.; Joung, J.K. CRISPR-Cas systems for editing, regulating and targeting genomes. Nat. Biotechnol. 2014, 32, 347–355. [Google Scholar] [CrossRef]
- Wright, A.V.; Nuñez, J.K.; Doudna, J.A. Biology and applications of CRISPR systems: Harnessing nature’s toolbox for genome engineering. Cell 2016, 164, 29–44. [Google Scholar]
- Chen, C.; Russu, I.M. Sequence-dependence of the energetics of opening of at basepairs in DNA. Biophys. J. 2004, 87, 2545–2551. [Google Scholar] [CrossRef]
- Englander, S.W.; Kallenbach, N.R. Hydrogen exchange and structural dynamics of proteins and nucleic acids. Q. Rev. Biophys. 1983, 16, 521–655. [Google Scholar] [CrossRef]
- Folta-Stogniew, E.; Russu, I.M. Sequence dependence of base-pair opening in a DNA dodecamer containing the CACA/GTGT sequence motif. Biochem. 1994, 33, 11016–11024. [Google Scholar] [CrossRef]
- Guéron, M.; Leroy, J.-L. [16] Studies of base pair kinetics by NMR measurement of proton exchange. Method. Enzymol. 1995, 261, 383–413. [Google Scholar]
- Krueger, A.; Protozanova, E.; Frank-Kamenetskii, M.D. Sequence-dependent basepair opening in DNA double helix. Biophys. J. 2006, 90, 3091–3099. [Google Scholar] [CrossRef]
- Steinert, H.S.; Rinnenthal, J.; Schwalbe, H. Individual basepair stability of DNA and RNA studied by NMR-detected solvent exchange. Biophys. J. 2012, 102, 2564–2574. [Google Scholar] [CrossRef]
- Altan-Bonnet, G.; Libchaber, A.; Krichevsky, O. Bubble dynamics in double-stranded DNA. Phys. Rev. Lett. 2003, 90, 138101. [Google Scholar] [CrossRef]
- Yin, Y.; Yang, L.; Zheng, G.; Gu, C.; Yi, C.; He, C.; Gao, Y.Q.; Zhao, X.S. Dynamics of spontaneous flipping of a mismatched base in DNA duplex. Proc. Natl. Acad. Sci. USA 2014, 111, 8043–8048. [Google Scholar] [CrossRef]
- Kilchherr, F.; Wachauf, C.; Pelz, B.; Rief, M.; Zacharias, M.; Dietz, H. Single-molecule dissection of stacking forces in DNA. Science 2016, 353, aaf5508. [Google Scholar] [CrossRef]
- Banavali, N.K.; MacKerell, A.D., Jr. Free energy and structural pathways of base flipping in a DNA GCGC containing sequence. J. Mol. Biol. 2002, 319, 141–160. [Google Scholar] [CrossRef]
- Giudice, E.; Várnai, P.; Lavery, R. Base pair opening within B–DNA: Free energy pathways for GC and AT pairs from umbrella sampling simulations. Nucleic Acids Res. 2003, 31, 1434–1443. [Google Scholar] [CrossRef]
- Hagan, M.F.; Dinner, A.R.; Chandler, D.; Chakraborty, A.K. Atomistic understanding of kinetic pathways for single base-pair binding and unbinding in DNA. Proc. Natl. Acad. Sci. USA 2003, 100, 13922–13927. [Google Scholar] [CrossRef]
- Häse, F.; Zacharias, M. Free energy analysis and mechanism of base pair stacking in nicked DNA. Nucleic Acids Res. 2016, 44, 7100–7108. [Google Scholar] [CrossRef]
- Lindahl, V.; Villa, A.; Hess, B. Sequence dependency of canonical base pair opening in the DNA double helix. PloS Comput. Biol. 2017, 13, e1005463. [Google Scholar] [CrossRef]
- Liu, T.; Yu, T.; Zhang, S.; Wang, Y.; Zhang, W. Thermodynamic and kinetic properties of a single base pair in A-DNA and B-DNA. Phys. Rev. E. 2021, 103, 042409. [Google Scholar] [CrossRef]
- Pan, Y.; MacKerell, A.D., Jr. Altered structural fluctuations in duplex RNA versus DNA: A conformational switch involving base pair opening. Nucleic Acids Res. 2003, 31, 7131–7140. [Google Scholar] [CrossRef]
- Várnai, P.; Canalia, M.; Leroy, J.-L. Opening Mechanism of G·T/U Pairs in DNA and RNA Duplexes: A Combined Study of Imino Proton Exchange and Molecular Dynamics Simulation. J. Am. Chem. Soc. 2004, 126, 14659–14667. [Google Scholar] [CrossRef]
- Várnai, P.; Lavery, R. Base flipping in DNA: Pathways and energetics studied with molecular dynamic simulations. J. Am. Chem. Soc. 2002, 124, 7272–7273. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, Y. Types and concentrations of metal ions affect local structure and dynamics of RNA. Phys. Rev. E 2016, 94, 040401. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, S.; Wang, Z.; Zhang, W. The thermodynamics and kinetics of a nucleotide base pair. J. Chem. Phys. 2016, 144, 115101. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, T.; Yu, T.; Tan, Z.-J.; Zhang, W. Salt effect on thermodynamics and kinetics of a single RNA base pair. RNA 2020, 26, 470–480. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Wang, Y.; Liu, T.; Zhang, W. The nearest neighbor and next nearest neighbor effects on the thermodynamic and kinetic properties of RNA base pair. J. Chem. Phys. 2018, 148, 045101. [Google Scholar] [CrossRef]
- Zgarbová, M.; Otyepka, M.; Sponer, J.; Lankas, F.; Jurecka, P. Base pair fraying in molecular dynamics simulations of DNA and RNA. J. Chem. Theory Comput. 2014, 10, 3177–3189. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Wang, W. Atomistic analysis of pseudoknotted RNA unfolding. J. Am. Chem. Soc. 2011, 133, 6882–6885. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, C.; Russu, I.M. Dynamics and stability of individual base pairs in two homologous RNA–DNA hybrids. Biochemistry 2009, 48, 3988–3997. [Google Scholar] [CrossRef]
- Huang, Y.; Russu, I.M. Dynamic and energetic signatures of adenine tracts in a rA-dT RNA-DNA hybrid and in homologous RNA-DNA, RNA-RNA, and DNA-DNA double helices. Biochemistry 2017, 56, 2446–2454. [Google Scholar] [CrossRef]
- Huang, Y.; Weng, X.; Russu, I.M. Structural energetics of the adenine tract from an intrinsic transcription terminator. J. Mol. Biol. 2010, 397, 677–688. [Google Scholar] [CrossRef][Green Version]
- Sugimoto, N.; Nakano, S.-i.; Katoh, M.; Matsumura, A.; Nakamuta, H.; Ohmichi, T.; Yoneyama, M.; Sasaki, M. Thermodynamic parameters to predict stability of RNA/DNA hybrid duplexes. Biochemistry 1995, 34, 11211–11216. [Google Scholar] [CrossRef]
- Banerjee, D.; Tateishi-Karimata, H.; Ohyama, T.; Ghosh, S.; Endoh, T.; Takahashi, S.; Sugimoto, N. Improved nearest-neighbor parameters for the stability of RNA/DNA hybrids under a physiological condition. Nucleic Acids Res. 2020, 48, 12042–12054. [Google Scholar] [CrossRef]
- Craig, M.E.; Crothers, D.M.; Doty, P. Relaxation kinetics of dimer formation by self complementary oligonucleotides. J. Mol. Biol. 1971, 62, 383–401. [Google Scholar] [CrossRef]
- Berne, B.J.; Borkovec, M.; Straub, J.E. Classical and modern methods in reaction rate theory. J. Phys. Chem. 1988, 92, 3711–3725. [Google Scholar]
- Chung, H.S.; Eaton, W.A. Single-molecule fluorescence probes dynamics of barrier crossing. Nature 2013, 502, 685–688. [Google Scholar]
- Kramers, H.A. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 1940, 7, 284–304. [Google Scholar]
- Chung, H.S.; Louis, J.M.; Eaton, W.A. Experimental determination of upper bound for transition path times in protein folding from single-molecule photon-byphoton trajectories. Proc. Natl. Acad. Sci. USA 2009, 106, 11837–11844. [Google Scholar]
- Hummer, G. From transition paths to transition states and rate coefficients. J. Chem. Phys. 2004, 120, 516–523. [Google Scholar] [CrossRef]
- Neupane, K.; Ritchie, D.B.; Yu, H.; Foster, D.A.; Wang, F.; Woodside, M.T. Transition path times for nucleic acid folding determined from energy-landscape analysis of single-molecule trajectories. Phys. Rev. Lett. 2012, 109, 068102. [Google Scholar]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar]
- Mahoney, M.W.; Jorgensen, W.L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys. 2000, 112, 8910–8922. [Google Scholar]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar]
- Ivani, I.; Dans, P.D.; Noy, A.; Pérez, A.; Faustino, I.; Hospital, A.; Walther, J.; Andrio, P.; Goñi, R.; Balaceanu, A. Parmbsc1: A refined force field for DNA simulations. Nat. Methods. 2016, 13, 55–58. [Google Scholar]
- Zgarbová, M.; Otyepka, M.; Sponer, J.; Mládek, A.T.; Banáš, P.; Cheatham, T.E.; Jurečka, P. Refinement of the Cornell et al. Nucleic Acids Force Field Based on Reference Quantum Chemical Calculations of Glycosidic Torsion Profiles. J. Chem. Theory Comput. 2011, 7, 2886–2902. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar]
- Dzyaloshinskii, I.E.E.; Lifshitz, E.M.; Pitaevskii, L.P. The general theory of van der Waals forces. Adv. Phys. 1961, 10, 165–209. [Google Scholar]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar]
| Temperature | Closed State (cs) | Open State (os) | Transition State (ctc) | Transition State (oto) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T(K) | (ns) | Ncl | pcl | (ns) | Nop | Pop | (ns) | Nctc | Pctc | (ns) | Noto | Poto |
| 370 | 27.41 | 78 | 0.53 | 24.18 | 77 | 0.47 | 0.23 | 435 | 0.025 | 0.205 | 663 | 0.034 |
| 380 | 21.21 | 89 | 0.47 | 23.74 | 89 | 0.53 | 0.225 | 441 | 0.025 | 0.201 | 736 | 0.037 |
| 390 | 16.16 | 102 | 0.41 | 23.06 | 102 | 0.59 | 0.216 | 447 | 0.024 | 0.195 | 762 | 0.037 |
| 400 | 12.95 | 114 | 0.37 | 22.14 | 114 | 0.63 | 0.211 | 462 | 0.023 | 0.188 | 821 | 0.039 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Bao, L.; Wang, Y. The Thermodynamic and Kinetic Properties of the dA-rU DNA-RNA Hybrid Base Pair Investigated via Molecular Dynamics Simulations. Molecules 2024, 29, 4920. https://doi.org/10.3390/molecules29204920
Liu T, Bao L, Wang Y. The Thermodynamic and Kinetic Properties of the dA-rU DNA-RNA Hybrid Base Pair Investigated via Molecular Dynamics Simulations. Molecules. 2024; 29(20):4920. https://doi.org/10.3390/molecules29204920
Chicago/Turabian StyleLiu, Taigang, Lei Bao, and Yujie Wang. 2024. "The Thermodynamic and Kinetic Properties of the dA-rU DNA-RNA Hybrid Base Pair Investigated via Molecular Dynamics Simulations" Molecules 29, no. 20: 4920. https://doi.org/10.3390/molecules29204920
APA StyleLiu, T., Bao, L., & Wang, Y. (2024). The Thermodynamic and Kinetic Properties of the dA-rU DNA-RNA Hybrid Base Pair Investigated via Molecular Dynamics Simulations. Molecules, 29(20), 4920. https://doi.org/10.3390/molecules29204920





