Exploration of the Solubility Hyperspace of Selected Active Pharmaceutical Ingredients in Choline- and Betaine-Based Deep Eutectic Solvents: Machine Learning Modeling and Experimental Validation
Abstract
1. Introduction
2. Results and Discussion
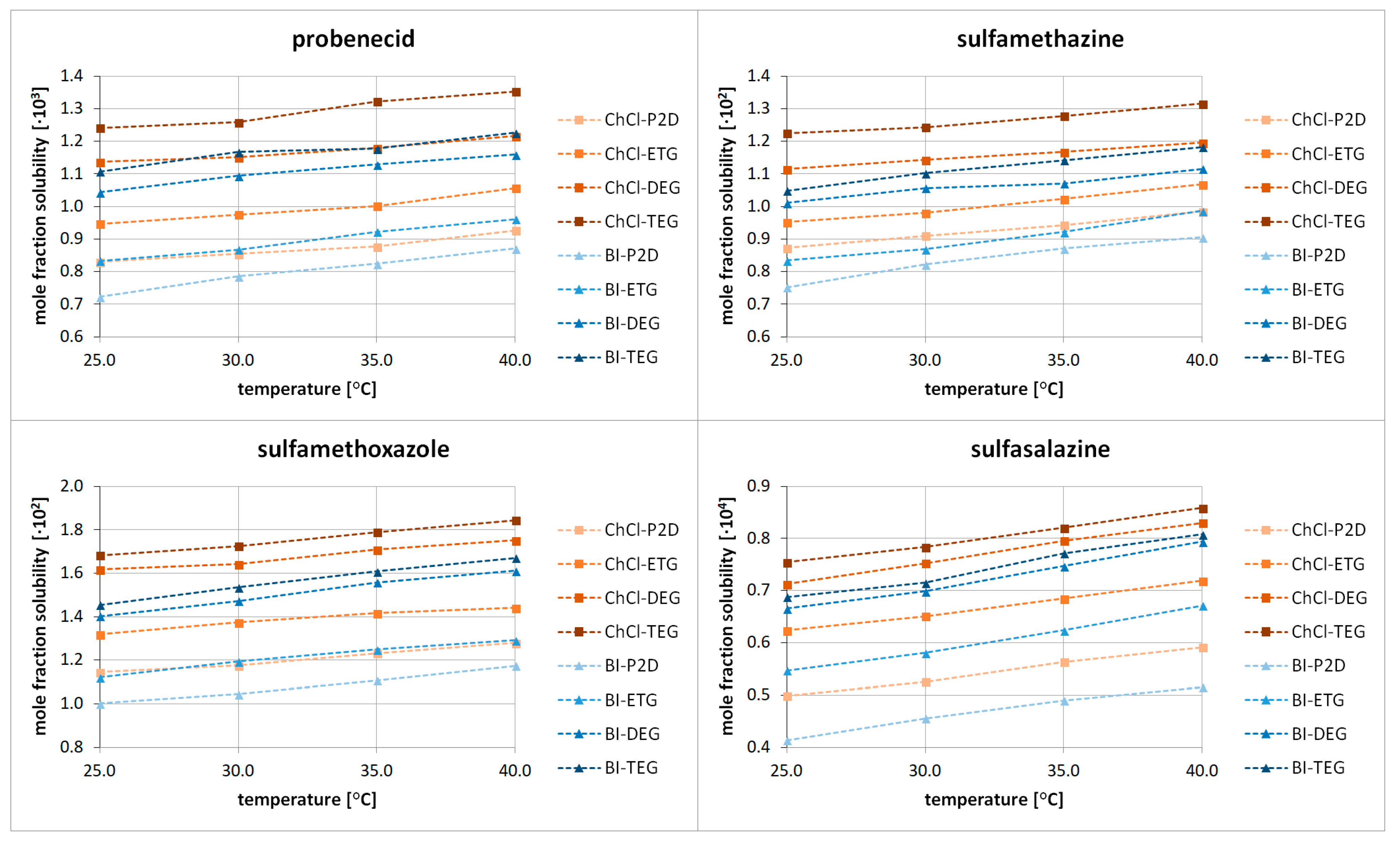
2.1. Experimental Extension of the Solubility Dataset in DESs
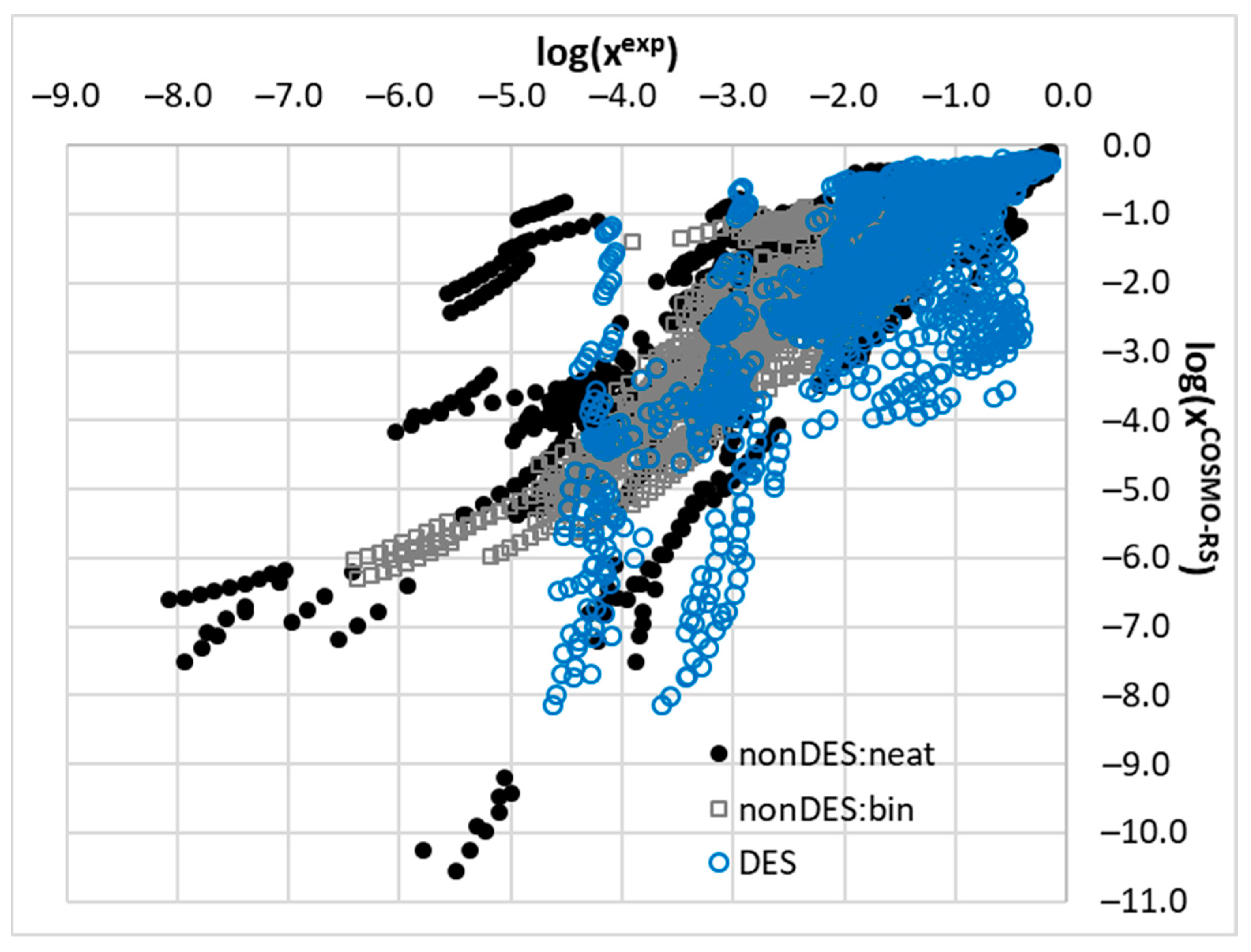
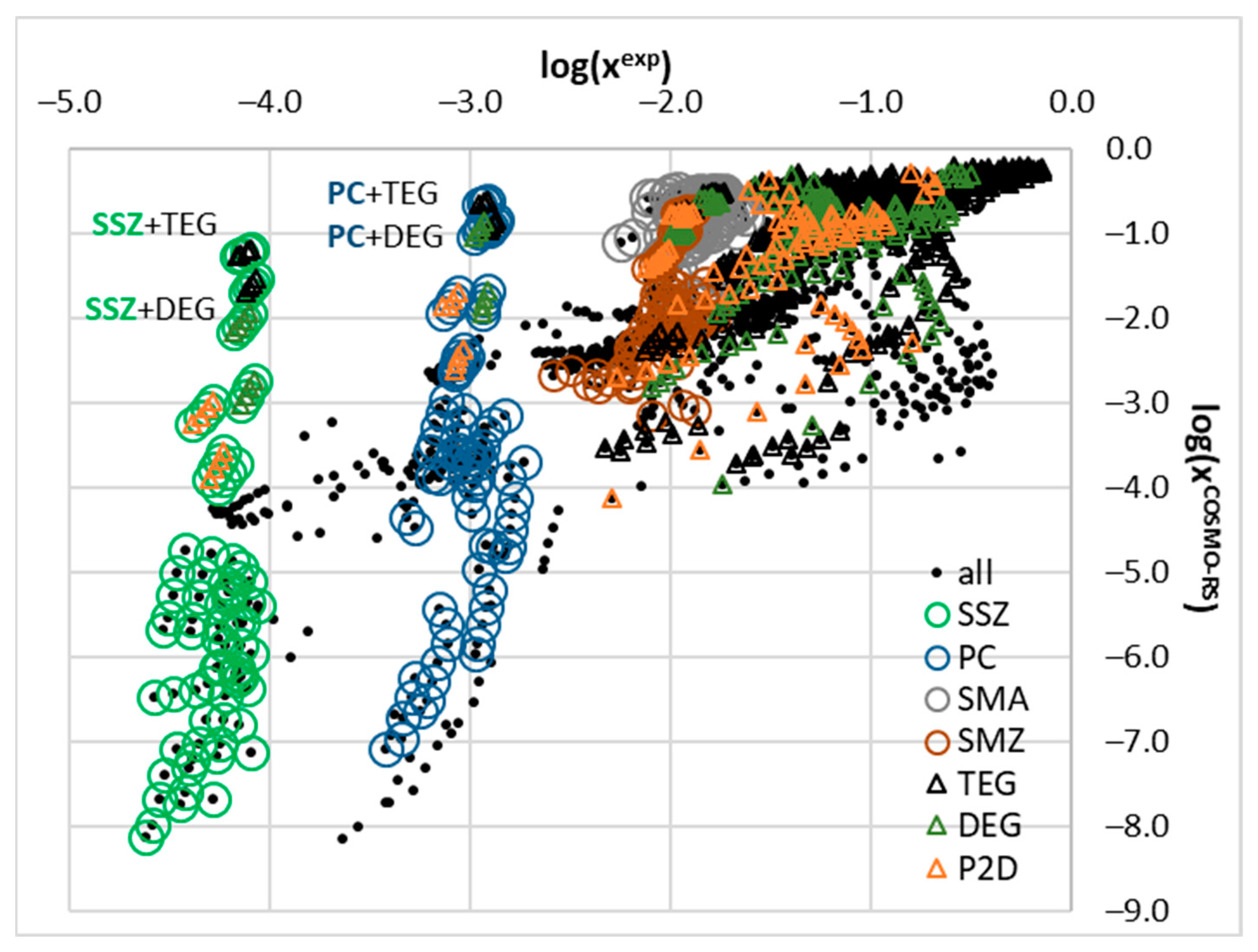
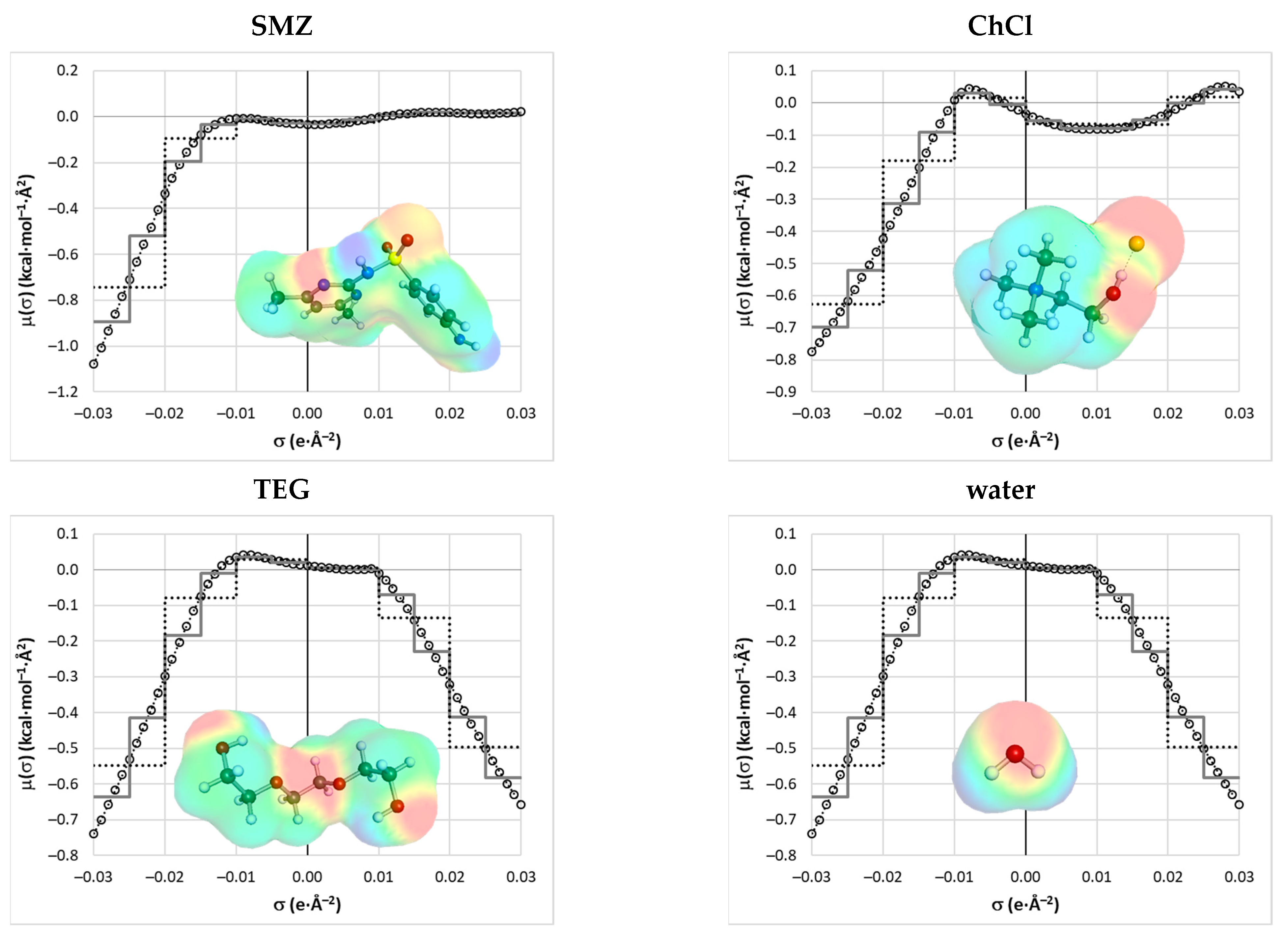
2.2. COSMO-RS Derived Solubility
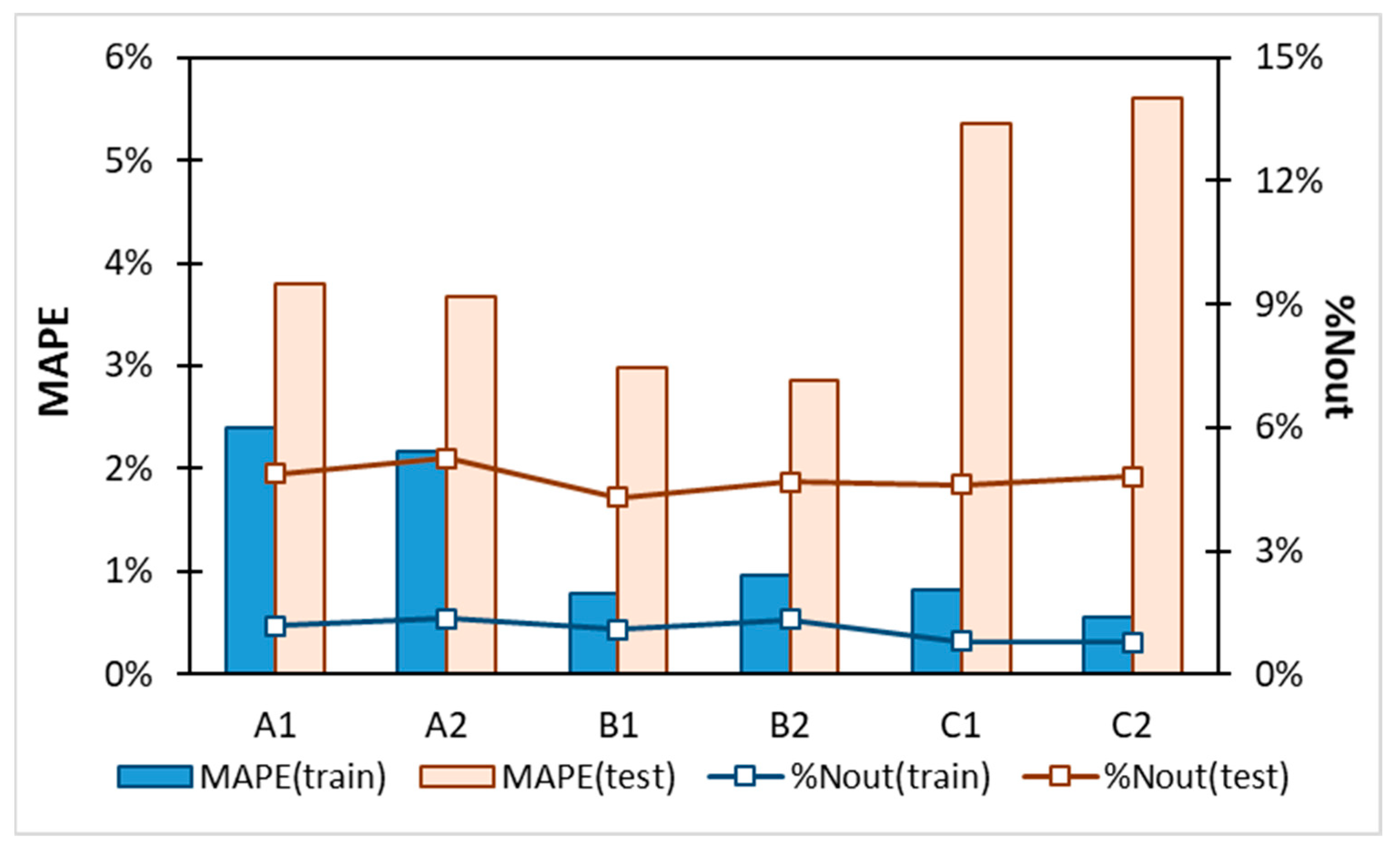
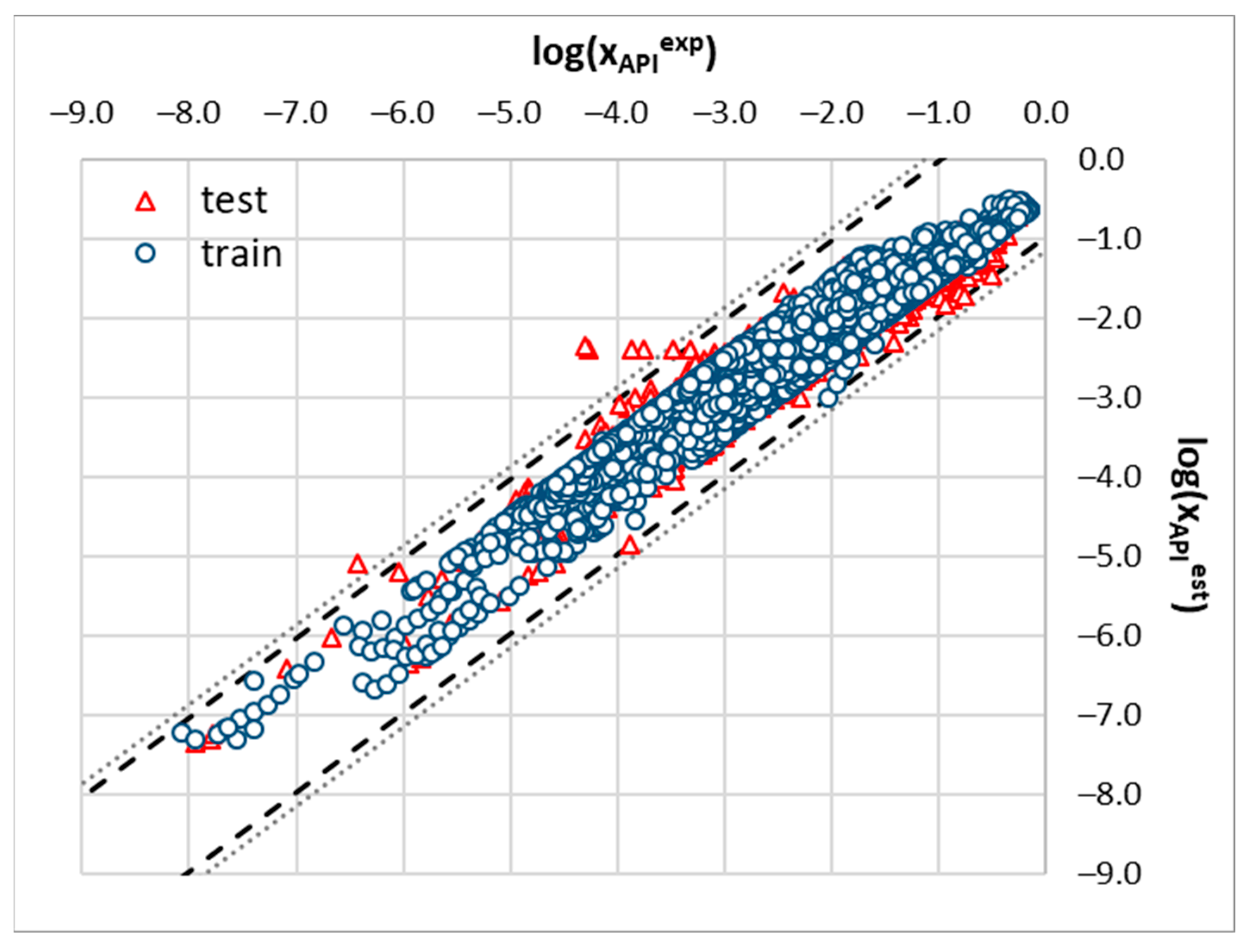
2.3. Machine Learning Solubility Model
3. Materials and Methods
3.1. Materials
3.2. Solubility Determination
3.3. Solubility Dataset
3.4. COSMO-RS Solubility Computations
3.5. Molecular Descriptors
3.6. Machine Learning Protocol
4. Conclusions
- C (6.8251) controls the trade-off between maximizing the margin and minimizing the training error. A higher value of C results in a model that prioritizes fitting the training data closely, potentially at the risk of overfitting.
- Degree (8) is relevant when using polynomial kernels and determines the degree of the polynomial. A degree of eight indicates a highly flexible model capable of capturing the complex relationships in the data.
- Gamma (0.8358) defines the influence of a single training example. A higher gamma value means the model will try to fit the data more closely, as each point has a significant influence on the shape of the decision boundary.
- Max_iter (61,378,442) sets the maximum number of iterations for the algorithm to converge. A high value ensures that the algorithm has sufficient iterations to find an optimal solution, which is especially important for complex models.
- Nu (0.4754) controls the proportion of support vectors and the margin of error, offering a balance between the number of support vectors used and the tolerance for deviations. An optimal value indicates a balanced trade-off, allowing the model to capture the underlying data patterns while controlling the margin of tolerance.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, V.; Bansal, V.; Madhavan, A.; Kumar, M.; Sindhu, R.; Awasthi, M.K.; Binod, P.; Saran, S. Active pharmaceutical ingredient (API) chemicals: A critical review of current biotechnological approaches. Bioengineered 2022, 13, 4309–4327. [Google Scholar] [CrossRef]
- Kątny, M.; Frankowski, M. Impurities in Drug Products and Active Pharmaceutical Ingredients. Crit. Rev. Anal. Chem. 2017, 47, 187–193. [Google Scholar] [CrossRef] [PubMed]
- Martínez, F.; Jouyban, A.; Acree, W.E. Pharmaceuticals solubility is still nowadays widely studied everywhere. Pharm. Sci. 2017, 23, 1–2. [Google Scholar] [CrossRef]
- Savjani, K.T.; Gajjar, A.K.; Savjani, J.K. Drug Solubility: Importance and Enhancement Techniques. ISRN Pharm. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Coltescu, A.R.; Butnariu, M.; Sarac, I. The importance of solubility for new drug molecules. Biomed. Pharmacol. J. 2020, 13, 577–583. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, Y.; Xia, M.; Dai, W.; Zhu, B.; Mei, X. Improving the dissolution behaviors and bioavailability of abiraterone acetate via multicomponent crystal forms. Int. J. Pharm. 2022, 614, 121460. [Google Scholar] [CrossRef]
- Kalam, M.A.; Alshamsan, A.; Alkholief, M.; Alsarra, I.A.; Ali, R.; Haq, N.; Anwer, M.K.; Shakeel, F. Solubility Measurement and Various Solubility Parameters of Glipizide in Different Neat Solvents. ACS Omega 2020, 5, 1708–1716. [Google Scholar] [CrossRef]
- Kim, H.-S.; Kim, C.-M.; Jo, A.-N.; Kim, J.-E. Studies on Preformulation and Formulation of JIN-001 Liquisolid Tablet with Enhanced Solubility. Pharmaceuticals 2022, 15, 412. [Google Scholar] [CrossRef]
- Khadka, P.; Ro, J.; Kim, H.; Kim, I.; Kim, J.T.; Kim, H.; Cho, J.M.; Yun, G.; Lee, J. Pharmaceutical particle technologies: An approach to improve drug solubility, dissolution and bioavailability. Asian J. Pharm. Sci. 2014, 9, 304–316. [Google Scholar] [CrossRef]
- Müller, C.E. Prodrug Approaches for Enhancing the Bioavailability of Drugs with Low Solubility. Chem. Biodivers. 2009, 6, 2071–2083. [Google Scholar] [CrossRef]
- Lipinski, C.A. Drug-like properties and the causes of poor solubility and poor permeability. J. Pharmacol. Toxicol. Methods 2000, 44, 235–249. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, F.L.O.; Marques, M.B.D.F.; Kato, K.C.; Carneiro, G. Nanonization techniques to overcome poor water-solubility with drugs. Expert Opin. Drug Discov. 2020, 15, 853–864. [Google Scholar] [CrossRef]
- Das, B.; Baidya, A.T.K.; Mathew, A.T.; Yadav, A.K.; Kumar, R. Structural modification aimed for improving solubility of lead compounds in early phase drug discovery. Bioorg. Med. Chem. 2022, 56, 116614. [Google Scholar] [CrossRef] [PubMed]
- Black, S.; Dang, L.; Liu, C.; Wei, H. On the measurement of solubility. Org. Process Res. Dev. 2013, 17, 486–492. [Google Scholar] [CrossRef]
- Bergström, C.A.S.; Avdeef, A. Perspectives in solubility measurement and interpretation. ADMET DMPK 2019, 7, 88–105. [Google Scholar] [CrossRef] [PubMed]
- Bhalani, D.V.; Nutan, B.; Kumar, A.; Singh Chandel, A.K. Bioavailability Enhancement Techniques for Poorly Aqueous Soluble Drugs and Therapeutics. Biomedicines 2022, 10, 2055. [Google Scholar] [CrossRef]
- Manallack, D.T.; Yuriev, E.; Chalmers, D.K. The influence and manipulation of acid/base properties in drug discovery. Drug Discov. Today Technol. 2018, 27, 41–47. [Google Scholar] [CrossRef]
- Merisko-Liversidge, E.; Liversidge, G.G. Nanosizing for oral and parenteral drug delivery: A perspective on formulating poorly-water soluble compounds using wet media milling technology. Adv. Drug Deliv. Rev. 2011, 63, 427–440. [Google Scholar] [CrossRef]
- Brewster, M.E.; Loftsson, T. Cyclodextrins as pharmaceutical solubilizers. Adv. Drug Deliv. Rev. 2007, 59, 645–666. [Google Scholar] [CrossRef]
- Korn, C.; Balbach, S. Compound selection for development—Is salt formation the ultimate answer? Experiences with an extended concept of the “100 mg approach”. Eur. J. Pharm. Sci. 2014, 57, 257–263. [Google Scholar] [CrossRef]
- Seedher, N.; Kanojia, M. Co-solvent solubilization of some poorly-soluble antidiabetic drugs. Pharm. Dev. Technol. 2009, 14, 185–192. [Google Scholar] [CrossRef] [PubMed]
- Boobier, S.; Hose, D.R.J.; Blacker, A.J.; Nguyen, B.N. Machine learning with physicochemical relationships: Solubility prediction in organic solvents and water. Nat. Commun. 2020, 11, 5753. [Google Scholar] [CrossRef] [PubMed]
- Lovrić, M.; Pavlović, K.; Žuvela, P.; Spataru, A.; Lučić, B.; Kern, R.; Wong, M.W. Machine learning in prediction of intrinsic aqueous solubility of drug-like compounds: Generalization, complexity, or predictive ability? J. Chemom. 2021, 35, e3349. [Google Scholar] [CrossRef]
- Hahnenkamp, I.; Graubner, G.; Gmehling, J. Measurement and prediction of solubilities of active pharmaceutical ingredients. Int. J. Pharm. 2010, 388, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.H.; Smith, R.E.; Luchtefeld, R.; Boorem, A.J.; Lou, R.; Acree, W.E. Prediction of solubility of drugs and other compounds in organic solvents. J. Pharm. Sci. 2010, 99, 1500–1515. [Google Scholar] [CrossRef] [PubMed]
- Hewitt, M.; Cronin, M.T.D.; Enoch, S.J.; Madden, J.C.; Roberts, D.W.; Dearden, J.C. In silico prediction of aqueous solubility: The solubility challenge. J. Chem. Inf. Model. 2009, 49, 2572–2587. [Google Scholar] [CrossRef]
- Lenoir, D.; Schramm, K.W.; Lalah, J.O. Green Chemistry: Some important forerunners and current issues. Sustain. Chem. Pharm. 2020, 18, 100313. [Google Scholar] [CrossRef]
- Kopach, M.; Leahy, D.; Manley, J. The green chemistry approach to pharma manufacturing. Innov. Pharm. Technol. 2012, 43, 72–75. [Google Scholar]
- González-Miquel, M.; Díaz, I. Green solvent screening using modeling and simulation. Curr. Opin. Green Sustain. Chem. 2021, 29, 100469. [Google Scholar] [CrossRef]
- Derbenev, I.N.; Dowden, J.; Twycross, J.; Hirst, J.D. Software tools for green and sustainable chemistry. Curr. Opin. Green Sustain. Chem. 2022, 35, 100623. [Google Scholar] [CrossRef]
- Sánchez-Camargo, A.d.P.; Bueno, M.; Parada-Alfonso, F.; Cifuentes, A.; Ibáñez, E. Hansen solubility parameters for selection of green extraction solvents. TrAC Trends Anal. Chem. 2019, 118, 227–237. [Google Scholar] [CrossRef]
- Wu, Y.c.; Feng, J.w. Development and Application of Artificial Neural Network. Wirel. Pers. Commun. 2018, 102, 1645–1656. [Google Scholar] [CrossRef]
- Sharifani, K.; Amini, M. Machine Learning and Deep Learning: A Review of Methods and Applications. World Inf. Technol. Eng. J. 2023, 10, 3897–3904. [Google Scholar]
- Tosca, E.M.; Bartolucci, R.; Magni, P. Application of artificial neural networks to predict the intrinsic solubility of drug-like molecules. Pharmaceutics 2021, 13, 1101. [Google Scholar] [CrossRef] [PubMed]
- Deng, T.; Jia, G. zhu Prediction of aqueous solubility of compounds based on neural network. Mol. Phys. 2020, 118, e1600754. [Google Scholar] [CrossRef]
- Wesolowski, M.; Suchacz, B. Artificial Neural Networks: Theoretical Background and Pharmaceutical Applications: A Review. J. AOAC Int. 2012, 95, 652–668. [Google Scholar] [CrossRef] [PubMed]
- Agatonovic-Kustrin, S.; Beresford, R. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef]
- Becker, J.; Manske, C.; Randl, S. Green chemistry and sustainability metrics in the pharmaceutical manufacturing sector. Curr. Opin. Green Sustain. Chem. 2022, 33, 100562. [Google Scholar] [CrossRef]
- Mishra, M.; Sharma, M.; Dubey, R.; Kumari, P.; Ranjan, V.; Pandey, J. Green synthesis interventions of pharmaceutical industries for sustainable development. Curr. Res. Green Sustain. Chem. 2021, 4, 100174. [Google Scholar] [CrossRef]
- DeSimone, J.M. Practical approaches to green solvents. Science 2002, 297, 799–803. [Google Scholar] [CrossRef]
- Häckl, K.; Kunz, W. Some aspects of green solvents. Comptes Rendus Chim. 2018, 21, 572–580. [Google Scholar] [CrossRef]
- Santana-Mayor, Á.; Rodríguez-Ramos, R.; Herrera-Herrera, A.V.; Socas-Rodríguez, B.; Rodríguez-Delgado, M.Á. Deep eutectic solvents. The new generation of green solvents in analytical chemistry. TrAC Trends Anal. Chem. 2021, 134, 116108. [Google Scholar] [CrossRef]
- Vanda, H.; Dai, Y.; Wilson, E.G.; Verpoorte, R.; Choi, Y.H. Green solvents from ionic liquids and deep eutectic solvents to natural deep eutectic solvents. Comptes Rendus Chim. 2018, 21, 628–638. [Google Scholar] [CrossRef]
- Smith, E.L.; Abbott, A.P.; Ryder, K.S. Deep Eutectic Solvents (DESs) and Their Applications. Chem. Rev. 2014, 114, 11060–11082. [Google Scholar] [CrossRef] [PubMed]
- El Achkar, T.; Greige-Gerges, H.; Fourmentin, S. Basics and properties of deep eutectic solvents: A review. Environ. Chem. Lett. 2021, 19, 3397–3408. [Google Scholar] [CrossRef]
- Omar, K.A.; Sadeghi, R. Physicochemical properties of deep eutectic solvents: A review. J. Mol. Liq. 2022, 360, 119524. [Google Scholar] [CrossRef]
- Paiva, A.; Craveiro, R.; Aroso, I.; Martins, M.; Reis, R.L.; Duarte, A.R.C. Natural Deep Eutectic Solvents—Solvents for the 21st Century. ACS Sustain. Chem. Eng. 2014, 2, 1063–1071. [Google Scholar] [CrossRef]
- Espino, M.; de los Ángeles Fernández, M.; Gomez, F.J.V.; Silva, M.F. Natural designer solvents for greening analytical chemistry. TrAC Trends Anal. Chem. 2016, 76, 126–136. [Google Scholar] [CrossRef]
- Xu, G.; Shi, M.; Zhang, P.; Tu, Z.; Hu, X.; Zhang, X.; Wu, Y. Tuning the composition of deep eutectic solvents consisting of tetrabutylammonium chloride and n-decanoic acid for adjustable separation of ethylene and ethane. Sep. Purif. Technol. 2022, 298, 121680. [Google Scholar] [CrossRef]
- Cao, Y.; Tao, X.; Jiang, S.; Gao, N.; Sun, Z. Tuning thermodynamic properties of deep eutectic solvents for achieving highly efficient photothermal sensor. J. Mol. Liq. 2020, 308, 113163. [Google Scholar] [CrossRef]
- Liu, Y.; Deak, N.; Wang, Z.; Yu, H.; Hameleers, L.; Jurak, E.; Deuss, P.J.; Barta, K. Tunable and functional deep eutectic solvents for lignocellulose valorization. Nat. Commun. 2021, 12, 5424. [Google Scholar] [CrossRef] [PubMed]
- Hansen, B.B.; Spittle, S.; Chen, B.; Poe, D.; Zhang, Y.; Klein, J.M.; Horton, A.; Adhikari, L.; Zelovich, T.; Doherty, B.W.; et al. Deep Eutectic Solvents: A Review of Fundamentals and Applications. Chem. Rev. 2021, 121, 1232–1285. [Google Scholar] [CrossRef] [PubMed]
- Bazzo, G.C.; Pezzini, B.R.; Stulzer, H.K. Eutectic mixtures as an approach to enhance solubility, dissolution rate and oral bioavailability of poorly water-soluble drugs. Int. J. Pharm. 2020, 588, 119741. [Google Scholar] [CrossRef]
- Kapre, S.; Palakurthi, S.S.; Jain, A.; Palakurthi, S. DES-igning the future of drug delivery: A journey from fundamentals to drug delivery applications. J. Mol. Liq. 2024, 400, 124517. [Google Scholar] [CrossRef]
- Jeliński, T.; Przybyłek, M.; Mianowana, M.; Misiak, K.; Cysewski, P. Deep Eutectic Solvents as Agents for Improving the Solubility of Edaravone: Experimental and Theoretical Considerations. Molecules 2024, 29, 1261. [Google Scholar] [CrossRef]
- Duarte, A.R.C.; Ferreira, A.S.D.; Barreiros, S.; Cabrita, E.; Reis, R.L.; Paiva, A. A comparison between pure active pharmaceutical ingredients and therapeutic deep eutectic solvents: Solubility and permeability studies. Eur. J. Pharm. Biopharm. 2017, 114, 296–304. [Google Scholar] [CrossRef]
- Nguyen, C.-H.; Augis, L.; Fourmentin, S.; Barratt, G.; Legrand, F.-X. Deep Eutectic Solvents for Innovative Pharmaceutical Formulations. In Deep Eutectic Solvents for Innovative Pharmaceutical Formulations; Springer: Berlin/Heidelberg, Germany, 2021; Volume 56, pp. 41–102. [Google Scholar]
- Liu, Y.; Wu, Y.; Liu, J.; Wang, W.; Yang, Q.; Yang, G. Deep eutectic solvents: Recent advances in fabrication approaches and pharmaceutical applications. Int. J. Pharm. 2022, 622, 121811. [Google Scholar] [CrossRef]
- Emami, S.; Shayanfar, A. Deep eutectic solvents for pharmaceutical formulation and drug delivery applications. Pharm. Dev. Technol. 2020, 25, 779–796. [Google Scholar] [CrossRef]
- Pedro, S.N.; Freire, M.G.; Freire, C.S.R.; Silvestre, A.J.D. Deep eutectic solvents comprising active pharmaceutical ingredients in the development of drug delivery systems. Expert Opin. Drug Deliv. 2019, 16, 497–506. [Google Scholar] [CrossRef]
- Mustafa, N.R.; Spelbos, V.S.; Witkamp, G.J.; Verpoorte, R.; Choi, Y.H. Solubility and stability of some pharmaceuticals in natural deep eutectic solvents-based formulations. Molecules 2021, 26, 2645. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Przybyłek, M.; Mai, A.; Kułak, J. Experimental and Machine-Learning-Assisted Design of Pharmaceutically Acceptable Deep Eutectic Solvents for the Solubility Improvement of Non-Selective COX Inhibitors Ibuprofen and Ketoprofen. Molecules 2024, 29, 2296. [Google Scholar] [CrossRef] [PubMed]
- Jeliński, T.; Przybyłek, M.; Różalski, R.; Romanek, K.; Wielewski, D.; Cysewski, P. Tuning Ferulic Acid Solubility in Choline-Chloride- and Betaine-Based Deep Eutectic Solvents: Experimental Determination and Machine Learning Modeling. Molecules 2024, 29, 3841. [Google Scholar] [CrossRef] [PubMed]
- Jeliński, T.; Przybyłek, M.; Cysewski, P. Natural Deep Eutectic Solvents as Agents for Improving Solubility, Stability and Delivery of Curcumin. Pharm. Res. 2019, 36, 116. [Google Scholar] [CrossRef] [PubMed]
- Jeliński, T.; Cysewski, P. Quantification of Caffeine Interactions in Choline Chloride Natural Deep Eutectic Solvents: Solubility Measurements and COSMO-RS-DARE Interpretation. Int. J. Mol. Sci. 2022, 23, 7832. [Google Scholar] [CrossRef] [PubMed]
- Jeliński, T.; Stasiak, D.; Kosmalski, T.; Cysewski, P. Experimental and theoretical study on theobromine solubility enhancement in binary aqueous solutions and ternary designed solvents. Pharmaceutics 2021, 13, 1118. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Cymerman, P.; Przybyłek, M. Solvent screening for solubility enhancement of theophylline in neat, binary and ternary NADES solvents: New measurements and ensemble machine learning. Int. J. Mol. Sci. 2021, 22, 7347. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Przybyłek, M. Experimental and Theoretical Insights into the Intermolecular Interactions in Saturated Systems of Dapsone in Conventional and Deep Eutectic Solvents. Molecules 2024, 29, 1743. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Przybyłek, M. Intermolecular Interactions of Edaravone in Aqueous Solutions of Ethaline and Glyceline Inferred from Experiments and Quantum Chemistry Computations. Molecules 2023, 28, 629. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T. Optimization, thermodynamic characteristics and solubility predictions of natural deep eutectic solvents used for sulfonamide dissolution. Int. J. Pharm. 2019, 570, 118682. [Google Scholar] [CrossRef]
- Lomba, L.; Ribate, M.P.; Zaragoza, E.; Concha, J.; Garralaga, M.P.; Errazquin, D.; García, C.B.; Giner, B. Deep Eutectic Solvents: Are They Safe? Appl. Sci. 2021, 11, 10061. [Google Scholar] [CrossRef]
- De Morais, P.; Gonçalves, F.; Coutinho, J.A.P.; Ventura, S.P.M. Ecotoxicity of Cholinium-Based Deep Eutectic Solvents. ACS Sustain. Chem. Eng. 2015, 3, 3398–3404. [Google Scholar] [CrossRef]
- Macário, I.P.E.; Jesus, F.; Pereira, J.L.; Ventura, S.P.M.; Gonçalves, A.M.M.; Coutinho, J.A.P.; Gonçalves, F.J.M. Unraveling the ecotoxicity of deep eutectic solvents using the mixture toxicity theory. Chemosphere 2018, 212, 890–897. [Google Scholar] [CrossRef] [PubMed]
- Nejrotti, S.; Antenucci, A.; Pontremoli, C.; Gontrani, L.; Barbero, N.; Carbone, M.; Bonomo, M. Critical Assessment of the Sustainability of Deep Eutectic Solvents: A Case Study on Six Choline Chloride-Based Mixtures. ACS Omega 2022, 7, 47449–47461. [Google Scholar] [CrossRef]
- Kovács, A.; Neyts, E.C.; Cornet, I.; Wijnants, M.; Billen, P. Modeling the Physicochemical Properties of Natural Deep Eutectic Solvents. ChemSusChem 2020, 13, 3789–3804. [Google Scholar] [CrossRef]
- Deglmann, P.; Hungenberg, K.-D.; Vale, H.M. Dependence of Copolymer Composition in Radical Polymerization on Solution Properties: A Quantitative Thermodynamic Interpretation. Ind. Eng. Chem. Res. 2021, 60, 10566–10583. [Google Scholar] [CrossRef]
- Klamt, A.; Schwöbel, J.; Huniar, U.; Koch, L.; Terzi, S.; Gaudin, T. COSMO plex: Self-consistent simulation of self-organizing inhomogeneous systems based on COSMO-RS. Phys. Chem. Chem. Phys. 2019, 21, 9225–9238. [Google Scholar] [CrossRef]
- Abraham, M.H.; Acree, W.E. Estimation of enthalpies of sublimation of organic, organometallic and inorganic compounds. Fluid Phase Equilib. 2020, 515, 112575. [Google Scholar] [CrossRef]
- Jasim, F.; Talib, T. Some observations on the thermal behaviour of curcumin under air and argon atmospheres. J. Therm. Anal. 1992, 38, 2549–2552. [Google Scholar] [CrossRef]
- Kulkarni, P.P.; Jafvert, C.T. Solubility of C60 in solvent mixtures. Environ. Sci. Technol. 2008, 42, 845–851. [Google Scholar] [CrossRef]
- Manin, A.N.; Drozd, K.V.; Voronin, A.P.; Churakov, A.V.; Perlovich, G.L. A Combined Experimental and Theoretical Study of Nitrofuran Antibiotics: Crystal Structures, DFT Computations, Sublimation and Solution Thermodynamics. Molecules 2021, 26, 3444. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Shi, P.; Du, S.; Liu, Y.; Han, D.; Sun, P.; Sun, M.; Xu, S.; Gong, J. Uncover the effect of solvent and temperature on solid-liquid equilibrium behavior of l-norvaline. J. Mol. Liq. 2017, 243, 273–284. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Przybyłek, M. Finding the Right Solvent: A Novel Screening Protocol for Identifying Environmentally Friendly and Cost-Effective Options for Benzenesulfonamide. Molecules 2023, 28, 5008. [Google Scholar] [CrossRef] [PubMed]
- Awad, M.; Khanna, R. Support Vector Regression. Effic. Learn. Mach. 2015, 67–80. [Google Scholar] [CrossRef]
- Ghanavati, M.A.; Ahmadi, S.; Rohani, S. A machine learning approach for the prediction of aqueous solubility of pharmaceuticals: A comparative model and dataset analysis. Digit. Discov. 2024, 3, 2085–2104. [Google Scholar] [CrossRef]
- Vassileiou, A.D.; Robertson, M.N.; Wareham, B.G.; Soundaranathan, M.; Ottoboni, S.; Florence, A.J.; Hartwig, T.; Johnston, B.F. A unified ML framework for solubility prediction across organic solvents. Digit. Discov. 2023, 2, 356–367. [Google Scholar] [CrossRef]
- Przybyłek, M.; Recki, Ł.; Mroczyńska, K.; Jeliński, T.; Cysewski, P. Experimental and theoretical solubility advantage screening of bi-component solid curcumin formulations. J. Drug Deliv. Sci. Technol. 2019, 50, 125–135. [Google Scholar] [CrossRef]
- Jeliński, T.; Przybyłek, M.; Cysewski, P. Solubility advantage of sulfanilamide and sulfacetamide in natural deep eutectic systems: Experimental and theoretical investigations. Drug Dev. Ind. Pharm. 2019, 45, 1120–1129. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Przybyłek, M. Application of COSMO-RS-DARE as a Tool for Testing Consistency of Solubility Data: Case of Coumarin in Neat Alcohols. Molecules 2022, 27, 5274. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-like screening model for real solvents: A new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Klamt, A. From Quantum Chemistry to Fluid Phase Thermodynamics and Drug Design; Elsevier: Amsterdam, The Netherlands, 2005; ISBN 978-0-444-51994-8. [Google Scholar]
- Klamt, A.; Eckert, F.; Arlt, W. COSMO-RS: An Alternative to Simulation for Calculating Thermodynamic Properties of Liquid Mixtures. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 101–122. [Google Scholar] [CrossRef]
- Klamt, A. COSMO-RS for aqueous solvation and interfaces. Fluid Phase Equilib. 2016, 407, 152–158. [Google Scholar] [CrossRef]
- Klamt, A. The COSMO and COSMO-RS solvation models. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 699–709. [Google Scholar] [CrossRef]
- Klamt, A.; Eckert, F. COSMO-RS: A novel and efficient method for the a priori prediction of thermophysical data of liquids. Fluid Phase Equilib. 2000, 172, 43–72. [Google Scholar] [CrossRef]
- Dassault Systèmes. COSMOconf, version 24.0.0; Dassault Systèmes; Biovia: San Diego, CA, USA, 2022.
- Dassault Systèmes. COSMOtherm, version 24.0.0; Dassault Systèmes; Biovia: San Diego, CA, USA, 2022.
- TURBOMOLE GmbH. TURBOMOLE, version 7.8; TURBOMOLE GmbH: Karlsruhe, Germany, 2023.
- Acree, W.; Chickos, J.S. Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds. Sublimation, Vaporization and Fusion Enthalpies From 1880 to 2015. Part 1. C 1–C 10. J. Phys. Chem. Ref. Data 2016, 45, 033101. [Google Scholar] [CrossRef]
- Acree, W.; Chickos, J.S. Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds and Ionic Liquids. Sublimation, Vaporization, and Fusion Enthalpies from 1880 to 2015. Part 2. C11–C192. J. Phys. Chem. Ref. Data 2017, 46, 013104. [Google Scholar] [CrossRef]
- Nordström, F.L.; Rasmuson, Å.C. Determination of the activity of a molecular solute in saturated solution. J. Chem. Thermodyn. 2008, 40, 1684–1692. [Google Scholar] [CrossRef]
- Svärd, M.; Valavi, M.; Khamar, D.; Kuhs, M.; Rasmuson, Å.C. Thermodynamic Stability Analysis of Tolbutamide Polymorphs and Solubility in Organic Solvents. J. Pharm. Sci. 2016, 105, 1901–1906. [Google Scholar] [CrossRef]
- Svärd, M.; Hjorth, T.; Bohlin, M.; Rasmuson, Å.C. Calorimetric Properties and Solubility in Five Pure Organic Solvents of N-Methyl- d -Glucamine (Meglumine). J. Chem. Eng. Data 2016, 61, 1199–1204. [Google Scholar] [CrossRef]
- Cysewski, P.; Jeliński, T.; Przybyłek, M.; Nowak, W.; Olczak, M. Solubility Characteristics of Acetaminophen and Phenacetin in Binary Mixtures of Aqueous Organic Solvents: Experimental and Deep Machine Learning Screening of Green Dissolution Media. Pharmaceutics 2022, 14, 2828. [Google Scholar] [CrossRef]
- Dragon, version 7.0; Talete srl: Milan, Italy, 2014.
- Yap, C.W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. [Google Scholar] [CrossRef]
- Jeliński, T.; Przybyłek, M.; Różalski, R.; Cysewski, P. Solubility of dapsone in deep eutectic solvents: Experimental analysis, molecular insights and machine learning predictions. Polym. Med. 2024, 54, 15–25. [Google Scholar] [CrossRef] [PubMed]
- Python Software Foundation. Python Language Reference, Version 3.10. Python Software Foundation: Wilmington, DE, USA. Available online: http://www.python.org (accessed on 12 October 2024).
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the KDD ‘19: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar] [CrossRef]

| Compound | λmax [nm] | Linear Regression Equation | R2 | LOD [mg/mL] | LOQ [mg/mL] |
|---|---|---|---|---|---|
| probenecid (PC) | 246 | A = 27.628 × C + 0.001 | 0.996 | 0.00126 | 0.00378 |
| sulfamethazine (SMZ) | 269 | A = 80.729 × C + 0.002 | 0.999 | 0.00052 | 0.00157 |
| sulfamethoxazole (SMA) | 270 | A = 69.820 × C + 0.001 | 0.998 | 0.00067 | 0.00202 |
| sulfasalazine (SSZ) | 364 | A = 87.917 × C + 0.002 | 0.998 | 0.00042 | 0.00127 |
| Model | Descriptors Set | Ndescr |
|---|---|---|
| A1 | Δσ- relative potential profiles simplified by step function (Ndescr = 6) intermolecular interactions (Ndescr = 5) COSMO-RS derived solubility(Ndescr = 1) | 12 |
| A2 | similar to model A1 but without COSMO-RS derived solubility | 11 |
| B1 | Δσ- relative potential profiles simplified by step function (Ndescr = 12) intermolecular interactions (Ndescr = 5) COSMO-RS derived solubility(Ndescr = 1) | 18 |
| B2 | similar to model A1 but without COSMO-RS derived solubility | 17 |
| C1 | Δσ- relative potential profiles as full profile (Ndescr = 61) COSMO-RS derived solubility | 62 |
| C2 | as model B1 is without COSMO-RS derived solubility | 61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cysewski, P.; Jeliński, T.; Przybyłek, M. Exploration of the Solubility Hyperspace of Selected Active Pharmaceutical Ingredients in Choline- and Betaine-Based Deep Eutectic Solvents: Machine Learning Modeling and Experimental Validation. Molecules 2024, 29, 4894. https://doi.org/10.3390/molecules29204894
Cysewski P, Jeliński T, Przybyłek M. Exploration of the Solubility Hyperspace of Selected Active Pharmaceutical Ingredients in Choline- and Betaine-Based Deep Eutectic Solvents: Machine Learning Modeling and Experimental Validation. Molecules. 2024; 29(20):4894. https://doi.org/10.3390/molecules29204894
Chicago/Turabian StyleCysewski, Piotr, Tomasz Jeliński, and Maciej Przybyłek. 2024. "Exploration of the Solubility Hyperspace of Selected Active Pharmaceutical Ingredients in Choline- and Betaine-Based Deep Eutectic Solvents: Machine Learning Modeling and Experimental Validation" Molecules 29, no. 20: 4894. https://doi.org/10.3390/molecules29204894
APA StyleCysewski, P., Jeliński, T., & Przybyłek, M. (2024). Exploration of the Solubility Hyperspace of Selected Active Pharmaceutical Ingredients in Choline- and Betaine-Based Deep Eutectic Solvents: Machine Learning Modeling and Experimental Validation. Molecules, 29(20), 4894. https://doi.org/10.3390/molecules29204894








