DFT Exploration of Metal Ion–Ligand Binding: Toward Rational Design of Chelating Agent in Semiconductor Manufacturing
Abstract
1. Introduction
2. Calculation Methods
2.1. Binding Strength
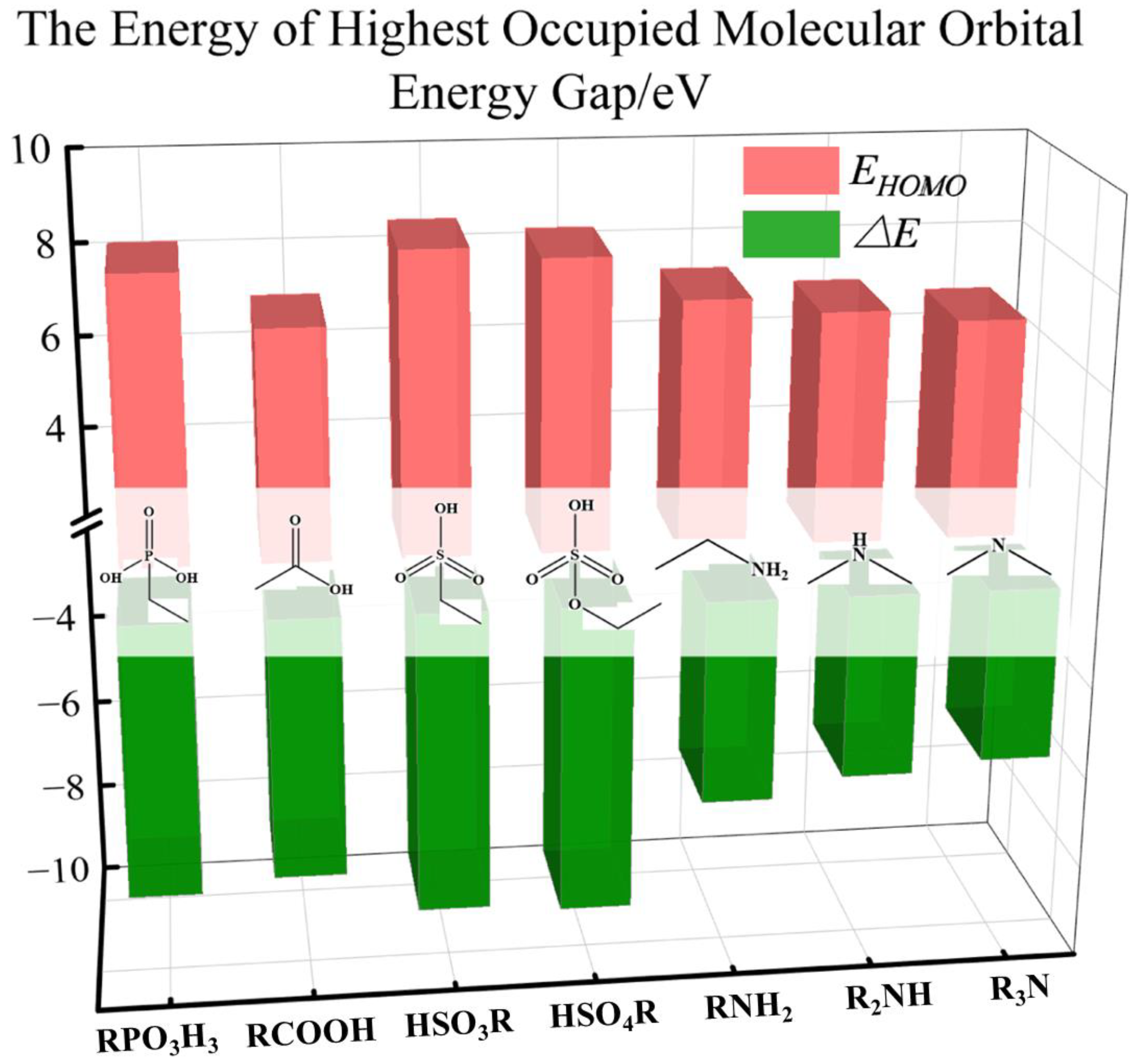
2.2. Frontier Molecular Orbitals (FMOs) and Energy Gaps
2.3. The Electrophilicity ω Index and the Nucleophilicity N Index
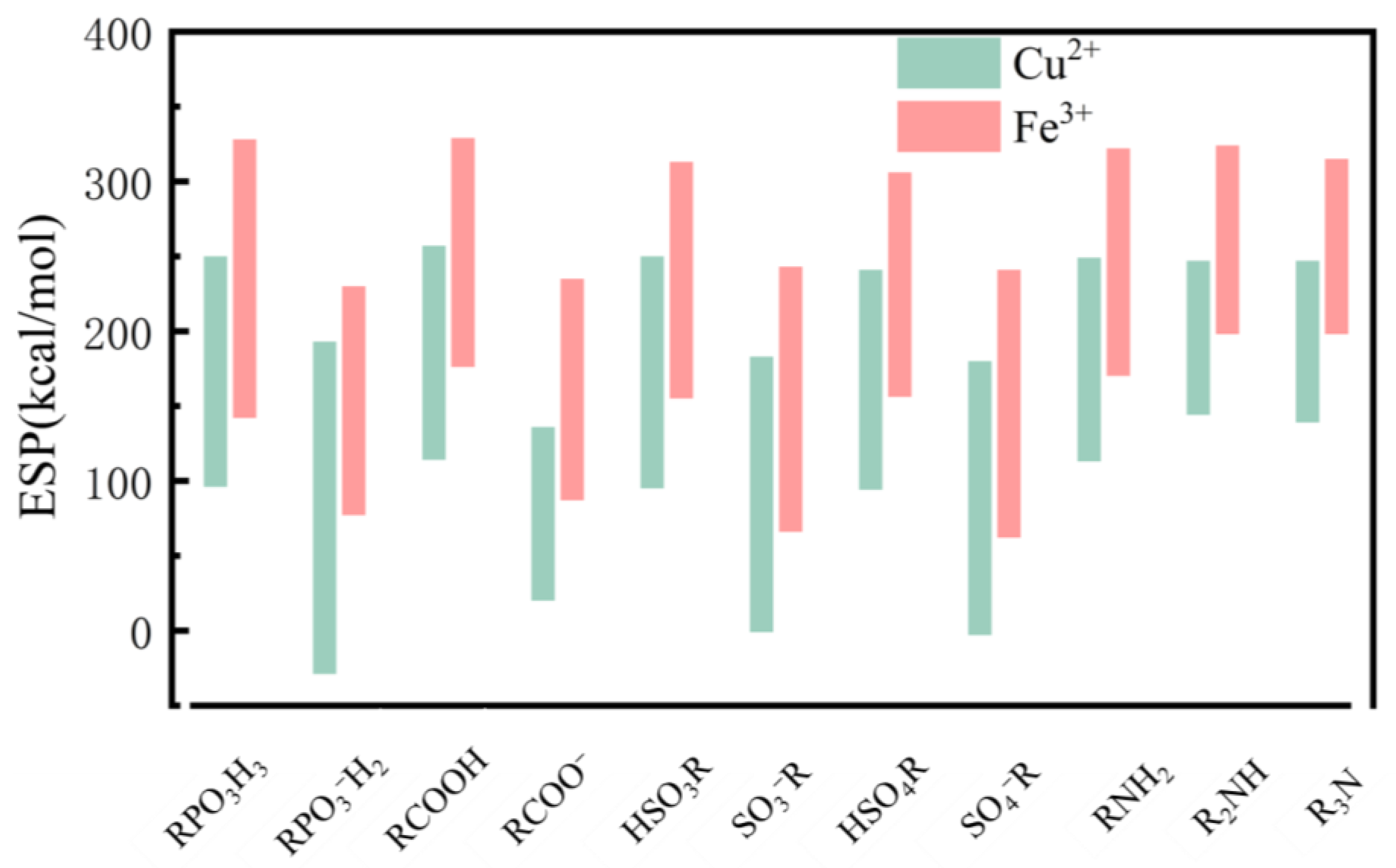
2.4. Electrostatic Potential
2.5. Energy Decomposition Analysis Based on Forcefield (EDA-FF)
3. Results
4. Discussion
4.1. Effect of Deprotonation on Binding Properties of Ligand
4.2. Differences in Binding Properties of Neutral Ligands
4.3. Differences in Electrostatic Properties of Divalent and Trivalent Metal Ion Complexes
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Polignano, M.L.; Borionetti, G.; Galbiati, A.; Grasso, S.; Mica, I.; Nutsch, A. Comparison of techniques for detecting metal contamination in silicon wafers. Spectrochim. Acta Part B At. Spectrosc. 2018, 149, 313–321. [Google Scholar] [CrossRef]
- McHugo, S.A.; Thompson, A.C.; Lamble, G.; Flink, C.; Weber, E.R. Metal impurity precipitates in silicon: Chemical state and stability. Phys. B Condens. Matter 1999, 273, 371–374. [Google Scholar] [CrossRef]
- Kim, J.-S. Cleaning Efficiencies of Various Chemical Solutions for Noble Metals such as Cu, Ag, and Au on Si Wafer Surfaces. J. Electrochem. Soc. 1999, 146, 4281–4289. [Google Scholar] [CrossRef]
- Feeney, R.E.; Bennett, N. Formation of Liesegang-like Rings by Metal Ions and Chelating or Complexing Agents. Nature 1957, 180, 979–980. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.H.; Wang, G.X. Study of Chelating Agents in Silicon Wafer Polishing Slurry. Adv. Mater. Res. 2012, 581–582, 790–793. [Google Scholar]
- Tung Ming, P.; Tan Fu, L.; Fu Hsiang, K.; Tien Sheng, C.; Tzu Huan, C.; Ying Hao, L.; Chih Peng, L. Comparison of novel cleaning solutions with various chelating agents for post-CMP cleaning on poly-Si film. IEEE Trans. Semicond. Manuf. 2001, 14, 365–371. [Google Scholar] [CrossRef]
- Zhang, X.G. Electrochemistry of Silicon and Its Oxide; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Kawase, A.; Miwa, T.; Sakamoto, K.; Hayashida, I. Polishing Composition and Rinsing Composition. US74819492B, 27 January 2009. [Google Scholar]
- Momota, K.T. Polishing Composition for Silicon Wafer and Polishing Method. US10273383B2, 30 April 2019. [Google Scholar]
- Roh, H.S.; Park, T.W.; Lee, T.Y.; Lee, I.K.; Lee, C.H.; Kim, Y.W.; Choi, M.R.; Kim, J.S. Polishing Slurry Composition and Method of Using the Same. US20060196850A1, 7 September 2006. [Google Scholar]
- Tan, B.M.; Niu, X.H.; He, Y.G.; Gao, B.H.; Liu, Y.L. Effect of FA/O Chelating Agent on Copper Ion Removing on Silicon Surface. Adv. Mater. Res. 2011, 183–185, 2284–2287. [Google Scholar]
- Zhang, K.; Niu, X.; Wang, C.; Wang, J.; Yin, D.; Wang, R. Effect of Chelating Agent and Ammonium Dodecyl Sulfate on the Interfacial Behavior of Copper CMP for GLSI. ECS J. Solid State Sci. Technol. 2018, 7, P509. [Google Scholar] [CrossRef]
- Li, X.; Pan, G.; Wang, C.; Guo, X.; He, P.; Li, Y. Effect of Chelating Agent on Reducing Galvanic Corrosion between Cobalt and Copper in Alkaline Slurry. ECS J. Solid State Sci. Technol. 2016, 5, P540. [Google Scholar] [CrossRef]
- Da Costa, L.M.; Stoyanov, S.R.; Damasceno, R.N.; de M. Carneiro, J.W. Density functional theory investigation of the binding interactions between phosphoryl, carbonyl, imino, and thiocarbonyl ligands and the pentaaqua nickel(II) complex: Coordination affinity and associated parameters. Int. J. Quantum Chem. 2013, 113, 2621–2628. [Google Scholar] [CrossRef]
- Quattrociocchi, D.S.G.; de M. Carneiro, J.W.; Ferreira, G.B.; Stoyanov, S.R.; Damasceno, R.N.; da Costa, L.M. Design of Molecular Building Blocks for the Development of Nickel(II)-Chelating Agents. ChemistrySelect 2017, 2, 4617–4625. [Google Scholar] [CrossRef]
- Meuser, M.V.M.; Quattrociocchi, D.G.S.; Da Costa, L.M.; Ferreira, G.B.; Carneiro, J.W.d.M. Computational study of the interaction between the [Pb(H2O)3]2+ cation and ligands containing oxygen, nitrogen and sulfur donor atoms. Polyhedron 2015, 102, 193–200. [Google Scholar] [CrossRef]
- Baskaran, S.; Venuvanalingam, P.; Sivasankar, C. Understanding the stability, electronic and molecular structure of some copper(III) complexes containing alkyl and non alkyl ligands: Insights from DFT calculations. J. Organomet. Chem. 2011, 696, 2627–2634. [Google Scholar] [CrossRef]
- Lopez, R.; Diaz, N.; Suarez, D. Alkali and Alkaline-Earth Cations in Complexes with Small Bioorganic Ligands: Ab Initio Benchmark Calculations and Bond Energy Decomposition. Chemphyschem 2020, 21, 99–112. [Google Scholar] [CrossRef] [PubMed]
- Quattrociocchi, D.G.S.; Ferreira, G.B.; da Costa, L.M.; Carneiro, J.W.d.M. DFT studies of the interactions between the [Ca(H 2 O) 5 ] 2+ cation and monofunctional oxo, aza, sulfur and phosphorous ligands. Comput. Theor. Chem. 2016, 1075, 104–110. [Google Scholar] [CrossRef]
- Shang, X.-Y.; An, H.-Y.; Zhang, T.; Lin, J.-H.; Hao, F.; Yu, D.-H.; Xiao, J.-C.; Li, T.-D. Evaluating and understanding the affinity of metal ions to water and ammonia using density functional theory calculation. Chem. Phys. Lett. 2021, 768, 138398. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016.
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Prejanò, M.; Alberto, M.E.; Russo, N.; Toscano, M.; Marino, T. The effects of the metal ion substitution into the active site of metalloenzymes: A theoretical insight on some selected cases. Catalysts 2020, 10, 1038. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Roosevelt, T. Benchmarks for HS-LS Energy Difference: NEVPT2, CASPT2 and DLPNO-CCSD (T) vs. TPSSh. Ph.D. Thesis, Univitat Rovira i Virgili, Tarragona, Spain, 2020. [Google Scholar]
- Starikov, A.; Starikova, A.; Minkin, V. Quantum Chemical Study of the Structures and Stability of Copper (II) Bis (diketonate) Dimers. Russ. J. Coord. Chem. 2021, 47, 174–179. [Google Scholar] [CrossRef]
- Li, G.; Stenlid, J.H.; Ahlquist, M.S.; Brinck, T. Utilizing the Surface Electrostatic Potential to Predict the Interactions of Pt and Ni Nanoparticles with Lewis Acids and Bases—σ-Lumps and σ-Holes Govern the Catalytic Activities. J. Phys. Chem. C 2020, 124, 14696–14705. [Google Scholar] [CrossRef]
- Reimann, M.; Bischoff, F.A.; Sauer, J. Thermochemistry of FeO m H nz Species: Assessment of Some DFT Functionals. J. Chem. Theory Comput. 2020, 16, 2430–2435. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, J.; Mennucci, B.; Cancès, E. The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level. J. Mol. Struct 1999, 464, 211–226. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F.-W. Calculation of molecular orbital composition. Acta Chim. Sin. 2011, 69, 2393. [Google Scholar]
- Lu, T.; Chen, F. Quantitative analysis of molecular surface based on improved Marching Tetrahedra algorithm. J. Mol. Graph. Model. 2012, 38, 314–323. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Peckelsen, K.; Martens, J.; Berden, G.; Oomens, J.; Dunbar, R.C.; Meijer, A.J.; Schäfer, M. Gas-phase complexes of Ni2+ and Ca2+ with deprotonated histidylhistidine (HisHis): A model case for polyhistidyl-metal binding motifs. J. Mol. Spectrosc. 2017, 332, 38–44. [Google Scholar] [CrossRef]
- Da Silva, V.H.M.; de Mesquita Carneiro, J.W.; da Costa, L.M.; Ferreira, G.B. DFT analysis of the interaction between Hg2+ and monodentate neutral ligands using NBO, EDA, and QTAIM. J. Mol. Model. 2020, 26, 146. [Google Scholar] [CrossRef] [PubMed]
- Da Costa, L.M.; Ferreira, G.B.; de M. Carneiro, J.W. DFT studies of imino and thiocarbonyl ligands with the pentaaqua Mg2+ cation: Affinity and associated parameters. J. Mol. Model. 2013, 19, 2669–2677. [Google Scholar] [CrossRef]
- Luque, I.; Freire, E. Structural parameterization of the binding enthalpy of small ligands. Proteins Struct. Funct. Bioinform. 2002, 49, 181–190. [Google Scholar] [CrossRef] [PubMed]
- Braga, L.S.; Leal, D.H.; Kuca, K.; Ramalho, T.C. Perspectives on the role of the frontier effective-for-reaction molecular orbital (FERMO) in the study of chemical reactivity: An updated review. Curr. Org. Chem. 2020, 24, 314–331. [Google Scholar] [CrossRef]
- Pal, R.; Chattaraj, P.K. Electrophilicity index revisited. J. Comput. Chem. 2023, 44, 278–297. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the conceptual density functional theory indices to organic chemistry reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Pérez, P. The nucleophilicity N index in organic chemistry. Org. Biomol. Chem. 2011, 9, 7168–7175. [Google Scholar] [CrossRef]
- Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels–Alder reactions. Tetrahedron 2002, 58, 4417–4423. [Google Scholar] [CrossRef]
- Jaramillo, P.; Domingo, L.R.; Chamorro, E.; Pérez, P. A further exploration of a nucleophilicity index based on the gas-phase ionization potentials. J. Mol. Struct. Theochem. 2008, 865, 68–72. [Google Scholar] [CrossRef]
- Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Quantitative characterization of the local electrophilicity of organic molecules. Understanding the regioselectivity on Diels—Alder reactions. J. Phys. Chem. A 2002, 106, 6871–6875. [Google Scholar] [CrossRef]
- Pérez, P.; Domingo, L.R.; Duque-Noreña, M.; Chamorro, E. A condensed-to-atom nucleophilicity index. An application to the director effects on the electrophilic aromatic substitutions. J. Mol. Struct. Theochem. 2009, 895, 86–91. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. The fundamental nature and role of the electrostatic potential in atoms and molecules. Theor. Chem. Acc. 2002, 108, 134–142. [Google Scholar] [CrossRef]
- Cao, J.; Ren, Q.; Chen, F.; Lu, T. Comparative study on the methods for predicting the reactive site of nucleophilic reaction. Sci. China Chem. 2015, 58, 1845–1852. [Google Scholar] [CrossRef]
- Bijina, P.V.; Suresh, C.H. Molecular electrostatic potential analysis of non-covalent complexes. J. Chem. Sci. 2016, 128, 1677–1686. [Google Scholar] [CrossRef]
- Suresh, C.H.; Remya, G.S.; Anjalikrishna, P.K. Molecular electrostatic potential analysis: A powerful tool to interpret and predict chemical reactivity. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1601. [Google Scholar] [CrossRef]
- Lu, T.; Liu, Z.; Chen, Q. Comment on “18 and 12–Member carbon rings (cyclo [n] carbons)–A density functional study”. Mater. Sci. Eng. B 2021, 273, 115425. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, X.; Lu, T.; Wang, J.; Yan, X.; Wu, Y.; Xu, J. Molecular assembly with figure-of-eight nanohoop as a strategy for collection and stabilization of cyclo[18]carbon. Phys. Chem. Chem. Phys. 2023, 25, 16707–16711. [Google Scholar] [CrossRef]
- Zhu, S.-f.; Gan, Q.; Feng, C. Multimolecular complexes of CL-20 with nitropyrazole derivatives: Geometric, electronic structure, and stability. ACS Omega 2019, 4, 13408–13417. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, Q.; Li, Z.; Hu, F. Intermolecular weak interactions of crystalline purine and uric acid investigated by terahertz spectroscopy and theoretical calculation. J. Lumin. 2020, 223, 117198. [Google Scholar] [CrossRef]
- Zhan, K.; Li, Z.; Chen, J.; Hou, Y.; Zhang, J.; Sun, R.; Bu, Z.; Wang, L.; Wang, M.; Chen, X. Tannic acid modified single nanopore with multivalent metal ions recognition and ultra-trace level detection. Nano Today 2020, 33, 100868. [Google Scholar] [CrossRef]
- Chen, X.; Sakurai, H.; Wang, H.; Gao, S.; Bi, H.-D.; Bai, F.-Q. Theoretical study on the molecular stacking interactions and charge transport properties of triazasumanene crystals–from explanation to prediction. Phys. Chem. Chem. Phys. 2021, 23, 4681–4689. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Chen, S.; Luo, F.; Sun, L. Absorption of toluene using deep eutectic solvents: Quantum chemical calculations and experimental investigation. Ind. Eng. Chem. Res. 2020, 59, 22605–22618. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
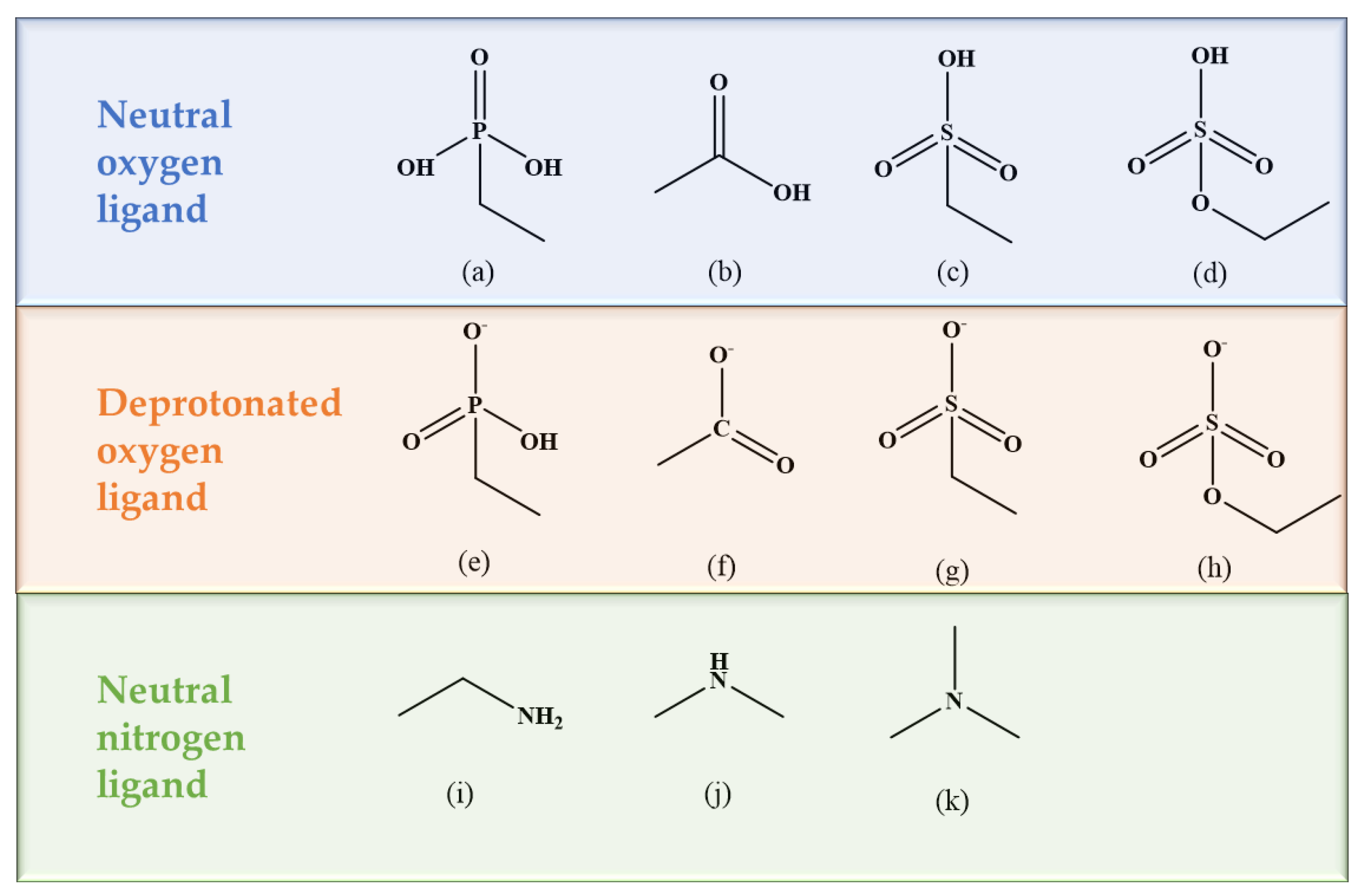
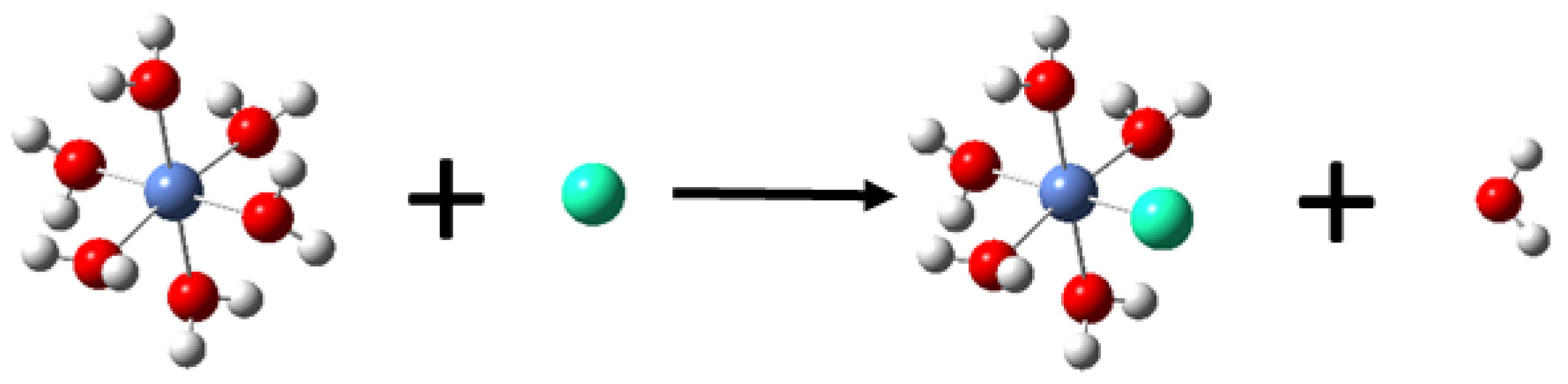
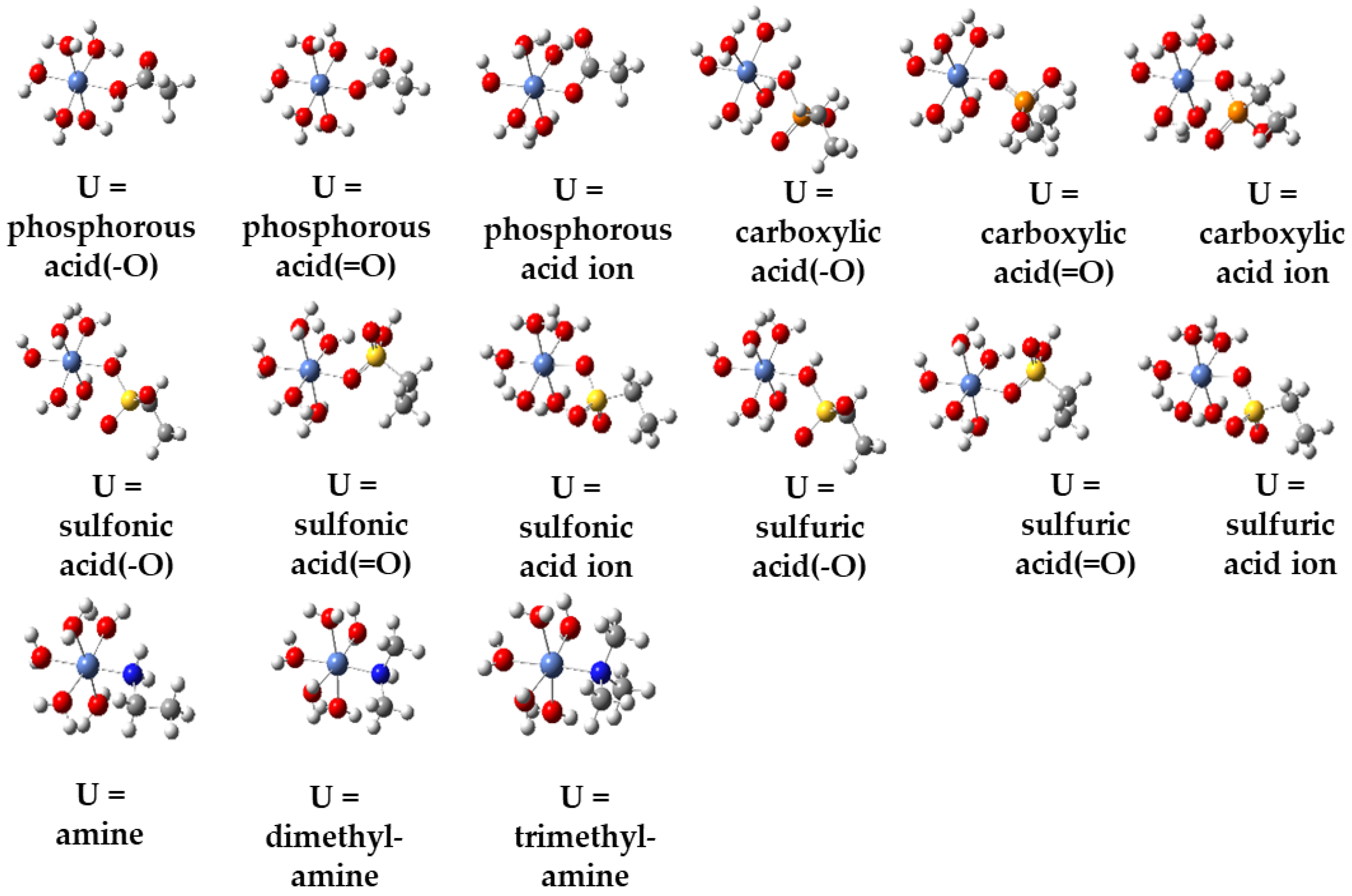


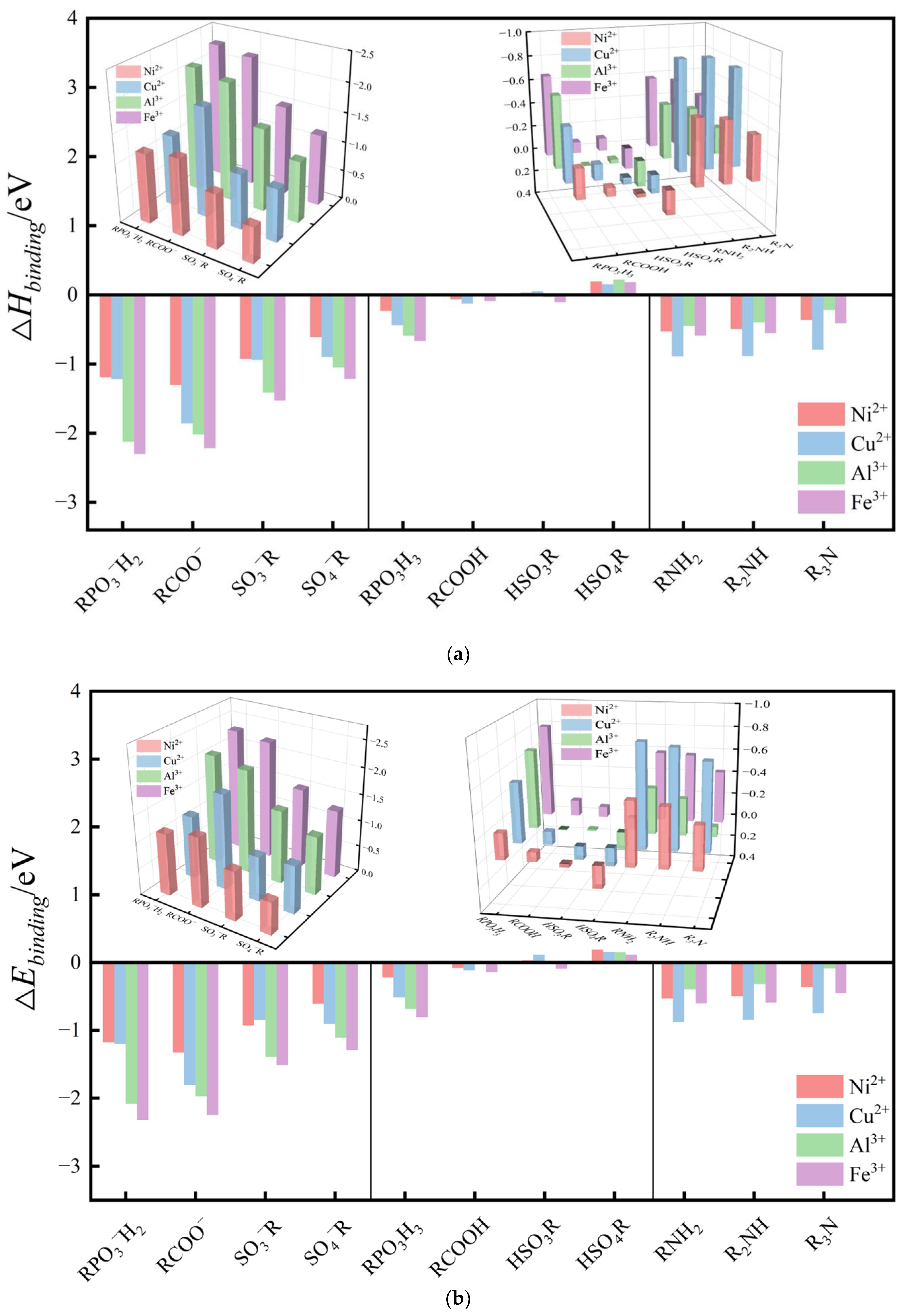



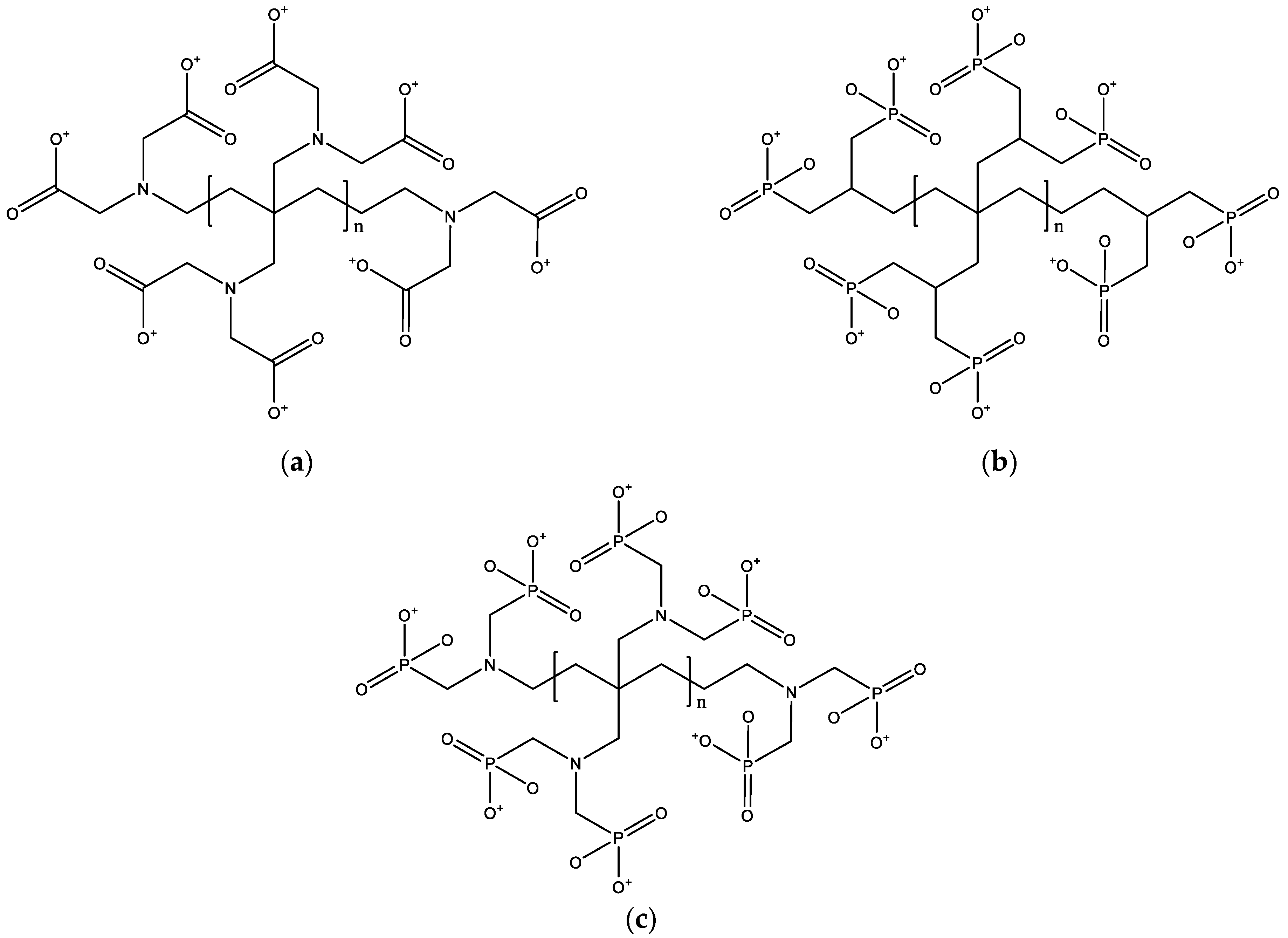
| Metal Ions | Edge Position Ligand | Center Position Ligand | ||||
|---|---|---|---|---|---|---|
| Ni2+ | carboxylic acid ion | phosphorous acid ion | sulfonic acid ion | amine | dimethylamine | trimethylamine |
| Cu2+ | carboxylic acid ion | phosphorous acid ion | sulfonic acid ion | amine | dimethylamine | trimethylamine |
| Al3+ | phosphorous acid ion | carboxylic acid ion | sulfonic acid ion | phosphorous acid | amine | dimethylamine |
| Fe3+ | phosphorous acid ion | carboxylic acid ion | sulfonic acid ion | phosphorous acid | amine | dimethylamine |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhu, J.; Huang, Q.; Zhu, L.; Wang, D.; Li, W.; Yu, W. DFT Exploration of Metal Ion–Ligand Binding: Toward Rational Design of Chelating Agent in Semiconductor Manufacturing. Molecules 2024, 29, 308. https://doi.org/10.3390/molecules29020308
Wang W, Zhu J, Huang Q, Zhu L, Wang D, Li W, Yu W. DFT Exploration of Metal Ion–Ligand Binding: Toward Rational Design of Chelating Agent in Semiconductor Manufacturing. Molecules. 2024; 29(2):308. https://doi.org/10.3390/molecules29020308
Chicago/Turabian StyleWang, Wenyuan, Junli Zhu, Qi Huang, Lei Zhu, Ding Wang, Weimin Li, and Wenjie Yu. 2024. "DFT Exploration of Metal Ion–Ligand Binding: Toward Rational Design of Chelating Agent in Semiconductor Manufacturing" Molecules 29, no. 2: 308. https://doi.org/10.3390/molecules29020308
APA StyleWang, W., Zhu, J., Huang, Q., Zhu, L., Wang, D., Li, W., & Yu, W. (2024). DFT Exploration of Metal Ion–Ligand Binding: Toward Rational Design of Chelating Agent in Semiconductor Manufacturing. Molecules, 29(2), 308. https://doi.org/10.3390/molecules29020308






