Computational Study of the Kinetics and Mechanisms of Gas-Phase Decomposition of N-Diacetamides Using Density Functional Theory
Abstract
1. Introduction
2. Computational Methodology
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soheil, M.; Alireza, F. Encyclopedia of Toxicology, 4th ed.; Wexler, P., Ed.; Academic Press: Cambridge, MA, USA, 2024; pp. 39–42. [Google Scholar] [CrossRef]
- Kuroda, Y.; Saito, Y.; Machida, K.; Uno, T. Infrared dichroism and out-of-plane vibrations of trans-cis diacetamide and its C- and N-deuterated derivatives. Spect. Acta Part A Mol. Spectrosc. 1973, 29, 411–421. [Google Scholar] [CrossRef]
- Kuroda, Y.; Saito, Y.; Machida, K.; Uno, T. Infrared spectra of trans-cis diacetamide and its C- and Ndeuterated compounds. Spectrochim. Acta Part A Mol. Spectrosc. 1971, 27, 1481–1493. [Google Scholar] [CrossRef]
- Gallaher, K.L.; Batter, S.H. Structure of diacetamide. Reference amido structures for polypeptide conformation analysis. J. Chem. Soc. Faraday Trans. 2 1975, 71, 1423–1435. [Google Scholar] [CrossRef]
- Ramondo, F.; Nunziante Cesaro, S.; Bencivenni, L. Effects of intermolecular hydrogen bonding on the molecular structure and vibrational spectrum of diacetamide. J. Mol. Struct. 1993, 291, 219–244. [Google Scholar] [CrossRef]
- Matias, P.M.; Jeffrey, G.A.; Ruble, J.R. Structures of the E,Z (cis–trans) isomer of diacetamide and the 1:1 complex with acetamide at 123 K. Ab-initio molecular orbital calculations on the Z,Z (trans–trans), E,Z (cis–trans) and E,E (cis–cis) isomers of diacetamide. Acta Cryst. Sect. B Struct. Sci. 1988, 44, 516–522. [Google Scholar] [CrossRef]
- Altarawneh, M.; Altarawneh, K. A theoretical study on the bimolecular reactions encountered in the pyrolysis of acetamide. J. Phys. Org. Chem. 2012, 25, 431–436. [Google Scholar] [CrossRef]
- Hurd, C.D. The Pyrolysis of Carbon Compounds; ACS Monograph Series No. 50; The Chemical Catalog Co., Ltd.: New York, NY, USA, 1929. [Google Scholar]
- Irwin, W.J. Analytical pyrolysis an overview. J. Anal. Appl. Pyrolysis 1979, 1, 89–122. [Google Scholar] [CrossRef]
- Ericsson, I.; Lattimer, R. Pyrolysis nomenclature. J. Anal. Appl. Pyrol. 1989, 14, 219–221. [Google Scholar] [CrossRef]
- Uden, P. Nomenclature and terminology for analytical pyrolysis (IUPAC Recommendations 1993). Pure Appl. Chem. 1993, 65, 2405–2409. [Google Scholar] [CrossRef][Green Version]
- Almeida-Neto, F.W.Q.; Matos, M.G.C.; Marinho, E.M.; Marinho, M.M.; Sampaio, T.L.; Bandeira, P.N.; Dos Santos, H.S. In silico study of the potential interactions of 4′-acetamidechalcones with protein targets in SARS-CoV-2. Biochem. Biophys. Res. Commun. 2021, 537, 71–77. [Google Scholar] [CrossRef]
- Hariyono, P.; Dwiastuti, R.; Yusuf, M.; Salin, N.H.; Hariono, M. 2-Phenoxyacetamide derivatives as SARSCoV-2 main protease inhibitor: In silico studies. Results Chem. 2022, 4, 100263. [Google Scholar] [CrossRef] [PubMed]
- Moldoveanu, S. Pyrolysis of Organic Molecules with Applications to Health and Environment; Techniques and Instrumentation in Analytical Chemistry; Elsevier: Amsterdam, The Netherlands, 2010; Volume 28, pp. 1–724. Available online: https://www.sciencedirect.com/bookseries/techniques-and-instrumentation-in-analytical-chemistry/vol/28/suppl/C (accessed on 5 August 2024).
- Al-Awadi, N.A.; Al-Omran, F.A. Gas-phase kinetics of N-substituted diacetamide. Int. J. Chem. Kinet. 1994, 26, 951–954. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, revision C.01-version 1.1; Gaussian, Inc.: Wallingford CT, USA, 2016. [Google Scholar]
- G09 Keywords: DFT Methods. Available online: http://www.chemistry4.me/gaussian/g09w/help/g09/l_keywords09.htm (accessed on 5 August 2024).
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 104552. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, C.; Rubez, G.; Khartabil, H.; Boisson, J.C.; Contreras-García, J.; Hénon, E. Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density. Phys. Chem. Chem. Phys. 2017, 19, 17928–17936. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, C.; Khartabil, H.; Boisson, J.C.; Contreras-García, J.; Piquemal, J.P.; Hénon, E. Independent Gradient Model: A new approach for probing strong and weak interactions in molecules from wave function calculations. Chem. Phys. Chem. 2018, 19, 724–735. [Google Scholar] [CrossRef] [PubMed]
- Ponce-Vargas, M.; Lefebvre, C.; Boisson, J.C.; Hénon, E. Atomic Decomposition Scheme of Noncovalent Interactions Applied to Host–Guest Assemblies. J. Chem. Inf. Model. 2020, 60, 268–278. [Google Scholar] [CrossRef] [PubMed]
- Klein, J.; Khartabil, H.; Boisson, J.C.; Contreras-García, J.; Piquemal, J.P.; Hénon, E. New Way for Probing Bond Strength. J. Phys. Chem. A 2020, 124, 1850–1860. [Google Scholar] [CrossRef]
- Lefebvre, C.; Khartabil, H.; Hénon, E. New insight into atomic-level interpretation of interactions in molecules and reacting systems. Phys. Chem. Chem. Phys. 2023, 25, 11398–11409. [Google Scholar] [CrossRef]
- Lefebvre, C.; Klein, J.; Khartabil, H.; Boisson, J.; Hénon, E. IGMPlot: A program to identify, characterize, and quantify molecular interactions. J. Comput. Chem. 2023, 44, 1750–1766. [Google Scholar] [CrossRef]
- McQuarrie, D. Statistical Mechanics; Harper & Row: New York, NY, USA, 1986. [Google Scholar]
- Tzeli, D.; Tsekouras, A.A. Mind the basis set superposition error. Chem. Phys. Lett. 2010, 496, 42–45. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtis, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
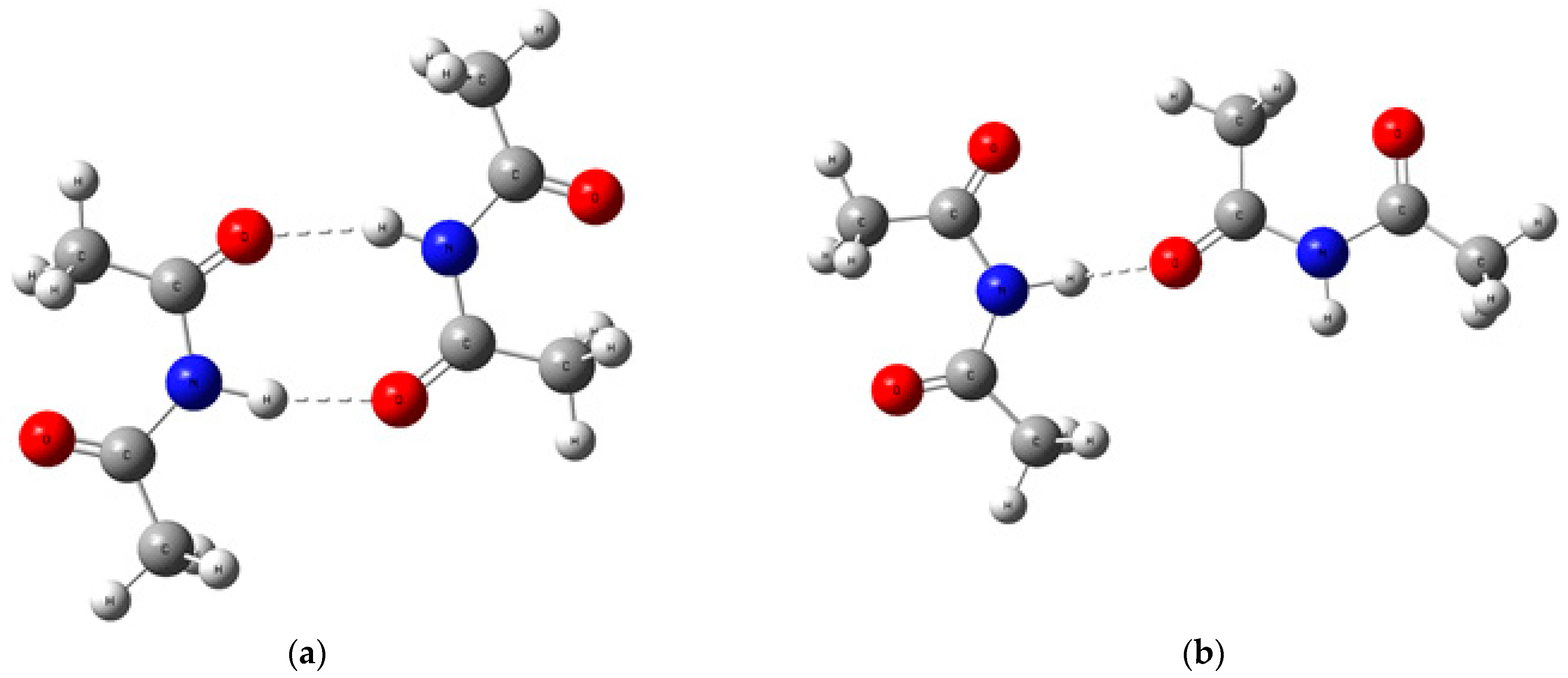
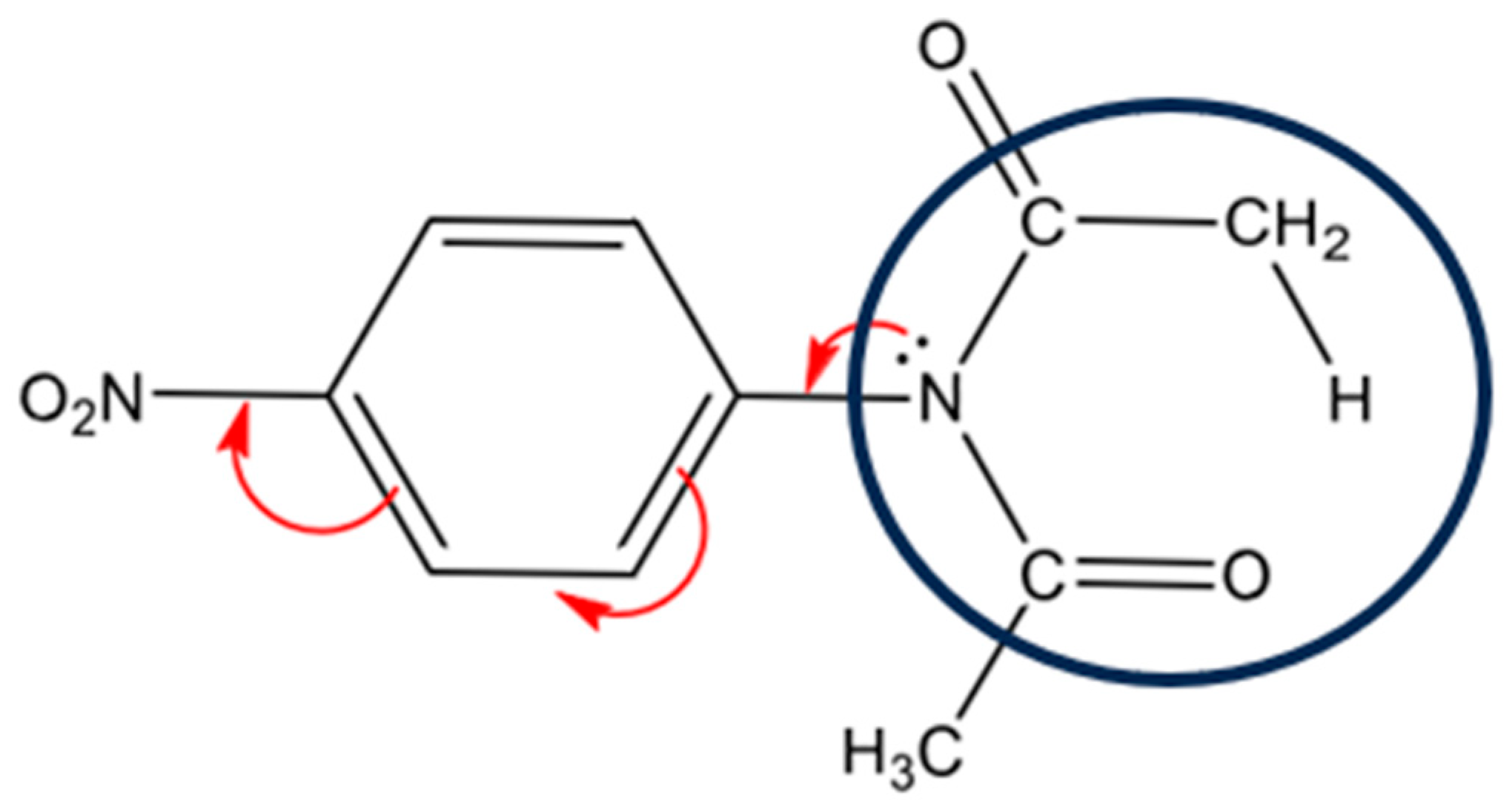
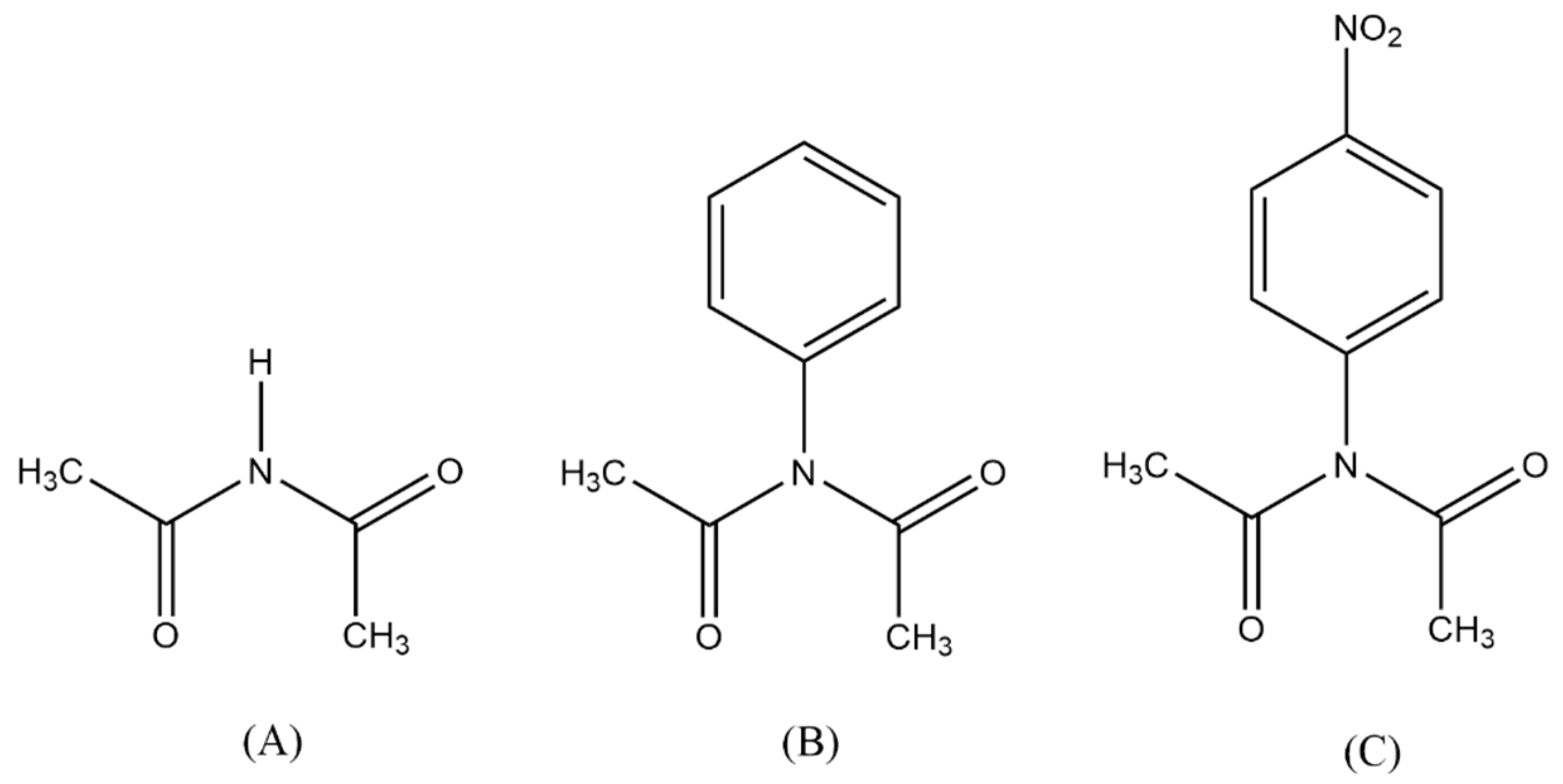
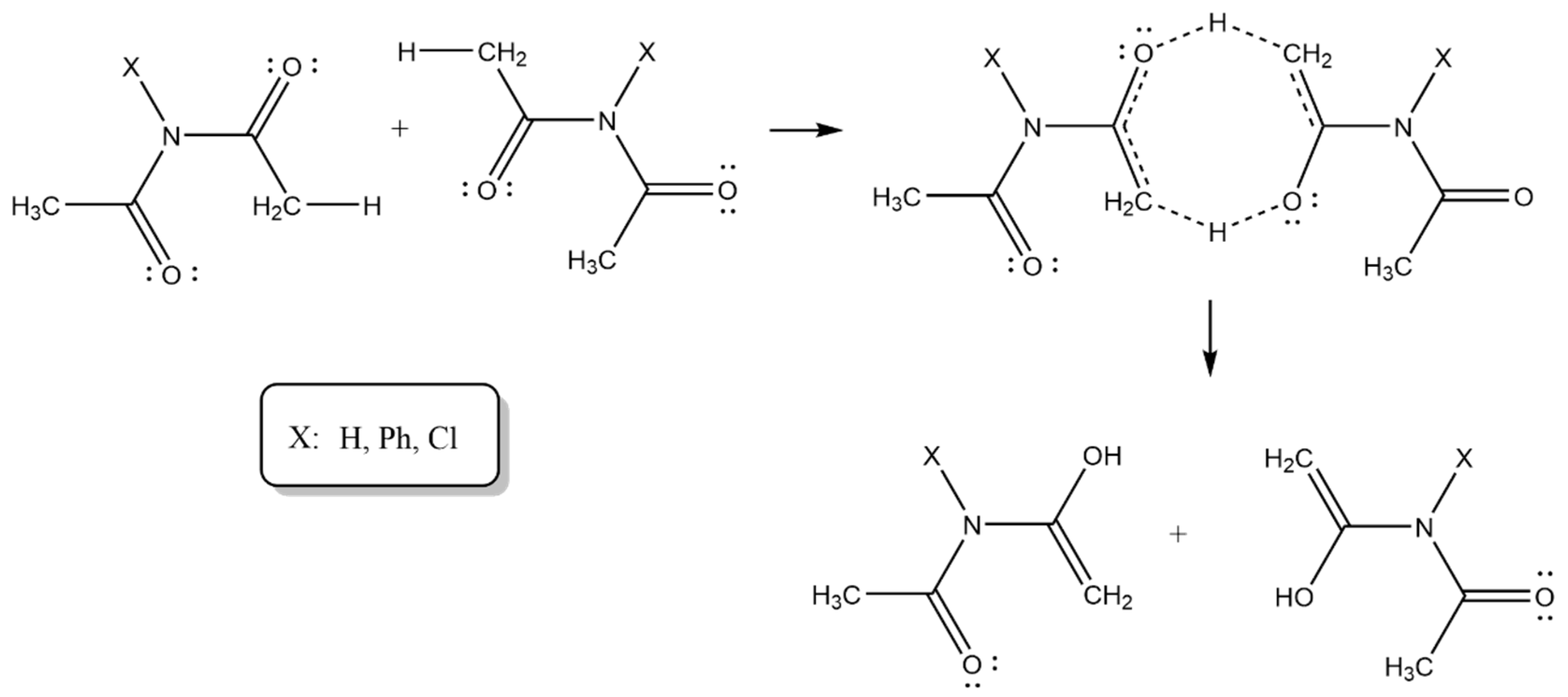
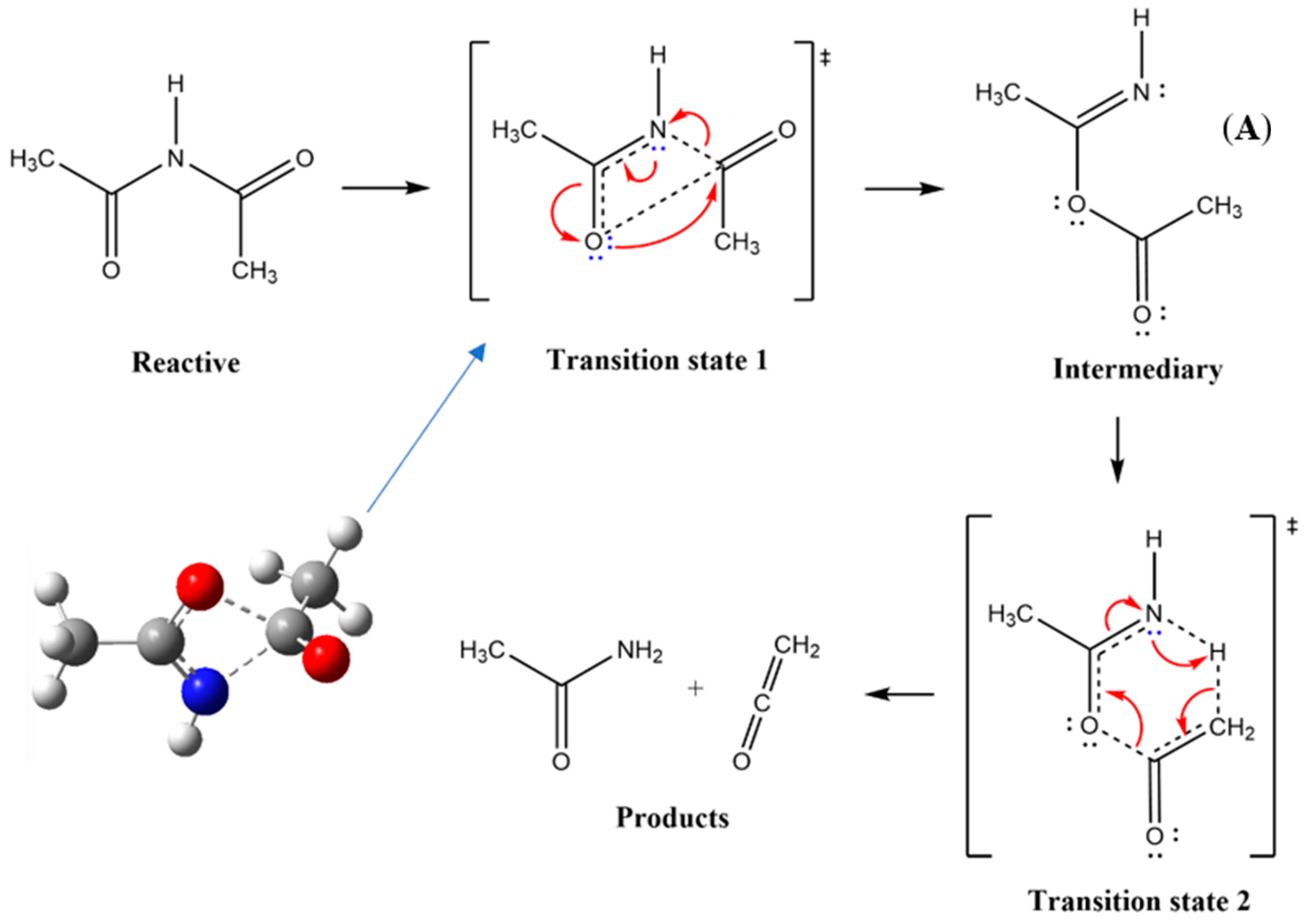


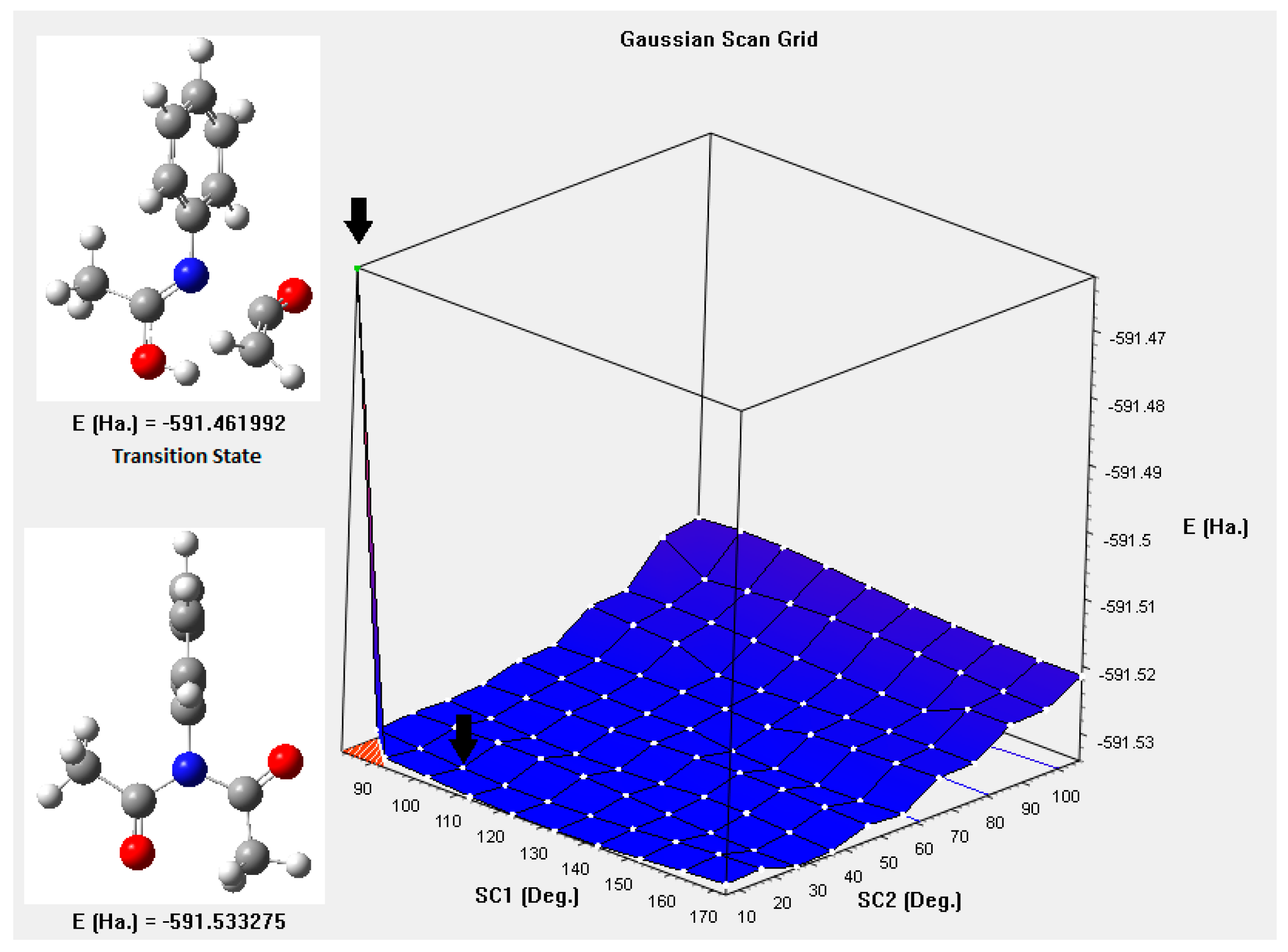
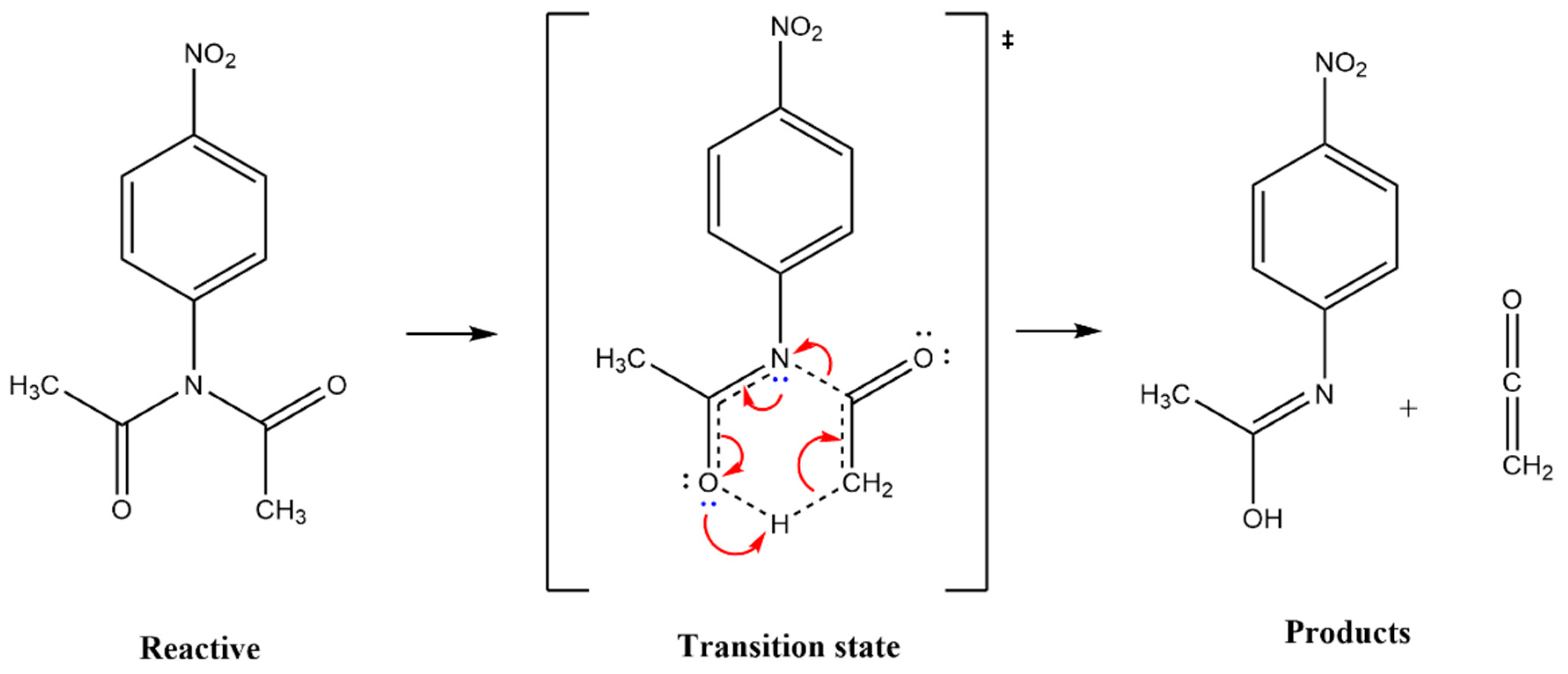
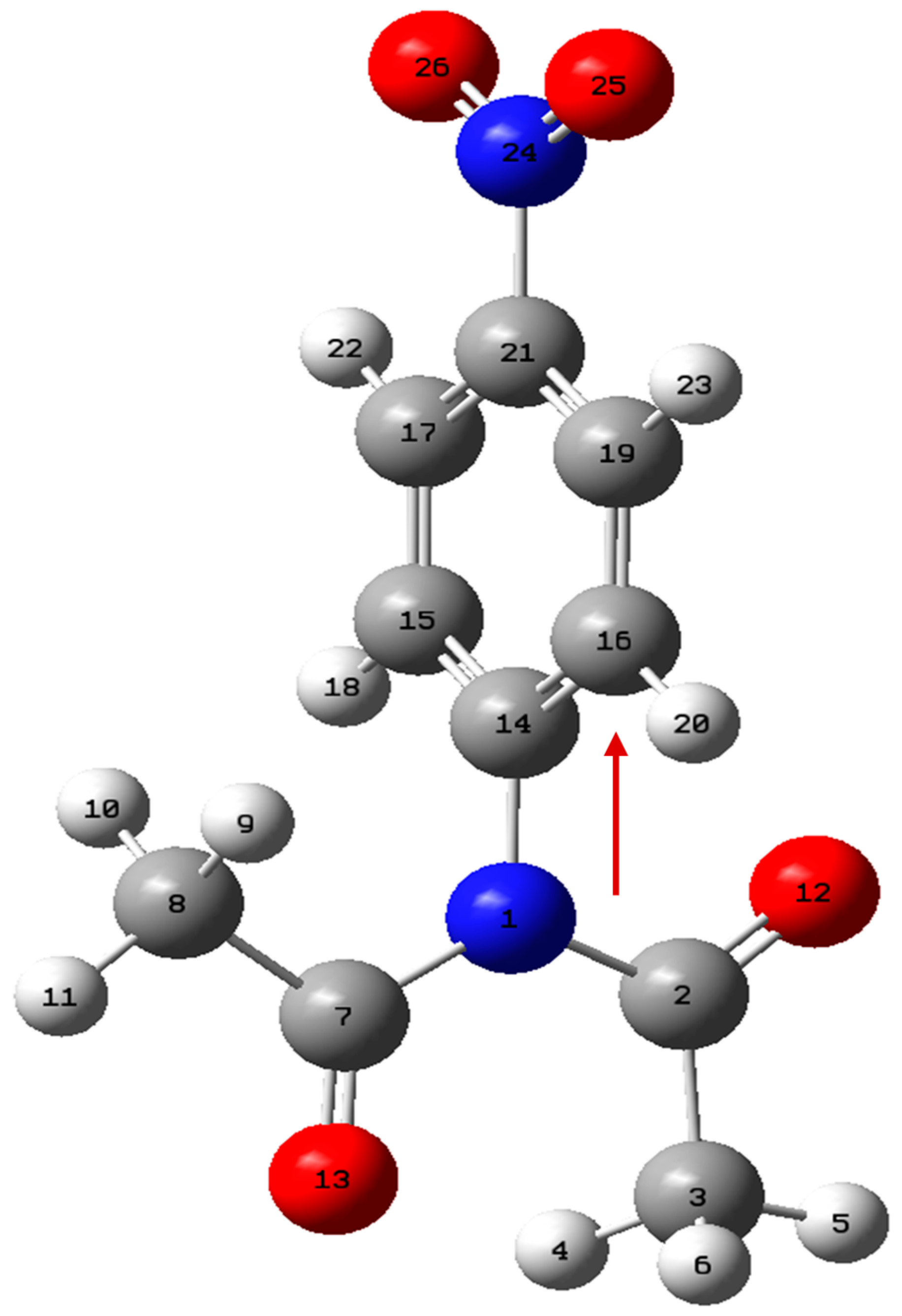

| X | Ea (kJ mol−1) |
|---|---|
| Hydrogen | 151.3 ± 2.7 |
| Phenyl | 185.7 ± 7.5 |
| 4-nitrophenyl | 192.0 |
| Properties | ΔG (kJ/mol) | ΔS (J/Kmol) | Ea (kJ/mol) | |
|---|---|---|---|---|
| Basis Set | ||||
| B3Pw91 | 6-311+G(3df,2p) | 163.67 | −18.00 | 155.34 |
| 6-311+G(3df,2p) * | 164.30 | −17.10 | 156.52 | |
| def2-TZVP | 165.00 | −17.67 | 159.39 | |
| X3LYP | def2-TZVP | 169.02 | −17.77 | 163.35 |
| 6-311+G(3df,2p) | 167.83 | −17.10 | 162.56 | |
| B1LYP | def2-TZVP | 172.22 | −17.66 | 166.62 |
| 6-311+G(3df,2p) | 171.19 | −17.12 | 163.39 | |
| LC-BLYP | def2-TZVP | 186.757 | −18.00 | 180.95 |
| 6-311+G(3df,2p) | 185.84 | −17.94 | 177.55 | |
| CAM-B3LYP | def2-TZVP | 176.625 | −17.70 | 175.99 |
| 6-311+G(3df,2p) | 175.65 | −17.24 | 167.78 | |
| ωB97X-D | def2-TZVP | 177.733 | −18.16 | 171.84 |
| M062-X | def2-TZVP | 175.415 | −13.72 | 172.17 |
| Properties. | ΔG (kJ/mol) | ΔS (J/Kmol) | Ea (kJ/mol) |
|---|---|---|---|
| Experimental | 165.05 | −31.23 | 154.0 |
| X3LYP | 189.00 | −14.00 | 185.61 |
| ωB97X-D | 201.96 | −10.55 | 200.62 |
| M062-X | 191.44 | −6.57 | 192.49 |
| LC-BLYP | 216.88 | −8.13 | 216.99 |
| CAM-B3LYP | 199.59 | −11.61 | 202.61 |
| B3PW91 | 187.67 | −11.53 | 185.75 |
| B1LYP | 192.30 | −14.88 | 188.37 |
| NX(COCH3)2 X=Cl | |||
| X3LYP | 158.04 | −15.30 | 153.85 |
| (158.02) * | (−17.07) * | (152.75) * | |
| B1LYP | 161.95 | −15.61 | 157.58 |
| NX(COCH3)2 X=CH3 | |||
| B1LYP | 167.82 | −7.07 | 168.57 |
| Tipo | Degrees | |||||||||
| 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | |
| Labels | NBO charges | |||||||||
| N1 | −0.557 | −0.557 | −0.556 | −0.554 | −0.552 | −0.551 | −0.550 | −0.549 | −0.550 | −0.551 |
| C14 | 0.152 | 0.152 | 0.150 | 0.150 | 0.150 | 0.150 | 0.151 | 0.150 | 0.153 | 0.154 |
| Bond | IBSI | |||||||||
| N1-C14 | 1.099 | 1.109 | 1.135 | 1.159 | 1.181 | 1.210 | 1.211 | 1.224 | 1.252 | 1.272 |
| NBO charges | ||||||||||
| C2 | 0.715 | 0.715 | 0.714 | 0.714 | 0.714 | 0.715 | 0.716 | 0.721 | 0.728 | 0.737 |
| Bond | IBSI | |||||||||
| N1-C2 | 1.204 | 1.203 | 1.201 | 1.194 | 1.185 | 1.170 | 1.150 | 1.120 | 1.081 | 1.048 |
| NBO charges | ||||||||||
| C7 | 0.721 | 0.721 | 0.722 | 0.722 | 0.722 | 0.722 | 0.721 | 0.719 | 0.715 | 0.708 |
| Bond | IBSI | |||||||||
| N1-C7 | 1.192 | 1.192 | 1.192 | 1.196 | 1.199 | 1.199 | 1.203 | 1.214 | 1.234 | 1.265 |
| Parameters | ΔG (kJ/mol) | ΔS (J/Kmol) | Ea (kJ/mol) |
|---|---|---|---|
| Experimental | 189.11 | −14.00 | 185.70 |
| B1LYP | |||
| 6-31G | 175.79 | −1.51 | 177.36 |
| 6-311G | 167.19 | −5.34 | 166.46 |
| 6-31G(d,) | 178.14 | −7.17 | 176.31 |
| 6-31+G(d) | 175.14 | −7.38 | 173.19 |
| 6-31G+G(d,p) | 161.58 | −5.81 | 160.57 |
| 6-31G+G(d,p) BSSE | 168.46 | −7.88 | 166.21 |
| def2-TZVP | 160.79 | −22.36 | 152.37 |
| B3Pw91 | |||
| 6-31G | 171.39 | 17.61 | 186.95 |
| 6-31G(d) | 173.54 | −0.76 | 178.07 |
| 6-311+G(2d,2p) | 154.48 | 1.36 | 160.29 |
| 6-311+G(3df,2p) | 151.98 | 3.27 | 156.42 |
| LC-BLYP | |||
| def2-TZVP | 183.98 | −4.14 | 186.48 |
| Parameters | ΔG (kJ/mol) | ΔS (J/Kmol) | Ea (kJ/mol) |
|---|---|---|---|
| Experimental | 189.11 | −14.00 | 185.70 |
| p-nitro | |||
| X3LYP | 157.110 | −22.97 | 148.32 |
| B3Pw91 | 294.038 | −11.32 | 292.26 |
| LC-BLYP | 182.877 | −8.92 | 182.51 |
| m-nitro | |||
| X3LYP | 158.176 | −24.66 | 148.38 |
| B3Pw91 | 294.636 | −9.67 | 293.83 |
| LC-BLYP | 183.113 | −7.49 | 183.61 |
| Point | Donor NBO (i) | Acceptor NBO (j) | E (2) kcal/mol | IBSI | |||
|---|---|---|---|---|---|---|---|
| N1-C2 | N1-C7 | N1-C14 | N24-C21 | ||||
| 01 (BTS) | LP (1)N1 | BD*(2) C2-O12 | 15.70 | 1.030 | |||
| LP (1)N1 | BD*(1) C14-C15 | 4.75 | 1.216 | ||||
| LP (3)O26 | BD*(2) N24-O25 | 173.79 | 1.105 | ||||
| 02 | LP (1)N1 | BD*(2) C2-O12 | 14.88 | 0.991 | |||
| LP (1)N1 | BD*(1) C14-C15 | 4.88 | 1.227 | ||||
| LP (3)O26 | BD*(2) N24-O25 | 173.63 | 1.105 | ||||
| 03 | LP (1)N1 | BD*(2) C2-O12 | 12.45 | 0.877 | |||
| LP (1)N1 | BD*(1) C14-C15 | 5.02 | 1.238 | ||||
| LP (3)O26 | BD*(2) N24-O25 | 173.51 | 1.104 | ||||
| 04 | LP (1)N1 | BD*(2) C2-O12 | 10.26 | 0.787 | |||
| LP (1)N1 | BD*(1) C14-C15 | 4.94 | 1.245 | ||||
| LP (3)O26 | BD*(2) N24-O25 | 173.6 | 1.102 | ||||
| (ST) | LP (1)N1 | BD*(1) C7–C8 | 9.75 | 1.621 | |||
| LP (1)N1 | BD*(2) C14-C16 | 16.81 | 1.293 | ||||
| LP (3)O26 | BD*(2) N24-O25 | 172.62 | 1.107 | ||||
| 06 (ATS) | LP (1)N1 | BD*(1) C7-O13 | 8.62 | 1.689 | |||
| LP (1)N1 | BD*(1) C14-C15 | 19.04 | 1.328 | ||||
| LP (3)O26 | BD*(2) N24-O25 | 170.83 | 1.120 | ||||
| 07 | LP (1)N1 | BD*(1) C7-O13 | 8.86 | 1.692 | |||
| LP (1)N1 | BD*(1) C14-C15 | 19.22 | 1.325 | ||||
| LP (3)O26 | BD*(2) N24-O25 | 170.69 | 1.120 | ||||
| 08 | LP (1)N1 | BD*(1) C7-O13 | 9.09 | 1.692 | |||
| LP (1)N1 | BD*(1) C14-C15 | 19.30 | 1.317 | ||||
| LP (3)O26 | BD*(2) N24-O25 | 170.59 | 1.120 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabidia Torres, O.L.; Loroño, M.; Paz Rojas, J.L.; Garrido Schaeffer, C.J.A.; Linares Fuentes, T.C.; Cordova Sintjago, T.C. Computational Study of the Kinetics and Mechanisms of Gas-Phase Decomposition of N-Diacetamides Using Density Functional Theory. Molecules 2024, 29, 3833. https://doi.org/10.3390/molecules29163833
Gabidia Torres OL, Loroño M, Paz Rojas JL, Garrido Schaeffer CJA, Linares Fuentes TC, Cordova Sintjago TC. Computational Study of the Kinetics and Mechanisms of Gas-Phase Decomposition of N-Diacetamides Using Density Functional Theory. Molecules. 2024; 29(16):3833. https://doi.org/10.3390/molecules29163833
Chicago/Turabian StyleGabidia Torres, Oswaldo Luis, Marcos Loroño, Jose Luis Paz Rojas, Cecilio Julio Alberto Garrido Schaeffer, Thais Cleofe Linares Fuentes, and Tania Cecilia Cordova Sintjago. 2024. "Computational Study of the Kinetics and Mechanisms of Gas-Phase Decomposition of N-Diacetamides Using Density Functional Theory" Molecules 29, no. 16: 3833. https://doi.org/10.3390/molecules29163833
APA StyleGabidia Torres, O. L., Loroño, M., Paz Rojas, J. L., Garrido Schaeffer, C. J. A., Linares Fuentes, T. C., & Cordova Sintjago, T. C. (2024). Computational Study of the Kinetics and Mechanisms of Gas-Phase Decomposition of N-Diacetamides Using Density Functional Theory. Molecules, 29(16), 3833. https://doi.org/10.3390/molecules29163833









