Quantitative Analysis of Pb in Soil Using Laser-Induced Breakdown Spectroscopy Based on Signal Enhancement of Conductive Materials
Abstract
1. Introduction
2. Results and Discussion
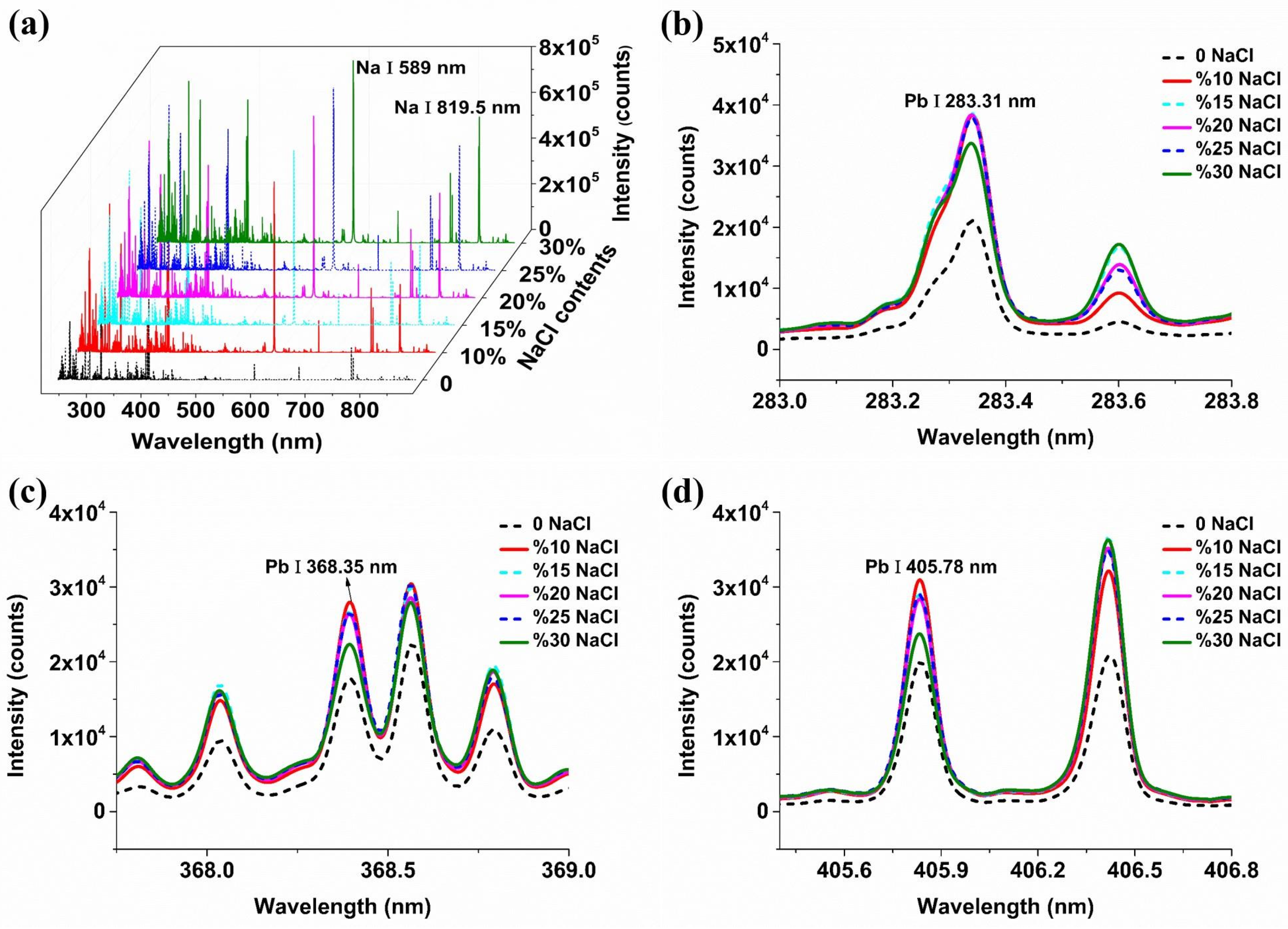
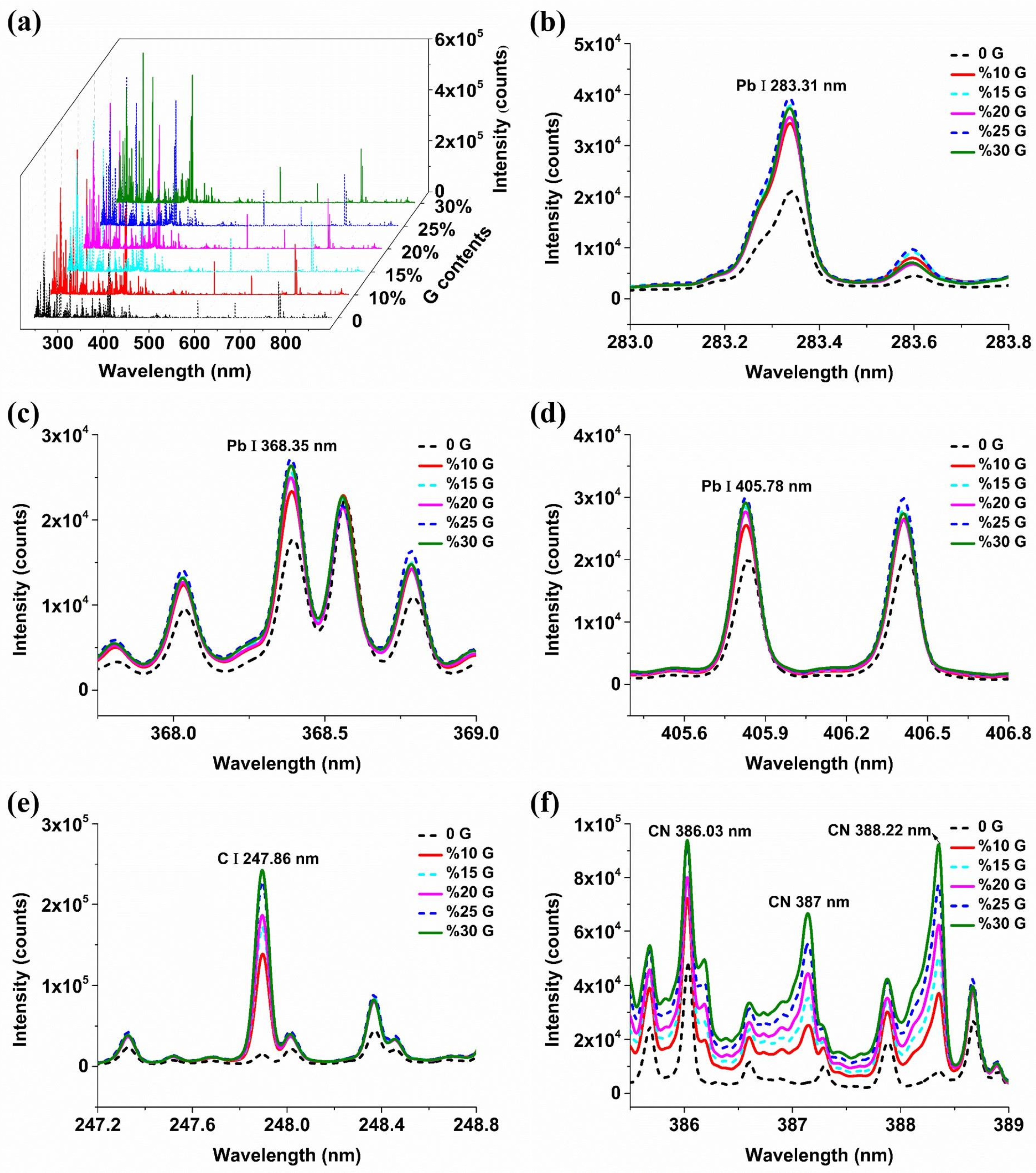
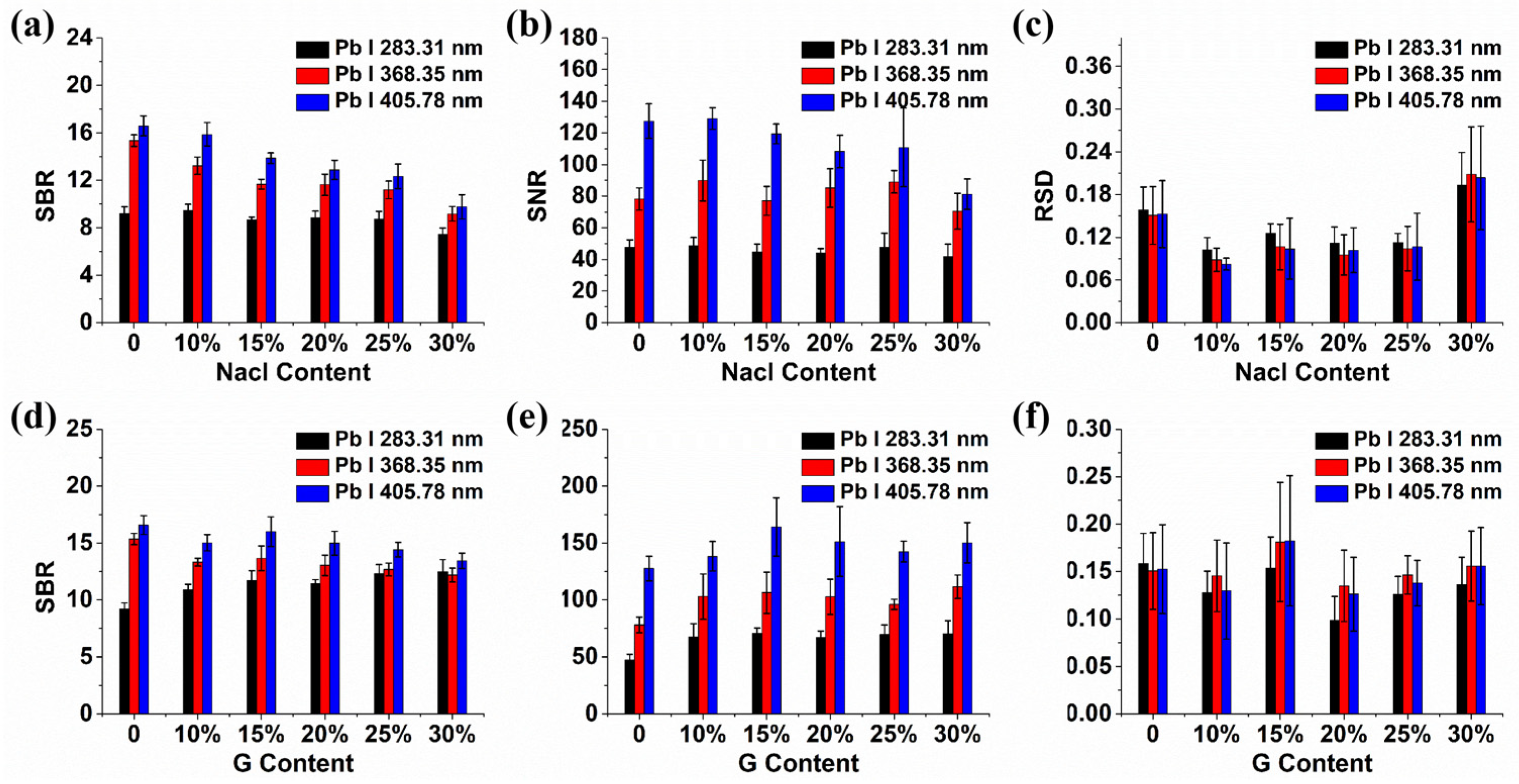
2.1. The Influence of Conductive Materials on Spectral Signals
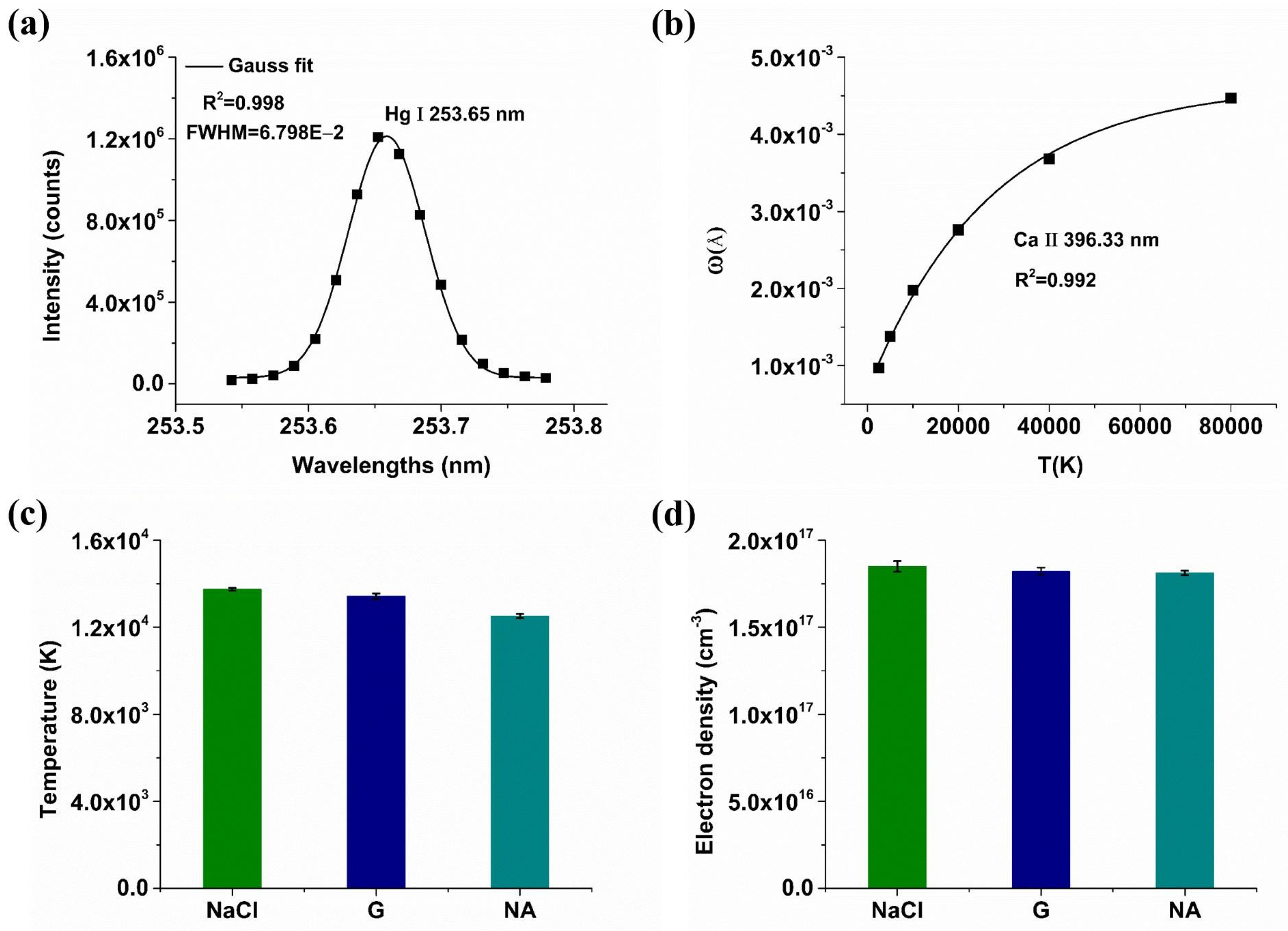
2.2. Mechanism Analysis of Enhancement of Spectral Signals by Conductive Materials
2.3. Quantitative Determination of Pb Based on Conductive Materials
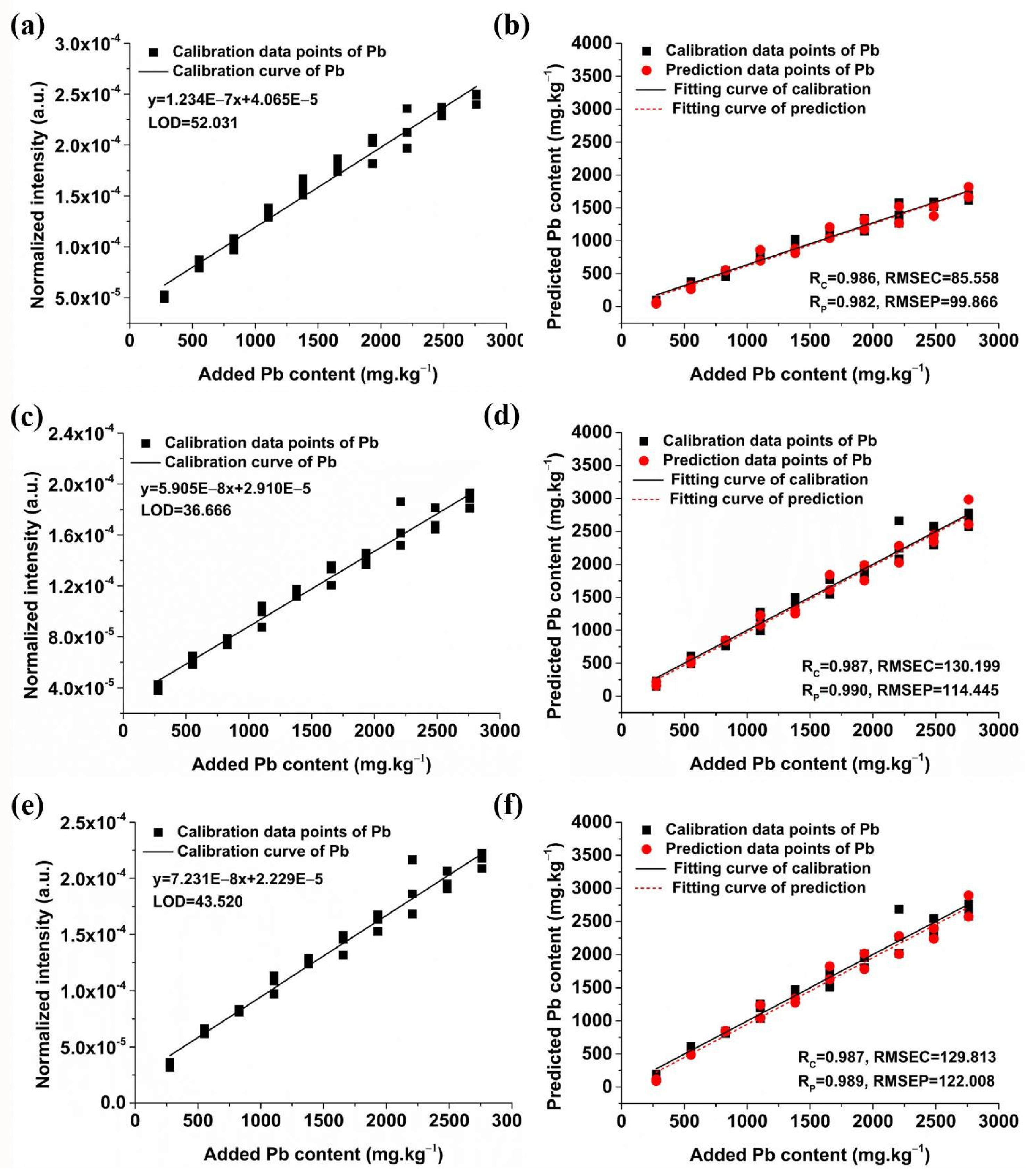
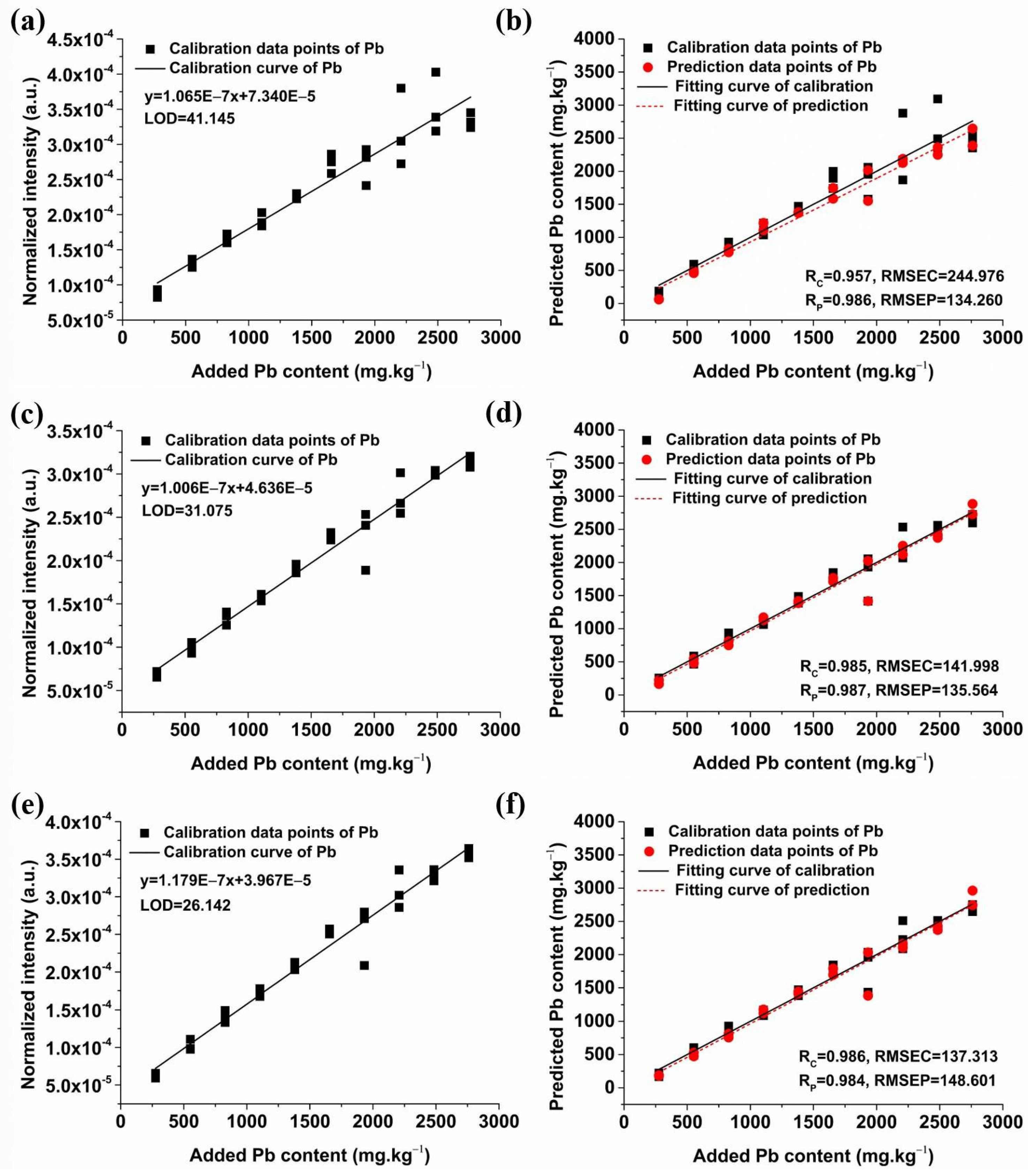
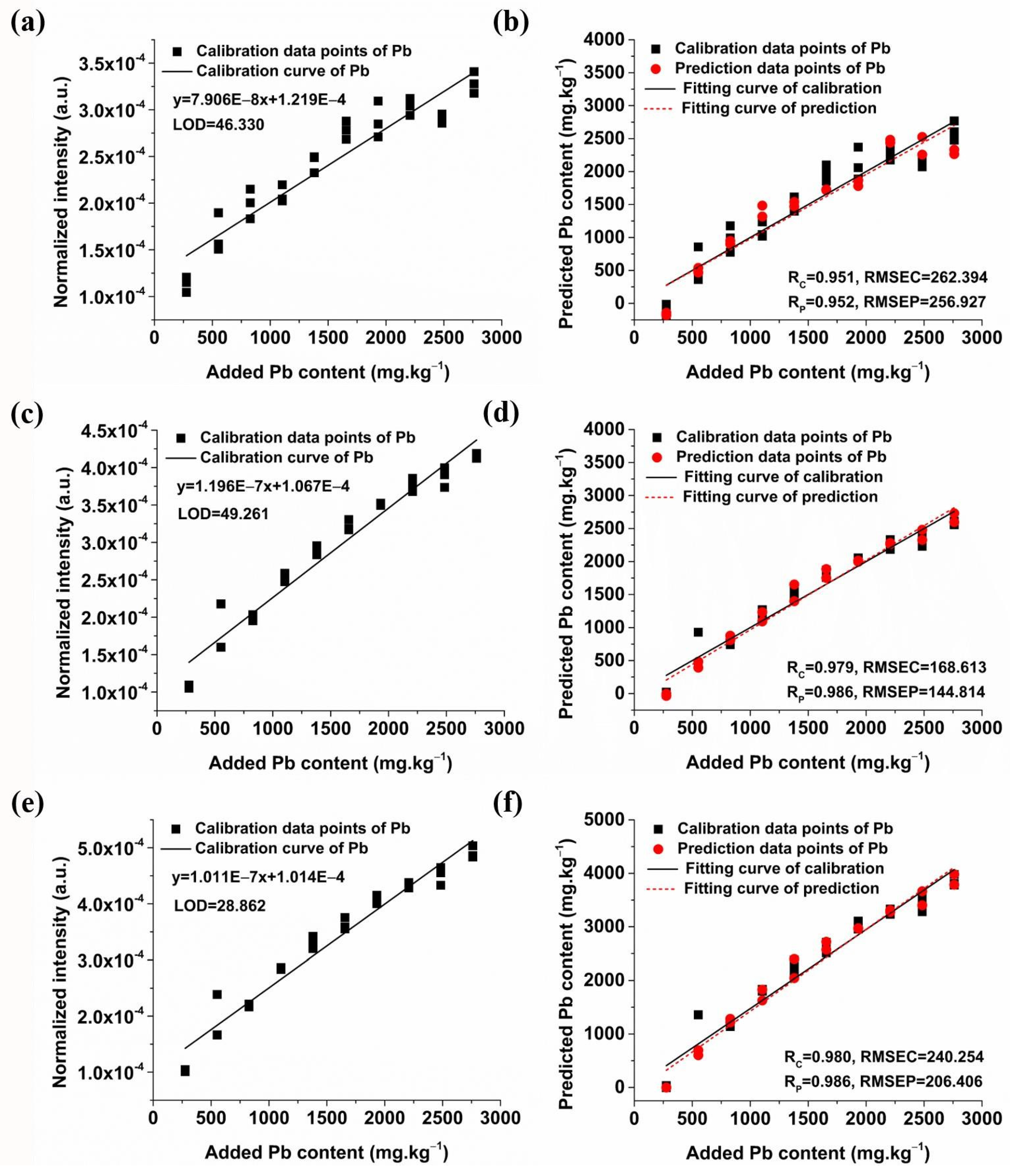
2.3.1. Quantitative Analysis of Pb Based on Univariate Models
2.3.2. Quantitative Analysis of Pb Based on Multivariate Models
3. Materials and Methods
3.1. Soil Samples
3.2. Spectral Acquisition
3.3. Data Analysis
3.3.1. Data Preprocessing
3.3.2. Quantitative Analysis Methods
3.4. Software Tools
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Basset, C. Soil security: The cornerstone of national security in an era of global disruptions. Soil Secur 2024, 16, 100154. [Google Scholar] [CrossRef]
- Telo da Gama, J. The Role of Soils in Sustainability, Climate Change, and Ecosystem Services: Challenges and Opportunities. Ecologies 2023, 4, 552–567. [Google Scholar] [CrossRef]
- Filote, C.; Roșca, M.; Hlihor, R.; Cozma, P.; Simion, I.; Apostol, M.; Gavrilescu, M. Sustainable Application of Biosorption and Bioaccumulation of Persistent Pollutants in Wastewater Treatment: Current Practice. Processes 2021, 9, 1696. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, T.; Gao, Y.; Li, D.; Cui, R.; Gu, C.; Wang, L.; Sun, H. Quantitative identification of the co-exposure effects of e-waste pollutants on human oxidative stress by explainable machine learning. J. Hazard. Mater. 2024, 466, 133560. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.; Singh, R.; Upreti, P.; Yadav, R.K. Geo-statistical assessment of soil quality and identification of Heavy metal contamination using Integrated GIS and Multivariate statistical analysis in Industrial region of Western India. Environ. Technol. Innov. 2022, 28, 102646. [Google Scholar] [CrossRef]
- Alengebawy, A.; Abdelkhalek, S.T.; Qureshi, S.R.; Wang, M.Q. Heavy Metals and Pesticides Toxicity in Agricultural Soil and Plants: Ecological Risks and Human Health Implications. Toxics 2021, 9, 42. [Google Scholar] [CrossRef]
- Jin, M.; Yuan, H.; Liu, B.; Peng, J.; Xu, L.; Yang, D. Review of the distribution and detection methods of heavy metals in the environment. Anal. Methods 2020, 12, 5747–5766. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, T.; Li, H. Application of laser-induced breakdown spectroscopy (LIBS) in environmental monitoring. Spectrochim. Acta B At. Spectrosc. 2021, 181, 106218. [Google Scholar] [CrossRef]
- Goncharova, I.; Guichaoua, D.; Taboukhat, S.; Tarbi, A.; Chtouki, T.; Erguig, H.; Sahraoui, B. Laser-induced breakdown spectroscopy application for heavy metals detection in water: A review. Spectrochim. Acta B At. Spectrosc. 2024, 217, 106943. [Google Scholar] [CrossRef]
- Meng, Y.; Li, H.; Wang, Y.; Lv, H.; Wang, C.; Wang, F.; Fang, L. Influence of Planar Mirror Confinement and Temperature Control upon the Elemental Analysis of Soil by Laser-Induced Breakdown Spectroscopy. Anal. Lett. 2023, 56, 2792–2802. [Google Scholar] [CrossRef]
- Park, K.; Cho, G.; Kwak, J.-H. Development of an Aerosol Focusing-Laser Induced Breakdown Spectroscopy (Aerosol Focusing-LIBS) for Determination of Fine and Ultrafine Metal Aerosols. Aerosol Sci. Technol. 2009, 43, 375–386. [Google Scholar] [CrossRef]
- Knight, A.K.; Scherbarth, N.L.; Cremers, D.A.; Ferris, M.J. Characterization of laser-induced breakdown spectroscopy (LIBS) for application to space exploration. Appl. Spectrosc. 2000, 54, 331–340. [Google Scholar] [CrossRef]
- Trejos, T.; Vander Pyl, C.; Menking-Hoggatt, K.; Alvarado, A.L.; Arroyo, L.E. Fast identification of inorganic and organic gunshot residues by LIBS and electrochemical methods. Forensic Chem. 2018, 8, 146–156. [Google Scholar] [CrossRef]
- Chen, T.; Sun, L.; Yu, H.; Zeng, P.; Qi, L. Online Fe grade monitoring of iron ore slurry by Morse wavelet transform and lightweight convolutional neural network based on LIBS. Spectrochim. Acta B At. Spectrosc. 2023, 210, 106821. [Google Scholar] [CrossRef]
- Nicolodelli, G.; Cabral, J.; Menegatti, C.R.; Marangoni, B.; Senesi, G.S. Recent advances and future trends in LIBS applications to agricultural materials and their food derivatives: An overview of developments in the last decade (2010–2019). Part I. Soils and fertilizers. Trends Anal. Chem. 2019, 115, 70–82. [Google Scholar] [CrossRef]
- Vaisakh, P.S.; Adarsh, U.K.; Amrutha, K.; Warrier, A.K.; Kartha, V.B.; Unnikrishnan, V.K. Integrated LIBS-Raman spectroscopy: A comprehensive approach to monitor microplastics and heavy metal contamination in water resources. Environ. Res. 2023, 231, 116198. [Google Scholar] [CrossRef]
- Agresti, J.; Indelicato, C.; Perotti, M.; Moreschi, R.; Osticioli, I.; Cacciari, I.; Mencaglia, A.A.; Siano, S. Quantitative Compositional Analyses of Calcareous Rocks for Lime Industry Using LIBS. Molecules 2022, 27, 1813. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Huang, J.; Chen, R.; You, Z.; Peng, J.; Shi, Q.; Li, G.; Liu, F. Chromium in soil detection using adaptive weighted normalization and linear weighted network framework for LIBS matrix effect reduction. J. Hazard. Mater. 2023, 448, 130885. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Tian, Y.; Gao, L.; Niu, Y.; Zhang, T.; Li, H.; Zhang, Y.; Yue, Z.; Delepine-Gilon, N.; Yu, J. Machine Learning Allows Calibration Models to Predict Trace Element Concentration in Soils with Generalized LIBS Spectra. Sci. Rep. 2019, 9, 11363. [Google Scholar] [CrossRef]
- Zhao, S.; Song, C.; Gao, X.; Lin, J. Quantitative analysis of Pb in soil by femtosecond-nanosecond double-pulse laser-induced breakdown spectroscopy. Results Phys. 2019, 15, 102736. [Google Scholar] [CrossRef]
- Ren, J.; Yang, Z.; Zhao, Y.; Yu, K. Collinear double-pulse laser-induced breakdown spectroscopy based Cd profiling in the soil. Opt. Express 2022, 30, 37711–37726. [Google Scholar] [CrossRef]
- Zhao, S.; Gao, X.; Chen, A.; Lin, J. Effect of spatial confinement on Pb measurements in soil by femtosecond laser-induced breakdown spectroscopy. Appl. Phys. B 2019, 126, 7. [Google Scholar] [CrossRef]
- Fu, X.; Li, G.; Tian, H.; Dong, D. Detection of cadmium in soils using laser-induced breakdown spectroscopy combined with spatial confinement and resin enrichment. RSC Adv. 2018, 8, 39635–39640. [Google Scholar] [CrossRef]
- Akhtar, M.; Jabbar, A.; Ahmed, N.; Mahmood, S.; Umar, Z.A.; Ahmed, R.; Baig, M.A. Analysis of lead and copper in soil samples by laser-induced breakdown spectroscopy under external magnetic field. Appl. Phys. B 2019, 125, 110. [Google Scholar] [CrossRef]
- Akhtar, M.; Jabbar, A.; Mehmood, S.; Ahmed, N.; Ahmed, R.; Baig, M.A. Magnetic field enhanced detection of heavy metals in soil using laser induced breakdown spectroscopy. Spectrochim. Acta B At. Spectrosc. 2018, 148, 143–151. [Google Scholar] [CrossRef]
- Liu, X.; Liu, F.; Huang, W.; Peng, J.; Shen, T.; He, Y. Quantitative Determination of Cd in Soil Using Laser-Induced Breakdown Spectroscopy in Air and Ar Conditions. Molecules 2018, 23, 2492. [Google Scholar] [CrossRef]
- Xu, X.; Li, A.; Wang, X.; Ding, C.; Qiu, S.; He, Y.; Lu, T.; He, F.; Zou, B.; Liu, R. The high-accuracy prediction of carbon content in semi-coke by laser-induced breakdown spectroscopy. J. Anal. At. Spectrom. 2020, 35, 984–992. [Google Scholar] [CrossRef]
- Goueguel, C.; Singh, J.P.; McIntyre, D.L.; Jain, J.; Karamalidis, A.K. Effect of sodium chloride concentration on elemental analysis of brines by laser-induced breakdown spectroscopy (LIBS). Appl. Spectrosc. 2014, 68, 213–221. [Google Scholar] [CrossRef]
- Liu, X.; Lin, Q.; Tian, Y.; Liao, W.; Yang, T.; Qian, C.; Zhang, T.; Duan, Y. Metal-chelate induced nanoparticle aggregation enhanced laser-induced breakdown spectroscopy for ultra-sensitive detection of trace metal ions in liquid samples. J. Anal. At. Spectrom. 2020, 35, 188–197. [Google Scholar] [CrossRef]
- Huang, Y.; Harilal, S.S.; Bais, A.; Hussein, A.E. Progress toward machine learning methodologies for laser-induced breakdown spectroscopy with an emphasis on soil analysis. IEEE Trans. Plasma Sci. 2023, 51, 1729–1749. [Google Scholar] [CrossRef]
- Zeng, L.; Wu, M.; Chen, S.; Zheng, R.; Rao, Y.; He, X.; Duan, Y.; Wang, X. Direct and sensitive determination of Cu, Pb, Cr and Ag in soil by laser ablation microwave plasma torch optical emission spectrometry. Talanta 2022, 246, 123516. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Lin, P.; Ma, S.; Xu, F.; Wen, X.; Fu, X.; Dong, D. Decreasing the effect of soil particle size on heavy metal measurement stability using a method involving laser-induced breakdown spectroscopy and solid-phase conversion. J. Anal. At. Spectrom. 2024, 39, 1087–1093. [Google Scholar] [CrossRef]
- Zhong, L.; Murphy, A.B.; Wang, X.; Rong, M. Calculation of two-temperature plasma composition: II. Consideration of condensed phases. J. Phys. D Appl. Phys. 2020, 53, 065203. [Google Scholar] [CrossRef]
- Wang, K.; Su, M.; Cao, S.; Ma, P.; Sun, D.; Min, Q.; Dong, C. Diagnosis of electron temperature and density in the early stage of laser-produced Si plasma expansion. Phys. Plasmas 2020, 27, 063513. [Google Scholar] [CrossRef]
- Inoue, K.; Takahashi, S.; Sakakibara, N.; Toko, S.; Ito, T.; Terashima, K. Spatiotemporal optical emission spectroscopy to estimate electron density and temperature of plasmas in solution. J. Phys. D Appl. Phys. 2020, 53, 235202. [Google Scholar] [CrossRef]
- Dojić, D.; Skočić, M.; Bukvić, S.; Djeniže, S. Stark broadening measurements of Al II, Al III and He I 388.86 nm spectral lines at high electron densities. Spectrochim. Acta B At. Spectrosc. 2020, 166, 105816. [Google Scholar] [CrossRef]
- Griem, H. Plasma Spectroscopy, 1st ed.; McGraw-Hill Book Company: New York, NY, USA, 1965; pp. 498–499. [Google Scholar]
- Fikry, M.; Tawfik, W.; Omar, M.M. Investigation on the effects of laser parameters on the plasma profile of copper using picosecond laser induced plasma spectroscopy. Opt. Quant. Electron. 2020, 52, 249. [Google Scholar] [CrossRef]
- Rhif, M.; Ben Abbes, A.; Farah, I.R.; Martínez, B.; Sang, Y. Wavelet Transform Application for/in Non-Stationary Time-Series Analysis: A Review. Appl. Sci. 2019, 9, 1345. [Google Scholar] [CrossRef]
- Zheng, Y.; Ban, D.; Li, N.; Song, J.; Zhang, J.; Luo, Y.; Guan, J.; Zhang, C.; Xue, C. Performance improvement of underwater LIBS qualitative and quantitative analysis by irradiating with long nanosecond pulses. Analyst 2024, 149, 768–777. [Google Scholar] [CrossRef]
- Lin, P.; Wen, X.; Ma, S.; Liu, X.; Xiao, R.; Gu, Y.; Chen, G.; Han, Y.; Dong, D. Rapid identification of the geographical origins of crops using laser-induced breakdown spectroscopy combined with transfer learning. Spectrochim. Acta B At. Spectrosc. 2023, 206, 106729. [Google Scholar] [CrossRef]
- Guezenoc, J.; Gallet-Budynek, A.; Bousquet, B. Critical review and advices on spectral-based normalization methods for LIBS quantitative analysis. Spectrochim. Acta B At. Spectrosc. 2019, 160, 105688. [Google Scholar] [CrossRef]
- Wang, C.; Li, H.; Sun, J.; Lü, H.; Wang, F.; Zhang, R. Study on enrichment characteristics of Chinese herbal medicine based on LIBS technology. Optoelectron. Lett. 2023, 19, 88–94. [Google Scholar] [CrossRef]
- Peng, J.; Liu, Y.; Ye, L.; Jiang, J.; Zhou, F.; Liu, F.; Huang, J. Fast detection of minerals in rice leaves under chromium stress based on laser-induced breakdown spectroscopy. Sci. Total Environ. 2023, 860, 160545. [Google Scholar] [CrossRef]
- Sharma, N.; Singh, V.K.; Lee, Y.; Kumar, S.; Rai, P.K.; Pathak, A.K.; Singh, V.K. Analysis of Mineral Elements in Medicinal Plant Samples Using LIBS and ICP-OES. At. Spectrosc. 2020, 41, 234–241. [Google Scholar] [CrossRef]
- Wang, H.; Chu, X.; Chen, P.; Li, J.; Liu, D.; Xu, Y. Partial least squares regression residual extreme learning machine (PLSRR-ELM) calibration algorithm applied in fast determination of gasoline octane number with near-infrared spectroscopy. Fuel 2022, 309, 122224. [Google Scholar] [CrossRef]
- Lv, S.; Wang, J.; Wang, S.; Wang, Q.; Wang, Z.; Fang, Y.; Zhai, W.; Wang, F.; Qu, G.; Ma, W. Quantitative analysis of chlorophyll in Catalpa bungei leaves based on partial least squares regression and spectral reflectance index. Sci. Hortic. 2024, 329, 113019. [Google Scholar] [CrossRef]
- Wu, Q.; Geng, Y.; Wang, X.; Wang, D.; Yoo, C.; Liu, H. A novel deep learning framework with variational auto-encoder for indoor air quality prediction. Front. Environ. Sci. Eng. 2023, 18, 8. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Q.; Kamruzzaman, M. Portable NIR spectroscopy and PLS based variable selection for adulteration detection in quinoa flour. Food Control 2022, 138, 108970. [Google Scholar] [CrossRef]
- Lin, B.-D.; Zhang, X.-Y.; Zhang, M.; Li, H.; Lu, G.-Q. Improved genetic algorithm-based research on optimization of least square support vector machines: An application of load forecasting. Soft Comput. 2021, 25, 11997–12005. [Google Scholar] [CrossRef]
- Zhongda, T. Kernel principal component analysis-based least squares support vector machine optimized by improved grey wolf optimization algorithm and application in dynamic liquid level forecasting of beam pump. Trans. Inst. Meas. Control 2019, 42, 1135–1150. [Google Scholar] [CrossRef]
- Wang, J.; Lu, S.; Wang, S.-H.; Zhang, Y.-D. A review on extreme learning machine. Multimed. Tools Appl. 2021, 81, 41611–41660. [Google Scholar] [CrossRef]
- Li, H.; Bai, L.; Gao, W.; Xie, J.; Huang, L. Many-objective coevolutionary learning algorithm with extreme learning machine auto-encoder for ensemble classifier of feedforward neural networks. Expert Syst. Appl. 2024, 246, 123186. [Google Scholar] [CrossRef]


| Spectral Line (nm) | Spontaneous Transition Probability Aki (108 s−1) | Excitation Energy of Upper Level Ek (ev) | Statistical Weight of Upper Level gk |
|---|---|---|---|
| Ca II 315.887 | 3.10 | 7.047168 | 2 |
| Ca II 317.933 | 3.60 | 7.049550 | 4 |
| Ca II 370.603 | 0.88 | 6.467875 | 2 |
| Ca II 373.731 | 1.70 | 6.467875 | 2 |
| Ca II 393.366 | 1.47 | 3.150984 | 2 |
| Ca II 386.847 | 1.40 | 3.123349 | 2 |
| Additive | Model | Parameter | Calibration | Prediction | ||
|---|---|---|---|---|---|---|
| RC | RMSEC | RP | RMSEP | |||
| NaCl | PLSR | 4 | 0.991 | 104.477 | 0.966 | 243.311 |
| LS-SVM | (5.002 × 1011, 1.361 × 1010) | 1.000 | 3.300 × 10−4 | 0.946 | 359.569 | |
| ELM | 15 | 0.990 | 113.134 | 0.971 | 350.716 | |
| PLSR | 5 | 0.996 | 74.009 | 0.993 | 108.609 | |
| graphite | LS-SVM | (5.002 × 1011, 1.361 × 1010) | 1.000 | 4.800 × 10−4 | 0.965 | 447.346 |
| ELM | 22 | 0.994 | 85.441 | 0.954 | 299.708 | |
| NA | PLSR | 3 | 0.985 | 136.911 | 0.978 | 179.760 |
| LS-SVM | (5.002 × 1011, 1.361 × 1010) | 1.000 | 4.442 × 10−4 | 0.880 | 433.261 | |
| ELM | 21 | 0.992 | 100.431 | 0.968 | 209.882 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zheng, Q.; Liu, X.; Liu, P.; Yu, L. Quantitative Analysis of Pb in Soil Using Laser-Induced Breakdown Spectroscopy Based on Signal Enhancement of Conductive Materials. Molecules 2024, 29, 3699. https://doi.org/10.3390/molecules29153699
Li S, Zheng Q, Liu X, Liu P, Yu L. Quantitative Analysis of Pb in Soil Using Laser-Induced Breakdown Spectroscopy Based on Signal Enhancement of Conductive Materials. Molecules. 2024; 29(15):3699. https://doi.org/10.3390/molecules29153699
Chicago/Turabian StyleLi, Shefeng, Qi Zheng, Xiaodan Liu, Peng Liu, and Long Yu. 2024. "Quantitative Analysis of Pb in Soil Using Laser-Induced Breakdown Spectroscopy Based on Signal Enhancement of Conductive Materials" Molecules 29, no. 15: 3699. https://doi.org/10.3390/molecules29153699
APA StyleLi, S., Zheng, Q., Liu, X., Liu, P., & Yu, L. (2024). Quantitative Analysis of Pb in Soil Using Laser-Induced Breakdown Spectroscopy Based on Signal Enhancement of Conductive Materials. Molecules, 29(15), 3699. https://doi.org/10.3390/molecules29153699






