The Salt-Induced Diffusiophoresis of Nonionic Micelles—Does the Salt-Induced Growth of Micelles Influence Diffusiophoresis?
Abstract
1. Introduction
2. Theory
2.1. Description of Micelle Diffusiophoresis
2.2. Effect of Salt on Micellization Thermodynamics
2.3. Preferential Hydration Diffusiophoresis
2.4. Micelle Growth Diffusiophoresis
2.5. Role of Multiple Equilibrium on Micelle Brownian Mobility and Diffusiophoresis
3. Discussion
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Ha, D.; Seo, S.; Lee, K.; Kim, T. Dynamic Transport Control of Colloidal Particles by Repeatable Active Switching of Solute Gradients. Acs Nano 2019, 13, 12939–12948. [Google Scholar] [CrossRef] [PubMed]
- Frimmel, F.H.; von der Kammer, F.; Flemming, H.C. Colloidal Transport in Porous Media; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Park, S.W.; Lee, J.; Yoon, H.; Shin, S. Microfluidic Investigation of Salinity-Induced Oil Recovery in Porous Media during Chemical Flooding. Energy Fuels 2021, 35, 4885–4892. [Google Scholar] [CrossRef]
- Shin, S. Diffusiophoretic separation of colloids in microfluidic flows. Phys. Fluids 2020, 32, 15. [Google Scholar] [CrossRef]
- Dey, K.K.; Das, S.; Poyton, M.F.; Sengupta, S.; Butler, P.J.; Cremer, P.S.; Sen, A. Chemotactic separation of enzymes. ACS Nano 2014, 8, 11941–11949. [Google Scholar] [CrossRef] [PubMed]
- Abecassis, B.; Cottin-Bizonne, C.; Ybert, C.; Ajdari, A.; Bocquet, L. Boosting migration of large particles by solute contrasts. Nat. Mater. 2008, 7, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Shardt, O.; Warren, P.B.; Stone, H.A. Membraneless water filtration using CO2. Nat. Commun. 2017, 8, 15181. [Google Scholar] [CrossRef] [PubMed]
- Guha, R.; Shang, X.; Zydney, A.L.; Velegol, D.; Kumar, M. Diffusiophoresis contributes significantly to colloidal fouling in low salinity reverse osmosis systems. J. Membr. Sci. 2015, 479, 67–76. [Google Scholar] [CrossRef]
- Sear, R.P.; Warren, P.B. Diffusiophoresis in nonadsorbing polymer solutions: The Asakura-Oosawa model and stratification in drying films. Phys. Rev. E 2017, 96, 11. [Google Scholar] [CrossRef]
- Larson, R.G. Transport and deposition patterns in drying sessile droplets. AIChE J. 2014, 60, 1538–1571. [Google Scholar] [CrossRef]
- Liu, R.; Du, D.-j.; Pu, W.-f.; Zhang, J.; Fan, X.-b. Enhanced Oil Recovery Potential of Alkyl Alcohol Polyoxyethylene Ether Sulfonate Surfactants in High-Temperature and High-Salinity Reservoirs. Energy Fuels 2018, 32, 12128–12140. [Google Scholar] [CrossRef]
- Sinz, D.K.N.; Hanyak, M.; Darhuber, A.A. Self-Induced Surfactant Transport along Discontinuous Liquid-Liquid Interfaces. J. Phys. Chem. Lett. 2013, 4, 1039–1043. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Doan, V.S.; Feng, J. Osmotic Delivery and Release of Lipid-Encapsulated Molecules via Sequential Solution Exchange. Phys. Rev. Appl. 2019, 12, 8. [Google Scholar] [CrossRef]
- Wesselingh, J.A. Controlling diffusion. J. Control. Release 1993, 24, 47–60. [Google Scholar] [CrossRef]
- Zhang, H.X.; Annunziata, O. Modulation of drug transport properties by multicomponent diffusion in surfactant aqueous solutions. Langmuir 2008, 24, 10680–10687. [Google Scholar] [CrossRef]
- Shin, S.; Warren, P.B.; Stone, H.A. Cleaning by Surfactant Gradients: Particulate Removal from Porous Materials and the Significance of Rinsing in Laundry Detergency. Phys. Rev. Appl. 2018, 9, 6. [Google Scholar] [CrossRef]
- Annunziata, O.; Buzatu, D.; Albright, J.G. Protein diffusiophoresis and salt osmotic diffusion in aqueous solutions. J. Phys. Chem. B 2012, 116, 12694–12705. [Google Scholar] [CrossRef] [PubMed]
- Fahim, A.; Annunziata, O. Amplification of Salt-Induced Protein Diffusiophoresis by Varying Salt from Potassium to Sodium to Magnesium Chloride in Water. Langmuir 2020, 36, 2635–2643. [Google Scholar] [CrossRef]
- McAfee, M.S.; Zhang, H.; Annunziata, O. Amplification of salt-induced polymer diffusiophoresis by increasing salting-out strength. Langmuir 2014, 30, 12210–12219. [Google Scholar] [CrossRef]
- Velegol, D.; Garg, A.; Guha, R.; Kar, A.; Kumar, M. Origins of concentration gradients for diffusiophoresis. Soft Matter 2016, 12, 4686–4703. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.L. Colloid Transport by Interfacial Forces. Ann. Rev. Fluid Mech. 1989, 21, 61–99. [Google Scholar] [CrossRef]
- Prieve, D.C. Migration of a colloidal particle in a gradient of electrolyte concentration. Adv. Colloid Interface Sci. 1982, 16, 321–335. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Wong, T.I.; Liu, X.; Zhou, X.; Liedberg, B. Electrofocusing-enhanced localized surface plasmon resonance biosensors. Nanoscale 2015, 7, 17244–17248. [Google Scholar] [CrossRef]
- Prieve, D.C.; Malone, S.M.; Khair, A.S.; Stout, R.F.; Kanj, M.Y. Diffusiophoresis of charged colloidal particles in the limit of very high salinity. Proc. Natl. Acad. Sci. USA 2019, 116, 18257–18262. [Google Scholar] [CrossRef] [PubMed]
- Kar, A.; Guha, R.; Dani, N.; Velegol, D.; Kumar, M. Particle Deposition on Microporous Membranes Can Be Enhanced or Reduced by Salt Gradients. Langmuir 2014, 30, 793–799. [Google Scholar] [CrossRef]
- Kar, A.; Chiang, T.Y.; Rivera, I.O.; Sen, A.; Velegol, D. Enhanced Transport into and out of Dead-End Pores. Acs Nano 2015, 9, 746–753. [Google Scholar] [CrossRef]
- Leaist, D.G. The role of supporting electrolytes in protein diffusion. J. Phys. Chem. 1989, 93, 474–479. [Google Scholar] [CrossRef]
- Gosting, L.J. Measurement and interpretation of diffusion coefficients of proteins. Adv. Prot. Chem. 1956, 11, 429–554. [Google Scholar] [CrossRef]
- Albright, J.G.; Annunziata, O.; Miller, D.G.; Paduano, L.; Pearlstein, A.J. Precision measurements of binary and multicomponent diffusion coefficients in protein solutions relevant to crystal growth: Lysozyme chloride in water and aqueous NaCl at pH 4.5 and 25 degrees C-perpendicular to. J. Am. Chem. Soc. 1999, 121, 3256–3266. [Google Scholar] [CrossRef]
- McAfee, M.S.; Annunziata, O. Effect of particle size on salt-induced diffusiophoresis compared to Brownian mobility. Langmuir 2014, 30, 4916–4923. [Google Scholar] [CrossRef] [PubMed]
- McAfee, M.S.; Annunziata, O. Effects of Salting-In Interactions on Macromolecule Diffusiophoresis and Salt Osmotic Diffusion. Langmuir 2015, 31, 1353–1361. [Google Scholar] [CrossRef] [PubMed]
- Leaist, D.G. Diffusion of ionic micelles in salt-solutions—Sodium dodecyl-sulfate + sodium-chloride + water. J. Colloid Interface Sci. 1986, 111, 240–249. [Google Scholar] [CrossRef]
- Barrios, E.C.; Penino, K.V.; Annunziata, O. Diffusiophoresis of a Nonionic Micelle in Salt Gradients; Roles of Preferential Hydration and Salt-Induced Surfactant Aggregation. Int. J. Mol. Sci. 2022, 23, 13710. [Google Scholar] [CrossRef]
- Barrios, E.C.; Krause, T.C.; Annunziata, O. Salt-induced diffusiophoresis of a nonionic micelle: Roles of salting out and proximity to surfactant cloud point. J. Mol. Liq. 2022, 359, 119271. [Google Scholar] [CrossRef]
- Chelazzi, D.; Giorgi, R.; Baglioni, P. Microemulsions, Micelles, and Functional Gels: How Colloids and Soft Matter Preserve Works of Art. Angew. Chem. Int. Ed. 2018, 57, 7296–7303. [Google Scholar] [CrossRef]
- Patist, A.; Kanicky, J.R.; Shukla, P.K.; Shah, D.O. Importance of micellar kinetics in relation to technological processes. J. Colloid Interface Sci. 2002, 245, 7955. [Google Scholar] [CrossRef] [PubMed]
- Shah, A.; Shahzad, S.; Munir, A.; Nadagouda, M.N.; Khan, G.S.; Shams, D.F.; Dionysiou, D.D.; Rana, U.A. Micelles as Soil and Water Decontamination Agents. Chem. Rev. 2016, 116, 6042–6074. [Google Scholar] [CrossRef] [PubMed]
- La Sorella, G.; Strukul, G.; Scarso, A. Recent advances in catalysis in micellar media. Green Chem. 2015, 17, 644–683. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, E.S.; Yang, J.H.; Cao, Z.Q. Strategies to improve micelle stability for drug delivery. Nano Res. 2018, 11, 4985–4998. [Google Scholar] [CrossRef]
- Mangiapia, G.; D’Errico, G.; Simeone, L.; Irace, C.; Radulescu, A.; Di Pascale, A.; Colonna, A.; Montesarchio, D.; Paduano, L. Ruthenium-based complex nanocarriers for cancer therapy. Biomaterials 2012, 33, 3770–3782. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Um, E.; Sabass, B.; Ault, J.T.; Rahimi, M.; Warren, P.B.; Stone, H.A. Size-dependent control of colloid transport via solute gradients in dead-end channels. Proc. Natl. Acad. Sci. USA 2016, 113, 257–261. [Google Scholar] [CrossRef] [PubMed]
- Dong, R.H.; Hao, J.C. Complex Fluids of Poly(oxyethylene) Monoalkyl Ether Nonionic Surfactants. Chem. Rev. 2010, 110, 4978–5022. [Google Scholar] [CrossRef]
- Anderson, C.F.; Courtenay, E.S.; Record, M.T. Thermodynamic Expressions Relating Different Types of Preferential Interaction Coefficients in Solutions Containing Two Solute Components. J. Phys. Chem. B 2002, 106, 418–433. [Google Scholar] [CrossRef]
- Molina-Bolívar, J.A.; Aguiar, J.; Ruiz, C.C. Growth and Hydration Of Triton X-100 Micelles In Monovalent Alkali Salts: A Light Scattering Study. J. Phys. Chem. B 2002, 106, 870–877. [Google Scholar] [CrossRef]
- Barrios, E.C.; Annunziata, O. Determination of Critical Micelle Concentration from the Diffusion-Driven Dilution of Micellar Aqueous Mixtures. Langmuir 2021, 37, 2855–2862. [Google Scholar] [CrossRef] [PubMed]
- Tanford, C. Theory of micelle formation in aqueous-solutions. J. Phys. Chem. 1974, 78, 2469–2479. [Google Scholar] [CrossRef]
- Li, Y.; Sato, T. Multiple Association-Dissociation Equilibria in Solutions of Amphiphilic Molecules. Langmuir 2020, 36, 8323–8343. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, R.; Ruckenstein, E. Relation between the transition point in micellar size distribution, the cmc, and the cooperativity of micellization. J. Colloid Interface Sci. 1983, 91, 500–506. [Google Scholar] [CrossRef]
- Huddleston, J.G.; Willauer, H.D.; Rogers, R.D. Phase diagram data for several PEG plus salt aqueous biphasic systems at 25 °C. J. Chem. Eng. Data 2003, 48, 1230–1236. [Google Scholar] [CrossRef]
- Tanford, C. Physical Chemistry of Macromolecules; Wiley: Hoboken, NJ, USA, 1963. [Google Scholar]
- Dharaiya, N.; Aswal, V.K.; Bahadur, P. Characterization of Triton X-100 and its oligomer (Tyloxapol) micelles vis-à-vis solubilization of bisphenol A by spectral and scattering techniques. Colloids Surf. A Physicochem. Eng. Asp. 2015, 470, 230–239. [Google Scholar] [CrossRef]
- Regev, O.; Zana, R. Aggregation Behavior of Tyloxapol, a Nonionic Surfactant Oligomer, in Aqueous Solution. J. Colloid Interface Sci. 1999, 210, 8–17. [Google Scholar] [CrossRef] [PubMed]
- Schott, H. Comparing the Surface Chemical Properties and the Effect of Salts on the Cloud Point of a Conventional Nonionic Surfactant, Octoxynol 9 (Triton X-100), and of Its Oligomer, Tyloxapol (Triton WR-1339). J. Colloid Interface Sci. 1998, 205, 496–502. [Google Scholar] [CrossRef] [PubMed]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011; pp. 1–674. [Google Scholar]
- Annunziata, O.; Fahim, A. A unified description of macroion diffusiophoresis, salt osmotic diffusion and collective diffusion coefficient. Int. J. Heat Mass Transf. 2020, 163, 11. [Google Scholar] [CrossRef]
- Lechlitner, L.R.; Annunziata, O. Macromolecule Diffusiophoresis Induced by Concentration Gradients of Aqueous Osmolytes. Langmuir 2018, 34, 9525–9531. [Google Scholar] [CrossRef]
- Annunziata, O. Diffusiophoresis of Macromolecules within the Framework of Multicomponent Diffusion. Molecules 2024, 29, 1367. [Google Scholar] [CrossRef]
- Zhang, H.X.; Annunziata, O. Macromolecular hydration compared with preferential hydration and their role on macromolecule-osmolyte coupled diffusion. Phys. Chem. Chem. Phys. 2009, 11, 8923–8932. [Google Scholar] [CrossRef] [PubMed]
- Miller, D.G.; Vitagliano, V.; Sartorio, R. Some comments on multicomponent diffusion—Negative main term diffusion-coefficients, 2nd law constraints, solvent choices, and reference frame transformations. J. Phys. Chem. 1986, 90, 1509–1519. [Google Scholar] [CrossRef]
- Fine, B.M.; Lomakin, A.; Ogun, O.O.; Benedek, G.B. Static structure factor and collective diffusion of globular proteins in concentrated aqueous solution. J. Chem. Phys. 1996, 104, 326–335. [Google Scholar] [CrossRef]
- Leaist, D.G.; Hao, L. Comparison of diffusion-coefficients of multicomponent solutions from light-scattering and macroscopic gradient techniques—Sodium dodecyl-sulfate micelles in aqueous salt-solutions. J. Phys. Chem. 1993, 97, 7763–7768. [Google Scholar] [CrossRef]
- Annunziata, O.; Buzatu, D.; Albright, J.G. Protein diffusion coefficients determined by macroscopic-gradient Rayleigh interferometry and dynamic light scattering. Langmuir 2005, 21, 12085–12089. [Google Scholar] [CrossRef] [PubMed]
- Corti, M.; Degiorgio, V. Micellar properties and critical fluctuations in aqueous solutions of nonionic amphiphiles. J. Phys. Chem. 1981, 85, 1442–1445. [Google Scholar] [CrossRef]
- Corti, M.; Degiorgio, V. Investigation of micelle formation in aqueous-solution by laser-light scattering. Chem. Phys. Lett. 1978, 53, 237–241. [Google Scholar] [CrossRef]
- Lindman, B.; Puyal, M.; Kamenka, N.; Rymden, R.; Stilbs, P. Micelle formation of anionic and cationic surfactants from fourier-transform H-1 and LI-7 nuclear magnetic-resonance and tracer self-diffusion studies. J. Phys. Chem. 1984, 88, 5048–5057. [Google Scholar] [CrossRef]
- Jansson, M.; Warr, G. Self-diffusion coefficients in attractive ionic micelle solutions. J. Colloid Interface Sci. 1990, 140, 541–544. [Google Scholar] [CrossRef]
- Annunziata, O.; Costantino, L.; D’Errico, G.; Paduano, L.; Vitagliano, V. Transport properties for aqueous sodium sulfonate surfactants—2. Intradiffusion measurements: Influence of the obstruction effect on the monomer and micelle mobilities. J. Colloid Interface Sci. 1999, 216, 16–24. [Google Scholar] [CrossRef] [PubMed]
- Annunziata, O. Role of preferential hydration on diffusiophoresis of globular proteins. Int. J. Heat Mass Transf. 2023, 216, 124503. [Google Scholar] [CrossRef]
- Hamer, W.J.; Wu, Y.C. Osmotic Coefficients and Mean Activity Coefficients of Uni-univalent Electrolytes in Water at 25 °C. J. Phys. Chem. Ref. Data 1972, 1, 1047–1100. [Google Scholar] [CrossRef]
- Lobo, V.M.M. Electrolyte Solutions: Literature Data on Thermodynamic and Transport Properties; Department of Chemistry, University of Coimbra: Coimbra, Portugal, 1984. [Google Scholar]
- Prieve, D.C.; Roman, R. Diffusiophoresis of a rigid sphere through a viscous electrolyte solution. J. Chem. Soc. Faraday Trans. 2 1987, 83, 1287–1306. [Google Scholar] [CrossRef]
- Henry, D.C. The cataphoresis of suspended particles. Part I.—The equation of cataphoresis. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1997, 133, 106–129. [Google Scholar] [CrossRef]
- Arakawa, T.; Timasheff, S.N. Preferential interactions of proteins with salts in concentrated-solutions. Biochemistry 1982, 21, 6545–6552. [Google Scholar] [CrossRef] [PubMed]
- Annunziata, O.; Costantino, L.; D’Errico, G.; Paduano, L.; Vitagliano, V. Transport properties for aqueous solution of sodium sulfonate surfactants—1. Mutual diffusion measurements: Evaluation of the equilibrium parameters for the micellization process. J. Colloid Interface Sci. 1999, 216, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Rard, J.A.; Miller, D.G. The mutual diffusion coefficients of NaCl-H2O and CaCl2-H2O at 25 °C from Rayleigh interferometry. J. Sol. Chem. 1979, 8, 701–716. [Google Scholar] [CrossRef]
- Giorgio, G.; Colafemmina, G.; Mavelli, F.; Murgia, S.; Palazzo, G. The impact of alkanes on the structure of Triton X100 micelles. RSC Adv. 2016, 6, 825–836. [Google Scholar] [CrossRef]
- Paradies, H. Shape and size of a non-ionic surfactant micelle—triton x-100 in aqueous-solution. J. Phys. Chem. 1980, 84, 599–607. [Google Scholar] [CrossRef]
- Zoeller, N.; Lue, L.; Blankschtein, D. Statistical-thermodynamic framework to model nonionic micellar solutions. Langmuir 1997, 13, 5258–5275. [Google Scholar] [CrossRef]
- Korosi, A.; Fabuss, B.M. Viscosities of binary aqueous solutions of sodium chloride, potassium chloride, sodium sulfate, and magnesium sulfate at concentrations and temperatures of interest in desalination processes. J. Chem. Eng. Data 2002, 13, 548–552. [Google Scholar] [CrossRef]

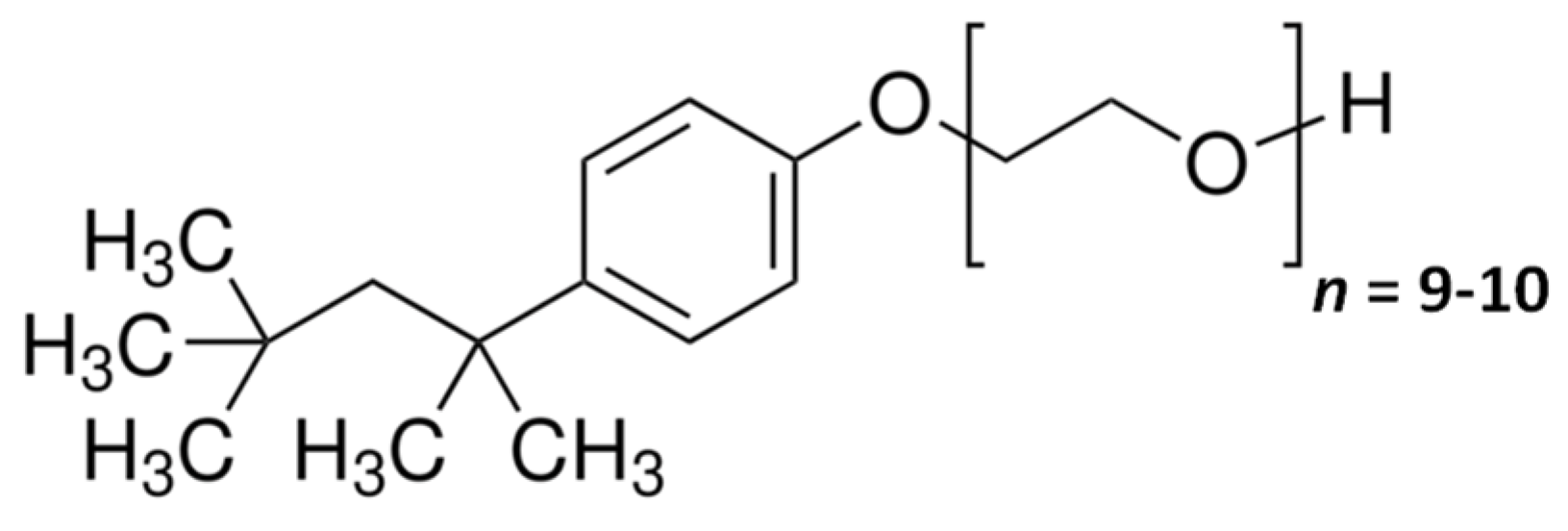

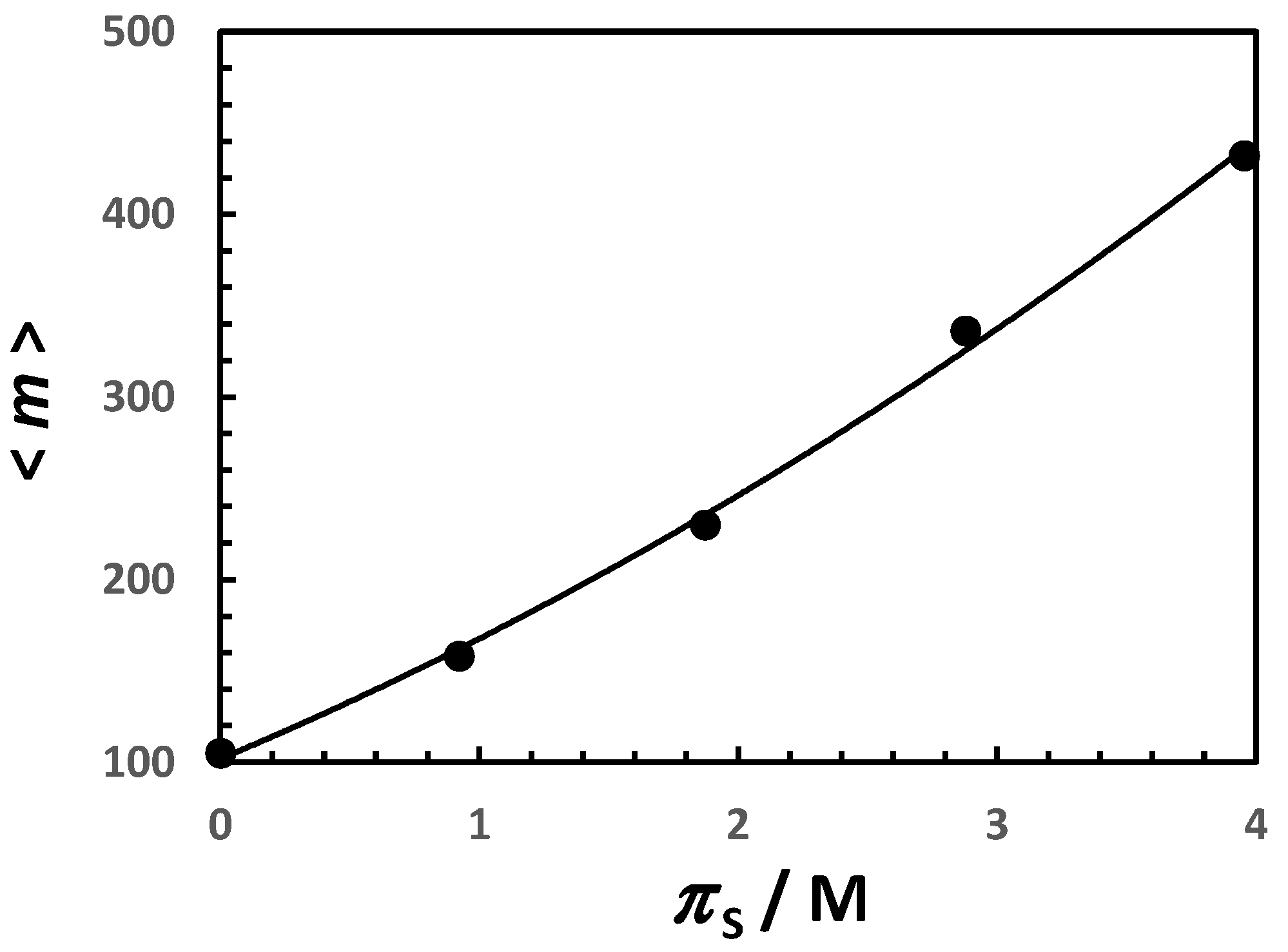

| 0 | 0 | 102 | 0.58 |
| 0.20 | 0.369 | 125 | 0.51 |
| 0.50 | 0.921 | 162 | 0.44 |
| 1.00 | 1.873 | 235 | 0.35 |
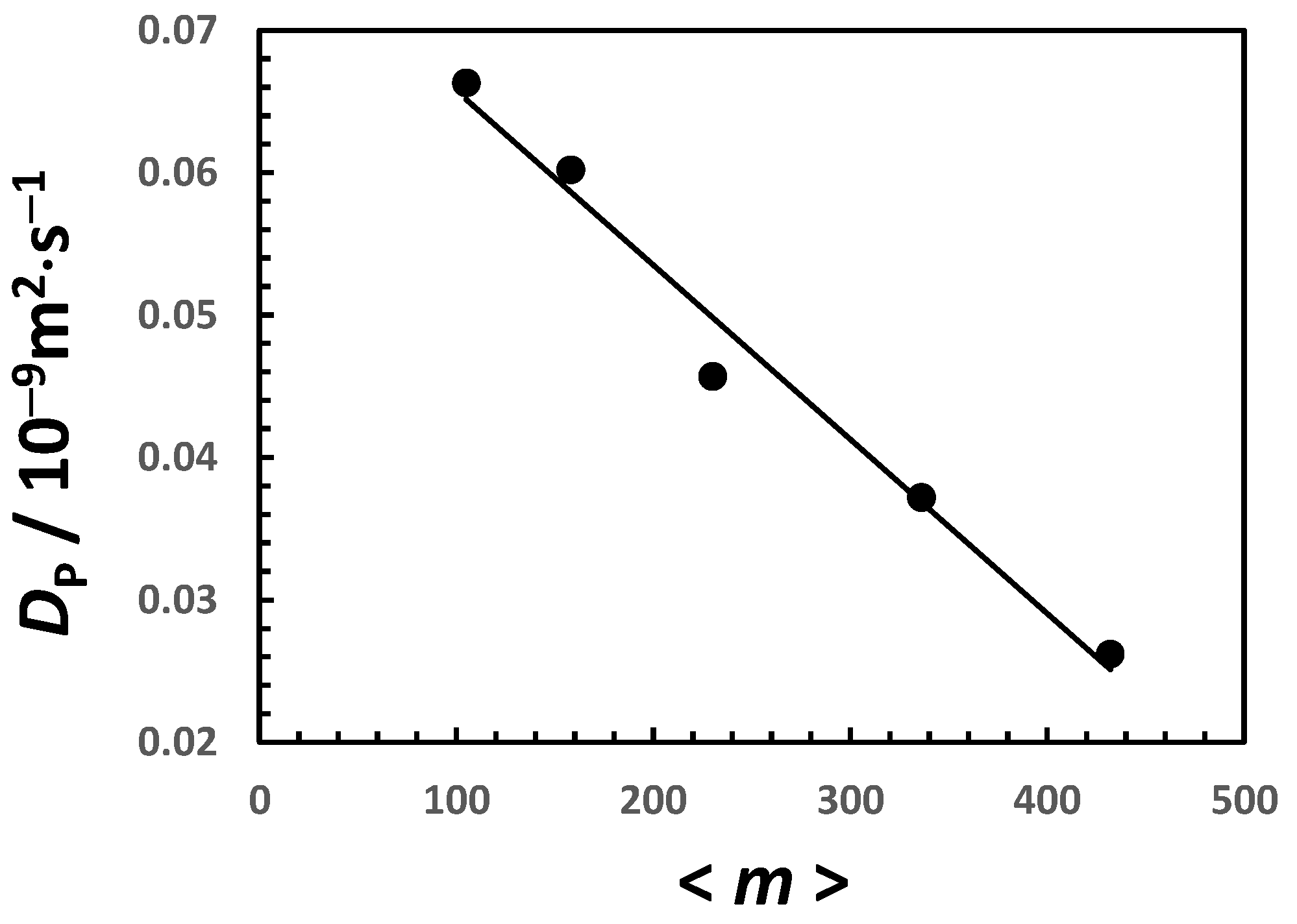
| 0 | 0.0678 | 0.0018 | −0.11 | 6.19 |
| 0.20 | 0.0636 | 0.0019 | −0.12 | 7.57 |
| 0.50 | 0.0574 | 0.0021 | −0.15 | 9.84 |
| 1.00 | 0.0471 | 0.0026 | −0.21 | 14.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Annunziata, O. The Salt-Induced Diffusiophoresis of Nonionic Micelles—Does the Salt-Induced Growth of Micelles Influence Diffusiophoresis? Molecules 2024, 29, 3618. https://doi.org/10.3390/molecules29153618
Annunziata O. The Salt-Induced Diffusiophoresis of Nonionic Micelles—Does the Salt-Induced Growth of Micelles Influence Diffusiophoresis? Molecules. 2024; 29(15):3618. https://doi.org/10.3390/molecules29153618
Chicago/Turabian StyleAnnunziata, Onofrio. 2024. "The Salt-Induced Diffusiophoresis of Nonionic Micelles—Does the Salt-Induced Growth of Micelles Influence Diffusiophoresis?" Molecules 29, no. 15: 3618. https://doi.org/10.3390/molecules29153618
APA StyleAnnunziata, O. (2024). The Salt-Induced Diffusiophoresis of Nonionic Micelles—Does the Salt-Induced Growth of Micelles Influence Diffusiophoresis? Molecules, 29(15), 3618. https://doi.org/10.3390/molecules29153618






