Insights into the Interaction Mechanisms of Peptide and Non-Peptide Inhibitors with MDM2 Using Gaussian-Accelerated Molecular Dynamics Simulations and Deep Learning
Abstract
1. Introduction
2. Results and Discussion
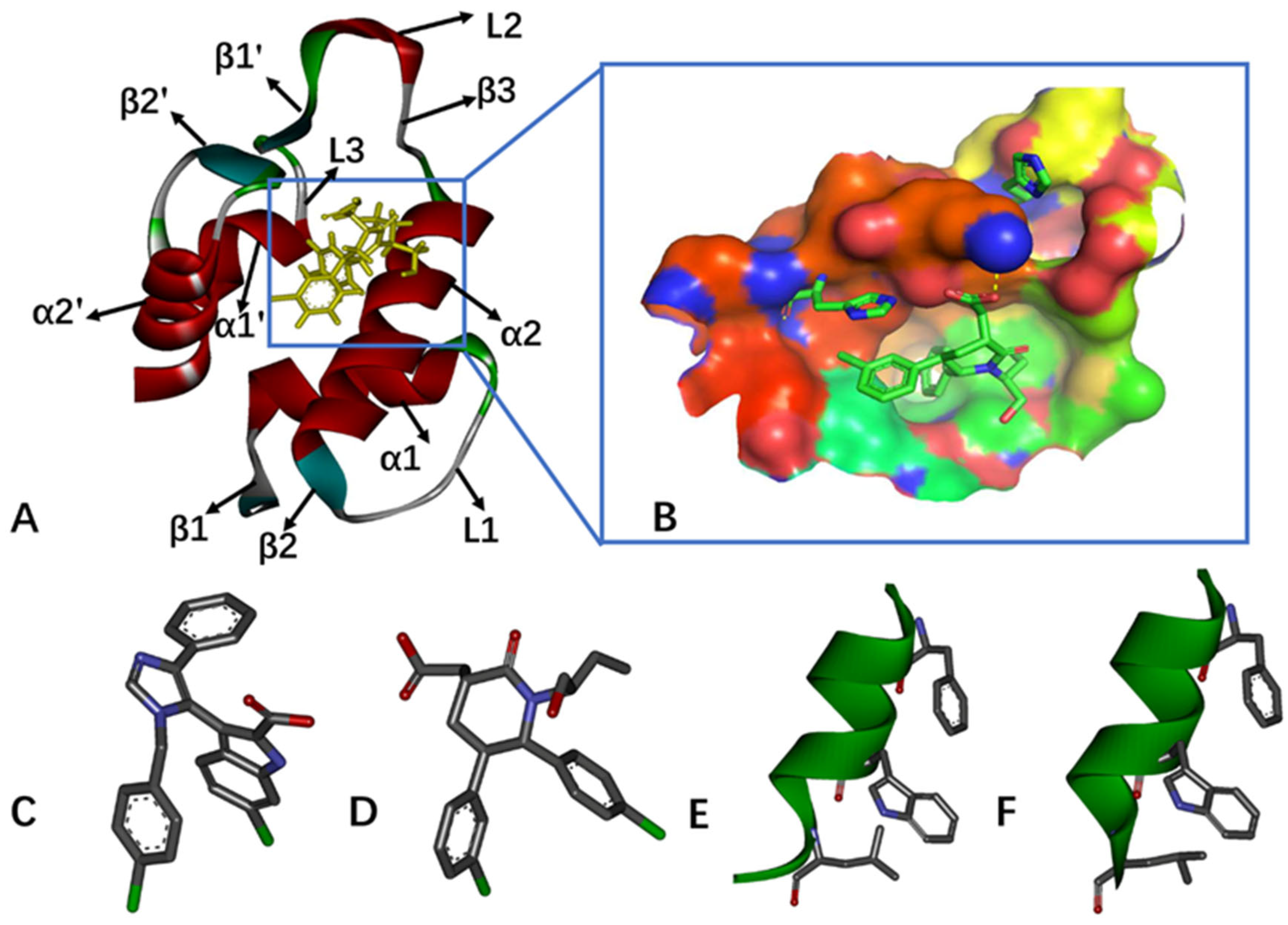
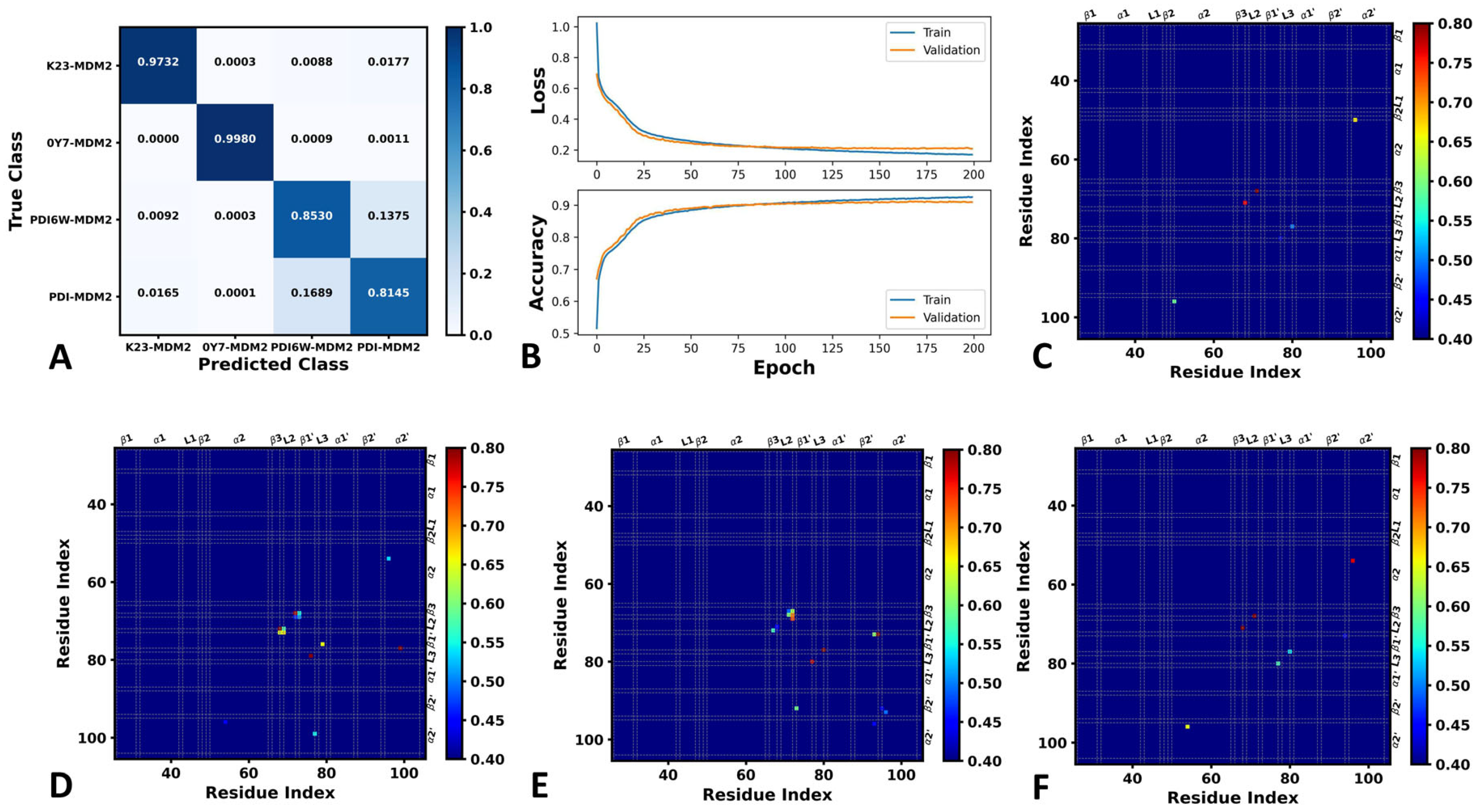
2.1. Differences in the Contacts of Structural Domains Revealed by Deep Learning
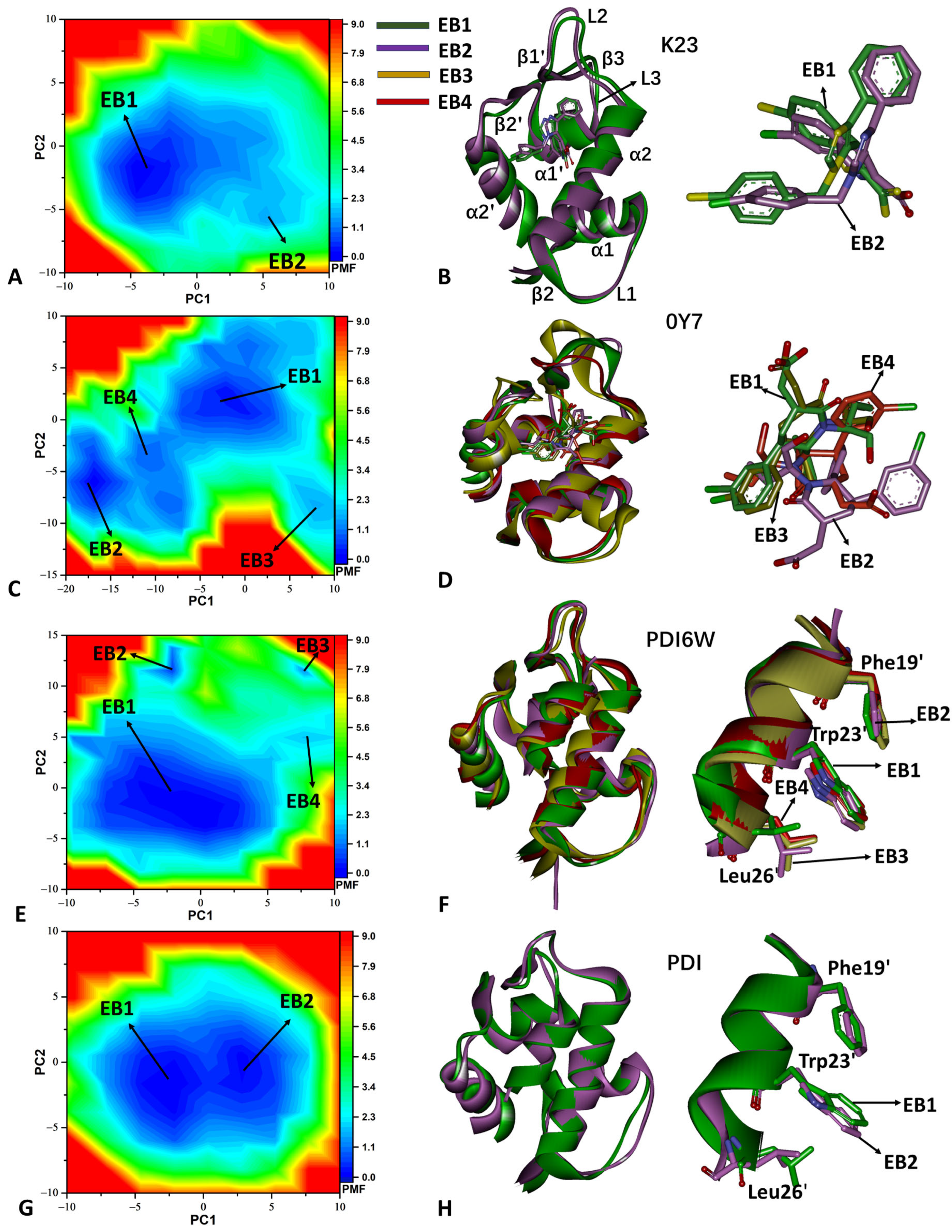
2.2. Free Energy Profiles and Structural Dynamics of MDM2
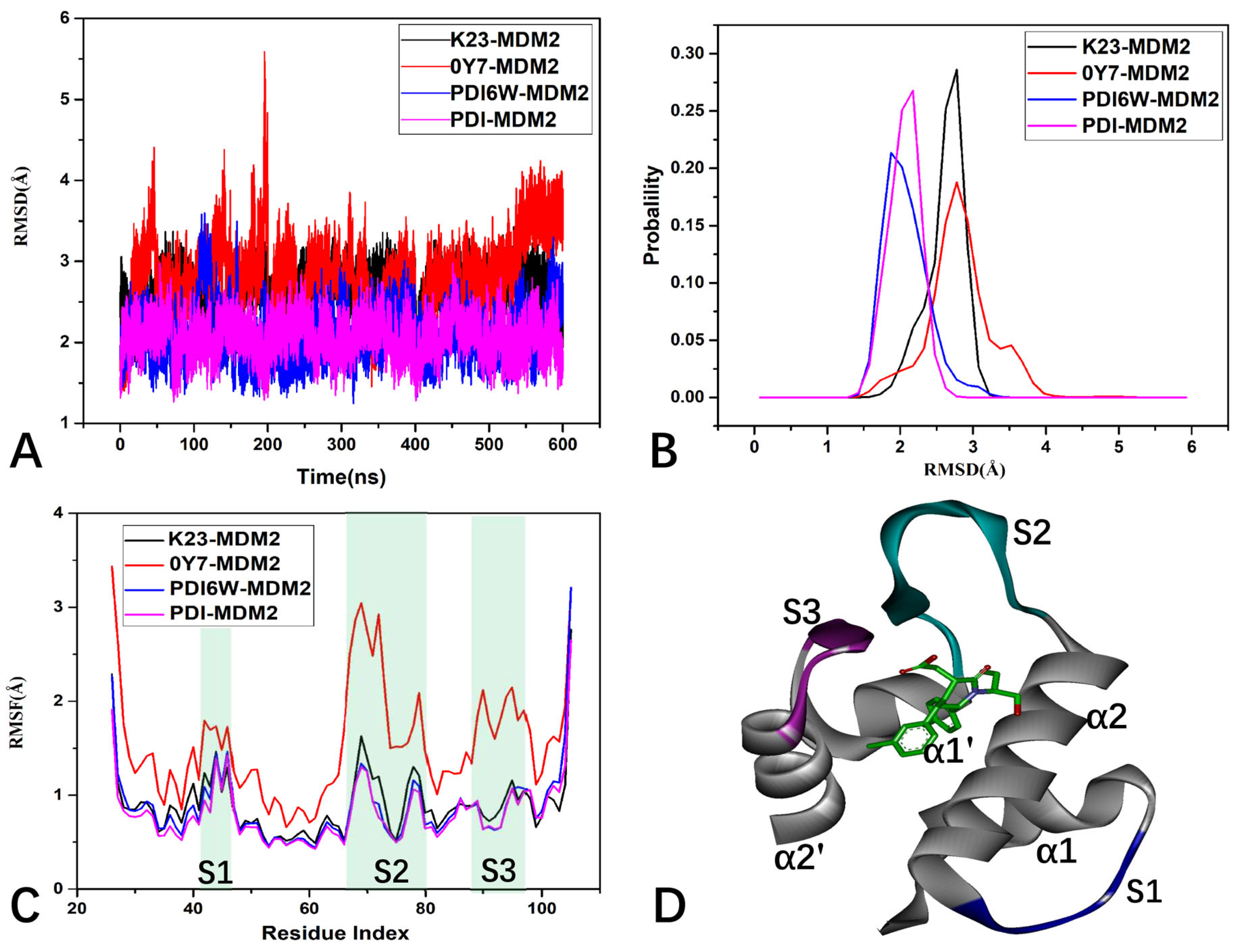
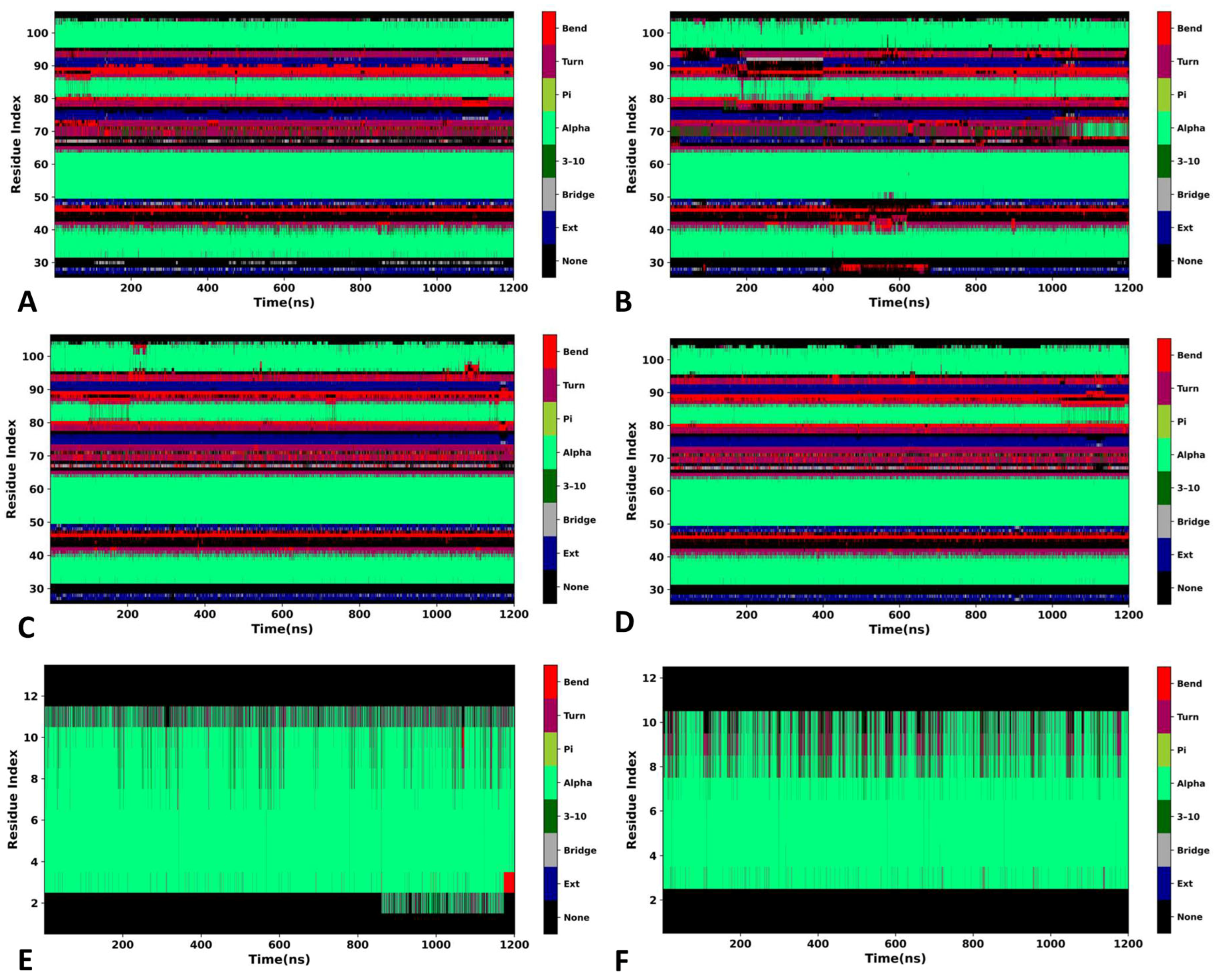
2.3. Structural Property of MDM2
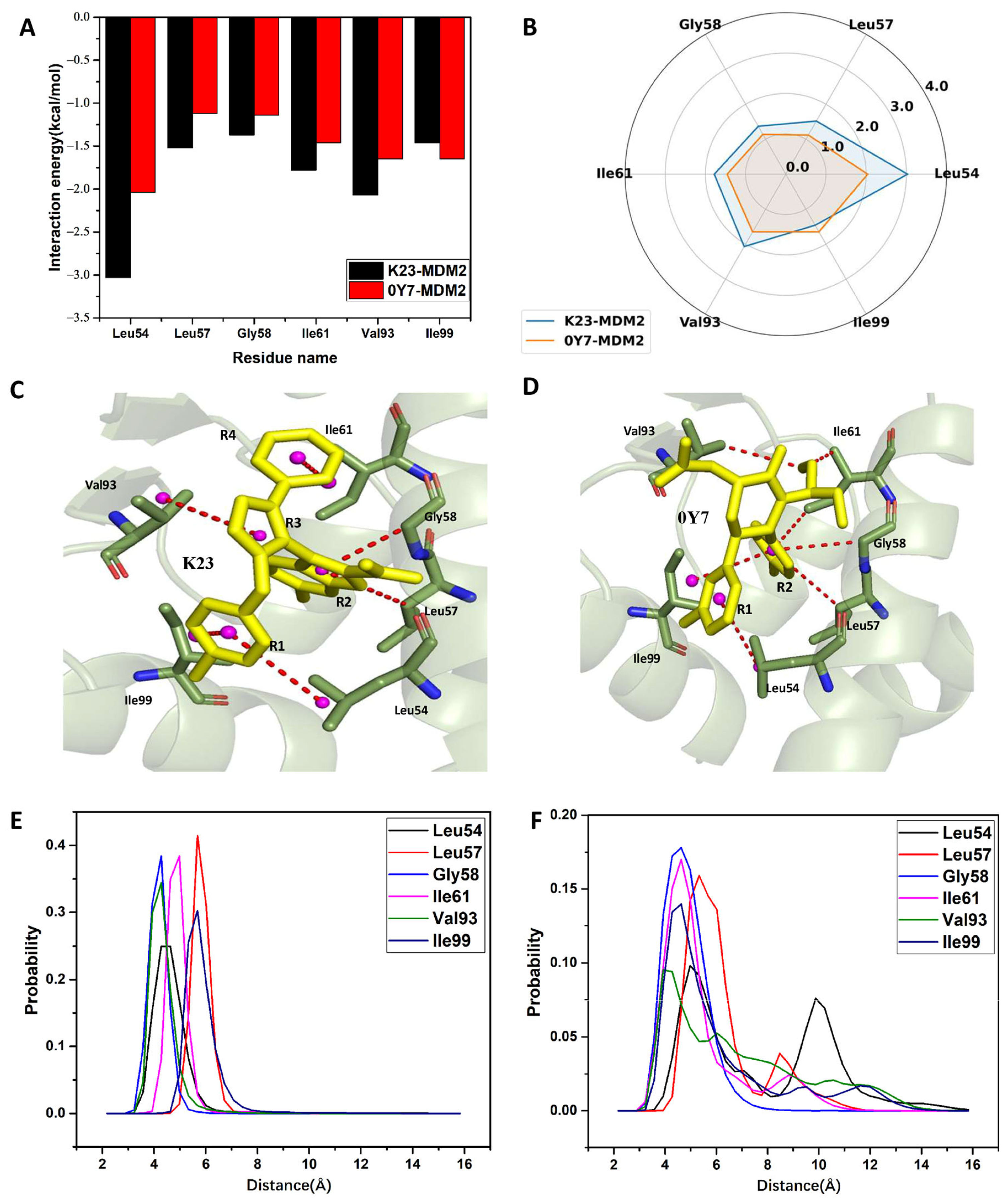
2.4. Comparative Calculations of Binding Free Energies
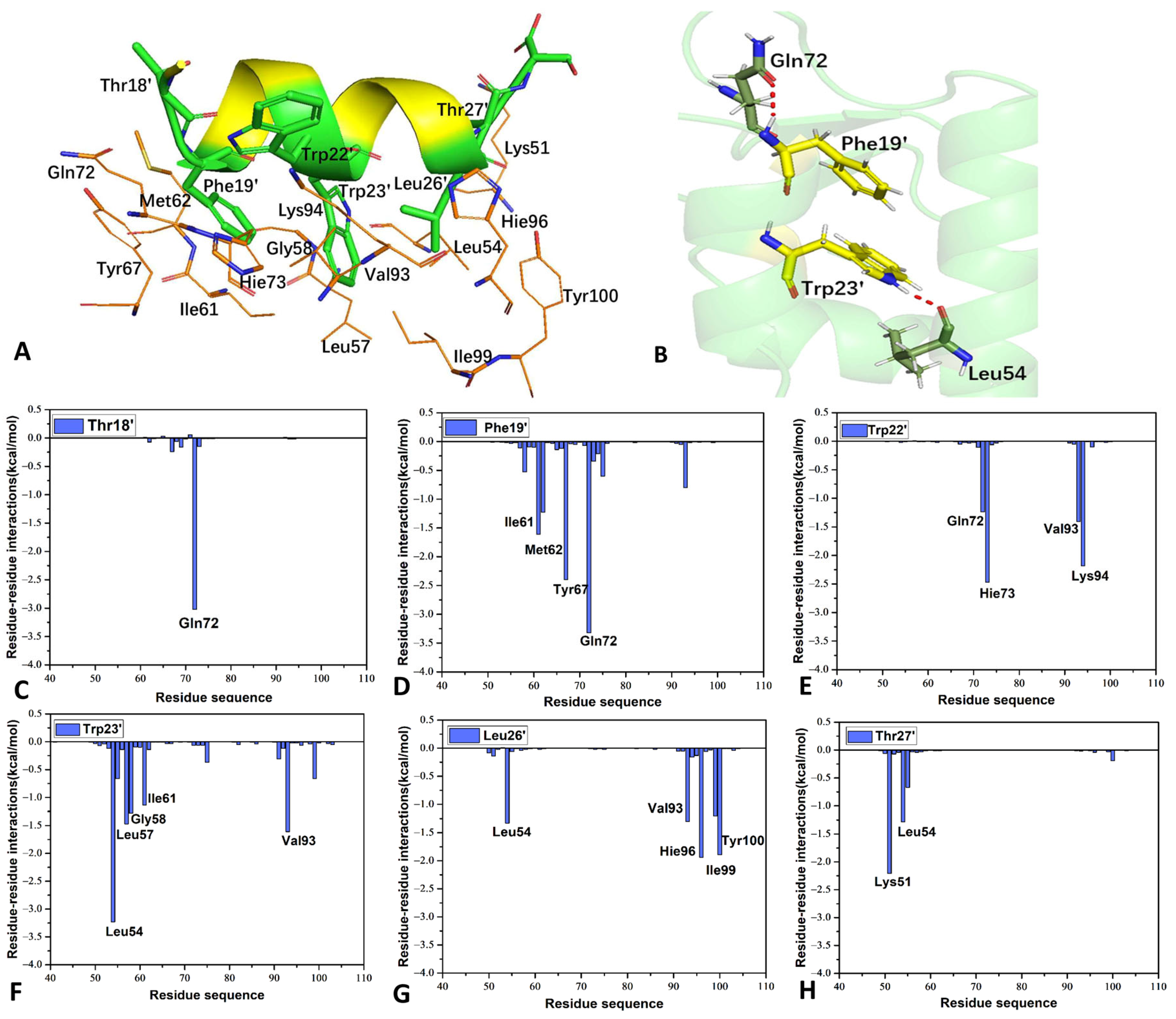
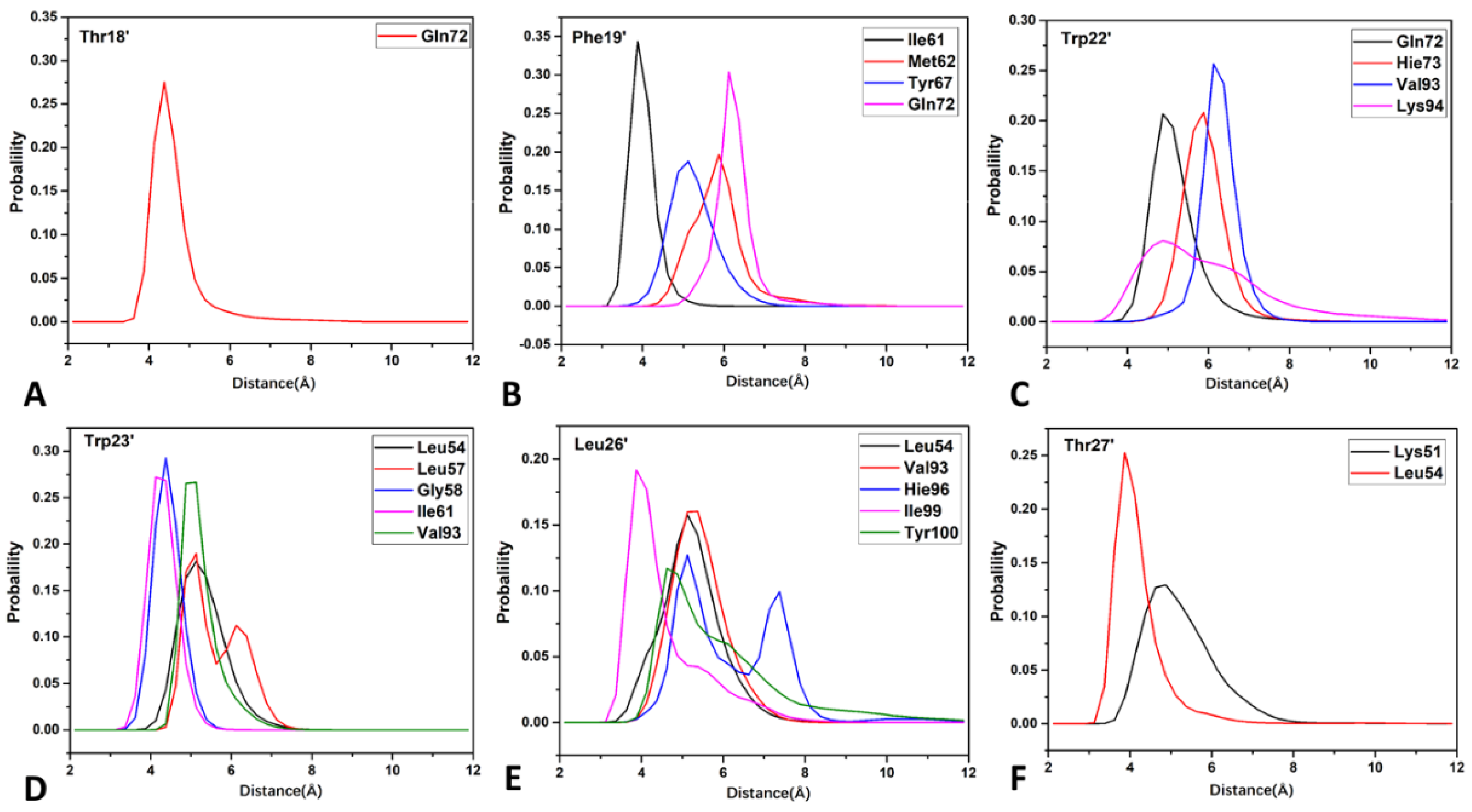
2.5. Interaction Network of Inhibitors with MDM2
3. Materials and Methods
3.1. System Preparation
3.2. Multiple Independent Gaussian-Accelerated Molecular Dynamics
3.3. Deep Learning
3.4. Principal Component Analysis and Dynamic Cross-Correlation Maps
3.5. Construction of Free Energy Landscapes
3.6. Binding Free Energies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Patil, M.R.; Bihari, A. A comprehensive study of p53 protein. J. Cell. Biochem. 2022, 123, 1891–1937. [Google Scholar] [CrossRef] [PubMed]
- Ozaki, T.; Nakagawara, A. p53: The attractive tumor suppressor in the cancer research field. J. Biomed. Biotechnol. 2011, 2011, 603925. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Miki, Y. The cell death machinery governed by the p53 tumor suppressor in response to DNA damage. Cancer Sci. 2010, 101, 831–835. [Google Scholar] [CrossRef] [PubMed]
- Bykov, V.J.N.; Eriksson, S.E.; Bianchi, J.; Wiman, K.G. Targeting mutant p53 for efficient cancer therapy. Nat. Rev. Cancer 2018, 18, 89–102. [Google Scholar] [CrossRef] [PubMed]
- Khoo, K.H.; Verma, C.S.; Lane, D.P. Drugging the p53 pathway: Understanding the route to clinical efficacy. Nat. Rev. Drug Discov. 2014, 13, 217–236. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Albadari, N.; Du, Y.; Fowler, J.F.; Sang, H.T.; Xian, W.; McKeon, F.; Li, W.; Zhou, J.; Zhang, R. MDM2 Inhibitors for Cancer Therapy: The Past, Present, and Future. Pharmacol. Rev. 2024, 76, 414–453. [Google Scholar] [CrossRef] [PubMed]
- Zafar, A.; Khan, M.J.; Naeem, A. MDM2- an indispensable player in tumorigenesis. Mol. Biol. Rep. 2023, 50, 6871–6883. [Google Scholar] [CrossRef] [PubMed]
- Wade, M.; Li, Y.C.; Wahl, G.M. MDM2, MDMX and p53 in oncogenesis and cancer therapy. Nat. Rev. Cancer 2013, 13, 83–96. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, M.; Mandani, G.; Momand, J. The MDM2 gene family. Biomol. Concepts 2014, 5, 9–19. [Google Scholar] [CrossRef]
- Momand, J.; Villegas, A.; Belyi, V.A. The evolution of MDM2 family genes. Gene 2011, 486, 23–30. [Google Scholar] [CrossRef]
- Tan, B.X.; Liew, H.P.; Chua, J.S.; Ghadessy, F.J.; Tan, Y.S.; Lane, D.P.; Coffill, C.R. Anatomy of Mdm2 and Mdm4 in evolution. J. Mol. Cell Biol. 2017, 9, 3–15. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.H.; Xu, Z.Y.; Mo, S.; Yuan, L.; Cheng, X.D.; Qin, J.J. Targeting MDMX for Cancer Therapy: Rationale, Strategies, and Challenges. Front. Oncol. 2020, 10, 1389. [Google Scholar] [CrossRef] [PubMed]
- Sanford, J.D.; Yang, J.; Han, J.; Tollini, L.A.; Jin, A.; Zhang, Y. MDMX is essential for the regulation of p53 protein levels in the absence of a functional MDM2 C-terminal tail. BMC Mol. Cell Biol. 2021, 22, 46. [Google Scholar] [CrossRef] [PubMed]
- Kussie, P.H.; Gorina, S.; Marechal, V.; Elenbaas, B.; Moreau, J.; Levine, A.J.; Pavletich, N.P. Structure of the MDM2 oncoprotein bound to the p53 tumor suppressor transactivation domain. Science 1996, 274, 948–953. [Google Scholar] [CrossRef] [PubMed]
- Koo, N.; Sharma, A.K.; Narayan, S. Therapeutics Targeting p53-MDM2 Interaction to Induce Cancer Cell Death. Int. J. Mol. Sci. 2022, 23, 5005. [Google Scholar] [CrossRef] [PubMed]
- Nayak, S.K.; Khatik, G.L.; Narang, R.; Monga, V.; Chopra, H.K. p53-Mdm2 Interaction Inhibitors as Novel Nongenotoxic Anticancer Agents. Curr. Cancer Drug Targets 2018, 18, 749–772. [Google Scholar] [CrossRef] [PubMed]
- Rasafar, N.; Barzegar, A.; Mehdizadeh Aghdam, E. Design and development of high affinity dual anticancer peptide-inhibitors against p53-MDM2/X interaction. Life Sci. 2020, 245, 117358. [Google Scholar] [CrossRef] [PubMed]
- Lemos, A.; Leão, M.; Soares, J.; Palmeira, A.; Pinto, M.; Saraiva, L.; Sousa, M.E. Medicinal Chemistry Strategies to Disrupt the p53-MDM2/MDMX Interaction. Med. Res. Rev. 2016, 36, 789–844. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Li, X.; Li, Y.; Yuan, X.; Geng, C.; Gao, S.; Li, J.; Ma, B.; Wang, Z.; Lu, W.; et al. Design of stapled peptide-based PROTACs for MDM2/MDMX atypical degradation and tumor suppression. Theranostics 2022, 12, 6665–6681. [Google Scholar] [CrossRef]
- Rasafar, N.; Barzegar, A.; Mehdizadeh Aghdam, E. Structure-based designing efficient peptides based on p53 binding site residues to disrupt p53-MDM2/X interaction. Sci. Rep. 2020, 10, 11449. [Google Scholar] [CrossRef]
- Wang, Y.T.; Cheng, T.L. Computational modeling of cyclic peptide inhibitor-MDM2/MDMX binding through global docking and Gaussian accelerated molecular dynamics simulations. J. Biomol. Struct. Dyn. 2021, 39, 4005–4014. [Google Scholar] [CrossRef] [PubMed]
- Phan, J.; Li, Z.; Kasprzak, A.; Li, B.; Sebti, S.; Guida, W.; Schönbrunn, E.; Chen, J. Structure-based design of high affinity peptides inhibiting the interaction of p53 with MDM2 and MDMX. J. Biol. Chem. 2010, 285, 2174–2183. [Google Scholar] [CrossRef] [PubMed]
- Czarna, A.; Popowicz, G.M.; Pecak, A.; Wolf, S.; Dubin, G.; Holak, T.A. High affinity interaction of the p53 peptide-analogue with human Mdm2 and Mdmx. Cell Cycle 2009, 8, 1176–1184. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Liao, G.; Yu, B. Small-molecule MDM2/X inhibitors and PROTAC degraders for cancer therapy: Advances and perspectives. Acta Pharm. Sin. B 2020, 10, 1253–1278. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Chen, F.E. Small-molecule MDM2 inhibitors in clinical trials for cancer therapy. Eur. J. Med. Chem. 2022, 236, 114334. [Google Scholar] [CrossRef] [PubMed]
- Beloglazkina, A.; Zyk, N.; Majouga, A.; Beloglazkina, E. Recent small-molecule inhibitors of the p53-MDM2 protein-protein Interaction. Molecules 2020, 25, 1211. [Google Scholar] [CrossRef] [PubMed]
- Rew, Y.; Sun, D. Discovery of a small molecule MDM2 inhibitor (AMG 232) for treating cancer. J. Med. Chem. 2014, 57, 6332–6341. [Google Scholar] [CrossRef] [PubMed]
- Liao, G.; Yang, D.; Ma, L.; Li, W.; Hu, L.; Zeng, L.; Wu, P.; Duan, L.; Liu, Z. The development of piperidinones as potent MDM2-P53 protein-protein interaction inhibitors for cancer therapy. Eur. J. Med. Chem. 2018, 159, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Wang, Y.; Zhu, J.; Bartberger, M.D.; Canon, J.; Chen, A.; Chow, D.; Eksterowicz, J.; Fox, B.; Fu, J.; et al. Discovery of Potent and Simplified Piperidinone-Based Inhibitors of the MDM2-p53 Interaction. ACS Med. Chem. Lett. 2014, 5, 894–899. [Google Scholar] [CrossRef]
- Gessier, F.; Kallen, J.; Jacoby, E.; Chène, P.; Stachyra-Valat, T.; Ruetz, S.; Jeay, S.; Holzer, P.; Masuya, K.; Furet, P. Discovery of dihydroisoquinolinone derivatives as novel inhibitors of the p53-MDM2 interaction with a distinct binding mode. Bioorg. Med. Chem. Lett. 2015, 25, 3621–3625. [Google Scholar] [CrossRef]
- Holzer, P.; Masuya, K.; Furet, P.; Kallen, J.; Valat-Stachyra, T.; Ferretti, S.; Berghausen, J.; Bouisset-Leonard, M.; Buschmann, N.; Pissot-Soldermann, C.; et al. Discovery of a Dihydroisoquinolinone Derivative (NVP-CGM097): A Highly Potent and Selective MDM2 Inhibitor Undergoing Phase 1 Clinical Trials in p53wt Tumors. J. Med. Chem. 2015, 58, 6348–6358. [Google Scholar] [CrossRef] [PubMed]
- de Weger, V.A.; de Jonge, M.; Langenberg, M.H.G.; Schellens, J.H.M.; Lolkema, M.; Varga, A.; Demers, B.; Thomas, K.; Hsu, K.; Tuffal, G.; et al. A phase I study of the HDM2 antagonist SAR405838 combined with the MEK inhibitor pimasertib in patients with advanced solid tumours. Br. J. Cancer 2019, 120, 286–293. [Google Scholar] [CrossRef]
- Vu, B.; Wovkulich, P.; Pizzolato, G.; Lovey, A.; Ding, Q.; Jiang, N.; Liu, J.J.; Zhao, C.; Glenn, K.; Wen, Y.; et al. Discovery of RG7112: A Small-Molecule MDM2 Inhibitor in Clinical Development. ACS Med. Chem. Lett. 2013, 4, 466–469. [Google Scholar] [CrossRef]
- Kang, M.H.; Reynolds, C.P.; Kolb, E.A.; Gorlick, R.; Carol, H.; Lock, R.; Keir, S.T.; Maris, J.M.; Wu, J.; Lyalin, D.; et al. Initial Testing (Stage 1) of MK-8242-A Novel MDM2 Inhibitor-by the Pediatric Preclinical Testing Program. Pediatr. Blood Cancer 2016, 63, 1744–1752. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, D.; Zhang, Y.; Li, G. Computational studies of difference in binding modes of peptide and non-peptide inhibitors to MDM2/MDMX based on molecular dynamics simulations. Int. J. Mol. Sci. 2012, 13, 2176–2195. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Xu, B.; Zhu, W.; Li, G. Insight into mechanism of small molecule inhibitors of the MDM2-p53 interaction: Molecular dynamics simulation and free energy analysis. J. Mol. Graph. Model. 2011, 30, 46–53. [Google Scholar] [CrossRef]
- Niu, R.J.; Zheng, Q.C.; Zhang, J.L.; Zhang, H.X. Molecular dynamics simulations studies and free energy analysis on inhibitors of MDM2-p53 interaction. J. Mol. Graph. Model. 2013, 46, 132–139. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Xu, S.; Wang, J. Characterizing the Free-Energy Landscape of MDM2 Protein-Ligand Interactions by Steered Molecular Dynamics Simulations. Chem. Biol. Drug Des. 2015, 86, 1351–1359. [Google Scholar] [CrossRef] [PubMed]
- Shoaib, T.H.; Abdelmoniem, N.; Mukhtar, R.M.; Alqhtani, A.T.; Alalawi, A.L.; Alawaji, R.; Althubyani, M.S.; Mohamed, S.G.A.; Mohamed, G.A.; Ibrahim, S.R.M.; et al. Molecular Docking and Molecular Dynamics Studies Reveal the Anticancer Potential of Medicinal-Plant-Derived Lignans as MDM2-P53 Interaction Inhibitors. Molecules 2023, 28, 6665. [Google Scholar] [CrossRef]
- Miao, Y.; Feher, V.A.; McCammon, J.A. Gaussian Accelerated Molecular Dynamics: Unconstrained Enhanced Sampling and Free Energy Calculation. J. Chem. Theory Comput. 2015, 11, 3584–3595. [Google Scholar] [CrossRef]
- Miao, Y.; McCammon, J.A. Gaussian Accelerated Molecular Dynamics: Theory, Implementation, and Applications. Annu. Rep. Comput. Chem. 2017, 13, 231–278. [Google Scholar] [PubMed]
- Wang, J.; Arantes, P.R.; Bhattarai, A.; Hsu, R.V.; Pawnikar, S.; Huang, Y.M.; Palermo, G.; Miao, Y. Gaussian accelerated molecular dynamics (GaMD): Principles and applications. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 11, e1521. [Google Scholar] [CrossRef] [PubMed]
- Pawnikar, S.; Bhattarai, A.; Wang, J.; Miao, Y. Binding Analysis Using Accelerated Molecular Dynamics Simulations and Future Perspectives. Adv. Appl. Bioinform. Chem. 2022, 15, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Li, W. Absolute Binding Free Energy Calculations for Highly Flexible Protein MDM2 and Its Inhibitors. Int. J. Mol. Sci. 2020, 21, 4765. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Wang, Y.; Yan, D.; Liu, Z.; Wei, B.; Chen, J.; He, W. Binding Mechanism of Inhibitors to Heat Shock Protein 90 Investigated by Multiple Independent Molecular Dynamics Simulations and Prediction of Binding Free Energy. Molecules 2023, 28, 4792. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, X.; Pang, L.; Zhang, J.Z.H.; Zhu, T. Effect of mutations on binding of ligands to guanine riboswitch probed by free energy perturbation and molecular dynamics simulations. Nucleic Acids Res. 2019, 47, 6618–6631. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Cong, Y.; Li, Y.; Zhong, S.; Wang, R.; Li, H.; Duan, L. Insight Into the Binding Mechanism of p53/pDIQ-MDMX/MDM2 With the Interaction Entropy Method. Front. Chem. 2019, 7, 33. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; McCammon, J.A. Graded activation and free energy landscapes of a muscarinic G-protein-coupled receptor. Proc. Natl. Acad. Sci. USA 2016, 113, 12162–12167. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zeng, Q.; Wang, W.; Sun, H.; Hu, G. Decoding the Identification Mechanism of an SAM-III Riboswitch on Ligands through Multiple Independent Gaussian-Accelerated Molecular Dynamics Simulations. J. Chem. Inf. Model. 2022, 62, 6118–6132. [Google Scholar] [CrossRef]
- Wang, J.; Miao, Y. Peptide Gaussian accelerated molecular dynamics (Pep-GaMD): Enhanced sampling and free energy and kinetics calculations of peptide binding. J. Chem. Phys. 2020, 153, 154109. [Google Scholar] [CrossRef]
- Miao, Y.; Bhattarai, A.; Wang, J. Ligand Gaussian Accelerated Molecular Dynamics (LiGaMD): Characterization of Ligand Binding Thermodynamics and Kinetics. J. Chem. Theory Comput. 2020, 16, 5526–5547. [Google Scholar] [CrossRef] [PubMed]
- N, S.D.; Shivakumar; Kumar, D.U.; Ghate, S.D.; Dixit, S.R.; Awasthi, A.; Revanasiddappa, B.C. Benzothiazole derivatives as p53-MDM2 inhibitors: In-silico design, ADMET predictions, molecular docking, MM-GBSA Assay, MD simulations studies. J. Biomol. Struct. Dyn. 2023, 1–12. [Google Scholar] [CrossRef]
- Dokainish, H.M.; Sugita, Y. Exploring Large Domain Motions in Proteins Using Atomistic Molecular Dynamics with Enhanced Conformational Sampling. Int. J. Mol. Sci. 2020, 22, 270. [Google Scholar] [CrossRef] [PubMed]
- Plante, A.; Shore, D.M.; Morra, G.; Khelashvili, G.; Weinstein, H. A Machine Learning Approach for the Discovery of Ligand-Specific Functional Mechanisms of GPCRs. Molecules 2019, 24, 2097. [Google Scholar] [CrossRef] [PubMed]
- Plante, A.; Weinstein, H. Ligand-Dependent Conformational Transitions in Molecular Dynamics Trajectories of GPCRs Revealed by a New Machine Learning Rare Event Detection Protocol. Molecules 2021, 26, 3059. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, W.; Zhao, L.; Wei, B.; Chen, J. Binding Mechanism of Inhibitors to BRD4 and BRD9 Decoded by Multiple Independent Molecular Dynamics Simulations and Deep Learning. Molecules 2024, 29, 1857. [Google Scholar] [CrossRef] [PubMed]
- Degiacomi, M.T. Coupling Molecular Dynamics and Deep Learning to Mine Protein Conformational Space. Structure 2019, 27, 1034–1040.e1033. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Jiao, Y.; Shi, C.; Zhang, Y. Deep learning-based molecular dynamics simulation for structure-based drug design against SARS-CoV-2. Comput. Struct. Biotechnol. J. 2022, 20, 5014–5027. [Google Scholar] [CrossRef] [PubMed]
- Do, H.N.; Wang, J.; Bhattarai, A.; Miao, Y. GLOW: A Workflow Integrating Gaussian-Accelerated Molecular Dynamics and Deep Learning for Free Energy Profiling. J. Chem. Theory Comput. 2022, 18, 1423–1436. [Google Scholar] [CrossRef]
- Do, H.N.; Wang, J.; Miao, Y. Deep Learning Dynamic Allostery of G-Protein-Coupled Receptors. JACS Au 2023, 3, 3165–3180. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Yang, W.; Zhao, L.; Zhao, J.; Hu, G. Molecular Mechanism of Phosphorylation-Mediated Impacts on the Conformation Dynamics of GTP-Bound KRAS Probed by GaMD Trajectory-Based Deep Learning. Molecules 2024, 29, 2317. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Yang, W.; Zhao, K.; Sun, Q.; Chen, J. Unveiling Conformational States of CDK6 Caused by Binding of Vcyclin Protein and Inhibitor by Combining Gaussian Accelerated Molecular Dynamics and Deep Learning. Molecules 2024, 29, 2681. [Google Scholar] [CrossRef] [PubMed]
- Genheden, S.; Ryde, U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discov. 2015, 10, 449–461. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.; Sun, H.; Wang, J.; Wang, Z.; Liu, H.; Zhang, J.Z.H.; Hou, T. End-Point Binding Free Energy Calculation with MM/PBSA and MM/GBSA: Strategies and Applications in Drug Design. Chem. Rev. 2019, 119, 9478–9508. [Google Scholar] [CrossRef] [PubMed]
- Molani, F.; Webb, S.; Cho, A.E. Combining QM/MM Calculations with Classical Mining Minima to Predict Protein-Ligand Binding Free Energy. J. Chem. Inf. Model. 2023, 63, 2728–2734. [Google Scholar] [CrossRef] [PubMed]
- Naïm, M.; Bhat, S.; Rankin, K.N.; Dennis, S.; Chowdhury, S.F.; Siddiqi, I.; Drabik, P.; Sulea, T.; Bayly, C.I.; Jakalian, A.; et al. Solvated interaction energy (SIE) for scoring protein-ligand binding affinities. 1. Exploring the parameter space. J. Chem. Inf. Model. 2007, 47, 122–133. [Google Scholar] [CrossRef] [PubMed]
- Popowicz, G.M.; Czarna, A.; Wolf, S.; Wang, K.; Wang, W.; Dömling, A.; Holak, T.A. Structures of low molecular weight inhibitors bound to MDMX and MDM2 reveal new approaches for p53-MDMX/MDM2 antagonist drug discovery. Cell Cycle 2010, 9, 1104–1111. [Google Scholar] [CrossRef] [PubMed]
- Michelsen, K.; Jordan, J.B.; Lewis, J.; Long, A.M.; Yang, E.; Rew, Y.; Zhou, J.; Yakowec, P.; Schnier, P.D.; Huang, X.; et al. Ordering of the N-terminus of human MDM2 by small molecule inhibitors. J. Am. Chem. Soc. 2012, 134, 17059–17067. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, S.S.; Iqbal, S.; Ayyadurai, N.; Gunasekaran, K. Insights in the structural understanding of amyloidogenicity and mutation-led conformational dynamics of amyloid beta (Aβ) through molecular dynamics simulations and principal component analysis. J. Biomol. Struct. Dyn. 2022, 40, 5577–5587. [Google Scholar] [CrossRef] [PubMed]
- Sittel, F.; Jain, A.; Stock, G. Principal component analysis of molecular dynamics: On the use of Cartesian vs. internal coordinates. J. Chem. Phys. 2014, 141, 014111. [Google Scholar] [CrossRef]
- Ichiye, T.; Karplus, M. Collective motions in proteins: A covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulations. Proteins 1991, 11, 205–217. [Google Scholar] [CrossRef]
- Chen, J.; Wang, L.; Wang, W.; Sun, H.; Pang, L.; Bao, H. Conformational transformation of switch domains in GDP/K-Ras induced by G13 mutants: An investigation through Gaussian accelerated molecular dynamics simulations and principal component analysis. Comput. Biol. Med. 2021, 135, 104639. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Li, C.; Pazgier, M.; Li, C.; Mao, Y.; Lv, Y.; Gu, B.; Wei, G.; Yuan, W.; Zhan, C.; et al. D-peptide inhibitors of the p53-MDM2 interaction for targeted molecular therapy of malignant neoplasms. Proc. Natl. Acad. Sci. USA 2010, 107, 14321–14326. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Pazgier, M.; Li, C.; Yuan, W.; Li, C.; Lu, W. A left-handed solution to peptide inhibition of the p53-MDM2 interaction. Angew. Chem. Int. Ed. Engl. 2010, 49, 3649–3652. [Google Scholar] [CrossRef] [PubMed]
- Strizhak, A.V.; Babii, O.; Afonin, S.; Bakanovich, I.; Pantelejevs, T.; Xu, W.; Fowler, E.; Eapen, R.; Sharma, K.; Platonov, M.O.; et al. Diarylethene moiety as an enthalpy-entropy switch: Photoisom-erizable stapled peptides for modulating p53/MDM2 interaction. Org. Biomol. Chem. 2020, 18, 5359–5369. [Google Scholar] [CrossRef]
- Anandakrishnan, R.; Aguilar, B.; Onufriev, A.V. H++ 3.0: Automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012, 40, W537–W541. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham, T.E., III; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Kasavajhala, K.; Belfon, K.A.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Man, V.H.; Yang, W.; Lee, T.S.; Wang, J. A fast and high-quality charge model for the next generation general AMBER force field. J. Chem. Phys. 2020, 153, 114502. [Google Scholar] [CrossRef] [PubMed]
- Nayar, D.; Agarwal, M.; Chakravarty, C. Comparison of Tetrahedral Order, Liquid State Anomalies, and Hydration Behavior of mTIP3P and TIP4P Water Models. J. Chem. Theory Comput. 2011, 7, 3354–3367. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E., III. Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E., III. Molecular dynamics simulations of the dynamic and energetic properties of alkali and halide ions using water-model-specific ion parameters. J. Phys. Chem. B 2009, 113, 13279–13290. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; Sinko, W.; Pierce, L.; Bucher, D.; Walker, R.C.; McCammon, J.A. Improved Reweighting of Accelerated Molecular Dynamics Simulations for Free Energy Calculation. J. Chem. Theory Comput. 2014, 10, 2677–2689. [Google Scholar] [CrossRef]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Izaguirre, J.A.; Catarello, D.P.; Wozniak, J.M.; Skeel, R.D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef] [PubMed]
- Götz, A.W.; Williamson, M.J.; Xu, D.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. [Google Scholar] [CrossRef] [PubMed]
- McGibbon, R.T.; Beauchamp, K.A.; Harrigan, M.P.; Klein, C.; Swails, J.M.; Hernández, C.X.; Schwantes, C.R.; Wang, L.P.; Lane, T.J.; Pande, V.S. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 2015, 109, 1528–1532. [Google Scholar] [CrossRef] [PubMed]
- Kotikalapudi, R. Keras-Vis; GitHub: San Francisco, CA, USA, 2017. [Google Scholar]
- Roe, D.R.; Cheatham, T.E., III. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins 2004, 55, 383–394. [Google Scholar] [CrossRef]
- Miller, B.R., III; McGee, T.D., Jr.; Swails, J.M.; Homeyer, N.; Gohlke, H.; Roitberg, A.E. MMPBSA.py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. [Google Scholar] [CrossRef]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into protein-protein binding by binding free energy calculation and free energy decomposition for the Ras-Raf and Ras-RalGDS complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef]
- Purisima, E.O. Fast summation boundary element method for calculating solvation free energies of macromolecules. J. Comput. Chem. 1998, 19, 1494–1504. [Google Scholar] [CrossRef]
- Purisima, E.O.; Nilar, S.H. A simple yet accurate boundary element method for continuum dielectric calculations. J. Comput. Chem. 1995, 16, 681–689. [Google Scholar] [CrossRef]
- Bhat, S.; Purisima, E.O. Molecular surface generation using a variableradius solvent probe. Proteins 2006, 62, 244–261. [Google Scholar] [CrossRef] [PubMed]
- Perdih, A.; Bren, U.; Solmajer, T. Binding free energy calculations of N-sulphonyl-glutamic acid inhibitors of MurD ligase. J. Mol. Model. 2009, 15, 983–996. [Google Scholar] [CrossRef] [PubMed]
- Cui, Q.; Sulea, T.; Schrag, J.D.; Munger, C.; Hung, M.N.; Naïm, M.; Cygler, M.; Purisima, E.O. Molecular dynamics-solvated interaction energy studies of protein-protein interactions: The MP1-p14 scaffolding complex. J. Mol. Biol. 2008, 379, 787–802. [Google Scholar] [CrossRef]

| Complex | K23-MDM2 | 0Y7-MDM2 | PDI-MDM2 | PDI6W-MDM2 | ||||
|---|---|---|---|---|---|---|---|---|
| Average | Std | Average | Std | Average | Std | Average | Std | |
| −105.32 | 9.38 | −2.43 | 7.63 | −222.94 | 36.30 | −250.13 | 33.93 | |
| −37.68 | 3.46 | −34.25 | 4.05 | −61.75 | 4.29 | −63.96 | 4.94 | |
| 119.19 | 9.40 | 12.76 | 6.45 | 244.68 | 34.79 | 272.15 | 32.41 | |
| −4.63 | 0.38 | −4.48 | 0.58 | −7.80 | 0.57 | −8.10 | 0.60 | |
| 13.87 | 1.67 | 10.33 | 2.96 | 21.73 | 3.55 | 22.03 | 4.00 | |
| −18.12 | 4.63 | −15.80 | 5.37 | −25.86 | 6.28 | −25.38 | 6.14 | |
| −10.31 | −12.61 | −21.96 | −24.67 | |||||
| −7.89 | −9.98 | −10.01 | −10.18 | |||||
| Complex | K23-MDM2 | 0Y7-MDM2 | PDI-MDM2 | PDI6W-MDM2 | ||||
|---|---|---|---|---|---|---|---|---|
| Average | Std | Average | Std | Average | Std | Average | Std | |
| −36.07 | 2.97 | −36.96 | 3.79 | −62.01 | 4.21 | −63.96 | 4.94 | |
| −47.60 | 4.02 | −3.06 | 4.14 | −99.20 | 17.98 | −111.21 | 15.07 | |
| −6.59 | 0.30 | −7.14 | 0.48 | −10.85 | 0.65 | −11.33 | 0.63 | |
| 49.23 | 4.16 | 5.56 | 2.71 | 99.09 | 16.43 | 111.10 | 13.82 | |
| −7.19 | −7.25 | −10.53 | −10.79 | |||||
| −7.89 | −9.98 | −10.01 | −10.18 | |||||
| Inhibitor | Donor | Acceptor | a Distance(Å) | a Angle(°) | b Occupied(%) |
|---|---|---|---|---|---|
| K23 | K23:N8-H4 | Leu54:O | 2.89 | 157.08 | 98.58 |
| PDI6W | Phe19’: N-H | Gln72: OE1 | 2.98 | 154.03 | 76.31 |
| Trp23’: NE1- HE1 | Leu54: O | 2.89 | 148.67 | 97.62 | |
| PDI | Phe19’: N-H | Gln72: OE1 | 2.98 | 154.83 | 81.36 |
| Trp23’: NE1- HE1 | Leu54: O | 2.92 | 149.58 | 95.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Wang, J.; Zhao, L.; Chen, J. Insights into the Interaction Mechanisms of Peptide and Non-Peptide Inhibitors with MDM2 Using Gaussian-Accelerated Molecular Dynamics Simulations and Deep Learning. Molecules 2024, 29, 3377. https://doi.org/10.3390/molecules29143377
Yang W, Wang J, Zhao L, Chen J. Insights into the Interaction Mechanisms of Peptide and Non-Peptide Inhibitors with MDM2 Using Gaussian-Accelerated Molecular Dynamics Simulations and Deep Learning. Molecules. 2024; 29(14):3377. https://doi.org/10.3390/molecules29143377
Chicago/Turabian StyleYang, Wanchun, Jian Wang, Lu Zhao, and Jianzhong Chen. 2024. "Insights into the Interaction Mechanisms of Peptide and Non-Peptide Inhibitors with MDM2 Using Gaussian-Accelerated Molecular Dynamics Simulations and Deep Learning" Molecules 29, no. 14: 3377. https://doi.org/10.3390/molecules29143377
APA StyleYang, W., Wang, J., Zhao, L., & Chen, J. (2024). Insights into the Interaction Mechanisms of Peptide and Non-Peptide Inhibitors with MDM2 Using Gaussian-Accelerated Molecular Dynamics Simulations and Deep Learning. Molecules, 29(14), 3377. https://doi.org/10.3390/molecules29143377






