Effect of Diffusion on the Ultimate Axial Load of Complex-Shaped Al-SiC Samples: A Molecular Dynamics Study
Abstract
1. Introduction
2. Simulation Results and Discussion
2.1. Effects of Diffusion on the Young’s Modulus of Al-SiC Composite
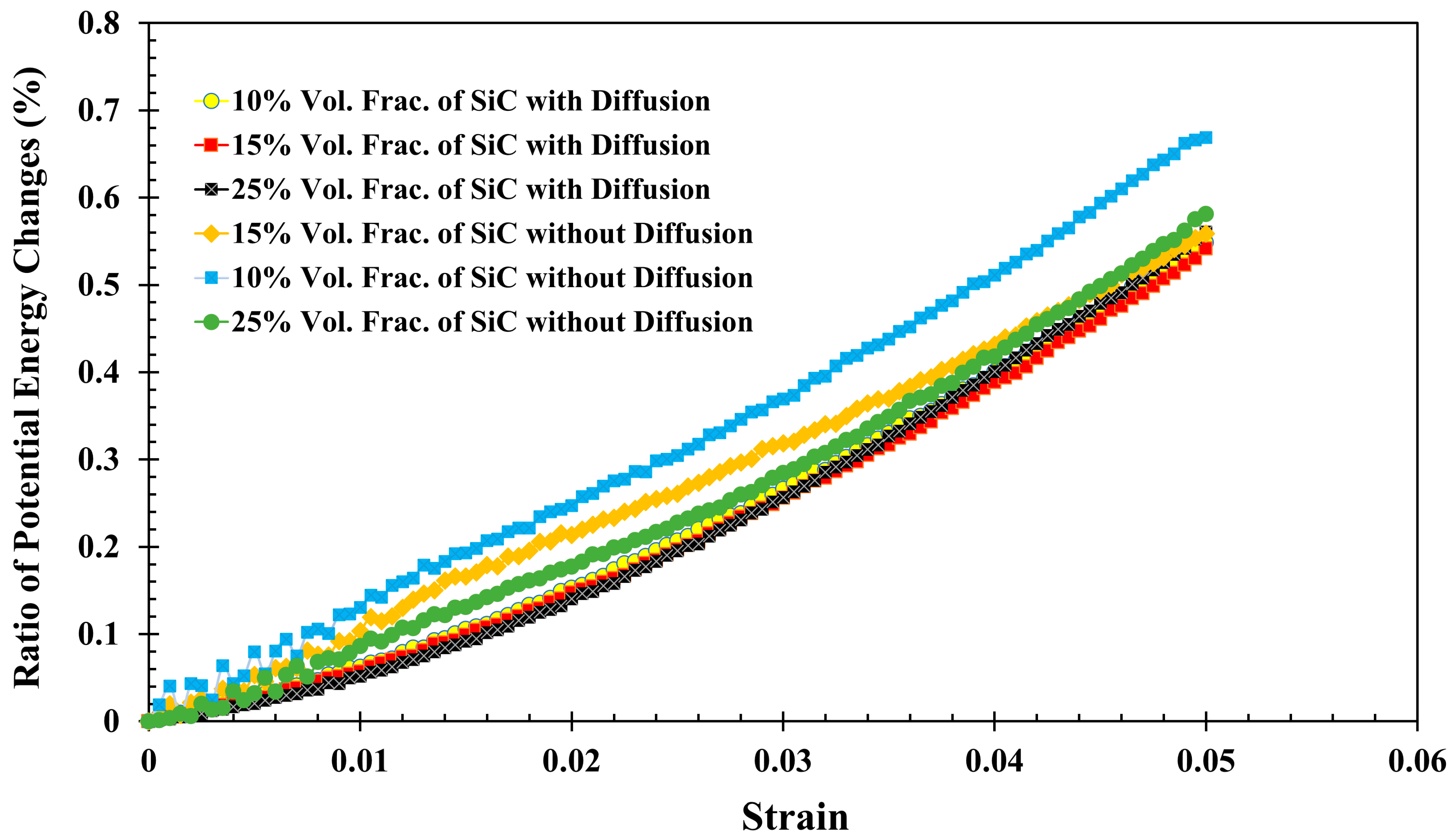
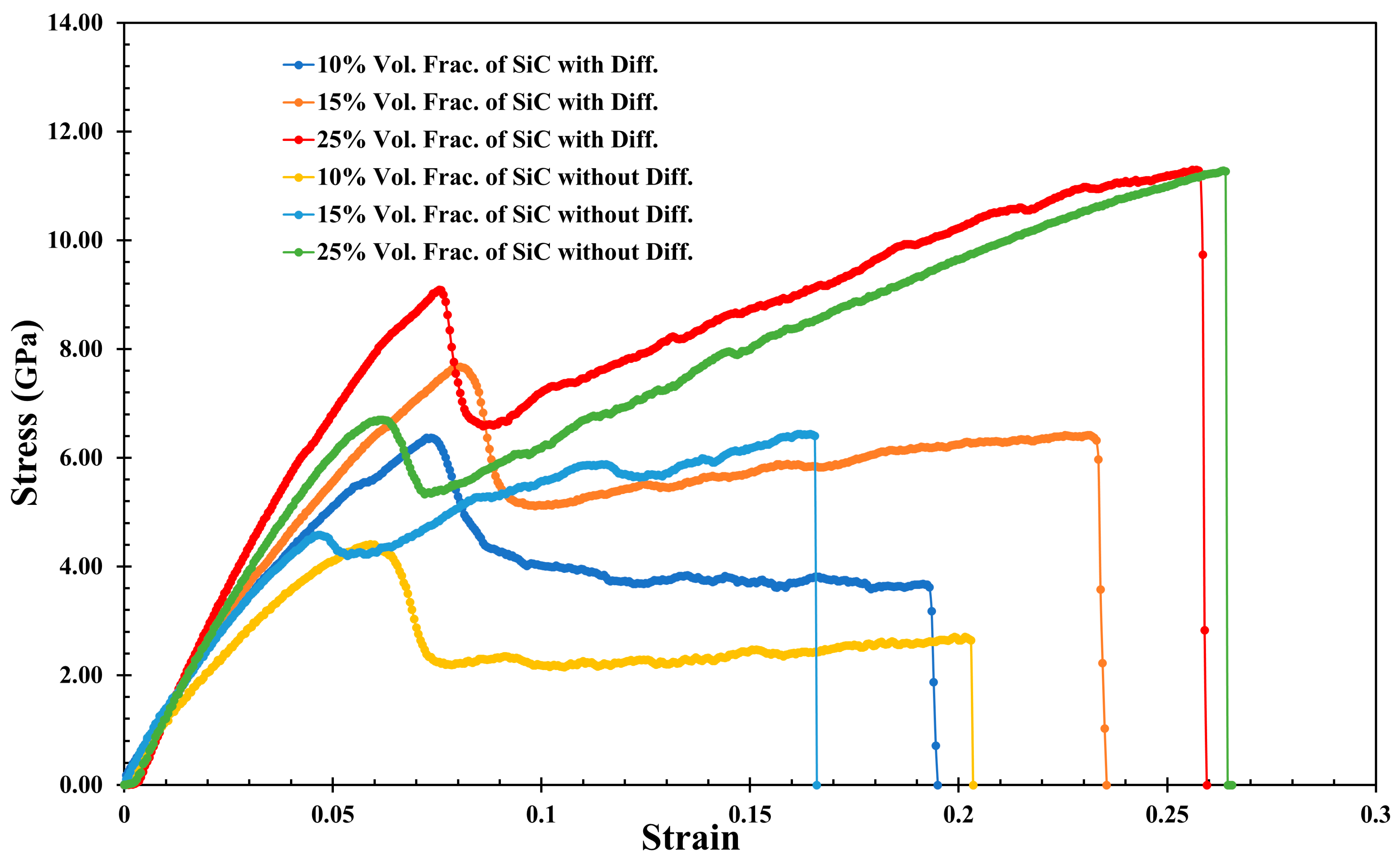
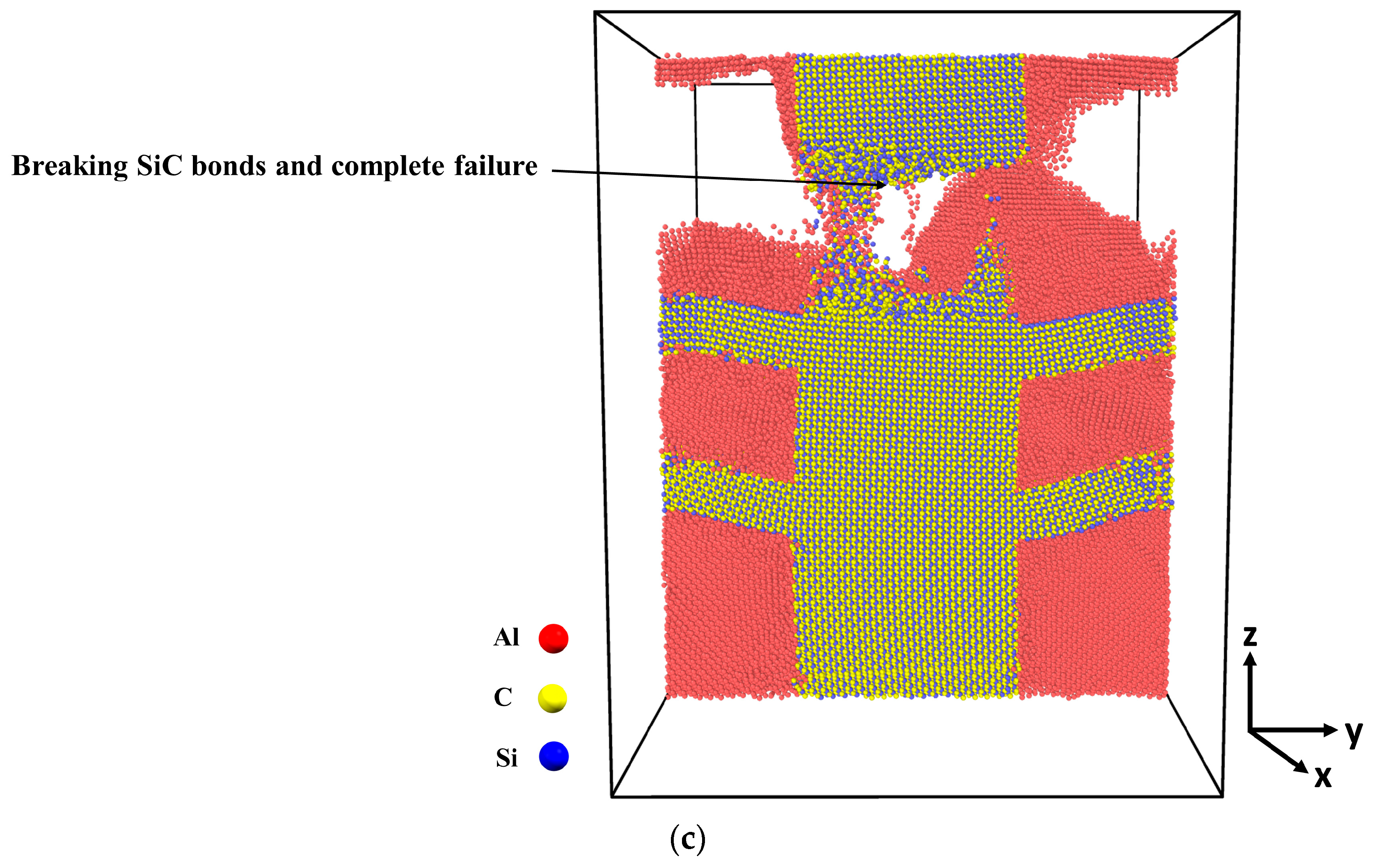
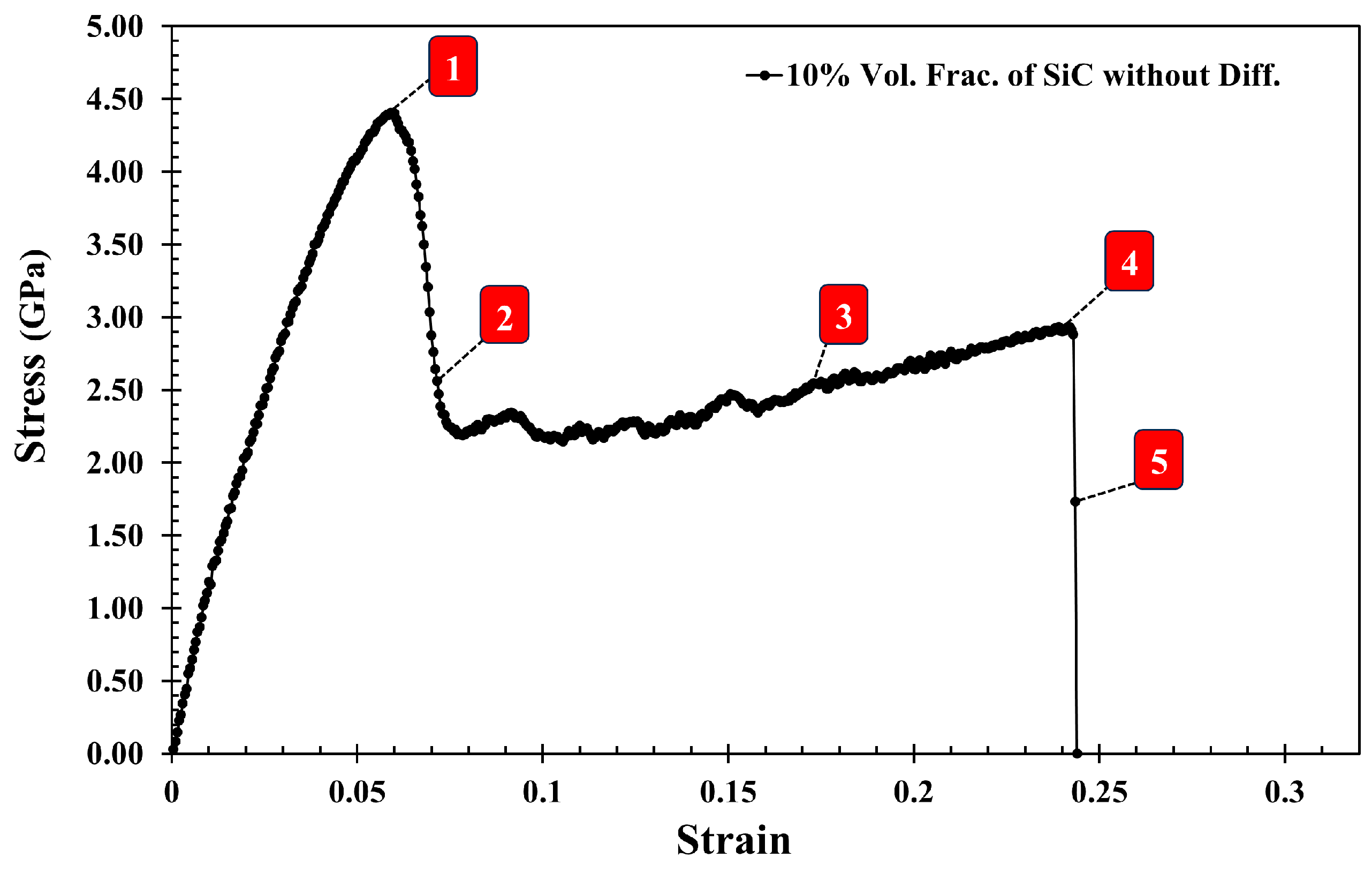
2.2. Tensile Test Simulation
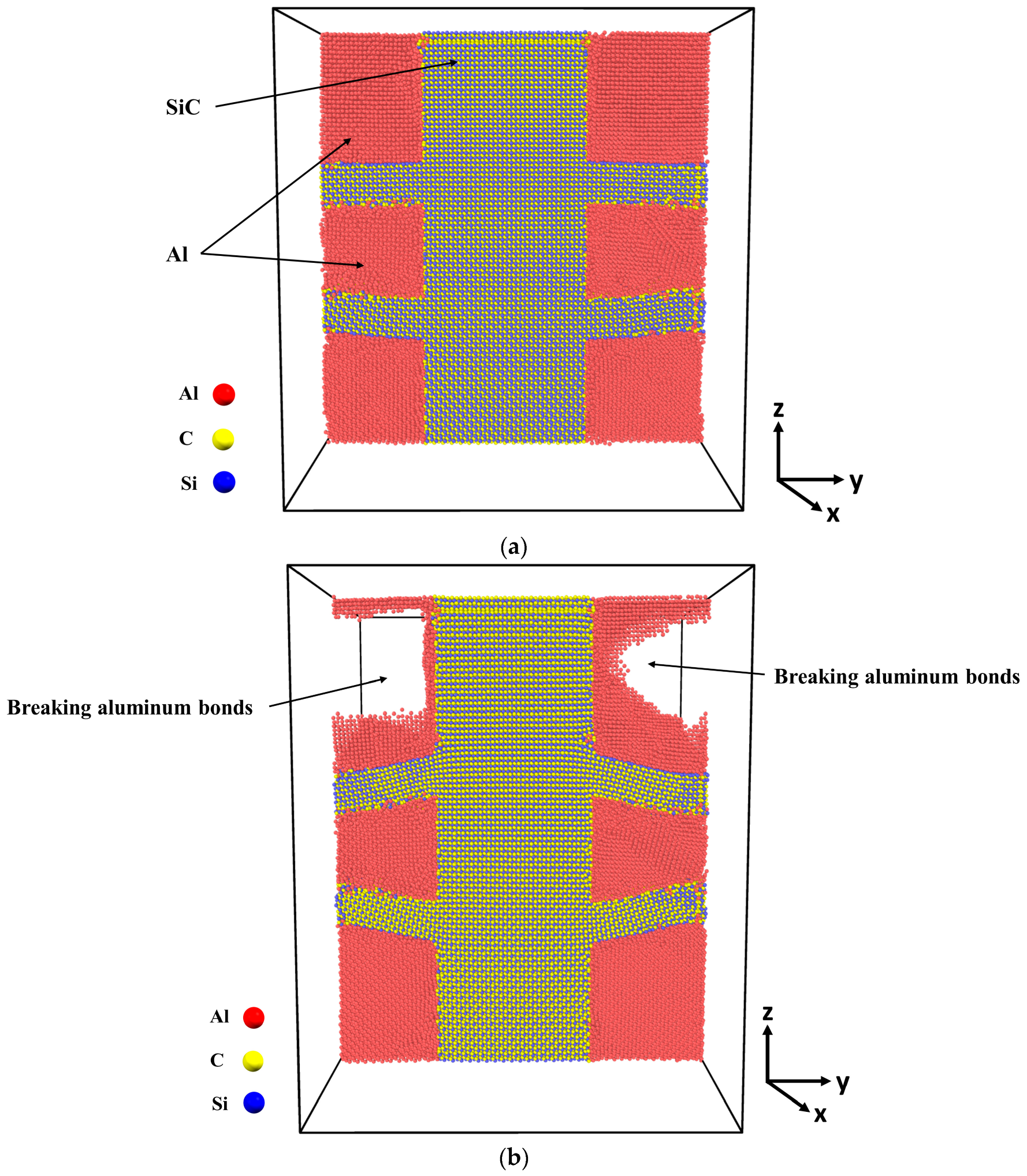
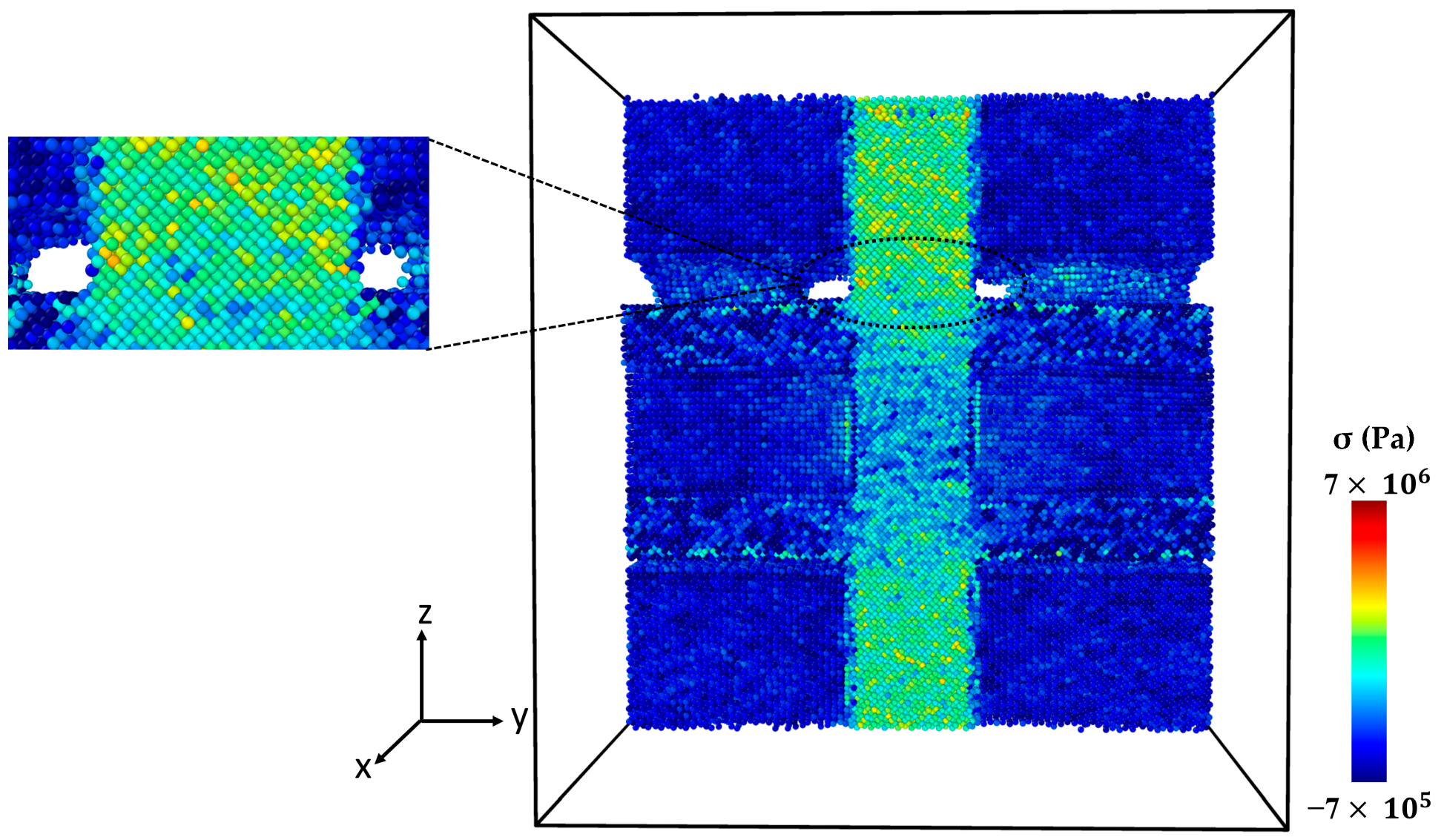
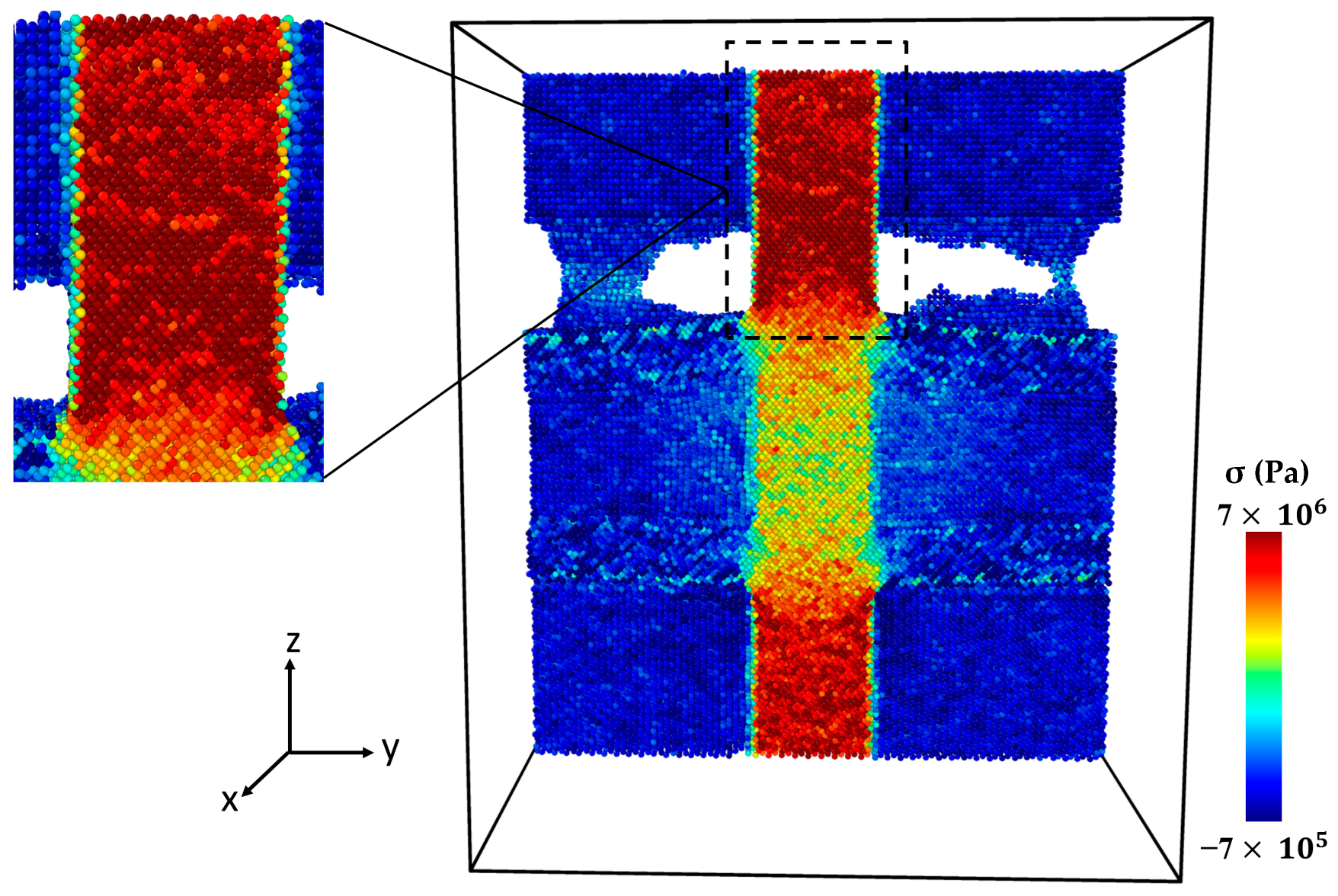
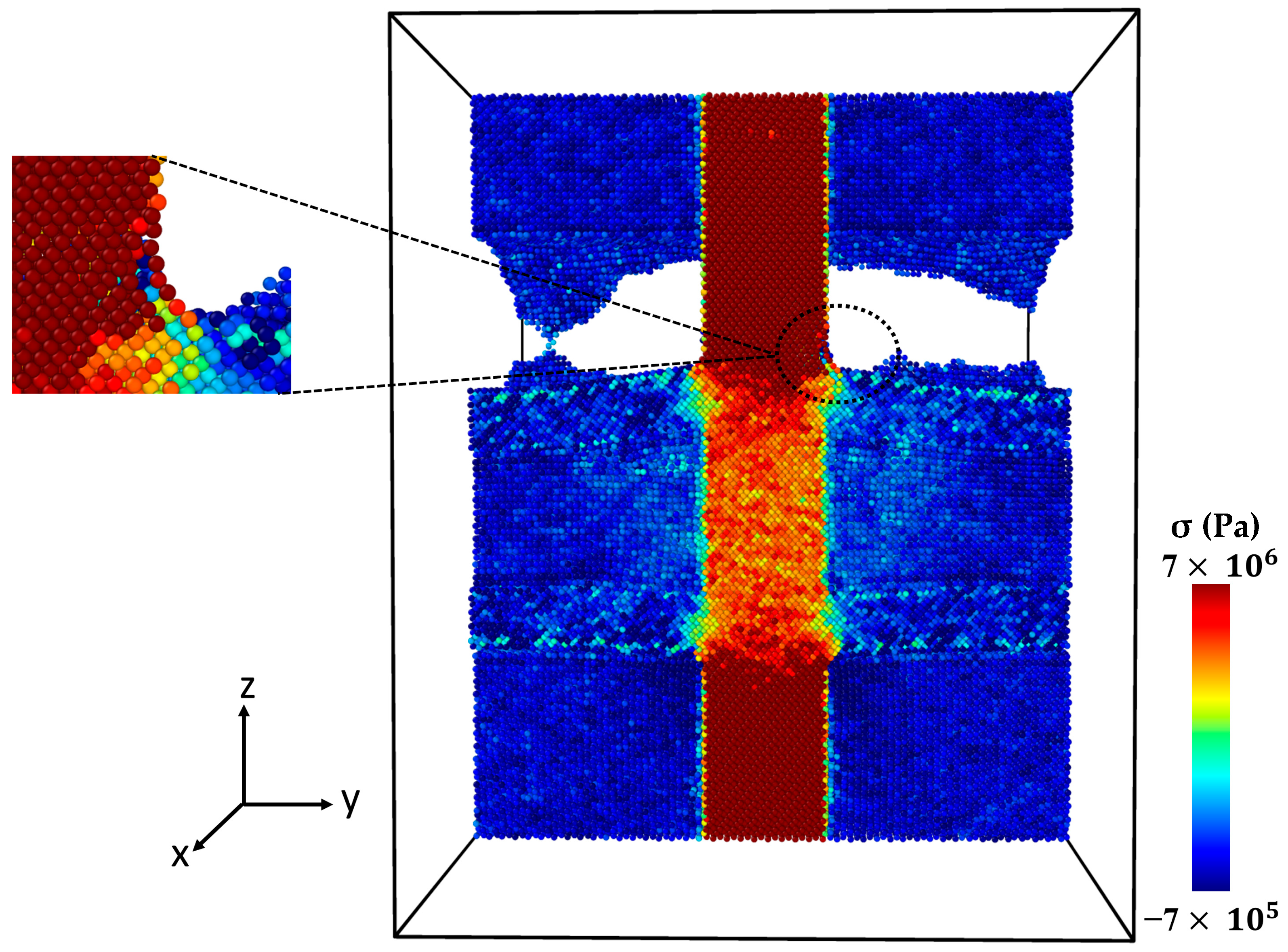
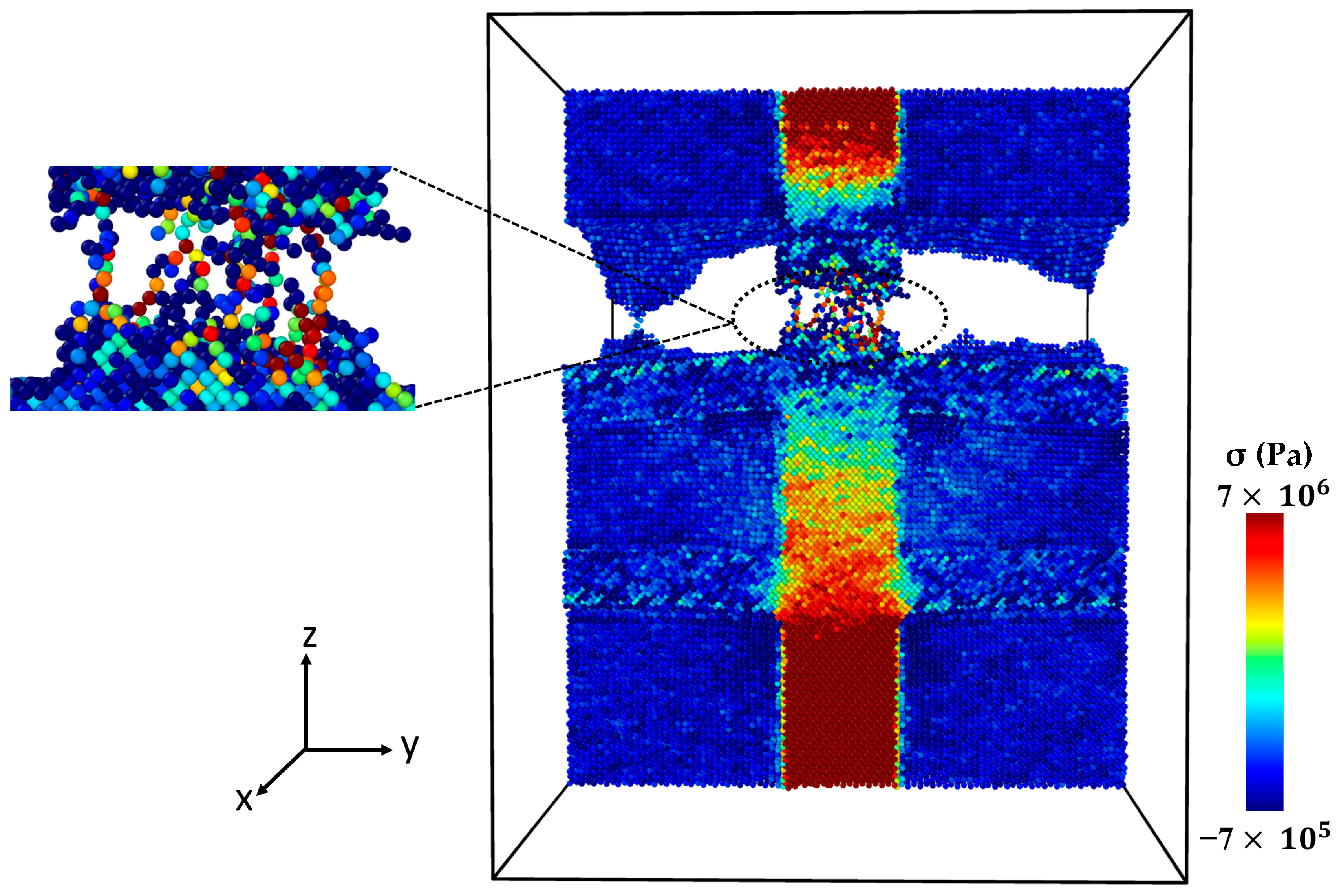
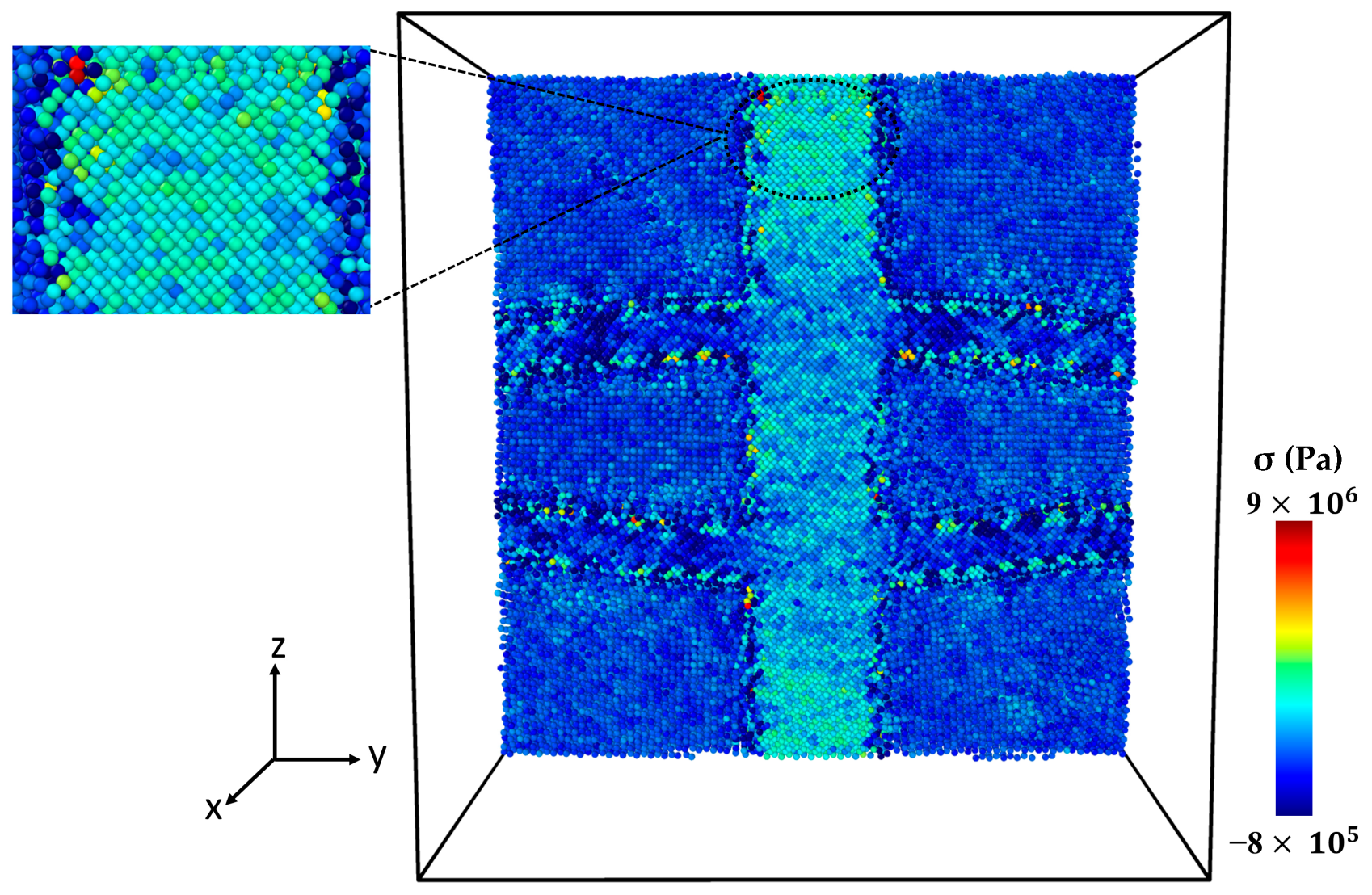
2.3. Analyzing Local Stress Distribution in Al-SiC Composites under Tensile Deformation
3. Methodology
3.1. Potential Functions
3.2. Molecular Dynamics Model
3.3. Loading Conditions
4. Conclusions
- As the volume fraction of SiC increased, Young’s modulus of the Al-SiC composite in all the models showed a significant increase.
- The Al-SiC composite strength rose dramatically with increasing SiC volume fraction in all the models.
- The results indicate that diffusion does not significantly affect Young’s modulus of the Al-SiC composite when compared to the scenarios without considering diffusion. However, diffusion does result in a notable increase in the strength of the composite.
- The strength properties of the Al-SiC composite were better along the z-axis than the x-axis, potentially due to its unique geometric shape.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhoi, N.K.; Singh, H.; Pratap, S. Developments in the Aluminum Metal Matrix Composites Reinforced by Micro/Nano Particles—A Review. J. Compos. Mater. 2020, 54, 813–833. [Google Scholar] [CrossRef]
- Hayat, M.D.; Singh, H.; He, Z.; Cao, P. Titanium Metal Matrix Composites: An Overview. Compos. Part A Appl. Sci. Manuf. 2019, 121, 418–438. [Google Scholar] [CrossRef]
- Imran, M.; Khan, A.R.A. Characterization of Al-7075 Metal Matrix Composites: A Review. J. Mater. Res. Technol. 2019, 8, 3347–3356. [Google Scholar] [CrossRef]
- Bodukuri, A.K.; Eswaraiah, K.; Rajendar, K.; Sampath, V. Fabrication of Al–SiC–B4C Metal Matrix Composite by Powder Metallurgy Technique and Evaluating Mechanical Properties. Perspect. Sci. 2016, 8, 428–431. [Google Scholar] [CrossRef]
- Baimova, J.A.; Shcherbinin, S.A. Metal/Graphene Composites: A Review on the Simulation of Fabrication and Study of Mechanical Properties. Materials 2022, 16, 202. [Google Scholar] [CrossRef]
- Hu, Z.; Tong, G.; Lin, D.; Chen, C.; Guo, H.; Xu, J.; Zhou, L. Graphene-Reinforced Metal Matrix Nanocomposites—A Review. Mater. Sci. Technol. 2016, 32, 930–953. [Google Scholar] [CrossRef]
- Previtali, B.; Pocci, D.; Taccardo, C. Application of Traditional Investment Casting Process to Aluminium Matrix Composites. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1606–1617. [Google Scholar] [CrossRef]
- Teng, F.; Yu, K.; Luo, J.; Fang, H.; Shi, C.; Dai, Y.; Xiong, H. Microstructures and Properties of Al–50%SiC Composites for Electronic Packaging Applications. Trans. Nonferrous Met. Soc. China 2016, 26, 2647–2652. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, H.; Wang, Z.; Li, Q.; Wu, J. Mechanical Properties and Corrosion Behavior of Al/SiC Composites. J. Alloys Compd. 2016, 678, 23–30. [Google Scholar] [CrossRef]
- Wang, J.; Yang, G. Numerical Modeling of the Damping Capacity of Al/SiC(p). Met. Mater. Trans. A 2003, 34, 1387–1392. [Google Scholar] [CrossRef]
- Kan, Y.; Liu, Z.G.; Zhang, S.H.; Zhang, L.W.; Cheng, M.; Song, H.W. Microstructure-Based Numerical Simulation of the Tensile Behavior of SiCp/Al Composites. J. Mater. Eng. Perform. 2014, 23, 1069–1076. [Google Scholar] [CrossRef]
- Gatea, S.; Jwad, T.; Chen, F.; Ou, H. Micromechanical Modeling of the Deformation and Damage Behavior of Al6092/SiC Particle Metal Matrix Composites. J. Mate. Eng. Perform. 2023, 32, 10680–10701. [Google Scholar] [CrossRef]
- Gelpi, J.; Hospital, A.; Goñi, R.; Orozco, M. Molecular Dynamics Simulations: Advances and Applications. Adv. Appl. Bioinform. Chem. 2015, 8, 37. [Google Scholar] [CrossRef]
- Wolf, D.; Yamakov, V.; Phillpot, S.R.; Mukherjee, A.; Gleiter, H. Deformation of Nanocrystalline Materials by Molecular-Dynamics Simulation: Relationship to Experiments? Acta Mater. 2005, 53, 1–40. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In ’T Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Huo, S.; Xie, L.; Xiang, J.; Pang, S.; Hu, F.; Umer, U. Atomic-Level Study on Mechanical Properties and Strengthening Mechanisms of Al/SiC Nano–Composites. Appl. Phys. A 2018, 124, 209. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Lu, C.; Xue, T.; Hu, B.; Zhang, C. Microscopic Residual Stress Evolution at the SiC/Al Interface during Nanoindentation via Molecular Dynamics Simulation. Surf. Interfaces 2022, 33, 102210. [Google Scholar] [CrossRef]
- Vu, X.-T.; Nguyen, V.-H.; Tran, T.-V.; Nguyen, Q.-M.; Doan, D.-Q. Mechanical Characteristics and Deformation Behavior of Al Polycrystal Reinforced with SiC Particles. J. Phys. Chem. Solids 2023, 183, 111617. [Google Scholar] [CrossRef]
- Lin, K.; Zeng, M.; Chen, H.; Tao, X.; Ouyang, Y.; Du, Y.; Peng, Q. Dynamic Strength, Reinforcing Mechanism and Damage of Ceramic Metal Composites. Int. J. Mech. Sci. 2022, 231, 107580. [Google Scholar] [CrossRef]
- Tahani, M.; Postek, E.; Sadowski, T. Investigating the Influence of Diffusion on the Cohesive Zone Model of the SiC/Al Composite Interface. Molecules 2023, 28, 6757. [Google Scholar] [CrossRef]
- Hamed Mashhadzadeh, A.; Ghorbanzadeh Ahangari, M.; Dadrasi, A.; Fathalian, M. Theoretical Studies on the Mechanical and Electronic Properties of 2D and 3D Structures of Beryllium-Oxide Graphene and Graphene Nanobud. Appl. Surf. Sci. 2019, 476, 36–48. [Google Scholar] [CrossRef]
- Ahangari, M.G.; Mashhadzadeh, A.H.; Fathalian, M.; Dadrasi, A.; Rostamiyan, Y.; Mallahi, A. Effect of Various Defects on Mechanical and Electronic Properties of Zinc-Oxide Graphene-like Structure: A DFT Study. Vacuum 2019, 165, 26–34. [Google Scholar] [CrossRef]
- Fathalian, M.; Postek, E.; Sadowski, T. Mechanical and Electronic Properties of Al(111)/6H-SiC Interfaces: A DFT Study. Molecules 2023, 28, 4345. [Google Scholar] [CrossRef]
- Fathalian, M.; Postek, E.; Tahani, M.; Sadowski, T. A Comprehensive Study of Al2O3 Mechanical Behavior Using Density Functional Theory and Molecular Dynamics. Molecules 2024, 29, 1165. [Google Scholar] [CrossRef]
- Agrawal, P.M.; Sudalayandi, B.S.; Raff, L.M.; Komanduri, R. A Comparison of Different Methods of Young’s Modulus Determination for Single-Wall Carbon Nanotubes (SWCNT) Using Molecular Dynamics (MD) Simulations. Comput. Mater. Sci. 2006, 38, 271–281. [Google Scholar] [CrossRef]
- Tahani, M.; Postek, E.; Motevalizadeh, L.; Sadowski, T. Effect of Vacancy Defect Content on the Interdiffusion of Cubic and Hexagonal SiC/Al Interfaces: A Molecular Dynamics Study. Molecules 2023, 28, 744. [Google Scholar] [CrossRef]
- Tayyebi, M.; Eghbali, B. Microstructure and Mechanical Properties of SiC-Particle-Strengthening Tri-Metal Al/Cu/Ni Composite Produced by Accumulative Roll Bonding Process. Int. J. Min. Met. Mater. 2018, 25, 357–364. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, L.; Chang, Y.; Yan, J. Identification of Post-Necking Stress–Strain Curve for Sheet Metals by Inverse Method. Mech. Mater. 2016, 92, 107–118. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO–the Open Visualization Tool. Modelling Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Kramer, M.J.; Becker, C.A.; Asta, M. Analysis of Semi-Empirical Interatomic Potentials Appropriate for Simulation of Crystalline and Liquid Al and Cu. Philos. Mag. 2008, 88, 1723–1750. [Google Scholar] [CrossRef]
- Mishin, Y.; Farkas, D.; Mehl, M.J.; Papaconstantopoulos, D.A. Interatomic Potentials for Monoatomic Metals from Experimental Data and Ab Initio Calculations. Phys. Rev. B 1999, 59, 3393–3407. [Google Scholar] [CrossRef]
- Erhart, P.; Albe, K. Analytical Potential for Atomistic Simulations of Silicon, Carbon, and Silicon Carbide. Phys. Rev. B 2005, 71, 035211. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, N. An Inverse Adhesion Problem for Extracting Interfacial Pair Potentials for the Al(0 0 1)/3C–SiC(0 0 1) Interface. Inverse Probl. 2008, 24, 035019. [Google Scholar] [CrossRef]
- Tahani, M.; Postek, E.; Sadowski, T. Molecular Dynamics Study of Interdiffusion for Cubic and Hexagonal SiC/Al Interfaces. Crystals 2022, 13, 46. [Google Scholar] [CrossRef]


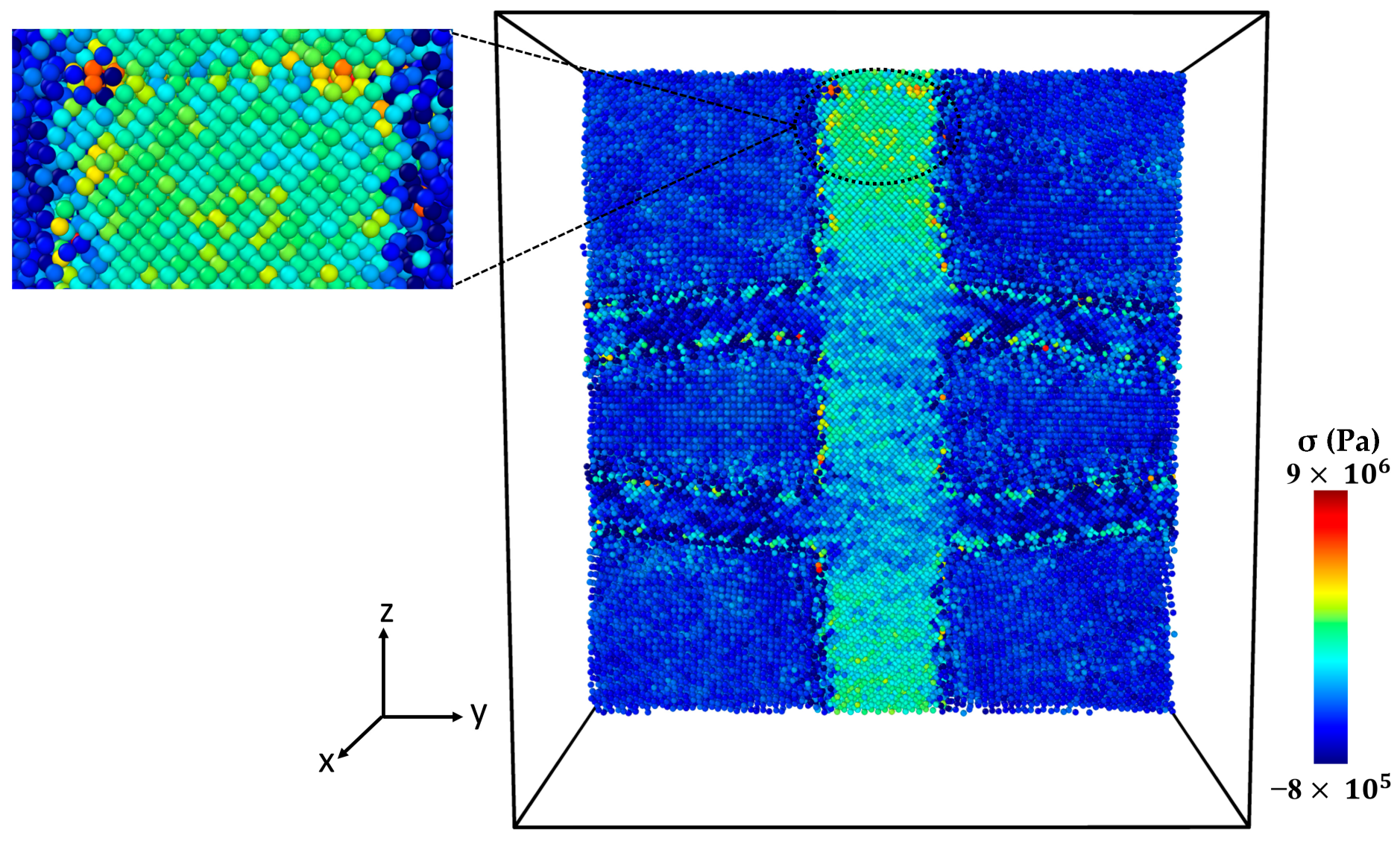
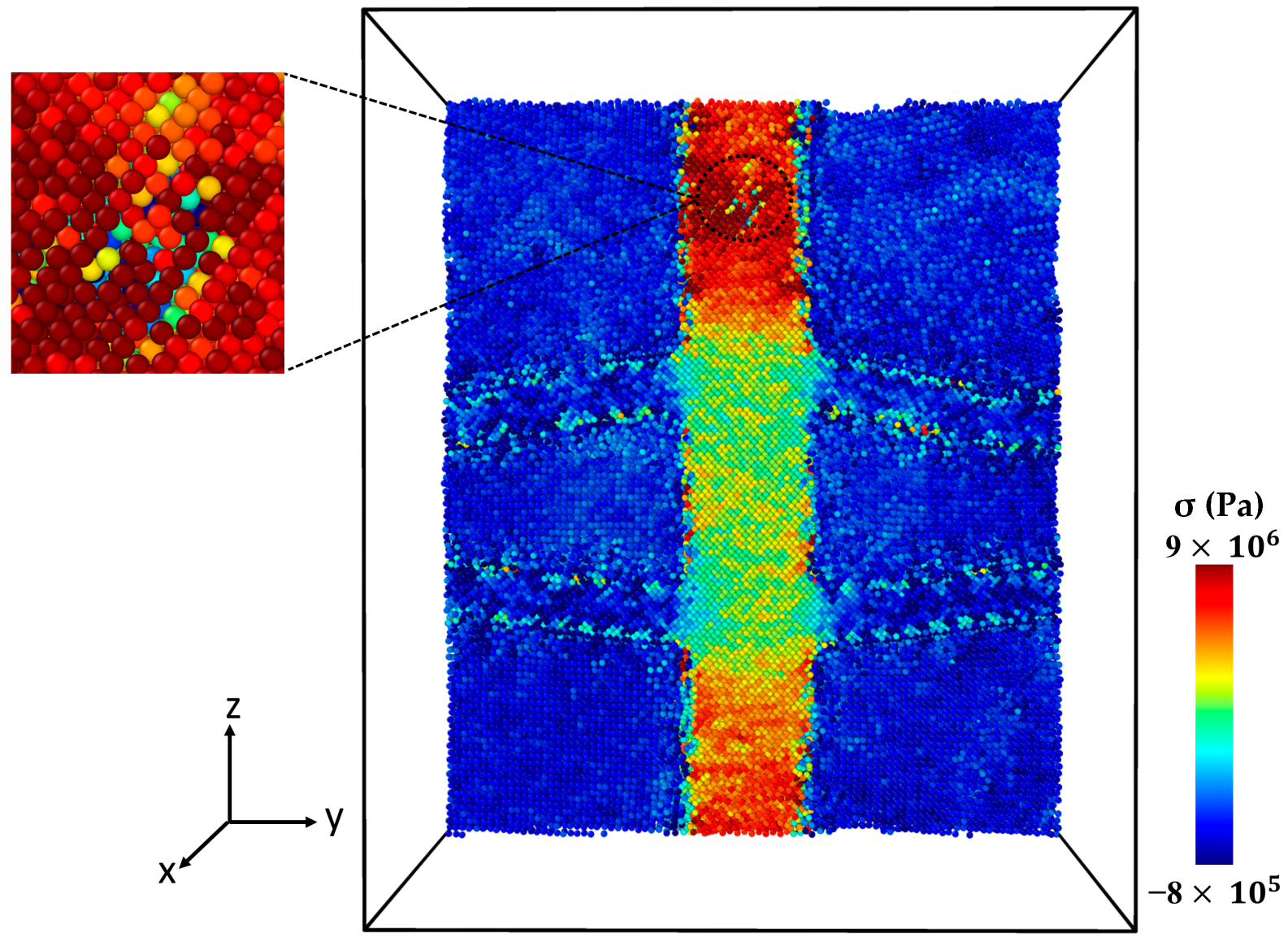
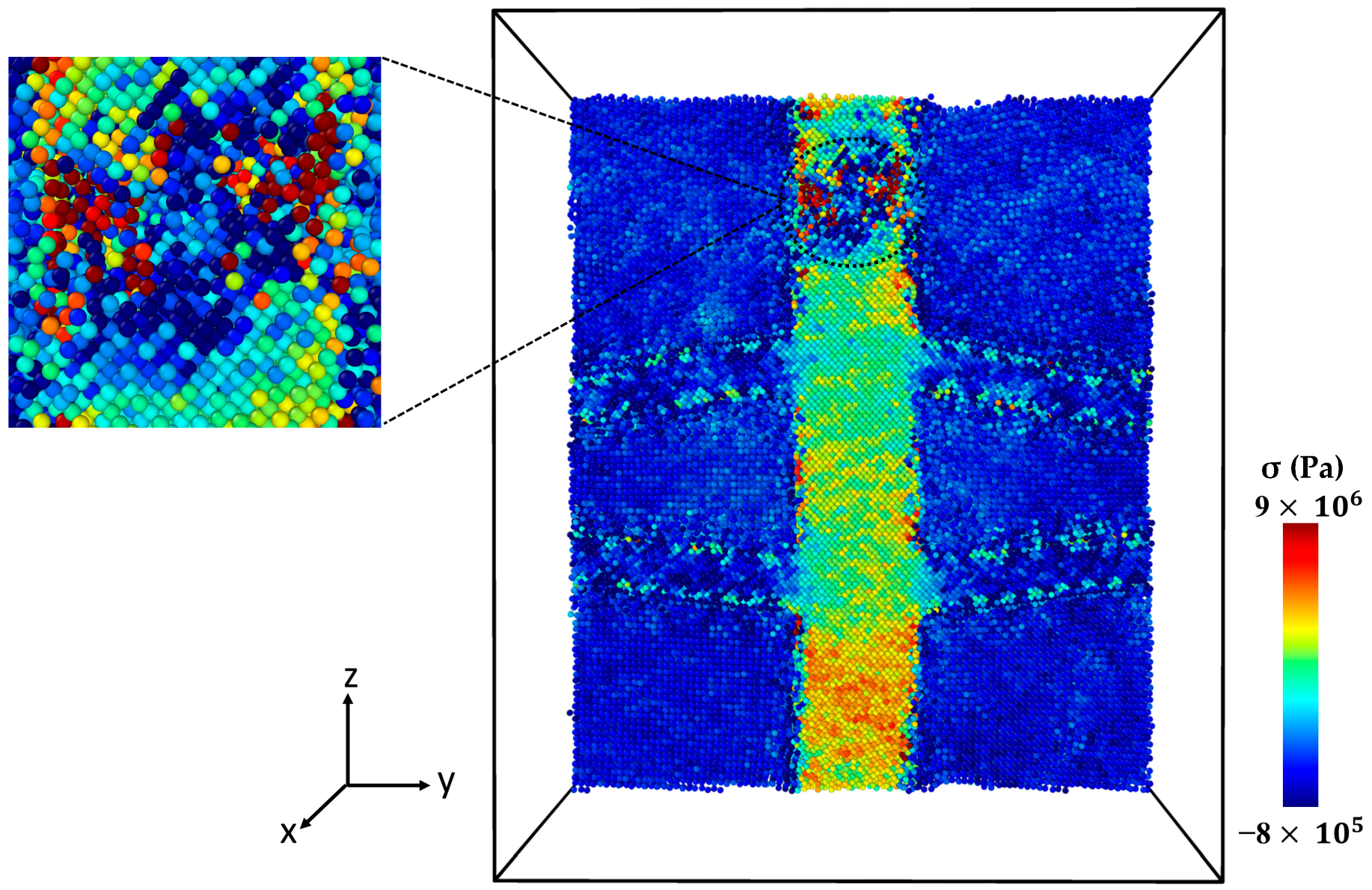
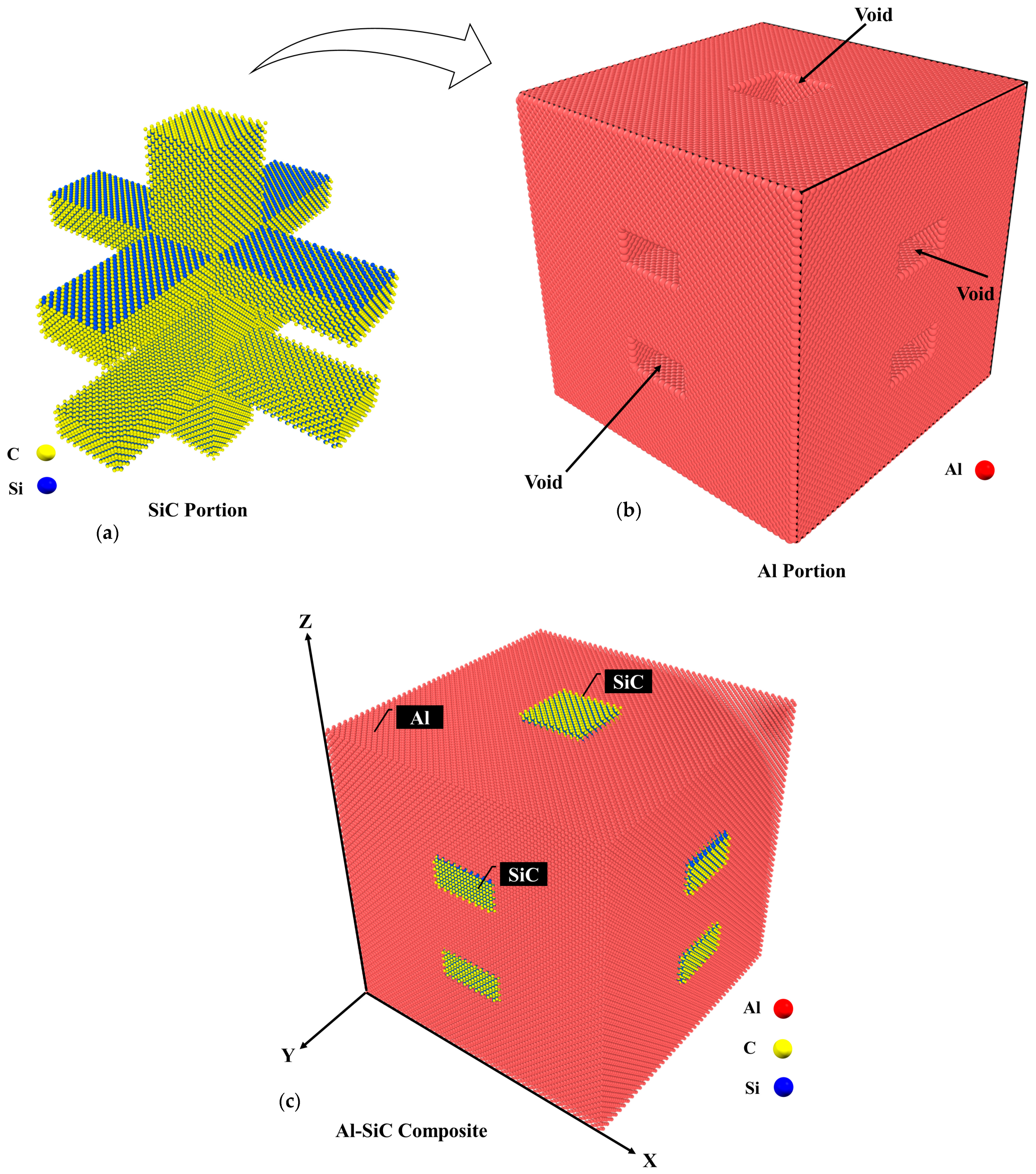
| Volume Fraction of SiC Phase | Young’s Modulus (GPa) | |
|---|---|---|
| 10% | 123.72 | |
| With diffusion | 15% | 135.21 |
| 25% | 141.32 | |
| 10% | 120.42 | |
| Without diffusion | 15% | 132.32 |
| 25% | 139.11 |
| Volume Fraction of SiC Phase | Tensile Ultimate Strength (GPa) | Toughness (GPa) | |
|---|---|---|---|
| With diffusion | 10% | 5.93 | 0.863 |
| 15% | 7.67 | 1.296 | |
| 25% | 11.29 | 2.086 | |
| Without diffusion | 10% | 4.105 | 0.628 |
| 15% | 6.110 | 1.206 | |
| 25% | 11.28 | 1.947 |
| Volume Fraction of SiC Phase | Tensile Ultimate Strength (GPa) | Toughness (GPa) | |
|---|---|---|---|
| 10% | 5.98 | 0.759 | |
| With diffusion | 15% | 6.35 | 0.768 |
| 25% | 6.63 | 0.557 | |
| 10% | 5.04 | 0.857 | |
| Without diffusion | 15% | 5.12 | 0.673 |
| 25% | 5.31 | 0.788 |
| System | Parameters | Value |
|---|---|---|
| Al-SiC | (eV) | 0.4824 |
| α (1/Å) | 1.322 | |
| (1/Å) | 2.92 | |
| Al-C | (eV) | 0.4691 |
| α (1/Å) | 1.738 | |
| (1/Å) | 2.246 |
| Volume Fraction (%) | Type of Atom | Number of Atoms |
|---|---|---|
| 10% | Al | 342,144 |
| Si | 35,964 | |
| C | 38,960 | |
| 15% | Al | 325,458 |
| Si | 52,504 | |
| C | 51,527 | |
| 25% | Al | 298,178 |
| Si | 71,928 | |
| C | 76,648 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathalian, M.; Postek, E.; Tahani, M.; Sadowski, T. Effect of Diffusion on the Ultimate Axial Load of Complex-Shaped Al-SiC Samples: A Molecular Dynamics Study. Molecules 2024, 29, 3343. https://doi.org/10.3390/molecules29143343
Fathalian M, Postek E, Tahani M, Sadowski T. Effect of Diffusion on the Ultimate Axial Load of Complex-Shaped Al-SiC Samples: A Molecular Dynamics Study. Molecules. 2024; 29(14):3343. https://doi.org/10.3390/molecules29143343
Chicago/Turabian StyleFathalian, Mostafa, Eligiusz Postek, Masoud Tahani, and Tomasz Sadowski. 2024. "Effect of Diffusion on the Ultimate Axial Load of Complex-Shaped Al-SiC Samples: A Molecular Dynamics Study" Molecules 29, no. 14: 3343. https://doi.org/10.3390/molecules29143343
APA StyleFathalian, M., Postek, E., Tahani, M., & Sadowski, T. (2024). Effect of Diffusion on the Ultimate Axial Load of Complex-Shaped Al-SiC Samples: A Molecular Dynamics Study. Molecules, 29(14), 3343. https://doi.org/10.3390/molecules29143343








