Electrochemical Circuit Model Based State of Health Prognostics for Evaluation of Reusability of Lithium-Ion Batteries from Electric Vehicle
Abstract
1. Introduction
2. Experimental and Theory Formulation
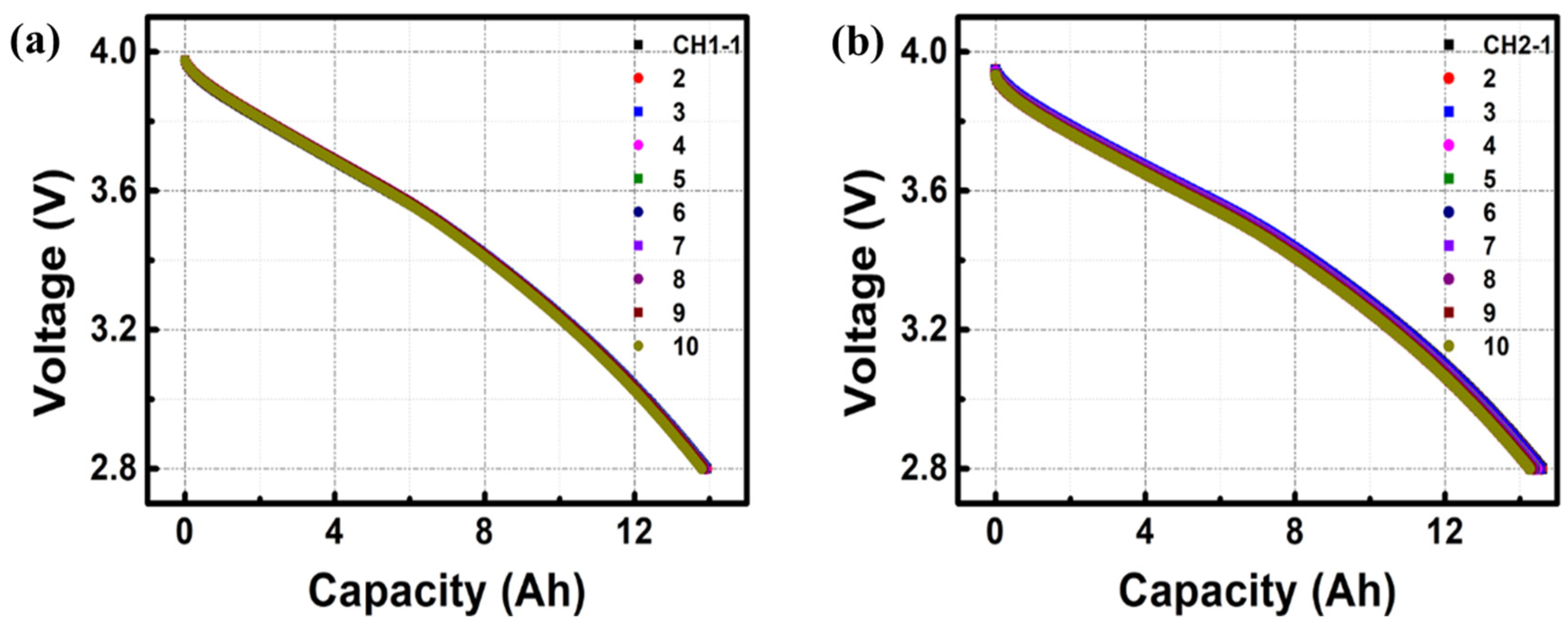
2.1. Experimental
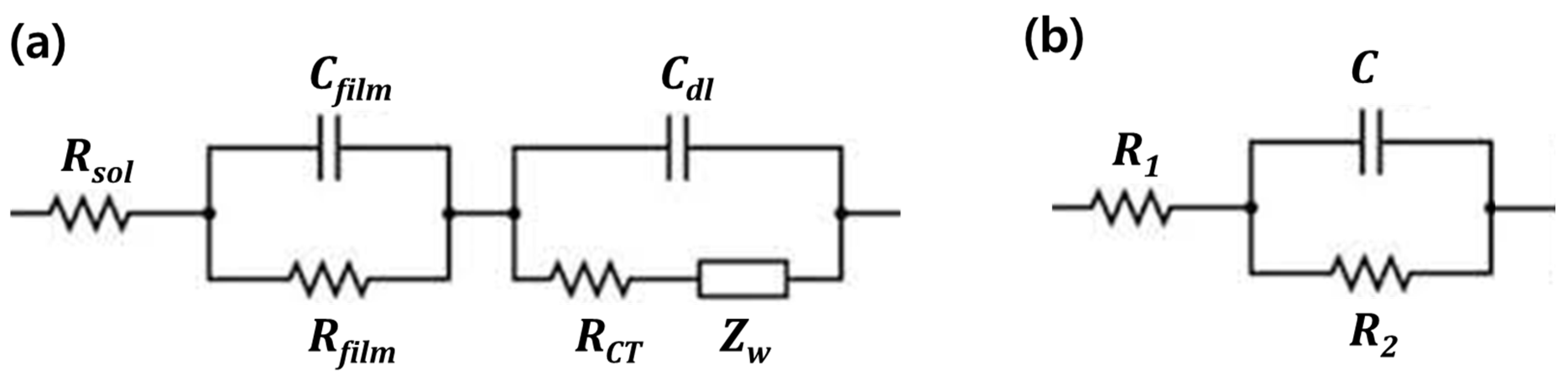
2.2. Cycle Performance Prediction Equation Based on Equivalent Circuit Model Theory
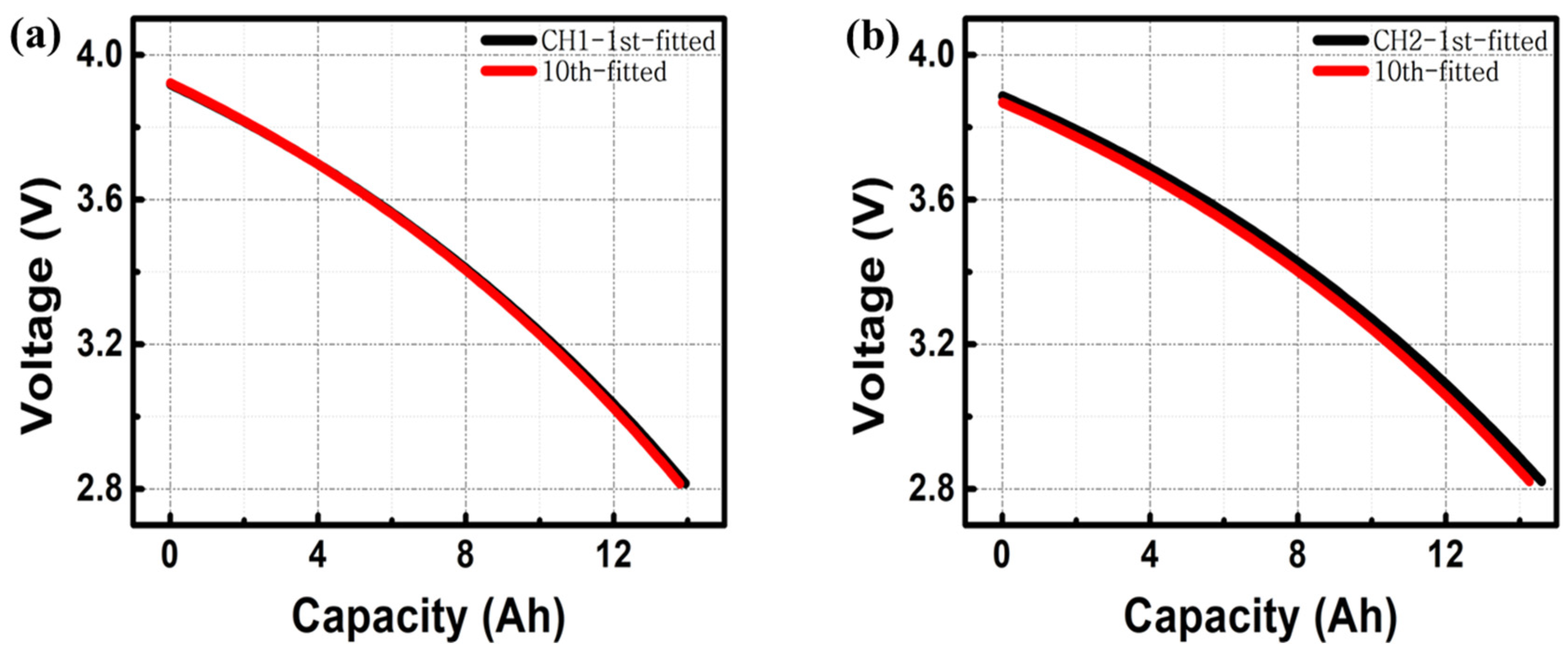
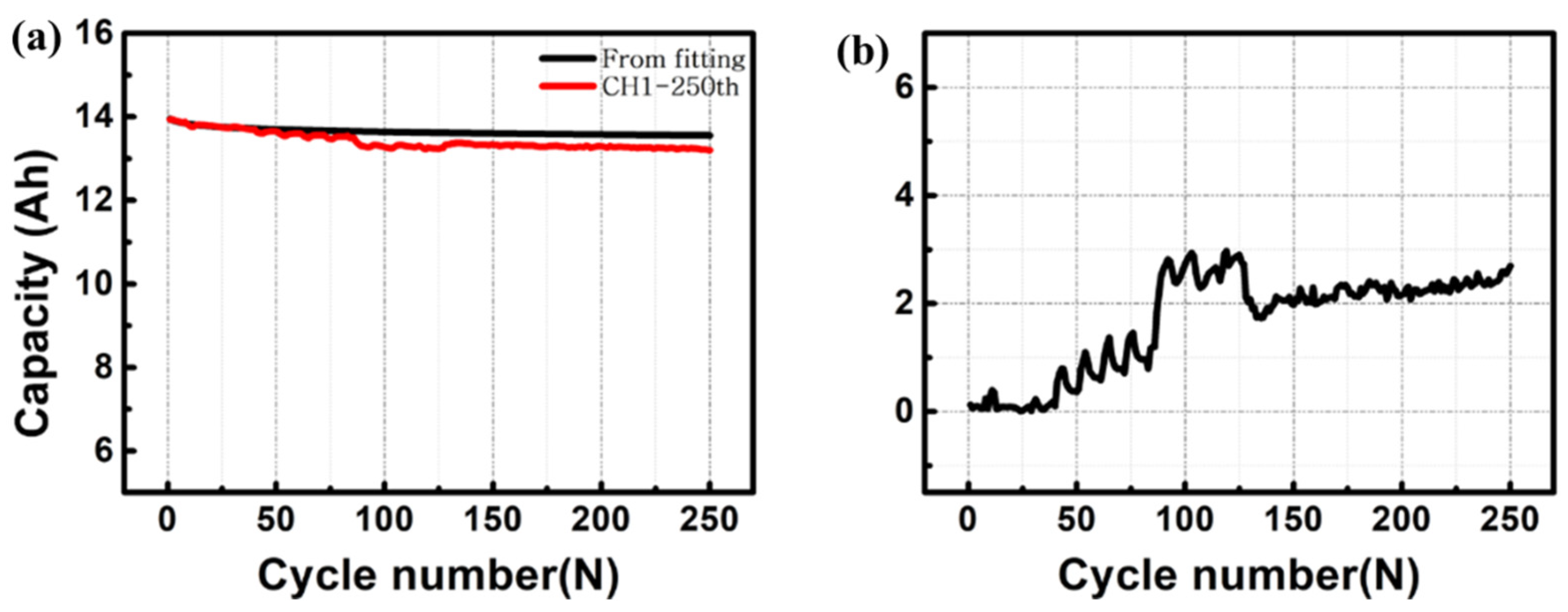
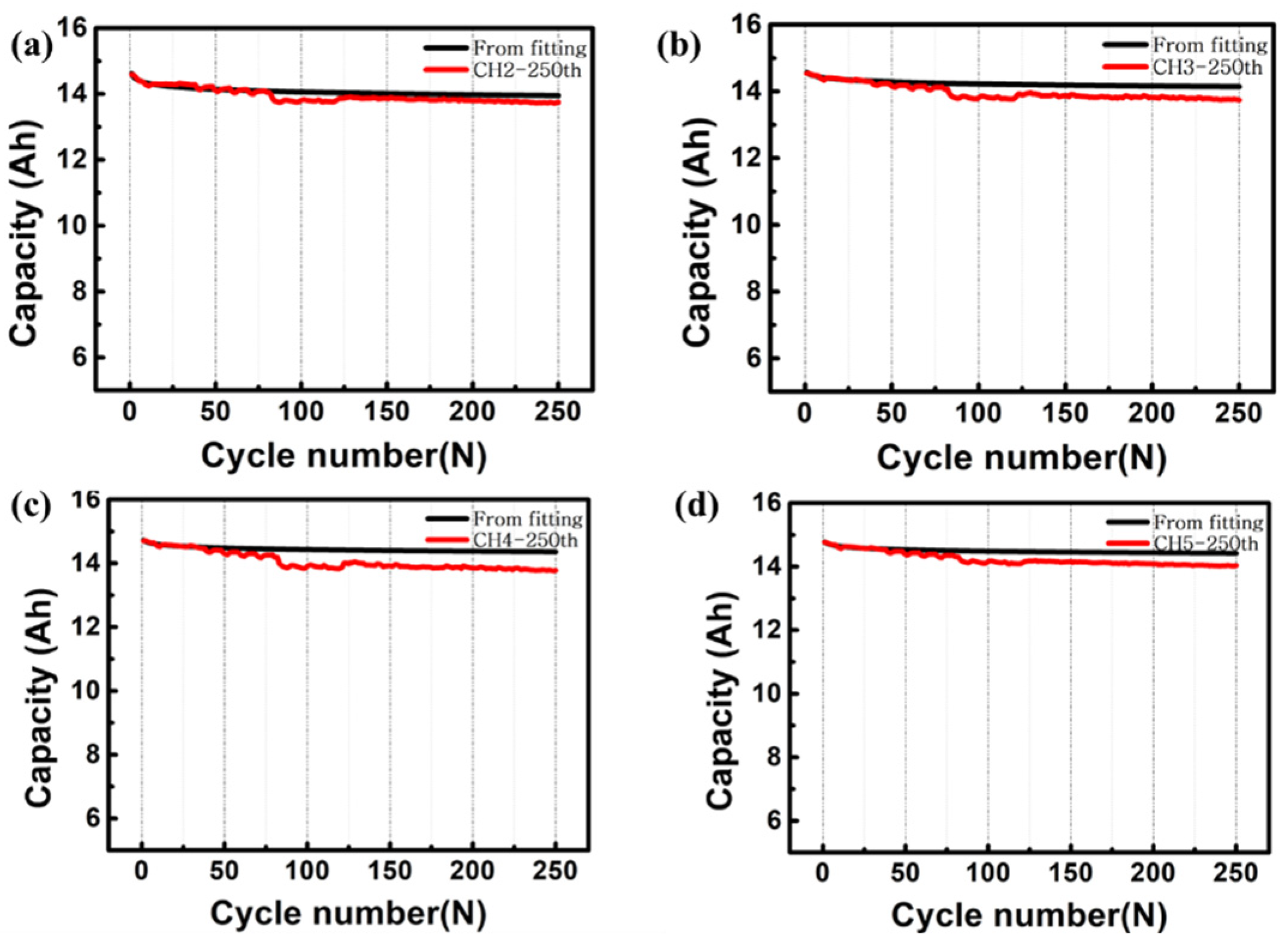
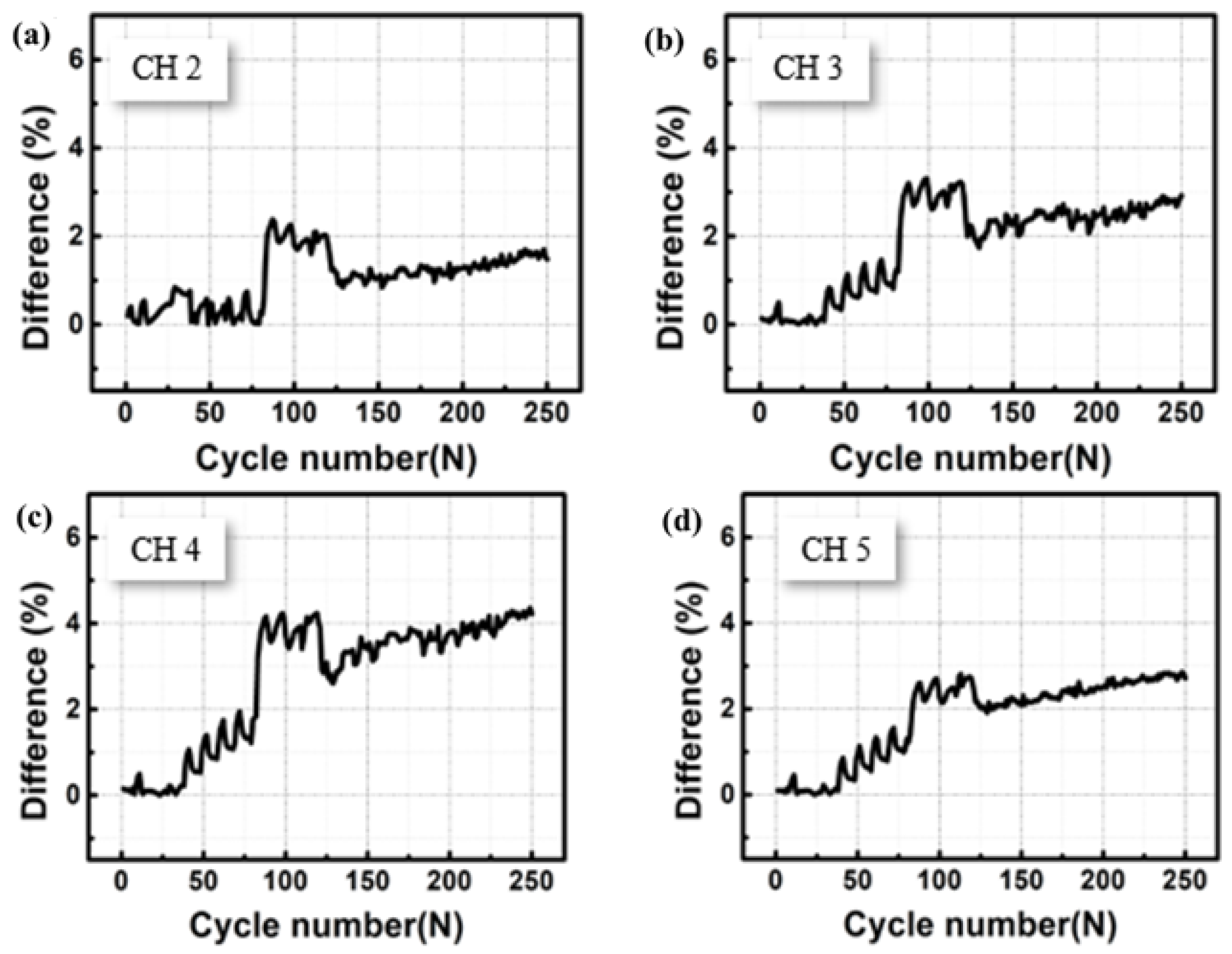
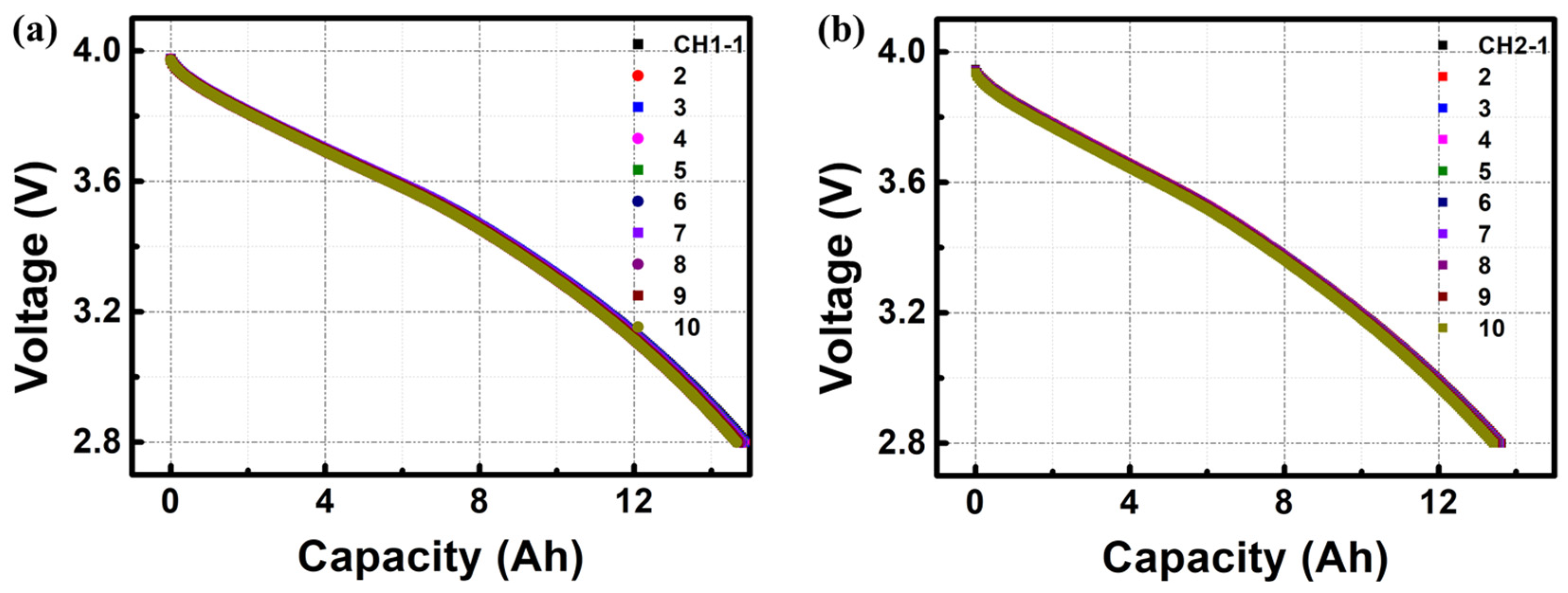
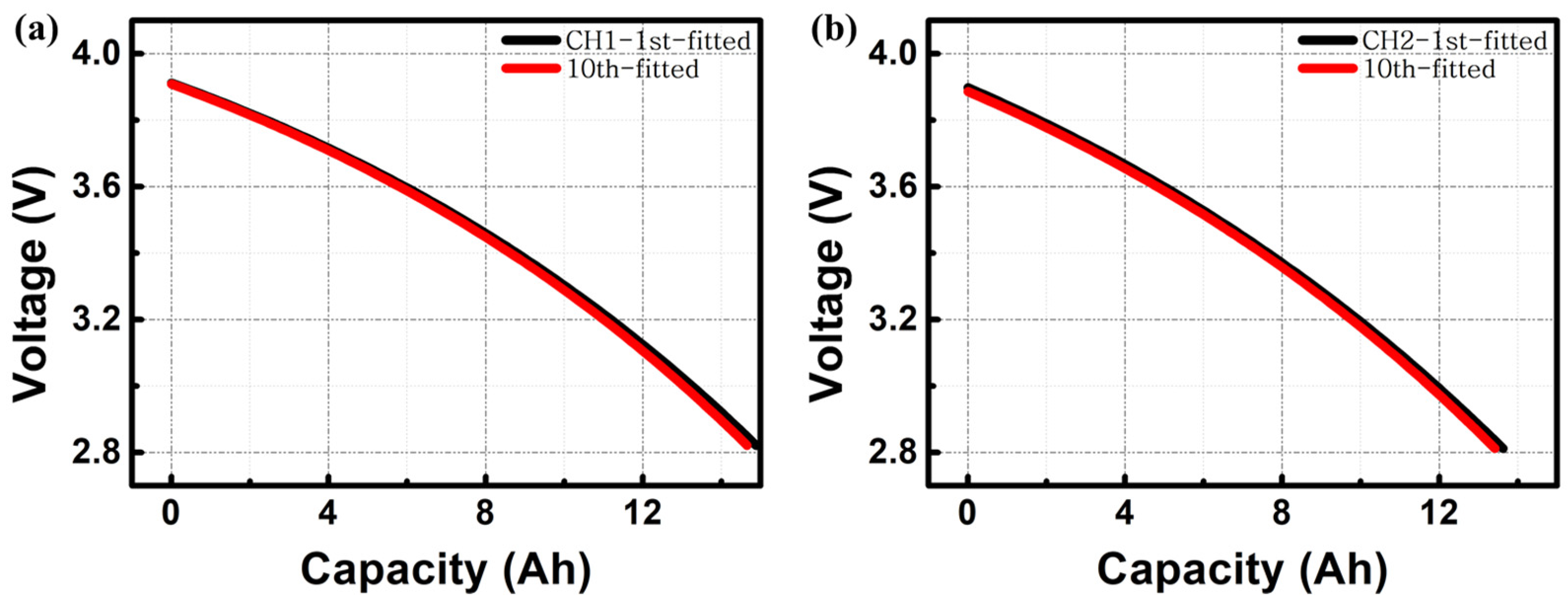
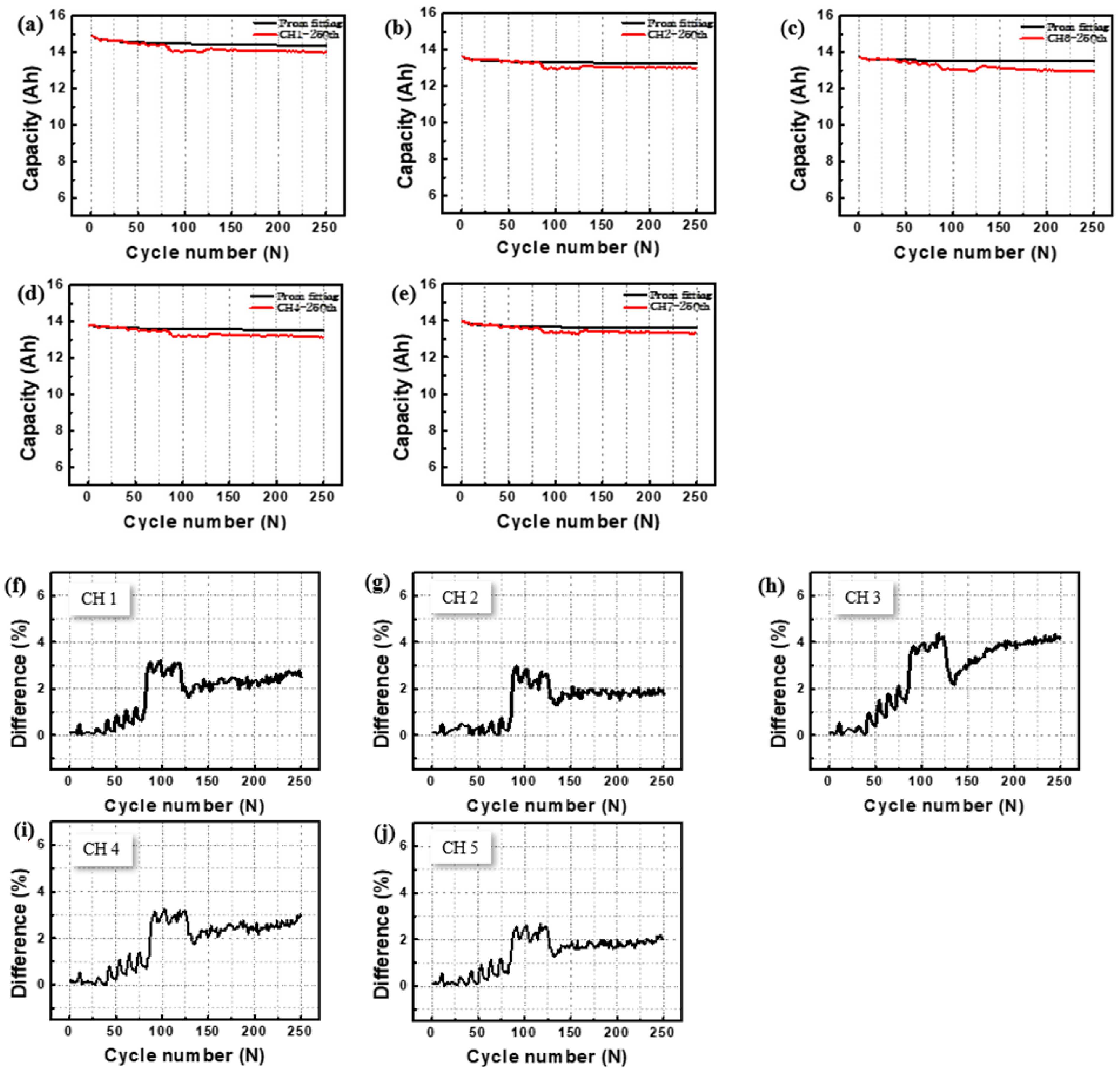
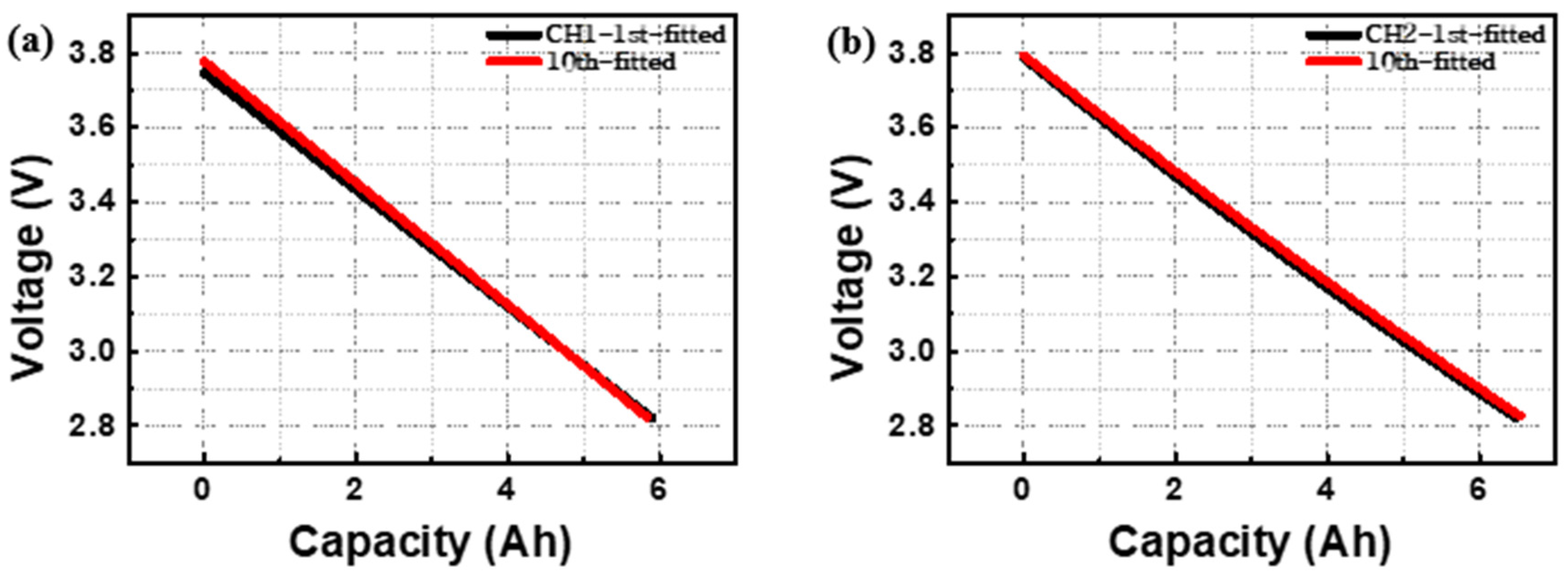
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, Z.-K.; Liu, X.; Wang, Y.; Zhang, Q.; Sun, C. The oxygen vacancy in Li-ion battery cathode materials. Nanoscale Horiz. 2020, 5, 1453–1466. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Li, S.; Zhang, C.; Chen, Z. State estimation for advanced battery management: Key challenges and future trends. Renew. Sustain. Energy Rev. 2019, 114, 109334. [Google Scholar] [CrossRef]
- Lü, X.; Li, Q.; Wang, Y.; Zhang, Z.; Li, W. A comprehensive review on hybrid power system for PEMFC-HEV: Issues and strategies. Energy Convers. Manag. 2018, 171, 1273–1291. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Cho, B.H. Complementary Cooperation Algorithm Based on DEKF Combined with Pattern Recognition for SOC/Capacity Estimation and SOH Prediction. IEEE Trans. Power Electron. 2012, 27, 436–451. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z. State of health estimation for Li-ion battery via partial incremental capacity analysis based on support vector regression. Energy 2020, 203, 117852. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, B.; Li, H.; Zhang, Y.; Xie, J. Environmental characteristics comparison of Li-ion batteries and Ni-MH batteries under the uncertainty of cycle performance. J. Hazard. Mater. 2012, 229–230, 455–460. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kim, T.; Kang, Y.; Kim, H.; Lee, S. State of health monitoring by gas generation patterns in commercial 18,650 lithium-ion batteries. J. Electroanal. Chem. 2022, 907, 115892. [Google Scholar] [CrossRef]
- Dong, G.; Wei, J.; Ling, Q. Battery Health Prognosis Using Brownian Motion Modeling and Particle Filtering. IEEE Trans. Ind. Electron. 2018, 65, 8646–8655. [Google Scholar] [CrossRef]
- Ungurean, L.; Boicea, V.; Micea, M.V. Battery state of health estimation: A structured review of models, methods and commercial devices. Int. J. Energy Res. 2017, 41, 151–181. [Google Scholar] [CrossRef]
- Burgos Mellado, C.D.; Roman, E.; Garcia, P.; Espinosa, J. Particle-filtering-based estimation of maximum available power state in Lithium-Ion batteries. Appl. Energy 2016, 161, 349–363. [Google Scholar] [CrossRef]
- Hatzell, K.; Sharma, A.; Fathy, H.K. A survey of long-term health modeling, estimation, and control of Lithium-ion batteries: Challenges and opportunities. In Proceedings of the American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 584–591. [Google Scholar] [CrossRef][Green Version]
- Ghorbani Kashkooli, A.; Farhad, S.; Kazemi, M.; Dees, D.W.; Jaguemont, J.; Van Mierlo, J.; Berecibar, M. Application of Artificial Intelligence to State-of-Charge and State-of-Health Estimation of Calendar-Aged Lithium-Ion Pouch Cells. J. Electrochem. Soc. 2019, 166, A605–A615. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hoque, M.M.; Mohamed, A.; Ayob, A. Neural Network Approach for Estimating State of Charge of Lithium-Ion Battery Using Backtracking Search Algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Landi, M.; Gross, G. Measurement Techniques for Online Battery State of Health Estimation in Vehicle-to-Grid Applications. IEEE Trans. Instrum. Meas. 2014, 63, 1224–1234. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Sources 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Hossain Lipu, M.S.; Hannan, M.A.; Hussain, A.; Ker, P.J.; Saad, M.H.M.; Ayob, A. A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 2018, 205, 115–133. [Google Scholar] [CrossRef]
- Venugopal, P. State-of-Health Estimation of Li-ion Batteries in Electric Vehicle Using IndRNN under Variable Load Condition. Energies 2019, 12, 4338. [Google Scholar] [CrossRef]
- Guo, Z.; Jin, C.; Liu, J.; Jiang, J.; Wan, C. State of health estimation for lithium ion batteries based on charging curves. J. Power Sources 2014, 249, 457–462. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Wiley: New York, NY, USA, 2001; pp. 580–632. [Google Scholar]
| CYC 1 | CYC 2 | CYC 3 | CYC 4 | CYC 5 | CYC 6 | CYC 7 | CYC 8 | CYC 9 | CYC10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ch 1 | P | 4.570 | 4.658 | 4.647 | 4.645 | 4.653 | 4.645 | 4.645 | 4.642 | 4.635 | 4.659 |
| Q (C) | −1.010 | −0.7381 | −0.7253 | −0.7229 | −0.7289 | −0.7222 | −0.7219 | −0.7186 | −0.7106 | −0.7348 | |
| τ1 | 12.41 | 15.24 | 15.04 | 14.98 | 15.04 | 14.94 | 14.91 | 14.85 | 14.75 | 15.01 | |
| Ch 2 | P (V) | 4.391 | 4.555 | 4.540 | 4.537 | 4.535 | 4.531 | 4.532 | 4.525 | 4.528 | 4.544 |
| Q (V) | −0.8308 | −0.6685 | −0.6538 | −0.6505 | −0.6536 | −0.6549 | −0.6564 | −0.6509 | −0.6555 | −0.6742 | |
| τ1 (s) | 11.29 | 15.31 | 15.07 | 14.98 | 14.99 | 14.99 | 15.00 | 14.92 | 14.99 | 15.22 | |
| Ch 3 | P (V) | 4.583 | 4.569 | 4.556 | 4.556 | 4.554 | 4.553 | 4.555 | 4.554 | 4.558 | 4.568 |
| Q (V) | −0.6897 | −0.6770 | −0.6608 | −0.6603 | −0.6580 | −0.6564 | −0.6588 | −0.6571 | −0.6604 | −0.6722 | |
| τ1 (s) | 15.50 | 15.32 | 15.05 | 15.02 | 14.96 | 14.91 | 14.93 | 14.90 | 14.93 | 15.06 | |
| Ch 4 | P (V) | 4.579 | 4.563 | 4.559 | 4.561 | 4.559 | 4.558 | 4.557 | 4.566 | 4.575 | 4.580 |
| Q (V) | −0.6769 | −0.6570 | −0.6522 | −0.6537 | −0.6510 | −0.6504 | −0.6481 | −0.6570 | −0.6680 | −0.6734 | |
| τ1 (s) | 15.42 | 15.09 | 14.99 | 14.99 | 14.92 | 14.89 | 14.85 | 14.96 | 15.09 | 15.15 | |
| Ch 5 | P (V) | 4.561 | 4.545 | 4.542 | 4.546 | 4.546 | 4.547 | 4.544 | 4.550 | 4.558 | 4.558 |
| Q (V) | −0.6578 | −0.6396 | −0.6364 | −0.6395 | −0.6398 | −0.6409 | −0.6366 | −0.6436 | −0.6531 | −0.6541 | |
| τ1 (s) | 15.19 | 14.88 | 14.80 | 14.83 | 14.82 | 14.82 | 14.75 | 14.84 | 14.94 | 14.94 |
| C 1–C 10 | C 1–C 15 | C 1–C 20 | C 1–C 250 | ||
|---|---|---|---|---|---|
| Ch 1 | l | 35.03 | 14.32 | 14.05 | 14.64 |
| m | 3.802 | 0.1751 | 0.08939 | 0.2592 | |
| n | 254.7 | 7.290 | 1.948 | 11.08 | |
| τ1 (s) | 35.03 | 14.32 | 14.05 | 14.64 | |
| Ch 2 | l | 16.35 | 14.73 | 14.60 | 15.13 |
| m | 0.6675 | 0.1742 | 0.1182 | 0.2547 | |
| n | 12.55 | 0.8836 | −0.1345 | 8.834 | |
| τ1 (s) | 137.3 | 35.83 | 24.31 | 52.40 | |
| Ch 3 | l | 43.27 | 14.78 | 14.64 | 15.28 |
| m | 5.127 | 0.1398 | 0.08999 | 0.2781 | |
| n | 269.6 | 3.912 | 1.382 | 10.15 | |
| τ1 (s) | 1055 | 28.76 | 18.51 | 57.20 | |
| Ch 4 | l | 45.43 | 14.92 | 14.78 | 15.92 |
| m | 5.409 | 0.1253 | 0.07553 | 0.3894 | |
| n | 290.8 | 3.685 | 1.070 | 17.26 | |
| τ1 (s) | 1113 | 25.78 | 15.54 | 80.10 | |
| Ch 5 | l | 39.52 | 14.91 | 14.81 | 15.55 |
| m | 4.521 | 0.1088 | 0.07058 | 0.2778 | |
| n | 237.2 | 2.161 | 0.4225 | 14.06 | |
| τ1 (s) | 930.0 | 22.38 | 14.52 | 57.14 |
| CYC 1 | CYC 2 | CYC 3 | CYC 4 | CYC 5 | CYC 6 | CYC 7 | CYC 8 | CYC 9 | CYC 10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ch 1 | P (V) | 4.555 | 4.534 | 4.524 | 4.521 | 4.534 | 4.534 | 4.532 | 4.544 | 4.549 | 4.552 |
| Q (V) | −0.6432 | −0.6214 | −0.6126 | −0.6100 | −0.6219 | −0.6216 | −0.6196 | −0.6308 | −0.6387 | −0.6428 | |
| τ1 (s) | 15.02 | 14.67 | 14.52 | 14.46 | 14.61 | 14.58 | 14.54 | 14.67 | 14.76 | 14.80 | |
| Ch 2 | P (V) | 4.735 | 4.712 | 0.01894 | 0.01871 | 0.01856 | 4.672 | 4.672 | 4.664 | 4.681 | 4.686 |
| Q (V) | −0.8373 | −0.8151 | 0.0178 | 0.0176 | 0.0175 | −0.7806 | −0.7812 | −0.7728 | −0.7931 | −0.7999 | |
| τ1 (s) | 16.39 | 16.07 | 0.2388 | 0.2359 | 0.2337 | 15.57 | 15.56 | 15.44 | 15.69 | 15.76 | |
| Ch 3 | P (V) | 4.686 | 4.674 | 4.673 | 4.667 | 4.665 | 4.666 | 4.660 | 4.647 | 4.667 | 4.668 |
| Q (V) | −0.7861 | −0.7764 | −0.7769 | −0.7707 | −0.7691 | −0.7689 | −0.7622 | −0.7490 | −0.7712 | −0.7741 | |
| τ1 (s) | 15.80 | 15.68 | 15.67 | 15.57 | 15.54 | 15.51 | 15.41 | 15.23 | 15.50 | 15.52 | |
| Ch 4 | P (V) | 4.659 | 4.647 | 4.648 | 4.644 | 4.646 | 4.646 | 4.644 | 4.637 | 4.652 | 4.659 |
| Q (V) | −0.7473 | −0.7331 | −0.7329 | −0.7281 | −0.7296 | −0.7290 | −0.7270 | −0.7192 | −0.7362 | −0.7444 | |
| τ1 (s) | 15.28 | 15.08 | 15.05 | 14.97 | 14.97 | 14.94 | 14.91 | 14.80 | 14.99 | 15.07 | |
| Ch 7 | P (V) | 4.655 | 4.645 | 4.628 | 4.637 | 4.625 | 4.623 | 4.622 | 4.635 | 4.652 | 4.652 |
| Q (V) | −0.7496 | −0.7377 | −0.7222 | −0.7303 | −0.7194 | −0.7178 | −0.7164 | −0.7275 | −0.7475 | −0.7483 | |
| τ1 (s) | 15.55 | 15.35 | 15.13 | 15.22 | 15.06 | 15.02 | 15.00 | 15.12 | 15.36 | 15.34 |
| C 1–C 15 | C 1–C 20 | C 1–C 250 | ||
|---|---|---|---|---|
| Ch 1 | l | 15.18 | 15.00 | 15.68 |
| m | 0.1799 | 0.1145 | 0.3094 | |
| n | 3.609 | 1.125 | 10.30 | |
| τ1 (s) | 37.00 | 23.55 | 63.64 | |
| Ch 2 | l | 13.79 | 13.64 | 14.29 |
| m | 0.1318 | 0.07195 | 0.2402 | |
| n | 2.338 | 0.05045 | 14.49 | |
| τ1 | 27.10 | 14.80 | 49.40 | |
| Ch 3 | l | 13.81 | 13.70 | 15.00 |
| m | 0.08054 | 0.03482 | 0.3687 | |
| n | 1.376 | −0.5738 | 26.29 | |
| τ1 (s) | 16.57 | 7.163 | 75.84 | |
| Ch 4 | l | 14.24 | 13.90 | 14.64 |
| m | 0.1735 | 0.06561 | 0.2695 | |
| n | 9.670 | 1.729 | 15.85 | |
| τ1 (s) | 35.69 | 13.50 | 55.44 | |
| Ch 7 | l | 14.20 | 14.01 | 14.69 |
| m | 0.1447 | 0.07837 | 0.2561 | |
| n | 3.761 | 0.6901 | 15.56 | |
| τ1 (s) | 29.78 | 16.12 | 52.69 |
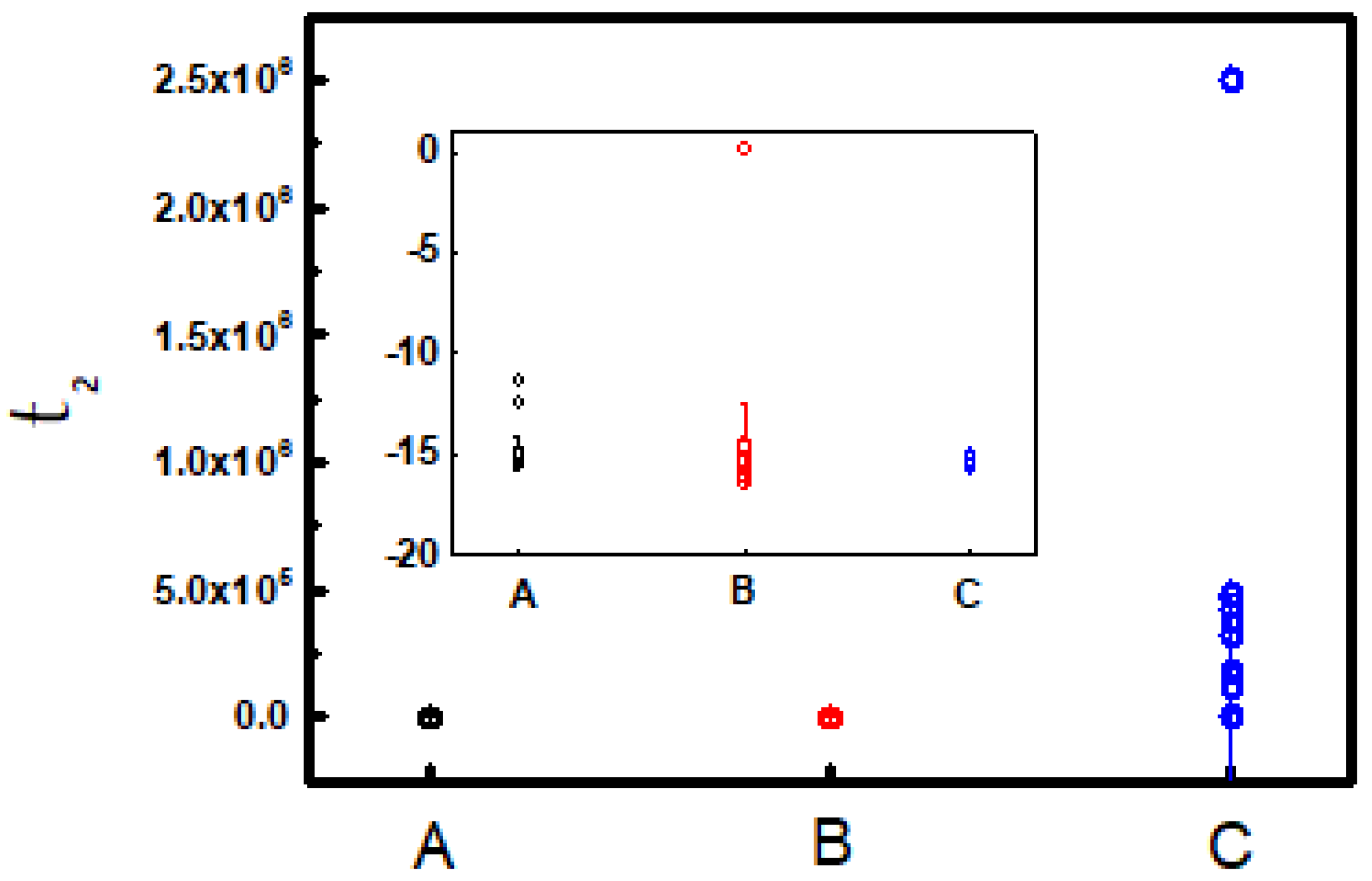
| C 1 | C 2 | C 3 | C 4 | C 5 | C 6 | C 7 | C 8 | C 9 | C 10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ch 1 | P (V) | −53,702.7 | −28,577.6 | −64,446.8 | −50,783.6 | −72,918.7 | 21.57107 | −67249 | −76,536.2 | −59,558 | 55.69349 |
| Q (V) | 53,706.46 | 28,581.38 | 64,450.59 | 50,787.33 | 72,922.47 | −17.7958 | 67,252.73 | 76,539.94 | 59,561.82 | −51.9156 | |
| τ1 (s) | 342,140 | 182,626.2 | 414,120.4 | 325,295.2 | 463,704.2 | 116.302 | 424,004.2 | 478,618.2 | 368,780.3 | 320.038 | |
| Ch 2 | P (V) | −1.60113 | −0.96858 | −4.6612 | −6.29289 | −5.14953 | −6.98678 | −6.24893 | −5.82573 | −5.43682 | −3.60366 |
| Q (V) | 5.38769 | 4.75587 | 8.45944 | 10.09036 | 8.94919 | 10.78696 | 10.04671 | 9.62309 | 9.23147 | 7.39686 | |
| τ1 (s) | 32.85228 | 28.76151 | 53.998 | 65.44687 | 57.67349 | 70.22137 | 65.07207 | 61.82811 | 59.12841 | 46.65805 | |
| Ch 3 | P (V) | 4.65828 | 4.64631 | 4.62864 | 4.63438 | 4.63265 | 4.63001 | 4.62903 | 4.62018 | 4.63154 | 4.63595 |
| Q (V) | −0.76585 | −0.75257 | −0.73937 | −0.74507 | −0.74277 | −0.7409 | −0.7395 | −0.72982 | −0.74946 | −0.75579 | |
| τ1 (s) | 15.5051 | 15.2741 | 15.0965 | 15.1587 | 15.1049 | 15.0758 | 15.0454 | 14.894 | 15.1051 | 15.1748 | |
| Ch 4 | P (V) | −364419 | −534.915 | −26482.2 | −19,372.5 | −43.7761 | −47.0712 | −19.1422 | −15.4416 | −10.3224 | −7.02494 |
| Q (V) | 364,422.8 | 538.7366 | 26,485.99 | 19,376.3 | 47.60398 | 50.90015 | 22.96835 | 19.2679 | 14.14652 | 10.84635 | |
| τ1 (s) | 2.50 × 106 | 3604.861 | 174,633.3 | 126,372.9 | 303.3228 | 320.7659 | 141.2039 | 115.9232 | 83.27393 | 62.16823 | |
| Ch 5 | P (V) | 4.67995 | 4.66087 | 4.65527 | 4.64273 | 4.64594 | 4.65252 | 4.64419 | 4.64762 | 4.66258 | 4.66295 |
| Q (V) | −0.78143 | −0.76618 | −0.76289 | −0.75163 | −0.75343 | −0.75912 | −0.75007 | −0.75064 | −0.77058 | −0.77211 | |
| τ1 (s) | 15.6637 | 15.4418 | 15.3726 | 15.2085 | 15.2155 | 15.2793 | 15.1445 | 15.1233 | 15.3842 | 15.3938 |
| C 1–C 15 | C 1–C 20 | C 1–C 250 | ||
|---|---|---|---|---|
| CH 1 | l | 138.2302 | 296.9051 | 9.48609 |
| m | 20.87784 | 44.77955 | 1.65587 | |
| n | 558.6958 | 657.4966 | 3.03309 | |
| τ1 (s) | 4294.87 | 9211.793 | 340.6361 | |
| CH 2 | l | 85.35705 | 216.0331 | 66.38358 |
| m | 12.05898 | 31.86752 | 10.67708 | |
| n | 682.1583 | 709.5324 | 258.836 | |
| τ1 (s) | 2480.704 | 6555.604 | 2196.428 | |
| CH 3 | l | 14.26526 | 13.77415 | 14.13861 |
| m | 0.29094 | 0.13671 | 0.25372 | |
| n | 7.63046 | 1.5465 | 4.86306 | |
| τ1 (s) | 59.85051 | 28.1232 | 52.19383 | |
| CH 4 | l | 157.7079 | 340.3363 | 9.58917 |
| m | 26.69073 | 54.0596 | 1.7819 | |
| n | 283.9487 | 475.7721 | 1.4131 | |
| τ1 (s) | 5490.664 | 11120.83 | 366.5623 | |
| CH5 | l | 13.63623 | 13.58724 | 14.46576 |
| m | 0.0729 | 0.04867 | 0.26786 | |
| n | 0.06429 | -0.62595 | 22.27892 | |
| τ1 (s) | 14.99657 | 10.01211 | 55.10263 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, H.; Oh, M.; Kim, J.; Shin, E.; Hwang, K.; Kim, S.; Chi, Y.; Park, C.; Yoon, S. Electrochemical Circuit Model Based State of Health Prognostics for Evaluation of Reusability of Lithium-Ion Batteries from Electric Vehicle. Molecules 2024, 29, 3325. https://doi.org/10.3390/molecules29143325
Kang H, Oh M, Kim J, Shin E, Hwang K, Kim S, Chi Y, Park C, Yoon S. Electrochemical Circuit Model Based State of Health Prognostics for Evaluation of Reusability of Lithium-Ion Batteries from Electric Vehicle. Molecules. 2024; 29(14):3325. https://doi.org/10.3390/molecules29143325
Chicago/Turabian StyleKang, Hyunchul, Minki Oh, Jaekwang Kim, Eunseon Shin, Keebum Hwang, Soyeon Kim, Youngmin Chi, Chulwan Park, and Songhun Yoon. 2024. "Electrochemical Circuit Model Based State of Health Prognostics for Evaluation of Reusability of Lithium-Ion Batteries from Electric Vehicle" Molecules 29, no. 14: 3325. https://doi.org/10.3390/molecules29143325
APA StyleKang, H., Oh, M., Kim, J., Shin, E., Hwang, K., Kim, S., Chi, Y., Park, C., & Yoon, S. (2024). Electrochemical Circuit Model Based State of Health Prognostics for Evaluation of Reusability of Lithium-Ion Batteries from Electric Vehicle. Molecules, 29(14), 3325. https://doi.org/10.3390/molecules29143325







