Application of Strain Engineering in Solar Cells
Abstract
1. Introduction
2. Origin of Strain in Solar Cells
2.1. External Conditions Induce Strain
2.2. Local Lattice Strain
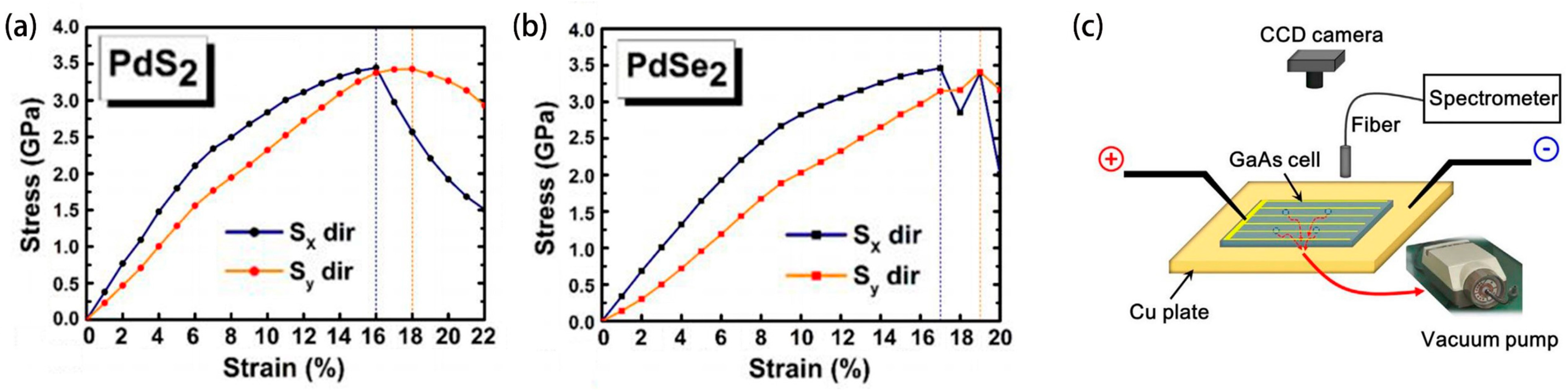
3. Characterization of Strain in Solar Cells
4. Effect of Strain on Solar Cells
4.1. Electron Band Structure
4.2. Optical and Electrical Properties

4.3. Power Degradation
4.4. Trap State Density
4.5. Ion Migration
4.6. PCE and Stability
5. Adjusting Method for Stabilizing Solar Cell Strain
5.1. Local Strain Regulation
5.2. External Conditions Induce Strain Regulation
5.3. Strain Modulation
6. Strategies to Improve Solar Cell Performance
6.1. Quantum Dots/Quantum Wells
6.2. Improve the Efficiency and Stability of Photoelectric Conversion
7. Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Fu, Q.; Tang, X.; Huang, B.; Hu, T.; Tan, L.; Chen, L.; Chen, Y. Recent progress on the long-term stability of perovskite solar cells. Nano Energy 2018, 5, 1700387. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Mujahid, M.; Duan, Y.; Wang, Z.K.; Xue, J.; Yang, Y. A review of perovskites solar cell stability. Adv. Funct. Mater. 2019, 29, 1808843. [Google Scholar] [CrossRef]
- Wen, J.; Zhao, Y.; Liu, Z.; Gao, H.; Lin, R.; Wan, S.; Ji, C.; Xiao, K.; Gao, Y.; Tian, Y.; et al. Steric engineering enables efficient and photostable wide-bandgap perovskites for all-perovskite tandem solar cells. Adv. Mater. 2022, 34, 2110356. [Google Scholar] [CrossRef] [PubMed]
- Gao, K.; Bi, Q.; Wang, X.; Liu, W.; Xing, C.; Li, K.; Xu, D.; Su, Z.; Zhang, C.; Yu, J.; et al. Progress and future prospects of wide-bandgap metal-compound-based passivating contacts for silicon solar cells. Adv. Mater. 2022, 34, 2200344. [Google Scholar] [CrossRef] [PubMed]
- Sharmoukh, W.; Kiey, S.A.A.; Ali, B.A.; Menon, L.; Allam, N.K. Recent progress in the development of hole-transport materials to boost the power conversion efficiency of perovskite solar cells. SMT 2020, 26, e00210. [Google Scholar] [CrossRef]
- Jošt, M.; Kegelmann, L.; Korte, L.; Albrecht, S. Monolithic perovskite tandem solar cells: A review of the present status and advanced characterization methods toward 30% efficiency. Adv. Energy Mater. 2020, 10, 1904102. [Google Scholar] [CrossRef]
- Venkatesan, S.; Lin, W.H.; Hsu, T.H.; Teng, H.; Lee, Y.L. Indoor dye-sensitized solar cells with efficiencies surpassing 26% using polymeric counter electrodes. ACS Sustain. Chem. Eng. 2022, 10, 2473–2483. [Google Scholar] [CrossRef]
- Yoo, J.J.; Shin, S.S.; Seo, J. Toward efficient perovskite solar cells: Progress, strategies, and perspectives. ACS Energy Lett. 2022, 7, 2084–2091. [Google Scholar] [CrossRef]
- Brinkmann, K.O.; Wang, P.; Lang, F.; Li, W.; Guo, X.; Zimmermann, F.; Olthof, S.; Neher, D.; Hou, Y.; Stolterfoht, M.; et al. Perovskite–organic tandem solar cells. Nat. Rev. Mater. 2024, 9, 202–217. [Google Scholar] [CrossRef]
- Li, F.; Lin, F.R.; Jen, A.K.-Y. Current state and future perspectives of printable organic and perovskite solar cells. Adv. Mater. 2023, 36, 2307161. [Google Scholar] [CrossRef] [PubMed]
- Rolston, N.; Bush, K.A.; Printz, A.D.; Gold-Parker, A.; Ding, Y.; Toney, M.F.; McGehee, M.D.; Dauskardt, R.H. Engineering stress in perovskite solar cells to improve stability. Adv. Energy Mater. 2018, 8, 1802139. [Google Scholar] [CrossRef]
- Li, N.; Niu, X.; Chen, Q.; Zhou, H. Towards commercialization: The operational stability of perovskite solar cells. Chem. Soc. Rev. 2020, 49, 8235. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Liu, S.C.; Li, Z.; Wang, S.; Xue, D.J.; Lin, Y.; Hu, J.S. Strain in perovskite solar cells: Origins, impacts and regulation. Natl. Sci. Rev. 2021, 8, nwab047. [Google Scholar] [CrossRef] [PubMed]
- Meng, L.; You, J.; Yang, Y. Addressing the stability issue of perovskite solar cells for commercial applications. Nat. Commun. 2018, 9, 5265. [Google Scholar] [CrossRef] [PubMed]
- Kapil, G.; Bessho, T.; Ng, C.H.; Hamada, K.; Pandey, M.; Kamarudin, M.; Hirotani, D.; Kinoshita, T.; Minemoto, T.; Shen, Q.; et al. Strain relaxation and light management in tin−lead perovskite solar cells to achieve high efficiencies. ACS Energy Lett. 2019, 4, 1991–1998. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, Z.L. Recent progress in piezo-phototronic effect enhanced solar cells. Adv. Funct. Mater. 2019, 29, 1808214. [Google Scholar] [CrossRef]
- Zhu, C.; Niu, X.; Fu, Y.; Li, N.; Hu, C.; Chen, Y.; He, X.; Na, G.; Liu, P.; Zai, H.; et al. Strain engineering in perovskite solar cells and its impacts on carrier dynamics. Nat. Commun. 2019, 10, 815. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Xie, L.; Pu, Z.; Liu, C.; Yang, M.; Chen, Y.; He, X.; Na, G.; Liu, P.; Zai, H.; et al. The synergistic effect of pemirolast potassium on carrier management and strain release for high-performance inverted perovskite solar cells. Adv. Funct. Mater. 2023, 33, 2301956. [Google Scholar] [CrossRef]
- Li, F.; Deng, X.; Qi, F.; Li, Z.; Liu, D.; Shen, D.; Qin, M.; Wu, S.; Lin, F.; Jang, S.H.; et al. Regulating surface termination for efficient inverted perovskite solar cells with greater than 23% efficiency. J. Am. Chem. Soc. 2020, 142, 20134–20142. [Google Scholar] [CrossRef]
- Saidaminov, M.I.; Kim, J.; Jain, A.; Quintero-Bermudez, R.; Tan, H.; Long, G.; Tan, F.; Johnston, A.; Zhao, Y.; Voznyy, O.; et al. Suppression of atomic vacancies via incorporation of isovalent small ions to increase the stability of halide perovskite solar cells in ambient air. Nat. Energy 2018, 3, 648–654. [Google Scholar] [CrossRef]
- Liu, K.; Yuan, S.; Xian, Y.; Long, Y.; Yao, Q.; Rahman, N.; Guo, Y.; Sun, M.; Xue, Q.; Yip, H.L.; et al. Architecturing 1D-2D-3D multidimensional coupled CsPbI2Br perovskites toward highly effective and stable solar cells. Small 2021, 17, 2100888. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Ding, L. Pushing commercialization of perovskite solar cells by improving their intrinsic stability. Energy Environ. Sci. 2021, 14, 3233. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Z.; Qin, M.; Ren, Z.; Liu, K.; Huang, J.; Shen, D.; Wu, Z.; Zhang, Y.; Hao, J.; et al. Multifunctional crosslinking-enabled strain-regulating crystallization for stable, efficient α-FAPbI3-based perovskite solar cells. Adv. Mater. 2021, 33, 2008487. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhu, C.; Liu, L.; Ma, S.; Liu, P.; Wu, J.; Shi, C.; Du, Q.; Hao, Y.; Xiang, S.; et al. Interfacial residual stress relaxation in perovskite solar cells with improved stability. Adv. Mater. 2019, 31, 1904408. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yang, J.; Dai, R.; Sheng, W.; Su, Y.; Zhong, Y.; Li, X.; Tan, L.; Chen, Y. Elimination of interfacial lattice mismatch and detrimental reaction by self-assembled layer dual-passivation for efficient and stable inverted perovskite solar cells. Adv. Energy Mater. 2022, 12, 2103674. [Google Scholar] [CrossRef]
- Dong, W.; Zhu, C.; Bai, C.; Ma, Y.; Lv, L.; Zhao, J.; Huang, F.; Cheng, Y.B.; Zhong, J. Low-cost hydroxyacid potassium synergists as an efficient in situ defect passivator for high performance tin-oxide-based perovskite solar cells. Angew. Chem. Int. Ed. 2023, 62, e202302507. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; Zhao, Y.; Zhang, S.; Shi, R.; Zhang, T. Strain engineering: A boosting strategy for photocatalysis. Adv. Mater. 2022, 34, 2200868. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Park, N.G. Strain control to stabilize perovskite solar cells. Angew. Chem. Int. Ed. 2022, 134, e202212268. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Z.; Qu, S.; Ding, L. Stress and strain in perovskite/silicon tandem solar cells. Nano-Micro Lett. 2023, 15, 59. [Google Scholar] [CrossRef] [PubMed]
- Tsai, H.; Asadpour, R.; Blancon, J.C.; Stoumpos, C.C.; Durand, O.; Strzalka, J.W.; Chen, B.; Verduzco, R.; Ajayan, P.M.; Tretiak, S.; et al. Light-induced lattice expansion leads to high-efficiency perovskite solar cells. Science 2018, 360, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Deng, Y.; Wei, H.; Zheng, X.; Yu, Z.; Shao, Y.; Shield, J.E.; Huang, J. Strained hybrid perovskite thin films and their impact on the intrinsic stability of perovskite solar cells. Sci. Adv. 2017, 3, eaao5616. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Su, Z.; Canil, L.; Hughes, D.; Aldamasy, M.H.; Dagar, J.; Trofimov, S.; Wang, L.; Zuo, W.; Jerónimo-Rendon, J.J.; et al. Highly efficient p-i-n perovskite solar cells that endure temperature variations. Science 2023, 379, 399–403. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, X.; Zhou, D.; Liu, S.; Shi, Z.; Sun, R.; Liang, J.; Jia, Y.; Bian, S.; Liu, Z.; Song, H. Trivalent europium-doped CsCl quantum dots for MA-free perovskite solar cells with inherent bandgap through lattice strain compensation. Adv. Mater. 2023, 35, 2302393. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Dong, H.; Xi, J.; Yang, Y.; Yu, Y.; Ma, L.; Chen, J.; Jiao, B.; Hou, X.; Li, J.; et al. Local nearly non-strained perovskite lattice approaching a broad environmental stability window of efficient solar cells. Nano Energy 2020, 75, 104940. [Google Scholar] [CrossRef]
- Jones, T.W.; Osherov, A.; Alsari, M.; Sponseller, M.; Duck, B.C.; Jung, Y.K.; Settens, C.; Niroui, F.; Brenes, R.; Stan, C.V.; et al. Lattice strain causes non-radiative losses in halide perovskites. Energy Environ. Sci. 2019, 12, 596. [Google Scholar] [CrossRef]
- Yang, B.; Bogachuk, D.; Suo, J.; Wagner, L.; Kim, H.; Lim, J.; Hinsch, A.; Boschloo, G.; Khaja Nazeeruddin, M.; Hagfeldt, A. Strain effects on halide perovskite solar cells. Chem. Soc. Rev. 2022, 51, 7509–7530. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Shi, J.; Li, Y.; Li, H.; Wu, H.; Luo, Y.; Li, D.; Meng, Q. Quantifying the interface defect for the stability origin of perovskite solar cells. Adv. Energy Mater. 2019, 9, 1901352. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Yang, Y.; Wang, Y.; Li, P.; Huang, J.; Li, J.; Lu, Y.; Li, Z.; Wang, Z.; et al. Kirigami-based highly stretchable thin film solar cells that are mechanically stable for more than 1000 cycles. ACS Nano 2020, 14, 1560–1568. [Google Scholar] [CrossRef] [PubMed]
- Nayak, P.K.; Sendner, M.; Wenger, B.; Wang, Z.; Sharma, K.; Ramadan, A.J.; Lovrinčić, R.; Pucci, A.; Madhu, P.K.; Snaith, H.J. Impact of Bi3+ heterovalent doping in organic-inorganic metal halide perovskite crystals. J. Am. Chem. Soc. 2018, 140, 574–577. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, D.; Acharya, D.; Zhou, L.; Nie, W.; Prezhdo, O.V.; Tretiak, S.; Neukirch, A.J. Lattice expansion in hybrid perovskites: Effect on optoelectronic properties and charge carrier dynamics. J. Phys. Chem. Lett. 2019, 10, 5000–5007. [Google Scholar] [CrossRef] [PubMed]
- Min, H.; Ji, S.-G.; Seok, S.I. Relaxation of externally strained halide perovskite thin layers with neutral ligands. Joule 2022, 6, 2175–2185. [Google Scholar] [CrossRef]
- Raval, D.; Gupta, S.K.; Gajjar, P.N.; Ahuja, R. Strain modulating electronic band gaps and SQ efficiencies of semiconductor 2D PdQ2 (Q=S, Se) monolayer. Sci. Rep. 2022, 12, 2964. [Google Scholar] [CrossRef]
- Hu, X.; Zhu, L.; Weng, G.; Chen, S. Accessing externally induced spatially-resolved strain in GaAs thin-film solar cells by electroluminescence imaging. Sol. Energy Mater Sol. Cells 2018, 179, 283–288. [Google Scholar] [CrossRef]
- Oksenberg, E.; Merdasa, A.; Houben, L.; Kaplan-Ashiri, I.; Rothman, A.; Scheblykin, I.G.; Unger, E.L.; Joselevich, E. Large lattice distortions and size-dependent bandgap modulation in epitaxial halide perovskite nanowires. Nat. Commun. 2020, 11, 489. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Yun, J.S.; Sharma, P.; Lee, D.S.; Kim, J.; Soufiani, A.M.; Huang, S.; Green, M.A.; Ho-Baillie, A.W.Y.; Seidel, J. Light- and bias-induced structural variations in metal halide perovskites. Nat. Commun. 2019, 10, 444. [Google Scholar] [CrossRef] [PubMed]
- Qiu, F.; Sun, J.; Qi, J. Crystal growth, defect passivation and strain release via in-situ self-polymerization strategy enables efficient and stable perovskite solar cells. Chem. Eng. J. 2022, 430, 132869. [Google Scholar] [CrossRef]
- Chen, Y.; Lei, Y.; Li, Y.; Yu, Y.; Cai, J.; Chiu, M.H.; Rao, R.; Gu, Y.; Wang, C.; Choi, W.; et al. Strain engineering and epitaxial stabilization of halide perovskites. Nature 2020, 577, 209–215. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Pratap, S.; Körstgens, V.; Vema, S.; Song, L.; Liang, S.; Davydok, A.; Krywka, C.; Müller-Buschbaum, P. Mapping structure heterogeneities and visualizing moisture degradation of perovskite films with nano-focus WAXS. Nat. Commun. 2022, 13, 6701. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Xu, Q.; Abdelwahab, I.; Cai, R.; Febriansyah, B.; Yin, T.; Ping Loh, K.; Mathews, N.; Sun, H.; Chien Sum, T. Strain propagation in layered two-dimensional halide perovskites. Sci. Adv. 2022, 8, eabq1971. [Google Scholar] [CrossRef] [PubMed]
- Gerthoffera, A.; Poulainb, C.; Rouxa, F.; Emieuxa, F.; Grenet, L.; Perraud, S. CIGS solar cells on ultra-thin glass substrates: Determination of mechanical properties by nanoindentation and application to bending-induced strain calculation. Sol. Energy Mater Sol. Cells 2017, 166, 254–261. [Google Scholar] [CrossRef]
- Kim, H.S.; Park, N.G. Importance of tailoring lattice strain in halide perovskite crystals. NPG Asia Mater. 2020, 12, 78. [Google Scholar] [CrossRef]
- Cui, Z.; Bu, K.; Zhuang, Y.; Donnelly, M.E.; Zhang, D.; Dalladay-Simpson, P.; Howie, R.T.; Zhang, J.; Lv, X.; Hu, Q. Phase transition mechanism and bandgap engineering of Sb2S3 at gigapascal pressures. Commun. Chem. 2021, 4, 125. [Google Scholar] [CrossRef] [PubMed]
- Meng, W.; Zhang, K.; Osvet, A.; Zhang, J.; Gruber, W.; Forberich, K.; Meyer, B.; Heiss, W.; Unruh, T.; Li, N.; et al. Revealing the strain-associated physical mechanisms impacting the performance and stability of perovskite solar cells. Joule 2022, 6, 458–475. [Google Scholar] [CrossRef]
- Kirchartz, T.; RauWhat, U. Makes a good solar cell? Adv. Energy Mater. 2018, 8, 1703385. [Google Scholar] [CrossRef]
- Luo, S.; Kazes, M.; Lin, H.; Oron, D. Strain-induced type II band alignment control in CdSe nanoplatelet/ZnS-sensitized solar cells. J. Phys. Chem. C 2017, 121, 11136–11143. [Google Scholar] [CrossRef]
- Park, H.K.; Cho, Y.; Kim, J.; Kim, S.; Kim, S.; Kim, J.; Yang, K.J.; Kim, D.H.; Kang, J.K.; Jo, W. Flexible kesterite thin-film solar cells under stress. npj Flex. Electron. 2022, 6, 91. [Google Scholar] [CrossRef]
- Guin, L.; Cabarrocas, P.R.; Jabbour, M.E.; Triantafyllidis, N. Effect of strain on the dark current-voltage characteristic of silicon heterojunction solar cells. Sol. Energy 2020, 196, 457–461. [Google Scholar] [CrossRef]
- Smith, A.M.; Mohs, A.M.; Nie, S. Tuning the optical and electronic properties of colloidal nanocrystals by lattice strain. Nat. Nanotechnol. 2009, 4, 56–63. [Google Scholar] [CrossRef] [PubMed]
- Bushick, K.; Chae, S.; Deng, Z.; Heron, J.T.; Kioupakis, E. Boron arsenide heterostructures: Lattice-matched heterointerfaces and strain effects on band alignments and mobility. npj Comput. Mater. 2020, 6, 3. [Google Scholar] [CrossRef]
- Rout, P.C.; Schwingenschlögl, U. Large spin coherence length and high photovoltaic efficiency of the room temperature ferrimagnet Ca2FeOsO6 by strain engineering. Adv. Sci. 2022, 9, 2106037. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.-H.; Song, B.; Meroueh, L.; Ding, Z.; Song, Q.; Zhou, J.; Li, M.; Chen, G. Simultaneously high electron and hole mobilities in cubic boron-V compounds: BP, BAs, and BSb. Phys. Rev. B 2018, 98, 081203. [Google Scholar] [CrossRef]
- Mark, V.K.; Anoop, K.M.; Eugene, A.K.; Iris, V.-F. Bias-dependent degradation of various solar cells: Lessons for stability of perovskite photovoltaics. Energy Environ. Sci. 2019, 12, 550–558. [Google Scholar]
- Yang, C.; Song, K.; Xu, X.; Yao, G.; Wu, Z. Strain dependent effect on power degradation of CIGS thin film solar cell. Sol. Energy 2020, 195, 121–128. [Google Scholar] [CrossRef]
- Cheraghizade, M.; Jamali-Sheini, F. Symmetric strain- and temperature-dependent optoelectronics performance of TiO2/SnS/Ag solar cells. Surf. Interfaces 2021, 25, 101223. [Google Scholar] [CrossRef]
- Wei, J.; Wang, Q.; Huo, J.; Gao, F.; Gan, Z.; Zhao, Q.; Li, H. Mechanisms and suppression of photoinduced degradation in perovskite solar cells. Adv. Energy Mater. 2021, 11, 2002326. [Google Scholar] [CrossRef]
- Zhao, Y.; Yavuz, I.; Wang, M.; Weber, M.H.; Lee, J.H.; Tan, S.; Huang, T.; Meng, D.; Wang, R.; Xue, J.; et al. Suppressing ion migration in metal halide perovskite via interstitial doping with a trace amount of multivalent cations. Nat. Mater. 2022, 21, 1396–1402. [Google Scholar] [CrossRef] [PubMed]
- Luo, T.; Chen, R.; Zhang, G.; Li, L.; Wu, H.; Zhang, W.; Chen, W.; Chang, H. MASCN surface treatment to reduce phase transition temperature and regulate strain for efficient and stable α-FAPbI3 perovskite solar cells. ACS Appl. Mater. Interfaces 2023, 15, 38496–38506. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ying, Z.; Zheng, J.; Wang, X.; Chen, Y.; Wu, M.; Xiao, C.; Sun, J.; Shou, C.; Yang, Z.; et al. Surface reconstruction for efficient and stable monolithic perovskite/silicon tandem solar cells with greatly suppressed residual strain. Adv. Mater. 2023, 35, 2211962. [Google Scholar] [CrossRef] [PubMed]
- Lv, W.; Hu, Z.; Qiu, W.; Yan, D.; Li, M.; Mei, A.; Xu, L.; Chen, R. Constructing soft perovskite–substrate interfaces for dynamic modulation of perovskite film in inverted solar cells with over 6200 hours photostability. Adv. Sci. 2022, 9, 2202028. [Google Scholar] [CrossRef] [PubMed]
- Yuan, G.; Xie, W.; Song, Q.; Ma, S.; Ma, Y.; Shi, C.; Xiao, M.; Pei, F.; Niu, X.; Zhang, Y.; et al. Inhibited crack development by compressive strain in perovskite solar cells with improved mechanical stability. Adv. Mater. 2023, 35, 2211257. [Google Scholar] [CrossRef] [PubMed]
- Shai, X.; Wang, J.; Sun, P.; Huang, W.; Liao, P.; Cheng, F.; Zhu, B.; Chang, S.Y.; Yao, E.P.; Shen, Y.; et al. Achieving ordered and stable binary metal perovskite via strain engineering. Nano Energy 2018, 48, 117–127. [Google Scholar] [CrossRef]
- Kim, G.; Min, H.; Lee, K.S.; Lee, D.Y.; Yoon, S.M.; Il Seok, S. Impact of strain relaxation on performance of α-formamidinium lead iodide perovskite solar cells. Science 2020, 370, 108–112. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Grassano, D.; Pulci, O.; Liu, Y.; Luo, Y.; Mosca Conte, A.; Vasilievich Kusmartsev, F.; Kusmartseva, A. Covalent bonded bilayers from germanene and stanene with topological giant capacitance effects. npj 2D Mater. Appl. 2023, 7, 27. [Google Scholar] [CrossRef]
- Cheng, Q.; Wang, B.; Huang, G.; Li, Y.; Li, X.; Chen, J.; Yue, S.; Li, K.; Zhang, H.; Zhang, Y.; et al. Impact of strain relaxation on 2D ruddlesden–popper perovskite solar cells. Angew. Chem. Int. Ed. 2022, 61, e202208264. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Zhu, C.; Zhang, W.; Wang, H.; Wang, J.; Ren, F.; Chen, R.; Liu, S.; Meng, X.; Zhou, J.; et al. Strain release of formamidinium-cesium perovskite with imprint-assisted organic ammonium halide compensation for efficient and stable solar cells. Nano Energy 2022, 101, 107594. [Google Scholar] [CrossRef]
- Kim, S.G.; Kim, J.H.; Ramming, P.; Zhong, Y.; Schötz, K.; Joon Kwon, S.; Huettner, S.; Panzer, F.; Park, N.G. How antisolvent miscibility affects perovskite film wrinkling and photovoltaic properties. Nat. Commun. 2021, 12, 1554. [Google Scholar] [CrossRef]
- Ye, T.; Wang, K.; Ma, S.; Wu, C.; Hou, Y.; Yang, D.; Wang, K.; Priya, S. Strain-relaxed tetragonal MAPbI3 results in efficient mesoporous solar cells. Nano Energy 2021, 83, 105788. [Google Scholar] [CrossRef]
- Heintz, A.; Ilahi, B.; Pofelski, A.; Botton, G.; Patriarche, G.; Barzaghi, A.; Fafard, S.; Arès, R.; Isella, G.; Boucherif, A. Defect free strain relaxation of microcrystals on mesoporous patterned silicon. Nat. Commun. 2022, 13, 6624. [Google Scholar] [CrossRef]
- Yu, H.; Li, X.; Zhang, Z.; Ban, H.; Gong, X.; Liu, Z.; Zhang, M.; Sun, Q.; Zhang, T.; Shen, Y.; et al. Strain-stabilized CsPbI3 perovskite via organopolysilazane for efficient solar cells with efficiency over 19%. Adv. Optical Mater. 2022, 10, 2201672. [Google Scholar] [CrossRef]
- Xue, D.J.; Hou, Y.; Liu, S.C.; Wei, M.; Chen, B.; Huang, Z.; Li, Z.; Sun, B.; Proppe, A.H.; Dong, Y.; et al. Regulating strain in perovskite thin films through charge-transport layers. Nat. Commun. 2020, 11, 1514. [Google Scholar] [CrossRef]
- Jung, K.; Chae, W.S.; Choi, J.W.; Kim, K.C.; Lee, M.J. Synergistic passivation of MAPbI3 perovskite solar cells by compositional engineering using acetamidinium bromide additives. J. Energy Chem. 2021, 59, 755–762. [Google Scholar] [CrossRef]
- Nishimura, K.; Hirotani, D.; Kamarudin, M.A.; Shen, Q.; Toyoda, T.; Iikubo, S.; Minemoto, T.; Yoshino, K.; Hayase, S. Relationship between lattice strain and efficiency for Sn-perovskite solar cells. ACS Appl. Mater. Interfaces 2019, 11, 31105–31110. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Song, Q.; Pei, F.; Chen, Y.; Dou, J.; Wang, H.; Shi, C.; Zhang, X.; Fan, R.; Zhou, W.; et al. Strain modulation for light-stable n–i–p perovskite/silicon tandem solar cells. Adv. Mater. 2022, 34, 2201315. [Google Scholar] [CrossRef] [PubMed]
- Park, J.I.; Heo, J.H.; Park, S.-H.; Hong, K.I.; Jeong, H.G.; Im, S.H.; Kim, H.-K. Highly flexible InSnO electrodes on thin colourless polyimide substrate for high-performance flexible CH3NH3PbI3 perovskite solar cells. J. Power Sources 2017, 341, 340–347. [Google Scholar] [CrossRef]
- Liang, H.; Yang, W.; Xia, J.; Gu, H.; Meng, X.; Yang, G.; Fu, Y.; Wang, B.; Cai, H.; Chen, Y.; et al. Strain effects on flexible perovskite solar cells. Adv. Sci. 2023, 10, 2304733. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Yossef, M.; Zhang, C. Strain effect on the performance of amorphous silicon and perovskite solar cells. Sol. Energy 2018, 163, 243–250. [Google Scholar] [CrossRef]
- Linares, P.G.; López, E.; Ramiro, I.; Datas, A.; Antolín, E.; Yoshida, S.; Sogabe, T.; Okada, Y.; Martí, A.; Luque, A. Voltage limitation analysis in strain-balanced InAs/GaAsN quantum dot solar cells applied to the intermediate band concept. Sol. Energy Mater Sol. Cells 2015, 132, 178–182. [Google Scholar] [CrossRef]
- Welser, R.E.; Polly, S.J.; Kacharia, M.; Fedorenko, A.; Sood, A.K.; Hubbard, S.M. Design and demonstration of high-efficiency quantum well solar cells employing thin strained superlattices. Sci. Rep. 2019, 9, 13955. [Google Scholar] [CrossRef] [PubMed]
- Ekins-Daukes, N.J.; Lee, K.-H.; Hirst, L.; Chan, A.; Fuhrer, M.; Adams, J.; Browne, B.; Barnham, K.W.J.; Stavrinou, P.; Connolly, J.; et al. Controlling radiative loss in quantum well solar cells. J. Phys. D Appl. Phys. 2013, 46, 264007. [Google Scholar] [CrossRef]
- Steiner, M.A.; France, R.M.; Buencuerpo, J.; Geisz, J.F.; Nielsen, M.P.; Pusch, A.; Olavarria, W.J.; Young, M.; Ekins-Daukes, N.J. High efficiency inverted GaAs and GaInP/GaAs solar cells with strain-balanced GaInAs/GaAsP quantum wells. Adv. Energy Mater. 2021, 11, 2002874. [Google Scholar] [CrossRef]
- Rafiquea, S.; Abdullaha, S.M.; Sulaimana, K.; Iwamoto, M. Fundamentals of bulk heterojunction organic solar cells: An overview of stability/degradation issues and strategies for improvement. Renew. Sustain. Energy Rev. 2018, 84, 43–53. [Google Scholar] [CrossRef]
- Girolamo, D.D.; Phung, N.; Kosasih, F.U.; Giacomo, F.D.; Matteocci, F.; Smith, J.A.; Flatken, M.A.; Köbler, H.; Turren Cruz, S.H.; Mattoni, A.; et al. Ion migration-induced amorphization and phase segregation as a degradation mechanism in planar perovskite solar cells. Adv. Energy Mater. 2020, 10, 2000310. [Google Scholar] [CrossRef]
- Zhong, T.; Guo, F.; Lei, S.; Xiao, B.; Li, Q.; Jia, T.; Wang, X.; Yang, R. Multi-scale mechanical properties of bulk-heterojunction films in polymer solar cells. npj Flex. Electron. 2023, 7, 2. [Google Scholar] [CrossRef]
- Qin, F.; Wang, W.; Sun, L.; Jiang, X.; Hu, L.; Xiong, S.; Liu, T.; Dong, X.; Li, J.; Jiang, Y.; et al. Robust metal ion-chelated polymer interfacial layer for ultraflexible non-fullerene organic solar cells. Nat. Commun. 2020, 11, 4508. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wang, J.; Deng, Y.; Xi, J.; Zhang, Y.; Liu, C.; Guo, W. Undoped hole transport layer toward efficient and stable inorganic perovskite solar cells. Adv. Funct. Mater. 2023, 33, 2214562. [Google Scholar] [CrossRef]
- Hang, P.; Kan, C.; Li, B.; Yao, Y.; Hu, Z.; Zhang, Y.; Xie, J.; Wang, Y.; Yang, D.; Yu, X. Highly efficient and stable wide-bandgap perovskite solar cells via strain management. Adv. Funct. Mater. 2023, 33, 2214381. [Google Scholar] [CrossRef]
- Chen, W.; Huang, Y.; Cui, H.; Li, S.; Feng, Y.; Zhang, B. Reduced VOC deficit of mixed lead–tin perovskite solar cells via strain-releasing and synergistic passivation additives. Small Methods 2023, 7, 2201276. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, H.; Shang, C.; Sang, D.; Li, C.; Ge, S.; Zou, L.; Wang, Q. Application of Strain Engineering in Solar Cells. Molecules 2024, 29, 3260. https://doi.org/10.3390/molecules29143260
Fei H, Shang C, Sang D, Li C, Ge S, Zou L, Wang Q. Application of Strain Engineering in Solar Cells. Molecules. 2024; 29(14):3260. https://doi.org/10.3390/molecules29143260
Chicago/Turabian StyleFei, Houzhi, Caiyi Shang, Dandan Sang, Changxing Li, Shunhao Ge, Liangrui Zou, and Qinglin Wang. 2024. "Application of Strain Engineering in Solar Cells" Molecules 29, no. 14: 3260. https://doi.org/10.3390/molecules29143260
APA StyleFei, H., Shang, C., Sang, D., Li, C., Ge, S., Zou, L., & Wang, Q. (2024). Application of Strain Engineering in Solar Cells. Molecules, 29(14), 3260. https://doi.org/10.3390/molecules29143260





