High-Performance One-Dimensional Sub-5 nm Transistors Based on Poly(p-phenylene ethynylene) Molecular Wires
Abstract
1. Introduction
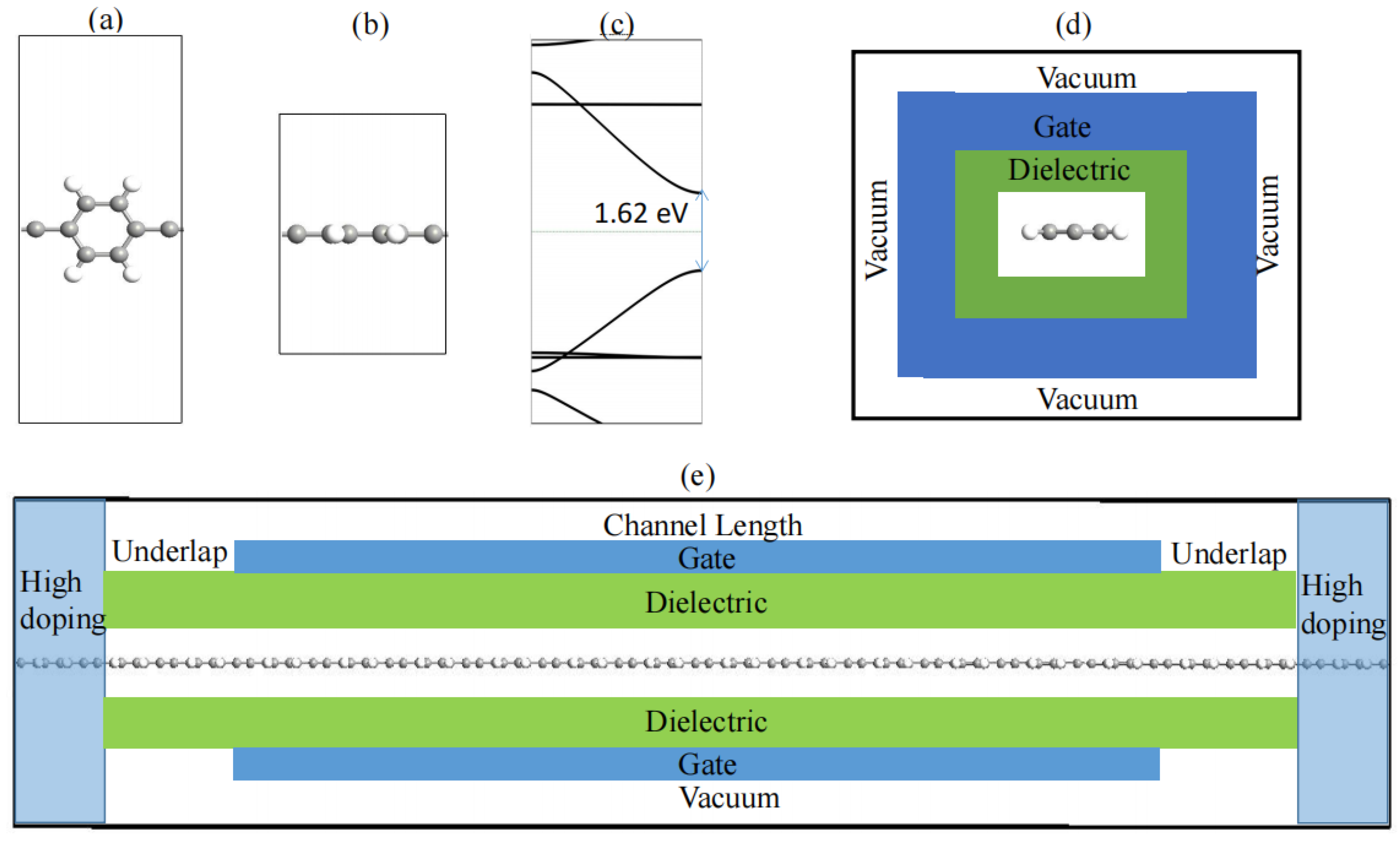
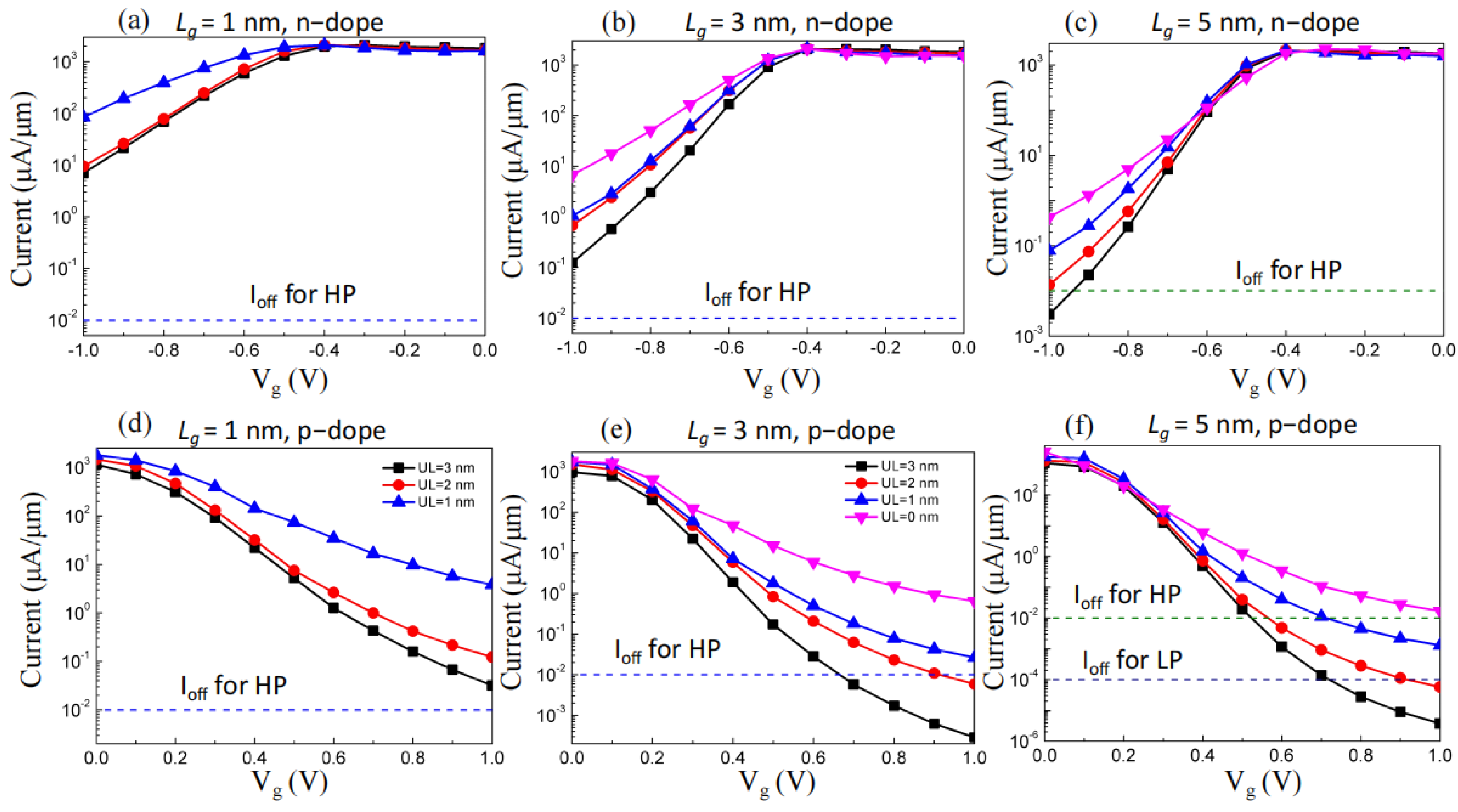
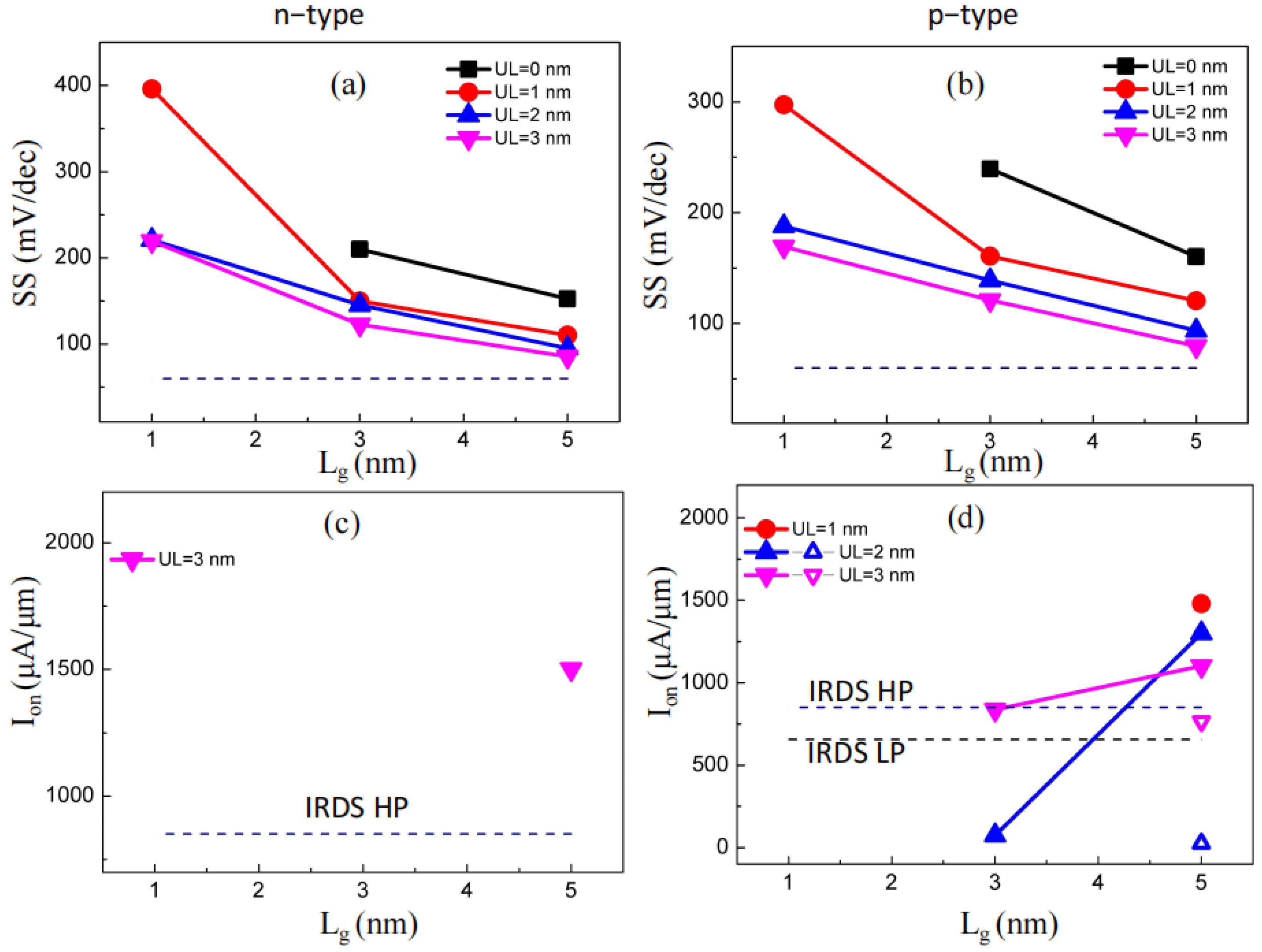
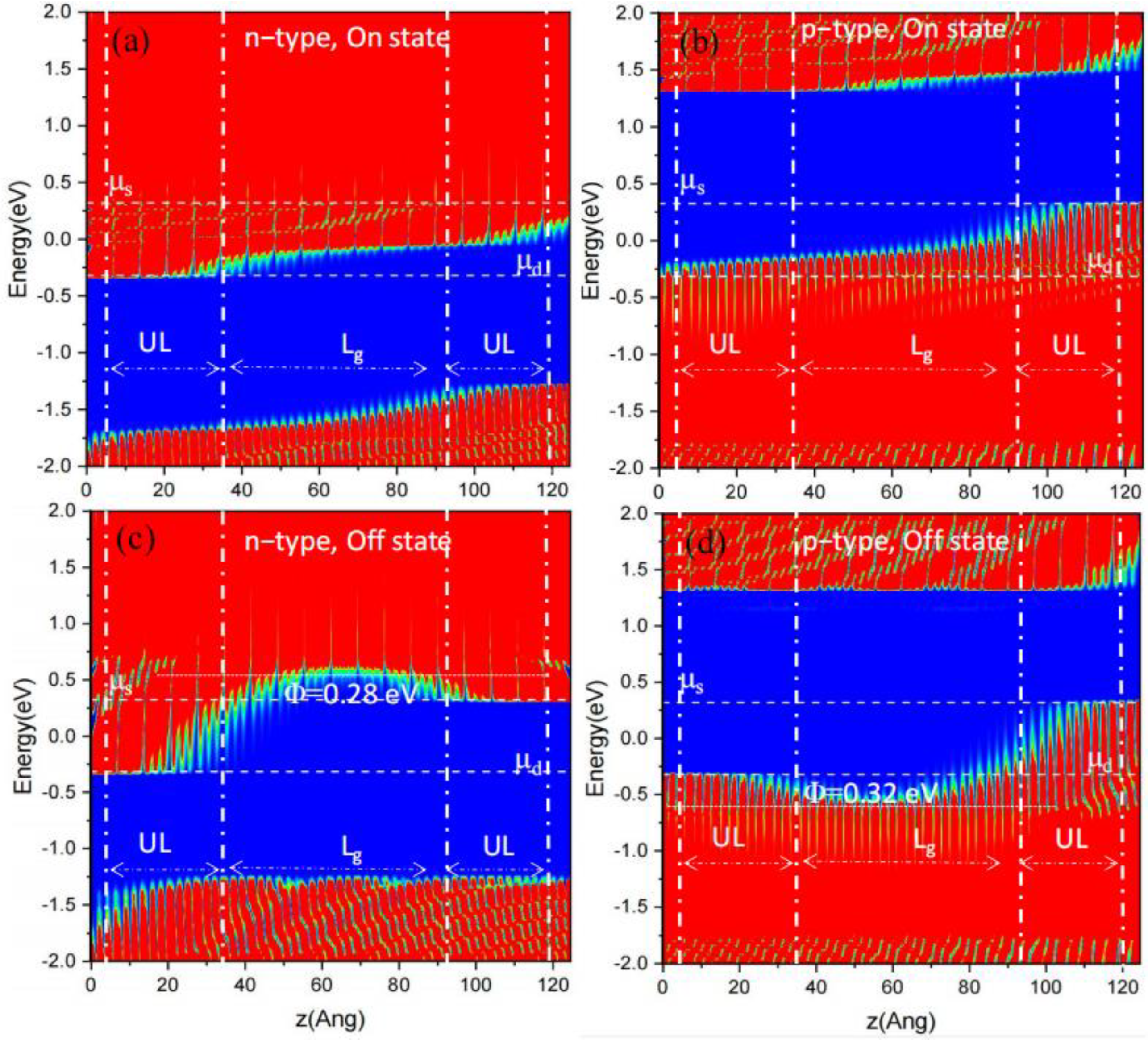
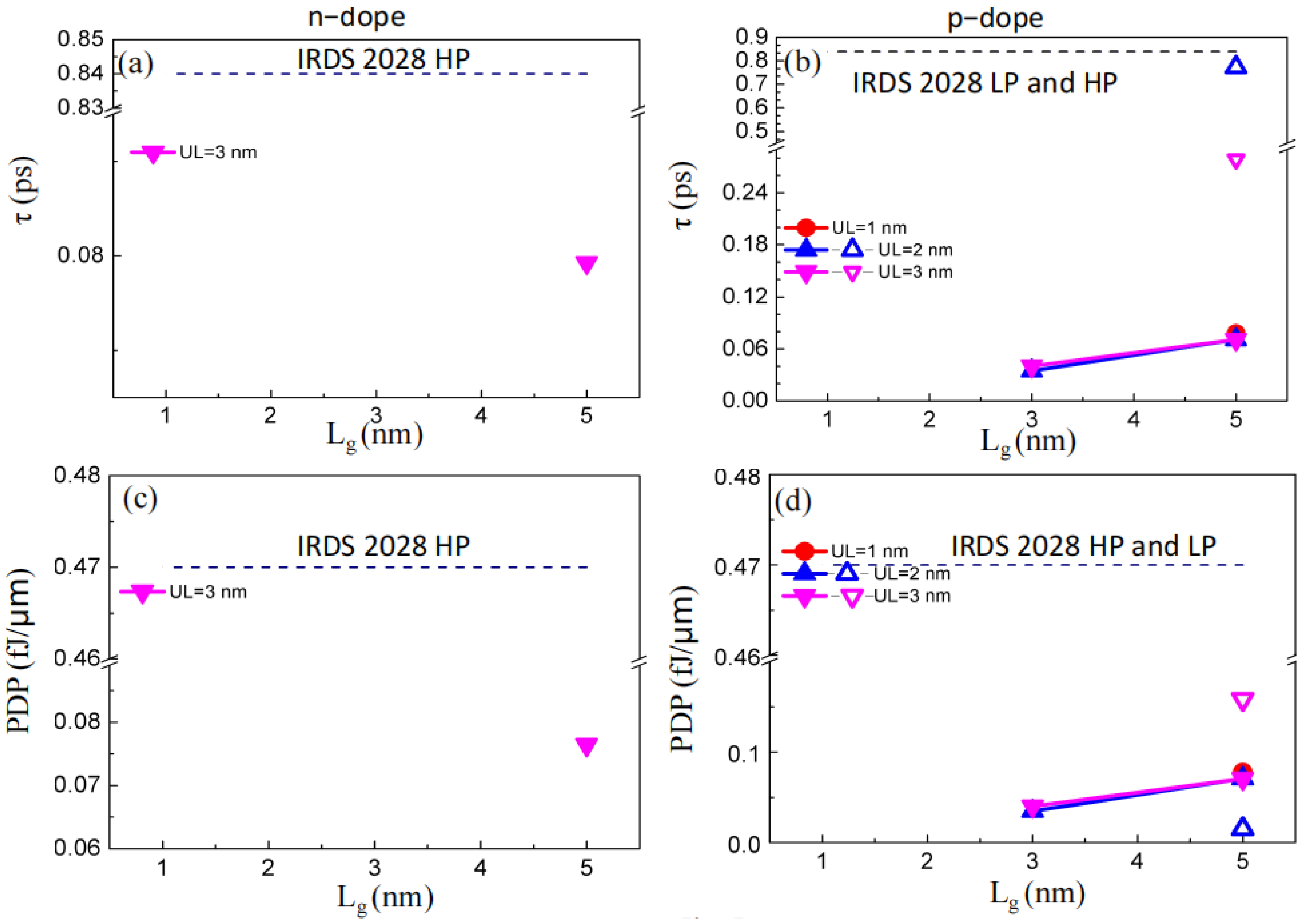
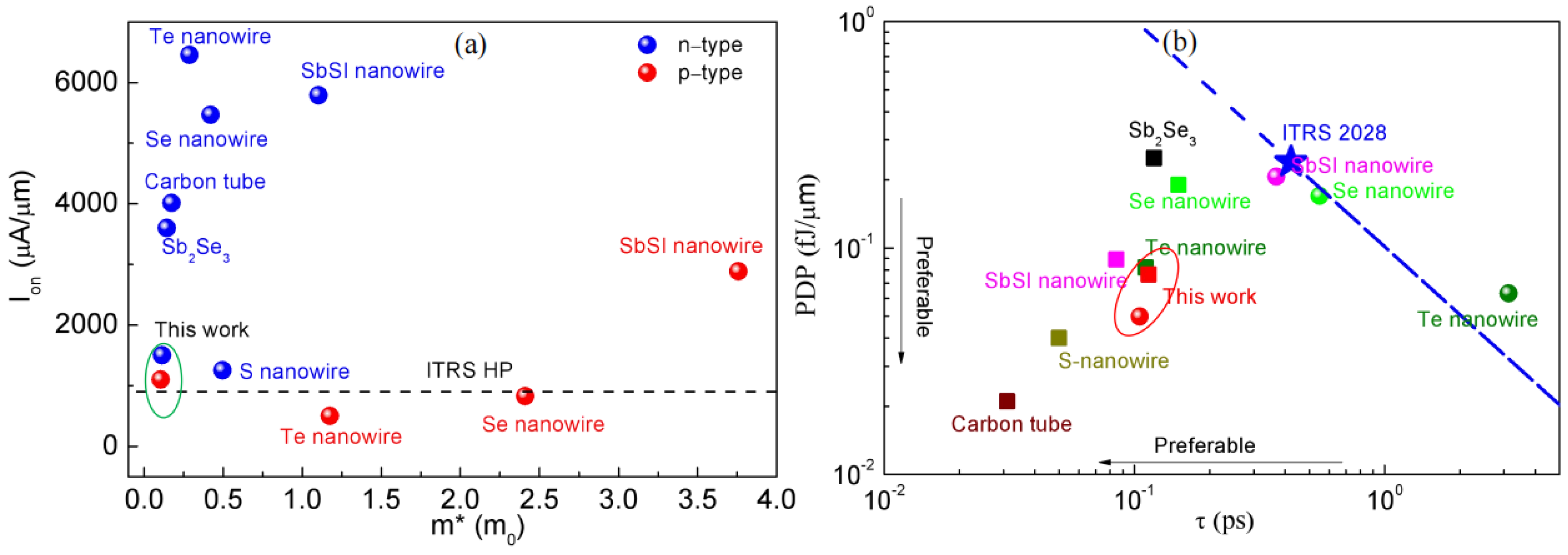
2. Results and Discussion
3. The Approach and the Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Quhe, R.; Xu, L.; Liu, S.; Yang, C.; Wang, Y.; Li, H.; Yang, J.; Li, Q.; Shi, B.; Li, Y. Sub-10 nm two-dimensional transistors: Theory and experiment. Phys. Rep. 2021, 938, 1–72. [Google Scholar] [CrossRef]
- Liu, Q.; Li, J.-J.; Wu, D.; Deng, X.-Q.; Zhang, Z.-H.; Fan, Z.-Q.; Chen, K.-Q. Gate-controlled reversible rectifying behavior investigated in a two-dimensional MoS2 diode. Phys. Rev. B 2021, 104, 045412. [Google Scholar] [CrossRef]
- Huang, X.-D.; Liu, Q.; Xie, H.-Q.; Deng, X.-Q.; Fan, Z.-Q.; Wu, D.; Chen, K.-Q. Transport Properties of 5-nm Tunnel Field-Effect Transistor for High-Performance Switches Decorated With Blue Phosphorene and Transition Metals. IEEE Trans. Electron Devices 2023, 70, 5462–5468. [Google Scholar] [CrossRef]
- Dastgeer, G.; Nisar, S.; Shahzad, Z.M.; Rasheed, A.; Kim, D.K.; Jaffery, S.H.A.; Wang, L.; Usman, M.; Eom, J. Low-Power Negative-Differential-Resistance Device for Sensing the Selective Protein via Supporter Molecule Engineering. Adv. Sci. 2023, 10, 2204779. [Google Scholar] [CrossRef] [PubMed]
- Nisar, S.; Dastgeer, G.; Shahzadi, M.; Shahzad, Z.M.; Elahi, E.; Irfan, A.; Eom, J.; Kim, H.; Kim, D.-k. Gate-assisted MoSe2 transistor to detect the streptavidin via supporter molecule engineering. Mater. Today Nano 2023, 24, 100405. [Google Scholar] [CrossRef]
- Tans, S.J.; Devoret, M.H.; Dai, H.; Thess, A.; Smalley, R.E.; Geerligs, L.; Dekker, C. Individual single-wall carbon nanotubes as quantum wires. Nature 1997, 386, 474–477. [Google Scholar] [CrossRef]
- Tans, S.J.; Verschueren, A.R.; Dekker, C. Room-temperature transistor based on a single carbon nanotube. Nature 1998, 393, 49–52. [Google Scholar] [CrossRef]
- Bachtold, A.; Hadley, P.; Nakanishi, T.; Dekker, C. Logic circuits with carbon nanotube transistors. Science 2001, 294, 1317–1320. [Google Scholar] [CrossRef] [PubMed]
- Javey, A.; Guo, J.; Wang, Q.; Lundstrom, M.; Dai, H. Ballistic carbon nanotube field-effect transistors. Nature 2003, 424, 654–657. [Google Scholar] [CrossRef]
- Franklin, A.D. The road to carbon nanotube transistors. Nature 2013, 498, 443–444. [Google Scholar] [CrossRef]
- Martel, R.; Schmidt, T.; Shea, H.; Hertel, T.; Avouris, P. Single-and multi-wall carbon nanotube field-effect transistors. Appl. Phys. Lett. 1998, 73, 2447–2449. [Google Scholar] [CrossRef]
- Qiu, C.; Zhang, Z.; Xiao, M.; Yang, Y.; Zhong, D.; Peng, L.-M. Scaling carbon nanotube complementary transistors to 5-nm gate lengths. Science 2017, 355, 271–276. [Google Scholar] [CrossRef] [PubMed]
- Franklin, A.D.; Luisier, M.; Han, S.-J.; Tulevski, G.; Breslin, C.M.; Gignac, L.; Lundstrom, M.S.; Haensch, W. Sub-10 nm carbon nanotube transistor. Nano Lett. 2012, 12, 758–762. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Yang, J.; Qiu, C.; Liu, S.; Zhou, W.; Li, Q.; Shi, B.; Ma, J.; Yang, C.; Lu, J. Can Carbon Nanotube Transistors Be Scaled Down to the Sub-5 nm Gate Length? ACS Appl. Mater. Interfaces 2021, 13, 31957–31967. [Google Scholar] [CrossRef] [PubMed]
- Appenzeller, J.; Lin, Y.-M.; Knoch, J.; Avouris, P. Band-to-band tunneling in carbon nanotube field-effect transistors. Phys. Rev. Lett. 2004, 93, 196805. [Google Scholar] [CrossRef] [PubMed]
- Lemme, M.C.; Echtermeyer, T.J.; Baus, M.; Kurz, H. A graphene field-effect device. IEEE Electron Device Lett. 2007, 28, 282–284. [Google Scholar] [CrossRef]
- Meric, I.; Han, M.Y.; Young, A.F.; Ozyilmaz, B.; Kim, P.; Shepard, K.L. Current saturation in zero-bandgap, top-gated graphene field-effect transistors. Nat. Nanotechnol. 2008, 3, 654–659. [Google Scholar] [CrossRef]
- Chen, Z.; Narita, A.; Müllen, K. Graphene nanoribbons: On-surface synthesis and integration into electronic devices. Adv. Mater. 2020, 32, 2001893. [Google Scholar] [CrossRef] [PubMed]
- Neto, A.C.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Kotov, V.N.; Uchoa, B.; Pereira, V.M.; Guinea, F.; Neto, A.C. Electron-electron interactions in graphene: Current status and perspectives. Rev. Mod. Phys. 2012, 84, 1067. [Google Scholar] [CrossRef]
- Wang, X.; Ouyang, Y.; Li, X.; Wang, H.; Guo, J.; Dai, H. Room-temperature all-semiconducting sub-10-nm graphene nanoribbon field-effect transistors. Phys. Rev. Lett. 2008, 100, 206803. [Google Scholar] [CrossRef]
- Bennett, P.B.; Pedramrazi, Z.; Madani, A.; Chen, Y.-C.; de Oteyza, D.G.; Chen, C.; Fischer, F.R.; Crommie, M.F.; Bokor, J. Bottom-up graphene nanoribbon field-effect transistors. Appl. Phys. Lett. 2013, 103, 253114. [Google Scholar] [CrossRef]
- Llinas, J.P.; Fairbrother, A.; Borin Barin, G.; Shi, W.; Lee, K.; Wu, S.; Yong Choi, B.; Braganza, R.; Lear, J.; Kau, N. Short-channel field-effect transistors with 9-atom and 13-atom wide graphene nanoribbons. Nat. Commun. 2017, 8, 633. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Kawagoe, Y.; Hirano, Y.; Iruka, T.; Yano, M.; Nakae, T. Width-Controlled Sub-Nanometer Graphene Nanoribbon Films Synthesized by Radical-Polymerized Chemical Vapor Deposition. Adv. Mater. 2014, 26, 4134–4138. [Google Scholar] [CrossRef]
- Tsumura, A.; Koezuka, H.; Ando, T. Macromolecular electronic device: Field-effect transistor with a polythiophene thin film. Appl. Phys. Lett. 1986, 49, 1210–1212. [Google Scholar] [CrossRef]
- Shu, C.-H.; Liu, M.-X.; Zha, Z.-Q.; Pan, J.-L.; Zhang, S.-Z.; Xie, Y.-L.; Chen, J.-L.; Yuan, D.-W.; Qiu, X.-H.; Liu, P.-N. On-surface synthesis of poly (p-phenylene ethynylene) molecular wires via in situ formation of carbon-carbon triple bond. Nat. Commun. 2018, 9, 2322. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.; Li, H.; Zhong, C.; Matsumoto, M.; Dichtel, W.R.; Bredas, J.-L. Electronic structure of two-dimensional π-conjugated covalent organic frameworks. Chem. Mater. 2019, 31, 3051–3065. [Google Scholar] [CrossRef]
- Quhe, R.; Li, Q.; Zhang, Q.; Wang, Y.; Zhang, H.; Li, J.; Zhang, X.; Chen, D.; Liu, K.; Ye, Y. Simulations of quantum transport in sub-5-nm monolayer phosphorene transistors. Phys. Rev. Appl. 2018, 10, 024022. [Google Scholar] [CrossRef]
- Li, Q.; Yang, J.; Li, Q.; Liu, S.; Xu, L.; Yang, C.; Xu, L.; Li, Y.; Sun, X.; Yang, J. Sub-5 nm Gate Length Monolayer MoTe2 Transistors. J. Phys. Chem. C 2021, 125, 19394–19404. [Google Scholar] [CrossRef]
- Cao, W.; Kang, J.; Sarkar, D.; Liu, W.; Banerjee, K. 2D semiconductor FETs—Projections and design for sub-10 nm VLSI. IEEE Trans. Electron Devices 2015, 62, 3459–3469. [Google Scholar] [CrossRef]
- Likharev, K.K. Classical and quantum limitations on energy consumption in computation. Int. J. Theor. Phys. 1982, 21, 311–326. [Google Scholar] [CrossRef]
- Keyes, R.W. Fundamental limits in digital information processing. Proc. IEEE 1981, 69, 267–278. [Google Scholar] [CrossRef]
- Zhirnov, V.V.; Cavin, R.K.; Hutchby, J.A.; Bourianoff, G.I. Limits to binary logic switch scaling-a gedanken model. Proc. IEEE 2003, 91, 1934–1939. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, Z.; Zhong, H.; Shao, C.; Wan, X.; Zhang, C.; Robertson, J.; Guo, Y. Tellurium nanowire gate-all-around MOSFETs for sub-5 nm applications. ACS Appl. Mater. Interfaces 2021, 13, 3387–3396. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Tan, X.; Yang, Y. Sub-5 nm Gate Length Selenium Nanowire Transistors: Implications for Nanoelectronics. ACS Appl. Nano Mater. 2023, 6, 4067–4077. [Google Scholar] [CrossRef]
- Tan, X.; Li, Q.; Ren, D. One dimensional MOSFETs for sub-5 nm high-performance applications: A case of Sb2Se3 nanowires. Phys. Chem. Chem. Phys. 2023, 25, 2056–2062. [Google Scholar] [CrossRef]
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Verstichel, B.; Stradi, D.; Khomyakov, P.A.; Vej-Hansen, U.G. QuantumATK: An integrated platform of electronic and atomic-scale modelling tools. J. Phys. Condens. Matter 2019, 32, 015901. [Google Scholar] [CrossRef]
- Imry, Y.; Landauer, R. Conductance viewed as transmission. Rev. Mod. Phys. 1999, 71, S306–S312. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Datta, S. Quantum Transport: Atom to Transistor; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Zhong, H.; Quhe, R.; Wang, Y.; Ni, Z.; Ye, M.; Song, Z.; Pan, Y.; Yang, J.; Yang, L.; Lei, M. Interfacial properties of monolayer and bilayer MoS2 contacts with metals: Beyond the energy band calculations. Sci. Rep. 2016, 6, 21786. [Google Scholar] [CrossRef]
- Gao, S.; Yang, L. Renormalization of the quasiparticle band gap in doped two-dimensional materials from many-body calculations. Phys. Rev. B 2017, 96, 155410. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Tan, X.; Li, Q.; Wan, J.; Xu, G. High-Performance One-Dimensional Sub-5 nm Transistors Based on Poly(p-phenylene ethynylene) Molecular Wires. Molecules 2024, 29, 3207. https://doi.org/10.3390/molecules29133207
Chen Z, Tan X, Li Q, Wan J, Xu G. High-Performance One-Dimensional Sub-5 nm Transistors Based on Poly(p-phenylene ethynylene) Molecular Wires. Molecules. 2024; 29(13):3207. https://doi.org/10.3390/molecules29133207
Chicago/Turabian StyleChen, Zhilin, Xingyi Tan, Qiang Li, Jing Wan, and Gang Xu. 2024. "High-Performance One-Dimensional Sub-5 nm Transistors Based on Poly(p-phenylene ethynylene) Molecular Wires" Molecules 29, no. 13: 3207. https://doi.org/10.3390/molecules29133207
APA StyleChen, Z., Tan, X., Li, Q., Wan, J., & Xu, G. (2024). High-Performance One-Dimensional Sub-5 nm Transistors Based on Poly(p-phenylene ethynylene) Molecular Wires. Molecules, 29(13), 3207. https://doi.org/10.3390/molecules29133207







