A Heterogeneous Viscosity Flow Model for Liquid Transport through Nanopores Considering Pore Size and Wettability
Abstract
1. Introduction
2. Results
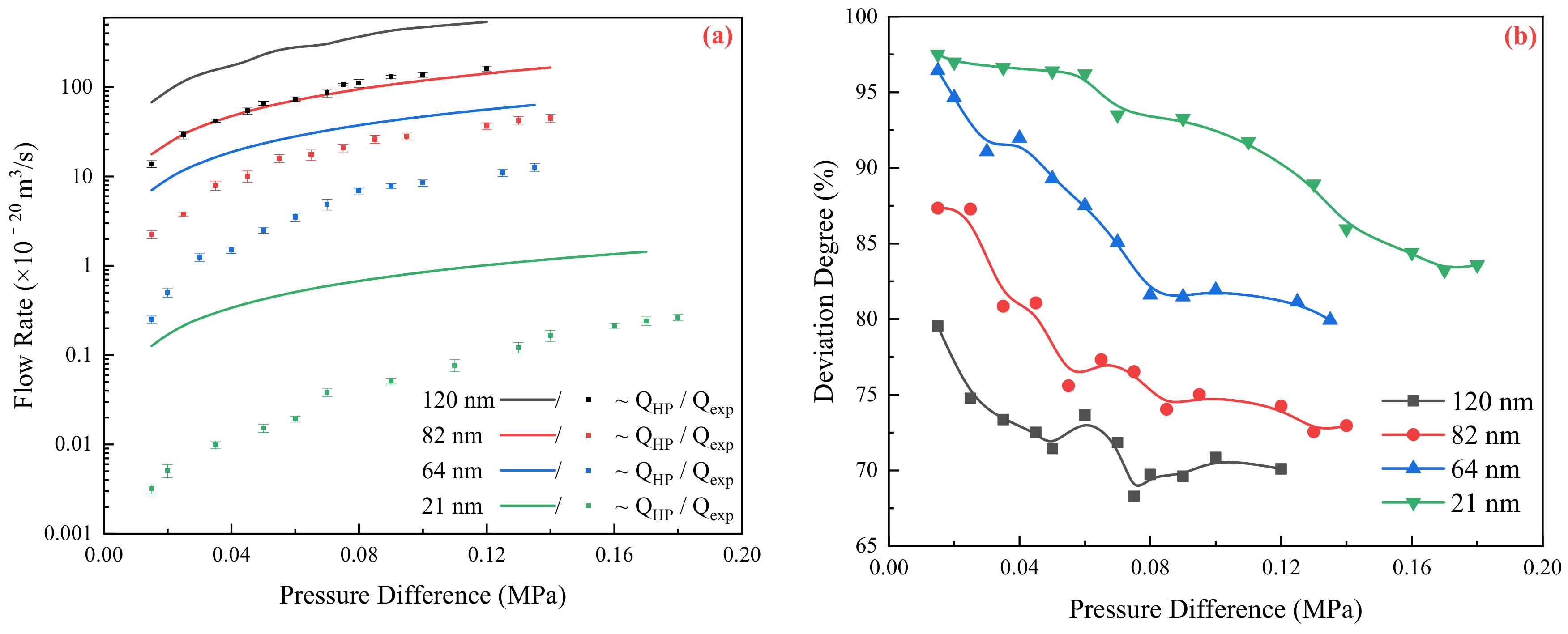
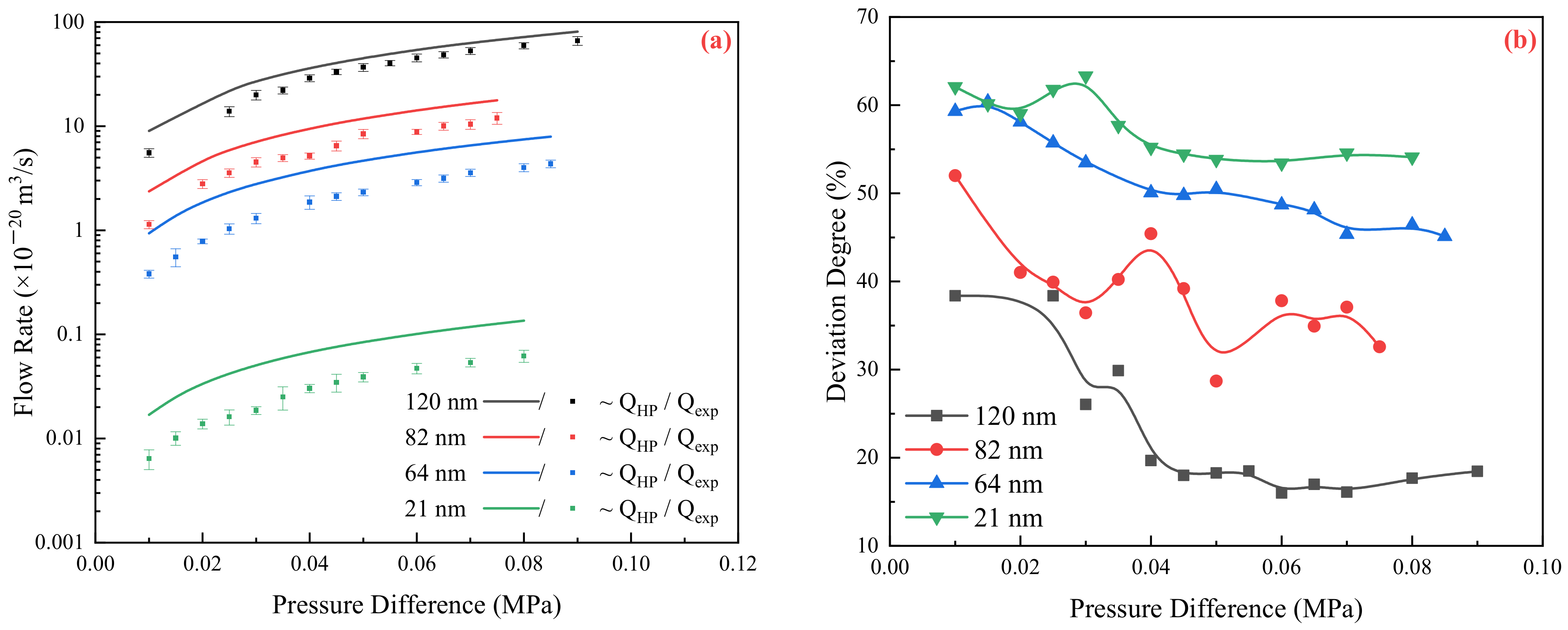
2.1. Relationship between Experimental and Theoretical Flow Rate
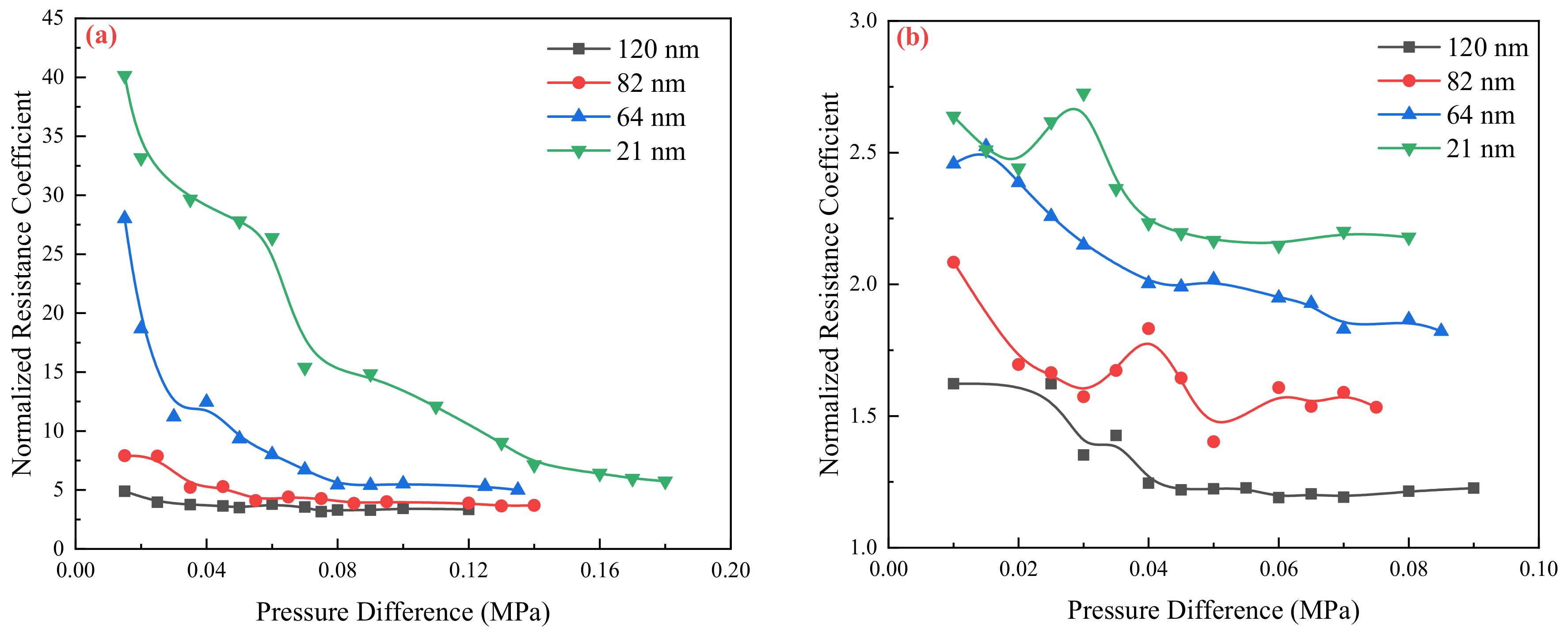
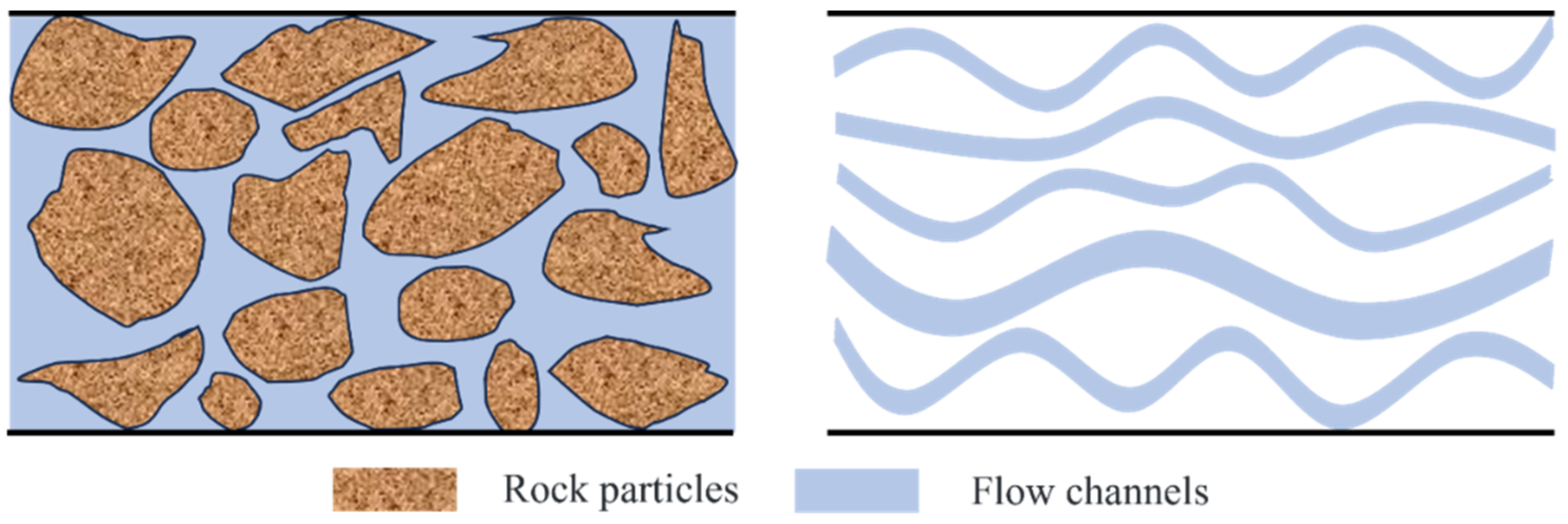
2.2. Flow Resistance of the Different Medium
3. Discussions
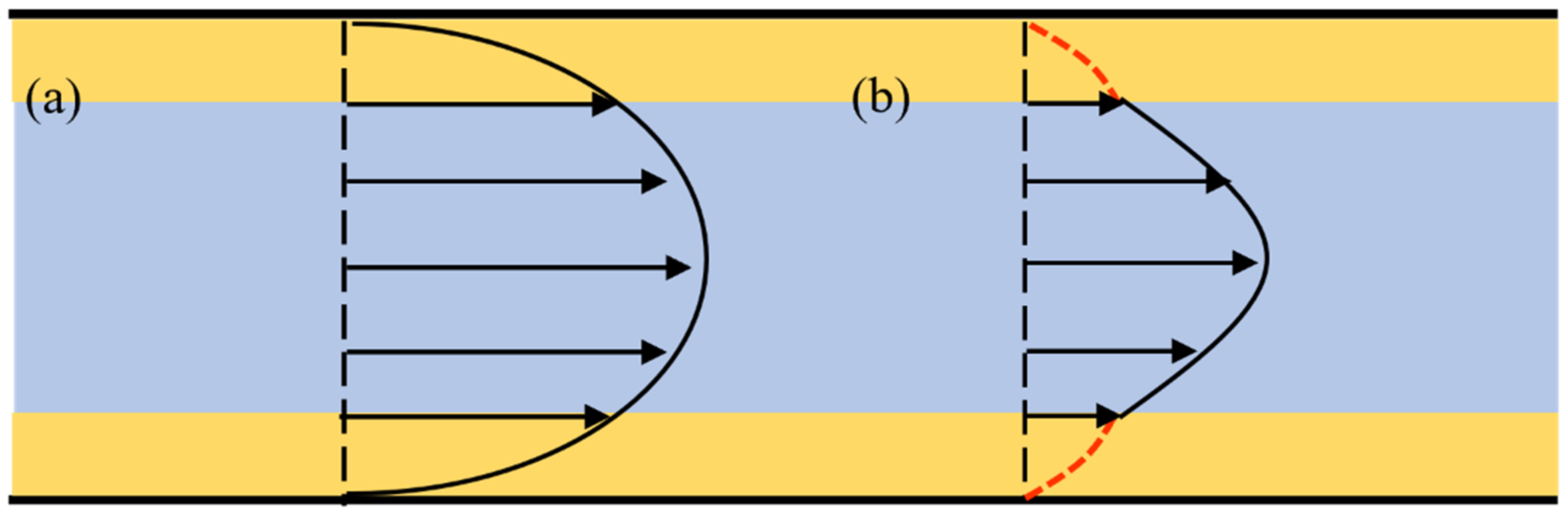
3.1. Heterogeneous Viscosity Flow Model
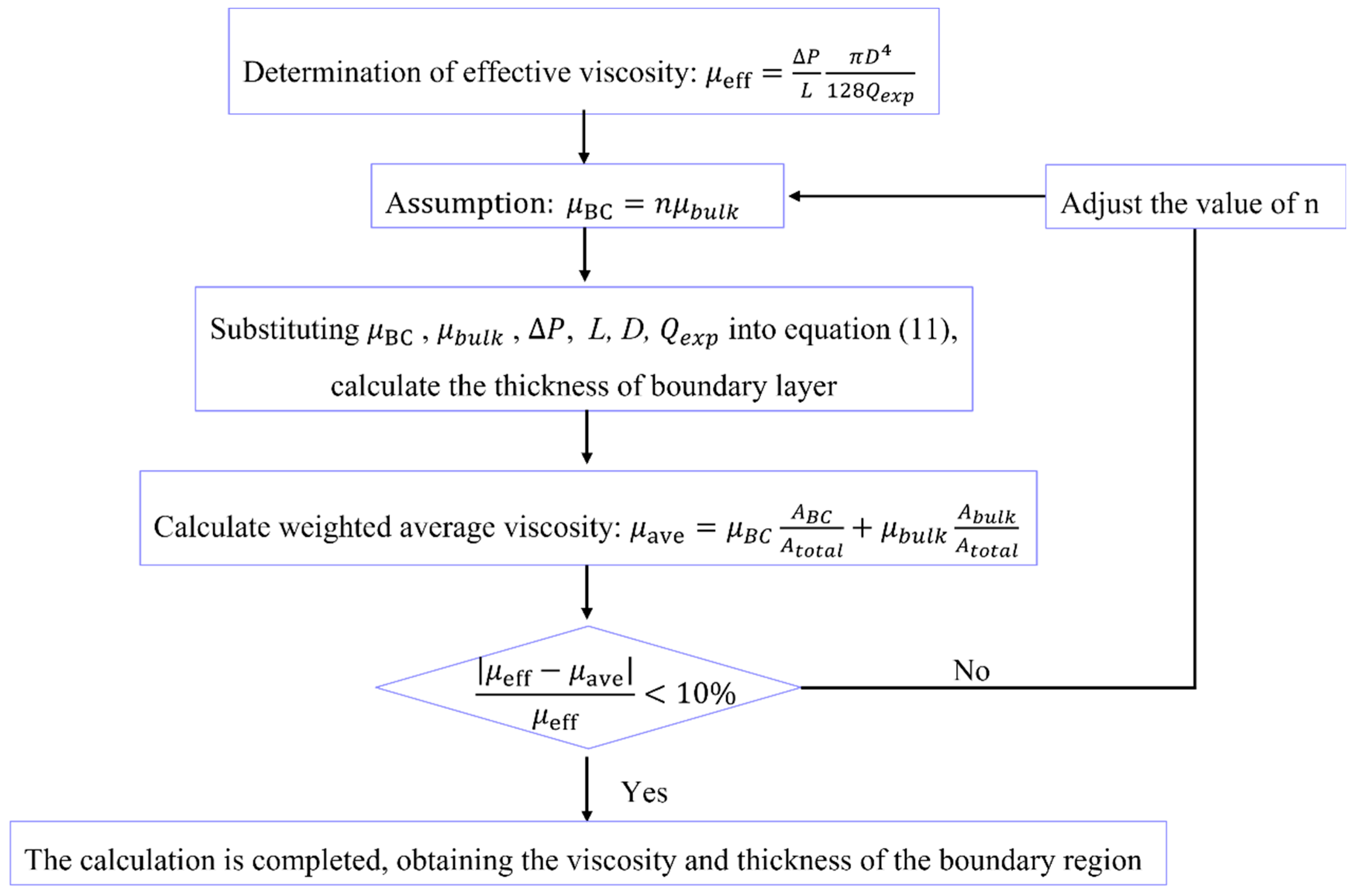
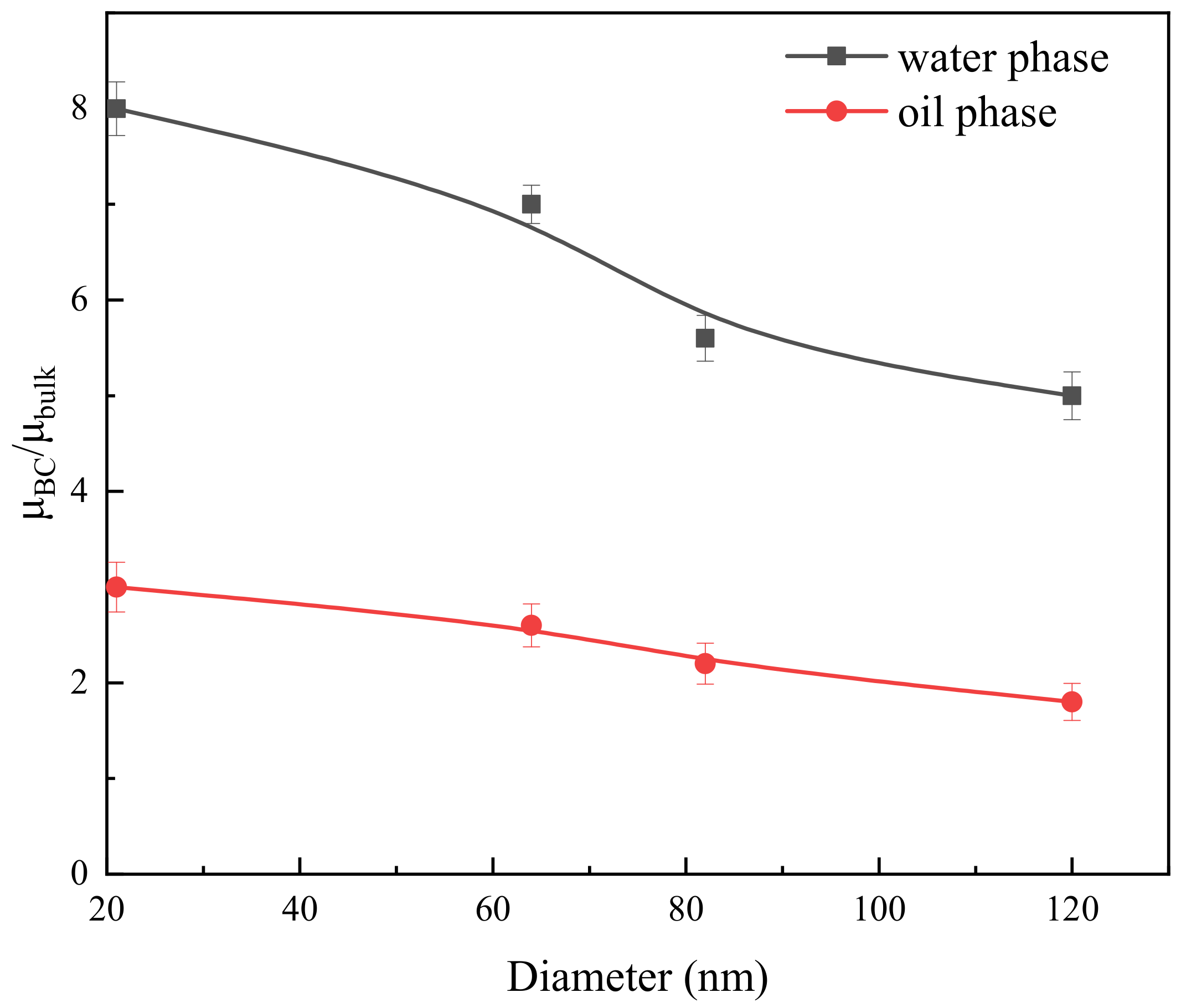
3.2. Fluid Viscosity and Thickness of the Boundary Region
- (1)
- Assuming the viscosity of the fluid is a necessary step in calculating the thickness of the boundary region when the fluid viscosity and thickness are unknown. To determine the appropriateness of the assumed fluid viscosity, a standard is required. In this case, the effective viscosity of the fluid can be calculated based on the HP equation and experimentally measured flow rate at different pore sizes and pressures, which serves as a benchmark for subsequent judgment.
- (2)
- Based on the given information, both the water phase and the oil phase are in a flow inhibition state in the nanochannel. This indicates that the viscosity of the boundary layer is greater than the bulk viscosity. Meanwhile, the fluid viscosity is also greater than the effective viscosity determined in the first step. Taking these factors into account, the ratio n of viscosity of boundary fluid and bulk fluid can be estimated.
- (3)
- Input the following parameters into Equation (12), boundary region fluid viscosity, bulk fluid viscosity, pressure gradient, experimental flow rate, and calculate the thickness h of the boundary layer.
- (4)
- After obtaining h, it is crucial to combine the viscosity of the boundary region fluid and bulk fluid to form an average viscosity for comparison with the effective viscosity. Calculate the weighted average viscosity of the fluid in the nanochannel according to Equation (7):
- (5)
- Calculate the relative error between the average viscosity and the effective viscosity. If the relative error is less than 10%, it indicates that the assumed boundary fluid viscosity is appropriate, and the calculation can be concluded. However, if the relative error is greater than 10%, it suggests that there is an issue with the initially selected boundary fluid viscosity. In this case, you should go back to step (2) and adjust the value of n to restart the calculation. Continue iterating and adjusting the n value until the relative error is less than 10%.
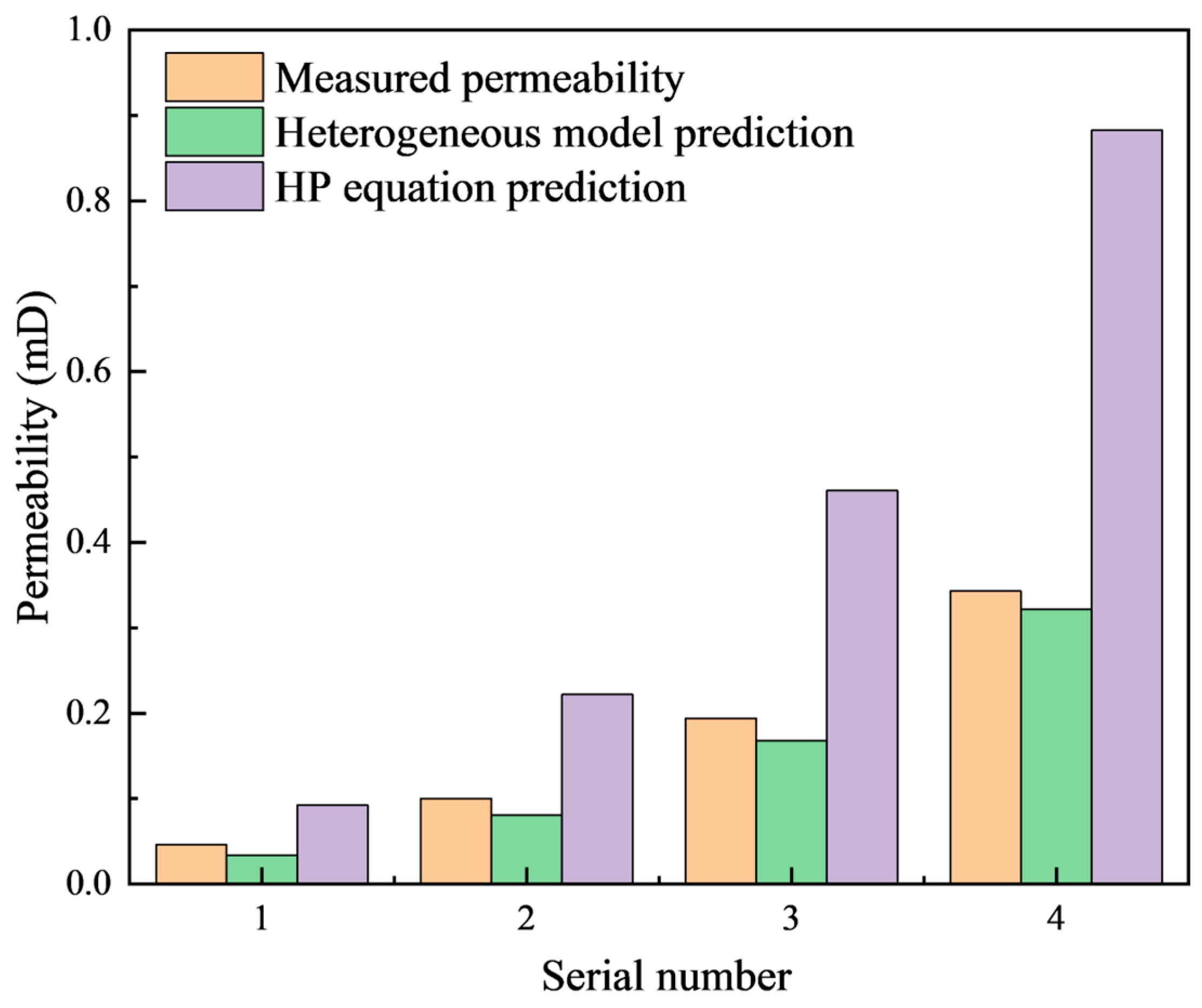
3.3. Model Application
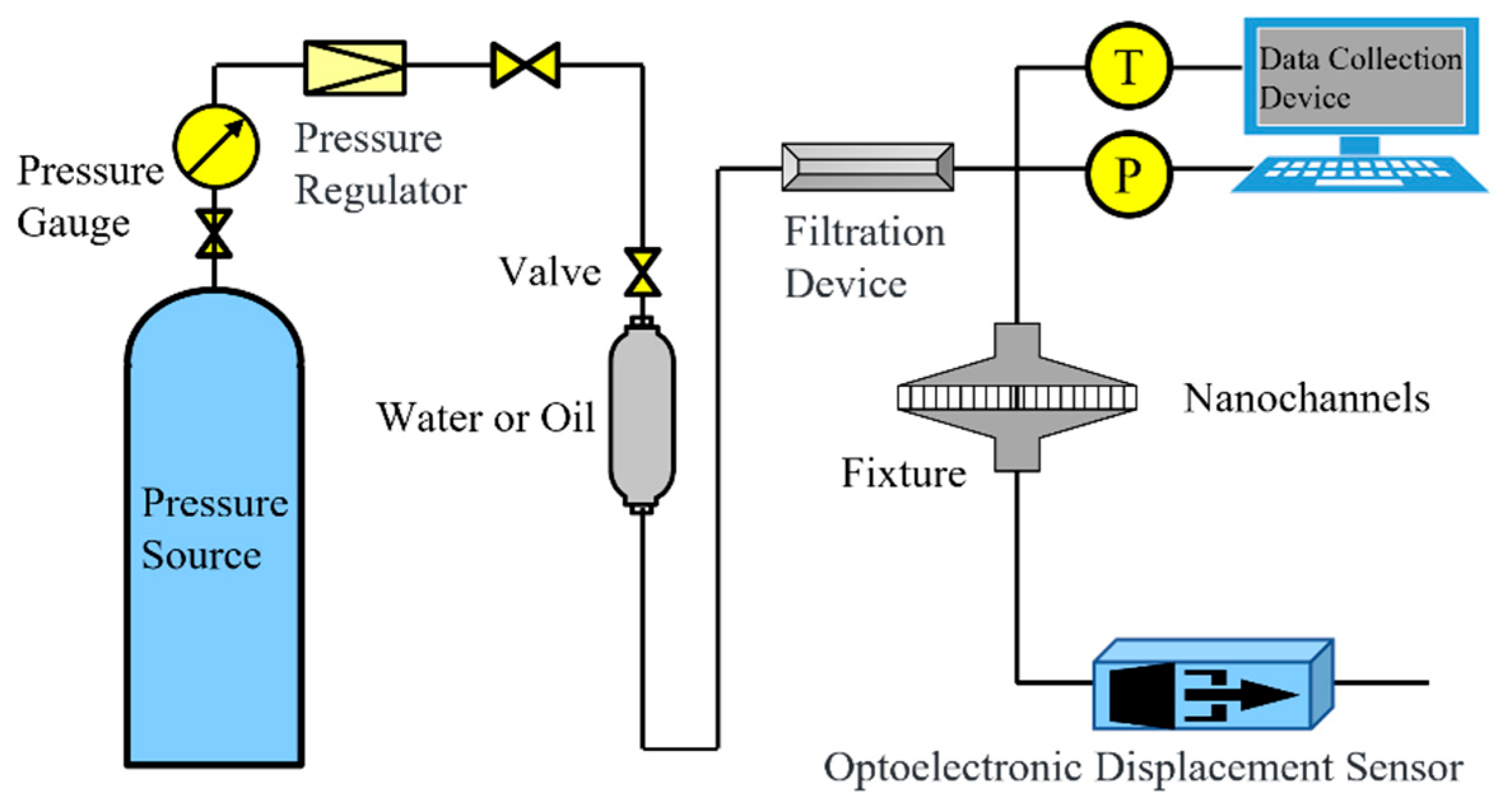
4. Experimental Section
4.1. Materials
4.2. Experimental Method
4.2.1. Experimental Procedure
4.2.2. Data Analysis Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, G.; Zhu, R. Progress, Challenges and key issues of unconventional oil and gas development of CNPC. China Pet. Explor. 2020, 25, 1–13. [Google Scholar]
- Fu, S.; Jin, Z.; Fu, J.; Li, S.; Yang, W. Transformation of understanding from tight oil to shale oil in the member 7 of Yanchang formation in Ordos basin and its significance of exploration and development. Acta Pet. Sin. 2021, 42, 561–569. [Google Scholar]
- Zhao, X.; Yang, Z.; Lin, W.; Xiong, S.; Luo, Y.; Wang, Z.; Chen, T.; Xia, D.; Wu, Z. Study on Pore Structures of Tight Sandstone Reservoirs Based on Nitrogen Adsorption, High-Pressure Mercury Intrusion, and Rate-Controlled Mercury Intrusion. J. Energy Resour. Technol.-Trans. ASME 2019, 141, 112903. [Google Scholar] [CrossRef]
- Zou, C.; Zhu, R.; Wu, S.; Yang, Z.; Tao, S.; Yuan, X.; Hou, L.; Yang, H.; Xu, C.; Hua, D.; et al. Types, Characteristics, genesis and prospects of conventional and unconventional hydrocarbon accumulations: Taking tight oil and tight gas in China as an instance. Acta Pet. Sin. 2012, 33, 173–187. [Google Scholar]
- Jia, C.; Zou, C.; Li, J.; Li, D.; Zheng, M. Assessment Criteria, main types, basic features and resource prospects of the tight oil in China. Acta Pet. Sin. 2012, 33, 343–350. [Google Scholar]
- Yu, C.; Zhao, J.; Wang, Z.; Guo, P.; Liu, H.; Su, Z.; Liao, H. Vapor-liquid phase equilibrium of n-pentane in quartz nanopores by grand canonical Monte Carlo calculation. J. Mol. Liq. 2022, 365, 120075. [Google Scholar] [CrossRef]
- Wang, H.; Su, Y.; Wang, W.; Sheng, G.; Li, H.; Zafar, A. Enhanced water flow and apparent viscosity model considering wettability and shape effects. Fuel 2019, 253, 1351–1360. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, X.; Yang, Z.; Wang, F.; Zhang, Y.; Liu, G.; Lin, W. Experimental study on physical modeling of flow mechanism in volumetric fracturing of tight oil reservoir. Phys. Fluids 2021, 33, 107118. [Google Scholar] [CrossRef]
- Nazari, M.; Davoodabadi, A.; Huang, D.; Luo, T.; Ghasemi, H. Transport Phenomena in Nano/Molecular Confinements. ACS Nano 2020, 14, 16348–16391. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zong, X.; Xue, S.; Liu, H.; He, M. Molecular structure and transport of ionic liquid confined in asymmetric graphene-coated silica nanochannel. J. Mol. Liq. 2022, 345, 117869. [Google Scholar] [CrossRef]
- Lee, K.P.; Leese, H.; Mattia, D. Water flow enhancement in hydrophilic nanochannels. Nanoscale 2012, 4, 2621–2627. [Google Scholar] [CrossRef] [PubMed]
- Holt, J.K. Methods for probing water at the nanoscale. Microfluid. Nanofluid. 2008, 5, 425–442. [Google Scholar] [CrossRef]
- Majumder, M.; Chopra, N.; Andrews, R.; Hinds, B.J. Nanoscale hydrodynamics—Enhanced flow in carbon nanotubes. Nature 2005, 438, 44. [Google Scholar] [CrossRef] [PubMed]
- Whitby, M.; Cagnon, L.; Thanou, M.; Quirke, N. Enhanced fluid flow through nanoscale carbon pipes. Nano Lett. 2008, 8, 2632–2637. [Google Scholar] [CrossRef] [PubMed]
- Secchi, E.; Marbach, S.; Nigues, A.; Stein, D.; Siria, A.; Bocquet, L. Massive radius-dependent flow slippage in carbon nanotubes. Nature 2016, 537, 210–213. [Google Scholar] [CrossRef]
- Kelly, S.; Balhoff, M.T.; Torres-Verdin, C. Quantification of Bulk Solution Limits for Liquid and Interfacial Transport in Nanoconfinements. Langmuir 2015, 31, 2167–2179. [Google Scholar] [CrossRef] [PubMed]
- Tomo, Y.; Askounis, A.; Ikuta, T.; Takata, Y.; Sefiane, K.; Takahashi, K. Superstable Ultrathin Water Film Confined in a Hydrophilized Carbon Nanotube. Nano Lett. 2018, 18, 1869–1874. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.; Yao, S.-C. Effect of surface roughness on laminar liquid flow in micro-channels. Appl. Therm. Eng. 2011, 31, 228–234. [Google Scholar] [CrossRef]
- Tao, J.; Song, X.; Zhao, T.; Zhao, S.; Liu, H. Confinement effect on water transport in CNT membranes. Chem. Eng. Sci. 2018, 192, 1252–1259. [Google Scholar] [CrossRef]
- Zhang, J.; Song, H.; Zhu, W.; Wang, J. Liquid Transport Through Nanoscale Porous Media with Strong Wettability. Transp. Porous Media 2021, 140, 697–711. [Google Scholar] [CrossRef]
- Wu, S.; Li, Z.; Zhang, C.; Lv, G.; Zhou, P. Nanohydrodynamic Model and Transport Mechanisms of Tight Oil Confined in Nanopores Considering Liquid-Solid Molecular Interaction Effect. Ind. Eng. Chem. Res. 2021, 60, 18154–18165. [Google Scholar] [CrossRef]
- Bocquet, L.; Charlaix, E. Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 2010, 39, 1073–1095. [Google Scholar] [CrossRef]
- Kohler, M.H.; da Silva, L.B. Size effects and the role of density on the viscosity of water confined in carbon nanotubes. Chem. Phys. Lett. 2016, 645, 38–41. [Google Scholar] [CrossRef]
- Srivastava, A.; Hassan, J.; Homouz, D. Effect of Size and Temperature on Water Dynamics inside Carbon Nano-Tubes Studied by Molecular Dynamics Simulation. Molecules 2021, 26, 6175. [Google Scholar] [CrossRef] [PubMed]
- Shirai, J.; Yoshida, K.; Koreeda, H.; Kitamori, T.; Yamaguchi, T.; Mawatari, K. Water structure in 100 nm nanochannels revealed by nano X-ray diffractometry and Raman spectroscopy. J. Mol. Liq. 2022, 350, 118567. [Google Scholar] [CrossRef]
- Thomas, J.A.; McGaughey, A.J.H.; Kuter-Arnebeck, O. Pressure-driven water flow through carbon nanotubes: Insights from molecular dynamics simulation. Int. J. Therm. Sci. 2010, 49, 281–289. [Google Scholar] [CrossRef]
- Thomas, J.A.; McGaughey, A.J.H. Reassessing fast water transport through carbon nanotubes. Nano Lett. 2008, 8, 2788–2793. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Chen, Z.; Xu, J.; Hu, Y. A Universal Model of Water Flow Through Nanopores in Unconventional Reservoirs: Relationships Between Slip, Wettability and Viscosity. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, UAE, 26 September 2016; p. 16. [Google Scholar]
- Wu, K.; Chen, Z.; Li, J.; Li, X.; Xu, J.; Dong, X. Wettability effect on nanoconfined water flow. Proc. Natl. Acad. Sci. USA 2017, 114, 3358. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Ok, J.T.; Sun, Y.; Retterer, S.T.; Neeves, K.B.; Yin, X.; Bai, B.; Ma, Y. Optic imaging of single and two-phase pressure-driven flows in nano-scale channels. Lab Chip 2013, 13, 1165–1171. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Yang, S.; Nie, X.; Wang, Z. Dynamic threshold pressure gradient in tight gas reservoir. J. Nat. Gas Sci. Eng. 2014, 20, 155–160. [Google Scholar] [CrossRef]
- Wang, H.; Tian, L.; Gu, D.; Li, M.; Chai, X.; Yang, Y. Method for Calculating Non-Darcy Flow Permeability in Tight Oil Reservoir. Transp. Porous Media 2020, 133, 357–372. [Google Scholar] [CrossRef]
- Wu, J.; Cheng, L.; Li, C.; Cao, R.; Chen, C.; Cao, M.; Xu, Z. Experimental Study of Nonlinear Flow in Micropores Under Low Pressure Gradient. Transp. Porous Media 2017, 119, 247–265. [Google Scholar] [CrossRef]
- Wang, H.; Su, Y.; Wang, W.; Sheng, G. Hydrodynamic resistance model of oil flow in nanopores coupling oil-wall molecular interactions and the pore-throat structures effect. Chem. Eng. Sci. 2019, 209, 115166. [Google Scholar] [CrossRef]
- Zeng, H.; Wu, K.; Cui, X.; Chen, Z. Wettability effect on nanoconfined water flow: Insights and perspectives. Nano Today 2017, 16, 7–8. [Google Scholar] [CrossRef]
- Din, X.D.; Michaelides, E.E. Kinetic theory and molecular dynamics simulations of microscopic flows. Phys. Fluids 1997, 9, 3915–3925. [Google Scholar] [CrossRef]
- Yu, B.M.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Wu, J.; Yu, B. A fractal resistance model for flow through porous media. Int. J. Heat Mass Transf. 2007, 50, 3925–3932. [Google Scholar] [CrossRef]
- Yu, B.M.; Li, J.H. A geometry model for tortuosity of flow path in porous media. Chin. Phys. Lett. 2004, 21, 1569–1571. [Google Scholar]
- Li, X.-G.; Yi, L.-P.; Yang, Z.-Z.; Huang, X. A new model for gas transport in fractal-like tight porous media. J. Appl. Phys. 2015, 117, 174304. [Google Scholar] [CrossRef]
- Cui, H.H.; Silber-Li, Z.H.; Zhu, S.N. Flow characteristics of liquids in microtubes driven by a high pressure. Phys. Fluids 2004, 16, 1803–1810. [Google Scholar] [CrossRef]


| Serial Number | Porosity/% | Permeability/mD | Df | DT |
|---|---|---|---|---|
| 1 | 5.14 | 0.046 | 1.35 | 1.52 |
| 2 | 6.32 | 0.1 | 1.27 | 1.48 |
| 3 | 8.45 | 0.194 | 1.17 | 1.44 |
| 4 | 10.19 | 0.343 | 1.08 | 1.42 |
| Pore Diameter/nm | 21 | 64 | 82 | 120 |
| Pore Length/μm | 56.4 | 88.1 | 93.7 | 113 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Zhang, Y.; Niu, Z.; Chen, X.; Du, M.; Yang, Z. A Heterogeneous Viscosity Flow Model for Liquid Transport through Nanopores Considering Pore Size and Wettability. Molecules 2024, 29, 3176. https://doi.org/10.3390/molecules29133176
Chang Y, Zhang Y, Niu Z, Chen X, Du M, Yang Z. A Heterogeneous Viscosity Flow Model for Liquid Transport through Nanopores Considering Pore Size and Wettability. Molecules. 2024; 29(13):3176. https://doi.org/10.3390/molecules29133176
Chicago/Turabian StyleChang, Yilin, Yapu Zhang, Zhongkun Niu, Xinliang Chen, Meng Du, and Zhengming Yang. 2024. "A Heterogeneous Viscosity Flow Model for Liquid Transport through Nanopores Considering Pore Size and Wettability" Molecules 29, no. 13: 3176. https://doi.org/10.3390/molecules29133176
APA StyleChang, Y., Zhang, Y., Niu, Z., Chen, X., Du, M., & Yang, Z. (2024). A Heterogeneous Viscosity Flow Model for Liquid Transport through Nanopores Considering Pore Size and Wettability. Molecules, 29(13), 3176. https://doi.org/10.3390/molecules29133176







