Theoretical Study of Copper Squarate as a Promising Adsorbent for Small Gases Pollutants
Abstract
1. Introduction
2. Results and Discussion
2.1. Crystal Bulk Structure and Analysis of Connolly Free Volume and Surface Area Properties
2.2. Adsorption Analysis
2.2.1. Pollutants and Water Adsorption
2.2.2. Co-Adsorption of Pollutants and Water
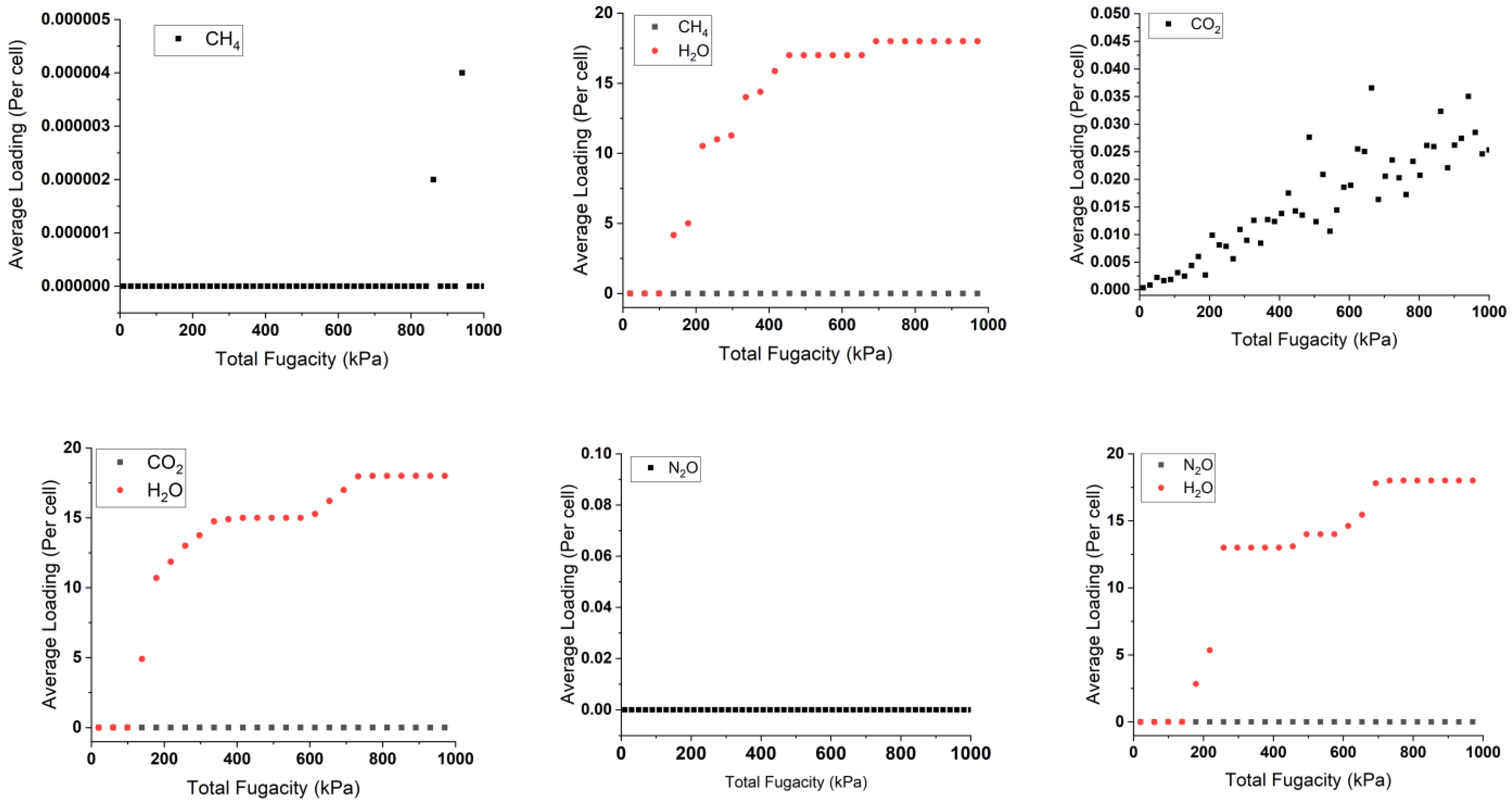
2.3. Sorption Isotherms
3. Quantum Computational Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Lotto, R. Assessment of Development and Regeneration Urban Projects: Cultural and Operational Implications in Metropolization Context. Int. J. Energy Environ. 2008, 2, 25–34. [Google Scholar]
- Molina, M.J.; Molina, L.T. Megacities and Atmospheric Pollution. J. Air Waste Manag. Assoc. 2004, 54, 644–680. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Jin, Y.; Lu, J. Experimental Study on Adsorption of SO2 and DCM from Air Pollutants by Modified Biochar. Biomass Convers. Biorefin 2023, 1–15. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, J.Z.; Xu, Z.P.; Li, Y.; Cao, T.; Zhao, J.; Ruan, X.; Liu, Q.; Qian, G. Decomposition of Potent Greenhouse Gas Sulfur Hexafluoride (SF6) by Kirschsteinite-Dominant Stainless Steel Slag. Environ. Sci. Technol. 2014, 48, 599–606. [Google Scholar] [CrossRef] [PubMed]
- Yao, Z.; Zheng, X.; Dong, H.; Wang, R.; Mei, B.; Zhu, J. A 3-Year Record of N2O and CH4 Emissions from a Sandy Loam Paddy during Rice Seasons as Affected by Different Nitrogen Application Rates. Agric. Ecosyst. Environ. 2012, 152, 1–9. [Google Scholar] [CrossRef]
- Ehhalt, D.; Prather, M.; Dentener, F.; Derwent, R.; Dlugokencky, E.; Holland, E.; Isaksen, I.; Katima, J.; Kirchhoff, V.; Matson, P.; et al. Atmospheric Chemistry and Greenhouse Gases. In Climate change 2001: The Scientific Basis; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2001. [Google Scholar]
- Arani, M.H.; Jaafarzadeh, N.; Moslemzadeh, M.; Ghalhari, M.R.; Arani, S.B.; Mohammadzadeh, M. Dispersion of NO2 and SO2 Pollutants in the Rolling Industry with AERMOD Model: A Case Study to Assess Human Health Risk. J. Environ. Health Sci. Eng. 2021, 19, 1287–1298. [Google Scholar] [CrossRef]
- García-Berríos, Z.I.; Arce, R. Photodegradation Mechanisms of 1-Nitropyrene, an Environmental Pollutant: The Effect of Organic Solvents, Water, Oxygen, Phenols, and Polycyclic Aromatics on the Destruction and Product Yields. J. Phys. Chem. A 2012, 116, 3662–3664. [Google Scholar] [CrossRef][Green Version]
- Wang, H.L.; Nie, L.; Li, J.; Wang, Y.F.; Wang, G.; Wang, J.H.; Hao, Z.P. Characterization and Assessment of Volatile Organic Compounds (VOCs) Emissions from Typical Industries. Chin. Sci. Bull. 2013, 58, 724–730. [Google Scholar] [CrossRef]
- Inomata, S.; Yamada, H.; Tanimoto, H. Investigation on VOC Emissions from Automobile Sources by Means of Online Mass Spectrometry. Curr. Pollut. Rep. 2016, 2, 188–199. [Google Scholar] [CrossRef]
- Lin, Y.; Qiu, X.; Ma, Y.; Ma, J.; Zheng, M.; Shao, M. Concentrations and Spatial Distribution of Polycyclic Aromatic Hydrocarbons (PAHs) and Nitrated PAHs (NPAHs) in the Atmosphere of North China, and the Transformation from PAHs to NPAHs. Environ. Pollut. 2015, 196, 164–170. [Google Scholar] [CrossRef]
- Keyte, I.J.; Albinet, A.; Harrison, R.M. On-Road Traffic Emissions of Polycyclic Aromatic Hydrocarbons and Their Oxy- and Nitro- Derivative Compounds Measured in Road Tunnel Environments. Sci. Total Environ. 2016, 566–567, 1131–1142. [Google Scholar] [CrossRef] [PubMed]
- Supong, A.; Bhomick, P.C.; Sinha, U.B.; Sinha, D. A Combined Experimental and Theoretical Investigation of the Adsorption of 4-Nitrophenol on Activated Biocarbon Using DFT Method. Korean J. Chem. Eng. 2019, 36, 2023–2034. [Google Scholar] [CrossRef]
- Ipek, I.; Kabay, N.; Yüksel, M. Separation of Bisphenol A and Phenol from Water by Polymer Adsorbents: Equilibrium and Kinetics Studies. J. Water Process Eng. 2017, 16, 206–211. [Google Scholar] [CrossRef]
- Plaza-Medina, E.F.; Rodríguez-Córdoba, W.; Morales-Cueto, R.; Peon, J. Primary Photochemistry of Nitrated Aromatic Compounds: Excited-State Dynamics and NO• Dissociation from 9-Nitroanthracene. J. Phys. Chem. A 2011, 115, 577–585. [Google Scholar] [CrossRef] [PubMed]
- Tian, M.; Bakovic, L.; Chen, A. Kinetics of the Electrochemical Oxidation of 2-Nitrophenol and 4-Nitrophenol Studied by in Situ UV Spectroscopy and Chemometrics. Electrochim. Acta 2007, 52, 6517–6524. [Google Scholar] [CrossRef]
- Bertinelli, L.; Camacho, C.; Zou, B. Carbon Capture and Storage and Transboundary Pollution: A Differential Game Approach. Eur. J. Oper. Res. 2014, 237, 721–728. [Google Scholar] [CrossRef]
- Shan, Y.; Du, J.; Zhang, Y.; Shan, W.; Shi, X.; Yu, Y.; Zhang, R.; Meng, X.; Xiao, F.S.; He, H. Selective Catalytic Reduction of NOx with NH3: Opportunities and Challenges of Cu-Based Small-Pore Zeolites. Natl. Sci. Rev. 2021, 8, nwab010. [Google Scholar] [CrossRef] [PubMed]
- Inomata, S.; Fushimi, A.; Sato, K.; Fujitani, Y.; Yamada, H. 4-Nitrophenol, 1-Nitropyrene, and 9-Nitroanthracene Emissions in Exhaust Particles from Diesel Vehicles with Different Exhaust Gas Treatments. Atmos. Environ. 2015, 110, 93–102. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, L.; Chen, L.; Han, C.; Akutagawa, T.; Endo, O.; Yamauchi, M.; Neroda, A.; Toriba, A.; Tang, N. Polycyclic Aromatic Hydrocarbons and Nitro-Polycyclic Aromatic Hydrocarbons in Five East Asian Cities: Seasonal Characteristics, Health Risks, and Yearly Variations. Environ. Pollut. 2021, 287. [Google Scholar] [CrossRef]
- Zeng, Y.; Zou, R.; Zhao, Y. Covalent Organic Frameworks for CO2 Capture. Adv. Mater. 2016, 28, 2855–2873. [Google Scholar] [CrossRef]
- Wang, S.M.; Mu, X.T.; Liu, H.R.; Zheng, S.T.; Yang, Q.Y. Pore-Structure Control in Metal–Organic Frameworks (MOFs) for Capture of the Greenhouse Gas SF6 with Record Separation. Angew. Chem. -Int. Ed. 2022, 61, e202207066. [Google Scholar] [CrossRef]
- Jang, Y.; Sekaran, B.; Singh, P.P.; Misra, R.; D’Souza, F. Accelerated Intramolecular Charge Transfer in Tetracyanobutadiene- and Expanded Tetracyanobutadiene-Incorporated Asymmetric Triphenylamine-Quinoxaline Push-Pull Conjugates. J. Phys. Chem. A 2023, 127, 4455–4462. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Chen, Y.; Ma, Y.; Bailey, J.; Wang, Z.; Lee, D.; Sheveleva, A.M.; Tuna, F.; McInnes, E.J.L.; Frogley, M.D.; et al. Control of the Pore Chemistry in Metal-Organic Frameworks for Efficient Adsorption of Benzene and Separation of Benzene/Cyclohexane. Chem 2023, 9, 739–754. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, Q.; Liu, X.; Qu, X.; Wei, Q.; Xie, G.; Chen, S.; Gao, S. High-Energy Metal-Organic Frameworks (HE-MOFs): Synthesis, Structure and Energetic Performance. Coord. Chem. Rev. 2016, 307, 292–312. [Google Scholar] [CrossRef]
- Thi Thuy Huong, T.; Ngoc Thanh, P.; Thi Xuan Huynh, N.; Ngoc Son, D. Metal-Organic Frameworks: State-of-the-Art Material for Gas Capture and Storage. VNU J. Sci. Math. Phys. 2016, 32, 67–85. [Google Scholar]
- Paudel, H.P.; Shi, W.; Hopkinson, D.; Steckel, J.A.; Duan, Y. Computational Modelling of Adsorption and Diffusion Properties of CO2 and CH4 in ZIF-8 for Gas Separation Applications: A Density Functional Theory Approach. React. Chem. Eng. 2021, 6, 990–1001. [Google Scholar] [CrossRef]
- Miyazaki, R.; Nakatani, N.; Levchenko, S.V.; Yokoya, T.; Nakajima, K.; Hara, K.; Fukuoka, A.; Hasegawa, J.Y. DFT Mechanistic Study on the Complete Oxidation of Ethylene by the Silica-Supported Pt Catalyst: C=C Activation via the Ethylene Dioxide Intermediate. J. Phys. Chem. C 2019, 123, 12706–12715. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Zhang, C.; Li, Z.; Lu, B.; Zhu, J. Molecular Simulation of C2H4/CO2/N2/O2 Adsorption Characteristics in Lignite and Anthracite. AIP Adv. 2021, 11, 085205. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, J.; Zhang, Y.; Ma, J.; Huang, L.; Yu, S.; Chen, L.; Song, G.; Qiu, M.; Wang, X. Applications of Water-Stable Metal-Organic Frameworks in the Removal of Water Pollutants: A Review. Environ. Pollut. 2021, 291, 118076. [Google Scholar] [CrossRef]
- Adjal, C.; Timón, V.; Guechtouli, N.; Boussassi, R.; Hammoutène, D.; Senent, M.L. The Role of Water in the Adsorption of Nitro-Organic Pollutants on Activated Carbon. J. Phys. Chem. A 2023, 127, 8146–8158. [Google Scholar] [CrossRef]
- Timón, V.; Senent, M.L.; Hochlaf, M. Structural Single and Multiple Molecular Adsorption of CO2 and H2O in Zeolitic Imidazolate Framework (ZIF) Crystals. Microporous Mesoporous Mater. 2015, 218, 33–41. [Google Scholar] [CrossRef]
- Furukawa, H.; Gándara, F.; Zhang, Y.B.; Jiang, J.; Queen, W.L.; Hudson, M.R.; Yaghi, O.M. Water Adsorption in Porous Metal-Organic Frameworks and Related Materials. J. Am. Chem. Soc. 2014, 136, 4369–4381. [Google Scholar] [CrossRef]
- Guo, S.; Huang, X.; Situ, Y.; Huang, Q.; Guan, K.; Huang, J.; Wang, W.; Bai, X.; Liu, Z.; Wu, Y.; et al. Interpretable Machine-Learning and Big Data Mining to Predict Gas Diffusivity in Metal-Organic Frameworks. Adv. Sci. 2023, 10, 2301461. [Google Scholar] [CrossRef] [PubMed]
- Dinnebier, R.E.; Nuss, H.; Jansen, M. Anhydrous CuC4O4, a Channel Structure Solved from X-Ray Powder Diffraction Data. Z. Anorg. Allg. Chem. 2005, 631, 2328–2332. [Google Scholar] [CrossRef]
- Colmenero, F.; Lobato, Á.; Timón, V. Compressing the Channels in the Crystal Structure of Copper Squarate Metal-Organic Framework. Solids 2022, 3, 374–384. [Google Scholar] [CrossRef]
- Colmenero, F. Negative Linear Compressibility in Nanoporous Metal-Organic Frameworks Rationalized by the Empty Channel Structural Mechanism. Phys. Chem. Chem. Phys. 2021, 23, 8508–8524. [Google Scholar] [CrossRef]
- Colmenero, F.; Cobos, J.; Timón, V. Negative Linear Compressibility in Uranyl Squarate Monohydrate. J. Phys. Condens. Matter 2019, 31, 175701. [Google Scholar] [CrossRef]
- Colmenero, F. Addendum: Anomalous Mechanical Behavior of the Deltic, Squaric and Croconic Cyclic Oxocarbon Acids. Mater. Res. Express 2019, 6, 045610. [Google Scholar] [CrossRef]
- Qiu, W.; Zeng, Q.; Li, C.; Hao, J.; Li, Y. Theoretical Investigation of Zero Linear Compressibility on Metal Squarates MC4O4 (M = Pb and Ba). J. Phys. Chem. C 2023, 127, 9957–9963. [Google Scholar] [CrossRef]
- Zhang, L.; He, Z.; Liu, Y.; You, J.; Lin, L.; Jia, J.; Chen, S.; Hua, N.; Ma, L.A.; Ye, X.; et al. A Robust Squarate-Cobalt Metal-Organic Framework for CO2/N2 Separation. ACS Appl. Mater. Interfaces 2023, 15, 30394–30401. [Google Scholar] [CrossRef]
- BIOVIA. Dassault Systemes, Materials Studio 2022. Dassault Systemes: San Diego, CA, USA, 2022. [Google Scholar]
- Delgado, M.R. Structure and Stability of Gas Adsorption Complexes in Periodic Porous Solids as Studied by VTIR Spectroscopy: An Overview. Appl. Sci. 2020, 10, 8589. [Google Scholar] [CrossRef]
- Manak, M.; Jirkovsky, L.; Kolingerova, I. Interactive Analysis of Connolly Surfaces for Various Probes. Comput. Graph. Forum 2017, 36, 160–172. [Google Scholar] [CrossRef]
- El, N.; Timón, V.; Boussessi, R.; Dalbouha, S.; Senent, M.L. DFT Studies of Single and Multiple Molecular Adsorption of CH4, SF6 and H2O in Zeolitic-Imidazolate Framework (ZIF-4 and ZIF-6). Inorganica Chim Acta 2019, 490, 272–281. [Google Scholar] [CrossRef]
- Akkermans, R.L.C.; Spenley, N.A.; Robertson, S.H. COMPASS III: Automated Fitting Workflows and Extension to Ionic Liquids. Mol. Simul. 2021, 47, 540–551. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Gautam, R.; Steiner, T. The Weak Hydrogen Bond. In Structural Chemistry and Biology; Oxford University Press: Oxford, UK, 1999; ISBN 9780198509707. [Google Scholar]
- Park, K.S.; Ni, Z.; Cô, A.P.; Choi, J.Y.; Huang, R.; Uribe-Romo, F.J.; Chae, H.K.; O’keeffe, M.; Yaghi, O.M. Exceptional Chemical and Thermal Stability of Zeolitic Imidazolate Frameworks. Proc. Natl. Acad. Sci. USA 2006, 103, 10186–10191. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, S.; Tanaka, Y. A Simple Step toward Enhancing Hydrothermal Stability of ZIF-8. ACS Omega 2019, 4, 19905–19912. [Google Scholar] [CrossRef] [PubMed]
- Shieh, F.K.; Wang, S.C.; Leo, S.Y.; Wu, K.C.W. Water-Based Synthesis of Zeolitic Imidazolate Framework-90 (ZIF-90) with a Controllable Particle Size. Chem.-A Eur. J. 2013, 19, 11139–11142. [Google Scholar] [CrossRef]
- Nalaparaju, A.; Zhao, X.S.; Jiang, J.W. Molecular Understanding for the Adsorption of Water and Alcohols in Hydrophilic and Hydrophobic Zeolitic Metal-Organic Frameworks. J. Phys. Chem. C 2010, 114, 11542–11550. [Google Scholar] [CrossRef]
- Benedict, W.S.; Gailar, N.; Plyler, E.K. Rotation-Vibration Spectra of Deuterated Water Vapor. J. Chem. Phys. 1956, 24, 1139–1165. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K. MC Payne. First Princ. Methods Using Castep. Z. Für Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar]
- Hai, G.; Wang, H. Theoretical Studies of Metal-Organic Frameworks: Calculation Methods and Applications in Catalysis, Gas Separation, and Energy Storage. Coord. Chem. Rev. 2022, 469, 214670. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Ailan, D.C.; Arias, T.A.; Joannopouios, J.D. Iterative Minimization Techniques for Ab Initio Total-Energy Calculations: Molecular Dynamics and Conjugate Gradients. Rev. Mod. Phys. 1992, 64, 1045. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Cô, M.; Louie, S.G.; Cohen, M.L. Relaxation of Crystals with the Quasi-Newton Method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Ehrlich, S.; Moellmann, J.; Reckien, W.; Bredow, T.; Grimme, S. System-Dependent Dispersion Coefficients for the DFT-D3 Treatment of Adsorption Processes on Ionic Surfaces. ChemPhysChem 2011, 12, 3414–3420. [Google Scholar] [CrossRef] [PubMed]
- Troullier, N.; Martins, J.L. EfFicient Pseudopotentials for Plane-Wave Calculations-II. Phys. Rev. B 1991, 8, 1993. [Google Scholar] [CrossRef] [PubMed]
- Baroni, S.; De Gironcoli, S.; Corso, A.D.; Giannozzi, P. Phonons and Related Crystal Properties from Density-Functional Perturbation Theor. Rev. Mod. Phys. 2001, 73, 515. [Google Scholar] [CrossRef]
- Refson, K.; Tulip, P.R.; Clark, S.J. Variational Density-Functional Perturbation Theory for Dielectrics and Lattice Dynamics. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 155114. [Google Scholar] [CrossRef]
- Khaled, K.F. Monte Carlo Simulations of Corrosion Inhibition of Mild Steel in 0.5 M Sulphuric Acid by Some Green Corrosion Inhibitors. J. Solid State Electrochem. 2009, 13, 1743–1756. [Google Scholar] [CrossRef]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A., III. DREIDING: A Generic Force Field for Molecular Simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Babarao, R.; Dai, S.; Jiang, D.E. Effect of Pore Topology and Accessibility on Gas Adsorption Capacity in Zeolitic-Imidazolate Frameworks: Bringing Molecular Simulation Close to Experiment. J. Phys. Chem. C 2011, 115, 8126–8135. [Google Scholar] [CrossRef]
- Gao, H.; Pishney, S.; Janik, M.J. First Principles Study on the Adsorption of CO2 and H2O on the K2CO3 (001) Surface. Surf. Sci. 2013, 609, 140–146. [Google Scholar] [CrossRef]
- Smit, B.; Frenkel, D. Understanding Molecular Simulation, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2023; Volume 1. [Google Scholar]
- NIST Computational Chemistry Comparison and Benchmark Database. NIST Standard Reference Database Number 101. Release 22, May 2022, Editor: Russell D. Johnson III. Available online: https://cccbdb.nist.gov/ (accessed on 23 May 2024).

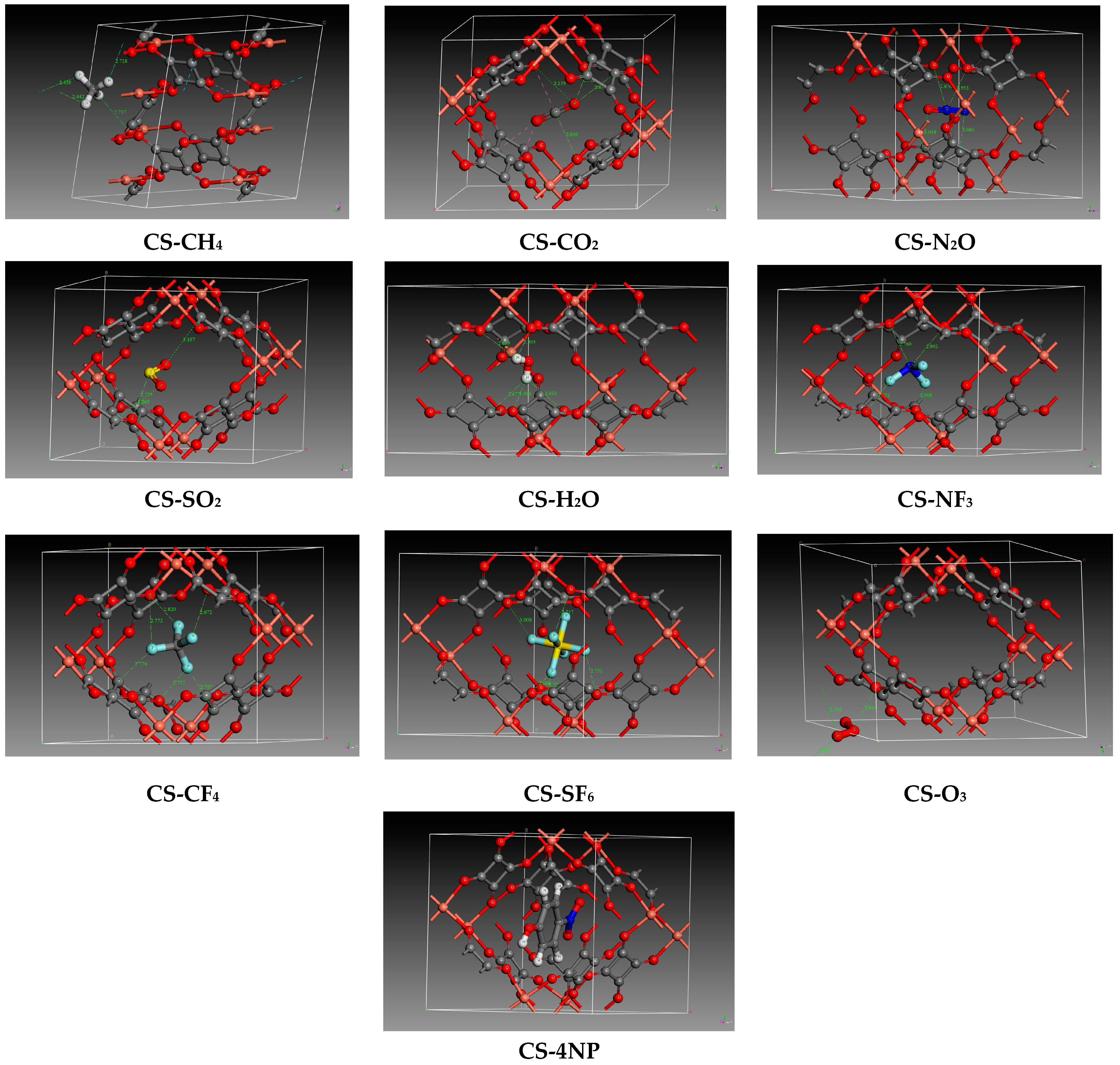


| Species | ) | ||||||
|---|---|---|---|---|---|---|---|
| C-S (1 × 1 × 2) | 11.017 | 9.352 | 11.288 | 89.918 | 117.636 | 90.082 | 1030.39 |
| Exp. (1 × 1 × 1) | 10.686 | 8.939 | 5.674 | 90.0 | 117.600 | 90.0 | 480.455 |
| 1 CH4 | 11.159 | 9.145 | 11.224 | 89.570 | 116.579 | 90.186 | 1024.40 |
| 4 CH4 | 10.707 | 9.812 | 11.394 | 90.089 | 117.974 | 89.977 | 1057.25 |
| 1 CO2 | 11.212 | 9.071 | 11.208 | 89.278 | 116.246 | 90.607 | 1022.29 |
| 2 CO2 | 11.096 | 9.264 | 11.276 | 89.356 | 116.571 | 90.410 | 1036.68 |
| 5 CO2 | 10.926 | 9.579 | 11.405 | 89.330 | 115.918 | 89.907 | 1073.61 |
| 1 O3 | 11.062 | 9.275 | 11.253 | 90.081 | 117.058 | 89.949 | 1027.85 |
| 3 O3 | 10.972 | 9.654 | 11.206 | 89.975 | 119.881 | 90.149 | 1029.24 |
| 5 O3 | 10.937 | 9.563 | 11.409 | 90.103 | 116.515 | 90.254 | 1067.79 |
| 1 SF6 | 10.904 | 9.754 | 11.226 | 89.641 | 118.322 | 89.846 | 1051.02 |
| 1 NF3 | 11.106 | 9.225 | 11.261 | 90.333 | 116.512 | 89.765 | 1023.45 |
| 1 CF4 | 11.015 | 9.610 | 11.192 | 89.801 | 119.085 | 90.008 | 1035.35 |
| 1 N2O | 10.925 | 9.683 | 11.217 | 90.014 | 120.345 | 90.007 | 1024.08 |
| 1 S2O | 11.139 | 9.167 | 11.215 | 90.160 | 116.500 | 90.140 | 1024.94 |
| 1 H2O | 11.214 | 9.015 | 11.187 | 90.279 | 116.117 | 89.714 | 1015.56 |
| 5 H2O | 11.070 | 9.431 | 11.155 | 90.185 | 117.025 | 89.544 | 1037.45 |
| 18 H2O | 10.907 | 9.524 | 12.334 | 93.334 | 106.045 | 89.533 | 1229.24 |
| 14NP | 10.027 | 10.51 | 11.722 | 88.364 | 114.868 | 90.152 | 1120.26 |
| Sample | ||||
|---|---|---|---|---|
| C-S Exp. [36] | 2.263 2.427 | 283.7 | 223.5 | 0.0958 |
| Mixture | |||||||
|---|---|---|---|---|---|---|---|
| 1 CH4 + 1 H2O | 11.088 | 9.246 | 11.231 | 89.983 | 116.856 | 89.765 | 1027.29 |
| 1 CO2 + 1 H2O | 11.082 | 9.249 | 11.216 | 90.009 | 116.896 | 89.695 | 1025.20 |
| 1 O3 +1 H2O | 11.134 | 9.192 | 11.229 | 89.511 | 116.154 | 90.203 | 1030.70 |
| 1 SF6 +1 H2O | 10.902 | 9.796 | 11.247 | 90.335 | 118.839 | 90.090 | 1051.76 |
| 1 NF3 +1 H2O | 11.021 | 9.376 | 11.298 | 89.924 | 116.777 | 89.956 | 1024.30 |
| 1 CF4 +1 H2O | 11.014 | 9.573 | 11.187 | 89.728 | 118.839 | 90.084 | 1033.19 |
| 1 N2O + 1 H2O | 11.053 | 9.533 | 11.185 | 90.004 | 119.398 | 90.076 | 1026.75 |
| 1 SO2 +1 H2O | 11.095 | 9.232 | 11.221 | 90.499 | 116.896 | 89.693 | 1025.20 |
| 1 4NP + 1 H2O | 9.9750 | 10.55 | 11.774 | 88.224 | 116.634 | 90.125 | 1107.77 |
| X | Pollutant | H2O | Energy (eV) | |||
|---|---|---|---|---|---|---|
| 1 | CH4 | 0 | −28,377.13 | −19.42 | ||
| 4 | CH4 | 0 | −29,036.92 | −23.02 | ||
| 1 | CO2 | 0 | −29,174.10 | −18.93 | ||
| 2 | CO2 | 0 | −30,190.92 | −17.72 | ||
| 5 | CO2 | 0 | −33,241.66 | −22.22 | ||
| 1 | O3 | 0 | −29,443.50 | −30.51 | ||
| 3 | O3 | 0 | −32,016.10 | −50.05 | ||
| 5 | O3 | 0 | −34,588.30 | −26.94 | ||
| 1 | SF6 | 0 | −32,355.32 | −3.785 | ||
| 1 | NF3 | 0 | −33,375.60 | −14.12 | ||
| 1 | CF4 | 0 | −30,908.98 | −3.400 | ||
| 1 | N2O | 0 | −29,137.72 | −63.32 | ||
| 1 | SO2 | 0 | −29,322.81 | −38.04 | ||
| 1 | H2O | 0 | −28,621.07 | −51.16 | ||
| 5 | H2O | 0 | −30,476.14 | −47.01 | ||
| 18 | H2O | 0 | −36,505.20 | −46.78 | ||
| 1 | 4NP | 0 | −30,730.94 | +47.94 | ||
| 1 | CH4 | 1 | −28,157.25 | −33.11 | +4.364 | |
| 1 | CO2 | 1 | −29,638.03 | −40.39 | −10.68 | |
| 1 | O3 | 1 | −29,907.21 | −35.52 | +10.63 | |
| 1 | SF6 | 1 | −32,818.70 | −6.186 | +42.67 | |
| 1 | NF3 | 1 | −30,839.30 | −26.83 | +11.01 | |
| 1 | CF4 | 1 | −31,373.09 | −41.31 | −27.96 | |
| 1 | N2O | 1 | −29,601.17 | −39.10 | +36.30 | |
| 1 | SO2 | 1 | −29,786.61 | −43.48 | +1.952 | |
| 1 | 4NP | 1 | −30,730.93 | +47.93 | −10.34 |
| X | H2O | dH-O | One Distance of (X) | Angles (X) | |
|---|---|---|---|---|---|
| CH4 | 1 | 0.961 | 105.9 | C-H = 1.094 | 109.255 |
| CO2 | 1 | 0.961 | 105.7 | C-O = 1.165 | 179.344 |
| O3 | 1 | 0.961 | 103.4 | O-O = 1.267 | 117.303 |
| SF6 | 1 | 0.960 | 104.8 | S-F = 1.584 | 89.787 |
| NF3 | 1 | 0.969 | 104.0 | N-F = 1.410 | 102.390 |
| CF4 | 1 | 0.961 | 106.6 | C-F = 1.345 | 109.673 |
| N2O | 1 | 0.961 | 105.9 | N-N = 1.140 N-O = 1.149 | 179.782 |
| SO2 | 1 | 0.962 | 103.8 | S-O = 1.440 | 118.205 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adjal, C.; Guechtouli, N.; Timón, V.; Colmenero, F.; Hammoutène, D. Theoretical Study of Copper Squarate as a Promising Adsorbent for Small Gases Pollutants. Molecules 2024, 29, 3140. https://doi.org/10.3390/molecules29133140
Adjal C, Guechtouli N, Timón V, Colmenero F, Hammoutène D. Theoretical Study of Copper Squarate as a Promising Adsorbent for Small Gases Pollutants. Molecules. 2024; 29(13):3140. https://doi.org/10.3390/molecules29133140
Chicago/Turabian StyleAdjal, Celia, Nabila Guechtouli, Vicente Timón, Francisco Colmenero, and Dalila Hammoutène. 2024. "Theoretical Study of Copper Squarate as a Promising Adsorbent for Small Gases Pollutants" Molecules 29, no. 13: 3140. https://doi.org/10.3390/molecules29133140
APA StyleAdjal, C., Guechtouli, N., Timón, V., Colmenero, F., & Hammoutène, D. (2024). Theoretical Study of Copper Squarate as a Promising Adsorbent for Small Gases Pollutants. Molecules, 29(13), 3140. https://doi.org/10.3390/molecules29133140








