Scrutinising the Conformational Ensemble of the Intrinsically Mixed-Folded Protein Galectin-3
Abstract
1. Introduction
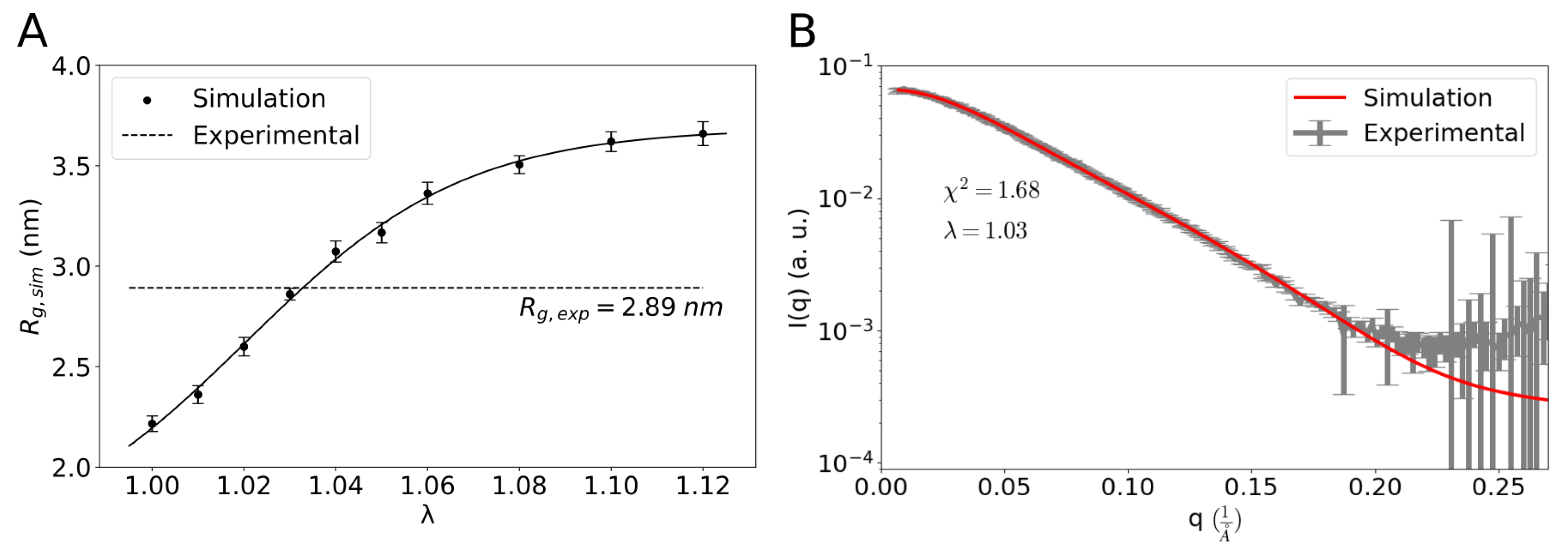
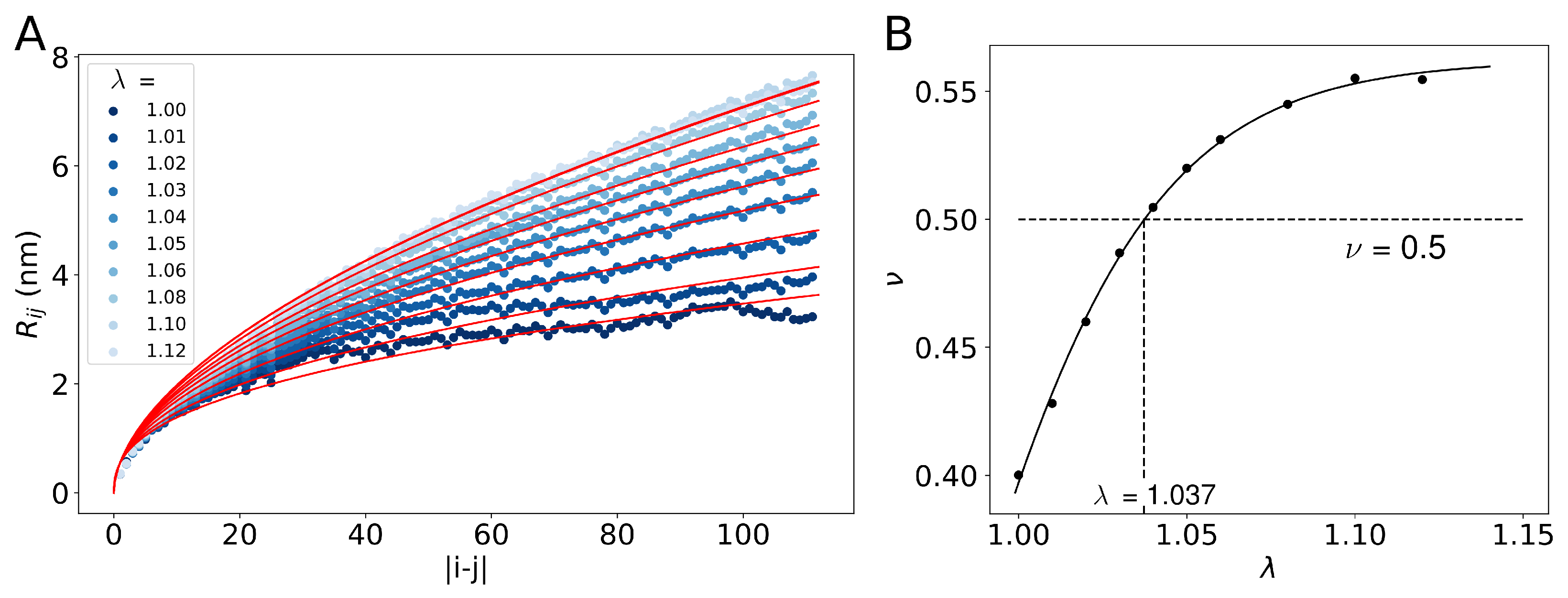
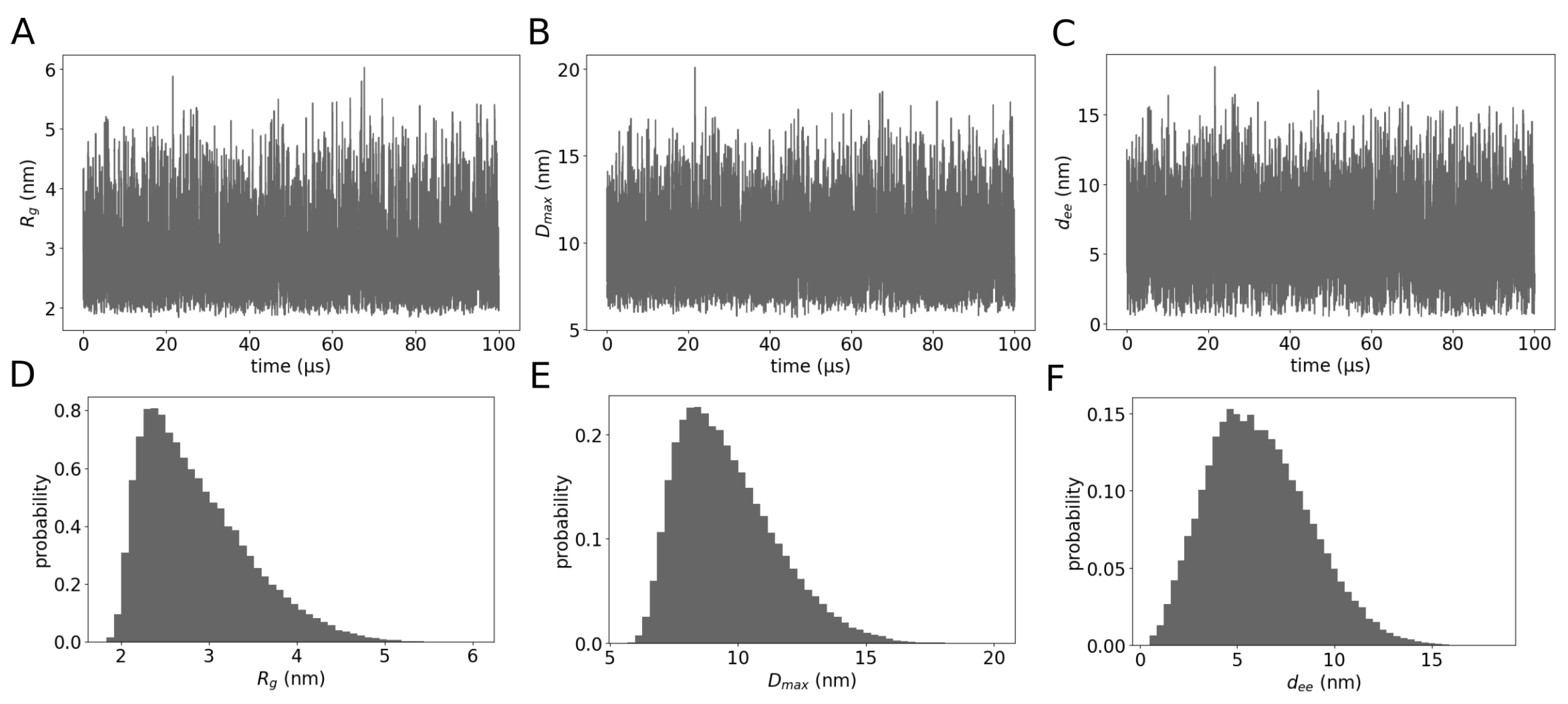
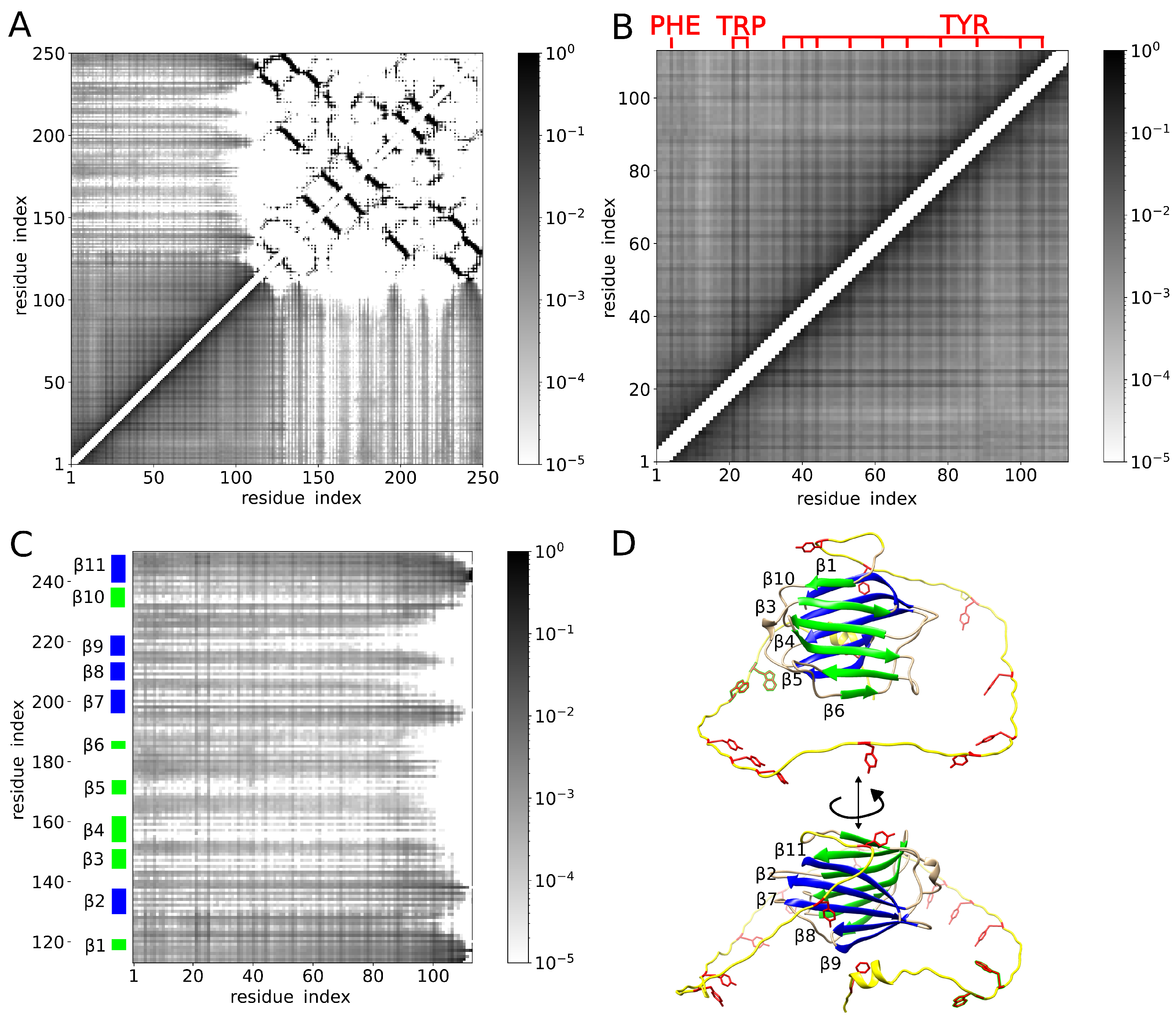
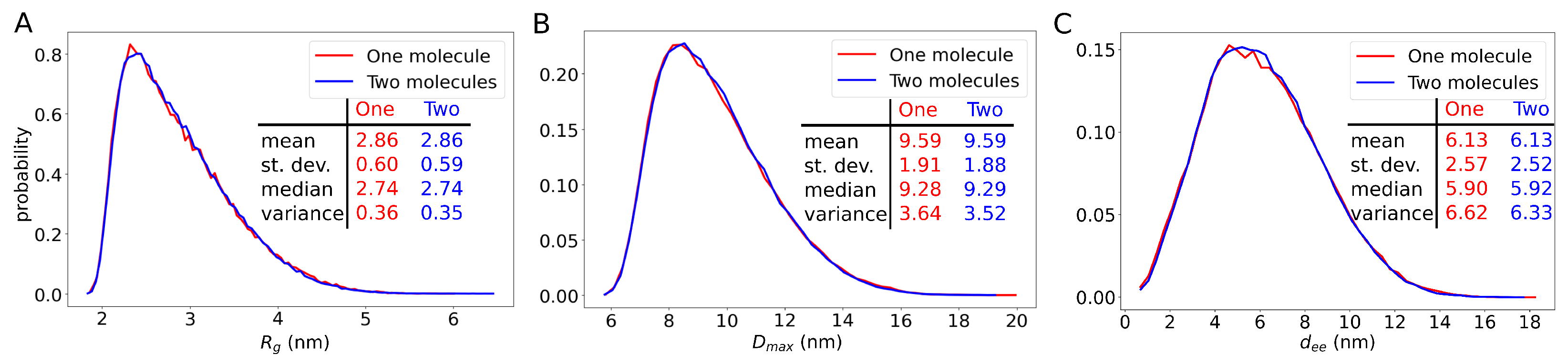
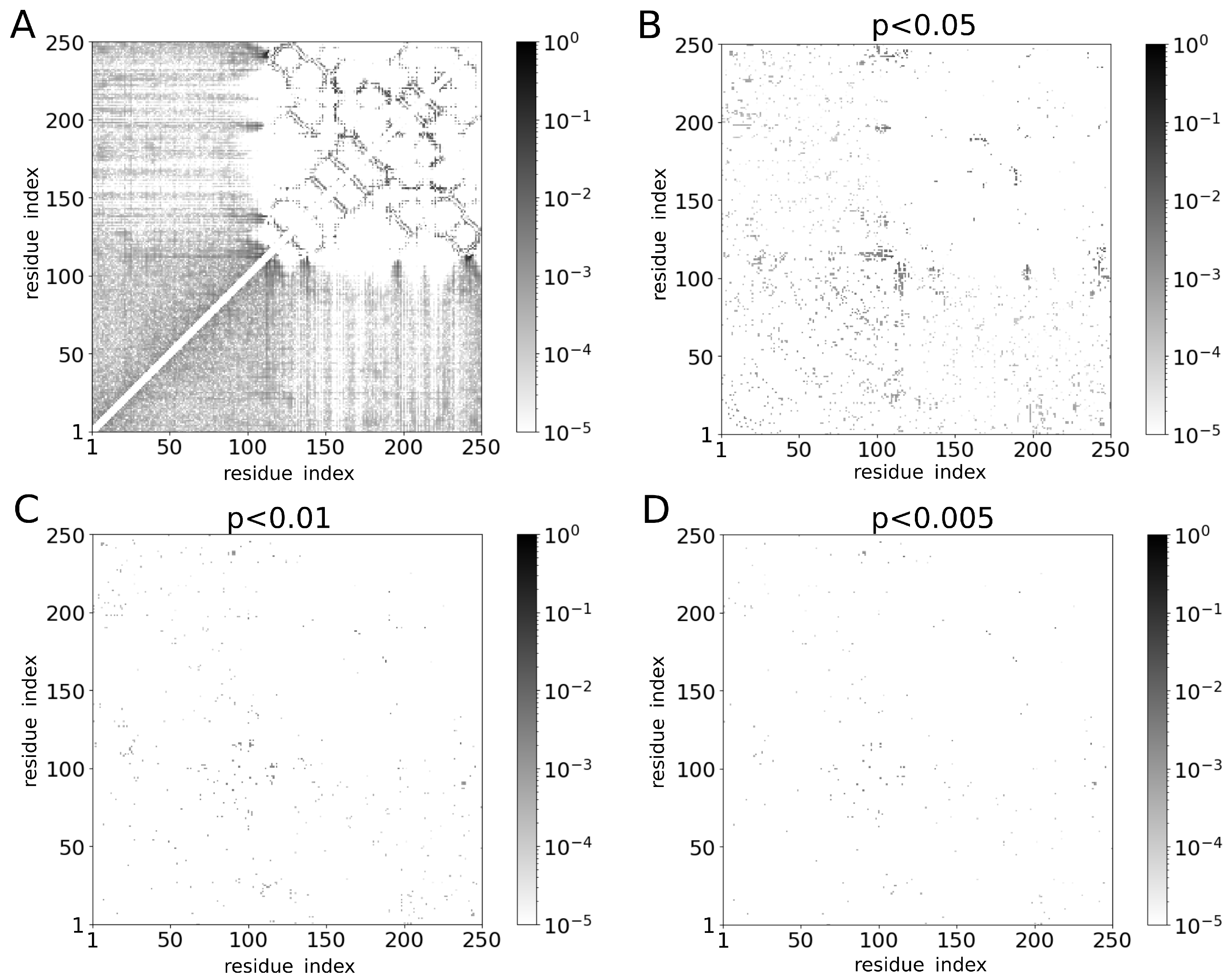
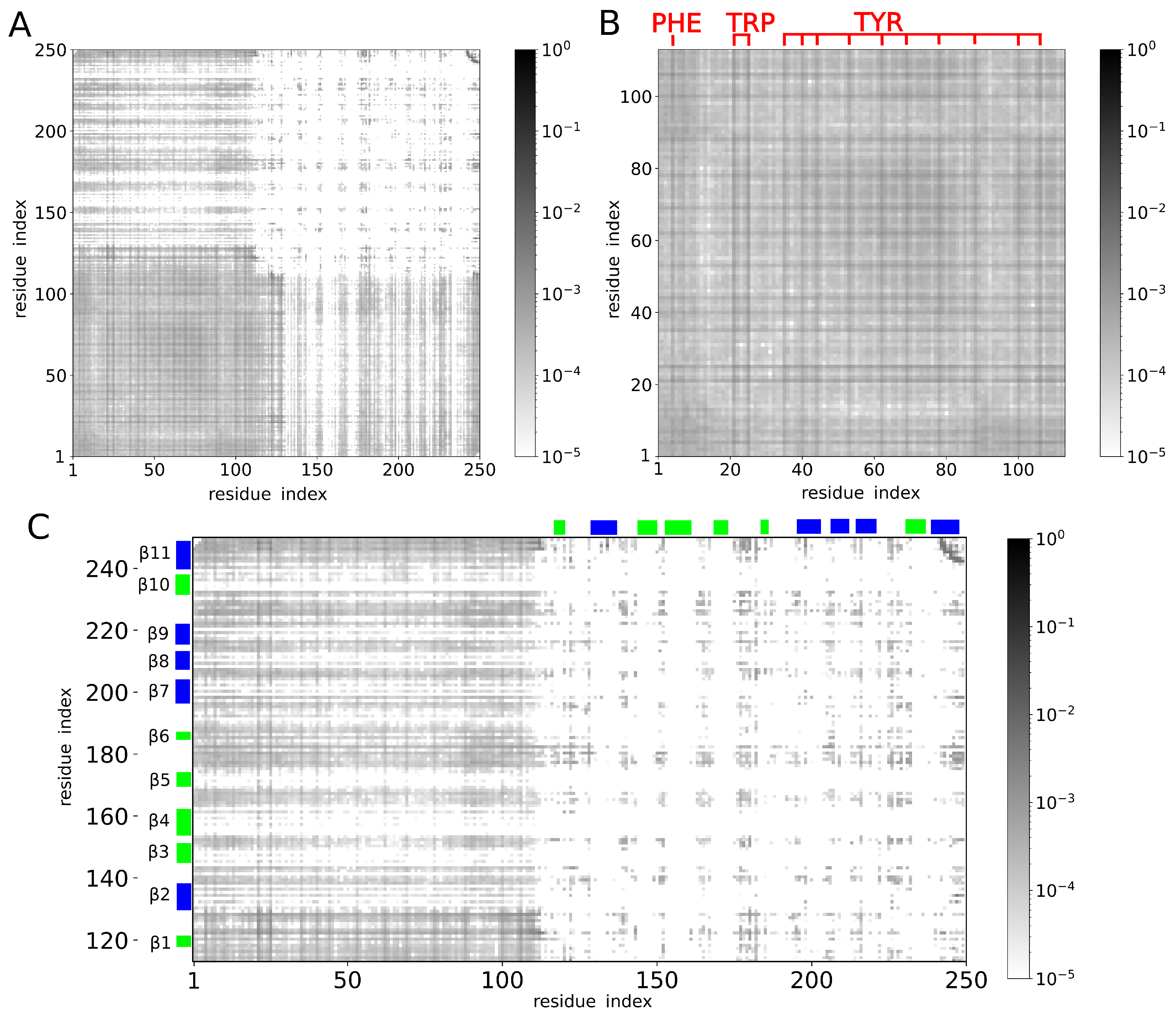
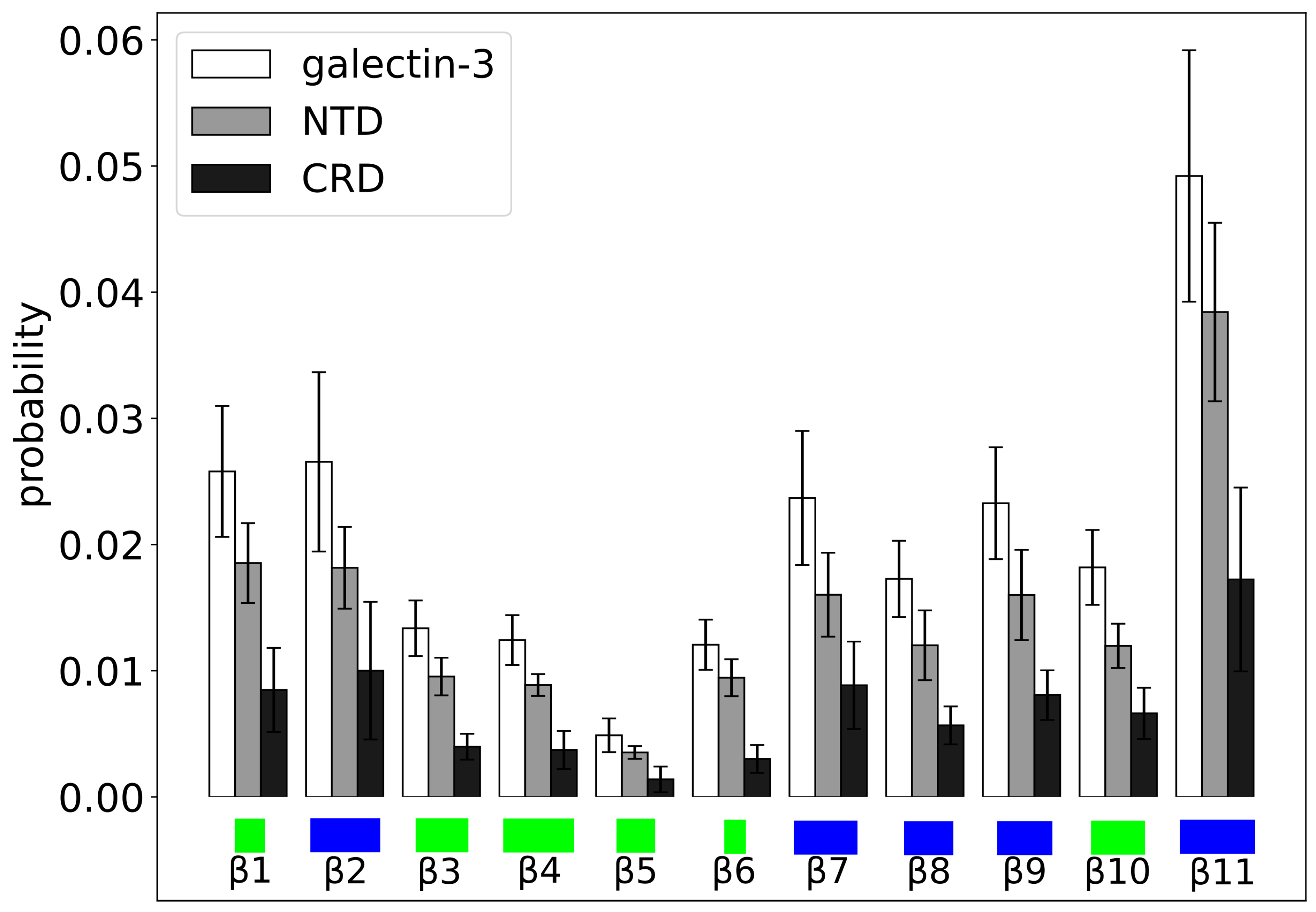
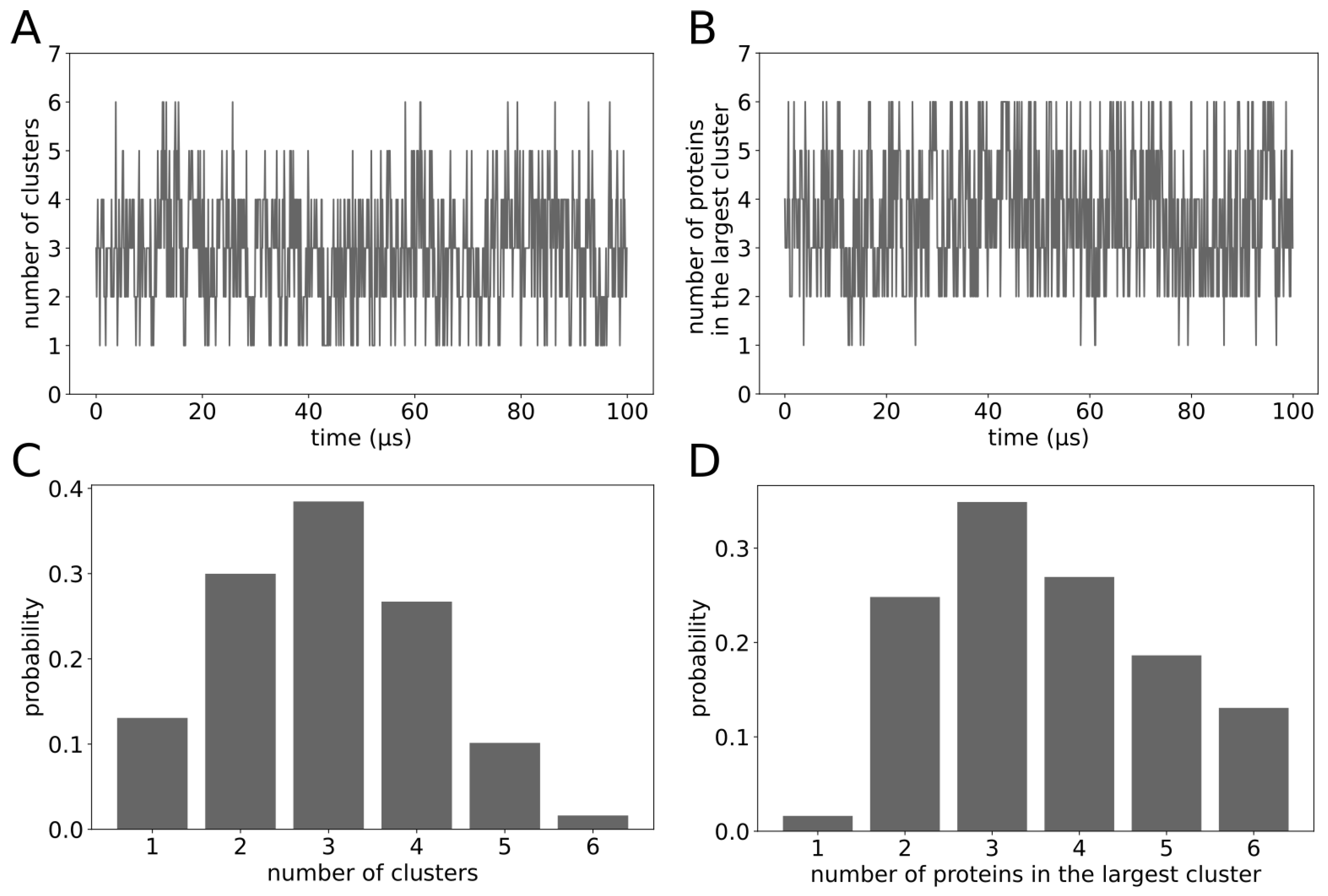
2. Results
3. Methods
3.1. Molecular Dynamics Simulations
3.2. Analysis of Molecular Dynamics Trajectories
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hirabayashi, J.; Kasai, K.-I. The family of metazoan metal-independent β-galactoside-binding lectins: Structure, function and molecular evolution. Glycobiology 1993, 3, 297–304. [Google Scholar] [CrossRef]
- Barondes, S.H.; Castronovo, V.; Cooper, D.; Cummings, R.D.; Drickamer, K.; Feizi, T.; Gitt, M.A.; Hirabayashi, J.; Hughes, C.; Kasai, K.-I. Galectins: A family of animal beta-galactoside-binding lectins. Cell 1994, 76, 597–598. [Google Scholar] [CrossRef] [PubMed]
- Bänfer, S.; Jacob, R. Galectins in intra-and extracellular vesicles. Biomolecules 2020, 10, 1232. [Google Scholar] [CrossRef] [PubMed]
- Johannes, L.; Jacob, R.; Leffler, H. Galectins at a glance. J. Cell Sci. 2018, 131, jcs208884. [Google Scholar] [CrossRef] [PubMed]
- Lepur, A.; Salomonsson, E.; Nilsson, U.J.; Leffler, H. Ligand induced galectin-3 protein self-association. J. Biol. Chem. 2012, 287, 21751–21756. [Google Scholar] [CrossRef]
- Ippel, H.; Miller, M.C.; Vértesy, S.; Zheng, Y.; Cañada, F.J.; Suylen, D.; Umemoto, K.; Romanò, C.; Hackeng, T.; Tai, G.; et al. Intra-and intermolecular interactions of human galectin-3: Assessment by full-assignment-based NMR. Glycobiology 2016, 26, 888–903. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.H.; Qiu, D.C.; Chang, W.H.; Yeh, Y.Q.; Jeng, U.S.; Liu, F.T.; Huang, J.R. The intrinsically disordered N-terminal domain of galectin-3 dynamically mediates multisite self-association of the protein through fuzzy interactions. J. Biol. Chem. 2017, 292, 17845–17856. [Google Scholar] [CrossRef] [PubMed]
- Funasaka, T.; Raz, A.; Nangia-Makker, P. Nuclear transport of galectin-3 and its therapeutic implications. Semin. Cancer Biol. 2014, 27, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Dumic, J.; Dabelic, S.; Flögel, M. Galectin-3: An open-ended story. Biochim. Biophys. Acta-(Bba)-Gen. Subj. 2006, 1760, 616–635. [Google Scholar] [CrossRef]
- Newlaczyl, A.U.; Yu, L.G. Galectin-3—A jack-of-all-trades in cancer. Cancer Lett. 2011, 313, 123–128. [Google Scholar] [CrossRef]
- Dong, R.; Zhang, M.; Hu, Q.; Zheng, S.; Soh, A.; Zheng, Y.; Yuan, H. Galectin-3 as a novel biomarker for disease diagnosis and a target for therapy. Int. J. Mol. Med. 2018, 41, 599–614. [Google Scholar] [CrossRef] [PubMed]
- Seetharaman, J.; Kanigsberg, A.; Slaaby, R.; Leffler, H.; Barondes, S.H.; Rini, J.M. X-ray crystal structure of the human galectin-3 carbohydrate recognition domain at 2.1-Å resolution. J. Biol. Chem. 1998, 273, 13047–13052. [Google Scholar] [CrossRef] [PubMed]
- Collins, P.M.; Hidari, K.I.; Blanchard, H. Slow diffusion of lactose out of galectin-3 crystals monitored by X-ray crystallography: Possible implications for ligand-exchange protocols. Acta Crystallogr. Sect. Biol. Crystallogr. 2007, 63, 415–419. [Google Scholar] [CrossRef] [PubMed]
- Souza, P.C.; Alessandri, R.; Barnoud, J.; Thallmair, S.; Faustino, I.; Grünewald, F.; Patmanidis, I.; Abdizadeh, H.; Bruininks, B.M.; Wassenaar, T.A.; et al. Martini 3: A general purpose force field for coarse-grained molecular dynamics. Nat. Methods 2021, 18, 382–388. [Google Scholar] [CrossRef] [PubMed]
- Thomasen, F.E.; Pesce, F.; Roesgaard, M.A.; Tesei, G.; Lindorff-Larsen, K. Improving Martini 3 for disordered and multidomain proteins. J. Chem. Theory Comput. 2022, 18, 2033–2041. [Google Scholar] [CrossRef] [PubMed]
- Koneru, J.K.; Sinha, S.; Mondal, J. Molecular dynamics simulations elucidate oligosaccharide recognition pathways by galectin-3 at atomic resolution. J. Biol. Chem. 2021, 297, 101271. [Google Scholar] [CrossRef] [PubMed]
- Vander Zanden, C.M.; Majewski, J.; Weissbarth, Y.; Browne, D.F.; Watkins, E.B.; Gabius, H.J. Structure of Galectin-3 bound to a model membrane containing ganglioside GM1. Biophys. J. 2023, 122, 1926–1937. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, S.; Zhang, M.; Hu, W.; Qi, T.; Heisterkamp, N. Targeting disordered-structured domain interactions in Galectin-3 based on NMR and enhanced MD. Biophys. J. 2022, 121, 4342–4357. [Google Scholar] [CrossRef] [PubMed]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-grained protein models and their applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef]
- Chiu, Y.P.; Sun, Y.C.; Qiu, D.C.; Lin, Y.H.; Chen, Y.Q.; Kuo, J.C.; Huang, J.R. Liquid-liquid phase separation and extracellular multivalent interactions in the tale of galectin-3. Nat. Commun. 2020, 11, 1229. [Google Scholar] [CrossRef] [PubMed]
- Dignon, G.L.; Zheng, W.; Best, R.B.; Kim, Y.C.; Mittal, J. Relation between single-molecule properties and phase behavior of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2018, 115, 9929–9934. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, H.; Soranno, A.; Borgia, A.; Gast, K.; Nettels, D.; Schuler, B. Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy. Proc. Natl. Acad. Sci. USA 2012, 109, 16155–16160. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Zerze, G.; Borgia, A.; Mittal, J.; Schuler, B.; Best, R.B. Inferring properties of disordered chains from FRET transfer efficiencies. Biophys. J. 2018, 114, 367a. [Google Scholar] [CrossRef]
- Mazur, J. Distribution function of the end-to-end distances of linear polymers with excluded volume effects. J. Res. Natl. Bur. Stand. Sect. Phys. Chem. 1965, 69, 355–363. [Google Scholar] [CrossRef] [PubMed]
- Farhadi, S.A.; Liu, R.; Becker, M.W.; Phelps, E.A.; Hudalla, G.A. Physical tuning of galectin-3 signaling. Proc. Natl. Acad. Sci. USA 2021, 118, e2024117118. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolym. Orig. Res. Biomol. 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Herzog, F.A.; Braun, L.; Schoen, I.; Vogel, V. Improved side chain dynamics in MARTINI simulations of protein—Lipid interfaces. J. Chem. Theory Comput. 2016, 12, 2446–2458. [Google Scholar] [CrossRef]
- Wassenaar, T.A.; Ingólfsson, H.I.; Bockmann, R.A.; Tieleman, D.P.; Marrink, S.J. Computational lipidomics with insane: A versatile tool for generating custom membranes for molecular simulations. J. Chem. Theory Comput. 2015, 11, 2144–2155. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Bruininks, B.M.H.; Wassenaar, T.A.; Vattulainen, I. Unbreaking Assemblies in Molecular Simulations with Periodic Boundaries. J. Chem. Inf. Model. 2023, 63, 3448–3452. [Google Scholar] [CrossRef]
- McGibbon, R.T.; Beauchamp, K.A.; Harrigan, M.P.; Klein, C.; Swails, J.M.; Hernández, C.X.; Schwantes, C.R.; Wang, L.P.; Lane, T.J.; Pande, V.S. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 2015, 109, 1528–1532. [Google Scholar] [CrossRef] [PubMed]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Flyvbjerg, H.; Petersen, H.G. Error estimates on averages of correlated data. J. Chem. Phys. 1989, 91, 461–466. [Google Scholar] [CrossRef]
- Wassenaar, T.A.; Pluhackova, K.; Bockmann, R.A.; Marrink, S.J.; Tieleman, D.P. Going backward: A flexible geometric approach to reverse transformation from coarse grained to atomistic models. J. Chem. Theory Comput. 2014, 10, 676–690. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; De Groot, B.L.; Grubmüller, H.; MacKerell, A.D., Jr. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [PubMed]
- Grudinin, S.; Garkavenko, M.; Kazennov, A. Pepsi-SAXS: An adaptive method for rapid and accurate computation of small-angle X-ray scattering profiles. Acta Crystallogr. Sect. Struct. Biol. 2017, 73, 449–464. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar]
- Swenson, D.W.H.; Revision, S.R. Contact Map Explorer. Available online: https://github.com/dwhswenson/contact_map (accessed on 25 April 2024).
- Anila, M.M.; Ghosh, R.; Różycki, B. Membrane curvature sensing by model biomolecular condensates. Soft Matter 2023, 19, 3723–3732. [Google Scholar] [CrossRef]
- Brosey, C.A.; Tainer, J.A. Evolving SAXS versatility: Solution X-ray scattering for macromolecular architecture, functional landscapes, and integrative structural biology. Curr. Opin. Struct. Biol. 2019, 58, 197–213. [Google Scholar] [CrossRef] [PubMed]
- Gräwert, T.W.; Svergun, D.I. Structural modeling using solution small-angle X-ray scattering (SAXS). J. Mol. Biol. 2020, 432, 3078–3092. [Google Scholar] [CrossRef] [PubMed]
- Petoukhov, M.V.; Svergun, D.I. Global rigid body modeling of macromolecular complexes against small-angle scattering data. Biophys. J. 2005, 89, 1237–1250. [Google Scholar] [CrossRef] [PubMed]
- Pelikan, M.; Hura, G.L.; Hammel, M. Structure and flexibility within proteins as identified through small angle X-ray scattering. Gen. Physiol. Biophys. 2009, 28, 174–189. [Google Scholar] [CrossRef] [PubMed]
- Różycki, B.; Kim, Y.C.; Hummer, G. SAXS ensemble refinement of ESCRT-III CHMP3 conformational transitions. Structure 2011, 19, 109–116. [Google Scholar] [CrossRef] [PubMed]
- Tria, G.; Mertens, H.D.; Kachala, M.; Svergun, D.I. Advanced ensemble modelling of flexible macromolecules using X-ray solution scattering. Int. Union Crystallogr. J. 2015, 2, 207–217. [Google Scholar] [CrossRef] [PubMed]
- Cordeiro, T.N.; Herranz-Trillo, F.; Urbanek, A.; Estaña, A.; Cortés, J.; Sibille, N.; Bernadó, P. Small-angle scattering studies of intrinsically disordered proteins and their complexes. Curr. Opin. Struct. Biol. 2017, 42, 15–23. [Google Scholar] [CrossRef] [PubMed]
- Różycki, B.; Boura, E. Large, dynamic, multi-protein complexes: A challenge for structural biology. J. Phys. Condens. Matter 2014, 26, 463103. [Google Scholar] [CrossRef] [PubMed]
- Różycki, B.; Cieplak, M.; Czjzek, M. Large conformational fluctuations of the multi-domain xylanase Z of Clostridium thermocellum. J. Struct. Biol. 2015, 191, 68–75. [Google Scholar] [CrossRef]
- Chalupska, D.; Eisenreichova, A.; Różycki, B.; Rezabkova, L.; Humpolickova, J.; Klima, M.; Boura, E. Structural analysis of phosphatidylinositol 4-kinase IIIβ (PI4KB)–14-3-3 protein complex reveals internal flexibility and explains 14-3-3 mediated protection from degradation in vitro. J. Struct. Biol. 2017, 200, 36–44. [Google Scholar] [CrossRef]
- Chalupska, D.; Różycki, B.; Klima, M.; Boura, E. Structural insights into Acyl-coenzyme A binding domain containing 3 (ACBD3) protein hijacking by picornaviruses. Protein Sci. 2019, 28, 2073–2079. [Google Scholar] [CrossRef] [PubMed]
- Chalupska, D.; Różycki, B.; Humpolickova, J.; Faltova, L.; Klima, M.; Boura, E. Phosphatidylinositol 4-kinase IIIβ (PI4KB) forms highly flexible heterocomplexes that include ACBD3, 14-3-3, and Rab11 proteins. Sci. Rep. 2019, 9, 567. [Google Scholar] [CrossRef] [PubMed]
- Sicorello, A.; Różycki, B.; Konarev, P.V.; Svergun, D.I.; Pastore, A. Capturing the conformational ensemble of the mixed folded polyglutamine protein ataxin-3. Structure 2021, 29, 70–81. [Google Scholar] [CrossRef] [PubMed]
- Dorival, J.; Moraïs, S.; Labourel, A.; Różycki, B.; Cazade, P.A.; Dabin, J.; Setter-Lamed, E.; Mizrahi, I.; Thompson, D.; Thureau, A.; et al. Mapping the deformability of natural and designed cellulosomes in solution. Biotechnol. Biofuels Bioprod. 2022, 15, 68. [Google Scholar] [CrossRef] [PubMed]
- Różycki, B.; Boura, E. Conformational ensemble of the full-length SARS-CoV-2 nucleocapsid (N) protein based on molecular simulations and SAXS data. Biophys. Chem. 2022, 288, 106843. [Google Scholar] [CrossRef]
- Lakshminarayan, R.; Wunder, C.; Becken, U.; Howes, M.T.; Benzing, C.; Arumugam, S.; Sales, S.; Ariotti, N.; Chambon, V.; Lamaze, C.; et al. Galectin-3 drives glycosphingolipid-dependent biogenesis of clathrin-independent carriers. Nat. Cell Biol. 2014, 16, 592–603. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anila, M.M.; Rogowski, P.; Różycki, B. Scrutinising the Conformational Ensemble of the Intrinsically Mixed-Folded Protein Galectin-3. Molecules 2024, 29, 2768. https://doi.org/10.3390/molecules29122768
Anila MM, Rogowski P, Różycki B. Scrutinising the Conformational Ensemble of the Intrinsically Mixed-Folded Protein Galectin-3. Molecules. 2024; 29(12):2768. https://doi.org/10.3390/molecules29122768
Chicago/Turabian StyleAnila, Midhun Mohan, Paweł Rogowski, and Bartosz Różycki. 2024. "Scrutinising the Conformational Ensemble of the Intrinsically Mixed-Folded Protein Galectin-3" Molecules 29, no. 12: 2768. https://doi.org/10.3390/molecules29122768
APA StyleAnila, M. M., Rogowski, P., & Różycki, B. (2024). Scrutinising the Conformational Ensemble of the Intrinsically Mixed-Folded Protein Galectin-3. Molecules, 29(12), 2768. https://doi.org/10.3390/molecules29122768





