Unveiling Conformational States of CDK6 Caused by Binding of Vcyclin Protein and Inhibitor by Combining Gaussian Accelerated Molecular Dynamics and Deep Learning
Abstract
1. Introduction
2. Results and Discussion
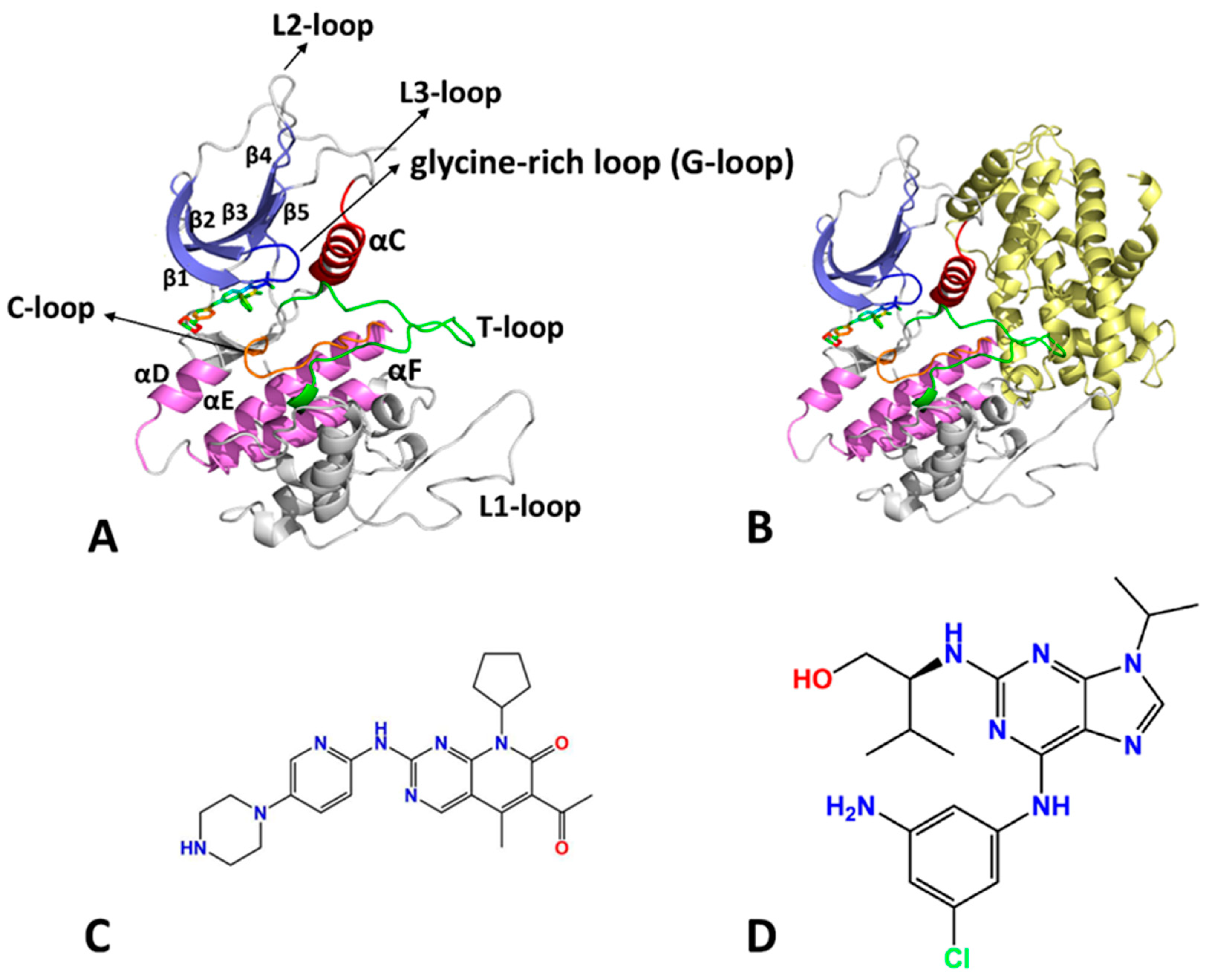
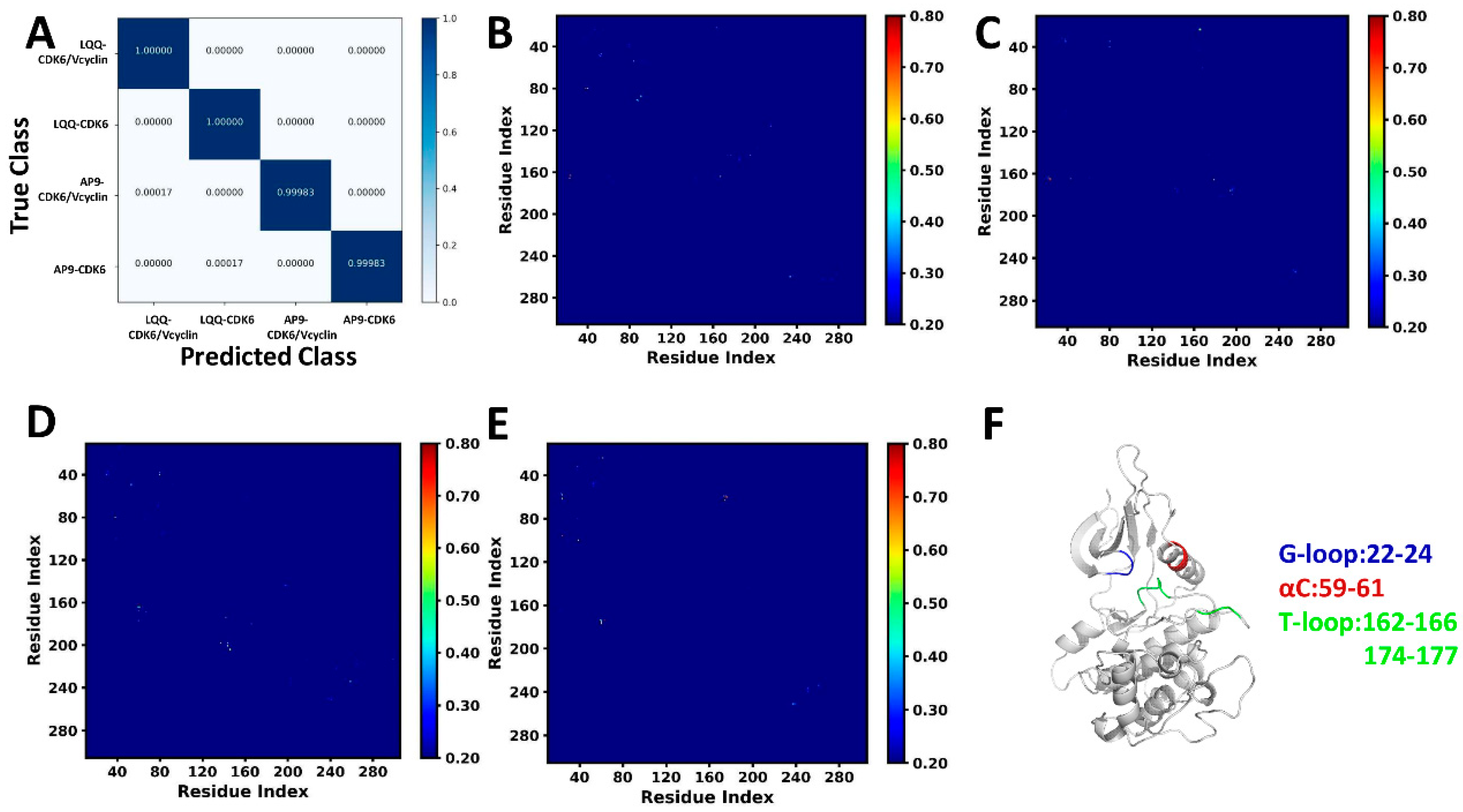
2.1. Characteristic Residue Contacts Revealed by Deep Learning
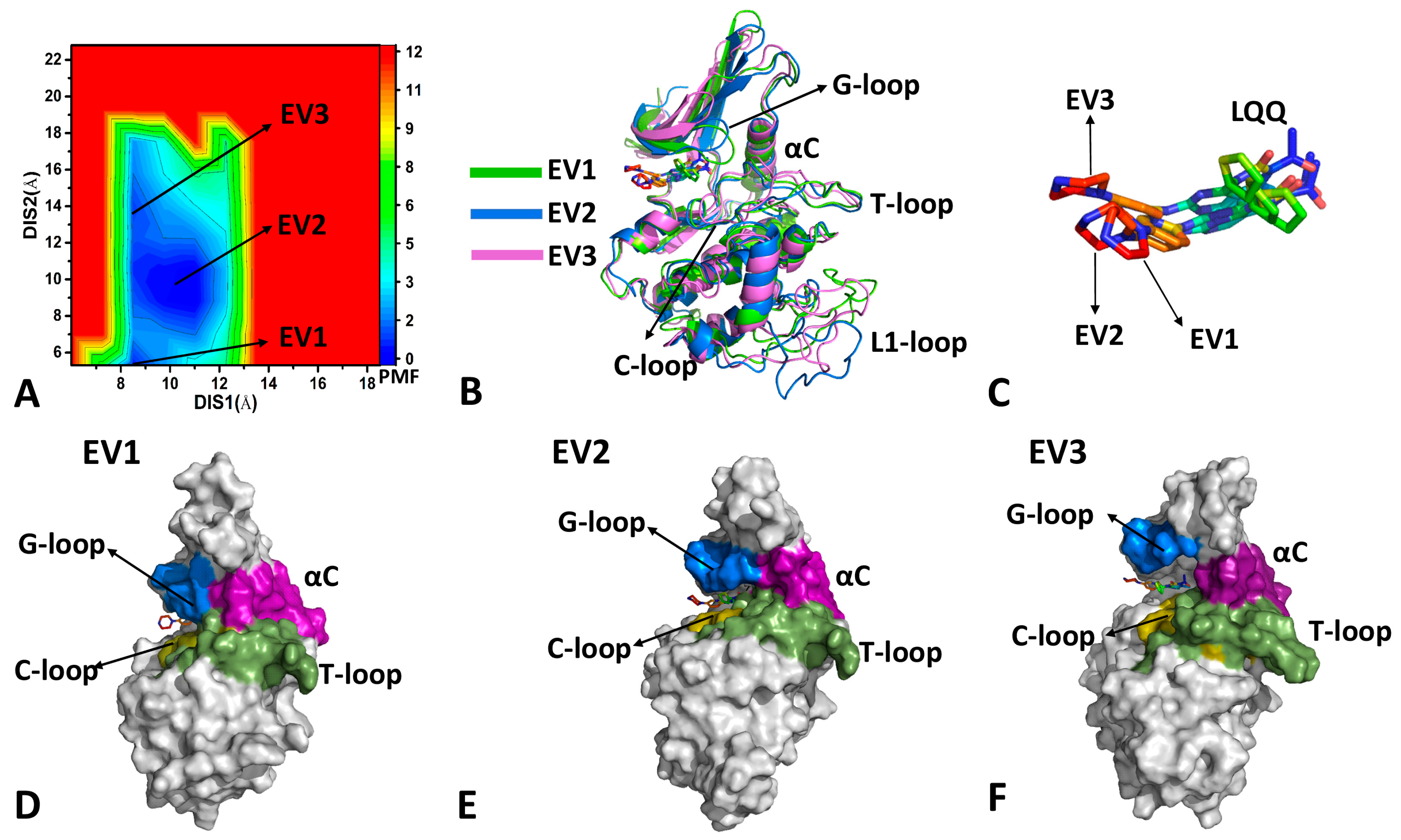
2.2. Conformational Transition of CDK6 from Free Energy Landscapes
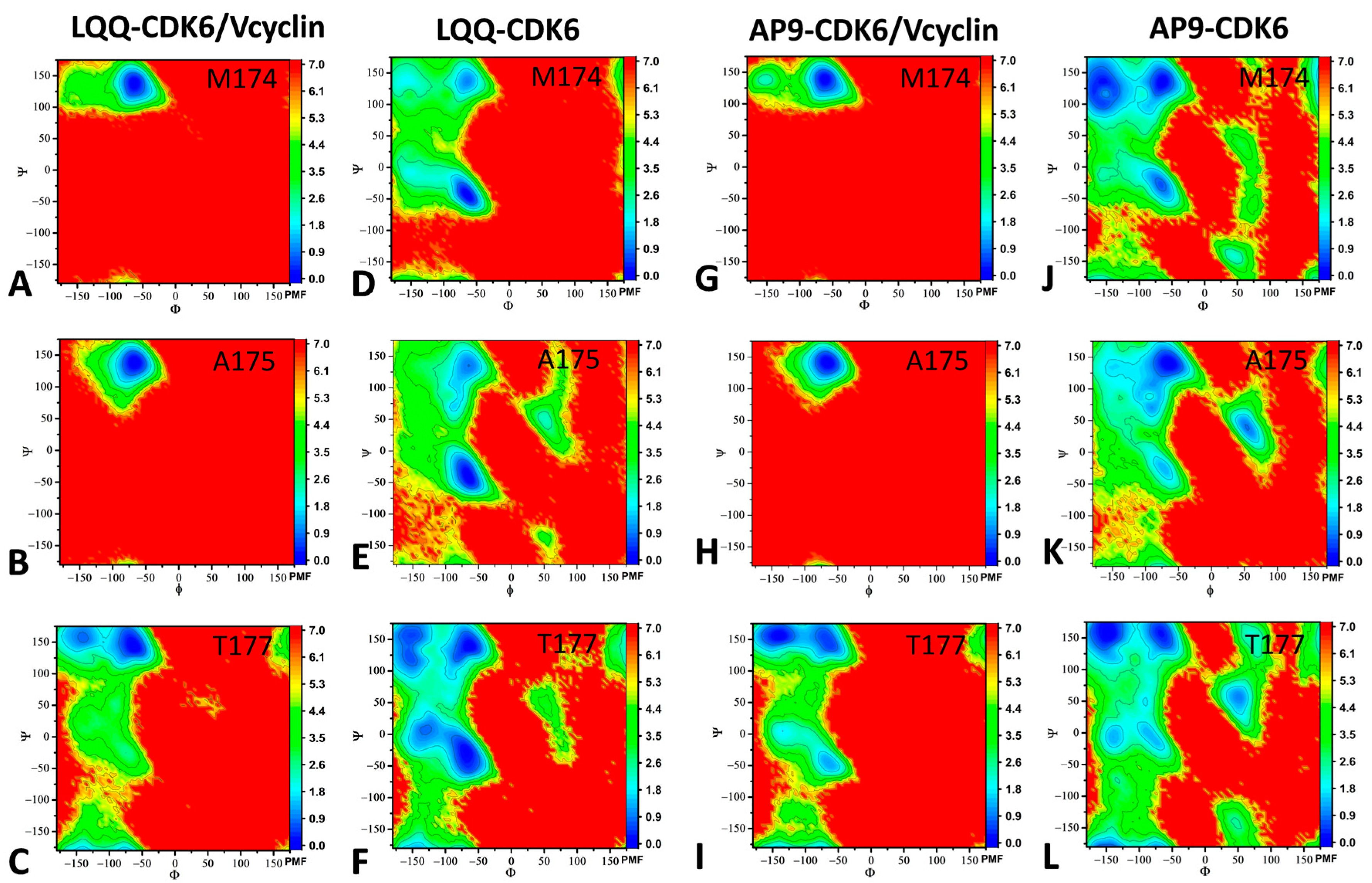
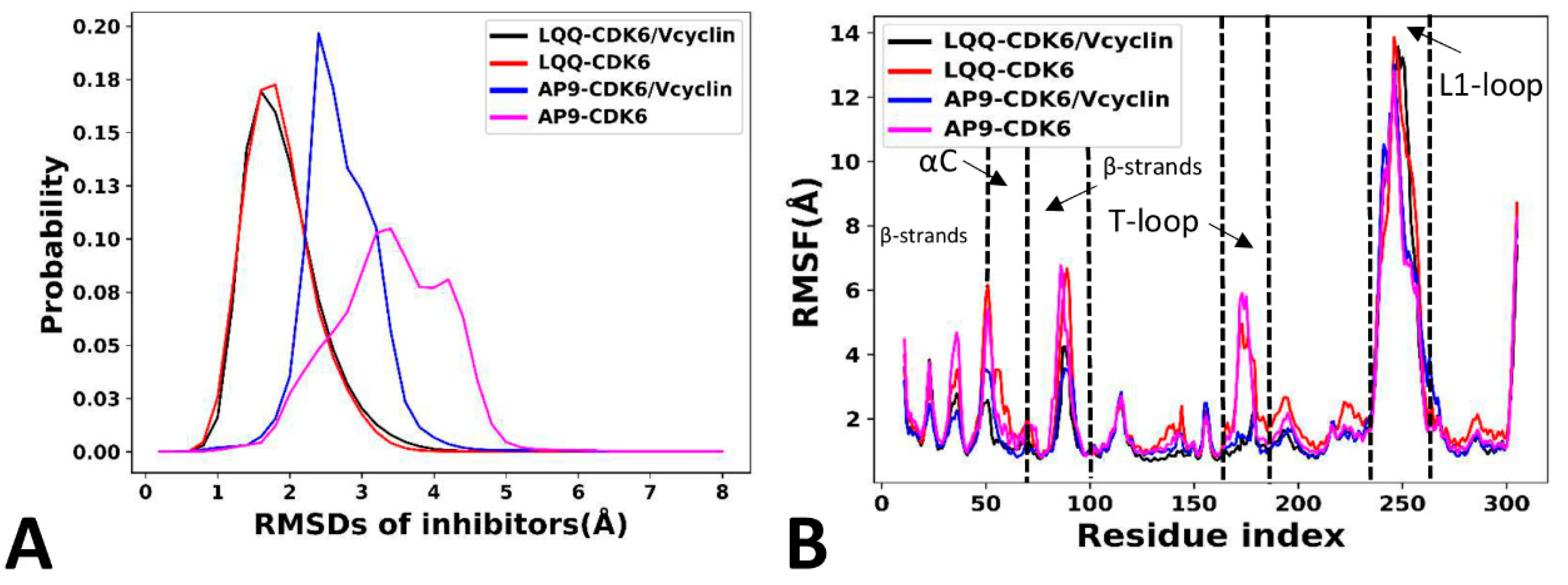
2.3. Dynamics Behavior of CDK6
2.4. Binding Free Energy Calculations
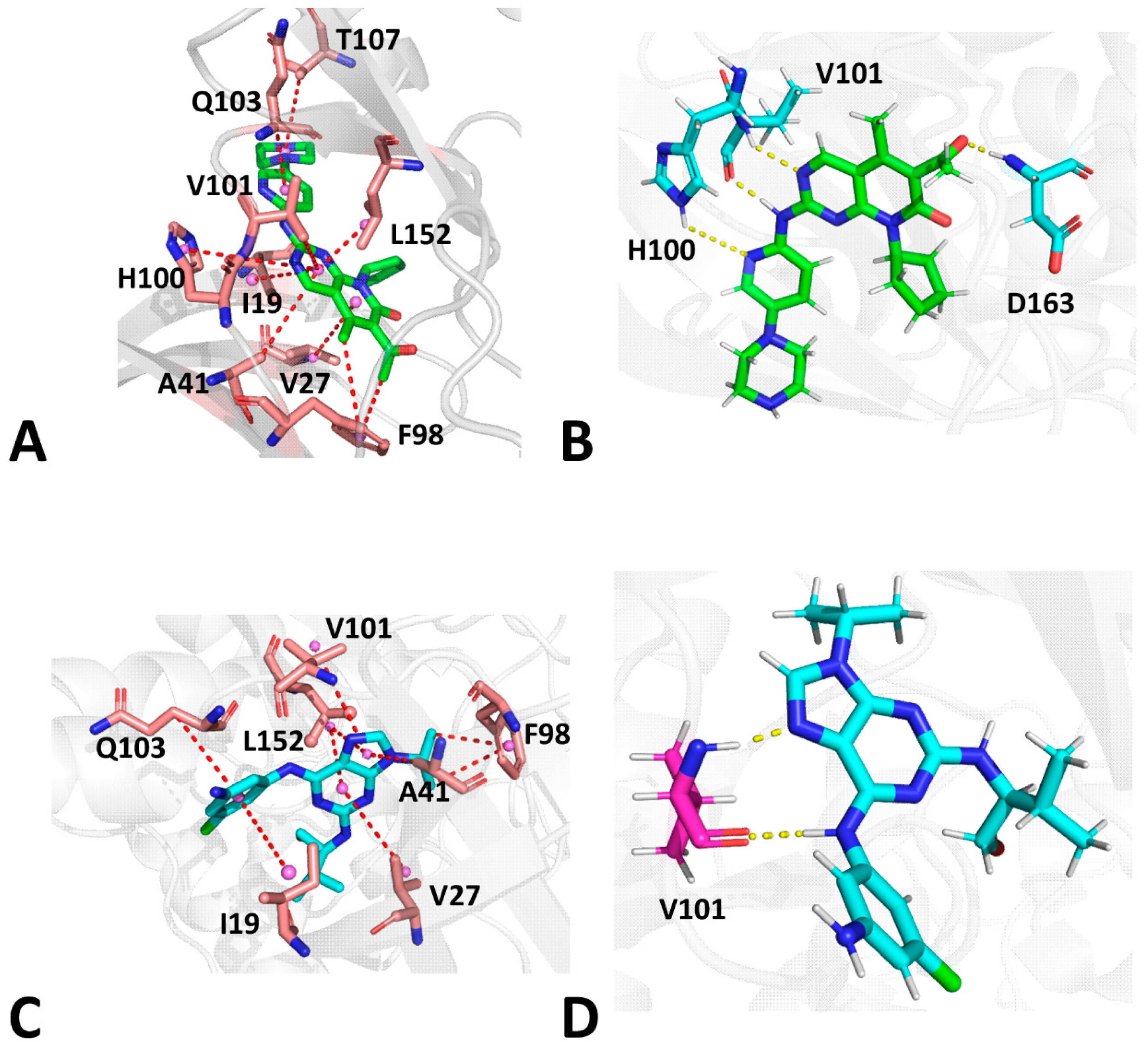
2.5. Analyses of Inhibitor–CDK6 Interaction Networks
3. Materials and Methods
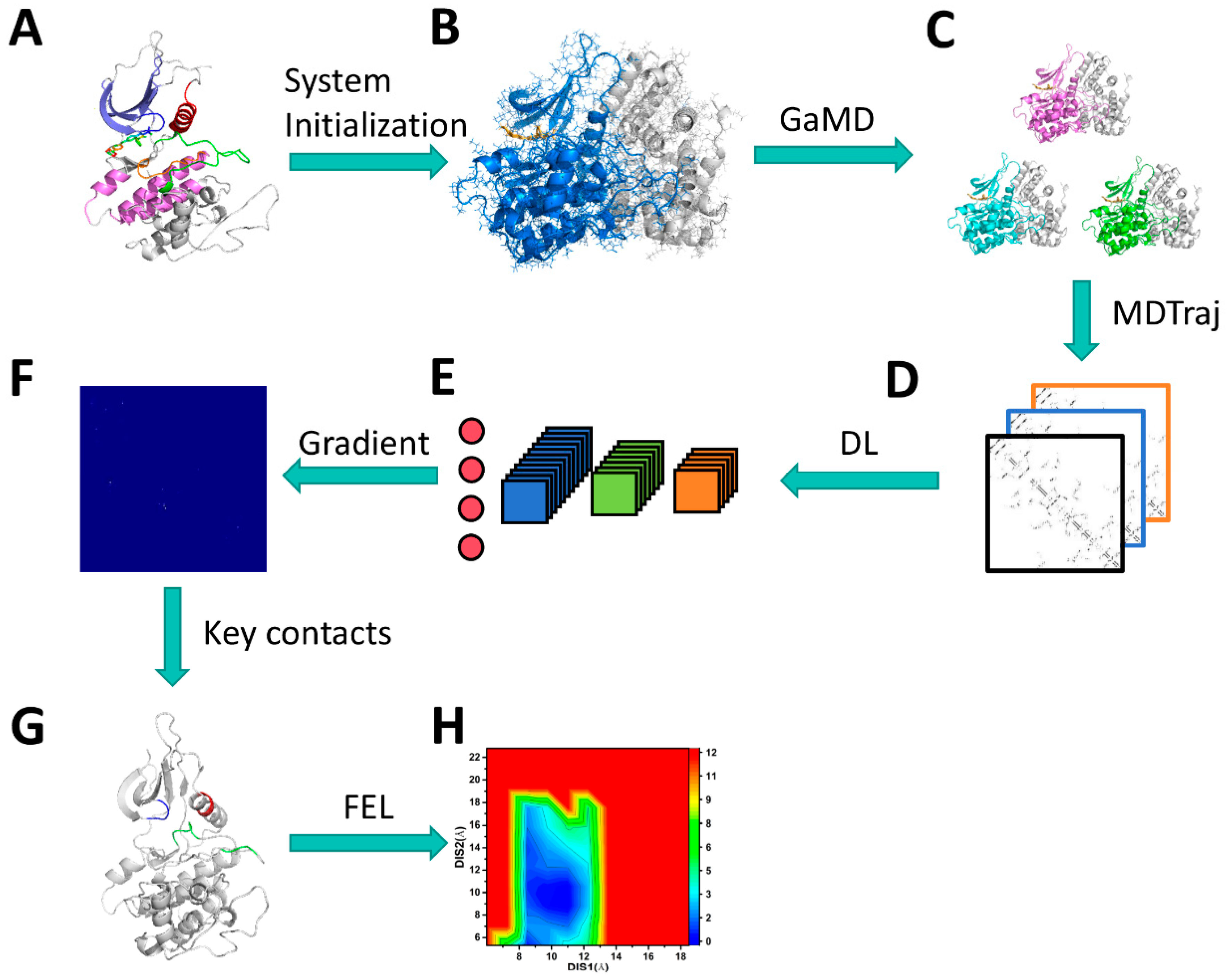
3.1. Scheme of Operating Calculations
3.2. Constructions of Simulated Systems
3.3. Multiple Separate Gaussian Accelerated Molecular Dynamics
3.4. Deep Learning
3.5. Construction of Free Energy Landscapes
3.6. Principal Component Analysis
3.7. QM/MM-GBSA Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schafer, K.A. The Cell Cycle: A Review. Vet. Pathol. 1998, 35, 461–478. [Google Scholar] [CrossRef] [PubMed]
- Bury, M.; Le Calvé, B.; Ferbeyre, G.; Blank, V.; Lessard, F. New insights into CDK regulators: Novel opportunities for cancer therapy. Trends Cell Biol. 2021, 31, 331–344. [Google Scholar] [CrossRef] [PubMed]
- Schulze-Gahmen, U.; Kim, S.-H. Structural basis for CDK6 activation by a virus-encoded cyclin. Nat. Struct. Mol. Biol. 2002, 9, 177–181. [Google Scholar] [CrossRef] [PubMed]
- Hunter, T.; Pines, J. Cyclins and cancer II: Cyclin D and CDK inhibitors come of age. Cell 1994, 79, 573–582. [Google Scholar] [CrossRef]
- Palermo, V.; Rinalducci, S.; Sanchez, M.; Grillini, F.; Sommers, J.A.; Brosh, R.M., Jr.; Zolla, L.; Franchitto, A.; Pichierri, P. CDK1 phosphorylates WRN at collapsed replication forks. Nat. Commun. 2016, 7, 12880. [Google Scholar] [CrossRef] [PubMed]
- Quelle, D.; Ashmun, R.; Shurtleff, S.; Kato, J.; Bar-Sagi, D.; Roussel, M.; Sherr, C. Overexpression of mouse D-type cyclins accelerates G1 phase in rodent fibroblasts. Genes Dev. 1993, 7, 1559–1571. [Google Scholar] [CrossRef] [PubMed]
- Malumbres, M.; Barbacid, M. Mammalian cyclin-dependent kinases. Trends Biochem. Sci. 2005, 30, 630–641. [Google Scholar] [CrossRef]
- Pagliuca, F.W.; Collins, M.O.; Choudhary, J.S. Coordinating Cell Cycle Progression via Cyclin Specificity; Taylor & Francis: Abingdon, UK, 2011; Volume 10, pp. 4195–4196. [Google Scholar]
- Malumbres, M. Cyclin-dependent kinases. Genome Biol. 2014, 15, 122. [Google Scholar] [CrossRef]
- Liang, S.S.; Liu, X.G.; Cui, Y.X.; Zhang, S.L.; Zhang, Q.G.; Chen, J.Z. Molecular mechanism concerning conformational changes of CDK2 mediated by binding of inhibitors using molecular dynamics simulations and principal component analysis. SAR QSAR Environ. Res. 2021, 32, 573–594. [Google Scholar] [CrossRef]
- Chohan, T.A.; Qayyum, A.; Rehman, K.; Tariq, M.; Akash, M.S.H. An insight into the emerging role of cyclin-dependent kinase inhibitors as potential therapeutic agents for the treatment of advanced cancers. Biomed. Pharmacother. 2018, 107, 1326–1341. [Google Scholar] [CrossRef]
- Sun, J.; Liang, S.; Liu, X.; Zhang, S.; Li, M.; Zhang, Q.; Chen, J. Insights into the selectivity of a brain-penetrant CDK4/6 vs. CDK1/2 inhibitor for glioblastoma used in multiple replica molecular dynamics simulations. J. Biomol. Struct. Dyn. 2023, 1–20. [Google Scholar] [CrossRef]
- Hamilton, E.; Infante, J.R. Targeting CDK4/6 in patients with cancer. Cancer Treat. Rev. 2016, 45, 129–138. [Google Scholar] [CrossRef] [PubMed]
- Goel, S.; Bergholz, J.S.; Zhao, J.J. Targeting CDK4 and CDK6 in cancer. Nat. Rev. Cancer 2022, 22, 356–372. [Google Scholar] [CrossRef] [PubMed]
- Asghar, U.; Witkiewicz, A.K.; Turner, N.C.; Knudsen, E.S. The history and future of targeting cyclin-dependent kinases in cancer therapy. Nat. Rev. Drug Discov. 2015, 14, 130–146. [Google Scholar] [CrossRef]
- Ingham, M.; Schwartz, G.K. Cell-cycle therapeutics come of age. J. Clin. Oncol. 2017, 35, 2949. [Google Scholar] [CrossRef] [PubMed]
- Fassl, A.; Geng, Y.; Sicinski, P. CDK4 and CDK6 kinases: From basic science to cancer therapy. Science 2022, 375, eabc1495. [Google Scholar] [CrossRef] [PubMed]
- Wood, D.J.; Endicott, J.A. Structural insights into the functional diversity of the CDK–cyclin family. Open Biol. 2018, 8, 180112. [Google Scholar] [CrossRef]
- Pavletich, N.P. Mechanisms of cyclin-dependent kinase regulation: Structures of Cdks, their cyclin activators, and Cip and INK4 inhibitors. J. Mol. Biol. 1999, 287, 821–828. [Google Scholar] [CrossRef] [PubMed]
- Lucas, J.J.; Szepesi, A.; Modiano, J.F.; Domenico, J.; Gelfand, E.W. Regulation of synthesis and activity of the PLSTIRE protein (cyclin-dependent kinase 6 (cdk6)), a major cyclin D-associated cdk4 homologue in normal human T lymphocytes. J. Immunol. 1995, 154, 6275–6284. [Google Scholar] [CrossRef] [PubMed]
- Russo, A.A.; Tong, L.; Lee, J.-O.; Jeffrey, P.D.; Pavletich, N.P. Structural basis for inhibition of the cyclin-dependent kinase Cdk6 by the tumour suppressor p16INK4a. Nature 1998, 395, 237–243. [Google Scholar] [CrossRef]
- Tadesse, S.; Yu, M.; Kumarasiri, M.; Le, B.T.; Wang, S. Targeting CDK6 in cancer: State of the art and new insights. Cell Cycle 2015, 14, 3220–3230. [Google Scholar] [CrossRef]
- Nebenfuehr, S.; Kollmann, K.; Sexl, V. The role of CDK6 in cancer. Int. J. Cancer 2020, 147, 2988–2995. [Google Scholar] [CrossRef]
- Mahony, D.; Parry, D.A.; Lees, E. Active cdk6 complexes are predominantly nuclear and represent only a minority of the cdk6 in T cells. Oncogene 1998, 16, 603–611. [Google Scholar] [CrossRef] [PubMed]
- Mateyak, M.K.; Obaya, A.J.; Sedivy, J.M. c-Myc regulates cyclin D-Cdk4 and-Cdk6 activity but affects cell cycle progression at multiple independent points. Mol. Cell. Biol. 1999, 19, 4672–4683. [Google Scholar] [CrossRef] [PubMed]
- Grossel, M.J.; Hinds, P.W. Beyond the cell cycle: A new role for Cdk6 in differentiation. J. Cell. Biochem. 2006, 97, 485–493. [Google Scholar] [CrossRef]
- Tigan, A.; Bellutti, F.; Kollmann, K.; Tebb, G.; Sexl, V. CDK6—A review of the past and a glimpse into the future: From cell-cycle control to transcriptional regulation. Oncogene 2016, 35, 3083–3091. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.T.; Mansukhani, M.; Weinstein, I.B. Cyclin-dependent kinase 6 associates with the androgen receptor and enhances its transcriptional activity in prostate cancer cells. Proc. Natl. Acad. Sci. USA 2005, 102, 5156–5161. [Google Scholar] [CrossRef]
- Sherr, C.J.; Beach, D.; Shapiro, G.I. Targeting CDK4 and CDK6: From discovery to therapy. Cancer Discov. 2016, 6, 353–367. [Google Scholar] [CrossRef] [PubMed]
- Meyerson, M.; Harlow, E. Identification of G1 kinase activity for cdk6, a novel cyclin D partner. Mol. Cell. Biol. 1994, 14, 2077–2086. [Google Scholar]
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Mol. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, F.; Yan, D.; Zeng, Y.; Wei, B.; Chen, J.; He, W. Identification Mechanism of BACE1 on Inhibitors Probed by Using Multiple Separate Molecular Dynamics Simulations and Comparative Calculations of Binding Free Energies. Molecules 2023, 28, 4773. [Google Scholar] [CrossRef]
- Xue, W.; Wang, P.; Tu, G.; Yang, F.; Zheng, G.; Li, X.; Li, X.; Chen, Y.; Yao, X.; Zhu, F. Computational identification of the binding mechanism of a triple reuptake inhibitor amitifadine for the treatment of major depressive disorder. Phys. Chem. Chem. Phys. 2018, 20, 6606–6616. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Gong, Z.; Xia, F.; He, X. Ion dynamics and selectivity of Nav channels from molecular dynamics simulation. Chem. Phys. 2021, 548, 111245. [Google Scholar] [CrossRef]
- Chen, J.; Wang, W.; Sun, H.; He, W. Roles of Accelerated Molecular Dynamics Simulations in Predictions of Binding Kinetic Parameters. Mini-Rev. Med. Chem. 2024, 24, 1323–1333. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Wang, Y.; Yan, D.; Liu, Z.; Wei, B.; Chen, J.; He, W. Binding Mechanism of Inhibitors to Heat Shock Protein 90 Investigated by Multiple Independent Molecular Dynamics Simulations and Prediction of Binding Free Energy. Molecules 2023, 28, 4792. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Yang, F.; Wang, P.; Zheng, G.; Chen, Y.; Yao, X.; Zhu, F. What Contributes to Serotonin–Norepinephrine Reuptake Inhibitors’ Dual-Targeting Mechanism? The Key Role of Transmembrane Domain 6 in Human Serotonin and Norepinephrine Transporters Revealed by Molecular Dynamics Simulation. ACS Chem. Neurosci. 2018, 9, 1128–1140. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Huai, Z.; He, Q.; Liu, Z. A General Picture of Cucurbit[8]uril Host–Guest Binding. J. Chem. Inf. Model. 2021, 61, 6107–6134. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, S.K.; Singh, S.K.; Singh, P.; Chellaperumal, P.; Reddy, K.K.; Selvaraj, C. Exploring the selectivity of a ligand complex with CDK2/CDK1: A molecular dynamics simulation approach. J. Mol. Recognit. 2012, 25, 504–512. [Google Scholar] [CrossRef] [PubMed]
- Pisani, P.; Caporuscio, F.; Carlino, L.; Rastelli, G. Molecular dynamics simulations and classical multidimensional scaling unveil new metastable states in the conformational landscape of CDK2. PLoS ONE 2016, 11, e0154066. [Google Scholar] [CrossRef]
- Chen, J.; Pang, L.; Wang, W.; Wang, L.; Zhang, J.Z.; Zhu, T. Decoding molecular mechanism of inhibitor bindings to CDK2 using molecular dynamics simulations and binding free energy calculations. J. Biomol. Struct. Dyn. 2020, 4, 985–996. [Google Scholar] [CrossRef]
- Wu, M.; Han, J.; Liu, Z.; Zhang, Y.; Huang, C.; Li, J.; Li, Z. Identification of novel CDK 9 inhibitors based on virtual screening, molecular dynamics simulation, and biological evaluation. Life Sci. 2020, 258, 118228. [Google Scholar] [CrossRef]
- Sofi, S.; Mehraj, U.; Qayoom, H.; Aisha, S.; Almilaibary, A.; Alkhanani, M.; Mir, M.A. Targeting cyclin-dependent kinase 1 (CDK1) in cancer: Molecular docking and dynamic simulations of potential CDK1 inhibitors. Med. Oncol. 2022, 39, 133. [Google Scholar] [CrossRef] [PubMed]
- Villacañas, Ó.; Pérez, J.J.; Rubio-Martínez, J. Structural analysis of the inhibition of Cdk4 and Cdk6 by p16INK4a through molecular dynamics simulations. J. Biomol. Struct. Dyn. 2002, 20, 347–358. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef] [PubMed]
- Harvey, M.J.; Giupponi, G.; Fabritiis, G.D. ACEMD: Accelerating biomolecular dynamics in the microsecond time scale. J. Chem. Theory Comput. 2009, 5, 1632–1639. [Google Scholar] [CrossRef] [PubMed]
- Shaw, D.E.; Maragakis, P.; Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Eastwood, M.P.; Bank, J.A.; Jumper, J.M.; Salmon, J.K.; Shan, Y. Atomic-level characterization of the structural dynamics of proteins. Science 2010, 330, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Johnston, J.M.; Filizola, M. Showcasing modern molecular dynamics simulations of membrane proteins through G protein-coupled receptors. Curr. Opin. Struc. Biol. 2011, 21, 552–558. [Google Scholar] [CrossRef] [PubMed]
- Lane, T.J.; Shukla, D.; Beauchamp, K.A.; Pande, V.S. To milliseconds and beyond: Challenges in the simulation of protein folding. Curr. Opin. Struc. Biol. 2013, 23, 58–65. [Google Scholar] [CrossRef]
- Miao, Y.; Feher, V.A.; McCammon, J.A. Gaussian accelerated molecular dynamics: Unconstrained enhanced sampling and free energy calculation. J. Chem. Theory Comput. 2015, 11, 3584–3595. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Arantes, P.R.; Bhattarai, A.; Hsu, R.V.; Pawnikar, S.; Huang, Y.m.M.; Palermo, G.; Miao, Y. Gaussian accelerated molecular dynamics: Principles and applications. WIREs Comput. Mol. Sci. 2021, 11, e1521. [Google Scholar] [CrossRef]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef]
- Shen, T.; Hamelberg, D. A statistical analysis of the precision of reweighting-based simulations. J. Chem. Phys. 2008, 129, 034103. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.T.; Miao, Y.; Wang, Y.; McCammon, J.A. Gaussian accelerated molecular dynamics in NAMD. J. Chem. Theory Comput. 2017, 13, 9–19. [Google Scholar] [CrossRef]
- Ricci, C.G.; Chen, J.S.; Miao, Y.; Jinek, M.; Doudna, J.A.; McCammon, J.A.; Palermo, G. Deciphering off-target effects in CRISPR-Cas9 through accelerated molecular dynamics. ACS Cent. Sci. 2019, 5, 651–662. [Google Scholar] [CrossRef]
- Bhattarai, A.; Wang, J.; Miao, Y. G-protein-coupled receptor–membrane interactions depend on the receptor activation state. J. Comput. Chem. 2020, 41, 460–471. [Google Scholar] [CrossRef] [PubMed]
- Bhattarai, A.; Devkota, S.; Bhattarai, S.; Wolfe, M.S.; Miao, Y. Mechanisms of γ-secretase activation and substrate processing. ACS Cent. Sci. 2020, 6, 969–983. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, Q.; Wang, W.; Sun, H.; Hu, G. Decoding the Identification Mechanism of an SAM-III Riboswitch on Ligands through Multiple Independent Gaussian-Accelerated Molecular Dynamics Simulations. J. Chem. Inf. Model. 2022, 62, 6118–6132. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, S.; Wang, W.; Pang, L.; Zhang, Q.; Liu, X. Mutation-Induced Impacts on the Switch Transformations of the GDP- and GTP-Bound K-Ras: Insights from Multiple Replica Gaussian Accelerated Molecular Dynamics and Free Energy Analysis. J. Chem. Inf. Model. 2021, 61, 1954–1969. [Google Scholar] [CrossRef]
- Wang, J.; Miao, Y. Mechanistic Insights into Specific G Protein Interactions with Adenosine Receptors. J. Phys. Chem. B 2019, 123, 6462–6473. [Google Scholar] [CrossRef]
- Plante, A.; Shore, D.M.; Morra, G.; Khelashvili, G.; Weinstein, H. A machine learning approach for the discovery of ligand-specific functional mechanisms of GPCRs. Molecules 2019, 24, 2097. [Google Scholar] [CrossRef]
- Plante, A.; Weinstein, H. Ligand-dependent conformational transitions in molecular dynamics trajectories of GPCRs revealed by a new machine learning rare event detection protocol. Molecules 2021, 26, 3059. [Google Scholar] [CrossRef]
- Do, H.N.; Wang, J.; Bhattarai, A.; Miao, Y. GLOW: A workflow integrating Gaussian-accelerated molecular dynamics and deep learning for free energy profiling. J. Chem. Theory Comput. 2022, 18, 1423–1436. [Google Scholar] [CrossRef]
- Do, H.N.; Wang, J.; Miao, Y. Deep learning dynamic allostery of G-protein-coupled receptors. JACS Au 2023, 3, 3165–3180. [Google Scholar] [CrossRef]
- Wang, J.; Yang, W.; Zhao, L.; Wei, B.; Chen, J. Binding Mechanism of Inhibitors to BRD4 and BRD9 Decoded by Multiple Independent Molecular Dynamics Simulations and Deep Learning. Molecules 2024, 29, 1857. [Google Scholar] [CrossRef]
- Lu, H.; Schulze-Gahmen, U. Toward understanding the structural basis of cyclin-dependent kinase 6 specific inhibition. J. Med. Chem. 2006, 49, 3826–3831. [Google Scholar] [CrossRef]
- Amadei, A.; Linssen, A.B.; Berendsen, H.J. Essential dynamics of proteins. Proteins 1993, 17, 412–425. [Google Scholar] [CrossRef]
- Ichiye, T.; Karplus, M. Collective motions in proteins: A covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulations. Proteins 1991, 11, 205–217. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.; Liu, X.; Zhang, S.; Su, J.; Zhang, Q.; Chen, J. Molecular dynamics exploration of selectivity of dual inhibitors 5M7, 65X, and 65Z toward fatty acid binding proteins 4 and 5. Int. J. Mol. Sci. 2018, 19, 2496. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.; Wang, W.; Sun, H.; Chen, J. Probing mutation-induced conformational transformation of the GTP/M-RAS complex through Gaussian accelerated molecular dynamics simulations. J. Enzym. Inhib. Med. Chem. 2023, 38, 2195995. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Xu, J.; Xie, W.; Guo, Q.-L.; Jiang, F.-L.; Liu, Y. Reduced state transition barrier of CDK6 from open to closed state induced by Thr177 phosphorylation and its implication in binding modes of inhibitors. BBA-Gen. Subj. 2018, 1862, 501–512. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Webb, B.; Sali, A. Comparative protein structure modeling using MODELLER. Curr. Protoc. Bioinform. 2016, 54, 5.6.1–5.6.37. [Google Scholar] [CrossRef] [PubMed]
- Anandakrishnan, R.; Aguilar, B.; Onufriev, A.V. H++ 3.0: Automating pK prediction and the preparation of biomolecular struc- tures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012, 40, W537–W541. [Google Scholar] [CrossRef] [PubMed]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham, T.E., III; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
- Joung, I.S.; Cheatham, T.E., III. Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef] [PubMed]
- Joung, I.S.; Cheatham, T.E., III. Molecular dynamics simulations of the dynamic and energetic properties of alkali and halide ions using water-model-specific ion parameters. J. Phys. Chem. B 2009, 113, 13279–13290. [Google Scholar] [CrossRef] [PubMed]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- He, X.; Man, V.H.; Yang, W.; Lee, T.-S.; Wang, J. A fast and high-quality charge model for the next generation general AMBER force field. J. Chem. Phys. 2020, 153, 114502. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Roe, D.R.; Cheatham, T.E., III. PTRAJ and CPPTRAJ: Software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Miao, Y.; Sinko, W.; Pierce, L.; Bucher, D.; Walker, R.C.; McCammon, J.A. Improved reweighting of accelerated molecular dynamics simulations for free energy calculation. J. Chem. Theory Comput. 2014, 10, 2677–2689. [Google Scholar] [CrossRef] [PubMed]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Izaguirre, J.A.; Catarello, D.P.; Wozniak, J.M.; Skeel, R.D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. [Google Scholar] [CrossRef]
- McGibbon, R.T.; Beauchamp, K.A.; Harrigan, M.P.; Klein, C.; Swails, J.M.; Hernández, C.X.; Schwantes, C.R.; Wang, L.-P.; Lane, T.J.; Pande, V.S. MDTraj: A modern open library for the analysis of molecular dynamics trajectories. Biophys. J. 2015, 109, 1528–1532. [Google Scholar] [CrossRef]
- McLachlan, A. Gene duplications in the structural evolution of chymotrypsin. J. Mol. Biol. 1979, 128, 49–79. [Google Scholar] [CrossRef]
- Wang, J.; Morin, P.; Wang, W.; Kollman, P.A. Use of MM-PBSA in Reproducing the Binding Free Energies to HIV-1 RT of TIBO Derivatives and Predicting the Binding Mode to HIV-1 RT of Efavirenz by Docking and MM-PBSA. J. Am. Chem. Soc. 2001, 123, 5221–5230. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Li, Y.; Shen, M.; Tian, S.; Xu, L.; Pan, P.; Guan, Y.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. 2014, 16, 22035–22045. [Google Scholar] [CrossRef]
- Sun, H.; Li, Y.; Tian, S.; Xu, L.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys. Chem. Chem. Phys. 2014, 16, 16719–16729. [Google Scholar] [CrossRef]
- Sun, H.; Duan, L.; Chen, F.; Liu, H.; Wang, Z.; Pan, P.; Zhu, F.; Zhang, J.Z.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 7. Entropy effects on the performance of end-point binding free energy calculation approaches. Phys. Chem. Chem. Phys. 2018, 20, 14450–14460. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Zhang, Q.; Chen, K.; Zhu, W. A comparative study of trypsin specificity based on QM/MM molecular dynamics simulation and QM/MM GBSA calculation. J. Biomol. Struct. Dyn. 2015, 33, 2606–2618. [Google Scholar] [CrossRef] [PubMed]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into Protein–Protein Binding by Binding Free Energy Calculation and Free Energy Decomposition for the Ras–Raf and Ras–RalGDS Complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef] [PubMed]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins 2004, 55, 383–394. [Google Scholar] [CrossRef]
- Miller, B.R., III; McGee, T.D., Jr.; Swails, J.M.; Homeyer, N.; Gohlke, H.; Roitberg, A.E. MMPBSA.py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. [Google Scholar] [CrossRef] [PubMed]





| a Components | LQQ-Bound CDK6/Vcyclin | LQQ-Bound CDK6 | AP9-Bound CDK6/Vcyclin | AP9-Bound CDK6 | ||||
|---|---|---|---|---|---|---|---|---|
| Average | b STD | Average | STD | Average | STD | Average | STD | |
| c | 0.09 | 0.00 | 0.07 | 0.00 | 0.08 | 0.00 | 0.08 | 0.00 |
| c | −52.14 | 0.21 | −51.73 | 0.21 | −48.89 | 0.17 | −42.90 | 0.22 |
| c | 30.43 | 0.32 | 28.75 | 0.32 | 29.68 | 0.44 | 25.33 | 0.43 |
| c | −5.90 | 0.02 | −5.95 | 0.02 | −5.90 | 0.02 | −5.26 | 0.02 |
| d | −10.72 | 0.30 | −11.54 | 0.28 | −5.62 | 0.44 | −3.78 | 0.50 |
| e | −38.23 | 0.26 | −40.39 | 0.28 | −30.62 | 0.19 | −26.52 | 0.29 |
| f | 17.20 | 1.18 | 20.98 | 1.05 | 21.08 | 1.17 | 19.22 | 0.97 |
| g | −21.03 | −19.41 | −9.54 | −7.3 | ||||
| h | −11.11 | −9.09 | ||||||
| Compound | Residue | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| LQQ-CDK6/Vcyclin | I19 | −2.75 | −0.95 | −3.7 | −0.22 | −0.32 | −0.54 | 0.18 | 1.5 | 1.68 | −3.1 |
| V27 | −1.53 | −0.15 | −1.68 | −0.12 | −0.07 | −0.19 | 0.11 | 0.04 | 0.15 | −1.94 | |
| A41 | −0.69 | −0.2 | −0.89 | 0.02 | 0.01 | 0.03 | −0.02 | 0.11 | 0.09 | −0.83 | |
| F98 | −1.15 | −0.13 | −1.28 | 0.21 | 0.17 | 0.38 | −0.05 | −0.04 | −0.09 | −1.1 | |
| H100 | −1.15 | −0.34 | −1.49 | −0.86 | −0.63 | −1.49 | 1.12 | 0.14 | 1.26 | −1.77 | |
| V101 | −0.92 | −0.2 | −1.12 | 0.01 | −2.17 | −2.16 | −0.03 | 1.0 | 0.97 | −2.37 | |
| Q103 | −1.02 | −0.84 | −1.86 | −0.17 | 0.13 | −0.04 | 0.23 | −0.02 | 0.21 | −1.83 | |
| T107 | −0.68 | −0.08 | −0.76 | −0.53 | 0.1 | −0.43 | 0.66 | −0.22 | 0.43 | −0.94 | |
| L152 | −2.32 | −0.1 | −2.41 | −0.04 | −0.03 | −0.08 | 0.1 | −0.08 | 0.02 | −2.74 | |
| LQQ-CDK6 | I19 | −2.69 | −0.62 | −3.3 | −0.19 | −0.23 | −0.42 | 0.2 | 0.88 | 1.09 | −3.11 |
| V27 | −1.57 | −0.15 | −1.72 | −0.08 | −0.02 | −0.1 | 0.09 | 0.02 | 0.11 | −1.94 | |
| A41 | −0.72 | −0.22 | −0.94 | 0.01 | −0.03 | −0.01 | −0.01 | 0.15 | 0.14 | −0.88 | |
| F98 | −1.19 | −0.13 | −1.32 | 0.22 | 0.16 | 0.38 | −0.06 | −0.06 | −0.12 | −1.17 | |
| H100 | −1.22 | −0.34 | −1.56 | −2.49 | −0.72 | −3.21 | 1.88 | 0.21 | 2.09 | −2.75 | |
| V101 | −0.82 | −0.18 | −1.0 | 0.0 | −2.41 | −2.41 | −0.02 | 1.1 | 1.08 | −2.38 | |
| Q103 | −0.96 | −0.81 | −1.77 | −0.14 | 0.05 | −0.09 | 0.16 | −0.1 | 0.07 | −1.91 | |
| T107 | −0.71 | −0.08 | −0.79 | −0.79 | 0.16 | −0.63 | 0.92 | −0.3 | 0.62 | −1.0 | |
| L152 | −2.36 | −0.09 | −2.46 | −0.07 | 0.0 | −0.07 | 0.14 | −0.11 | 0.03 | −2.78 | |
| AP9-CDK6/Vcyclin | I19 | −2.36 | −0.5 | −2.86 | −0.2 | 0.28 | 0.08 | 0.24 | 0.01 | 0.26 | −2.95 |
| V27 | −1.68 | −0.16 | −1.84 | −0.12 | 0.15 | 0.03 | 0.09 | −0.27 | −0.18 | −2.22 | |
| A41 | −0.73 | −0.3 | −1.03 | 0.07 | −0.33 | −0.26 | −0.04 | 0.42 | 0.38 | −0.98 | |
| F98 | −1.43 | −0.15 | −1.58 | −0.12 | 0.22 | 0.1 | 0.02 | −0.14 | −0.12 | −1.68 | |
| V101 | −1.0 | −0.62 | −1.62 | −0.05 | −2.65 | −2.7 | −0.01 | 1.7 | 1.69 | −2.71 | |
| Q103 | −0.91 | −0.76 | −1.67 | −0.18 | −0.8 | −0.98 | 0.25 | 0.51 | 0.76 | −2.0 | |
| L152 | −2.51 | −0.09 | −2.6 | −0.17 | −0.2 | −0.38 | 0.24 | 0.08 | 0.32 | −2.95 | |
| AP9-CDK6 | I19 | −2.18 | −0.39 | −2.57 | −0.23 | 0.2 | −0.03 | 0.26 | 0.01 | 0.27 | −2.76 |
| V27 | −1.52 | −0.15 | −1.66 | −0.12 | 0.16 | 0.03 | 0.11 | −0.3 | −0.18 | −2.06 | |
| A41 | −0.62 | −0.26 | −0.88 | 0.07 | −0.31 | −0.24 | −0.04 | 0.41 | 0.38 | −0.81 | |
| F98 | −1.18 | −0.17 | −1.34 | −0.12 | 0.23 | 0.11 | 0.12 | −0.17 | −0.05 | −1.39 | |
| V101 | −0.93 | −0.65 | −1.58 | −0.02 | −2.35 | −2.37 | −0.04 | 1.7 | 1.66 | −2.4 | |
| Q103 | −0.8 | −0.69 | −1.5 | −0.15 | −1.0 | −1.15 | 0.2 | 0.69 | 0.88 | −1.87 | |
| L152 | −2.38 | −0.09 | −2.47 | −0.09 | −0.2 | −0.29 | 0.2 | 0.07 | 0.27 | −2.82 |
| Compound | a Hydrogen Bonds | Distance (Å) | Angle (°) | b Occupancy(%) |
|---|---|---|---|---|
| LQQ-CDK6/Vcyclin | V101-O…LQQ-N04-H4 | 2.8 | 153.5 | 98.8 |
| V101-N-H…LQQ-N01 | 3.2 | 147.7 | 77.7 | |
| H100-NE2-HE2…LQQ-N05 | 3.0 | 155.0 | 65.4 | |
| D163-N-H…LQQ-O01 | 3.2 | 151.2 | 53.0 | |
| LQQ-CDK6 | V101-O…LQQ-N04-H4 | 2.8 | 153.4 | 98.7 |
| V101-N-H…LQQ-N01 | 3.2 | 148.0 | 79.7 | |
| H100-NE2-HE2…LQQ-N05 | 3.0 | 155.3 | 58.8 | |
| D163-N-H…LQQ-O01 | 3.1 | 151.1 | 51.6 | |
| AP9-CDK6/Vcyclin | V101-O…AP9-N6-H6 | 3.0 | 151.6 | 95.6 |
| V101-N-H…AP9-N7 | 3.3 | 138.1 | 59.7 | |
| AP9-CDK6 | V101-O…AP9-N6-H6 | 3.0 | 154.3 | 91.6 |
| V101-N-H…AP9-N7 | 3.2 | 141.1 | 67.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Wang, J.; Yang, W.; Zhao, K.; Sun, Q.; Chen, J. Unveiling Conformational States of CDK6 Caused by Binding of Vcyclin Protein and Inhibitor by Combining Gaussian Accelerated Molecular Dynamics and Deep Learning. Molecules 2024, 29, 2681. https://doi.org/10.3390/molecules29112681
Zhao L, Wang J, Yang W, Zhao K, Sun Q, Chen J. Unveiling Conformational States of CDK6 Caused by Binding of Vcyclin Protein and Inhibitor by Combining Gaussian Accelerated Molecular Dynamics and Deep Learning. Molecules. 2024; 29(11):2681. https://doi.org/10.3390/molecules29112681
Chicago/Turabian StyleZhao, Lu, Jian Wang, Wanchun Yang, Kunpeng Zhao, Qingtao Sun, and Jianzhong Chen. 2024. "Unveiling Conformational States of CDK6 Caused by Binding of Vcyclin Protein and Inhibitor by Combining Gaussian Accelerated Molecular Dynamics and Deep Learning" Molecules 29, no. 11: 2681. https://doi.org/10.3390/molecules29112681
APA StyleZhao, L., Wang, J., Yang, W., Zhao, K., Sun, Q., & Chen, J. (2024). Unveiling Conformational States of CDK6 Caused by Binding of Vcyclin Protein and Inhibitor by Combining Gaussian Accelerated Molecular Dynamics and Deep Learning. Molecules, 29(11), 2681. https://doi.org/10.3390/molecules29112681






