Identification of Anticancer Enzymes and Biomarkers for Hepatocellular Carcinoma through Constraint-Based Modeling
Abstract
1. Introduction
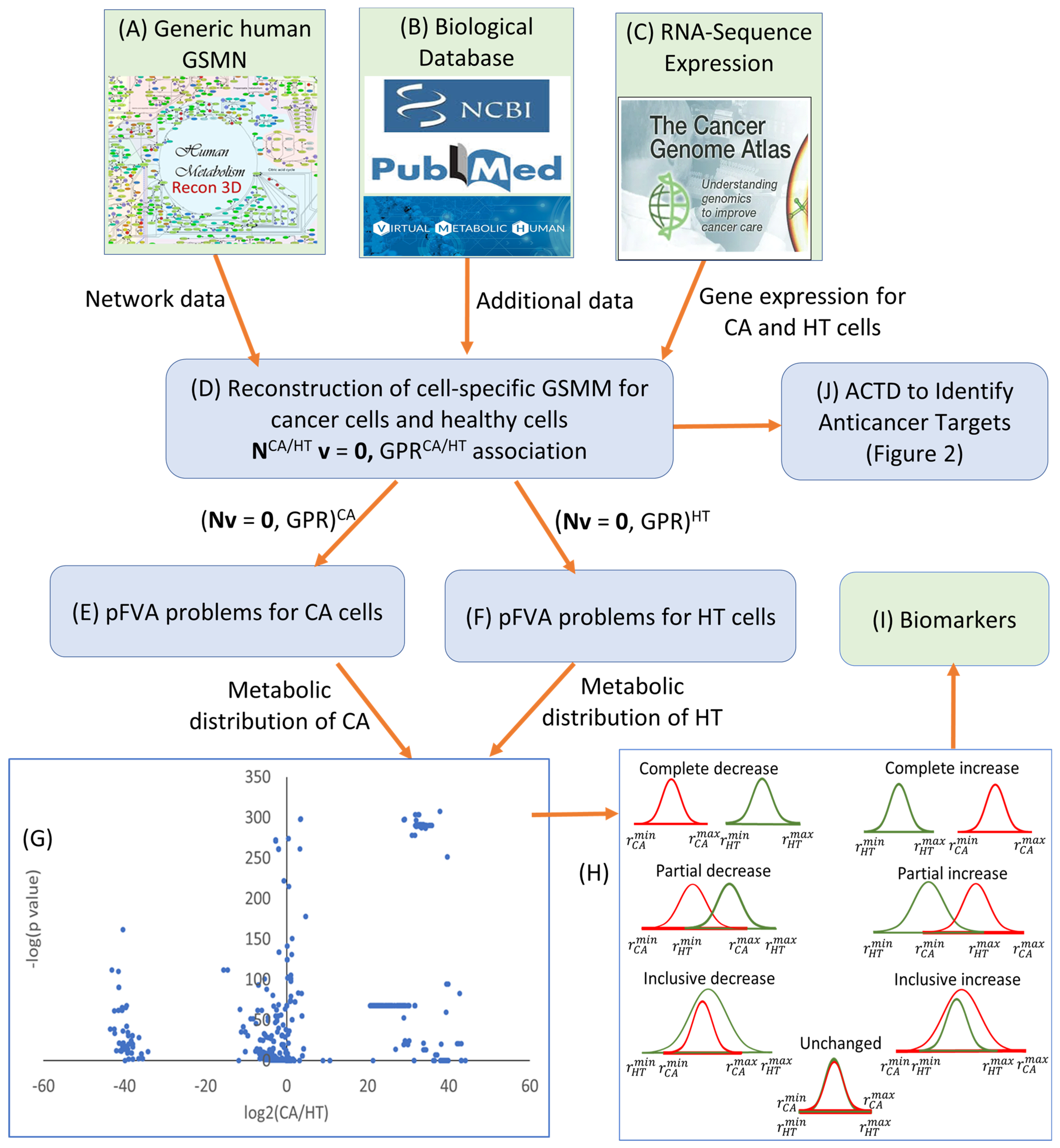
2. Results and Discussion
2.1. Weighting Factors in the UFD Problem
2.2. Single Anticancer Targets
2.3. Various Nutrient Media
2.4. Combination of Targets with Exchange Reactions
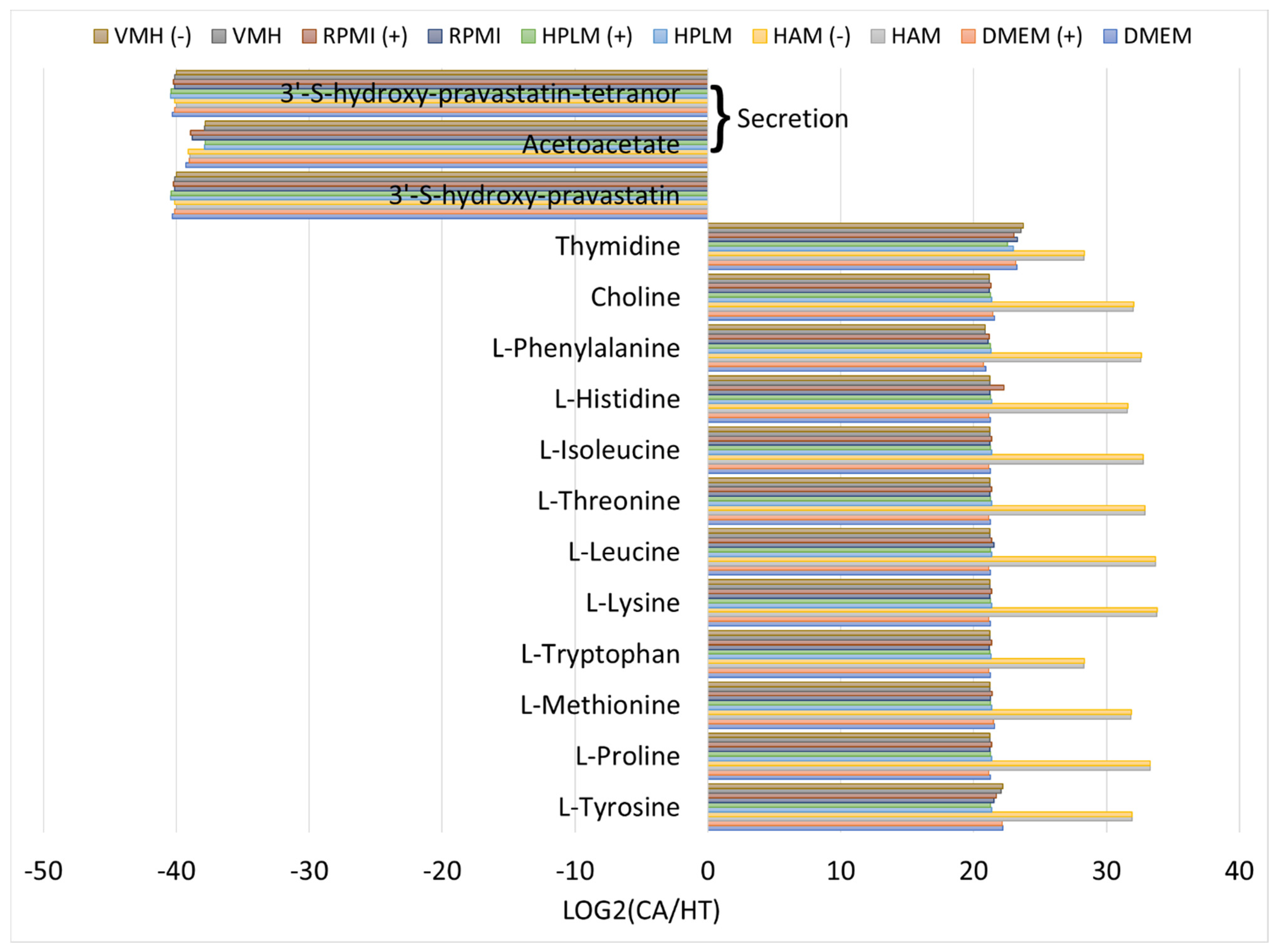
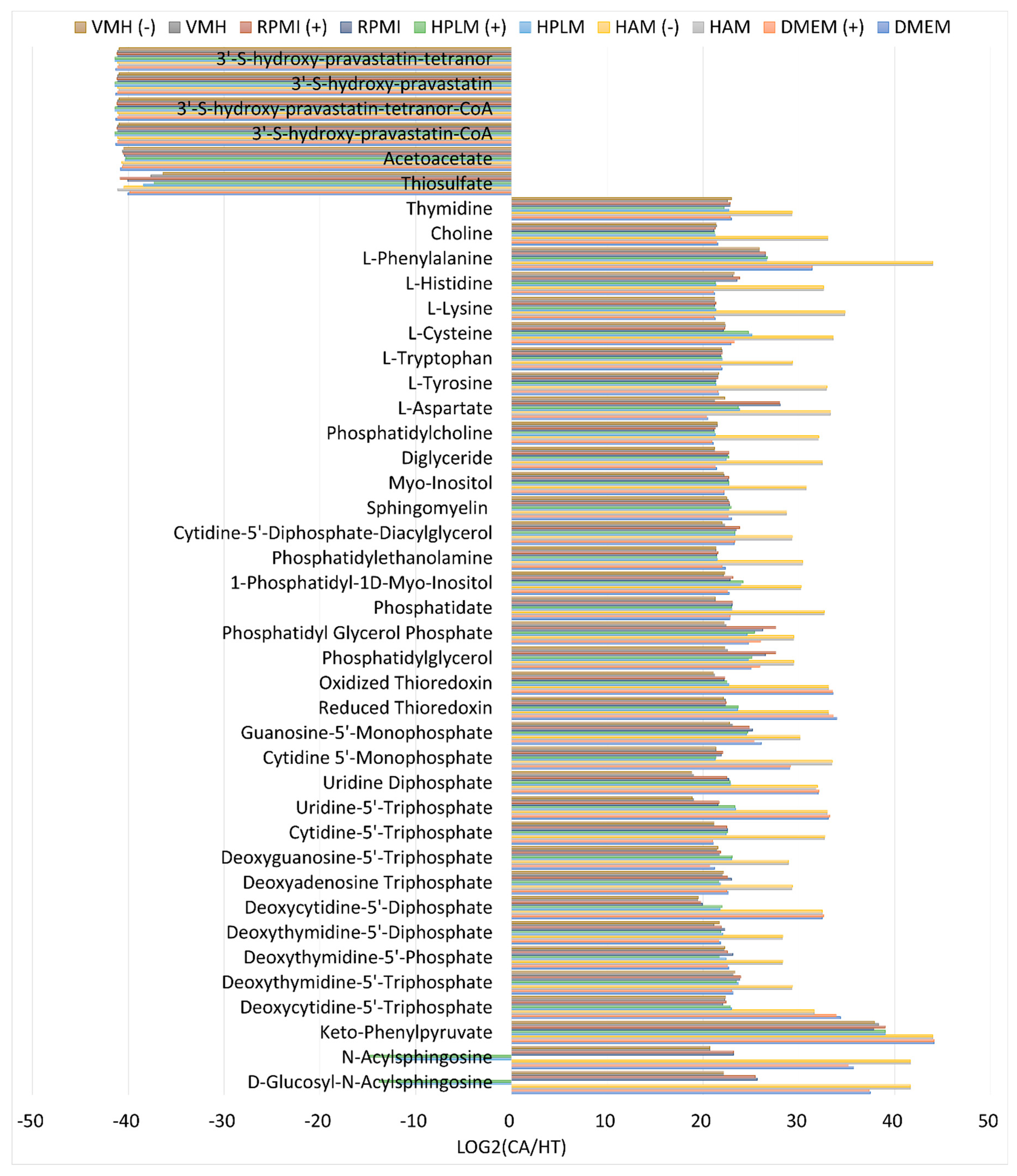
2.5. Biomarker Identification
3. Methods
3.1. Parsimonious Flux Balance Analysis and Flux Variability Analysis
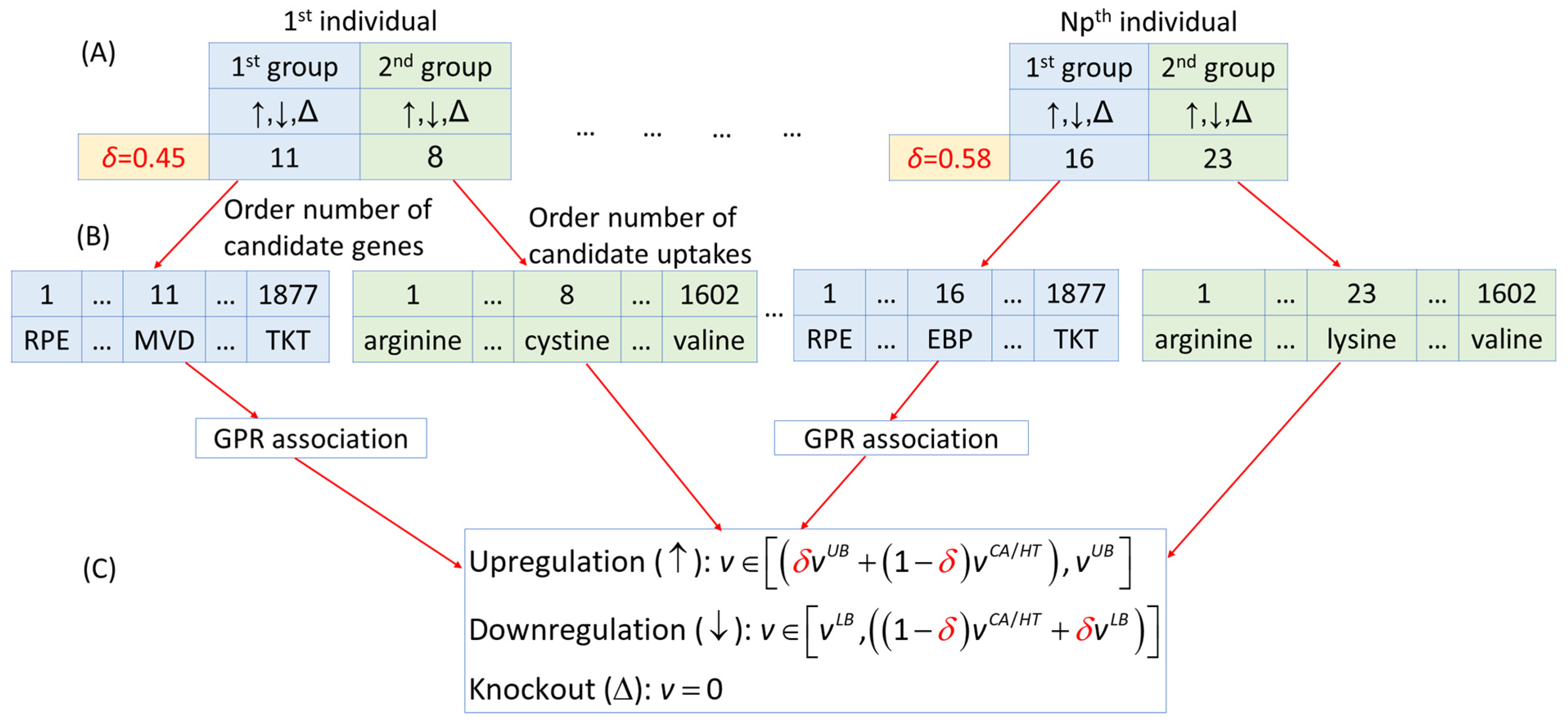
3.2. Anticancer Target Discovery Problem
3.3. Fuzzy Multi-Objective Hierarchical Optimization Problem
3.4. Computational Procedures
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Z.; Xu, M.J.; Gao, B. Hepatocytes: A key cell type for innate immunity. Cell. Mol. Immunol. 2016, 13, 301–315. [Google Scholar] [CrossRef] [PubMed]
- Tenen, D.G.; Chai, L.; Tan, J.L. Metabolic alterations and vulnerabilities in hepatocellular carcinoma. Gastroenterol. Rep. 2021, 9, 1–13. [Google Scholar] [CrossRef]
- Siegel, R.L.; Miller, K.D.; Wagle, N.S.; Jemal, A. Cancer statistics, 2023. CA Cancer J. Clin. 2023, 73, 17–48. [Google Scholar] [CrossRef] [PubMed]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Satriano, L.; Lewinska, M.; Rodrigues, P.M.; Banales, J.M.; Andersen, J.B. Metabolic rearrangements in primary liver cancers: Cause and consequences. Nat. Rev. Gastroenterol. Hepatol. 2019, 16, 748–766. [Google Scholar] [CrossRef] [PubMed]
- Pavlova, N.N.; Thompson, C.B. The emerging hallmarks of cancer metabolism. Cell Metab. 2016, 23, 27–47. [Google Scholar] [CrossRef] [PubMed]
- DeBerardinis, R.J.; Chandel, N.S. Fundamentals of cancer metabolism. Sci. Adv. 2016, 2, e1600200. [Google Scholar] [CrossRef] [PubMed]
- Pavlova, N.N.; Zhu, J.; Thompson, C.B. The hallmarks of cancer metabolism: Still emerging. Cell Metab. 2022, 34, 355–377. [Google Scholar] [CrossRef]
- Konda, P.; Garinet SVan Allen EMViswanathan, S.R. Genome-guided discovery of cancer therapeutic targets. Cell Rep. 2023, 42, 112978. [Google Scholar] [CrossRef]
- Finley, L.W.S. What is cancer metabolism? Cell 2023, 186, 1670–1688. [Google Scholar] [CrossRef]
- Ge, M.; Luo, J.; Wu, Y.; Shen, G.; Kuang, X. The biological essence of synthetic lethality: Bringing new opportunities for cancer therapy. Oncology 2024, 3, e70. [Google Scholar] [CrossRef]
- Su, M.C.; Lee Am Zhang, W.; Maeser, D.; Gruener, R.F.; Deng, Y.; Huang, R.S. Computational modeling to identify drugs targeting metastatic castration-resistant prostate cancer characterized by heightened glycolysis. Pharmaceuticals 2024, 17, 569. [Google Scholar] [CrossRef] [PubMed]
- Folger, O.; Jerby, L.; Frezza, C.; Gottlieb, E.; Ruppin, E.; Shlomi, T. Predicting selective drug targets in cancer through metabolic networks. Mol. Syst. Biol. 2011, 7, 501. [Google Scholar] [CrossRef] [PubMed]
- Yizhak, K.; Gaude, E.; Le Dévédec, S.; Waldman, Y.Y.; Stein, G.Y.; Water, B.V.D.; Frezza, C.; Ruppin, E. Phenotype-based cell-specific metabolic modeling reveals metabolic liabilities of cancer. eLife 2014, 3, e03641. [Google Scholar] [CrossRef] [PubMed]
- Ghaffari, P.; Mardinoglu, A.; Nielsen, J. Cancer metabolism: A modeling perspective. Front. Physiol. 2015, 6, 382. [Google Scholar] [CrossRef] [PubMed]
- Jerby, L.; Ruppin, E. Predicting drug targets and biomarkers of cancer via genome-scale metabolic modeling. Clin. Cancer Res. 2012, 18, 5572–5584. [Google Scholar] [CrossRef] [PubMed]
- Lewis, N.E.; Abdel-Haleem, A.M. The evolution of genome-scale models of cancer metabolism. Front. Physiol. 2013, 4, 237. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, A.; Nielsen, J. Genome scale metabolic modeling of cancer. Metab. Eng. 2017, 43, 103–112. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J.L.; Nielsen, J. Anticancer drug discovery through genome-scale metabolic modeling. Curr. Opin. Syst. Biol. 2017, 4, 1–8. [Google Scholar] [CrossRef]
- Wu, H.Q.; Cheng, M.L.; Lai, J.M.; Wu, H.H.; Chen, M.C.; Liu, W.H.; Wu, W.H.; Chang, P.M.H.; Huang, C.Y.F.; Tsou, A.P.; et al. Flux balance analysis predicts Warburg-like effects of mouse hepatocyte deficient in miR-122a. PLoS Comput. Biol. 2017, 13, e1005618. [Google Scholar] [CrossRef]
- Wang, F.S.; Wu, W.H.; Hsiu, W.S.; Liu, Y.J.; Chuang, K.W. Genome-scale metabolic modeling with protein expressions of normal and cancerous colorectal tissues for oncogene inference. Metabolites 2020, 10, 16. [Google Scholar] [CrossRef]
- Wang, Y.T.; Lin, M.R.; Chen, W.C.; Wu, W.H.; Wang, F.S. Optimization of a modeling platform to predict oncogenes from genome-scale metabolic networks of non-small-cell lung cancers. FEBS OpenBio 2021, 11, 2078–2094. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.T.; Wang, T.Y.; Chen, P.R.; Wu, W.H.; Lai, J.M.; Chang, P.M.H.; Hong, Y.R.; Huang, C.Y.F.; Wang, F.S. Computer-aided design for identifying anticancer targets in genome-scale metabolic models of colon cancer. Biology 2021, 10, 1115. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.S.; Chen, P.R.; Chen, T.Y.; Zhang, H.X. Fuzzy optimization for identifying anticancer targets with few side effects in constraint-based models of head and neck cancer. R. Soc. Open Sci. 2022, 9, 220633. [Google Scholar] [CrossRef] [PubMed]
- MohammadiPeyhani, H.; Chiappino-Pepe, A.; Haddadi, K.; Hafner, J.; Hadadi, N.; Hatzimanikatis, V. NICEdru, a workflow for rational drug design and systems-level analysis of drug metabolism. eLife 2021, 10, e65543. [Google Scholar] [CrossRef] [PubMed]
- You, Y.; Lai, X.; Pan, Y.; Zheng, H.; Vera, J.; Liu, S.; Deng, S.; Zhang, L. Artificial intelligence in cancer target identification and drug discovery. Signal Transduct. Target. Ther. 2022, 7, 156. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.; Aouidate, A.; Wang, S.; Yu, Q.; Li, Y.; Yuan, S. Discovering anti-cancer drugs via computational methods. Front. Pharmacol. 2020, 11, 733. [Google Scholar] [CrossRef] [PubMed]
- Huang, A.; Garraway, L.A.; Ashworth, A.; Weber, B. Synthetic lethality as an engine for cancer drug target discovery. Nat. Rev. Drug Discov. 2019, 19, 23–38. [Google Scholar] [CrossRef]
- Rinschen, M.M.; Ivanisevic, J.; Giera, M.; Siuzdak, G. Identification of bioactive metabolites using activity metabolomics. Nat. Rev. Mol. Cell Biol. 2019, 20, 353–367. [Google Scholar] [CrossRef]
- Lewis, J.E.; Kemp, M.L. Integration of machine learning and genome-scale metabolic modeling identifies multi-omics biomarkers for radiation resistance. Nat. Commun. 2021, 12, 2700. [Google Scholar] [CrossRef]
- Moškon, M.; Režen, T. Context-specific genome-scale metabolic modelling and its application to the analysis of COVID-19 metabolic signatures. Metabolites 2023, 13, 126. [Google Scholar] [CrossRef] [PubMed]
- Jenior, M.L.; Moutinho, T.J., Jr.; Dougherty, B.V.; Papin, J.A. Transcriptome-guided parsimonious lux analysis improves predictions with metabolic Networks in complex environments. PLoS Comput. Biol. 2020, 16, e1007099. [Google Scholar] [CrossRef] [PubMed]
- National Cancer Institute of U.S. The Cancer Genome Atlas Program. Department of Health and Human Services. Available online: https://www.cancer.gov/about-nci/organization/ccg/research/structural-genomics/tcga (accessed on 27 May 2024).
- Schultz, A.; Qutub, A.A. Reconstruction of tissue-specific metabolic networks using CORDA. PLoS Comput. Biol. 2016, 12, e1004808. [Google Scholar] [CrossRef] [PubMed]
- Heiden, M.G.V.; Locasale, J.W.; Swanson, K.D.; Sharfi, H.; Heffron, G.J.; Daniel Amador-Noguez, D.; Christofk, H.R.; Wagner, G.; Rabinowitz, J.D.; Asara, J.M.; et al. Evidence for an alternative glycolytic pathway in rapidly proliferating cells. Science 2010, 329, 1492–1499. [Google Scholar] [CrossRef] [PubMed]
- Jain, M.; Nilsson, R.; Sharma, S.; Madhusudhan, N.; Kitami, T.; Souza, A.L.; Kafri, R.; Kirschner, M.W.; Clish, C.B.; Mootha, V.K. Metabolite profiling identifies a key role for glycine in rapid cancer cell proliferation. Science 2012, 336, 1040–1044. [Google Scholar] [CrossRef] [PubMed]
- Asgari, Y.; Zabihinpour, Z.; Salehzadeh-Yazdi, A.; Schreiber, F.; Masoudi-Nejad, A. Alterations in cancer cell metabolism: The Warburg effect and metabolic adaptation. Genomics 2015, 105, 275–281. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.S.; Wang, T.Y.; Wu, W.H. Fuzzy multiobjective hierarchical optimization with application to identify antienzymes of colon cancer cells. J. Taiwan Inst. Chem. Eng. 2022, 132, 10412. [Google Scholar] [CrossRef]
- Wishart, D.S.; Feunang, Y.D.; Guo, A.C.; Lo, E.J.; Marcu, A.; Grant, J.R.; Sajed, T.; Johnson, D.; Li, C.; Sayeeda, Z.; et al. DrugBank 5.0: A major update to the DrugBank database for 2018. Nucleic Acids Res. 2018, 46, D1074–D1082. [Google Scholar] [CrossRef]
- Brunk, E.; Sahoo, S.; Zielinski, D.C.; Altunkaya, A.; Dräger, A.; Mih, N.; Gatto, F.; Nilsson, A.; Andres Gonzalez, A.P.; Aurich, M.K.; et al. Recon3D enables a three-dimensional view of gene variation in human metabolism. Nat. Biotechnol. 2018, 36, 272–281. [Google Scholar] [CrossRef]
- Zur, H.; Ruppin, E.; Shlomi, T. iMAT: An integrative metabolic analysis tool. Bioinformatics 2010, 26, 3140–3142. [Google Scholar] [CrossRef]
- Vaskan, P.; Guillén-Gosálbez, G.; Sorribas, A.; Alves, R.; Jiménez, L. Multi-level optimization framework applied to the systematic evaluation of metabolic objective functions. Comput. Aided Chem. Eng. 2014, 33, 961–966. [Google Scholar] [CrossRef]
- Pozo, C.; Miró, A.; Guillén-Gosálbez, G.; Sorribas, A.; Alves, R.; Jiménez, L. Global optimization of hybrid kinetic/FBA models via outer-approximation. Comput. Chem. Eng. 2015, 72, 325–333. [Google Scholar] [CrossRef]
- Chiou, J.P.; Wang, F.S. Hybrid method of evolutionary algorithms for static and dynamic optimization problems with application to a fed-batch fermentation process. Comput. Chem. Eng. 1999, 23, 1277–1291. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]


| DMEM | HAM | HPLM | RPMI | VMH | D/T | No. Drugs | Pathway | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Target | CV | MD | CV | MD | CV | MD | CV | MD | CV | MD | |||
| CMPK1 | 0.869 | 0.472 | 0.842 | 0.594 | -- | -- | -- | -- | -- | -- | 40/43 | 9 | Gemcitabine pathway |
| DCTD | 0.869 | 0.451 | 0.842 | 0.561 | 0.980 | 0.479 | -- | -- | -- | -- | 1/43 | 1 | Gemcitabine pathway |
| PGS1 | 0.833 | 0.431 | 0.842 | 0.625 | 0.980 | 0.518 | 0.980 | 0.496 | 0.980 | 0.530 | 36/43 | 0 | Glycerophospholipid biosynthesis |
| CRLS1 | 0.833 | 0.424 | 0.842 | 0.586 | 0.980 | 0.479 | 0.980 | 0.550 | 0.980 | 0.565 | 25/43 | 0 | Glycerophospholipid biosynthesis |
| MVD | 0.833 | 0.421 | -- | -- | 0.980 | 0.500 | 0.980 | 0.551 | -- | -- | 31/43 | 0 | Cholesterol biosynthesis |
| MVK | 0.833 | 0.421 | -- | -- | 0.980 | 0.510 | 0.980 | 0.507 | -- | -- | 34/43 | 1 | Cholesterol biosynthesis |
| PMVK | 0.833 | 0.421 | -- | -- | 0.980 | 0.500 | 0.980 | 0.507 | -- | -- | 10/43 | 0 | Cholesterol biosynthesis |
| SC5D | 0.833 | 0.411 | -- | -- | 0.980 | 0.511 | 0.980 | 0.559 | -- | -- | 0/43 | 0 | Cholesterol biosynthesis |
| HMGCR | 0.833 | 0.411 | -- | -- | 0.980 | 0.519 | 0.980 | 0.545 | -- | -- | 43/43 | 20 | Cholesterol biosynthesis |
| ADSL | 0.833 | 0.410 | 0.842 | 0.615 | 0.980 | 0.506 | 0.980 | 0.516 | -- | -- | 28/43 | 0 | Metabolism of nucleotides |
| ADSS2 | 0.833 | 0.408 | 0.842 | 0.604 | 0.980 | 0.506 | 0.980 | 0.506 | -- | -- | 22/43 | 2 | Metabolism of nucleotides |
| LSS | 0.833 | 0.407 | -- | -- | 0.980 | 0.489 | 0.980 | 0.567 | -- | -- | 0/43 | 2 | Cholesterol biosynthesis |
| SQLE | 0.833 | 0.407 | -- | -- | 0.980 | 0.541 | 0.980 | 0.567 | -- | -- | 1/43 | 4 | Cholesterol biosynthesis |
| GK | 0.833 | 0.406 | 0.842 | 0.562 | 0.980 | 0.482 | -- | -- | -- | -- | 0/43 | 0 | Glycerophospholipid biosynthesis |
| DHCR24 | 0.833 | 0.405 | -- | -- | 0.980 | 0.479 | 0.980 | 0.520 | -- | -- | 0/43 | 0 | Cholesterol biosynthesis |
| FDFT1 | 0.833 | 0.402 | -- | -- | 0.980 | 0.507 | 0.980 | 0.530 | -- | -- | 2/43 | 1 | Cholesterol biosynthesis |
| EBP | 0.833 | 0.402 | -- | -- | 0.980 | 0.510 | 0.980 | 0.507 | -- | -- | 0/43 | 0 | Cholesterol biosynthesis |
| CTSA * | 0.812 | 0.479 | -- | -- | -- | -- | 0.980 | 0.565 | 0.980 | 0.448 | 0/43 | 3 | Sphingolipid metabolism |
| GMPR2 | 0.534 | 0.371 | -- | -- | 0.447 | 0.465 | 0.564 | 0.375 | -- | -- | 0/43 | 1 | Metabolism of nucleotides |
| CEPT1 | 0.307 | 0.288 | 0.308 | 0.328 | -- | -- | -- | -- | -- | -- | 9/43 | 2 | Glycerophospholipid biosynthesis |
| PTDSS2 | 0.234 | 0.317 | 0.250 | 0.379 | -- | -- | -- | -- | 0.564 | 0.320 | 0/43 | 1 | Glycerophospholipid biosynthesis |
| NSDHL | 0.224 | 0.269 | 0.842 | 0.594 | 0.273 | 0.279 | 0.265 | 0.290 | 0/43 | 1 | Cholesterol biosynthesis | ||
| DMEM+Cholesterol | HAM−Cholesterol | HPLM+Cholesterol | RPMI+Cholesterol | VMH−Cholesterol | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Target | CV | MD | CV | MD | CV | MD | CV | MD | CV | MD |
| CMPK1 | 0.869 | 0.480 | 0.842 | 0.594 | -- | -- | -- | -- | -- | -- |
| DCTD | 0.869 | 0.449 | 0.842 | 0.560 | 0.980 | 0.477 | -- | -- | -- | -- |
| PGS1 | 0.833 | 0.421 | 0.842 | 0.590 | 0.980 | 0.563 | 0.980 | 0.457 | 0.980 | 0.550 |
| CRLS1 | 0.833 | 0.423 | 0.842 | 0.579 | 0.980 | 0.486 | 0.980 | 0.510 | 0.980 | 0.547 |
| MVD | -- | -- | 0.842 | 0.656 | -- | -- | -- | -- | 0.980 | 0.574 |
| MVK | -- | -- | 0.842 | 0.656 | -- | -- | -- | -- | 0.980 | 0.574 |
| PMVK | -- | -- | 0.842 | 0.656 | -- | -- | -- | -- | 0.980 | 0.574 |
| SC5D | -- | -- | 0.842 | 0.617 | -- | -- | -- | -- | 0.980 | 0.527 |
| HMGCR | -- | -- | 0.842 | 0.600 | -- | -- | -- | -- | 0.980 | 0.533 |
| ADSL | 0.833 | 0.413 | 0.842 | 0.604 | 0.980 | 0.480 | 0.980 | 0.454 | -- | -- |
| ADSS2 | 0.833 | 0.414 | 0.842 | 0.596 | 0.980 | 0.499 | 0.980 | 0.476 | -- | -- |
| LSS | -- | -- | 0.842 | 0.601 | -- | -- | -- | -- | 0.980 | 0.574 |
| SQLE | -- | -- | 0.842 | 0.601 | -- | -- | -- | -- | 0.980 | 0.574 |
| GK | 0.833 | 0.438 | 0.842 | 0.567 | 0.980 | 0.501 | -- | -- | -- | -- |
| DHCR24 | -- | -- | 0.842 | 0.590 | -- | -- | -- | -- | 0.980 | 0.555 |
| FDFT1 | -- | -- | 0.842 | 0.596 | -- | -- | -- | -- | 0.980 | 0.580 |
| EBP | -- | -- | 0.842 | 0.604 | -- | -- | -- | -- | 0.980 | 0.567 |
| CTSA * | 0.812 | 0.486 | -- | -- | -- | -- | 0.980 | 0.533 | 0.980 | 0.460 |
| GMPR2 | -- | -- | -- | -- | 0.447 | 0.428 | 0.564 | 0.373 | -- | -- |
| CEPT1 | 0.307 | 0.292 | 0.308 | 0.321 | -- | -- | -- | -- | -- | -- |
| PTDSS2 | -- | -- | -- | -- | -- | -- | -- | -- | 0.564 | 0.324 |
| NSDHL | -- | -- | -- | -- | -- | -- | -- | -- | 0.273 | 0.275 |
| DMEM | HAM | VMH | ||||||
|---|---|---|---|---|---|---|---|---|
| Two-Target Combinations | CV | MD | Two-Target Combinations | CV | MD | Two-Target Combinations | CV | MD |
| (CMPK1Δ, R_EX_galt[e]↓) | 0.980 | 0.432 | (CMPK1Δ, R_EX_glyc_R[e]↓) | 0.980 | 0.526 | (CMPK1Δ, R_EX_thymd[e]Δ) | 0.980 | 0.552 |
| (DCTD↓, R_EX_glyc2p[e]↓) | 0.980 | 0.475 | (DCTD↓, R_EX_glyc_R[e]↓) | 0.980 | 0.493 | (DCTDΔ, R_EX_trp_L[e]Δ) | 0.980 | 0.577 |
| (PGS1Δ, R_EX_glyc3p[e]↓) | 0.980 | 0.494 | (PGS1Δ, R_EX_CE5304[e]↓) | 0.980 | 0.561 | (PGS1Δ, R_EX_sphs1p[e]↓) | 0.980 | 0.582 |
| (CRLS1Δ, R_EX_glyc2p[e]↓) | 0.980 | 0.477 | (CRLS1Δ, R_EX_CE5304[e]↓) | 0.980 | 0.564 | (CRLS1Δ, R_EX_lstnm1[e]Δ) | 0.980 | 0.577 |
| (MVDΔ, R_EX_icit[e]↓) | 0.980 | 0.476 | (MVDΔ, R_EX_chsterol[e]Δ) | 0.842 | 0.656 | (MVDΔ, R_EX_thymd[e]Δ) | 0.980 | 0.533 |
| (MVKΔ, R_EX_34dhpha[e]↓) | 0.980 | 0.464 | (MVKΔ, R_EX_thymd[e]Δ) | 0.842 | 0.610 | (MVK↓, R_EX_asn_L[e]Δ) | 0.980 | 0.370 |
| (PMVK↓, R_EX_glyc_R[e]↑) | 0.980 | 0.455 | (PMVK↓, R_EX_phe_L[e]Δ) | 0.842 | 0.518 | (PMVKΔ, R_EX_chsterol[e]Δ) | 0.980 | 0.574 |
| (SC5DΔ, R_EX_icit[e]↓) | 0.980 | 0.508 | (SC5DΔ, R_EX_thymd[e]Δ) | 0.842 | 0.603 | (SC5DΔ, R_EX_chsterol[e]Δ) | 0.980 | 0.527 |
| (HMGCRΔ, R_EX_glyc[e]↓) | 0.980 | 0.446 | (HMGCRΔ, R_EX_met_L[e]Δ) | 0.842 | 0.603 | (HMGCRΔ, R_EX_phe_L[e]Δ) | 0.980 | 0.399 |
| (LSSΔ, R_EX_icit[e]↓) | 0.980 | 0.517 | (LSSΔ, R_EX_his_L[e]Δ) | 0.842 | 0.611 | (LSSΔ, R_EX_chsterol[e]Δ) | 0.980 | 0.574 |
| (SQLEΔ, R_EX_icit[e]↓) | 0.980 | 0.524 | (SQLEΔ, R_EX_asn_L[e]Δ) | 0.842 | 0.512 | (SQLE↓, R_EX_trp_L[e]Δ) | 0.980 | 0.574 |
| (DHCR24Δ, R_EX_34dhpha[e]↓) | 0.980 | 0.474 | (DHCR24Δ, R_EX_his_L[e]Δ) | 0.842 | 0.593 | (DHCR24Δ, R_EX_chsterol[e]Δ) | 0.980 | 0.555 |
| (CTPS1Δ, R_EX_icit[e]↓) | 0.980 | 0.481 | (CTPS1Δ, R_EX_strch1[e]↓) | 0.959 | 0.555 | (CTPS1↓, R_EX_thymd[e]Δ) | 0.980 | 0.552 |
| (ATICΔ, R_EX_acald[e]↑) | 0.944 | 0.341 | (ATICΔ, R_EX_lnlc[e]Δ) | 0.842 | 0.593 | (ATIC↓, R_EX_thymd[e]Δ) | 0.980 | 0.562 |
| (CDIPTΔ, R_EX_acald[e]↑) | 0.941 | 0.345 | (CDIPTΔ, R_EX_trp_L[e]Δ) | 0.842 | 0.602 | (CDIPTΔ, R_EX_thymd[e]Δ) | 0.980 | 0.553 |
| (PRPS1L1Δ, R_EX_HC01444[e]↑) | 0.911 | 0.424 | (PRPS1L1Δ, R_EX_met_L[e]Δ) | 0.842 | 0.617 | (PRPS1L1Δ, R_EX_trp_L[e]Δ) | 0.980 | 0.549 |
| (GLA↓, R_EX_thymd[e]Δ) | 0.896 | 0.433 | (GLA↓, R_EX_thymd[e]Δ) | 0.842 | 0.609 | (GLA↓, R_EX_mi1p_D[e]Δ) | 0.980 | 0.547 |
| (SLC2A13↓, R_EX_thymd[e]Δ) | 0.884 | 0.440 | (SLC2A13↓, R_EX_thymd[e]Δ) | 0.842 | 0.613 | (SLC2A13↓, R_EX_trp_L[e]Δ) | 0.980 | 0.558 |
| (RPEΔ, R_EX_trp_L[e]Δ) | 0.869 | 0.425 | (RPEΔ, R_EX_met_L[e]Δ) | 0.842 | 0.455 | (RPEΔ, R_EX_mi1p_D[e]Δ) | 0.980 | 0.555 |
| (NSDHLΔ, R_EX_chsterol[e]↓, R_EX_ga1_hs[e]Δ) | 0.812 | 0.489 | (NSDHLΔ, R_EX_met_L[e]Δ) | 0.842 | 0.616 | (NSDHL↓, R_EX_mi1p_D[e]Δ) | 0.980 | 0.528 |
| (MVDΔ, GOT1Δ) | 0.980 | 0.491 | (MVDΔ, CRLS1Δ) | 0.842 | 0.592 | (MVD↓, PSAPΔ) | 0.980 | 0.434 |
| (MVKΔ, GMPR2↓) | 0.980 | 0.503 | (MVK↓, ADSS2Δ) | 0.842 | 0.627 | (MVKΔ, PGS1Δ) | 0.980 | 0.567 |
| (PMVKΔ, GLA↓) | 0.980 | 0.479 | (PMVKΔ, ADSL↓) | 0.842 | 0.605 | (PMVK↓, CRLS1Δ) | 0.980 | 0.507 |
| (SC5DΔ, SLC25A10Δ) | 0.980 | 0.454 | (SC5D↓, CMPK1Δ) | 0.842 | 0.599 | (SC5D↓, PSAPΔ) | 0.980 | 0.446 |
| (HMGCRΔ, MPC2Δ) | 0.980 | 0.480 | (HMGCRΔ, NEU3Δ) | 0.710 | 0.604 | (HMGCRΔ, SLC27A4Δ) | 0.980 | 0.495 |
| (LSSΔ, GLA↓) | 0.980 | 0.491 | (LSSΔ, CMPK1Δ) | 0.842 | 0.604 | (LSS↓, PSAPΔ) | 0.980 | 0.459 |
| (SQLEΔ, SLC17A1↓) | 0.941 | 0.487 | (SQLE↓, PGS1Δ) | 0.842 | 0.581 | (SQLE↓, CRLS1↓) | 0.980 | 0.547 |
| (DHCR24Δ, MPC2Δ) | 0.980 | 0.480 | (DHCR24Δ, ADSS2Δ) | 0.842 | 0.587 | (DHCR24Δ, SLC27A4Δ) | 0.980 | 0.506 |
| (FDFT1Δ, GLA↓) | 0.980 | 0.533 | (FDFT1Δ, CMPK1Δ) | 0.842 | 0.609 | (FDFT1Δ, PGS1Δ) | 0.980 | 0.552 |
| (EBPΔ, GLA↓) | 0.980 | 0.507 | (EBPΔ, PGS1↓) | 0.842 | 0.609 | (EBPΔ, CRLS1Δ) | 0.980 | 0.515 |
| (NSDHL↓, CRLS1Δ) | 0.834 | 0.392 | (NSDHL↓, ADSS2Δ) | 0.842 | 0.600 | (NSDHLΔ, CRLS1Δ) | 0.980 | 0.525 |
| NHDE |
|---|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.-S.; Zhang, H.-X. Identification of Anticancer Enzymes and Biomarkers for Hepatocellular Carcinoma through Constraint-Based Modeling. Molecules 2024, 29, 2594. https://doi.org/10.3390/molecules29112594
Wang F-S, Zhang H-X. Identification of Anticancer Enzymes and Biomarkers for Hepatocellular Carcinoma through Constraint-Based Modeling. Molecules. 2024; 29(11):2594. https://doi.org/10.3390/molecules29112594
Chicago/Turabian StyleWang, Feng-Sheng, and Hao-Xiang Zhang. 2024. "Identification of Anticancer Enzymes and Biomarkers for Hepatocellular Carcinoma through Constraint-Based Modeling" Molecules 29, no. 11: 2594. https://doi.org/10.3390/molecules29112594
APA StyleWang, F.-S., & Zhang, H.-X. (2024). Identification of Anticancer Enzymes and Biomarkers for Hepatocellular Carcinoma through Constraint-Based Modeling. Molecules, 29(11), 2594. https://doi.org/10.3390/molecules29112594







