Effects of La-N Co-Doping of BaTiO3 on Its Electron-Optical Properties for Photocatalysis: A DFT Study
Abstract
1. Introduction
2. Results and Discussion
2.1. Mono-Doped BaTiO3 with La or N
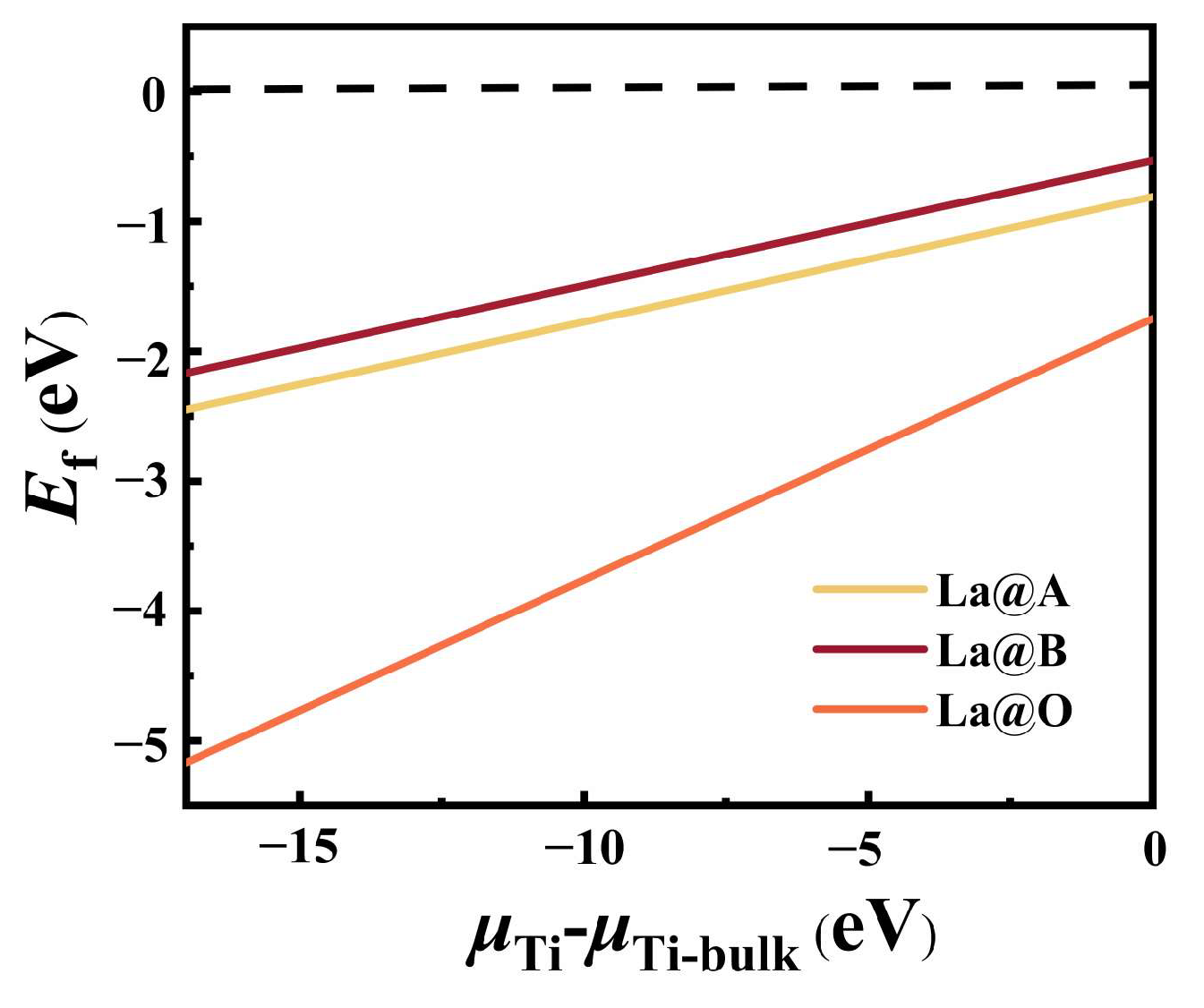
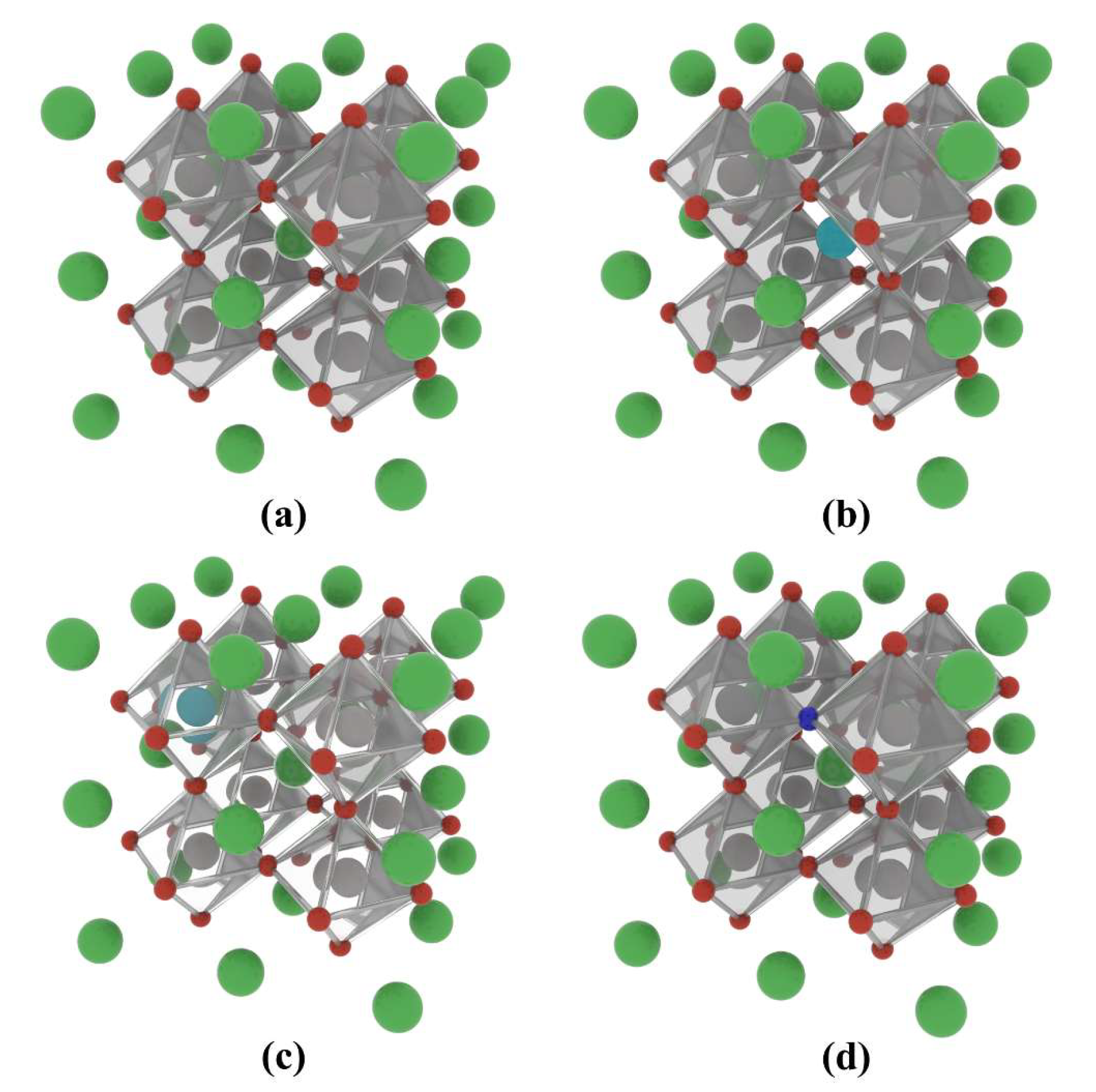
2.1.1. Atomic Structure and Formation Energy
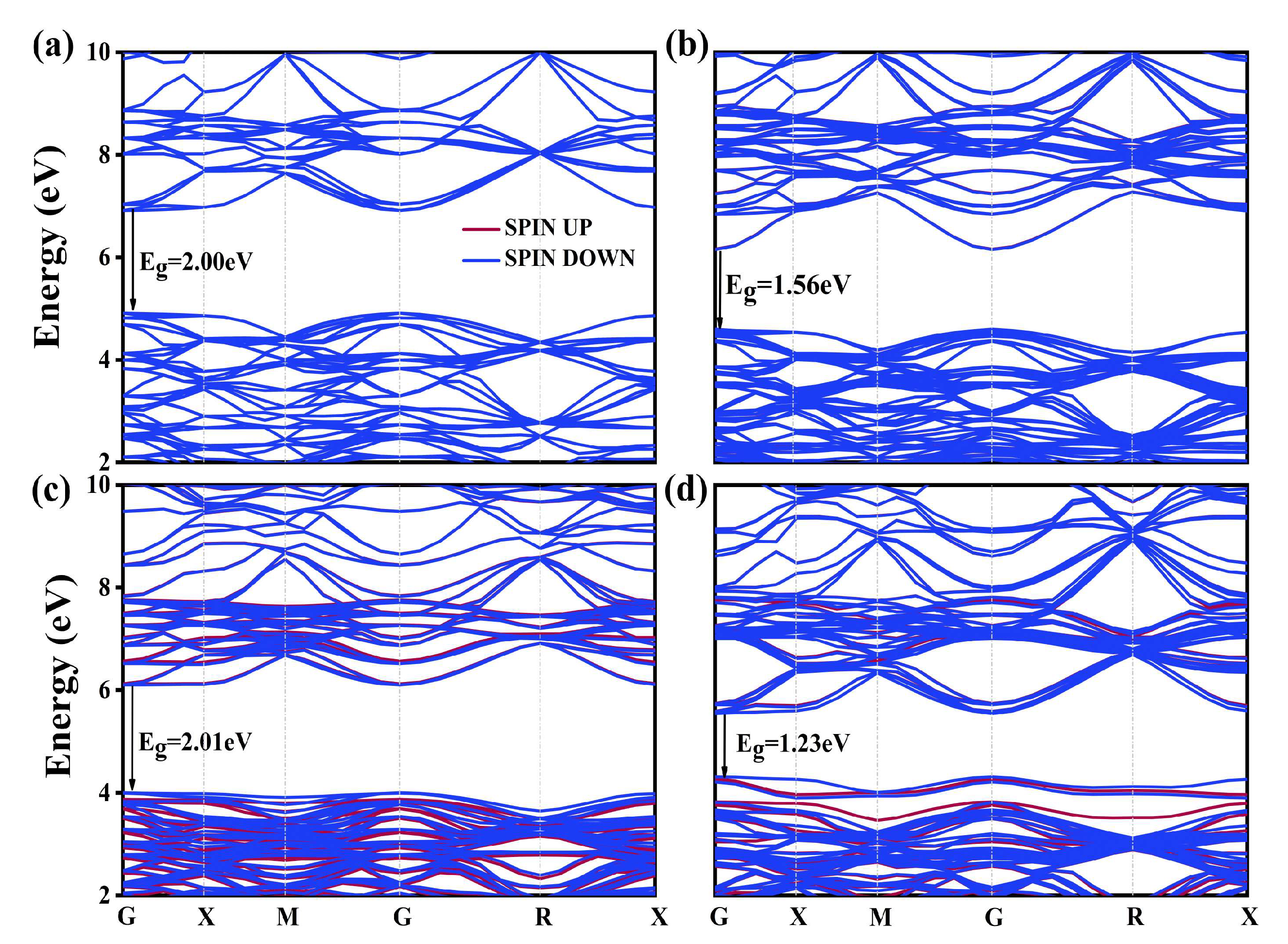
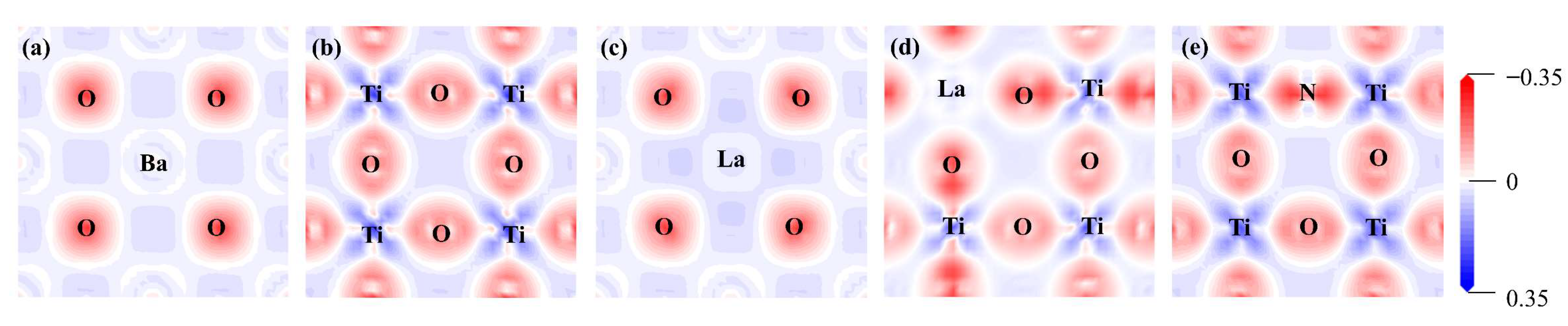
2.1.2. Electronic Structure
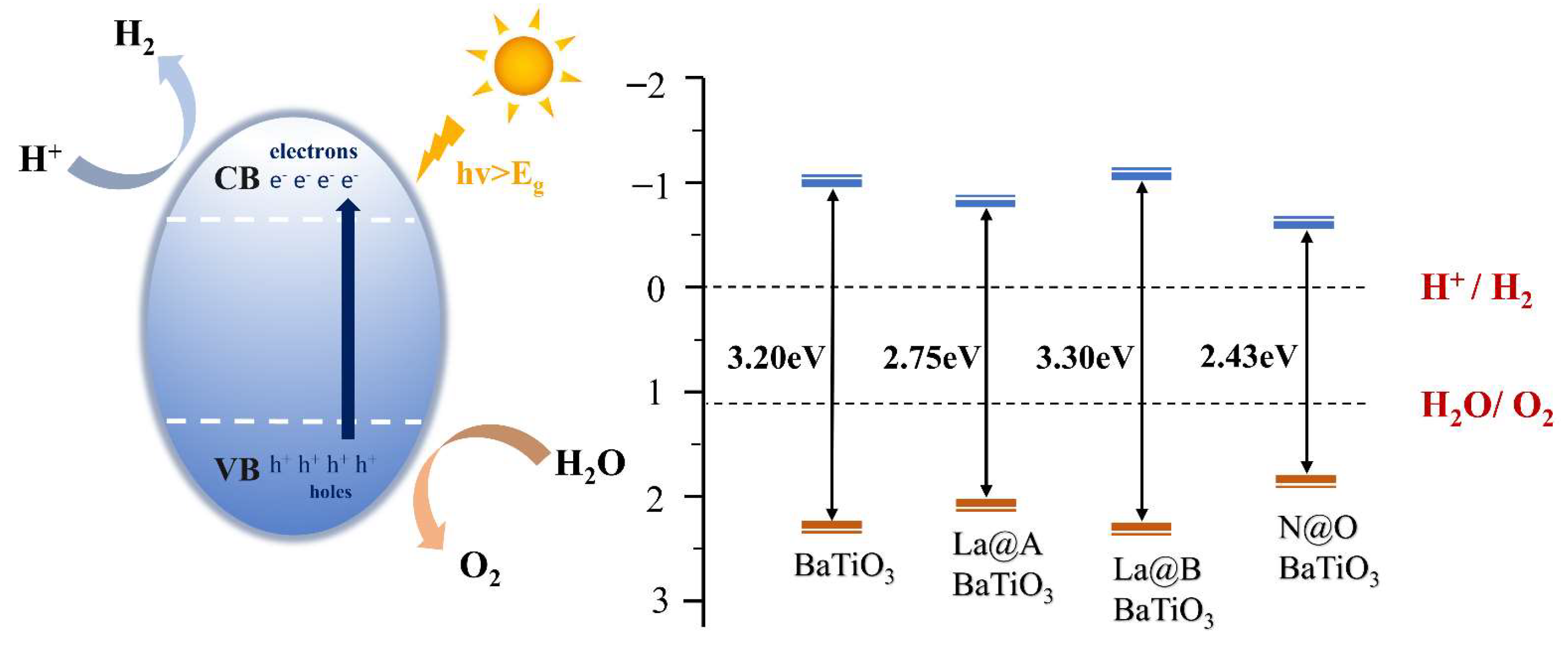
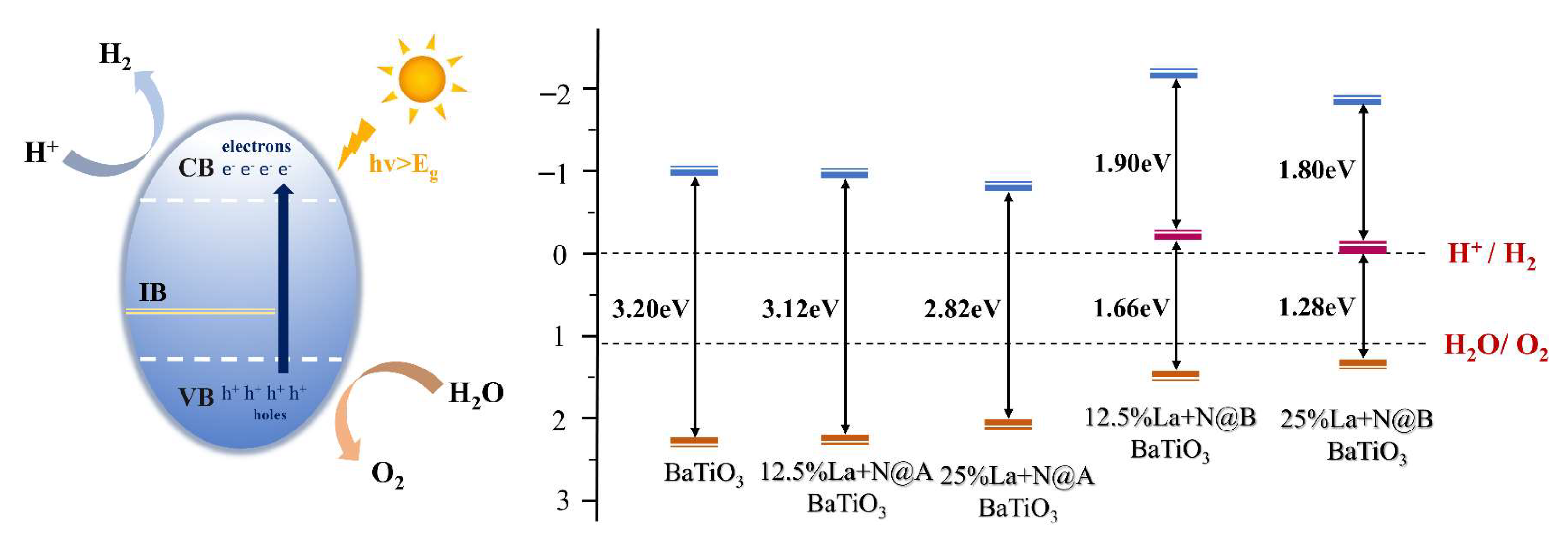
2.1.3. Water Redox Potential
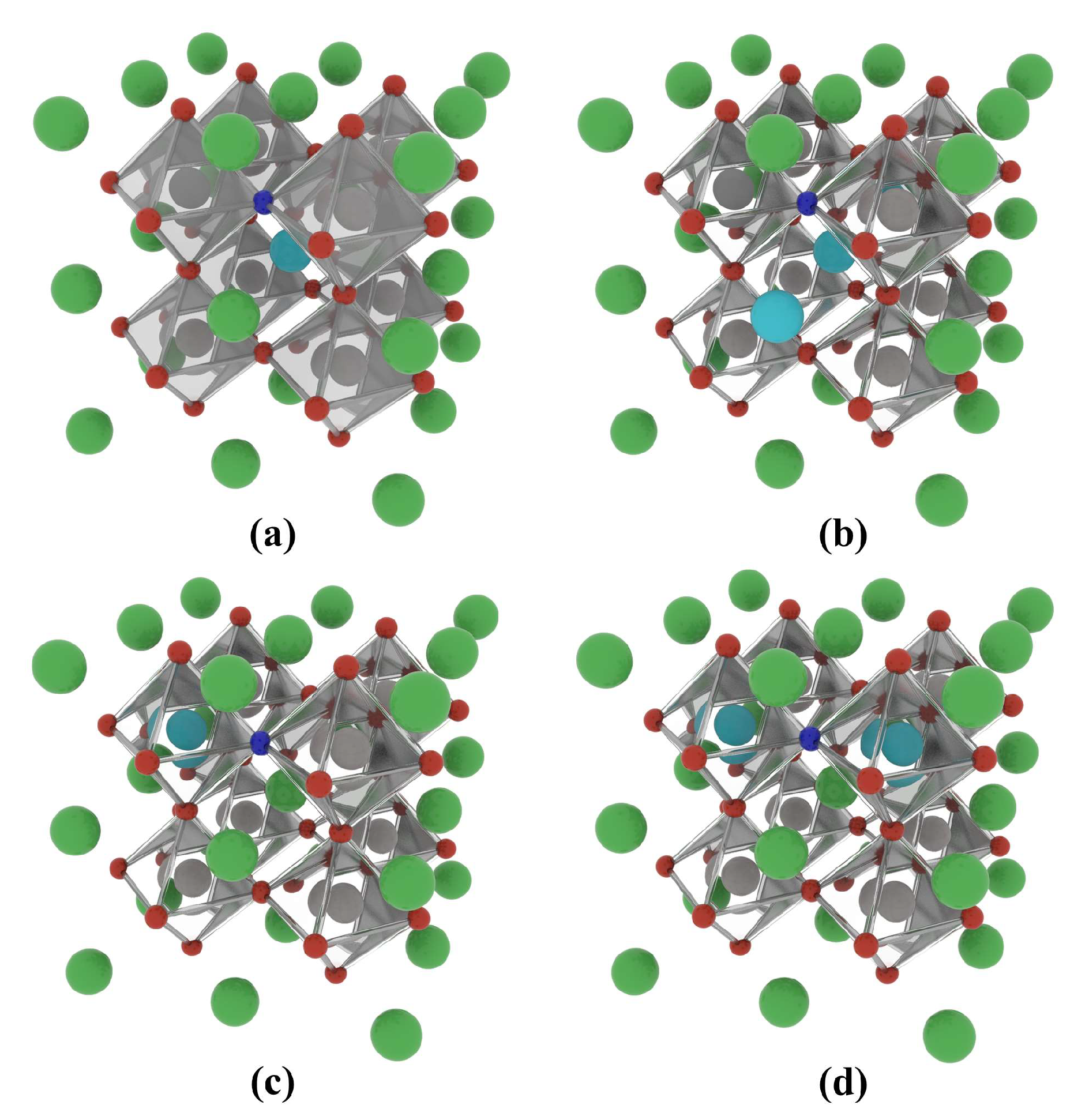
2.2. La-N Co-Doped BaTiO3
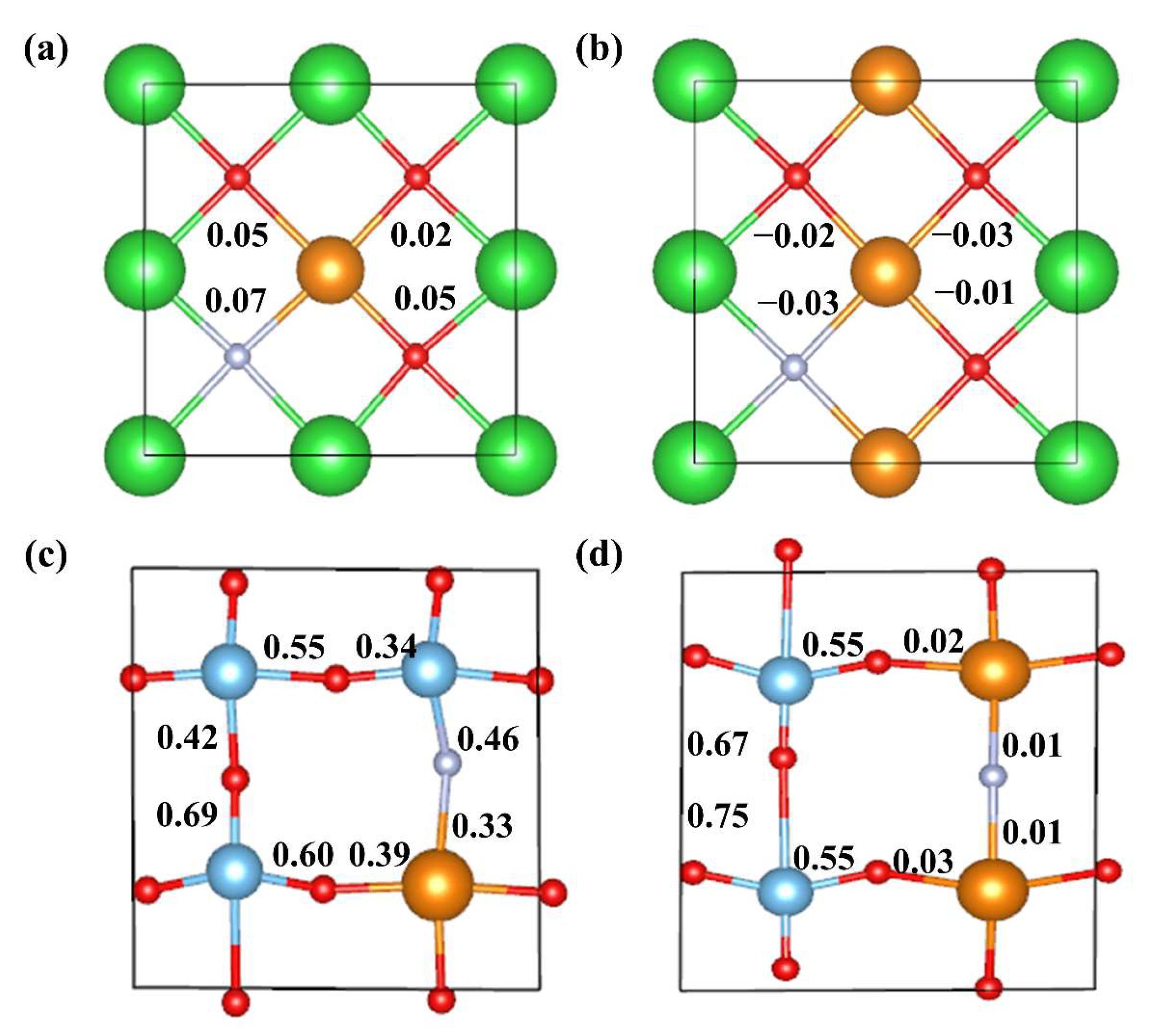
2.2.1. Formation Energy and Binding Energy
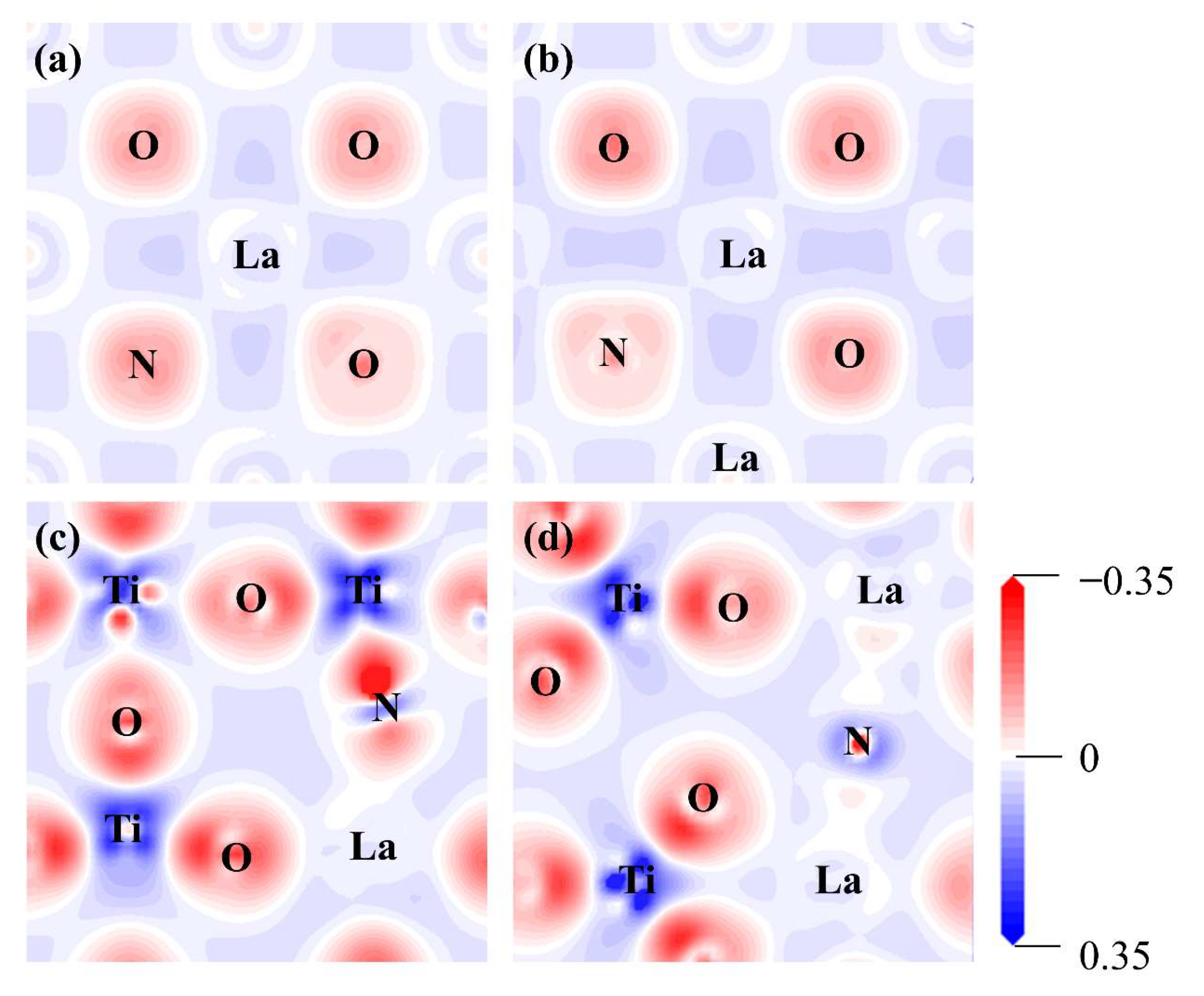
2.2.2. Electronic Structure
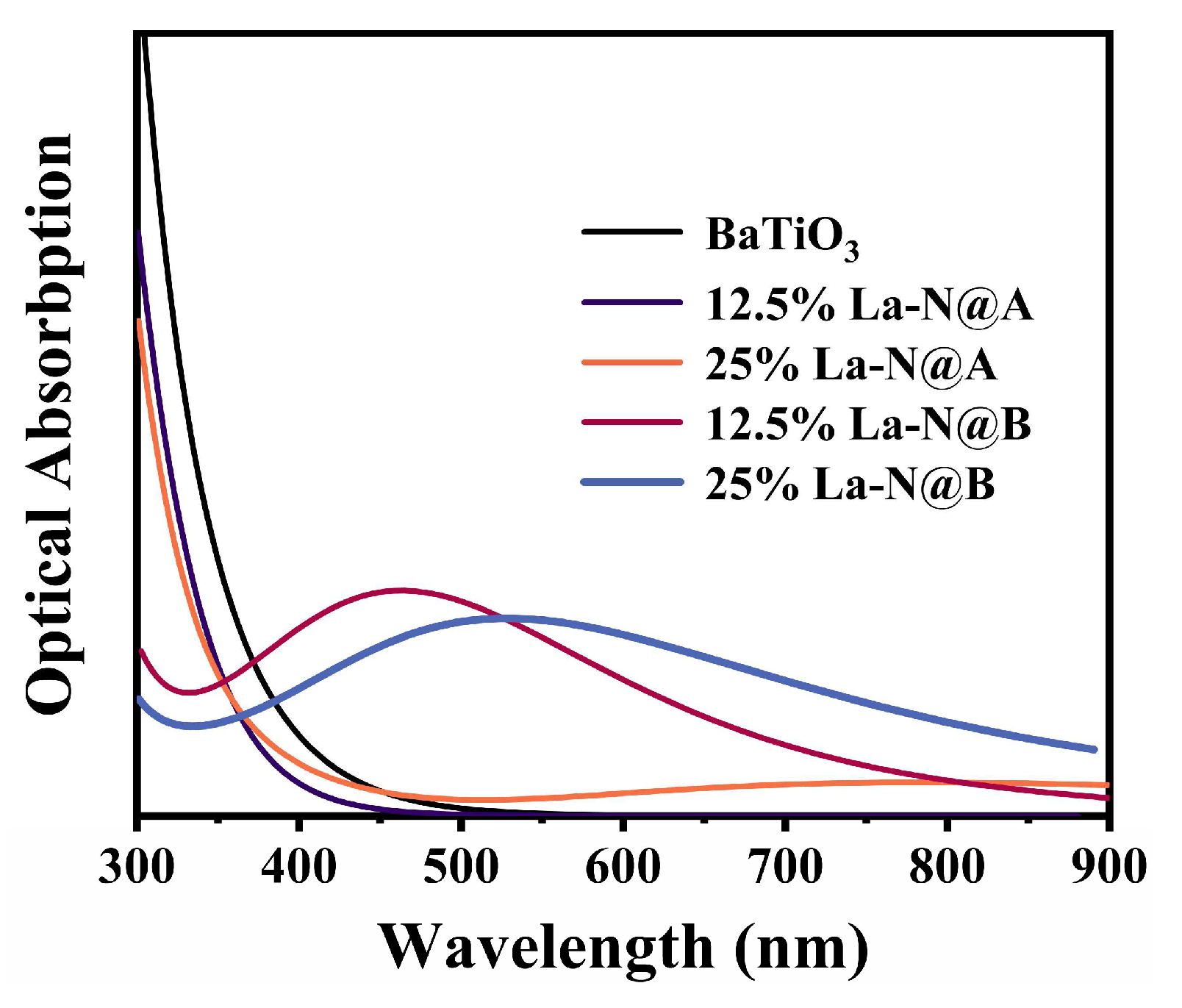
2.2.3. Optical Properties
2.2.4. Water Redox Potential
3. Calculation Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, X.; Wang, T.; Yang, P.; Zhang, G.; Gong, J. The Development of Cocatalysts for Photoelectrochemical CO2 Reduction. Adv. Mater. 2019, 31, 1804710. [Google Scholar] [CrossRef]
- Lin, B.; Li, Z. Towards World’s Low Carbon Development: The Role of Clean Energy. Appl. Energy 2022, 307, 118160. [Google Scholar] [CrossRef]
- Zhang, Z.; Nagasaki, Y.; Miyagi, D.; Tsuda, M.; Komagome, T.; Tsukada, K.; Hamajima, T.; Ayakawa, H.; Ishii, Y.; Yonekura, D. Stored Energy Control for Long-Term Continuous Operation of an Electric and Hydrogen Hybrid Energy Storage System for Emergency Power Supply and Solar Power Fluctuation Compensation. Int. J. Hydrog. Energy 2019, 44, 8403–8414. [Google Scholar] [CrossRef]
- Opoku, F.; Govender, K.K.; Van Sittert, C.G.C.E.; Govender, P.P. Recent Progress in the Development of Semiconductor-Based Photocatalyst Materials for Applications in Photocatalytic Water Splitting and Degradation of Pollutants. Adv. Sustain. Syst. 2017, 1, 1700006. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H.; Liang, J.; Luo, Y.; Chen, G.; Shi, X.; Lu, S.; Gao, S.; Hu, J.; Liu, Q.; et al. A-Site Perovskite Oxides: An Emerging Functional Material for Electrocatalysis and Photocatalysis. J. Mater. Chem. A 2021, 9, 6650–6670. [Google Scholar] [CrossRef]
- Chen, T.; Meng, J.; Wu, S.; Pei, J.; Lin, Q.; Wei, X.; Li, J.; Zhang, Z. Room Temperature Synthesized BaTiO3 for Photocatalytic Hydrogen Evolution. J. Alloys Compd. 2018, 754, 184–189. [Google Scholar] [CrossRef]
- Chakraborty, A.; Liton, M.N.H.; Sarker, M.S.I.; Rahman, M.M.; Khan, M.K.R. A Comprehensive DFT Evaluation of Catalytic and Optoelectronic Properties of BaTiO3 Polymorphs. Phys. B Condens. Matter 2023, 648, 414418. [Google Scholar] [CrossRef]
- Anitha, B.G.; Devi, L.G. Photocatalytic Activity of Fluorine Doped SrTiO3 under the Irradiation of UV/Solar Light: Extended Visible Light Absorption by the Bulk Lattice F− Ions and Suppression of Photogenerated Charge Carrier Recombination by the Surface F− Ions. Chem. Phys. Lett. 2020, 742, 137138. [Google Scholar] [CrossRef]
- Cao, J.; Ji, Y.; Tian, C.; Yi, Z. Synthesis and Enhancement of Visible Light Activities of Nitrogen-Doped BaTiO3. J. Alloys Compd. 2014, 615, 243–248. [Google Scholar] [CrossRef]
- Teng, Z.; Jiang, J.; Chen, G.; Ma, C.; Zhang, F. The Electronic Structures and Optical Properties of B, C or N Doped BaTiO3. AIP Adv. 2018, 8, 095216. [Google Scholar] [CrossRef]
- Rehman, J.U.; Rehman, M.A.; Tahir, M.B.; Hussain, A.; Iqbal, T.; Sagir, M.; Usman, M.; Kebaili, I.; Alrobei, H.; Alzaid, M. Electronic and Optical Properties of Nitrogen and Sulfur Doped Strontium Titanate as Efficient Photocatalyst for Water Splitting: A DFT Study. Int. J. Hydrog. Energy 2022, 47, 1605–1612. [Google Scholar] [CrossRef]
- Xie, P.; Yang, F.; Li, R.; Ai, C.; Lin, C.; Lin, S. Improving Hydrogen Evolution Activity of Perovskite BaTiO3 with Mo Doping: Experiments and First-Principles Analysis. Int. J. Hydrog. Energy 2019, 44, 11695–11704. [Google Scholar] [CrossRef]
- Issam, D.; Achehboune, M.; Boukhoubza, I.; Hatel, R.; El Adnani, Z.; Rezzouk, A. Investigation of the Crystal Structure, Electronic and Optical Properties of Cr-Doped BaTiO3 on the Ti Site Using First Principles Calculations. J. Phys. Chem. Solids 2023, 175, 111209. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Y.; Guo, W.; Xing, Z.; Wang, H.; Lu, Z.; Zhang, Z. First-Principles Calculations of Electronic and Optical Properties of A and B Site Substituted BaTiO3. Vacuum 2021, 193, 110530. [Google Scholar] [CrossRef]
- Martha, S.; Chandra Sahoo, P.; Parida, K.M. An Overview on Visible Light Responsive Metal Oxide Based Photocatalysts for Hydrogen Energy Production. RSC Adv. 2015, 5, 61535–61553. [Google Scholar] [CrossRef]
- Zeba, I.; Bashir, N.; Ahmad, R.; Shakil, M.; Rizwan, M.; Rafique, M.; Rashid, F.; Gillani, S.S.A. Cubic to Pseudo-Cubic Tetragonal Phase Transformation with Lithium and Beryllium Doping in CaTiO3 and Its Impact on Electronic and Optical Properties: A DFT Approach. Bull. Mater. Sci. 2020, 43, 244. [Google Scholar] [CrossRef]
- Pal, P.; Rudrapal, K.; Maji, P.; Chaudhuri, A.R.; Choudhury, D. Toward an Enhanced Room-Temperature Photovoltaic Effect in Ferroelectric Bismuth and Iron Codoped BaTiO3. J. Phys. Chem. C 2021, 125, 5315–5326. [Google Scholar] [CrossRef]
- Fadlallah, M.M.; Shibl, M.F.; Vlugt, T.J.H.; Schwingenschlögl, U. Theoretical Study on Cation Codoped SrTiO3 Photocatalysts for Water Splitting. J. Mater. Chem. A 2018, 6, 24342–24349. [Google Scholar] [CrossRef]
- Niishiro, R.; Tanaka, S.; Kudo, A. Hydrothermal-Synthesized SrTiO3 Photocatalyst Codoped with Rhodium and Antimony with Visible-Light Response for Sacrificial H2 and O2 Evolution and Application to Overall Water Splitting. Appl. Catal. B Environ. 2014, 150–151, 187–196. [Google Scholar] [CrossRef]
- Ohno, T.; Tsubota, T.; Nakamura, Y.; Sayama, K. Preparation of S, C Cation-Codoped SrTiO3 and Its Photocatalytic Activity under Visible Light. Appl. Catal. A Gen. 2005, 288, 74–79. [Google Scholar] [CrossRef]
- Kenmoe, S.; Spohr, E. Photooxidation of Water on Pristine, S- and N-Doped TiO2 (001) Nanotube Surfaces: A DFT + U Study. J. Phys. Chem. C 2019, 123, 22691–22698. [Google Scholar] [CrossRef]
- Ma, Z.-Q.; Pan, H.; Wang, Z.-S.; Wong, P.K. Effects of Non-Metal Dopants and Defects on Electronic Properties of Barium Titanate as Photocatalyst. Int. J. Hydrog. Energy 2015, 40, 4766–4776. [Google Scholar] [CrossRef]
- Akhtar, S.; Alay-e-Abbas, S.M.; Abbas, S.M.G.; Arshad, M.I.; Batool, J.; Amin, N. First-Principles Evaluation of Electronic and Optical Properties of (Mo, C) Codoped BaHfO3 for Applications in Photocatalysis. J. Appl. Phys. 2018, 123, 161569. [Google Scholar] [CrossRef]
- Bentour, H.; Belasfar, K.; Boujnah, M.; El Yadari, M.; Benyoussef, A.; El Kenz, A. DFT Study of Se/Mn and Te/Mn Codoped SrTiO3 for Visible Light-Driven Photocatlytic Hydrogen Production. Opt. Mater. 2022, 129, 112431. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Lian, W.; Liu, Y. Insight into the Enhanced Photocatalytic Activity of Mo and P Codoped SrTiO3 from First-Principles Prediction. RSC Adv. 2020, 10, 40117–40126. [Google Scholar] [CrossRef] [PubMed]
- Amaechi, I.C.; Hadj Youssef, A.; Rawach, D.; Claverie, J.P.; Sun, S.; Ruediger, A. Ferroelectric Fe–Cr Codoped BaTiO3 Nanoparticles for the Photocatalytic Oxidation of Azo Dyes. ACS Appl. Nano Mater. 2019, 2, 2890–2901. [Google Scholar] [CrossRef]
- Qin, Y.; Fang, F.; Xie, Z.; Lin, H.; Zhang, K.; Yu, X.; Chang, K. La, Al-Codoped SrTiO3 as a Photocatalyst in Overall Water Splitting: Significant Surface Engineering Effects on Defect Engineering. ACS Catal. 2021, 11, 11429–11439. [Google Scholar] [CrossRef]
- Purkayastha, M.D.; Singh, N.; Darbha, G.K.; Majumder, T.P. Strain Influence on the Structural Properties of Nitrogen and Fluorine Codoped TiO2. Optik 2020, 206, 164029. [Google Scholar] [CrossRef]
- Fo, Y.; Ma, Y.; Dong, H.; Zhou, X. Tuning the Electronic Structure of BaTiO3 for an Enhanced Photocatalytic Performance Using Cation–Anion Codoping: A First-Principles Study. New J. Chem. 2021, 45, 8228–8239. [Google Scholar] [CrossRef]
- Yang, K.; Dai, Y.; Huang, B. Review of First-Principles Studies of TiO2: Nanocluster, Bulk, and Material Interface. Catalysts 2020, 10, 972. [Google Scholar] [CrossRef]
- Zulfiqar, W.; Alay-e-Abbas, S.M. Improved Thermodynamic Stability and Visible Light Absorption in Zr + X Codoped (X = S, Se and Te) BaTiO3 Photocatalysts: A First-Principles Study. Mater. Today Commun. 2022, 32, 103867. [Google Scholar] [CrossRef]
- Miyauchi, M.; Takashio, M.; Tobimatsu, H. Photocatalytic Activity of SrTiO3 Codoped with Nitrogen and Lanthanum under Visible Light Illumination. Langmuir 2004, 20, 232–236. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Jiang, N.; Xu, S.; Li, Z.; Liu, X.; Cheng, T.; Han, A.; Lv, H.; Sun, W.; Hou, Y. Towards High Visible Light Photocatalytic Activity in Rare Earth and N Co-Doped SrTiO3: A First Principles Evaluation and Prediction. RSC Adv. 2017, 7, 16282–16289. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, H.; Inoue, T.; Yao, Q. Highly Active SrTiO3 for Visible Light Photocatalysis: A First-Principles Prediction. Solid State Commun. 2014, 181, 5–8. [Google Scholar] [CrossRef]
- Gao, H.; Cao, J.; Liu, L.; Yang, Y. Theoretical Investigation on the Structure and Electronic Properties of Barium Titanate. J. Mol. Struct. 2011, 1003, 75–81. [Google Scholar] [CrossRef]
- Hasan, M.; Akther Hossain, A.K.M. Structural, Electronic and Optical Properties of Strontium and Nickel Co-Doped BaTiO3: A DFT Based Study. Comput. Condens. Matter 2021, 28, e00578. [Google Scholar] [CrossRef]
- Ravel, B.; Stern, E.A.; Vedrinskii, R.I.; Kraizman, V. Local Structure and the Phase Transitions of BaTiO3. Ferroelectrics 1998, 206, 407–430. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Wang, Y.; Zhang, X.; Fan, Y.; Liu, Y.; Yi, Z. Role of P in Improving V-Doped SrTiO3 Visible Light Photocatalytic Activity for Water Splitting: A First—Principles Study. Int. J. Hydrog. Energy 2021, 46, 20492–20502. [Google Scholar] [CrossRef]
- Van De Walle, C.G.; Neugebauer, J. First-Principles Calculations for Defects and Impurities: Applications to III-Nitrides. J. Appl. Phys. 2004, 95, 3851–3879. [Google Scholar] [CrossRef]
- Rizwan, M.; Zeba, I.; Shakil, M.; Gillani, S.S.A.; Usman, Z. Electronic, Structural and Optical Properties of BaTiO3 Doped with Lanthanum (La): Insight from DFT Calculation. Optik 2020, 211, 164611. [Google Scholar] [CrossRef]
- Naz, A.; Aldaghfag, S.A.; Yaseen, M.; Butt, M.K.; Kashif, M.; Zahid, M.; Mubashir, S.; Somaily, H.H. Investigation of Ce Doped BaTiO3 Compound for Optoelectronic Devices. Phys. B Condens. Matter 2022, 631, 413714. [Google Scholar] [CrossRef]
- Saleem, S.; Ishfaq, M.; Aldaghfag, S.A.; Sajid, M.; Yaseen, M. DFT Insight into Magnetoelectronic and Optical Properties of Mo-Modified BaTiO3. Phys. B Condens. Matter 2023, 667, 415163. [Google Scholar] [CrossRef]
- Yang, F.; Yang, L.; Ai, C.; Xie, P.; Lin, S.; Wang, C.-Z.; Lu, X. Tailoring Bandgap of Perovskite BaTiO3 by Transition Metals Co-Doping for Visible-Light Photoelectrical Applications: A First-Principles Study. Nanomaterials 2018, 8, 455. [Google Scholar] [CrossRef]
- Pitriana, P.; Wungu, T.D.K.; Hidayat, R. The Characteristics of Band Structures and Crystal Binding in All-Inorganic Perovskite APbBr3 Studied by the First Principle Calculations Using the Density Functional Theory (DFT) Method. Results Phys. 2019, 15, 102592. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic Population Analysis on LCAO–MO Molecular Wave Functions. II. Overlap Populations, Bond Orders, and Covalent Bond Energies. J. Chem. Phys. 1955, 23, 1841–1846. [Google Scholar] [CrossRef]
- Wen, Y.; Wang, L.; Liu, H.; Song, L. Ab Initio Study of the Elastic and Mechanical Properties of B19TiAl. Crystals 2017, 7, 39. [Google Scholar] [CrossRef]
- Ali, M.L.; Khan, M.; Al Asad, M.A.; Rahaman, M.Z. Highly Efficient and Stable Lead-Free Cesium Copper Halide Perovskites for Optoelectronic Applications: A DFT Based Study. Heliyon 2023, 9, e18816. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, R.; Zhu, G.; Li, G.; Cao, Y. A DFT Study on the Effect of Lattice Defects on the Electronic Structures and Floatability of Spodumene. Phys. B Condens. Matter 2024, 676, 415657. [Google Scholar] [CrossRef]
- Barman, P.; Rahman, M.F.; Islam, M.R.; Hasan, M.; Chowdhury, M.; Hossain, M.K.; Modak, J.K.; Ezzine, S.; Amami, M. Lead-Free Novel Perovskite Ba3AsI3: First-Principles Insights into Its Electrical, Optical, and Mechanical Properties. Heliyon 2023, 9, e21675. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Duan, H.; Wang, B.; Han, C.; Wei, D. The Adsorption Mechanism of Calcium Ion on Quartz (101) Surface: A DFT Study. Powder Technol. 2018, 329, 158–166. [Google Scholar] [CrossRef]
- Wang, M.M.; Wang, C.; Liu, Y.; Zhou, X. Hybrid density functional theory description of non-metal doping in perovskite BaTiO3 for visible-light photocatalysis. J. Solid State Chem. 2019, 280, 121018. [Google Scholar] [CrossRef]
- Huang, H.-C.; Yang, C.-L.; Wang, M.-S.; Ma, X.-G. Chalcogens Doped BaTiO3 for Visible Light Photocatalytic Hydrogen Production from Water Splitting. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 208, 65–72. [Google Scholar] [CrossRef] [PubMed]
- Yin, W.J.; Wei, S.H.; Al-Jassim, M.M. Double-hole-mediated coupling of dopants and its impact on band gap engineering in TiO2. Phys. Rev. Lett. 2011, 106, 066801. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Wang, Y.; Jia, Y.; Yan, W.; Li, Q.; Zhou, J.; Wu, K. Engineering the Electronic Structure Towards Visible Lights Photocatalysis of CaTiO3 Perovskites by Cation (La/Ce)-Anion (N/S) Co-doping: A First-Principles Study. Molecules 2023, 28, 7134. [Google Scholar] [CrossRef] [PubMed]
- Modak, B. An Efficient Strategy to Enhance the Photocatalytic Activity of Ir-Doped SrTiO3: A Hybrid DFT Approach. New J. Chem. 2022, 46, 1507–1515. [Google Scholar] [CrossRef]
- Zhu, W.; Qiu, X.; Iancu, V.; Chen, X.-Q.; Pan, H.; Wang, W.; Dimitrijevic, N.M.; Rajh, T.; Meyer, H.M.; Paranthaman, M.P.; et al. Band Gap Narrowing of Titanium Oxide Semiconductors by Noncompensated Anion-Cation Codoping for Enhanced Visible-Light Photoactivity. Phys. Rev. Lett. 2009, 103, 226401. [Google Scholar] [CrossRef] [PubMed]
- Gai, Y.; Li, J.; Li, S.-S.; Xia, J.-B.; Wei, S.-H. Design of Narrow-Gap TiO2: A Passivated Codoping Approach for Enhanced Photoelectrochemical Activity. Phys. Rev. Lett. 2009, 102, 036402. [Google Scholar] [CrossRef]
- Yin, W.-J.; Tang, H.; Wei, S.-H.; Al-Jassim, M.M.; Turner, J.; Yan, Y. Band structure engineering of semiconductors for enhanced photoelectrochemical water splitting: The case of TiO2. Phys. Rev. B 2010, 82, 045106. [Google Scholar] [CrossRef]
- Weber, D.; Marisa, C.; Marcelo, A.; Renan, A.; Ariadne, C.; Marcio, D.; Gilmar, E.; Mário, G.; Elson, L.; Maria, F. Unraveling the relationship between bulk structure and exposed surfaces and its effect on the electronic structure and photoluminescent properties of Ba0.5Sr0.5TiO3: A joint experimental and theoretical approach. Mater. Res. Bull. 2021, 143, 111442. [Google Scholar]
- Gajdoš, M.; Hummer, K.; Kresse, G.; Furthmüller, J.; Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 2006, 73, 045112. [Google Scholar] [CrossRef]
- Shi, W.J.; Xiong, S.J. Ab initio study on band-gap narrowing in SrTiO3 with Nb–C–Nb cooping. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 84, 1541–1545. [Google Scholar] [CrossRef]
- Mishra, V.; Sagdeo, A.; Kumar, V.; Warshi, M.K.; Rai, H.M.; Saxena, S.K.; Roy, D.R.; Mishra, V.; Kumar, R.; Sagdeo, P.R. Electronic and Optical Properties of BaTiO3 across Tetragonal to Cubic Phase Transition: An Experimental and Theoretical Investigation. J. Appl. Phys. 2017, 122, 065105. [Google Scholar] [CrossRef]
- Jin, Y.; Yu, V.W.; Govoni, M.; Xu, A.C.; Galli, G. Excited State Properties of Point Defects in Semiconductors and Insulators Investigated with Time-Dependent Density Functional Theory. J. Chem. Theory Comput. 2023, 19, 8689–8705. [Google Scholar] [CrossRef] [PubMed]
- Basera, P.; Saini, S.; Bhattacharya, S. Self Energy and Excitonic Effect in (Un)Doped TiO2 Anatase: A Comparative Study of Hybrid DFT, GW and BSE to Explore Optical Properties. J. Mater. Chem. C 2019, 7, 14284–14293. [Google Scholar] [CrossRef]
- Matta, S.K.; Liao, T.; Russo, S.P. New Janus Structure Photocatalyst Having Widely Tunable Electronic and Optical Properties with Strain Engineering. J. Mater. Sci. Technol. 2023, 155, 142–147. [Google Scholar] [CrossRef]
- Usman, M.; Rehman, J.U.; Tahir, M.B.; Hussain, A. First-Principles Calculations to Investigate the Effect of Cs-Doping in BaTiO3 for Water-Splitting Application. Solid State Commun. 2022, 355, 114920. [Google Scholar] [CrossRef]
- Sikam, P.; Moontragoon, P.; Sararat, C.; Karaphun, A.; Swatsitang, E.; Pinitsoontorn, S.; Thongbai, P. DFT Calculation and Experimental Study on Structural, Optical and Magnetic Properties of Co-Doped SrTiO3. Appl. Surf. Sci. 2018, 446, 92–113. [Google Scholar] [CrossRef]
- Sanna, S.; Thierfelder, C.; Wippermann, S.; Sinha, T.P.; Schmidt, W.G. Barium Titanate Ground- and Excited-State Properties from First-Principles Calculations. Phys. Rev. B 2011, 83, 054112. [Google Scholar] [CrossRef]
- Han, S.; Li, Y.; Wang, Z. PtSe2/SiH van Der Waals Type-II Heterostructure: A High Efficiency Photocatalyst for Water Splitting. Phys. Chem. Chem. Phys. 2020, 22, 17145–17151. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Wang, Z.; Zhang, Z. Homogeneous and heterogeneous reaction mechanisms and kinetics of mercury oxidation in coal-fired flue gas with bromine addition. Proc. Combust. Inst. 2017, 36, 4039–4049. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Setyawan, W.; Curtarolo, S. High-Throughput Electronic Band Structure Calculations: Challenges and Tools. Comput. Mater. Sci. 2010, 49, 299–312. [Google Scholar] [CrossRef]
- Derkaoui, I.; Achehboune, M.; Boukhoubza, I.; El Adnani, Z.; Rezzouk, A. Improved First-Principles Electronic Band Structure for Cubic (Pm3m) and Tetragonal (P4mm, P4/Mmm) Phases of BaTiO3 Using the Hubbard U Correction. Comput. Mater. Sci. 2023, 217, 111913. [Google Scholar] [CrossRef]
- Laurita, G.; Page, K.; Suzuki, S.; Seshadri, R. Average and local structure of the Pb-free ferroelectric perovskites (Sr, Sn)TiO3 and (Ba, Ca, Sn)TiO3. Phys. Rev. B 2015, 9, 214109. [Google Scholar] [CrossRef]
- Chandrappa, S.; Myakala, S.N.; Koshi, N.A.; Galbao, S.J.; Lee, S.-C.; Bhattacharjee, S.; Eder, D.; Cherevan, A.; Murthy, D.H.K. Unveiling Valence State-Dependent Photocatalytic Water Splitting Activity and Photocathodic Behavior in Visible Light-Active Iridium-Doped BaTiO3. ACS Appl. Mater. Interfaces 2024, 16, 8763–8771. [Google Scholar] [CrossRef] [PubMed]
- Uma, P.I.; Shenoy, U.S.; Bhat, D.K. Electronic Structure Engineering of BaTiO3 Cuboctahedrons by Doping Copper to Enhance the Photocatalytic Activity for Environmental Remediation. J. Alloys Compd. 2023, 948, 169600. [Google Scholar] [CrossRef]
- Goumri-Said, S.; Kanoun, M.B. Insight into the Effect of Anionic–Anionic Co-Doping on BaTiO3 for Visible Light Photocatalytic Water Splitting: A First-Principles Hybrid Computational Study. Catalysts 2022, 12, 1672. [Google Scholar] [CrossRef]






| Model | Ba | Ti | O | La | N |
|---|---|---|---|---|---|
| OPT | 1.57 | 2.17 | −1.25 | - | - |
| La@A | 1.56 | 2.10 | −1.24 | 2.14 | - |
| La@B | 1.57 | 2.18 | −1.24 | 2.04 | - |
| N@O | 1.57 | 2.17 | −1.25 | - | −1.22 |
| Model | Eb (eV) |
|---|---|
| OPT | - |
| 12.5%La-N@A | 1.86 |
| 25%La-N@A | 1.41 |
| 12.5%La-N@B | −15.19 |
| 25%La-N@B | −15.59 |
| Model | Ba | Ti | O | La | N |
| OPT | 1.57 | 2.17 | −1.25 | - | - |
| 12.5%La-N@A | 1.57 | 2.15 | −1.26 | 2.12 | −1.44 |
| 25%La-N@A | 1.57 | 2.11 | −1.12 | 2.10 | −1.45 |
| 12.5%La-N@B | 1.56 | 2.14 | −1.23 | 2.05 | −1.17 |
| 25%La-N@B | 1.48 | 2.18 | −1.22 | 2.06 | −1.09 |
| Calculation Methods | Bandgap of Pristine BaTiO3 (eV) |
| CBM-VBM | 2.000 |
| HOMO-LOMO | 2.298 |
| Tauc plot | 3.790 |
| Experimental measurement [68] | 3.200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhou, Q.; Zhang, Q.; Ren, Y.; Cui, K.; Cheng, C.; Wu, K. Effects of La-N Co-Doping of BaTiO3 on Its Electron-Optical Properties for Photocatalysis: A DFT Study. Molecules 2024, 29, 2250. https://doi.org/10.3390/molecules29102250
Wang Y, Zhou Q, Zhang Q, Ren Y, Cui K, Cheng C, Wu K. Effects of La-N Co-Doping of BaTiO3 on Its Electron-Optical Properties for Photocatalysis: A DFT Study. Molecules. 2024; 29(10):2250. https://doi.org/10.3390/molecules29102250
Chicago/Turabian StyleWang, Yang, Qinyan Zhou, Qiankai Zhang, Yuanyang Ren, Kunqi Cui, Chuanhui Cheng, and Kai Wu. 2024. "Effects of La-N Co-Doping of BaTiO3 on Its Electron-Optical Properties for Photocatalysis: A DFT Study" Molecules 29, no. 10: 2250. https://doi.org/10.3390/molecules29102250
APA StyleWang, Y., Zhou, Q., Zhang, Q., Ren, Y., Cui, K., Cheng, C., & Wu, K. (2024). Effects of La-N Co-Doping of BaTiO3 on Its Electron-Optical Properties for Photocatalysis: A DFT Study. Molecules, 29(10), 2250. https://doi.org/10.3390/molecules29102250







