Next Article in Journal
Preparation of Dye Semiconductors via Coupling Polymerization Catalyzed by Two Catalysts and Application to Transistor
Previous Article in Journal
Antiallergic Activity of 3-O-Dodecyl-l-ascorbic Acid
Previous Article in Special Issue
Highly Substituted 10-RO-(hetero)acenes—Electric Properties of Vacuum-Deposited Molecular Films
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 29
Issue 1
10.3390/molecules29010070
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

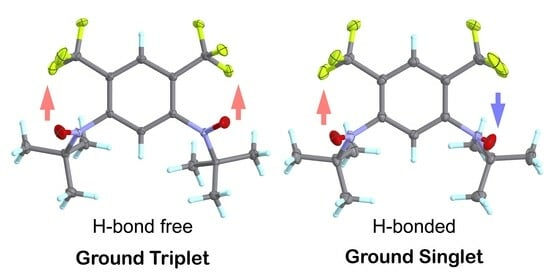
A Triplet/Singlet Ground-State Switch via the Steric Inhibition of Conjugation in 4,6-Bis(trifluoromethyl)-1,3-phenylene Bisnitroxide

by
Nagito Haga
and
Takayuki Ishida
*
Department of Engineering Science, The University of Electro-Communications, Chofu 182-8585, Tokyo Prefecture, Japan
*
Author to whom correspondence should be addressed.
Molecules 2024, 29(1), 70; https://doi.org/10.3390/molecules29010070
Submission received: 30 October 2023 / Revised: 12 December 2023 / Accepted: 19 December 2023 / Published: 21 December 2023
(This article belongs to the Special Issue Computational Studies of Novel Function Materials)
Browse Figures
Versions Notes

Abstract

:
Ground triplet 4,6-bis(trifluoromethyl)-1,3-phenylene bis(tert-butyl nitroxide) (TF2PBN) reacted with [Y(hfac)3(H2O)2] (hfac = 1,1,1,5,5,5-hexafluoropentane-2,4-dionate), affording a doubly hydrogen-bonded adduct [Y(hfac)3(H2O)2(TF2PBN)]. The biradical was recovered from the adduct through recrystallization. Crystallographic analysis indicates that the torsion angles (|θ| ≤ 90°) between the benzene ring and nitroxide groups were 74.9 and 84.8° in the adduct, which are larger than those of the starting material TF2PBN. Steric congestion due to o-trifluoromethyl groups gives rise to the reduction of π-conjugation. Two hydrogen bonds enhance this deformation. Susceptometry of the adduct indicates a ground singlet with 2J/kB = −128(2) K, where 2J corresponds to the singlet–triplet gap. The observed magneto-structure relation is qualitatively consistent with Rajca’s pioneering work. A density functional theory calculation at the UB3LYP/6-311+G(2d,p) level using the atomic coordinates determined provided a result of 2J/kB = −162.3 K for the adduct, whilst the corresponding calculation on intact TF2PBN provided +87.2 K. After a comparison among a few known compounds, the 2J vs. |θ| plot shows a negative slope with a critical torsion of 65(3)°. The ferro- and antiferromagnetic coupling contributions are balanced in TF2PBN, being responsible for ground-state interconversion by means of small structural perturbation like hydrogen bonds.

Graphical Abstract

1. Introduction

Coordination compounds provide us a great opportunity for the development of spin-related functional materials [1,2,3,4,5]. Rational design, chemical modification, and physical modulation, etc. have attracted great attention to magnetic materials controlled by external stimuli [6,7]. To apply ground triplet biradicals and ground high-spin oligoradicals to materials chemistry [8,9,10,11,12,13,14,15,16], the choice of radical species is crucial. It has been theoretically and experimentally clarified that 1,3-phenylene-bridges serve as a robust ferromagnetic coupler in the context of the spin-polarization mechanism or topological rule [4,5,11,12,13,14,15,16,17,18,19]. Triphenylmethyls and diphenylcarbenes are the most popular paramagnetic centers in this research field, but heteroatomic ones can also be utilized as a spin source [17,18,19,20,21,22]. Nitroxides or aminoxyls are persistent radicals and are available for various aspects in chemistry, physics, and biology [20,21,22,23] thanks to the stability achieved through the resonance of the following canonical formulas: R1–N(–O•)–R2←→R1–N+•(–O–)–R2. The non-bonding molecular orbital (NBMO) belongs to a π* symmetry and has comparable contributions from N and O atomic orbitals. The nitroxide oxygen atom can participate in hydrogen (H) bonds [24] as well as coordination bonds [1,2,3,4,5] and is reasonably understood from the latter canonical formula.
There are two typical ways to stabilize organic radicals [25,26]. Bulky substituents will raise the energy level of a transition state and decrease the reaction rate, which is comprehended in terms of steric protection or kinetic persistency. π-Conjugated substituents will suppress the energy level of a reactant due to spin delocalization, often called the resonance effect or thermodynamic stability. Aromatic substituents usually have both contributions. The biphenyl-3,5-diyl bis(tert-butyl nitroxide) (BPBN) biradical and several related derivatives [27,28,29] (Scheme 1a) have enough persistency to be isolated under ambient conditions. They seem to be promising for the development of 2p, 2p-3d, and 2p-4f homo-/heterospin magnets. However, decomposition reactions of BPBNs have also been reported during further chemical reactions [30,31,32]. As for bulky aliphatic groups, 5-tert-butyl-1,3-phenylene bis(tert-butyl nitroxide), tBuPBN [33] (Scheme 1a), appears to be another attractive candidate with improved persistency and has actually been applied in coordination chemistry [34,35].
The sterically protecting groups of BPBN and tBuPBN, peripheral aryl and tert-butyl substituents, are located at the m-position with respect to the nitroxide groups. On the other hand, 4,6-bis(trifluoromethyl)-1,3-phenylene bis(tert-butyl nitroxide) (TF2PBN, Scheme 1a), originally synthesized by Rajca et al. [36], takes advantage of the o- and p-positions. This structural feature will enhance effective protection and, accordingly, persistency. In fact, it can be isolated and manipulated under ambient aerobic conditions. Furthermore, TF2PBN was reported to have triplet spin multiplicity at the ground state [36,37]. These characters seem to be suitable for magnetism-based materials chemistry. A methyl group at the o- or p-position is reported to destabilize phenyl nitroxides owing to a hydrogen abstraction producing quinoid compounds [32]. Thus, the roles of methyl and trifluoromethyl groups are strikingly different from each other in nitroxide chemistry.
We found that TF2PBN reacted with [Y(hfac)3(H2O)2] (hfac = 1,1,1,5,5,5-hexafluoropentane-2,4-dionate) [38] to produce a supramolecular discrete adduct, [Y(hfac)3(H2O)2(TF2PBN)] (abbreviated as 1 hereafter; Scheme 1b). The TF2PBN and [Y(hfac)3(H2O)2] portions are connected only with double H bonds and not coordination bonds. There is a 12-membered ring which seems to be rather rare in chelate chemistry, to our knowledge. Since Y3+ is diamagnetic, the present study is attributed to a research on genuine organic magnetism. Rajca and co-workers have already reported [Mn(hfac)2(TF2PBN)2] coordination compounds [37]. The nitroxide oxygen atoms are directly coordinated to the Mn2+ center, giving rise to considerable 2p-3d exchange coupling. Interestingly, the m-phenylene bridge was assumed to play the role of an antiferromagnetic coupler. In comparison with Rajca’s work, the present compound has an advantage in the unequivocal analysis of the exchange interaction in a ligand. In this report, we attempt to construct a framework for predicting J from the molecular structure and tuning J by structural deformation after conducting detailed structural and magnetic analyses of 1 together with related compounds.

2. Materials and Methods

The following procedure for the preparation of 1 is typical. After [Y(hfac)3(H2O)2] [38] (74.9 mg; 0.104 mmol) was dissolved in heptane (10 mL) at 90 °C, the resultant solution was combined with a dichloromethane solution (1 mL) containing TF2PBN [37] (38.4 mg; 0.0995 mmol) at room temperature. After 5 days, orange polycrystals of 1 and unchanged colorless [Y(hfac)3(H2O)2] were both precipitated; they were collected on a filter, washed, and air-dried. The total mass was 17.0 mg. IR (neat, attenuated total reflection) 3473, 3260, 3151, 2990, 1649, 1619, 1566, 1539, 1474, 1328, 1253, 1226, 1204, 1138, 1100, 1062, 953, 919, 808, 743, 662 cm−1. Anal. Calcd. for C47.5H34.7N2O18.8F43.8Y2.1 ([Y(hfac)3(H2O)2(TF2PBN)]· [Y(hfac)3(H2O)2]1.1: C, 29.21; H, 1.79; N, 1.43%. Found: C, 28.35; H, 1.56; N, 1.98%. On the basis of the elemental and magnetic analysis, the yield of 1 was estimated to be 8.8%. M.p. 123 °C (decomp.).
The above orange product was recrystallized from ethanol. Recovered red crystals were determined to be identical to the starting material TF2PBN, as confirmed by means of IR spectroscopy and a single-crystal X-ray diffraction analysis.
X-ray diffraction data of a single crystal of 1 and [Y(hfac)3(H2O)2] recovered from the above reaction were recorded on a Rigaku XtaLAB Synergy R HyPix diffractometer with graphite monochromated Mo Kα radiation (λ = 0.71073 Å) at 100 K. The hkl and intensity data were extracted using CrysAlisPro [39]. The structure was solved directly and expanded using Fourier techniques in the Olex2 program [40]. Hydrogen atoms were located at calculated positions. The parameters were refined using Shelxl [41]. Disorder models were applied to three CF3 groups in the [Y(hfac)3(H2O)2] moiety in 1 and to all CF3 groups in [Y(hfac)3(H2O)2]. The crystal data of 1 are as follows: C31H27N2O10F24Y, triclinic, P 1 ¯ , a = 11.8139(2), b = 11.8703(2), c = 16.8620(3) Å, α = 79.8250(10), β = 84.9680(10), γ = 66.348(2)°, V = 2131.57(7) Å3, Z = 2, dcalc = 1.764 g cm−3, μ(Mo Kα) = 1.527 mm−1, Rint = 0.0201, R1(I > 2σ(I)) = 0.0295, Rw(all data) = 0.0804, and GOF = 1.040 at 99.9(3) K with 11,851 independent reflections. Selected bond distances and angles are listed in Table 1. The crystal data of [Y(hfac)3(H2O)2] are as follows: C15H7F18O8Y, triclinic, P 1 ¯ , a = 9.9136(4), b = 11.5271(4), c = 12.3329(4) Å, α = 67.952(3), β = 73.764(3), γ = 75.973(3)°, V = 1239.13(9) Å3, Z = 2, dcalc = 2.000 g cm−3, μ(Mo Kα) = 2.528 mm−1, Rint = 0.0179, R1(I > 2σ(I)) = 0.0299, Rw(all data) = 0.0720, and GOF = 1.031 at 100.0(1) K with 6556 independent reflections. The experimental details and full geometrical parameter tables can be obtained using the CCDC reference numbers 2301482 and 2303226 for 1 and [Y(hfac)3(H2O)2], respectively. Powder X-ray diffraction (PXRD) data were recorded on a Rigaku SmartLab diffractometer using Cu Kα radiation (λ = 1.54178 Å) at room temperature.
The magnetic susceptibilities of TF2PBN and 1 were measured on a Quantum Design MPMS3 SQUID magnetometer. The data were acquired at 0.5 T in a temperature range from 1.8 to 300 K. The magnetic responses were corrected with diamagnetic blank data of a gelatin capsule sample holder measured separately, and a further diamagnetic contribution was estimated from Pascal’s constants [42].
Density functional theory (DFT) calculations on TF2PBN, 1, and related known compounds MO2PBN, BrMO2PBN, and MesBN (see below) were carried out using Gaussian16 Revision C.01 [43]. For molecular structures, see the Results section. The broken symmetry method [44,45,46] and the unrestricted B3LYP theory were applied to the basis sets of lanl2dz for Y and 6-311+G(2d,p) for other elements. Self-consistent field energies were calculated using the experimentally determined coordinates. In the spin Hamiltonian provided as Equation (1), the exchange coupling parameter was reduced using Yamaguchi’s equation (Equation (2)) [47,48].
H ^ = − 2 J S ^ 1 · S ^ 2
J = E B S L S − E H S     S ^ 2 H S − S ^ 2 B S L S      

3. Results

3.1. Synthesis and Structural Analysis

The adduct, [Y(hfac)3(H2O)2(TF2PBN)] (1), was obtained by simply mixing the two starting materials. The product is completely stable below at least the melting point (123 °C (decomp.)) under ambient conditions. It should also be noted that no degradation was observed, unlike the BPBN case [30,31]. An IR absorption appeared around 3260 cm−1 after adduct formation, which can be assigned to H-bonded O-H stretching [49]. The reaction product was afforded as a mixture of 1 and the starting material, [Y(hfac)3(H2O)2], with a molar ratio 1/1.1, as evidenced by the elemental and IR spectroscopic analyses as well as the powder X-ray diffraction study (see below). The impurity, [Y(hfac)3(H2O)2], was present as a mixture at a crystalline level. Biradical TF2PBN can be recovered from 1 via recrystallization from ethanol. This finding indicates that not only are the present H bonds weak but also that the ground-state interconversion is reversible.
Figure 1a,b display the X-ray crystal structure of 1, and experimental and simulated powder X-ray diffraction results are also shown in Figure 1c. No lattice solvent molecules are involved. The positions of three hfac groups cannot be symmetrically arranged and, accordingly, the two nitroxide groups are unequal. Double H bonds can be found in O1⋯H9A–O9 and O2⋯H10A–O10. The O1⋯O9 and O2⋯O10 distances are 2.70552(6) and 2.72070(5) Å, respectively. The N1–O1⋯O9 and N2–O2⋯O10 angles are 113.1067(13) and 123.2740(12)°, respectively, and the O1⋯O9–Y1 and O2⋯O10–Y1 angles are 141.6666(8) and 136.1056(13)°, respectively, being consistent with the H bond angles. The adduct molecule is discrete and magnetically isolated because the peripheral trifluoromethyl and tert-butyl groups bring about only a weak van der Waals interaction.
The N1–O1 and N2–O2 bond lengths in 1 are 1.2842(16) and 1.2850(16) Å, respectively, typical of nitroxide radicals [50]. Now, we compare the geometries between the intact TF2PBN molecule [36] and the TF2PBN moiety in 1 (Table 1). The geometrical parameters of the TF2PBN portion in [Mn(hfac)2(TF2PBN)2] [37] are also included in Table 1. All the geometrical parameters are quite similar to each other except for the torsion angles along O–N–Cα(Ar)–Cβ(Ar) and the intramolecular O1⋯O2 distance. The torsion angles of TF2BN in 1 are closer to the right angle than those of the intact TF2PBN and the TF2PBN moiety in [Mn(hfac)2(TF2PBN)2], and the O1⋯O2 distance in 1 is the shortest. This finding indicates that the nitroxide oxygen atoms in 1 are the most dislocated from the benzene plane. As a consequence, the π-conjugation in 1 is the most severely inhibited between the benzene ring and nitroxide groups.
The Y3+ ion in 1 was eight-coordinate, and the coordination structure is best described as a square antiprism (SAPR) (Figure 2a). The SHAPE analysis [51] indicates that the continuous shape measure was 0.485 with respect to an ideal SAPR-8 reference. The H-donor OH groups in two aqua ligands (O9 and O10) are arranged in a trans position in a basal square. The O9–Y1–O10 angle is 104.79(4)°, and the interatomic distance between O9 and O10 is 3.73555(7) Å in 1. The X-ray crystal structure of [Y(hfac)3(H2O)2] was also determined (Figure 2b), and those of lanthanide analogs [Ln(hfac)3(H2O)2] (Ln = Gd [CCDC 2300883], Ho [52] and Er [53]) are known. They are isomorphous, which can be reasonably understood from the ionic radii (1.05, 1.02, and 1.00 Å, respectively, vs. 1.02 Å for Y [54]). Two aqua ligands are always located in a cis position of a basal plane of the SAPR. The Oaq–RE–Oaq angle is ca. 70.7–70.8°, with an Oaq⋯Oaq distance of ca. 2.69–2.77 Å. Such structural flexibility seems to be beneficial to accommodate the strain accompanied by the 12-membered ring formation.
Interestingly, intact TF2PBN already has a disrotatory conformation of the two nitroxide groups, leading to an approximate CS symmetry and not C2 symmetry, as indicated by the positive and negative torsion angles (Scheme 2, left). Here, the torsion angle θ was chosen as |θ| ≤ 90°. After the association reaction, the O1⋯O2 distance in TF2PBN became shorter (Scheme 2, right), while the Oaq⋯Oaq distance in [Y(hfac)3(H2O)2] became wider (6.339(16) vs. 5.8868(1) Å, Table 1) thanks to an attractive H-bonding interaction. This motion brings about the larger torsion around the O–N–Cα(Ar)–Cβ(Ar).

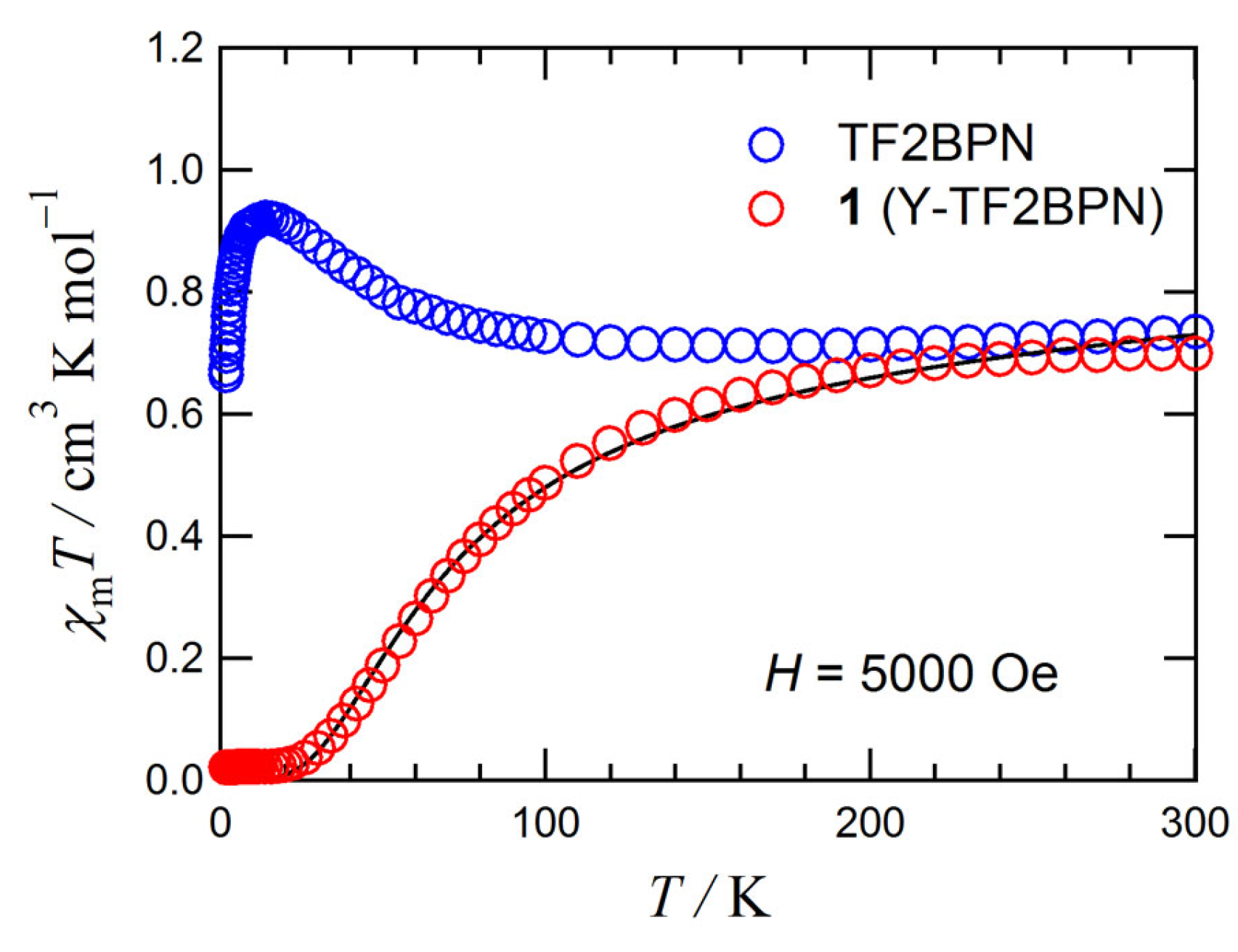
3.2. Magnetic Analysis

Figure 3 shows the magnetic susceptibility results for the starting material TF2PBN and 1·[Y(hfac)3(H2O)2]1.1. The diamagnetic impurity at a polycrystalline level does not disturb the magnetic analysis, so the plot can practically be regarded as that of 1. The χmT value of 1 shows a monotonic decrease upon cooling, indicating the presence of antiferromagnetic coupling. Finally, the χmT value was practically null at the base temperature (1.8 K), indicating the high purity of the biradical species as a paramagnetic source. If unreacted or overreacted species were present, the χmT bias would appear as an S = 1/2 Curie impurity.
In sharp contrast, the ground sate of TF2PBN has been reported to be triplet with 2J/kB = 40–80 K [36,37], which we were able to confirm independently (Figure 3). The χmT value of TF2PBN shows an increase upon cooling, indicating the presence of ferromagnetic coupling. The final drop may originate in an intermolecular interaction.
The data of 1 were analyzed according to the Bleaney-Bowers formula (Equation (3)) [55]. Here, χm is the molar magnetic susceptibility, T is the absolute temperature, J is the exchange coupling constant, g is the Landé g factor, NA is Avogadro’s number, μB is the Bohr magneton, and kB is the Boltzmann constant. The singlet–triplet energy gap corresponds to 2J. The best optimized parameter was 2J/kB = −128(2) K with the g value fixed to 2.006, a typical value for nitroxides [10]. The calculation curve almost reproduces the experimental data.
χ m = 2 N A g 2 μ B 2 k B T   1 3 + e x p ( − 2 J / k B )
There seem to be two possible radical–radical exchange pathways. One is through the m-phenylene bridge, and the other occurs through the diamagnetic Y3+ ion, namely, a superexchange mechanism across (N)O-H-O-Y-O-H-O(N). As shown in the plot for 1, much stronger exchange coupling is observed than expected from the superexchange mechanism, which is typically of the order of 10 to 20 K [56,57]. The observed antiferromagnetic exchange coupling must be ascribed to the m-phenylene bridge.
There have been several reports on rule-breaking compounds regarding the ground states anticipated from Kekulé or non-Kekulé structural formulas [58,59,60,61]. Rajca et al. reported a pioneering work in which antiferromagnetic coupling was assigned to the m-phenylene-bridge in TF2PBN-MnII(hfac)2-TF2PBN according to the approximate spin model (S = 1/2)–(S = 3/2)–(S = 1/2) [37]. In comparison to the Mn complex, compound 1 carries only two radical spins with only slight perturbations, leading to a highly reliable evaluation of J. To confirm these assumptions and construct a possible magneto-structure relationship, we performed calculations.

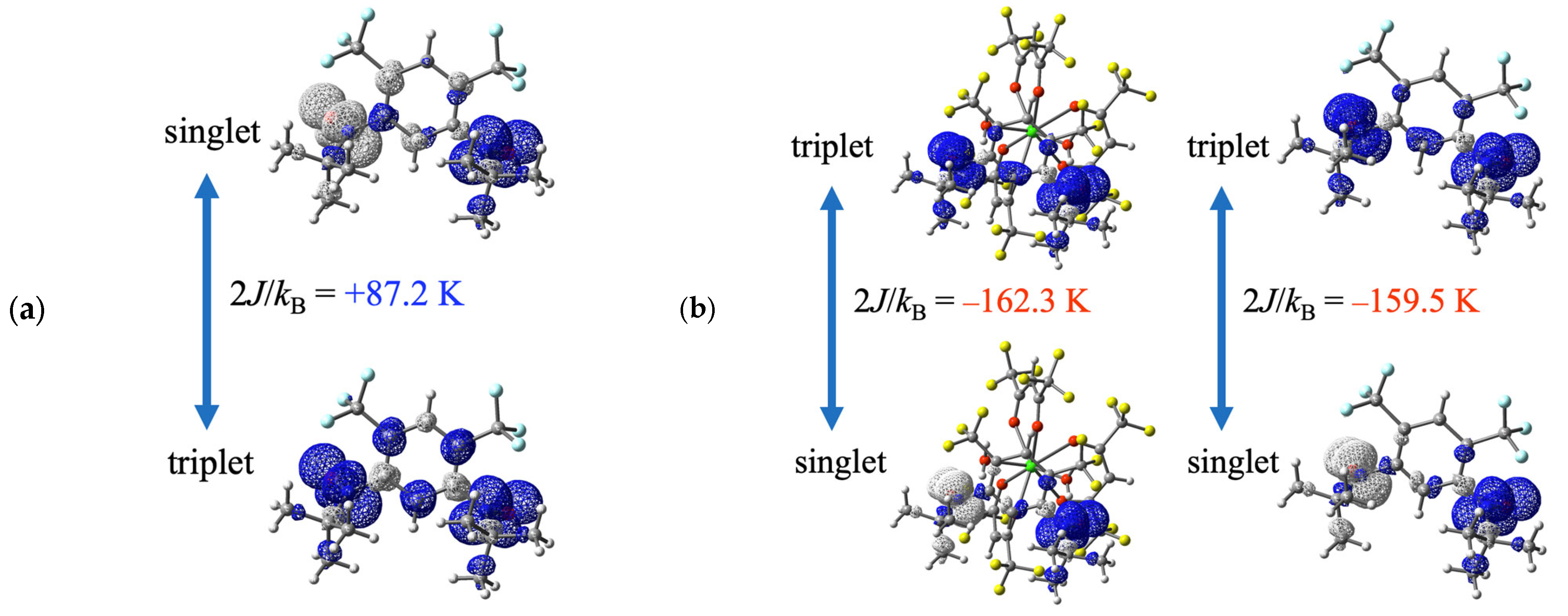
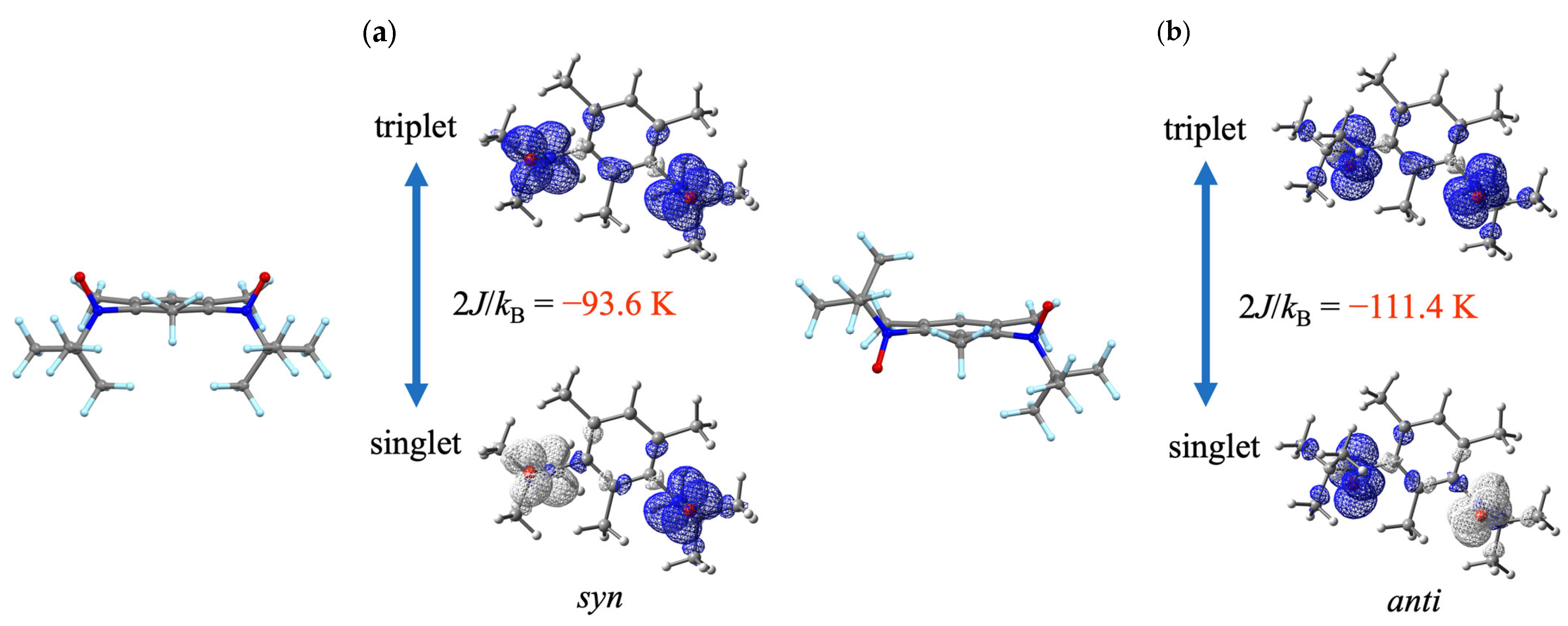
3.3. DFT Calculation Analysis

A density functional theory (DFT) calculation on the UB3LYP/6-311+G(2d,p) level using the geometry determined for TF2PBN [36] afforded a triplet ground state with 2J/kB = +87.2 K (Figure 4a). The intramolecular coupling was semi-quantitatively supported by the theoretical calculation. It is quite normal that m-phenylene bis(nitroxides) possesses a ground triplet state [62,63,64,65]. On the other hand, the corresponding calculation for 1 provided an antiferromagnetic interaction with 2J/kB = −162.3 K (Figure 4b, left). To elucidate the presence or absence of superexchange coupling through the H-O-Y-O-H bridge, we applied the same calculation protocol to the virtual molecule TF2PBN after the [Y(hfac)3(H2O)2] portion was removed from 1 (Figure 4b, right). Antiferromagnetic coupling was again calculated to be 2J/kB = −159.5 K. The two comparable 2J values tell us that the antiferromagnetic m-phenylene pathway is plausible. m-Phenylene bis(nitroxides) with a ground singlet state seem to be rather rare [37,66,67,68].

4. Discussion

Figure 4a indicates the spin distribution on the m-phenylene ring, while Figure 4b shows a much smaller spin density there. This picture clarifies that the spin polarization scheme hardly works in 1. The o-trifluoromethyl group has interference against the adjacent tert-butyl nitroxide group, giving rise to the steric inhibition of π-conjugation. Instead, in the out-of-plane deformed structure, a through-space interaction seems to be operative [66,69] because σ-type bonding and antibonding contributions appeared in the benzene bridge and a possible interaction produced a syn conformation. According to the ab initio study, the antiferromagnetic couplings are due to a through-bond interaction which increases the energy difference between the symmetric and antisymmetric NBMOs [70].
The present result is consistent with the previous work on the post-Hartree-Fock CAS calculation of TF2PBN [71,72]. The exchange coupling values are plotted in the matrix of two torsion angles, θ1 and θ2, and almost four basins showing antiferromagnetic or very small coupling appeared regarding the severe out-of-plane conformation. The present values (Scheme 2), θ1 = −48.8° and θ2 = 69.7° for the starting material TF2PBN and θ1 = −74.9° and θ2 = 84.8° for complex 1, belong to the ferro- and antiferromagnetic regions, respectively. Therefore, both post-Hartree-Fock CAS [71,72] and DFT (this work) calculations reproduced the experimental results well. This finding seems to be very helpful for researchers who do not specialize in calculation because a low-cost DFT treatment could afford a reliable output.
Iwamura et al. reported that biradical 4,6-dimethoxy-1,3-phenylene bis(tert-butyl nitroxide) (abbreviated as MO2PBN, Scheme 3) has θ1 = −75.3 and θ2 = 65.1° [66], which are considerably large. The same DFT protocol was applied to MO2PBN, and the geometrical parameters are available from the experiment, affording antiferromagnetic 2J/kB = −56.1 K. The experimental value was −73.8 K in the crystalline form [66]. The following known derivative also adds a supportive instance; 5-bromo-2,4-dimethoxy-1,3-phenylene bis(tert-butyl nitroxide) (BrMO2PBN, Scheme 3) [67] was reported to have larger torsion (θ1 = −79.1 and θ2 = 82.5°). Our DFT calculation suggested 2J/kB = −109.9 K, while the experiments showed 2J/kB = −79.3 K. Another sterically crowded biradical, 2,4,6-trimethyl-m-phenylene bis(tert-butyl nitroxide) (MesBN, Scheme 3), was reported by Rassat et al. [68], and MesBN was separated as syn- and anti-isomers, each of which was characterized as a ground singlet species. Unfortunately, their crystal structures are unknown. The same DFT protocol was applied to MesBN except that the geometries of the syn (CS) and anti (C2) conformers were computationally optimized at the UB3LYP/6-31G(d) level. The exchange coupling constants were computed as 2J/kB = −93.6 and −111.4 K, respectively (Figure 5). The observed values are reported to be 2J/kB = −66 to −86 K by means of electron spin resonance spectroscopy. Further attempts toward novel switching materials using MO2PBN, BrMO2PBN, or MesBN with [Y(hfac)3(H2O)2], based on the same strategy as that of TF2PBN, were aborted in our project since they are already singlet species.
The exchange constant is clarified to be very sensitive to the conformation of the nitroxide group. Now, we can propose a possible magneto-structure relationship (Figure 6). The protecting groups are various (CF3, CH3, Br, and CH3O), but we simplify a model by ignoring such a substituent effect. The exchange coupling constant 2J was plotted against the averaged out-of-conjugation torsion angle, θ = (|θ1| + |θ2|)/2. We can find an almost monotonic negative slope in the observed 2Jexp vs. torsion angle as well as the calculated 2Jcalc vs. torsion angle. Unexpectedly, electronic substituent effects are hardly observed. The angular dependence of the overlap between the nitrogen 2pz and ipso carbon 2pz orbitals may obey the cos2 θ law [73,74,75], as expected from the two-fold symmetry of pπ-pπ orbital overlap. Barone et al. reported the computational results from m- and p-phenylene bridged bisnitroxide models of HNO-C6H4-NOH [76], and the singlet–triplet energy gap approximately traced cos2 θ. In magnetic resonance spectroscopy, one may recall the Karplus-Conroy equation [76,77,78,79] and McConnell-Heller equation [11,80], which tell us the NMR and ESR coupling constants, respectively, as functions of the dihedral angle. Here, the angular range is rather small; therefore, an empirical equation is determined via approximate linear fitting. The critical angle, where the sign of 2Jexp changes from positive (ferromagnetic) to negative (antiferromagnetic), is 65(3)° for the experimental data. For the calculation, the critical angle (66.7(14)°) is very close to the experimental one. The calculation somewhat overestimates the angular sensitivity as a slope. We can verify the literature data on [Mn(hfac)2(TF2PBN)2] (Table 1). The average θ = 63.5° belongs to the border or the ferromagnetic region. The coordination to a divalent cation, Mn2+, may cause an electronic state modification of the nitroxide group, for example, the increasing contribution of the canonical formula R1–N+•(–O–)–R2 [35], and the magneto-structure picture would be slightly altered for coordination compounds.
We must comment on the role of the H bonds in 1. The essential function of the H-bonding formation in 1 is to force the π-electron systems to bend more to violate the spin-polarization mechanism or topological rule. A question arises here: why does the J value become antiferromagnetic and not approach null? The observable exchange interaction comprises ferro- and antiferromagnetic contributions, namely Equation (4), according to Kahn’s interpretation [81]. The JF term originates in the two-electron exchange integral, which is always positive. The JAF term is regulated with the overlap and transfer integrals between the two magnetic orbitals, which are negative. According to this model, when the JF term is reduced, the JAF term becomes decisive. The two terms make comparable contributions in TF2PBN, being responsible for the ground-state switching behavior by means of small structural perturbations like H bonds.
J = JF + JAF
The empirical equation is given as 2Jexp kB−1/K = 467 − 7.2θ (Figure 6). The first and second terms partly imply JF and JAF, respectively. This equation holds for a relatively narrow region of torsional angles, and therefore extrapolation to zero torsion seems to be risky according to a linear or cos2 function.

5. Conclusions

Steric congestion due to o-trifluoromethyl groups seems to decrease ferromagnetic interactions in TF2PBN. A further reduction in ferromagnetic interactions originates in the U-shaped bending deformation owing to attractive H-bonding toward the aqua ligands in the [Y(hfac)3(H2O)2] portion. Here, the DFT calculation provided a reliable explanation and prediction. After comparison of the results among a few known compounds, we found a magneto-structure relationship, namely, the observed 2J value vs. the out-of-conjugation torsion angle shows a monotonic negative slope, and the critical torsion angle, at which the sign of 2J changes from ferro- to antiferromagnetic, is 65(3)°. The conformational effects on the intramolecular magnetic properties are clearly demonstrated. The ferro- and antiferromagnetic interactions have balanced contributions in TF2PBN and are responsible for the ground-state interconversion between triplet and singlet states by means of small structural perturbations like the presence or absence of H bonds. Since TF2PBN can be recovered from the adduct, a triplet/singlet ground-state switchable material has been successfully realized.
Very recently, H-bonding-assisted molecular design has been proposed for flattening conformation and enhancing ferromagnetic exchange coupling [82]. Combining their strategy and related ideas with the present conclusion, control over coplanar or twisted configurations between aryl and nitroxide groups seems to be feasible, which accelerates the development of novel magnetic-switch-based functional materials.

Author Contributions

N.H. participated in the preparation, characterization, magnetic measurements, and DFT calculation. T.I. supervised the research and wrote the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research was financially supported by JSPS (No. 22K19006) and The Murata Science Foundation. A part of this work was conducted in the UEC Coordinated Center Research Facilities, supported by the MEXT Advanced Research Infrastructure for Materials and Nanotechnology in Japan (ARIM) (No. JPMXP1222UE0016).

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Acknowledgments

The authors thank Hiroyasu Sekine and Saki Ito for information on complexation reaction conditions between TF2PBN and lanthanide hfac salts.

Conflicts of Interest

The authors declare no competing financial interests.

References

  1. Demir, S.; Jeon, I.R.; Long, J.R.; Harris, T.D. Radical ligand-containing single-molecule magnets. Coord. Chem. Rev. 2015, 289, 149–176. [Google Scholar] [CrossRef]
  2. Caneschi, A.; Gatteschi, D.; Sessoli, R.; Rey, P. Toward molecular magnets: The metal-radical approach. Acc. Chem. Res. 1989, 22, 392–398. [Google Scholar] [CrossRef]
  3. Tan, Y.; Hsu, S.-N.; Tahir, H.; Dou, L.; Savoie, B.M.; Boudouris, B.W. Electronic and Spintronic Open-Shell Macromolecules, Quo Vadis? J. Am. Chem. Soc. 2022, 144, 626–647. [Google Scholar] [CrossRef] [PubMed]
  4. Iwamura, H. What role has organic chemistry played in the development of molecule-based magnets? Polyhedron 2013, 66, 3–14. [Google Scholar] [CrossRef]
  5. Iwamura, H. High-spin organic molecules and spin alignment in organic molecular assemblies. Adv. Phys. Org. Chem. 1990, 26, 179–253. [Google Scholar]
  6. Sato, O. Dynamic molecular crystals with switchable physical properties. Nat. Chem. 2016, 8, 644–656. [Google Scholar] [CrossRef] [PubMed]
  7. Ratera, I.; Veciana, J. Playing with organic radicals as building blocks for functional molecular materials. Chem. Soc. Rev. 2012, 41, 303–349. [Google Scholar] [CrossRef] [PubMed]
  8. Dong, S.; Li, Z. Recent progress in open-shell organic conjugated materials and their aggregated states. J. Mater. Chem. C 2022, 10, 2431–2449. [Google Scholar] [CrossRef]
  9. Xie, Y.; Zhang, K.; Yamauchi, Y.; Oyaizu, K.; Jia, Z. Nitroxide radical polymers for emerging plastic energy storage and organic electronics: Fundamentals, materials, and applications. Mater. Horiz. 2021, 8, 803–829. [Google Scholar] [CrossRef]
  10. Chen, Z.X.; Li, Y.; Huang, F. Persistent and stable organic radicals: Design, synthesis, and applications. Chem 2021, 7, 288–332. [Google Scholar] [CrossRef]
  11. Shu, C.; Yang, Z.; Rajca, A. From Stable Radicals to Thermally Robust High-Spin Diradicals and Triradicals. Chem. Rev. 2023, 123, 11954–12003. [Google Scholar] [CrossRef]
  12. Rajca, A. Magnetism of Nitroxides. In Nitroxides: Synthesis, Properties and Applications; The Royal Society of Chemistry: London, UK, 2021; Chapter 9. [Google Scholar]
  13. Datta, S.N.; Pal, A.K.; Panda, A. Design of Magnetic Organic Molecules and Organic Magnets: Experiment, Theory and Computation with Application and Recent Advances. Chem. Phys. Impact 2023, 7, 100379. [Google Scholar] [CrossRef]
  14. Baumgarten, M. High spin molecules directed towards molecular magnets. In EPR of Free Radicals in Solids II; Springer: Dordrecht, The Netherlands, 2012; pp. 205–244. [Google Scholar]
  15. Baumgarten, M. High spin organic molecules. In World Scientific Reference on Spin in Organics; Spin in Organics; World Scientific Publishing: Singapore, 2018; Volume 4, pp. 1–93. [Google Scholar]
  16. Gallagher, N.M.; Olankitwanit, A.; Rajca, A. High-spin organic molecules. J. Org. Chem. 2015, 80, 1291–1298. [Google Scholar] [CrossRef] [PubMed]
  17. Chapyshev, S.V.; Mendez-Vega, E.; Sander, W. Molecular Magnets: The Synthesis and Characterization of High-Spin Nitrenes. Chem. Eur. J. 2021, 27, 1258–1269. [Google Scholar] [CrossRef] [PubMed]
  18. Zhang, H.; Pink, M.; Wang, Y.; Rajca, S.; Rajca, A. High-spin S = 3/2 ground-state aminyl triradicals: Toward high-spin oligo-aza nanographenes. J. Am. Chem. Soc. 2022, 144, 19576–19591. [Google Scholar] [CrossRef] [PubMed]
  19. Pomikło, D.; Kaszyński, P. Blatter diradicals with a spin coupler at the N(1) position. Chem. Eur. J. 2023, 29, e202301069. [Google Scholar] [CrossRef] [PubMed]
  20. Tretyakov, E.V.; Ovcharenko, V.I.; Terent’ev, A.O.; Krylov, I.B.; Magdesieva, T.V.; Mazhukin, D.G.; Gritsan, N.P. Conjugated nitroxides. Russ. Chem. Rev. 2022, 91, RCR5025. [Google Scholar] [CrossRef]
  21. Zaytseva, E.V.; Mazhukin, D.G. Spirocyclic nitroxides as versatile tools in modern natural sciences: From synthesis to applications. Part I. Old and new synthetic approaches to spirocyclic nitroxyl radicals. Molecules 2021, 26, 677. [Google Scholar] [CrossRef] [PubMed]
  22. Likhtenshtein, G.I. (Ed.) Nitroxides: Brief History, Fundamentals, and Recent Developments; Springer: Cham, Switzerland, 2020. [Google Scholar]
  23. Bonucci, A.; Ouari, O.; Guigliarelli, B.; Belle, V.; Mileo, E. In-cell EPR: Progress towards structural studies inside cells. ChemBioChem 2020, 21, 451–460. [Google Scholar] [CrossRef]
  24. Kotake, Y.; Kuwata, K. Formation of Intramolecular Hydrogen Bond in Hydroxy-substituted Nitroxide Radicals as Evidenced by Electron Spin Resonance. Bull. Chem. Soc. Jpn. 1982, 55, 3686–3689. [Google Scholar] [CrossRef]
  25. Hicks, R.G. What’s new in stable radical chemistry? Org. Biomol. Chem. 2007, 5, 1321–1338. [Google Scholar] [CrossRef] [PubMed]
  26. Kubo, T. Synthesis, physical properties, and reactivity of stable, π-conjugated, carbon-centered radicals. Molecules 2019, 24, 665. [Google Scholar] [CrossRef] [PubMed]
  27. Kurokawa, G.; Ishida, T.; Nogami, T. Remarkably strong intermolecular antiferromagnetic couplings in the crystal of biphenyl-3,5-diyl bis(tert-butyl nitroxide). Chem. Phys. Lett. 2004, 392, 74–79. [Google Scholar] [CrossRef]
  28. Katoh, K.; Hosokoshi, Y.; Inoue, K.; Goto, T. Singlet ground states in an organic S = 1/2 spin ladder and a novel double spin chain of ferromagnetic dimers formed by an organic tetraradical. J. Phys. Soc. Jpn. 2000, 69, 1008–1011. [Google Scholar] [CrossRef]
  29. Iwamura, H.; Inoue, K. Spontaneous magnetization in a 2:3 complex formed by 3,4′,5-tris(N-oxy-tert-butylamino) biphenyl and manganese(II) bis(hexafluoroacetylacetonate). Adv. Mater. 1996, 8, 73–76. [Google Scholar] [CrossRef]
  30. Sekine, H.; Ishida, T. Unexpected Complexes of a [3+3] Cycloadduct from Biphenyl-3,5-diyl Bis(tert-butyl Nitroxide) with Gadolinium(III) 1,1,1,5,5,5-hexafluoropentane-2,4-dionate. Chem. Lett. 2018, 47, 74–77. [Google Scholar] [CrossRef]
  31. Ito, S.; Yoshitake, T.; Ishida, T. Ferromagnetic 2p-2p and 4f-2p Couplings in a Macrocycle from Two Biradicals and Two Gadolinium(III) Ions. Molecules 2022, 27, 4930. [Google Scholar] [CrossRef] [PubMed]
  32. Calder, A.; Forrester, A.R. The stability of aryl-t-butylnitroxides. Chem. Commun. 1967, 682–684. [Google Scholar] [CrossRef]
  33. Chiarelli, R.; Gambarelli, S.; Rassat, A. Exchange interactions in nitroxide biradicals. Mol. Cryst. Liq. Cryst. 1997, 305, 455–478. [Google Scholar] [CrossRef]
  34. Ito, S.; Ishida, T. Practically Diamagnetic Macrocycle Consisting of Nickel-Biradical Heterospins with the Largest Out-of-Plane Torsion at Coordination Bonds. Chem. Lett. 2020, 49, 1062–1065. [Google Scholar] [CrossRef]
  35. Ito, S.; Takano, R.; Hatanaka, S.I.; Ishida, T. Rare-Earth (RE = Y, Gd, Tb, Dy, Ho, and Er) Chains Bridged with a Triplet Biradical and Magnetic Hysteresis Recorded for RE = Tb. Inorg. Chem. 2022, 61, 10619–10623. [Google Scholar] [CrossRef] [PubMed]
  36. Rajca, A.; Lu, K.; Rajca, S.; Ross, C.R., II. Singlet–triplet bistability in a 1,3-phenylene-based bis(aminoxyl) diradical. Chem. Commun. 1999, 13, 1249–1250. [Google Scholar] [CrossRef]
  37. Rajca, A.; Rajca, S.; Wongsriratanakul, J.; Ross, C.R., II. 4,6-Bis(trifluoromethyl)-N,N′-di-tert-butyl-1,3-phenylenebis(aminoxyl) and its bis(hexafluoroacetylacetonato)manganese(II) complex: Synthesis, X-ray crystallography, and magnetism. Polyhedron 2001, 20, 1669–1675. [Google Scholar] [CrossRef]
  38. Richardson, M.F.; Wagner, W.F.; Sands, D.E. Rare-earth trishexafluoroacetylacetonates and related compounds. J. Inorg. Nucl. Chem. 1968, 30, 1275–1289. [Google Scholar] [CrossRef]
  39. CrysAlisPRO; Oxford Diffraction/Agilent Technologies UK Ltd.: Yarnton, UK, 2021.
  40. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.; Puschmann, H. Olex2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  41. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
  42. Bain, G.A.; Berry, J.F. Diamagnetic corrections and Pascal’s constants. J. Chem. Educ. 2008, 85, 532–536. [Google Scholar] [CrossRef]
  43. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
  44. Neese, F. Prediction of molecular properties and molecular spectroscopy with density functional theory: From fundamental theory to exchange-coupling. Coord. Chem. Rev. 2009, 253, 526–563. [Google Scholar] [CrossRef]
  45. Noodleman, L.; Norman, J.G., Jr. The Xα valence bond theory of weak electronic coupling. Application to the low-lying states of Mo2Cl84−. J. Chem. Phys. 1979, 70, 4903–4906. [Google Scholar] [CrossRef]
  46. Noodleman, L. Valence bond description of antiferromagnetic coupling in transition metal dimers. J. Chem. Phys. 1981, 74, 5737–5743. [Google Scholar] [CrossRef]
  47. Yamaguchi, K.; Toyoda, Y.; Fueno, T. A generalized MO (GMO) approach to unstable molecules with quasi-degenerate electronic states: Ab initio GMO calculations of intramolecular effective exchange integrals and designing of organic magnetic polymers. Synth. Met. 1987, 19, 81–86. [Google Scholar] [CrossRef]
  48. Soda, T.; Kitagawa, Y.; Onishi, T.; Takano, Y.; Shigeta, Y.; Nagao, H.; Yoshioka, Y.; Yamaguchi, K. Ab initio computations of effective exchange integrals for H–H, H–He–H and Mn2O2 complex: Comparison of broken-symmetry approaches. Chem. Phys. Lett. 2000, 319, 223–230. [Google Scholar] [CrossRef]
  49. Nakamoto, K.; Margoshes, M.; Rundle, R.E. Stretching frequencies as a function of distances in hydrogen bonds. J. Am. Chem. Soc. 1955, 77, 6480–6486. [Google Scholar] [CrossRef]
  50. Ishida, T.; Ito, S.; Homma, Y.; Kyoden, Y. Molecular S = 2 High-Spin, S = 0 Low-Spin and S = 0 ⇄ 2 Spin-Transition/-Crossover Nickel(II)-Bis(nitroxide) Coordination Compounds. Inorganics 2021, 9, 10. [Google Scholar] [CrossRef]
  51. Lluncll, M.; Casanova, D.; Circra, J.; Bofill, J.M.; Alcmany, P.; Alvarez, S.; Pinsky, M.; Avnir, D. SHAPE, Version 2.1; University of Barcelona: Barcelona, Spain; Hebrew University of Jerusalem: Jerusalem, Israel, 2005. [Google Scholar]
  52. Lee, J.H.; Jung, Y.S.; Sohn, Y.S.; Kang, S.-J. Synthesis and Characterization of Holmium Complexes Containing β-Diketonate Ligands. Bull. Korean Chem. Soc. 1998, 19, 231–235. [Google Scholar]
  53. Tan, R.H.C.; Motevalli, M.; Abrahams, I.; Wyatt, P.B.; Gillin, W.P. Quenching of IR Luminiescence of Erbium, Neodymium and Ytterbium β-diketonate Complexes by Ligand C-H and C-D bonds. J. Phys. Chem. B 2006, 110, 24476–24479. [Google Scholar] [CrossRef] [PubMed]
  54. Shannon, R. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr. Sect. A Cryst. Phys. Diffr. Theor. Gen. Crystallogr. 1976, 32, 751–767. [Google Scholar] [CrossRef]
  55. Bleaney, B.; Bowers, K.D. Anomalous paramagnetism of copper acetate. Proc. Royal Soc. Ser. A 1952, 214, 451–465. [Google Scholar] [CrossRef]
  56. Nakamura, T.; Ishida, T. Strong exchange couplings in lanthanide complexes with an aliphatic nitroxide radical 1,1,3,3-tetramethylisoindolin-2-oxyl. Polyhedron 2015, 87, 302–306. [Google Scholar] [CrossRef]
  57. Murakami, R.; Nakamura, T.; Ishida, T. Doubly TEMPO-coordinated gadolinium(III), lanthanum(III), and yttrium(III) complexes. Strong superexchange coupling across rare earth ions. Dalton Trans. 2014, 43, 5893–5898. [Google Scholar] [CrossRef]
  58. Baumgarten, M.; Karabunarliev, S. Reverting the effect of magnetic couplers in bridged di-and polyradicals. Chem. Phys. 1999, 244, 35–47. [Google Scholar] [CrossRef]
  59. Zeng, Z.; Sung, Y.M.; Bao, N.; Tan, D.; Lee, R.; Zafra, J.L.; Lee, B.S.; Ishida, M.; Ding, J.; López Navarrete, J.T.; et al. Stable Tetrabenzo-Chichibabin’s Hydrocarbons: Tunable Ground State and Unusual Transition between Their Closed-Shell and Open-Shell Resonance Forms. J. Am. Chem. Soc. 2012, 134, 14513–14525. [Google Scholar] [CrossRef] [PubMed]
  60. Wu, J.I.; van Eikema Hommes, N.J.; Lenoir, D.; Bachrach, S.M. The quest for a triplet ground-state alkene: Highly twisted C=C double bonds. J. Phys. Org. Chem. 2019, 32, e3965. [Google Scholar] [CrossRef]
  61. Shimizu, A.; Morikoshi, T.; Sugisaki, K.; Shiomi, D.; Sato, K.; Takui, T.; Shintani, R. Synthesis and Isolation of a Kekulé Hydrocarbon with a Triplet Ground State. Angew. Chem. Int. Ed. 2022, 61, e202205729. [Google Scholar] [CrossRef] [PubMed]
  62. Nishimaki, H.; Mashiyama, S.; Yasui, M.; Nogami, T.; Ishida, T. Bistable Polymorphs Showing Diamagnetic and Paramagnetic States of an Organic Crystalline Biradical Biphenyl-3,5-diyl Bis(tert-butylnitroxide). Chem. Mater. 2006, 18, 3602–3604. [Google Scholar] [CrossRef]
  63. Nishimaki, H.; Ishida, T. Organic two-step spin-transition-like behavior in a linear S = 1 array: 3’-methylbiphenyl-3,5-diyl bis(tert-butylnitroxide) and related compounds. J. Am. Chem. Soc. 2010, 132, 9598–9599. [Google Scholar] [CrossRef] [PubMed]
  64. Konno, T.; Kudo, H.; Ishida, T. Intermediate-paramagnetic phases with a half and a quarter spin entities in fluorinated biphenyl-3,5-diyl bis(tert-butyl nitroxides). J. Mater. Chem. C 2015, 3, 7813–7818. [Google Scholar] [CrossRef]
  65. Yoshitake, T.; Kudo, H.; Ishida, T. Thermally Activated Paramagnets from Diamagnetic Polymers of Biphenyl-3,5-diyl Bis(tert-butyl Nitroxides) with Methyl and Fluoro Groups at the 2’- and 5’-Positions. Crystals 2016, 6, 30. [Google Scholar] [CrossRef]
  66. Kanno, F.; Inoue, K.; Koga, N.; Iwamura, H. 4,6-Dimethoxy-1,3-phenylenebis(N-tert-butyl nitroxide) with a singlet ground state. Formal violation of a rule that m-phenylene serves as a robust ferromagnetic coupling unit. J. Am. Chem. Soc. 1993, 115, 847–850. [Google Scholar] [CrossRef]
  67. Fujita, J.; Tanaka, M.; Suemune, H.; Koga, N.; Matsuda, K.; Iwamura, H. Antiferromagnetic exchange interaction among the three spins placed in an isosceles triangular configuration in 2,4-dimethoxy-1,3,5-benzenetriyltris(N-tert-butyl nitroxide). J. Am. Chem. Soc. 1996, 118, 9347–9351. [Google Scholar] [CrossRef]
  68. Dvolaitzky, M.; Chiarelli, R.; Rassat, A. Stable N,N′-Di-tert-butyl-meta-phenylene-bisnitroxides—Unexpected Ground-State Singlets. Angew. Chem. Int. Ed. Engl. 1992, 31, 180–181. [Google Scholar] [CrossRef]
  69. Yoshizawa, K.; Kuga, T.; Sato, T.; Hatanaka, M.; Tanaka, K.; Yamabe, T. Through-bond and through-space interactions of organic radicals coupled by m-phenylene. Bull. Chem. Soc. Jpn. 1996, 69, 3443–3450. [Google Scholar] [CrossRef]
  70. Fang, S.; Lee, M.S.; Hrovat, D.A.; Borden, W.T. Ab initio calculations show why m-phenylene is not always a ferromagnetic coupler. J. Am. Chem. Soc. 1995, 117, 6727–6731. [Google Scholar] [CrossRef]
  71. Barone, V.; Cacelli, I.; Ferretti, A.; Monti, S.; Prampolini, G. An integrated protocol for the accurate calculation of magnetic interactions in organic magnets. J. Chem. Theory Comput. 2011, 7, 699–706. [Google Scholar] [CrossRef] [PubMed]
  72. Barone, V.; Boilleau, C.; Cacelli, I.; Ferretti, A.; Prampolini, G. Conformational effects on the magnetic properties of an organic diradical: A computational study. J. Chem. Theory Comput. 2013, 9, 1958–1963. [Google Scholar] [CrossRef] [PubMed]
  73. Venkataraman, L.; Klare, J.E.; Nuckolls, C.; Hyberstsen, M.S.; Steigerwald, M.L. Dependence of single-molecule junction conductance on molecular conformation. Nature 2006, 442, 904–907. [Google Scholar] [CrossRef] [PubMed]
  74. Vonlanthen, D.; Mishchenko, A.; Elbing, M.; Neuburger, M.; Wandlowski, T.; Mayor, M. Chemically controlled conductivity: Torsion-angle dependence in a single-molecule biphenyldithiol junction. Angew. Chem. Int. Ed. 2009, 48, 8886–8890. [Google Scholar] [CrossRef] [PubMed]
  75. Nishizawa, S.; Hasegawa, J.Y.; Matsuda, K. Theoretical investigation of the dependence of exchange interaction on dihedral angle between two aromatic rings in a wire unit. Chem. Lett. 2014, 43, 530–532. [Google Scholar] [CrossRef]
  76. Barone, V.; Cacelli, I.; Cimino, P.A.; Ferretti, S. Monti and G. Prampolini, Magnetic Interactions in Phenyl-Bridged Nitroxide Diradicals: Conformational Effects by Multireference and Broken Symmetry DFT Approaches. J. Phys. Chem. A 2009, 113, 15150–15155. [Google Scholar] [CrossRef]
  77. Shultz, D.A.; Fico, R.M.; Lee, H.; Kampf, J.W.; Kirschbaum, K.; Pinkerton, A.A.; Boyle, P.D. Mechanisms of exchange modulation in trimethylenemethane-type biradicals: The roles of conformation and spin density. J. Am. Chem. Soc. 2003, 125, 15426–15432. [Google Scholar] [CrossRef]
  78. Shultz, D.A.; Fico, R.M.; Bodnar, S.H.; Kumar, R.K.; Vostrikova, K.E.; Kampf, J.W.; Boyle, P.D. Trends in exchange coupling for trimethylenemethane-type bis(semiquinone) biradicals and correlation of magnetic exchange with mixed valency for cross-conjugated systems. J. Am. Chem. Soc. 2003, 125, 11761–11771. [Google Scholar] [CrossRef]
  79. Karplus, M. Vicinal proton coupling in nuclear magnetic resonance. J. Am. Chem. Soc. 1963, 85, 2870–2871. [Google Scholar] [CrossRef]
  80. Heller, C.; McConnell, H.M. Radiation damage in organic crystals. II. Electron spin resonance of (CO2H)CH2CH(CO2H) in β-succinic acid. J. Chem. Phys. 1960, 32, 1535–1539. [Google Scholar] [CrossRef]
  81. Kahn, O. Molecular Magnetism; VCH: New York, NY, USA, 1993. [Google Scholar]
  82. Zheng, X.; Bu, Y. Hydrogen-Bonding-Assisted Substituent Engineering for Modulating Magnetic Spin Couplings and Switching in m-Phenylene Nitroxide Diradicals. J. Phys. Chem. A 2023, 127, 7443–7451. [Google Scholar] [CrossRef] [PubMed]
Molecules 29 00070 sch001
Scheme 1. (a) Structural formulas of BPBN, tBuPBN, and TF2PBN. (b) Reaction Scheme for [Y(hfac)3(H2O)2(TF2PBN)] (1).
Scheme 1. (a) Structural formulas of BPBN, tBuPBN, and TF2PBN. (b) Reaction Scheme for [Y(hfac)3(H2O)2(TF2PBN)] (1).
Molecules 29 00070 sch001
Molecules 29 00070 g001
Figure 1. (a) Crystal structure of 1 with thermal ellipsoids at the 50% probability level. Major conformations are drawn for disordered CF3 groups at C17 (occupancy 0.640(4)), C26 (0.770(5)), and C31 (0.68(2)). Dotted lines stand for H bonds, denoted between the oxygen atoms. Selected atomic numbering is also shown. Atomic color codes: C, gray; H, turquoise; N, blue; O, red; F, yellow; Y, green. (b) An important portion after the C, H, and F atoms in hfac is omitted for the sake of clarity. (c) Simulated PXRD profiles for 1 and [Y(hfac)3(H2O)2] and experimental PXRD data for the product, 1·[Y(hfac)3(H2O)2]1.1.
Figure 1. (a) Crystal structure of 1 with thermal ellipsoids at the 50% probability level. Major conformations are drawn for disordered CF3 groups at C17 (occupancy 0.640(4)), C26 (0.770(5)), and C31 (0.68(2)). Dotted lines stand for H bonds, denoted between the oxygen atoms. Selected atomic numbering is also shown. Atomic color codes: C, gray; H, turquoise; N, blue; O, red; F, yellow; Y, green. (b) An important portion after the C, H, and F atoms in hfac is omitted for the sake of clarity. (c) Simulated PXRD profiles for 1 and [Y(hfac)3(H2O)2] and experimental PXRD data for the product, 1·[Y(hfac)3(H2O)2]1.1.
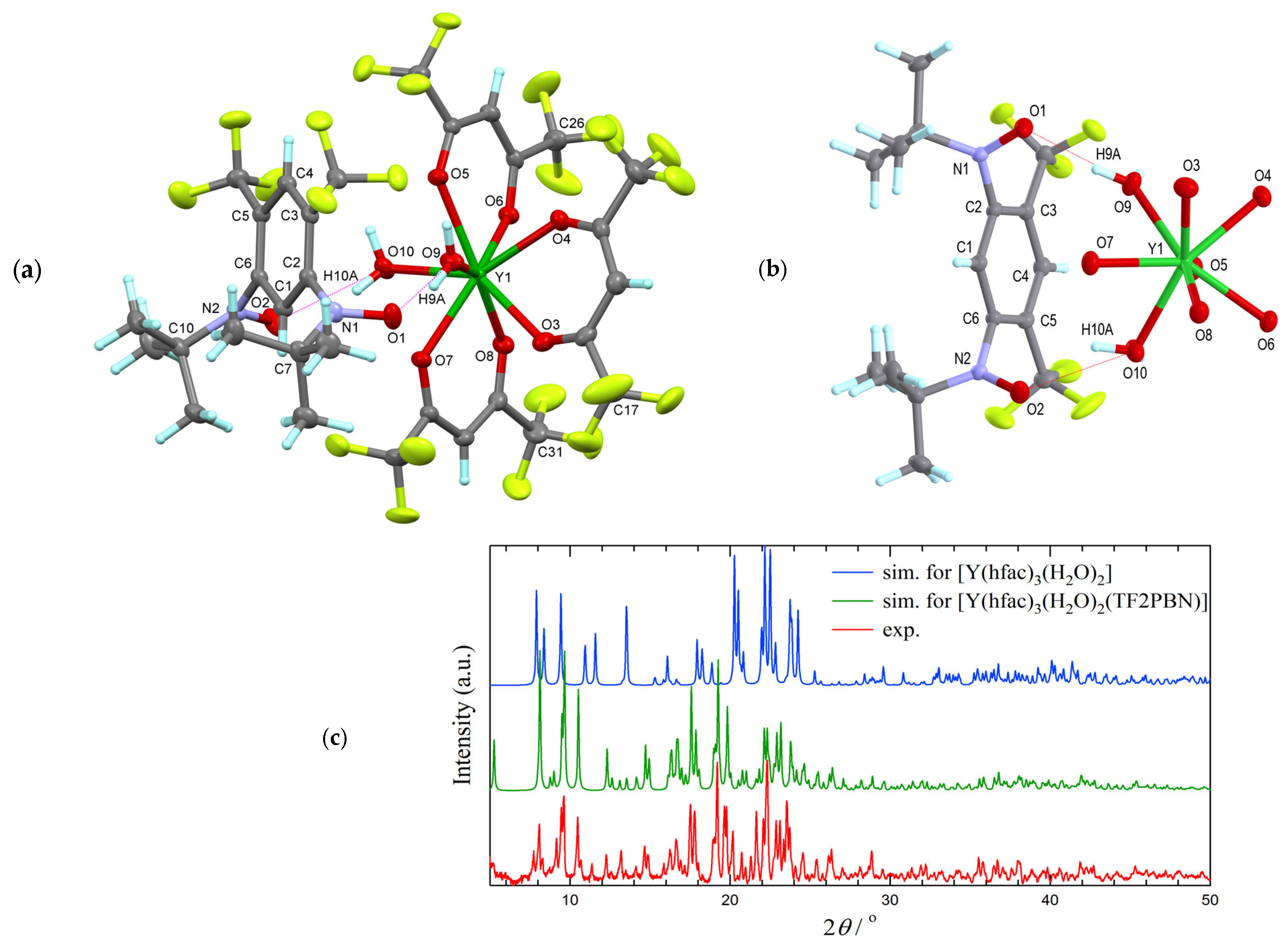
Molecules 29 00070 g001
Molecules 29 00070 g002
Figure 2. Crystal structure of (a) the [Y(hfac)3(H2O)2] moiety in 1 and (b) [Y(hfac)3(H2O)2] with thermal ellipsoids at the 50% probability level. Major conformations are drawn for disordered CF3 groups. Selected atomic numbering is also shown. For the atomic color codes, see Figure 1.
Figure 2. Crystal structure of (a) the [Y(hfac)3(H2O)2] moiety in 1 and (b) [Y(hfac)3(H2O)2] with thermal ellipsoids at the 50% probability level. Major conformations are drawn for disordered CF3 groups. Selected atomic numbering is also shown. For the atomic color codes, see Figure 1.
Molecules 29 00070 g002
Molecules 29 00070 sch002
Scheme 2. The torsion angles (left) before and (right) after adduct formation. θ1 and θ2 are shown.
Scheme 2. The torsion angles (left) before and (right) after adduct formation. θ1 and θ2 are shown.
Molecules 29 00070 sch002
Molecules 29 00070 g003
Figure 3. The χmT vs. T plot for TF2PBN and 1. The solid line represents the theoretical fit to the data on 1. For the equation and parameters, see the text.
Figure 3. The χmT vs. T plot for TF2PBN and 1. The solid line represents the theoretical fit to the data on 1. For the equation and parameters, see the text.
Molecules 29 00070 g003
Molecules 29 00070 g004
Figure 4. Relative energy levels of triplet and broken-symmetry singlet states, calculated at the UB3LYP/6-311+G(2d,p) level. Spin density surfaces are drawn at the 0.002 e− Å−3 level with blue and white lobes for the positive and negative spin densities, respectively. (a) The self-consistent field (SCF) energies of TF2PBN are −1480.8374662573 au with <S2> = 2.0114 and −1480.8373276154 au with <S2> = 1.0080 for the triplet and singlet states, respectively. (b) (Left) The SCF energies of 1 are −4494.9085419557 au with <S2> = 2.0094 and −4494.9088003966 au with <S2> = 1.0041 for the triplet and singlet states, respectively. (Right) The SCF energies of the TF2PBN portion in 1 are −1480.9064795589 au with <S2> = 2.0094 and −1480.9067334369 au with <S2> = 1.0045 for the triplet and singlet states, respectively. Ferro- and antiferromagnetic J values are marked in blue and red, respectively. For the atomic color codes, see Figure 1.
Figure 4. Relative energy levels of triplet and broken-symmetry singlet states, calculated at the UB3LYP/6-311+G(2d,p) level. Spin density surfaces are drawn at the 0.002 e− Å−3 level with blue and white lobes for the positive and negative spin densities, respectively. (a) The self-consistent field (SCF) energies of TF2PBN are −1480.8374662573 au with <S2> = 2.0114 and −1480.8373276154 au with <S2> = 1.0080 for the triplet and singlet states, respectively. (b) (Left) The SCF energies of 1 are −4494.9085419557 au with <S2> = 2.0094 and −4494.9088003966 au with <S2> = 1.0041 for the triplet and singlet states, respectively. (Right) The SCF energies of the TF2PBN portion in 1 are −1480.9064795589 au with <S2> = 2.0094 and −1480.9067334369 au with <S2> = 1.0045 for the triplet and singlet states, respectively. Ferro- and antiferromagnetic J values are marked in blue and red, respectively. For the atomic color codes, see Figure 1.
Molecules 29 00070 g004
Molecules 29 00070 sch003
Scheme 3. Structural formulas of MO2PBN, BrMO2PBN, syn-CS-MesBN, and anti-C2-MesBN.
Scheme 3. Structural formulas of MO2PBN, BrMO2PBN, syn-CS-MesBN, and anti-C2-MesBN.
Molecules 29 00070 sch003
Molecules 29 00070 g005
Figure 5. Relative energy levels of triplet and broken-symmetry singlet states, calculated at the UB3LYP/6-311+G(2d,p)//UB3LYP/6-31G(d) level. Optimized geometries were also shown. (a) The SCF energies of syn-MesBN are −924.7811231198 au with <S2> = 2.0095 and −924.7812718628 au with <S2> = 1.0060 for the triplet and singlet states, respectively. (b) The SCF energies of anti-MesBN are −924.7809370560 au with <S2> = 2.0096 and −924.7811143077 au with <S2> = 1.0056 for the triplet and singlet states, respectively. Spin density surfaces are drawn at the 0.002 e− Å−3 level with blue and white lobes for the positive and negative spin densities, respectively. Antiferromagnetic J values are marked in red. For the atomic color codes, see Figure 1.
Figure 5. Relative energy levels of triplet and broken-symmetry singlet states, calculated at the UB3LYP/6-311+G(2d,p)//UB3LYP/6-31G(d) level. Optimized geometries were also shown. (a) The SCF energies of syn-MesBN are −924.7811231198 au with <S2> = 2.0095 and −924.7812718628 au with <S2> = 1.0060 for the triplet and singlet states, respectively. (b) The SCF energies of anti-MesBN are −924.7809370560 au with <S2> = 2.0096 and −924.7811143077 au with <S2> = 1.0056 for the triplet and singlet states, respectively. Spin density surfaces are drawn at the 0.002 e− Å−3 level with blue and white lobes for the positive and negative spin densities, respectively. Antiferromagnetic J values are marked in red. For the atomic color codes, see Figure 1.
Molecules 29 00070 g005
Molecules 29 00070 g006
Figure 6. Plot of the exchange coupling constant, 2J, vs. the averaged out-of-conjugation torsion angle, θ = (|θ1| + |θ2|)/2. For the definition of θ1 and θ2, see Scheme 2, and the angular error bar implies |θ1| and |θ2|. The experimental and calculated 2J data are marked in filled and open circles, respectively. The lines represent an empirical linear relationship.
Figure 6. Plot of the exchange coupling constant, 2J, vs. the averaged out-of-conjugation torsion angle, θ = (|θ1| + |θ2|)/2. For the definition of θ1 and θ2, see Scheme 2, and the angular error bar implies |θ1| and |θ2|. The experimental and calculated 2J data are marked in filled and open circles, respectively. The lines represent an empirical linear relationship.
Molecules 29 00070 g006
Table 1. Selected bond lengths, angles, and dihedral (torsion) angles for TF2PBN, 1, and [Mn(hfac)2(TF2PBN)2].
Table 1. Selected bond lengths, angles, and dihedral (torsion) angles for TF2PBN, 1, and [Mn(hfac)2(TF2PBN)2].
CompoundTF2PBN 11[Mn(hfac)2(TF2PBN)2]
N1–O11.2863(19)1.2842(16)1.294(3)
N2–O21.2826(13)1.2850(16)1.2779(17)
N1–C21.423(8)1.4389(16)1.421(3)
N2–C61.4361(14)1.4393(16)1.433(2)
N1–C71.505(3)1.5043(17)1.512(5)
N2–C101.5051(16)1.5004(17)1.499(4)
O1–N1–C2115.80(15)116.44(11)115.9(2)
O2–N2–C6116.58(9)115.83(11)115.74(15)
O1–N1–C7117.8(3)118.29(11)117.59(18)
O2–N2–C10119.81(8)117.73(11)119.63(12)
C2–N1–C7126.36(18)124.33(11)126.47(12)
C6–N2–C10123.58(9)124.12(11)123.56(13)
N1–C2–C1119.55(9)117.96(12)118.23(19)
N1–C2–C3121.0(3)121.94(12)121.83(13)
N2–C6–C1118.85(9)118.30(12)118.84(19)
N2–C6–C5121.4(3)121.53(11)121.15(15)
O1–N1–C2–C1126.69(11) 2101.2262(14)130.08(16) 3
O1–N1–C2–C3−48.78(14) 2−74.9312(14)−46.05(19) 3
O2–N2–C6–C1−107.53(14) 2−91.264(2)−94.9(2) 3
O2–N2–C6–C569.65(15) 284.7612(19)81.4(2) 3
O1⋯O26.339(16) 25.8868(1)6.231(11) 3
referenceref. [36]this workRef. [37]
1 Measured at 50 K. 2 Calculated in Olex2 [40] from CCDC 182/1278 [36]. 3 Calculated in Olex2 [40] from CCDC 151603 [37].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Haga, N.; Ishida, T. A Triplet/Singlet Ground-State Switch via the Steric Inhibition of Conjugation in 4,6-Bis(trifluoromethyl)-1,3-phenylene Bisnitroxide. Molecules 2024, 29, 70. https://doi.org/10.3390/molecules29010070

AMA Style

Haga N, Ishida T. A Triplet/Singlet Ground-State Switch via the Steric Inhibition of Conjugation in 4,6-Bis(trifluoromethyl)-1,3-phenylene Bisnitroxide. Molecules. 2024; 29(1):70. https://doi.org/10.3390/molecules29010070

Chicago/Turabian Style

Haga, Nagito, and Takayuki Ishida. 2024. "A Triplet/Singlet Ground-State Switch via the Steric Inhibition of Conjugation in 4,6-Bis(trifluoromethyl)-1,3-phenylene Bisnitroxide" Molecules 29, no. 1: 70. https://doi.org/10.3390/molecules29010070

APA Style

Haga, N., & Ishida, T. (2024). A Triplet/Singlet Ground-State Switch via the Steric Inhibition of Conjugation in 4,6-Bis(trifluoromethyl)-1,3-phenylene Bisnitroxide. Molecules, 29(1), 70. https://doi.org/10.3390/molecules29010070

Article Metrics

Back to TopTop