2.1. OPA Spectrum
Triangulene consists of six aromatic benzene ring-like units with radial p-orbitals. The presence of two unpaired electrons [
26] exists in a single triangulene. Under optical excitation, the two unpaired electrons form electron–hole pairs, which determine the optical absorption properties of triangulene; these pairs have a spin-chain structure containing multiple unpaired electrons. Some relevant information is given in
Figures S1–S3. The spin density distribution is shown at the edges of the serration [
26] (
Figure S3). This distribution can hinder or prevent the compounding of photoexcited electron and hole pairs in the catalyst and the promotion of photogeneration for electron–hole pairs [
27].
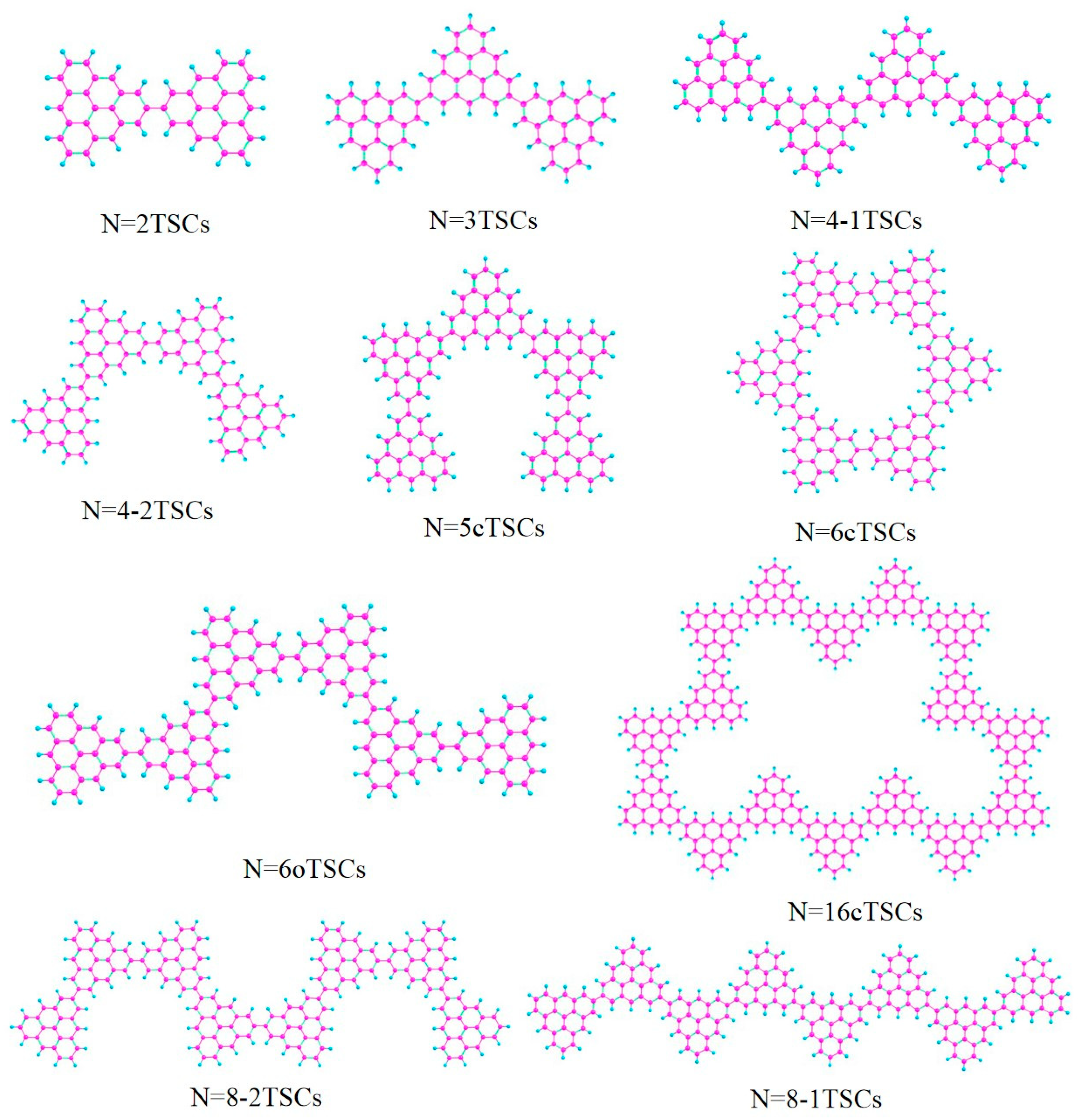
In order to investigate the effect of conformational changes on the optical absorption properties of TSCs, we selected several TSCs that were representative of conformation (
Figure 1). On the basis of the TSCs (N = 2TSCs) connected by two triangulene units, the TSCs units were added, and the triangulene connection sites were changed. We then constructed 10 kinds of TSC quantum dots with different structures and periodic micro-nano sizes. Each two adjacent triangulene units were joined in such a way that the C-C bond centers at the junction points were combined as an axis of symmetry. The corresponding OPA spectra are presented in
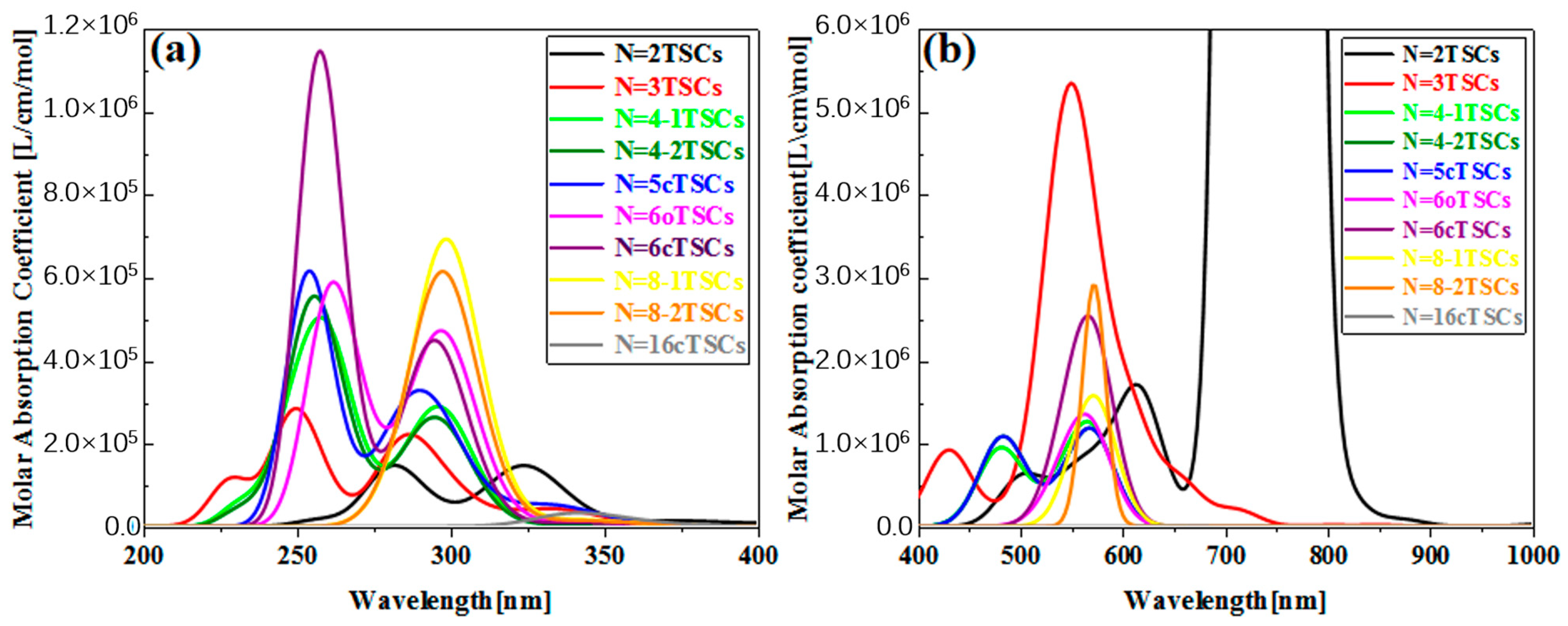
Figure S1. The vertical coordinate is the molar absorption coefficient, the magnitude of which can be used to compare the probability of electrons transitioning between the energy levels of different compounds. Their absorption peaks are located in the UV region between 200 and 400 nm and consist mainly of two strong absorption peaks. The primary absorption peaks of N = 2, 3, 4-1, 4-2, 5c, 6, 6cTSCs were caused by S
73, S
66, S
62, S
62, S
91, S
94, and S
98, and the secondary absorption peaks were caused by S
38, S
37, S
36, S
35, S
55, S
53, and S
55, respectively. Since N = 3TSCs also has an excited state with a similar vibronic intensity near S
66, when the intensity of an oscillator is broadened into the curve of the absorption spectrum, it is subjected to the intensity of that oscillator and forms an even stronger absorption peak. Thus, although S
37 has a higher oscillator intensity, it has a smaller molar absorptivity. With the addition of a triangulene unit, the two main absorption peaks of N = 4-1TSCs were red-shifted. The main absorption peak was shifted to 261.1 nm, caused by S
62, and the secondary absorption peak was caused by S
36 near 297 nm (
Figure S1c).
Figure S1d shows the OPA spectrum of 4-2TSCs with a main absorption peak of
= 261.4 nm, caused by S
62. The secondary absorption peak was caused by S
35 at 297.1 nm, which is spectroscopically very close to N = 4-1TSCs. This small gap may have occurred because triangulene forms two completely different conformations due to different attachment sites, resulting in different excitation energy between the two configurations at the same wavelength. This difference leads to an increase with increasing size, indicating that the change in conformation has a significant effect on the optical absorption properties of triangulene. When the TSCs form a closed six-membered ring,
= 257.6 nm of the main absorption peak of the N = 6c TSCs is caused by the excited state S
98, and the secondary absorption peak is caused by S55 near 294.5 nm (
Figure S1g). The distinctive feature of the absorption spectrum of N = 6cTSCs is greatly enhanced absorbance. The main absorption peaks show a color enhancement effect, mainly due to the large vibrational intensity of the system.
Figure 2b shows the TPA spectrum of triangulene. The vertical coordinate is the TPA cross-section. TPA is a third-order nonlinear optical absorption process caused by the absorption of two photons at twice the excitation wavelength of OPA. The main absorption peak of the TPA spectrum is located at 600–800 nm. Therefore, compared to the OPA spectrum, the main site is excited by high-energy-region photoluminescence, which can effectively avoid optical damage to the material caused by the excitation beam. For TPA, attention needs to be paid to excited states with large TPA cross sections.
Figure S2 shows the TPA spectra of four triangulene spin chains with large two-photon cross sections. After changing the attachment point of triangulene,
= 544.5 nm for N = 3TSCs, where the absorption peak is mainly caused by S
50;
= 573 nm for N = 4-1TSCs, where the absorption peak is mainly caused by S
40; and
= 573.6 nm for N = 4-2TSCs, with absorption peaks mainly caused by S
40 and reduced two-photon cross sections compared to N = 4-1TSCs. After changing the connection point of triangulene, N = 4-2TSCs and
= 573.6 nm. Here, the absorption peak is mainly caused by S
40, and the two-photon cross-section decreases compared to N = 4-1TSCs; N = 6cTSCs and
= 573.8 nm are mainly caused by S
60.
Figure S2 presents a composite diagram of the two-step transition summation terms of the four configurations of the TPA spectra. It can be seen that the molar absorption intensity of TPA with N = 3TSCs is the largest. In addition, the TPA peak of N = 6cTSCs changes from two to one, mainly because the excited state of the two-photon cross-section is concentrated around 550 nm.
In order to study the physical mechanism of the change in absorption spectrum caused by the change of the triangulene spin chain configuration in essence, it is necessary to analyze the transition density matrix (TDM) of excited states. For a single electronic state, the density matrix is a disguised form of the wave function of a specific electronic state. TDM can reflect the transition between two states, and the electronic distribution from the ground state to the excited state can be easily obtained, enabling one to determine and analyze the detailed optical absorption characteristics of the triangulene spin chain. The real spatial form of TDM between the ground state and excited state in a multi-electron system is as follows:
where
is the ground state wave function,
is an excited state wave function,
is the spin + space coordinate of the electron,
is the spin coordinate, and
is the space coordinate. When calculating the excited state using TDDFT with the reference method, the excited state wave function is described by the linear combination of various single excited configuration functions, and TDM is expressed as
where TDM is a six-dimensional function. The, take the diagonal elements of Formula (2) to obtain the three-dimensional transition density
:
where, the transition of orbital electrons from occupied orbit
to empty orbit
can be easily observed through image processing. The larger the
is, the more obvious the overlap of the
and
orbits becomes. Generally, electron excitation includes the excitation of multiple orbitals, so it is broadly described as “hole → electron”. The definition of a hole is as follows:
which is composed of the local term
and the
cross term, where
is the coordinate vector,
is the orbital wave function,
or
is the occupied orbital label,
or
is the empty orbital label, and the definition of the electron is similar. When the absolute value of the product of the wave functions of the two orbits is large, the greater the transition density is, the greater the overlap of the corresponding
and
orbits becomes. Conversely, the smaller the absolute value of the product of the two orbital wave functions is, the smaller the overlap of
and
becomes. Therefore, it can be approximately considered that the place with high transition density will present a large overlap of holes and electrons.
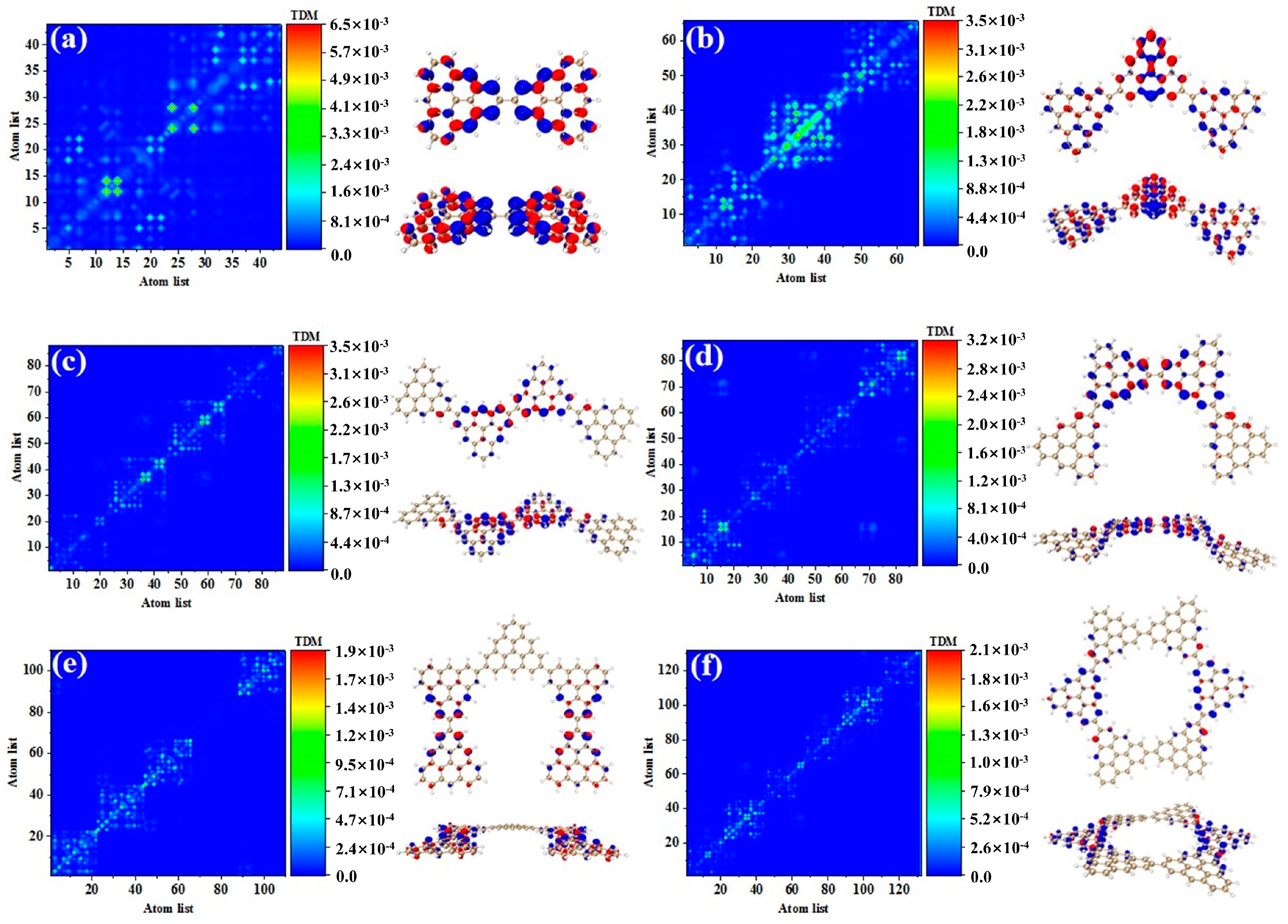
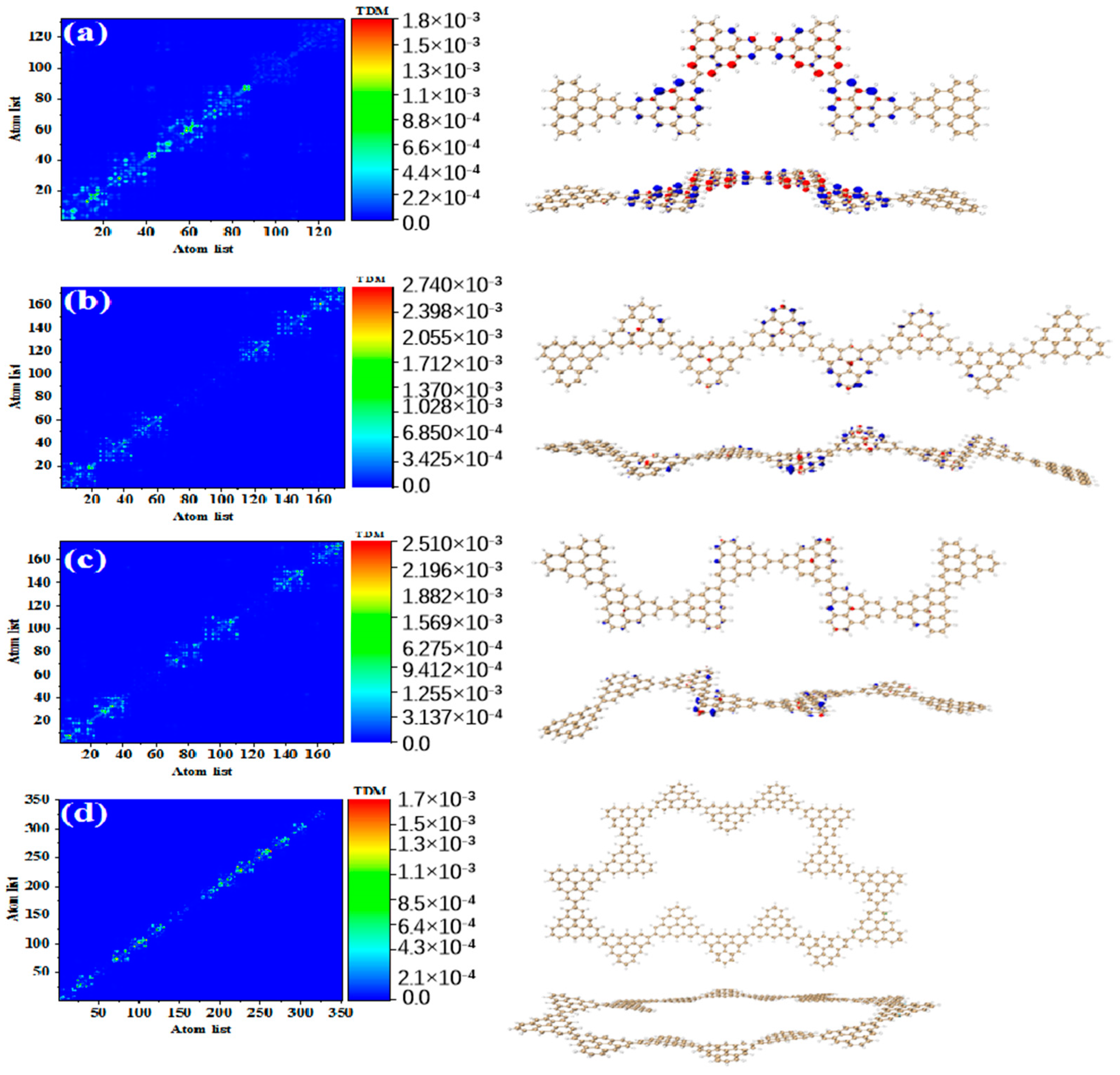
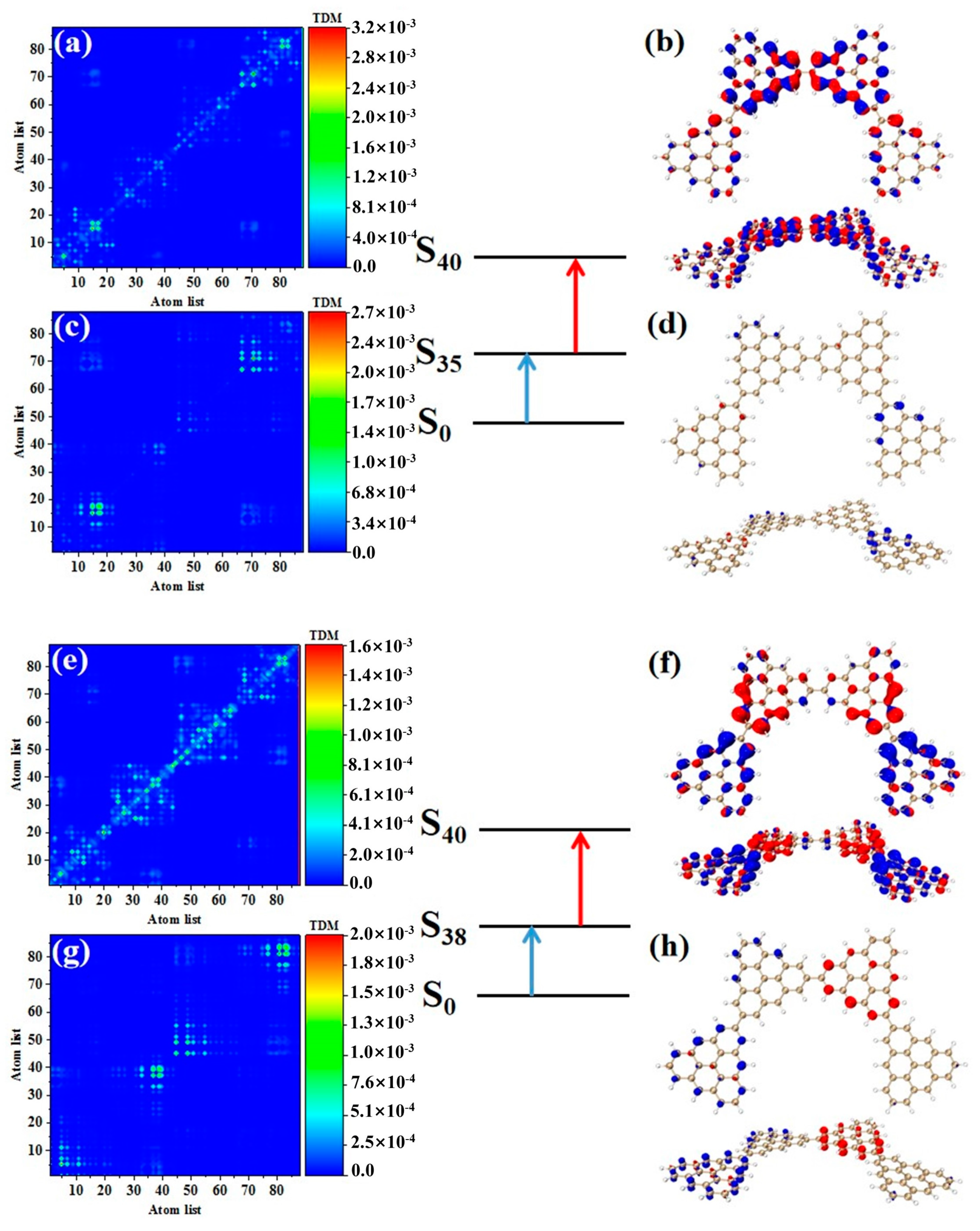
Figure 3 shows the TDM and hole-electron pair density of the secondary absorption peak of the triangulene spin chain with different configurations. TDM is displayed in the form of a heat map, and the abscissa and ordinates are atomic numbers. The brighter the matrix element color is, the greater the transition density is.
Figure 3a shows the TDM and hole-electron pair density of N = 2TSCs in S
38. TDM shows that there are significant green and yellow areas on the main diagonal. There are also some transition density distributions on both sides of the main diagonal, which are caused by the charge transfer. The density of the hole-electron pairs shows that the holes are mainly distributed at the junctions of two triangulene sheets, and the electrons are distributed on both sides. Therefore, the electronic transition of S
38 has obvious charge transfer characteristics. After adding a triangle, TDM shows that the transition density is almost completely distributed on the main diagonal, corresponding to atoms 25–40, namely, the triangle unit in the middle of the triangulene dimer. The blue isosurface on the hole-electron pair represents the area where the electron decreases during the electron transition, and the red isosurface represents the area where the electron increases. In addition to a small number of hole-electron pairs on the triangulene units on both sides, the main isosurface is distributed on the triangulene in the middle, which is very consistent with the distribution of transition density, as shown in
Figure 3b. In addition to the relatively high transition density of the intermediate triangulene, there are two areas with weak brightness at the upper-left and upper-right sides of the TDM, which represent the transition density on the left and right sides of the triangulene trimer, respectively. Because these transition densities are mainly distributed on the diagonal, the TDM reflects the local excitation characteristics between adjacent carbon atoms. After adding a triangulene unit, the main diagonal of TDM shows two connected areas with similar brightness, which can be speculated to represent the local excitation of the middle two pieces of triangulene in N = 4-1TSCs. The hole-electron pair density diagram on the right also indicates that the hole-electron is mainly distributed at the connection point of the middle two pieces of triangulene, as shown in
Figure 3c. After changing the connection point of triangulene, the distribution of bright areas on TDM is similar, belonging to the local excitation of the middle two pieces of triangulene, as shown in
Figure 3d. The ring triangulene spin chain composed of five triangulene N = 5cTSCs also belongs to local excitation in S
55, and the hole-electrons are mainly distributed at the junction of triangulene units on both sides (
Figure 3e). After triangulene forms a closed six-member ring, TDM shows that the transition density is also divided into two bright regions, but the transition density of this system is the smallest of the four configurations. From the perspective of the density of hole-electron pairs, the distribution of the hole-electron-equivalent surface is central symmetry. At the same isosurface value (iso value = 0.001), the density of the hole-electron pair is the smallest (
Figure 3f), which shows that the electron transition is weakened in this stable ring structure.
Compared to the secondary absorption peak, the main absorption peak has higher oscillator strength. This result shows that the absorption intensity of the system is enhanced.
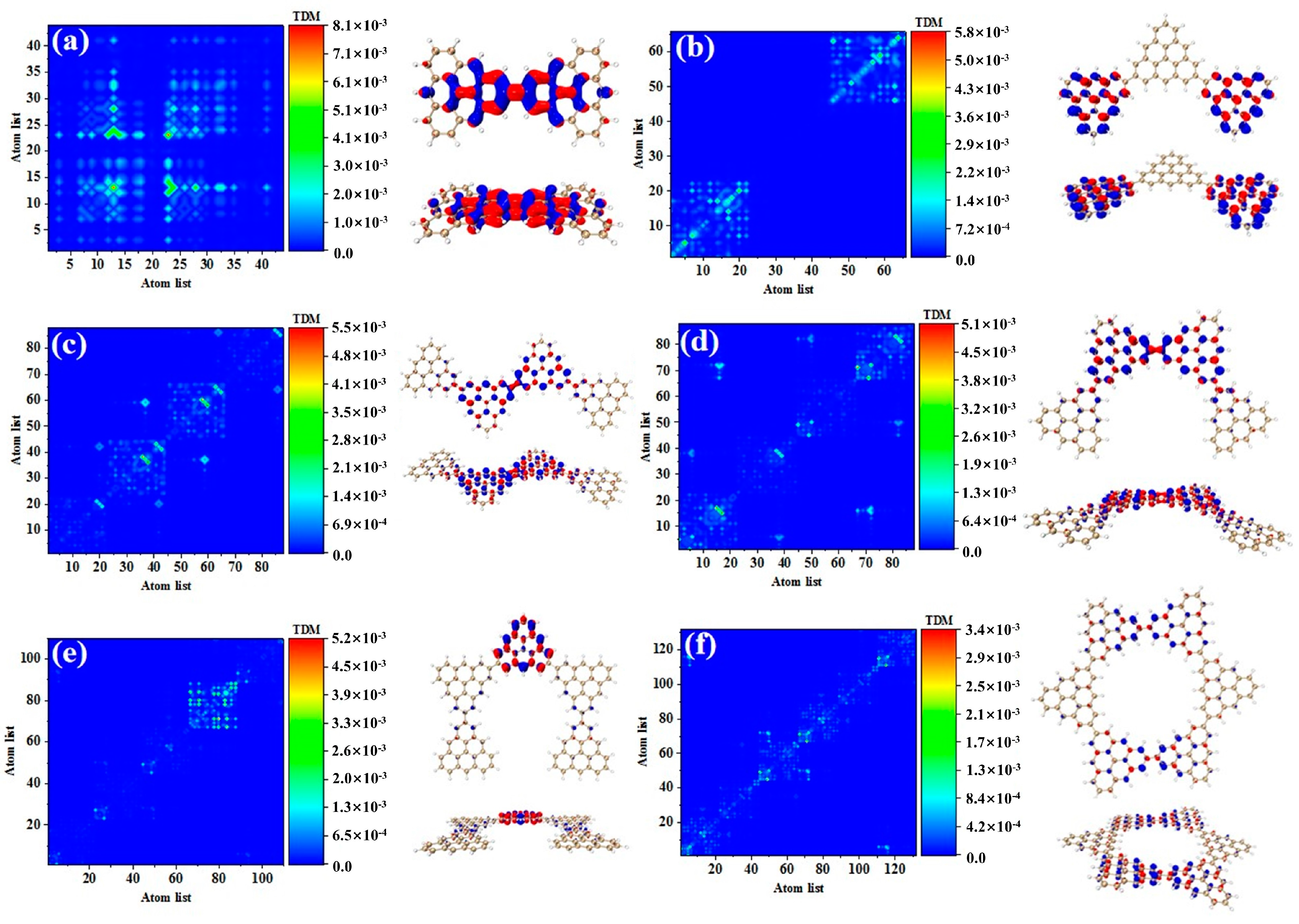
Figure 4 shows the TDM and hole-electron pair densities of the excited states of the main absorption peak of the triangulene spin chain with different configurations. The TDM of N = 2TSCs shows that the excitation characteristics of S
73 belong to local excitation and the hole-electrons overlap at the junction of two triangulene units, as shown in
Figure 4a. The excitation characteristics of N = 3TSCs in S
66 are opposite to the secondary absorption peak. From the TDM, the bright yellow and green areas are mainly located at the lower left and upper right areas of the main diagonal. Compared to S
37, the distribution range of the bright regions is greatly enlarged, and their atomic numbers correspond to triangulene on both sides of the system. From the perspective of hole-electron pair density, the hole-electron isosurface is very significant and almost completely distributed on both sides of triangulene, belonging to local excitation between adjacent carbon atoms of triangulene on both sides, as shown in
Figure 4b. The electron excitation of N = 4-1TSCs in S
62 was transferred to the middle two triangulene units. TDM shows that compared to S
36, the degree of electronic excitation is enhanced. Based on the density of the hole-electron pairs, there is also electron distribution on the middle two triangulene junction points, as shown in
Figure 4c. After changing the connection point, the electronic excitation characteristics of N = 4-2TSCs in S
62 also belong to local excitation, as shown in
Figure 4d. The electronic transition of N = 5cTSCs in S
91 comes from the triangulene unit in the middle part, which belongs to local excitation, as shown in
Figure 4e. The degree of electronic excitation in the closed six-member ring in S
98 is still the smallest, belonging to weak local excitation. Compared to the secondary absorption peak, the hole-electron pairs are distributed on the triangulene unit adjacent to the two directions, as shown in
Figure 4f.
Figure 5 shows the TDM and hole-electron pair density of the main absorption peak of the N = 6, 8-1, 8-2, and 16cTSCs, where the N = 8-1, 8-2, and 16cTSCs have only one absorption peak. Compared to the previous structure, the transition density of TDM is only distributed on the main diagonal as the system increases. Here, the isosurface of the hole-electron is significantly reduced, indicating that the degree of electron transition is weakened (
Figure 5a–c). When the quantum dot is composed of 16 triangulene units, the distribution of the hole-electron disappears, as shown in
Figure 5d.
2.2. Analysis of Transition Index of Excited State
Visualization of the TDM and hole-electron pair density is used to qualitatively investigate the electronic transition characteristics of excited states. In order to investigate the characteristics of electron excitation, the wave function analysis of electronic states is also needed from a quantitative perspective. We also calculated the transition index of one-photon excited states and selected four triangulene spin chain structures, as shown in
Table 1. The
H index represents the overall distribution breadth of hole-electron pairs, which is defined as
where
and
are used to characterize the spatial distribution breadth of electrons and holes, including the root mean square difference of the distribution of electrons and holes in the three directions of xyz.
in the direction of
is defined as
It can be seen that the
H index of the excited state at the secondary absorption peak increases with size, which is caused by a gradual increase in the system structure. In addition, the configuration change will cause a change in excited state energy, with the excitation energy of S
37 being the largest among the four configurations. The D index is the distance between the hole and the electron centroid, which is derived from the Cartesian coordinates of the hole and the electron centroid and obtained from the following formula:
The
D index of N = 3TSCs in S
66 reached 0.173 Å, which is the largest among all one-photon excited states. This result was mainly due to the location of the hole-electron exchange on both sides of the triangulene. Additionally, on a triangulene, the holes are mainly distributed at the edge of the triangulene, while the electrons are mainly distributed in the interior. Therefore, compared to other excited states, the electron migration path in S
66 is longer. Corresponding to the distance between the centroid of the hole-electron is the separation degree t of the electron and the hole, which is defined as
where
is the average extent of electrons and holes in the direction of charge transfer,
and
are the vector sum of the average extent of holes in the three directions of xyz, and
is the unit vector in the direction of charge transfer. Generally, a combination of these two indexes can be used to examine the strength of charge transfer in the process of electron excitation.
Table 1 and
Table 2 show that all excited states
t < 0, indicating that there is no significant separation of holes–electrons in the direction of charge transfer because the distance between the center of mass of the hole and the electron is far less than their average extension on the triangulene spin chain. We also define the
index, which is used to characterize the coincidence degree of electrons and holes. The physical meaning of this index is opposite to that of the
index. The definition is as follows:
This index is the full space integral of the function . When the value is 1, the electron and hole completely coincide. Based on the table, the Sr indexes of all excited states are very close to the maximum value of 1, indicating that the overlap of electrons and holes is quite large. The above analysis of the transition index of the electronically excited states shows that local excitation between adjacent carbon atoms dominates the electronic transition of the triangulene spin chain quantum dots. After adding triangulene, with the growth of the conjugated chain, the energy difference between the levels of the triangulene spin chain decreases. This decrease reduces the excitation energy of electrons and causes absorption to move toward the long wave spectrum.
2.4. Two-Photon Transition
Photon-excited spectral analysis shows that the absorption of the triangulene spin chain is located in the ultraviolet region, which limits its application. Here, the large-section TPA with two photons at the same time under an intense laser pulse presented many excellent characteristics, such as the ability to produce an excited state with half the nominal excitation energy, improve the penetration ability of the absorbing or scattering medium, and transfer the optical absorption to the visible light region, greatly improving the application ability. Therefore, we calculated the first and second transition characteristics for the TPA of the triangulene spin chain through the three-state model [
1,
2] of Formula (1).
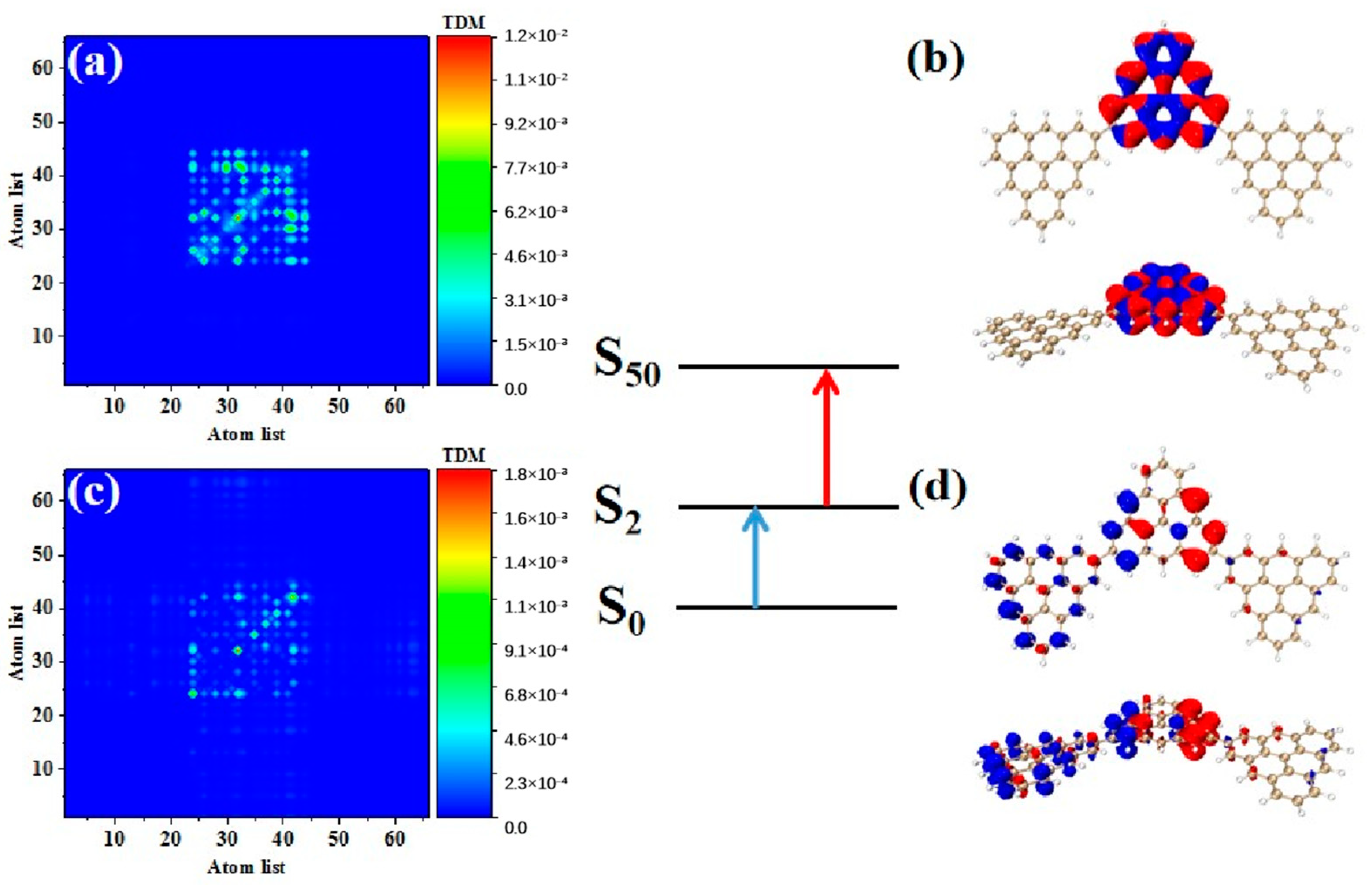
Table 3 shows the transition dipole moment elements of the maximum two-photon cross-section. Here, N = 3TSCs have the largest TPA cross section among the four configurations, and the maximum value is caused by the two-step transition of S
50.
Figure 7a,b show the TDM and hole-electron pair density from the ground state to the excited state (
). The TDM shows that the transition density is mainly distributed in the middle of the diagonal, and the hole-electron density value is concentrated on the intermediate triangulene. Therefore, the first step of transition belongs to strong local excitation between adjacent carbon atoms on the intermediate triangulene. The second transition comes from the second part of Formula (1), that is, the electronic transition from the excited state to the final state (
). TDM shows that in addition to the transition density on the main diagonal, there are weak bright areas on the non-diagonal, as shown in
Figure 7c. Combined with the density of hole-electron pairs, it can be seen that the electrons transfer from the left triangulene of N = 3TSCs to the middle triangulene, as shown in
Figure 7d. Therefore, the second transition can be observed as local charge transfer excitation.
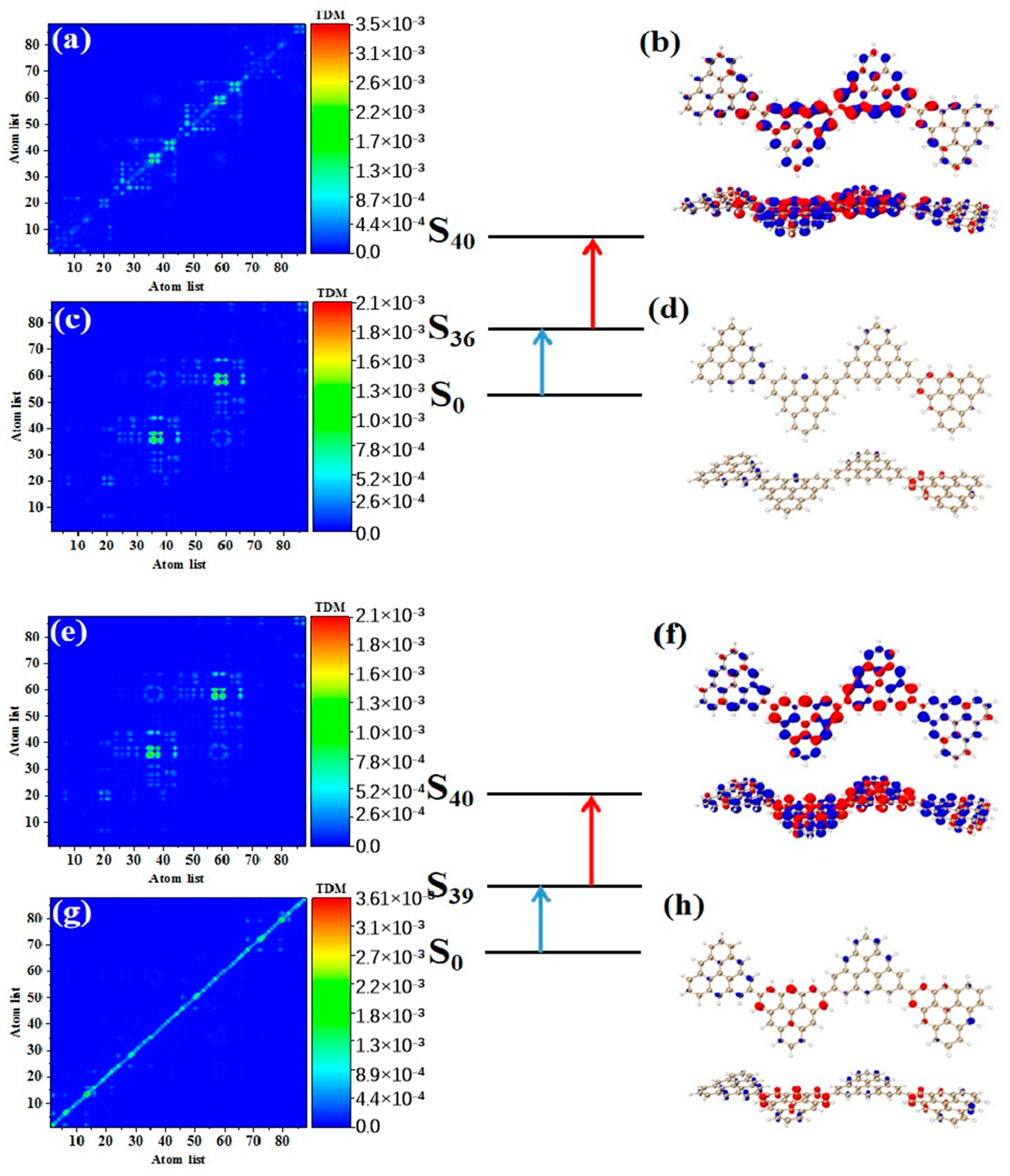
As shown in
Table 3, after adding one triangulene, the maximum two-photon cross section of N = 4-1TSCs has an S
40 contribution, and its two-photon transition consists of two channels, where the intermediate state of channel I is S
36. From the perspective of TDM and hole-electron pair density, the first step of transition
belongs to local excitation between the two adjacent atoms of the middle triangle alkene, as shown in
Figure 8a,b. The transition density of transition
in the second step is significantly lower than that in the first step, and there is almost no hole-electron pair density (
Figure 8c,d). When the intermediate state is S
36, the TPA is mainly caused by the first step. The intermediate state of the other channel in the two-photon transition of S
40 is S
39. The TDM of
shows that the first step of the transition still belongs to local excitation. Compared to channel I, the degree of local excitation is enhanced. Based on the distribution of the hole-electron pair density, the hole-electron distribution has a very obvious distribution on the four triangles (
Figure 8e,f), and the transition characteristics of the second step of transition
are similar to those of channel I. The two-photon transition of N = 4-1TSCs shows that the TPA of the triangulene spin chain is mainly caused by the first transition after the system increases.
It can be seen from the TPA spectrum in
Figure 2 that after changing the triangulene junction point, the absorption spectra of two triangulene spin chains with the same size are very similar.
Table 3 shows that the maximum two-photon cross section of N = 4-2TSCs is caused by S
40 and consists of two channels. The dipole moment distance of the first step is smaller than that of the second step. The intermediate state of channel I is S
35, and the TDM and hole-electron pair density of the two-step transition is very similar to those of N = 4-1TSCs, as shown in
Figure 9a–d. The other channel, the intermediate state, is S
38. The TDM of
shows that in addition to the relatively large transition density on the diagonal, there is also significant transition density distribution in the non-diagonal region, as shown in
Figure 9e. Based on the density of hole-electron pairs, the electrons are mainly concentrated on the two triangulene units in the upper half, as shown in
Figure 9f. This result indicates that the electron transfer direction extends from the two triangulene units in the lower part to the adjacent triangulene units in the upper part, presenting the characteristics of charge transfer. The second transition
belongs to weak charge transfer excitation, as shown in
Figure 9g,h. Therefore, a comparison of the two configurations shows that the charge transfer ratio of the two-step transition can be significantly increased by changing the triangulene junction point, and the electronic transition ability can be enhanced.
After triangulene forms a closed six-member ring, the maximum two-photon cross-section is caused by S
61. The two-photon transition process includes two channels. The intermediate state of channel I is S
56. From the perspective of TDM, the first step of transition
belongs to local excitation. As shown in
Figure 10a, the density of the hole-electron pairs shows that the hole-electrons are distributed on the adjacent triangulene units on the upper and lower sides (
Figure 10b). Combined with the second transition characteristics of the triangulene spin chain in the previous three configurations, we found that with a further increase in size, the electronic transition degree of the second transition of N = 6cTSCs further decreased, and the distribution of hole-electrons almost disappeared (
Figure 10c,d). The intermediate state of channel II is S
55, and the first step of transition
also belongs to local excitation. The second step of transition
has the same excitation characteristics as channel I. However, unlike channel I, the hole-electron distribution is exactly the opposite, with hole-electrons mainly distributed on left and right single triangulene units.
2.6. Chiral Physical Mechanism
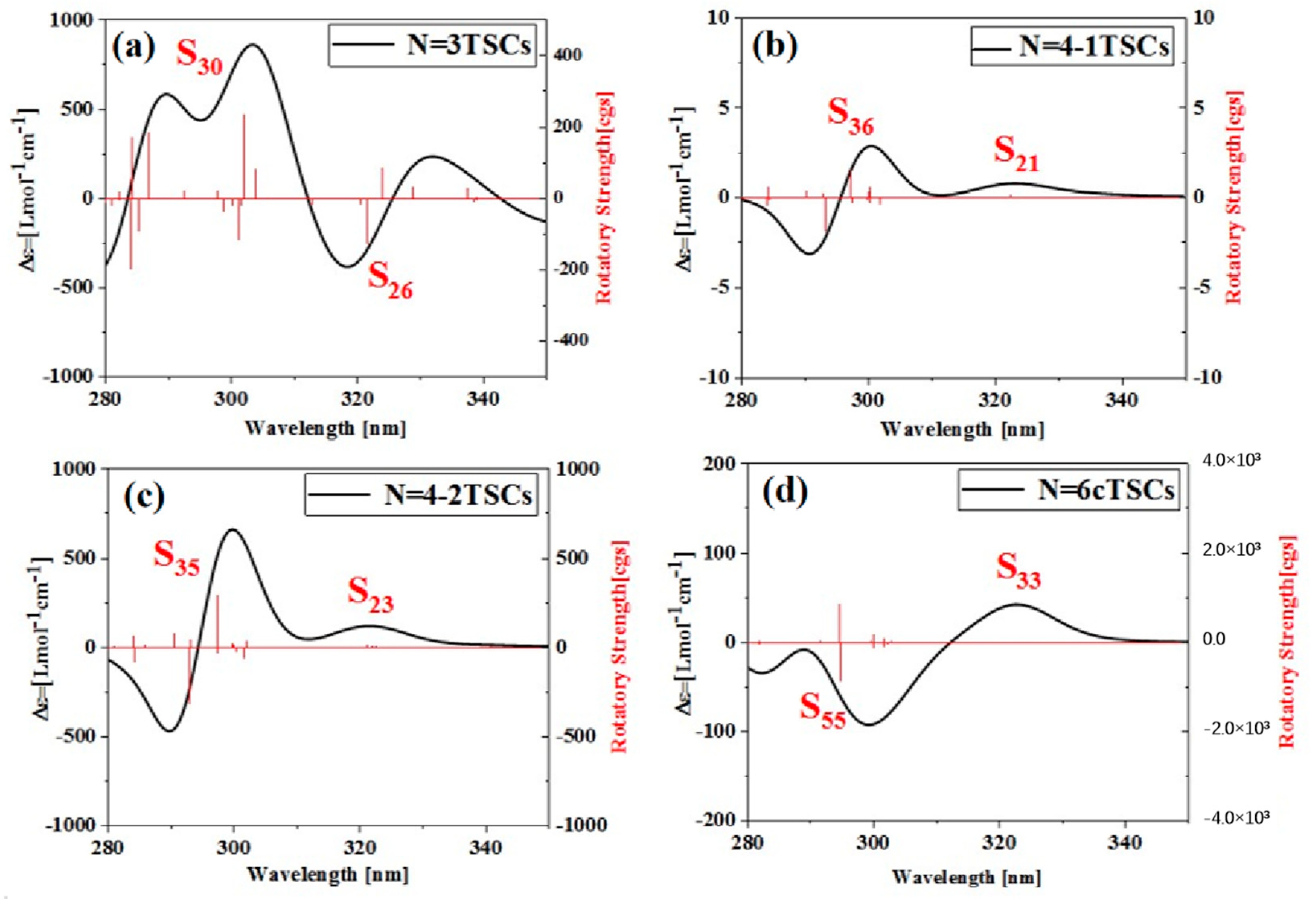
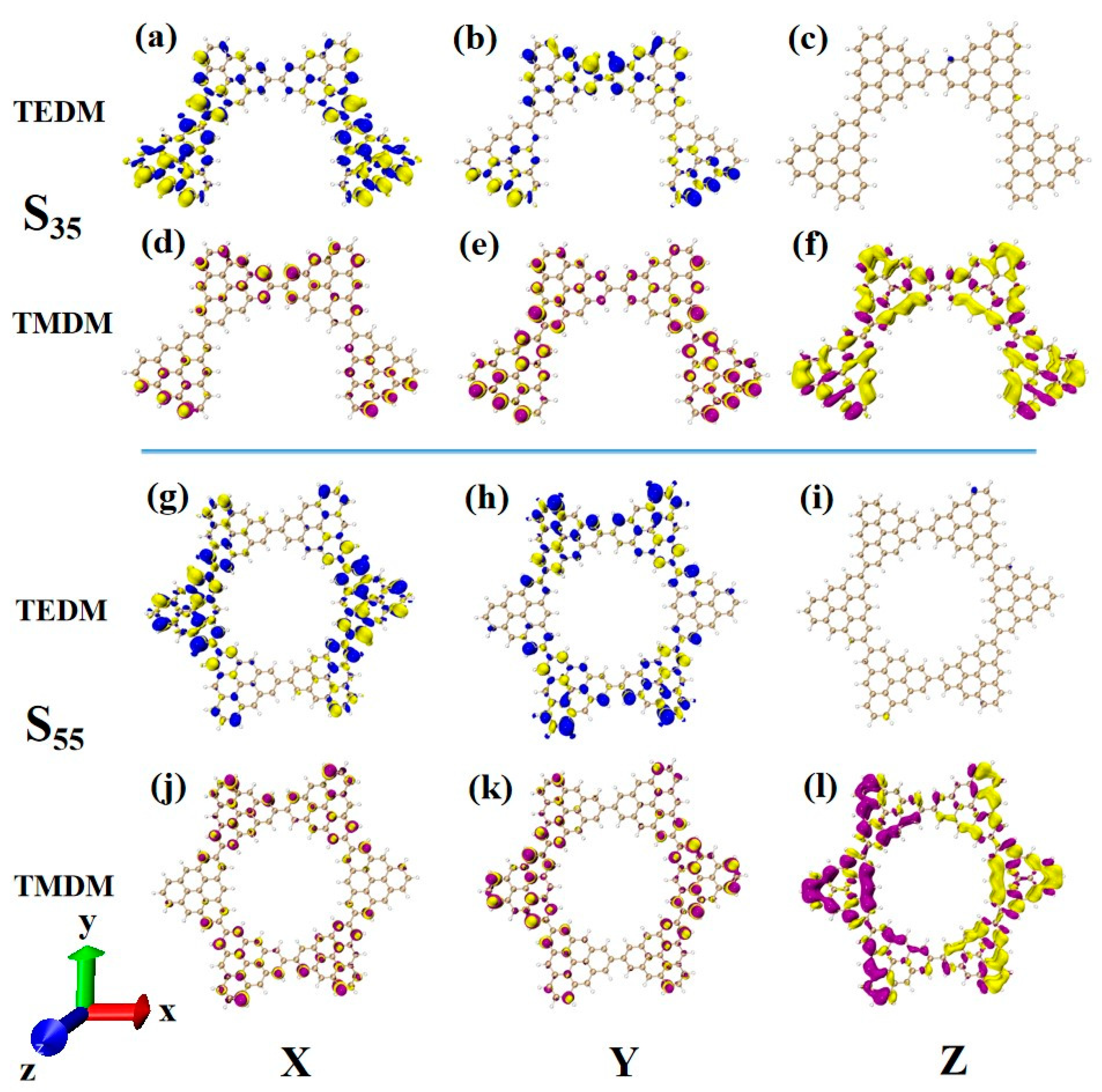
In order to deeply analyze the physical mechanism of ECD chirality inversion after the configuration changes of TSCs, the visual transition electric dipole moment density (TEDM, where the positive value is purple, and the negative value is yellow) and transition magnetic dipole moment density (TMDM, where the positive value is blue, and the negative value is yellow) are drawn, and the isosurface value is set to 0.008. At 321.4 nm, N = 3TSCs have a strong transition dipole moment in the X component, mainly distributed on the triangulene sheets on both sides. There is almost no transition dipole moment density on the Y and Z components, as shown in
Figure 12a–c. The transition magnetic dipole moment is mainly distributed on the Y and Z components, with a large isosurface; these components are clustered on the triangulene sheets on both sides, as shown in
Figure 12d,f. After adding a triangulene unit, the distribution of the transition electric dipole moment density and the transition magnetic dipole moment density of the two configuration molecules are the same in the Z component, but there are significant differences in the X and Y components. The isosurface of the transition dipole moment density on the three components is not very large. The transition dipole moment on the Y component spreads to the entire triangulene spin chain, as shown in
Figure 12g–i. The distribution of the transition magnetic dipole moment density is also similar, and the transition magnetic dipole moment on the X component also presents a diffusion distribution trend, as shown in
Figure 12j–l. Therefore, overall, the transition electric dipole moment and transition magnetic dipole moment of N = 4-1TSCs are less than those of N = 3TSCs. The transition dipole distance density of N = 4-1TSCs on the X component is mainly distributed on the middle two triangulene units. However, the transition magnetic dipole moment is mainly distributed on both sides. The Y component is exactly the opposite, with the transition electric dipole moment density distributed on both sides and the transition magnetic dipole moment density distributed in the middle, and the distribution range is complementary. In this case, the transition electric dipole distance and transition magnetic dipole strength are completely opposite in the same direction on N = 3TSCs because TEDM and TMDM can reveal the responses of molecular and electromagnetic waves of triangulene spin chains in the process of light excitation. Because the direction of the electric field and the magnetic field are vertical, the distribution range of these fields is complementary. In addition, from the perspective of rotor strength, ECD shows that the circular dichroic absorption intensity of N = 4-1TSCs became significantly reduced. According to Formula (6) in
Section 2.3, the rotor strength depends on the tensor product
of electricity and magnetism in three directions. Because the transition electric dipole moment and transition magnetic dipole moment of N = 4-1TSCs on the X and Y components are small, the overall tensor product becomes smaller; ultimately, the smaller rotor strength can be determined.
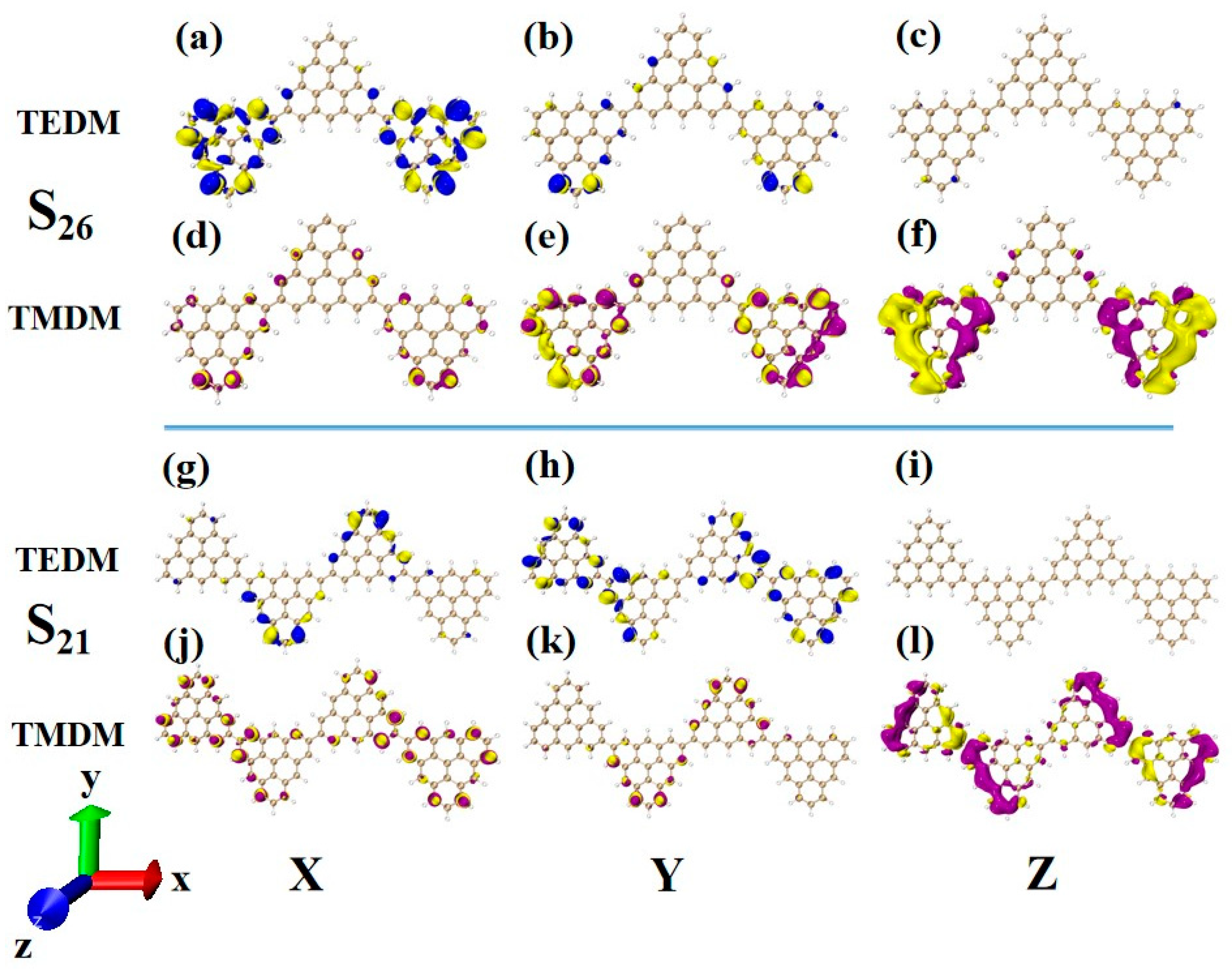
Another ECD excited state of N = 3TSCs is S
30. Compared to S
26, the transition electric dipole moment density and transition magnetic dipole moment density of S
30 in the three components are similar, but the distribution trend is very different. The yellow isosurface and purple isosurface of S
26 on the Y and Z components are relatively independent, so the positive and negative values of the transition magnetic dipole moment are highly separated, as shown in
Figure 13a–c. The positive and negative values of the transition magnetic dipole moment density of S
30 on the Y and Z components are evenly distributed, as shown in
Figure 12d–f, which is why circular dichroism changes from negative to positive. After adding a triangulene unit, the transition electric dipole of S
36 is mainly caused by the Y component, as shown in
Figure 13h. The transition magnetic dipole is mainly caused by the Z component, and the X component also contributes a portion of the transition magnetic dipole moment (as shown in
Figure 13j–l). Compared to N = 3TSCs, the transition dipole moment of these components is mainly caused by a single square quantity. However, the density of the transition magnetic coupling of S
30 is larger in the Y and Z components, while the transition magnetic coupling of S
36 is only larger in the Z component, so the overall tensor product is smaller than S
30, and its rotor strength is also relatively small. Unlike N = 3TSCs, the absorption peak of S
36 still shows positive circular dichroism because the isosurface size of the transition electric dipole moment density and the transition magnetic dipole moment density on the three components of S
36 are similar to those of S
21, and the distribution trends are also similar. In both, the positive and negative values of the transition electric dipole moment are uniformly distributed on the Y component, and the positive and negative values of the transition magnetic dipole moment are separated on the Z component (as shown in
Figure 12g–l and
Figure 13g–l. In addition, since the transition dipole moment of S
36 on the Y component is significantly greater than that of S
21 (
Figure 12h and
Figure 13h), it has strong circular dichroism.
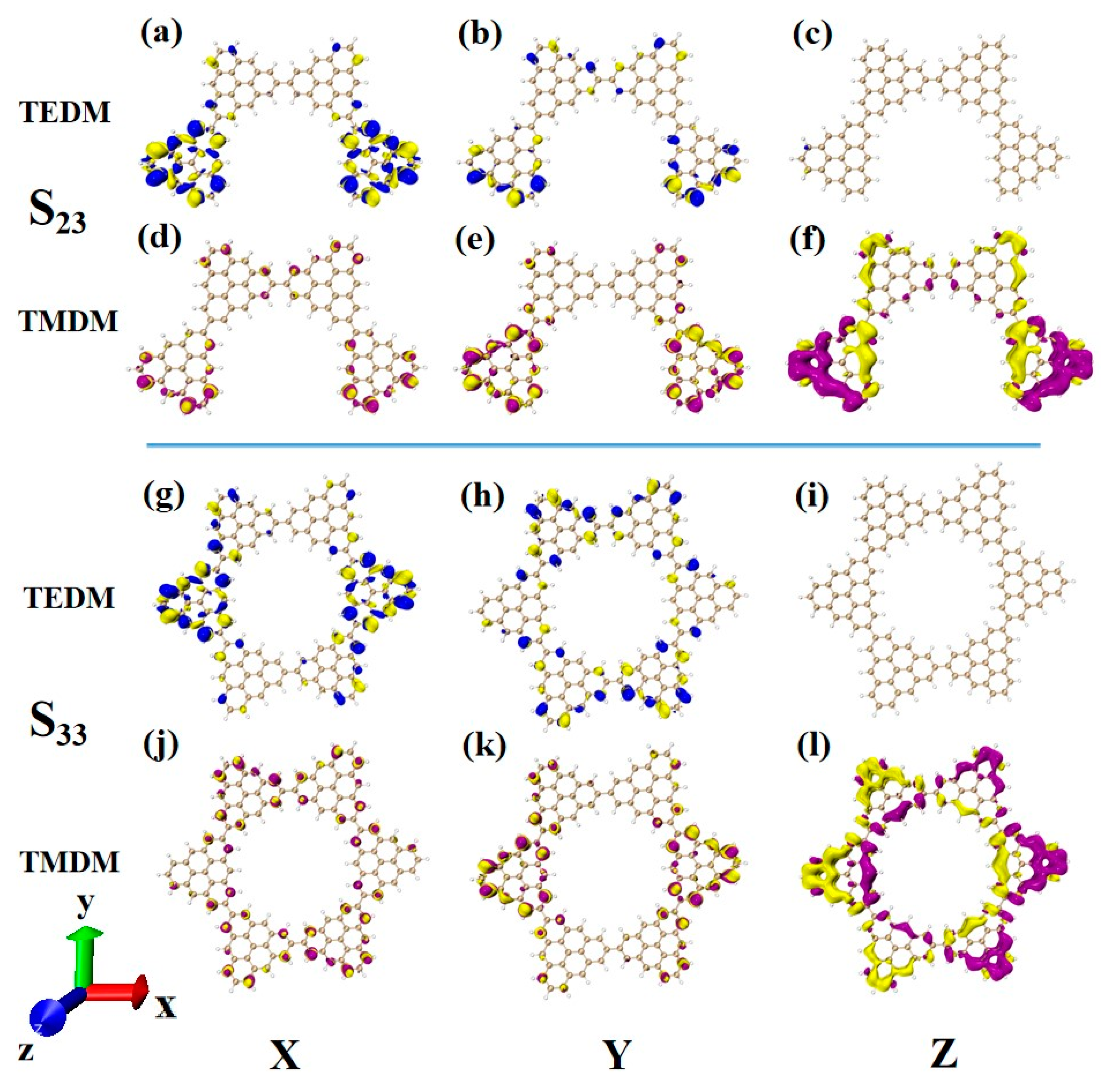
After changing the junction site, the ECD absorption peak of N = 4-2TSs at 320 nm is caused by S
23. The upper part of
Figure 14 shows the density of the transition electric dipole moment and transition magnetic dipole moment of S
23 in Cartesian coordinates. Here, the transition dipole moment is mainly caused by the X component, and there are also some values on the Y component. The transition dipole moment density on the Z component completely disappears, as shown in
Figure 14a,b. The transition magnetic dipole moment is mainly caused by the Z component, with only a small distribution on the X and Y components, as shown in
Figure 14d–f. Compared to N = 4-1TSCs, the transition magnetic dipole moments of the two systems are similar, and the difference between the system and the photon electromagnetic interaction mainly comes from the transition electric dipole moment. When the connection mode of the added triangulene sheet unit and triangulene trimer is in periodic superposition, the distribution of the transition dipole moment on the three components becomes relatively uniform, and the value is relatively small. When triangulene changes the linkage site and triangulene trimer connection, a large transition dipole moment is generated in the X component. Therefore, this semi-closed triangulene spin chain has a larger tensor product of electricity and magnetism and will present greater rotor strength and stronger circular dichroism.
After triangulene forms a closed six-membered ring structure, the absorption peak near 300 nm is mainly caused by S
33. Due to its unique ring structure, the complementary characteristics of the transition electric dipole moment and the transition magnetic dipole moment are more significant than the chain structure, and the distribution trend is similar to that of N = 4-2TSCs (
Figure 14a–f,g–l.) Therefore, the circular dichroism of the two structures at this wavelength is positive.
The main absorption peak of N = 4-2TSCs is caused by S
35, whose circular dichroism is significantly enhanced compared to that of S
23. For the transition dipole moment, the density values on the X and Y components are larger than those of S
23, as shown in
Figure 15a,b. This result mainly shows that the two triangulenes in the upper half of the semi-closed triangulene spin chain also produce a small amount of transition dipole moment density. The change in the transition magnetic dipole moment in the X and Y components is the same. The Z component has an obvious transition magnetic dipole moment density in the whole semi-closed triangulene spin chain, as shown in
Figure 15d–f. The large transition electric dipole moment response and transition magnetic dipole moment response on each component make the rotor strength of S
35 much greater than that of S
23. The circular dichroism of the closed triangulene six-membered ring N = 6cTSCs at 322.6 nm is negative, and greater chiral inversion occurs compared to N = 4-2TSCs at the same wavelength. The distribution of the transition electric dipole moment density and the transition magnetic dipole moment density in the X and Y components of the two configurations is approximate (
Figure 15a–f,g–l). However, there are great differences in the Z component. The transition magnetic coupling of N = 4-2TSCs in the Z component is mainly caused by the yellow isosurface representing a negative value. However, the transition dipole moment density on the closed six-membered ring triangulene spin chain is composed of yellow and purple isosurfaces, and positive and negative values have the same contribution, as shown in
Figure 15f–l. This contribution is due to the uneven distribution of transition magnetic dipole moments caused by changes in the triangulene spin chain configuration, resulting in chiral inversion.