Size–Pore-Dependent Methanol Sequestration from Water–Methanol Mixtures by an Embedded Graphene Slit
Abstract
1. Introduction
| Material | Method | Selective to | Main Result | Ref. |
|---|---|---|---|---|
| Porous BNNS -H, -F -OH | Simulations | Methanol Water | Each molecule has higher free energy in correspondence to the pores it cannot permeate through. | [16] |
| BNNT | Simulations | Alcohols | Alcohols can easily break their hydrogen bonds to enter and occupy the nanotubes, having a strong interaction with them. | [17] |
| Pristine graphene | Simulations | Methanol | Methanol gets preferentially absorbed into a graphene slit pore. When mixed with water, the two liquids couple and diffuse. | [18] |
| Graphite plates | Simulations | Methanol | Preferential absorption of methanol on graphite sheets due to Van der Walls interactions between the methyl groups and the carbon. | [19] |
| GO | Experiments | Water | Low friction flow of a water monolayer through 2D channels between graphene sheets, while helium remains in feed. | [21] |
| SA/PVA | Experiments | Water | ↑ T ⇒ ↑ mobility of the polymer chain⇒ ↑ flux, little selectivity reduction. At 5% PVA composition, the material has surface pores, and at 20% has cracks. Optimum PVA composition at 10%. | [22] |
| PHB | Experiments | Water | Pure substance pervaporation shows good MeOH permeation. It has water selectivity in a mixture due to the hydrogen bond network. MeOH has reduced mobility when mixed with water. | [23] |
| rGO/CS | Experiments | Water | The interlayer space due to the CS leads to molecularly sieve water, and the hydrophobicity of GO provides good flux. | [24] |
| ZIF-8/PVDF ZIF-67/PVDF | Experiments | Water | ZIF-67/PVDF membrane enhances flux due to its hydrophilicity. However, ↑ water % in the feed ⇒ ↑ swelling ⇒ ↓ selectivity as volume increases and MeOH molecules can also pass through. ↑ T ⇒ ↑ polymer chain mobility ⇒ ↑ flux, ↓ selectivity. | [25] |
2. Results and Discussion
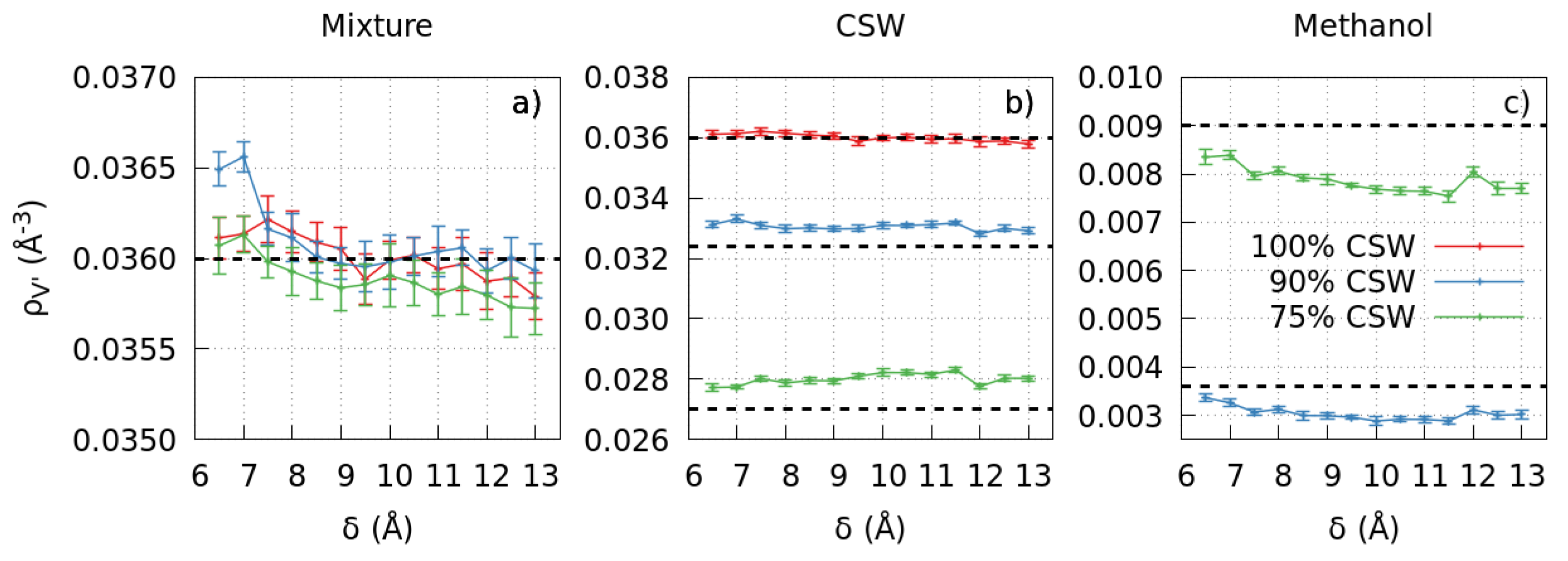
2.1. Number Density
2.1.1. The Pure CSW Case
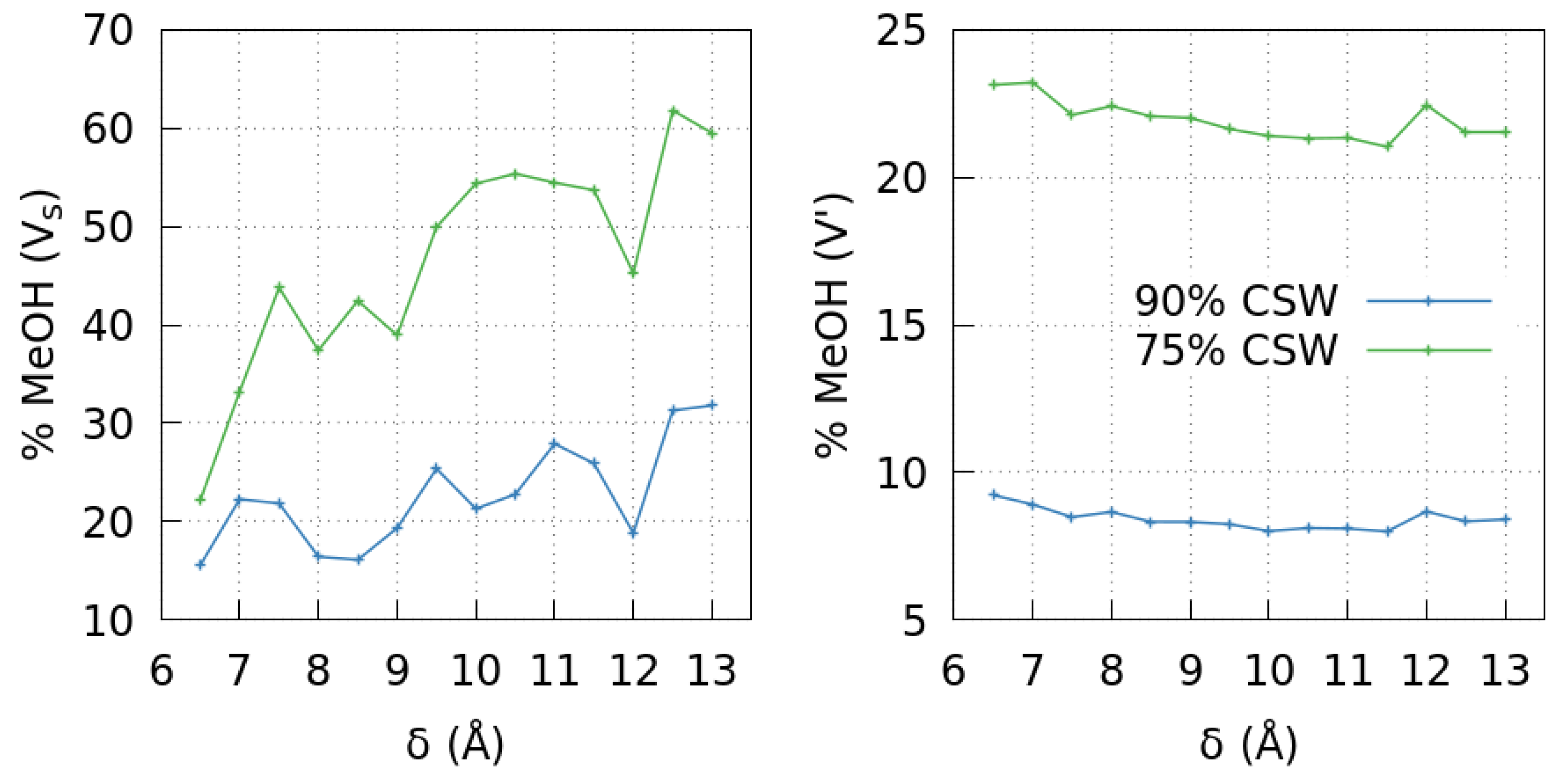
2.1.2. The Mixture Case
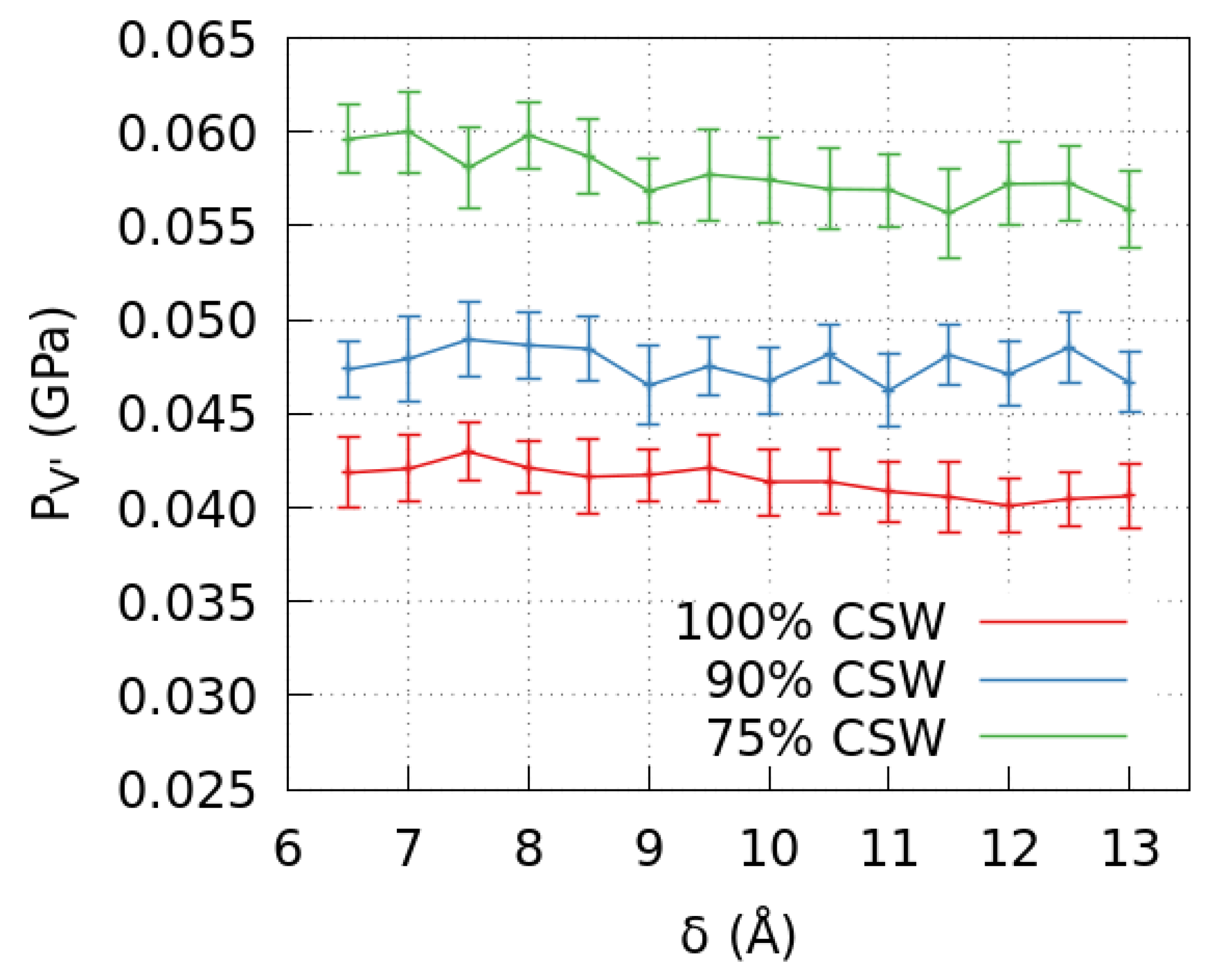
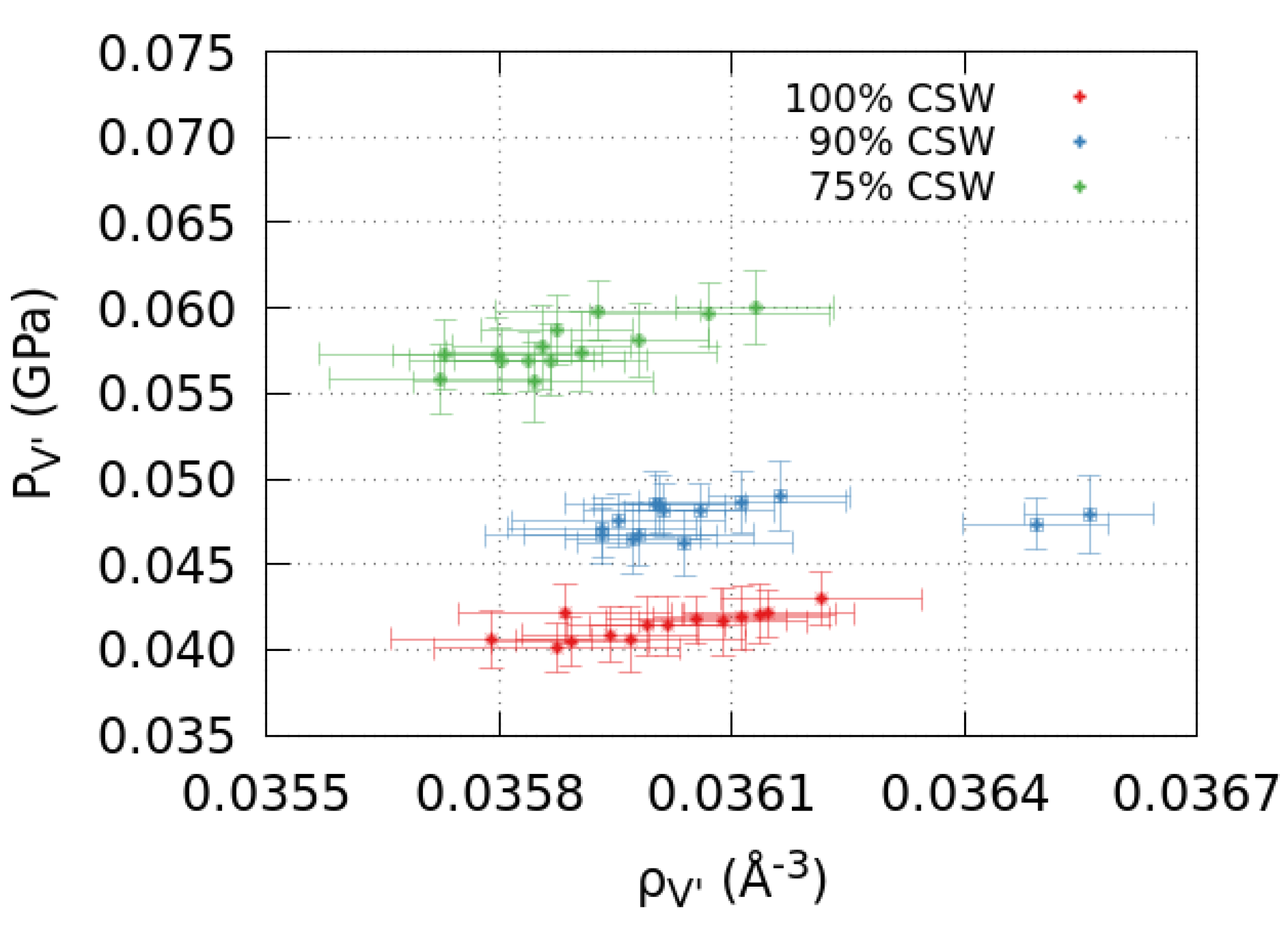
2.2. Pressure in
3. Materials and Methods
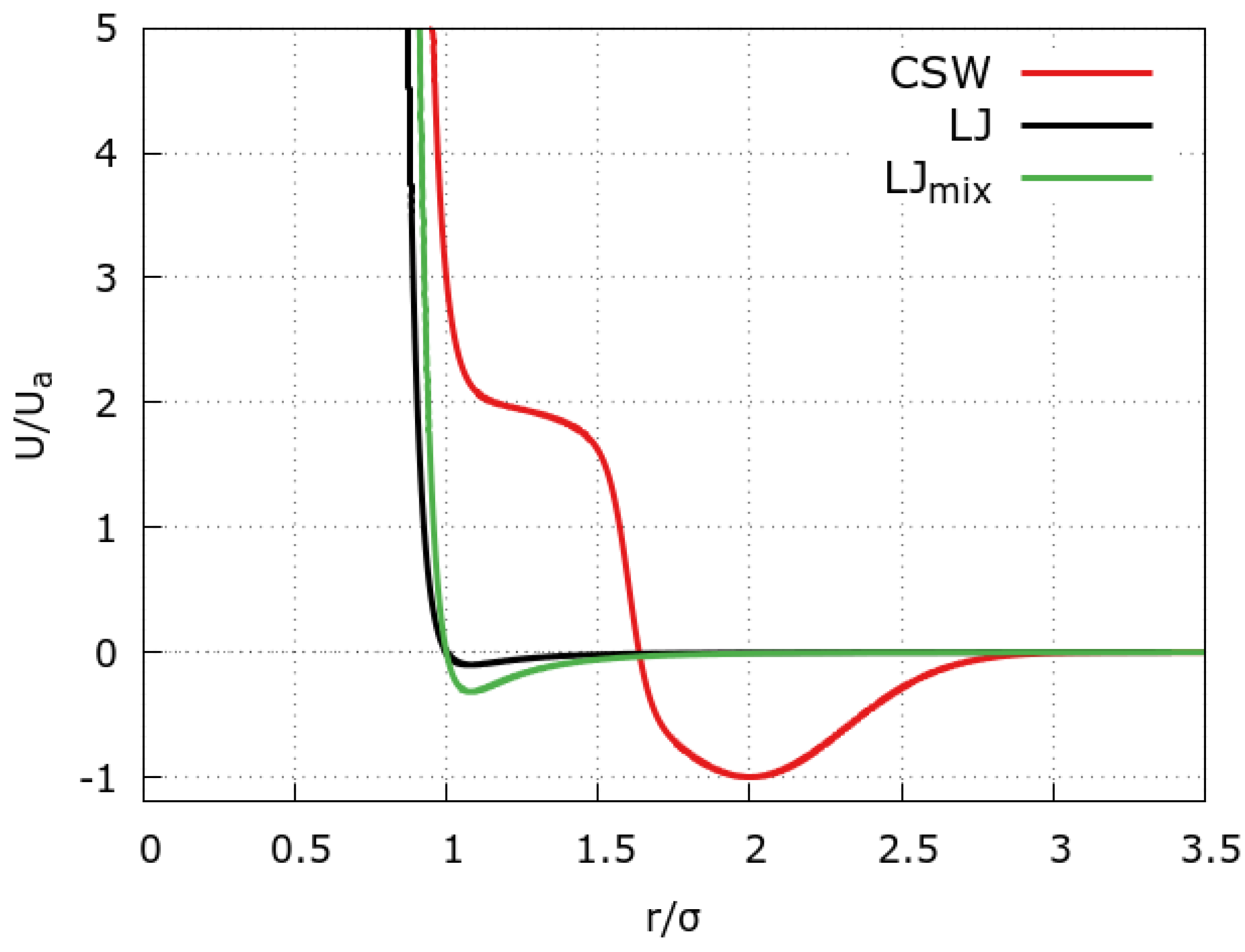
3.1. The Coarse-Grained Models for the Mixture
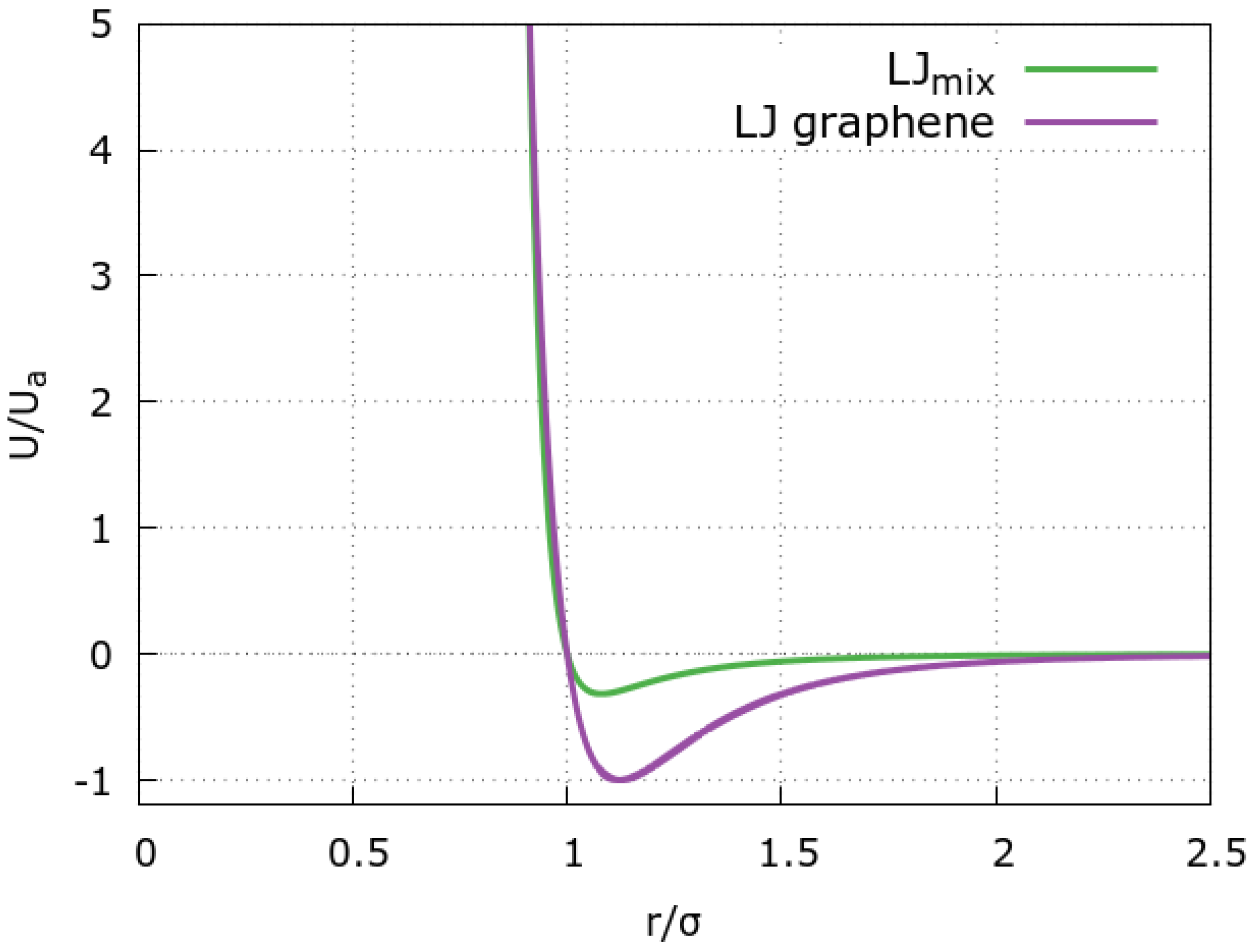
3.2. The Model for the Graphene Slit Pore
3.3. Graphene Slit-Pore Geometry
3.4. Molecular Dynamics
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| CSW | Continuous shouldered well |
| MSD | Mean square displacement |
| CM | Center of mass |
| LJ | Lennard-Jones |
| MD | Molecular dynamics |
References
- Fetisov, V.; Gonopolsky, A.M.; Zemenkova, M.Y.; Andrey, S.; Davardoost, H.; Mohammadi, A.H.; Riazi, M. On the Integration of CO2 Capture Technologies for an Oil Refinery. Energies 2023, 16, 865. [Google Scholar] [CrossRef]
- Fetisov, V.; Gonopolsky, A.M.; Davardoost, H.; Ghanbari, A.R.; Mohammadi, A.H. Regulation and impact of VOC and CO2 emissions on low-carbon energy systems resilient to climate change: A case study on an environmental issue in the oil and gas industry. Energy Sci. Eng. 2023, 11, 1516–1535. [Google Scholar] [CrossRef]
- Soetens, J.C.; Bopp, P.A. Water–Methanol Mixtures: Simulations of Mixing Properties over the Entire Range of Mole Fractions. J. Phys. Chem. B 2015, 119, 8593–8599. [Google Scholar] [CrossRef]
- Ren, X.; Zelenay, P.; Thomas, S.; Davey, J.; Gottesfeld, S. Recent advances in direct methanol fuel cells at Los Alamos National Laboratory. J. Power Sources 2000, 86, 111–116. [Google Scholar] [CrossRef]
- Boysen, D.A.; Uda, T.; Chisholm, C.R.I.; Haile, S.M. High-Performance Solid Acid Fuel Cells Through Humidity Stabilization. Science 2004, 303, 68–70. [Google Scholar] [CrossRef]
- Liu, S.; Clemente, E.R.C.; Hu, T.; Wei, Y. Study of spark ignition engine fueled with methanol/gasoline fuel blends. Appl. Therm. Eng. 2004, 27, 1904–1910. [Google Scholar] [CrossRef]
- Wei, Y.; Liu, S.; Li, H.; Yang, R.; Liu, J.; Wang, Y. Effects of Methanol/Gasoline Blends on a Spark Ignition Engine Performance and Emissions. Energy Fuels 2008, 22, 1254–1259. [Google Scholar] [CrossRef]
- Miganakallu, N.; Yang, Z.; Rogóż, R.; Kapusta, Ł.J.; Christensen, C.; Barros, S.; Naber, J. Effect of water–methanol blends on engine performance at borderline knock conditions in gasoline direct injection engines. Appl. Energy 2020, 264, 114750. [Google Scholar] [CrossRef]
- Toledo-Camacho, S.Y.; Rey, A.; Maldonado, M.I.; Llorca, J.; Contreras, S.; Medina, F. Photocatalytic hydrogen production from water–methanol and -glycerol mixtures using Pd/TiO2(-WO3) catalysts and validation in a solar pilot plant. Int. J. Hydrogen Energy 2021, 46, 36152–36166. [Google Scholar] [CrossRef]
- Miller, G.A.; Carpenter, D.K. Solid-Liquid Phase Diagram of the System Methanol-Water. J. Chem. Eng. Data 1964, 9, 371–373. [Google Scholar] [CrossRef]
- Sun, M.; Wang, L.M.; Tian, Y.; Liu, R.; Ngai, K.L.; Tan, C. Component Dynamics in Miscible Mixtures of Water and Methanol. J. Phys. Chem. B 2011, 115, 8242–8248. [Google Scholar] [CrossRef]
- Cortright, R.D.; Davda, R.R.; Dumesic, J.A. Hydrogen from catalytic reforming of biomass-derived hydrocarbons in liquid water. Nature 2002, 418, 964–967. [Google Scholar] [CrossRef]
- Masoumi, S.; Dalai, A.K. Techno-economic and life cycle analysis of biofuel production via hydrothermal liquefaction of microalgae in a methanol-water system and catalytic hydrotreatment using hydrochar as a catalyst support. Biomass Bioenergy 2021, 151, 106168. [Google Scholar] [CrossRef]
- Dalena, F.; Senatore, A.; Marino, A.; Gordano, A.; Basile, M.; Basile, A. Chapter 1—Methanol Production and Applications: An Overview. In Methanol; Basile, A., Dalena, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 3–28. [Google Scholar] [CrossRef]
- Liang, K.; Li, W.; Luo, H.; Xia, M.; Xu, C. Energy-Efficient Extractive Distillation Process by Combining Preconcentration Column and Entrainer Recovery Column. Ind. Eng. Chem. Res. 2014, 53, 7121–7131. [Google Scholar] [CrossRef]
- Azamat, J. Selective separation of methanol-water mixture using functionalized boron nitride nanosheet membrane: A computer simulation study. Struct. Chem. 2019, 30, 1451–1457. [Google Scholar] [CrossRef]
- Azamat, J.; Ghasemi, F.; Jahanbin Sardroodi, J.; Jahanshahi, D. Molecular dynamics simulation of separation of water/methanol and water/ethanol mixture using boron nitride nanotubes. J. Mol. Liq. 2021, 331, 115774. [Google Scholar] [CrossRef]
- Pršlja, P.; Lomba, E.; Gómez-Álvarez, P.; Urbič, T.; Noya, E.G. Adsorption of water, methanol, and their mixtures in slit graphite pores. J. Chem. Phys. 2019, 150, 024705. [Google Scholar] [CrossRef]
- Mosaddeghi, H.; Alavi, S.; Kowsari, M.H.; Najafi, B.; Az’hari, S.; Afshar, Y. Molecular dynamics simulations of nano-confined methanol and methanol-water mixtures between infinite graphite plates: Structure and dynamics. J. Chem. Phys. 2019, 150, 144510. [Google Scholar] [CrossRef]
- Esplandiu, M.J.; Bastus, N.; Fraxedas, J.; Ihmaz, I.; Puntes, V.; Radjenovic, J.; Sepúlveda, B.; Serrá, A.; Suárez-García, S.; Franzese, G. Interfacial phenomena in nanotechnological applications for water remediation. In Reference Module in Chemistry, Molecular Sciences and Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar] [CrossRef]
- Nair, R.R.; Wu, H.A.; Jayaram, P.N.; Grigorieva, I.V.; Geim, A.K. Unimpeded Permeation of Water Through Helium-Leak–Tight Graphene-Based Membranes. Science 2012, 335, 442–444. [Google Scholar] [CrossRef]
- Mahmood, A.; Bano, S.; Kim, S.G.; Lee, K.H. Water–methanol separation characteristics of annealed SA/PVA complex membranes. J. Membr. Sci. 2012, 415–416, 360–367. [Google Scholar] [CrossRef]
- Villegas, M.; Castro Vidaurre, E.F.; Gottifredi, J.C. Sorption and pervaporation of methanol/water mixtures with poly(3-hydroxybutyrate) membranes. Chem. Eng. Res. Des. 2015, 94, 254–265. [Google Scholar] [CrossRef]
- Hung, W.S.; Chang, S.M.; Lecaros, R.L.G.; Ji, Y.L.; An, Q.F.; Hu, C.C.; Lee, K.R.; Lai, J.Y. Fabrication of hydrothermally reduced graphene oxide/chitosan composite membranes with a lamellar structure on methanol dehydration. Carbon 2017, 117, 112–119. [Google Scholar] [CrossRef]
- Kachhadiya, D.D.; Murthy, Z. Preparation and characterization of ZIF-8 and ZIF-67 incorporated poly(vinylidene fluoride) membranes for pervaporative separation of methanol/water mixtures. Mater. Today Chem. 2021, 22, 100591. [Google Scholar] [CrossRef]
- Calero, C.; Franzese, G. Water under extreme confinement in graphene: Oscillatory dynamics, structure, and hydration pressure explained as a function of the confinement width. J. Mol. Liq. 2020, 317, 114027. [Google Scholar] [CrossRef]
- Leoni, F.; Calero, C.; Franzese, G. Nanoconfined Fluids: Uniqueness of Water Compared to Other Liquids. ACS Nano 2021, 15, 19864–19876. [Google Scholar] [CrossRef] [PubMed]
- Leoni, F.; Franzese, G. Structural behavior and dynamics of an anomalous fluid between attractive and repulsive walls: Templating, molding, and superdiffusion. J. Chem. Phys. 2014, 141, 174501. [Google Scholar] [CrossRef]
- Leoni, F.; Franzese, G. Effects of confinement between attractive and repulsive walls on the thermodynamics of an anomalous fluid. Phys. Rev. E 2016, 94, 062604. [Google Scholar] [CrossRef]
- Franzese, G.; Stanley, H.E. Understanding the Unusual Properties of Water. In Water and Life: The Unique Properties of H2O; Lynden-Bell, R.M., Conway Morris, S., Barrow, J.D., Finney, J.L., Harper, C., Eds.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Bianco, V.; Franzese, G.; Ruberto, R.; Ancherbak, S. Water and anomalous liquids. In Complex Materials in Physics and Biology: Proceedings of the International School of Physics "Enrico Fermi"; Mallamace, F., Stanley, H.E., Eds.; IOS Press: Amsterdam, The Netherlands, 2012; Volume 176, pp. 113–128. [Google Scholar]
- Gallo, P.; Bachler, J.; Bove, L.E.; Böhmer, R.; Camisasca, G.; Coronas, L.E.; Corti, H.R.; de Almeida Ribeiro, I.; de Koning, M.; Franzese, G.; et al. Advances in the study of supercooled water. Eur. Phys. J. E 2021, 44, 143. [Google Scholar] [CrossRef]
- Martí, J.; Calero, C.; Franzese, G. Structure and Dynamics of Water at Carbon-Based Interfaces. Entropy 2017, 19, 135. [Google Scholar] [CrossRef]
- Corti, H.R.; Appignanesi, G.A.; Barbosa, M.C.; Bordin, J.R.; Calero, C.; Camisasca, G.; Elola, M.D.; Franzese, G.; Gallo, P.; Hassanali, A.; et al. Structure and dynamics of nanoconfined water and aqueous solutions. Eur. Phys. J. E 2021, 44, 136. [Google Scholar] [CrossRef]
- Huš, M.; Urbic, T. Existence of a liquid-liquid phase transition in methanol. Phys. Rev. E 2014, 90, 062306. [Google Scholar] [CrossRef] [PubMed]
- Baptista-Pires, L.; Norra, G.F.; Radjenovic, J. Graphene-based sponges for electrochemical degradation of persistent organic contaminants. Water Res. 2021, 203, 117492. [Google Scholar] [CrossRef] [PubMed]
- Park, K.S.; Ni, Z.; Côté, A.P.; Choi, J.Y.; Huang, R.; Uribe-Romo, F.J.; Chae, H.K.; O’Keeffe, M.; Yaghi, O.M. Exceptional chemical and thermal stability of zeolitic imidazolate frameworks. Proc. Natl. Acad. Sci. USA 2006, 103, 10186–10191. [Google Scholar] [CrossRef] [PubMed]
- Sentenac, P.; Bur, Y.; Rauzy, E.; Berro, C. Density of Methanol + Water between 250 K and 440 K and up to 40 MPa and Vapor-Liquid Equilibria from 363 K to 440 K. J. Chem. Eng. Data 1998, 43, 592–600. [Google Scholar] [CrossRef]
- Perry, R.; Green, D.; Maloney, J. Perry’s Chemical Engineers’ Handbook; McGraw-Hill CD-ROM Handbooks; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Marques, M.S.; Hernandes, V.F.; Lomba, E.; Bordin, J. Competing interactions near the liquid-liquid phase transition of core-softened water/methanol mixtures. J. Mol. Liq. 2020, 320, 114420. [Google Scholar] [CrossRef]
- Vilaseca, P.; Franzese, G. Isotropic soft-core potentials with two characteristic length scales and anomalous behaviour. J. Non-Cryst. Solids 2011, 357, 419–426. [Google Scholar] [CrossRef]
- Franzese, G. Differences between discontinuous and continuous soft-core attractive potentials: The appearance of density anomaly. J. Mol. Liq. 2007, 136, 267–273. [Google Scholar] [CrossRef]
- Huš, M.; Munaò, G.; Urbic, T. Properties of a soft-core model of methanol: An integral equation theory and computer simulation study. J. Chem. Phys. 2014, 141, 164505. [Google Scholar] [CrossRef]
- Huš, M.; Zalar, M.; Urbic, T. Correctness of certain integral equation theories for core-softened fluids. J. Chem. Phys. 2013, 138, 224508. [Google Scholar] [CrossRef]
- Hus, M.; Urbic, T. Core-softened fluids as a model for water and the hydrophobic effect. J. Chem. Phys. 2013, 139, 114504. [Google Scholar] [CrossRef]
- Munaò, G.; Urbic, T. Structure and thermodynamics of core-softened models for alcohols. J. Chem. Phys. 2015, 142, 214508. [Google Scholar] [CrossRef] [PubMed]
- Vilaseca, P.; Franzese, G. Softness dependence of the anomalies for the continuous shouldered well potential. J. Chem. Phys. 2010, 133, 084507. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kalé, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comp. Phys. Comm. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Birdsall, C.; Langdon, A. Plasma Physics via Computer Simulation; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar] [CrossRef]
- de Oliveira, A.B.; Franzese, G.; Netz, P.A.; Barbosa, M.C. Waterlike hierarchy of anomalies in a continuous spherical shouldered potential. J. Chem. Phys. 2008, 128, 064901. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellido-Peralta, R.; Leoni, F.; Calero, C.; Franzese, G. Size–Pore-Dependent Methanol Sequestration from Water–Methanol Mixtures by an Embedded Graphene Slit. Molecules 2023, 28, 3697. https://doi.org/10.3390/molecules28093697
Bellido-Peralta R, Leoni F, Calero C, Franzese G. Size–Pore-Dependent Methanol Sequestration from Water–Methanol Mixtures by an Embedded Graphene Slit. Molecules. 2023; 28(9):3697. https://doi.org/10.3390/molecules28093697
Chicago/Turabian StyleBellido-Peralta, Roger, Fabio Leoni, Carles Calero, and Giancarlo Franzese. 2023. "Size–Pore-Dependent Methanol Sequestration from Water–Methanol Mixtures by an Embedded Graphene Slit" Molecules 28, no. 9: 3697. https://doi.org/10.3390/molecules28093697
APA StyleBellido-Peralta, R., Leoni, F., Calero, C., & Franzese, G. (2023). Size–Pore-Dependent Methanol Sequestration from Water–Methanol Mixtures by an Embedded Graphene Slit. Molecules, 28(9), 3697. https://doi.org/10.3390/molecules28093697







