Abstract
Electronic properties and absorption spectra are the grounds to investigate molecular electronic states and their interactions with the environment. Modeling and computations are required for the molecular understanding and design strategies of photo-active materials and sensors. However, the interpretation of such properties demands expensive computations and dealing with the interplay of electronic excited states with the conformational freedom of the chromophores in complex matrices (i.e., solvents, biomolecules, crystals) at finite temperature. Computational protocols combining time dependent density functional theory and ab initio molecular dynamics (MD) have become very powerful in this field, although they require still a large number of computations for a detailed reproduction of electronic properties, such as band shapes. Besides the ongoing research in more traditional computational chemistry fields, data analysis and machine learning methods have been increasingly employed as complementary approaches for efficient data exploration, prediction and model development, starting from the data resulting from MD simulations and electronic structure calculations. In this work, dataset reduction capabilities by unsupervised clustering techniques applied to MD trajectories are proposed and tested for the ab initio modeling of electronic absorption spectra of two challenging case studies: a non-covalent charge-transfer dimer and a ruthenium complex in solution at room temperature. The K-medoids clustering technique is applied and is proven to be able to reduce by ∼100 times the total cost of excited state calculations on an MD sampling with no loss in the accuracy and it also provides an easier understanding of the representative structures (medoids) to be analyzed on the molecular scale.
1. Introduction
Photo-induced phenomena and optical properties are the grounds to investigate electronic states and their interactions with the environment [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Experimental spectra can be interpreted via computational approaches at the molecular scale, understanding the microscopic characteristics that determine the position, width and shape of absorption bands [23,24,25,26,27,28,29,30,31,32,33,34]. However, a number of challenges remain open and mainly concern the modeling of either floppy molecules or non-covalent complexes in solution. Ideal approaches to deal with the complexity of the conformational freedom have to ensure an adequate sampling of the phase space of the potential energy surface (PES) at a given temperature, since such systems cannot be easily described by minimum energy structures as starting points for subsequent more computationally expensive calculations required to compute electronic transitions and excited state properties [34,35,36]. Molecular dynamics (MD) is the perfect technique for this goal since it can simultaneously describe the conformational freedom and the complexity of the environment (i.e., explicit solvent models) and can guarantee a satisfactory sampling of the phase space of the PES for selecting the initial states of the electronic transitions. On these bases, it is possible to reproduce the thermal fluctuations in a classical manner and simulate the shape of the electronic spectrum by classically considering the spreading of the vertical transitions of a representative sample of snapshots of the MD trajectory [37,38,39].
An accurate description of the electronic layout of a system is very important for the excited state properties and optical absorption. The electronic state separation, and the resulting UV-Vis absorption, strongly depend on the reference structure(s), indeed. A very detailed description of the PES ruling the system dynamics is demanded when standard force fields cannot by easily used, i.e., with non-covalent charge-transfer complexes [40,41,42,43,44,45,46,47,48], metal compounds or usually when the electronic density reorganization is involved during the time, even in the ground state. This is usually quite common also when an environment reorganization is involved as well. Since parameterized force fields cannot account for explicit electronic effects, an explicit treatment of electronic degrees of freedom is mandatory via ab initio methods. However, when reasonable large systems (≥1000 atoms) are studied, accurate wavefunction-based methods cannot be employed due to their high computational cost (above all, for excited state properties), although some progress has been recently achieved using graphical processing units [49] and localization procedures [50,51]. Thus, density functional theory (DFT) and time dependent (TD-) DFT, the latter required for excited state quantities, are usually chosen as a good compromise between accuracy and computational costs [10,52,53,54,55,56,57,58,59,60,61,62].
Besides canonical computational chemistry fields, data analysis and machine learning (ML) methods have been increasingly employed as complementary approaches for an efficient data exploration, prediction and model development, starting from experimental data (structure, properties, reactivity) or from MD simulations and electronic structure calculations [63,64,65,66,67,68,69,70,71,72,73,74,75,76]. In particular, MD simulations often produce very big datasets (i.e., the collected trajectory in the phase-space), especially for long simulation times and extended systems, which can be difficult to manually inspect. Automated ML data analysis techniques thus can offer a valuable and efficient option to extract the significant and “physical” information from MD trajectories. In particular, unsupervised ML methods, such as clustering analysis, are able to partition a dataset according to similarities in some features space, employing only the input values and not requiring any output ones supplied by the user. Clustering proved a valuable tool for MD simulation analysis, allowing one to reduce the high number of sampled structures into a few representative ones, approximating conformational energy minima [77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92].
The simulation of electronic band-shapes at finite temperature through an MD sampling potentially requires hundreds of excited state calculations. Therefore, alternative routes such as the selection of a small number of representative frames could both reduce the computational cost of spectra calculations and simplify their interpretation [78,82]. In this work, dataset reduction capabilities via clustering techniques applied to MD trajectories in specifically tailored feature spaces were tested in the simulation of electronic absorption spectra of two model compounds. In particular, spectra computed only from the clusters’ representative frames showed a remarkable reproduction of the main spectral features if compared to spectra from a uniform sampling of frames of the trajectory (a subset of ∼500 structures). This approach also allowed an easier interpretation of the calculated bands, which could result from many states close in energy but differing for their spatial properties.
Dataset reduction capabilities via unsupervised clustering techniques applied to MD trajectories are proposed and tested for the ab initio modeling of electronic absorption spectra of two challenging case studies. The first investigated model system is a prototypical -stacked non-covalent dimer in dichloromethane (DCM) solvent (see Figure 1, left panel), consisting of an electron donor (1-chloronaphthalene, 1ClN) and an electron acceptor (tetracyanoethylene, TCNE). This represents a challenging case study with respect to evaluating the performance of ML clustering techniques in reproducing its electronic/optical properties, considering that the potential energy surface of weakly bound systems, ruled by dispersive intermolecular forces, is quite flat and numerous isoenergetic orientational isomers can be present in the solution. The TCNE::1ClN dimer has been thoroughly investigated in recent years by means of Femtosecond Stimulated Raman Spectroscopy [93] and through electronic structure methods for the detailed characterization of the ground state properties [35] and to unveil the nuclear relaxation upon photoexcitation downhill from the Franck–Condon region of the first charge-transfer state [34,94]. The second system is instead a Ru(II) complex, [Ru(dcbpy)2(NCS)2]4− (dcbpy = 4,4′-dicarboxy-2,2′-bipyridine) in water solution, also called “N34−” (Figure 1, right panel), which is a popular example of Ru-based dye sensitizers for solar cells and light-harvesting applications [95,96,97]. Light absorption by N34− in the visible region induced excitation to a dense manifold of metal-to-ligand charge-transfer (1MLCT) states. N34− photo-physical behavior is characterized by an ultrafast relaxation pathway among the singlet and triplet manifolds, induced by a complex interplay between closely spaced coupled electronic states, nuclear motion and solvent rearrangement [98,99,100,101,102,103,104,105], potentially influencing the dynamics and efficiency of the electron injection into a semiconductor substrate [106,107,108,109,110]. The N34− complex, both for its dense 1MLCT manifold and its conformational dynamics in the solution [111], represents therefore another ideal model system for testing an efficient MD/ML clustering approach for the simulation of electronic spectra including finite-temperature effects.
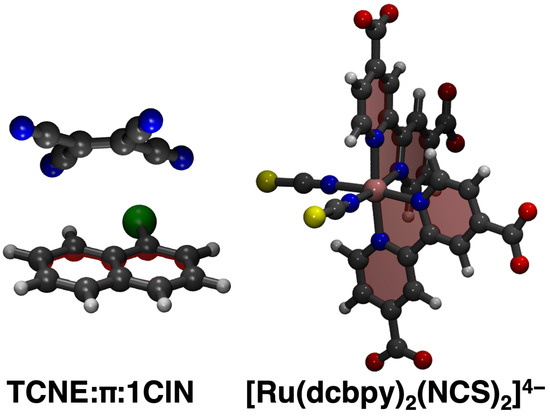
Figure 1.
Case studies investigated in the present work. The TCNE::1ClN non-covalent dimer and Ru(II) complex ([Ru(dcbpy)2(NCS)2]4− or “N34−”, dcbpy = 4,4′-dicarboxy-2,2′-bipyridine) are presented from left to right, respectively (Carbon is in gray, Hydrogen in white, Chlorine in green, Sulphur in yellow, Oxygen in red, Nitrogen in blue, Ruthenium in pink).
2. Results and Discussion
2.1. The TCNE::1ClN Case Study
The massive amount of data acquired during an MD simulation requires analyses that are capable of going beyond the visual inspection of snapshots and average structures. In this regard, the statistical analysis of the trajectories through the calculation of the distribution functions represents an advantageous choice with respect to taking into account conformational dynamics, solute–solvent interactions and so on. In Figure 2, a three-dimensional spatial distribution function (SDF) [112,113] is presented, computed along the 10 ps-long AIMD trajectory by considering the 1ClN as reference molecule (for which a local three points coordinate system was defined) and the center of the mass of the TCNE unit. From the SDF, it is observed that the TCNE remains on the same side of the ClN and slips on both rings during the exploration of the ground state PES, proving the presence of different mutual configurations and distances due to the weak Coulombic interactions that rule the -stacked arrangement.
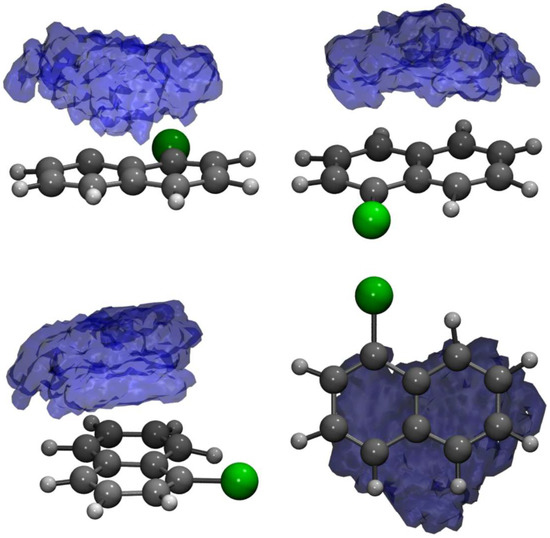
Figure 2.
Side, front and top views of the spatial distribution function of the center-of-mass of the TCNE acceptor monomer around the 1ClN subunit.
According to the procedure presented in Section 3.2, the MD trajectory clustering thus yielded, for the TCNE::1ClN case study, five medoids (each one is representative of the corresponding cluster), characteristic of the accessible conformational space, in agreement with the SDF previously discussed. The clustering structural feature values shown by the five medoids, namely the rotation angle () and the rotation axis () of the two subunits molecular planes and the position vector between the two geometric centers (), are collected in Table 1 (see also Section 3.2 for features definitions). A detailed analysis of medoid structural features reveals that they do not significantly differ in the rotation angle between the two TCNE and 1ClN planes (values within a small range, ∼5 degrees), but mainly in the planes’ relative orientation, as suggested by clearly different axis components and secondarily in the TCNE-1ClN relative position. A closer inspection of the rotation axis components for medoids 2 and 4 reveals that they differ along the x- and z-axes (see Table 1), while for medoids 3 and 5 only the component along the z-axis is reoriented for these latter. Additionally, analyzing the five medoids obtained from the clustering approach (side view presented in the right panel of Figure 3), considerable geometric deformations are present and the relative position of the molecular planes is also different. In order to acquire a visual representation of such clustering, the trajectory was projected onto the subspace of the features’ first two principal components (PCs; please refer to Section 3.3 for technical details). A clear cluster separation was obtained, with each medoid representing a different portion of the conformational space (see Figure 4). The partial superposition of cluster 5 with cluster 3 in the principal components subspace is only an artifact (being instead separated in the full space) due to the reduced variance explained by the first two PCs (∼55.5% of the total variance).

Table 1.
Clustering feature values of the five cluster medoids from TCNE::1ClN trajectory. : rotation angle (angle between versors normal to the two molecular planes, degrees), : rotation axis (versor normal to the former ones), : relative position vector (between 1ClN and TCNE geometric centers). Vector quantities are given as cartesian components (Å) in a fixed frame of reference.
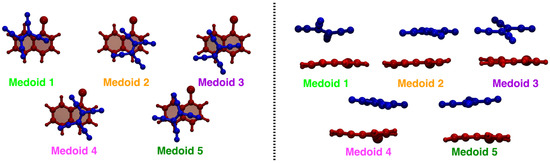
Figure 3.
Structures of the five cluster medoids in top (left panel) and side (right panel) views. The TCNE and 1ClN are represented as ball and stick in blue and red, respectively. The color code is uniform with that of Figure 4.
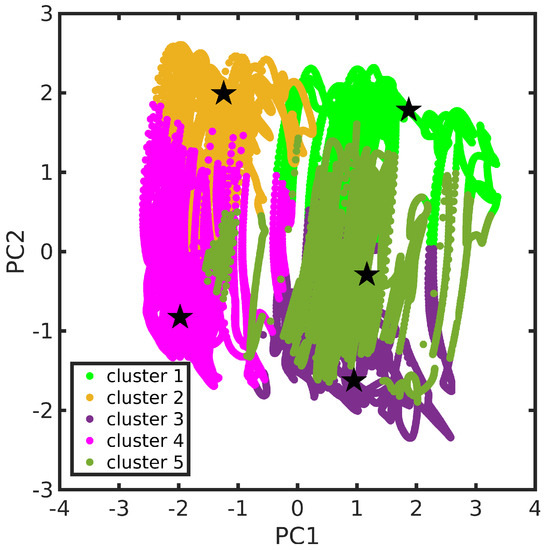
Figure 4.
TCNE::1ClN trajectory in the features’ first two principal components space. Cluster partition is represented through different colors. Cluster medoids are also highlighted (as star symbols). The color scheme adopted is kept fixed throughout this section.
From Figure 3, the found medoids overall show pairwise structural similarities (see 2–4 and 3–5) if observed in a top-down direction; see Table 1 for a more quantitative evaluation. The conformational flexibility of the TCNE:1ClN -stacked complex, which is due to the weak dispersion forces, is thus fully captured with the trajectory clustering approach.
The UV-Vis spectrum comprising the first low-lying singlet states computed for each medoid within linear response TD-DFT formalism is reported in Figure 5. The estimation of the whole electronic spectrum (red curve) was obtained according to Equation (5) and the procedure explained in Section 3.4. A comprehensive analysis of the electronic spectrum has been recently provided by some of the authors in Ref. [35]. On the other hand, we report a detailed summary of the characterization of the transitions towards the S1 and S2 excited states in Table 2. We recall that the weaker electronic transitions below 4.00 eV have a charge transfer (CT) nature (for S1 and S2 see charge transfer descriptor parameter in Table 2). Conversely, the very bright ones are characterized by electronic density reorganization occurring in the same molecular unit, hence they are of a local excitation (LE) character. For medoid 1, the TCNE is located on an edge of the 1ClN ring and it mainly contributes to the absorption bands above 2.50 eV (see light green curve in Figure 5), while for the S0–S1 electronic transition at 1.807 eV characterized by a strong CT nature () the probability is negligible, . For medoids 2 and 4, the TCNE lies on the ring bearing the chlorine atom and they share roughly the same electronic properties in terms of transition probability and energy range (see orange and magenta curves in Figure 5, respectively). Both show absorption bands in all regions of the spectrum. In this case, the first two states S1 and S2 of both medoids contribute, respectively, to the bands at ∼2.00 and 2.80 eV. Also in these cases, the S1 and S2 states are characterized by a strong charge transfer nature as can be easily deduced from the values of the descriptor close to unity, reported in Table 2. In medoids 3 and 5, the TCNE is placed on the unfunctionalized six-membered ring of the 1ClN and we observe that the electronic properties show considerable differences. The electronic features of medoid 3 (violet curve in Figure 5) cover the entire spectral range considered, 1.50–5.00 eV, while only high energy electronic transitions (>3.50 eV) are bright for medoid 5 (dark green curve in Figure 5).
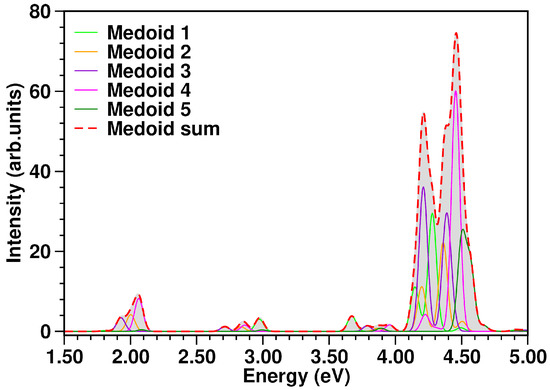
Figure 5.
TCNE::1ClN absorption spectrum (in eV) calculated at TD-CAM-B3LYP/6-31G(d,p)/GD3/C-PCM(DCM) level of theory from each medoid and as the sum spectrum of the structures representative of the conformational equilibrium in the ground state. The color code is presented in the graph legend. The sum spectrum (red dashed curve) was obtained as the sum of individual medoid contributions (presented in the figure as well, see color legend), each one already multiplied by the k-th cluster population. See Equation (5) and the procedure explained in Section 3.4 for more details.

Table 2.
Characterization of S1 and S2 excited states of TCNE::1ClN cluster medoids. (eV): vertical excitation energy, : oscillator strength (arb. units), : transition density population analysis for A (hole) and B (electron) fragments, : charge transfer descriptor (please refer to Section 3.4 for definitions). Fragment labels: E: TCNE, N: 1ClN.
Comparing the spectrum from the five medoids to that from the complete MD sampling, an excellent agreement is observed (Figure 6, top panel). The experimental optical spectrum profile in solution (Figure 6, bottom panel) shows two distinct absorption bands with maxima centered at 408 nm (3.04 eV) and 537 nm (2.31 eV), as well as the calculated spectrum. In particular, the first calculated band at ∼2.00 eV has contributions from the S1 states of representative frames 4, 2 and 3, each having, in turn, a clear 1ClN → TCNE charge-transfer character. Analogously, the second band at ∼2.80 eV appears constituted by the S2 CT states of medoids 1, 4, 3 and 2.
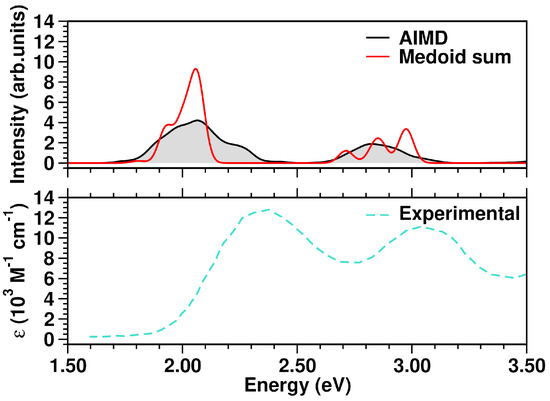
Figure 6.
Top panel: comparison of TCNE::1ClN simulated absorption spectra in the 1.50–3.50 eV range. Bottom panel: experimental UV-Vis spectrum, retrieved from Ref. [93], of the TCNE::1ClN complex measured in DCM solution (molar absorptivity, ). The color code is presented in the graph legend.
Such a case study proves the clustering technique to be an efficient way to estimate the electronic spectrum at finite temperature, avoiding excited state calculations on a large number of frames (for TCNE::1ClN model system, a 100-fold decrease in total computational cost). Moreover, the medoid excited state characterization (Table 2) allows one to perform a more accurate spectral assignment of the absorption bands. This further confirms that the cluster medoids, taken as representative frames, can efficiently resume the collected conformational dynamics.
2.2. The N34− Case Study
The N34− dynamics at room temperature in water solution is characterized, on the one hand, by the rigidity of the dcbpy ligands, due to the chelation to the Ru center and, on the other hand, by the flexibility of the NCS− ligands, exploring conical-shaped regions (please see Figure 1, right panel, to recall the system under investigation). The vibrational dynamics induce therefore instantaneous deviations from the ideal symmetry, which could improve the transition probability of otherwise dark excited states [111]. The clustering procedure applied to the collected N34− trajectory suggested a partition into seven distinct clusters. Projection into the two-dimensional principal component subspace (actually accounting for 56.9% of the total variance) shows indeed a quite clear separation between the clusters and the medoids representing them (Figure 7). Again, the observed partial superposition could be a spurious effect of data visualization through a low-dimensional PCA. According to the feature values shown by the cluster medoids, these representative structures (reported in Figure 8) actually seem to capture both the conformational (torsional) freedom of the coordinated NCS− ligands ( and torsional angles) and the different degrees of asymmetry sampled by the N34− dynamics (Table 3, please refer also to Section 3.2 for N34− features definitions). In particular, the values of continuous symmetry measure of deviation from symmetry (-CSM, Section 3.2) most sampled by the MD trajectory (distribution maxima at 0.09, 0.17, 0.22, 0.31, Figure 9) are close to the values by the cluster medoids, further confirming the representation capabilities of the latter.
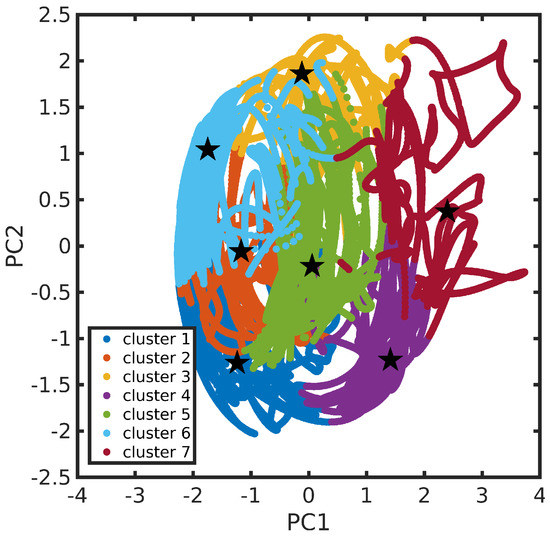
Figure 7.
N34− trajectory in the features’ first two principal components subspace. Cluster partition is represented through different colors. Cluster medoids are also highlighted (as star symbols).
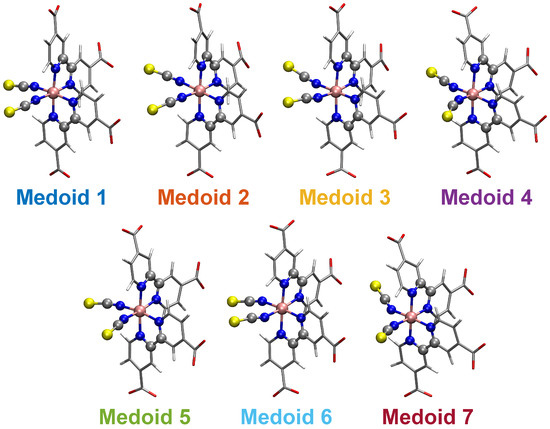
Figure 8.
Structures of the N34− seven cluster medoids. The atoms determining the features employed for clustering analysis are highlighted as ball and stick. The color code is uniform with that of Figure 7.

Table 3.
Clustering feature values of the seven cluster medoids from N34− trajectory. : C(NCS1)-N(NCS1)-Ru-N(dcbpy) dihedral angle (degrees), : C(NCS2)-N(NCS2)-Ru-N(dcbpy) dihedral angle (degrees), -CSM: continuous symmetry measure for deviation from symmetry.
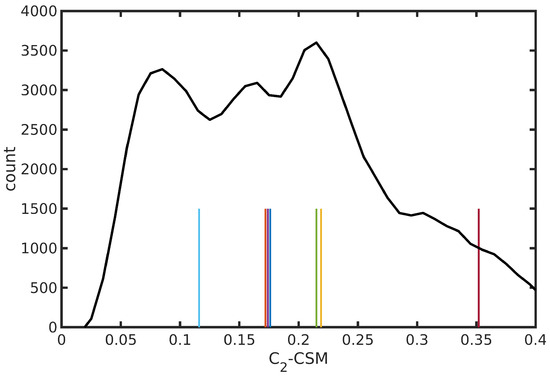
Figure 9.
Distribution of -CSM symmetry deviation parameter from N34− trajectory in water solution. Values of the medoid structures from trajectory clustering analysis are also shown as vertical bars (with arbitrary heights). The color code is uniform with that of Figure 7.
Electronic absorption spectra of transition metal complexes are determined by several, closely spaced, excited states, differing in their spatial properties (i.e., metal and ligand-localized transitions, metal-to-ligand (ML) and ligand-to-metal (LM) charge-transfer (CT) transitions). From a practical point of view, this implies the computation (and characterization) of a high number of excited states with some level of theory to simulate the spectrum in a given energy range. Therefore, a clustering analysis performed on an MD trajectory (and so reducing the complete configuration dataset to a few, representative, structures) potentially appears even more convenient for the simulation and the interpretation of transition metal complex electronic spectra including finite-temperature effects.
The N34− electronic spectrum was simulated up to ∼3.7 eV, comprising the two experimentally characterized bands at ∼2.50 and ∼3.36 eV [114]. The spectra calculated for each cluster medoid actually slightly differ in the absorption band positions (energies) and intensities, since the medoids represent different regions of the accessible conformational space (Figure 10). In particular, the spectrum obtained from the only seven representative frames can actually quite well reproduce that from the complete MD sampling at in water solution (Figure 11), although with an increased sub-structure, due to the lower number of frames involved in the spectrum calculation. The selection of representative frames through a clustering analysis allowed one therefore to achieve a remarkable ∼70-fold decrease in the total computational cost for N34− electronic spectrum simulation.
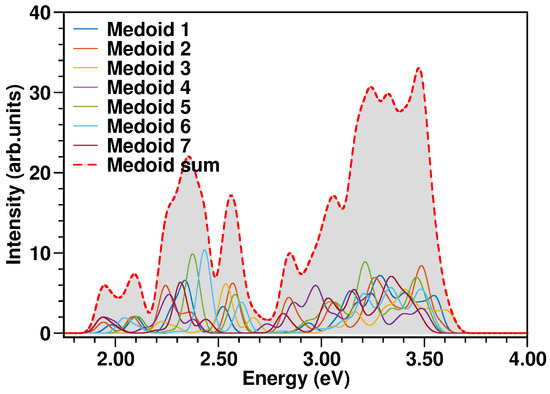
Figure 10.
N34− absorption spectra (in eV) calculated at TD-B3LYP/C-PCM/def2-SVP/SDD(Ru) level of theory from each medoid, weighted by the population of the corresponding cluster and the spectrum resulting from the sum over the medoids (red dashed curve). The color code is presented in the graph legend. See Equation (5) and the procedure explained in Section 3.4 for more details.
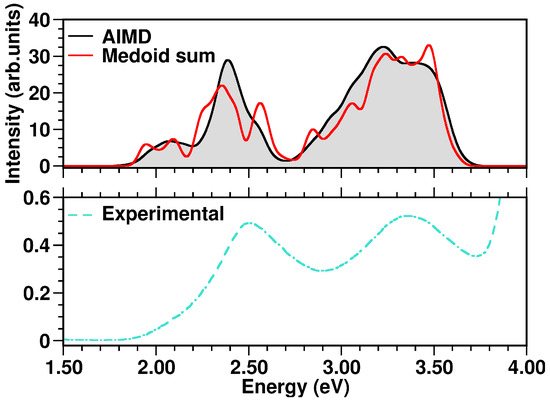
Figure 11.
Top panel: comparison of N34− simulated absorption spectra in the 1.50–4.00 eV range. Bottom panel: experimental N34− UV-Vis spectrum, retrieved from Ref. [114], measured in water solution. The color code is presented in the graph legend.
Especially for transition metal complexes, the observed absorption bands can each be the result of many close transitions. Dataset reduction through a clustering analysis allowed an accurate N34− spectral characterization, which could be otherwise difficult to perform. In particular, the calculated band at 2.07 eV (Figure 11) results from medoid 1 S2, medoid 2 S2, medoid 7 S1, medoid 6 S1 and medoid 5 S2 states, which are mainly Ru → (dcbpy)2 (, , Table 4) CT states. Analogously, medoid 6 S5, medoid 7 S5, medoid 2 S6, medoid 1 S5 and medoid 3 S5, with similar metal-to-ligand charge-transfer (MLCT) spatial features, contribute to the more intense calculated band at 2.39 eV. The higher-energy bands are characterized instead by a less homogeneous set of excited states. In fact, the calculated band at 3.23 eV results from medoid 2 S8, medoid 7 S13 Ru → (dcbpy)2 states (, , Table 4), medoid 2 S18 Ru → (dcbpy)2 state, but with an increased dcbpy localized-excitation character (, ), medoid 4 S15 Ru → (dcbpy)2 state, with increased (NCS)2 donor contribution (, ) and medoid 7 S19 state, which is mainly an (NCS)2 → (dcbpy)2 CT state (, ). The close calculated 3.38 eV band has instead a quite different average character. In fact, the contributing medoid 1 S40 state is mostly an (NCS)2 → (dcbpy)2 CT state (), medoid 2 S37 and medoid 5 S33 states have an increased localized character (, ), while medoid 3 S21 and medoid 6 S34 are localized excitations on dcbpy ligands ( and , respectively).

Table 4.
Characterization of the excited states of N34− cluster medoids most contributing to the calculated absorption bands. (eV): vertical excitation energy, : oscillator strength, : transition density population analysis for A (hole) and B (electron) fragments, : charge transfer descriptor (please refer to Section 3.4 for definitions). Fragment labels: S: (NCS)2, R: Ru, P: (dcbpy)2.
3. Materials and Methods
3.1. Ab Initio Molecular Dynamics
The conformational flexibility of the TCNE::1ClN and N34− model systems were sampled through ab initio molecular dynamics simulations. In particular, the Atom-centered Density Matrix Propagation (ADMP) method was employed: the density matrix in an orthonormalized atomic basis is included in an extended Lagrangian as an additional degree of freedom and propagated together with the nuclear degrees, avoiding a self-consistent procedure at each step [115,116,117,118,119].
The TCNE::1ClN ground state trajectory was collected for 10 ps with a 0.2 fs time step, at the B3LYP/6-31G(d,p) [120,121,122] level of theory [35,94]. Temperature was kept at 298 K, through a velocity rescaling every 1 ps. Dichloromethane solvent effects were included through the conductor-like polarizable continuum model (C-PCM) [123,124,125,126,127,128]. Moreover, due to the -stacked, non-covalent nature of the TCNE:1ClN complex, dispersion forces had to be modeled, employing Grimme’s correcting potential (GD3) [129,130,131,132,133,134].
The N34− system was simulated instead for 8.6 ps with a 0.1 fs time step [111]. A velocity rescaling every 1 ps allowed to keep a 298 K temperature. Explicit water solvation was included in the N34− ground state sampling, in order to better model the specific solute–solvent interactions at the several solvation sites. A 22 Å-radius spherical solvent box (∼1500 molecules) was extracted from a pre-equilibrated cubic one and placed around N34−. A hybrid quantum mechanics/molecular mechanics potential was employed: B3LYP/def2-SVP [135] for the QM portion (the N34− molecule) with associated electronic core potential for the Ru atom [136] and the TIP3P water model [137] for the MM part (the water spherical box), re-parametrized to allow a bending motion [11]. The QM and MM potentials were combined through the ONIOM QM/MM scheme [138,139,140], including the MM charges into the QM hamiltonian (i.e., an “electronic embedding”). General AMBER Force Field [141] atom types (and so van der Waals non-bonding parameters) were assigned, moreover, to N34− atoms. Non-periodic boundary conditions were introduced through a hybrid explicit/implicit solvent model. Long-range electrostatic effects and short-range dispersion–repulsion forces between the explicit and the bulk solvent were, respectively, modeled through C-PCM self-reaction field and an empirical confining potential, which has to be parametrized for the specific solvent model [10,124,142,143,144]. We refer the reader to previous works for more details about the ab initio molecular dynamics simulations of the model systems and the employed potentials [34,94,111].
3.2. Feature Selection and Clustering of Molecular Dynamics Trajectories
Due to its large dimensions, it is often useful to transform the original dataset of the collected, N-frames long, trajectory (the configurations, i.e., the positions of each of the atoms in the system, at each time step) into a matrix , representing the data in some d-dimensional () feature space, different from the coordinate space. The chosen features should adequately describe the properties of interest, without much loss of information [77]. Internal coordinates, such as bonds, angles and dihedrals or more specifically tailored parameters, according to the problem under study, can be employed as features.
In particular, the TCNE::1ClN trajectory was transformed into a feature space able to describe the orientation of the two molecular planes and the relative position of the two molecules, comprising the angle () between the versors normal to the TCNE and ClN planes, the versor representing the axis of rotation of the two planes (i.e., the versor orthogonal to the former ones) and the relative position vector (i.e., the vector between the two geometric centers). For N34−, instead, a continuous symmetry measure of deviation from the ideal symmetry [145,146,147], calculated as the minimized root-mean-square deviation from the images generated through the symmetry operations, was considered. In particular, -CSM was evaluated on the smallest subset of N34− atoms showing a symmetry not higher than , as the complete molecule. Since the non-linearity of the NCS− coordination in the water solution (C(NCS)-N(NCS)-Ru angle less than 180°) and their torsional mobility were previously recognized [111], the C(NCS)-N(NCS)-Ru-N(dcbpy) dihedrals describing the NCS− orientations were also included. In this regard, to avoid problems due to the periodicity around ±180°, each dihedral was included as a pair to keep a metric feature space [148]. The MD datasets in the feature space were standardized (i.e., shifted to zero mean and scaled to unit variance) before following analyses.
Clustering machine learning techniques allow one to partition a dataset, grouping similar instances according to a similarity measure, such as a metric (for instance, Euclidean) in the feature space [149]. Instances within a cluster should be similar to each other and different from those belonging to the other clusters. In K-Means [150] and K-Medoids [151,152,153] approaches, for a given number K of clusters, K cluster centers are obtained. The feature space is partitioned (tessellated) by assigning each instance to the closest center. The latter are found by minimization of a loss function, defined as the sum of the squared distances between each instance and the cluster center to which it is assigned:
where belongs to the cluster k, is the corresponding center in the feature space and N is the number of “observations” (trajectory frames). While in the K-Means algorithm the cluster center is the mean of the cluster members and so does not have to correspond to any instance of the dataset, in the K-Medoids approach it is forced to be some , such that the sum of the squared distances from the cluster members is the lowest (like a median).
MD trajectories of TCNE::1ClN and N34− model systems in their respective feature spaces were clusterized with the K-Medoids algorithm [152], since the cluster medoids, which are representative of the corresponding clusters, are trajectory frames themselves and, compared to K-Means centroids, should be less sensitive to possible outliers [151].
The optimal number of clusters K was chosen searching for an “elbow” (i.e., a slope change) in the plot of the inertia parameter (i.e., the minimized value of Equation (1)) as a function of K and evaluating the Calinski–Harabasz index [154], which is the ratio of between-cluster and within-cluster dispersions, being higher for a better clusterization into compact and separated clusters.
3.3. Dimensionality Reduction for MD Data Visualization
Principal component analysis (PCA) [155] is a popular dimensionality reduction technique. For some centered (i.e., zero-mean) data matrix , its principal components are the eigenvectors of its covariance matrix :
It can be shown that (the eigenvector corresponding to the largest eigenvalue ) is the direction along which the variance of the data is highest, is the direction of highest variance in the subspace orthogonal to , etc., while the eigenvalues are the variance of the data along each . Projection of the data on the subspace of the first principal components can be performed via the following:
where is the variance retained in the PC subspace.
PCA dimensionality reduction () of TCNE::1ClN and N34− trajectories was performed only for data visualization purposes on two-dimensional plots and not as a pre-processing step for clustering analysis. In fact, the dimensionalities of their respective feature spaces (Section 3.2) are actually quite small, likely not involving any “curse of dimensionality” issues.
3.4. Excited State Characterization and Spectra Simulations
TCNE::1ClN and N34− excited states were computed with the linear-response TD-DFT approach at CAM-B3LYP/GD3/C-PCM(DCM)/6-31+G(d,p) and B3LYP/C-PCM(water)/def2-SVP/SDD(Ru) levels of theory, respectively. Electronic spectra in the solution at K were simulated on 500 frame subsets of the collected MD samplings (i.e., every 20 fs and 17.2 fs, respectively). The first 8 and 40 singlet excited states were calculated for TCNE::1ClN and N34−, respectively. The complete spectra were obtained by summation of Gaussian-shaped contributions over each frame and each calculated excited state:
where and are the oscillator strength and excitation energy of the i-th state of l-th frame and is a width parameter, set at . Spectra estimated from the only cluster medoids were similarly calculated:
where K is the number of clusters and is the k-th cluster population.
Cluster medoid excited states were further characterized by fragment-based transition density Löwdin population analysis and related charge transfer descriptors, calculated with the TheoDORE package [156,157]:
where A and B are two molecular fragments and is the transition density matrix for the S ← S0 excitation.
Ab initio molecular dynamics simulations and excited state calculations were performed with the Gaussian16 software package [158].
4. Conclusions
Unsupervised clustering methods have been employed as complementary approaches for an efficient exploration of the data resulting from MD simulations and electronic structure calculations. In this work, MD dataset reduction capabilities via unsupervised clustering techniques were applied for the ab initio modeling of electronic absorption spectra of the non-covalent charge-transfer TCNE::1ClN dimer and the [Ru(dcbpy)2(NCS)2]4− complex in solution at room temperature. Cluster medoids, taken as representative structures, were found and analyzed in terms of main structural parameters, principal component dynamics, electronic excitations and charge transfer indices, showing how such medoids can satisfactorily cover the system dynamics and optical properties with a very good agreement with experiments.
The simulation of electronic absorption spectra usually demands expensive computations and requires dealing with the interplay of electronic excited states with the conformational freedom of the chromophores in complex matrices (i.e., solvents, biomolecules, crystals) at finite temperature. This work highlights the power of the unsupervised K-medoid clustering technique combined with a tailored selection of the feature space in reducing by ∼100 times the total cost of electronic and optical property computations on an MD sampling with no loss of accuracy and in preserving the molecular interpretation via the cluster medoids. In this regard, it could be very interesting to study how the medoids and the several conformational minima are related and this is a subject for further spectroscopic and weighting scheme developments.
Author Contributions
F.P.: data curation, formal analysis, software, investigation, writing—original draft, writing—review & editing; F.C.: data curation, formal analysis, investigation, writing—original draft, writing—review & editing; N.R.: conceptualization, funding acquisition, methodology, writing—review & editing; A.P.: conceptualization, methodology, supervision, validation, writing—original draft, writing—review & editing. All authors have read and agreed to the published version of the manuscript.
Funding
Authors thank Gaussian Inc. and the Italian Ministry of University and Research (Projects: PRIN 2017YJMPZN001, PRIN 202082CE3T_002) for financial support.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 1ClN | 1-chloronaphthalene |
| ADMP | Atom-centered density matrix propagation |
| C-PCM | Conductor-like polarizable continuum model |
| CT | Charge transfer |
| dcbpy | 4,4′-dicarboxy-2,2′-bipyridine |
| DCM | dichloromethane |
| DFT | Density functional theory |
| LMCT | Ligand-to-metal charge-transfer |
| MD | Molecular dynamics |
| ML | Machine learning |
| MLCT | Metal-to-ligand charge-transfer |
| MM | Molecular mechanics |
| N34− | [Ru(dcbpy)2(NCS)2]4− |
| PC | Principal component |
| PCA | Principal component analysis |
| PES | Potential energy surface |
| QM | Quantum mechanics |
| SDF | Spatial distribution function |
| TCNE | Tetracyanoethylene |
| TD-DFT | Time dependent density functional theory |
References
- Adamo, C.; Cossi, M.; Rega, N.; Barone, V. Chapter 12—New computational strategies for the quantum mechanical study of biological systems in condensed phases. In Theoretical Biochemistry; Eriksson, L.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 9: Theoretical and Computational Chemistry; pp. 467–538. [Google Scholar] [CrossRef]
- Barone, V.; Improta, R.; Rega, N. Quantum Mechanical Computations and Spectroscopy: From Small Rigid Molecules in the Gas Phase to Large Flexible Molecules in Solution. Acc. Chem. Res. 2008, 41, 605–616. [Google Scholar] [CrossRef] [PubMed]
- Reichardt, C. Solvatochromic Dyes as Solvent Polarity Indicators. Chem. Rev. 1994, 94, 2319–2358. [Google Scholar] [CrossRef]
- Barone, V.; Polimeno, A. Integrated computational strategies for UV/vis spectra of large molecules in solution. Chem. Soc. Rev. 2007, 36, 1724–1731. [Google Scholar] [CrossRef] [PubMed]
- Krystkowiak, E.; Dobek, K.; Maciejewski, A. Origin of the strong effect of protic solvents on the emission spectra, quantum yield of fluorescence and fluorescence lifetime of 4-aminophthalimide: Role of hydrogen bonds in deactivation of S1-4-aminophthalimide. J. Photochem. Photobiol. 2006, 184, 250–264. [Google Scholar] [CrossRef]
- Solntsev, K.M.; Huppert, D.; Agmon, N. Photochemistry of “Super”-Photoacids. Solvent Effects. J. Phys. Chem. A 1999, 103, 6984–6997. [Google Scholar] [CrossRef]
- Solntsev, K.M.; Huppert, D.; Tolbert, L.M.; Agmon, N. Solvatochromic shifts of “super” photoacids. J. Am. Chem. Soc. 1998, 120, 7981–7982. [Google Scholar] [CrossRef]
- Coppola, F.; Nucci, M.; Marazzi, M.; Rocca, D.; Pastore, M. Norbornadiene/Quadricyclane System in the Spotlight: The Role of Rydberg States and Dynamic Electronic Correlation in a Solar-Thermal Building Block. ChemPhotoChem 2023, e202200214. [Google Scholar] [CrossRef]
- Frank, H.A.; Bautista, J.A.; Josue, J.; Pendon, Z.; Hiller, R.G.; Sharples, F.P.; Gosztola, D.; Wasielewski, M.R. Effect of the Solvent Environment on the Spectroscopic Properties and Dynamics of the Lowest Excited States of Carotenoids. J. Phys. Chem. B 2000, 104, 4569–4577. [Google Scholar] [CrossRef]
- Raucci, U.; Perrella, F.; Donati, G.; Zoppi, M.; Petrone, A.; Rega, N. Ab-initio molecular dynamics and hybrid explicit-implicit solvation model for aqueous and nonaqueous solvents: GFP chromophore in water and methanol solution as case study. J. Comput. Chem. 2020, 41, 2228–2239. [Google Scholar] [CrossRef]
- Donati, G.; Petrone, A.; Rega, N. Multiresolution continuous wavelet transform for studying coupled solute–solvent vibrations via ab initio molecular dynamics. Phys. Chem. Chem. Phys. 2020, 22, 22645–22661. [Google Scholar] [CrossRef]
- Coppola, F.; Perrella, F.; Petrone, A.; Donati, G.; Rega, N. A not obvious correlation between the structure of green fluorescent protein chromophore pocket and hydrogen bond dynamics: A choreography from ab initio molecular dynamics. Front. Mol. Biosci. 2020, 7, 569990. [Google Scholar] [CrossRef]
- Raucci, U.; Savarese, M.; Adamo, C.; Ciofini, I.; Rega, N. Intrinsic and Dynamical Reaction Pathways of an Excited State Proton Transfer. J. Phys. Chem. B 2015, 119, 2650–2657. [Google Scholar] [CrossRef]
- Petrone, A.; Caruso, P.; Tenuta, S.; Rega, N. On the optical absorption of the anionic GFP chromophore in vacuum, solution, and protein. Phys. Chem. Chem. Phys. 2013, 15, 20536–20544. [Google Scholar] [CrossRef]
- Langella, E.; Rega, N.; Improta, R.; Crescenzi, O.; Barone, V. Conformational analysis of the tyrosine dipeptide analogue in the gas phase and in aqueous solution by a density functional/continuum solvent model. J. Comput. Chem. 2002, 23, 650–661. [Google Scholar] [CrossRef]
- Cerezo, J.; Petrone, A.; Ferrer, F.J.A.; Donati, G.; Santoro, F.; Improta, R.; Rega, N. Electronic spectroscopy of a solvatochromic dye in water: Comparison of static cluster/implicit and dynamical/explicit solvent models on structures and energies. Theor. Chem. Acc. 2016, 135, 263. [Google Scholar] [CrossRef]
- Cimino, P.; Raucci, U.; Donati, G.; Chiariello, M.G.; Schiazza, M.; Coppola, F.; Rega, N. On the different strength of photoacids. Theor. Chem. Acc. 2016, 135, 117. [Google Scholar] [CrossRef]
- Kim, P.; Valentine, A.J.S.; Roy, S.; Mills, A.W.; Chakraborty, A.; Castellano, F.N.; Li, X.; Chen, L.X. Ultrafast Excited-State Dynamics of Photoluminescent Pt(II) Dimers Probed by a Coherent Vibrational Wavepacket. J. Phys. Chem. Lett. 2021, 12, 6794–6803. [Google Scholar] [CrossRef]
- Lu, L.; Wildman, A.; Jenkins, A.J.; Young, L.; Clark, A.E.; Li, X. The “Hole” Story in Ionized Water from the Perspective of Ehrenfest Dynamics. J. Phys. Chem. Lett. 2020, 11, 9946–9951. [Google Scholar] [CrossRef]
- Leger, J.D.; Friedfeld, M.R.; Beck, R.A.; Gaynor, J.D.; Petrone, A.; Li, X.; Cossairt, B.M.; Khalil, M. Carboxylate Anchors Act as Exciton Reporters in 1.3 nm Indium Phosphide Nanoclusters. J. Phys. Chem. Lett. 2019, 10, 1833–1839. [Google Scholar] [CrossRef]
- Nascimento, D.R.; Zhang, Y.; Bergmann, U.; Govind, N. Near-Edge X-ray Absorption Fine Structure Spectroscopy of Heteroatomic Core-Hole States as a Probe for Nearly Indistinguishable Chemical Environments. J. Phys. Chem. Lett. 2020, 11, 556–561. [Google Scholar] [CrossRef]
- Alberto, M.E.; De Simone, B.C.; Mazzone, G.; Quartarolo, A.D.; Russo, N. Theoretical Determination of Electronic Spectra and Intersystem Spin–Orbit Coupling: The Case of Isoindole-BODIPY Dyes. J. Chem. Theory Comput. 2014, 10, 4006–4013. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Alessandrini, S.; Biczysko, M.; Cheeseman, J.R.; Clary, D.C.; McCoy, A.B.; DiRisio, R.J.; Neese, F.; Melosso, M.; Puzzarini, C. Computational molecular spectroscopy. Nat. Rev. Methods Prim. 2021, 1, 38. [Google Scholar] [CrossRef]
- Barone, V.; Bloino, J.; Biczysko, M.; Santoro, F. Fully Integrated Approach to Compute Vibrationally Resolved Optical Spectra: From Small Molecules to Macrosystems. J. Chem. Theory Comput. 2009, 5, 540–554. [Google Scholar] [CrossRef] [PubMed]
- Santoro, F.; Lami, A.; Improta, R.; Barone, V. Effective method to compute vibrationally resolved optical spectra of large molecules at finite temperature in the gas phase and in solution. J. Chem. Phys. 2007, 126, 184102. [Google Scholar] [CrossRef]
- Avila Ferrer, F.J.; Cerezo, J.; Stendardo, E.; Improta, R.; Santoro, F. Insights for an Accurate Comparison of Computational Data to Experimental Absorption and Emission Spectra: Beyond the Vertical Transition Approximation. J. Chem. Theory Comput. 2013, 9, 2072–2082. [Google Scholar] [CrossRef]
- Dierksen, M.; Grimme, S. Density functional calculations of the vibronic structure of electronic absorption spectra. J. Chem. Phys. 2004, 120, 3544–3554. [Google Scholar] [CrossRef]
- Isborn, C.M.; Gotz, A.W.; Clark, M.A.; Walker, R.C.; Martínez, T.J. Electronic absorption spectra from MM and ab initio QM/MM molecular dynamics: Environmental effects on the absorption spectrum of photoactive yellow protein. J. Chem. Theory Comput. 2012, 8, 5092–5106. [Google Scholar] [CrossRef]
- Pagliai, M.; Mancini, G.; Carnimeo, I.; De Mitri, N.; Barone, V. Electronic absorption spectra of pyridine and nicotine in aqueous solution with a combined molecular dynamics and polarizable QM/MM approach. J. Chem. Theory Comput. 2017, 38, 319–335. [Google Scholar] [CrossRef]
- Mendanha, K.; Prado, R.C.; Oliveira, L.B.; Colherinhas, G. TD-DFT absorption spectrum of (poly) threonine in water: A study combining molecular dynamics and quantum mechanics calculations. Chem. Phys. Lett. 2021, 779, 138876. [Google Scholar] [CrossRef]
- Kasper, J.M.; Williams-Young, D.B.; Vecharynski, E.; Yang, C.; Li, X. A Well-Tempered Hybrid Method for Solving Challenging Time-Dependent Density Functional Theory (TDDFT) Systems. J. Chem. Theory Comput. 2018, 14, 2034–2041. [Google Scholar] [CrossRef]
- Van Beeumen, R.; Williams-Young, D.B.; Kasper, J.M.; Yang, C.; Ng, E.G.; Li, X. Model Order Reduction Algorithm for Estimating the Absorption Spectrum. J. Chem. Theory Comput. 2017, 13, 4950–4961. [Google Scholar] [CrossRef]
- Alberto, M.E.; Mazzone, G.; Quartarolo, A.D.; Sousa, F.F.R.; Sicilia, E.; Russo, N. Electronic spectra and intersystem spin-orbit coupling in 1,2- and 1,3-squaraines. J. Comput. Chem. 2014, 35, 2107–2113. [Google Scholar] [CrossRef]
- Petrone, A.; Perrella, F.; Coppola, F.; Crisci, L.; Donati, G.; Cimino, P.; Rega, N. Ultrafast photo-induced processes in complex environments: The role of accuracy in excited-state energy potentials and initial conditions. Chem. Phys. Rev. 2022, 3, 021307. [Google Scholar] [CrossRef]
- Coppola, F.; Cimino, P.; Perrella, F.; Crisci, L.; Petrone, A.; Rega, N. Electronic and Vibrational Manifold of Tetracyanoethylene–Chloronaphthalene Charge Transfer Complex in Solution: Insights from TD-DFT and Ab Initio Molecular Dynamics. J. Phys. Chem. A 2022, 126, 7179–7192. [Google Scholar] [CrossRef]
- Segatta, F.; Nenov, A.; Nascimento, D.R.; Govind, N.; Mukamel, S.; Garavelli, M. iSPECTRON: A simulation interface for linear and nonlinear spectra with ab-initio quantum chemistry software. J. Comput. Chem. 2021, 42, 644–659. [Google Scholar] [CrossRef]
- Petrenko, T.; Neese, F. Analysis and prediction of absorption band shapes, fluorescence band shapes, resonance Raman intensities and excitation profiles using the time-dependent theory of electronic spectroscopy. J. Chem. Phys. 2007, 127, 164319. [Google Scholar] [CrossRef]
- Petrone, A.; Cerezo, J.; Ferrer, F.J.A.; Donati, G.; Improta, R.; Rega, N.; Santoro, F. Absorption and Emission Spectral Shapes of a Prototype Dye in Water by Combining Classical/Dynamical and Quantum/Static Approaches. J. Phys. Chem. A 2015, 119, 5426–5438. [Google Scholar] [CrossRef]
- De Mitri, N.; Monti, S.; Prampolini, G.; Barone, V. Absorption and emission spectra of a flexible dye in solution: A computational time-dependent approach. J. Chem. Theory Comput. 2013, 9, 4507–4516. [Google Scholar] [CrossRef]
- Hoffman, D.P.; Ellis, S.R.; Mathies, R.A. Characterization of a conical intersection in a charge-transfer dimer with two-dimensional time-resolved stimulated Raman spectroscopy. J. Phys. Chem. A 2014, 118, 4955–4965. [Google Scholar] [CrossRef]
- Dubinets, N.; Safonov, A.; Bagaturyants, A. Structures and binding energies of the naphthalene dimer in its ground and excited states. J. Phys. Chem. A 2016, 120, 2779–2782. [Google Scholar] [CrossRef]
- Hancock, A.C.; Goerigk, L. Noncovalently bound excited-state dimers: A perspective on current time-dependent density functional theory approaches applied to aromatic excimer models. RSC Adv. 2022, 12, 13014–13034. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.h.; Lischka, H.; Mueller, T.; Plasser, F.; Kertesz, M. Study of the Diradicaloid Character in a Prototypical Pancake-Bonded Dimer: The Stacked Tetracyanoethylene (TCNE) Anion Dimer and the Neutral K2TCNE2 Complex. ChemPhysChem 2014, 15, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Valente, D.C.A.; Do Casal, M.T.; Barbatti, M.; Niehaus, T.A.; Aquino, A.J.; Lischka, H.; Cardozo, T.M. Excitonic and charge transfer interactions in tetracene stacked and T-shaped dimers. J. Chem. Phys. 2021, 154, 044306. [Google Scholar] [CrossRef] [PubMed]
- Siddique, F.; Barbatti, M.; Cui, Z.; Lischka, H.; Aquino, A.J. Nonadiabatic dynamics of charge-transfer states using the anthracene–tetracyanoethylene complex as a prototype. J. Phys. Chem. A 2020, 124, 3347–3357. [Google Scholar] [CrossRef] [PubMed]
- Mauck, C.M.; Bae, Y.J.; Chen, M.; Powers-Riggs, N.; Wu, Y.L.; Wasielewski, M.R. Charge-transfer character in a covalent diketopyrrolopyrrole dimer: Implications for singlet fission. ChemPhotoChem 2018, 2, 223–233. [Google Scholar] [CrossRef]
- Cui, Z.h.; Aquino, A.J.; Sue, A.C.H.; Lischka, H. Analysis of charge transfer transitions in stacked π-electron donor–acceptor complexes. Phys. Chem. Chem. Phys. 2018, 20, 26957–26967. [Google Scholar] [CrossRef]
- Müller-Dethlefs, K.; Hobza, P. Noncovalent interactions: A challenge for experiment and theory. Chem. Rev. 2000, 100, 143–168. [Google Scholar] [CrossRef]
- Snyder, J.W.; Fales, B.S.; Hohenstein, E.G.; Levine, B.G.; Martínez, T.J. A direct-compatible formulation of the coupled perturbed complete active space self-consistent field equations on graphical processing units. J. Chem. Phys. 2017, 146, 174113. [Google Scholar] [CrossRef]
- Demel, O.; Pittner, J.; Neese, F. A Local Pair Natural Orbital-Based Multireference Mukherjee’s Coupled Cluster Method. J. Chem. Theory Comput. 2015, 11, 3104–3114. [Google Scholar] [CrossRef]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef]
- Chiariello, M.G.; Donati, G.; Raucci, U.; Perrella, F.; Rega, N. Structural Origin and Vibrational Fingerprints of the Ultrafast Excited State Proton Transfer of the Pyranine-Acetate Complex in Aqueous Solution. J. Phys. Chem. B 2021, 125, 10273–10281. [Google Scholar] [CrossRef]
- Chiariello, M.G.; Raucci, U.; Donati, G.; Rega, N. Water-mediated excited state proton transfer of pyranine–acetate in aqueous solution: Vibrational fingerprints from ab initio molecular dynamics. J. Phys. Chem. A 2021, 125, 3569–3578. [Google Scholar] [CrossRef]
- De Simone, B.C.; Alberto, M.E.; Marino, T.; Russo, N.; Toscano, M. The Contribution of Density Functional Theory to the Atomistic Knowledge of Electrochromic Processes. Molecules 2021, 26, 5793. [Google Scholar] [CrossRef]
- Raucci, U.; Chiariello, M.G.; Rega, N. Modeling excited-state proton transfer to solvent: A dynamics study of a super photoacid with a hybrid implicit/explicit solvent model. J. Chem. Theory Comput. 2020, 16, 7033–7043. [Google Scholar] [CrossRef]
- Chiariello, M.G.; Donati, G.; Rega, N. Time-resolved vibrational analysis of excited state ab initio molecular dynamics to understand photorelaxation: The case of the pyranine photoacid in aqueous solution. J. Chem. Theory Comput. 2020, 16, 6007–6013. [Google Scholar] [CrossRef]
- Raucci, U.; Chiariello, M.G.; Coppola, F.; Perrella, F.; Savarese, M.; Ciofini, I.; Rega, N. An electron density based analysis to establish the electronic adiabaticity of proton coupled electron transfer reactions. J. Comput. Chem. 2020, 41, 1835–1841. [Google Scholar] [CrossRef]
- Chiariello, M.G.; Raucci, U.; Coppola, F.; Rega, N. Unveiling anharmonic coupling by means of excited state ab initio dynamics: Application to diarylethene photoreactivity. Phys. Chem. Chem. Phys. 2019, 21, 3606–3614. [Google Scholar] [CrossRef]
- Chiariello, M.G.; Rega, N. Exploring nuclear photorelaxation of pyranine in aqueous solution: An integrated ab-initio molecular dynamics and time resolved vibrational analysis approach. J. Phys. Chem. A 2018, 122, 2884–2893. [Google Scholar] [CrossRef]
- Perrella, F.; Raucci, U.; Chiariello, M.G.; Chino, M.; Maglio, O.; Lombardi, A.; Rega, N. Unveiling the structure of a novel artificial heme-enzyme with peroxidase-like activity: A theoretical investigation. Biopolymers 2018, 109, e23225. [Google Scholar] [CrossRef]
- Williams-Young, D.B.; Bagusetty, A.; de Jong, W.A.; Doerfler, D.; van Dam, H.J.; Vázquez-Mayagoitia, Á.; Windus, T.L.; Yang, C. Achieving performance portability in Gaussian basis set density functional theory on accelerator based architectures in NWChemEx. Parallel Comput. 2021, 108, 102829. [Google Scholar] [CrossRef]
- Williams-Young, D.B.; Petrone, A.; Sun, S.; Stetina, T.F.; Lestrange, P.; Hoyer, C.E.; Nascimento, D.R.; Koulias, L.; Wildman, A.; Kasper, J.; et al. The Chronus Quantum software package. WIREs Comput. Mol. Sci. 2020, 10, e1436. [Google Scholar] [CrossRef]
- Artrith, N.; Butler, K.T.; Coudert, F.X.; Han, S.; Isayev, O.; Jain, A.; Walsh, A. Best practices in machine learning for chemistry. Nat. Chem. 2021, 13, 505–508. [Google Scholar] [CrossRef] [PubMed]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Pflüger, P.M.; Glorius, F. Molecular Machine Learning: The Future of Synthetic Chemistry? Angew. Chem. 2020, 59, 18860–18865. [Google Scholar] [CrossRef] [PubMed]
- Stocker, S.; Csányi, G.; Reuter, K.; Margraf, J.T. Machine learning in chemical reaction space. Nat. Chem. 2020, 11, 5505. [Google Scholar] [CrossRef]
- Sanchez-Lengeling, B.; Aspuru-Guzik, A. Inverse molecular design using machine learning: Generative models for matter engineering. Science 2018, 361, 360–365. [Google Scholar] [CrossRef]
- Dral, P.O. Quantum Chemistry in the Age of Machine Learning. J. Phys. Chem. Lett. 2020, 11, 2336–2347. [Google Scholar] [CrossRef]
- Keith, J.A.; Vassilev-Galindo, V.; Cheng, B.; Chmiela, S.; Gastegger, M.; Müller, K.R.; Tkatchenko, A. Combining Machine Learning and Computational Chemistry for Predictive Insights Into Chemical Systems. Chem. Rev. 2021, 121, 9816–9872. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Dral, P.O.; Rupp, M.; von Lilienfeld, O.A. Big Data Meets Quantum Chemistry Approximations: The Δ-Machine Learning Approach. J. Chem. Theory Comput. 2015, 11, 2087–2096. [Google Scholar] [CrossRef]
- von Lilienfeld, O.A.; Müller, K.R.; Tkatchenko, A. Exploring chemical compound space with quantum-based machine learning. Nat. Rev. Chem. 2020, 4, 347–358. [Google Scholar] [CrossRef]
- Häse, F.; Roch, L.M.; Friederich, P.; Aspuru-Guzik, A. Designing and understanding light-harvesting devices with machine learning. Nat. Chem. 2020, 11, 4587. [Google Scholar] [CrossRef]
- Rosen, A.S.; Iyer, S.M.; Ray, D.; Yao, Z.; Aspuru-Guzik, A.; Gagliardi, L.; Notestein, J.M.; Snurr, R.Q. Machine learning the quantum-chemical properties of metal–organic frameworks for accelerated materials discovery. Matter 2021, 4, 1578–1597. [Google Scholar] [CrossRef]
- Häse, F.; Galván, I.F.; Aspuru-Guzik, A.; Lindh, R.; Vacher, M. How machine learning can assist the interpretation of ab initio molecular dynamics simulations and conceptual understanding of chemistry. Chem. Sci. 2019, 10, 2298–2307. [Google Scholar] [CrossRef]
- Häse, F.; Valleau, S.; Pyzer-Knapp, E.; Aspuru-Guzik, A. Machine learning exciton dynamics. Chem. Sci. 2016, 7, 5139–5147. [Google Scholar] [CrossRef]
- Schriber, J.B.; Nascimento, D.R.; Koutsoukas, A.; Spronk, S.A.; Cheney, D.L.; Sherrill, C.D. CLIFF: A component-based, machine-learned, intermolecular force field. J. Chem. Phys. 2021, 154, 184110. [Google Scholar] [CrossRef]
- Glielmo, A.; Husic, B.E.; Rodriguez, A.; Clementi, C.; Noé, F.; Laio, A. Unsupervised Learning Methods for Molecular Simulation Data. Chem. Rev. 2021, 121, 9722–9758. [Google Scholar] [CrossRef]
- Falbo, E.; Fusè, M.; Lazzari, F.; Mancini, G.; Barone, V. Integration of Quantum Chemistry, Statistical Mechanics and Artificial Intelligence for Computational Spectroscopy: The UV–Vis Spectrum of TEMPO Radical in Different Solvents. J. Chem. Theory Comput. 2022, 18, 6203–6216. [Google Scholar] [CrossRef]
- Mancini, G.; Fusè, M.; Lipparini, F.; Nottoli, M.; Scalmani, G.; Barone, V. Molecular Dynamics Simulations Enforcing Nonperiodic Boundary Conditions: New Developments and Application to the Solvent Shifts of Nitroxide Magnetic Parameters. J. Chem. Theory Comput. 2022, 18, 2479–2493. [Google Scholar] [CrossRef]
- Mancini, G.; Fusè, M.; Lazzari, F.; Barone, V. Fast exploration of potential energy surfaces with a joint venture of quantum chemistry, evolutionary algorithms and unsupervised learning. Digit. Discov. 2022, 1, 790–805. [Google Scholar] [CrossRef]
- Barone, V.; Puzzarini, C.; Mancini, G. Integration of theory, simulation, artificial intelligence and virtual reality: A four-pillar approach for reconciling accuracy and interpretability in computational spectroscopy. Phys. Chem. Chem. Phys. 2021, 23, 17079–17096. [Google Scholar] [CrossRef]
- Mancini, G.; Del Galdo, S.; Chandramouli, B.; Pagliai, M.; Barone, V. Computational Spectroscopy in Solution by Integration of Variational and Perturbative Approaches on Top of Clusterized Molecular Dynamics. J. Chem. Theory Comput. 2020, 16, 5747–5761. [Google Scholar] [CrossRef] [PubMed]
- Del Galdo, S.; Chandramouli, B.; Mancini, G.; Barone, V. Assessment of Multi-Scale Approaches for Computing UV–Vis Spectra in Condensed Phases: Toward an Effective yet Reliable Integration of Variational and Perturbative QM/MM Approaches. J. Chem. Theory Comput. 2019, 15, 3170–3184. [Google Scholar] [CrossRef] [PubMed]
- Troyer, J.M.; Cohen, F.E. Protein conformational landscapes: Energy minimization and clustering of a long molecular dynamics trajectory. Proteins 1995, 23, 97–110. [Google Scholar] [CrossRef] [PubMed]
- Wolf, A.; Kirschner, K.N. Principal component and clustering analysis on molecular dynamics data of the ribosomal L11·23S subdomain. J. Mol. Model. 2013, 19, 539–549. [Google Scholar] [CrossRef] [PubMed]
- Papaleo, E.; Mereghetti, P.; Fantucci, P.; Grandori, R.; De Gioia, L. Free-energy landscape, principal component analysis and structural clustering to identify representative conformations from molecular dynamics simulations: The myoglobin case. J. Mol. Graph. Model. 2009, 27, 889–899. [Google Scholar] [CrossRef]
- Shao, J.; Tanner, S.W.; Thompson, N.; Cheatham, T.E. Clustering Molecular Dynamics Trajectories: 1. Characterizing the Performance of Different Clustering Algorithms. J. Chem. Theory Comput. 2007, 3, 2312–2334. [Google Scholar] [CrossRef]
- Torda, A.E.; van Gunsteren, W.F. Algorithms for clustering molecular dynamics configurations. J. Comput. Chem. 1994, 15, 1331–1340. [Google Scholar] [CrossRef]
- Phillips, J.L.; Colvin, M.E.; Newsam, S. Validating clustering of molecular dynamics simulations using polymer models. BMC Bioinform. 2011, 12, 445. [Google Scholar] [CrossRef]
- Karpen, M.E.; Tobias, D.J.; Brooks, C.L.I. Statistical clustering techniques for the analysis of long molecular dynamics trajectories: Analysis of 2.2-ns trajectories of YPGDV. Biochemistry 1993, 32, 412–420. [Google Scholar] [CrossRef]
- Peng, J.H.; Wang, W.; Yu, Y.Q.; Gu, H.L.; Huang, X. Clustering algorithms to analyze molecular dynamics simulation trajectories for complex chemical and biological systems. Chin. J. Chem. Phys. 2018, 31, 404–420. [Google Scholar] [CrossRef]
- González-Alemán, R.; Hernández-Castillo, D.; Rodríguez-Serradet, A.; Caballero, J.; Hernández-Rodríguez, E.W.; Montero-Cabrera, L. BitClust: Fast Geometrical Clustering of Long Molecular Dynamics Simulations. J. Chem. Inf. Model. 2020, 60, 444–448. [Google Scholar] [CrossRef]
- Ellis, S.R.; Hoffman, D.P.; Park, M.; Mathies, R.A. Difference bands in time-resolved femtosecond stimulated Raman spectra of photoexcited intermolecular electron transfer from chloronaphthalene to tetracyanoethylene. J. Phys. Chem. A 2018, 122, 3594–3605. [Google Scholar] [CrossRef]
- Coppola, F.; Cimino, P.; Raucci, U.; Chiariello, M.G.; Petrone, A.; Rega, N. Exploring the Franck–Condon region of a photoexcited charge transfer complex in solution to interpret femtosecond stimulated Raman spectroscopy: Excited state electronic structure methods to unveil non-radiative pathways. Chem. Sci. 2021, 12, 8058–8072. [Google Scholar] [CrossRef]
- Hagfeldt, A.; Boschloo, G.; Sun, L.; Kloo, L.; Pettersson, H. Dye-Sensitized Solar Cells. Chem. Rev. 2010, 110, 6595–6663. [Google Scholar] [CrossRef]
- Grätzel, M. Dye-sensitized solar cells. J. Photochem. Photobiol. C 2003, 4, 145–153. [Google Scholar] [CrossRef]
- Grätzel, M. Solar Energy Conversion by Dye-Sensitized Photovoltaic Cells. Inorg. Chem. 2005, 44, 6841–6851. [Google Scholar] [CrossRef]
- McCusker, J.K.; Vlcek, A., Jr. Ultrafast Excited-State Processes in Inorganic Systems. Acc. Chem. Res. 2015, 48, 1207–1208. [Google Scholar] [CrossRef]
- Chergui, M. Ultrafast Photophysics of Transition Metal Complexes. Acc. Chem. Res. 2015, 48, 801–808. [Google Scholar] [CrossRef]
- Pettersson Rimgard, B.; Föhlinger, J.; Petersson, J.; Lundberg, M.; Zietz, B.; Woys, A.M.; Miller, S.A.; Wasielewski, M.R.; Hammarström, L. Ultrafast interligand electron transfer in cis-[Ru(4,4′-dicarboxylate-2,2′-bipyridine)2(NCS)2]4− and implications for electron injection limitations in dye sensitized solar cells. Chem. Sci. 2018, 9, 7958–7967. [Google Scholar] [CrossRef]
- Waterland, M.R.; Kelley, D.F. Photophysics and Relaxation Dynamics of Ru(4,4′-Dicarboxy-2,2′-bipyridine)2cis(NCS)2 in Solution. J. Phys. Chem. A 2001, 105, 4019–4028. [Google Scholar] [CrossRef]
- Atkins, A.J.; González, L. Trajectory Surface-Hopping Dynamics Including Intersystem Crossing in [Ru(bpy)3]2+. J. Phys. Chem. Lett. 2017, 8, 3840–3845. [Google Scholar] [CrossRef] [PubMed]
- Zobel, J.P.; González, L. The Quest to Simulate Excited-State Dynamics of Transition Metal Complexes. JACS Au 2021, 1, 1116–1140. [Google Scholar] [CrossRef] [PubMed]
- Perrella, F.; Li, X.; Petrone, A.; Rega, N. Nature of the Ultrafast Interligands Electron Transfers in Dye-Sensitized Solar Cells. JACS Au 2023, 3, 70–79. [Google Scholar] [CrossRef] [PubMed]
- Perrella, F.; Petrone, A.; Rega, N. Understanding Charge Dynamics in Dense Electronic Manifolds in Complex Environments. J. Chem. Theory Comput. 2023, 19, 626–639. [Google Scholar] [CrossRef] [PubMed]
- Baldini, E.; Palmieri, T.; Rossi, T.; Oppermann, M.; Pomarico, E.; Auböck, G.; Chergui, M. Interfacial Electron Injection Probed by a Substrate-Specific Excitonic Signature. J. Am. Chem. Soc. 2017, 139, 11584–11589. [Google Scholar] [CrossRef]
- Wei, H.; Luo, J.W.; Li, S.S.; Wang, L.W. Revealing the Origin of Fast Electron Transfer in TiO2-Based Dye-Sensitized Solar Cells. J. Am. Chem. Soc. 2016, 138, 8165–8174. [Google Scholar] [CrossRef]
- Tiwana, P.; Docampo, P.; Johnston, M.B.; Snaith, H.J.; Herz, L.M. Electron Mobility and Injection Dynamics in Mesoporous ZnO, SnO2 and TiO2 Films Used in Dye-Sensitized Solar Cells. ACS Nano 2011, 5, 5158–5166. [Google Scholar] [CrossRef]
- Katoh, R.; Furube, A.; Yoshihara, T.; Hara, K.; Fujihashi, G.; Takano, S.; Murata, S.; Arakawa, H.; Tachiya, M. Efficiencies of Electron Injection from Excited N3 Dye into Nanocrystalline Semiconductor (ZrO2, TiO2, ZnO, Nb2O2, SnO2, In2O2) Films. J. Phys. Chem. B 2004, 108, 4818–4822. [Google Scholar] [CrossRef]
- Asbury, J.B.; Ellingson, R.J.; Ghosh, H.N.; Ferrere, S.; Nozik, A.J.; Lian, T. Femtosecond IR Study of Excited-State Relaxation and Electron-Injection Dynamics of Ru(dcbpy)2(NCS)2 in Solution and on Nanocrystalline TiO2 and Al2O2 Thin Films. J. Phys. Chem. B 1999, 103, 3110–3119. [Google Scholar] [CrossRef]
- Perrella, F.; Petrone, A.; Rega, N. Direct observation of the solvent organization and nuclear vibrations of [Ru(dcbpy)2(NCS)2]4−, [dcbpy = (4,4′-dicarboxy-2,2′-bipyridine)], via ab initio molecular dynamics. Phys. Chem. Chem. Phys. 2021, 23, 22885–22896. [Google Scholar] [CrossRef]
- Brehm, M.; Thomas, M.; Gehrke, S.; Kirchner, B. TRAVIS—A free analyzer for trajectories from molecular simulation. J. Chem. Phys. 2020, 152, 164105. [Google Scholar] [CrossRef]
- Brehm, M.; Kirchner, B. TRAVIS—A free analyzer and visualizer for Monte Carlo and molecular dynamics trajectories. J. Chem. Inf. Model. 2011, 51, 8. [Google Scholar] [CrossRef]
- De Angelis, F.; Fantacci, S.; Selloni, A.; Nazeeruddin, M.K. Time dependent density functional theory study of the absorption spectrum of the [Ru(4,4′-COO−-2,2′-bpy)2(X)2]4− (X=NCS, Cl) dyes in water solution. Chem. Phys. Lett. 2005, 415, 115–120. [Google Scholar] [CrossRef]
- Schlegel, H.B.; Millam, J.M.; Iyengar, S.S.; Voth, G.A.; Daniels, A.D.; Scuseria, G.E.; Frisch, M.J. Ab initio molecular dynamics: Propagating the density matrix with Gaussian orbitals. J. Chem. Phys. 2001, 114, 9758–9763. [Google Scholar] [CrossRef]
- Iyengar, S.S.; Schlegel, H.B.; Millam, J.M.; Voth, G.A.; Scuseria, G.E.; Frisch, M.J. Ab initio molecular dynamics: Propagating the density matrix with Gaussian orbitals. II. Generalizations based on mass-weighting, idempotency, energy conservation and choice of initial conditions. J. Chem. Phys. 2001, 115, 10291–10302. [Google Scholar] [CrossRef]
- Schlegel, H.B.; Iyengar, S.S.; Li, X.; Millam, J.M.; Voth, G.A.; Scuseria, G.E.; Frisch, M.J. Ab initio molecular dynamics: Propagating the density matrix with Gaussian orbitals. III. Comparison with Born–Oppenheimer dynamics. J. Chem. Phys. 2002, 117, 8694–8704. [Google Scholar] [CrossRef]
- Iyengar, S.S.; Schlegel, H.B.; Voth, G.A.; Millam, J.M.; Scuseria, G.E.; Frisch, M.J. Ab initio molecular dynamics: Propagating the density matrix with Gaussian orbitals. IV. Formal analysis of the deviations from born-oppenheimer dynamics. Isr. J. Chem. 2002, 42, 191–202. [Google Scholar] [CrossRef]
- Rega, N.; Iyengar, S.S.; Voth, G.A.; Schlegel, H.B.; Vreven, T.; Frisch, M.J. Hybrid Ab-Initio/Empirical Molecular Dynamics: Combining the ONIOM Scheme with the Atom-Centered Density Matrix Propagation (ADMP) Approach. J. Phys. Chem. B 2004, 108, 4210–4220. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results obtained with the correlation energy density functionals of becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Brancato, G.; Rega, N.; Barone, V. A hybrid explicit/implicit solvation method for first-principle molecular dynamics simulations. J. Chem. Phys. 2008, 128, 144501. [Google Scholar] [CrossRef] [PubMed]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Cossi, M.; Scalmani, G.; Rega, N.; Barone, V. New developments in the polarizable continuum model for quantum mechanical and classical calculations on molecules in solution. J. Chem. Phys. 2002, 117, 43–54. [Google Scholar] [CrossRef]
- Mennucci, B. Polarizable continuum model. WIREs Comput. Mol. Sci. 2012, 2, 386–404. [Google Scholar] [CrossRef]
- Cossi, M.; Barone, V. Solvent effect on vertical electronic transitions by the polarizable continuum model. J. Chem. Phys. 2000, 112, 2427–2435. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Grimme, S. Density functional theory with London dispersion corrections. WIREs Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Ehrlich, S.; Moellmann, J.; Grimme, S. Dispersion-Corrected Density Functional Theory for Aromatic Interactions in Complex Systems. Acc. Chem. Res. 2013, 46, 916–926. [Google Scholar] [CrossRef] [PubMed]
- Risthaus, T.; Grimme, S. Benchmarking of London Dispersion-Accounting Density Functional Theory Methods on Very Large Molecular Complexes. J. Chem. Theory Comput. 2013, 9, 1580–1591. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Do Special Noncovalent π–π Stacking Interactions Really Exist? Angew. Chem. 2008, 47, 3430–3434. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Andrae, D.; Haeussermann, U.; Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the second and third row transition elements. Theor. Chem. Acc. 1990, 77, 123–141. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Svensson, M.; Humbel, S.; Froese, R.D.J.; Matsubara, T.; Sieber, S.; Morokuma, K. ONIOM: A Multilayered Integrated MO + MM Method for Geometry Optimizations and Single Point Energy Predictions. A Test for Diels-Alder Reactions and Pt(P(t-Bu)3)2 + H2 Oxidative Addition. J. Phys. Chem. 1996, 100, 19357–19363. [Google Scholar] [CrossRef]
- Vreven, T.; Byun, K.S.; Komáromi, I.; Dapprich, S.; Montgomery, J.A.J.; Morokuma, K.; Frisch, M.J. Combining Quantum Mechanics Methods with Molecular Mechanics Methods in ONIOM. J. Chem. Theory Comput. 2006, 2, 815–826. [Google Scholar] [CrossRef]
- Chung, L.W.; Sameera, W.M.C.; Ramozzi, R.; Page, A.J.; Hatanaka, M.; Petrova, G.P.; Harris, T.V.; Li, X.; Ke, Z.; Liu, F.; et al. The ONIOM Method and Its Applications. Chem. Rev. 2015, 115, 5678–5796. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Brancato, G.; Rega, N.; Barone, V. Molecular dynamics simulations in a NpT ensemble using non-periodic boundary conditions. Chem. Phys. Lett. 2009, 483, 177–181. [Google Scholar] [CrossRef]
- Rega, N.; Brancato, G.; Barone, V. Non-periodic boundary conditions for ab initio molecular dynamics in condensed phase using localized basis functions. Chem. Phys. Lett. 2006, 422, 367–371. [Google Scholar] [CrossRef]
- Brancato, G.; Barone, V.; Rega, N. Theoretical modeling of spectroscopic properties of molecules in solution: Toward an effective dynamical discrete/continuum approach. Theor. Chem. Acc. 2007, 117, 1001–1015. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. [Google Scholar] [CrossRef]
- Pinsky, M.; Casanova, D.; Alemany, P.; Alvarez, S.; Avnir, D.; Dryzun, C.; Kizner, Z.; Sterkin, A. Symmetry operation measures. J. Comput. Chem. 2008, 29, 190–197. [Google Scholar] [CrossRef]
- Pinsky, M.; Dryzun, C.; Casanova, D.; Alemany, P.; Avnir, D. Analytical methods for calculating Continuous Symmetry Measures and the Chirality Measure. J. Comput. Chem. 2008, 29, 2712–2721. [Google Scholar] [CrossRef]
- Mu, Y.; Nguyen, P.H.; Stock, G. Energy landscape of a small peptide revealed by dihedral angle principal component analysis. Proteins 2005, 58, 45–52. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras and TensorFlow: Concepts, Tools and Techniques to Build Intelligent Systems; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Schubert, E.; Lenssen, L. Fast k-medoids Clustering in Rust and Python. J. Open Source Softw. 2022, 7, 4183. [Google Scholar] [CrossRef]
- Schubert, E.; Rousseeuw, P.J. Fast and eager k-medoids clustering: O(k) runtime improvement of the PAM, CLARA and CLARANS algorithms. Inform. Syst. 2021, 101, 101804. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Phil. Trans. R. Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Plasser, F. TheoDORE: A toolbox for a detailed and automated analysis of electronic excited state computations. J. Chem. Phys. 2020, 152, 084108. [Google Scholar] [CrossRef] [PubMed]
- Plasser, F.; Lischka, H. Analysis of Excitonic and Charge Transfer Interactions from Quantum Chemical Calculations. J. Chem. Theory Comput. 2012, 8, 2777–2789. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).