Elucidating the Role of Noncovalent Interactions in Favipiravir, a Drug Active against Various Human RNA Viruses; a 1H-14N NQDR/Periodic DFT/QTAIM/RDS/3D Hirshfeld Surfaces Combined Study
Abstract
1. Introduction
2. Results and Discussion
2.1. 1H-14N NQDR Spectrum
- (i)
- Polarization field for time Typically,, where is the proton spin-lattice relaxation time in the field so that an equilibrium proton magnetization is established.
- (ii)
- Relaxation (also called “mixing”) field for time . Here the proton magnetization relaxes towards the equilibrium value with a time constant .
- (iii)
- Acquisition field , at which the proton NMR signal amplitude, which is proportional to the proton magnetization at the end of interval, is measured.
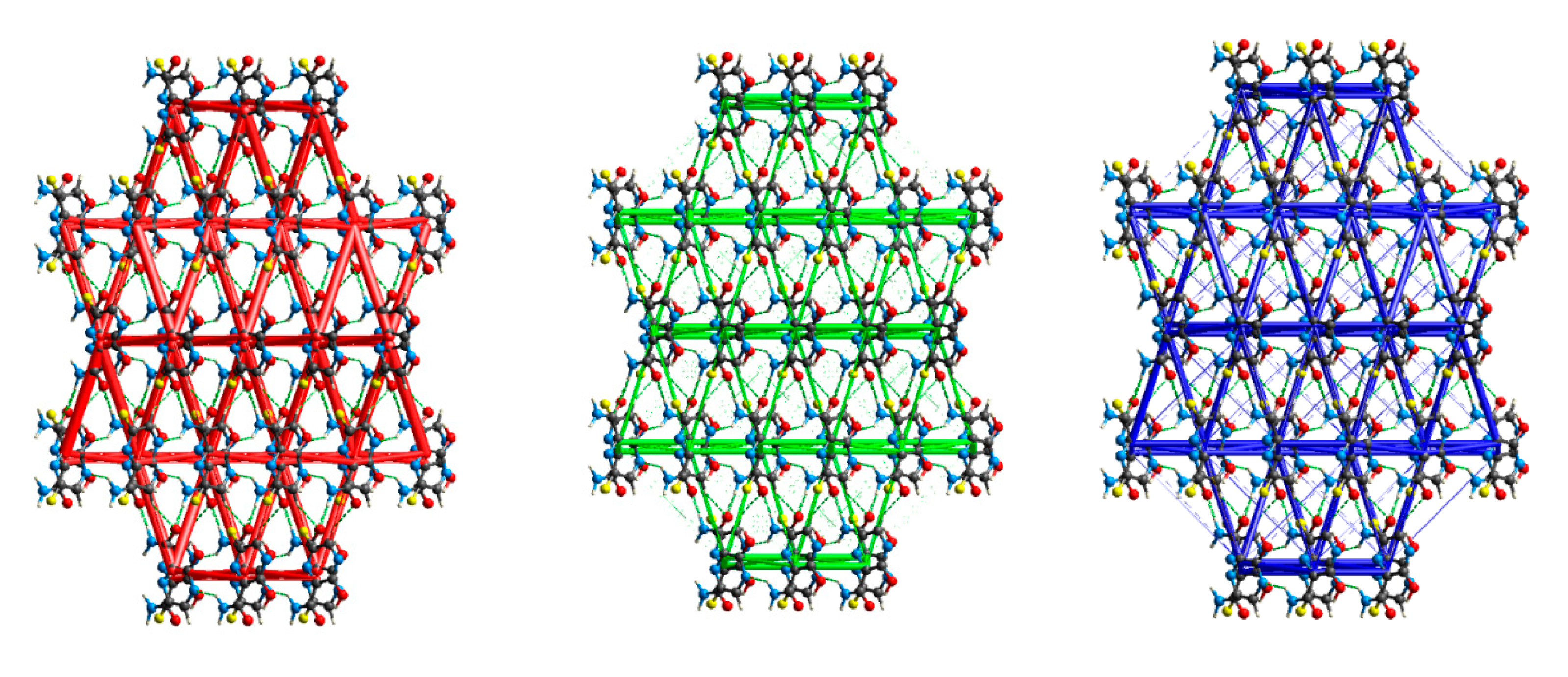
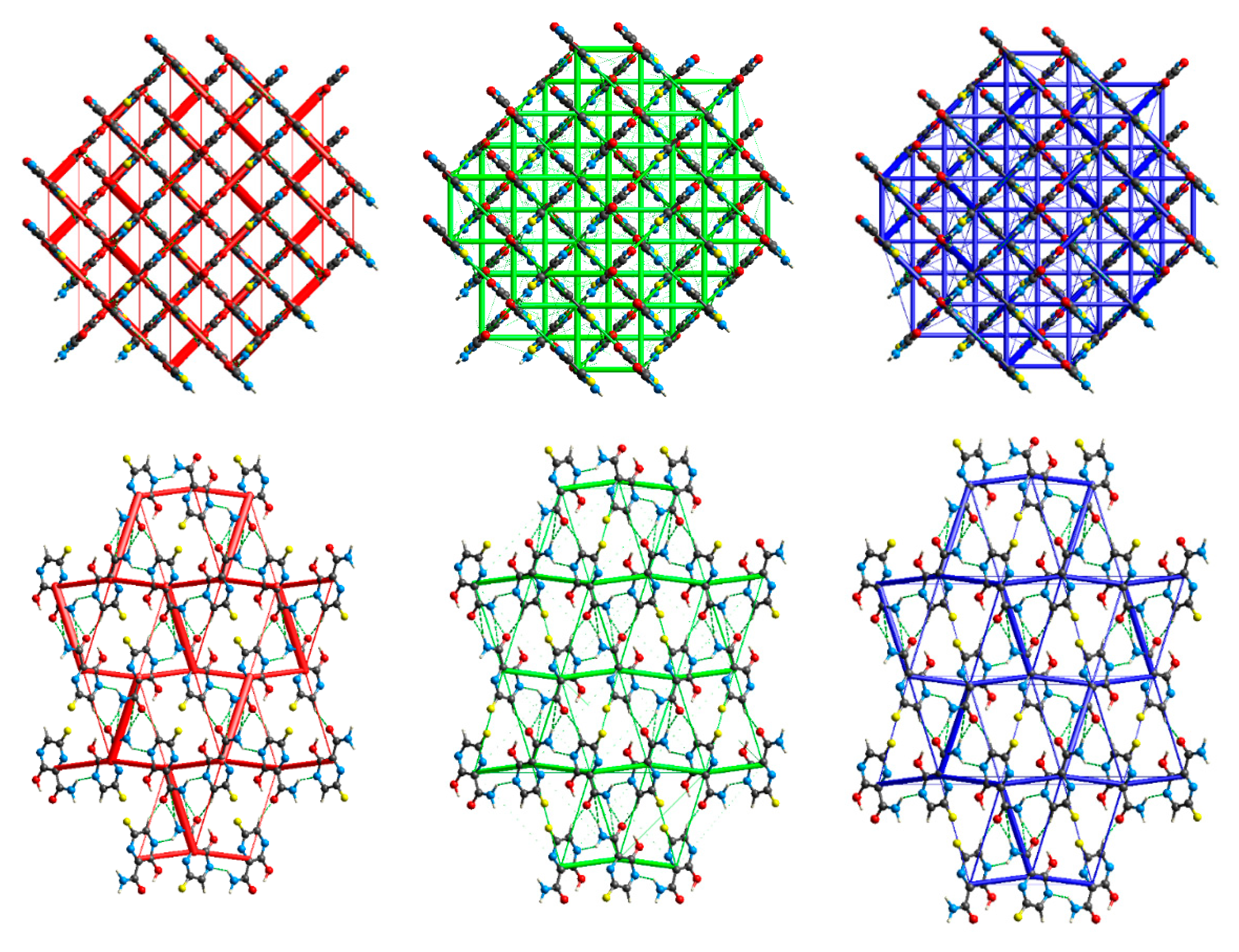
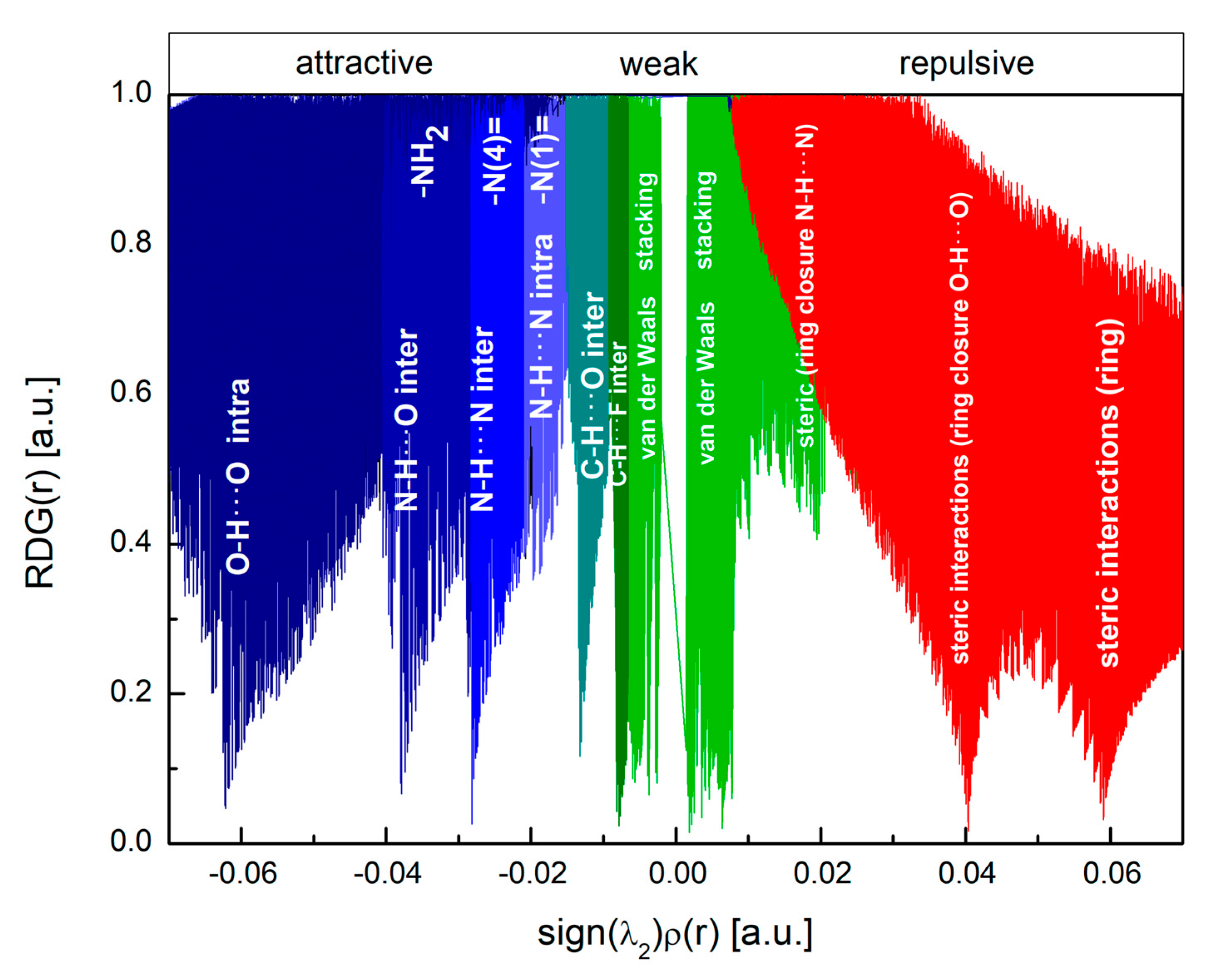
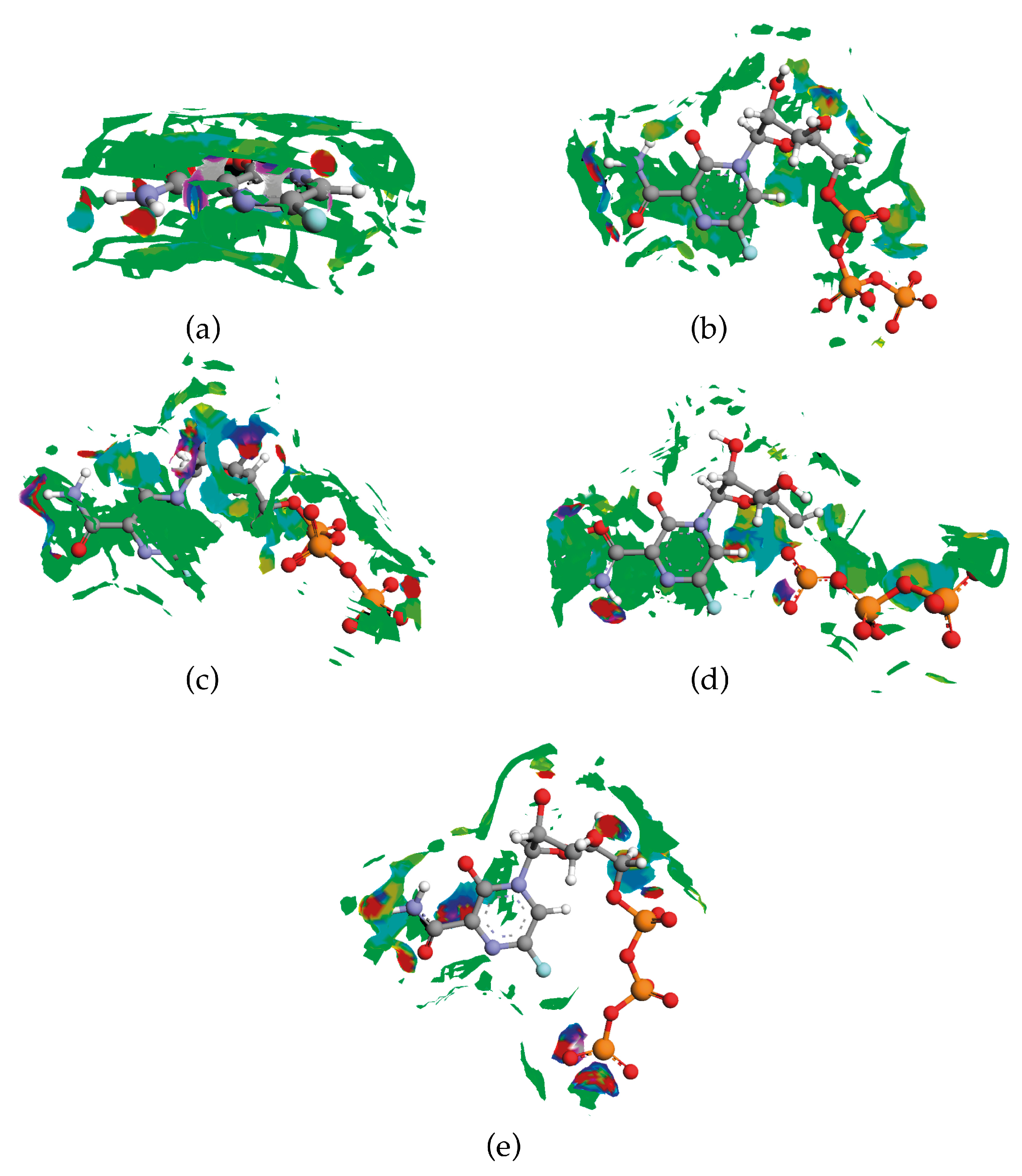
2.2. Interactions Pattern
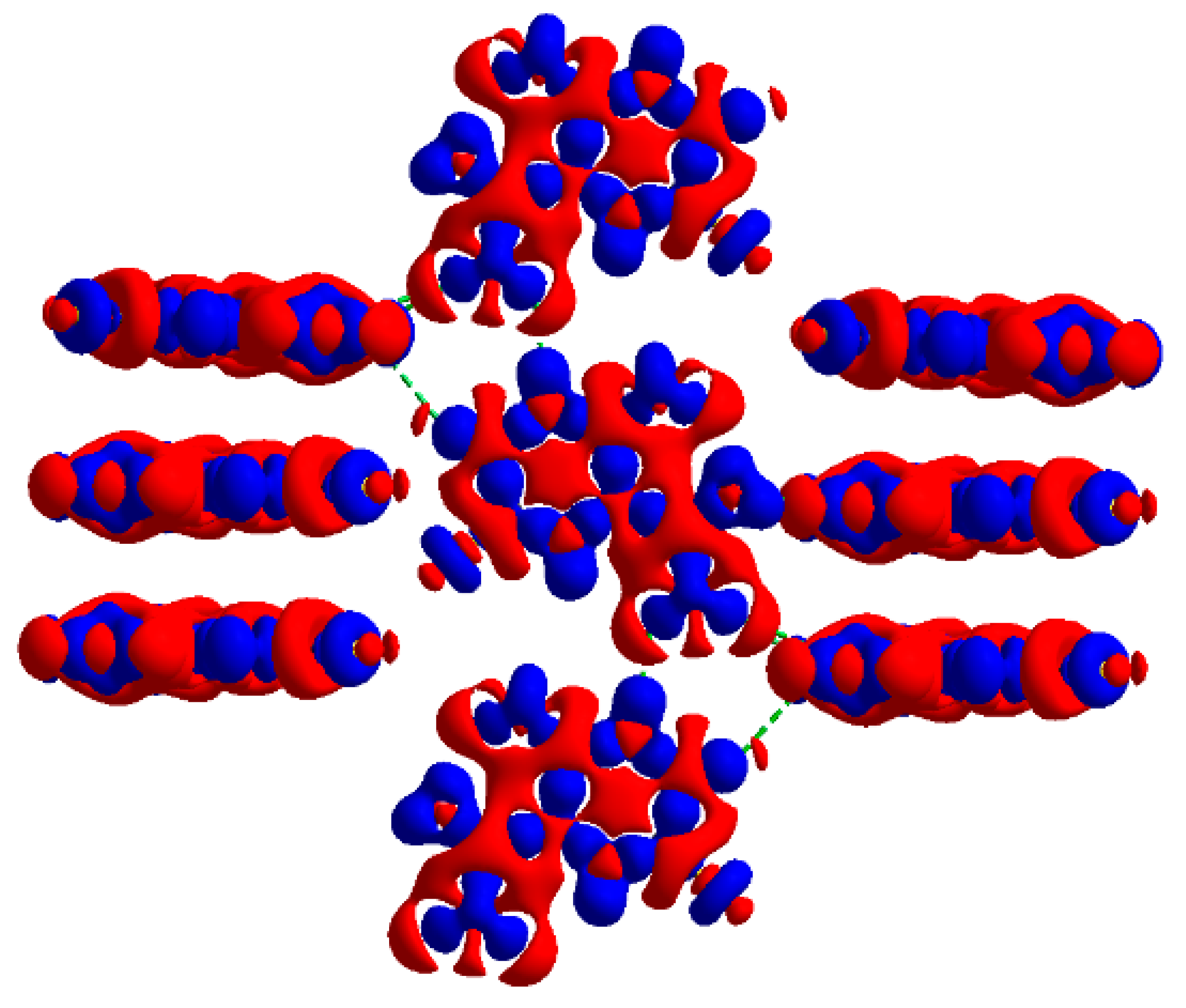
2.2.1. Hirshfeld Surfaces
2.2.2. Characterization of the Strength of the Interactions
The Total Interaction Energy Partitioning
Electrostatic Potential
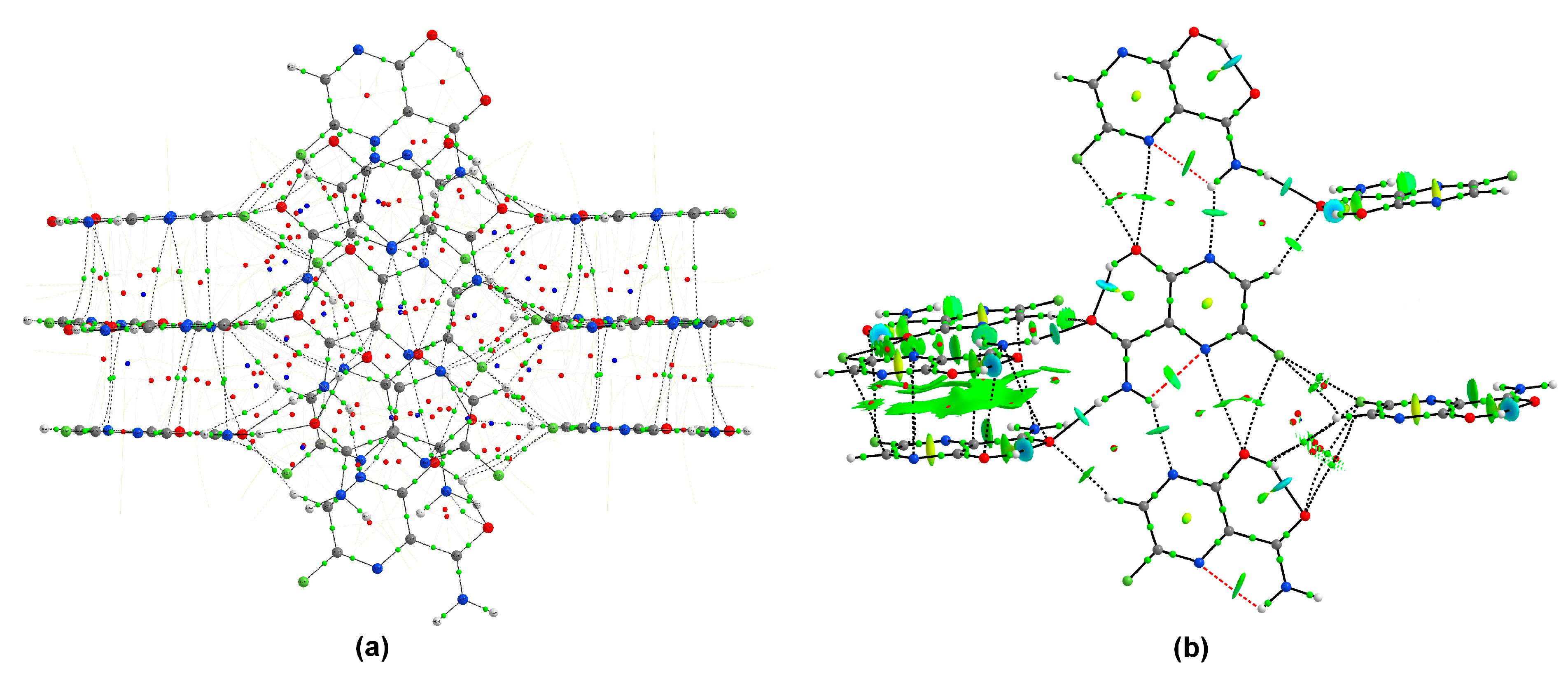
Quantum Theory of Atoms in Molecules
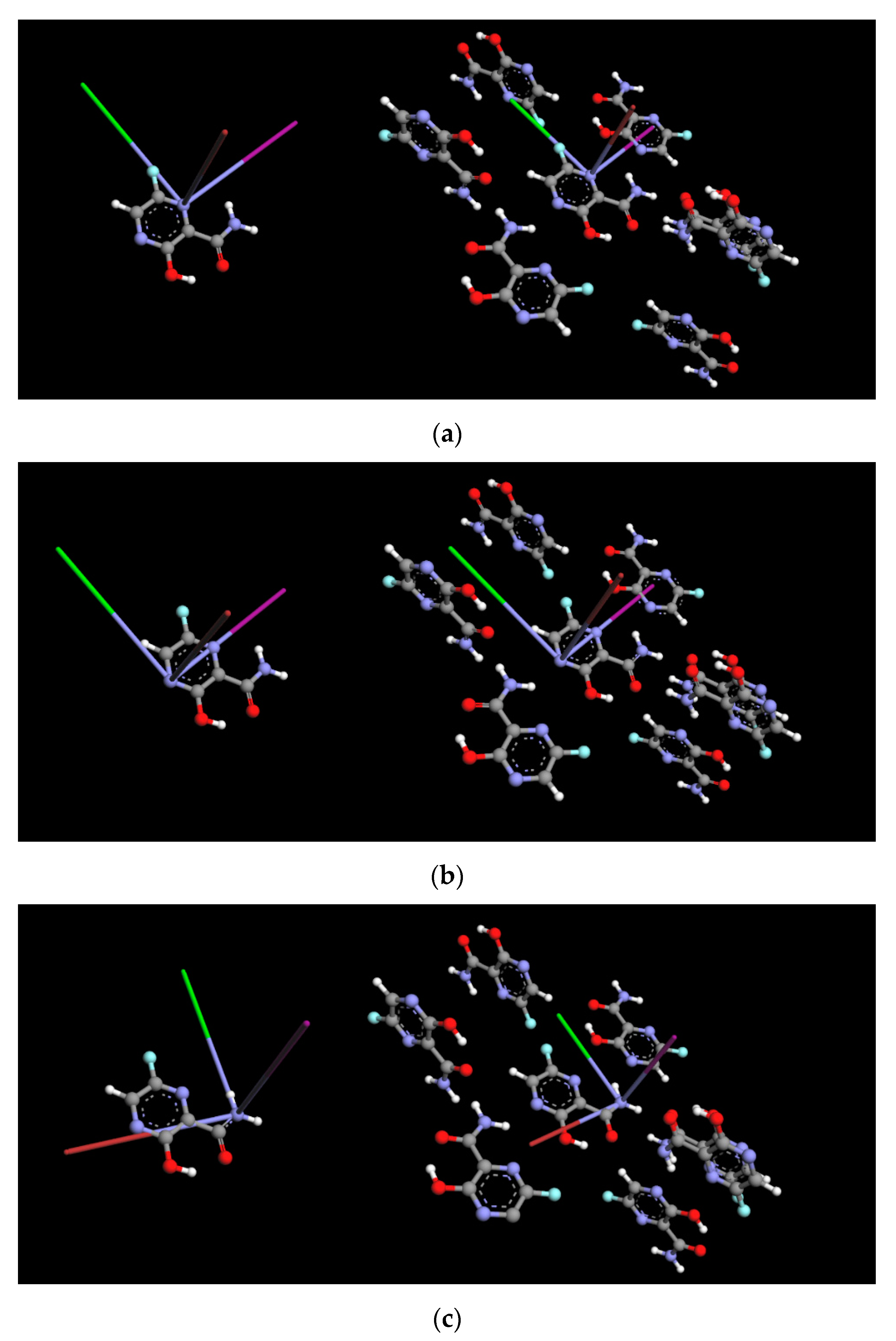
2.3. Binding Mode of Biologically Active Form
3. Material
4. Methods
4.1. Experimental—1H-14N NQDR
4.2. Spectra Simulations—Density Functional Theory (DFT)
4.3. Quantum Theory of Atoms in Molecules (QTAIM)
4.4. Hirshfeld Surfaces (3D HS)
4.5. Molecular Docking
5. Conclusions
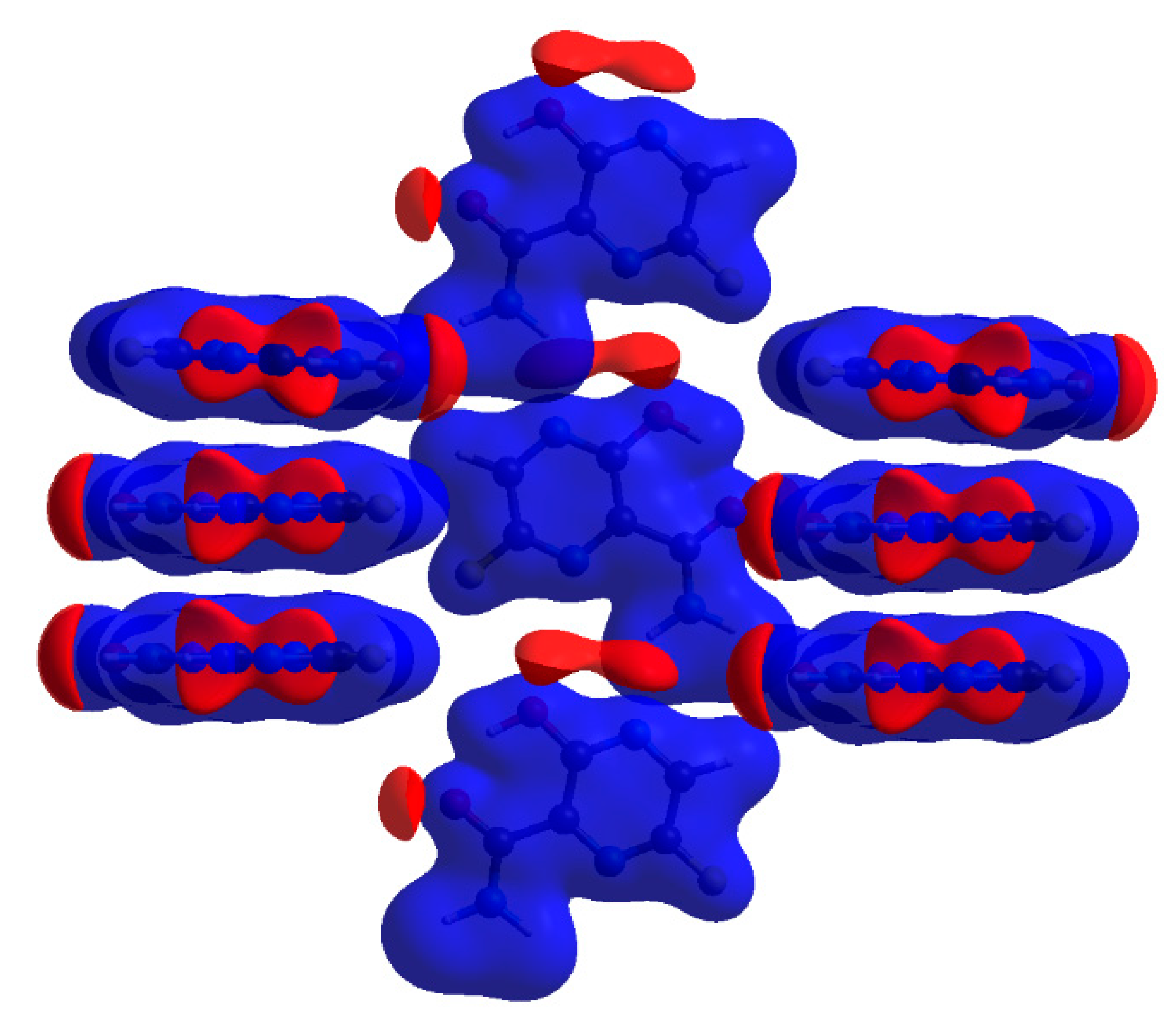
≈ π⋯π stacking (flipped molecules) > C–H⋯O >> F⋯F > F–H⋯C,
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Perlman, S. Another Decade, Another Coronavirus. N. Engl. J. Med. 2020, 382, 760–762. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, Q.; Zhang, Z. Probable Pangolin Origin of SARS-CoV-2 Associated with the COVID-19 Outbreak. Curr. Biol. 2020, 30, 1578. [Google Scholar] [CrossRef]
- WHO. Tracking SARS-CoV-2 Variants. Available online: https://www.who.int/activities/tracking-SARS-CoV-2-variants (accessed on 3 March 2023).
- Jordan, P.C.; Stevens, S.K.; Deval, J. Nucleosides for the treatment of respiratory RNA virus infections. Antivir. Chem. Chemother. 2018, 26, 204020661876448. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, M. The COVID-19 Pandemic in Japan. Surg. Today 2020, 50, 787–793. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Gupta, N.; Kodan, P.; Mittal, A.; Soneja, M.; Wig, N. Battling COVID-19: Using old weapons for a new enemy. Trop. Dis. Travel Med. Vaccines 2020, 6, 6. [Google Scholar] [CrossRef] [PubMed]
- Yavuz, S.; Ünal, S. Antiviral treatment of COVID-19. Turk. J. Med. Sci. 2020, 50, 611–619. [Google Scholar] [CrossRef]
- Delang, L.; Abdelnabi, R.; Neyts, J. Favipiravir as a potential countermeasure against neglected and emerging RNA viruses. Antivir. Res. 2018, 153, 85–94. [Google Scholar] [CrossRef]
- Furuta, Y.; Komeno, T.; Nakamura, T. Favipiravir (T-705), a broad-spectrum inhibitor of viral RNA polymerase. Proc. Jpn. Acad. Ser. B 2017, 93, 449–463. [Google Scholar] [CrossRef]
- Shiraki, K.; Daikoku, T. Favipiravir, an anti-influenza drug against life-threatening RNA virus infections. Pharmacol. Ther. 2020, 209, 107512. [Google Scholar] [CrossRef]
- Bai, C.-Q.; Mu, J.-S.; Kargbo, D.; Song, Y.-B.; Niu, W.-K.; Nie, W.-M.; Kanu, A.; Liu, W.-W.; Wang, Y.-P.; Dafae, F.; et al. Clinical and Virological Characteristics of Ebola Virus Disease Patients Treated with Favipiravir (T-705)—Sierra Leone, 2014. Clin. Infect. Dis. 2016, 63, 1288–1294. [Google Scholar] [CrossRef]
- Rosenke, K.; Feldmann, H.; Westover, J.B.; Hanley, P.W.; Martellaro, C.; Feldmann, F.; Saturday, G.; Lovaglio, J.; Scott, D.P.; Furuta, Y.; et al. Use of Favipiravir to Treat Lassa Virus Infection in Macaques. Emerg. Infect. Dis. 2018, 24, 1696–1699. [Google Scholar] [CrossRef] [PubMed]
- Escribano-Romero, E.; de Oya, N.J.; Domingo, E.; Saiz, J.C. Extinction of West Nile Virus by Favipiravir through Lethal Mutagenesis. Antimicrob. Agents Chemother. 2017, 61, e01400-17. [Google Scholar] [CrossRef] [PubMed]
- Marlin, R.; Desjardins, D.; Contreras, V.; Lingas, G.; Solas, C.; Roques, P.; Naninck, T.; Pascal, Q.; Behillil, S.; Maisonnasse, P.; et al. Antiviral efficacy of favipiravir against Zika and SARS-CoV-2 viruses in non-human primates. Nat. Commun. 2022, 13, 5108. [Google Scholar] [CrossRef] [PubMed]
- Bologheanu, R.; Schubert, L.; Thurnher, M.; Schiefer, J.; Santonja, I.; Holzmann, H.; Oesterreicher, Z.; Tobudic, S.; Winkler, S.; Faybik, P.; et al. Unexpected complete recovery of a patient with severe tick-borne encephalitis treated with favipiravir. Antivir. Res. 2020, 184, 104952. [Google Scholar] [CrossRef]
- Banyard, A.C.; Mansfield, K.L.; Wu, G.; Selden, D.; Thorne, L.; Birch, C.; Koraka, P.; Osterhaus, A.D.; Fooks, A.R. Re-evaluating the effect of Favipiravir treatment on rabies virus infection. Vaccine 2019, 37, 4686–4693. [Google Scholar] [CrossRef]
- Shannon, A.; Canard, B. Kill or corrupt: Mechanisms of action and drug-resistance of nucleotide analogues against SARS-CoV-2. Antivir. Res. 2023, 210, 105501. [Google Scholar] [CrossRef]
- Shannon, A.; Selisko, B.; Le, N.-T.; Huchting, J.; Touret, F.; Piorkowski, G.; Fattorini, V.; Ferron, F.; Decroly, E.; Meier, C.; et al. Rapid incorporation of Favipiravir by the fast and permissive viral RNA polymerase complex results in SARS-CoV-2 lethal mutagenesis. Nat. Commun. 2020, 11, 4682. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, C.; Xu, X.; Chong, T.H.; Zhang, L.; Cheung, P.P.-H.; Huang, X. The mechanism of action of T-705 as a unique delayed chain terminator on influenza viral polymerase transcription. Biophys. Chem. 2021, 277, 106652. [Google Scholar] [CrossRef]
- Driouich, J.-S.; Cochin, M.; Lingas, G.; Moureau, G.; Touret, F.; Petit, P.-R.; Piorkowski, G.; Barthélémy, K.; Laprie, C.; Coutard, B.; et al. Favipiravir antiviral efficacy against SARS-CoV-2 in a hamster model. Nat. Commun. 2021, 12, 1735. [Google Scholar] [CrossRef]
- Kaptein, S.J.F.; Jacobs, S.; Langendries, L.; Seldeslachts, L.; ter Horst, S.; Liesenborghs, L.; Hens, B.; Vergote, V.; Heylen, E.; Barthelemy, K.; et al. Favipiravir at high doses has potent antiviral activity in SARS-CoV-2−infected hamsters, whereas hydroxychloroquine lacks activity. Proc. Natl. Acad. Sci. USA. 2020, 117, 26955–26965. [Google Scholar] [CrossRef]
- Agrawal, U.; Raju, R.; Udwadia, Z.F. Favipiravir: A new and emerging antiviral option in COVID-19. Med. J. Armed Forces India 2020, 76, 370–376. [Google Scholar] [CrossRef] [PubMed]
- Joshi, S.; Parkar, J.; Ansari, A.; Vora, A.; Talwar, D.; Tiwaskar, M.; Patil, S.; Barkate, H. Role of favipiravir in the treatment of COVID-19. Int. J. Infect. Dis. 2021, 102, 501–508. [Google Scholar] [CrossRef] [PubMed]
- Manabe, T.; Kambayashi, D.; Akatsu, H.; Kudo, K. Favipiravir for the treatment of patients with COVID-19: A systematic review and meta-analysis. BMC Infect. Dis. 2021, 21, 489. [Google Scholar] [CrossRef]
- Sirijatuphat, R.; Manosuthi, W.; Niyomnaitham, S.; Owen, A.; Copeland, K.K.; Charoenpong, L.; Rattanasompattikul, M.; Mahasirimongkol, S.; Wichukchinda, N.; Chokephaibulkit, K. Early treatment of Favipiravir in COVID-19 patients without pneumonia: A multicentre, open-labelled, randomized control study. Emerg. Microbes Infect. 2022, 11, 2197–2206. [Google Scholar] [CrossRef]
- Etter, M.C. Encoding and decoding hydrogen-bond patterns of organic compounds. Accounts Chem. Res. 2002, 23, 120–126. [Google Scholar] [CrossRef]
- Etter, M.C. Hydrogen bonds as design elements in organic chemistry. J. Phys. Chem. 2002, 95, 4601–4610. [Google Scholar] [CrossRef]
- Latosińska, J.N. NQR parameters: Electric field gradient tensor and asymmetry parameter studied in terms of density functional theory. Int. J. Quantum Chem. 2003, 91, 284–296. [Google Scholar] [CrossRef]
- Latosińska, J.N.; Koput, J. Analysis of the NQR parameters in 2-nitro-5-methylimidazole derivatives by quantum chemical calculations. Phys. Chem. Chem. Phys. 2000, 2, 145–150. [Google Scholar] [CrossRef]
- Latosińska, J.N.; Latosińska, M.; Koput, J. The tautomeric equilibria of cytosine studied by NQR spectroscopy and HF, MP2 and DFT calculations. J. Mol. Struct. 2003, 648, 9–18. [Google Scholar] [CrossRef]
- Bader, R. Atoms in Molecules: A Quantum Theory (International Series of Monographs on Chemistry); Oxford: Clarendon press, Oxford, UK, 1994. [Google Scholar]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Spackman, M.A.; McKinnon, J.J. Fingerprinting intermolecular interactions in molecular crystals. CrystEngComm 2002, 4, 378–392. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. The electrostatic potential: An overview. WIREs Comput. Mol. Sci. 2011, 1, 153–163. [Google Scholar] [CrossRef]
- Latosińska, J.N.; Latosińska, M.; Seliger, J.; Žagar, V.; Kazimierczuk, Z. An Insight into Prototropism and Supramolecular Motifs in Solid-State Structures of Allopurinol, Hypoxanthine, Xanthine, and Uric Acid. A 1H–14N NQDR Spectroscopy, Hybrid DFT/QTAIM, and Hirshfeld Surface-Based Study. J. Phys. Chem. B 2014, 118, 10837–10853. [Google Scholar] [CrossRef] [PubMed]
- Latosińska, J.N.; Latosińska, M.; Seliger, J.; Žagar, V.; Maurin, J.K.; Orzeszko, A.; Kazimierczuk, Z. Structural Study of Selected Polyhalogenated Benzimidazoles (Protein Kinase CK2 Inhibitors) by Nuclear Quadrupole Double Resonance, X-ray, and Density Functional Theory. J. Phys. Chem. A 2010, 114, 563–575. [Google Scholar] [CrossRef]
- Latosińska, J.N.; Latosińska, M.; Olejniczak, G.A.; Seliger, J.; Žagar, V. Topology of the Interactions Pattern in Pharmaceutically Relevant Polymorphs of Methylxanthines (Caffeine, Theobromine, and Theophiline): Combined Experimental (1H–14N Nuclear Quadrupole Double Resonance) and Computational (DFT and Hirshfeld-Based) Study. J. Chem. Inf. Model. 2014, 54, 2570–2584. [Google Scholar] [CrossRef]
- Seliger, J.; Osredkar, R.; Mali, M.; Blinc, R. 14N quadrupole resonance of some liquid crystalline compounds in the solid. J. Chem. Phys. 1976, 65, 2887–2891. [Google Scholar] [CrossRef]
- Stephenson, D.; Smith, J.A.S. Nitrogen-14 quadrupole cross-relaxation spectroscopy. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1988, 416, 149–178. [Google Scholar] [CrossRef]
- Gregorovič, A.; Apih, T.; Seliger, J. 1 H– 14 N cross-relaxation spectrum analysis in sildenafil and sildenafil citrate. Solid State Nucl. Magn. Reson. 2016, 78, 16–23. [Google Scholar] [CrossRef]
- Seliger, J.; Zagar, V.; Blinc, R. A New Highly Sensitive 1H-14N Nuclear-Quandrupole Double-Resonance Technique. J. Magn. Reson. Ser. A 1994, 106, 214–222. [Google Scholar] [CrossRef]
- Seliger, J.; Žagar, V.; Blinc, R. 1H -14N Nuclear Quadrupole Double Resonance with Multiple Frequency Sweeps. Z. Für Nat. A 1994, 49, 31–34. [Google Scholar] [CrossRef]
- Schempp, E.; Bray, P.J. Nuclear Quadrupole Resonance in Solid Diazines. J. Chem. Phys. 1967, 46, 1186–1190. [Google Scholar] [CrossRef]
- Hunt, M.; Mackay, A. Deuterium and nitrogen pure quadrupole resonance in amino acids. II. J. Magn. Reson. 1976, 22, 295–301. [Google Scholar] [CrossRef]
- Blinc, R.; Mali, M.; Osredkar, R.; Prelesnik, A.; Seliger, J.; Zupančič, I.; Ehrenberg, L. 14N NQR Spectroscopy of Some Amino Acids and Nucleic Bases via Double Resonance in the Laboratory Frame. J. Chem. Phys. 1972, 57, 5087–5093. [Google Scholar] [CrossRef]
- Purohit, C.S.; Ghosh, P.; Panda, S.J. A New Short Synthesis route for Favipiravir and its Analogue: Their Tautomerization Behaviour. New J. Chem. 2022, 46, 18824–18831. [Google Scholar] [CrossRef]
- Tiyasakulchai, T.; Charoensetakul, N.; Khamkhenshorngphanuch, T.; Thongpanchang, C.; Srikun, O.; Yuthavong, Y.; Srimongkolpithak, N. Scalable synthesis of favipiravir via conventional and continuous flow chemistry. RSC Adv. 2021, 11, 38691–38693. [Google Scholar] [CrossRef] [PubMed]
- Shi, F.; Li, Z.; Kong, L.; Xie, Y.; Zhang, T.; Xu, W. Synthesis and crystal structure of 6-fluoro-3-hydroxypyrazine-2-carboxamide. Drug Discov. Ther. 2014, 8, 117–120. [Google Scholar] [CrossRef]
- Goloveshkin, A.; Korlyukov, A.; Vologzhanina, A. Novel Polymorph of Favipiravir—An Antiviral Medication. Pharmaceutics 2021, 13, 139. [Google Scholar] [CrossRef]
- Loots, L.; Barbour, L.J. A simple and robust method for the identification of π–π packing motifs of aromatic compounds. Crystengcomm 2011, 14, 300–304. [Google Scholar] [CrossRef]
- Gilli, G.; Gilli, P. The Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory, 1st ed.Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Li, Z.; Zhou, Z.; Yu, X. Structure of COVID-19 RNA-dependent RNA polymerase bound to favipiravir. Proc. Natl. Acad. Sci. USA 2021, 118, e2021946118. [Google Scholar] [CrossRef]
- Naydenova, K.; Muir, K.W.; Wu, L.-F.; Zhang, Z.; Coscia, F.; Peet, M.J.; Castro-Hartmann, P.; Qian, P.; Sader, K.; Dent, K.; et al. Structure of the SARS-CoV-2 RNA-dependent RNA polymerase in the presence of favipiravir-RTP. Proc. Natl. Acad. Sci. USA 2021, 118, e2021946118. [Google Scholar] [CrossRef] [PubMed]
- Peng, Q.; Peng, R.; Yuan, B.; Wang, M.; Zhao, J.; Fu, L.; Qi, J.; Shi, Y. Structural Basis of SARS-CoV-2 Polymerase Inhibition by Favipiravir. Innovation 2021, 2, 100080. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Yan, L.; Huang, Y.; Liu, F.; Zhao, Y.; Cao, L.; Wang, T.; Sun, Q.; Ming, Z.; Zhang, L.; et al. Structure of the RNA-dependent RNA polymerase from COVID-19 virus. Science 2020, 368, 779–782. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Lu, S.; Huang, Z.; Liu, X.; Mou, L.; Luo, Y.; Zhao, Y.; Liu, Y.; Chen, Z.; Hou, T.; et al. Allosite: A method for predicting allosteric sites. Bioinformatics 2013, 29, 2357–2359. [Google Scholar] [CrossRef]
- Tian, H.; Jiang, X.; Tao, P. PASSer: Prediction of allosteric sites server. Mach. Learn. Sci. Technol. 2021, 2, 035015. [Google Scholar] [CrossRef]
- Faisal, S.; Badshah, S.L.; Kubra, B.; Sharaf, M.; Emwas, A.-H.; Jaremko, M.; Abdalla, M. Identification and Inhibition of the Druggable Allosteric Site of SARS-CoV-2 NSP10/NSP16 Methyltransferase through Computational Approaches. Molecules 2022, 27, 5241. [Google Scholar] [CrossRef]
- Kijewska, M.; Sharfalddin, A.A.; Jaremko, Ł.; Cal, M.; Setner, B.; Siczek, M.; Stefanowicz, P.; Hussien, M.A.; Emwas, A.-H.; Jaremko, M. Lossen Rearrangement of p-Toluenesulfonates of N-Oxyimides in Basic Condition, Theoretical Study, and Molecular Docking. Front. Chem. 2021, 9, 662533. [Google Scholar] [CrossRef]
- Latosińska, J.N.; Latosińska, M.; Orzeszko, A.; Maurin, J.K. Synthesis and Crystal Structure of Adamantylated 4,5,6,7-Tetrahalogeno-1H-benzimidazoles Novel Multi-Target Ligands (Potential CK2, M2 and SARS-CoV-2 Inhibitors); X-ray/DFT/QTAIM/Hirshfeld Surfaces/Molecular Docking Study. Molecules 2022, 28, 147. [Google Scholar] [CrossRef] [PubMed]
- Latosińska, J.N.; Latosińska, M.; Maurin, J.K.; Orzeszko, A.; Kazimierczuk, Z. Quantum-Chemical Insight into Structure–Reactivity Relationship in 4,5,6,7-Tetrahalogeno-1H-benzimidazoles: A Combined X-ray, DSC, DFT/QTAIM, Hirshfeld Surface-Based, and Molecular Docking Approach. J. Phys. Chem. A 2014, 118, 2089–2106. [Google Scholar] [CrossRef]
- Golan, Y.; Campos, J.A.S.; Woolson, R.; Cilla, D.; Hanabergh, R.; Gonzales-Rojas, Y.; Lopez, R.; Finberg, R.; Balboni, A. Favipiravir in Patients with Early Mild-to-moderate Coronavirus Disease 2019 (COVID-19): A Randomized Controlled Trial. Clin. Infect. Dis. 2022, 76, e10–e17. [Google Scholar] [CrossRef]
- Eloy, P.; Le Grand, R.; Malvy, D.; Guedj, J. Combined treatment of molnupiravir and favipiravir against SARS-CoV-2 infection: One + zero equals two? EBioMedicine 2021, 74, 103663. [Google Scholar] [CrossRef]
- Klein, J.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. New Way for Probing Bond Strength. J. Phys. Chem. A 2020, 124, 1850–1860. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Levy, M. Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v -representability problem. Proc. Natl. Acad. Sci. USA 1979, 76, 6062–6065. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Wu, Z.; Cohen, R.E. More accurate generalized gradient approximation for solids. Phys. Rev. B 2006, 73, 235116. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Erratum: Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1993, 48, 4978. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. für Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Pyykkö, P. Year-2008 nuclear quadrupole moments. Mol. Phys. 2008, 106, 1965–1974. [Google Scholar] [CrossRef]
- Jabłoński, M. A Critical Overview of Current Theoretical Methods of Estimating the Energy of Intramolecular Interactions. Molecules 2020, 25, 5512. [Google Scholar] [CrossRef]
- Abramov, Y.A. On the Possibility of Kinetic Energy Density Evaluation from the Experimental Electron-Density Distribution. Acta Crystallogr. Sect. A Found. Crystallogr. 1997, 53, 264–272. [Google Scholar] [CrossRef]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Mata, I.; Alkorta, I.; Espinosa, E.; Molins, E. Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields. Chem. Phys. Lett. 2011, 507, 185–189. [Google Scholar] [CrossRef]
- Emamian, S.; Lu, T.; Kruse, H.; Emamian, H. Exploring Nature and Predicting Strength of Hydrogen Bonds: A Correlation Analysis between Atoms-in-Molecules Descriptors, Binding Energies, and Energy Components of Symmetry-Adapted Perturbation Theory. J. Comput. Chem. 2019, 40, 2868–2881. [Google Scholar] [CrossRef] [PubMed]
- Afonin, A.V.; Vashchenko, A.V.; Sigalov, M.V. Estimating the energy of intramolecular hydrogen bonds from 1H NMR and QTAIM calculations. Org. Biomol. Chem. 2016, 14, 11199–11211. [Google Scholar] [CrossRef] [PubMed]
- Nikolaienko, T.Y.; Bulavin, L.A.; Hovorun, D.M. Bridging QTAIM with vibrational spectroscopy: The energy of intramolecular hydrogen bonds in DNA-related biomolecules. Phys. Chem. Chem. Phys. 2012, 14, 7441–7447. [Google Scholar] [CrossRef] [PubMed]
- Jelsch, C.; Ejsmont, K.; Huder, L. The enrichment ratio of atomic contacts in crystals, an indicator derived from the Hirshfeld surface analysis. IUCrJ 2014, 1, 119–128. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Peralta-Inga, Z. Molecular surface electrostatic potentials in relation to noncovalent interactions in biological systems. Int. J. Quantum Chem. 2001, 85, 676–684. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Quantitative Analyses of Molecular Surface Electrostatic Potentials in Relation to Hydrogen Bonding and Co-Crystallization. Cryst. Growth Des. 2015, 15, 3767–3774. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef]
- Eberhardt, J.; Santos-Martins, D.; Tillack, A.F.; Forli, S. AutoDock Vina 1.2.0: New Docking Methods, Expanded Force Field, and Python Bindings. J. Chem. Inf. Model. 2021, 61, 3891–3898. [Google Scholar] [CrossRef] [PubMed]
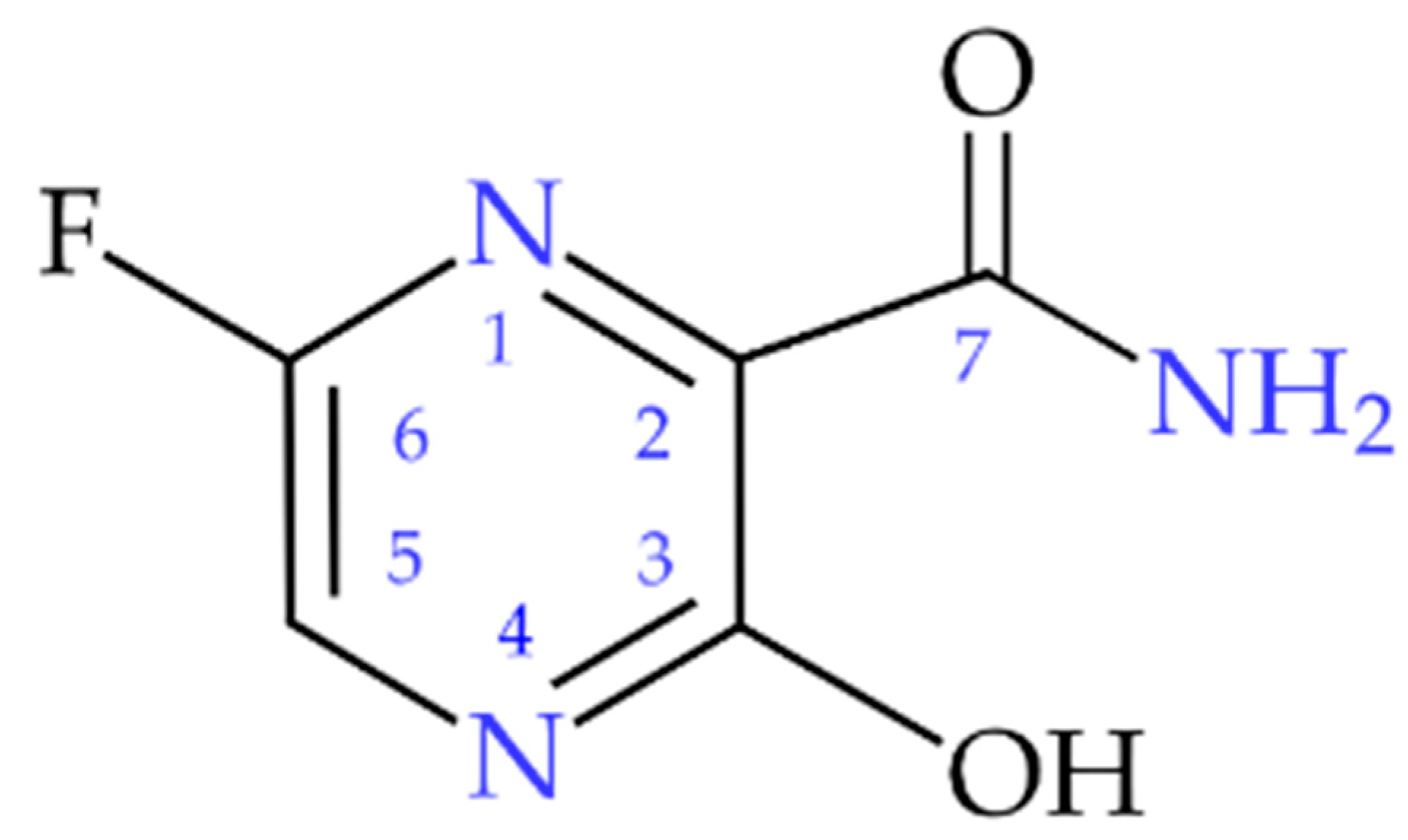
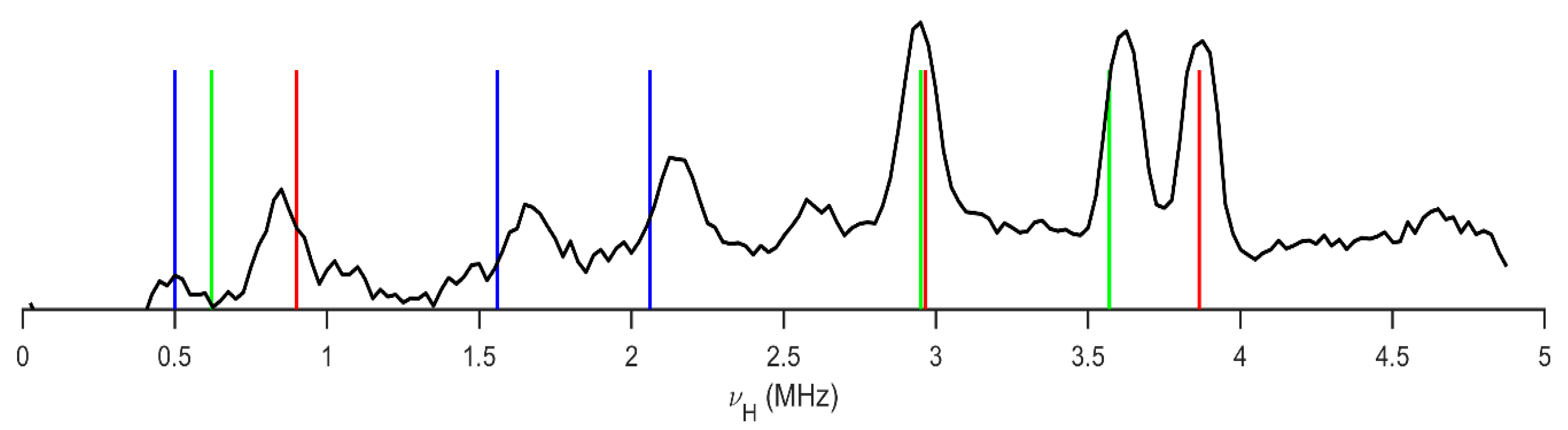
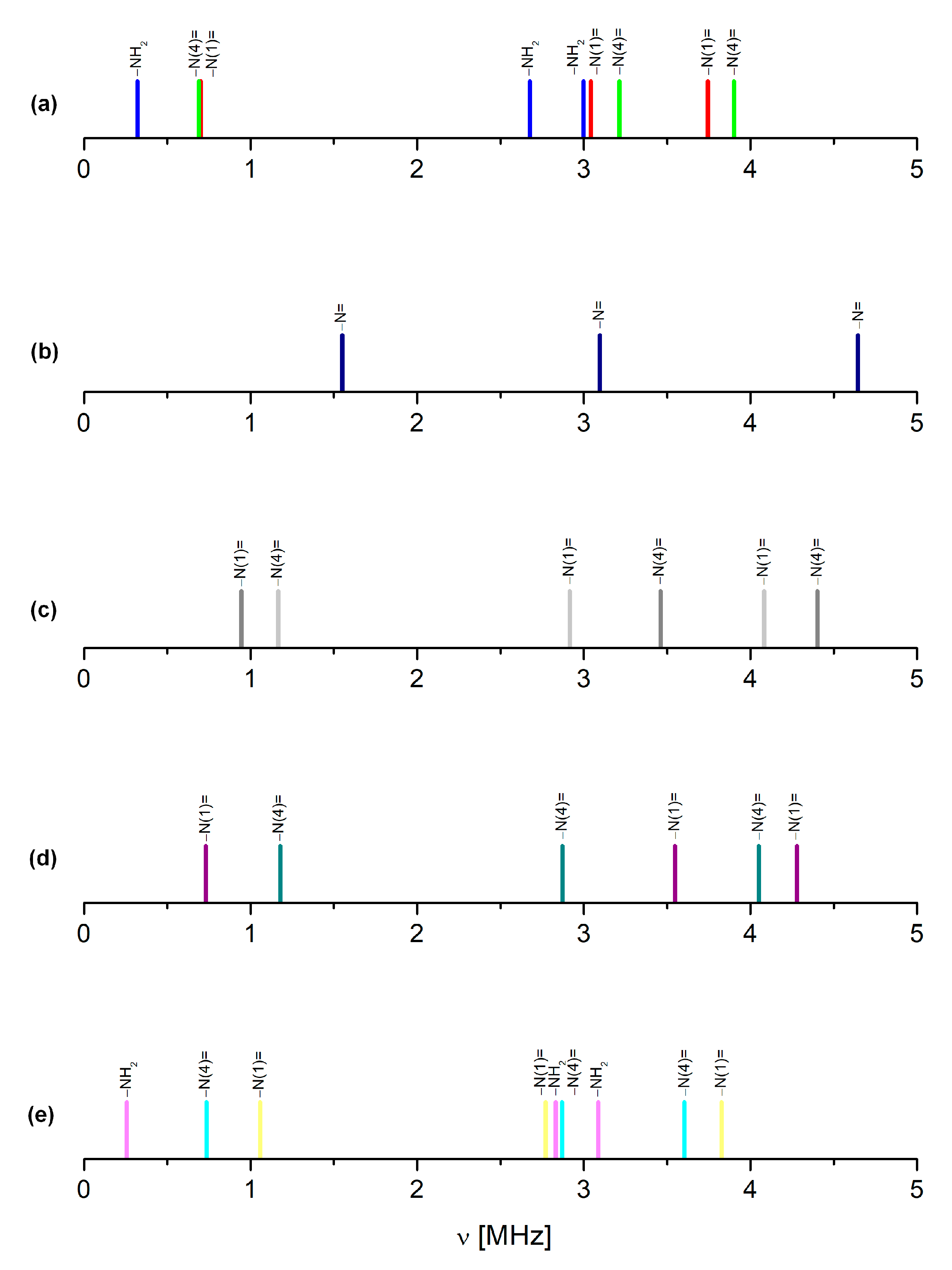
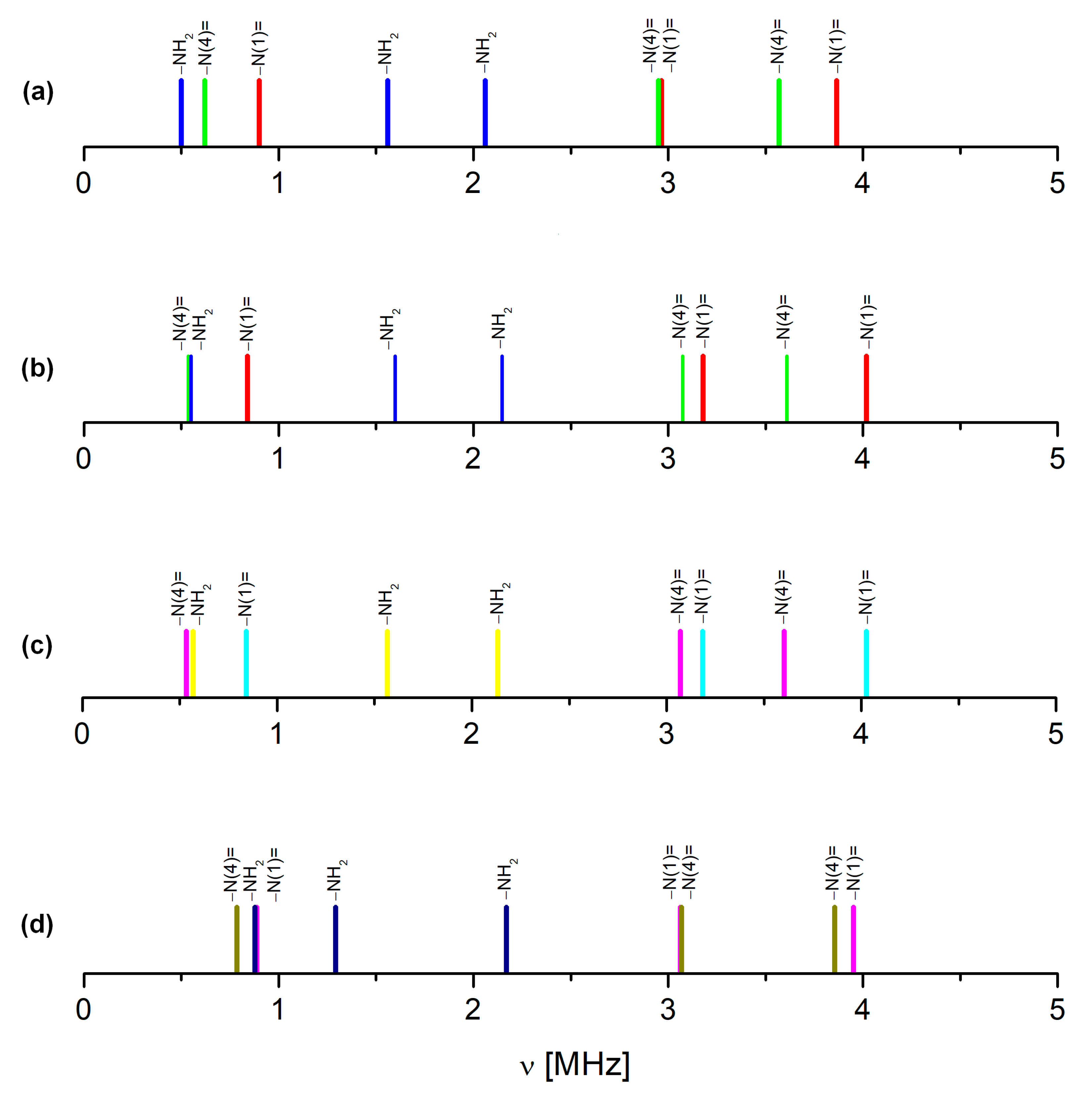
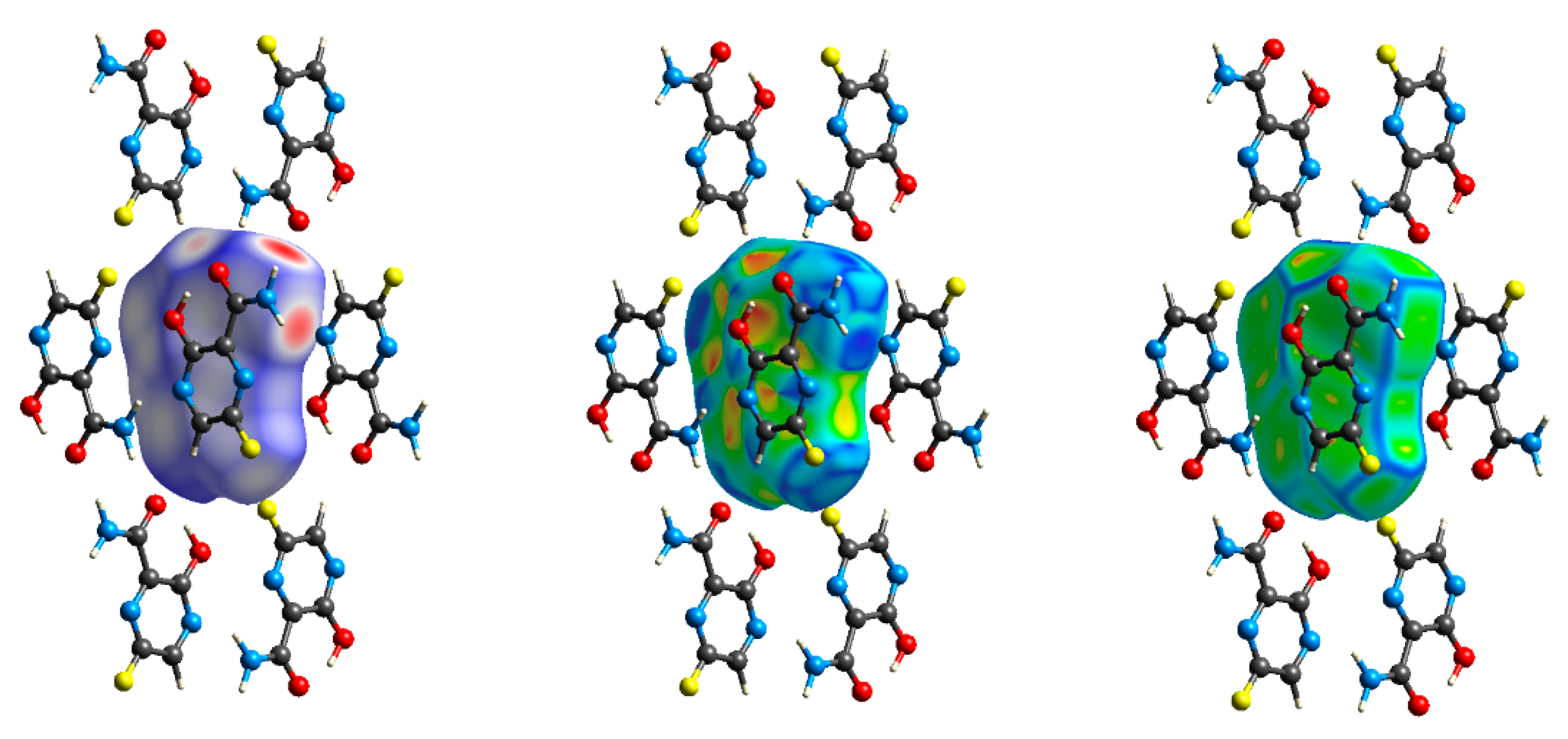
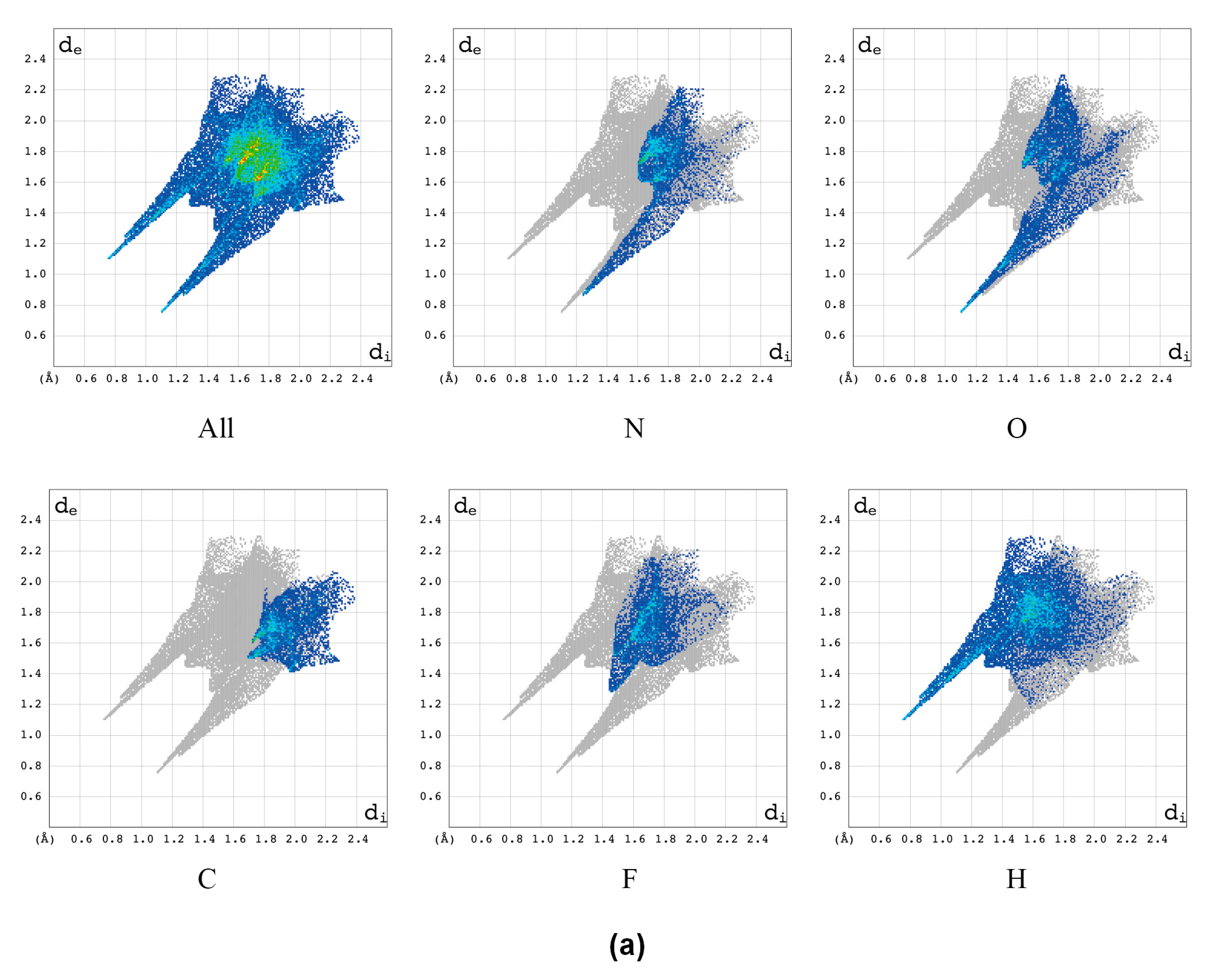
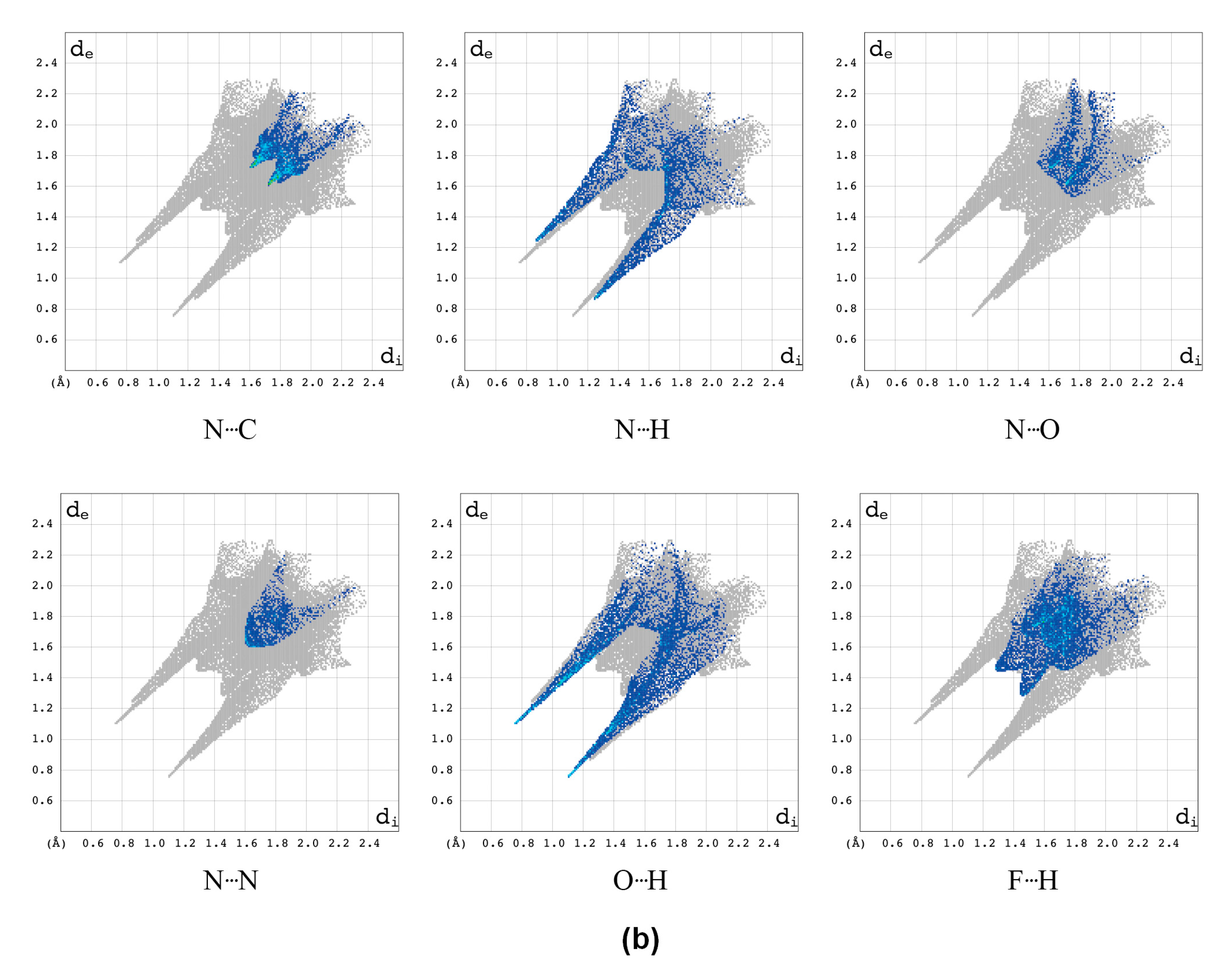
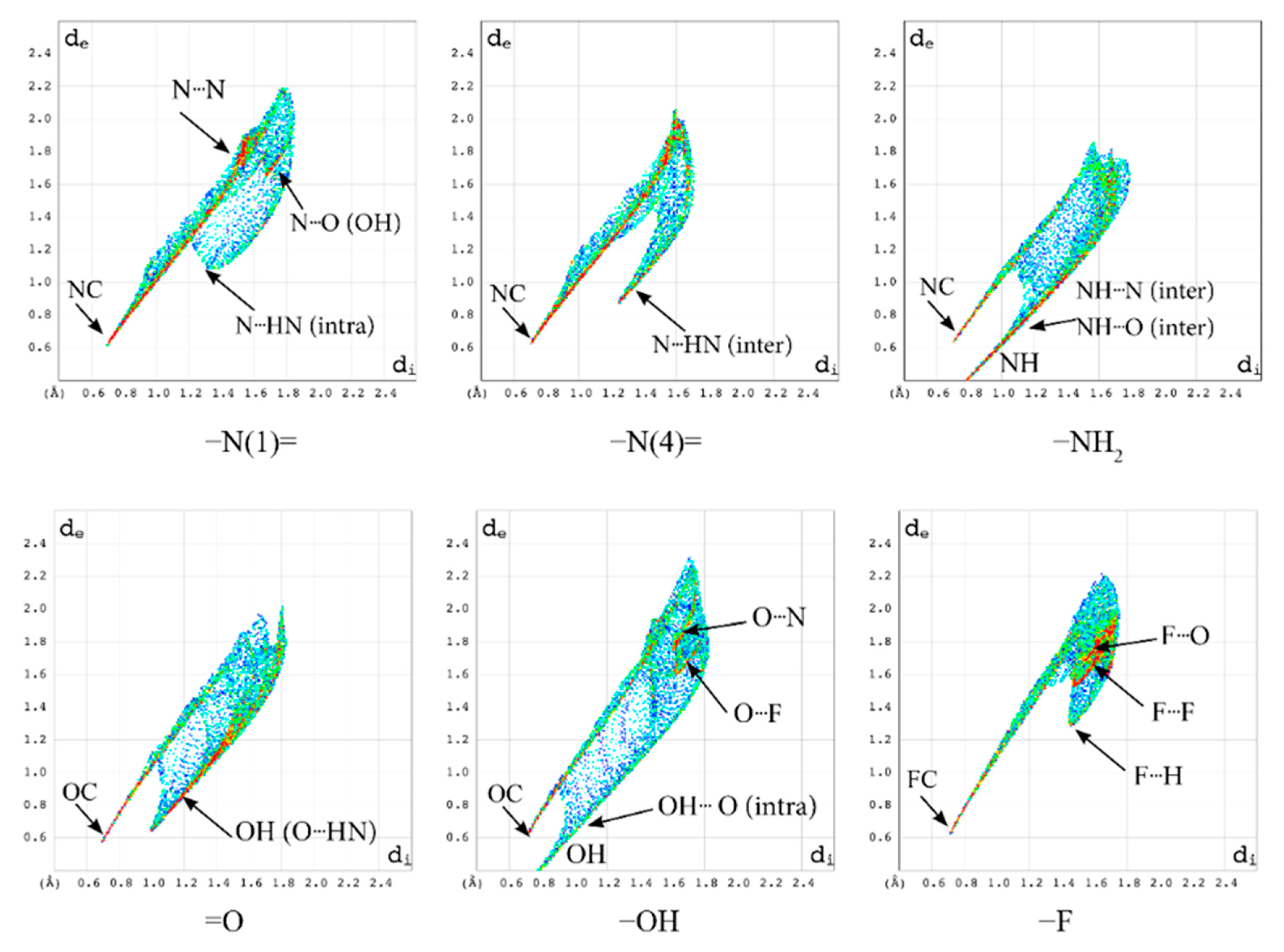
| Site | ν+ [MHz] | ν− [MHz] | ν0 [MHz] | |e2qQ/h|[MHz] | η | T [K] | Final Assignment * |
|---|---|---|---|---|---|---|---|
| pyrazine nitrogens | 3.865 | 2.965 | 0.900 | 4.553 | 0.395 | 295 | −N(1)= |
| 3.570 | 2.950 | 0.620 | 4.347 | 0.285 | −N(4)= | ||
| amide nitrogen | 2.060 | 1.560 | 0.500 | 2.413 | 0.414 | −NH2 | |
| pyrazine [44] | 4.329 | 3.017 | 1.312 | 4.897 | 0.536 | 295 | −N= |
| Substituent | Site | ν+ [MHz] | ν− [MHz] | ν0 [MHz] | e2qQ/h [MHz] | η | Correlation |
|---|---|---|---|---|---|---|---|
| FPV | −N(1)= | 3.744 | 3.043 | 0.701 | −4.538 | 0.300 | νGGA = 1.025νNQR + 0.203 r2 = 0.8685; s = 1.8060 |
| −N(4)= | 3.902 | 3.214 | 0.688 | −4.731 | 0.290 | ||
| −NH2 | 2.997 | 2.676 | 0.321 | −3.789 | 0.160 | ||
| pyrazine | −N= | 4.646 | 3.097 | 1.549 | −5.162 | 0.600 | νGGA = 1.021νNQR + 0.152 r2 = 0.9887; s = 0.0271 |
| 2-fluoro-pyrazine | −N(1)= | 4.403 | 3.460 | 0.944 | −5.242↑ | 0.36↓ | experimental data unavailable |
| −N(4)= | 4.082 | 2.916 | 1.166 | −4.665↓ | 0.50↓ | ||
| 2-hydroxy-pyrazine | −N(1)= | 4.279 | 3.548 | 0.731 | −5.218↑ | 0.28↓ | |
| −N(4)= | 4.049 | 2.872 | 1.177 | −4.614↓ | 0.51↓ | ||
| pyrazine-2-carboxamide | −N(1)= | 3.826 | 2.771 | 1.056 | −4.398↓ | 0.48↓ | |
| −N(4)= | 3.603 | 2.869 | 0.734 | −4.315↓ | 0.34↓ | ||
| −NH2 | 3.087 | 2.831 | 0.256 | −3.945↓ | 0.13↓ |
| Structure, CCDC | Site | ν+ [MHz] | ν− [MHz] | ν0 [MHz] | e2qQ/h [MHz] | η | Calculations Level | Correlation |
|---|---|---|---|---|---|---|---|---|
| 2106318, 100 K monomer | −N(1)= | 3.772 | 2.964 | 0.808 | −4.491 | 0.36 | GGA/RPBE | νGGA = 1.005νNQR + 0.188 r2 = 0.9647; s = 0.4256 |
| −N(4)= | 4.055 | 3.186 | 0.869 | −4.827 | 0.36 | |||
| −NH2 | 2.558 | 1.943 | 0.615 | −3.001 | 0.41 | |||
| 2106318, 100 K solid | −N(1)= | 3.885 | 2.971 | 0.914 | −4.570 | 0.40 | GGA/PBEsol | νGGA = 0.989νNQR + 0.042 r2 = 0.9686; s = 0.3650 |
| −N(4)= | 3.759 | 2.994 | 0.765 | −4.502 | 0.34 | |||
| −NH2 | 1.938 | 1.119 | 0.819 | −2.038 | 0.80 | |||
| −N(1)= | 3.938 | 3.052 | 0.885 | −4.660 | 0.38 | GGA/PBE | νGGA = 1.009νNQR + 0.054 r2 = 0.9756; s = 0.2937 | |
| −N(4)= | 3.809 | 3.075 | 0.734 | −4.589 | 0.32 | |||
| −NH2 | 2.075 | 1.219 | 0.856 | −2.196 | 0.78 | |||
| −N(1)= | 3.958 | 3.047 | 0.911 | −4.670 | 0.39 | GGA/WC Wu-Cohen | νGGA = 1.007νNQR + 0.057 r2 = 0.9686; s = 0.3892 | |
| −N(4)= | 3.835 | 3.054 | 0.781 | −4.593 | 0.34 | |||
| −NH2 | 2.021 | 1.153 | 0.868 | −2.116 | 0.82 | |||
| −N(1)= | 4.008 | 3.086 | 0.922 | −4.729 | 0.39 | GGA/PW91 | νGGA = 1.023νNQR + 0.053 r2 = 0.9754; s = 0.3041 | |
| −N(4)= | 3.870 | 3.103 | 0.767 | −4.649 | 0.33 | |||
| −NH2 | 2.071 | 1.225 | 0.846 | −2.197 | 0.77 | |||
| −N(1)= | 3.895 | 3.060 | 0.835 | −4.637 | 0.36 | GGA/RPBE | νGGA = 1.009νNQR + 0.047 r2 = 0.9827; s = 0.2068 | |
| −N(4)= | 3.762 | 3.078 | 0.684 | −4.560 | 0.30 | |||
| −NH2 | 2.133 | 1.308 | 0.826 | −2.294 | 0.720 | |||
| X-ray 2048895 100 K monomer | −N(1)= | 3.796 | 2.942 | 0.853 | −4.492 | 0.38 | GGA/RPBE | νGGA = 1.001νNQR + 0.203 r2 = 0.9654; s = 0.4143 |
| −N(4)= | 4.086 | 3.168 | 0.919 | −4.836 | 0.38 | |||
| −NH2 | 2.539 | 1.942 | 0.597 | −2.987 | 0.40 | |||
| X-ray 2048895 100 K solid | −N(1)= | 3.896 | 2.959 | 0.937 | −4.570 | 0.41 | GGA/PBESol | νGGA = 0.984νNQR + 0.061 r2 = 0.9643; s = 0.4133 |
| −N(4)= | 3.792 | 2.979 | 0.813 | −4.514 | 0.36 | |||
| −NH2 | 1.933 | 1.103 | 0.830 | −2.024 | 0.82 | |||
| −N(1)= | 3.949 | 3.041 | 0.909 | −4.660 | 0.39 | GGA/PBE | νGGA = 1.008νNQR + 0.061 r2 = 0.9756; s = 0.2933 | |
| −N(4)= | 3.842 | 3.060 | 0.782 | −4.601 | 0.34 | |||
| −NH2 | 2.051 | 1.222 | 0.829 | −2.182 | 0.76 | |||
| −N(1)= | 3.980 | 3.023 | 0.957 | −4.669 | 0.41 | GGA/WC Wu-Cohen | νGGA = 1.005νNQR + 0.068 r2 = 0.9677; s = 0.3888 | |
| −N(4)= | 3.868 | 3,039 | 0.829 | −4.605 | 0.36 | |||
| −NH2 | 1.996 | 1.156 | 0.840 | −2.101 | 0.80 | |||
| −N(1)= | 4.021 | 3.075 | 0.946 | −4.731 | 0.40 | GGA/PW91 | νGGA = 1.021νNQR + 0.061 r2 = 0.9840; s = 0.3222 | |
| −N(4)= | 3.904 | 3.088 | 0.816 | −4.661 | 0.35 | |||
| −NH2 | 2.049 | 1.221 | 0.828 | −2.180 | 0.76 | |||
| −N(1)= | 3.908 | 3.049 | 0.858 | −4.638 | 0.37 | GGA/RPBE | νGGA = 1.009νNQR + 0.052 r2 = 0.9836; s = 0.1955 | |
| −N(4)= | 3.796 | 3.065 | 0.732 | −4.574 | 0.32 | |||
| −NH2 | 2.108 | 1.310 | 0.798 | −2.279 | 0.70 | |||
| X-ray 969968 296 K monomer | −N(1)= | 3.852 | 2.966 | 0.886 | −4.545 | 0.39 | GGA/RPBE | νGGA = 0.994νNQR + 0.239 r2 = 0.9696; s = 0.3569 |
| −N(4)= | 4.113 | 3.145 | 0.968 | −4.839 | 0.40 | |||
| −NH2 | 2.553 | 1.849 | 0.704 | −2.935 | 0.48 | |||
| X-ray 969968 296 K solid | −N(1)= | 3.941 | 2.973 | 0.968 | −4.609 | 0.42 | GGA/PBESol | νGGA = 0.980νNQR + 0.108 r2 = 0.9572; s = 0.4941 |
| −N(4)= | 3.849 | 2.984 | 0.865 | −4.555 | 0.38 | |||
| −NH2 | 1.999 | 1.092 | 0.907 | −2.061 | 0.88 | |||
| −N(1)= | 3.988 | 3.050 | 0.938 | −4.692 | 0.40 | GGA/PBE | νGGA = 0.999νNQR + 0.110 r2 = 0.9671; s = 0.3911 | |
| −N(4)= | 3.880 | 3.049 | 0.831 | −4.619 | 0.36 | |||
| −NH2 | 2.110 | 1.187 | 0.923 | −2.198 | 0.84 | |||
| −N(1)= | 4.016 | 3.050 | 0.966 | −4.711 | 0.41 | GGA/WC Wu-Cohen | νGGA = 1.001νNQR + 0.1173 r2 = 0.9630; s = 0.4437 | |
| −N(4)= | 3.918 | 3.057 | 0.860 | −4.650 | 0.37 | |||
| −NH2 | 2.099 | 1.164 | 0.935 | −2.175 | 0.86 | |||
| −N(1)= | 4.067 | 3.089 | 0.978 | −4.771 | 0.41 | GGA/PW91 | νGGA = 1.017νNQR + 0.108 r2 = 0.9673; s = 0.4026 | |
| −N(4)= | 3.962 | 3.092 | 0.870 | −4.703 | 0.37 | |||
| −NH2 | 2.113 | 1.206 | 0.907 | −2.213 | 0.82 | |||
| −N(1)= | 3.951 | 3.063 | 0.888 | −4.676 | 0.38 | GGA/RPBE | νGGA = 1.004νNQR + 0.098 r2 = 0.9779; s = 0.2628 | |
| −N(4)= | 3.854 | 3.069 | 0.785 | −4.615 | 0.34 | |||
| −NH2 | 2.170 | 1.292 | 0.877 | −2.308 | 0.76 |
| Structure, CCDC | Site | ν+ [MHz] | ν− [MHz] | ν0 [MHz] | e2qQ/h [MHz] | η | Calculations Level | Correlation |
|---|---|---|---|---|---|---|---|---|
| X-ray 2047143 monomer | −N(1)= | 3.800 | 3.046 | 0.753 | −4.564 | 0.33 | GGA/RPBE | νGGA = 1.014νNQR + 0.1734 r2 = 0.9676; s = 0.3975 |
| −N(4)= | 4.008 | 3.235 | 0.773 | −4.829 | 0.32 | |||
| −NH2 | 2.604 | 1.848 | 0.757 | −2.968 | 0.51 | |||
| X-ray 2047143 solid | −N(1)= | 3.965 | 3.052 | 0.912 | −4.678 | 0.42 | GGA/PBESol | νGGA = 0.998νNQR + 0.060 r2 = 0.9589; s = 0.4912 |
| −N(4)= | 3.714 | 3.059 | 0.655 | −4.555 | 0.38 | |||
| −NH2 | 2.063 | 1.078 | 0.984 | −2.061 | 0.88 | |||
| −N(1)= | 4.017 | 3.135 | 0.882 | −4.768 | 0.37 | GGA/PBE | νGGA = 1.023νNQR + 0.050 r2 = 0.9667; s = 0.4165 | |
| −N(4)= | 3.744 | 3.147 | 0.597 | −4.594 | 0.26 | |||
| −NH2 | 2.177 | 1.189 | 0.987 | −2.244 | 0.88 | |||
| −N(1)= | 4.038 | 3.130 | 0.908 | −4.779 | 0.38 | GGA/WC Wu-Cohen | νGGA = 1.019νNQR + 0.062 r2 = 0.9616; s = 0.4768 | |
| −N(4)= | 3.788 | 3.121 | 0.668 | −4.606 | 0.29 | |||
| −NH2 | 2.129 | 1.129 | 0.999 | −2.172 | 0.92 | |||
| −N(1)= | 4.092 | 3.172 | 0.920 | −4.843 | 0.38 | GGA/PW91 | νGGA = 1.037νNQR + 0.052 r2 = 0.9669; s = 0.4233 | |
| −N(4)= | 3.805 | 3.177 | 0.628 | −4.655 | 0.27 | |||
| −NH2 | 2.179 | 1.190 | 0.988 | −2.246 | 0.88 | |||
| −N(1)= | 3.969 | 3.140 | 0.829 | −4.739 | 0.35 | GGA/RPBE | νGGA = 1.023νNQR + 0.039 r2 = 0.9730; s = 0.3354 | |
| −N(4)= | 3.694 | 3.146 | 0.547 | −4.560 | 0.24 | |||
| −NH2 | 2.225 | 1.279 | 0.946 | −2.336 | 0.81 |
| Structure, CCDC | Site | ν+ [MHz] | ν− [MHz] | ν0 [MHz] | e2qQ/h [MHz] | η | Calculations Level | Correlation |
|---|---|---|---|---|---|---|---|---|
| X-ray 2048895 optimized at RPBE with fixed cell parameters | −N(1)= | 3.898 | 3.062 | 0.835 | −4.640 | 0.360 | GGA/PBESol | νGGA = 1.013νNQR − 0.484 r2 = 0.9960; s = 0.0478 |
| −N(4)= | 3.507 | 2.948 | 0,559 | −4.303 | 0.260 | |||
| −NH2 | 1.995 | 1.415 | 0.580 | −2.273 | 0.510 | |||
| −N(1)= −N(4)= | 3.954 | 3.149 | 0.805 | −4.735 | 0.34 | GGA/PBE | νGGA = 1.040νNQR − 0.0545 r2 = 0.9964; s = 0.0526 | |
| 3.547 | 3.042 | 0.505 | −4.393 | 0.23 | ||||
| −NH2 | 2.129 | 1.563 | 0.566 | −2.461 | 0.46 | |||
| −N(1)= | 3.983 | 3.130 | 0.854 | −4.742 | 0.360 | GGA/WC Wu-Cohen | νGGA = 1.035νNQR − 0.046 r2 = 0.9967; s = 0.0461 | |
| −N(4)= | 3.564 | 3.016 | 0.548 | −4.387 | 0.250 | |||
| −NH2 | 2.067 | 1.476 | 0.591 | −2.362 | 0.500 | |||
| −N(1)= | 4.026 | 3.185 | 0.841 | −4.807 | 0.350 | GGA/PW91 | νGGA = 1.053νNQR − 0.053 r2 = 0.9972; s = 0.0767 | |
| −N(4)= | 3.604 | 3.070 | 0.534 | −4.449 | 0.240 | |||
| −NH2 | 2.132 | 1.565 | 0.567 | −2.465 | 0.460 | |||
| −N(1)= | 3.911 | 3.157 | 0.754 | −4.712 | 0.320 | GGA/RPBE | νGGA = 1.041νNQR − 0.055 r2 = 0.9919; s = 0.1022 | |
| −N(4)= | 3.512 | 3.052 | 0.459 | −4.376 | 0.210 | |||
| −NH2 | 2.200 | 1.660 | 0.540 | −2.573 | 0.420 | |||
| 2106318 100 K optimized at RPBE with fixed cell parameters | −N(1)= | 3.892 | 3.058 | 0.834 | −4.633 | 0.360 | GGA/PBESol | νGGA = 1.011νNQR − 0.042 r2 = 0.9967; s = 0.0388 |
| −N(4)= | 3.511 | 2.951 | 0.560 | −4.308 | 0.260 | |||
| −NH2 | 2.015 | 1.439 | 0.576 | −2.303 | 0.500 | |||
| −N(1)= | 3.948 | 3.144 | 0.804 | −4.728 | 0.340 | GGA/PBE | νGGA = 1.039νNQR − 0.049 r2 = 0.9959; s = 0.0518 | |
| −N(4)= | 3.552 | 3.046 | 0.506 | −4.399 | 0.230 | |||
| −NH2 | 2.148 | 1.588 | 0.560 | −2.491 | 0.450 | |||
| −N(1)= | 3.977 | 3.125 | 0.852 | −4.735 | 0.360 | GGA/WC Wu-Cohen | νGGA = 1.033νNQR − 0.038 r2 = 0.9975; s = 0.0314 | |
| −N(4)= | 3.580 | 3.009 | 0.571 | −4.393 | 0.260 | |||
| −NH2 | 2.082 | 1.508 | 0.574 | −2.393 | 0.480 | |||
| −N(1)= | 4.017 | 3.178 | 0.839 | −4.797 | 0.350 | GGA/PW91 | νGGA = 1.054νNQR − 0.051 r2 = 0.9975; s = 0.0714 | |
| −N(4)= | 3.609 | 3.075 | 0.535 | −4.456 | 0.240 | |||
| −NH2 | 2.146 | 1.597 | 0.549 | −2.495 | 0.440 | |||
| −N(1)= | 3.904 | 3.152 | 0.753 | −4.704 | 0.320 | GGA/RPBE | νGGA = 1.040νNQR − 0.051 r2 = 0.9924; s = 0.1252 | |
| −N(4)= | 3.509 | 3.050 | 0.459 | −4.373 | 0.210 | |||
| −NH2 | 2.212 | 1.691 | 0.520 | −2.602 | 0.400 |
| Structure, CCDC | Site | ν+ [MHz] | ν− [MHz] | ν0 [MHz] | e2qQ/h [MHz] | η | Correlation |
|---|---|---|---|---|---|---|---|
| 2048895 monomer | −N(1)= | 4.251 | 3.170 | 1.081 | −4.947 | 0.437 | νDFT = 1.116νNQR + 0.241 r2 = 0.9197; s = 1.2453 |
| −N(4)= | 4.503 | 3.469 | 1.034 | −5.315 | 0.389 | ||
| −NH2 | 2.930 | 2.659 | 0.270 | −3.726 | 0.145 | ||
| 2048895 cluster | −N(1)= | 4.475 | 3.280 | 1.194 | −5.170 | 0.462 | νDFT = 1.125νNQR + 0.040 r2 = 0.9926; s = 0.1115 |
| −N(4)= | 4.235 | 3.348 | 0.887 | −5.055 | 0.351 | ||
| −NH2 | 2.247 | 1.752 | 0.495 | −2.666 | 0.371 |
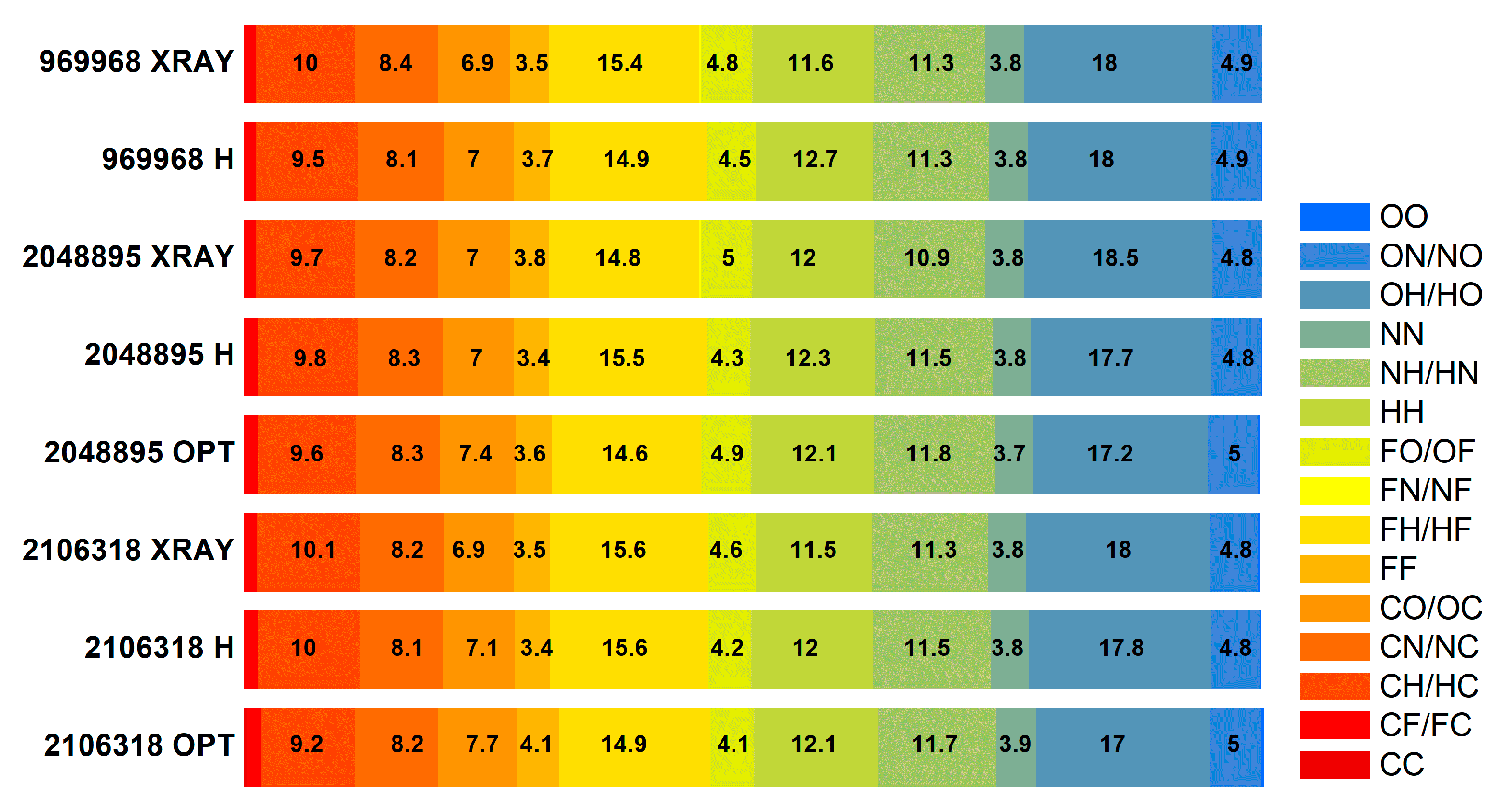
| Structure, CCDC | Homonuclear | Heteronuclear * | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C···C | F···F | N···N | O···O | H···H | C···F | C···H | C···N | C···O | F···H | F···N | F···O | N···H | O···H | N···O | |
| 2106318 X-ray | 0 | 3.4 | 3.8 | 0.1 | 12.0 | 1.3 | 10.1 | 8.2 | 7.1 | 15.6 | 0 | 4.2 | 11.5 | 17.8 | 4.8 |
| 2106318 optimized protons | 0 | 3.4 | 3.8 | 0.1 | 12.0 | 1.4 | 10.0 | 8.1 | 7.1 | 15.6 | 0 | 4.2 | 11.5 | 17.8 | 4.8 |
| 2106318 full optimization | 0.3 | 4.1 | 3.9 | 0.3 | 12.1 | 1.4 | 9.2 | 8.2 | 7.7 | 14.9 | 0 | 4.3 | 11.7 | 17.0 | 5.0 |
| 2048895 X-ray | 0 | 3.4 | 3.8 | 0.1 | 12 | 1.2 | 10 | 8.4 | 7.1 | 15.6 | 0 | 4.2 | 11.5 | 17.8 | 4.8 |
| 2048895 optimized protons | 0 | 3.4 | 3.8 | 0.1 | 12 | 1.4 | 9.8 | 8.3 | 7.1 | 15.6 | 0 | 4.2 | 11.5 | 17.8 | 4.8 |
| 2048895 full optimization | 0 | 3.4 | 3.8 | 0.1 | 12 | 1.4 | 9.6 | 8.3 | 7.1 | 15.6 | 0 | 4.2 | 11.5 | 17.8 | 4.8 |
| 969968 X-ray | 0 | 3.4 | 3.8 | 0.1 | 12 | 1.2 | 9.7 | 8.2 | 7.1 | 15.6 | 0 | 4.2 | 11.5 | 17.8 | 4.8 |
| 969968 optimized protons | 0 | 3.4 | 3.8 | 0.1 | 12 | 1.2 | 10 | 8.4 | 7.1 | 15.6 | 0 | 4.2 | 11.5 | 17.8 | 4.8 |
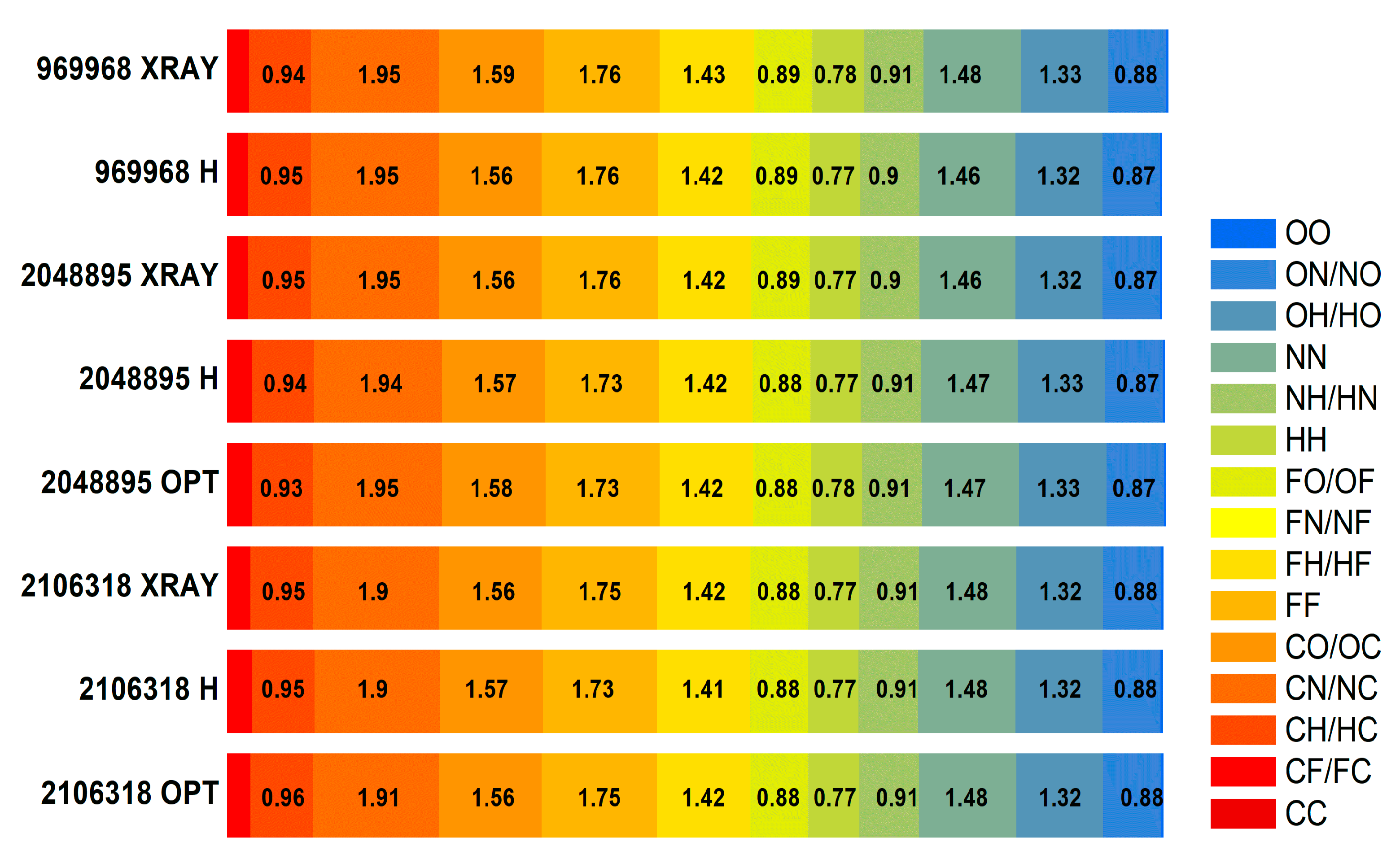
| Structure, CCDC | Atom | C | F | H | N | O |
|---|---|---|---|---|---|---|
| 2106318 X-ray | Surface % | 13.35 | 13.95 | 39.5 | 16.5 | 17.05 |
| C | 0 | - | - | - | - | |
| F | 0.35 | 1.75 | - | - | - | |
| H | 0.96 | 1.42 | 0.77 | - | - | |
| N | 1.91 | 0.00 | 0.91 | 1.48 | - | |
| O | 1.56 | 0.88 | 1.32 | 0.88 | 0.03 | |
| 2106318 optimized protons | Surface % | 13.3 | 14.0 | 39.5 | 16.0 | 17.5 |
| C | 0 | - | - | - | - | |
| F | 0.38 | 1.73 | - | - | - | |
| H | 0.95 | 1.41 | 0.77 | - | - | |
| N | 1.90 | 0.00 | 0.91 | 1.48 | - | |
| O | 1.57 | 0.88 | 1.32 | 0.88 | 0.03 | |
| 2106318 full optimization unit cell fixed | Surface % | 13.55 | 14.4 | 38.5 | 16.3 | 17.3 |
| C | 0.16 | - | - | - | ||
| F | 0.36 | 1.98 | - | - | ||
| H | 0.88 | 1.34 | 0.82 | - | ||
| N | 1.85 | 0.00 | 0.93 | 1.46 | ||
| O | 1.64 | 0.86 | 1.28 | 0.88 | 0.10 | |
| 2048895 X-ray | Surface % | 13.35 | 13.9 | 39.45 | 16.15 | 17.05 |
| C | 0 | - | - | - | - | |
| F | 0.32 | 1.76 | - | - | - | |
| H | 0.95 | 1.42 | 0.77 | - | - | |
| N | 1.95 | 0 | 0.90 | 1.46 | - | |
| O | 1.56 | 0.89 | 1.32 | 0.87 | 0.03 | |
| 2048895 optimized protons | Surface % | 13.3 | 14.0 | 39.35 | 16.1 | 17.05 |
| C | 0 | - | - | - | - | |
| F | 0.38 | 1.73 | - | - | - | |
| H | 0.94 | 1.42 | 0.77 | - | - | |
| N | 1.94 | 0 | 0.91 | 1.47 | - | |
| O | 1.57 | 0.88 | 1.33 | 0.87 | 0.03 | |
| 2048895 full optimization unit cell fixed | Surface % | 13.2 | 14.0 | 39.25 | 16.1 | 17.05 |
| C | 0 | - | - | - | - | |
| F | 0.38 | 1.73 | - | - | - | |
| H | 0.93 | 1.42 | 0.78 | - | - | |
| N | 1.95 | 0 | 0.91 | 1.47 | - | |
| O | 1.58 | 0.88 | 1.33 | 0.87 | 0.03 | |
| 969968 X-ray | Surface % | 13.1 | 13.9 | 39.3 | 16.05 | 17.05 |
| C | 0 | - | - | - | - | |
| F | 0.33 | 1.76 | - | - | - | |
| H | 0.94 | 1.43 | 0.78 | - | - | |
| N | 1.95 | 0 | 0.91 | 1.48 | - | |
| O | 1.59 | 0.89 | 1.33 | 0.88 | 0.03 | |
| 969968 optimized protons | Surface % | 13.35 | 13.9 | 39.45 | 16.15 | 17.05 |
| C | 0 | - | - | - | - | |
| F | 0.32 | 1.76 | - | - | - | |
| H | 0.95 | 1.42 | 0.77 | - | - | |
| N | 1.95 | 0 | 0.90 | 1.46 | - | |
| O | 1.56 | 0.89 | 1.32 | 0.87 | 0.03 |
| Contact Type | –N(1)= | –N(4)= | –NH2 | Contact Type | =O | –OH | Contact Type | F |
|---|---|---|---|---|---|---|---|---|
| N···C | 59.9 | 59.7 | 19.3 | O···C | 22.9 | 30 | F···C | 29.3 |
| N···H | 20.4 | 35.2 | 80.7 | O···H | 76.4 | 51.5 | F···H | 43.1 |
| N···O | 9.2 | 1 | - | O···O | 0 | 0 | F···O | 8.2 |
| N···N | 5.3 | 4.1 | - | O···N | 0 | 9.7 | F···N | 1.6 |
| N···F | 5.1 | - | - | O···F | 0.7 | 8.9 | F···F | 17.9 |
| Interaction | Eel. [kJ/mol] | Ep [kJ/mol] | Ed [kJ/mol] | Er [kJ/mol] | Etotal [kJ/mol] | Structure, CCDC |
|---|---|---|---|---|---|---|
| N–H⋯O | −37.6 | −5.9 | −6.9 | 25.6 | −24.8 | 2048895 optimized |
| N–H⋯N | −22.0 | −5.6 | −10.8 | 18.7 | −19.6 | |
| C–H⋯O | −6.0 | −1.1 | −5.0 | 4.5 | −7.6 | |
| F⋯F | −1.2 | −0.1 | −4.4 | 1.2 | −4.6 | |
| π⋯π stacking (flip) | −2.5 | −1.2 | −20.8 | 7.5 | −17.0 | |
| π⋯π stacking (parallel) | −4.1 | −1.3 | −21.1 | 7.5 | −19.0 | |
| N–H⋯O | −25.7 | −3.9 | −6.4 | 13.1 | −22.9 | 2048895 X-ray |
| N–H⋯N | −4.9 | −1.1 | −21.2 | 6.8 | −20.4 | |
| C–H⋯O | −4.0 | −0.9 | −4.5 | 2.2 | −7.4 | |
| F⋯F | −1.4 | −0.1 | −3.0 | 0.1 | −4.5 | |
| π⋯π stacking (flip) | −14.0 | −3.9 | −10.7 | 11.7 | −16.8 | |
| π⋯π stacking (parallel) | −3.2 | −1.0 | −21.2 | 7.4 | −17.9 |
| Interaction | Nitrogen Site | RX⋯Y, <XHY | ρBCP(r) [a.u.] | ΔρBCP(r) [a.u.] | VBCP [a.u.] | GBCP [a.u.] | EE [kJ/mol] | EM [kJ/mol] | EEM [kJ/mol] | EA [kJ/mol] | EG [kJ/mol] | EN [kJ/mol] | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| hydrogen bonds | N-H⋯N * | -NH2, -N(1)= | 2.321, 101.8 | - | - | - | - | - | - | - | - | - | - |
| O-H⋯O | - | 2.591, 142.6 | 0.042481 | 0.143112 | −0.04196 | 0.038869 | −55.08 | −43.77 | −36.54 | −30.97 | −25.92 | −29.55 | |
| hydrogen bonds | N–H⋯O | -NH2 | 2.880, 166.9 | 0.026747 | 0.110269 | −0.02233 | 0.024948 | −29.31 | −28.10 | −21.86 | −16.69 | - | −16.69 |
| N–H⋯N | -NH2, -N(4)= | 2.961, 133.8 | 0.018429 | 0.06814 | −0.01189 | 0.014461 | −15.61 | −16.29 | −14.10 | - | - | - | |
| C–H⋯O | - | 3.420, 148.9 | 0.009161 | 0.030523 | −0.00555 | 0.006589 | −7.28 | −7.42 | −5.44 | −4.48 | - | - | |
| F–H⋯C | - | 3.459, 118.8 | 0.00343 | 0.015936 | −0.00238 | 0.003182 | −3.12 | −3.58 | −0.10 | −2.18 | - | - | |
| F⋯F | - | 3.067 | 0.003874 | 0.021766 | −0.00353 | 0.004488 | −4.64 | −5.06 | - | - | - | - | |
| π⋯π stacking (flip) | F⋯C | - | 6.535 | 0.002768 | 0.012361 | −0.00158 | 0.002333 | −2.06 | - | - | - | - | - |
| N⋯N | -N(1)=, -N(4)= | 6.166 | 0.005919 | 0.018211 | −0.00326 | 0.003905 | −4.28 | - | - | - | - | - | |
| N⋯O | -NH2 | 6.472 | 0.005106 | 0.016997 | −0.00309 | 0.003668 | −4.05 | - | - | - | - | - | |
| N⋯O | -NH2 | 6.679 | 0.003988 | 0.012019 | −0.00228 | 0.002642 | −2.99 | - | - | - | - | - | |
| π⋯π stacking (parallel) | O⋯F | - | 6.682 | 0.001989 | 0.010403 | −0.00126 | 0.00193 | −1.65 | - | - | - | - | - |
| N⋯C | -N(4)= | 6.785 | 0.005659 | 0.01542 | −0.00285 | 0.003354 | −3.75 | - | - | - | - | - | |
| O⋯C | - | 6.075 | 0.006435 | 0.021031 | −0.00384 | 0.004551 | −5.04 | - | - | - | - | - | |
| N⋯C | -N(4)= | 6.404 | 0.003977 | 0.011922 | −0.00208 | 0.002532 | −2.74 | - | - | - | - | - | |
| stabilising (in a layer) | N⋯O | -N(1)= | 6.385 | 0.004228 | 0.015145 | −0.00252 | 0.003155 | −3.31 | - | - | - | - | - |
| F⋯O | - | 6.167 | 0.003083 | 0.016013 | −0.00236 | 0.003182 | −3.09 | - | - | - | - | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latosińska, J.N.; Latosińska, M.; Seliger, J.; Žagar, V.; Apih, T.; Grieb, P. Elucidating the Role of Noncovalent Interactions in Favipiravir, a Drug Active against Various Human RNA Viruses; a 1H-14N NQDR/Periodic DFT/QTAIM/RDS/3D Hirshfeld Surfaces Combined Study. Molecules 2023, 28, 3308. https://doi.org/10.3390/molecules28083308
Latosińska JN, Latosińska M, Seliger J, Žagar V, Apih T, Grieb P. Elucidating the Role of Noncovalent Interactions in Favipiravir, a Drug Active against Various Human RNA Viruses; a 1H-14N NQDR/Periodic DFT/QTAIM/RDS/3D Hirshfeld Surfaces Combined Study. Molecules. 2023; 28(8):3308. https://doi.org/10.3390/molecules28083308
Chicago/Turabian StyleLatosińska, Jolanta Natalia, Magdalena Latosińska, Janez Seliger, Veselko Žagar, Tomaž Apih, and Paweł Grieb. 2023. "Elucidating the Role of Noncovalent Interactions in Favipiravir, a Drug Active against Various Human RNA Viruses; a 1H-14N NQDR/Periodic DFT/QTAIM/RDS/3D Hirshfeld Surfaces Combined Study" Molecules 28, no. 8: 3308. https://doi.org/10.3390/molecules28083308
APA StyleLatosińska, J. N., Latosińska, M., Seliger, J., Žagar, V., Apih, T., & Grieb, P. (2023). Elucidating the Role of Noncovalent Interactions in Favipiravir, a Drug Active against Various Human RNA Viruses; a 1H-14N NQDR/Periodic DFT/QTAIM/RDS/3D Hirshfeld Surfaces Combined Study. Molecules, 28(8), 3308. https://doi.org/10.3390/molecules28083308






