Benchmark Study on Phosphorescence Energies of Anthraquinone Compounds: Comparison between TDDFT and UDFT
Abstract
1. Introduction
2. Computational Details
3. Results
3.1. Geometry Optimization
3.2. Phosphorescence Energy
| PBE | PBE0 | B3LYP | CAM-B3LYP | ωB97XD | M06-2X | M06-HF | |
|---|---|---|---|---|---|---|---|
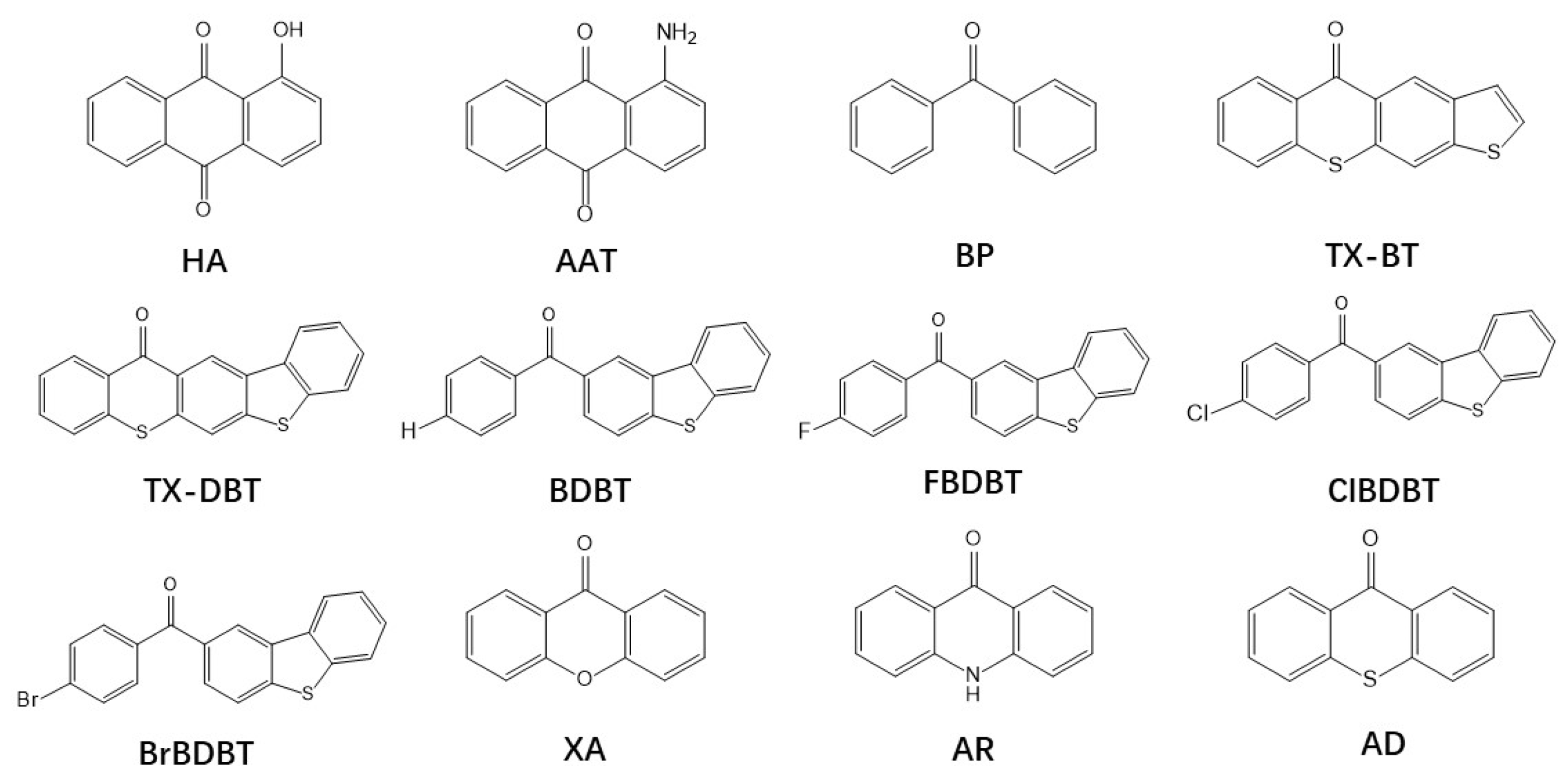
| HA | 1.47 | −0.49 | −0.47 | −0.36 | −0.31 | −0.23 | −0.09 |
| AAT | −0.40 | −0.41 | −0.38 | −0.34 | −0.3 | − 0.24 | −0.17 |
| BP | −0.24 | −0.28 | −0.18 | −0.15 | −0.11 | −0.05 | −0.02 |
| TX−BT | −0.35 | −0.34 | −0.32 | −0.30 | −0.23 | −0.07 | 0.14 |
| TX-DBT | −0.62 | −0.42 | −0.44 | −0.21 | −0.14 | −0.12 | 0.06 |
| BDBT | −0.37 | −0.28 | −0.22 | −0.14 | −0.10 | −0.03 | 0.75 |
| FBDBT | −0.39 | −0.29 | −0.23 | −0.15 | −0.11 | −0.04 | 0.75 |
| ClBDBT | −0.39 | −0.29 | −0.23 | −0.15 | −0.10 | −0.03 | 0.00 |
| BrBDBT | −0.39 | −0.29 | −0.23 | −0.15 | −0.10 | −0.03 | 0.78 |
| XA | −0.59 | −0.65 | −0.53 | −0.28 | −0.23 | −0.47 | 0.01 |
| AR | 1.19 | −0.32 | −0.44 | −0.26 | −0.20 | −0.16 | 0.04 |
| AD | 1.50 | −0.45 | −0.45 | −0.27 | −0.20 | −0.17 | −0.02 |
| MUE (a) | 0.66 | 0.37 | 0.34 | 0.23 | 0.18 | 0.14 | 0.24 |
| MUE (b) | 0.56 | 0.25 | 0.23 | 0.22 | 0.21 | 0.25 | 0.46 |
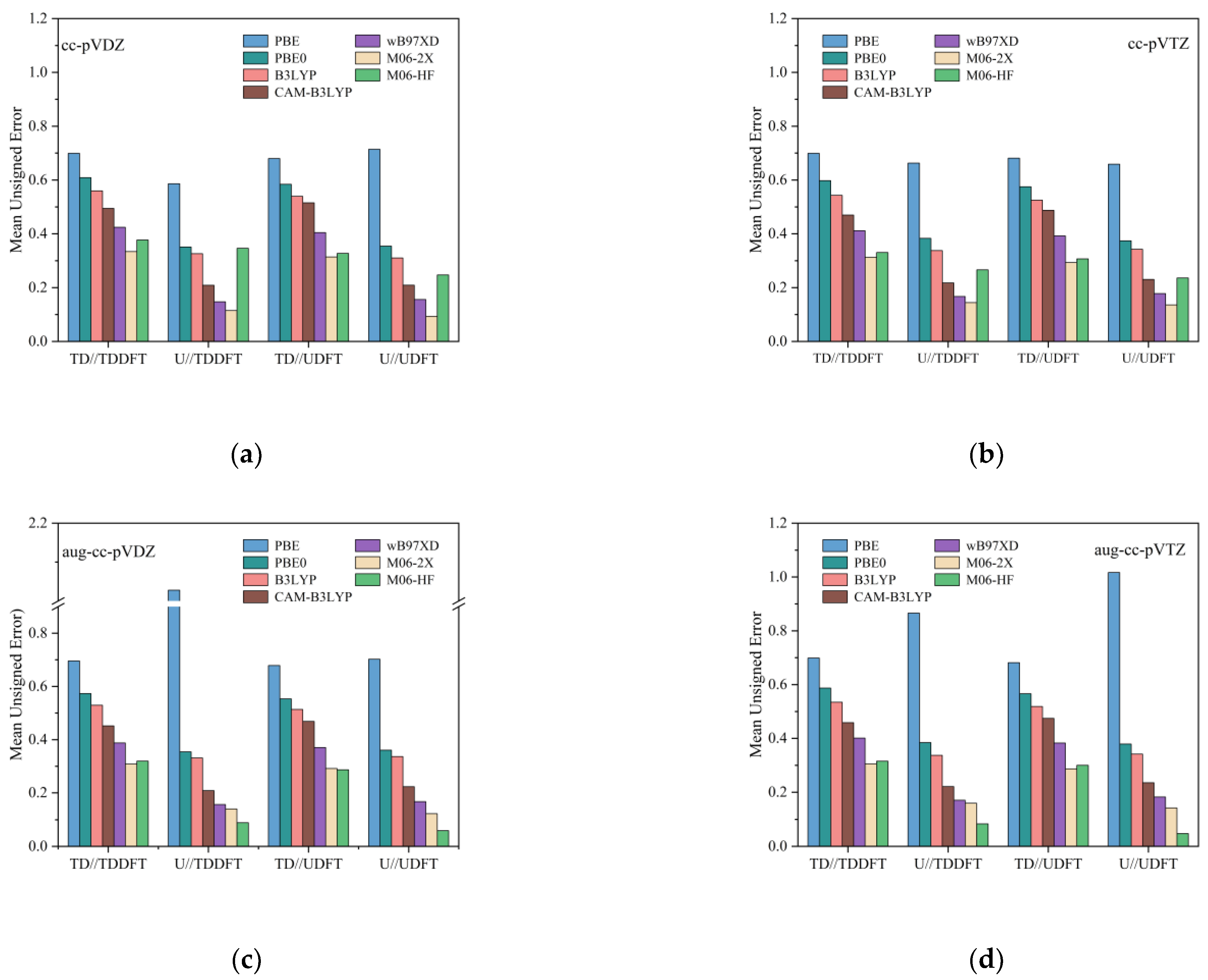
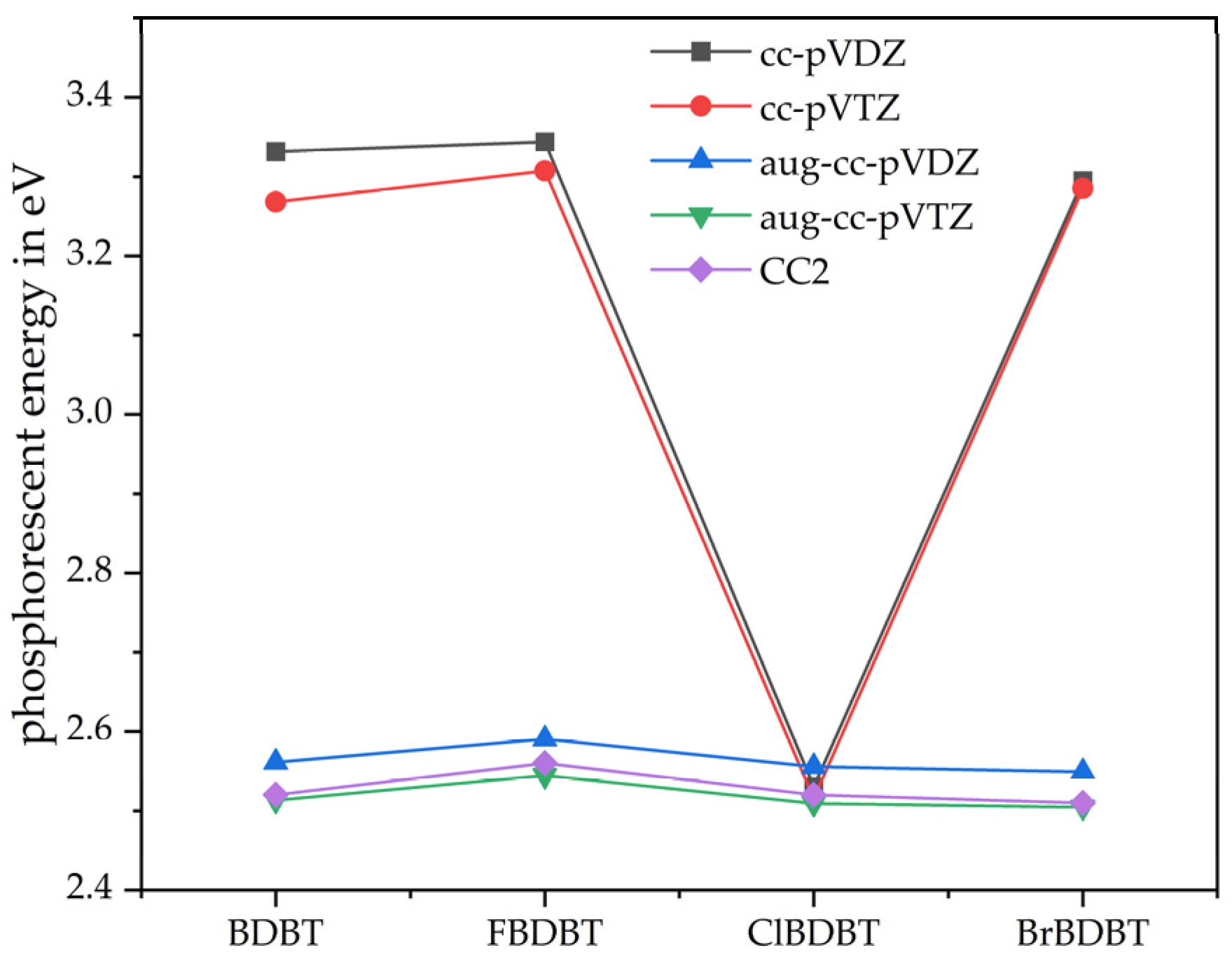
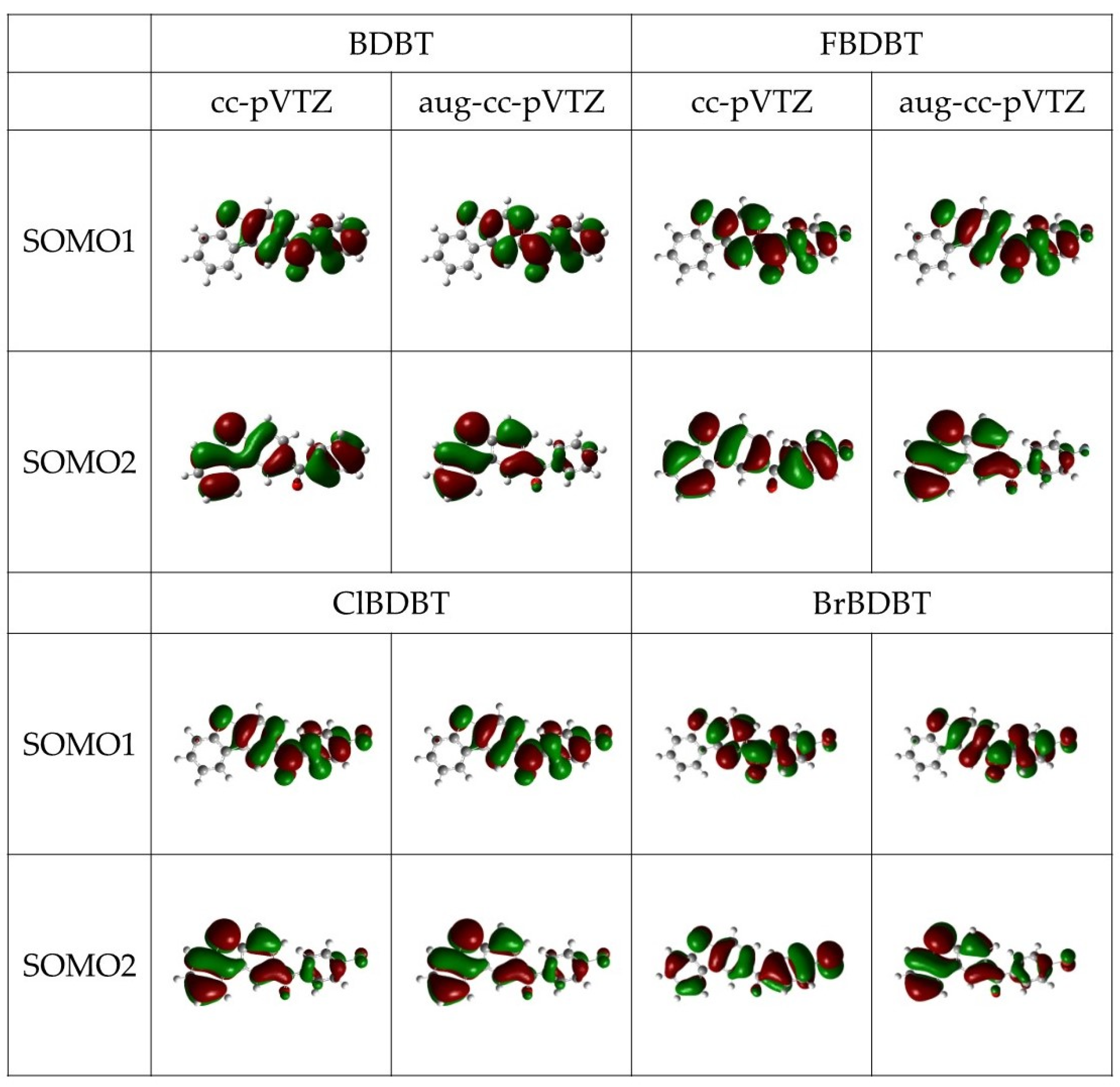
3.3. Basis Sets Effect
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, W.; He, Z.; Tang, B.Z. Room-temperature phosphorescence from organic aggregates. Nat. Rev. Mater. 2020, 5, 869–885. [Google Scholar] [CrossRef]
- Jacquemin, D.; Wathelet, V.; Perpete, E.A.; Adamo, C. Extensive TD-DFT Benchmark: Singlet-Excited States of Organic Molecules. J. Chem. Theory Comput. 2009, 5, 2420–2435. [Google Scholar] [CrossRef]
- Mukherjee, S.; Thilagar, P. Recent advances in purely organic phosphorescent materials. Chem. Commun. 2015, 51, 10988–11003. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W. Critical Assessment of Time-Dependent Density Functional Theory for Excited States of Open-Shell Systems: II. Doublet-Quartet Transitions. J. Chem. Theory Comput. 2016, 12, 2517–2527. [Google Scholar] [CrossRef] [PubMed]
- Baryshnikov, G.; Minaev, B.; Agren, H. Theory and Calculation of the Phosphorescence Phenomenon. Chem. Rev. 2017, 117, 6500–6537. [Google Scholar] [CrossRef]
- Niehaus, T.A.; Hofbeck, T.; Yersin, H. Charge-transfer excited states in phosphorescent organo-transition metal compounds: A difficult case for time dependent density functional theory? RSC Adv. 2015, 5, 63318–63329. [Google Scholar] [CrossRef]
- De Souza, B.; Farias, G.; Neese, F.; Izsak, R. Predicting Phosphorescence Rates of Light Organic Molecules Using Time-Dependent Density Functional Theory and the Path Integral Approach to Dynamics. J. Chem. Theory Comput. 2019, 15, 1896–1904. [Google Scholar] [CrossRef] [PubMed]
- Grotjahn, R.; Kaupp, M. Reliable TDDFT Protocol Based on a Local Hybrid Functional for the Prediction of Vibronic Phosphorescence Spectra Applied to Tris(2,2’-bipyridine)-Metal Complexes. J. Phys. Chem. A 2021, 125, 7099–7110. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; An, Z.; Li, P.-Z.; Yin, J.; Xing, G.; He, T.; Chen, H.; Wang, J.; Sun, H.; Huang, W.; et al. Enhancing Organic Phosphorescence by Manipulating Heavy-Atom Interaction. Cryst. Growth Des. 2016, 16, 808–813. [Google Scholar] [CrossRef]
- Kenry; Chen, C.; Liu, B. Enhancing the performance of pure organic room-temperature phosphorescent luminophores. Nat. Commun. 2019, 10, 2111. [Google Scholar] [CrossRef]
- El-Sayed, M.A. Spin—Orbit Coupling and the Radiationless Processes in Nitrogen Heterocyclics. J. Chem. Phys. 1963, 38, 2834–2838. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, Y.; Wu, Z.; Wang, Y.; Sun, Y.; Feng, X.; Wang, H.; Zhao, G. Unveiling the theoretical mechanism of purely organic room temperature phosphorescence emission and heteroatomic effects on singlet-triplet intersystem crossing for isopropylthioxanthone derivatives. J. Lumin. 2021, 232, 117864. [Google Scholar] [CrossRef]
- Jacquemin, D.; Assfeld, X.; Preat, J.; Perpète, E.A. Comparison of theoretical approaches for predicting the UV/Vis spectra of anthraquinones. Mol. Phys. 2007, 105, 325–331. [Google Scholar] [CrossRef]
- Goudappagouda; Nidhankar, A.D.; Nayak, R.A.; Santhosh Babu, S. Aggregation-induced phosphorescence of an anthraquinone based emitter. Org. Biomol. Chem. 2021, 19, 1004–1008. [Google Scholar] [CrossRef] [PubMed]
- Diaz, A.N. Absorption and Emission Spectroscopy and Photochemistry of 1,10-Anthraquinone D erivatives: A Review. J. Photochem. Photobiol. A-Chem. 1989, 53, 141–167. [Google Scholar] [CrossRef]
- Schreiber, M.; Silva-Junior, M.R.; Sauer, S.P.; Thiel, W. Benchmarks for electronically excited states: CASPT2, CC2, CCSD, and CC3. J. Chem. Phys. 2008, 128, 134110. [Google Scholar] [CrossRef]
- Sauer, S.P.; Schreiber, M.; Silva-Junior, M.R.; Thiel, W. Benchmarks for Electronically Excited States: A Comparison of Noniterative and Iterative Triples Corrections in Linear Response Coupled Cluster Methods: CCSDR(3) versus CC3. J. Chem. Theory Comput. 2009, 5, 555–564. [Google Scholar] [CrossRef]
- Christiansen, O.; Koch, H.; Jørgensen, P. Response functions in the CC3 iterative triple excitation model. J. Chem. Phys. 1995, 103, 7429–7441. [Google Scholar] [CrossRef]
- Christiansen, O.; Koch, H.; Jo/rgensen, P. Perturbative triple excitation corrections to coupled cluster singles and doubles excitation energies. J. Chem. Phys. 1996, 105, 1451–1459. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.Å.; Roos, B.O. Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys. 1992, 96, 1218–1226. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.A.; Roos, B.O.; Sadlej, A.J.; Wolinski, K. Second-Order Perturbation Theory with a CASSCF Reference Function. J. Phys. Chem. 1990, 94, 5483–5488. [Google Scholar] [CrossRef]
- Christiansen, O.; Koch, H.; Jørgensen, P. The second-order approximate coupled cluster singles and doubles model CC2. Chem. Phys. Lett. 1995, 243, 409–418. [Google Scholar] [CrossRef]
- Dominique Guillaumont, S.N. Calculation of the absorption wavelength of dyes using time-dependent density-functional theory (TD-DFT). Dye. Pigment. 2000, 46, 85–92. [Google Scholar] [CrossRef]
- Serrano-Andrés, L.; Roos, B.O. A Theoretical Study of the Indigoid Dyes and Their Chromophore. Clwm. Eztr. J. 1997, 3, 717–725. [Google Scholar] [CrossRef]
- Parac, M.; Grimme, S. Comparison of Multireference Møller-Plesset Theory and Time-Dependent Methods for the Calculation of Vertical Excitation Energies of Molecules. J. Phys. Chem. A 2002, 106, 6844–6850. [Google Scholar] [CrossRef]
- Fabian, J.; Diaz, L.A.; Seifert, G.; Niehaus, T. Calculation of excitation energies of organic chromophores: A critical evaluation. J. Mol. Struct. 2002, 594, 41–53. [Google Scholar] [CrossRef]
- Blancafort, L.; Robb, M.A. Key Role of a Threefold State Crossing in the Ultrafast Decay of Electronically Excited Cytosine. J. Phys. Chem. A 2004, 108, 10609–10614. [Google Scholar] [CrossRef]
- Shemesh, D.; Sobolewski, A.L.; Domcke, W. Efficient Excited-State Deactivation of the Gly-Phe-Ala Tripeptide via an Electron-Driven Proton-Transfer Process. J. Comput. Chem. 2009, 131, 1374–1375. [Google Scholar] [CrossRef] [PubMed]
- Blancafort, L.; Voityuk, A.A. MS-CASPT2 Calculation of Excess Electron Transfer in Stacked DNA Nucleobases. J. Phys. Chem. A 2007, 111, 4714–4719. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Stratmann, R.E.; Scuseria, G.E.; Frisch, M.J. An efficient implementation of time-dependent density-functional theory for the calculation of excitation energies of large molecules. J. Chem. Phys. 1998, 109, 8218–8224. [Google Scholar] [CrossRef]
- Petersilka, M.G.U.J.; Gossmann, U.J.; Gross, E.K.U. Excitation Energies from Time-Dependent Density-Functional Theory. Phys. Rev. Lett. 1996, 76, 1212–1214. [Google Scholar] [CrossRef] [PubMed]
- Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Andreas Dreuw, M.H.-G. Single-Reference ab Initio Methods for the Calculation of Excited States of Large Molecules. Chem. Rev. 2005, 105, 4009–4037. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Tao, J.; Staroverov, V.N.; Scuseria, G.E.; Csonka, G.I. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. J. Chem. Phys. 2005, 123, 62201. [Google Scholar] [CrossRef] [PubMed]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Hirata, S.; Lee, T.J.; Head-Gordon, M. Time-dependent density functional study on the electronic excitation energies of polycyclic aromatic hydrocarbon radical cations of naphthalene, anthracene, pyrene, and perylene. J. Chem. Phys. 1999, 111, 8904–8912. [Google Scholar] [CrossRef]
- Hirata, S.; Head-Gordon, M. Time-dependent density functional theory within the Tamm–Dancoff approximation. Chem. Phys. Lett. 1999, 314, 291–299. [Google Scholar] [CrossRef]
- Handy, N.C.; Tozer, D.J. Excitation Energies of Benzene from Kohn᎐Sham Theory. J. Comput. Chem. 1998, 20, 106–113. [Google Scholar] [CrossRef]
- Peach, M.J.; Benfield, P.; Helgaker, T.; Tozer, D.J. Excitation energies in density functional theory: An evaluation and a diagnostic test. J. Chem. Phys. 2008, 128, 044118. [Google Scholar] [CrossRef] [PubMed]
- Isegawa, M.; Peverati, R.; Truhlar, D.G. Performance of recent and high-performance approximate density functionals for time-dependent density functional theory calculations of valence and Rydberg electronic transition energies. J. Chem. Phys. 2012, 137, 244104. [Google Scholar] [CrossRef] [PubMed]
- Peverati, R.; Truhlar, D.G. Performance of the M11 and M11-L density functionals for calculations of electronic excitation energies by adiabatic time-dependent density functional theory. Phys. Chem. Chem. Phys. 2012, 14, 11363–11370. [Google Scholar] [CrossRef] [PubMed]
- Jacquemin, D.; Perpete, E.A.; Ciofini, I.; Adamo, C.; Valero, R.; Zhao, Y.; Truhlar, D.G. On the Performances of the M06 Family of Density Functionals for Electronic Excitation Energies. J. Chem. Theory Comput. 2010, 6, 2071–2085. [Google Scholar] [CrossRef] [PubMed]
- Schira, R.; Latouche, C. DFT vs. TDDFT vs. TDA to simulate phosphorescence spectra of Pt- and Ir-based complexes. Dalton Trans. 2021, 50, 746–753. [Google Scholar] [CrossRef] [PubMed]
- Nakatsuji, H. Cluster Expansion of the Wavefunction-Excited States. Chem. Phys. Lett. 1978, 59, 362–364. [Google Scholar] [CrossRef]
- Bousquet, D.; Fukuda, R.; Jacquemin, D.; Ciofini, I.; Adamo, C.; Ehara, M. Benchmark Study on the Triplet Excited-State Geometries and Phosphorescence Energies of Heterocyclic Compounds: Comparison Between TD-PBE0 and SAC-CI. J. Chem. Theory Comput. 2014, 10, 3969–3979. [Google Scholar] [CrossRef]
- Khalid, M.; Hussain, R.; Hussain, A.; Ali, B.; Jaleel, F.; Imran, M.; Assiri, M.A.; Usman Khan, M.; Ahmed, S.; Abid, S.; et al. Electron Donor and Acceptor Influence on the Nonlinear Optical Response of Diacetylene-Functionalized Organic Materials (DFOMs): Density Functional Theory Calculations. Molecules 2019, 24, 2096. [Google Scholar] [CrossRef]
- Haroon, M.; Khalid, M.; Akhtar, T.; Tahir, M.N.; Khan, M.U.; Muhammad, S.; Al-Sehemi, A.G.; Hameed, S. Synthesis, crystal structure, spectroscopic, electronic and nonlinear optical properties of potent thiazole based derivatives: Joint experimental and computational insight. J. Mol. Struct. 2020, 1202, 127354. [Google Scholar] [CrossRef]
- Khalid, M.; Naseer, S.; Tahir, M.S.; Shafiq, I.; Munawar, K.S.; de Alcântara Morais, S.F.; Braga, A.A. A theoretical approach towards designing of banana shaped non-fullerene chromophores using efficient acceptors moieties: Exploration of their NLO response properties. Opt. Quantum Electron. 2023, 55, 258. [Google Scholar] [CrossRef]
- Baek, Y.S.; Lee, S.; Filatov, M.; Choi, C.H. Optimization of Three State Conical Intersections by Adaptive Penalty Function Algorithm in Connection with the Mixed-Reference Spin-Flip Time-Dependent Density Functional Theory Method (MRSF-TDDFT). J. Phys. Chem. A 2021, 125, 1994–2006. [Google Scholar] [CrossRef]
- Yu, H.S.; Li, S.L.; Truhlar, D.G. Perspective: Kohn-Sham density functional theory descending a staircase. J. Chem. Phys. 2016, 145, 130901. [Google Scholar] [CrossRef] [PubMed]
- Gräfenstein, J.; Kraka, E.; Filatov, M.; Cremer, D. Can Unrestricted Density-Functional Theory Describe Open Shell Singlet Biradicals? Int. J. Mol. Sci. 2002, 3, 360–394. [Google Scholar] [CrossRef]
- Gräfenstein, J.; Hjerpe, A.M.; Kraka, E.; Cremer, D. An accurate description of the Bergman reaction using restricted and unrestricted DFT: Stability test, spin density, and on-top pair density. J. Phys. Chem. A 2000, 104, 1748–1761. [Google Scholar] [CrossRef]
- Richtol, H.H.; Fitch, B.R. Triplet State Acidity Constants for Hydroxy and Amino Substituted Anthraquinones and Related Compounds. Anal. Chem. 1974, 46, 1860–1862. [Google Scholar] [CrossRef]
- Bayrakceken, F. Triplet-triplet optical energy transfer from benzophenone to naphthalene in the vapor phase. Spectrochim. Acta Part A-Mol. Biomol. Spectrosc. 2008, 71, 603–608. [Google Scholar] [CrossRef]
- Karaca, N.; Ocal, N.; Arsu, N.; Jockusch, S. Thioxanthone-benzothiophenes as photoinitiator for free radical polymerization. J. Photochem. Photobiol. A-Chem. 2016, 331, 22–28. [Google Scholar] [CrossRef]
- He, Z.; Zhao, W.; Lam, J.W.Y.; Peng, Q.; Ma, H.; Liang, G.; Shuai, Z.; Tang, B.Z. White light emission from a single organic molecule with dual phosphorescence at room temperature. Nat. Commun. 2017, 8, 416. [Google Scholar] [CrossRef]
- McMorrow, D.; Wyche, M.I.; Chou, P.T.; Kasha, M. On the dual phosphorescence of xanthone and chromone in glassy hydrocarbon hosts. Photochem. Photobiol. 2015, 91, 576–585. [Google Scholar] [CrossRef]
- De Silva, J.A.F.; Strojny, N.; Stika, K. Luminescence determination of pharmaceuticals of the tetrahydrocarbazole, carbazole, and 1, 4-benzodiazepine class. Anal. Chem. 1976, 48, 144–155. [Google Scholar] [CrossRef]
- Dansholm, C.N.; Junker, A.K.R.; Nielsen, L.G.; Kofod, N.; Pal, R.; Sorensen, T.J. pi-Expanded Thioxanthones—Engineering the Triplet Level of Thioxanthone Sensitizers for Lanthanide-Based Luminescent Probes with Visible Excitation. Chempluschem 2019, 84, 1778–1788. [Google Scholar] [CrossRef]
- Shukla, D.; Ahearn, W.G.; Farid, S. Chain Amplification in Photoreactions of N-Alkoxypyridinium Salts with Alcohols: Mechanism and Kinetics. J. Org. Chem. 2005, 70, 6809–6819. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
- Reiher, M.; Salomon, O.; Artur Hess, B. Reparameterization of hybrid functionals based on energy differences of states of different multiplicity. Theor. Chem. Acc. 2001, 107, 48–55. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2007, 120, 215–241. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Comparative DFT Study of van der Waals Complexes: Rare-Gas Dimers, Alkaline-Earth Dimers, Zinc Dimer, and Zinc-Rare-Gas Dimers. J. Phys. Chem. A 2006, 110, 5121–5129. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density Functional for Spectroscopy: No Long-Range Self-Interaction Error, Good Performance for Rydberg and Charge-Transfer States, and Better Performance on Average than B3LYP for Ground States. J. Phys. Chem. A 2006, 110, 13126–13130. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J.; Manby, F.R.; Black, J.A.; Doll, K.; Hesselmann, A.; Kats, D.; Kohn, A.; Korona, T.; Kreplin, D.A.; et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020, 152, 144107. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
| Molecular | RMSD | Molecular | RMSD |
|---|---|---|---|
| HA | 0.00 | FBDBT | 0.02 |
| AAT | 0.05 | ClBDBT | 0.03 |
| BP | 0.01 | BrBDBT | 0.03 |
| TX-BT | 0.14 | XA | 0.03 |
| TX-DBT | 0.01 | AR | 0.02 |
| BDBT | 0.02 | AD | 0.01 |
| CC2 | PBE | PBE0 | B3LYP | CAM-B3LYP | ωB97XD | M06-2X | M06-HF | |
|---|---|---|---|---|---|---|---|---|
| HA | 2.55 | −0.87 * | –0.80 | −0.75 | −0.68 | −0.57 | −0.41 | −0.25 * |
| AAT | 2.03 | −0.75 | −0.67 | −0.64 | −0.53 | −0.46 | −0.33 | −0.11 |
| BP | 2.50 | −0.62 | −0.39 | −0.34 | −0.27 | −0.18 | −0.11 | −0.26 |
| TX−BT | 2.67 | −0.49 | −0.71 | −0.59 | −0.83 | −0.68 | −0.28 | −0.14 |
| TX−DBT | 2.91 | −0.77 | −0.58 | −0.57 | −0.47 | −0.39 | −0.36 | −0.32 |
| BDBT | 2.52 | −0.65 | −0.42 | −0.37 | −0.30 | −0.21 | −0.13 | −0.25 |
| FBDBT | 2.56 | −0.65 | −0.44 | −0.39 | −0.33 | −0.23 | −0.15 | −0.27 |
| ClBDBT | 2.52 | −0.66 | −0.43 | −0.39 | −0.31 | −0.22 | −0.14 | −0.26 |
| BrBDBT | 2.51 | −0.66 | −0.43 | −0.38 | −0.31 | −0.21 | −0.14 | −0.25 |
| XA | 3.16 | −0.68 * | −0.76 | −0.68 * | −0.71 | −0.60 | −0.55 | −0.59 |
| AR | 2.83 | − 0.65 * | −0.63 | −0.59 | −0.54 | − 0.47 | −0.48 | −0.53 |
| AD | 2.93 | −0.71 * | −0.64 | −0.60 | −0.56 | −0.48 | −0.44 | − 0.44 |
| MUE(a) | − | 0.68 | 0.57 | 0.53 | 0.49 | 0.39 | 0.29 | 0.31 |
| cc-pVTZ | aug-cc-pVTZ | |||
|---|---|---|---|---|
| Charge Transfer | E (2) kcal/mol | Charge Transfer | E (2) kcal/mol | |
| HA | σ* (C7-C10) → σ* (C3-C4) | 176.24 | σ* (C7-C10) → σ* (C3-C4) | 176.24 |
| AAT | σ* (C8-C9) → σ* (C7-C10) | 105.28 | σ* (C8-C9) → σ* (C7-C10) | 105.28 |
| BP | σ* (C19-C21) → σ* (C15-C17) | 271.00 | σ* (C19-C21) → σ* (C15-C17) | 271.00 |
| TX-BT | σ* (C3-C4) → σ* (C5-C6) | 180.49 | σ* (C3-C4) → σ* (C5-C6) | 180.49 |
| TX-DBT | σ* (C3-C4) → σ* (C7-C8) | 249.08 | σ* (C3-C4) → σ* (C7-C8) | 249.08 |
| BDBT | σ* (C14-C15) → σ* (C11-C16) | 516.26 | σ* (C3-C4) → σ* (C1-C2) | 236.54 |
| FBDBT | σ* (C14-C15) → σ* (C11-C16) | 307.23 | σ* (C11-C16) → σ* (C27-H31) | 1100.56 |
| ClBDBT | σ* (C3-C4) → σ* (C1-C2) | 228.33 | σ* (C3-C4) → σ* (C1-C2) | 228.32 |
| BrBDBT | σ* (C14-C15) → σ* (C11-C16) | 457.47 | σ* (C22-C23) → σ* (C25-C29) | 441.75 |
| XA | σ* (C4-C5) → σ* (C1-C6) | 191.23 | σ* (C4-C5) → σ* (C1-C6) | 191.23 |
| AR | σ* (C4-C5) →σ* (C1-C6) | 258.20 | σ* (C4-C5) →σ* (C1-C6) | 258.20 |
| AD | σ* (C8-C9) →σ* (C4-C7) | 191.85 | σ* (C8-C9) →σ* (C4-C7) | 191.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Zhang, L.; Qu, Z. Benchmark Study on Phosphorescence Energies of Anthraquinone Compounds: Comparison between TDDFT and UDFT. Molecules 2023, 28, 3257. https://doi.org/10.3390/molecules28073257
Guo Y, Zhang L, Qu Z. Benchmark Study on Phosphorescence Energies of Anthraquinone Compounds: Comparison between TDDFT and UDFT. Molecules. 2023; 28(7):3257. https://doi.org/10.3390/molecules28073257
Chicago/Turabian StyleGuo, Yujie, Lingyu Zhang, and Zexing Qu. 2023. "Benchmark Study on Phosphorescence Energies of Anthraquinone Compounds: Comparison between TDDFT and UDFT" Molecules 28, no. 7: 3257. https://doi.org/10.3390/molecules28073257
APA StyleGuo, Y., Zhang, L., & Qu, Z. (2023). Benchmark Study on Phosphorescence Energies of Anthraquinone Compounds: Comparison between TDDFT and UDFT. Molecules, 28(7), 3257. https://doi.org/10.3390/molecules28073257





