1. Introduction
The need to control harmful gas emissions and improve environmental quality is becoming increasingly strong, with global environmental pollution becoming increasingly prominent and people’s awareness of environmental protection gradually strengthening. Nitrogen oxides (NO
x) are one of the main harmful emissions from diesel engines, which has caused great harm to human health, the ecological environment and the climate. Nowadays, selective catalytic reduction (SCR) systems [
1] have been increasingly used in diesel as the mainstream device to deal with NO
x emissions [
2,
3].
Urea-SCR technology is to spray urea aqueous solution into the exhaust pipe of a diesel engine at a suitable location; it produces the reducing agent NH
3 after evaporation, pyrolysis and hydrolysis, and NH
3 converts the harmful NO
x into harmless N
2 and H
2O under the action of a catalyst. Numerous studies [
4,
5,
6,
7,
8] have revealed that the exhaust pipe wall of diesel engines with urea-SCR systems was prone to form deposits consisting of undecomposed urea, biuret, and cyanuric acid (CYA). The deposits easily lead to partial or even total blockage of the exhaust pipe, which increases the exhaust back pressure and seriously affects the performance of diesel engines [
9].
The mechanism of the urea pyrolysis reaction is complex. Dong, et al. [
10] have studied the pyrolysis process of urea using thermogravimetric combined with Fourier infrared spectroscopy analytical methods. The result indicated that the urea pyrolysis process went through three stages. Each stage occurred at 193 °C, 250 °C and 400 °C, corresponding to residual mass fractions of 46.2%, 39.5% and 9.2%, respectively. The polymerization of HNCO and the condensation reaction with urea and biuret are the main reasons for producing polymeric compounds. Schaber, et al. [
11] have studied the thermal decomposition process of urea in detail. The results indicated that the urea pyrolysis process could be divided into four reaction stages, where the first and second stages were the main reaction processes. The mass loss was mainly related to the urea decomposition in the first reaction stage (room temperature to 190 °C). The urea was decomposed into the biuret and began to slowly synthesize complex products, such as cyanuric acid and cyanuric acid monoamide. The urea continued to decompose and the biuret began to decompose at the second reaction stage (190~250 °C). The production rate of cyanuric acid and cyanuric acid monoamide increased, while little cyanuric acid amide and melamine began to be generated. The third reaction stage (250~360 °C) and the fourth reaction stage (>360 °C) were mainly the decomposition and sublimation of residues. Zhao [
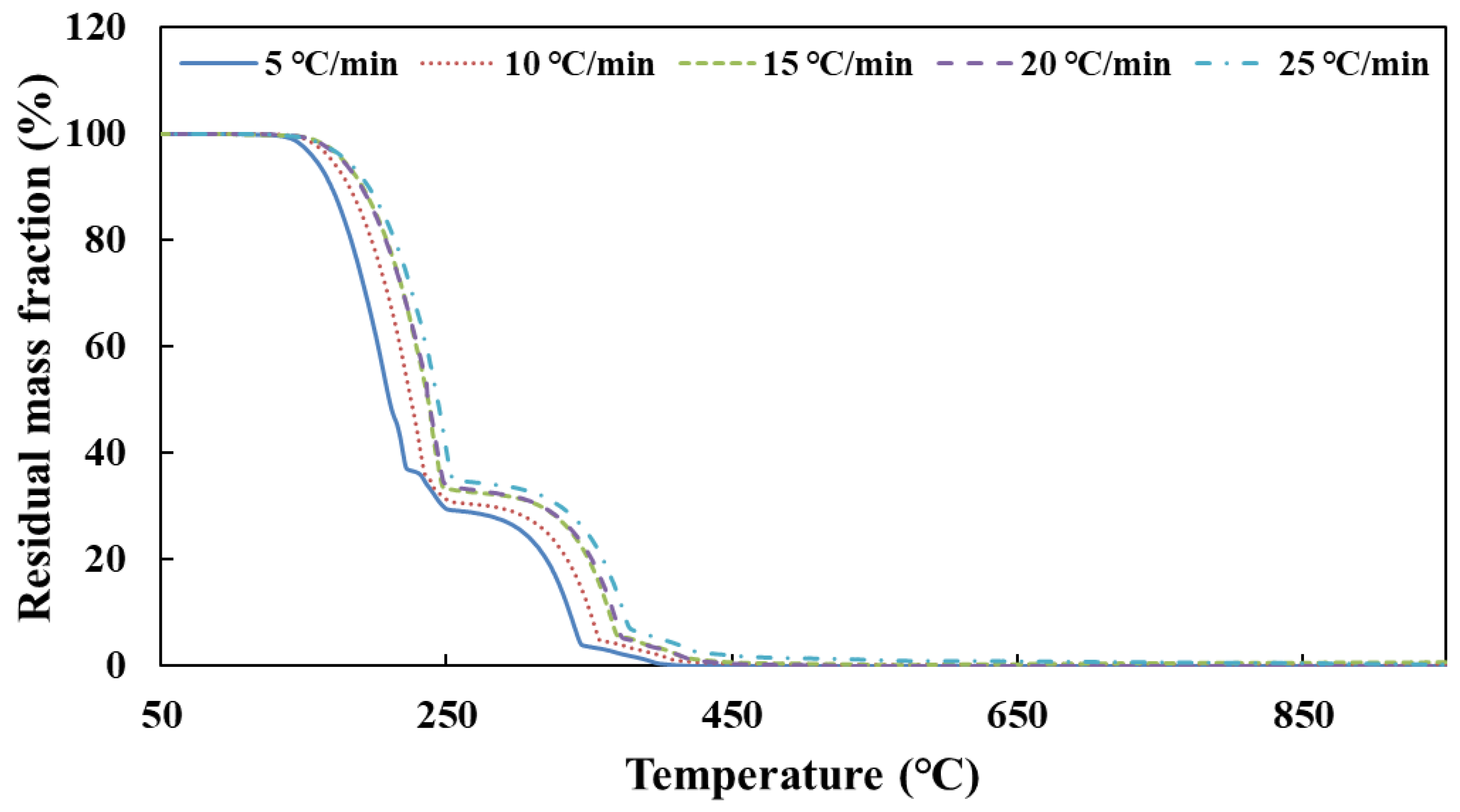
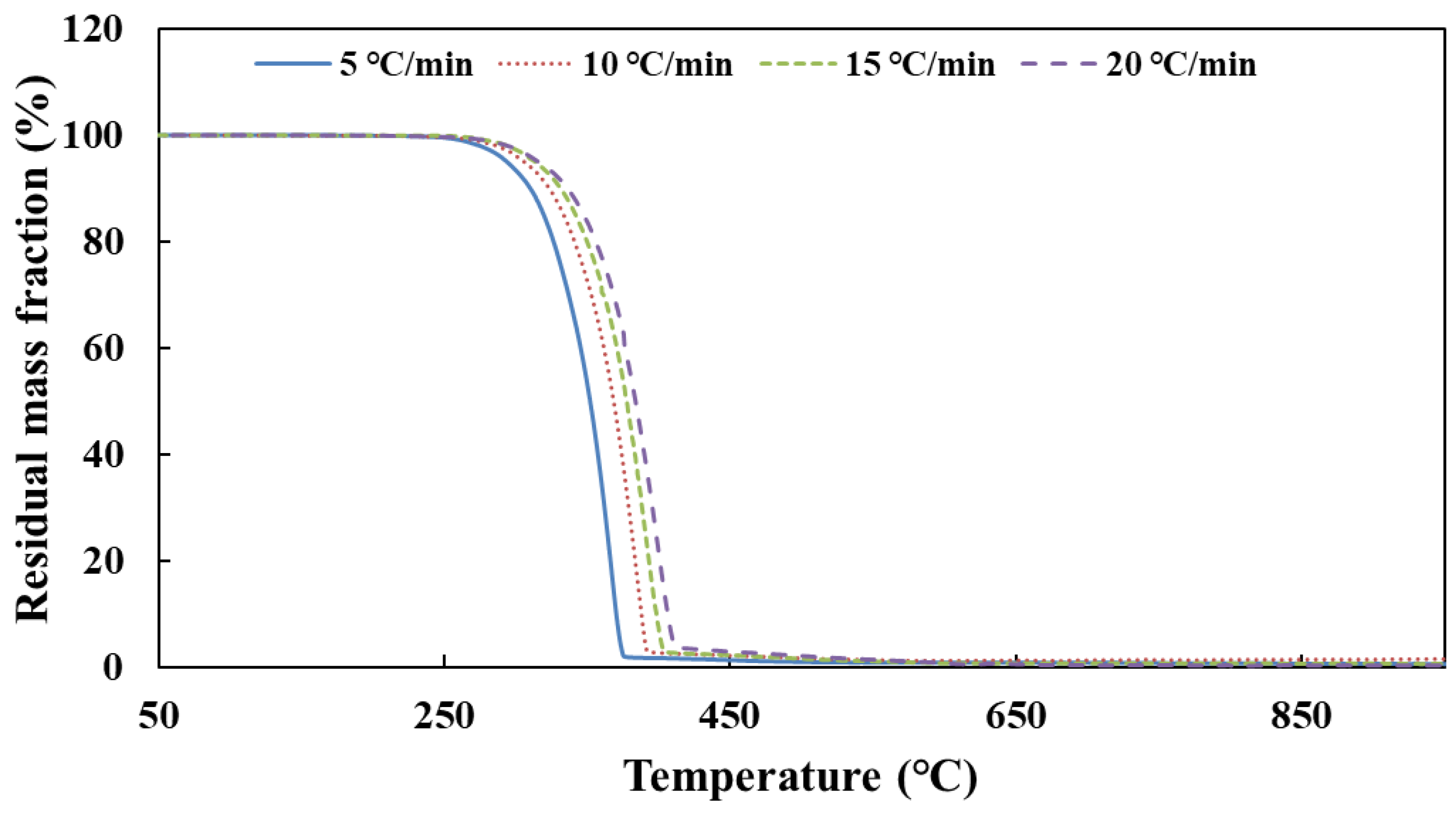
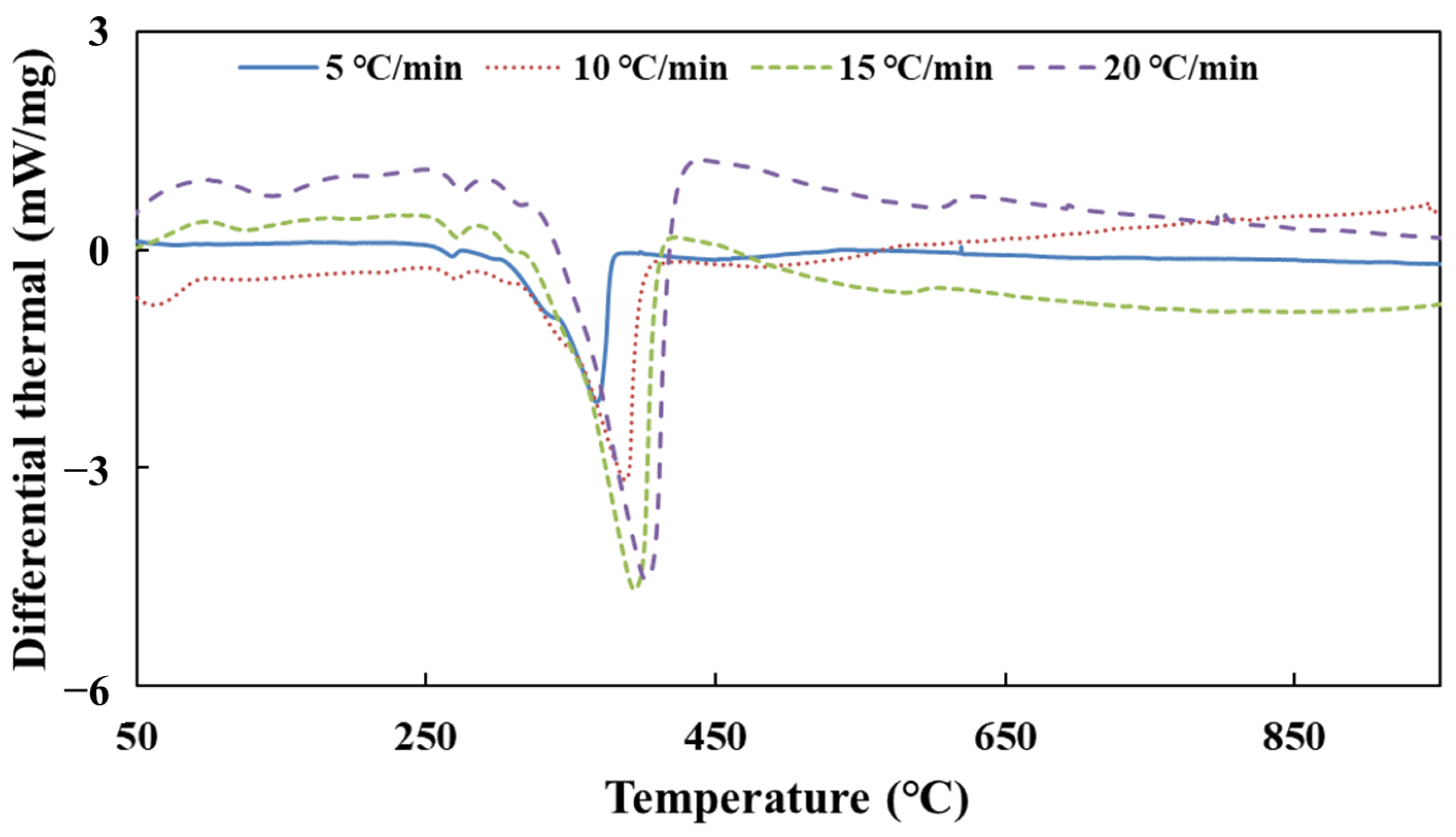
12] from Tsinghua University studied the influence of the urea pyrolysis process at different temperatures and different heating rates by thermogravimetric tests. Thagard [
13] has analyzed the urea pyrolysis process at 150–200 °C using the DBD method. The results indicated there was no difference in the urea pyrolysis by-products whether in wet or dry air, the main gaseous products were NH
3 and HNCO, and the residual solid product was CYA. In addition, Stradella [
14], Carp [
15] and Lundström [
16] have conducted studies related to urea pyrolysis as well.
The detailed kinetic model of the deposit reaction is required to quantitatively describe the production of the deposit. Ebrahimian [
17] has established the reaction kinetic model of the urea pyrolysis process. It considered four kinds of components of deposit, including urea, biuret, CYA and ammelide, which provided a guide for the quantitative study of deposit formation. Brack, et al. [
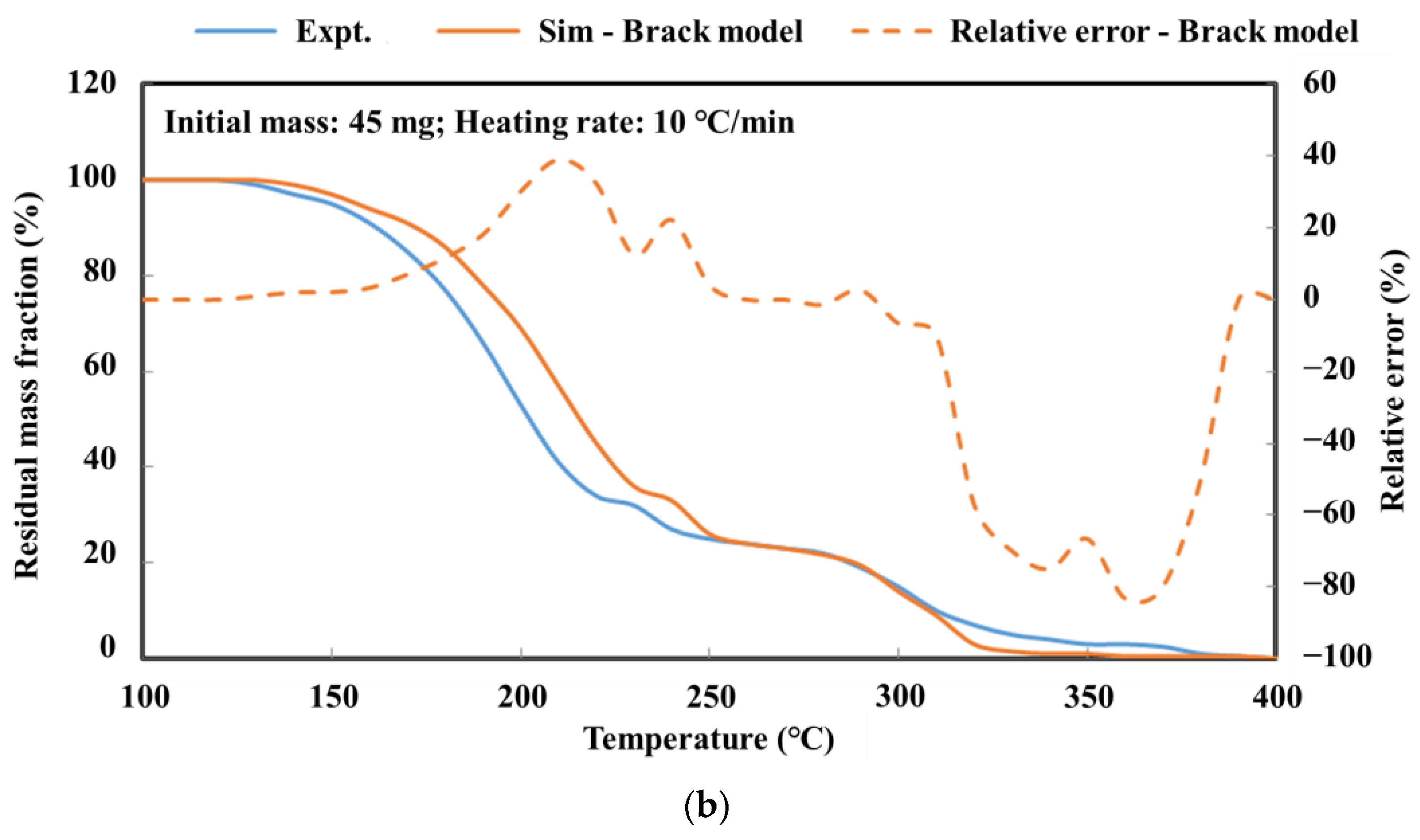
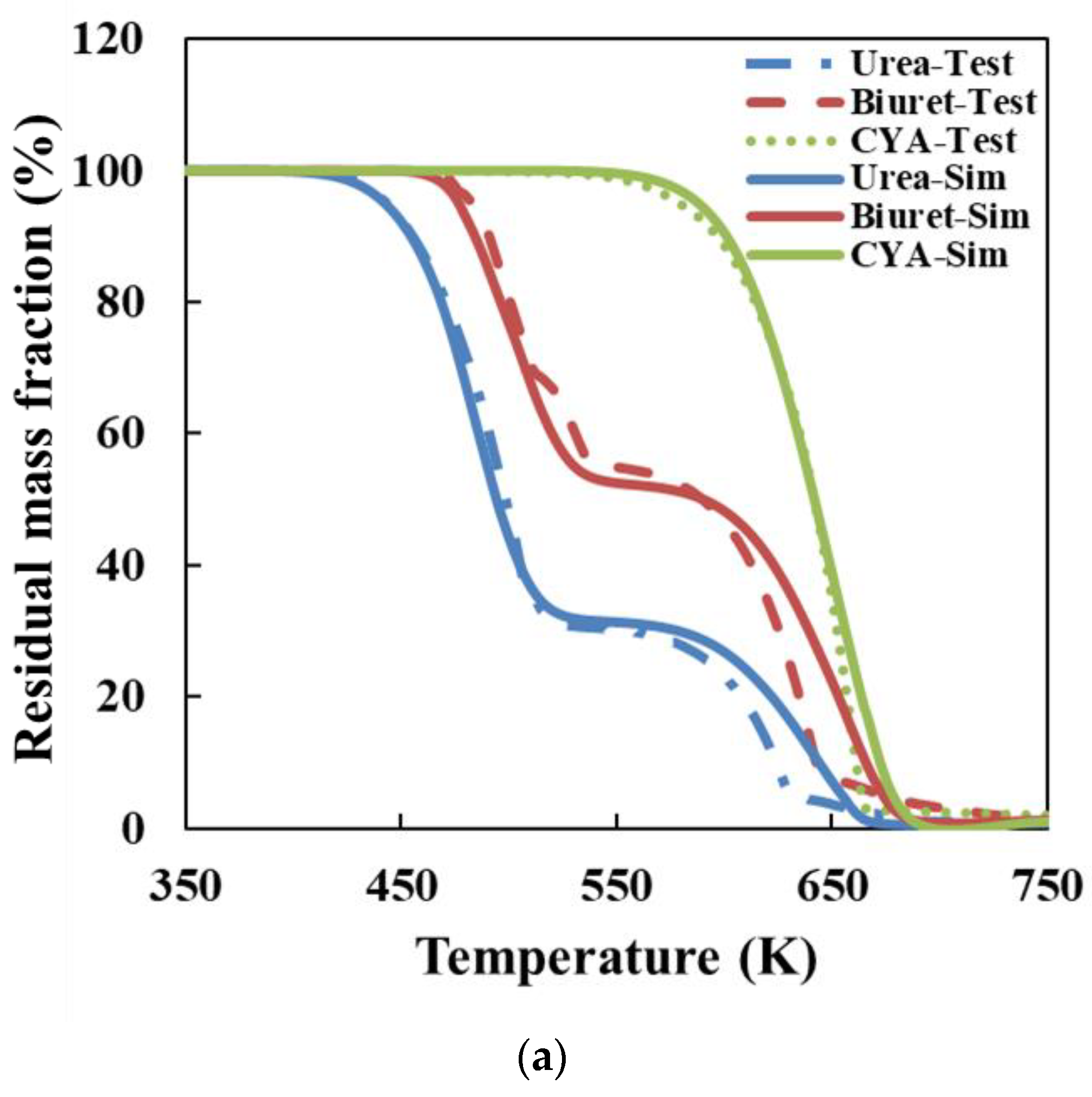
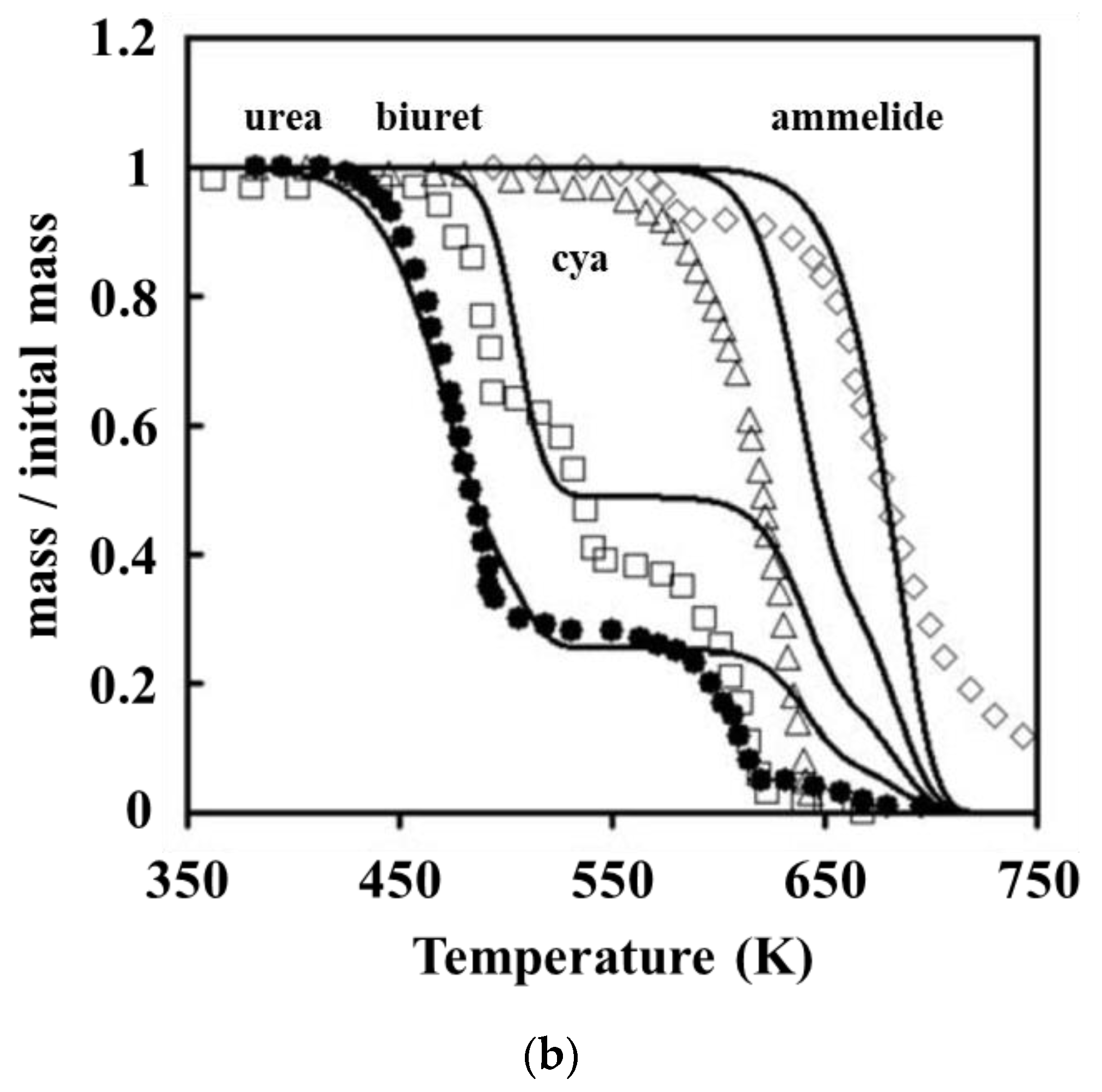
18] have revised the reaction path based on the Ebrahimian mechanism model. They re-identified the reaction kinetic parameters, according to the results of thermogravimetric tests with different urea initial masses, temperature heating rates and reactor configurations. However,
Figure 1 shows that the simulation values of urea pyrolysis, respectively, from the above reaction kinetic models established by Ebrahimian and Brack, are different from the experimental values.
In this study, thermal analysis technology was applied to the investigation of chemical reaction kinetics, and various classical thermal analysis kinetic methods were used to solve the activation energy of the decomposition reactions of urea and CYA. According to the Ebrahimian mechanism model, we re-identified the reaction kinetic parameters and established a deposit reaction kinetic model to describe the decomposition process of the key components in the deposit, attempting to provide a reference for the quantitative study of the deposit formation.
4. Conclusions
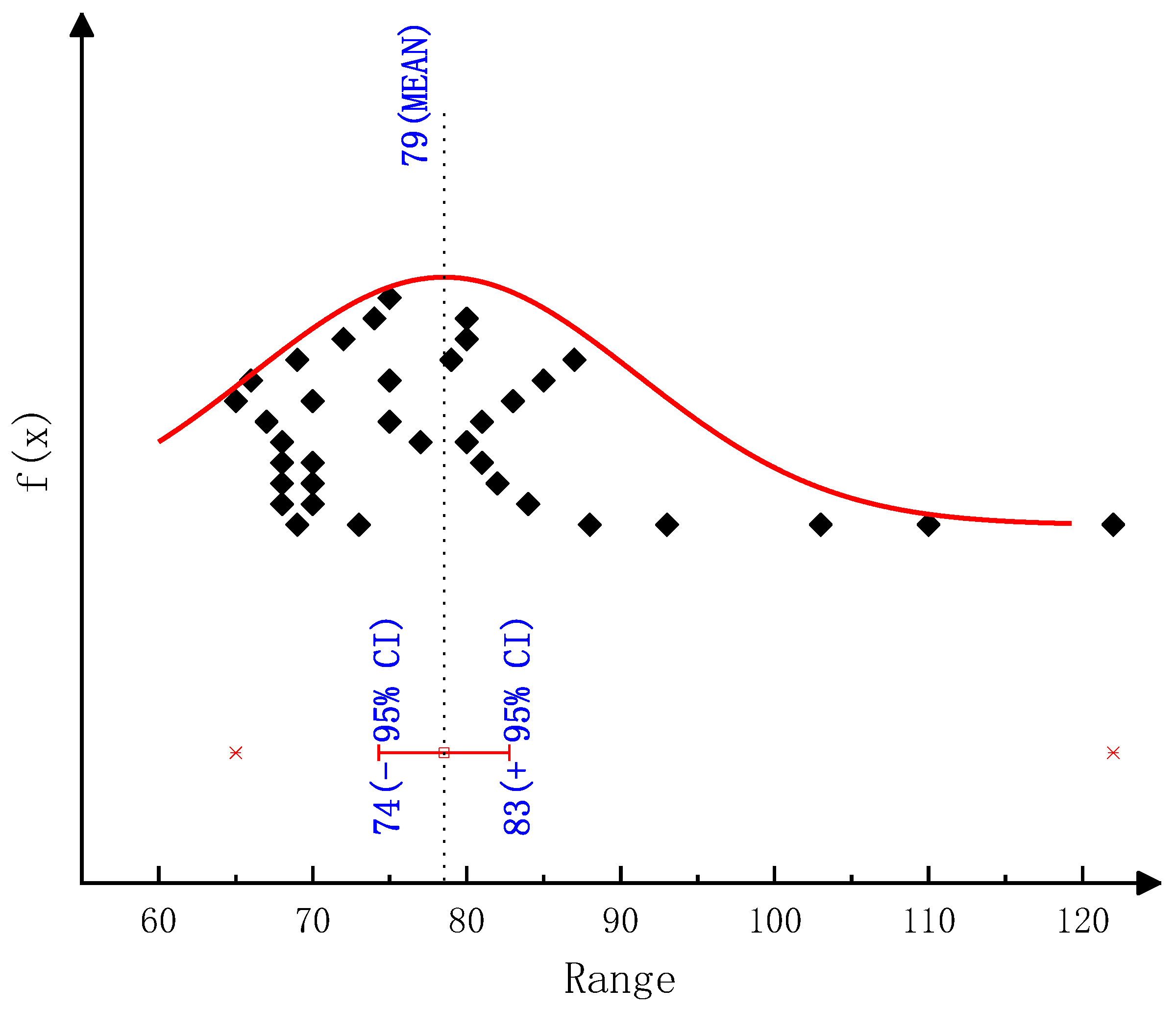
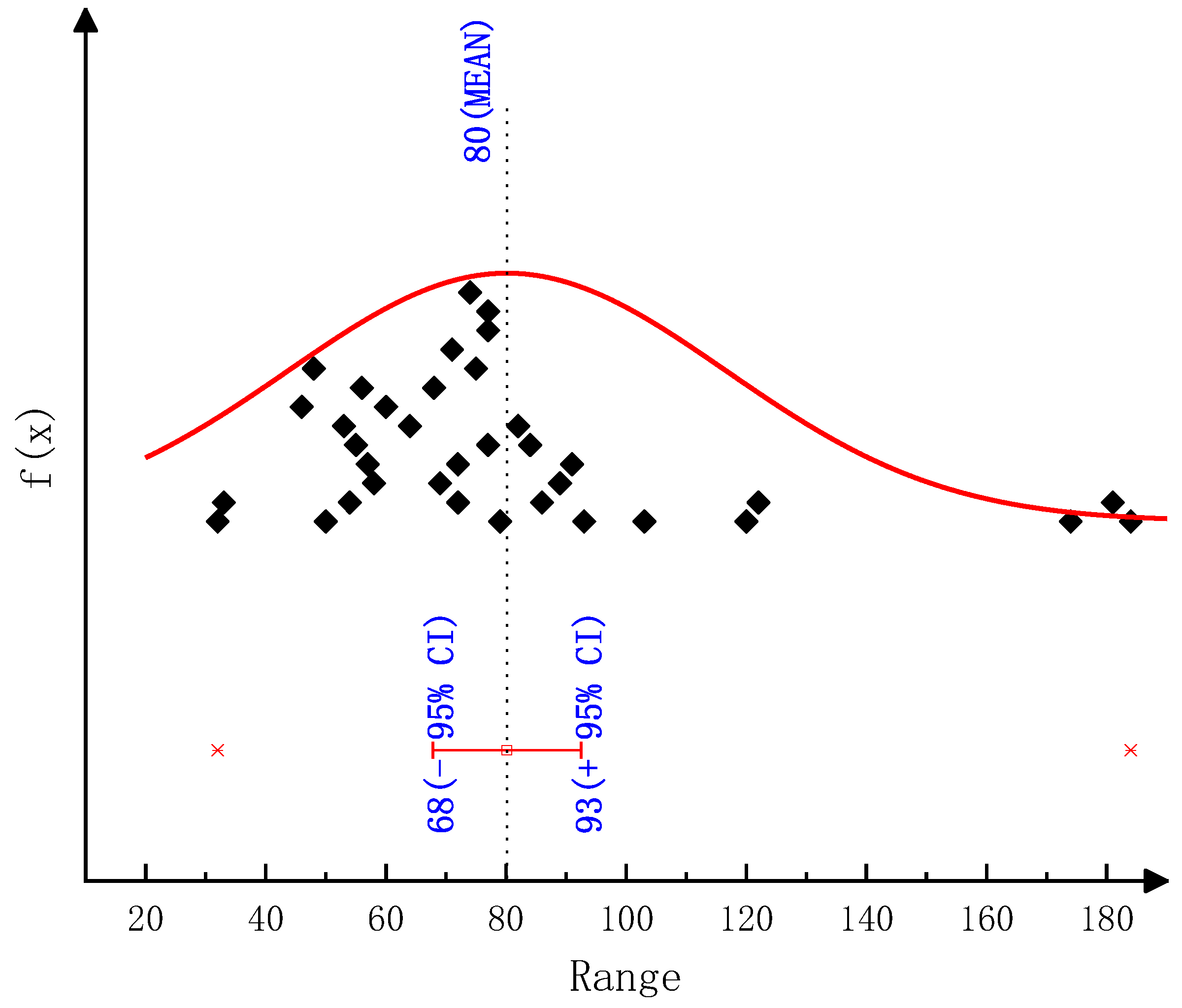
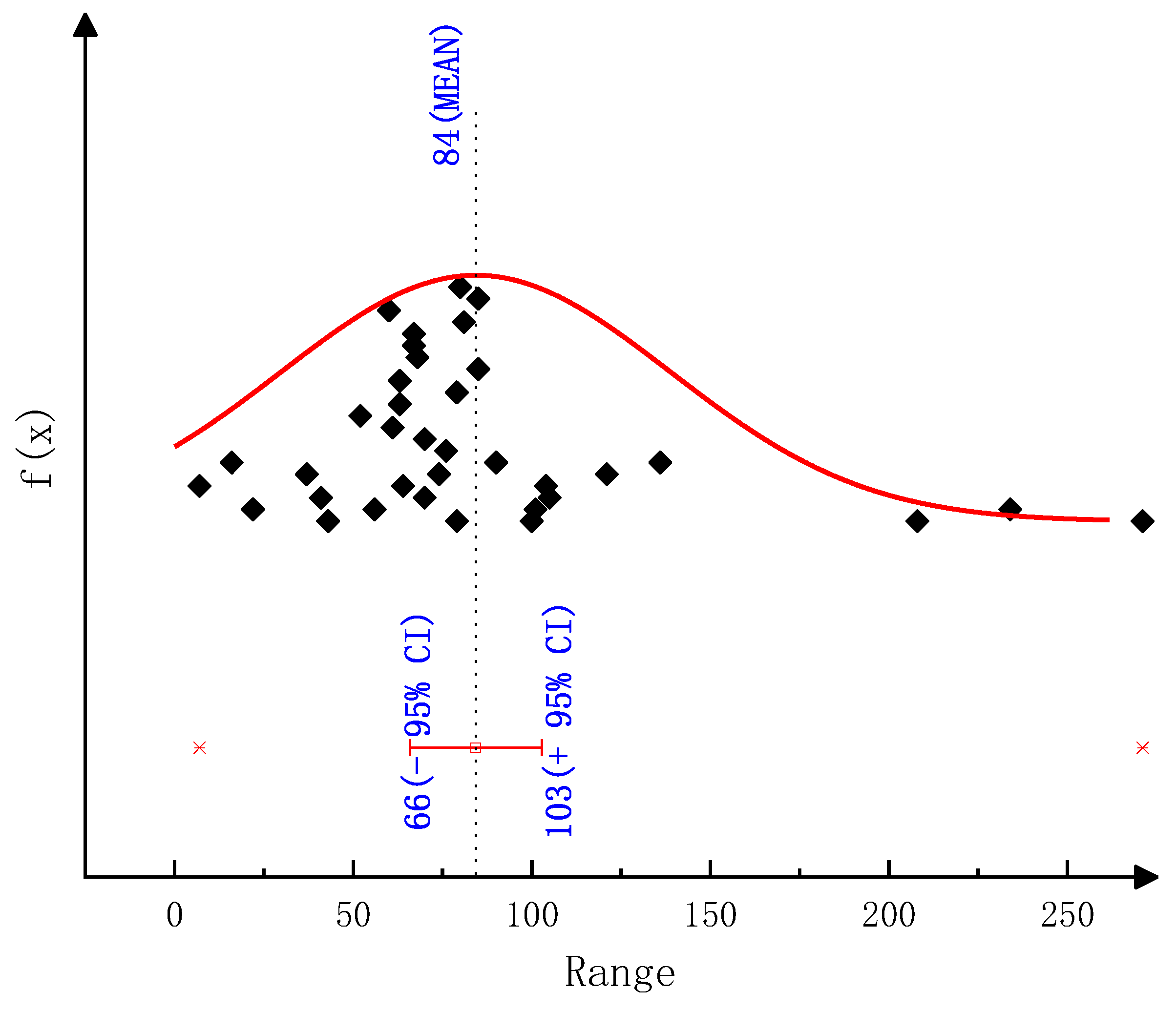
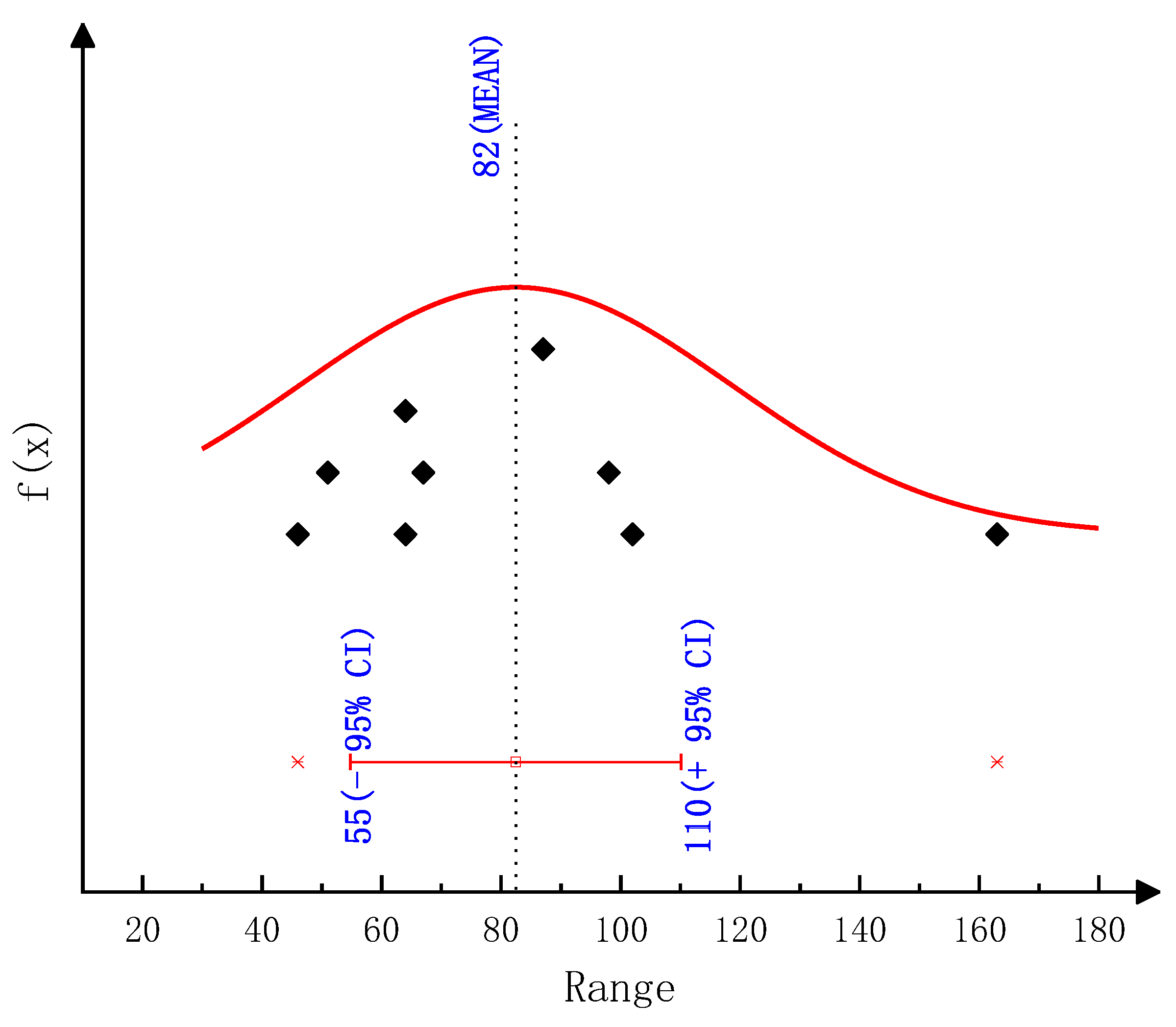
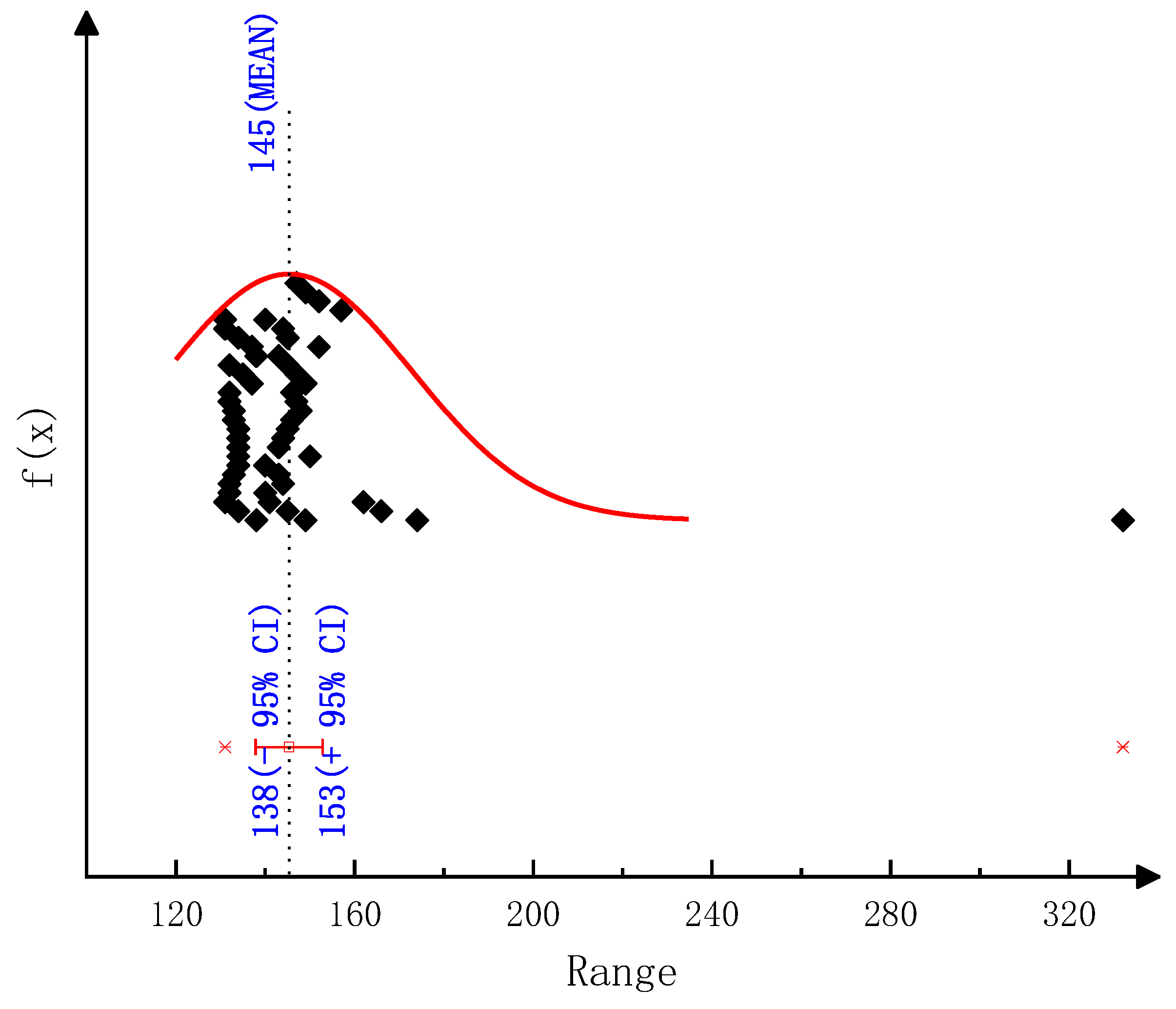
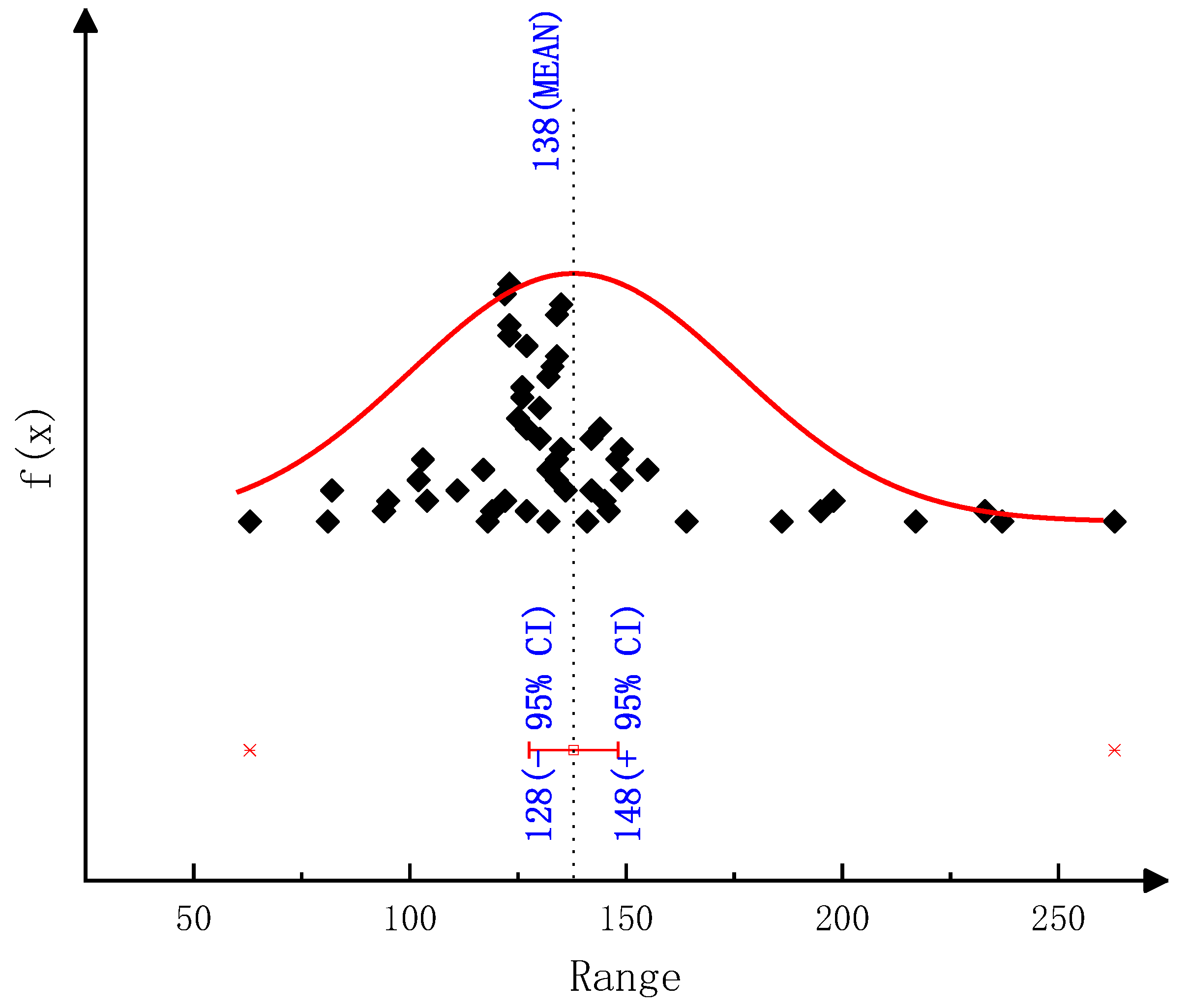
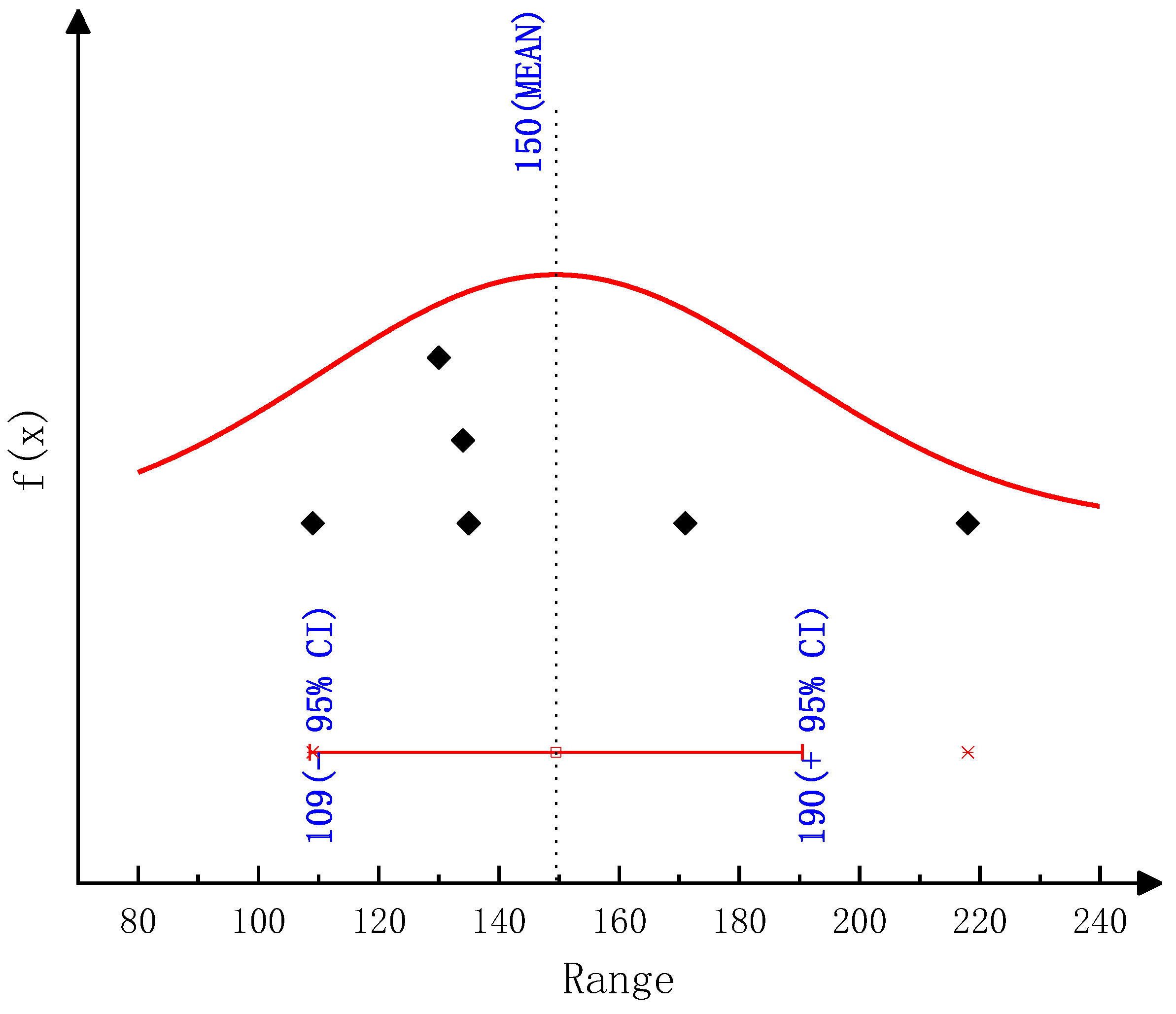
According to the thermogravimetric test results, we employed various classical thermal analysis kinetic methods to solve the activation energies of the thermal decomposition reactions of urea and CYA. The activation energy of the urea decomposition reaction: the result is 78.44 kJ/mol by the Ozawa method, 80.12 kJ/mol by the Friedman two-interval method, 84.34 kJ/mol by the Friedman one-interval method and 82.64 kJ/mol by the Kissinger method. The activation energy of CYA decomposition reaction: the result is 145.38 kJ/mol by the Ozawa method, 137.83 kJ/mol by the Friedman two-interval method, 152.57 kJ/mol by the Friedman one-interval method and 149.34 kJ/mol by the Kissinger method. After identifying the reaction kinetic parameters in the model of this paper, the activation energies of the decomposition reactions of urea and CYA are 84 kJ/mol and 152 kJ/mol, respectively. The established deposit reaction kinetic model can accurately describe the decomposition process of each key component of deposits. What is more, the simulation accuracy is significantly improved above 600 K, which can provide a reference for the quantitative study of deposit formation.