Next Article in Journal
Research on Improved MOF Materials Modified by Functional Groups for Purification of Water
Previous Article in Journal
The Effect of Poria cocos Polysaccharide PCP-1C on M1 Macrophage Polarization via the Notch Signaling Pathway
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 5
10.3390/molecules28052139
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Series of Metal–Organic Frameworks with 2,2′-Bipyridyl Derivatives: Synthesis vs. Structure Relationships, Adsorption, and Magnetic Studies

by
Vadim A. Dubskikh
1,
Aleksei A. Kolosov
1,2,
Anna A. Lysova
1,*,
Denis G. Samsonenko
1,
Alexander N. Lavrov
1,
Konstantin A. Kovalenko
1,
Danil N. Dybtsev
1,* and
Vladimir P. Fedin
1
1
Nikolaev Institute of Inorganic Chemistry, Siberian Branch of the Russian Academy of Sciences, Novosibirsk 630090, Russia
2
Department of Natural Sciences, Novosibirsk State University, Novosibirsk 630090, Russia
*
Authors to whom correspondence should be addressed.
Molecules 2023, 28(5), 2139; https://doi.org/10.3390/molecules28052139
Submission received: 26 January 2023 / Revised: 16 February 2023 / Accepted: 22 February 2023 / Published: 24 February 2023
(This article belongs to the Section Inorganic Chemistry)
Browse Figures
Versions Notes

Abstract

:
Five new metal–organic frameworks based on Mn(II) and 2,2′-bithiophen-5,5′-dicarboxylate (btdc2–) with various chelating N-donor ligands (2,2′-bipyridyl = bpy; 5,5′-dimethyl-2,2′-bipyridyl = 5,5′-dmbpy; 4,4′-dimethyl-2,2′-bipyridyl = 4,4′-dmbpy) [Mn3(btdc)3(bpy)2]·4DMF, 1; [Mn3(btdc)3(5,5′-dmbpy)2]·5DMF, 2; [Mn(btdc)(4,4;-dmbpy)], 3; [Mn2(btdc)2(bpy)(dmf)]·0.5DMF, 4; [Mn2(btdc)2(5,5′-dmbpy)(dmf)]·DMF, 5 (dmf, DMF = N,N-dimethylformamide) have been synthesized, and their crystal structure has been established using single-crystal X-ray diffraction analysis (XRD). The chemical and phase purities of Compounds 1–3 have been confirmed via powder X-ray diffraction, thermogravimetric, and chemical analyses as well as IR spectroscopy. The influence of the bulkiness of the chelating N-donor ligand on the dimensionality and structure of the coordination polymer has been analyzed, and the decrease in the framework dimensionality, as well as the secondary building unit’s nuclearity and connectivity, has been observed for bulkier ligands. For three-dimensional (3D) coordination polymer 1, the textural and gas adsorption properties have been studied, revealing noticeable ideal adsorbed solution theory (IAST) CO2/N2 and CO2/CO selectivity factors (31.0 at 273 K and 19.1 at 298 K and 25.7 at 273 K and 17.0 at 298 K, respectively, for the equimolar composition and the total pressure of 1 bar). Moreover, significant adsorption selectivity for binary C2–C1 hydrocarbons mixtures (33.4 and 24.9 for C2H6/CH4, 24.8 and 17.7 for C2H4/CH4, 29.3 and 19.1 for C2H2/CH4 at 273 K and 298 K, respectively, for the equimolar composition and the total pressure of 1 bar) has been observed, making it possible to separate on 1 natural, shale, and associated petroleum gas into valuable individual components. The ability of Compound 1 to separate benzene and cyclohexane in a vapor phase has also been analyzed based on the adsorption isotherms of individual components measured at 298 K. The preferable adsorption of C6H6 over C6H12 by 1 at high vapor pressures (VB/VCH = 1.36) can be explained by the existence of multiple van der Waals interactions between guest benzene molecules and the metal–organic host revealed by the XRD analysis of 1 immersed in pure benzene for several days (1≅2C6H6). Interestingly, at low vapor pressures, an inversed behavior of 1 with preferable adsorption of C6H12 over C6H6 (KCH/KB = 6.33) was observed; this is a very rare phenomenon. Moreover, magnetic properties (the temperature-dependent molar magnetic susceptibility, χp(T) and effective magnetic moments, μeff(T), as well as the field-dependent magnetization, M(H)) have been studied for Compounds 1–3, revealing paramagnetic behavior consistent with their crystal structure.

Graphical Abstract

1. Introduction

Metal–organic frameworks (MOFs) are a class of inorganic materials consisting of metal ions or clusters connected by organic ligands into one- (1D), two- (2D), or three- (3D) dimensional structures with pores whose size is determined by the length and geometry of the organic ligand [1,2,3,4,5,6]. Currently, various ligands with two or more carboxylate functions are the most extensively used types of linkers for the MOF design. Polydentate carboxylate groups are known to assist an assemblage of metal cations into polynuclear clusters or complexes known as secondary building units (SBUs) to be connected into regular periodic networks. Auxiliary monodentate linkers, e.g., with pyridine functions, such as 4,4′-bipyridyl, further enrich the connectivity of SBUs and the complexity of the topology of MOFs, which, however, may have a negative impact on the porosity of the material [7,8,9,10]. In this regard, a reduction in the structural complexity might often be a promising strategy in the design of sufficiently porous structures. Additionally, a suppression of the connectivity of the SBUs is likely the only rational way to obtain low-dimensional coordination networks (1D or 2D), which are valuable targets for magnetic or electronic materials with highly anisotropic properties [11,12,13,14,15]. Chelate organic ligands are known to form stronger coordination complexes with metal cations ensuring higher competitively over the other type of ligands. Partial substitution of carboxylate linkers to a chelate pendant in the inner coordination sphere of metal cations inevitably reduces the connectivity of the SBUs. Additionally, a substitution of coordinated solvent molecules by a chelate ligand improves the general stability of the porous architecture of the MOF since the expected detachment of the poorly bind moieties may destabilize the coordination environment of the metal nodes. Moreover, electron-rich aromatic chelate molecules, such as 1,10-phenantroline or 2,2′-bipyridyl, feature excellent UV light absorbance, resulting in a remarkable luminescence or photocatalytic properties of the corresponding coordination compounds [16,17,18,19]. In short, the utilization of auxiliary chelate ligands is a powerful tool for a deliberate modulation of a MOF topology, an enhancement of the stability and porosity of the coordination framework, as well as a versatile functionalization of the products.
Despite obvious advantages, the systematic study of the effects of the chelating ligands on the structure and functional properties of the MOFs is somewhat underdeveloped [20,21,22,23,24,25,26]. In this account we investigate a synthesis of a series of five new MOFs prepared from Mn(II) cations; 2,2′-bithiophen-5,5′-dicarboxylate anions as ditopic linkers; and 2,2′-bipyridyl derivatives (2,2′-bipyridyl = bpy; 5,5′-dimethyl-2,2′-bipyridyl = 5,5′-dmbpy; 4,4′-dimethyl-2,2′-bipyridyl = 4,4′-dmbpy) as chelate ligands. An influence of the bipyridyl derivative on the structure of SBUs and topology of coordination networks was revealed. The adsorption and potential selective separation properties of one of the MOFs featuring 3D porous structure towards some industrially important gases or vapors have been systematically investigated. Moreover, various magnetic properties of the MOFs have been characterized and rationalized according to their crystal structures.

2. Results and Discussion

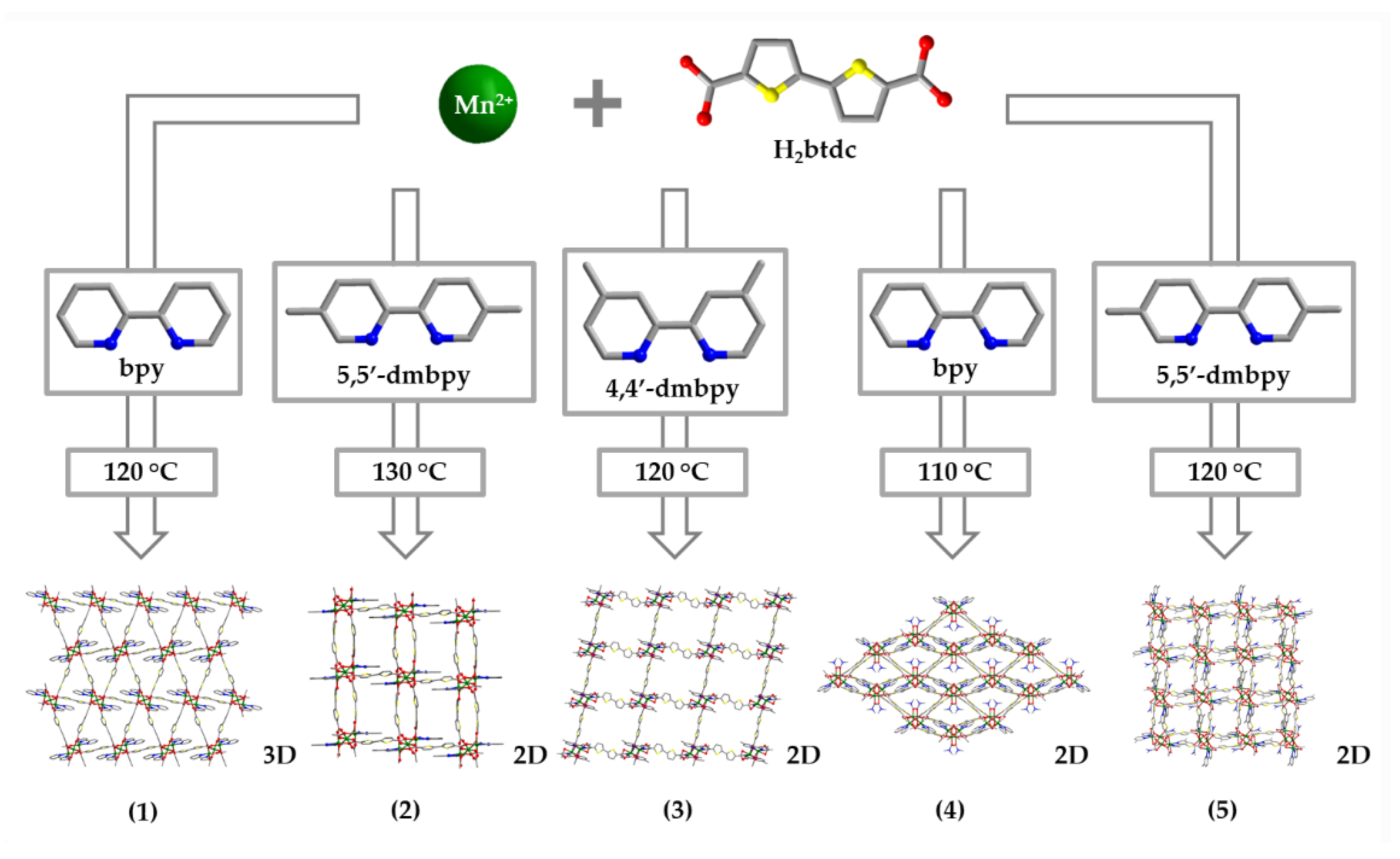
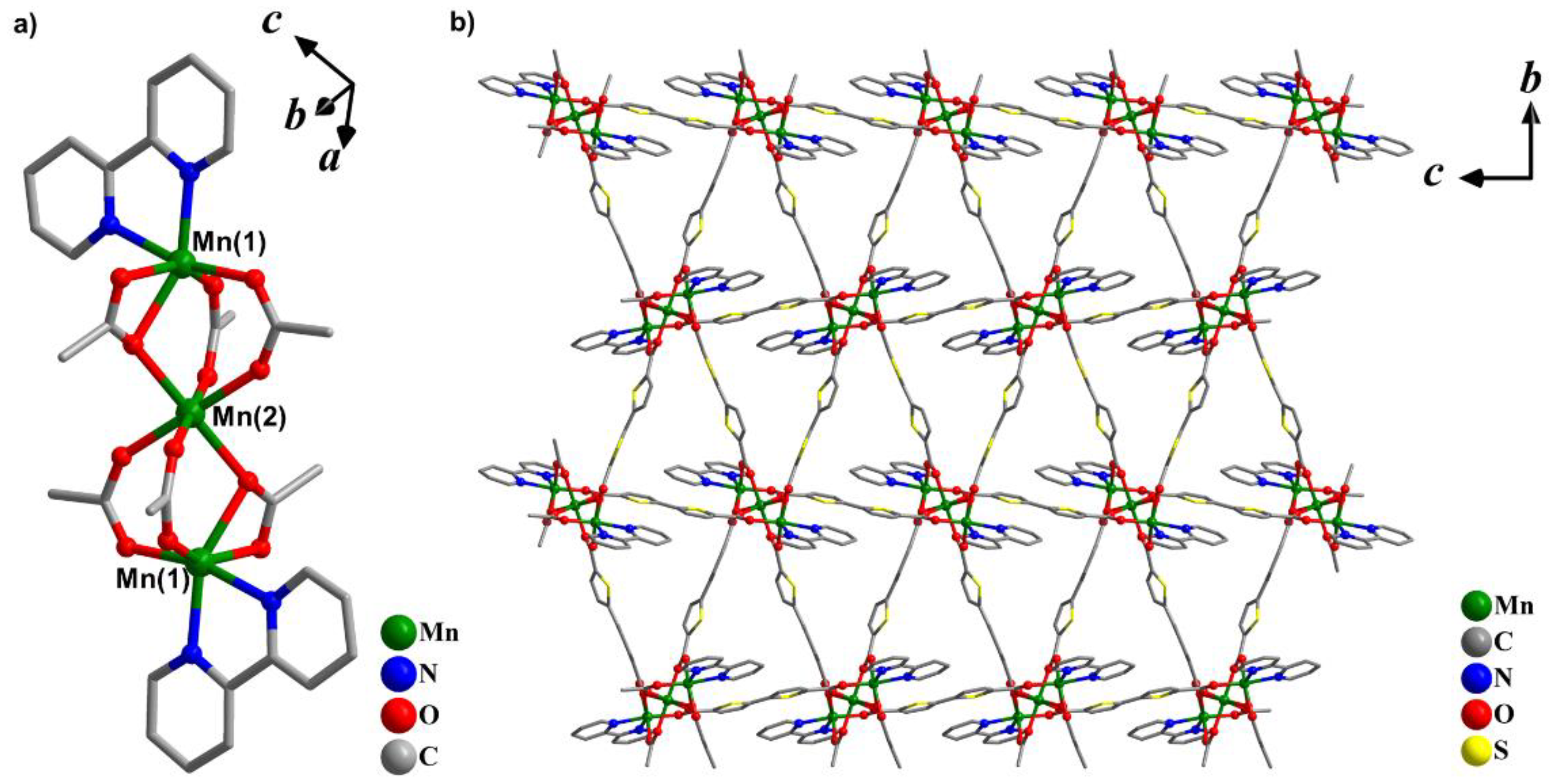
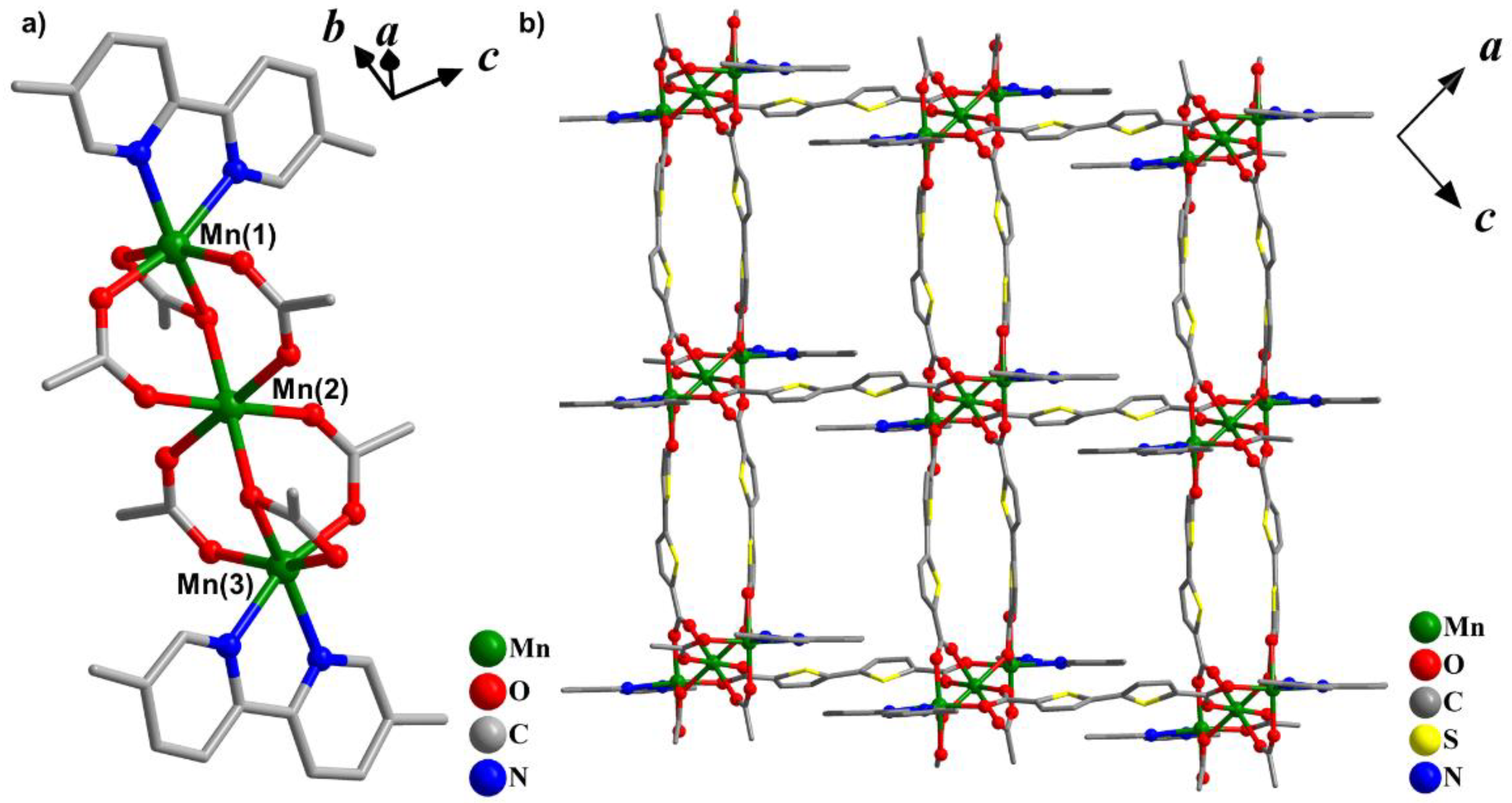
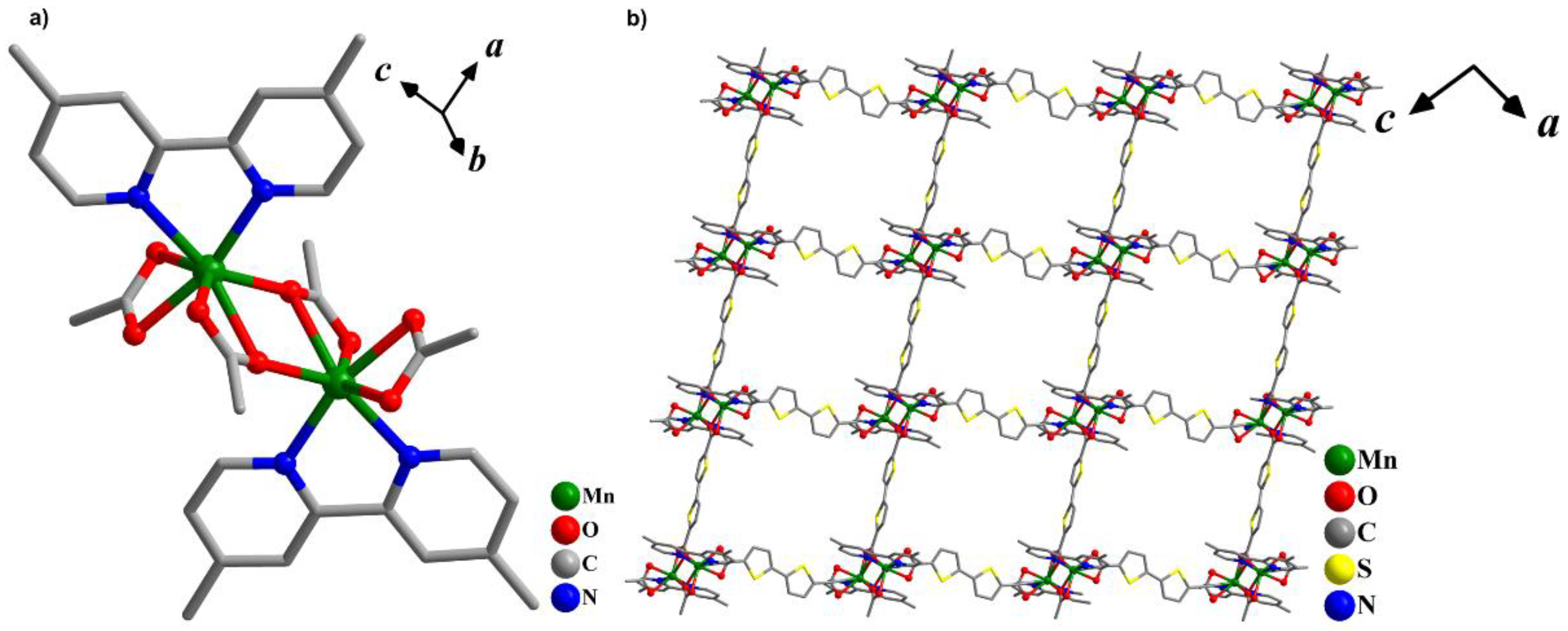
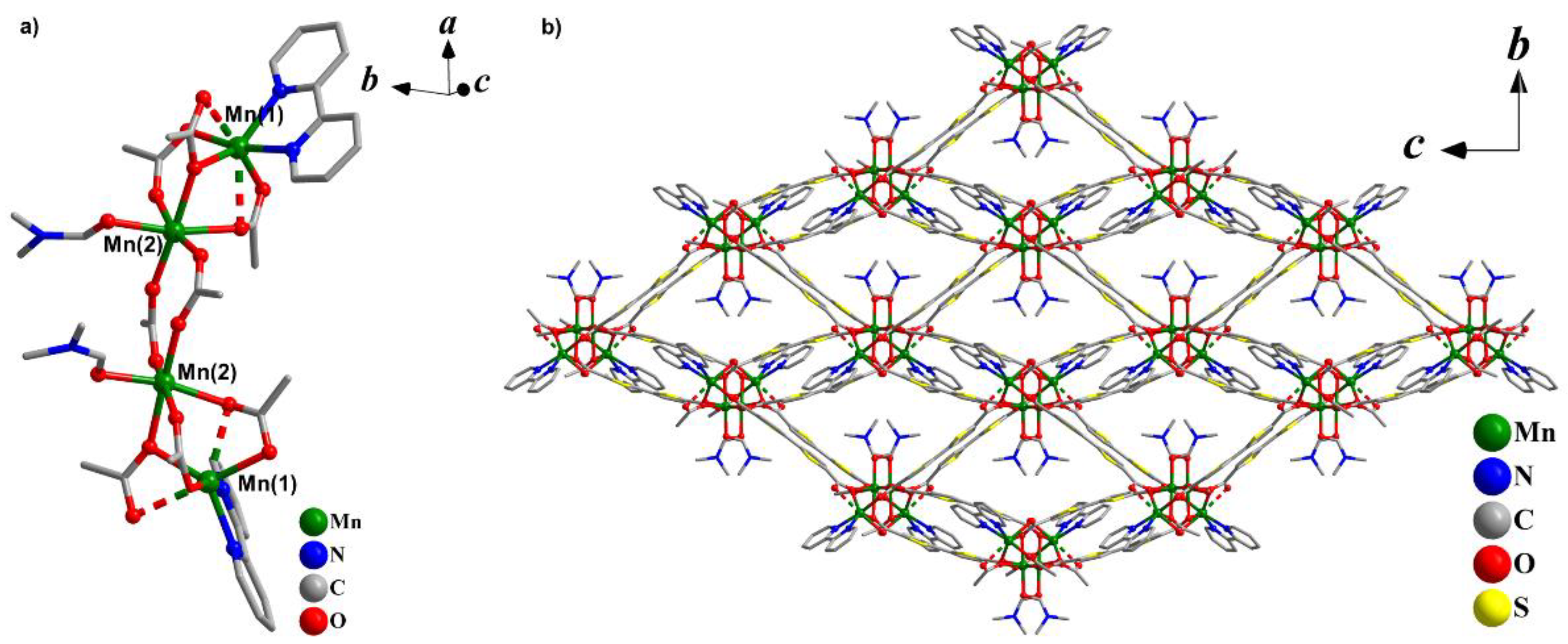
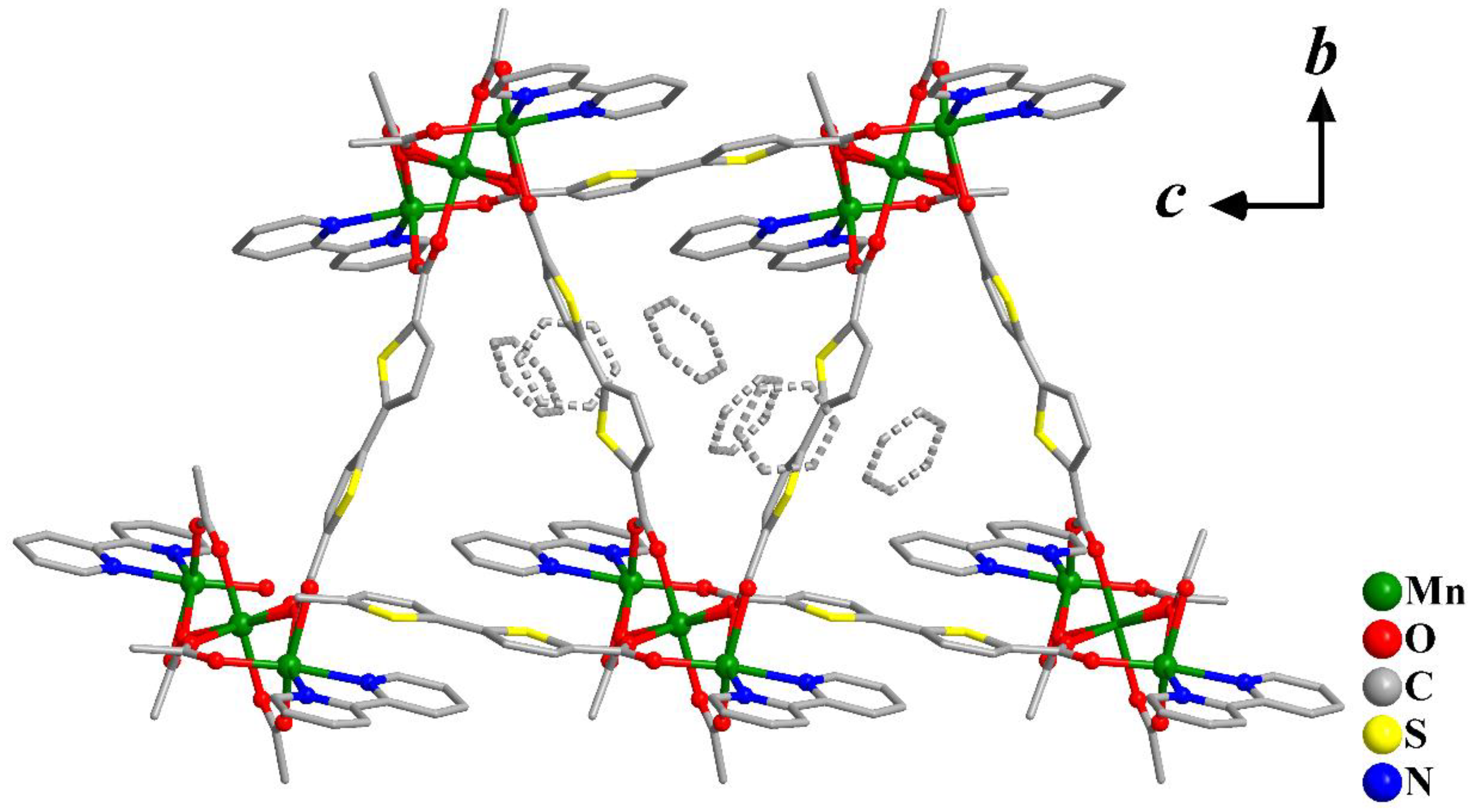
2.1. Synthesis and Structural Characterization

All compounds are formed under similar reaction conditions: manganese(II) perchlorate hexahydrate as a source of the metal ions, the equimolar ratio of the metal ions and H2btdc, DMF as a solvent, and high synthesis temperature (110–130 °C) (Scheme 1). The syntheses of Compounds 1–3, which have been obtained as pure phases, are reproducible with comparable yields (46–61%). Compounds 4 and 5 were obtained as impurities to Compounds 1 and 2, respectively, when trying to synthesize them under other conditions.
The colorless plate crystals of [Mn3(btdc)3(bpy)2]·4DMF (1) are formed by heating the Mn(ClO4)2·6H2O, H2btdc and bpy mixture in DMF at 120 °C for two days. According to the X-ray crystallography data, Compound 1 has a 3D framework structure. An asymmetric unit contains two Mn(II) cations. Mn(1) cation is in a distorted octahedral coordination environment consisted from two oxygen atoms of two monodentate carboxylate groups, two oxygen atoms of a chelating bidentate carboxylate group, and two nitrogen atoms from a chelating bpy molecule. One of the rings of the bpy molecule is disordered over two half-occupied positions. Mn(2) adopts an octahedral geometry with six oxygen atoms of six different carboxylate groups. Mn(2) and two Mn(1) cations are interconnected via bridging COO groups to form a trinuclear secondary building unit (SBU) {Mn3(μ-RCOO-κ1,κ1)4(μ-RCOO-κ1,κ2)2(bpy)2} (Figure 1a). The Mn(1)–O bond lengths are in the range 2.065(2)–2.272(2) Å, the Mn(1)–N distances are in the range 2.201(2)–2.294(5) Å, and the Mn(2)–O distances lay in the range 2.1313(17)–2.1969(16) Å. Each trinuclear unit in 1 is linked to six others via six bridging btdc2– anions, which results in a 3D framework (Figure 1b). The thiophene rings of all btdc2– anions are in trans positions, and the angles between them are ~157° and ~180°. Compound 1 possesses 1D quadrilateral channels of the size of 5×4 Å running along the c axis. The channels are occupied by disordered guest DMF molecules. The guest composition is defined from the single crystal X-ray diffraction (XRD). The guest accessible void volume of 1 estimated by a PLATON software [27] is 34%.
The colorless plate crystal of [Mn3(btdc)3(5,5′-dmbpy)2]·5DMF (2) is formed by heating the Mn(ClO4)2·6H2O, H2btdc and 5,5′-dmbpy mixture in DMF at 130 °C for two days. According to the X-ray crystallography data, Compound 2 contains similar trinuclear SBU (Figure 2a). However, the coordination environments of two terminal Mn(II) ions slightly differ in dihedral angles and bond lengths. An asymmetric unit of 2 contains three nonequivalent manganese ions. The Mn(1)–O bond lengths are in the range 2.1025(12)–2.3296(11) Å, the Mn(1)–N distances are 2.2233(14) Å and 2.2595(14) Å, the Mn(2)–O distances lay in the range 2.1423(11)–2.2057(11) Å, the Mn(3)–O bond lengths are in the range 2.0990(11)–2.3372(11) Å, and the Mn(3)–N distances are 2.2120(14) Å and 2.2635(14) Å. In contrast to Compound 1, the thiophene rings of the btdc2− anion are in the cis positions. At the moment, only one coordination polymer has been published where the btdc2− ligand adopts the cis position [28]. Each SBU in 2 is linked to four others via two double and two single btdc2− bridges, which results in a two-dimensional (2D) network with rectangular windows of 4×6 Å (Figure 2b). The layers are parallel to the ac plane and alternate along the b axis to form two-layered crystal packing. Partially disordered guest DMF molecules are located in the interlayer space and in the windows of the layers. The guest-accessible void volume of 2 estimated by a PLATON software [27] is 41%.
The trinuclear linear SBU are very common in the chemistry of MOFs resulting in 2D or 3D structures [29,30,31,32,33]. The terminal positions in the coordination environment of the terminal metal ions are commonly occupied by coordinated solvent molecules. In our case, we intentionally used an additional chelating N-donor ligand in order to move away from the [Mn3(btdc)3(dmf)4] compound, which is based on the trinuclear SBU with coordinated DMF molecules on both terminal manganese(II) ions formed typically in the system with Mn(II) and H2btdc in the DMF solvent [34].
The colorless plate crystal of [Mn(btdc)(4,4′-dmbpy)] (3) is obtained by heating the Mn(ClO4)2·6H2O, H2btdc and 4,4′-dmbpy mixture in DMF at 120 °C for two days. The much bulkier N-donor ligand results in the decrease of the nuclearity of SBU; Compound 3 is based on a binuclear {Mn2(RCOO)4} building block consisting of two equivalent manganese(II) ions. According to X-ray crystallography data, Mn(II) has distorted pentagonal bipyramidal coordination environment, which contains two oxygen atoms of one chelating carboxylate group, three oxygen atoms of two bridging carboxylate groups, and two nitrogen atoms of a chelating 4,4′-dmbpy molecule. Two Mn(II) cations are interconnected via two bridging COO groups to form binuclear unit {Mn2(μ-RCOO-κ1,κ2)2(4,4′-dmbpy)2(RCOO-κ2)2} (Figure 3a). The Mn–O bond lengths are in the range 2.1980(16)–2.3390(16) Å, and the Mn–N distances are 2.2331(19) Å and 2.2881(18) Å. The thiophene rings of all btdc2– anions are in trans positions, with the dihedral angle of 180° between their planes. Each binuclear building unit in 3 is connected by four single btdc2− bridges to four others acting as a four-connecting node. This leads to the formation of layers with rectangular windows of 5 × 11 Å. The layers are situated on (−2 4 −2) and (2 −4 2) crystallographic planes to form two-layered crystal packing. The layers are tightly packed without the free volume available for guest solvent molecules.
At a lower temperature (110 °C), the colorless block crystals of [Mn2(btdc)2(bpy)(dmf)]·0.5DMF (4) are isolated as a byproduct during the synthesis of Compound 1 with the reagent ratio [Mn2+]:[btdc2-]:[bpy] = 2:2:1. According to X-ray crystallography data, an asymmetric unit of 4 contains two Mn(II) cations. The coordination environment of Mn(1) ion contains 5 oxygen atoms of 3 carboxylic groups and 2 nitrogen atoms of a bpy molecule. Two of three COO groups are coordinated in a bidentate manner with a short Mn–O bond and a longer Mn···O contact. Coordination number of Mn(1) could be described as 5 + 2. The Mn(1)–O bond lengths are in the range 2.113(2)–2.239(3) Å, Mn(1)···O contacts are 2.506(3) and 2.663(3) Å, and Mn(1)–N bond lengths are 2.228(3) Å and 2.234(3) Å. Mn(2) are in octahedral coordination environment, which consists of 5 oxygen atoms of 5 carboxylate groups, and one oxygen atom of a coordinated DMF molecule disordered over four positions. Mn(2)–O distances are in the range 2.086(3)–2.227(3) Å. Mn(1) and Mn(2) cations are interconnected via 3 bridging COO-groups to form a binuclear unit. Two binuclear units are interconnected via two bridging carboxylic groups to form a tetranuclear building unit {Mn4(μ-RCOO-κ1,κ1)4(μ-RCOO-κ1,κ2)4(bpy)2(dmf)2} (Figure 4a). The thiophene rings of a half btdc2− anions are in the cis positions, whereas those of another half btdc2− anions are in the trans positions. Each tetranuclear SBU is connected by four double btdc2− bridges to four neighboring ones, which leads to the formation of wide layers (Figure 4b) parallel to the bc plane. The layers alternate along the a axis to form the one-layered crystal packing. Compound 4 has triangular channels of the size of 5 × 8 Å running along the a axis. The channels are occupied by disordered coordinated and guest DMF molecules. The guest-accessible void volume of 4 estimated using PLATON software [27] is only 7%.
At a slightly lower temperature than for the synthesis of pure phase 2 (120 °C) the colorless block crystals of [Mn2(btdc)2(5,5′-dmbpy)(dmf)]·DMF (5) are isolated as a byproduct in the course of the synthesis of Compound 2 with the reagent ratio [Mn2+]:[btdc2−]:[5,5′-dmbpy] = 2:2:1. According to the X-ray crystallography data, Compound 5 is also based on a tetranuclear SBU, but its structure is different from that in Compound 4. The asymmetric unit of 5 contains two Mn(II) cations. The Mn(1) cations are in a distorted octahedral coordination environment composed of four oxygen atoms of three carboxylic groups and two nitrogen atoms of a chelating 4,4′-dmbpy molecule. The octahedral coordination environment of Mn(2) consists of five oxygen atoms of five carboxylic groups and an oxygen atom of a coordinated DMF molecule. The Mn(1)–O bond lengths are in the range 2.0861(17)–2.3848(18) Å, the Mn(1)–N distances are 2.221(2) Å and 2.246(2) Å, and the Mn(2)–O distances lay in the range 2.1242(16)–2.2310(17) Å. By the use of the bridging carboxylate groups, the manganese atoms are interconnected in sequence Mn(1)–Mn(2)–Mn(2)–Mn(1) in the form of a linear tetranuclear building unit {Mn4(μ-RCOO-κ1,κ1)6(μ-RCOO-κ1,κ2)2(4,4′-dmbpy)2(dmf)2} (Figure 5a). The center of the tetranuclear unit is situated in the inversion center. The thiophene rings of all btdc2− anions are in the trans-positions. Each tetranuclear SBU is connected by four double btdc2− bridges to four neighboring ones resulting in the formation of wide layers with quadrilateral windows of 5 × 3 Å (Figure 5b). The layers alternate along [1 0 −1] direction to form two-layered crystal packing. There are channels running along the a axis, which are filled by the coordinated and guest DMF molecules. The guest-accessible void volume of 5 estimated using PLATON software [27] is 25%.
The majority of the synthetic conditions ([Mn2+]/[btdc2-] ratio, concentrations, temperature range, solvent, reaction time) for 1–5 are either identical or very similar, while [Mn2+]/[bpy] ratio as well as positions of the methyl substituents in the bpy molecule are the only variable parameters. Such experimental design reveals a number of interesting relationships between the reaction conditions and the structure of SBUs as well as the topology of the MOF products. Decreasing the [Mn2+]/[bpy] molar ratio in the reaction mixture from 2:1 in the synthesis of 4 and 5 to 1:2 in the synthesis of 1 and 2 consequently lowers the [Mn2+]/[bpy] composition in the chemical formulae of the products since [Mn2+]/[bpy] = 4:2 in 4 and 5 and 3:2 in 1 and 2. Additionally, the structure of the carboxylate SBUs in those compounds is changed accordingly. The effect of the chemical functionalization of the bpy core could be seen via comparison of 1 vs. 2 and 4 vs. 5. In those cases, the methyl substituents in bpy ligands do not seem to influence the chemical composition or local features of the crystal structure (i.e., building blocks, SBU). To a certain extent, such a result could be expected since the structure of the SBU is mainly determined by a coordination arrangement of the ligands around the metal cations; however, the methyl groups in 5,5′-dmbpy neither have an impact on the geometry of the bpy molecule nor impose a steric hindrance for the bpy coordination. On the other hand, the methyl pendants attached to the bpy ligands decorate a periphery of the carboxylate SBUs and may develop some limitations to the packing of those large units as well as the topology of the coordination network. As a result, the same trinuclear SBU {Mn3(RCOO)6(bpy)2} in Compound 1 acts as a six-connecting node to form a 3D framework, while in 2, its connectivity is reduced to 4, forming a 2D layered net. Additionally, the relative porosity of 1 (34%) and 4 (7%) containing bare bpy ligands turns out to be lower than that of 2 (41%) and 5 (25%) containing 5,5′-dmbpy, respectively. We can speculate that the pendant methyl groups on the surface of the SBUs create certain sterical constraints, which hinder a denser packing of these units and eventually lead to an increase in pore volumes of the final MOF products. Quite strikingly, Compound 3, containing 4,4′-dmbpy ligand, features completely different chemical formula and structure of the SBU. The electron-donor group, such as methyl, in para-position is known to increase the nucleophility of the N donor atom of the pyridine ring and, eventually, the strength of the coordination interactions. This seems to be a deciding factor as the ratio [bpy]/[Mn2+] = 1:1 in 3 is the highest among the title series 1–5, which clearly suggests stronger coordination ability of the 4,4′-dmbpy ligand compared to that of 5,5′-dmbpy or nonsubstituted bpy molecules.

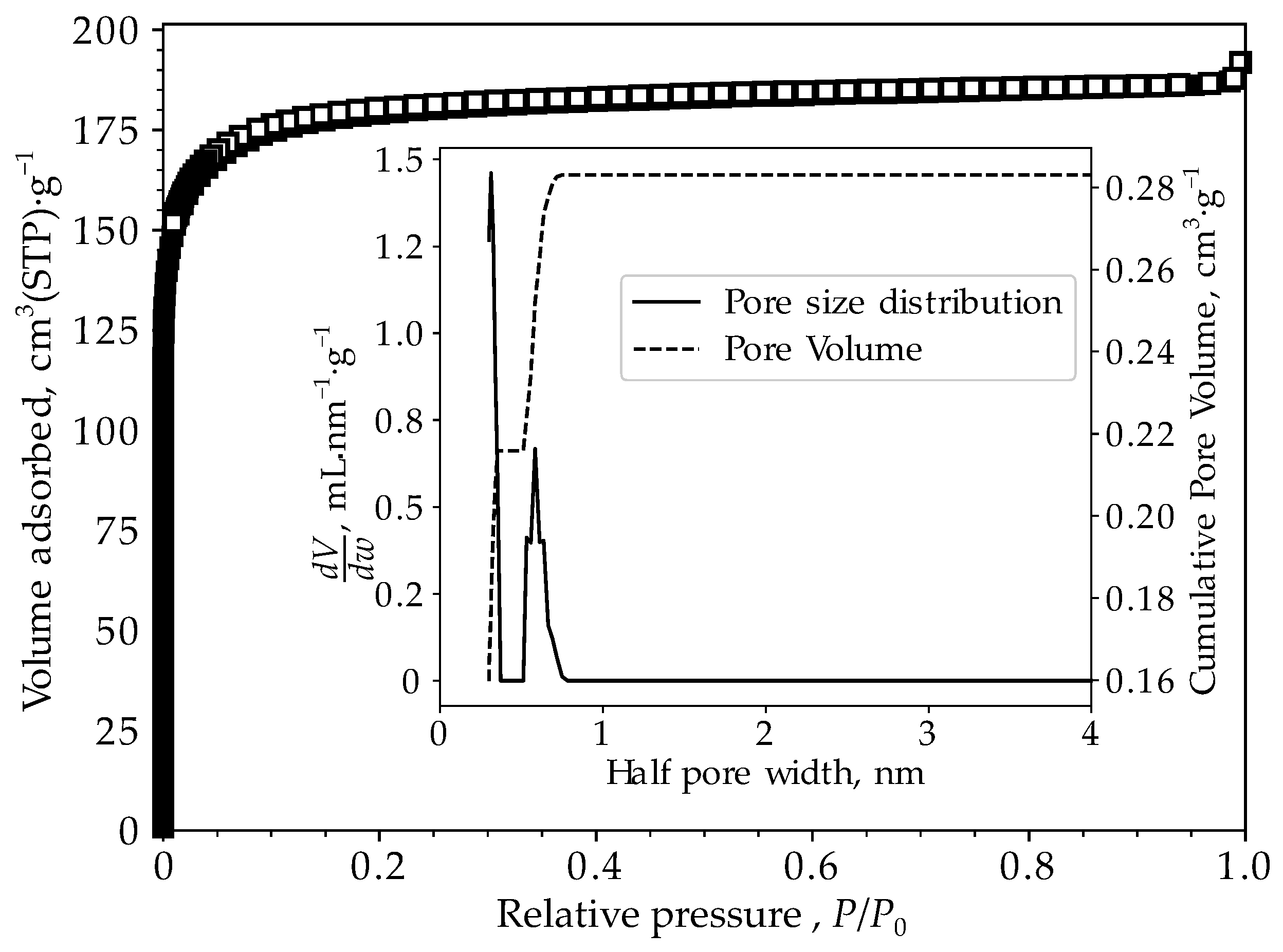
2.2. IR spectroscopy, Thermal and Textural Properties

Compounds 1–3 were obtained as pure phases, as confirmed using the powder X-ray diffraction method (Figures S1–S3), chemical analyses, and optical images (Figure S4); hence, their functional properties were further characterized.
The IR spectra of 1–3 contain bands at 770 cm−1 (1), 764 and 805 cm−1 (2), and 773 cm−1 (3), which can be related to the nonplanar deformation vibrations of C–H bonds in the thiophene fragment (Figures S5–S7). It is surprising that the spectrum of Compound 2 contains two bands corresponding to this vibration. This may be due to the cis position of the thiophene rings of the btdc2– anion in this compound. The characteristic bands of the carboxylate groups at 1377 and 1436 cm−1 (1), at 1389 and 1439 cm−1 (2), and at 1378 and 1426 cm−1 (3) are related to the symmetric stretching vibrations. The strong bands of the stretching asymmetric vibrations of the C=O bond in the carboxylate groups are observed at 1515 and 1594 cm–1 (1), at 1519 and 1564 cm–1 (2), and at 1522 and 1595 cm–1 (3). The bands at 1665 cm−1 (1) and 1612 cm−1 (2) can be referred to C=O bonds in DMF molecules, whereas the low-intensity bands in the range from 2850 cm−1 to 3091 cm−1 correspond to the valence vibrations of the C–H bonds in the CH3 fragment of the DMF molecule (1), the DMF or 5,5′-dmbpy molecules (2), and the 4,4′-dmbpy molecule (3). The broad bands at 3352 cm−1 (1), 3415 cm−1 (2), 3432 cm−1 (3) correspond to the airborne water on the surface of the crystals.
The thermogravimetric (TG) analysis of Compound 1 shows a continuous loss of mass in a wide temperature range (up to ~220 °C) of ca. 19%, which is associated with removal of the guest solvent molecules (calculated: 19% for 4 DMF) followed by a broad flat region up to ca. 310 °C, where the MOF starts to degrade quickly (Figure S8). Compound 2 demonstrates similar behavior: mass loss of ~17% up to ~175 °C associated with the solvent removal (calculated: 18% for 4 DMF) and degradation of the MOF starting at ~325 °C (Figure S9). For Compound 3, since—according to the XRD and chemical analyses—it does not have any guest solvent molecules, only one step on the TG curve is observed to be related to the degradation of the framework at ~370 °C and higher (Figure S10).
The permanent porosity of 1, which has a 3D structure, was confirmed via the measurements of a N2 gas adsorption isotherm at 77 K. The as-synthesized crystals of 1 were activated by the solvent exchange (CH2Cl2) followed by a dynamic vacuum treatment at 180 °C for 6 h directly in a gas adsorption analyzer. The nitrogen adsorption-desorption isotherm plot at 77 K is represented in Figure 6 and belongs to the Ia isotherm type according to the official IUPAC classification [35], which is typical for microporous compounds with narrow slit pores. The measured pore volume of 0.288 cm3·g–1 (at p/p0 = 0.95, Table S3) matches the expected value (0.308 mL·g–1) estimated from the PLATON pore volume calculations, which confirms the structural integrity of 1 as well as the completeness of the framework activation. The PXRD patterns of 1 after activation and adsorption in comparison to the as-synthesized sample (Figure S16) also confirm its phase stability upon activation and adsorption. The calculated surface areas are 806 m2·g–1 (Langmuir model), 707 m2·g–1 (BET model), and 918 m2·g–1 (DFT model). The pore size distribution plot of 1, calculated using the DFT model (Figure 6, inset), shows the presence of narrow pores with diameters less than ~1 nm, which is in a good agreement with the XRD structural data.

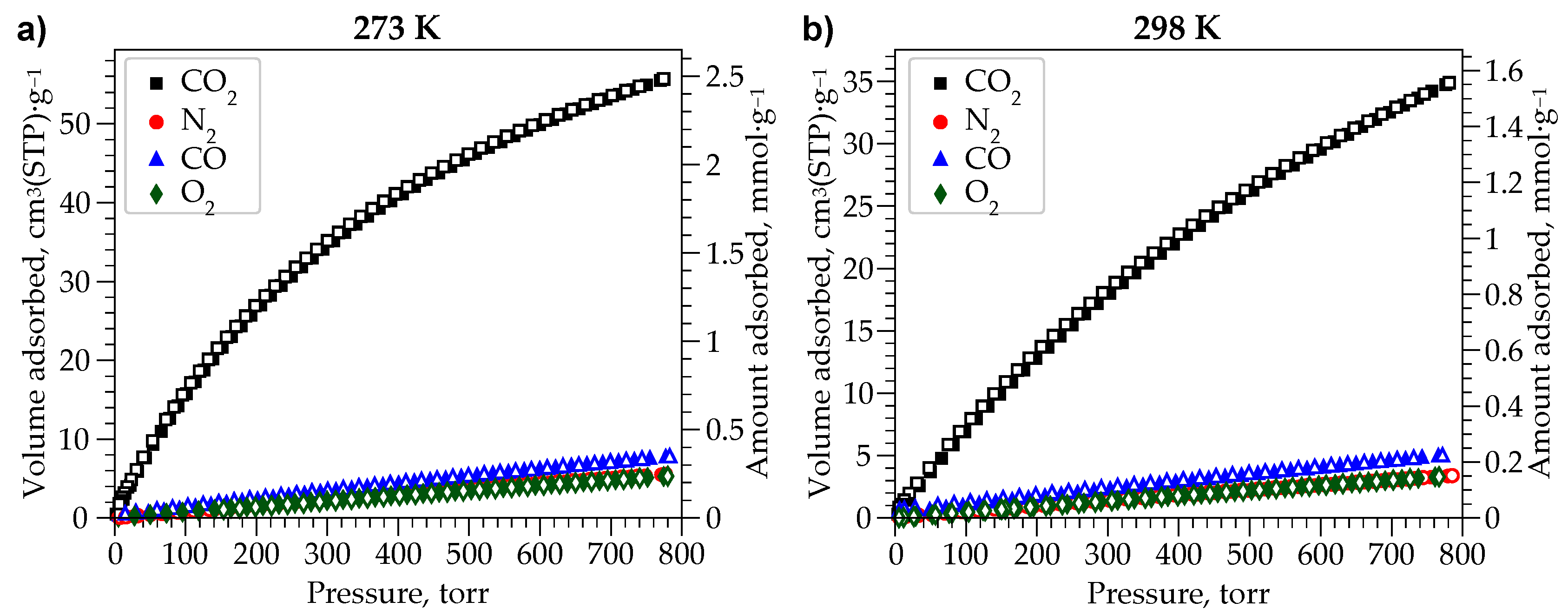
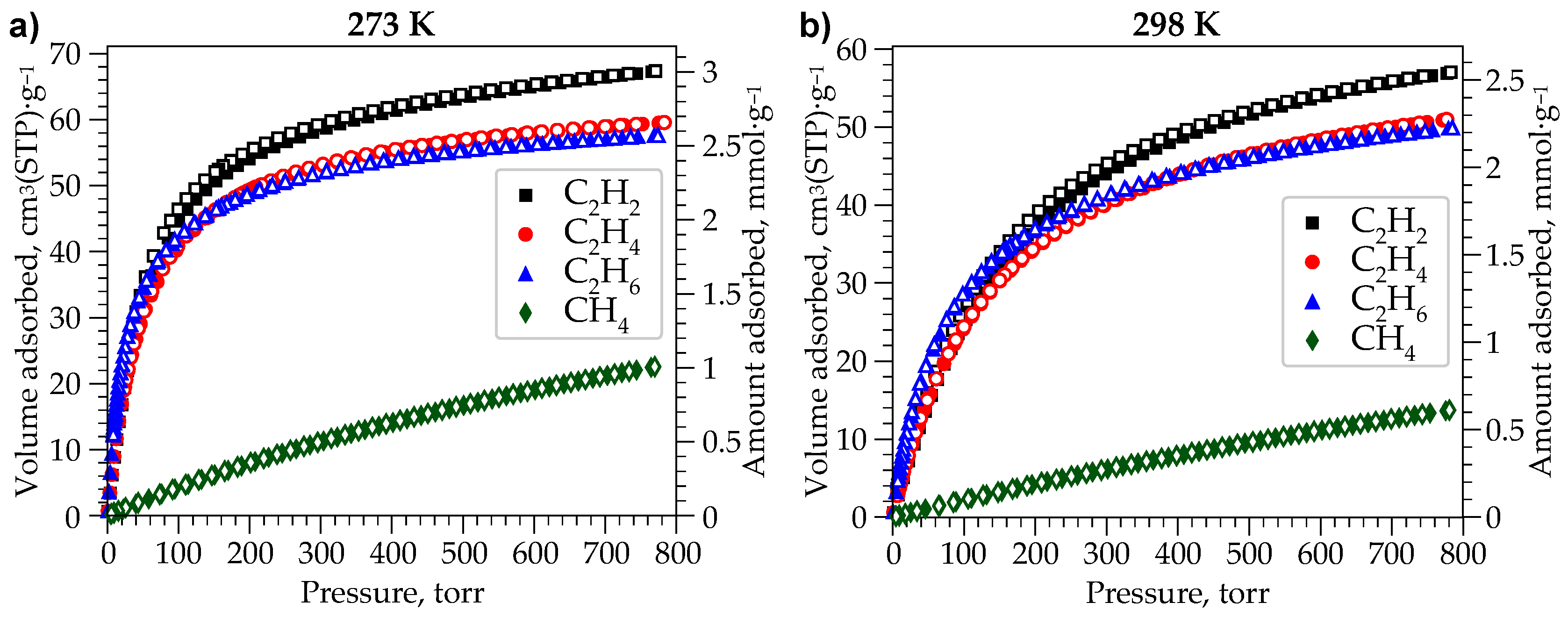
2.3. Gas Adsorption Studies

The surface of the porous channels in 1 is lined by sulfur heteroatoms of the btdc2– ligands. Such functional groups are known to enhance the adsorption uptake and selectivity of the corresponding MOFs towards small gas molecules, particularly CO2 [36,37]. The carbon dioxide is the most infamous anthropogenic pollutant causing global climate changes. Its acidic nature causes a chemical corrosion of valuable equipment unless the CO2 content in the gas mixture is reduced to a safe level before further processing. CO2 sequestration using adsorption technologies is one of the most efficient solutions for the purification of many industrially relevant gas mixtures, such as CO2/N2 (the main flue gas components), CO2/CH4 (the main components of biogas), and CO2/CO (production of steel). In this regard, a thorough investigation of the adsorption properties of 1 towards CO2 as well as other gases was performed within the current work. The adsorption–desorption isotherm data for “inorganic” (CO2, CO, N2, O2) and “organic” (CH4, C2H2, C2H4 and C2H6) gases at T = 273 K and 298 K were systematically measured. The corresponding isotherms are shown in Figure 7 and Figure 8; the gas uptakes in different units are summarized in Table 1.
The measured CO2, CH4, and C2 adsorption uptakes are comparable to those reported for other MOFs with modest porosity and specific surface area [38,39,40]. The calculated isosteric heats of adsorption at zero coverage Qst(0) for “inert” inorganic gases are typically low (12.1 kJ·mol−1 for CO, 13.6 kJ·mol−1 for O2, and 15.0 kJ·mol−1 for N2), whereas the adsorption heat for a polar CO2 molecule is somewhat higher, 25.3 kJ·mol–1 (Table S6, Figure S12). The adsorption heat for light hydrocarbons steadily increases from methane (19.4 kJ·mol–1) through acetylene (27.9 kJ·mol–1) and ethylene (28.2 kJ·mol–1) to ethane (30.8 kJ·mol–1) consistently with the increase in the number of atoms in the molecule capable of the interactions with the microporous surface. The isosteric heats of the gas adsorption for 1 are generally low confirming weak intermolecular interactions during the physical adsorption. From the practical point of view, such low adsorption heat values are considered an advantage since they reduce the energy costs in a desorption cycle.
The adsorption selectivity factors for the separation of binary gas mixtures were evaluated using three different methods: (i) as a ratio of the amount adsorbed; (ii) as a ratio of the corresponding Henry constants; and (iii) using ideal adsorbed solution theory (IAST) [41] calculations, which allowed an estimation of the selectivity factors for the different gas mixture compositions and total pressures. The results are summarized in Table 2 and in Figure S14. Among the “inorganic gases”, carbon dioxide adsorption is rather substantial (54.9 cm3·g−1 at 273 K and 34.0 cm3·g−1 at 298 K), suggesting a significant CO2/N2 adsorption selectivity, which was confirmed experimentally by the corresponding IAST adsorption selectivity factors (31.0 at 273 K and 19.1 at 298 K for the equimolar gas mixture at 1 bar). The calculated adsorption selectivity values are quite remarkable for a porous compound with no specific CO2 adsorption sites, such as coordinatively unsaturated metal sites (CUSs) or amine groups. Moreover, a low CO2 isosteric adsorption heat Qst(0) = 25.3 kJ·mol–1 minimizes parasite energy loss during the regeneration of the porous material in a practical gas separation process. Other than CO2/N2, promising IAST adsorption selectivity values at 298 K were also obtained for CO2/CO (17.0) and CO2/CH4 (3.6), which are comparable to other high-performing porous MOFs [42,43,44].
The adsorption uptakes for C2-hydrocarbons are very similar, suggesting no adsorption selectivity in their binary mixtures. At the same time, remarkable C2H6/CH4, C2H4/CH4, and C2H2/CH4 adsorption selectivity factors were calculated: 33.4, 24.8, and 29.3 at 273 K and 24.6, 17.7, and 19.1 at 298 K, respectively (1 bar, equimolar gas mixtures). By the combination C2H6/CH4 adsorption selectivity and the C2H6 adsorption capacity Compound 1 can be included in the top ten MOFs [45,46,47,48,49,50,51,52], and C2H4/CH4 and C2H2/CH4 adsorption selectivity factors are also high enough to consider 1 as a promising material for the adsorption separation of natural, shale and associated petroleum gas into individual components valuable for chemical industry. Moreover, the values of C2H6/CH4 adsorption selectivity become even higher as the content of C2H6 in the mixture shifts closer to the actual ethane composition in the natural gas, typically 5–10% (Table 2). Great CO2/N2, CO2/CO, and C2H6/CH4 adsorption selectivity potential and one of the lowest adsorption heats place the porous material 1 among the most promising materials for the practical sequestration of CO2 as well as efficient separation of mixtures of light hydrocarbons, which are highly demanding tasks for many environmental, industrial, and safety applications.

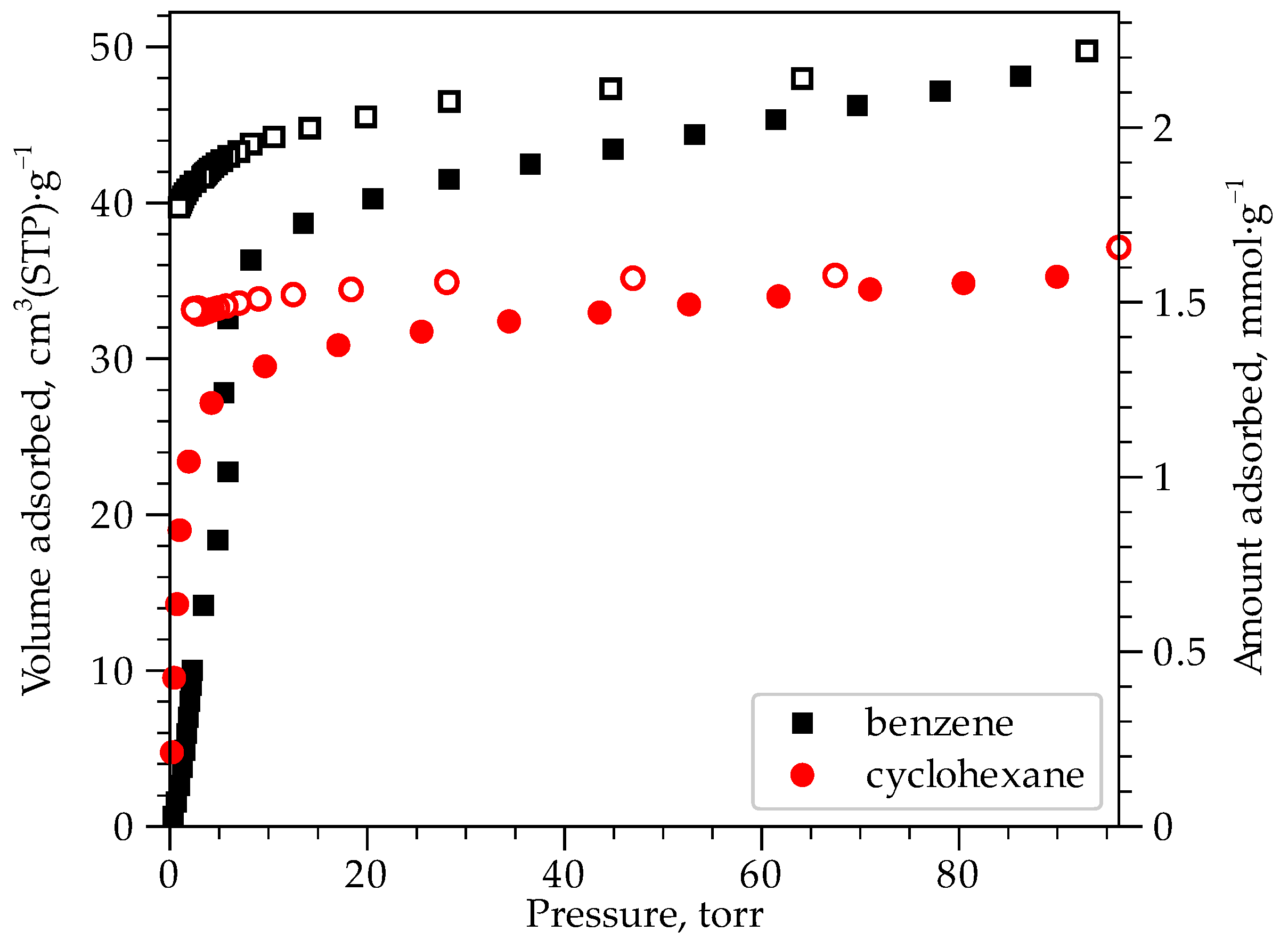
2.4. Vapor Phase Adsorption of Benzene and Cyclohexane

We have also studied adsorption of benzene (C6H6) and cyclohexane (C6H12) vapors at T = 298 K on the activated 1; the corresponding adsorption isotherms are presented in Figure 9. The adsorption uptake at saturation is 50.2 cm3·g–1 (2.24 mmol·g–1, or 14.9 wt.%) for C6H6 and 36.8 cm3·g–1 (1.64 mmol·g–1, or 12.1 wt.%) for C6H12. It is interesting that despite the fact that at high vapor pressures there is an obvious preference for benzene adsorption compared to cyclohexane (VB/VCH = 1.36 at the saturation pressure), at low pressures cyclohexane adsorbs on 1 better than benzene, which is confirmed by the ratio of the Henry constants (KB/KCH = 0.16, or KCH/KB = 6.33, Figure S15), and this is a very rare phenomenon observed previously only in few works [53,54,55].
Preferable adsorption of benzene at high vapor pressures can be explained on the basis of the single crystal X-ray diffraction analysis of a 1 crystal immersed in pure benzene for several days (100% of pore saturation). According to X-ray crystallography data, benzene molecules are disordered over three positions with s.o.f. 0.365(2)/0.289(2)/0.346(2) (Figure 10). The total amount is two benzene molecules per formula unit of Framework 1. A thorough analysis of the structure shows the existence of the relatively short host–guest interaction: C-H(benzene)···C(bpy) = 3.170–3.810 Å for the interactions of the first benzene molecule and a pyridyl ring, C-H(benzene)···C(btdc2−) = 2.996–3.275 Å for the interactions of the first benzene molecule and a thiophene ring of one btdc2− ligand, and C-H(benzene)···C(btdc2−) = 3.197–3.910 Å for the interactions of the second benzene molecule and a thiophene ring of another btdc2− ligand. Therefore, numerous van der Waals interactions are responsible for a preferable adsorption of benzene over cyclohexane on the activated 1 at 100% pore saturation.

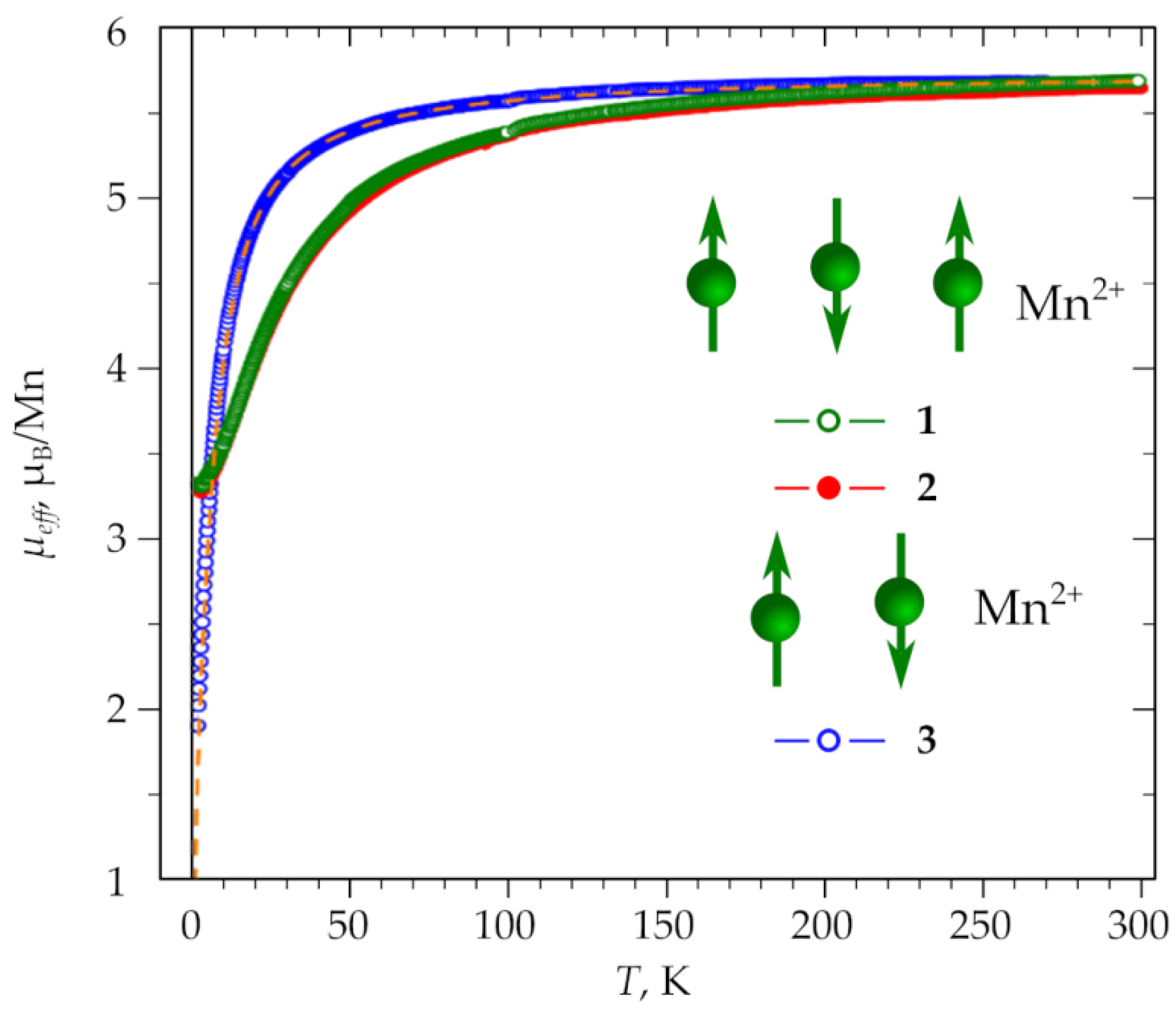
2.5. Magnetic Properties of Compounds 1–3

Temperature dependences of the molar magnetic susceptibility χ were measured for 1–3 in the range 1.77–330 K at magnetic fields H up to 10 kOe under zero-field-cooled and field-cooled conditions (Figures S17a–S19a). All the compounds studied kept a paramagnetic state down to the lowest accessible temperature without any anomaly that could be attributed to long-range magnetic ordering or any sign of magnetothermal irreversibility associated with spin freezing. Data analysis has shown, however, that the paramagnetic part of the magnetic susceptibility, χp(T), obtained by subtracting the diamagnetic contribution does not follow the conventional Curie–Weiss dependence χp(T) = Na·μeff2/(3·kB·(T − θ)) (Figures S17b–S19b). Instead, the χp(T) curves demonstrate almost perfect canonical behavior of trinuclear (1 and 2) and binuclear (3) compounds with an antiferromagnetic (AF) coupling of the magnetic moments within magnetic clusters [56] and negligible interaction between them. This is not surprising given that the crystal structures of Compounds 1, 2, and 3 are indeed built of trinuclear and binuclear SBUs, respectively. As can be seen in Figure 11 (see also Figures S17b–S19b), the effective magnetic moments, μeff, calculated for one manganese ion gradually decrease upon cooling, tending to saturate at a constant value of 3.25–3.31 μB in the case of Compounds 1 and 2—built of trinuclear SBUs—or tending to zero in the case of binuclear Compound 3. In the former case, the low-temperature values of μeff differ from the high-temperature ones of 5.65–5.69 μB by eactly √3 times, implying that the magnetic response of a trinuclear SBU is reduced at low temperatures by 3 times (proportionally to μeff2), that is, to a response of a single ion. This is quite expected given that the AF interaction in a linear trimer should fix the relative orientation of magnetic moments in the ground state so that the resulting moment is equal to that of a single ion (inset in Figure 11). In turn, the binuclear Compound 3 demonstrates the effective magnetic moment tending to zero at low temperatures owing to the singlet ground state in dimers with AF exchange interaction between ions (inset in Figure 11).
In the high-temperature region, the effective magnetic moments of all Compounds 1–3 reach similar values of 5.65–5.69 μB per manganese ion (Figure 11), which are very close to the μeff ≈ 5.92 μB expected for isolated Mn2+ ions (S = 5/2, L = 0), especially if the AF interaction within dimers and trimers still slightly affecting the magnetic susceptibility at high T is taken into account. Given that Mn2+ ions have no orbital moments (L = 0), the effects associated with the contribution of orbital moments and with zero-field splitting that usually affect the magnetic susceptibility behavior are expected to be rather weak in the compounds studied. This justifies the above description where the temperature dependences of μeff were attributed solely to the AF interactions within trinuclear (1 and 2) and binuclear (3) SBUs.
An additional confirmation for the description based on AF dimers and trimers comes from the magnetic field dependences of the magnetization, M(H), measured for 1–3 at T = 1.77 K (Figures S17c–S19c). The M(H) curves for 1 and 2 can be well fitted—both the shape and magnitude—by a conventional expression based on the Brillouin function with S = 5/2, as expected for the ground state of AF Mn2+ trimers. In the case of 3, the M(H) dependence is close to linear, and the magnetization stays below 1 μB per Mn2+ dimer at H = 10 kOe, in agreement with the singlet ground state of dimers.
To evaluate the magnitude of the AF exchange interaction in 3, we have fitted the magnetic susceptibility data with the model of Mn2+-Mn2+ dimers [56]; a rather good fit has been obtained for J/kB = 2.0 K (orange dashed line in Figure 11). Though this value appears small, this intradimer interaction is sufficient to govern the magnetic behavior of 3 and to cause its magnetic susceptibility to saturate (or pass through a maximum) at T < 2 K (Figure S19a). Fitting of the trimer’s magnetic behavior is a more difficult and less reliable procedure going beyond the scope of this work. Here, we simply point out that the AF exchange interactions in Compounds 1 and 2 have the same strength, which is quite expected due to the similar structure of both compounds based on trinuclear building blocks, and that this interaction is noticeably stronger than in the binuclear Compound 3.
In the low-temperature region where Mn2+ trimers acquire their ground state resembling that of a single ion, one can use a conventional Curie–Weiss fitting to evaluate the strength of the interaction between the trimers. Such analysis for 1 and 2 has shown that the temperature dependence of the reversed magnetic susceptibility at low T goes exactly to the origin (Figures S17b and S18b), and the Weiss constant θ equals zero within the experimental accuracy (|θ| < 0.1 K), pointing to the negligible interaction between trinuclear SBUs located rather far from each other in the crystal structure.

3. Conclusions

Five new metal–organic frameworks based on Mn(II), 2,2′-bithiophen-5,5′-dicarboxylate (btdc2–) and chelating N-donor ligands ([Mn3(btdc)3(bpy)2]·4DMF (1), [Mn3(btdc)3(5,5′-dmbpy)2]·5DMF (2), [Mn(btdc)(4,4′-dmbpy)] (3), [Mn2(btdc)2(bpy)(dmf)]·0.5DMF (4), [Mn2(btdc)2(4,4′dmbpy)(dmf)]·DMF (5) (bpy = 2,2′-bipyridyl, 5,5′-dmbpy = 5,5′-dimethyl-2,2′-bipyridyl, 4,4′-dmbpy = 4,4′-dimethyl-2,2′-bipyridyl, dmf, DMF = N,N-dimethylformamide) were synthesized and characterized using a number of physical–chemical methods, such as powder X-ray diffraction, TG analysis, and IR spectroscopy. The influence of the bulkiness of the chelating N-donor ligand on the dimensionality and structure of the coordination polymer has been analyzed, and the decrease in the framework dimensionality as well as the secondary building unit’s nuclearity and connectivity has been observed. For the 3D coordination polymer 1, the textural and gas adsorption properties have been studied, revealing noticeable ideal adsorbed solution theory (IAST) CO2/N2 and CO2/CO selectivity factors as well as a significant adsorption selectivity for binary C2-C1 hydrocarbons mixtures, which makes it possible to separate natural, shale, and associated petroleum gas into valuable individual components. The ability of Compound 1 to separate benzene and cyclohexane in a vapor phase has been also analyzed. The preferable adsorption of benzene by 1 has been explained by multiple van der Waals interactions between guest benzene molecules and the metal–organic host, as it was revealed by the XRD analysis of 1 immersed in pure benzene for several days (1≅2C6H6). It is interesting that at low vapor pressures, an inversed behavior of 1 with preferable adsorption of cyclohexane over benzene was observed. This is a very rare phenomenon. Moreover, magnetic properties (the temperature-dependent molar magnetic susceptibility, χp(T), and effective magnetic moments, μeff(T) as well as the field-dependent magnetization, M(H)) have been studied for Compounds 1–3, revealing paramagnetic behavior consistent with their crystal structure.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28052139/s1, Table S1: Crystal data and structure refinement for 1–3; Table S2: Crystal data and structure refinement for 4, 5, and 1≅2C6H6; Figure S1: PXRD patterns of 1 (experimental—red, calculated from the single crystal X-ray diffraction data—black); Figure S2: PXRD patterns of 2 (experimental—red, calculated from the single crystal X-ray diffraction data—black); Figure S3: PXRD patterns of 3 (experimental—red, calculated from the single crystal X-ray diffraction data—black); Figure S4. Optical images of the crystals: (a) pure phase 1; (b) pure phase 2; (c) pure phase 3; (d) mixture of Compounds 1 and 4; (e) mixture of Compounds 2 and 5; Figure S5: IR spectrum of 1; Figure S6: IR spectrum of 2; Figure S7: IR spectrum of 3; Figure S8: TG curve of 1; Figure S9: TG curve of 2; Figure S10: TG curve of 3; Table S3: The textural parameters of the porous structure of 1; Table S4: Virial coefficients Ai and Bj for gas adsorption isotherms at 273 K and 298 K on 1; Figure S11: Fits of isotherms by virial equation; Table S5: Henry constants for gas adsorption on 1 in mmol·g−1·bar−1 at 273 K and 298 K obtained by virial approach; Table S6: Zero coverage heats of adsorption in kJ/mol; Figure S12: Isosteric heats of gas adsorption on 1 calculated by a virial approach; Table S7: Fitted parameters for the adsorption isotherms on 1 at 273 K and 298 K and the corresponding Henry constants for comparison obtained by fitting and calculations performed using a virial approach, in brackets the deviations from a virial Henry constant are given; Figure S13: Fits of isotherms by an appropriate model; Figure S14: The prediction of an adsorption equilibrium by IAST (solid lines) and dependence of selectivity factors on a gas phase composition (dashed lines) as well as their pressure dependence for binary gas mixtures: (a) CO2/N2; (b) CO2/CO; (c) CO2/CH4; (d) C2H6/CH4; (e) C2H4/CH4; (f) C2H2/CH4; Figure S15: Fit of the initial (linear) parts of vapor adsorption isotherms by the Henry law, [k] = mmol·g–1·torr–1; Figure S16: PXRD patterns of 1: as-synthesized (red), activated (blue), and after adsorption (purple); Figure S17: (a) Temperature dependences of the magnetic susceptibility χ of 1 measured at magnetic fields H = 1; 10 kOe. (b) Temperature dependences of the effective magnetic moment μeff and the reversed magnetic susceptibility 1/χp for 1. (c) Magnetic field dependence of the magnetization M measured for 1 at T = 1.77 K; Figure S18: (a) Temperature dependences of the magnetic susceptibility χ of 2 measured at magnetic fields H = 1; 10 kOe. (b) Temperature dependences of the effective magnetic moment μeff and the reversed magnetic susceptibility 1/χp for 2. (c) Magnetic field dependence of the magnetization M measured for 2 at T = 1.77 K; Figure S19: (a) Temperature dependences of the magnetic susceptibility χ of 3 measured at magnetic fields H = 1; 10 kOe. (b) Temperature dependences of the effective magnetic moment μeff and the reversed magnetic susceptibility 1/χp for 3. (c) Magnetic field dependence of the magnetization M measured for 3 at T = 1.77 K. References [57,58,59,60,61,62,63] are cited in the Supplementary Materials.

Author Contributions

V.A.D., A.A.K., D.G.S., A.N.L. and K.A.K. performed the experimental work. V.A.D. and A.A.L. prepared the original manuscript. D.N.D. and V.P.F. reviewed and edited the manuscript. V.P.F. carried out the project administration and funding acquisition. All authors have read and agreed to the published version of the manuscript.

Funding

The authors are grateful to the Ministry of Science and Higher Education of the Russian Federation for financial support (Agreement No. 075-15-2022-263), providing an access to the large-scale research facility “EXAFS spectroscopy beamline”. Analytical services were provided by project No 121031700321-3.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in Supplementary Materials. CCDC 2227366–2227371 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge from The Cambridge Crystallographic Data Center at https://www.ccdc.cam.ac.uk/structures/ (accessed on 25 January 2023).

Acknowledgments

The authors thank P. V. Dorovatovskii and V. A. Lazarenko (National Research Center “Kurchatov Institute”, Moscow, Russia) for their assistance during the synchrotron XRD experiment.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Leong, W.L.; Vittal, J.J. One-dimensional coordination polymers: Complexity and diversity in structures, properties, and applications. Chem. Rev. 2011, 111, 688–764. [Google Scholar] [CrossRef] [PubMed]
  2. Yaghi, O.M.; O’Keeffe, M.; Ockwig, N.W.; Chae, H.K.; Eddaoudi, M.; Kim, J. Reticular synthesis and the design of new materials. Nature 2003, 423, 705–714. [Google Scholar] [CrossRef] [PubMed]
  3. Stock, N.; Biswas, S. Synthesis of metal-organic frameworks (MOFs): Routes to various MOF topologies, morphologies, and composites. Chem. Rev. 2012, 112, 933–969. [Google Scholar] [CrossRef] [PubMed]
  4. Ferey, G. Hybrid porous solids: Past, present, future. Chem. Soc. Rev. 2008, 37, 191–214. [Google Scholar] [CrossRef]
  5. Agafonov, M.A.; Alexandrov, E.V.; Artyukhova, N.A.; Bekmukhamedov, G.E.; Blatov, V.A.; Butova, V.V.; Gayfulin, Y.M.; Garibyan, A.A.; Gafurov, Z.N.; Gorbunova, Y.G.; et al. Metal-organic frameworks in Russia: From the synthesis and structure to functional properties and materials. J. Struct. Chem. 2022, 63, 671–843. [Google Scholar] [CrossRef]
  6. Guillerm, V.; Kim, D.; Eubank, J.F.; Luebke, R.; Liu, X.; Adil, K.; Lah, M.S.; Eddaoudi, M. A supermolecular building approach for the design and construction of metal–organic frameworks. Chem. Soc. Rev. 2014, 43, 6141–6172. [Google Scholar] [CrossRef] [Green Version]
  7. Li, Q.; Qian, J. Multifarious zinc coordination polymers based on biphenyl-3,3’,5,5’-tetracarboxylate and different flexibility of N-donor ligands. RSC Adv. 2014, 4, 32391–32397. [Google Scholar] [CrossRef]
  8. Tapas, S.B.; Maji, K. Multi-dimensional metal-organic frameworks based on mixed linkers: Interplay between structural flexibility and functionality. Coord. Chem. Rev. 2022, 469, e214645. [Google Scholar]
  9. Dutta, A.; Pan, Y.; Liu, J.-Q.; Kumar, A. Multicomponent isoreticular metal-organic frameworks: Principles, current status and challenges. Coord. Chem. Rev. 2021, 445, e214074. [Google Scholar] [CrossRef]
  10. Furukawa, H.; Müller, U.; Yaghi, O.M. “Heterogeneity within order” in metal–organic frameworks. Angew. Chem. Int. Ed. 2015, 54, 2–16. [Google Scholar] [CrossRef]
  11. Tolstikov, S.; Smirnova, K.; Kolesnikov, A.; Letyagin, G.; Bogomyakov, A.; Romanenko, G.; Ovcharenko, V. Relationship between phase transition temperature and accessible volume for substituent in Cu(hfac)2 chain-polymer complexes with pyridine-based nitroxides. Polyhedron 2023, 230, e116212. [Google Scholar] [CrossRef]
  12. Portoles-Gil, N.; Gomez-Coca, S.; Vallcorba, O.; Marban, G.; Aliaga-Alcalde, N.; Lopez-Periago, A.; Ayllon, J.A.; Domingo, C. Single molecule magnets of cobalt and zinc homo- and heterometallic coordination polymers prepared by a one-step synthetic procedure. RSC Adv. 2020, 10, 45090–45094. [Google Scholar] [CrossRef]
  13. Liu, X.; Ma, X.; Cen, P.; An, F.; Wang, Z.; Song, W.; Zhang, Y.-Q. One-dimensional cobalt(II) coordination polymer featuring single-ion-magnet-type field-induced slow magnetic relaxation. New J. Chem. 2018, 42, 9612–9619. [Google Scholar] [CrossRef]
  14. Sun, L.; Campbell, M.G.; Dincă, M. Electrically conductive porous metal–organic frameworks. Angew. Chem. Intern. Ed. 2016, 55, 3566–3579. [Google Scholar] [CrossRef]
  15. Liu, H.; Wang, Y.; Qin, Z.; Liu, D.; Xu, H.; Dong, H.; Hu, W. Electrically conductive coordination polymers for electronic and optoelectronic device applications. J. Phys. Chem. Lett. 2021, 12, 1612–1630. [Google Scholar] [CrossRef]
  16. Kaes, C.; Katz, A.; Hosseini, M.W. Bipyridine:  the most widely used ligand. A review of molecules comprising at least two 2,2‘-bipyridine units. Chem. Rev. 2000, 100, 3553–3590. [Google Scholar] [CrossRef]
  17. Ye, B.-H.; Tong, M.-L.; Chen, X.-M. Metal-organic molecular architectures with 2,2′-bipyridyl-like and carboxylate ligands. Coord. Chem. Rev. 2005, 249, 545–565. [Google Scholar] [CrossRef]
  18. Kent, C.A.; Liu, D.; Meyer, T.J.; Lin, W. Amplified luminescence quenching of phosphorescent metal–organic frameworks. J. Am. Chem. Soc. 2012, 134, 3991–3994. [Google Scholar] [CrossRef]
  19. McGee, K.A.; Veltkamp, D.J.; Marquardt, B.J.; Mann, K.R. Porous crystalline ruthenium complexes are oxygen sensors. J. Am. Chem. Soc. 2007, 129, 15092–15093. [Google Scholar] [CrossRef]
  20. Qian, J.; Jiang, F.; Su, K.; Pan, J.; Zhang, L.; Li, X.; Yuan, D.; Hong, M. Sorption behaviour in a unique 3,12-connected zinc–organic framework with 2.4 nm cages. J. Mater. Chem. A 2013, 1, 10631–10634. [Google Scholar] [CrossRef]
  21. Sotnik, S.A.; Polunin, R.A.; Kiskin, M.A.; Kirillov, A.M.; Dorofeeva, V.N.; Gavrilenko, K.S.; Eremenko, I.L.; Novotortsev, V.M.; Kolotilov, S.V. Heterometallic coordination polymers assembled from trigonalt Fe2Ni-pivalate blocks and polypyridine spacers: Topological diversity, sorption, and catalytic properties. Inorg. Chem. 2015, 54, 5169–5181. [Google Scholar] [CrossRef] [PubMed]
  22. Wu, X.; Ding, N.; Zhang, W.; Xue, F.; Hor, T.S.A. Spacer-directed selective assembly of copper square or hexagon and ring-stacks or coordination nanotubes. Inorg. Chem. 2015, 54, 6680–6686. [Google Scholar] [CrossRef]
  23. Pachfule, P.; Dey, C.; Panda, T.; Banerjee, R. Synthesis and structural comparisons of five new fluorinated metal organic frameworks (F-MOFs). CrystEngComm 2010, 12, 1600–1609. [Google Scholar] [CrossRef]
  24. Zou, G.-D.; Gong, L.-K.; Liu, L.; Zhang, Q.; Zhao, X.-H. Two low-dimensional transition metal coordination polymers constructed from thiophene-2,5-dicarboxylic acid and N/O-donor ligands: Syntheses, structures and magnetic property. Inorg. Chem. Commun. 2019, 99, 140–144. [Google Scholar] [CrossRef]
  25. Jaramillo-García, J.; Sánchez-Mendieta, V.; García-Orozco, I.; Morales-Luckie, R.A.; Martínez-Otero, D.; Téllez-López, A.; Rosales-Vázquez, L.D.; Escudero, R.; Morales, F. Muconato-bridged Manganese Coordination Polymer exhibiting rare Distorted-trigonal Prismatic Coordination Arrangement. Z. Anorg. Allg. Chem. 2018, 644, 19–22. [Google Scholar] [CrossRef] [Green Version]
  26. Shi, J.; Zhang, J.; Liang, T.; Tan, D.; Tan, X.; Wan, Q.; Cheng, X.; Zhang, B.; Han, B.; Liu, L.; et al. Bipyridyl-Containing Cadmium–Organic Frameworks for Efficient Photocatalytic Oxidation of Benzylamine. ACS Appl. Mater. Interfaces 2019, 11, 30953–30958. [Google Scholar] [CrossRef]
  27. Spek, A.L. PLATON SQUEEZE: A tool for the calculation of the disordered solvent contribution to the calculated structure factors. Acta Crystallogr. 2015, C71, 9–18. [Google Scholar]
  28. Zhao, J.; Shi, X.; Li, G.; Wang, X.; Li, C.; Yang, Q. Zinc and cadmium coordination polymers assembled with 2,2’-bipyridine and bithiophenedicarboxylic acid: Effect of metal ions on the conformation of ligand. Inorg. Chim. Acta 2012, 383, 185–189. [Google Scholar] [CrossRef]
  29. Tranchemontagne, D.J.; Mendoza-Cortés, J.L.; O’Keeffe, M.; Yaghi, O.M. Secondary building units, nets and bonding in the chemistry of metal–organic frameworks. Chem. Soc. Rev. 2009, 38, 1257–1283. [Google Scholar] [CrossRef] [Green Version]
  30. Dubskikh, V.A.; Lysova, A.A.; Samsonenko, D.G.; Dybtsev, D.N.; Fedin, V.P. Topological polymorphism and temperature-driven topotactical transitions of metal-organic coordination polymers. CrystEngComm 2020, 22, 6295–6301. [Google Scholar] [CrossRef]
  31. Lysova, A.A.; Samsonenko, D.G.; Dybtsev, D.N.; Fedin, V.P. Cadmium(II) terephthalates based on trinuclear units {Cd3(bdc)3}: Control of coordination structure dimensionality and luminescence properties. Russ. Chem. Bull. 2017, 66, 1580–1588. [Google Scholar] [CrossRef]
  32. Marakulin, A.V.; Lysova, A.A.; Samsonenko, D.G.; Dorovatovskii, P.V.; Lazarenko, V.A.; Dybtsev, D.N.; Fedin, V.P. New one-, two-, and three-dimensional metal-organic frameworks based on magnesium(II): Synthesis and structure. Russ. Chem. Bull. 2020, 69, 360–368. [Google Scholar] [CrossRef]
  33. Yang, S.-Y.; Yuan, H.-B.; Xu, X.-B.; Huang, R.-B. Influential factors on assembly of first-row transition metal coordination polymers. Inorg. Chim. Acta 2013, 403, 53–62. [Google Scholar] [CrossRef]
  34. Zhao, J.; Wang, X.-L.; Shi, X.; Yang, Q.-H.; Li, C. Synthesis, structure, and photoluminescent properties of metal−organic coordination polymers assembled with bithiophenedicarboxylic acid. Inorg. Chem. 2011, 50, 3198–3205. [Google Scholar] [CrossRef]
  35. Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC technical report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
  36. Yoon, M.; Moon, D. New Zr (IV) based metal-organic framework comprising a sulfur-containing ligand: Enhancement of CO2 and H2 storage capacity. Microporous Mesoporous Mater. 2015, 215, 116–122. [Google Scholar] [CrossRef]
  37. Dubskikh, V.A.; Kovalenko, K.A.; Nizovtsev, A.S.; Lysova, A.A.; Samsonenko, D.G.; Dybtsev, D.N.; Fedin, V.P. Enhanced adsorption selectivity of carbon dioxide and ethane on porous metal–organic framework functionalized by a sulfur-rich heterocycle. Nanomaterials 2022, 12, e4281. [Google Scholar] [CrossRef]
  38. Mahajan, S.; Lahtinen, M. Recent progress in metal-organic frameworks (MOFs) for CO2 capture at different pressures. J. Environ. Chem. Eng. 2022, 10, e108930. [Google Scholar] [CrossRef]
  39. Ursueguía, D.; Díaz, E.; Ordóñez, S. Metal-organic frameworks (MOFs) as methane adsorbents: From storage to diluted coal mining streams concentration. Sci. Total Environ. 2021, 790, e148211. [Google Scholar] [CrossRef]
  40. Jia, T.; Gu, Y.; Li, F. Progress and potential of metal-organic frameworks (MOFs) for gas storage and separation: A review. J. Environ. Chem. Eng. 2022, 10, e108300. [Google Scholar] [CrossRef]
  41. Myers, A.L.; Prausnitz, J.M. Thermodynamics of mixed-gas adsorption. AIChE J. 1965, 11, 121–127. [Google Scholar] [CrossRef]
  42. Karra, J.R.; Walton, K.S. Molecular simulations and experimental studies of CO2, CO, and N2 adsorption in metal-organic frameworks. J. Phys. Chem. C 2010, 114, 15735–15740. [Google Scholar] [CrossRef]
  43. Rallapalli, P.; Prasanth, K.P.; Patil, D.; Somani, R.S.; Jasra, R.V.; Bajaj, H.C. Sorption studies of CO2, CH4, N2, CO, O2 and Ar on nanoporous aluminum terephthalate [MIL-53(Al)]. J. Porous Mater. 2011, 18, 205–210. [Google Scholar] [CrossRef]
  44. Mishra, P.; Uppara, H.P.; Mandal, B.; Gumma, S. Adsorption and separation of carbon dioxide using MIL-53(Al) metal-organic framework. Ind. Eng. Chem. Res. 2014, 53, 19747–19753. [Google Scholar] [CrossRef]
  45. Luo, J.; Wang, J.; Cao, Y.; Yao, S.; Zhang, L.; Huo, Q.; Liu, Y. Assembly of an indium–porphyrin framework JLU-Liu7: A mesoporous metal–organic framework with high gas adsorption and separation of light hydrocarbons. Inorg. Chem. Front. 2017, 4, 139–143. [Google Scholar] [CrossRef]
  46. Li, L.; Wang, X.; Liang, J.; Huang, Y.-B.; Li, H.-F.; Lin, Z.-L.; Cao, R. A water-stable anionic metal-organic framework for highly selective separation of methane from natural gas and pyrolysis gas. ACS Appl. Mater. Interfaces 2016, 8, 9777–9781. [Google Scholar] [CrossRef]
  47. Luo, X.; Sun, L.; Zhao, J.; Li, D.-S.; Wang, D.; Li, G.; Huo, Q.; Liu, Y. Three metal-organic frameworks based on binodal inorganic building units and hetero-O, N donor ligand: Solvothermal syntheses, structures, and gas sorption properties. Cryst. Growth Des. 2015, 15, 4901–4907. [Google Scholar] [CrossRef]
  48. Li, J.; Guo, Y.; Fu, H.-R.; Zhang, J.; Huang, R.-B.; Zheng, L.-S.; Tao, J. A spin-canted NiII4-based metal–organic framework with gas sorption properties and high adsorptive selectivity for light hydrocarbons. Chem. Commun. 2014, 50, 9161–9164. [Google Scholar] [CrossRef]
  49. Fan, W.; Wang, X.; Xu, B.; Wang, Y.; Liu, D.; Zhang, M.; Shang, Y.; Dai, F.; Zhang, L.; Sun, D. Amino-functionalized MOFs with high physicochemical stability for efficient gas storage/separation, dye adsorption and catalytic performance. J. Mater. Chem. A 2018, 6, 24486–24495. [Google Scholar] [CrossRef]
  50. Plonka, A.M.; Chen, X.; Wang, H.; Krishna, R.; Dong, X.; Banerjee, D.; Woerner, W.R.; Han, Y.; Li, J.; Parise, J.B. Light hydrocarbon adsorption mechanisms in two calcium-based microporous metal organic frameworks. Chem. Mater. 2016, 28, 1636–1646. [Google Scholar] [CrossRef] [Green Version]
  51. Wang, D.; Zhang, Y.; Gao, J.; Ge, G.; Li, C. A polyhedron-based heterometallic MOF constructed by HSAB theory and SBB strategy: Synthesis, structure, and adsorption properties. Cryst. Growth Des. 2019, 19, 4571–4578. [Google Scholar] [CrossRef]
  52. Chen, Q.; Ying, Y.; Wang, L.; Guo, Z.; Zhou, Y.; Wang, D.; Li, C. A heterometallic MOF based on monofunctional linker by “one-pot” solvothermal method for highly selective gas adsorption. Z. Anorg. Allg. Chem. 2020, 646, 437–443. [Google Scholar] [CrossRef]
  53. Lysova, A.A.; Samsonenko, D.G.; Dorovatovskii, P.V.; Lazarenko, V.A.; Khrustalev, V.N.; Kovalenko, K.A.; Dybtsev, D.N.; Fedin, V.P. Tuning the molecular and cationic affinity in a series of multifunctional metal–organic frameworks based on dodecanuclear Zn(II) carboxylate wheels. J. Am. Chem. Soc. 2019, 141, 17260–17269. [Google Scholar] [CrossRef]
  54. Macreadie, L.K.; Babarao, R.; Setter, C.J.; Lee, S.J.; Qazvini, O.T.; Seeber, A.J.; Tsanaktsidis, J.; Telfer, S.G.; Batten, S.R.; Hill, M.R. Enhancing multicomponent metal–organic frameworks for low pressure liquid organic hydrogen carrier separations. Angew. Chem. Int. Ed. 2020, 59, 6090–6098. [Google Scholar] [CrossRef]
  55. Macreadie, L.K.; Qazvini, O.T.; Babarao, R. Reversing benzene/cyclohexane selectivity through varying supramolecular interactions using aliphatic, isoreticular MOFs. ACS Appl. Mater. Interfaces 2021, 13, 30885–30890. [Google Scholar] [CrossRef]
  56. Griffith, J.S. On the general theory of magnetic susceptibilities of polynuclear transition-metal compounds. In Structure and Bonding; Springer: Berlin/Heidelberg, Germany, 1972; pp. 87–126. [Google Scholar]
  57. CrysAlisPro Software System, version 1.171.41.98a; Rigaku Oxford Diffraction, Rigaku Corporation: Wrocław, Poland, 2021.
  58. Svetogorov, R.D.; Dorovatovskii, P.V.; Lazarenko, V.A. Belok/XSA diffraction beamline for studying crystalline samples at Kurchatov Synchrotron Radiation Source. Cryst. Res. Technol. 2020, 55, 1900184. [Google Scholar] [CrossRef]
  59. Lazarenko, V.A.; Dorovatovskii, P.V.; Zubavichus, Y.V.; Burlov, A.S.; Koshchienko, Y.V.; Vlasenko, V.G.; Khrustalev, V.N. High-throughput small-molecule crystallography at the ‘Belok’ beamline of the Kurchatov synchrotron radiation source: Transition metal complexes with azomethine ligands as a case study. Crystals 2017, 7, 325. [Google Scholar] [CrossRef] [Green Version]
  60. Kabsch, W. XDS. Acta Crystallogr. Sect. D. 2010, 66, 125–132. [Google Scholar] [CrossRef] [Green Version]
  61. Sheldrick, G.M. SHELXT – Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A 2015, 71, 3–8. [Google Scholar] [CrossRef] [Green Version]
  62. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [Green Version]
  63. Einkauf, J.D.; Ortega, R.E.; Mathivathanan, L.; de Lill, D.T. Nitroaromatic sensing with a new lanthanide coordination polymer [Er2(C10H4O4S2)3(H2O)6]n assembled by 2,2’-bithiophene-5,5’-dicarboxylate. New J. Chem. 2017, 41, 10929–10934. [Google Scholar] [CrossRef]
Molecules 28 02139 sch001 550
Scheme 1. Schematic description of the synthesis conditions for 1–5.
Scheme 1. Schematic description of the synthesis conditions for 1–5.
Molecules 28 02139 sch001
Molecules 28 02139 g001 550
Figure 1. (a) Structure of {Mn3(μ-RCOO-κ1,κ1)4(μ-RCOO-κ1,κ2)2(bpy)2} building unit in 1; (b) fragment of the crystal structure of 1 (projection on the bc plane).
Figure 1. (a) Structure of {Mn3(μ-RCOO-κ1,κ1)4(μ-RCOO-κ1,κ2)2(bpy)2} building unit in 1; (b) fragment of the crystal structure of 1 (projection on the bc plane).
Molecules 28 02139 g001
Molecules 28 02139 g002 550
Figure 2. (a) Structure of {Mn3(μ-RCOO-κ1,κ1)4(μ-RCOO-κ1,κ2)2(5,5′-dmbpy)2} building unit in 2; (b) fragment of the layer in Structure 2 (projection on the ac plane).
Figure 2. (a) Structure of {Mn3(μ-RCOO-κ1,κ1)4(μ-RCOO-κ1,κ2)2(5,5′-dmbpy)2} building unit in 2; (b) fragment of the layer in Structure 2 (projection on the ac plane).
Molecules 28 02139 g002
Molecules 28 02139 g003 550
Figure 3. (a) Structure of {Mn2(μ-RCOO-κ1,κ2)2(4,4′-dmbpy)2(RCOO-κ2)2} building unit in 3; (b) fragment of the layer in Structure 3 (projection on the ac plane).
Figure 3. (a) Structure of {Mn2(μ-RCOO-κ1,κ2)2(4,4′-dmbpy)2(RCOO-κ2)2} building unit in 3; (b) fragment of the layer in Structure 3 (projection on the ac plane).
Molecules 28 02139 g003
Molecules 28 02139 g004 550
Figure 4. (a) Structure of {Mn4(μ-RCOO-κ1,κ1)4(μ-RCOO-κ1,κ2)4(bpy)2(dmf)2} building unit in 4; (b) fragment of the layer in Structure 4 (projection on the bc plane). Only one of four positions of coordinated DMF molecules is shown.
Figure 4. (a) Structure of {Mn4(μ-RCOO-κ1,κ1)4(μ-RCOO-κ1,κ2)4(bpy)2(dmf)2} building unit in 4; (b) fragment of the layer in Structure 4 (projection on the bc plane). Only one of four positions of coordinated DMF molecules is shown.
Molecules 28 02139 g004
Molecules 28 02139 g005 550
Figure 5. (a) Structure of {Mn4(μ-RCOO-κ1,κ1)6(μ-RCOO-κ1,κ2)2(4,4′-dmbpy)2(dmf)2} building unit in 5; (b) fragment of the layer in Structure 5 (projection on the bc plane).
Figure 5. (a) Structure of {Mn4(μ-RCOO-κ1,κ1)6(μ-RCOO-κ1,κ2)2(4,4′-dmbpy)2(dmf)2} building unit in 5; (b) fragment of the layer in Structure 5 (projection on the bc plane).
Molecules 28 02139 g005
Molecules 28 02139 g006 550
Figure 6. Nitrogen adsorption (filled squares) and desorption (open squares) isotherms at 77 K for Compound 1. The inset shows the pore size distribution.
Figure 6. Nitrogen adsorption (filled squares) and desorption (open squares) isotherms at 77 K for Compound 1. The inset shows the pore size distribution.
Molecules 28 02139 g006
Molecules 28 02139 g007 550
Figure 7. CO2, CO, N2, and O2 gas adsorption isotherms for Compound 1: (a) at 273 K; (b) at 298 K.
Figure 7. CO2, CO, N2, and O2 gas adsorption isotherms for Compound 1: (a) at 273 K; (b) at 298 K.
Molecules 28 02139 g007
Molecules 28 02139 g008 550
Figure 8. CH4, C2H2, C2H4, and C2H6 gas adsorption isotherms for Compound 1: (a) at 273 K; (b) at 298 K.
Figure 8. CH4, C2H2, C2H4, and C2H6 gas adsorption isotherms for Compound 1: (a) at 273 K; (b) at 298 K.
Molecules 28 02139 g008
Molecules 28 02139 g009 550
Figure 9. C6H6 and C6H12 vapor adsorption (filled symbols) and desorption (open symbols) isotherms for Compound 1 at 298 K.
Figure 9. C6H6 and C6H12 vapor adsorption (filled symbols) and desorption (open symbols) isotherms for Compound 1 at 298 K.
Molecules 28 02139 g009
Molecules 28 02139 g010 550
Figure 10. Fragment of the crystal structure of 1≅2C6H6. The disordered positions of the guest benzene molecules are shown by a dashed line.
Figure 10. Fragment of the crystal structure of 1≅2C6H6. The disordered positions of the guest benzene molecules are shown by a dashed line.
Molecules 28 02139 g010
Molecules 28 02139 g011 550
Figure 11. Temperature dependences of the effective magnetic moments per one Mn ion, μeff, measured for 1–3. Inset illustrates the magnetic ground states of the trinuclear (1 and 2) and binuclear (3) SBUs. The orange dashed line shows a fit to the data of the Mn2+-Mn2+ dimer model [56] with the intradimer exchange interaction J/kB = 2.0 K.
Figure 11. Temperature dependences of the effective magnetic moments per one Mn ion, μeff, measured for 1–3. Inset illustrates the magnetic ground states of the trinuclear (1 and 2) and binuclear (3) SBUs. The orange dashed line shows a fit to the data of the Mn2+-Mn2+ dimer model [56] with the intradimer exchange interaction J/kB = 2.0 K.
Molecules 28 02139 g011
Table
Table 1. Gas uptakes on 1 at 1 bar.
Table 1. Gas uptakes on 1 at 1 bar.
Gas273 K298 K
cm3·g−1mmol·g−1wt.%cm3·g−1mmol·g−1wt.%
CO254.92.459.734.01.526.3
CO7.60.340.94.90.220.6
N25.40.240.73.20.140.4
O25.10.230.73.20.140.5
CH422.20.991.613.30.590.9
C2H267.12.997.256.52.526.2
C2H459.32.656.950.62.266.0
C2H657.52.567.249.52.216.2
Table
Table 2. Adsorption selectivity factors for separation of binary gas mixtures evaluated via different approaches.
Table 2. Adsorption selectivity factors for separation of binary gas mixtures evaluated via different approaches.
Gas Mixture273 K298 K
V1/V2KH1/KH2IAST aV1/V2KH1/KH2IAST a
CO2/N210.223.831.010.616.219.1
CO2/CO7.28.125.76.95.017.0
CO2/CH42.54.24.82.63.43.6
C2H6/CH42.644.933.4
37.7 b		3.729.524.6
27.2 b
C2H4/CH42.724.624.83.817.817.7
C2H2/CH43.021.129.34.215.419.1
a for the equimolar gas mixture composition at the total pressure of 1 bar; b C2H6:CH4 = 1:9 (v/v).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Dubskikh, V.A.; Kolosov, A.A.; Lysova, A.A.; Samsonenko, D.G.; Lavrov, A.N.; Kovalenko, K.A.; Dybtsev, D.N.; Fedin, V.P. A Series of Metal–Organic Frameworks with 2,2′-Bipyridyl Derivatives: Synthesis vs. Structure Relationships, Adsorption, and Magnetic Studies. Molecules 2023, 28, 2139. https://doi.org/10.3390/molecules28052139

AMA Style

Dubskikh VA, Kolosov AA, Lysova AA, Samsonenko DG, Lavrov AN, Kovalenko KA, Dybtsev DN, Fedin VP. A Series of Metal–Organic Frameworks with 2,2′-Bipyridyl Derivatives: Synthesis vs. Structure Relationships, Adsorption, and Magnetic Studies. Molecules. 2023; 28(5):2139. https://doi.org/10.3390/molecules28052139

Chicago/Turabian Style

Dubskikh, Vadim A., Aleksei A. Kolosov, Anna A. Lysova, Denis G. Samsonenko, Alexander N. Lavrov, Konstantin A. Kovalenko, Danil N. Dybtsev, and Vladimir P. Fedin. 2023. "A Series of Metal–Organic Frameworks with 2,2′-Bipyridyl Derivatives: Synthesis vs. Structure Relationships, Adsorption, and Magnetic Studies" Molecules 28, no. 5: 2139. https://doi.org/10.3390/molecules28052139

APA Style

Dubskikh, V. A., Kolosov, A. A., Lysova, A. A., Samsonenko, D. G., Lavrov, A. N., Kovalenko, K. A., Dybtsev, D. N., & Fedin, V. P. (2023). A Series of Metal–Organic Frameworks with 2,2′-Bipyridyl Derivatives: Synthesis vs. Structure Relationships, Adsorption, and Magnetic Studies. Molecules, 28(5), 2139. https://doi.org/10.3390/molecules28052139

Article Metrics

Back to TopTop