Investigation of Thermodynamic Properties of Dimethyl Phosphate-Based ILs for Use as Working Fluids in Absorption Refrigeration Technology
Abstract
1. Introduction
2. Results
2.1. DSC Measurements
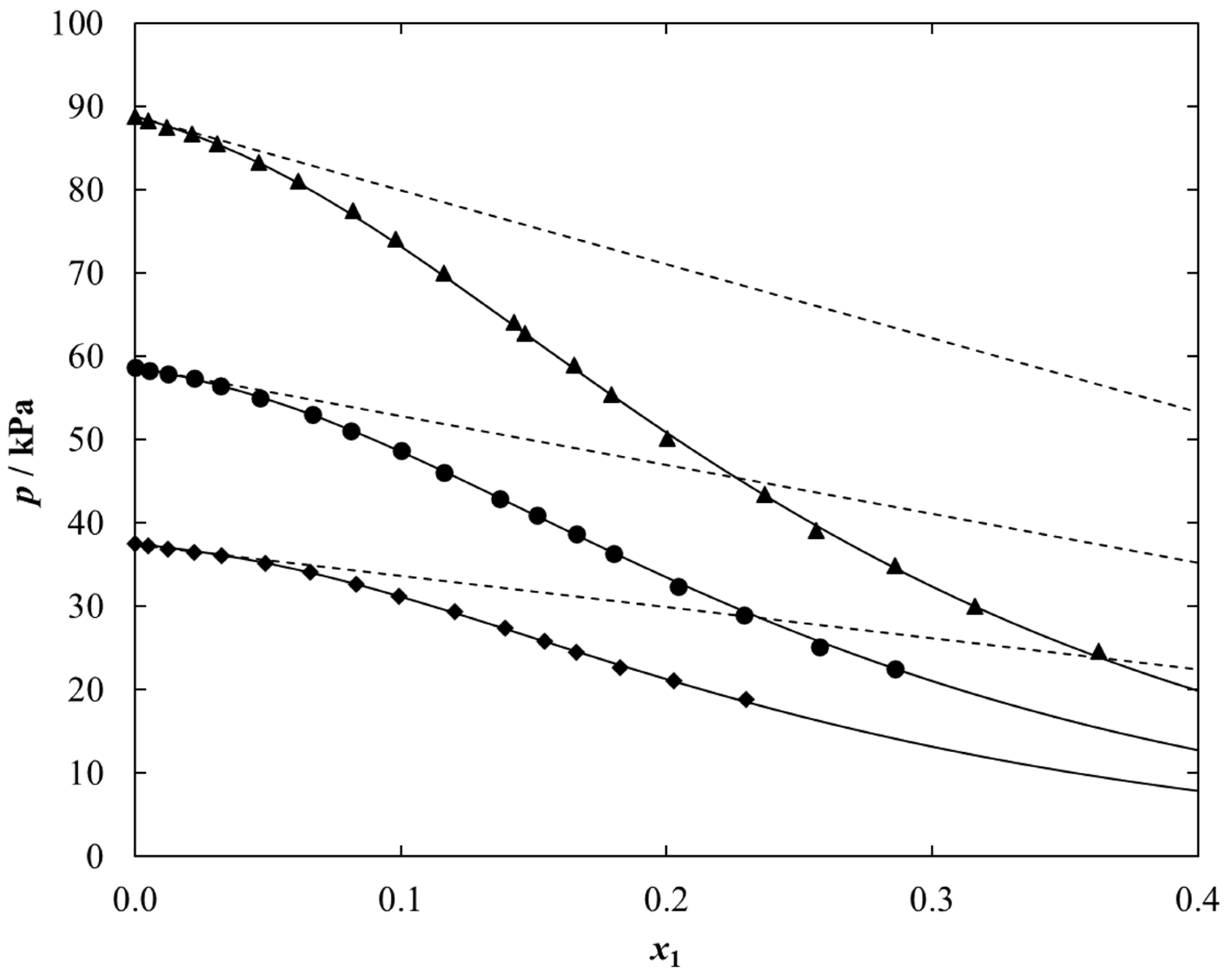
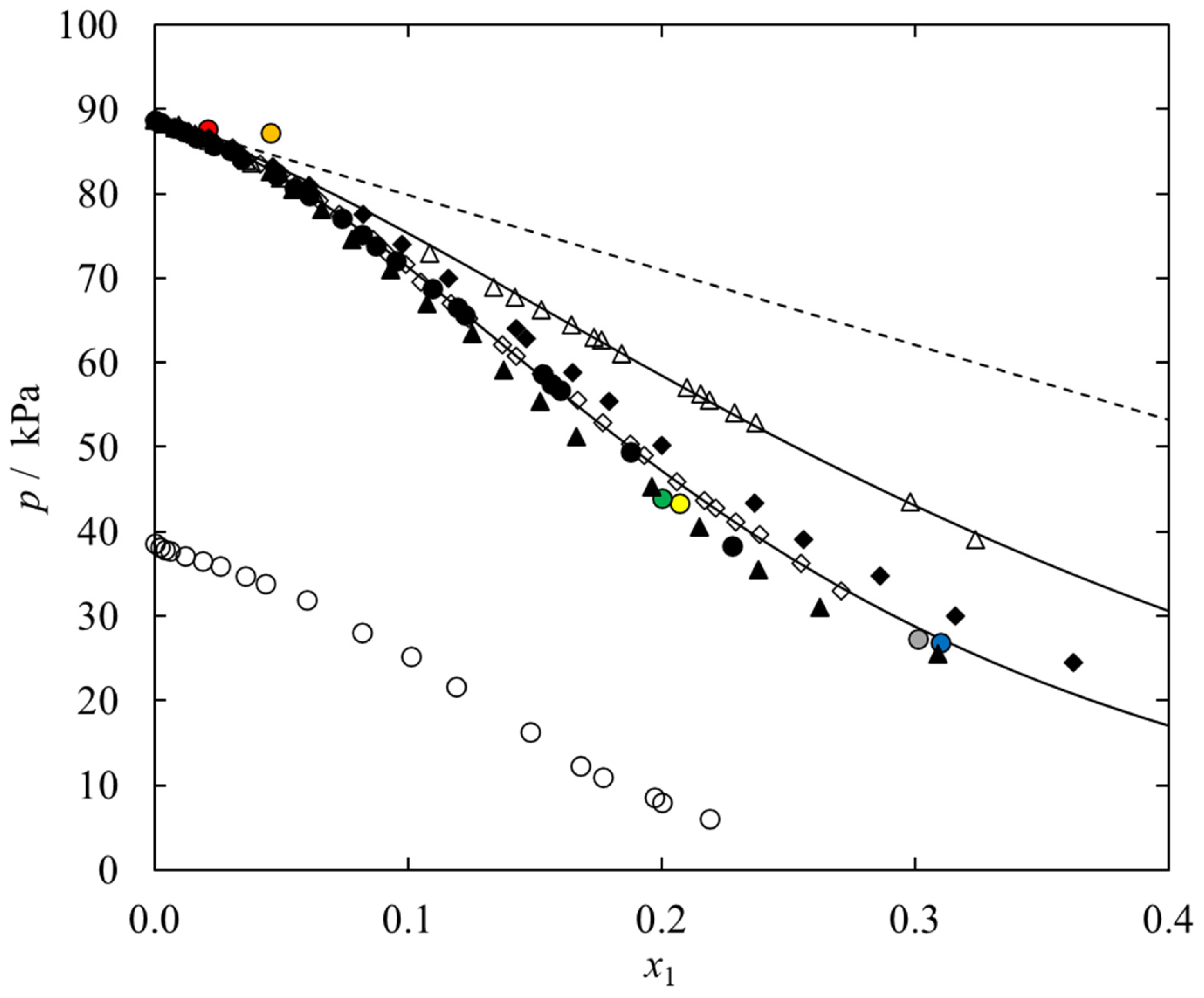
2.2. (Vapor-Liquid) Phase Equilibria Measurements
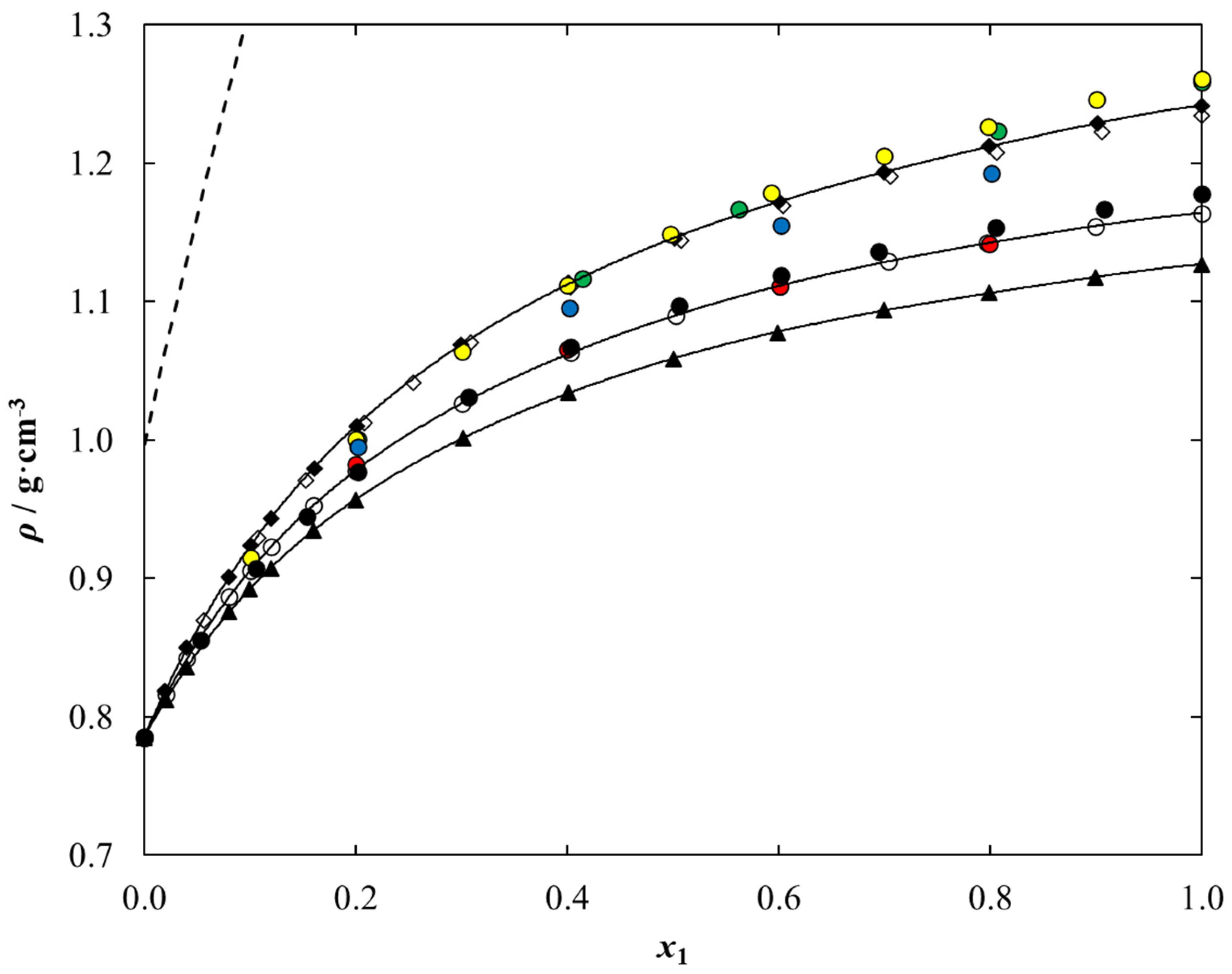
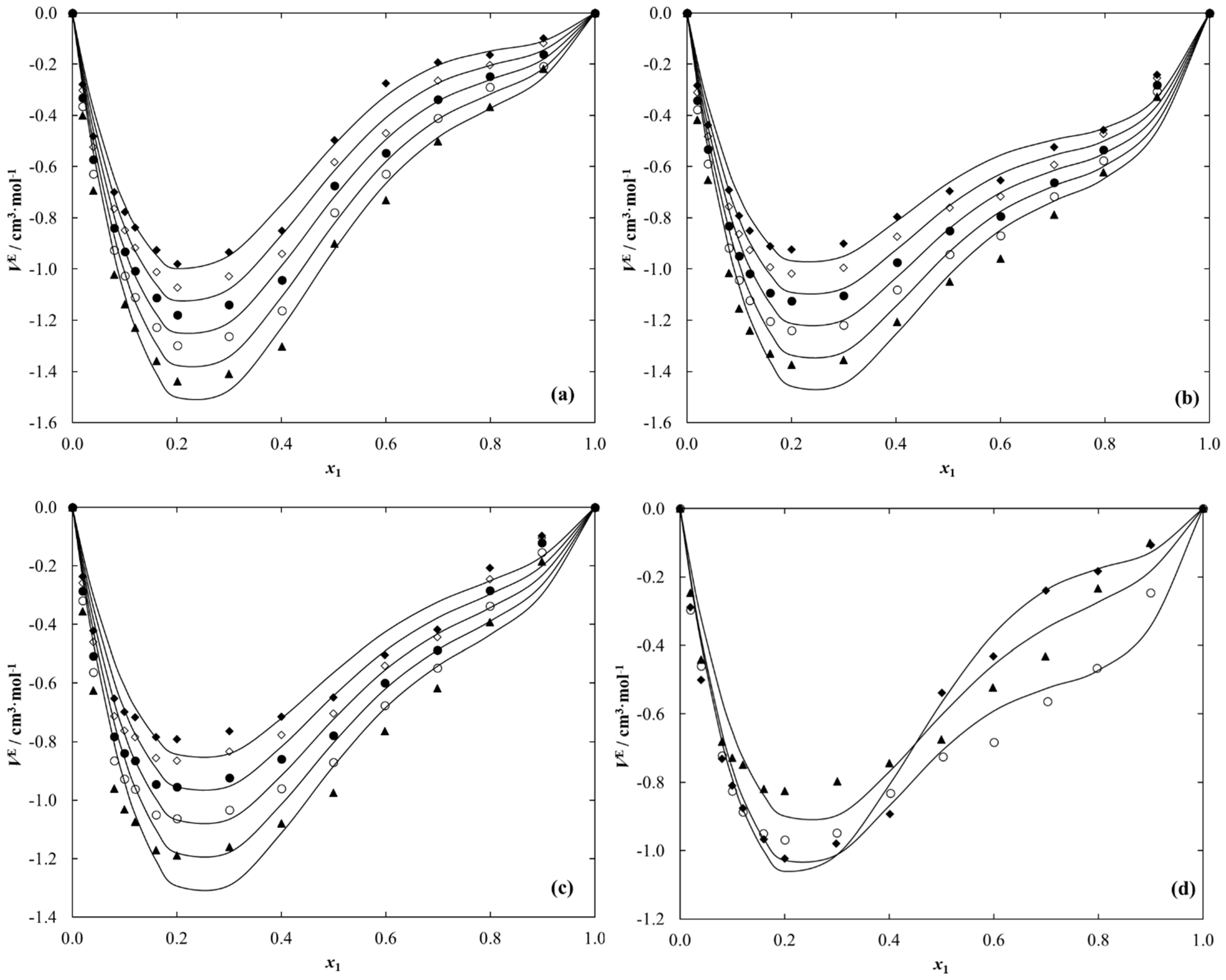
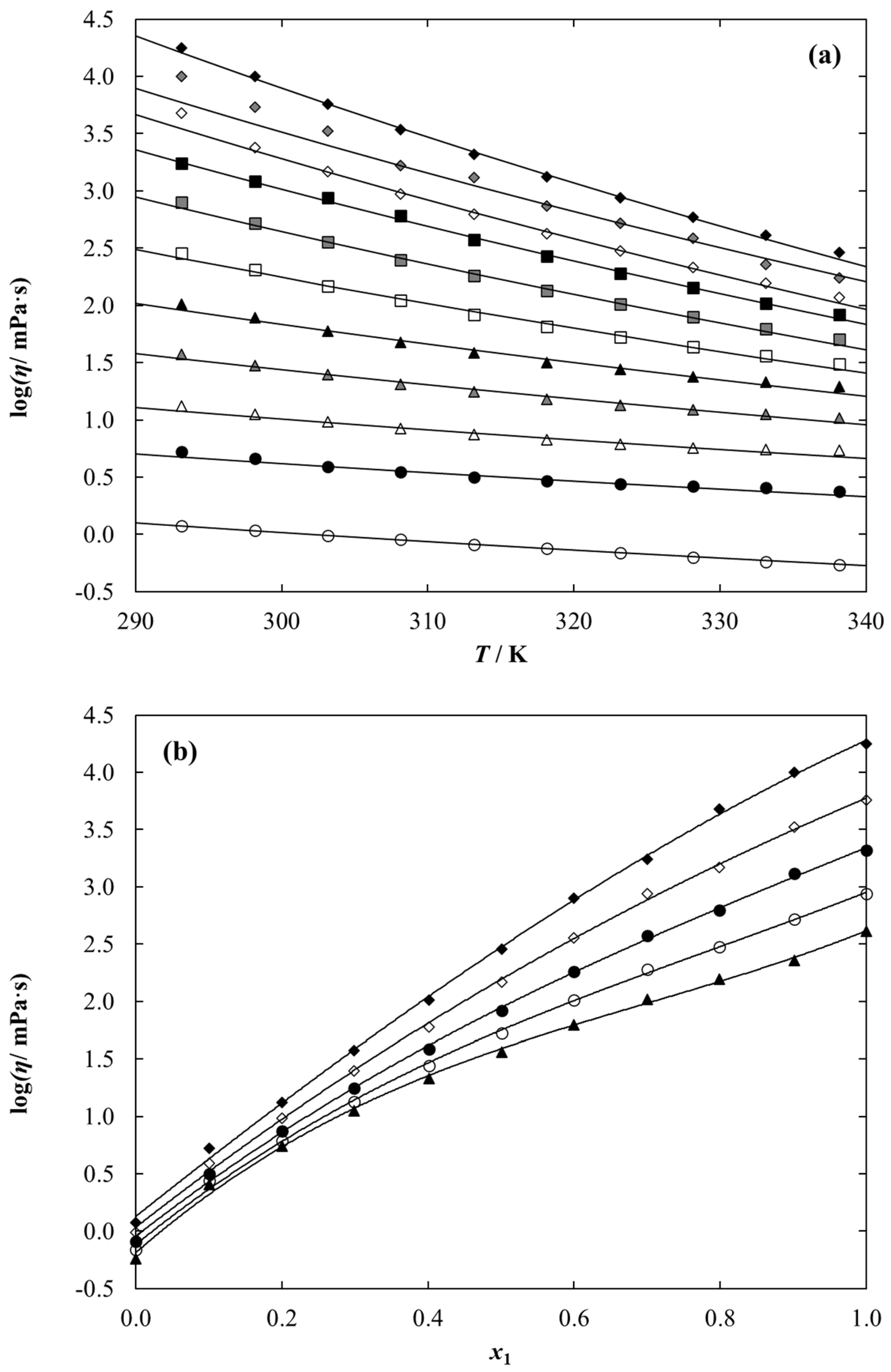
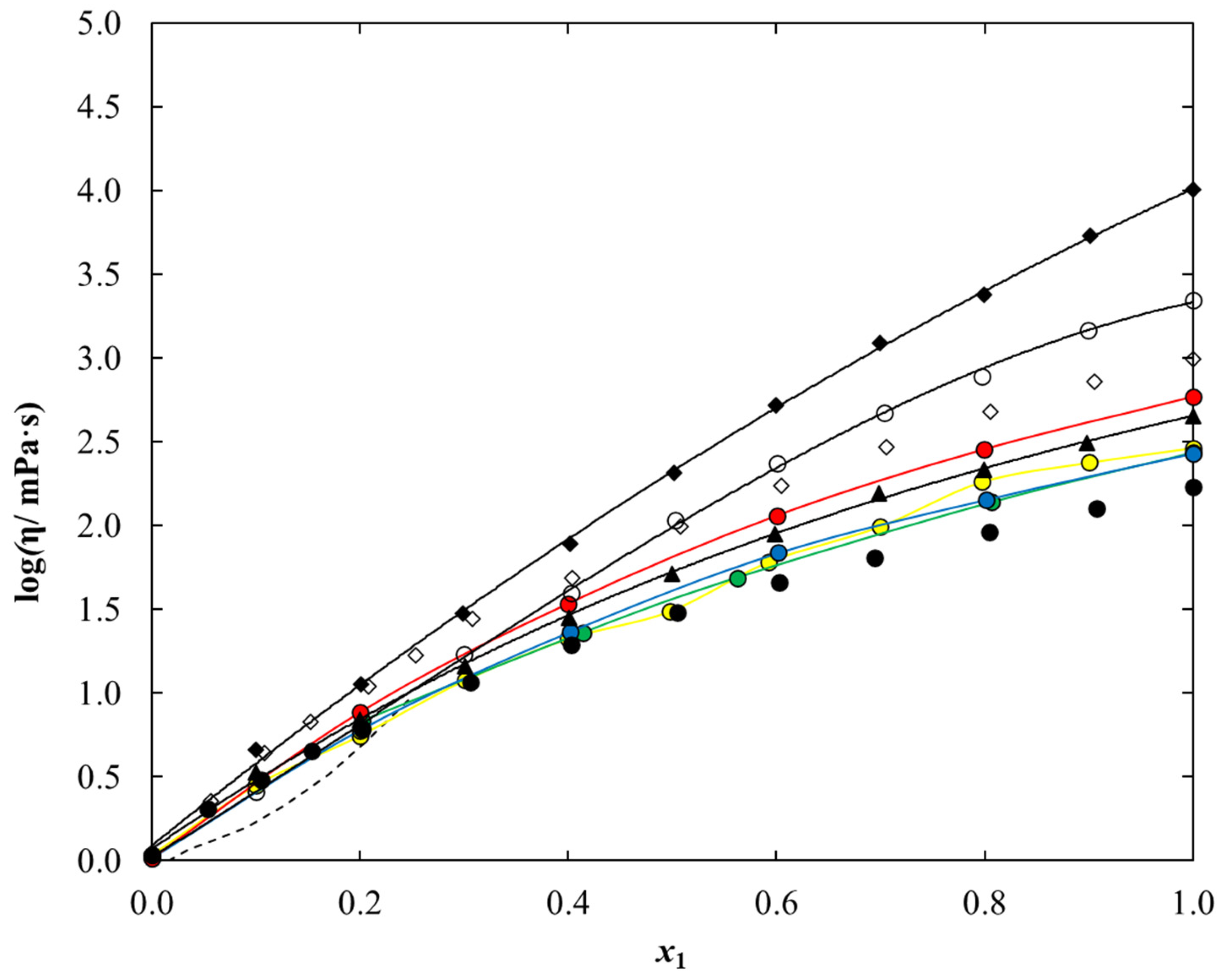
2.3. Density and Dynamic Viscosity Data
3. Discussion
4. Materials and Methods
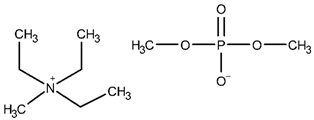
4.1. Materials
Synthesis of 1-ethyl-1-methylmorpholinium dimethyl phosphate, [C1C2MOR][DMP]
4.2. Experimental Apparatus and Procedure
4.2.1. Differential Scanning Calorimetry (DSC)
4.2.2. (Vapor-Liquid) Phase Equilibria Measurements
4.2.3. Density Measurement
4.2.4. Dynamic Viscosity Measurements
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Sun, J.; Fu, L.; Zhang, S. A review of working fluids of absorption cycles. Renew. Sustain. Energy Rev. 2012, 16, 1899–1906. [Google Scholar] [CrossRef]
- Zhuo, C.Z.; Machielsen, C.H.M. Thermophysical properties of the trifluoroethanol-pyrrolidone system for absorption heat transformers. Int. J. Refrig. 1993, 16, 357–363. [Google Scholar] [CrossRef]
- Srikhirin, P.; Aphornratana, S.; Chungpaibulpatana, S. A review of absorption refrigeration technologies. Renew. Sust. Energy Rev. 2001, 5, 343–372. [Google Scholar] [CrossRef]
- Aphornratana, S.; Chungpaibulpatana, S.; Srikhirin, P. Experimental investigation of an ejector refrigerator: Effect of mixing chamber geometry on system performance. Int. J. Energy Res. 2001, 25, 397–411. [Google Scholar] [CrossRef]
- Khamooshi, M.; Parham, K.; Atikol, U. Overview of Ionic Liquids Used as Working Fluids in Absorption Cycles. Adv. Mech. Eng. 2013, 2013, 1–7. [Google Scholar] [CrossRef]
- Jelinek, M.; Borde, I. Single and double stage absorption cycles based on fluorocarbon refrigerants and organic absorbents. Appl. Therm. Eng. 1998, 18, 765–771. [Google Scholar] [CrossRef]
- Kim, J.S.; Park, Y.; Lee, H. Performance evaluation of absorption chiller using LiBr + H2N(CH2)2OH + H2O, LiBr + HO(CH2)2OH + H2O, and LiBr + (HOCH2CH2)2NH + H2O as working fluids. Appl. Therm. Eng. 1999, 19, 217–225. [Google Scholar] [CrossRef]
- Kim, J.S.; Lee, H.S.; Lee, H. Thermal property measurements and enthalpy calculation of the LiBr + lithium iodide + 1,3-propanediol + H2O system. Int. J. Thermophys. 2000, 21, 1407–1418. [Google Scholar] [CrossRef]
- Yin, J.; Shi, L.; Zhu, M.S.; Han, L.Z. Performance analysis of an absorption heat transformer with different working fluid combinations. Appl. Energy 2000, 67, 281–292. [Google Scholar] [CrossRef]
- Zhao, Z.C.; Zhang, X.D.; Ma, X.H. Thermodynamic performance of a double-effect absorption heat-transformer using TFE/E181 as the working fluid. Appl. Energy 2005, 82, 107–116. [Google Scholar] [CrossRef]
- Ali, K.; Salman, A. Thermodynamic analysis of an absorption refrigeration machine with new working fluid for solar applications. Heat Mass Transf. 2008, 45, 71–81. [Google Scholar]
- Rogers, R.D.; Seddon, K.R. Ionic Liquids-Solvents of the Future? Science 2003, 302, 792–793. [Google Scholar] [CrossRef]
- Chinchilla, R.; Mazon, P.; Najera, C. New dimeric anthracenyl-derived Cinchona quaternary ammonium salts as phase-transfer catalysts for the asymmetric synthesis of α-amino acids. Tetrahedron Asymmetry 2009, 13, 927–931. [Google Scholar] [CrossRef]
- Welton, T. Ionic liquids: A brief history. Biophys. Rev. 2018, 10, 691–706. [Google Scholar] [CrossRef]
- Ray, A.; Saruhan, B. Application of Ionic Liquids for Batteries and Supercapacitors. Materials 2021, 14, 2942. [Google Scholar] [CrossRef]
- Kaur, G.; Kumar, H.; Singla, M. Diverse applications of ionic liquids: A comprehensive review. J. Mol. Liq. 2022, 351, 118556. [Google Scholar] [CrossRef]
- Yokozeki, A.; Shiflett, M.B. Vapor–liquid equilibria of ammonia + ionic liquid mixtures. Appl. Energy 2007, 84, 1258–1273. [Google Scholar] [CrossRef]
- Yokozeki, A.; Shiflett, M.B. Water solubility in ionic liquids and application to absorption cycles. Ind. Eng. Chem. Res. 2010, 49, 9496–9503. [Google Scholar] [CrossRef]
- Liang, S.Q.; Zhao, J.; Wang, L.; Huai, X.L. Absorption refrigeration cycle utilizing a new working pair of ionic liquid type. J. Chem. Thermophys. 2010, 31, 1627–1630. [Google Scholar]
- Liu, X.; Li, J.; Hou, K.; Wang, S.; He, M. New environment friendly working pairs of dimethyl ether and ionic liquids for absorption refrigeration with high COP. Int. J. Refrig. 2022, 134, 159–167. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, S.; Joshic, Y.K.; Fedorov, A.G.; Kohl, P.A. Thermodynamic analysis of an absorption refrigeration system with ionic-liquid/refrigerant mixture as a working fluid. Energy 2012, 44, 1005–1016. [Google Scholar] [CrossRef]
- Dong, L.; Zheng, D.; Nie, N.; Li, Y. Performance prediction of absorption refrigeration cycle based on the measurements of vapor pressure and heat capacity of H2O + [DMIM]DMP system. Appl. Energy 2012, 98, 326–332. [Google Scholar] [CrossRef]
- Currás, M.R.; Husson, P.; Pádua, A.A.H.; Costa Gomes, M.F.; García, J. High-Pressure Densities of 2,2,2-Trifluoroethanol + Ionic Liquid Mixtures Useful for Possible Applications in Absorption Cycles. Ind. Eng. Chem. Res. 2014, 53, 10791–11082. [Google Scholar] [CrossRef]
- Zawadzki, M.; Królikowska, M.; Antonowicz, J.; Lipiński, P.; Karpińska, M. physicochemical and thermodynamic properties of the {1-alkyl-1-methylmorpholinium bromide, [C1Cn=3,4,5MOR]Br, or 1-methyl-1-pentylpiperidinium bromide, [C1C5PIP]Br + water} binary systems. J. Chem. Thermodyn. 2018, 98, 324–337. [Google Scholar] [CrossRef]
- Wang, M.; Ferreira, C.A.I. Absorption heat pump cycles with NH3—Ionic liquid working pairs. Appl. Energy 2017, 204, 819–830. [Google Scholar]
- Cera-Manjarres, A.; Salavera, D.; Coronas, A. Vapour pressure measurements of ammonia/ionic liquids mixtures as suitable alternative working fluids for absorption refrigeration technology. Fluid Phase Equilib. 2018, 476, 48–60. [Google Scholar] [CrossRef]
- Takalkar, G.D.; Bhosale, R.R.; Mali, N.A.; Bhagwat, S.S. Thermodynamic analysis of EMISE–Water as a working pair for absorption refrigeration system. Appl. Therm. Eng. 2019, 148, 787–795. [Google Scholar] [CrossRef]
- Królikowska, M.; Paduszyński, K.; Zawadzki, M. (Vapor + liquid) phase equilibria of an aqueous solution of bromide-based ionic liquids—Measurements, correlations and application to absorption cycles. Fluid Phase Equilib. 2019, 494, 201–211. [Google Scholar] [CrossRef]
- Xuan, Y.; Fang, K.; Duan, B.; Gao, N.; Chen, G. Vapor Pressure Measurement of Ternary Systems LiBr + [Emim]I + H2O and LiBr + [Dmim]I + H2O. J. Chem. Eng. Data 2020, 65, 487–494. [Google Scholar] [CrossRef]
- Zhang, F.F.; Li, X.Y.; Chen, G.; Wang, T.; Jin, T.X.; Cheng, C.X.; Li, G.P.; Zhang, L.G.; Zhang, B.; Zheng, F.F. Thermophysical properties and water sorption characteristics of 1-ethyl-3-methylimidazolium acetate ionic liquid and water binary systems. Int. Comm. Heat Mass Transfer. 2021, 127, 105558. [Google Scholar] [CrossRef]
- Królikowska, M.; Grzeszyk, K.; Skonieczny, M. Thermodynamic characterization of {1-ethyl-1-methyl-pyrrolidinium dimethylphosphate, [C1C2PYR][DMP], or 1-hydroxyethyl-1-methylpyrrolidinium dimethylphosphate, [C1C2OHPYR][DMP] (1) + ethanol (2)} binary systems. Fluid Phase Equilib. 2021, 547, 113175. [Google Scholar] [CrossRef]
- de Araújo, H.V.; Massuchetto, L.H.P.; do Nascimento, R.B.C.; de Carvalho, S.M.R.; Dangelo, J.V.H. Thermodynamic performance analysis of a single-effect absorption refrigeration system operating with water and 1-ethyl-3-methylimidazolium-based ionic liquids mixtures. Appl. Therma. Eng. 2022, 201, 117761. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, T.; Zhao, T.; Hea, Y. Thermodynamic analysis of H2O-3-aminopropyl tributyl phosphonium glycinate as a working pair for absorption refrigeration system. Appl. Therm. Eng. 2022, 213, 118658. [Google Scholar] [CrossRef]
- Skonieczny, M.; Królikowska, M. Thermodynamic Properties of {Diethyl Phosphate-Based Ionic Liquid (1) + Ethanol (2)} Systems, Experimental Data and Correlation. J. Chem. Eng. Data 2022, 67, 869–885. [Google Scholar] [CrossRef]
- He, Z.; Zhao, Z.; Zhang, X.; Feng, H. Thermodynamic properties of new heat pump working pairs: 1,3-Dimethylimidazolium dimethylphosphate and water, ethanol and methanol. Fluid Phase Equilib. 2010, 298, 83–91. [Google Scholar] [CrossRef]
- Kato, R.; Gmehling, J. Activity coefficients at infinite dilution of various solutes in the ionic liquids [MMIM]+[CH3SO4]−, [MMIM]+[CH3OC2H4SO4]−, [MMIM]+[(CH3)2PO4]−, [C5H5NC2H5]+[(CF3SO2)2N]− and [C5H5NH]+[C2H5OC2H4OSO3]−. Fluid Phase Equilib. 2004, 226, 37–44. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, X.C.; Li, C.X.; Wang, Z.H. Vapor pressure measurement for binary and ternary systems containing a phosphoric ionic liquid. Fluid Phase Equilib. 2006, 247, 190–198. [Google Scholar] [CrossRef]
- Ren, J.; Zhao, Z.; Zhang, X. Vapor pressures, excess enthalpies, and specific heat capacities of the binary working pairs containing the ionic liquid 1-ethyl-3-methylimidazolium dimethylphosphate. J. Chem. Thermodyn. 2011, 43, 576–583. [Google Scholar] [CrossRef]
- Wang, J.F.; Li, C.X.; Wang, Z.H.; Li, Z.J.; Jiang, Y.B. Vapor pressure measurement for water, methanol, ethanol, and their binary mixtures in the presence of an ionic liquid 1-ethyl-3-methylimidazolium dimethylphosphate. Fluid Phase Equilib. 2007, 255, 186–192. [Google Scholar] [CrossRef]
- Shen, C.; Lu, Y.Z.; Li, X.M.; Li, C.X. Effect of the Ionic Liquid Triethylmethylammonium Dimethylphosphate on the Vapor Pressure of Water, Methanol, Ethanol, and Their Binary Mixtures. J. Chem. Eng. Data 2011, 56, 1933–1940. [Google Scholar] [CrossRef]
- Skonieczny, M.; Królikowska, M. Experimental data and correlation of the excess enthalpy for {ionic liquid (1) + ethanol (2)} binary systems. J. Chem. Thermodyn. under review. 2023. [Google Scholar]
- Hiraga, Y.; Goto, M.; Sato, Y.; Smith, R.L., Jr. Measurement of high pressure densities and atmospheric pressure viscosities of alkyl phosphate anion ionic liquids and correlation with the ɛ*-modified Sanchez-Lacombe equation of state. J. Chem. Thermodyn. 2017, 104, 73–81. [Google Scholar] [CrossRef]
- Gaciño, F.M.; Regueira, T.; Bolotov, A.V.; Sharipov, A.; Lugo, L.; Comuñas, M.J.P.; Fernández, J. Volumetric behaviour of six ionic liquids from T = (278 to 398) K and up to 120 MPa. J. Chem. Thermodyn. 2016, 93, 24–33. [Google Scholar] [CrossRef]
- Almeida, H.F.D.; Lopes, J.N.C.; Rebelo, L.P.N.; Coutinho, J.A.P.; Freire, M.G.; Marrucho, I.M. Densities and Viscosities of Mixtures of Two Ionic Liquids Containing a Common Cation. J. Chem. Eng. Data 2016, 61, 2828–2843. [Google Scholar] [CrossRef]
- Martins, M.A.R.; Coutinho, J.A.P.; Pinho, S.P.; Domańska, U. Measurements of activity coefficients at infinite dilution of organic solutes and water on polar imidazolium-based ionic liquids. J. Chem. Thermodyn. 2015, 91, 194–203. [Google Scholar] [CrossRef]
- Mac Dowell, N.; Llovell, F.; Sun, N.; Hallett, J.P.; George, A.; Hunt, P.A.; Welton, T.; Simmons, B.A.; Vega, L.F. New Experimental Density Data and Soft-SAFT Models of Alkylimidazolium ([CnC1im]+) Chloride (Cl−), Methylsulfate ([MeSO4]−), and Dimethyl-phosphate ([Me2PO4]−) Based Ionic Liquids. J. Phys. Chem. B 2014, 118, 6206–6221. [Google Scholar] [CrossRef]
- Freire, M.G.; Teles, A.R.R.; Rocha, M.A.A.; Schroder, B.; Neves, C.M.S.S.; Carvalho, P.J.; Evtuguin, D.V.; Santos, L.M.N.B.F.; Coutinho, J.A.P. Thermophysical Characterization of Ionic Liquids Able To Dissolve Biomass. J. Chem. Eng. Data 2011, 56, 4813–4822. [Google Scholar] [CrossRef]
- Wang, J.Y.; Zhao, F.Y.; Liu, R.J.; Hu, Y.Q. Thermophysical properties of 1-methyl-3-methylimidazolium dimethylphosphate and 1-ethyl-3-methylimidazolium diethyl-phosphate. J. Chem. Thermodyn. 2011, 43, 47–50. [Google Scholar] [CrossRef]
- Gong, Y.H.; Shen, C.; Lu, Y.Z.; Meng, H.; Li, C.X. Viscosity and density measurement for six binary mixtures of water (methanol or ethanol) with an ionic liquid [BMIM][DMP] or [EMIM][DMP] at atmospheric pressure in the temperature range of (293.15 to 333.15) K. J. Chem. Eng. Data 2012, 57, 33–39. [Google Scholar] [CrossRef]
- Krannich, M.; Heym, F.; Jess, A. Characterization of Six Hygroscopic Ionic Liquids with Regard to Their Suitability for Gas Dehydration: Density, Viscosity, Thermal and Oxidative Stability, Vapor Pressure, Diffusion Coefficient, and Activity Coefficient of Water. J. Chem. Eng. Data 2016, 61, 1162–1176. [Google Scholar] [CrossRef]
- Paduszyński, K.; Królikowska, M. Interactions between molecular solutes and task-specific ionic liquid: Measurements of infinite dilution activity coefficients and modelling. J. Mol. Liq. 2016, 221, 235–244. [Google Scholar] [CrossRef]
- Sánchez, P.B.; González, B.; Salgado, J.; Pádua, A.A.H.; García, J. Cosolvent effect on physical properties of 1,3-dimethylimidazolium dimethylphosphate and some theoretical insights on cellulose dissolution. J. Mol. Liq. 2018, 265, 114–120. [Google Scholar] [CrossRef]
- Wang, J.; Li, C.; Shen, C.; Wang, Z. Towards understanding the effect of electrostatic interactions on the density of ionic liquids. Fluid Phase Equilib. 2009, 279, 87–91. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Q.; Lu, X.; Qiao, C.; Zhang, S. Densities and Viscosities of Binary Mixtures Containing 1,3-Dimethylimidazolium Dimethylphosphate and Alcohols. J. Chem. Eng. Data 2014, 59, 2377–2388. [Google Scholar] [CrossRef]
- Królikowska, M.; Skonieczny, M.; Paduszyński, L.; Zawadzki, M. An influence of ionic liquid based additives on vapour pressure and physicochemical properties of {LiBr + water} mixtures—Measurements and COSMO-RS predictions. J. Solution Chem. 2021, 50, 473–502. [Google Scholar] [CrossRef]
- Andrade, E.N. da C. XLI. A theory of the viscosity of liquids—Part I. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1934, 17, 497–511. [Google Scholar] [CrossRef]
- Domańska, U.; Łachwa, J. Thermodynamics of Binary Mixtures of N-Methyl-2-Pyrrolidinone and Ketone. Experimental Results and Modelling of the (Solid + Liquid) Equilibrium and the (Vapour + Liquid) Equilibrium. The Modified UNIFAC (Do) Model Characterization. J. Chem. Thermodyn. 2005, 37, 692–704. [Google Scholar] [CrossRef]
- Vapor Pressure, Liquid Phase. Available online: https://app.knovel.com/hotlink/toc/id:kt00CZDV51/dippr-project-801-full/vapor-pressure-liquid (accessed on 22 December 2022).
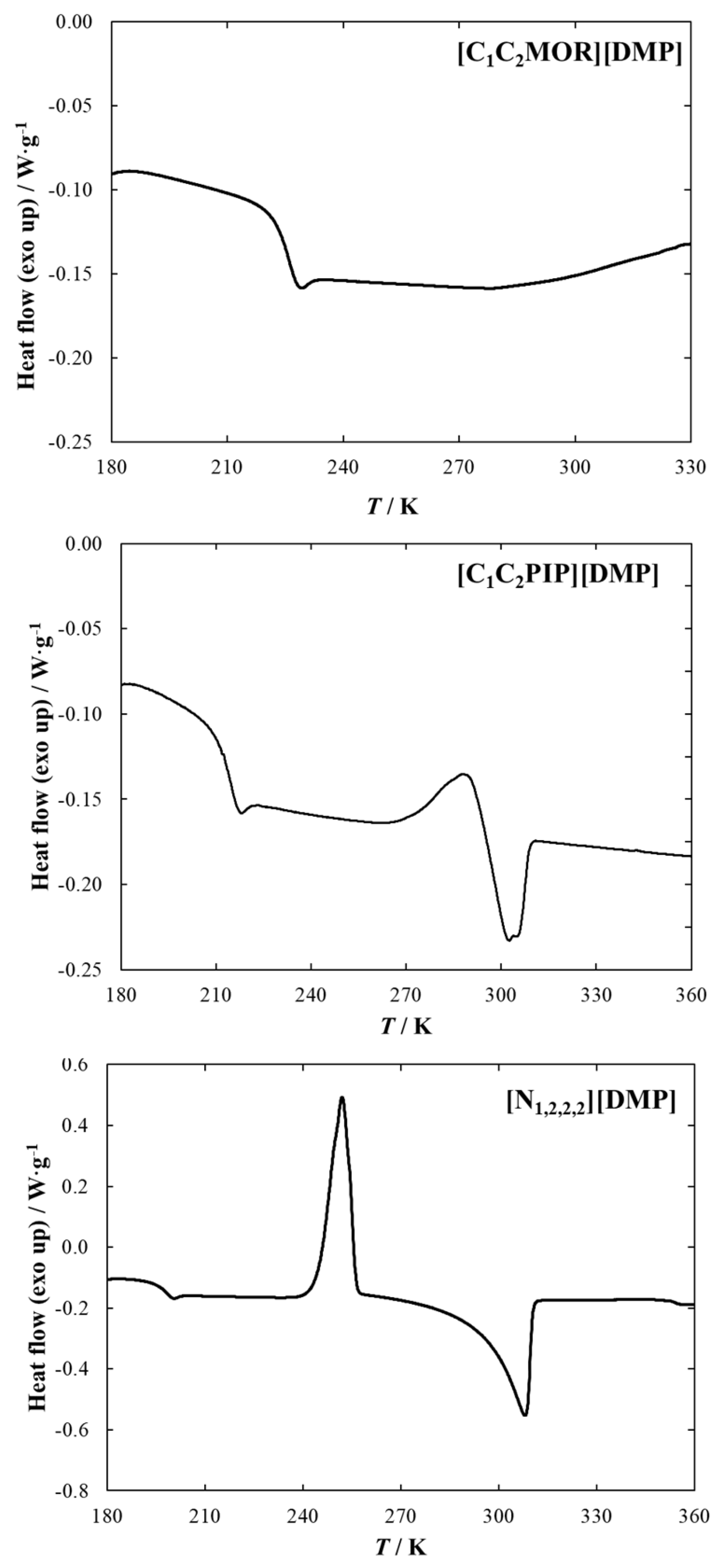


| IL | Tg/ (K) | ΔgCp/ (J mol−1 K−1) | Ttr,1/ (K) | Δtr,1H/ (kJ mol−1) | Tm/ (K) | ΔmH/ (kJ mol−1) |
|---|---|---|---|---|---|---|
| [C1C2MOR][DMP] (this work) | 222.2 | 132.7 | – | – | – | – |
| [C1C2PIP][DMP] (this work) | 211.0 | 103.9 | – | – | 295.2 | 2.026 |
| [N1,2,2,2][DMP] (this work) | 194.4 | 154.4 | – | – | 294.9 | 13.97 |
| [C1C2PYR][DMP] [42] | 189.7 | 119.6 | 274.5 | 0.861 | 285.2 | 0.727 |
| [C1C2OHPYR][DMP] [42] | 194.9 [42] 198.0 [51] | 148.1 [42] 132.7 [51] | – | – | – | – |
| x1 | P/(kPa) | γ2 | x1 | P/(kPa) | γ2 |
|---|---|---|---|---|---|
| T = 328.15 K | |||||
| 0.000 | 37.4 | 1.000 | 0.099 | 31.2 | 0.926 |
| 0.005 | 37.2 | 0.998 | 0.120 | 29.3 | 0.890 |
| 0.012 | 36.9 | 0.998 | 0.139 | 27.3 | 0.848 |
| 0.022 | 36.4 | 0.995 | 0.154 | 25.8 | 0.814 |
| 0.033 | 36.0 | 0.994 | 0.166 | 24.4 | 0.783 |
| 0.049 | 35.1 | 0.986 | 0.182 | 22.6 | 0.740 |
| 0.066 | 34.1 | 0.975 | 0.203 | 21.0 | 0.704 |
| 0.083 | 32.6 | 0.949 | 0.230 | 18.8 | 0.651 |
| T = 338.15 K | |||||
| 0.000 | 58.6 | 1.000 | 0.116 | 46.1 | 0.890 |
| 0.005 | 58.3 | 0.999 | 0.137 | 42.9 | 0.849 |
| 0.012 | 57.8 | 0.998 | 0.151 | 40.9 | 0.821 |
| 0.022 | 57.3 | 0.999 | 0.166 | 38.6 | 0.789 |
| 0.032 | 56.4 | 0.993 | 0.180 | 36.3 | 0.754 |
| 0.047 | 54.9 | 0.983 | 0.204 | 32.3 | 0.692 |
| 0.067 | 53.0 | 0.969 | 0.229 | 29.0 | 0.641 |
| 0.081 | 51.1 | 0.948 | 0.257 | 25.2 | 0.578 |
| 0.100 | 48.7 | 0.923 | 0.286 | 22.5 | 0.536 |
| T = 348.15 K | |||||
| 0.000 | 88.8 | 1.000 | 0.143 | 64.1 | 0.842 |
| 0.005 | 88.2 | 0.998 | 0.147 | 62.8 | 0.829 |
| 0.012 | 87.4 | 0.997 | 0.165 | 58.9 | 0.795 |
| 0.022 | 86.6 | 0.997 | 0.179 | 55.4 | 0.760 |
| 0.031 | 85.4 | 0.993 | 0.200 | 50.2 | 0.706 |
| 0.047 | 83.3 | 0.984 | 0.237 | 43.4 | 0.640 |
| 0.061 | 81.0 | 0.972 | 0.256 | 39.1 | 0.591 |
| 0.082 | 77.5 | 0.951 | 0.286 | 34.8 | 0.549 |
| 0.098 | 74.1 | 0.925 | 0.316 | 30.0 | 0.495 |
| 0.116 | 69.9 | 0.891 | 0.363 | 24.5 | 0.434 |
| x1 | P/(kPa) | γ2 | x1 | P/(kPa) | γ2 |
|---|---|---|---|---|---|
| T = 328.15 K | |||||
| 0.000 | 37.4 | 1.000 | 0.082 | 31.7 | 0.922 |
| 0.002 | 37.3 | 1.000 | 0.092 | 30.7 | 0.904 |
| 0.008 | 37.2 | 1.001 | 0.101 | 29.8 | 0.886 |
| 0.013 | 36.9 | 1.000 | 0.113 | 28.6 | 0.862 |
| 0.019 | 36.6 | 0.998 | 0.122 | 27.5 | 0.838 |
| 0.025 | 36.3 | 0.994 | 0.130 | 26.5 | 0.815 |
| 0.030 | 35.9 | 0.990 | 0.144 | 25.0 | 0.781 |
| 0.036 | 35.5 | 0.984 | 0.150 | 24.3 | 0.764 |
| 0.049 | 34.5 | 0.970 | 0.162 | 23.0 | 0.734 |
| 0.057 | 33.9 | 0.962 | 0.177 | 21.2 | 0.689 |
| 0.065 | 33.2 | 0.950 | 0.199 | 18.3 | 0.611 |
| 0.074 | 32.4 | 0.935 | |||
| T = 338.15 K | |||||
| 0.000 | 58.6 | 1.000 | 0.082 | 49.4 | 0.919 |
| 0.002 | 58.5 | 1.001 | 0.089 | 48.4 | 0.907 |
| 0.008 | 58.1 | 0.999 | 0.099 | 46.6 | 0.883 |
| 0.013 | 57.7 | 0.998 | 0.109 | 45.0 | 0.862 |
| 0.018 | 57.3 | 0.996 | 0.118 | 43.5 | 0.841 |
| 0.025 | 56.7 | 0.993 | 0.129 | 41.7 | 0.817 |
| 0.030 | 56.1 | 0.988 | 0.145 | 38.9 | 0.777 |
| 0.038 | 55.4 | 0.983 | 0.152 | 37.9 | 0.762 |
| 0.049 | 54.1 | 0.971 | 0.159 | 36.8 | 0.747 |
| 0.057 | 53.0 | 0.960 | 0.173 | 34.2 | 0.705 |
| 0.063 | 52.1 | 0.949 | 0.220 | 26.7 | 0.584 |
| 0.072 | 50.9 | 0.936 | |||
| T = 348.15 K | |||||
| 0.000 | 88.8 | 1.000 | 0.082 | 75.2 | 0.923 |
| 0.002 | 88.4 | 0.998 | 0.087 | 73.8 | 0.911 |
| 0.008 | 87.9 | 0.998 | 0.095 | 72.1 | 0.898 |
| 0.012 | 87.3 | 0.995 | 0.110 | 68.8 | 0.871 |
| 0.017 | 86.6 | 0.992 | 0.119 | 66.5 | 0.850 |
| 0.023 | 85.8 | 0.990 | 0.122 | 65.7 | 0.843 |
| 0.030 | 85.1 | 0.988 | 0.153 | 58.7 | 0.781 |
| 0.034 | 84.1 | 0.981 | 0.157 | 57.5 | 0.768 |
| 0.048 | 82.2 | 0.973 | 0.160 | 56.7 | 0.760 |
| 0.055 | 80.8 | 0.963 | 0.188 | 49.5 | 0.687 |
| 0.061 | 79.8 | 0.957 | 0.228 | 38.3 | 0.559 |
| 0.074 | 77.1 | 0.938 | |||
| x1 | P/(kPa) | γ2 | x1 | P/(kPa) | γ2 |
|---|---|---|---|---|---|
| T = 328.15 K | |||||
| 0.000 | 37.4 | 1.000 | 0.083 | 31.3 | 0.913 |
| 0.004 | 37.3 | 1.003 | 0.100 | 29.6 | 0.879 |
| 0.010 | 37.2 | 1.004 | 0.113 | 28.0 | 0.843 |
| 0.014 | 37.0 | 1.003 | 0.127 | 26.1 | 0.799 |
| 0.020 | 36.6 | 0.999 | 0.140 | 24.6 | 0.765 |
| 0.025 | 36.4 | 0.998 | 0.154 | 23.0 | 0.727 |
| 0.035 | 35.5 | 0.985 | 0.169 | 21.4 | 0.688 |
| 0.046 | 34.6 | 0.971 | 0.197 | 18.3 | 0.610 |
| 0.058 | 33.9 | 0.963 | 0.214 | 16.3 | 0.555 |
| 0.070 | 32.7 | 0.942 | |||
| T = 338.15 K | |||||
| 0.000 | 58.6 | 1.000 | 0.098 | 46.6 | 0.881 |
| 0.004 | 58.5 | 1.001 | 0.112 | 44.0 | 0.846 |
| 0.009 | 58.1 | 1.000 | 0.126 | 41.3 | 0.806 |
| 0.014 | 57.7 | 0.998 | 0.139 | 38.7 | 0.766 |
| 0.019 | 57.3 | 0.996 | 0.154 | 36.2 | 0.729 |
| 0.024 | 56.8 | 0.993 | 0.167 | 33.7 | 0.690 |
| 0.035 | 55.8 | 0.987 | 0.197 | 29.4 | 0.624 |
| 0.047 | 54.4 | 0.973 | 0.214 | 26.5 | 0.575 |
| 0.057 | 53.0 | 0.957 | 0.238 | 22.7 | 0.508 |
| 0.068 | 51.3 | 0.939 | 0.258 | 20.4 | 0.468 |
| 0.082 | 48.9 | 0.909 | |||
| T = 348.15 K | |||||
| 0.000 | 88.9 | 1.000 | 0.093 | 71.1 | 0.882 |
| 0.004 | 88.3 | 0.998 | 0.108 | 66.9 | 0.844 |
| 0.008 | 87.9 | 0.997 | 0.125 | 63.4 | 0.816 |
| 0.014 | 87.3 | 0.996 | 0.138 | 59.1 | 0.771 |
| 0.019 | 86.7 | 0.994 | 0.152 | 55.5 | 0.736 |
| 0.025 | 86.0 | 0.992 | 0.167 | 51.3 | 0.693 |
| 0.035 | 84.6 | 0.986 | 0.196 | 45.4 | 0.635 |
| 0.046 | 82.6 | 0.973 | 0.215 | 40.6 | 0.582 |
| 0.055 | 80.6 | 0.959 | 0.238 | 35.5 | 0.525 |
| 0.066 | 78.1 | 0.941 | 0.263 | 31.0 | 0.473 |
| 0.078 | 74.6 | 0.911 | 0.309 | 25.5 | 0.416 |
| NRTL Parameters | %AAD | ||||
|---|---|---|---|---|---|
| P/kPa | |||||
| {[C1C2MOR][DMP] (1) + Ethanol (2)} | |||||
| −18.842 | −4021.68 | −35.693 | 28191.0 | 0.3 | 0.34 |
| {[C1C2PIP][DMP] (1) + Ethanol (2)} | |||||
| −20.868 | −4174.55 | 9.473 | 14494.33 | 0.3 | 0.45 |
| {[N1,2,2,2][DMP] (1) + Ethanol (2)} | |||||
| −9.940 | −8120.8 | −139.231 | 64746.06 | 0.3 | 0.36 |
| T/K | 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | 318.15 | 323.15 | 328.15 | 333.15 | 338.15 |
|---|---|---|---|---|---|---|---|---|---|---|
| x1 | ρ/g∙cm−3 | |||||||||
| 1.0000 | 1.24485 | 1.24171 | 1.23856 | 1.23542 | 1.23228 | 1.22916 | 1.22604 | 1.22292 | 1.21975 | 1.21670 |
| 0.9012 | 1.23170 | 1.22853 | 1.22537 | 1.22226 | 1.21921 | 1.21617 | 1.21307 | 1.20987 | 1.20665 | 1.20307 |
| 0.7990 | 1.21554 | 1.21237 | 1.20919 | 1.20601 | 1.20285 | 1.19961 | 1.19649 | 1.19339 | 1.19030 | 1.18720 |
| 0.6997 | 1.19667 | 1.19362 | 1.19038 | 1.18721 | 1.18406 | 1.18091 | 1.17774 | 1.17457 | 1.17141 | 1.16825 |
| 0.5994 | 1.17423 | 1.17198 | 1.16874 | 1.16549 | 1.16224 | 1.15899 | 1.15574 | 1.15250 | 1.14927 | 1.14605 |
| 0.5012 | 1.14860 | 1.14533 | 1.14203 | 1.13874 | 1.13544 | 1.13215 | 1.12887 | 1.12559 | 1.12232 | 1.11905 |
| 0.4012 | 1.11712 | 1.11373 | 1.11033 | 1.10694 | 1.10356 | 1.10019 | 1.09683 | 1.09347 | 1.09012 | 1.08677 |
| 0.2991 | 1.07234 | 1.06885 | 1.06534 | 1.06185 | 1.05836 | 1.05487 | 1.05139 | 1.04791 | 1.04443 | 1.04095 |
| 0.2005 | 1.01399 | 1.01035 | 1.00670 | 1.00305 | 0.99939 | 0.99574 | 0.99208 | 0.98842 | 0.98475 | 0.98108 |
| 0.1605 | 0.98349 | 0.97977 | 0.97604 | 0.97230 | 0.96856 | 0.96482 | 0.96107 | 0.95730 | 0.95353 | 0.94975 |
| 0.1200 | 0.94739 | 0.94359 | 0.93976 | 0.93592 | 0.93207 | 0.92822 | 0.92434 | 0.92046 | 0.91656 | 0.91263 |
| 0.1001 | 0.92727 | 0.92341 | 0.91953 | 0.91563 | 0.91173 | 0.90781 | 0.90387 | 0.89991 | 0.89593 | 0.89193 |
| 0.0799 | 0.90493 | 0.90102 | 0.89707 | 0.89312 | 0.88914 | 0.88515 | 0.88114 | 0.87710 | 0.87303 | 0.86893 |
| 0.0401 | 0.85415 | 0.85009 | 0.84599 | 0.84187 | 0.83773 | 0.83356 | 0.82936 | 0.82512 | 0.82084 | 0.81650 |
| 0.0197 | 0.82326 | 0.81910 | 0.81491 | 0.81068 | 0.80643 | 0.80214 | 0.79782 | 0.79344 | 0.78901 | 0.78453 |
| 0.0000 | 0.78953 | 0.78528 | 0.78096 | 0.77660 | 0.77221 | 0.76777 | 0.76328 | 0.75874 | 0.75413 | 0.74944 |
| VE/cm3·mol−1 | ||||||||||
| 0.9012 | −0.0993 | −0.1064 | −0.1172 | −0.1349 | −0.1625 | −0.1895 | −0.2077 | −0.2106 | −0.2187 | −0.1509 |
| 0.7990 | −0.1645 | −0.1836 | −0.2041 | −0.2243 | −0.2483 | −0.2591 | −0.2889 | −0.3230 | −0.3672 | −0.3955 |
| 0.6997 | −0.1922 | −0.2390 | −0.2635 | −0.2979 | −0.3363 | −0.3744 | −0.4116 | −0.4507 | −0.4998 | −0.5374 |
| 0.5994 | −0.2751 | −0.4320 | −0.4699 | −0.5075 | −0.5469 | −0.5866 | −0.6289 | −0.6749 | −0.7307 | −0.7792 |
| 0.5012 | −0.4964 | −0.5388 | −0.5820 | −0.6280 | −0.6750 | −0.7244 | −0.7781 | −0.8350 | −0.9015 | −0.9622 |
| 0.4012 | −0.8506 | −0.8936 | −0.9403 | −0.9903 | −1.0439 | −1.1007 | −1.1622 | −1.2275 | −1.3021 | −1.3740 |
| 0.2991 | −0.9330 | −0.9788 | −1.0279 | −1.0816 | −1.1382 | −1.1978 | −1.2625 | −1.3315 | −1.4086 | −1.4858 |
| 0.2005 | −0.9800 | −1.0239 | −1.0725 | −1.1242 | −1.1782 | −1.2368 | −1.2990 | −1.3658 | −1.4396 | −1.5163 |
| 0.1605 | −0.9257 | −0.9667 | −1.0125 | −1.0608 | −1.1122 | −1.1676 | −1.2268 | −1.2890 | −1.3588 | −1.4316 |
| 0.1200 | −0.8387 | −0.8763 | −0.9173 | −0.9610 | −1.0069 | −1.0570 | −1.1092 | −1.1663 | −1.2291 | −1.2942 |
| 0.1001 | −0.7763 | −0.8104 | −0.8486 | −0.8888 | −0.9319 | −0.9777 | −1.0266 | −1.0786 | −1.1362 | −1.1974 |
| 0.0799 | −0.6999 | −0.7309 | −0.7645 | −0.8016 | −0.8394 | −0.8806 | −0.9249 | −0.9715 | −1.0228 | −1.0772 |
| 0.0401 | −0.4815 | −0.5010 | −0.5230 | −0.5470 | −0.5722 | −0.5993 | −0.6285 | −0.6591 | −0.6931 | −0.7285 |
| 0.0197 | −0.2785 | −0.2887 | −0.3022 | −0.3158 | −0.3305 | −0.3463 | −0.3640 | −0.3812 | −0.4006 | −0.4225 |
| η/mPa·s | ||||||||||
| 1.0000 | 18870 | 10070 | 5752 | 3414 | 2093 | 1333 | 875.7 | 592.2 | 410.8 | 289.6 |
| 0.9012 | 5816 | 3534 | 2350 | 1658 | 1318 | 740.6 | 521.5 | 388.3 | 229.6 | 172.8 |
| 0.7990 | 3981 | 2398 | 1466 | 934.0 | 627.2 | 426.0 | 299.5 | 214.6 | 157.6 | 118.1 |
| 0.6997 | 1755 | 1223 | 866.5 | 608.0 | 376.0 | 268.0 | 190.9 | 142.1 | 104.6 | 82.77 |
| 0.5994 | 792.2 | 522.3 | 358.3 | 251.1 | 181.6 | 134.0 | 102.3 | 79.03 | 62.38 | 50.49 |
| 0.5012 | 285.4 | 205.2 | 148.3 | 110.4 | 83.74 | 65.41 | 53.11 | 43.2 | 36.04 | 30.87 |
| 0.4012 | 103.3 | 78.36 | 59.78 | 47.38 | 38.49 | 31.84 | 27.51 | 23.96 | 21.39 | 19.48 |
| 0.2991 | 37.30 | 30.04 | 24.79 | 20.6 | 17.57 | 15.14 | 13.45 | 12.35 | 11.22 | 10.47 |
| 0.2005 | 13.18 | 11.22 | 9.63 | 8.38 | 7.43 | 6.71 | 6.16 | 5.69 | 5.52 | 5.41 |
| 0.1001 | 5.27 | 4.59 | 3.92 | 3.51 | 3.17 | 2.92 | 2.78 | 2.65 | 2.56 | 2.38 |
| 0.0000 | 1.19 | 1.08 | 0.98 | 0.90 | 0.82 | 0.75 | 0.69 | 0.63 | 0.58 | 0.54 |
| T/K | 293.15 b | 298.15 | 303.15 | 308.15 | 313.15 | 318.15 | 323.15 | 328.15 | 333.15 | 338.15 |
|---|---|---|---|---|---|---|---|---|---|---|
| x1 | ρ/g∙cm−3 | |||||||||
| 1.0000 | 1.16712 | 1.16404 | 1.16094 | 1.15782 | 1.15465 | 1.15157 | 1.14852 | 1.14548 | 1.14242 | 1.13937 |
| 0.8993 | 1.15746 | 1.15434 | 1.15121 | 1.14802 | 1.14492 | 1.14184 | 1.13876 | 1.13567 | 1.13259 | 1.12952 |
| 0.7968 | 1.14571 | 1.14253 | 1.13930 | 1.13617 | 1.13306 | 1.12994 | 1.12682 | 1.12370 | 1.12060 | 1.11751 |
| 0.7031 | 1.13206 | 1.12901 | 1.12586 | 1.12269 | 1.11952 | 1.11635 | 1.11318 | 1.11004 | 1.10691 | 1.10379 |
| 0.6007 | 1.11454 | 1.11134 | 1.10812 | 1.10489 | 1.10166 | 1.09844 | 1.09524 | 1.09205 | 1.08888 | 1.08572 |
| 0.5028 | 1.09324 | 1.08994 | 1.08664 | 1.08335 | 1.08008 | 1.07682 | 1.07357 | 1.07033 | 1.06710 | 1.06388 |
| 0.4027 | 1.06633 | 1.06297 | 1.05961 | 1.05626 | 1.05291 | 1.04958 | 1.04626 | 1.04295 | 1.03965 | 1.03635 |
| 0.3001 | 1.03024 | 1.02685 | 1.02341 | 1.01997 | 1.01653 | 1.01310 | 1.00967 | 1.00625 | 1.00283 | 0.99942 |
| 0.2001 | 0.98145 | 0.97792 | 0.97436 | 0.97078 | 0.96720 | 0.96360 | 0.96001 | 0.95642 | 0.95282 | 0.94922 |
| 0.1597 | 0.95621 | 0.95255 | 0.94887 | 0.94520 | 0.94152 | 0.93784 | 0.93416 | 0.93046 | 0.92673 | 0.92299 |
| 0.1203 | 0.92693 | 0.92318 | 0.91941 | 0.91564 | 0.91186 | 0.90808 | 0.90429 | 0.90048 | 0.89666 | 0.89282 |
| 0.1001 | 0.90964 | 0.90583 | 0.90201 | 0.89818 | 0.89434 | 0.89049 | 0.88662 | 0.88274 | 0.87884 | 0.87492 |
| 0.0803 | 0.89065 | 0.88678 | 0.88289 | 0.87899 | 0.87508 | 0.87116 | 0.86721 | 0.86325 | 0.85926 | 0.85524 |
| 0.0402 | 0.84613 | 0.84214 | 0.83808 | 0.83400 | 0.82990 | 0.82577 | 0.82162 | 0.81743 | 0.81320 | 0.80892 |
| 0.0203 | 0.82031 | 0.81621 | 0.81204 | 0.80785 | 0.80363 | 0.79937 | 0.79508 | 0.79074 | 0.78636 | 0.78191 |
| 0.0000 | 0.78953 | 0.78528 | 0.78096 | 0.77660 | 0.77221 | 0.76777 | 0.76328 | 0.75874 | 0.75413 | 0.74944 |
| VE/cm3·mol−1 | ||||||||||
| 0.8993 | −0.2409 | −0.2463 | −0.2541 | −0.2552 | −0.2811 | −0.2959 | −0.3062 | −0.3136 | −0.3271 | −0.3416 |
| 0.7968 | −0.4575 | −0.4662 | −0.4711 | −0.4963 | −0.5332 | −0.5561 | −0.5758 | −0.5952 | −0.6227 | −0.6522 |
| 0.7031 | −0.5227 | −0.5626 | −0.5923 | −0.6231 | −0.6619 | −0.6905 | −0.7169 | −0.7484 | −0.7866 | −0.8278 |
| 0.6007 | −0.6526 | −0.6831 | −0.7158 | −0.7514 | −0.7943 | −0.8308 | −0.8690 | −0.9100 | −0.9594 | −1.0128 |
| 0.5028 | −0.6951 | −0.7248 | −0.7597 | −0.8001 | −0.8499 | −0.8954 | −0.9422 | −0.9925 | −1.0500 | −1.1123 |
| 0.4027 | −0.7960 | −0.8320 | −0.8735 | −0.9205 | −0.9738 | −1.0259 | −1.0805 | −1.1391 | −1.2052 | −1.2760 |
| 0.3001 | −0.9006 | −0.9471 | −0.9944 | −1.0459 | −1.1031 | −1.1602 | −1.2197 | −1.2838 | −1.3545 | −1.4320 |
| 0.2001 | −0.9233 | −0.9689 | −1.0178 | −1.0692 | −1.1255 | −1.1809 | −1.2405 | −1.3044 | −1.3741 | −1.4504 |
| 0.1597 | −0.9110 | −0.9501 | −0.9933 | −1.0417 | −1.0937 | −1.1475 | −1.2049 | −1.2650 | −1.3291 | −1.3991 |
| 0.1203 | −0.8506 | −0.8864 | −0.9265 | −0.9707 | −1.0182 | −1.0683 | −1.1215 | −1.1775 | −1.2394 | −1.3066 |
| 0.1001 | −0.7927 | −0.8255 | −0.8634 | −0.9045 | −0.9488 | −0.9951 | −1.0438 | −1.0963 | −1.1538 | −1.2168 |
| 0.0803 | −0.6922 | −0.7216 | −0.7552 | −0.7920 | −0.8317 | −0.8737 | −0.9175 | −0.9650 | −1.0167 | −1.0731 |
| 0.0402 | −0.4381 | −0.4596 | −0.4816 | −0.5055 | −0.5311 | −0.5580 | −0.5876 | −0.6184 | −0.6523 | −0.6891 |
| 0.0203 | −0.2836 | −0.2968 | −0.3102 | −0.3255 | −0.3413 | −0.3579 | −0.3762 | −0.3948 | −0.4164 | −0.4391 |
| η/mPa·s | ||||||||||
| 1.0000 | 3276 | 2213 | 1485 | 1029 | 717.2 | 489.7 | 342.4 | 247.4 | 180.2 | 136.7 |
| 0.8993 | 2174 | 1473 | 1011 | 679.9 | 463.3 | 326.6 | 235.3 | 174.4 | 131.1 | 101.0 |
| 0.7968 | 1088 | 775.1 | 547.7 | 399.5 | 277.5 | 205.8 | 153.8 | 116.2 | 90.21 | 70.84 |
| 0.7031 | 662.0 | 471.0 | 330.4 | 235.7 | 172.9 | 129.7 | 99.70 | 77.71 | 61.75 | 49.88 |
| 0.6007 | 308.6 | 235.6 | 172.2 | 128.8 | 99.0 | 77.0 | 61.03 | 49.02 | 40.06 | 33.11 |
| 0.5028 | 135.7 | 108.4 | 83.4 | 65.52 | 52.1 | 42.3 | 34.63 | 28.72 | 24.06 | 20.59 |
| 0.4027 | 47.36 | 39.73 | 32.3 | 26.66 | 22.3 | 18.9 | 16.13 | 13.90 | 12.15 | 10.70 |
| 0.3001 | 19.86 | 17.06 | 14.5 | 12.48 | 10.8 | 9.4 | 8.27 | 7.29 | 6.45 | 5.90 |
| 0.2001 | 6.73 | 6.02 | 5.3 | 4.66 | 4.1 | 3.7 | 3.37 | 3.03 | 2.85 | 2.58 |
| 0.1001 | 2.85 | 2.59 | 2.3 | 2.09 | 1.9 | 1.7 | 1.58 | 1.45 | 1.34 | 1.27 |
| 0.0000 | 1.19 | 1.08 | 0.98 | 0.90 | 0.82 | 0.75 | 0.69 | 0.63 | 0.58 | 0.54 |
| T/K | 293.15 b | 298.15 | 303.15 | 308.15 | 313.15 | 318.15 | 323.15 | 328.15 | 333.15 | 338.15 |
|---|---|---|---|---|---|---|---|---|---|---|
| x1 | ρ/g∙cm−3 | |||||||||
| 1.0000 | 1.13000 | 1.12703 | 1.12405 | 1.12104 | 1.11800 | 1.11495 | 1.11191 | 1.10888 | 1.10585 | 1.10284 |
| 0.8987 | 1.12037 | 1.11735 | 1.11432 | 1.11127 | 1.10822 | 1.10519 | 1.10215 | 1.09912 | 1.09609 | 1.09306 |
| 0.7991 | 1.10938 | 1.10642 | 1.10336 | 1.10029 | 1.09722 | 1.09417 | 1.09111 | 1.08806 | 1.08500 | 1.08194 |
| 0.6988 | 1.09687 | 1.09374 | 1.09059 | 1.08745 | 1.08431 | 1.08119 | 1.07806 | 1.07495 | 1.07184 | 1.06874 |
| 0.5986 | 1.08088 | 1.07769 | 1.07448 | 1.07129 | 1.06810 | 1.06493 | 1.06176 | 1.05860 | 1.05545 | 1.05231 |
| 0.4998 | 1.06194 | 1.05871 | 1.05546 | 1.05222 | 1.04899 | 1.04576 | 1.04253 | 1.03931 | 1.03610 | 1.03289 |
| 0.4004 | 1.03727 | 1.03394 | 1.03061 | 1.02728 | 1.02396 | 1.02064 | 1.01733 | 1.01403 | 1.01074 | 1.00744 |
| 0.3011 | 1.00514 | 1.00171 | 0.99827 | 0.99484 | 0.99141 | 0.98799 | 0.98457 | 0.98116 | 0.97774 | 0.97433 |
| 0.1999 | 0.96064 | 0.95707 | 0.95349 | 0.94990 | 0.94631 | 0.94273 | 0.93914 | 0.93555 | 0.93196 | 0.92836 |
| 0.1600 | 0.93820 | 0.93455 | 0.93089 | 0.92723 | 0.92356 | 0.91989 | 0.91622 | 0.91253 | 0.90884 | 0.90514 |
| 0.1201 | 0.91144 | 0.90770 | 0.90394 | 0.90018 | 0.89641 | 0.89263 | 0.88885 | 0.88504 | 0.88123 | 0.87739 |
| 0.0998 | 0.89627 | 0.89248 | 0.88867 | 0.88485 | 0.88102 | 0.87717 | 0.87331 | 0.86944 | 0.86554 | 0.86162 |
| 0.0802 | 0.88003 | 0.87618 | 0.87231 | 0.86842 | 0.86453 | 0.86061 | 0.85668 | 0.85272 | 0.84874 | 0.84472 |
| 0.0402 | 0.84022 | 0.83621 | 0.83216 | 0.82810 | 0.82401 | 0.81989 | 0.81574 | 0.81156 | 0.80734 | 0.80306 |
| 0.0201 | 0.81643 | 0.81231 | 0.80814 | 0.80395 | 0.79974 | 0.79549 | 0.79119 | 0.78686 | 0.78247 | 0.77802 |
| 0.0000 | 0.78953 | 0.78528 | 0.78096 | 0.77660 | 0.77221 | 0.76777 | 0.76328 | 0.75874 | 0.75413 | 0.74944 |
| VE/cm3·mol−1 | ||||||||||
| 0.8987 | −0.0968 | −0.1001 | −0.1040 | −0.1100 | −0.1215 | −0.1391 | −0.1538 | −0.1692 | −0.1855 | −0.1992 |
| 0.7991 | −0.2078 | −0.2336 | −0.2458 | −0.2620 | −0.2835 | −0.3113 | −0.3370 | −0.3643 | −0.3915 | −0.4175 |
| 0.6988 | −0.4187 | −0.4309 | −0.4434 | −0.4628 | −0.4874 | −0.5182 | −0.5480 | −0.5814 | −0.6172 | −0.6547 |
| 0.5986 | −0.5048 | −0.5222 | −0.5406 | −0.5670 | −0.5985 | −0.6363 | −0.6754 | −0.7172 | −0.7638 | −0.8131 |
| 0.4998 | −0.6481 | −0.6746 | −0.7028 | −0.7375 | −0.7784 | −0.8231 | −0.8698 | −0.9200 | −0.9755 | −1.0335 |
| 0.4004 | −0.7140 | −0.7430 | −0.7766 | −0.8152 | −0.8596 | −0.9083 | −0.9608 | −1.0173 | −1.0798 | −1.1449 |
| 0.3011 | −0.7638 | −0.7968 | −0.8339 | −0.8768 | −0.9241 | −0.9769 | −1.0332 | −1.0940 | −1.1592 | −1.2304 |
| 0.1999 | −0.7911 | −0.8258 | −0.8651 | −0.9080 | −0.9550 | −1.0076 | −1.0632 | −1.1230 | −1.1888 | −1.2597 |
| 0.1600 | −0.7849 | −0.8185 | −0.8567 | −0.8993 | −0.9450 | −0.9953 | −1.0499 | −1.1070 | −1.1703 | −1.2390 |
| 0.1201 | −0.7174 | −0.7486 | −0.7838 | −0.8232 | −0.8654 | −0.9115 | −0.9620 | −1.0143 | −1.0729 | −1.1356 |
| 0.0998 | −0.6978 | −0.7277 | −0.7616 | −0.7988 | −0.8387 | −0.8816 | −0.9281 | −0.9783 | −1.0322 | −1.0912 |
| 0.0802 | −0.6532 | −0.6805 | −0.7120 | −0.7459 | −0.7831 | −0.8226 | −0.8657 | −0.9108 | −0.9605 | −1.0138 |
| 0.0402 | −0.4220 | −0.4400 | −0.4606 | −0.4840 | −0.5081 | −0.5342 | −0.5623 | −0.5924 | −0.6254 | −0.6603 |
| 0.0201 | −0.2362 | −0.2464 | −0.2583 | −0.2720 | −0.2869 | −0.3029 | −0.3191 | −0.3372 | −0.3564 | −0.3776 |
| η/mPa·s | ||||||||||
| 1.0000 | 679.6 | 453.4 | 308.3 | 216.5 | 155.8 | 115.9 | 87.38 | 66.80 | 52.33 | 41.46 |
| 0.8987 | 456.3 | 311.7 | 217.0 | 156.6 | 115.0 | 86.57 | 66.31 | 51.39 | 40.64 | 32.77 |
| 0.7991 | 307.3 | 214.3 | 152.2 | 112.1 | 83.82 | 64.08 | 50.21 | 39.51 | 31.60 | 25.66 |
| 0.6988 | 197.2 | 156.8 | 115.5 | 84.00 | 64.38 | 50.80 | 40.12 | 31.19 | 25.37 | 20.88 |
| 0.5986 | 119.4 | 89.15 | 66.95 | 51.50 | 40.53 | 32.31 | 26.40 | 21.80 | 18.30 | 15.48 |
| 0.4998 | 67.67 | 51.89 | 40.71 | 32.43 | 26.40 | 21.70 | 18.21 | 15.45 | 13.17 | 11.50 |
| 0.4004 | 34.79 | 28.01 | 22.84 | 18.91 | 16.00 | 13.57 | 11.71 | 10.20 | 9.14 | 8.13 |
| 0.3011 | 17.41 | 14.58 | 12.43 | 10.65 | 9.24 | 8.15 | 7.20 | 6.45 | 5.88 | 5.39 |
| 0.1999 | 7.99 | 6.99 | 6.12 | 5.40 | 4.85 | 4.41 | 4.06 | 3.76 | 3.51 | 3.32 |
| 0.0998 | 3.77 | 3.38 | 3.01 | 2.71 | 2.46 | 2.27 | 2.12 | 1.98 | 1.80 | 1.65 |
| 0.0000 | 1.19 | 1.08 | 0.98 | 0.90 | 0.82 | 0.75 | 0.69 | 0.63 | 0.58 | 0.54 |
| x1 | 104·σ | ||
|---|---|---|---|
| {[C1C2MOR][DMP] (1) + Ethanol (2)} | |||
| 1.0000 | 1.24171 | 5.087 | 0.225 |
| 0.9012 | 1.22862 | 5.167 | 1.970 |
| 0.7990 | 1.21235 | 5.250 | 0.390 |
| 0.6997 | 1.19357 | 5.350 | 0.478 |
| 0.5994 | 1.17171 | 5.498 | 3.060 |
| 0.5012 | 1.14533 | 5.796 | 0.282 |
| 0.4012 | 1.11373 | 6.121 | 0.139 |
| 0.2991 | 1.06886 | 6.602 | 0.344 |
| 0.2005 | 1.01038 | 7.332 | 0.671 |
| 0.1605 | 0.97981 | 7.756 | 0.878 |
| 0.1200 | 0.94364 | 8.304 | 1.190 |
| 0.1001 | 0.92348 | 8.632 | 1.370 |
| 0.0799 | 0.90109 | 9.016 | 1.610 |
| 0.0401 | 0.85019 | 10.007 | 2.150 |
| 0.0197 | 0.81923 | 10.697 | 2.530 |
| 0.0000 | 0.78543 | 11.568 | 3.019 |
| {[C1C2PIP][DMP] (1) + Ethanol (2)} | |||
| 1.0000 | 1.16401 | 5.354 | 0.332 |
| 0.8993 | 1.15432 | 5.430 | 0.235 |
| 0.7968 | 1.14251 | 5.533 | 0.271 |
| 0.7031 | 1.12899 | 5.638 | 0.521 |
| 0.6007 | 1.11133 | 5.830 | 0.183 |
| 0.5028 | 1.08993 | 6.050 | 0.059 |
| 0.4027 | 1.06297 | 6.338 | 0.063 |
| 0.3001 | 1.02685 | 6.757 | 0.426 |
| 0.2001 | 0.97795 | 7.426 | 0.811 |
| 0.1597 | 0.95259 | 7.851 | 0.932 |
| 0.1203 | 0.92323 | 8.328 | 1.031 |
| 0.1001 | 0.90589 | 8.644 | 1.223 |
| 0.0803 | 0.88685 | 9.009 | 1.424 |
| 0.0402 | 0.84223 | 9.990 | 2.095 |
| 0.0203 | 0.81632 | 10.646 | 2.498 |
| 0.0000 | 0.78565 | 11.572 | 3.019 |
| {[N1,2,2,2][DMP] (1) + Ethanol (2)} | |||
| 1.0000 | 1.12706 | 5.418 | 0.625 |
| 0.8987 | 1.11736 | 5.487 | 0.315 |
| 0.7991 | 1.10640 | 5.576 | 0.533 |
| 0.6988 | 1.09374 | 5.776 | 0.149 |
| 0.5986 | 1.07768 | 5.955 | 0.747 |
| 0.4998 | 1.05871 | 6.166 | 0.231 |
| 0.4004 | 1.03395 | 6.485 | 0.210 |
| 0.3011 | 1.00172 | 6.918 | 0.341 |
| 0.1999 | 0.95710 | 7.596 | 0.635 |
| 0.1600 | 0.93459 | 7.970 | 0.826 |
| 0.1201 | 0.90775 | 8.457 | 1.079 |
| 0.0998 | 0.89254 | 8.758 | 1.292 |
| 0.0802 | 0.87625 | 9.094 | 1.512 |
| 0.0402 | 0.83631 | 10.043 | 2.095 |
| 0.0201 | 0.81243 | 10.696 | 2.495 |
| 0.0000 | 0.78699 | 11.537 | 3.019 |
| σ | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [C1C2MOR][DMP] (1) + Ethanol (2) | −0.369 | 0.109 | 0.882 | 0.058 | −0.937 | 0.018 | 0.487 | 0.073 | −0.159 | 1.276 | 0.004 |
| [C1C2PIP][DMP] (1) + Ethanol (2) | −0.229 | −0.311 | 0.910 | −0.174 | −0.906 | 0.163 | 0.285 | 0.511 | −0.105 | 1.105 | 0.004 |
| [N1,2,2,2][DMP] (1) + Ethanol (2) | −0.307 | 0.119 | 0.694 | 0.076 | −0.745 | 0.032 | 0.403 | −0.028 | −0.143 | 1.226 | 0.003 |
| 102·a0 | 102·a1 | 102·a2 | b0 | b1 | b2 | σ/cm3·mol−1 | |
|---|---|---|---|---|---|---|---|
| [C1C2MOR][DMP] (1) + Ethanol (2) | −4.121 | 3.644 | −4.329 | 10.020 | −6.258 | 8.474 | 0.058 |
| [C1C2PIP][DMP] (1) + Ethanol (2) | −3.627 | 3.834 | −4.850 | 7.978 | −8.537 | 9.304 | 0.071 |
| [N1,2,2,2][DMP] (1) + Ethanol (2) | −3.198 | 3.472 | −4.904 | 7.122 | −7.092 | 11.145 | 0.084 |
| x1 | A | 10−3B/K | RMSE |
|---|---|---|---|
| {[C1C2MOR][DMP] (1) + Ethanol (2)} | |||
| 1.0000 | −21.526 | −9.150 | |
| 0.9012 | −17.479 | −7.670 | |
| 0.7990 | −18.216 | −7.732 | |
| 0.6997 | −16.160 | −6.929 | |
| 0.5994 | −14.097 | −6.056 | 0.091 |
| 0.5012 | −11.247 | −4.925 | |
| 0.4012 | −8.077 | −3.688 | |
| 0.2991 | −6.062 | −2.811 | |
| 0.2005 | −4.407 | −2.017 | |
| 0.1001 | −4.223 | −1.695 | |
| 0.0000 | −5.519 | −1.666 | |
| {[C1C2PIP][DMP] (1) + Ethanol (2)} | |||
| 1.0000 | −15.911 | −7.034 | |
| 0.8993 | −16.125 | −6.977 | |
| 0.7968 | −13.820 | −6.098 | |
| 0.7031 | −13.965 | −5.995 | |
| 0.6007 | −11.382 | −5.014 | 6.073 |
| 0.5028 | −9.439 | −4.204 | |
| 0.4027 | −7.433 | −3.307 | |
| 0.3001 | −6.238 | −2.702 | |
| 0.2001 | −5.338 | −2.121 | |
| 0.1001 | −5.155 | −1.815 | |
| 0.0000 | −5.502 | −1.666 | |
| {[N1,2,2,2][DMP] (1) + Ethanol (2)} | |||
| 1.0000 | −14.534 | −6.143 | |
| 0.8987 | −13.720 | −5.790 | |
| 0.7991 | −12.935 | −5.445 | |
| 0.6988 | −11.951 | −5.053 | |
| 0.5986 | −10.640 | −4.500 | |
| 0.4998 | −9.152 | −3.898 | 0.124 |
| 0.4004 | −7.440 | −3.204 | |
| 0.3011 | −6.036 | −2.593 | |
| 0.1999 | −4.607 | −1.946 | |
| 0.0998 | −4.758 | −1.778 | |
| 0.0000 | −5.517 | −1.666 | |
| Structure | Name, Abbreviation, CAS No. | M/ g·mol−1 | ρ/ g·cm−3 | η/ mPa·s |
|---|---|---|---|---|
 | 1-ethyl-1-methylmorpholinium dimethyl phosphate, [C1C2MOR][DMP]; CAS No. – | 255.25 | 1.23228 | 2093 |
 | 1-ethyl-1-methylpiperidinium dimethyl phosphate, [C1C2PIP][DMP]; CAS No. – | 253.28 | 1.15465 | 717.2 |
 | N,N,N-trimethyl-N-methylammonium dimethyl phosphate, [N1,2,2,2][DMP]; CAS No. – | 241.26 | 1.11800 | 155.8 |
| Sample | Source | Water Content/ppm | Initial Mass Fraction Purity | Purification Method | Final Mass Fraction Purity | Analysis Method |
|---|---|---|---|---|---|---|
| [C1C2MOR][DMP] | Own synthesis | 9000 | − | Vacuum heating | ≥0.950 | Karl-Fischer, 1H NMR |
| [C1C2PIP][DMP] | Io-li-tec | 7000 | − | Vacuum heating extraction | ≥0.970 | Karl-Fischer, 1H NMR |
| [N1,2,2,2][DMP] | Own synthesis [41] | 8000 | − | Vacuum heating, extraction | ≥0.950 | Karl-Fischer, 1H NMR |
| Water | Own source | − | − | Reversed osmosis, ion exchange | 0.9999 | Density |
| Ethanol | POCH | 90 | 0.998 | − | 0.998 | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skonieczny, M.; Królikowska, M.; Królikowski, M. Investigation of Thermodynamic Properties of Dimethyl Phosphate-Based ILs for Use as Working Fluids in Absorption Refrigeration Technology. Molecules 2023, 28, 1940. https://doi.org/10.3390/molecules28041940
Skonieczny M, Królikowska M, Królikowski M. Investigation of Thermodynamic Properties of Dimethyl Phosphate-Based ILs for Use as Working Fluids in Absorption Refrigeration Technology. Molecules. 2023; 28(4):1940. https://doi.org/10.3390/molecules28041940
Chicago/Turabian StyleSkonieczny, Michał, Marta Królikowska, and Marek Królikowski. 2023. "Investigation of Thermodynamic Properties of Dimethyl Phosphate-Based ILs for Use as Working Fluids in Absorption Refrigeration Technology" Molecules 28, no. 4: 1940. https://doi.org/10.3390/molecules28041940
APA StyleSkonieczny, M., Królikowska, M., & Królikowski, M. (2023). Investigation of Thermodynamic Properties of Dimethyl Phosphate-Based ILs for Use as Working Fluids in Absorption Refrigeration Technology. Molecules, 28(4), 1940. https://doi.org/10.3390/molecules28041940






