Modification of Multiwalled Carbon Nanotubes and Their Mechanism of Demanganization
Abstract
1. Introduction
2. Results and Discussion
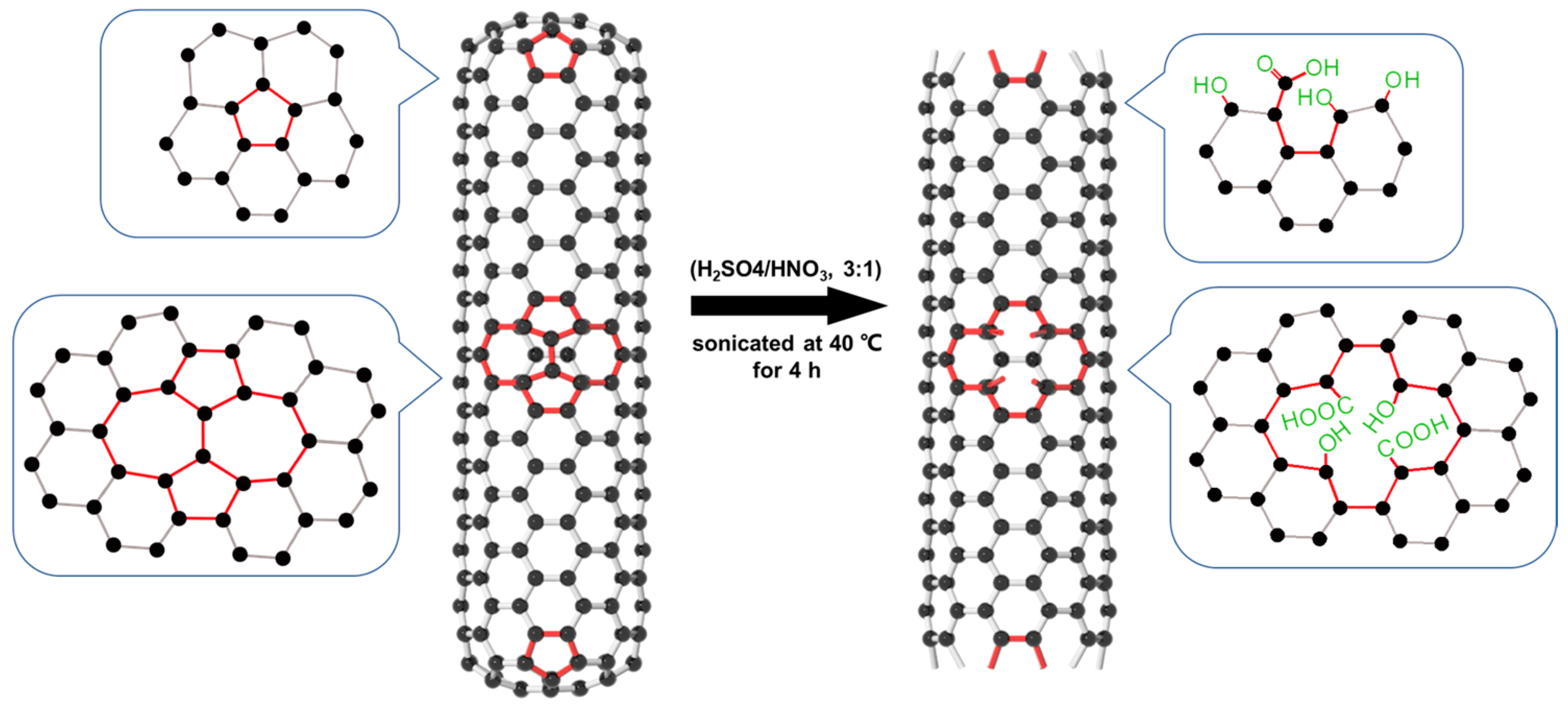
2.1. Characterization of MWCNTs and M-MWCNTs
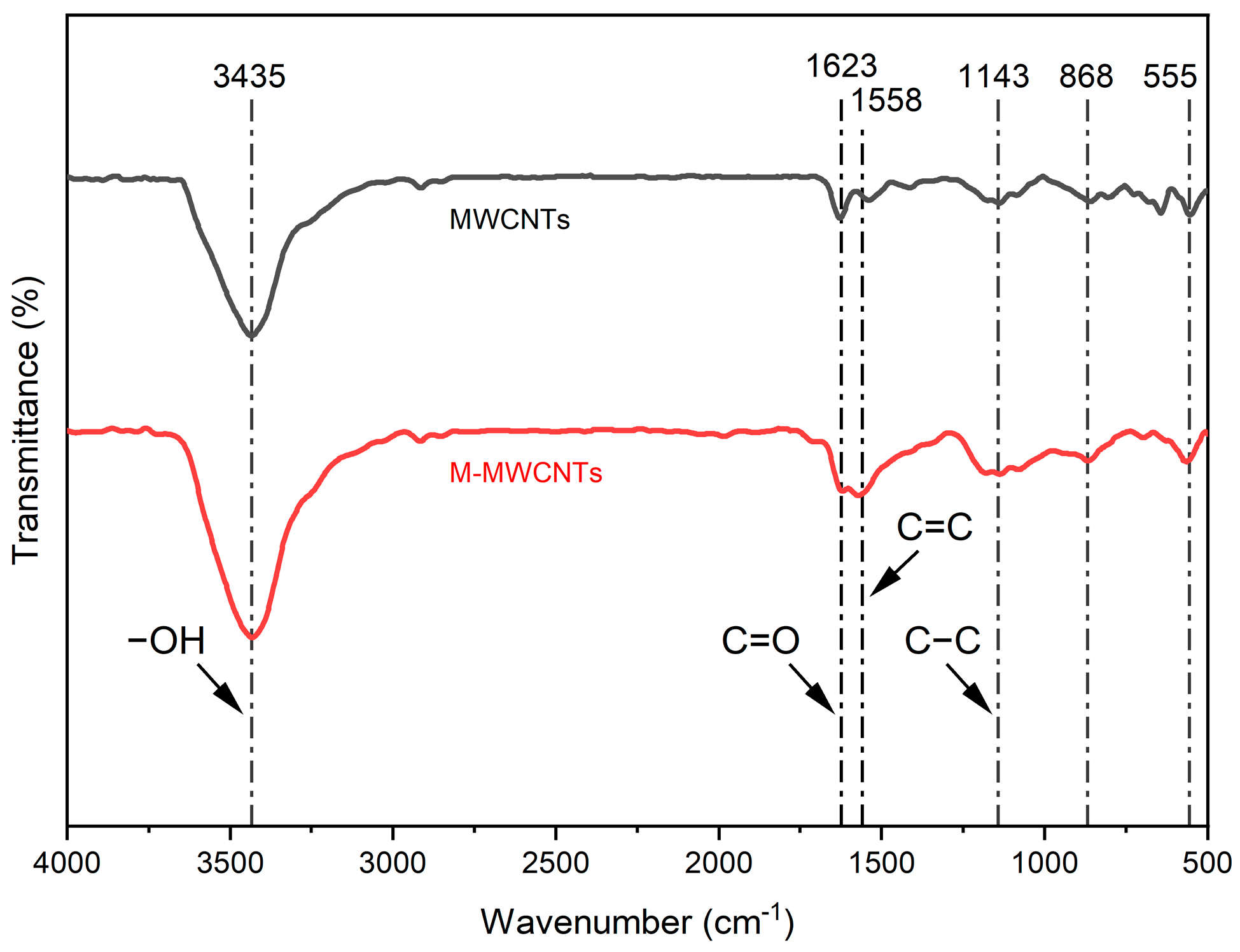
2.1.1. FT-IR
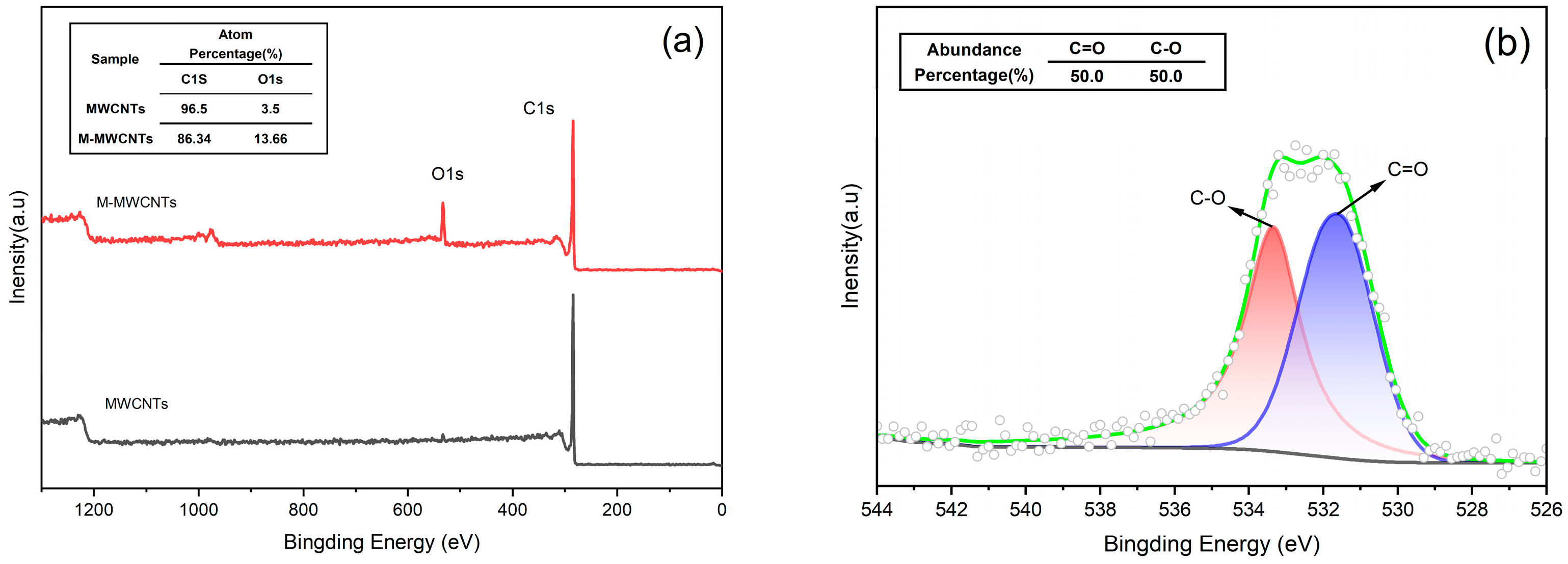
2.1.2. XPS
2.1.3. SEM
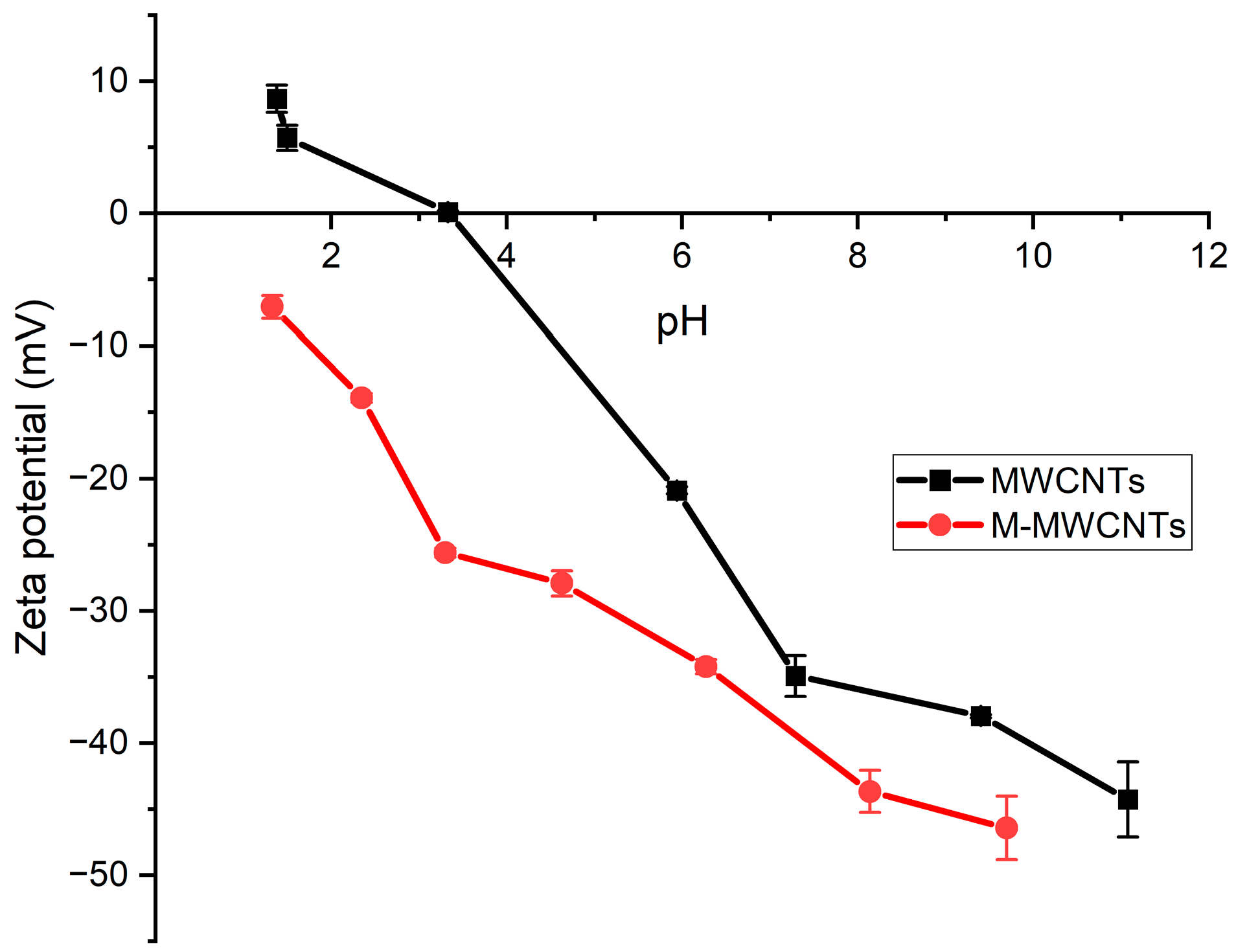
2.1.4. Zeta Potentials
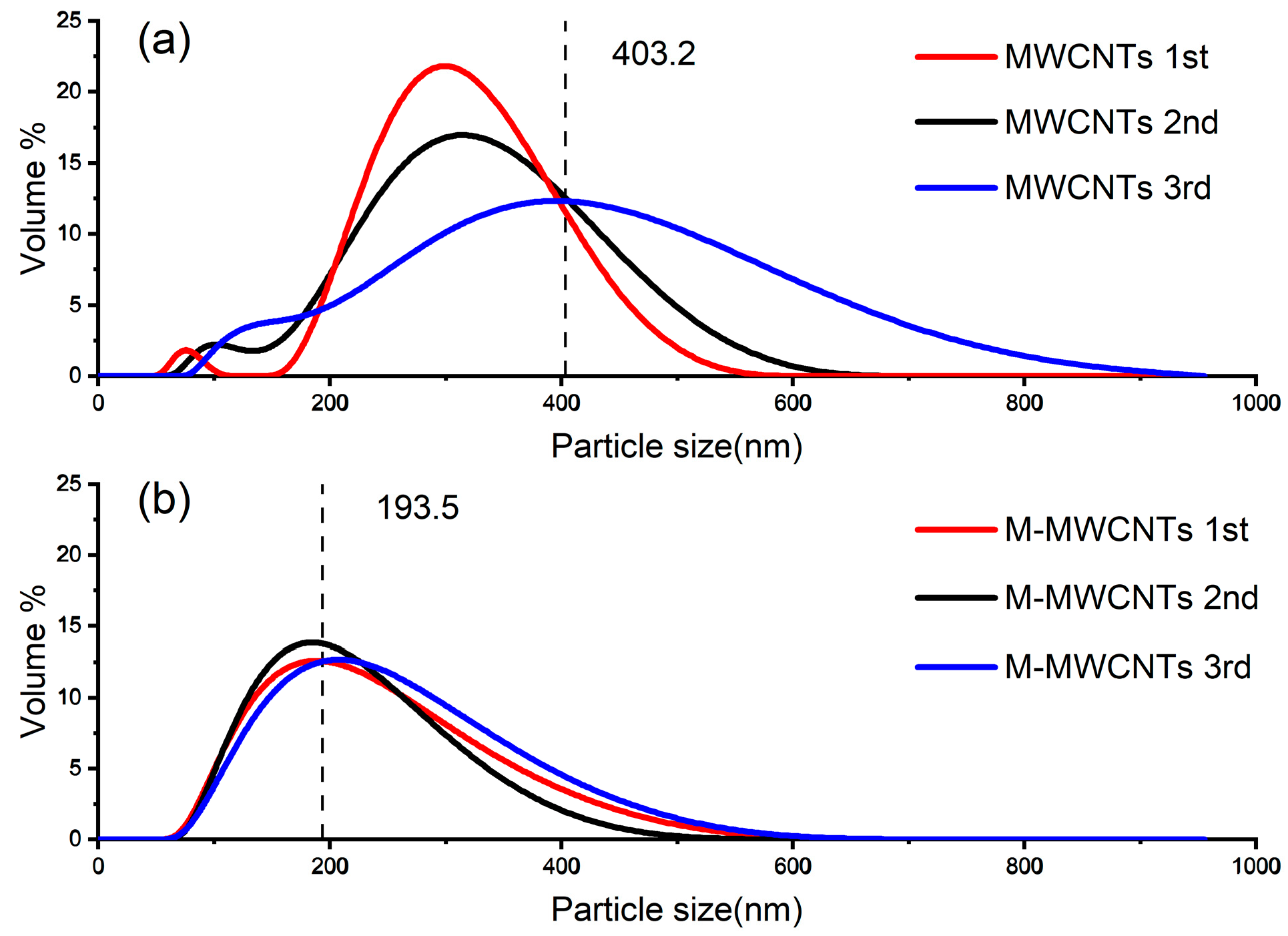
2.1.5. Size
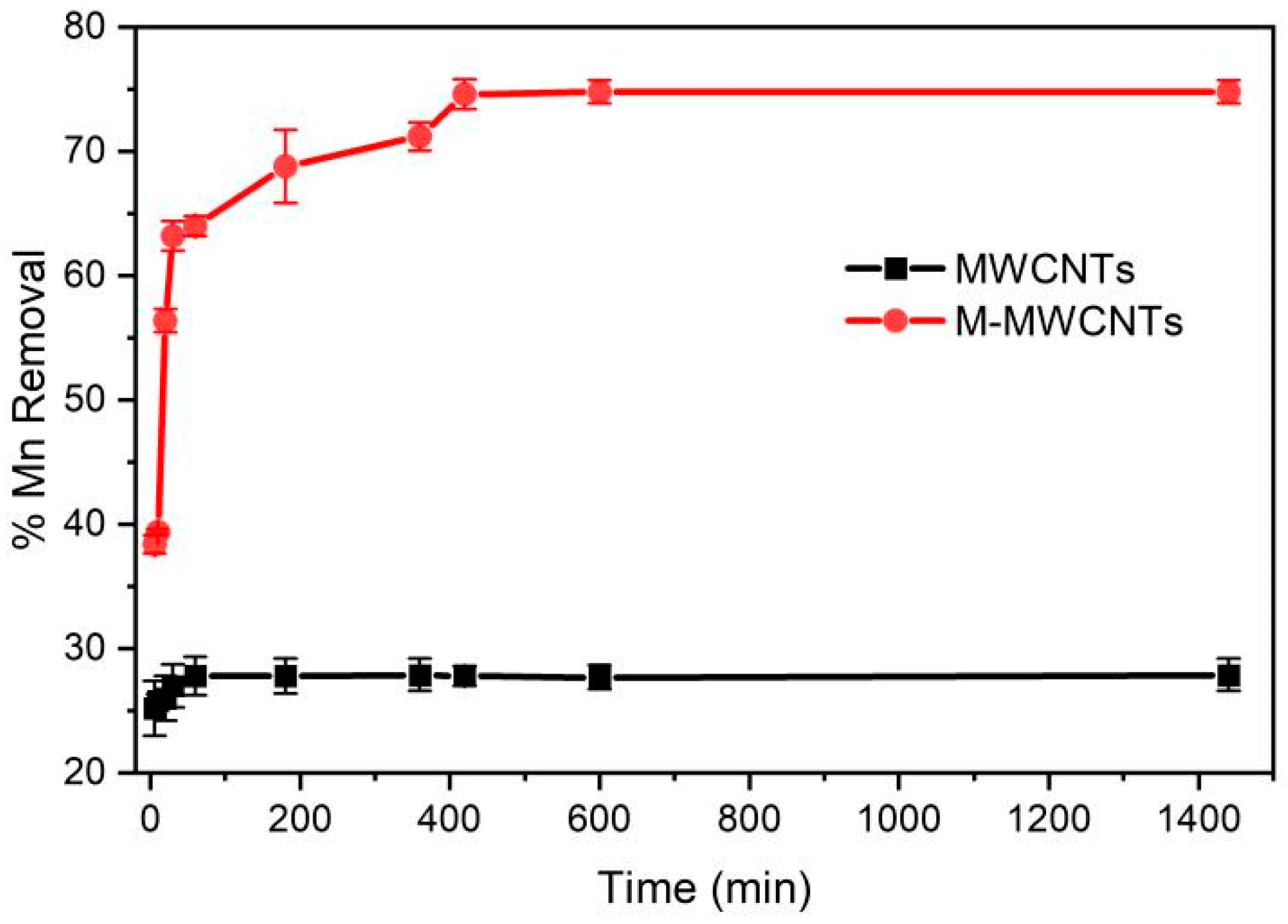
2.2. Effect of Contact Time
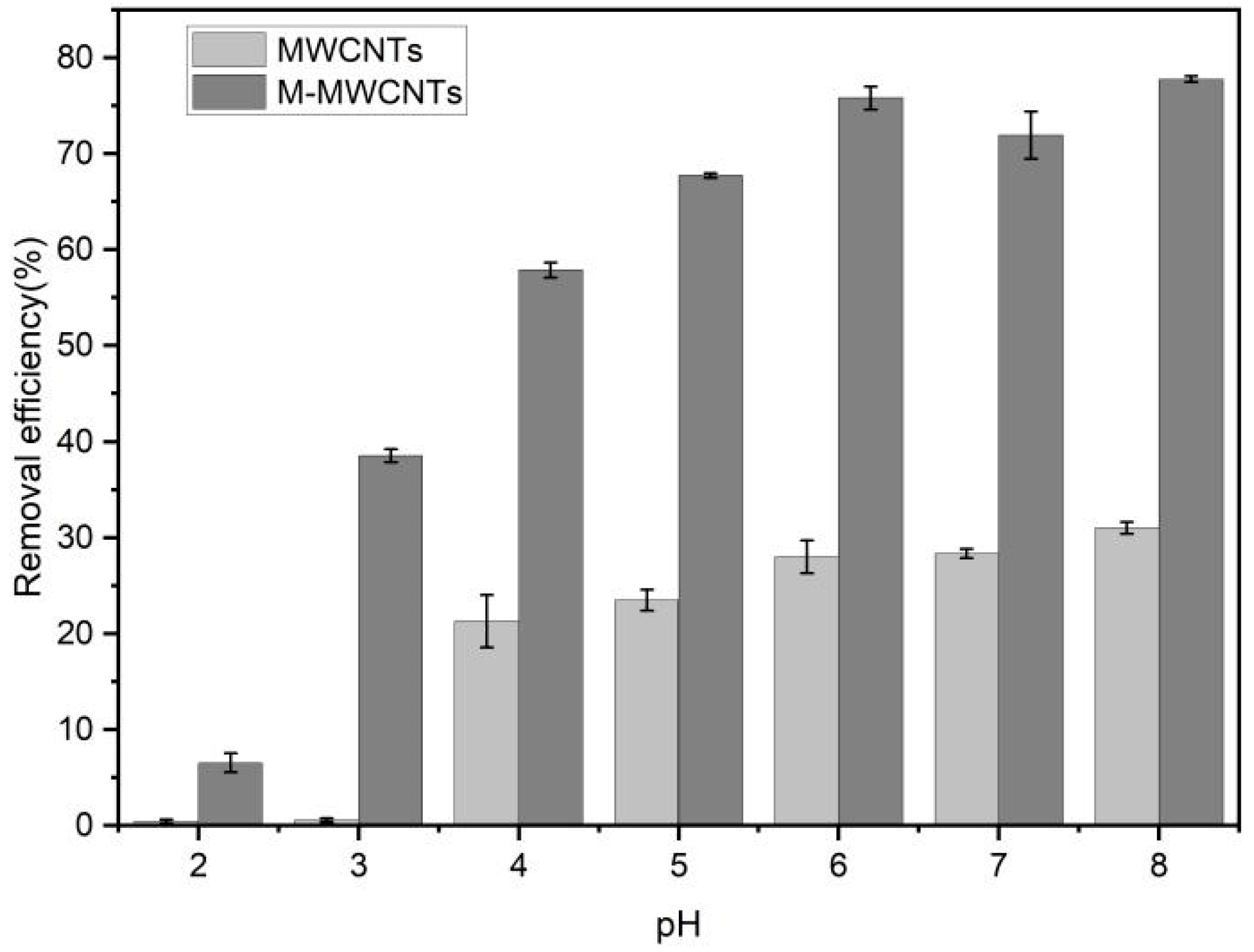
2.3. Effect of pH
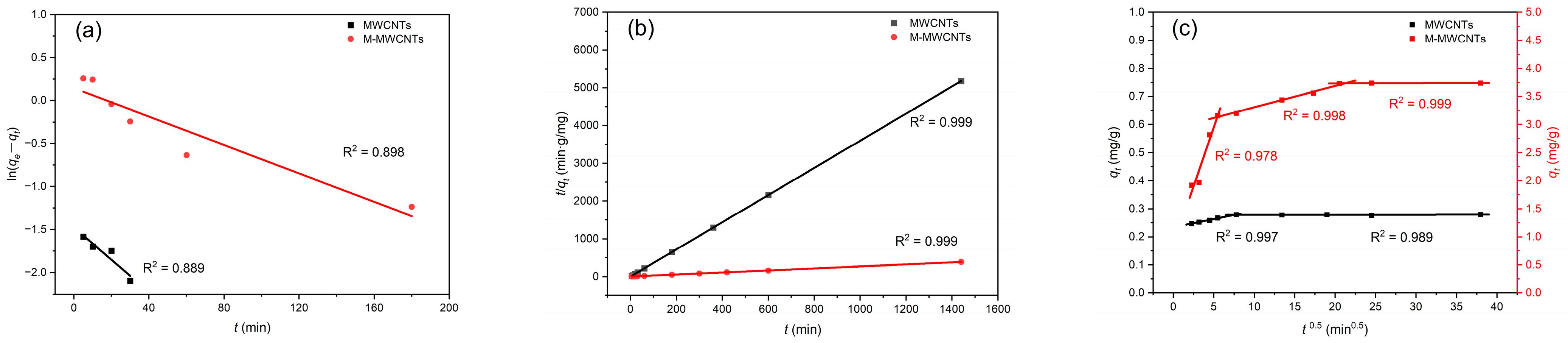
2.4. Kinetic Modeling
2.5. Isotherm Modeling
2.6. PSO–BP Modeling
3. Materials and Methods
3.1. Materials
3.2. Preparation of M-MWCNTs
3.3. Characterization Analysis Methods
3.4. Batch Experiments
3.5. Theory
3.5.1. Kinetic Modeling
3.5.2. Isotherm Modeling
3.5.3. PSO-BP Modeling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Appendix A
| (a) | |||||
| No. | pH | C/mg/L | Time/h | T/K | Adsorption Rate % |
| 1 | 2.18 | 5 | 180 | 298 | 0.4 |
| 2 | 3.23 | 5 | 180 | 298 | 0.6 |
| 3 | 4.17 | 5 | 180 | 298 | 20.4 |
| 4 | 5.15 | 5 | 180 | 298 | 23.5 |
| 5 | 6.17 | 5 | 180 | 298 | 28.5 |
| 6 | 7.18 | 5 | 180 | 298 | 28.31 |
| 7 | 8.25 | 5 | 180 | 298 | 30.4 |
| 8 | 5.58 | 1 | 180 | 298 | 58 |
| 9 | 5.58 | 2 | 180 | 298 | 42 |
| 10 | 5.58 | 5 | 180 | 298 | 28.6 |
| 11 | 5.58 | 10 | 180 | 298 | 9.6 |
| 12 | 5.58 | 20 | 180 | 298 | 11 |
| 13 | 5.58 | 50 | 180 | 298 | 6.5 |
| 14 | 5.58 | 5 | 5 | 298 | 22.2 |
| 15 | 5.58 | 5 | 10 | 298 | 25.8 |
| 16 | 5.58 | 5 | 20 | 298 | 26.8 |
| 17 | 5.58 | 5 | 30 | 298 | 28 |
| 18 | 5.58 | 5 | 60 | 298 | 27 |
| 19 | 5.58 | 5 | 180 | 298 | 28.6 |
| 20 | 5.58 | 5 | 180 | 298 | 28.2 |
| 21 | 5.58 | 10 | 180 | 298 | 15.99 |
| 22 | 5.58 | 20 | 180 | 298 | 11.01 |
| 23 | 5.58 | 50 | 180 | 298 | 5.45 |
| 24 | 5.58 | 5 | 180 | 308 | 29.34 |
| 25 | 5.58 | 10 | 180 | 308 | 16.61 |
| 26 | 5.58 | 20 | 180 | 308 | 12.38 |
| 27 | 5.58 | 50 | 180 | 308 | 5.89 |
| 28 | 5.58 | 5 | 180 | 318 | 29.6 |
| 29 | 5.58 | 10 | 180 | 318 | 18.01 |
| 30 | 5.58 | 20 | 180 | 318 | 14.95 |
| 31 | 5.58 | 50 | 180 | 318 | 6.7 |
| 32 | 5.58 | 5 | 180 | 328 | 32.45 |
| 33 | 5.58 | 10 | 180 | 328 | 18.59 |
| 34 | 5.58 | 20 | 180 | 328 | 15.22 |
| 35 | 5.58 | 50 | 180 | 328 | 7.03 |
| 36 | 2.18 | 5 | 180 | 298 | 0.4 |
| 37 | 3.23 | 5 | 180 | 298 | 0.58 |
| 38 | 4.17 | 5 | 180 | 298 | 19.4 |
| 39 | 5.15 | 5 | 180 | 298 | 23.18 |
| 40 | 6.17 | 5 | 180 | 298 | 27.5 |
| 41 | 7.18 | 5 | 180 | 298 | 28.5 |
| 42 | 8.25 | 5 | 180 | 298 | 31 |
| 43 | 5.58 | 1 | 180 | 298 | 59 |
| 44 | 5.58 | 2 | 180 | 298 | 43 |
| 45 | 5.58 | 5 | 180 | 298 | 26.2 |
| 46 | 5.58 | 10 | 180 | 298 | 29.6 |
| 47 | 5.58 | 20 | 180 | 298 | 10.75 |
| 48 | 5.58 | 50 | 180 | 298 | 6 |
| 49 | 5.58 | 5 | 5 | 298 | 26.4 |
| 50 | 5.58 | 5 | 10 | 298 | 25.2 |
| 51 | 5.58 | 5 | 20 | 298 | 23.8 |
| 52 | 5.58 | 5 | 30 | 298 | 27.6 |
| 53 | 5.58 | 5 | 60 | 298 | 27 |
| 54 | 5.58 | 5 | 180 | 298 | 26.2 |
| 55 | 5.58 | 5 | 180 | 298 | 27.8 |
| 56 | 5.58 | 10 | 180 | 298 | 15.45 |
| 57 | 5.58 | 20 | 180 | 298 | 11.05 |
| 58 | 5.58 | 50 | 180 | 298 | 5.59 |
| 59 | 5.58 | 5 | 180 | 308 | 28.5 |
| 60 | 5.58 | 10 | 180 | 308 | 17.12 |
| 61 | 5.58 | 20 | 180 | 308 | 12.51 |
| 62 | 5.58 | 50 | 180 | 308 | 6.05 |
| 63 | 5.58 | 5 | 180 | 318 | 29.8 |
| 64 | 5.58 | 10 | 180 | 318 | 17.8 |
| 65 | 5.58 | 20 | 180 | 318 | 14.5 |
| 66 | 5.58 | 50 | 180 | 318 | 6.58 |
| 67 | 5.58 | 5 | 180 | 328 | 32.5 |
| 68 | 5.58 | 10 | 180 | 328 | 18.51 |
| 69 | 5.58 | 20 | 180 | 328 | 15.1 |
| 70 | 5.58 | 50 | 180 | 328 | 7.22 |
| 71 | 2.18 | 5 | 180 | 298 | 0.4 |
| 72 | 3.23 | 5 | 180 | 298 | 0.51 |
| 73 | 4.17 | 5 | 180 | 298 | 24.2 |
| 74 | 5.15 | 5 | 180 | 298 | 23.8 |
| 75 | 6.17 | 5 | 180 | 298 | 28.1 |
| 76 | 7.18 | 5 | 180 | 298 | 28.2 |
| 77 | 8.25 | 5 | 180 | 298 | 31.6 |
| 78 | 5.58 | 1 | 180 | 298 | 49 |
| 79 | 5.58 | 2 | 180 | 298 | 40.5 |
| 80 | 5.58 | 5 | 180 | 298 | 28.6 |
| 81 | 5.58 | 10 | 180 | 298 | 8.6 |
| 82 | 5.58 | 20 | 180 | 298 | 11.5 |
| 83 | 5.58 | 50 | 180 | 298 | 4 |
| 84 | 5.58 | 5 | 5 | 298 | 25.6 |
| 85 | 5.58 | 5 | 10 | 298 | 24.8 |
| 86 | 5.58 | 5 | 20 | 298 | 27 |
| 87 | 5.58 | 5 | 30 | 298 | 24.8 |
| 88 | 5.58 | 5 | 60 | 298 | 29.6 |
| 89 | 5.58 | 5 | 180 | 298 | 28.6 |
| 90 | 5.58 | 5 | 180 | 298 | 27.6 |
| 91 | 5.58 | 10 | 180 | 298 | 16.5 |
| 92 | 5.58 | 20 | 180 | 298 | 10.9 |
| 93 | 5.58 | 50 | 180 | 298 | 5.5 |
| 94 | 5.58 | 5 | 180 | 308 | 28.2 |
| 95 | 5.58 | 10 | 180 | 308 | 16.98 |
| 96 | 5.58 | 20 | 180 | 308 | 12.63 |
| 97 | 5.58 | 50 | 180 | 308 | 6.09 |
| 98 | 5.58 | 5 | 180 | 318 | 28.6 |
| 99 | 5.58 | 10 | 180 | 318 | 17.1 |
| 100 | 5.58 | 20 | 180 | 318 | 14 |
| 101 | 5.58 | 50 | 180 | 318 | 6.04 |
| 102 | 5.58 | 5 | 180 | 328 | 32.49 |
| 103 | 5.58 | 10 | 180 | 328 | 18.58 |
| 104 | 5.58 | 20 | 180 | 328 | 14.8 |
| 105 | 5.58 | 50 | 180 | 328 | 7.31 |
| (b) | |||||
| No. | pH | C/mg/L | Time/h | T/K | Adsorption Rate % |
| 1 | 2.36 | 5 | 1440 | 298 | 5.6 |
| 2 | 3.38 | 5 | 1440 | 298 | 37.8 |
| 3 | 4.32 | 5 | 1440 | 298 | 57 |
| 4 | 5.31 | 5 | 1440 | 298 | 74.3 |
| 5 | 6.3 | 5 | 1440 | 298 | 76.1 |
| 6 | 7.37 | 5 | 1440 | 298 | 75.6 |
| 7 | 8.32 | 5 | 1440 | 298 | 77.8 |
| 8 | 5.58 | 5 | 1440 | 298 | 75.8 |
| 9 | 5.58 | 10 | 1440 | 298 | 48.8 |
| 10 | 5.58 | 20 | 1440 | 298 | 27.6 |
| 11 | 5.58 | 50 | 1440 | 298 | 12.4 |
| 12 | 5.58 | 80 | 1440 | 298 | 11.8 |
| 13 | 5.58 | 100 | 1440 | 298 | 5.69 |
| 14 | 5.58 | 5 | 5 | 298 | 38.2 |
| 15 | 5.58 | 5 | 10 | 298 | 39.2 |
| 16 | 5.58 | 5 | 20 | 298 | 53.6 |
| 17 | 5.58 | 5 | 30 | 298 | 64 |
| 18 | 5.58 | 5 | 60 | 298 | 64.4 |
| 19 | 5.58 | 5 | 180 | 298 | 68.8 |
| 20 | 5.58 | 5 | 300 | 298 | 69.8 |
| 21 | 5.58 | 5 | 420 | 298 | 75.8 |
| 22 | 5.58 | 5 | 600 | 298 | 75.8 |
| 23 | 5.58 | 5 | 1440 | 298 | 75.8 |
| 24 | 5.58 | 5 | 1440 | 298 | 75.1 |
| 25 | 5.58 | 10 | 1440 | 298 | 47.1 |
| 26 | 5.58 | 20 | 1440 | 298 | 27.5 |
| 27 | 5.58 | 50 | 1440 | 298 | 11.4 |
| 28 | 5.58 | 5 | 1440 | 308 | 77.2 |
| 29 | 5.58 | 10 | 1440 | 308 | 49.8 |
| 30 | 5.58 | 20 | 1440 | 308 | 29 |
| 31 | 5.58 | 50 | 1440 | 308 | 12.4 |
| 32 | 5.58 | 5 | 1440 | 318 | 80.4 |
| 33 | 5.58 | 10 | 1440 | 318 | 50.9 |
| 34 | 5.58 | 20 | 1440 | 318 | 30 |
| 35 | 5.58 | 50 | 1440 | 318 | 12.4 |
| 36 | 5.58 | 5 | 1440 | 328 | 81 |
| 37 | 5.58 | 10 | 1440 | 328 | 52 |
| 38 | 5.58 | 20 | 1440 | 328 | 30.4 |
| 39 | 5.58 | 50 | 1440 | 328 | 13 |
| 40 | 2.36 | 5 | 1440 | 298 | 7.6 |
| 41 | 3.38 | 5 | 1440 | 298 | 38.6 |
| 42 | 4.32 | 5 | 1440 | 298 | 58.4 |
| 43 | 5.31 | 5 | 1440 | 298 | 73.8 |
| 44 | 6.3 | 5 | 1440 | 298 | 76.3 |
| 45 | 7.37 | 5 | 1440 | 298 | 75.4 |
| 46 | 8.32 | 5 | 1440 | 298 | 77.9 |
| 47 | 5.58 | 5 | 1440 | 298 | 77 |
| 48 | 5.58 | 10 | 1440 | 298 | 47 |
| 49 | 5.58 | 20 | 1440 | 298 | 27.4 |
| 50 | 5.58 | 50 | 1440 | 298 | 10.4 |
| 51 | 5.58 | 80 | 1440 | 298 | 10.2 |
| 52 | 5.58 | 100 | 1440 | 298 | 5.8 |
| 53 | 5.58 | 5 | 5 | 298 | 37.8 |
| 54 | 5.58 | 5 | 10 | 298 | 39.2 |
| 55 | 5.58 | 5 | 20 | 298 | 62.4 |
| 56 | 5.58 | 5 | 30 | 298 | 61.8 |
| 57 | 5.58 | 5 | 60 | 298 | 63.5 |
| 58 | 5.58 | 5 | 180 | 298 | 68.5 |
| 59 | 5.58 | 5 | 300 | 298 | 72 |
| 60 | 5.58 | 5 | 420 | 298 | 72.5 |
| 61 | 5.58 | 5 | 600 | 298 | 74.2 |
| 62 | 5.58 | 5 | 1440 | 298 | 74.2 |
| 63 | 5.58 | 5 | 1440 | 298 | 74.8 |
| 64 | 5.58 | 10 | 1440 | 298 | 47.8 |
| 65 | 5.58 | 20 | 1440 | 298 | 27.29 |
| 66 | 5.58 | 50 | 1440 | 298 | 11.41 |
| 67 | 5.58 | 5 | 1440 | 308 | 77.8 |
| 68 | 5.58 | 10 | 1440 | 308 | 49.8 |
| 69 | 5.58 | 20 | 1440 | 308 | 28.8 |
| 70 | 5.58 | 50 | 1440 | 308 | 11.9 |
| 71 | 5.58 | 5 | 1440 | 318 | 79.8 |
| 72 | 5.58 | 10 | 1440 | 318 | 51.2 |
| 73 | 5.58 | 20 | 1440 | 318 | 30.1 |
| 74 | 5.58 | 50 | 1440 | 318 | 12.5 |
| 75 | 5.58 | 5 | 1440 | 328 | 81.5 |
| 76 | 5.58 | 10 | 1440 | 328 | 51.1 |
| 77 | 5.58 | 20 | 1440 | 328 | 30.5 |
| 78 | 5.58 | 50 | 1440 | 328 | 13.1 |
| 79 | 2.36 | 5 | 1440 | 298 | 6.4 |
| 80 | 3.38 | 5 | 1440 | 298 | 39.2 |
| 81 | 4.32 | 5 | 1440 | 298 | 58.2 |
| 82 | 5.31 | 5 | 1440 | 298 | 74.5 |
| 83 | 6.3 | 5 | 1440 | 298 | 75.9 |
| 84 | 7.37 | 5 | 1440 | 298 | 75.2 |
| 85 | 8.32 | 5 | 1440 | 298 | 77.8 |
| 86 | 5.58 | 5 | 1440 | 298 | 74.6 |
| 87 | 5.58 | 10 | 1440 | 298 | 46.2 |
| 88 | 5.58 | 20 | 1440 | 298 | 28 |
| 89 | 5.58 | 50 | 1440 | 298 | 11.3 |
| 90 | 5.58 | 80 | 1440 | 298 | 10.6 |
| 91 | 5.58 | 100 | 1440 | 298 | 5.71 |
| 92 | 5.58 | 5 | 5 | 298 | 39.2 |
| 93 | 5.58 | 5 | 10 | 298 | 39.6 |
| 94 | 5.58 | 5 | 20 | 298 | 53 |
| 95 | 5.58 | 5 | 30 | 298 | 63.6 |
| 96 | 5.58 | 5 | 60 | 298 | 64.4 |
| 97 | 5.58 | 5 | 180 | 298 | 69 |
| 98 | 5.58 | 5 | 300 | 298 | 71.6 |
| 99 | 5.58 | 5 | 420 | 298 | 74.6 |
| 100 | 5.58 | 5 | 600 | 298 | 74.4 |
| 101 | 5.58 | 5 | 1440 | 298 | 74.5 |
| 102 | 5.58 | 5 | 1440 | 298 | 74.9 |
| 103 | 5.58 | 10 | 1440 | 298 | 47.1 |
| 104 | 5.58 | 20 | 1440 | 298 | 27.5 |
| 105 | 5.58 | 50 | 1440 | 298 | 11.39 |
| 106 | 5.58 | 5 | 1440 | 308 | 77.3 |
| 107 | 5.58 | 10 | 1440 | 308 | 49.8 |
| 108 | 5.58 | 20 | 1440 | 308 | 29.1 |
| 109 | 5.58 | 50 | 1440 | 308 | 11.7 |
| 110 | 5.58 | 5 | 1440 | 318 | 78.9 |
| 111 | 5.58 | 10 | 1440 | 318 | 51 |
| 112 | 5.58 | 20 | 1440 | 318 | 30 |
| 113 | 5.58 | 50 | 1440 | 318 | 12.3 |
| 114 | 5.58 | 5 | 1440 | 328 | 81.2 |
| 115 | 5.58 | 10 | 1440 | 328 | 51.6 |
| 116 | 5.58 | 20 | 1440 | 328 | 30.6 |
| 117 | 5.58 | 50 | 1440 | 328 | 13.1 |
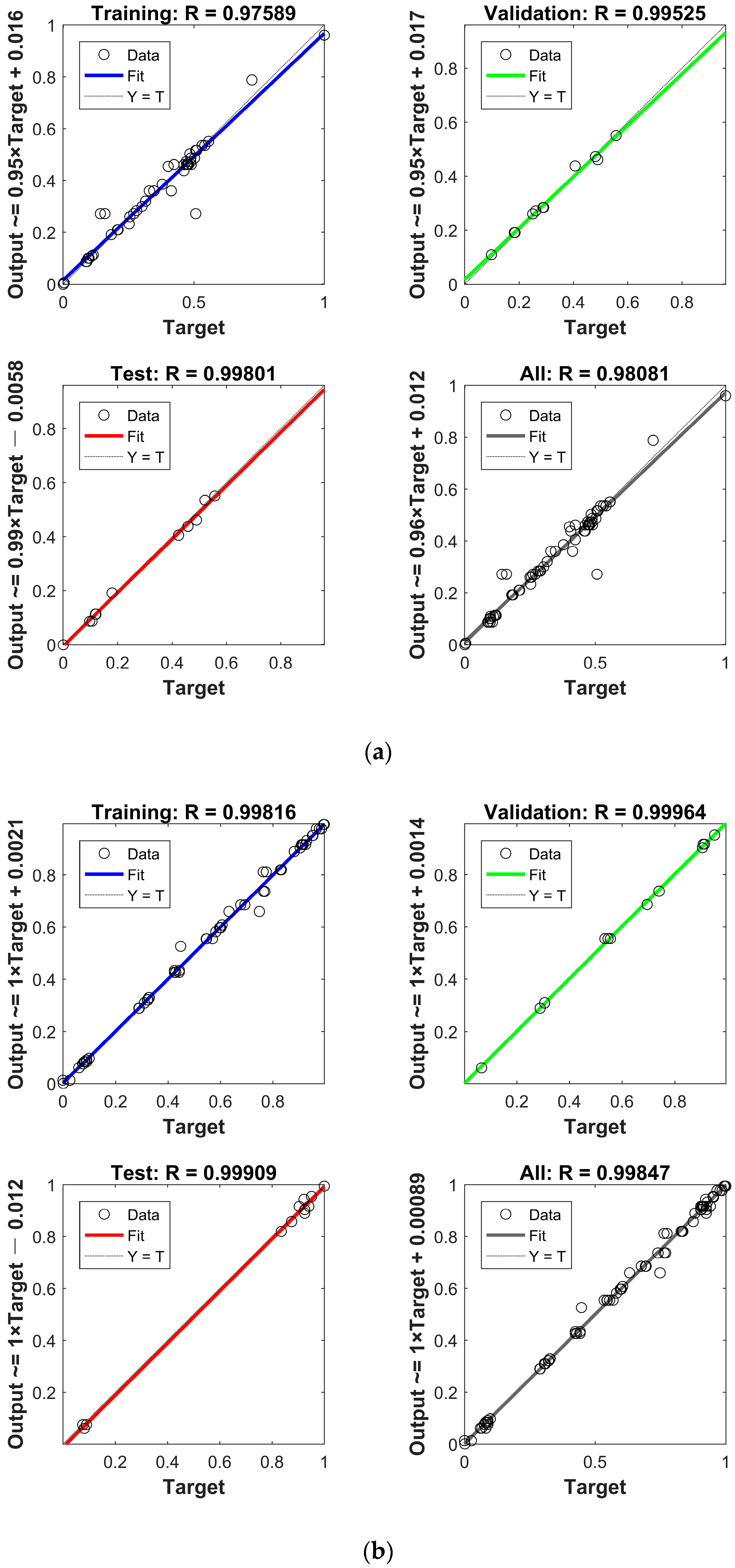
| (a) | ||||||
| Input (4)-Hidden Layer (4) | Hidden Layer (4)-Output (1) | |||||
| Weights | Bias | Weights | Bias | |||
| −0.0021 | −0.0998 | 0.0628 | 0.1912 | −0.4088 | −0.5668 | −0.1690 |
| −0.3308 | −0.3013 | 0.0358 | −0.0908 | −0.3962 | 0.2999 | |
| −0.1177 | 0.7891 | 0.1748 | 0.2355 | −0.3528 | −0.3022 | |
| −0.2683 | 0.1825 | 0.0773 | −0.4901 | 0.1691 | −0.0722 | |
| (b) | ||||||
| Input (4)-Hidden Layer (5) | Hidden Layer (5)-Output (1) | |||||
| Weights | Bias | Weights | Bias | |||
| 0.8852 | −0.6705 | −0.3712 | 0.0612 | 0.2464 | 0.1556 | −0.3376 |
| 0.2801 | 0.1780 | 0.1084 | −0.4348 | 0.3055 | 1 | |
| −0.1308 | 0.4948 | −0.0209 | 0.0709 | −0.0502 | 0.3046 | |
| −0.9012 | −0.2605 | −0.4838 | −0.8644 | 0.2783 | −0.4782 | |
| 0.6520 | −1 | −0.7253 | 0.1455 | 0.6593 | −0.2843 | |
References
- Clarke, C.; Upson, S. A global portrait of the manganese industry—A socioeconomic perspective. NeuroToxicology 2017, 58, 173–179. [Google Scholar] [CrossRef] [PubMed]
- Singh, T. A Review of Low Grade Manganese Ore Upgradation Processes. Miner. Process. Extr. Metall. Rev. 2020, 41, 417–438. [Google Scholar] [CrossRef]
- Jandieri, G. A generalized model for assessing and intensifying the recycling of metal-bearing industrial waste: A new approach to the resource policy of manganese industry in Georgia. Resour. Policy 2022, 75, S0301420721004700. [Google Scholar] [CrossRef]
- Ghosh, S.; Mohanty, S.; Akcil, A.; Sukla, L.B.; Das, A.P. A greener approach for resource recycling: Manganese bioleaching. Chemosphere 2016, 154, 628–639. [Google Scholar] [CrossRef] [PubMed]
- Marks, A. Aquatic environmental risk assessment of manganese processing industries. Neurotoxicology 2017, 58, 187–193. [Google Scholar] [CrossRef]
- Vetrimurugan, E.; Brindha, K.; Elango, L.; Ndwandwe, O.M. Human exposure risk to heavy metals through groundwater used for drinking in an intensively irrigated river delta. Appl. Water Sci. 2017, 7, 3267–3280. [Google Scholar] [CrossRef]
- Therdkiattikul, N.; Ratpukdi, T.; Kidkhunthod, P.; Chanlek, N.; Siripattanakul-Ratpukdi, S. Manganese-contaminated groundwater treatment by novel bacterial isolates: Kinetic study and mechanism analysis using synchrotron-based techniques. Sci. Rep. 2020, 10, 13391. [Google Scholar] [CrossRef]
- Masoud, A.A.; Koike, K.; Mashaly, H.A.; Gergis, F. Spatio-temporal trends and change factors of groundwater quality in an arid area with peat rich aquifers: Emergence of water environmental problems in Tanta District, Egypt. J. Arid. Environ. 2016, 124, 360–376. [Google Scholar] [CrossRef]
- Yu, D.; Zhou, J.; Zhang, J.; Sun, Y.; Zeng, Y. Hydrogeochemistry and evolution of iron and manganese in groundwater in Kashgar, Xinjiang. Acta Sci. Circumst 2021, 41, 2169–2181. [Google Scholar]
- Abubakar, B.; Jiun, O.D.; Ismail, M.; Imam, M.U. Nutrigenomics and Antioxidants. In Nutraceuticals and Natural Product Pharmaceuticals; Academic Press: Cambridge, MA, USA, 2019; pp. 33–70. [Google Scholar]
- Blanc, P.D. The Early History of Manganese and the Recognition of its Neurotoxicity, 1837–1936. Neurotoxicology 2017, 64, 5–11. [Google Scholar] [CrossRef]
- Dey, S.; Tripathy, B.; Kumar, M.S.; Das, A.P. Ecotoxicological consequences of manganese mining pollutants and their biological remediation. Environ. Chem. Ecotoxicol. 2023, 5, 55–61. [Google Scholar] [CrossRef]
- Hou, Q.; Zhang, Q.; Huang, G.; Liu, C.; Zhang, Y. Elevated manganese concentrations in shallow groundwater of various aquifers in a rapidly urbanized delta, south China. Sci. Total Environ. 2020, 701, 134777. [Google Scholar] [CrossRef] [PubMed]
- Champ, D.R.; Gulens, J.; Jackson, R.E. Oxidation–reduction sequences in ground water flow systems. Can. J. Earth Sci. 1979, 16, 12–23. [Google Scholar] [CrossRef]
- Dou, Y.; Li, M.; Liu, Z.; Fang, R.; Yan, K. Simulation of magnesium chloride vertical transport in column experiments. Hum. Ecol. Risk Assess. Int. J. 2020, 26, 2407–2419. [Google Scholar] [CrossRef]
- Szymoniak, L.; Claveau-Mallet, D.; Haddad, M.; Barbeau, B. Improving remineralization and manganese-removal of soft waters using a mixed CaCO3/MgO contactor. J. Water Process Eng. 2022, 49, 102995. [Google Scholar] [CrossRef]
- Bikiaris, D.; Vassiliou, A.; Chrissafis, K.; Paraskevopoulos, K.M.; Jannakoudakis, A.; Docoslis, A. Effect of acid treated multi-walled carbon nanotubes on the mechanical, permeability, thermal properties and thermo-oxidative stability of isotactic polypropylene. Polym. Degrad. Stab. 2008, 93, 952–967. [Google Scholar] [CrossRef]
- Stein, S.; Sivan, O.; Yechieli, Y.; Kasher, R. Redox condition of saline groundwater from coastal aquifers influences reverse osmosis desalination process. Water Res. 2021, 188, 116508. [Google Scholar] [CrossRef]
- Li, M.; Kuang, S.; Kang, Y.; Ma, H.; Dong, J.; Guo, Z. Recent advances in application of iron-manganese oxide nanomaterials for removal of heavy metals in the aquatic environment. Sci. Total Environ. 2022, 819, 153157. [Google Scholar] [CrossRef]
- Nassar, M.Y.; El-Shahat, M.F.; Osman, A.; Sobeih, M.M.; Zaid, M.A. Adsorptive Removal of Manganese Ions from Polluted Aqueous Media by Glauconite Clay-Functionalized Chitosan Nanocomposites. J. Inorg. Organomet. Polym. Mater. 2021, 31, 4050–4064. [Google Scholar] [CrossRef]
- Vasile, E.; Covaliu, C.I.; Stoian, O.; Paraschiv, G.; Ciric, A. Manganese Ions Removal from Industrial Wastewater. Rev. De Chim.-Buchar. Orig. Ed. 2020, 71, 391–396. [Google Scholar] [CrossRef]
- Dehghani, M.H.; Haghighat, G.A.; Yetilmezsoy, K.; McKay, G.; Heibati, B.; Tyagi, I.; Agarwal, S.; Gupta, V.K. Adsorptive removal of fluoride from aqueous solution using single- and multi-walled carbon nanotubes. J. Mol. Liq. 2016, 216, 401–410. [Google Scholar] [CrossRef]
- Rodríguez, C.; Leiva, E. Enhanced Heavy Metal Removal from Acid Mine Drainage Wastewater Using Double-Oxidized Multiwalled Carbon Nanotubes. Molecules 2020, 25, 111. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S.; Sundaram, B. Efficacy and Challenges of Carbon Nanotube in Wastewater and Water Treatment. Environ. Nanotechnol. Monit. Manage. 2022, 28, 100764. [Google Scholar] [CrossRef]
- Aslam, M.; Kuo, H.W.; Den, W.; Usman, M.; Ashraf, H. Functionalized Carbon Nanotubes (CNTs) for Water and Wastewater Treatment: Preparation to Application. Sustainability 2021, 13, 5717. [Google Scholar] [CrossRef]
- Ihsanullah; Abbas, A.; Al-Amer, A.M.; Laoui, T.; Al-Marri, M.J.; Nasser, M.S.; Khraisheh, M.; Atieh, M.A. Heavy metal removal from aqueous solution by advanced carbon nanotubes: Critical review of adsorption applications. Sep. Purif. Technol. 2016, 157, 141–161. [Google Scholar] [CrossRef]
- Hong, C.-E.; Lee, J.-H.; Kalappa, P.; Advani, S.G. Effects of oxidative conditions on properties of multi-walled carbon nanotubes in polymer nanocomposites. Compos. Sci. Technol. 2007, 67, 1027–1034. [Google Scholar] [CrossRef]
- Aghav, R.M.; Kumar, S.; Mukherjee, S.N. Artificial neural network modeling in competitive adsorption of phenol and resorcinol from water environment using some carbonaceous adsorbents. J. Hazard. Mater. 2011, 188, 67–77. [Google Scholar] [CrossRef]
- Tariq, R.; Abatal, M.; Bassam, A. Computational intelligence for empirical modeling and optimization of methylene blue adsorption phenomena using available local zeolites and clay of Morocco. J. Clean. Prod. 2022, 370. [Google Scholar] [CrossRef]
- Du, J.; Shang, X.; Shi, J.; Guan, Y. Removal of chromium from industrial wastewater by magnetic flocculation treatment: Experimental studies and PSO-BP modelling. J. Water Process Eng. 2022, 47, 102822. [Google Scholar] [CrossRef]
- Ganesan, P.; Kamaraj, R.; Sozhan, G.; Vasudevan, S. Oxidized multiwalled carbon nanotubes as adsorbent for the removal of manganese from aqueous solution. Environ. Sci. Pollut. Res. 2013, 20, 987–996. [Google Scholar] [CrossRef]
- Mohamed, I.M.A.; Dao, V.-D.; Yasin, A.S.; Barakat, N.A.M.; Choi, H.-S. Design of an efficient photoanode for dye-sensitized solar cells using electrospun one-dimensional GO/N-doped nanocomposite SnO2/TiO2. Appl. Surf. Sci. 2017, 400, 355–364. [Google Scholar] [CrossRef]
- Basahel, S.N.; Al Thabaiti, S.A.; Obaid, A.Y.; Mokhtar, M.; Salam, M.A. Chemical modification of multi-walled carbon nanotubes using different oxidising agents: Optimisation and characterisation. Int. J. Nanopart. 2009, 2, 200–208. [Google Scholar] [CrossRef]
- Pillay, K.; Cukrowska, E.M.; Coville, N.J. Multi-walled carbon nanotubes as adsorbents for the removal of parts per billion levels of hexavalent chromium from aqueous solution - ScienceDirect. J. Hazard. Mater. 2009, 166, 1067–1075. [Google Scholar] [CrossRef] [PubMed]
- Ali, I.; Kuznetsova, T.S.; Burakov, A.E.; Burakova, I.V.; Pasko, T.V.; Dyachkova, T.P.; Mkrtchyan, E.S.; Babkin, A.V.; Tkachev, A.G.; Albishri, H.M.; et al. Polyaniline Modified CNTs and Graphene Nanocomposite for Removal of Lead and Zinc Metal Ions: Kinetics, Thermodynamics and Desorption Studies. Molecules 2022, 27, 5623. [Google Scholar] [CrossRef]
- Mohamed, I.M.A.; Yasin, A.S.; Liu, C. Synthesis, surface characterization and electrochemical performance of ZnO @ activated carbon as a supercapacitor electrode material in acidic and alkaline electrolytes. Ceram. Int. 2020, 46, 3912–3920. [Google Scholar] [CrossRef]
- Sadri, R.; Hosseini, M.; Kazi, S.N.; Bagheri, S.; Zubir, N.; Solangi, K.H.; Zaharinie, T.; Badarudin, A. A bio-based, facile approach for the preparation of covalently functionalized carbon nanotubes aqueous suspensions and their potential as heat transfer fluids. J. Colloid Interface Sci. 2017, 504, 115–123. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, M.; Yang, B.; Feng, Q.; Liu, D. Enhanced sulfidization flotation mechanism of smithsonite in the synergistic activation system of copper–ammonium species. Miner. Eng. 2022, 187, 107796. [Google Scholar] [CrossRef]
- Lemya, B.; Zohra, S.F.; Houari, S.; Esma, C.-B.; Boumediene, B.; Ould, K.S.; Farouk, Z. Removal of Zn(II) and Ni(II) heavy metal ions by new alginic acid-ester derivatives materials. Carbohydr. Polym. 2021, 272, 118439. [Google Scholar]
- Silvestro, L.; Ruviaro, A.S.; de Matos, P.R.; Pelisser, F.; Mezalira, D.Z.; Gleize, P.J.P. Functionalization of multi-walled carbon nanotubes with 3-aminopropyltriethoxysilane for application in cementitious matrix. Constr. Build. Mater. 2021, 311, 125358. [Google Scholar] [CrossRef]
- Al-Wakeel, K.Z.; Abd El Monem, H.; Khalil, M.M.H. Removal of divalent manganese from aqueous solution using glycine modified chitosan resin. J. Environ. Chem. Eng. 2015, 3, 179–186. [Google Scholar] [CrossRef]
- Li, Y.; Shang, H.; Cao, Y.; Yang, C.; Feng, Y.; Yu, Y. Quantification of adsorption mechanisms distribution of sulfamethoxazole onto biochar by competition relationship in a wide pH range. J. Environ. Chem. Eng. 2022, 10, 108755. [Google Scholar] [CrossRef]
- Stafiej, A.; Pyrzynska, K. Adsorption of heavy metal ions with carbon nanotubes. Sep. Purif. Technol. 2007, 58, 49–52. [Google Scholar] [CrossRef]
- Tsai, Y.P.; Doong, R.A.; Yang, J.C.; Chuang, P.C.; Chou, C.C.; Lin, J.W. Removal of Humic Acids in Water by Carbon Nanotubes. Adv. Mater. Res. 2013, 747, 221–224. [Google Scholar] [CrossRef]
- Özcan, A.S.; Erdem, B.; Özcan, A. Adsorption of Acid Blue 193 from aqueous solutions onto BTMA-bentonite. Colloids Surf. A 2005, 266, 73–81. [Google Scholar] [CrossRef]
- Jun, L.Y.; Karri, R.R.; Yon, L.S.; Mubarak, N.M.; Bing, C.H.; Mohammad, K.; Jagadish, P.; Abdullah, E.C. Modeling and optimization by particle swarm embedded neural network for adsorption of methylene blue by jicama peroxidase immobilized on buckypaper/polyvinyl alcohol membrane. Environ. Res. 2020, 183, 109158. [Google Scholar] [CrossRef] [PubMed]
- Piao, Y.; Tondare, V.N.; Davis, C.S.; Gorham, J.M.; Walker, A. Comparative Study of Multiwall Carbon Nanotube Nanocomposites by Raman, SEM, and XPS Measurement Techniques. Compos. Sci. Technol. 2021, 208, 108753. [Google Scholar] [CrossRef]
- Jwa, B.; Xuan, G.A. Adsorption kinetic models: Physical meanings, applications, and solving methods—ScienceDirect. J. Hazard. Mater. 2020, 390, 122156. [Google Scholar]
- Wang, J.; Guo, X. Rethinking of the intraparticle diffusion adsorption kinetics model: Interpretation, solving methods and applications. Chemosphere 2022, 309, 136732. [Google Scholar] [CrossRef]
- Lagergren, S.K. About the theory of so-called adsorption of soluble substances. Sven. Vetenskapsakad. Handingarl 1898, 24, 1–39. [Google Scholar]
- Ho, Y.S.; McKay, G. Sorption of dye from aqueous solution by peat. Chem. Eng. J. 1998, 70, 115–124. [Google Scholar] [CrossRef]
- Allen, S.; Mckay, G.; Khader, K. Intraparticle diffusion of a basic dye during adsorption onto sphagnum peat. Environ. Pollut. 1989, 56, 39–50. [Google Scholar] [CrossRef] [PubMed]
- Weber, W.J.; Morris, J.C. Proceedings of International Conference Water pollution symposium Pergamon. Oxford 1962, 2, 231–262. [Google Scholar]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- McKay, G.; Blair, H.S.; Gardner, J.R. Adsorption of dyes on chitin. I. Equilibrium studies. J. Appl. Polym. Sci. 1982, 27, 3043–3057. [Google Scholar] [CrossRef]
- Hameed, B.H.; El-Khaiary, M.I. Malachite green adsorption by rattan sawdust: Isotherm, kinetic and mechanism modeling. J. Hazard. Mater. 2008, 159, 574–579. [Google Scholar] [CrossRef]
- Freundlich, H. Uber die adsorption in losungen. Z. Für Phys. Chem. 1907, 57, 385–470. [Google Scholar] [CrossRef]
- Foo, K.Y.; Hameed, B.H. Insights into the Modeling of Adsorption Isotherm Systems; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Yulia, F.; Chairina, I.; Zulys, A. Multi-objective Genetic Algorithm Optimization with an Artificial Neural Network for CO2/CH4 Adsorption Prediction in Metal-Organic Framework. Therm. Sci. Eng. Prog. 2021, 25, 100967. [Google Scholar] [CrossRef]
- Khan, H.; Hussain, S.; Hussain, S.F.; Gul, S.; Ahmad, A.; Ullah, S. Multivariate modeling and optimization of Cr(VI) adsorption onto carbonaceous material via response surface models assisted with multiple regression analysis and particle swarm embedded neural network. Environ. Technol. Innov. 2021, 24. [Google Scholar] [CrossRef]



| Model | Parameter | MWCNTs | M-MWCNTs |
|---|---|---|---|
| qe.experiment | 0.278 | 3.74 | |
| Pseudo-first-order model | qe.calculate (mg/g) | 0.229 | 1.16 |
| kf (1/min) | 0.0433 | 0.019 | |
| R2 | 0.889 | 0.898 | |
| Pseudo-second-order model | qe.calculate (mg/g) | 0.279 | 3.76 |
| ks (1/min) | 4.12 | 0.030 | |
| R2 | 0.999 | 0.999 | |
| Weber–Morris | kw | / | / |
| C | / | / | |
| R2 | / | / |
| Model | Parameter | MWCNTs | M-MWCNTs |
|---|---|---|---|
| Langmuir isotherm | qmax1 (mg/g) | 0.585 | 5.78 |
| b (L/mg) | 0.249 | 1.19 | |
| RL (L/mg) | 0.801 | 0.456 | |
| R2 | 0.989 | 0.999 | |
| Freundlich isotherm | Kf (mg/g (L/mg)1/n) | 0.159 | 3.96 |
| 1/n | 0.344 | 0.009 | |
| R2 | 0.978 | 0.872 | |
| Dubinin–Radushkevich | qmax2 (mg/g) | 1.4083 | 7.43 |
| β | 0.0030 | 0.0009 | |
| ES | 12.95 | 23.64 | |
| R2 | 0.989 | 0.913 |
| Parameter | Model A: MWCNTs | Model B: M-MWCNTs |
|---|---|---|
| Number of samples | 117 | 105 |
| Number of hidden layers | 1 | 1 |
| Hidden nodes | 4 | 5 |
| PSO swarm size | 50 | 50 |
| Cognitive component (c1) | 1.5 | 1.49554 |
| Social component (c2) | 1.5 | 1.49554 |
| Number of iterations | 1000 | 1000 |
| Statistical Metric | Model A: MWCNTs | Model B: M-MWCNTs |
|---|---|---|
| R2 (train/test) | 0.962/0.966 | 0.997/0.995 |
| RMSE (train/test) | 2.20/2.26 | 1.38/1.76 |
| MAE (train/test) | 1.404/1.58 | 0.769/0.909 |
| MAPE | 0.074/0.067 | 0.0202/0.0223 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; He, Y.; Wang, R.; Mao, Y.; Bai, J.; Dou, Y. Modification of Multiwalled Carbon Nanotubes and Their Mechanism of Demanganization. Molecules 2023, 28, 1870. https://doi.org/10.3390/molecules28041870
Zhou Y, He Y, Wang R, Mao Y, Bai J, Dou Y. Modification of Multiwalled Carbon Nanotubes and Their Mechanism of Demanganization. Molecules. 2023; 28(4):1870. https://doi.org/10.3390/molecules28041870
Chicago/Turabian StyleZhou, Yuan, Yingying He, Ruixue Wang, Yongwei Mao, Jun Bai, and Yan Dou. 2023. "Modification of Multiwalled Carbon Nanotubes and Their Mechanism of Demanganization" Molecules 28, no. 4: 1870. https://doi.org/10.3390/molecules28041870
APA StyleZhou, Y., He, Y., Wang, R., Mao, Y., Bai, J., & Dou, Y. (2023). Modification of Multiwalled Carbon Nanotubes and Their Mechanism of Demanganization. Molecules, 28(4), 1870. https://doi.org/10.3390/molecules28041870






