Abstract
CO2 is the most abundant greenhouse gas, and for this reason, it is the main target for finding solutions to climatic change. A strategy of environmental remediation is the transformation of CO2 to an aggregated value product to generate a carbon-neutral cycle. CO2 reduction is a great challenge because of the large C=O dissociation energy, ~179 kcal/mol. Heterogeneous photocatalysis is a strategy to address this issue, where the adsorption process is the fundamental step. The focus of this work is the role of adsorption in CO2 reduction by means of modeling the CO2 adsorption in rutile metallic oxides (TiO2, GeO2, SnO2, IrO2 and PbO2) using Density Functional Theory (DFT) and periodic DFT methods. The comparison of adsorption on different metal oxides forming the same type of crystal structure allowed us to observe the influence of the metal in the adsorption process. In the same way, we performed a comparison of the adsorption capability between two different surface planes, (001) and (110). Two CO2 configurations were observed, linear and folded: the folded conformations were observed in TiO2, GeO2 and SnO2, while the linear conformations were present in IrO2 and PbO2. The largest adsorption efficiency was displayed by the (001) surface planes. The CO2 linear and folded configurations were related to the interaction of the oxygen on the metallic surface with the adsorbate carbon, and the linear conformations were associated with the physisorption and folded configurations with chemisorption. TiO2 was the material with the best performance for CO2 interactions during the adsorption.
1. Introduction
CO2 is the most relevant greenhouse gas; the climatic change caused by high concentrations of this gas is related directly to human activity [1,2,3], and the impact of such climatic change is observed in the global economy and social wealth [4]. Several technological solutions were developed to reduce atmospheric emissions of CO2 [5,6,7], for instance, the use of emission gases as raw materials for low contaminant technological processes. The transformation of CO2 in aggregate-value products generates a carbon neutral cycle, which artificially reduces atmospheric emissions and relieves pressure on the traditional industry for energy production [8], considering the renewable production of combustibles. Nevertheless, a fundamental problem must be considered: CO2 is a highly stable molecule due to its linear geometry and efficient reduction potential, −1.9 V [9]. In addition, the C=O bond holds a dissociation energy of ~179 kcal/mol, which is around twice the C-H and C-C dissociation energies displaying values of 430 and 335 kJ/mol, respectively [10]. The reduction of CO2 is nonselective; depending on the reaction media and catalyzer, several chemical species are formed (CO, CH4, CH3OH, HCOOH, C2H6, C2H5OH) [11,12,13]. There are homogeneous and heterogeneous catalytic processes for CO2 reduction and activation [14,15,16,17]; nevertheless, heterogeneous catalysis has been proved to be more efficient and “clean” to obtain aggregate-value chemical species [18,19].
The synthesis of methane and methanol from CO2 and water has attracted great attention from the clean energy industry because of the enormous potential for the sustainable production of fuels using solar energy [20,21]. CO2 reduction mechanisms have been extensively studied in anatase and the rutile phases of TiO2 [22,23,24], and those results indicated that reduction occurs with multiple intermediates, suggesting that the disturbed geometry of CO2 during adsorption is the fundamental step for the reduction process. Another crucial factor is the efficiency of the catalyst, and relevant factors to consider are the charge separation displayed by the semiconductor [22,23] and the presence of water molecules during the process. The adsorption of water on the catalysts’ surface causes H2O dissociation [12,24,25,26], and such a process generates reactive species that are relevant in CO2 catalysis [26].
There are reports of semiconductor metal oxides capable of reducing CO2 in the presence of irradiation [24,27,28,29,30,31] despite the high reduction potential in the area that the reaction takes place. This indicates that the interaction between the CO2 and the semiconductor surface decreases the activation energy. Several experiments reported the detection of adsorbed CO2, which displayed modified structures [32,33,34,35,36]. DFT studies have analyzed the interactions between CO2 and different photocatalysts to study the role of adsorption on CO2 reduction [23,37,38,39,40,41,42,43,44,45,46].
Effective adsorption and activation are key steps for CO2 photoreduction [47], and adsorption models have been reported in the literature from kinetic and thermodynamic perspectives [48]. Therefore, the adsorption and subsequent activation of CO2 on the surfaces of heterogeneous catalysts are both crucial for the reduction process and for the suppression of the Hydrogen Evolution Reaction (HER). Under this perspective, the interactions of the CO2 molecule with the surface produce the formation of partially charged species (CO2δ−). Besides the linearity of gaseous carbon dioxide and the absence of a permanent dipole momentum, each oxygen atom has free electronic pairs that attack metal centers behaving as Lewis’s acids; therefore, the carbon atom is suitable to be attacked by a nucleophilic moiety. Considering these characteristics, CO2 has several coordination points, and this provides the possibility of having multiple geometries associated with the adsorption of CO2 on the surfaces of heterogeneous catalysts [37]. The morphology of the surface is relevant for the catalytic performance, and in addition, the adsorbed CO2 geometries are determined by the surface–adsorbate interactions, and the main anchor points of CO2 are the oxygen atoms. The preference of certain crystalline faces to adsorb CO2 has been observed, and this is favored for those surfaces with a large number of exposed metal atoms [38,39].
DFT studies showed that the coordination geometry of the surface controls the arrangement of the active sites, usually displaying cation behavior [40,41,42,43]. However, it is evident that due to the CO2 linearity, the possible adsorbed geometries are limited. Two adsorption configurations have been reported for CO2: linear and bent. The former occurs selectively on surfaces of certain metal oxides such as TiO2, CeO2, ZnO, SnO2 and CuO [41,42], while the latter is more common since it occurs on other metallic surfaces such as Au and Cu [41]. There is a third less common possibility in which a dissociation is carried out to M-CO and O-M during the CO2 adsorption, and the latter has been studied in detail using DFT calculations in surface models of Fe-Ni bimetallic catalysts [44].
Photochemical activation requires an electron transfer from the surface to the adsorbed CO2 molecule. The charge transfer from the metal to the CO2 is related to the way in which the adsorbate is coordinated, and this is the fundamental step of photoreduction. Ab initio calculations showed that bidentate CO2 adsorption on TiO2-anatase formed a hybrid LUMO between the CO2 orbitals and titanium 3d orbitals. Such LUMO showed a decrease in energy compared with the LUMO of nonadsorbed CO2, which suggests that the adsorption favored the electronic transfer by the 3d titanium orbitals to CO2 [43]. This ability to donate charge has also been studied and detected in TiO2 brookite models [45].
Surface defects are among the most reactive sites, and these sites experience electron density accumulation and change the surface reactivity properties. It has been proposed that oxygen vacancies play a vital role in several surface reactions [49], and those vacancies are particularly relevant in the adsorption and activation of CO2. Surface defects can promote higher-energy species during CO2 adsorption compared with perfect surfaces, although the defects are able to stabilize anionic CO2 [43]. Ab initio modeling has highlighted the importance of crystal defects for the description of adsorption and surface–adsorbate charge transfer for TiO2 models (brookite and anatase). Even so, it must be considered that perfect surfaces display similar adsorption properties to those with vacancies, at least regarding CO2 adsorption [23,45,46].
In this work, DFT studies were carried out on CO2 adsorption models on rutile-type structures from diverse metal oxides. We used one type of polymorph (rutile) to evince the cation’s role in adsorption, and we investigated the cation effect by comparing the adsorbed conformations and the cation effect in the adsorption energy. Additionally, we tested the adsorption in two different surfaces generated from two different lattice planes (001) and (110) to find the plane with the largest adsorption capability. Furthermore, we modeled the dissociative adsorption of water on these surfaces to analyze the competition for active sites with CO2, and finally, the formation of catalytic reactive species is proposed.
2. Methodology
We designed finite models of different metal oxide (MO) surfaces with rutile-like crystal structures. All of them were based on the structure reported in the crystallographic data banks followed by a geometry optimization; then, surface plane modeling was performed based on the Miller indices (001) and (110). The modeled MO surfaces were TiO2, GeO2, SnO2, PbO2 and IrO2. In the case of TiO2, the anatase surfaces were also modeled based on the (001) and (110) Miller indices. Molecules of CO2 and H2O (in individual systems) that were previously optimized were added to the models. Subsequently, the geometry optimization of the entire system was carried out, and the lowest energy configuration was obtained. Modeling was performed using the ADF (Amsterdam Density Functional) computational package [50,51,52] and its supplement for periodic systems BAND [53,54,55,56] in version adf2014.01. The MO optimizations and adsorption modeling were performed using a TZP basis set with the PBEsol [57] functional with the D3 Grimme dispersion correction [58], which is a modification of the PBE functional [59] designed to obtain an improvement in the equilibrium properties of solids in bulk and surface systems [60]. The PBE functional was successfully used to study CO2 adsorption in metal oxide systems [40,41,42,43]. The adsorbates were previously optimized with a B3LYP/TZP level [61,62]. The ZORA pseudopotential [63,64,65,66] was used for relativistic corrections on the metals. The atomic charges were computed using the Hirshfeld scheme [67]. For details, see the supporting information (SI).
To build the surface of the finite models, we used the bulk structure of the metal oxide as the starting point and the crystallographic parameters available in the BAND software databank. The bulk structure was optimized using BAND software with the PBEsol-D3/TZP level of theory. Finally, the surface planes were obtained from Miller’s indices (001) and (110) using BAND to build the slabs. The adsorbates were individually optimized using the B3LYP/TZP level of theory. Afterwards, an optimized adsorbate slab was generated and then used to perform optimizations over the optimized solid bulk surface slab, and the initial distance between the adsorbate molecules and metallic center surfaces was 5 Å. Different initial adsorbate orientations were tested which resulted in similar optimized geometries, and the conformations with the lowest energy were used to perform the analysis. For details, see the Supplementary Materials.
3. Results
3.1. CO2 Adsorption on TiO2 Surfaces
TiO2 belongs to the most studied substances related to the catalytic photoreduction of greenhouse gases due to its excellent photocatalytic properties. For this reason, we modeled the adsorption of CO2 on rutile and anatase phases, which are the most relevant phases for adsorption purposes [14]. Our results showed that both phases displayed an attractive interaction with CO2, and Figure 1 shows the optimized geometries for both studied phases for the rutile (001) and (110) planes and for the anatase (001) and (101) planes. The adsorbate geometry was bent in the rutile; meanwhile, in the anatase, the adsorbate geometry maintained its linearity. During the optimization, CO2 displayed a perpendicular orientation to the metallic surface; for this reason, an adsorbate oxygen atom (OA) approached directly to a surface titanium atom (Ti). At this stage of the optimization, the adsorption process differed for each phase. In the case of rutile, a second interaction appeared between the carbon and a surface oxygen (OS), and therefore the CO2 was bent; meanwhile, for the anatase, such an interaction and bending was not observed, and such results were the same for any plane (see Figure 2). The observed CO2 bent geometry in rutile is indicative of the capability to generate reactive species of CO2 during adsorption on the exposed surfaces.
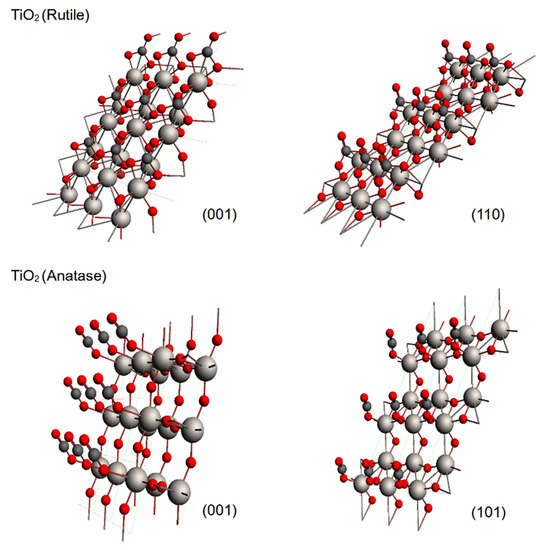
Figure 1.
Optimized geometries for the adsorption models over the crystalline phases of TiO2: top: (001) and (110) rutile planes; bottom: (001) and (101) anatase planes. Atomic representations: titanium atoms as white spheres, oxygen atoms as red spheres and carbon atoms as dark gray spheres.
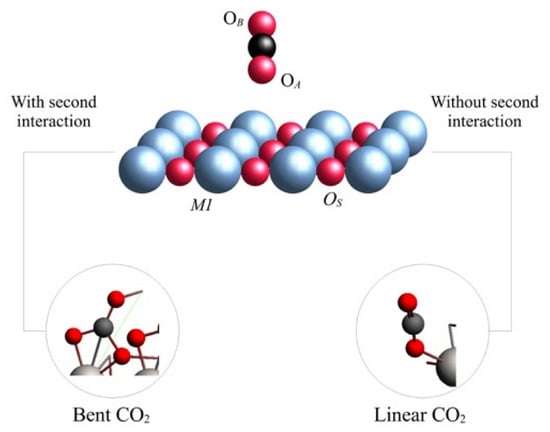
Figure 2.
Representation of CO2 adsorption on TiO2 on rutile (right) and anatase (left). Atoms are labeled as follows: OA is the oxygen atom of CO2 which displays the first interaction with the surface; OB is the second oxygen atom of CO2; OS is the metallic oxide oxygen; M1 is the metallic center.
The differences in the CO2 adsorbed structures, depending on the TiO2 phases, suggest that the capability of the surface to interact with the adsorbate is related to the phase topology. For the case of the (110) rutile plane, there was an oxygen out of the surface, which was the responsible of the interaction C--OS, denoted by the yellow oval on top of Figure 3. Additionally, rutile (001) displayed cavities between the connected layers and the alternation of the metallic atoms’ positions; consequently, there were regions with oxygens connecting layers that were capable of performing the C--OS interaction, as depicted by the blue oval on top of Figure 3. Nevertheless, the anatase (101) and (001) planes were flat surfaces without relevant cavities or prominences, and this situation reduced the exposition of the OS to have an interaction with the CO2 carbon.
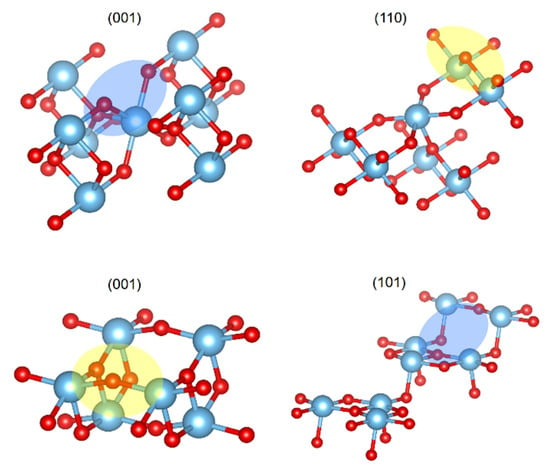
Figure 3.
Representation of rutile (top) and anatase (bottom) studied planes. Regions top of the plane in yellow ovals and regions below of the plane in blue ovals. Titanium atoms are depicted as blue spheres and oxygen as red spheres.
3.2. CO2 Adsorption on SnO2, GeO2, PbO2 and IrO2 Rutile-Type Surfaces
The effect of the metallic cation on rutile-type surfaces on CO2 adsorption is a relevant issue to consider, and for this reason, we modeled the adsorption of CO2 on GeO2, SnO2, IrO2 and PbO2 rutile-type surfaces; the result of the optimization of CO2 over these surfaces is displayed in Figure 4. As in the case of TiO2, an attractive adsorbate–surface interaction was observed, displaying bended CO2 for the case of the GeO2 and SnO2 surfaces, and linear geometry for IrO2 and PbO2. Such behavior is apparently related to the weight of the metallic cation, as the surfaces with lighter metallic cations (GeO2and SnO2) displayed bended CO2 geometries and surfaces with heavier metallic cations (IrO2 and PbO2) displayed linear CO2 geometries. So, additionally to the topology of the metallic oxide surface, the size of the metallic cation must be considered for CO2 catalytic purposes. Larger sizes of metallic atoms (M1) sterically block accessibility to OS and neglect the possibility of a C--OS effective interaction, which is the critic step of the effective CO2 adsorption for catalytic purposes.
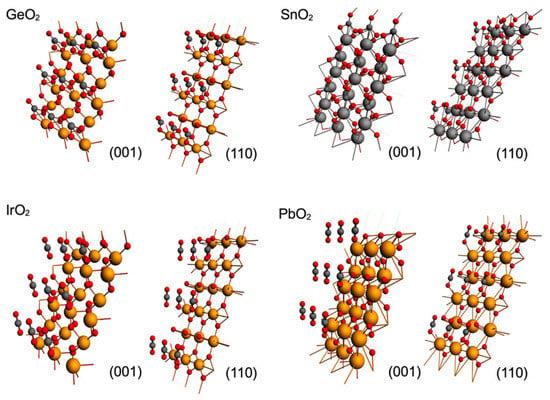
Figure 4.
Optimized geometries for GeO2, SnO2, IrO2 and PbO2 rutile-type surfaces on (001) and (001) planes. Metallic cations are shown as large orange spheres, oxygen atoms as red spheres and carbons as dark grey spheres.
The adsorption energy is relevant when classifying a process as chemisorption or physisorption because weak intermolecular forces (van der Waals) are related with physisorption; meanwhile, chemisorption involves a structural transformation and formation (or elimination) of chemical bonds. Our criterion for the classification of adsorption is combining the energetic and structural values, whereby the largest adsorption energies with relevant structural changes in adsorbates are related to chemisorption; meanwhile, the lowest adsorption energies with an absence of structural changes are related to physisorption. The calculated values for the adsorption energies per CO2 molecule are displayed in Table 1. For the case of the (001) plane, a large interaction energy was displayed for the bended CO2 structures on TiO2, GeO2 and SnO2, followed by a less energetic adsorption for the linear CO2 structures on IrO2 and PbO2. A similar behavior was displayed for the (110) TiO2 and GeO2 planes, displaying the largest adsorption energies for the bended CO2 structures. However, the SnO2 and PbO2 showed similar adsorption energies displaying different CO2 adsorbed geometries, bended for SnO2 and linear for PbO2. The values of adsorption on the (001) planes were larger than those displayed by the (110) planes in general, except for the PbO2. In Table 2, some geometric parameters are displayed for the different adsorption geometries. It is evident that the distances M1-OA and C-OS were larger for the (110) planes in general, except for PbO2 and TiO2. A larger interaction distance was related to a weaker interaction, with the consequence of a lower interaction energy and less bending effect for the CO2 geometry. Therefore, the displayed adsorption energy for the exceptional case of PbO2 was related to the M1-OA distance, which was smaller for the (110) plane, which caused a larger adsorption energy.

Table 1.
Adsorption CO2 energies for TiO2, GeO2, SnO2, IrO2 and PbO2 on (001) and (110) planes.

Table 2.
Distances and angles of the adsorption geometries for TiO2, GeO2, SnO2, IrO2 and PbO2.
The graph in Figure 5 shows the values of the adsorption energy against the bond distance M1--OA. On the left side of the graph, the presence of lighter metal oxides is observed, which shows that the shorter the bond distance, the greater the adsorption energy. This is consistent with the nature of this interaction, which is a Lewis acid–base reaction. Similarly, Figure 6 shows the adsorption energy graph against the change in angle of CO2. Again, there was a correspondence between the highest adsorption energies with the highest degree of modification in the structure of CO2. This suggests that both the first (M1--OA) and the second interactions (C1--OS) were the largest contributors to the adsorption energy. Our results suggest that chemisorption was observed for both planes of TiO2, GeO2 and SnO2, while physisorption was observed for both planes of IrO2 and for PbO2. Physisorption was related to the linear CO2 adsorbed geometries in general, and the bended CO2 adsorbed geometries were related to chemisorption, which is the expected behavior for a material with CO2 catalytic properties.
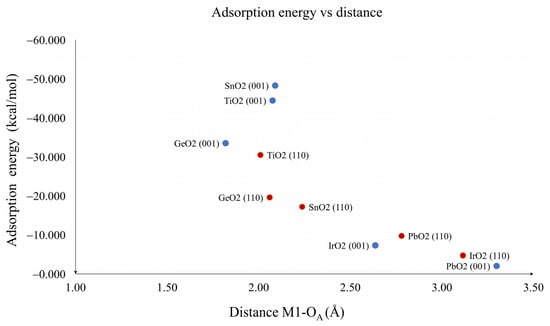
Figure 5.
Relation between adsorption energy and M1-OA distance for TiO2, GeO2, SnO2, IrO2 and PbO2. (001) planes are blue dots and (110) planes are red dots.
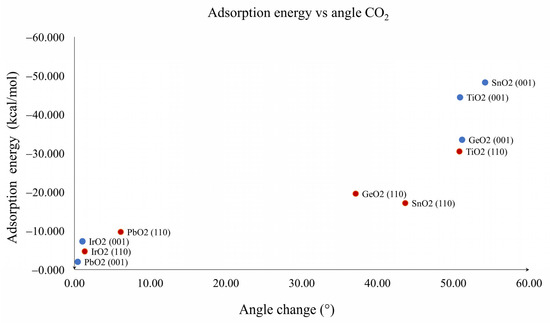
Figure 6.
Relation between adsorption energy and CO2 angle for TiO2, GeO2, SnO2, IrO2 and PbO2. (001) planes are blue dots and (110) planes are red dots.
The strength of the adsorption of a molecule depends on the surface energy, which can be defined as the increase in the energy of the crystalline structure because of the generation of a surface, whereby an asymmetric environment is therefore produced. The bonding energies of the metallic oxides were calculated and are shown in Table 3, and such energies can be considered the relative surface energies because all the calculated metallic oxides held the same molecular structure and shared the number and type of dangling bonds. The results in Table 3 indicate that the (110) surfaces held larger negative energies that the (001) ones, which agree with the previous discussion on the chemisorption/physisorption properties of such planes. There was a trend observed by the elements of the 14(IVA) group whereby the binding energy increased with the period. Nonetheless, the transition metals did not follow the trend; the Ir surface should have displayed a larger binding energy than Ge and Sn surfaces because it is a heavier atom, but the Ir surface displayed lower binding energies than the Ge and Sn ones. This behavior was rationalized from the coordination sphere perspective. For the case of rutile, each cation was coordinated with six oxygen atoms and an octahedral geometry was obtained, isolating this six-coordinated system from the crystal. The combination of the s, p and d orbitals generated d2sp3 orbitals for the transition metals and sp3d2 orbitals for the IVA group elements; therefore, the different electronic configurations for Ti and Ir displayed the same crystal arrangement. Additionally, for the case of the IVA group, the d orbitals participating in hybridization displayed the same n quantum number as the s and p orbitals. Meanwhile, the transition metal d orbitals were in a lower n-1 level than the s and p orbitals; for this reason, the generated hybrid orbitals of the IVA group were higher in energy than those at an n-1 level, and therefore, the IVA group surfaces displayed higher binding energies. The surface energy is a useful descriptor of the adsorption capability of a material; nevertheless, it is evident that the characterization of the interaction between the metallic cation and the adsorbed molecule is a relevant issue to consider.

Table 3.
Bonding energies for (001) and (110) planes of TiO2, GeO2, SnO2, IrO2 and PbO2.
3.3. Charge Redistribution and Effects over CO2
The redistribution of the charge density can be approximated by the analysis of the Hirshfeld atomic charges for the adsorption process. The change in atomic charges (AC) can be used as a measure of the charge transference during the adsorption process. In Figure 6 and Figure 7, the changes in charges for planes (001) and (110) are listed, as well as the metallic center (M1), the neighbored metallic atom (M2), the surface oxygen (OS) and the adsorbate oxygens (OA) and (OB). In Figure 8 we show a model of the charge redistribution based on the data in Figure 6 and Figure 7. Each CO2 adsorption conformation, bent or linear, displayed different charge redistribution mechanisms. In the case of the CO2 bent geometries, there were three regions where the change was larger than in the rest of the surface: the metallic cation (M1), responsible of the first interaction with adsorbate; the surface oxygen (OS), which bent the adsorbate through a second interaction with the adsorbate; and the CO2 carbon atom (C1), because of such a second interaction. In the case of linear geometries, the relevant charge transference was observed between OA and the metallic cation M1.
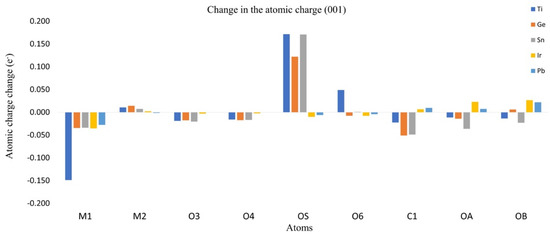
Figure 7.
Atomic charge change for plane (001).
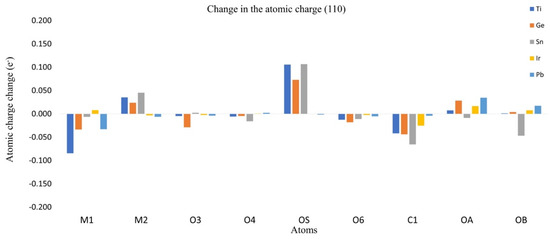
Figure 8.
Atomic charge change for plane (110).
For the CO2 bent geometries on plane (001), the initial interaction generated an electron density gain for M1, followed by a charge transference to the neighbored surface oxygens, labeled as O3 and O4 in Figure 9. Then, the attack of Os on the CO2 carbon generated a charge transference from OS to C1. For the case of TiO2, the large charge gain was due to the largest CO2 deformation, which produced a large charge delocalization of ¶ electrons of CO2. Regarding the CO2 bent geometries in plane (001), a similar situation was observed; a gain in the electronic charge of M1 followed by a charge transference to O3 and O4, and then Os attacked the CO2 carbon. However, in this case, a large charge donation of the metallic cation M2 to OS was observed. Along the series, the charge gaining of atom M1 was diminished and the transference to the adsorbate carbon was increased. For CO2 linear geometries in planes (001), the relevant charge transference was observed between the adsorbate oxygen (OA) and the metallic cation (M1). Meanwhile, for the linear geometries in the (110) plane, the charge transference of IrO2 to M1 was negligible, followed by a small charge change in the OA. Nevertheless, for PbO2, a significant charge gain was displayed for M1 obtained from OA. This analysis showed the relevance of the study on AC redistribution along the adsorption process.
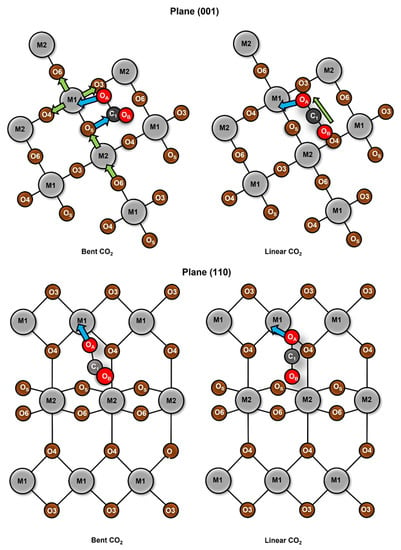
Figure 9.
Mechanism of atomic charge redistribution for plane (001) left and (110) right.
The relevance of the adsorption in catalytic processes is to diminish the activation energy to reduce the CO2 molecule. To quantify how bent CO2 structures are less stable than linear ones, we performed calculation of single points of isolated molecules from the geometries of the generated species along the adsorption process. In addition, relative energies were calculated using the formula , where is the energy of the linear-isolated CO2 structure and is the energy of the isolated CO2 molecule, using the adsorbed geometry, Table 4. It is evident that the energies of the bent structures (from TiO2, GeO2 and SnO2 oxides) were larger than the linear species (from IrO2 and PbO2 oxides). Additionally, the relative energies shown in Table 4 displayed a similar behavior to the adsorption energies, whereby the species generated by the (001) plane were less stable than the (110) plane ones in general. TiO2 displayed the lowest difference in the relative energy between planes. There was a significant difference between the planes for the case of GeO2 and SnO2, showing values of 37 and 25 kcal/mol, respectively. The IrO2 and PbO2 oxides displayed significant small values of relative energy; therefore, the adsorbed species on these surfaces displayed a large degree of stability. The electron affinity (EA) can be used to approximate the reduction potential using empirical parameters [68,69,70]. For this reason, we calculated EA using the expression , where is the energy of the anionic molecule and is the energy of the neutral molecule. We used the geometry of the adsorbed species and the geometry of the linear CO2 molecule as the reference. A comparison of the EA with the relative energies (D) and with the O-C-O angles showed that the large D was related to the large EA and had smaller O-C-O angles, which suggests the correlation between CO2 bending and the surface reduction capability.

Table 4.
Relative energy (D) of CO2 species generated during adsorption; electron affinities (EA) of adsorbed CO2 molecules. The linear CO2 molecule display EA of −4.19 eV.
3.4. Water Molecules Dissociation
The phenomenon of the adsorption of water molecules is important for several reasons. Water is a relevant substance in atmosphere phenomena as it plays a fundamental role in photocatalysis and electrochemistry on metal oxides and aqueous interfaces [71,72,73]. Several studies have shown that water molecules are completely dissociated on the surface of some metal oxides, generating hydroxylated surfaces [71,74,75,76,77]. TiO2 and SnO2 rutile are capable of dissociating H2O [32,74,78]. The (110) plane adsorbs H2O in a dissociative manner and the proton is attached to one of the bridge oxygens of the surface while the hydroxyl is attached to the metal center [79]. Water molecular adsorption is possible through hydrogen bond formation with OH groups; nevertheless, it makes it difficult to estimate the dissociation energy from experimental results. Gercher and Cox [78] used thermal desorption spectroscopy (TDS) and ultraviolet photoemission techniques to study water adsorption on surfaces. Their results showed that water is absorbed in a dissociative conformation on a perfect surface; this fact was attributed to a peak at 435 K in the desorption spectrum, and peaks at 200 and 300 K were also attributed to molecular water desorption.
We performed H2O adsorption processes over TiO2, GeO2 and SnO2 surfaces, and we did not consider IrO2 and PbO2 because these oxides display low adsorbate affinity. The adsorption models are displayed in Figure 10. The active site was the same as in the case of CO2 adsorption and similar processes occurred during H2O adsorption; there were two surface interactions that formed M1-OH and OS-H, and this observation agreed with the results reported by Lindan [79]. The surface dissociation energies of the water molecules dissociating into metal oxides are shown in Table 5; our values were larger than those reported in previous studies [71,79,80], in which the dissociation of H2O on SnO2 and TiO2 (001) displayed values around −40 kcal/mol. Table 5 shows that the process of H2O surface dissociation was preferred over the adsorption of CO2, considering that H-OH bond breaking took place. The study of the processes that occur after surface H2O dissociation is needed to consider what the probable reactive species for CO2 catalysis are. A relevant question must be addressed: is there a chance of liberation of H and OH as free radicals? Or do these species stay on the surface? To obtain a close connection with the experimental conditions of photocatalysis, adsorbates mixes must be modeled (H2O and CO2) on surfaces together with a characterization of vertical excitations, excited states relaxation and electromagnetic emissions. This study will be addressed in future work.
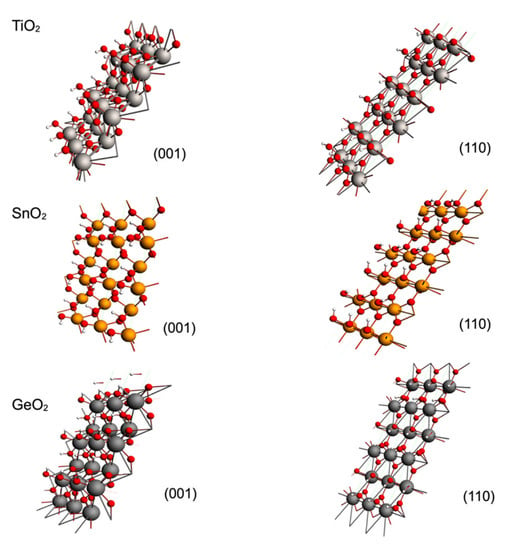
Figure 10.
H2O adsorption–dissociation geometries for TiO2, GeO2 and SnO2 surfaces in planes (001) and (110). Oxygen are red spheres, metals are large gray spheres and hydrogen are small white spheres.

Table 5.
H2O surface dissociation energies in TiO2, GeO2 and SnO2 oxides for (001) and (110) planes.
4. Conclusions
The results showed two adsorbate geometries for CO2 adsorption on rutile and anatase surfaces: one of them was a bended structure and the second one was linear. The observation of one of these geometries depended on the interaction between a surface oxygen and the carbon atom of adsorbate (C-Os) as this interaction was responsible for the CO2 bending. The main difference between the adsorption behavior of the TiO2 phases was the availability of the surface oxygens to interact with the adsorbate. Additionally, the surface topology was relevant to perform secondary interactions with adsorbates. The studied oxides (TiO2, GeO2, SnO2, IrO2 and PbO2) were capable of adsorbing CO2; nevertheless, the lighter oxides, TiO2, GeO2 and SnO2, bent CO2 during adsorption. Meanwhile, the heaviest oxides (IrO2 and PbO2) maintained a linear CO2 geometry. Chemisorption was observed for both planes of TiO2, GeO2 and SnO2, while physisorption was observed for both planes of IrO2 and PbO2. Therefore, the size of the metallic cation was relevant to the final adsorbed geometries. The planes (001) displayed the largest CO2 affinities compared with the (110) planes. Additionally, the bent CO2 geometries were related to chemisorption processes, lower CO2 stability and a large positive and therefore a positive reduction potential. Finally, it was found that the water molecules dissociated during the adsorption process on the TiO2, GeO2 and SnO2 surfaces, displaying the same active sites as in the case of CO2 adsorption, whereby the M1-O-H and OS-H species were observed in the adsorbed H2O. These reactive species with bent CO2 geometries suggested the generation of multiple secondary products that will be studied in future work.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28041776/s1, Figure S1: Scheme of models formation; Coordinates of adsorption models.
Author Contributions
Conceptualization, M.A.G.-R. and R.C.-R.; methodology, M.A.G.-R. and R.C.-R.; software, A.B.-J.; hardware, A.B.-J.; validation, J.R., I.M.-S., I.V.-R. and J.H.-L.; formal analysis, I.M.-S.; investigation, I.V.-R.; resources, J.H.-L.; data curation, I.M.-S.; writing—original draft preparation, R.C.-R.; writing—review and editing, M.A.G.-R., J.R. and R.C.-R.; visualization, I.V.-R. and J.H.-L.; supervision, M.A.G.-R. and J.R.; project administration, M.A.G.-R.; funding acquisition, A.B.-J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CONACYT for R.C.-R., grant number CVU: 1020083, and J.H-L., CVU: 270750.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The National Laboratory UG-UAA-CONACYT (316011) is acknowledged for providing the supercomputing resources. R.C.-R. and J.-H.-L. acknowledge CONACYT for providing their scholarships (1020083 and 270750). Paulina Lozano-Sotomayor and Lilia Bernabé are acknowledged for revising the language of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Le Quéré, C.; Takahashi, T.; Buitenhuis, E.T.; Rödenbeck, C.; Sutherland, S.C. Impact of climate change and variability on the global oceanic sink of CO2. Glob. Biogeochem. Cycles 2010, 24, 1–10. [Google Scholar] [CrossRef]
- Hao, Y.; Chen, H.; Wei, Y.-M.; Li, Y.-M. The influence of climate change on CO2 (carbon dioxide) emissions: An empirical estimation based on Chinese provincial panel data. J. Clean. Prod. 2016, 131, 667–677. [Google Scholar] [CrossRef]
- Shine Keith, P.; Sturges William, T. CO2 Is Not the Only Gas. Science 2007, 315, 1804–1805. [Google Scholar] [CrossRef] [PubMed]
- Dellink, R.; Lanzi, E.; Chateau, J. The Sectoral and Regional Economic Consequences of Climate Change to 2060. Environ. Resour. Econ. 2019, 72, 309–363. [Google Scholar] [CrossRef]
- Socolow, R.; Hotinski, R.; Greenblatt, J.B.; Pacala, S. Solving the Climate Problem: Technologies Available to Curb CO2 Emissions. Environ. Sci. Policy Sustain. Dev. 2004, 46, 8–19. [Google Scholar] [CrossRef]
- Steinberg, M.; Cheng, H.C. Advanced technologies for reduced CO2 emissions. In Proceedings of the Annual Meeting of Air Pollution Control Association, Dallas, TX, USA, 19–24 June 1988. [Google Scholar]
- Ward, H.; Radebach, A.; Vierhaus, I.; Fügenschuh, A.; Steckel, J.C. Reducing global CO2 emissions with the technologies we have. Resour. Energy Econ. 2017, 49, 201–217. [Google Scholar] [CrossRef]
- Olah, G.A.; Prakash, G.K.S.; Goeppert, A. Anthropogenic Chemical Carbon Cycle for a Sustainable Future. J. Am. Chem. Soc. 2011, 133, 12881–12898. [Google Scholar] [CrossRef]
- Surdhar, P.S.; Mezyk, S.P.; Armstrong, D.A. Reduction potential of the carboxyl radical anion in aqueous solutions. J. Phys. Chem. 1989, 93, 3360–3363. [Google Scholar] [CrossRef]
- Xie, S.; Zhang, Q.; Liu, G.; Wang, Y. Photocatalytic and photoelectrocatalytic reduction of CO2 using heterogeneous catalysts with controlled nanostructures. Chem. Commun. 2016, 52, 35–59. [Google Scholar] [CrossRef]
- Chang, X.; Wang, T.; Gong, J. CO2 photo-reduction: Insights into CO2 activation and reaction on surfaces of photocatalysts. Energy Environ. Sci. 2016, 9, 2177–2196. [Google Scholar] [CrossRef]
- Habisreutinger, S.N.; Schmidt-Mende, L.; Stolarczyk, J.K. Photocatalytic Reduction of CO2 on TiO2 and Other Semiconductors. Angew. Chem. Int. Ed. 2013, 52, 7372–7408. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, D.; Deng, X.; Li, Z. Metal–organic frameworks (MOFs) for photocatalytic CO2 reduction. Catal. Sci. Technol. 2017, 7, 4893–4904. [Google Scholar] [CrossRef]
- Abdullah, H.; Khan, M.M.R.; Ong, H.R.; Yaakob, Z. Modified TiO2 photocatalyst for CO2 photocatalytic reduction: An overview. J. CO2 Util. 2017, 22, 15–32. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, H.; Wu, J.; Zhao, R.; Lu, Y.; Xin, B. Controlled facile synthesis and photocatalytic activity of ultrafine high crystallinity TiO2 nanocrystals with tunable anatase/rutile ratios. Appl. Surf. Sci. 2014, 294, 36–41. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, L.; Andino, J.M.; Li, Y. Bicrystalline TiO2 with controllable anatase–brookite phase content for enhanced CO2 photoreduction to fuels. J. Mater. Chem. A 2013, 1, 8209–8216. [Google Scholar] [CrossRef]
- Li, X.; Yu, J.; Jaroniec, M.; Chen, X. Cocatalysts for Selective Photoreduction of CO2 into Solar Fuels. Chem. Rev. 2019, 119, 3962–4179. [Google Scholar] [CrossRef] [PubMed]
- Guil-López, R.; Mota, N.; Llorente, J.; Millán, E.; Pawelec, B.; Fierro, J.L.G.; Navarro, R.M. Methanol Synthesis from CO2: A Review of the Latest Developments in Heterogeneous Catalysis. Materials 2019, 12, 3902. [Google Scholar] [CrossRef]
- Handoko, A.D.; Li, K.; Tang, J. Recent progress in artificial photosynthesis: CO2 photoreduction to valuable chemicals in a heterogeneous system. Curr. Opin. Chem. Eng. 2013, 2, 200–206. [Google Scholar] [CrossRef]
- Centi, G.; Perathoner, S. Opportunities and prospects in the chemical recycling of carbon dioxide to fuels. Catal. Today 2009, 148, 191–205. [Google Scholar] [CrossRef]
- Omae, I. Aspects of carbon dioxide utilization. Catal. Today 2006, 115, 33–52. [Google Scholar] [CrossRef]
- Ji, Y.; Luo, Y. Theoretical Study on the Mechanism of Photoreduction of CO2 to CH4 on the Anatase TiO2(101) Surface. ACS Catal. 2016, 6, 2018–2025. [Google Scholar] [CrossRef]
- Pipornpong, W.; Wanbayor, R.; Ruangpornvisuti, V. Adsorption CO2 on the perfect and oxygen vacancy defect surfaces of anatase TiO2 and its photocatalytic mechanism of conversion to CO. Appl. Surf. Sci. 2011, 257, 10322–10328. [Google Scholar] [CrossRef]
- Anpo, M.; Yamashita, H.; Ichihashi, Y.; Ehara, S. Photocatalytic reduction of CO2 with H2O on various titanium oxide catalysts. J. Electroanal. Chem. 1995, 396, 21–26. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, H.; Andino, J.M.; Li, Y. Photocatalytic CO2 Reduction with H2O on TiO2 Nanocrystals: Comparison of Anatase, Rutile, and Brookite Polymorphs and Exploration of Surface Chemistry. ACS Catal. 2012, 2, 1817–1828. [Google Scholar] [CrossRef]
- Umezawa, N.; Kristoffersen, H.H.; Vilhelmsen, L.B.; Hammer, B. Reduction of CO2 with Water on Pt-Loaded Rutile TiO2(110) Modeled with Density Functional Theory. J. Phys. Chem. C 2016, 120, 9160–9164. [Google Scholar] [CrossRef]
- Matsumoto, Y. Energy Positions of Oxide Semiconductors and Photocatalysis with Iron Complex Oxides. J. Solid State Chem. 1996, 126, 227–234. [Google Scholar] [CrossRef]
- Peng, C.; Reid, G.; Wang, H.; Hu, P. Perspective: Photocatalytic reduction of CO2 to solar fuels over semiconductors. J. Chem. Phys. 2017, 147, 030901. [Google Scholar] [CrossRef]
- Dhakshinamoorthy, A.; Navalon, S.; Corma, A.; Garcia, H. Photocatalytic CO2 reduction by TiO2 and related titanium containing solids. Energy Environ. Sci. 2012, 5, 9217–9233. [Google Scholar] [CrossRef]
- Wu, H.-L.; Li, X.-B.; Tung, C.-H.; Wu, L.-Z. Semiconductor Quantum Dots: An Emerging Candidate for CO2 Photoreduction. Adv. Mater. 2019, 31, 1900709. [Google Scholar] [CrossRef]
- Yan, Y.-l.; Fang, Q.-J.; Pan, J.-k.; Yang, J.; Zhang, L.-l.; Zhang, W.; Zhuang, G.-l.; Zhong, X.; Deng, S.-w.; Wang, J.-g. Efficient photocatalytic reduction of CO2 using Fe-based covalent triazine frameworks decorated with in situ grown ZnFe2O4 nanoparticles. Chem. Eng. J. 2021, 408, 127358. [Google Scholar] [CrossRef]
- Krischok, S.; Höfft, O.; Kempter, V. The chemisorption of H2O and CO2 on TiO2 surfaces: Studies with MIES and UPS (HeI/II). Surf. Sci. 2002, 507–510, 69–73. [Google Scholar] [CrossRef]
- Liang, L.; Ling, P.; Li, Y.; Li, L.; Liu, J.; Luo, Q.; Zhang, H.; Xu, Q.; Pan, Y.; Zhu, J.; et al. Atmospheric CO2 capture and photofixation to near-unity CO by Ti3+-Vo-Ti3+ sites confined in TiO2 ultrathin layers. Sci. China Chem. 2021, 64, 953–958. [Google Scholar] [CrossRef]
- Sorescu, D.C.; Al-Saidi, W.A.; Jordan, K.D. CO2 adsorption on TiO2(101) anatase: A dispersion-corrected density functional theory study. J. Chem. Phys. 2011, 135, 124701. [Google Scholar] [CrossRef] [PubMed]
- Mino, L.; Spoto, G.; Ferrari, A.M. CO2 Capture by TiO2 Anatase Surfaces: A Combined DFT and FTIR Study. J. Phys. Chem. C 2014, 118, 25016–25026. [Google Scholar] [CrossRef]
- Li, H.; Rameshan, C.; Bukhtiyarov, A.V.; Prosvirin, I.P.; Bukhtiyarov, V.I.; Rupprechter, G. CO2 activation on ultrathin ZrO2 film by H2O co-adsorption: In situ NAP-XPS and IRAS studies. Surf. Sci. 2019, 679, 139–146. [Google Scholar] [CrossRef]
- Gattrell, M.; Gupta, N.; Co, A. A review of the aqueous electrochemical reduction of CO2 to hydrocarbons at copper. J. Electroanal. Chem. 2006, 594, 1–19. [Google Scholar] [CrossRef]
- Cadi-Essadek, A.; Roldan, A.; de Leeuw, N.H. Density functional theory study of the interaction of H2O, CO2 and CO with the ZrO2 (111), Ni/ZrO2 (111), YSZ (111) and Ni/YSZ (111) surfaces. Surf. Sci. 2016, 653, 153–162. [Google Scholar] [CrossRef]
- Chen, H.-Y.T.; Tosoni, S.; Pacchioni, G. A DFT study of the acid–base properties of anatase TiO2 and tetragonal ZrO2 by adsorption of CO and CO2 probe molecules. Surf. Sci. 2016, 652, 163–171. [Google Scholar] [CrossRef]
- Bendavid, L.I.; Carter, E.A. CO2 Adsorption on Cu2O(111): A DFT+U and DFT-D Study. J. Phys. Chem. C 2013, 117, 26048–26059. [Google Scholar] [CrossRef]
- Zhu, S.; Guo, L.; Li, P.; Zhang, B.; Zhao, G.; He, T. A computational study on linear and bent adsorption of CO2 on different surfaces for its photoreduction. Catal. Today 2019, 335, 278–285. [Google Scholar] [CrossRef]
- Tang, Q.-L.; Luo, Q.-H. Adsorption of CO2 at ZnO: A Surface Structure Effect from DFT+U Calculations. J. Phys. Chem. C 2013, 117, 22954–22966. [Google Scholar] [CrossRef]
- He, H.; Zapol, P.; Curtiss, L.A. A Theoretical Study of CO2 Anions on Anatase (101) Surface. J. Phys. Chem. C 2010, 114, 21474–21481. [Google Scholar] [CrossRef]
- Nie, X.; Wang, H.; Liang, Z.; Yu, Z.; Zhang, J.; Janik, M.J.; Guo, X.; Song, C. Comparative computational study of CO2 dissociation and hydrogenation over Fe-M (M = Pd, Ni, Co) bimetallic catalysts: The effect of surface metal content. J. CO2 Util. 2019, 29, 179–195. [Google Scholar] [CrossRef]
- Rodriguez, M.M.; Peng, X.; Liu, L.; Li, Y.; Andino, J.M. A Density Functional Theory and Experimental Study of CO2 Interaction with Brookite TiO2. J. Phys. Chem. C 2012, 116, 19755–19764. [Google Scholar] [CrossRef]
- Indrakanti, V.P.; Schobert, H.H.; Kubicki, J.D. Quantum Mechanical Modeling of CO2 Interactions with Irradiated Stoichiometric and Oxygen-Deficient Anatase TiO2 Surfaces: Implications for the Photocatalytic Reduction of CO2. Energy Fuels 2009, 23, 5247–5256. [Google Scholar] [CrossRef]
- Li, X.; Yu, J.; Jiang, C. Chapter 1—Principle and surface science of photocatalysis. In Interface Science and Technology; Yu, J., Jaroniec, M., Jiang, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Volume 31, pp. 1–38. [Google Scholar]
- Zhang, L.; Jaroniec, M. Chapter 2—Fundamentals of adsorption for photocatalysis. In Interface Science and Technology; Yu, J., Jaroniec, M., Jiang, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Volume 31, pp. 39–62. [Google Scholar]
- Huygh, S.; Bogaerts, A.; Neyts, E.C. How Oxygen Vacancies Activate CO2 Dissociation on TiO2 Anatase (001). J. Phys. Chem. C 2016, 120, 21659–21669. [Google Scholar] [CrossRef]
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Snijders, J.G.; te Velde, G.; Baerends, E.J. Towards an order-N DFT method. Theor. Chem. Acc. 1998, 99, 391–403. [Google Scholar] [CrossRef]
- ADF2014, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. Available online: https://www.scm.com/ (accessed on 2 May 2022).
- te Velde, G.; Baerends, E.J. Precise density-functional method for periodic structures. Phys. Rev. B 1991, 44, 7888–7903. [Google Scholar] [CrossRef]
- Wiesenekker, G.; Baerends, E.J. Quadratic integration over the three-dimensional Brillouin zone. J. Phys. Condens. Matter 1991, 3, 6721–6742. [Google Scholar] [CrossRef]
- Franchini, M.; Philipsen, P.H.T.; Visscher, L. The Becke Fuzzy Cells Integration Scheme in the Amsterdam Density Functional Program Suite. J. Comput. Chem. 2013, 34, 1819–1827. [Google Scholar] [CrossRef] [PubMed]
- Franchini, M.; Philipsen, P.H.T.; van Lenthe, E.; Visscher, L. Accurate Coulomb Potentials for Periodic and Molecular Systems through Density Fitting. J. Chem. Theory Comput. 2014, 10, 1994–2004. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Erratum: Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces [Phys. Rev. Lett. 100, 136406 (2008)]. Phys. Rev. Lett. 2009, 102, 039902. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- van Lenthe, E.; van Leeuwen, R.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. Int. J. Quantum Chem. 1996, 57, 281–293. [Google Scholar] [CrossRef]
- van Lenthe, E.; Snijders, J.G.; Baerends, E.J. The zero-order regular approximation for relativistic effects: The effect of spin–orbit coupling in closed shell molecules. J. Chem. Phys. 1996, 105, 6505–6516. [Google Scholar] [CrossRef]
- van Lenthe, E.; Ehlers, A.; Baerends, E.-J. Geometry optimizations in the zero order regular approximation for relativistic effects. J. Chem. Phys. 1999, 110, 8943–8953. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Ruoff, R.S.; Kadish, K.M.; Boulas, P.; Chen, E.C.M. Relationship between the Electron Affinities and Half-Wave Reduction Potentials of Fullerenes, Aromatic Hydrocarbons, and Metal Complexes. J. Phys. Chem. 1995, 99, 8843–8850. [Google Scholar] [CrossRef]
- Conradie, J. A Frontier orbital energy approach to redox potentials. J. Phys. Conf. Ser. 2015, 633, 012045. [Google Scholar] [CrossRef]
- Bateni, S.B.; England, K.R.; Galatti, A.T.; Kaur, H.; Mendiola, V.A.; Mitchell, A.R.; Vu, M.H.; Gherman, B.F.; Miranda, J.A. Prediction of reduction potentials from calculated electron affinities for metal-salen compounds. Beilstein J. Org. Chem. 2009, 5, 82. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, R.Q.; Ng, A.M.C.; Djurišić, A.B.; Chan, H.T.; Chan, W.K.; Tong, S.Y. Splitting Water on Metal Oxide Surfaces. J. Phys. Chem. C 2011, 115, 19710–19715. [Google Scholar] [CrossRef]
- Verdaguer, A.; Sacha, G.M.; Bluhm, H.; Salmeron, M. Molecular Structure of Water at Interfaces: Wetting at the Nanometer Scale. Chem. Rev. 2006, 106, 1478–1510. [Google Scholar] [CrossRef]
- Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
- Thiel, P.A.; Madey, T.E. The interaction of water with solid surfaces: Fundamental aspects. Surf. Sci. Rep. 1987, 7, 211–385. [Google Scholar] [CrossRef]
- Zwicker, G.; Jacobi, K. Site-specific interaction of H2O with ZnO single-crystal surfaces studied by thermal desorption and UV photoelectron spectroscopy. Surf. Sci. 1983, 131, 179–194. [Google Scholar] [CrossRef]
- Henrich, V.E. Ultraviolet photoemission studies of molecular adsorption on oxide surfaces. Prog. Surf. Sci. 1979, 9, 143–164. [Google Scholar] [CrossRef]
- McKay, J.M.; Henrich, V.E. Surface electronic structure of NiO: Defect states, O2 and H2O interactions. Phys. Rev. B 1985, 32, 6764–6772. [Google Scholar] [CrossRef] [PubMed]
- Gercher, V.A.; Cox, D.F. Water adsorption on stoichiometric and defective SnO2(110) surfaces. Surf. Sci. 1995, 322, 177–184. [Google Scholar] [CrossRef]
- Lindan, P.J.D. Water chemistry at the SnO2(110) surface: The role of inter-molecular interactions and surface geometry. Chem. Phys. Lett. 2000, 328, 325–329. [Google Scholar] [CrossRef]
- Slater, B.; Richard, C.; Catlow, A.; Williams, D.E.; Stoneham, A.M. Competitive Adsorption of O2 and H2O at the Neutral and Defective SnO2 (110) Surface. MRS Online Proc. Libr. 2001, 658, 933. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).