Rational Design of a Low-Data Regime of Pyrrole Antioxidants for Radical Scavenging Activities Using Quantum Chemical Descriptors and QSAR with the GA-MLR and ANN Concepts
Abstract
:1. Introduction
2. Results and Discussion
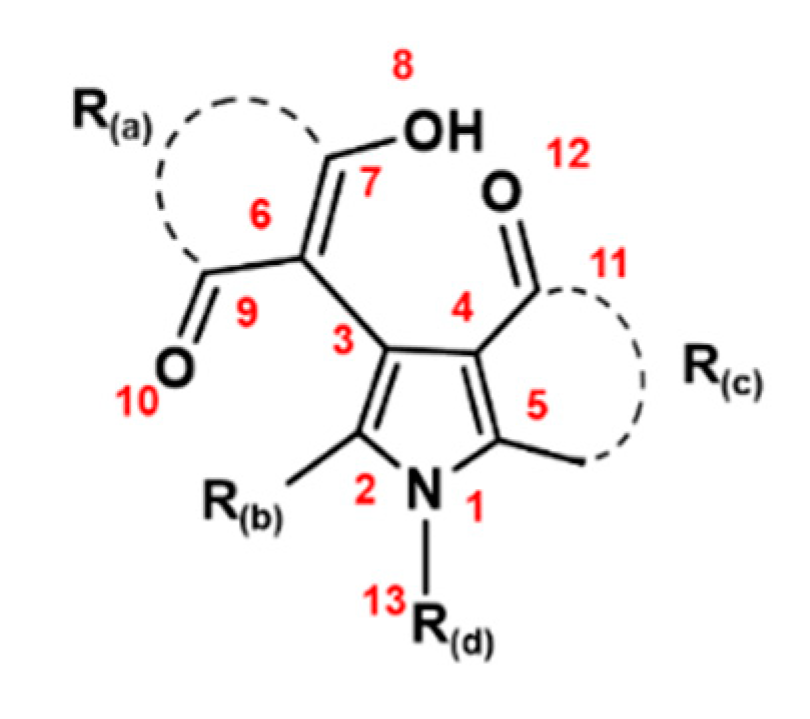
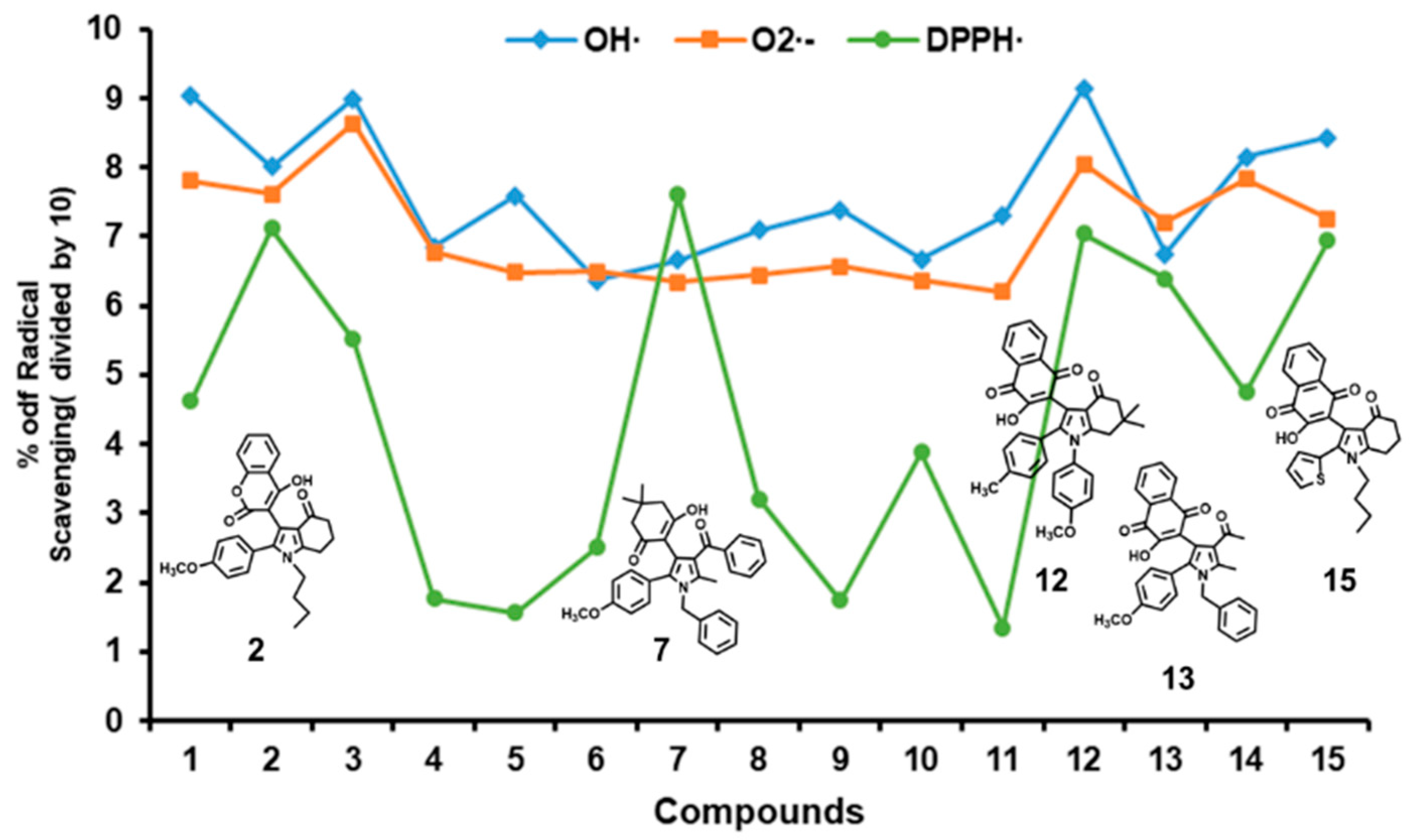
2.1. Scavenging Activities of Studied Pyrrole Derivatives
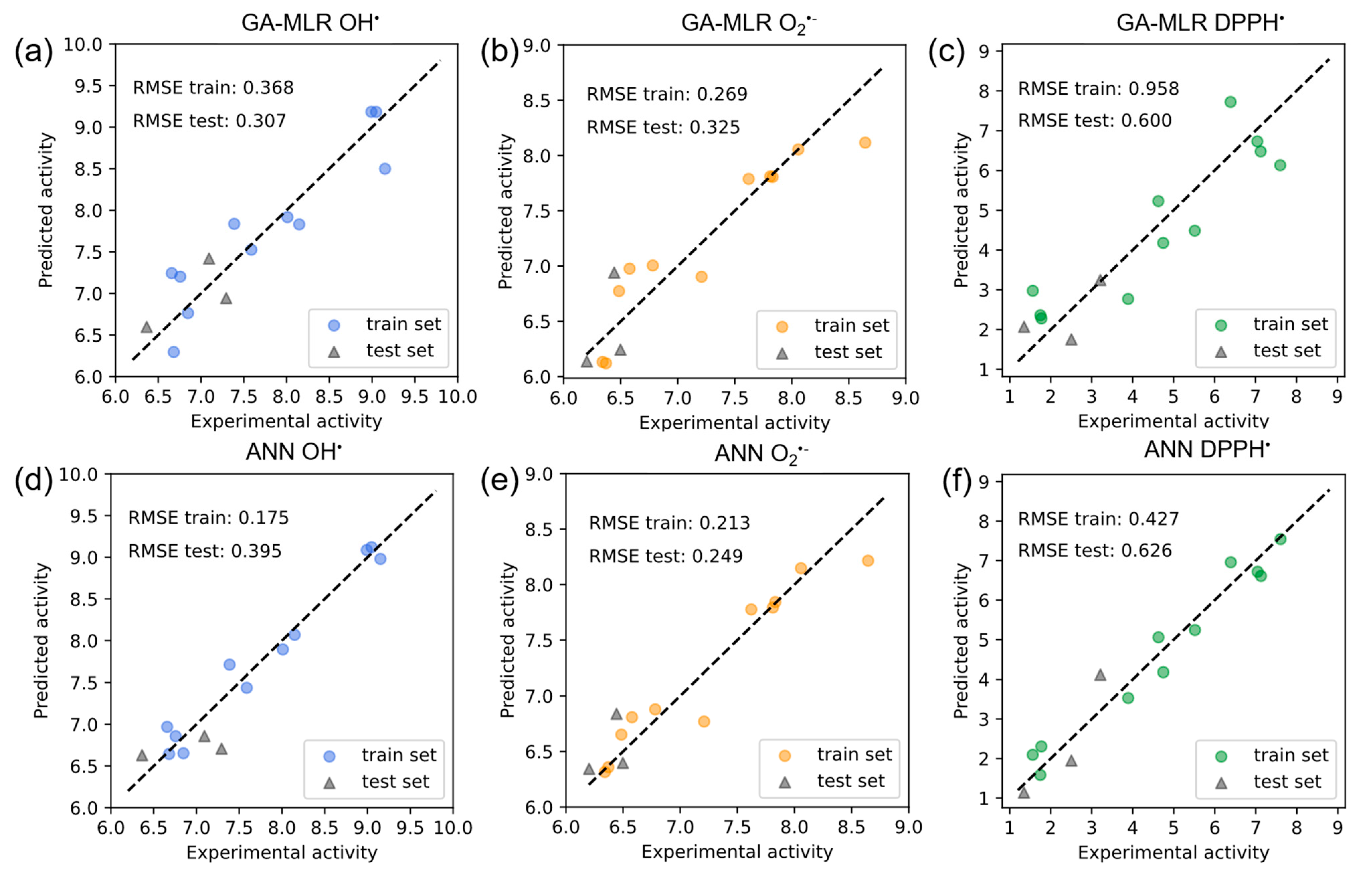
2.2. QSAR GA-MLR Models
2.3. QSAR ANN Models
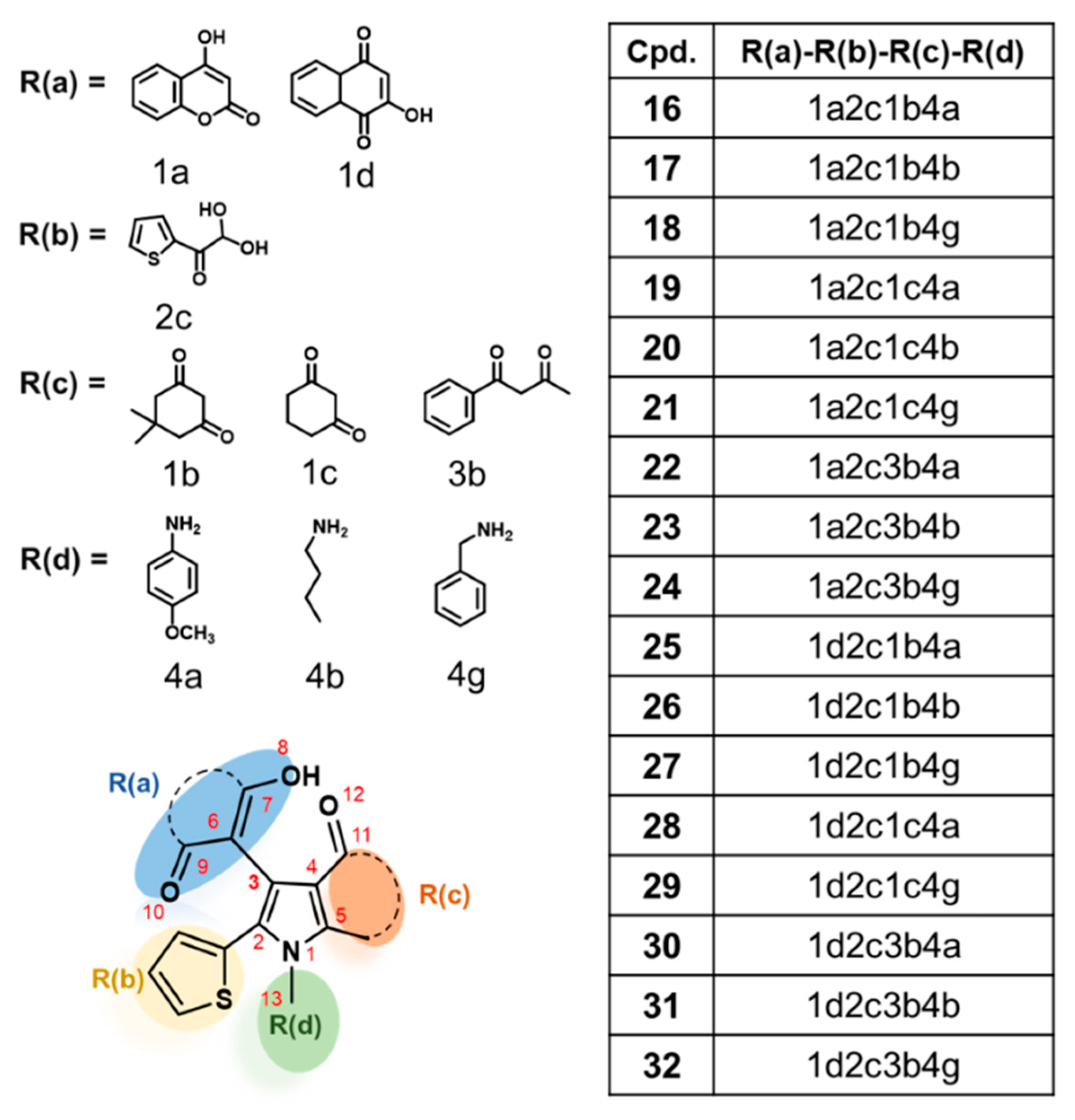
2.4. Newly Designed Compounds with Predicted ROS Activities
3. Methods

4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Lobo, V.; Patil, A.; Phatak, A.; Chandra, N. Free radicals, antioxidants and functional foods: Impact on human health. Pharmacogn. Rev. 2010, 4, 118–126. [Google Scholar] [CrossRef]
- Kim, G.H.; Kim, J.E.; Rhie, S.J.; Yoon, S. The Role of Oxidative Stress in Neurodegenerative Diseases. Exp. Neurobiol. 2015, 24, 325–340. [Google Scholar] [CrossRef]
- Thanan, R.; Oikawa, S.; Hiraku, Y.; Ohnishi, S.; Ma, N.; Pinlaor, S.; Yongvanit, P.; Kawanishi, S.; Murata, M. Oxidative stress and its significant roles in neurodegenerative diseases and cancer. Int. J. Mol. Sci. 2014, 16, 193–217. [Google Scholar] [CrossRef]
- Kayama, Y.; Raaz, U.; Jagger, A.; Adam, M.; Schellinger, I.N.; Sakamoto, M.; Suzuki, H.; Toyama, K.; Spin, J.M.; Tsao, P.S. Diabetic Cardiovascular Disease Induced by Oxidative Stress. Int. J. Mol. Sci. 2015, 16, 25234–25263. [Google Scholar] [CrossRef]
- Luo, J.; Mills, K.; le Cessie, S.; Noordam, R.; van Heemst, D. Ageing, age-related diseases and oxidative stress: What to do next? Ageing Res. Rev. 2020, 57, 100982. [Google Scholar] [CrossRef]
- Sharifi-Rad, M.; Anil Kumar, N.V.; Zucca, P.; Varoni, E.M.; Dini, L.; Panzarini, E.; Rajkovic, J.; Tsouh Fokou, P.V.; Azzini, E.; Peluso, I.; et al. Lifestyle, Oxidative Stress, and Antioxidants: Back and Forth in the Pathophysiology of Chronic Diseases. Front. Physiol. 2020, 11, 694. [Google Scholar] [CrossRef]
- Nimse, S.B.; Pal, D. Free radicals, natural antioxidants, and their reaction mechanisms. RSC Adv. 2015, 5, 27986–28006. [Google Scholar] [CrossRef]
- Kurutas, E.B. The importance of antioxidants which play the role in cellular response against oxidative/nitrosative stress: Current state. Nutr. J. 2016, 15, 71. [Google Scholar] [CrossRef]
- Seppanen, C.M.; Song, Q.; Saari Csallany, A. The Antioxidant Functions of Tocopherol. and Tocotrienol. Homologues in Oils, Fats, and Food Systems. J. Am. Oil Chem. Soc. 2010, 87, 469–481. [Google Scholar] [CrossRef]
- Perez-Gonzalez, A.; Galano, A. OH radical scavenging activity of Edaravone: Mechanism and kinetics. J. Phys. Chem. B 2011, 115, 1306–1314. [Google Scholar] [CrossRef]
- Im, S.; Nam, T.G.; Lee, S.G.; Kim, Y.J.; Chun, O.K.; Kim, D.-O. Additive antioxidant capacity of vitamin C and tocopherols in combination. Food Sci. Biotechnol. 2014, 23, 693–699. [Google Scholar] [CrossRef]
- Ingold, K.U.; Pratt, D.A. Advances in radical-trapping antioxidant chemistry in the 21st century: A kinetics and mechanisms perspective. Chem. Rev. 2014, 114, 9022–9046. [Google Scholar] [CrossRef] [PubMed]
- Kandasamy, S.; Baggu, C.; Javagal, M.R.; Lingamallu, J.R.; Yenamandra, V.; Aradhya, S.M. Antioxidant properties of isolated compounds from banana rhizome. J. Food Sci. 2014, 79, H988–H1001. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.P.; Li, Y.; Meng, X.; Zhou, T.; Zhou, Y.; Zheng, J.; Zhang, J.J.; Li, H.B. Natural Antioxidants in Foods and Medicinal Plants: Extraction, Assessment and Resources. Int. J. Mol. Sci. 2017, 18, 96. [Google Scholar] [CrossRef]
- Rasulev, B.F.; Abdullaev, N.D.; Syrov, V.N.; Leszczynski, J. A Quantitative Structure-Activity Relationship (QSAR) Study of the Antioxidant Activity of Flavonoids. QSAR Comb. Sci. 2005, 24, 1056–1065. [Google Scholar] [CrossRef]
- Di Meo, F.; Lemaur, V.; Cornil, J.; Lazzaroni, R.; Duroux, J.L.; Olivier, Y.; Trouillas, P. Free radical scavenging by natural polyphenols: Atom versus electron transfer. J. Phys. Chem. A 2013, 117, 2082–2092. [Google Scholar] [CrossRef] [PubMed]
- Khairullina, V.; Safarova, I.; Sharipova, G.; Martynova, Y.; Gerchikov, A. QSAR Assessing the Efficiency of Antioxidants in the Termination of Radical-Chain Oxidation Processes of Organic Compounds. Molecules 2021, 26, 421. [Google Scholar] [CrossRef]
- Fujita, T.; Winkler, D.A. Understanding the Roles of the “Two QSARs”. J. Chem. Inf. Model. 2016, 56, 269–274. [Google Scholar] [CrossRef]
- Rastija, V.; Medic-Saric, M. QSAR study of antioxidant activity of wine polyphenols. Eur. J. Med. Chem. 2009, 44, 400–408. [Google Scholar] [CrossRef]
- El Aissouq, A.; Toufik, H.; Lamchouri, F.; Stitou, M.; Ouammou, A. QSAR study of isonicotinamides derivatives as Alzheimer’s disease inhibitors using PLS-R and ANN methods. In Proceedings of the ISACS Conference 2019, Taza, Morocco, 26–27 December 2019; pp. 1–7. [Google Scholar]
- Choi, H.; Kang, H.; Chung, K.C.; Park, H. Development and application of a comprehensive machine learning program for predicting molecular biochemical and pharmacological properties. Phys. Chem. Chem. Phys. 2019, 21, 5189–5199. [Google Scholar] [CrossRef]
- Hu, S.; Chen, P.; Gu, P.; Wang, B. A Deep Learning-Based Chemical System for QSAR Prediction. IEEE J. BioMed. Health Inform. 2020, 24, 3020–3028. [Google Scholar] [CrossRef] [PubMed]
- Amic, D.; Davidovic-Amic, D.; Beslo, D.; Rastija, V.; Lucic, B.; Trinajstic, N. SAR and QSAR of the antioxidant activity of flavonoids. Curr. Med. Chem. 2007, 14, 827–845. [Google Scholar] [CrossRef] [PubMed]
- Lavarda, F.C. Relation between antioxidant activity and electronic structure of phenols. Int. J. Quantum Chem. 2003, 95, 219–223. [Google Scholar] [CrossRef]
- Reis, M.; Lobato, B.; Lameira, J.; Santos, A.S.; Alves, C.N. A theoretical study of phenolic compounds with antioxidant properties. Eur. J. Med. Chem. 2007, 42, 440–446. [Google Scholar] [CrossRef]
- Farrokhnia, M. Density Functional Theory Studies on the Antioxidant Mechanism and Electronic Properties of Some Bioactive Marine Meroterpenoids: Sargahydroquionic Acid and Sargachromanol. ACS Omega 2020, 5, 20382–20390. [Google Scholar] [CrossRef]
- Boudergua, S.; Alloui, M.; Belaidi, S.; Al Mogren, M.M.; Ellatif Ibrahim, U.A.A.; Hochlaf, M. QSAR Modeling and Drug-Likeness Screening for Antioxidant Activity of Benzofuran Derivatives. J. Mol. Struct. 2019, 1189, 307–314. [Google Scholar] [CrossRef]
- Zuvela, P.; David, J.; Yang, X.; Huang, D.; Wong, M.W. Non-Linear Quantitative Structure(-)Activity Relationships Modelling, Mechanistic Study and In-Silico Design of Flavonoids as Potent Antioxidants. Int. J. Mol. Sci. 2019, 20, 2328. [Google Scholar] [CrossRef]
- Worachartcheewan, A.; Prachayasittikul, V.; Prachayasittikul, S.; Tantivit, V.; Yeeyahya, C.; Prachayasittikul, V. Rational design of novel coumarins: A potential trend for antioxidants in cosmetics. EXCLI J. 2020, 19, 209–226. [Google Scholar]
- Kundu, T.; Pramanik, A. Expeditious and eco-friendly synthesis of new multifunctionalized pyrrole derivatives and evaluation of their antioxidant property. Bioorg. Chem. 2020, 98, 103734. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Materials Studio Modeling, Release 7.0; Accelrys Software, Inc.: San Diego, CA, USA, 2013.
- Kennard, R.W.; Stone, L.A. Computer Aided Design of Experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Sivakumar, P.M.; Babu, S.K.; Mukesh, D. QSAR studies on chalcones and flavonoids as anti-tuberculosis agents using genetic function approximation (GFA) method. Chem. Pharm. Bull. 2007, 55, 44–49. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, C.; Lin, W.; Chen, Q.; Guo, X.; Qian, Y.; Zhang, L. Quantitative structure-property relationship (QSPR) modeling of drug-loaded polymeric micelles via genetic function approximation. PLoS ONE 2015, 10, e0119575. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Jan-carlo, M.D.; Francisco, J.A.; Xerardo, G.; Francisco, J.P. New Theoretical Model for the Study of New β-Secretase Inhibitors. Mol2Net 2015, 1, 1–6. [Google Scholar]
- Terfloth, L. Neural networks and genetic algorithms in drug design. Drug Discov. Today 2001, 6, 102–108. [Google Scholar] [CrossRef]
- Cheng, F. Applications of Artificial Neural Network Modeling in Drug Discovery. Clin. Exp. Pharmacol. 2012, 2, 1–2. [Google Scholar] [CrossRef]
- Zuvela, P.; David, J.; Wong, M.W. Interpretation of ANN-based QSAR models for prediction of antioxidant activity of flavonoids. J. Comput. Chem. 2018, 39, 953–963. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Singh, V.; Gupta, I.; Gupta, H.O. ANN-based estimator for distillation using Levenberg–Marquardt approach. Eng. Appl. Artif. Intell. 2007, 20, 249–259. [Google Scholar] [CrossRef]
- MATLAB, version R2021b ed; The MathWorks, Inc.: Natick, MA, USA, 2021.


| Equation | Definitions | R2 | R2(CV) | b F | c Fcr (0.05) |
|---|---|---|---|---|---|
| Equation (1) a Y1 = −90.879 ∗ X17 −47.988 ∗ X19 +0.016 ∗ X20 +207.384 | X17: Bond C2-R(b) X19: Bond C4-C11 X20: Polarizability | 0.848 | 0.711 | 14.917 | 4.236 |
| Equation (2) Y2 = −43.836 ∗ X19 +0.005 ∗ X20 −75.277 ∗ X21 +47.527 | X19: Bond C4-C11 X20: Polarizability X21: HOMO energy | 0.863 | 0.731 | 16.770 | 4.236 |
| Equation (3) Y3 = 61.220 ∗ X16 −1.240 ∗ X26 +0.052 ∗ X30 −102.072 | X16: Bond N1-C13 X26: AlogP X30: Connolly surface area | 0.810 | 0.559 | 11.388 | 4.236 |
| Descriptors | Group Type | Definition |
|---|---|---|
| X16: Bond N1–C13 | Steric | The bond distance between atoms N1 and C13. |
| X17: Bond C2-R(b) | Steric | The bond distance between atom C2 and substituent R(b). |
| X19: Bond C4–C11 | Steric | The bond distance between atoms C4 and C11. |
| X20: Polarizability | Electronic | The relative tendency of charge distribution in a molecule. |
| X21: HOMO energy | Electronic | The energy of the Highest Occupied Molecular Orbital. |
| X26: AlogP | Hydrophobic | the logarithm of the octanol/water partition coefficient. |
| X30: Connolly surface area | Steric | The surface area of an atom volume surface, derived from the Connolly algorithm. |
| Model | GA-MLR | ANN | ||||
|---|---|---|---|---|---|---|
| R2 (Train) | RMSE (Train) | RMSE (Test) | R2 (Train) | RMSE (Train) | RMSE (Test) | |
| •OH | 0.848 | 0.368 | 0.307 | 0.965 | 0.175 | 0.395 |
| O2•− | 0.863 | 0.269 | 0.325 | 0.920 | 0.213 | 0.249 |
| DPPH• | 0.810 | 0.958 | 0.600 | 0.961 | 0.427 | 0.626 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, W.; Wiriyarattanakul, S.; Rungrotmongkol, T.; Shi, L.; Wiriyarattanakul, A.; Maitarad, P. Rational Design of a Low-Data Regime of Pyrrole Antioxidants for Radical Scavenging Activities Using Quantum Chemical Descriptors and QSAR with the GA-MLR and ANN Concepts. Molecules 2023, 28, 1596. https://doi.org/10.3390/molecules28041596
Xie W, Wiriyarattanakul S, Rungrotmongkol T, Shi L, Wiriyarattanakul A, Maitarad P. Rational Design of a Low-Data Regime of Pyrrole Antioxidants for Radical Scavenging Activities Using Quantum Chemical Descriptors and QSAR with the GA-MLR and ANN Concepts. Molecules. 2023; 28(4):1596. https://doi.org/10.3390/molecules28041596
Chicago/Turabian StyleXie, Wanting, Sopon Wiriyarattanakul, Thanyada Rungrotmongkol, Liyi Shi, Amphawan Wiriyarattanakul, and Phornphimon Maitarad. 2023. "Rational Design of a Low-Data Regime of Pyrrole Antioxidants for Radical Scavenging Activities Using Quantum Chemical Descriptors and QSAR with the GA-MLR and ANN Concepts" Molecules 28, no. 4: 1596. https://doi.org/10.3390/molecules28041596
APA StyleXie, W., Wiriyarattanakul, S., Rungrotmongkol, T., Shi, L., Wiriyarattanakul, A., & Maitarad, P. (2023). Rational Design of a Low-Data Regime of Pyrrole Antioxidants for Radical Scavenging Activities Using Quantum Chemical Descriptors and QSAR with the GA-MLR and ANN Concepts. Molecules, 28(4), 1596. https://doi.org/10.3390/molecules28041596







