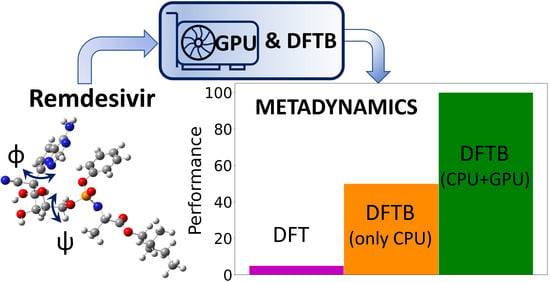
GPU-Enhanced DFTB Metadynamics for Efficiently Predicting Free Energies of Biochemical Systems
Abstract
1. Introduction
2. Theory and Methodology
2.1. DFTB Formalism
2.2. Hamiltonian Diagonalization
2.3. Divide-and-Conquer
2.4. Metadynamics
3. Computational Details
3.1. Amber Calculations
3.2. DFTB Calculations
4. Results and Discussion
4.1. Timing Benchmarks
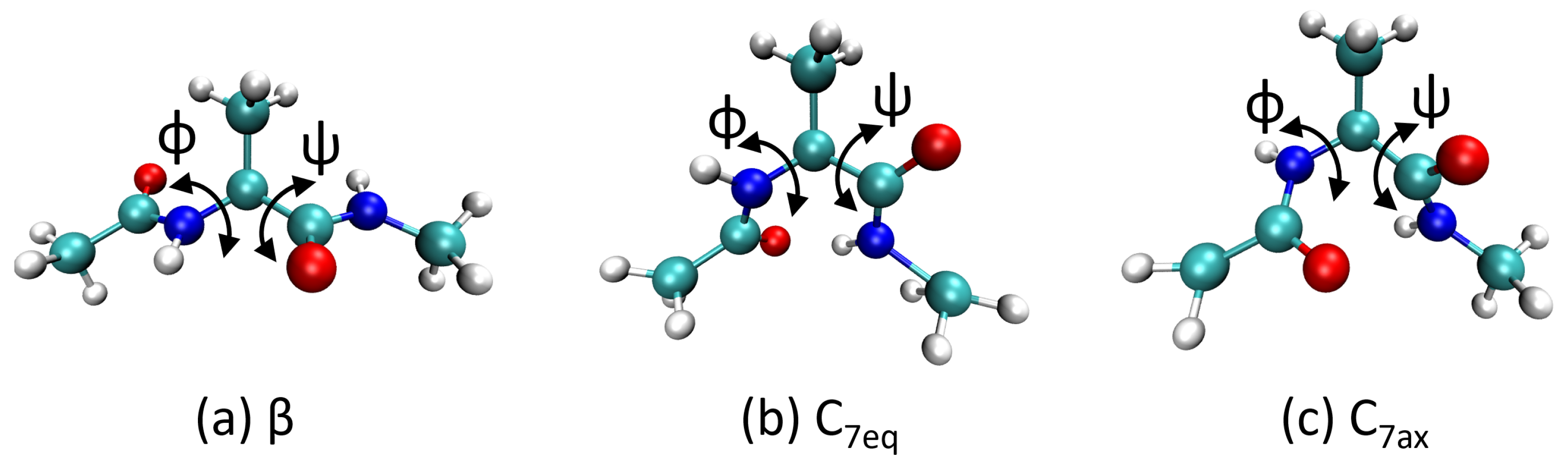
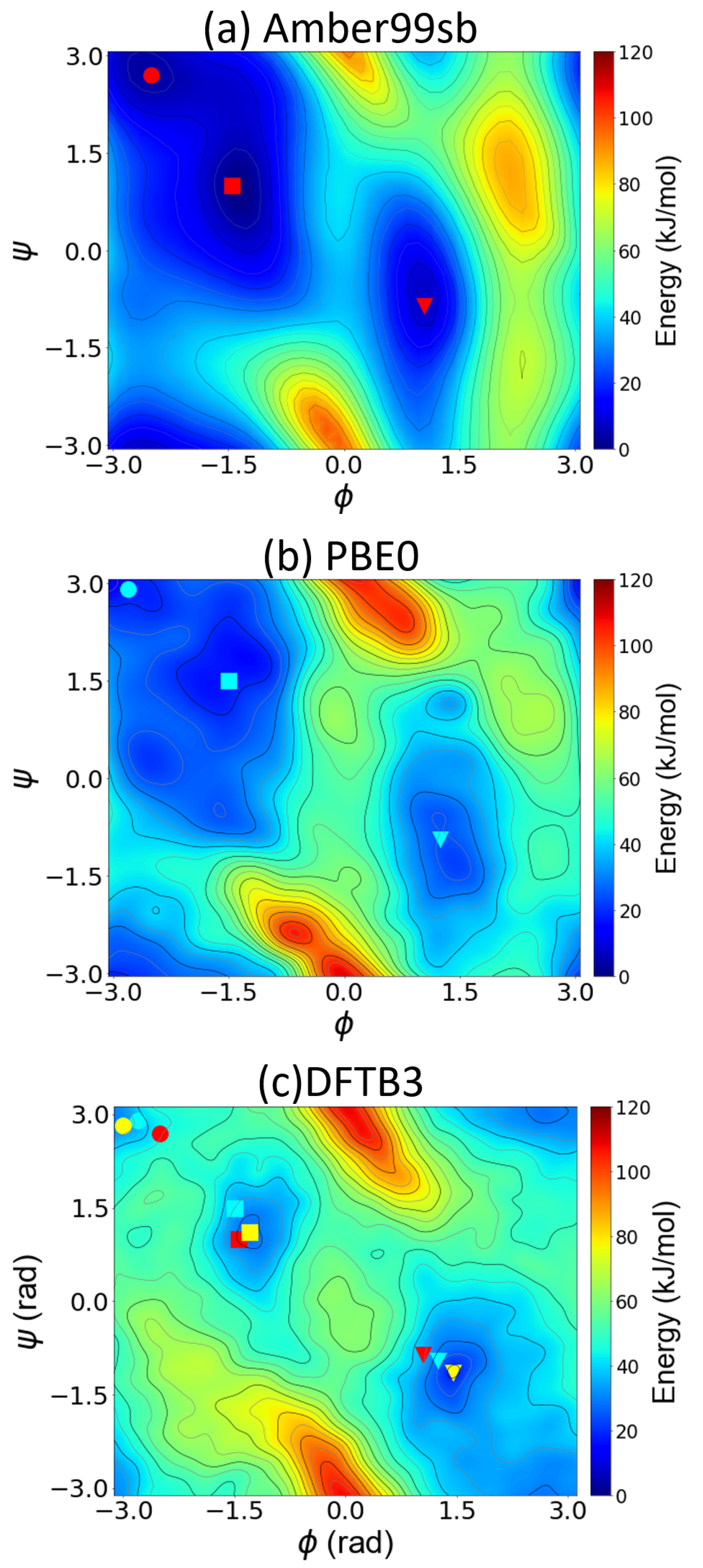
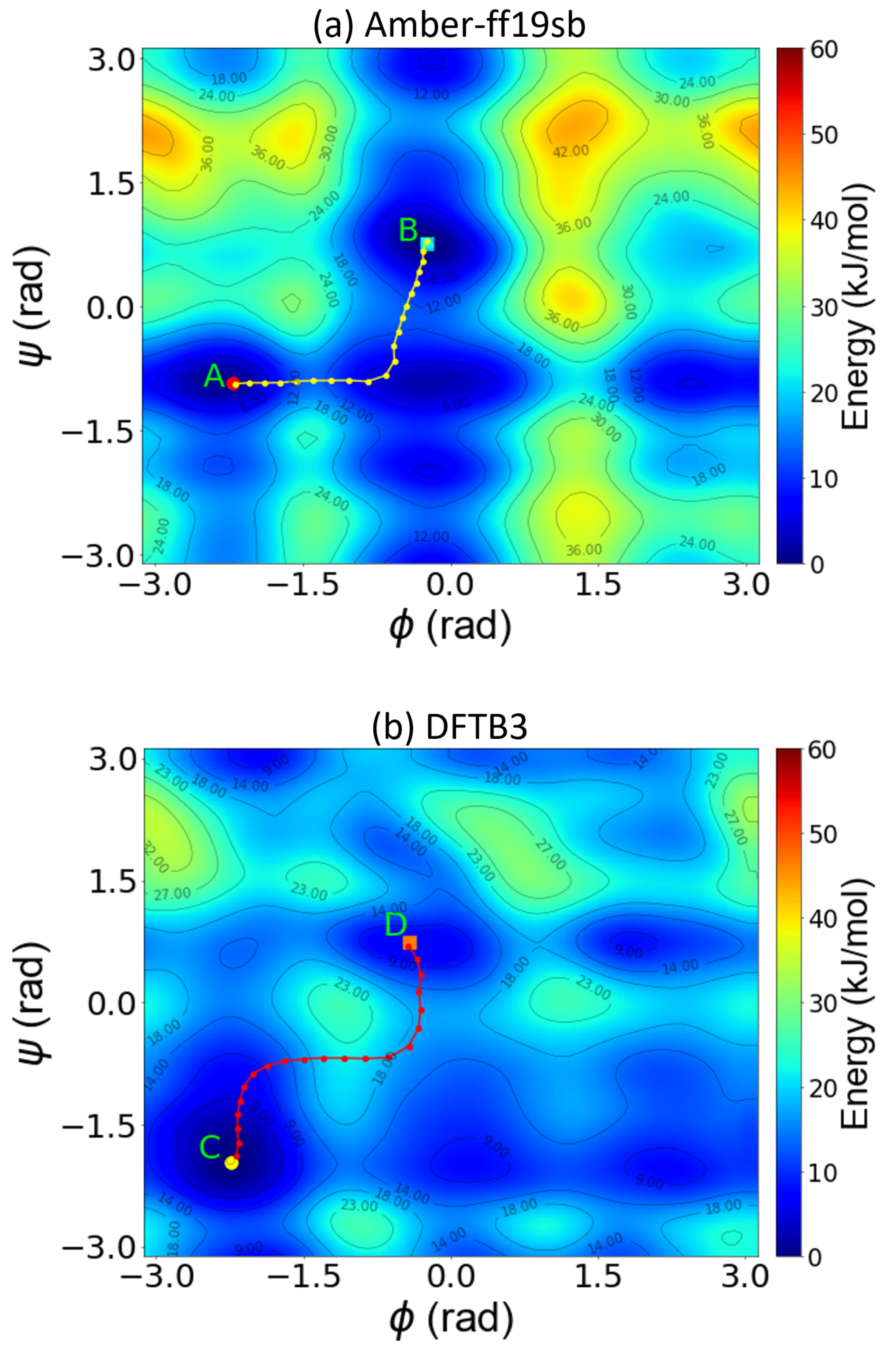
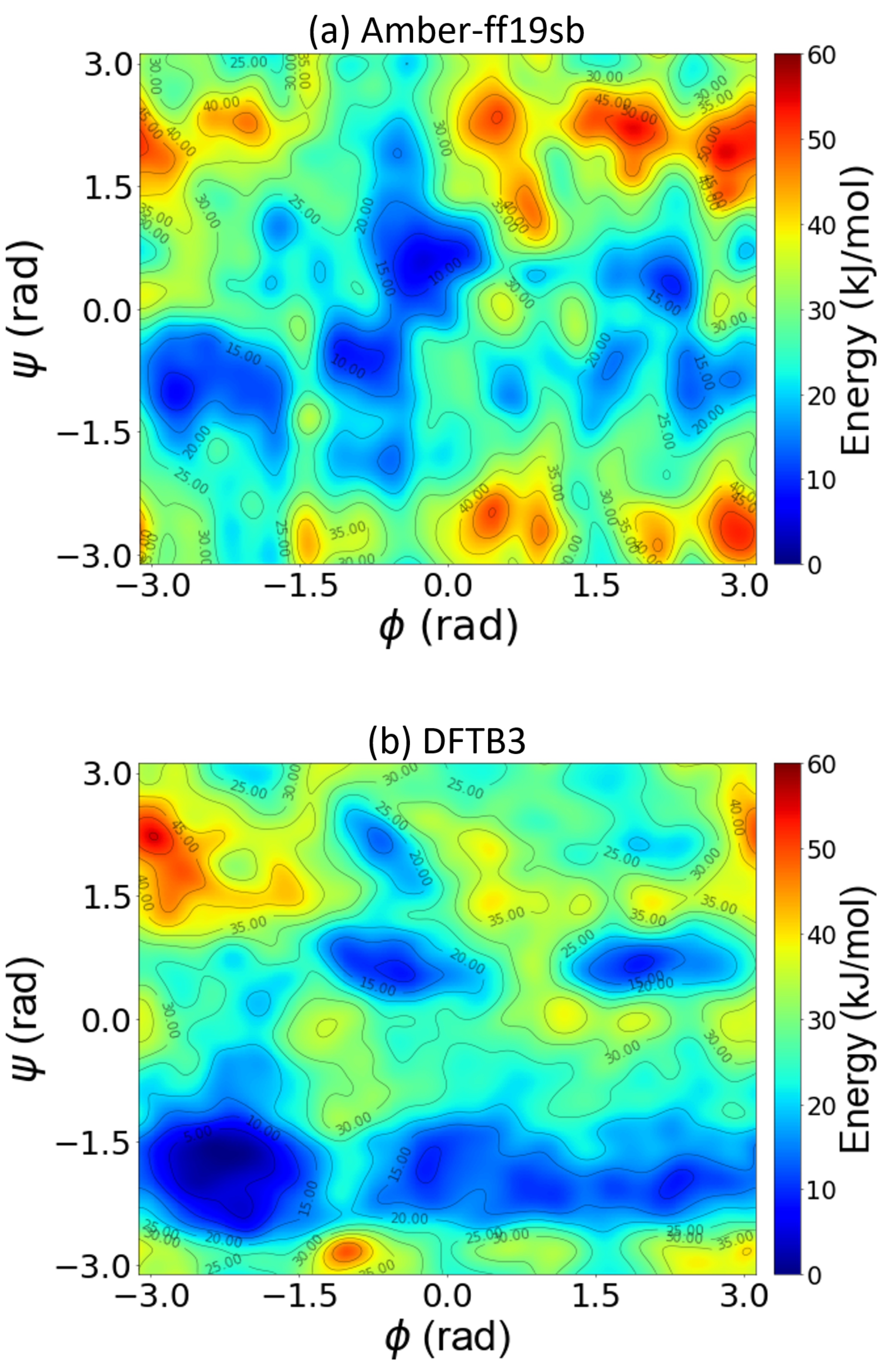
4.2. Metadynamics Benchmarks on Alanine Dipeptide
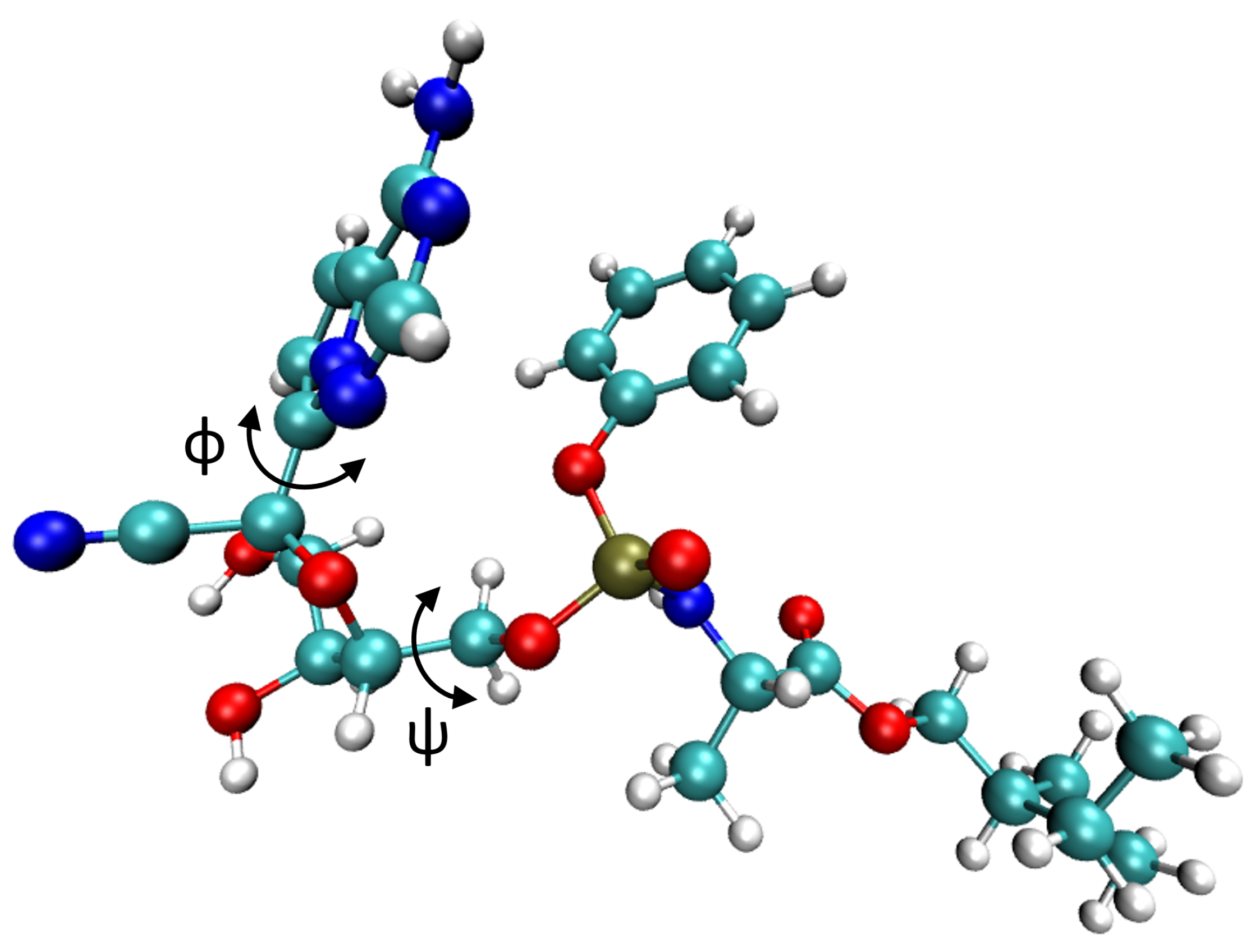
4.3. Large-Scale GPU-DFTB Metadynamics Simulations of Remdesivir
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Tuckerman, M. Statistical Mechanics: Theory and Molecular Simulation; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Tuckerman, M.E.; Martyna, G.J. Understanding Modern Molecular Dynamics: Techniques and Applications. J. Phys. Chem. B 2000, 104, 159–178. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Elsevier: Amsterdam, The Netherlands, 2001; Volume 1. [Google Scholar]
- Chodera, J.D.; Noé, F. Markov State Models of Biomolecular Conformational Dynamics. Curr. Opin. Struct. Biol. 2014, 25, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; Feixas, F.; Eun, C.; McCammon, J.A. Accelerated Molecular Dynamics Simulations of Protein Folding. J. Comput. Chem. 2015, 36, 1536–1549. [Google Scholar] [CrossRef] [PubMed]
- Perilla, J.R.; Goh, B.C.; Cassidy, C.K.; Liu, B.; Bernardi, R.C.; Rudack, T.; Yu, H.; Wu, Z.; Schulten, K. Molecular Dynamics Simulations of Large Macromolecular Complexes. Curr. Opin. Struct. Biol. 2015, 31, 64–74. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Ceriotti, M. Bridging the Gap Between Atomistic and Macroscopic Models of Homogeneous Nucleation. J. Chem. Phys. 2017, 146, 034106. [Google Scholar] [CrossRef]
- Giberti, F.; Salvalaglio, M.; Parrinello, M. Metadynamics Studies of Crystal Nucleation. IUCrJ 2015, 2, 256–266. [Google Scholar] [CrossRef] [PubMed]
- Giberti, F.; Salvalaglio, M.; Mazzotti, M.; Parrinello, M. 1, 3, 5-Tris (4-Bromophenyl)-Benzene Nucleation: From Dimers to Needle-like Clusters. Cryst. Growth Des. 2017, 17, 4137–4143. [Google Scholar] [CrossRef]
- Reid, D.R.; Lyubimov, I.; Ediger, M.; De Pablo, J.J. Age and Structure of a Model Vapour-Deposited Glass. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef]
- Helfferich, J.; Lyubimov, I.; Reid, D.; de Pablo, J.J. Inherent Structure Energy is a Good Indicator of Molecular Mobility in Glasses. Soft Matter 2016, 12, 5898–5904. [Google Scholar] [CrossRef]
- Pham, T.A.; Ping, Y.; Galli, G. Modelling Heterogeneous Interfaces for Solar Water Splitting. Nat. Mater. 2017, 16, 401–408. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping Free-Energy Minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef] [PubMed]
- Mitsutake, A.; Mori, Y.; Okamoto, Y. Enhanced Sampling Algorithms. In Biomolecular Simulations; Springer: Berlin/Heidelberg, Germany, 2013; pp. 153–195. [Google Scholar]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Amer. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins: Struct. Funct. Genet. 2006, 65, 712–725. [Google Scholar] [CrossRef] [PubMed]
- Henriques, J.; Skepö, M. Molecular Dynamics Simulations of Intrinsically Disordered Proteins: On the Accuracy of the TIP4P-D Water Model and the Representativeness of Protein Disorder Models. J. Chem. Theory Comput. 2016, 12, 3407–3415. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Rabinovich, A.L. Force Field Development for Lipid Membrane Simulations. Biochim. Biophys. Acta-Biomembr. 2016, 1858, 2483–2497. [Google Scholar] [CrossRef]
- Car, R.; Parrinello, M. Unified Approach for Molecular Dynamics and Density-Functional Theory. Phys. Rev. Lett. 1985, 55, 2471. [Google Scholar] [CrossRef]
- Marx, D.; Hutter, J. Ab initio Molecular Dynamics: Basic Theory and Advanced Methods; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Sevgen, E.; Giberti, F.; Sidky, H.; Whitmer, J.K.; Galli, G.; Gygi, F.; de Pablo, J.J. Hierarchical Coupling of First-Principles Molecular Dynamics with Advanced Sampling Methods. J. Chem. Theory Comput. 2018, 14, 2881–2888. [Google Scholar] [CrossRef]
- Seifert, G.; Joswig, J.O. Density-Functional Tight Binding—An Approximate Density-Functional Theory Method. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 456–465. [Google Scholar] [CrossRef]
- Gaus, M.; Cui, Q.; Elstner, M. Density Functional Tight Binding: Application to Organic and Biological Molecules. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 49–61. [Google Scholar] [CrossRef]
- Oviedo, M.B.; Wong, B.M. Real-Time Quantum Dynamics Reveals Complex, Many-Body Interactions in Solvated Nanodroplets. J. Chem. Theory Comput. 2016, 12, 1862–1871. [Google Scholar] [CrossRef] [PubMed]
- Ilawe, N.V.; Oviedo, M.B.; Wong, B.M. Real-Time Quantum Dynamics of Long-Range Electronic Excitation Transfer in Plasmonic Nanoantennas. J. Chem. Theory Comput. 2017, 13, 3442–3454. [Google Scholar] [CrossRef] [PubMed]
- Ilawe, N.V.; Oviedo, M.B.; Wong, B.M. Effect of Quantum Tunneling on the Efficiency of Excitation Energy Transfer in Plasmonic Nanoparticle Chain Waveguides. J. Mater. Chem. C 2018, 6, 5857–5864. [Google Scholar] [CrossRef]
- Allec, S.I.; Sun, Y.; Sun, J.; Chang, C.e.A.; Wong, B.M. Heterogeneous CPU+ GPU-Enabled Simulations for DFTB Molecular Dynamics of Large Chemical and Biological Systems. J. Chem. Theory. Comput. 2019, 15, 2807–2815. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Borbón, J.M.; Kalantar, A.; Yamijala, S.S.R.K.C.; Oviedo, M.B.; Najjar, W.; Wong, B.M. Field Programmable Gate Arrays for Enhancing the Speed and Energy Efficiency of Quantum Dynamics Simulations. J. Chem. Theory Comput. 2020, 16, 2085–2098. [Google Scholar] [CrossRef]
- Yamijala, S.S.; Oviedo, M.B.; Wong, B.M. Density Functional Tight Binding Calculations for Probing Electronic-Excited States of Large Systems. In Reviews in Computational Chemistry, Volume 32; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2022; Chapter 2; pp. 45–79. [Google Scholar]
- Kumar, A.; Ali, Z.A.; Wong, B.M. Efficient Predictions of Formation Energies and Convex Hulls from Density Functional Tight Binding Calculations. J. Mater. Sci. Technol. 2023, 141, 236–244. [Google Scholar] [CrossRef]
- Porezag, D.; Frauenheim, T.; Köhler, T.; Seifert, G.; Kaschner, R. Construction of Tight-Binding-like Potentials on the Basis of Density-Functional Theory: Application to Carbon. Phys. Rev. B 1995, 51, 12947. [Google Scholar] [CrossRef]
- Wahiduzzaman, M.; Oliveira, A.F.; Philipsen, P.; Zhechkov, L.; Van Lenthe, E.; Witek, H.A.; Heine, T. DFTB Parameters for the Periodic Table: Part 1, Electronic Structure. J. Chem. Theory. Comput. 2013, 9, 4006–4017. [Google Scholar] [CrossRef]
- Elstner, M.; Seifert, G. Density Functional Tight Binding. Philos. Trans. A Math. Phys. Eng. Sci. 2014, 372, 20120483. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Gaus, M.; Cui, Q.; Elstner, M. DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yu, H.; York, D.; Cui, Q.; Elstner, M. Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method: Third-Order Expansion of the Density Functional Theory Total Energy and Introduction of a Modified Effective Coulomb Interaction. J. Phys. Chem. A 2007, 111, 10861–10873. [Google Scholar] [CrossRef] [PubMed]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-Consistent-Charge Density-Functional Tight-Binding Method for Simulations of Complex Materials Properties. Phys. Rev. B 1998, 58, 7260. [Google Scholar] [CrossRef]
- Hourahine, B.; Aradi, B.; Blum, V.; Bonafe, F.; Buccheri, A.; Camacho, C.; Cevallos, C.; Deshaye, M.; Dumitrică, T.; Dominguez, A.; et al. DFTB+, A Software Package for Efficient Approximate Density Functional Theory Based Atomistic Simulations. J. Chem. Phys. 2020, 152, 124101. [Google Scholar] [CrossRef] [PubMed]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, S.; Dongarra, J.D.J.; Croz, J.D.; Greenbaum, A.; Hammarling, S.; McKenney, A.; Sorensen, D. LAPACK Users’ Guide, 3rd ed.; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Tomov, S.; Dongarra, J.; Baboulin, M. Towards Dense Linear Algebra for Hybrid GPU Accelerated Manycore Systems. Parallel Comput. 2010, 36, 232–240. [Google Scholar] [CrossRef]
- Cuppen, J.J. A Divide and Conquer Method for the Symmetric Tridiagonal Eigenproblem. Numer. Math. 1980, 36, 177–195. [Google Scholar] [CrossRef]
- Liao, X.; Li, S.; Lu, Y.; Roman, J.E. A Parallel Structured Divide-And-Conquer Algorithm for Symmetric Tridiagonal Eigenvalue Problems. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 367–378. [Google Scholar] [CrossRef]
- Oruganti, B.; Friedman, R. Activation of Abl1 Kinase Explored Using Well-Tempered Metadynamics Simulations on an Essential Dynamics Sampled Path. J. Chem. Theory Comput. 2021, 17, 7260–7270. [Google Scholar] [CrossRef]
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 826–843. [Google Scholar] [CrossRef]
- Sucerquia, D.; Parra, C.; Cossio, P.; Lopez-Acevedo, O. Ab Initio Metadynamics Determination of Temperature-Dependent Free-Energy Landscape in Ultrasmall Silver Clusters. J. Chem. Phys. 2022, 156, 154301. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Tian, C.; Kasavajhala, K.; Belfon, K.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2019, 16, 528–552. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, N.; Tan, Y.; Fu, F.; Liu, G.; Fang, Y.; Zhang, X.x.; Liu, M.; Cheng, Y.; Yu, J. Sweat-Resistant Silk Fibroin-Based Double Network Hydrogel Adhesives. ACS Appl. Mater. Interfaces 2022, 14, 21945–21953. [Google Scholar] [CrossRef] [PubMed]
- Marklund, E.G.; Larsson, D.S.; van der Spoel, D.; Patriksson, A.; Caleman, C. Structural Stability of Electrosprayed Proteins: Temperature and Hydration Effects. Phys. Chem. Chem. Phys. 2009, 11, 8069–8078. [Google Scholar] [CrossRef]
- Reimann, C.; Velázquez, I.; Bittner, M.; Tapia, O. Proteins in vacuo: A Molecular Dynamics Study of the Unfolding Behavior of Highly Charged Disulfide-Bond-Intact Lysozyme Subjected to a Temperature Pulse. Phys. Rev. E 1999, 60, 7277. [Google Scholar] [CrossRef]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.; et al. Gaussian 09, Revision D. 01. 2009. Available online: https://gaussian.com/ (accessed on 16 January 2023).
- Turq, P.; Lantelme, F.; Friedman, H.L. Brownian Dynamics: Its Application to Ionic Solutions. J. Chem. Phys. 1977, 66, 3039–3044. [Google Scholar] [CrossRef]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Ben-Shalom, I.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; et al. Amber 2021; University of California: San Francisco, CA, USA, 2021. [Google Scholar]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Hess, B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 116–122. [Google Scholar] [CrossRef]
- Tribello, G.A.; Bonomi, M.; Branduardi, D.; Camilloni, C.; Bussi, G. PLUMED 2: New Feathers for an Old Bird. Comput. Phys. Commun. 2014, 185, 604–613. [Google Scholar] [CrossRef]
- McMillan, S. Making Containers Easier with HPC Container Maker. In Proceedings of the In HPCSYSPROS18: HPC System Professionals Workshop, Dallas, TX, USA, 11 November 2018. [Google Scholar]
- Zhang, P.; Wood, G.P.; Ma, J.; Yang, M.; Liu, Y.; Sun, G.; Jiang, Y.A.; Hancock, B.C.; Wen, S. Harnessing Cloud Architecture for Crystal Structure Prediction Calculations. Cryst. Growth Des. 2018, 18, 6891–6900. [Google Scholar] [CrossRef]
- Wang, Y.; Murlidaran, S.; Pearlman, D.A. Quantum Simulations of SARS-CoV-2 Main Protease Mpro Enable High-Quality Scoring of Diverse Ligands. J. Comput. Aided Mol. Des. 2021, 35, 963–971. [Google Scholar] [CrossRef] [PubMed]
- Riccardi, D.; König, P.; Guo, H.; Cui, Q. Proton Transfer in Carbonic Anhydrase Is Controlled by Electrostatics Rather than the Orientation of the Acceptor. Biochem. 2008, 47, 2369–2378. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yu, H.; Cui, Q. Extensive Conformational Transitions are Required to Turn on ATP Hydrolysis in Myosin. J. Mol. Biol. 2008, 381, 1407–1420. [Google Scholar] [CrossRef]
- Yang, Y.; Cui, Q. Does Water Relay Play an Important Role in Phosphoryl Transfer Reactions? Insights from Theoretical Study of a Model Reaction in Water and Tert-Butanol. J. Phys. Chem. B 2009, 113, 4930–4939. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Nosé, S. A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical Dynamics: Equilibrium Phase-Space Dstributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Wes McKinney. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar]
- Gustafson, J.L. Reevaluating Amdahl’s Law. Commun. ACM 1988, 31, 532–533. [Google Scholar] [CrossRef]
- Strodel, B.; Wales, D.J. Free Energy Surfaces from an Extended Harmonic Superposition Approach and Kinetics for Alanine Dipeptide. Chem. Phys. Lett. 2008, 466, 105–115. [Google Scholar] [CrossRef]
- Liu, P.; Kim, B.; Friesner, R.A.; Berne, B.J. Replica Exchange with Solute Tempering: A Method for Sampling Biological Systems in Explicit Water. Proc. Natl. Acad. Sci. USA 2005, 102, 13749–13754. [Google Scholar] [CrossRef] [PubMed]
- Maragliano, L.; Fischer, A.; Vanden-Eijnden, E.; Ciccotti, G. String Method in Collective Variables: Minimum Free Energy Paths and Isocommittor Surfaces. J. Chem. Phys. 2006, 125, 024106. [Google Scholar] [CrossRef]
- Marsili, S.; Barducci, A.; Chelli, R.; Procacci, P.; Schettino, V. Self-healing Umbrella Sampling: A Non-equilibrium Approach for Quantitative Free Energy Calculations. J. Phys. Chem. B 2006, 110, 14011–14013. [Google Scholar] [CrossRef] [PubMed]
- Sidky, H.; Whitmer, J.K. Learning Free Energy Landscapes using Artificial Neural Networks. J. Chem. Phys. 2018, 148, 104111. [Google Scholar] [CrossRef]
- Cuny, J.; Korchagina, K.; Menakbi, C.; Mineva, T. Metadynamics Combined with Auxiliary Density Functional and Density Functional Tight-Binding Methods: Alanine Dipeptide as a Case Study. J. Mol. Model. 2017, 23, 72. [Google Scholar] [CrossRef]
- Malin, J.J.; Suárez, I.; Priesner, V.; Fätkenheuer, G.; Rybniker, J. Remdesivir against COVID-19 and Other Viral Diseases. Clin. Microbiol. Rev. 2020, 34, e00162–20. [Google Scholar] [CrossRef]
- Gralinski, L.E.; Menachery, V.D. Return of the Coronavirus: 2019-nCoV. Viruses 2020, 12, 135. [Google Scholar] [CrossRef] [PubMed]
- Sheahan, T.P.; Sims, A.C.; Leist, S.R.; Schäfer, A.; Won, J.; Brown, A.J.; Montgomery, S.A.; Hogg, A.; Babusis, D.; Clarke, M.O.; et al. Comparative Therapeutic Efficacy of Remdesivir and Combination Lopinavir, Ritonavir, and Interferon Beta against MERS-CoV. Nat. Commun. 2020, 11, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Hošek, P.; Spiwok, V. Metadyn View: Fast Web-Based Viewer of Free Energy Surfaces Calculated by Metadynamics. Comput. Phys. Commun. 2016, 198, 222–229. [Google Scholar] [CrossRef]

| Hardware Configurations | Wall Clock (min) | |
|---|---|---|
| Number of CPUs | Number of GPUs | |
| 40 | 4 | 23.43 |
| 20 | 4 | 7.74 |
| 10 | 4 | 7.98 |
| 8 | 4 | 7.89 |
| 4 | 4 | 5.59 |
| 8 | 2 | 5.87 |
| 4 | 2 | 5.17 |
| 2 | 2 | 3.89 |
| 8 | 1 | 6.05 |
| 4 | 1 | 3.95 |
| 2 | 1 | 3.93 |
| 1 | 1 | 32.45 |
| 8 | 0 | 14.74 |
| 1 | 0 | 59.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Arantes, P.R.; Saha, A.; Palermo, G.; Wong, B.M. GPU-Enhanced DFTB Metadynamics for Efficiently Predicting Free Energies of Biochemical Systems. Molecules 2023, 28, 1277. https://doi.org/10.3390/molecules28031277
Kumar A, Arantes PR, Saha A, Palermo G, Wong BM. GPU-Enhanced DFTB Metadynamics for Efficiently Predicting Free Energies of Biochemical Systems. Molecules. 2023; 28(3):1277. https://doi.org/10.3390/molecules28031277
Chicago/Turabian StyleKumar, Anshuman, Pablo R. Arantes, Aakash Saha, Giulia Palermo, and Bryan M. Wong. 2023. "GPU-Enhanced DFTB Metadynamics for Efficiently Predicting Free Energies of Biochemical Systems" Molecules 28, no. 3: 1277. https://doi.org/10.3390/molecules28031277
APA StyleKumar, A., Arantes, P. R., Saha, A., Palermo, G., & Wong, B. M. (2023). GPU-Enhanced DFTB Metadynamics for Efficiently Predicting Free Energies of Biochemical Systems. Molecules, 28(3), 1277. https://doi.org/10.3390/molecules28031277