Next Article in Journal
Therapeutic Potential of Ginsenoside Rb1-PLGA Nanoparticles for Heart Failure Treatment via the ROS/PPARα/PGC1α Pathway
Previous Article in Journal
New ψ-Santonin Derivatives from Crossostephium chinense and Their Anti-Proliferative Activities against Leishmania major and Human Cancer Cells A549
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 28
Issue 24
10.3390/molecules28248117
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Mechanistic Study on the Possibility of Converting Dissociated Oxygen into Formic Acid on χ-Fe5C2(510) for Resource Recovery in Fischer–Tropsch Synthesis

by
Ning Ai
1,2,3,
Changyi Lai
1,2,
Wanpeng Hu
2,
Qining Wang
3 and
Jie Ren
2,4,*
1
College of Chemical Engineering, Zhejiang University of Technology, Hangzhou 310014, China
2
College of Biological, Chemical Sciences and Engineering, Jiaxing University, Jiaxing 314001, China
3
National Demonstration Center for Experimental Chemistry and Chemical Engineering Education, Zhejiang University of Technology, Hangzhou 310014, China
4
Key Laboratory for Green Chemical Technology of Ministry of Education, R&D Center for Petrochemical Technology, Tianjin University, Tianjin 300072, China
*
Author to whom correspondence should be addressed.
Molecules 2023, 28(24), 8117; https://doi.org/10.3390/molecules28248117
Submission received: 22 September 2023 / Revised: 30 November 2023 / Accepted: 3 December 2023 / Published: 15 December 2023
(This article belongs to the Special Issue Molecular Simulation and Applied Catalysis in CO2 Utilization)
Browse Figures
Review Reports Versions Notes

Abstract

:
During Fischer–Tropsch synthesis, O atoms are dissociated on the surface of Fe-based catalysts. However, most of the dissociated O would be removed as H2O or CO2, which results in a low atom economy. Hence, a comprehensive study of the O removal pathway as formic acid has been investigated using the combination of density functional theory (DFT) and kinetic Monte Carlo (kMC) to improve the economics of Fischer–Tropsch synthesis on Fe-based catalysts. The results show that the optimal pathway for the removal of dissociated O as formic acid is the OH pathway, of which the effective barrier energy (0.936 eV) is close to that of the CO activation pathway (0.730 eV), meaning that the removal of dissociated O as formic acid is possible. The main factor in an inability to form formic acid is the competition between the formic acid formation pathway and other oxygenated compound formation pathways (H2O, CO2, methanol-formaldehyde); the details are as follows: 1. If the CO is hydrogenated first, then the subsequent reaction would be impossible due to its high effective Gibbs barrier energy. 2. If CO reacts first with O to become CO2, it is difficult for it to be hydrogenated further to become HCOOH because of the low adsorption energy of CO2. 3. When the CO + OH pathway is considered, OH would react easily with H atoms to form H2O due to the hydrogen coverage effect. Finally, the removal of dissociated O to formic acid is proposed via improving the catalyst to increase the CO2 adsorption energy or CO coverage.

1. Introduction

Fischer–Tropsch synthesis, which is able to convert synthesis gas into hydrocarbons (alkane and olefin) and oxygenated organic compounds (higher alcohols) [1,2,3], could develop the diversification of the world’s fuel supply [4] and the possibility of cleaner fuels free of sulfur, nitrogen, and aromatic compounds [5,6,7]. Fischer–Tropsch synthesis is a very complex multiphase catalytic process [8], with the shortcomings of wide product distribution, low target selectivity, and poor catalyst stability [9,10]. However, improving the economics of Fischer–Tropsch synthesis requires not only better selectivity [4] but also higher atom utilization. A literature review revealed that O atoms are dissociated and left on the catalyst surface during Fischer–Tropsch synthesis [11,12,13,14,15], and the majority of these dissociated O are removed from the surface in the form of H2O or CO2 [16,17,18,19], which would reduce the atom economy. There are two ways to solve this problem: one is to promote the further reaction of oxygen-containing compounds in the product to form valuable products, such as the hydrogenation of CO2 to hydrocarbons [20]; the other is to find a product with high economic benefits that can replace CO2 and H2O. The former improves the economic benefit to a certain extent. However, it does not solve the problem of using the oxygen atoms, so it is better to find a substitute.
Theoretically, there are three main ways to remove dissociated O in Fischer–Tropsch synthesis (as shown in Figure 1): 1. Dissociated O would react with hydrogen to be removed as H2O (a by-product with no economic value) [12,14]; 2. dissociated O would react with CO to be removed as CO2 (a by-product with no economic value and an additional greenhouse effect) [14,21]; and 3. dissociated O would react with hydrogen and CO to be removed as formic acid or polyacid. It is worth noting that when dissociated O is removed as alcohol [22,23,24], though it appears to produce an economically valuable product, the dissociated O that produces the alcohol is derived from CO, and essentially no additional dissociated O is removed, Therefore, it is necessary to form a product in which one C atom could take away two or more O atoms; the products that meet this condition are formic acid and polyacids. In particular, formic acid, besides being nontoxic, having a high energy density, and being renewable and degradable, has great potential in green organic synthesis and biomass conversion [25] and has wide applications in new energy utilization [26,27]. However, formic acid has not been found in Fischer–Tropsch synthesis in the literature, which could be attributed to unsatisfied catalysts or the failure of the reaction itself. Therefore, to investigate whether formic acid can theoretically be formed or not and to analyze the main factors limiting the formation of formic acid on the catalyst surface, the O removal pathway from the catalyst surface must be discussed.
At present, the O removal pathways from the surface of Fischer–Tropsch synthesis catalysts are not frequently reported, and studies have mainly investigated the removal mechanism of dissociated O in the form of H2O or CO2. For example, the mechanism of O removal on Fe(710) has been completed [21]; the following aspects were considered: the direct addition and disproportionation reactions of OH with OH to produce H2O; the direct reaction of dissociated O with CO, and the dehydrogenation of COOH to produce CO2. Analyzing the apparent Gibbs barrier energy, the results show that the removal of dissociated O from on the Fe(710) surface favors the production of H2O rather than CO2. In addition, it was shown that the hydrogen coverage effect has an impact on the O removal pathway [14]. At low hydrogen coverage, carbon dioxide is more likely to be produced through the decomposition of CO and OH, and H2O is produced through the pathway of two OH. At high hydrogen coverage, CO2 is more likely to be formed via the CO + O → CO2, and H2O is formed via the OH + H → H2O. The results of this study show that CO2 is more likely to be formed via the decomposition of CO + OH → COOH. However, it is inconclusive whether dissociated oxygen can be removed from the catalyst surface in the form of formic acid.
Fe-based comprises one of the representatives of traditional Fischer–Tropsch synthesis catalysts, due to its cost, wide operating temperature, and high activity [28,29]. The χ-Fe5C2 phase is considered to be the main active phase of Fe-based Fischer–Tropsch synthesis catalysts [30], and the χ-Fe5C2(510) surface is the main exposed surface of this carbide phase [31], so, in this paper, the χ-Fe5C2(510) surface is chosen as the represent facet to investigate the O removal pathway and reaction mechanism in Fischer–Tropsch synthesis on the χ-Fe5C2 (510) surface. Therefore, whether the Fischer–Tropsch synthesis itself is conducive to the formation of formic acid products is considered first, through examining the major reaction pathways for formic acid formation. Then, representative and relatively simple oxygen-containing products (carbon dioxide, hydrogen, formaldehyde, and methanol) are selected, and the competing relationships of formic acid to their formation processes are discussed to explain the failure to remove dissociated O as formic acid.
In this work, the elementary reactions of the Fischer–Tropsch synthesis O removal pathway on the surface of χ-Fe5C2(510) are first considered as comprehensively as possible using density functional theory (DFT) calculations. The basic data obtained via DFT calculations are applied to kinetic Monte Carlo (kMC) simulations, and the reaction frequencies of various elementary reactions are obtained. The major reaction pathways and the rate control steps when the O atom are removed as CO2, H2O, formaldehyde, methanol, and formic acid are clarified, according to the form in which the oxygen atoms are removed; also, the main factors limiting the dissociated O removed as formic acid are determined. This study could provide a theoretical basis and direction for the simultaneous production of Fischer–Tropsch synthesis products, using carbon resources in CO and formic acid, using dissociated oxygen resources in Fischer–Tropsch synthesis.

2. Results and Discussion

2.1. Computational Models and Methods

2.1.1. DFT Calculation Method

In this work, the effect of the magnetic properties of the χ-Fe5C2 phase on the energy and structure of the system is considered using the Vienna Ab initio Simulation Package (VASP) based on the periodic flat plate model and the spin polarization DFT method [32,33,34,35]. The exchange correlation energy is described via the projective affixed plane wave (PAW) method using the Perdew–Burke–Ernzerhof (PBE) function of the generalized gradient approximation (GGA) [33,36]. The plane wave cut-off energy is set to 400 eV [37]. The Brillouin zone integrals calculated via the bulk phase model and the surface model were modeled with 3×5×5 and 2×2×1 grids, respectively [38]. The electron occupancy state is determined using the Methfessel–Paxton method, where the smearing parameter is set to 0.2 eV [39]. The Jonson (BJ) damped DFT-D3 method is used to correct for van der Waals effects [40,41].
The transition state search is implemented using the climbing image nudged elastic band (CI-NEB) method [42,43]. The accuracy of the DFT calculations is set as follows: the convergence criteria for the self-consistent calculation of the electrons (SCF), the geometrically optimized calculation, and the transition state calculation are 1.0 × 10−6 eV, 0.03 eV/Å and 0.05 eV/Å, respectively. After the convergence of the transition state calculation, the transition state structure is subjected to frequency analysis and verified, and if only one imaginary frequency exists in the calculated structure, then the structure passes the test. The adsorption energy Eads (eV) is calculated using Equation (1):
E a d s = E ( a d s o r b a t e / s l a b ) − [ E ( s l a b ) + E ( a d s o r b a t e ) ]  
where E ( a d s o r b a t e / s l a b ) (eV), E ( s l a b ) (eV), and E ( a d s o r b a t e ) (eV) represent the total energy of the adsorption system, the surface energy of the unadsorbed mass, and the energy of the adsorbent itself, respectively.
The effects of the zero point energy (ZPE) correction, the standard molar vibrational internal energy contribution, and the standard molar vibrational entropy were considered to better evaluate the standard molar Gibbs free energy for each species. The standard molar Gibbs free energy ( G 0 ) for each species was calculated using Equation (2), as follows:
G 0 = E + z P E + U 0 + γ R T ( 1 + l n p p 0 ) − T S 0
Using the standard molar Gibbs free energy ( G 0 ) calculated using the above equation, insert it into the Gibbs reaction energy and Gibbs free energy formulae Gr = G(FS) − G(IS) and Ga = G(TS) − G(IS), respectively, where G(IS) represents the initial Gibbs energy (IS), G(FS) represents the final Gibbs energy (FS), and G(TS) represents the transition Gibbs energy (TS) for the final Gibbs energy (FS), and G(TS) for the transition Gibbs energy (TS).
As the reaction network studied in this work is complex, with a large number of concatenated and parallel reactions, the coverage of the intermediates in the concatenated reactions is an important parameter affecting the reaction rates according to the mass low. Therefore, when searching for the optimal reaction path, it is not sufficient to determine whether an elementary reaction is a tachyonic step or not simply by characterizing its reaction rate in terms of its Gibbs barrier energy. In this paper, the effective Gibbs barrier energy G a , e f f k is used to account for the effect of the coverage of the reactants on the catalyst surface on the rate of formation of different products [44,45]. The effective Gibbs barrier energy G a , e f f k (eV) for the kth reaction step in a given cascade is given by Equation (3):
G a , e f f k = G a k + ∑ i = j k − 1 G r i
where G a k (eV) and G r i (eV) are the Gibbs barrier energy of the kth step and the heat of reaction of the ith step, respectively. j is the jth reaction step, which is the primitive step with the lowest product energy in the reaction chain.

2.1.2. DFT Calculation Model

In this paper, the bulk phase χ-Fe5C2 model is optimized as a = 11.570Å, b = 4.501Å, c = 4.986Å, and β = 97.56°, which is consistent with the experimental cell parameters of a = 11.588Å, b = 4.579Å, c = 5.059Å, and β = 97.95° [46]; therefore, the calculation results are reliable. Based on the optimized bulk phase χ-Fe5C2 model, a χ-Fe5C2(510) surface model with two layers of Fe atoms and four layers of C atoms was developed. The lower one layer of Fe atoms and two layers of C atoms were fixed, while the other atoms and adsorbates were allowed to relax. The vacuum layer was set to 13 Å. And the geometry optimization and transition state searches for adsorbed species on the χ-Fe5C2(510) surface were performed on the p(2 × 1) supercell surface.
According to previous studies [14], hydrogen coverage has a great influence on the Fischer–Tropsch synthesis mechanism. The results show that on the surface of clean χ-Fe5C2(510), H2 dissociates to produce H atoms adsorbed at the triplet position first and accumulates on the surface to form hydrogen-covered χ-Fe5C2(510) facets. Then, on the hydrogen-covered χ-Fe5C2(510), H2 dissociates to form bridge-site H atoms with strong hydrogenation radical reaction activity, which are the main H atoms involved in the surface hydrogenation radical reaction. The consideration of hydrogen-covering effects can make the simulated catalyst surface more realistic. Hence, one layer of inlet hydrogen is also considered in the modelling. Top and side views of the investigated H-covered χ-Fe5C2(510) surface are shown in Figure 2.

2.1.3. Models and Methods for Calculating kMC

The lattice gas model (LGM), with the variable step size method (VSSM), was used for the kMC simulations in this work [47,48]. A number of processes, adsorption, dissociation, migration, and reaction, as well as the associated species, were defined based on the DFT calculations. For the adsorption process, the adsorption rate kads (1/s) [49] of the reactants is described by Equation (4):
k a d s = P A s i t e σ 2 π m k B T
where σ is the dimensionless adhesion coefficient, the value of which is often taken as 1 [50]. p (Pa) and T (K) are the partial pressure and absolute temperature of CO under the simulated conditions, Asite (m2) is the area of the adsorption site of a single molecule, and m (kg) is the molecular mass; kB (J/K) is the Boltzmann constant. The rate constants krec of activated processes were all calculated according to the transition state theory by Equation (5):
k i , j T = q T S v i b q i v i b k B T h e − ∆ E i j k B T
where TS stands for the transition state joining the initial state i with the final state j, T (K) is the absolute temperature, kB (J/K) is defined as above, and h (J*s) is the Planck constant. q T S v i b and q i v i b   are the vibrational partition functions for the TS and i states, respectively, the latter being approximated from the vibrational frequencies of the respective state using the harmonic approximation. ∆ E i j stands for the activation energy barrier of the process obtained through DFT calculations.
The lattice gas model is the model used for the kMC simulations in this paper. The calculations were performed using a 64 × 64 two-dimensional periodic model, with each lattice representing a p(1 × 1) χ-Fe5C2(510) surface. A total of 32 adsorption sites are set up within the lattice, of which 10 sites represent the top sites for Fe atoms corresponding to the p(1 × 1) χ-Fe5C2(510) surface atoms one at a time. Another 10 sites represent triple-adsorption sites of Fe atoms, 9 sites represent bridge sites of Fe atoms, and 3 sites represent quadruple-adsorption sites of Fe atoms, of which 2 quadruple-adsorption sites are top sites for C atoms, and 1 quadruple adsorption site is empty. Figure 3 shows the kMC model used for the calculation and the corresponding DFT model.

2.2. The Design of Dissociated O Removal Pathways on Hydrogen-Covered χ-Fe5C2(510) Surface

To achieve the objectives of this paper, a possible dissociated O removal reaction network is designed for the generation of water, carbon dioxide, formic acid, and methanol species on hydrogen-covered χ-Fe5C2(510) surfaces with dissociated O, bridge site H, top site CO, and OH as feedstock, as shown in Figure 4.
The ideas for the designed possible reaction network is as follows: firstly, for the dissociated O removal pathway in the form of H2O and CO2, the two-step hydrogenation of dissociated O to produce H2O, as well as the direct reaction of CO with dissociated O to produce CO2, are considered, mainly based on the research results of Zhang et al. [14]. Secondly, the reaction pathway for the stepwise hydrogenation of CO to produce methanol is considered, and contains the following two parallel reactions: 1. hydrogenation reaction at the C site; 2. hydrogenation reaction at the O site, which is the main reaction pathway for the black channel in Figure 4. Finally, finding the possible surface species that can react with dissociated O or OH in the main pathway to form formic acid are considered and denoted as the red O pathway or the blue OH pathway.

2.3. The Formic Acid Formation Pathway on Hydrogen-Covered χ-Fe5C2(510) Surface

According to the designed reaction pathway in Figure 4, there are eight possible reaction pathways for the formation of formic acid on χ-Fe5C2(510). They could be divided into three categories for discussion, as shown in Table 1, which are: 1, CO pathway (pathways 1, 2, 3, and 4); 2, OH pathway (pathways 5 and 6); 3, CO2 pathway (pathways 7 and 8). Table 1, below, gives a detailed description of the elementary reactions for each pathway.

2.3.1. Analysis of Formic Acid Formation Pathway on Hydrogen-Covered χ-Fe5C2 (510) Surface

The OH pathway and CO2 pathway are discussed first, and are shown in Figure 5. It is found that the Gibbs barrier energy of the first step of the elementary reaction in pathway 5 (yellow) is higher at 1.022 eV than that in pathway 6 (violet) at 0.744 eV. The former Gibbs reaction energy was 0.815 eV, whereas the latter Gibbs reaction energy was −0.160 eV; hence, the latter is more stable. Therefore, the first step of pathway 6, the elementary reaction O + H → OH, could occur more easily. In the second elementary reaction of pathway 6, CO + OH → COOH has a Gibbs barrier energy of 0.836 eV, but its effective Gibbs reaction energy is 0.588 eV, so the reverse reaction is more likely to occur. In contrast, Figure 5 shows that the effective Gibbs barrier energy of pathway 6 is 0.936 eV, which is determined by the last two steps of the radical reaction, while the effective Gibbs barrier energy of pathway 5 is 1.437 eV, and is much higher than that of pathway 6, so the effective Gibbs barrier energy of the OH pathway is defined as 0.936 eV.
For the CO2 pathway (e.g., reaction pathways 7 and 8 in Figure 5), the Gibbs barrier energy for the dissociated O with CO to produce CO2 is 0.853 eV, which is lower than that of the OH pathway. The Gibbs barrier energy in the second step of CO2 + H1 → COOH1 in reaction pathway 7 is 0.801 eV, while that of CO2 + H2 → COOH2 in reaction pathway 8 is 0.431 eV, which suggest that the O2 site of CO2 is more likely to undergo hydrogenation to produce COOH2. Thus, globally, the effective Gibbs barrier energy of reaction pathway 7 is 1.080 eV, determined by the first and second steps of the radical reaction, and that of reaction pathway 8 is 0.853 eV, determined by the first step of the radical reaction. It seems that the CO2 pathway is preferred, as its effective Gibbs barrier energy is 0.853 eV. However, the CO2 pathway is impossible, as the adsorption energy of CO2 is only 0.203 eV, which is much lower than the Gibbs barrier energy of CO2 + H2 → COOH2 (0.431 eV). After the formation of adsorption CO2, it is desorbed from the surface rather than undergoing the hydrogenation reaction.
The CO pathway is shown in Figure 6. The Gibbs barrier energy for the first-step elementary reaction CO + HO → COH in reaction pathways 1 and 2 is 1.788 eV; hence, its effective Gibbs barrier energy is theoretically ≥1.788 eV, and these two reaction pathways do not occur easily. As for reaction pathways 3 and 4, the Gibbs barrier energy of the first-step elementary reaction CO + HC → CHO is 1.022 eV, and its Gibbs reaction energy is 0.815 eV, so the generation of CHO is unfavorable, which means that the occurrence of this reaction pathway is difficult. From Figure 6, it can be seen that the effective Gibbs barrier energies of reaction pathways 3 and 4 are 1.542 eV and 1.710 eV, respectively, and the effective Gibbs barrier energy of reaction pathways 1 and 2 is theoretically ≥1.788 eV. Therefore, the effective Gibbs barrier energy of the CO pathway is 1.542 eV, which is much higher than that of the OH pathway (0.936 eV) and the CO2 pathway (0.853 eV). It is very difficult for the CO pathway to occur.

2.3.2. Charge Analysis of the Rate-Control Step in the Formation of Formic Acid on a Hydrogen-Covered χ-Fe5C2(510) Surface

The above analyses show that the effective Gibbs barrier energy for the CO hydrogenation reaction to form CHO (1.022 eV) and COH (1.788 eV) are high. In comparison, the effective Gibbs reaction barrier energy of O + CO → CO2 and OH + CO → COOH are only 0.853 eV and 0.836 eV, respectively. These four elementary reactions are the rate-controlled steps of their respective pathways, and their Gibbs barrier energies are very different from each other. Bader charge analysis is carried out to investigate the reasons in detail. The results are given in Table 2.
All these four elementary reactions take place all on the C reaction sites in CO; hence, the charges at the C reaction site of each elementary reaction transition state would be important and are shown in Table 2: elementary reaction 2 (3.665) > elementary reaction 1 (3.423) > elementary reaction 3 (3.092) > elementary reaction 4 (3.014). This result is consistent with the magnitude of the corresponding Gibbs barrier energy and suggests that the high Gibbs barrier energy for these four elementary reactions is mainly determined by the charge density of the C reaction site. The greater the charge density of the C site during the reaction, the more difficult it is for other species to react with CO. Thus, CO in the vicinity of dissociated O is more likely to react with oxygen atoms to form CO2 or with OH to form COOH.

2.3.3. Summary

The above analyses show that formic acid is difficult to produce via the CO and CO2 pathways, and the optimal pathways of the three pathways (OH, CO2, and CO pathways) for the removal of dissociated oxygen in the form of formic acid are summarized and comparatively analyzed in Figure 7. It is found that the effective Gibbs barrier energy for the formation of formic acid via the CO pathway (green) is 0.936 eV, which is much lower compared to that of the CO pathway (red) of 1.437 eV. In addition, formic acid cannot be produced via the CO2 pathway (black 0.853 eV) either, because CO2 desorbs very easily. Therefore, CO + OH → COOH + H → HCOOH is the optimal pathway for the formation of formic acid when all pathways are compared.
In summary, the lowest effective Gibbs barrier energy for the removal of dissociated O in the form of formic acid is 0.936 eV, which is not much higher than that of the CO activation pathway (0.730 eV) [15]. Therefore, formic acid formation is kinetically feasible if the Fischer–Tropsch synthesis reaction can proceed. However, there are no literature reports of formic acid production in the Fischer–Tropsch synthesis reaction, which may be due to competition from other species. Hence, the reaction pathways for the removal of dissociated O in the form of CO2, H2O, and alcohols will be discussed in the next part to find the limiting factors for formic acid formation.

2.4. Other Represented Oxygenated Species Formation Pathways on the Hydrogen–Covered χ-Fe5C2(510) Surface and their Competition with Formic Acid

The possibility of formic acid formation was discussed and demonstrated in Section 2.3, but no formic acid formation has been reported in experiments, which may be because the formic acid formation pathway is unable to outcompete other species. Therefore, the O removal pathway with other oxygenated compounds (mainly CO2, H2O, alcohols, and aldehydes) are discussed, and the comparison between the formic acid formation pathway and other oxygenated compound formation pathways is investigated to identify the key factors limiting the formation of formic acid.

2.4.1. The H2O and CO2 Formation Pathway on the Hydrogen-Covered χ-Fe5C2(510) Surface

CO2 and H2O are the main products of the removal of dissociated oxygen from the Fischer–Tropsch synthesis process and have been studied thoroughly [14,21]. However, the reaction pathways and effective Gibbs barrier energy for the removal of dissociated O in the form of H2O and CO2 are still considered based on the modelling and calculation accuracy of this work, so a comparison between the formic acid formation pathway and other oxygenated compound formation pathways is meaningful. The results are shown in Figure 8.
On the hydrogen-covered χ-Fe5C2(510) surface, the two-step hydrogenation reaction of dissociated O to produce H2O is mainly considered in the H2O formation pathway, the effective Gibbs barrier energy of which is 0.744 eV. Meanwhile, for the CO2 formation pathway, the CO + O (0.852 eV) route < CO + OH → COOH (1.342 eV) route < CO + H + O → COOH dehydrogenation (1.788 eV) route, indicating that if the dissociated O on the surface of χ-Fe5C2(510) is removed in the form of CO2, then the direct reaction of CO with dissociated O to produce CO2 is preferred. The Gibbs barrier energy of the reaction for the formation of CO2 (0.852 eV) is slightly higher than the Gibbs barrier energy for the formation of H2O (0.744 eV). Therefore, the dissociated O on the Fischer–Tropsch synthesis surface is preferentially removed as H2O, which is consistent with the results of Zhang’s [14] study and provides evidence that the calculations in this paper are credible.

2.4.2. The Methanol Formation Pathway on a Hydrogen-Covered χ-Fe5C2(510) Surface

Monohydric alcohols are also one of the possible products of the O removal pathway, of which methanol is representative [51]. In the designed reaction network shown in Figure 4, the black main channel represents the stepwise hydrogenation of CO to methanol, where it can be divided into four levels in terms of product classification: 1, CHO and COH; 2, CHOH and CH2O; 3, CH2OH and CH3O; and 4, CH3OH. Figure 9 shows the Gibbs barrier energy for the stepwise hydrogenation of CO to produce methanol on hydrogen-covered χ-Fe5C2(510).
At level 1, the effective Gibbs barrier energy for the hydrogenation of CO to CHO (1.022 eV) is much lower than that for COH (1.788 eV). Therefore, CO is more likely to undergo hydrogenation at the C site to produce CHO species. Similarly, comparing the effective Gibbs barrier energy of each basic reaction at levels 2 and 3, it is found that the corresponding species also tend to undergo hydrogenation at the C site first, such as CHO + H → CH2O, CH2O + H → CH3O, with the effective Gibbs barrier energy of 0.251 eV and 0.221 eV, respectively. Finally, when the C site is saturated, only then does hydrogenation occur at the O site: CH3O + H → CH3OH.
In short, it is easy to see that the Gibbs barrier energy of the stepwise hydrogenation from CO to methanol is higher on the C-site than on the O-site hydrogenation at all levels. The Gibbs barrier energy of the O-site hydrogenation reaction decreases with the increase in the number of H atoms at the C-site (the effective reaction Gibbs barrier energy for the O-site hydrogenation at all levels: 1, 1. 7611 eV > 2, 1.275 eV > 3, 0.4835 eV > 4, 0.2739 eV). Thus, the main reaction pathway for the stepwise hydrogenation of CO to methanol is CO + H → CHO + H → CH2O + H → CH3O + H → CH3OH, with the effective Gibbs barrier energy of 1.412 eV, which is the highest effective Gibbs barrier energy of the generated species considered. In addition, the stepwise hydrogenation of CO to methanol involves the formation of formaldehyde (at level 2), of which the effective energy barrier is mainly determined by the first step CO + H → HCO of 1.022 eV.

2.4.3. Competitive Analysis of the Formic acid Formation Pathway with the Formation Pathways of other Oxygenated Species on the Reaction of the Hydrogen-Covered χ-Fe5C2(510) Surface

After clarifying the preferred typical O removal product formation pathway, the Gibbs barrier energy of the formic acid formation pathway and each other product formation pathway can now be plotted in Figure 10.
Comparison of the effective Gibbs barrier energy of the optimal formation pathways for the different products in Figure 10, in order from smallest to largest: H2O (0.744 eV) < CO2 (0.853 eV) < HCOOH (0.936 eV) < CH2O (1.022 eV) < CH3OH (1.421 eV). The effective Gibbs barrier energy of the pathways for methanol and formaldehyde formation are much higher than those for the formation of other products, so that the production of alcohols and formaldehyde is kinetically unfavorable. In addition, it is seen in detail in Section 2.3.1. that it is also difficult to obtain formic acid via the CO pathway due to the fact that the effective reaction energy barrier of the CO pathway (1.542 eV) is much higher than that of the OH and CO2 pathways. It is found that there is a competitive relationship between CO + OH → COOH and H + OH → H2O, and the effective Gibbs barrier energy of the elementary reaction is COOH (0.836 eV) > H2O (0.553 eV). Because there are a large number of H atoms on the surface of χ-Fe5C2, which is favorable for the hydrogenation of OH to water, it is difficult for formic acid to be formed via the OH pathway reaction. In addition, it is discussed in Section 2.3 that the formation of formic acid via the CO2 pathway is difficult due to the low desorption energy of CO2. In summary, on the catalyst surface, the fact that formic acid is in competition with, and in a disadvantageous position with respect to, the pathways for the formation of H2O and CO2, results in the absence of formic acid formation.
What is more, the kMC simulation is applied to assist in finding the major reaction pathways, as only drawing energy profile diagrams and then determining reaction pathways cannot exhaust all the possible reaction pathways. Based on the kinetic data provided via DFT calculations, the kMC simulation could produce the reaction frequency of each elementary reaction, and the reaction pathways can be accurately obtained via the comparison of their reaction frequencies.
The DFT results regarding the radical reactions considered are given in Table S1, while the radical reactions considered in the kMC simulation are given in Table S2; the simulated temperature was 600 K, the simulated pressure was 2 MPa, the ratio of CO to H2 in the feed composition was 1:1, and the simulation time was 1.0 × 10−3 s. When the kMC simulation system reached stability, the kMC product distribution and reaction frequency data were obtained, and the results are shown in Figure 9 (black arrows indicate that species undergo hydrogenation; red arrows indicate that species react with O; blue arrows indicate that species react with OH; green numbers indicate the net reaction frequency; and the absence of a number next to the arrow indicates that the reaction did not occur).
In the kMC simulation system (Figure 11), the reaction frequency of the formic acid, formaldehyde, and methanol formation pathway is 0; the reaction frequency of the elementary reaction H + OH → H2O is 3450, and the reaction frequency of the dissociated O removal in the form of CO2 is 1207, suggesting that H2O and CO2 are the main oxygen-containing compounds in the iron-based iron Fischer–Tropsch synthesis catalysts, and that the dissociated O is also more easily removed as H2O. While the primitive reaction CO + OH → COOH did not occur, surprisingly, there was still a very small amount (net reaction frequency = 22) of CO2 hydrogenation to produce COOH, but no progress in the reaction to produce HCOOH, which can be attributed to the increase in energy required due to the change in conformation of COOH.

2.4.4. Summary

In summary, the combination use of DFT and kMC shows that the dissociated oxygen on χ-Fe5C2(510) is mainly removed in the form of CO2 and H2O, and the effective Gibbs barrier energy of the H2O production pathway is relatively lower, so more H2O is produced, while it is actually more difficult to produce HCOOH on χ-Fe5C2(510). The main reasons for the limitation of formic acid production are as follows: 1. If CO is hydrogenated first to form COH (1.788 eV) or CHO (1.022 eV), then it is difficult to form HCOOH due to the effective Gibbs barrier energy. 2. When CO reacts with O to form CO2, CO2 cannot be further hydrogenated to form HCOOH because it is easily desorbed. 3. When considering the OH pathway, because there are a large number of H atoms on the hydrogen-covered surface, OH is more likely to react with H atoms to form H2O, which also blocks the formation of HCOOH.
Based on the results of this work, two solutions are proposed to try to remove the dissociated O in the form of formic acid: firstly, increasing the adsorption energy of the catalyst for CO2 and the probability of the CO2 hydrogenation reaction occurring, by modifying the iron-based catalyst with other elements. Secondly, increasing the CO coverage on the catalyst surface so that CO could occupy more top-site iron atoms on the catalyst surface and reduce the occupancy of the hydrogen at the same time to prevent the hydrogenation reaction of OH species. The above analysis makes it possible to remove the dissociated O in the form of formic acid and, thus, achieve the resourceful use of dissociated O.

3. Conclusions

In this paper, the possibility of removing dissociated O by replacing H2O or CO2 (economically worthless byproducts) with HCOOH is proposed and discussed. First, the reaction mechanism of Fischer–Tropsch synthesis of formic acid was investigated via DFT simulation, and it was found that the best pathway to remove dissociated O in the form of formic acid is the OH pathway, through which OH + CO → COOH + H → HCOOH, with the effective Gibbs barrier energy of 0.936 eV. This result is close to the effective Gibbs barrier energy of 0.73 eV for the CO activation pathway, suggesting theoretical formic acid formation on the surface of iron-based Fischer–Tropsch synthesis catalysts. However, formic acid was not found in the experimental results, which could be attributed to the fact that the process used to form formic acid cannot compete with other species.
To prove this hypothesis, the removal of dissociated oxygen in the form of formic acid was compared with the formation pathways of CO2, H2O, and alcohol via DFT-kMC. Three main factors limiting the formation of formic acid were identified. 1. If the hydrogenation of CO is considered first, then the formation of HCOOH is hindered by the high effective Gibbs barrier energy for the formation of COH (1.788 eV) or CHO (1.022 eV). 2. If CO reacts first with O to form CO2, then it is difficult to hydrogenate it to HCOOH because CO2 is readily desorbed. 3. If the CO + OH pathway is considered, then OH reacts more readily with H atoms to form H2O than with CO to form COOH due to the hydrogen-covered effect.
There are two ways to attempt to remove dissociated oxygen in the form of formic acid, based on the reaction mechanism that limits the formation of formic acid. Firstly, the ability of the catalyst to adsorb carbon dioxide and the possibility of a carbon dioxide hydrogenation reaction can be improved by modifying the iron-based catalyst with other elements, which can be considered as the introduction of elements such as Cr, Mn, and Pd [52]. Secondly, by increasing the CO coverage on the catalyst surface while decreasing the hydrogen coverage, the likelihood of OH species undergoing a hydrogenation reaction is reduced. The introduction of the element Pb can also be considered, drawing on the idea of Pb electrocatalytic Fischer–Tropsch synthesis for the highly selective generation of formic acid [53].

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28248117/s1, Figure S1: Conformations of COOH species; Figure S2: Interconversion processes of different adsorption structures of HCOH; Figure S3: The initial, transition, and final states of the basic dissociative O removal reaction. Table S1: Gibbs barrier energy (Ga, eV), Gibbs reaction energy (Gr, eV), and effective Gibbs barrier energy (Geff, eV) for the basic reaction of the dissociative O removal reaction on χ-Fe5C2 (510); Table S2: The elementary reactions and corresponding kinetic parameters included in the kMC simulation about the Fischer-Tropsch reaction pathway on χ-Fe5C2(510); Table S3: Indicates the basic reaction corresponding to the transition state (TS) of Figure 5. Table S4: Indicates the basic reaction corresponding to the transition state (TS) of Figure 6. Table S5: Indicates the basic reaction corresponding to the transition state (TS) of Figure 7. Table S6: Indicates the basic reaction corresponding to the transition state (TS) of Figure 8. Table S7: Indicates the basic reaction corresponding to the transition state (TS) of Figure 9. Table S8 Indicates the basic reaction corresponding to the transition state (TS) of Figure 10.

Author Contributions

Conceptualization, J.R. and N.A.; data curation, C.L. and J.R.; formal analysis, N.A., C.L., Q.W., W.H. and J.R.; funding acquisition, N.A.; investigation, C.L. and J.R.; methodology, C.L., J.R. and N.A.; project administration, N.A.; resources, N.A.; software, J.R. and N.A; supervision, Q.W. and W.H.; validation, Q.W. and W.H.; visualization, C.L.; writing—original draft, N.A., C.L., Q.W., W.H. and J.R.; writing—review and editing, N.A., C.L., Q.W., W.H. and J.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used to support the findings of this study are included within the article.

Acknowledgments

The authors would like to acknowledge everyone who provided helpful guidance and would also like to thank the anonymous reviewers for their useful comments.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kulikova, M.V.; Chudakova, M.V.; Kulikov, A.B.; Krylova, A.Y. Fischer–Tropsch Synthesis in the Presence of Catalysts Based on Unmodified Iron Ores. Russ. J. Appl. Chem. 2021, 94, 104–109. [Google Scholar] [CrossRef]
  2. Mubenesha, S.; Okoye-Chine, C.G.; Ramutsindela, F.K.; Gorimbo, J.; Moyo, M.; Liu, X. The Potential Use of Raw Iron Ore in Fischer-Tropsch Synthesis. Int. J. Pet. Technol. 2021, 8, 99–115. [Google Scholar] [CrossRef]
  3. Ramutsindela, F.K.; Okoye-Chine, C.G.; Mbuya, C.O.L.; Mubenesha, S.; Gorimbo, J.; Okonye, L.U.; Liu, X.; Hildebrandt, D. The effect of reducing gases on raw iron ore catalyst for Fischer-Tropsch synthesis. J. Taiwan Inst. Chem. Eng. 2022, 131, 104163. [Google Scholar] [CrossRef]
  4. Ncube, S.; Moyo, M. A Review of the Use of Carbon Nanostructures and Other Reducing Agents During Auto-reduction for Fischer–Tropsch Synthesis and Other Applications. Catal. Lett. 2023, 1–21. [Google Scholar] [CrossRef]
  5. Chen, Y.; Wei, J.; Duyar, M.S.; Ordomsky, V.V.; Khodakov, A.Y.; Liu, J. Carbon-based catalysts for Fischer-Tropsch synthesis. Chem. Soc. Rev. 2021, 50, 2337–2366. [Google Scholar] [CrossRef]
  6. Mahmoudi, H.; Mahmoudi, M.; Doustdar, O.; Jahangiri, H.; Tsolakis, A.; Gu, S.; LechWyszynski, M. A review of Fischer Tropsch synthesis process, mechanism, surface chemistry and catalyst formulation. Biofuels Eng. 2017, 2, 11–31. [Google Scholar] [CrossRef]
  7. Okoye-Chine, C.G.; Mubenesha, S. The Use of Iron Ore as a Catalyst in Fischer–Tropsch Synthesis—A Review. Crystals 2022, 12, 1349. [Google Scholar] [CrossRef]
  8. Van Der Laan, G.P.; Beenackers, A.A.C.M. Kinetics and Selectivity of the Fischer–Tropsch Synthesis: A Literature Review. Catal. Rev. 1999, 41, 255–318. [Google Scholar] [CrossRef]
  9. Lin, T.; An, Y.; Yu, F.; Gong, K.; Yu, H.; Wang, C.; Sun, Y.; Zhong, L. Advances in Selectivity Control for Fischer–Tropsch Synthesis to Fuels and Chemicals with High Carbon Efficiency. ACS Catal. 2022, 12, 12092–12112. [Google Scholar] [CrossRef]
  10. Tavares, M.; Westphalen, G.; Araujo Ribeiro de Almeida, J.M.; Romano, P.N.; Sousa-Aguiar, E.F. Modified fischer-tropsch synthesis: A review of highly selective catalysts for yielding olefins and higher hydrocarbons. Front. Nanotechnol. 2022, 4, 978358. [Google Scholar] [CrossRef]
  11. Filot, I.A.; van Santen, R.A.; Hensen, E.J. The optimally performing Fischer-Tropsch catalyst. Angew. Chem. Int. Ed. 2014, 53, 12746–12750. [Google Scholar] [CrossRef] [PubMed]
  12. Gao, R.; Cao, D.-B.; Liu, S.; Yang, Y.; Li, Y.-W.; Wang, J.; Jiao, H. Density functional theory study into H2O dissociative adsorption on the Fe5C2(010) surface. Appl. Catal. A Gen. 2013, 468, 370–383. [Google Scholar] [CrossRef]
  13. Pham, T.H.; Duan, X.; Qian, G.; Zhou, X.; Chen, D. CO Activation Pathways of Fischer–Tropsch Synthesis on χ-Fe5C2 (510): Direct versus Hydrogen-Assisted CO Dissociation. J. Phys. Chem. C 2014, 118, 10170–10176. [Google Scholar] [CrossRef]
  14. Zhang, M.; Guan, X.; Yu, Y. Theoretical insights into the removal pathways of adsorbed oxygen on the surface of χ-Fe5C2(5 1 0). Chem. Eng. Sci. 2023, 271, 118576. [Google Scholar] [CrossRef]
  15. Zhang, M.; Ren, J.; Yu, Y. Insights into the Hydrogen Coverage Effect and the Mechanism of Fischer–Tropsch to Olefins Process on Fe5C2 (510). ACS Catal. 2020, 10, 689–701. [Google Scholar] [CrossRef]
  16. Andersson, R.; Boutonnet, M.; Järås, S. On-line gas chromatographic analysis of higher alcohol synthesis products from syngas. J. Chromatogr. A 2012, 1247, 134–145. [Google Scholar] [CrossRef] [PubMed]
  17. Liu, S.; Tian, X.; Wang, T.; Wen, X.; Li, Y.-W.; Wang, J.; Jiao, H. Coverage dependent water dissociative adsorption on Fe(110) from DFT computation. Phys. Chem. Chem. Phys. PCCP 2015, 17, 8811–8821. [Google Scholar] [CrossRef] [PubMed]
  18. Ojeda, M.; Nabar, R.; Nilekar, A.U.; Ishikawa, A.; Mavrikakis, M.; Iglesia, E. CO activation pathways and the mechanism of Fischer–Tropsch synthesis. J. Catal. 2010, 272, 287–297. [Google Scholar] [CrossRef]
  19. Seomoon, K. On-line GC and GC–MS analyses of the Fischer–Tropsch products synthesized using ferrihydrite catalyst. J. Ind. Eng. Chem. 2013, 19, 2108–2114. [Google Scholar] [CrossRef]
  20. Wang, H.Z.; Nie, X.W.; Liu, Y.; Janik, M.J.; Han, X.P.; Deng, Y.D.; Hu, W.B.; Song, C.S.; Guo, X.W. Mechanistic Insight into Hydrocarbon Synthesis via CO2 Hydrogenation on χ-Fe5C2 Catalysts. Acs Appl. Mater. Interfaces 2022, 14, 37637–37651. [Google Scholar] [CrossRef]
  21. Li, T.; Wen, X.; Li, Y.-W.; Jiao, H. Mechanisms of CO Activation, Surface Oxygen Removal, Surface Carbon Hydrogenation, and C–C Coupling on the Stepped Fe(710) Surface from Computation. J. Phys. Chem. C 2018, 122, 15505–15519. [Google Scholar] [CrossRef]
  22. Zhao, Q.; Liu, Y.; Ma, H.; Qiao, Y.; Chao, J.; Hou, X.; Wang, Y.; Wang, Y. Combination of pure shift NMR and chemical shift selective filters for analysis of Fischer-Tropsch waste-water. Anal. Chim. Acta 2020, 1110, 131–140. [Google Scholar] [CrossRef] [PubMed]
  23. Van der Westhuizen, R.; Crous, R.; de Villiers, A.; Sandra, P. Comprehensive two-dimensional gas chromatography for the analysis of Fischer–Tropsch oil products. J. Chromatogr. A 2010, 1217, 8334–8339. [Google Scholar] [CrossRef] [PubMed]
  24. Fernandes, D.R.; Pereira, V.B.; Stelzer, K.T.; Gomes, A.O.; Neto, F.R.; Azevedo, D.A. Quantification of trace O-containing compounds in GTL process samples via Fischer-Tropsch reaction by comprehensive two-dimensional gas chromatography/mass spectrometry. Talanta 2015, 144, 627–635. [Google Scholar] [CrossRef]
  25. Liu, X.; Li, S.; Liu, Y.; Cao, Y. Formic acid: A versatile renewable reagent for green and sustainable chemical synthesis. Chin. J. Catal. 2015, 36, 1461–1475. [Google Scholar] [CrossRef]
  26. Gibson, H.W. Chemistry of formic acid and its simple derivatives. Chem. Rev. 1969, 69, 673–692. [Google Scholar] [CrossRef]
  27. Grasemann, M.; Laurenczy, G. Formic acid as a hydrogen source—Recent developments and future trends. Energy Environ. Sci. 2012, 5, 8171–8181. [Google Scholar] [CrossRef]
  28. Yang, Y.; Zhang, H.; Ma, H.; Qian, W.; Sun, Q.; Ying, W. Effect of alkalis (Li, Na, and K) on precipitated iron-based catalysts for high-temperature Fischer-Tropsch synthesis. Fuel 2022, 326, 125090. [Google Scholar] [CrossRef]
  29. Song, L.; Ouyang, S.; Li, P.; Ye, J. Highly selective light olefin production via photothermal Fischer–Tropsch synthesis over α/γ-Fe2O3-derived Fe5C2 under low pressure. J. Mater. Chem. 2022, 10, 16243–16248. [Google Scholar] [CrossRef]
  30. Cheng, J.; Gong, X.-Q.; Hu, P.; Lok, C.M.; Ellis, P.; French, S. A quantitative determination of reaction mechanisms from density functional theory calculations: Fischer–Tropsch synthesis on flat and stepped cobalt surfaces. J. Catal. 2008, 254, 285–295. [Google Scholar] [CrossRef]
  31. Yang, C.; Zhao, H.; Hou, Y.; Ma, D. Fe5C2 Nanoparticles: A Facile Bromide-Induced Synthesis and as an Active Phase for Fischer–Tropsch Synthesis. J. Am. Chem. Soc. 2012, 134, 15814–15821. [Google Scholar] [CrossRef] [PubMed]
  32. Hacene, M.; Anciaux-Sedrakian, A.; Rozanska, X.; Klahr, D.; Guignon, T.; Fleurat-Lessard, P. Accelerating VASP electronic structure calculations using graphic processing units. J. Comput. Chem. 2012, 33, 2581–2589. [Google Scholar] [CrossRef] [PubMed]
  33. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  34. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
  35. Hutchinson, M.; Widom, M. VASP on a GPU: Application to exact-exchange calculations of the stability of elemental boron. Comput. Phys. Commun. 2012, 183, 1422–1426. [Google Scholar] [CrossRef]
  36. Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
  37. Ren, J.; Ai, N.; Ou, D.; Yu, Y. Insights into the Fischer–Tropsch mechanism on χ-Fe5C2(510) based on the hydrogen coverage effect. Mol. Catal. 2023, 538, 112990. [Google Scholar] [CrossRef]
  38. MacDonald, A.H. Comment on special points for Brillouin-zone integrations. Phys. Rev. B 1978, 18, 5897–5899. [Google Scholar] [CrossRef]
  39. Methfesel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
  40. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  41. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
  42. Sheppard, D.; Xiao, P.; Chemelewski, W.; Johnson, D.D.; Henkelman, G. A generalized solid-state nudged elastic band method. J. Chem. Phys. 2012, 136, 074103. [Google Scholar] [CrossRef] [PubMed]
  43. Sheppard, D.; Terrell, R.; Henkelman, G. Optimization methods for finding minimum energy paths. J. Chem. Phys. 2008, 128, 134106. [Google Scholar] [CrossRef] [PubMed]
  44. Chen, Y.; Cui, Y.; Deng, D.; Ai, N. Density Functional Theory Study on the Absorption of CO2 by the Ionic Liquid of 1-butyl-3-methylimidazolium Acetate. Adv. Mater. Res. 2013, 807–809, 543–548. [Google Scholar]
  45. Cheng, J.; Hu, P.; Ellis, P.; French, S.; Kelly, G.; Lok, C.M. An Energy Descriptor to Quantify Methane Selectivity in Fischer−Tropsch Synthesis: A Density Functional Theory Study. J. Phys. Chem. C 2009, 113, 8858–8863. [Google Scholar] [CrossRef]
  46. Retief, J.J. Powder diffraction data and Rietveld refinement of Hägg-carbide, χ-Fe5C2. Powder Diffr. 1999, 14, 130–132. [Google Scholar] [CrossRef]
  47. Sun, F.; Huang, W.L.; Li, J. Mesoscale Structures in the Adlayer of A-B 2 Heterogeneous Catalysis. Langmuir 2017, 33, 11582–11589. [Google Scholar] [CrossRef] [PubMed]
  48. Kattel, S.; Ramírez, P.J.; Chen, J.G.; Rodriguez, J.A.; Liu, P. Active sites for CO₂ hydrogenation to methanol on Cu/ZnO catalysts. Science 2017, 355, 1296–1299. [Google Scholar] [CrossRef]
  49. Jansen, A.P.J. An Introduction to Monte Carlo Simulations of Surface Reactions. arXiv 2003, arXiv:cond-mat/0303028. [Google Scholar]
  50. Turner, C.H.; Ji, J.; Lu, Z.; Lei, Y. Analysis of the propylene epoxidation mechanism on supported gold nanoparticles. Chem. Eng. Sci. 2017, 174, 229–237. [Google Scholar] [CrossRef]
  51. Dieterich, V.; Buttler, A.; Hanel, A.; Spliethoff, H.; Fendt, S. Power-to-liquid via synthesis of methanol, DME or Fischer–Tropsch-fuels: A review. Energy Environ. Sci. 2020, 13, 3207–3252. [Google Scholar] [CrossRef]
  52. Zhang, M.M.; Wang, S.; Nie, X.W.; Ding, F.S.; Song, C.S.; Guo, X.W. Mechanistic Understanding of Hydrocarbon Formation from CO2 Hydrogenation over χ-Fe5C2(111) and the Effect of H2O and Transition Metal Addition. Energy Fuels 2023, 37, 16842–16855. [Google Scholar] [CrossRef]
  53. Back, S.; Kim, J.H.; Kim, Y.T.; Jung, Y. On the mechanism of high product selectivity for HCOOH using Pb in CO2 electroreduction. Phys. Chem. Chem. Phys. 2016, 18, 9652–9657. [Google Scholar] [CrossRef] [PubMed]
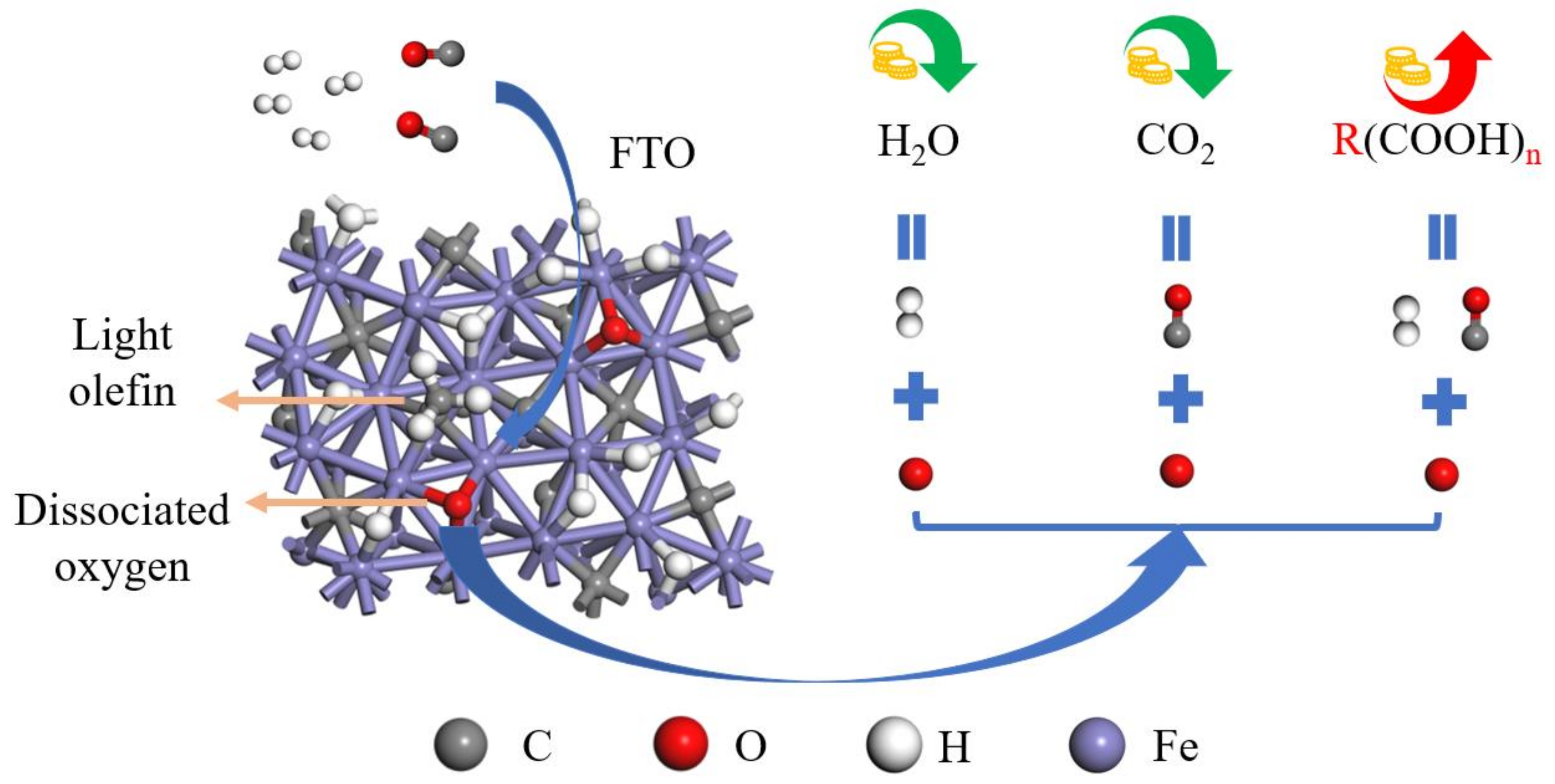
Molecules 28 08117 g001
Figure 1. Possible forms of removal of dissociated oxygen in Fischer–Tropsch synthesis.
Figure 1. Possible forms of removal of dissociated oxygen in Fischer–Tropsch synthesis.
Molecules 28 08117 g001
Molecules 28 08117 g002
Figure 2. Model used for DFT computation (blue: iron atoms, grey: carbon atoms, white: hydrogen atoms). (a) Top view of χ-Fe5C2(510) with consideration of the hydrogen coverage effect; (b) side view of χ-Fe5C2(510) with consideration of the hydrogen coverage effect.
Figure 2. Model used for DFT computation (blue: iron atoms, grey: carbon atoms, white: hydrogen atoms). (a) Top view of χ-Fe5C2(510) with consideration of the hydrogen coverage effect; (b) side view of χ-Fe5C2(510) with consideration of the hydrogen coverage effect.
Molecules 28 08117 g002
Molecules 28 08117 g003
Figure 3. Model used in the DFT calculation based on the kMC method. (a) kMC model (blue: top sites of the iron atoms; green: bridge sites of the iron atoms; white: 3-fold sites of the iron atoms; gray: 4-fold sites of the iron atoms); (b) corresponding DFT model (blue: iron atoms; gray: carbon atoms; white: hydrogen atoms).
Figure 3. Model used in the DFT calculation based on the kMC method. (a) kMC model (blue: top sites of the iron atoms; green: bridge sites of the iron atoms; white: 3-fold sites of the iron atoms; gray: 4-fold sites of the iron atoms); (b) corresponding DFT model (blue: iron atoms; gray: carbon atoms; white: hydrogen atoms).
Molecules 28 08117 g003
Molecules 28 08117 g004
Figure 4. Possible dissociated O removal pathways for χ-Fe5C2(510) surfaces covered with hydrogen.
Figure 4. Possible dissociated O removal pathways for χ-Fe5C2(510) surfaces covered with hydrogen.
Molecules 28 08117 g004
Molecules 28 08117 g005
Figure 5. The effective Gibbs barrier energy diagram of the pathway for the removal of dissociated O from the surface of hydrogen-covered χ-Fe5C2(510) in the form of (OH and CO2 pathway) formic acid.
Figure 5. The effective Gibbs barrier energy diagram of the pathway for the removal of dissociated O from the surface of hydrogen-covered χ-Fe5C2(510) in the form of (OH and CO2 pathway) formic acid.
Molecules 28 08117 g005
Molecules 28 08117 g006
Figure 6. The effective Gibbs barrier energy diagram for the pathway of dissociated O removal from the hydrogen-covered χ-Fe5C2(510) surface in the form of (CO pathway) formic acid.
Figure 6. The effective Gibbs barrier energy diagram for the pathway of dissociated O removal from the hydrogen-covered χ-Fe5C2(510) surface in the form of (CO pathway) formic acid.
Molecules 28 08117 g006
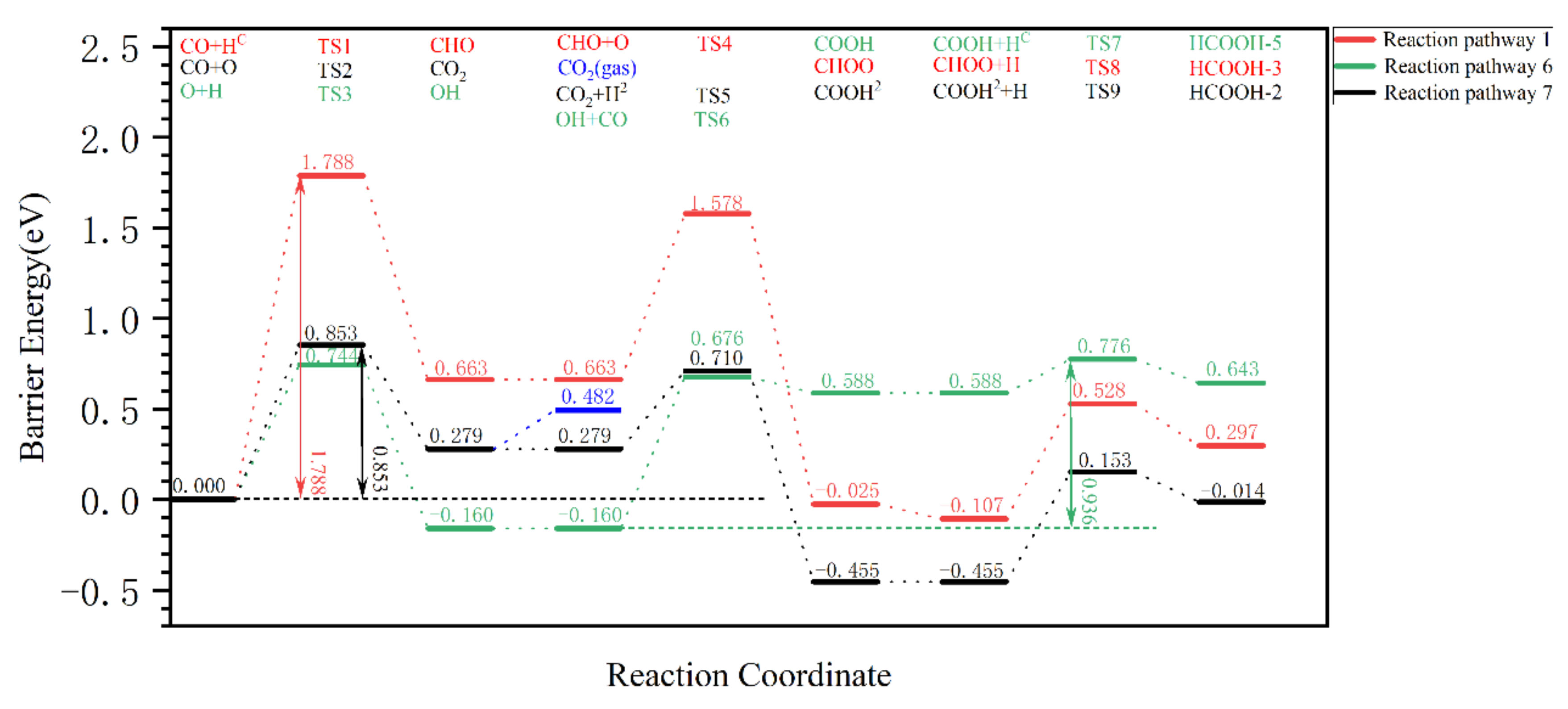
Molecules 28 08117 g007
Figure 7. The effective Gibbs barrier energy diagram for the removal pathway of dissociated oxygen from the surface of hydrogen-covered χ-Fe5C2(510) in the form of (OH, CO2, CO pathway optimal pathway) formic acid.
Figure 7. The effective Gibbs barrier energy diagram for the removal pathway of dissociated oxygen from the surface of hydrogen-covered χ-Fe5C2(510) in the form of (OH, CO2, CO pathway optimal pathway) formic acid.
Molecules 28 08117 g007
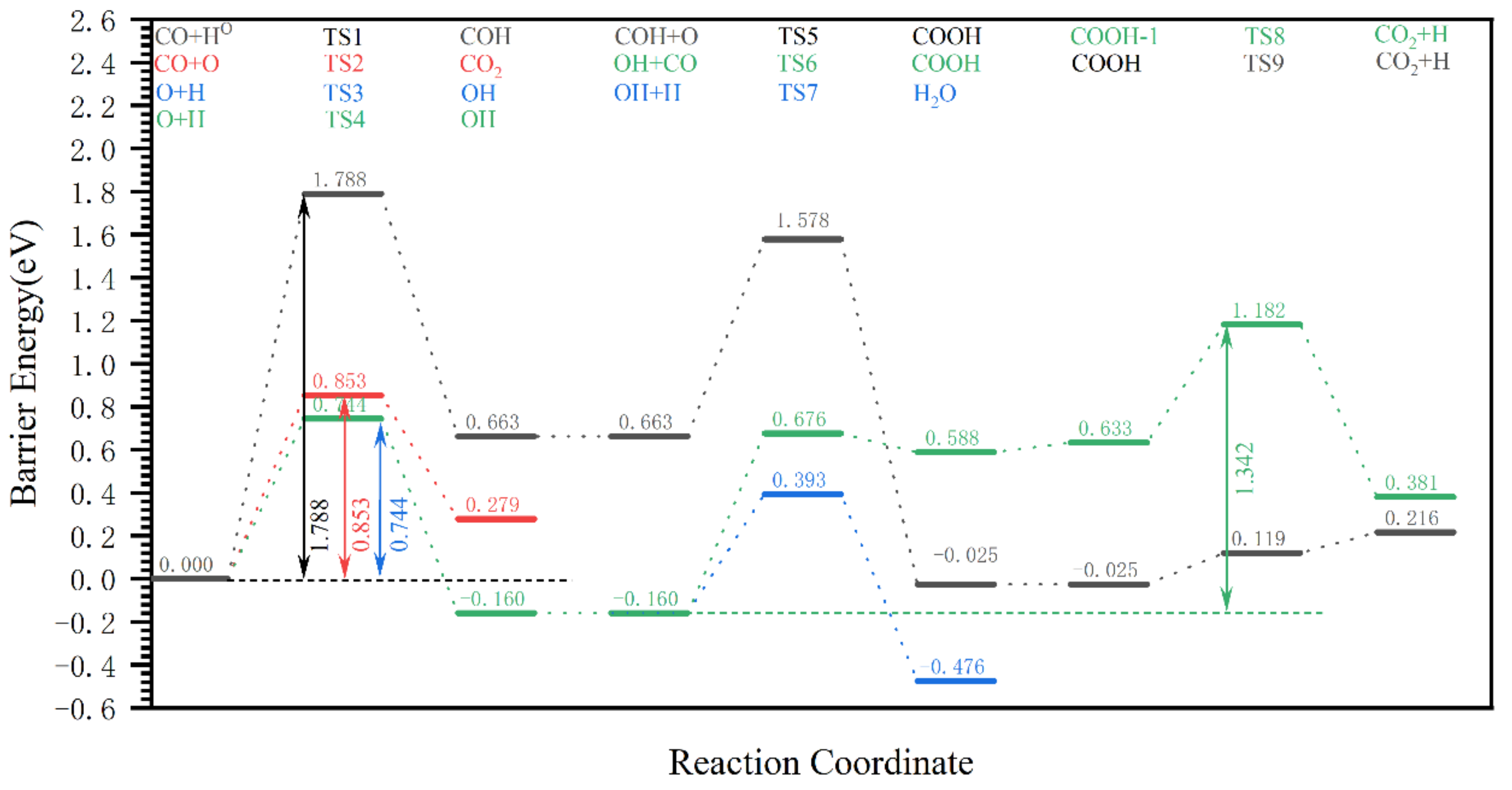
Molecules 28 08117 g008
Figure 8. The Gibbs barrier energy diagram for the pathway of dissociated O removal as CO2/H2O on the hydrogen-covered χ-Fe5C2(510) surface.
Figure 8. The Gibbs barrier energy diagram for the pathway of dissociated O removal as CO2/H2O on the hydrogen-covered χ-Fe5C2(510) surface.
Molecules 28 08117 g008
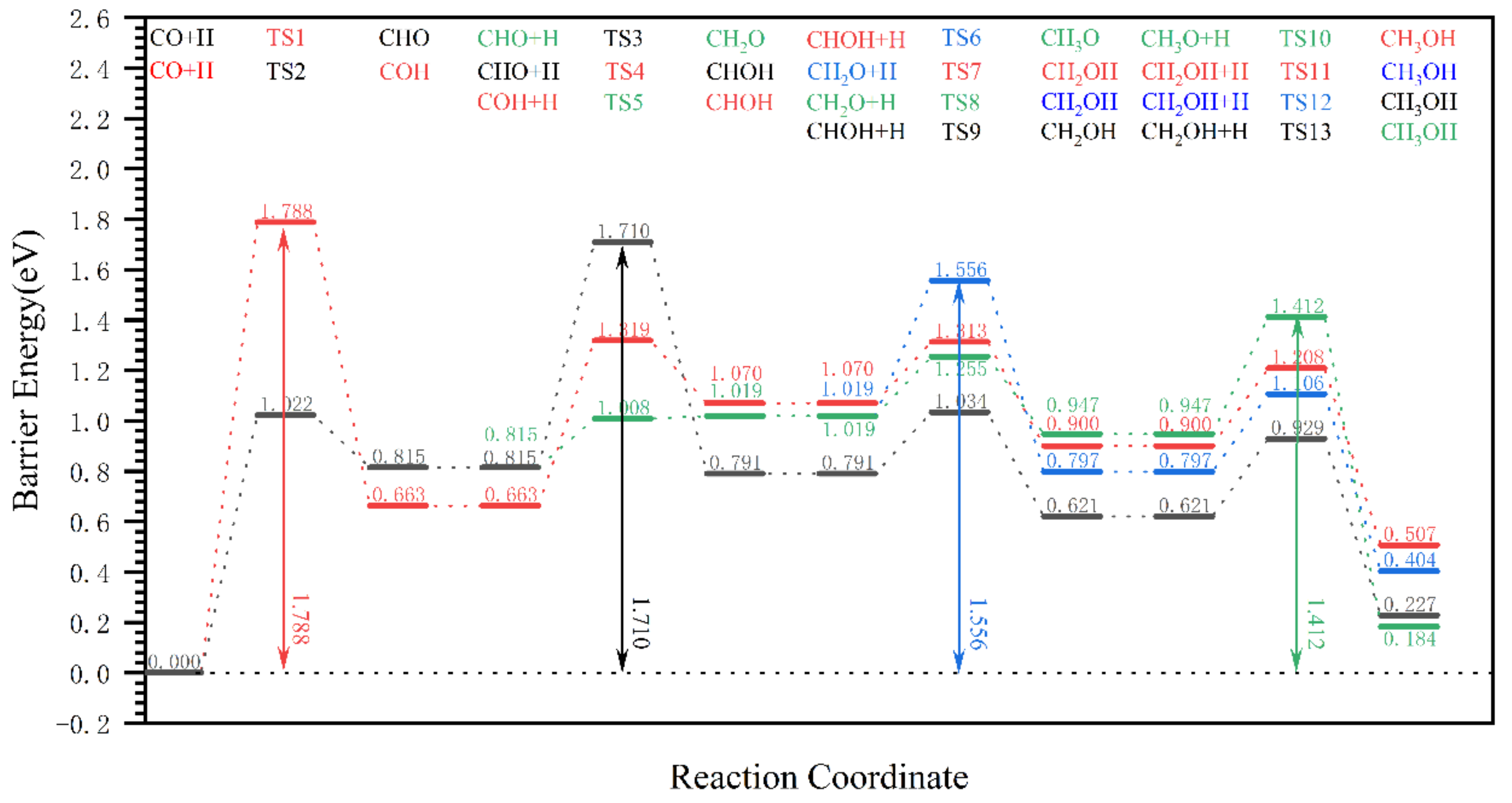
Molecules 28 08117 g009
Figure 9. The effective Gibbs barrier energy diagram for the dissociated O removal pathway in the form of methanol on the hydrogen-covered χ-Fe5C2(510) surface.
Figure 9. The effective Gibbs barrier energy diagram for the dissociated O removal pathway in the form of methanol on the hydrogen-covered χ-Fe5C2(510) surface.
Molecules 28 08117 g009
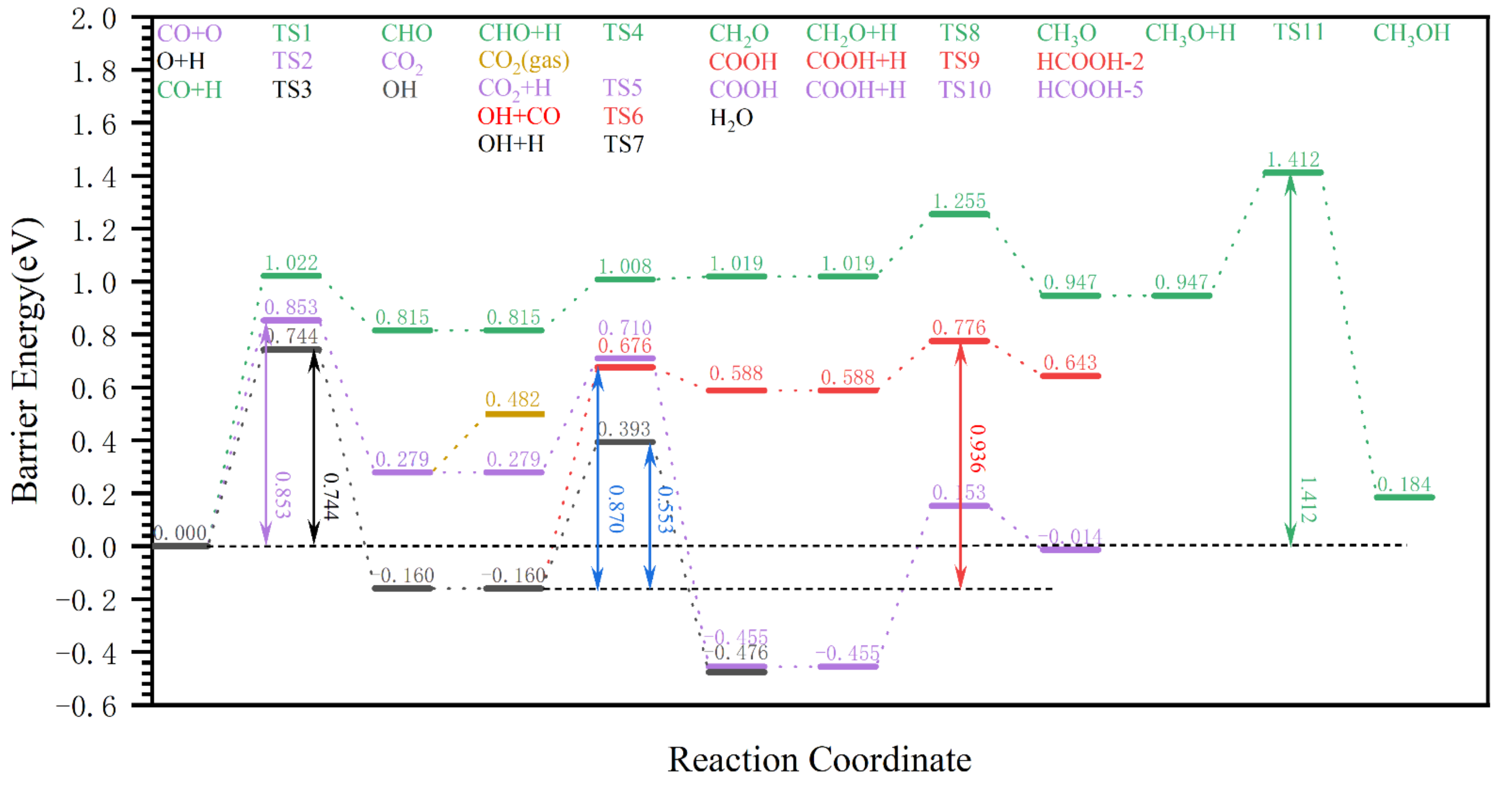
Molecules 28 08117 g010
Figure 10. Comparison of the effective Gibbs barrier energy for the optimal removal pathways for each form of dissociated O from the hydrogen-covered χ-Fe5C2(510) surface.
Figure 10. Comparison of the effective Gibbs barrier energy for the optimal removal pathways for each form of dissociated O from the hydrogen-covered χ-Fe5C2(510) surface.
Molecules 28 08117 g010
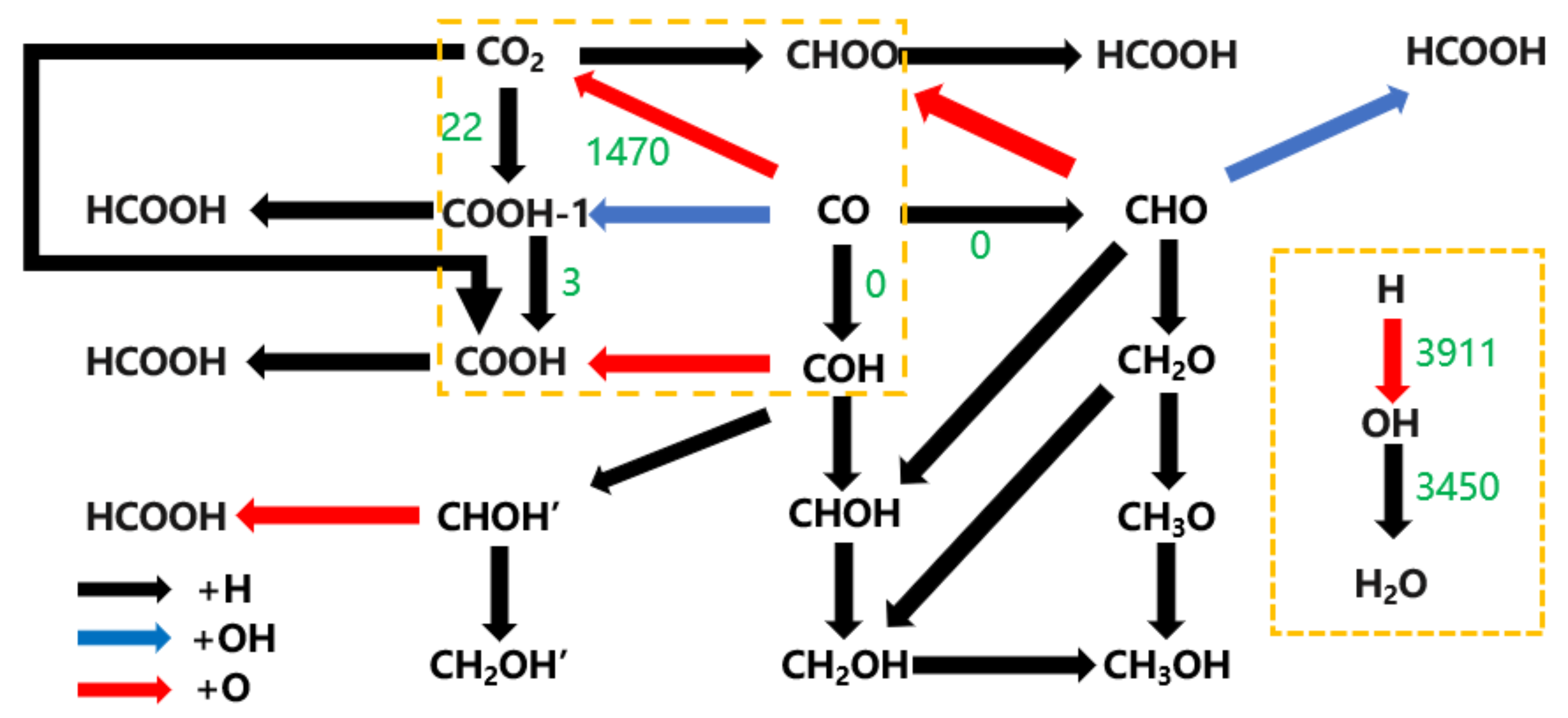
Molecules 28 08117 g011
Figure 11. Schematic representation of the process of dissociated O removal from the hydrogen-covered χ-Fe5C2(510) surface.
Figure 11. Schematic representation of the process of dissociated O removal from the hydrogen-covered χ-Fe5C2(510) surface.
Molecules 28 08117 g011
Table 1. Detailed table of the elementary reactions for the reaction pathway of the hydrogen-covered surface reaction of χ-Fe5C2(510) to formic acid.
Table 1. Detailed table of the elementary reactions for the reaction pathway of the hydrogen-covered surface reaction of χ-Fe5C2(510) to formic acid.
Reaction PathwayStep 1: Elementary ReactionStep 2: Elementary ReactionStep 3: Elementary Reaction
1CO Oxygen side hydrogenation
CO + HO → COH		COH carbon site oxygenated
COH + O → COOH		COOH carbon site hydrogenation
COOH + HC → HCOOH
2COH carbon site hydrogenation
COH + HC → CHOH		CHOH carbon site oxygenated
CHOH + O → HCOOH
3CO carbon site hydrogenation
CO + HC → CHO		CHO carbon site hydrogenation
CHO + O → CHOO		CHOO Oxygen side hydrogenation
CHOO + HO → HCOOH
4CHO Oxygen side hydrogenation
CHO + HO → CHOH		CHOH carbon site oxygenated
CHOH + O → HCOOH
5CO carbon site hydrogenation
CO + HC → CHO		Dissociation O hydrogenation
O + H → OH		CHO reacts with OH
HCO + OH → HCOOH
6Dissociation O hydrogenation
O + H → OH		OH attacks the carbon site of CO
OH + CO → COOH		COOH carbon site hydrogenation
COOH + HC → HCOOH
7CO carbon site oxygenated
CO + O → CO2		Hydrogenation of CO2 at the O1
Site
CO2 + H → COOH		COOH carbon site hydrogenation
COOH + HC → HCOOH
8CO carbon site oxygenated
CO + O → CO2		Hydrogenation of CO2 at the O2
CO2 + H → COOH		COOH carbon site hydrogenation
COOH + HC → HCOOH
Table 2. Charge analyses of the rate-determining steps of the reaction pathway for the hydrogen-covered χ-Fe5C2(510) surface reaction to produce formic acid.
Table 2. Charge analyses of the rate-determining steps of the reaction pathway for the hydrogen-covered χ-Fe5C2(510) surface reaction to produce formic acid.
Elementary ReactionReaction SiteCHARGE
Initial State Transition State End State
1. CO + H → CHOH0.7950.8401.170
C3.4933.4223.147
O7.0137.0027.070
2. CO + H → COHH1.1840.5840.277
C3.1263.6653.757
O7.0367.0087.201
3. CO + O → CO2Dissociated O6.8206.7747.012
C3.1203.0922.542
O7.0316.9767.015
4. CO + OH → COOHH0.2060.4070.296
C3.1963.0142.774
OH 7.2927.0117.193
OC7.0357.0267.080
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ai, N.; Lai, C.; Hu, W.; Wang, Q.; Ren, J. Mechanistic Study on the Possibility of Converting Dissociated Oxygen into Formic Acid on χ-Fe5C2(510) for Resource Recovery in Fischer–Tropsch Synthesis. Molecules 2023, 28, 8117. https://doi.org/10.3390/molecules28248117

AMA Style

Ai N, Lai C, Hu W, Wang Q, Ren J. Mechanistic Study on the Possibility of Converting Dissociated Oxygen into Formic Acid on χ-Fe5C2(510) for Resource Recovery in Fischer–Tropsch Synthesis. Molecules. 2023; 28(24):8117. https://doi.org/10.3390/molecules28248117

Chicago/Turabian Style

Ai, Ning, Changyi Lai, Wanpeng Hu, Qining Wang, and Jie Ren. 2023. "Mechanistic Study on the Possibility of Converting Dissociated Oxygen into Formic Acid on χ-Fe5C2(510) for Resource Recovery in Fischer–Tropsch Synthesis" Molecules 28, no. 24: 8117. https://doi.org/10.3390/molecules28248117

APA Style

Ai, N., Lai, C., Hu, W., Wang, Q., & Ren, J. (2023). Mechanistic Study on the Possibility of Converting Dissociated Oxygen into Formic Acid on χ-Fe5C2(510) for Resource Recovery in Fischer–Tropsch Synthesis. Molecules, 28(24), 8117. https://doi.org/10.3390/molecules28248117

Article Metrics

Back to TopTop