Abstract
Currently, two-dimensional (2D) materials with intrinsic antiferromagnetism have stimulated research interest due to their insensitivity to external magnetic fields and absence of stray fields. Here, we predict a family of stable transition metal (TM) borides, TMB12 (TM = V, Cr, Mn, Fe) monolayers, by combining TM atoms and B12 icosahedra based on first-principles calculations. Our results show that the four TMB12 monolayers have stable antiferromagnetic (AFM) ground states with large magnetic anisotropic energy. Among them, three TMB12 (TM=V, Cr, Mn) monolayers display an in-plane easy magnetization axis, while the FeB12 monolayer has an out-of-plane easy magnetization axis. Among them, the CrB12 and the FeB12 monolayers are AFM semiconductors with band gaps of 0.13 eV and 0.35 eV, respectively. In particular, the AFM FeB12 monolayer is a spin-polarized AFM material with a Néel temperature of 125 K. Moreover, the electronic and magnetic properties of the CrB12 and the FeB12 monolayers can be modulated by imposing external biaxial strains. Our findings show that the TMB12 monolayers are candidates for designing 2D AFM materials, with potential applications in electronic devices.
1. Introduction
With the development of spintronics, the search for magnetic semiconductors has become a prominent topic in both scientific and industrial communities due to their great potential to act as next-generation information storage devices. Compared to three-dimensional (3D) magnetic materials, two-dimensional (2D) magnetic materials hold appealing properties such as high crystallinity and flexibility, high optical transparency, large carrier mobility, etc., which are promising in low-power and ultra-compact spintronics at nanoscale [1,2,3,4,5,6,7,8]. Spintronics can combine standard microelectronics with spin-dependent effects, in which the electron spin carries information and provides opportunities for a new platform for designing devices, arising from the interaction between the spin of the carrier and the magnetic properties of the materials. Unfortunately, many 2D materials synthesized in experiments are nonmagnetic, such as graphene [9], silicene [10], phosphorus [11], etc.
To date, various approaches have been proposed to regulate the spin configurations of 2D materials, such as applying an electric field, imposing external strains, doping, building heterostructures, and so on. However, finding 2D materials with intrinsic magnetism is still a prominent topic and many efforts have been devoted to it. A milestone finding of 2D magnetic materials research is the successful fabrication of an atomically thick CrI3 monolayer and a Cr2Ge2Te6 bilayer by exfoliation from their van der Waals bulks, illustrated in 2017 by Gong et al. [12] and Huang et al. [13], respectively [12,13], which highly accelerated the development of 2D magnetic materials. To date, numerous 2D magnetic materials have been reported theoretically or experimentally, such as transition metal (TM) trihalide monolayers (TMX3, X = F, Cl, Br, I) [14,15,16,17], TM dichalcogenides or dihalides (TMX2, TM = V, Mn, Fe, Co, Ni; X = S, Se, Cl, Br, I) [18,19,20], and ternary materials like Fe3GeTe2 [21,22,23], TMPX3 (X = S, Se, Te) [24,25], TMSiTe3 [26,27], CrSnTe3 [28], CrGaSe3 [29], Cr2x3S3 (X = Br, I) [30], CrSBr [31,32], EuSn2X2 (X = P, As) [33], TMInX3 (X = Te, Se) [34,35], etc., all of which have been widely studied in terms of magnetoelectric coupling, magnetoresistance, and proximity effects. However, the transition temperatures of most of the known 2D magnetic materials are significantly lower than room temperature, which largely hinders their practical applications. For example, the Curie temperature for the ferromagnetic (FM) bilayer Cr2Ge2Te6 [12], the monolayer CrX3 (X = Cl, Br, I) [13,14,15,16,17], and Fe3GeTe2 [21] are 40 K, 45 K (X = I)/17 K (X = Cl)/34 K (X = Br) and 130 K, respectively. Moreover, compared to FM semiconductors, antiferromagnetic (AFM) semiconductors have become a promising research field due to their robustness against magnetic field perturbation, no stray fields, high-frequency dynamics, etc., which enable them to potentially replace ferromagnets as the active components of spintronic devices [36].
Among the discovered 2D magnetic materials, 2D TM borides composed of TM atoms and boron (B) atoms have attracted great attention in recent years and have become potential candidates for designing 2D magnetic materials. As the valence states of the B atom are unsaturated, it can easily hybridize with exotic atoms and display distinct electronic properties. Currently, a number of 2D TM borides with rich stoichiometries and geometric configurations have been predicted in theory and synthesized in experiments, such as TMBx (x = 1-6, 8, 9, 12) [37,38,39,40,41,42,43,44,45,46,47], TMnBn (n = 1, 2) [37,38,48], TMnBm (n = 2, m = 3, 6, 12) [49,50,51], etc., and robust magnetic properties have been found in these TM borides. For example, Ozdemir et al. found that an Fe2B2 monolayer with rectangular lattice and Fe atoms in different atomic planes has a stable columnar AFM ground state, which can change to an FM order with double hysteresis behavior [48]. Zhang et al. [39] found that the hexagonal FeB2 monolayer is a Dirac material with a Fermi velocity comparable to that of graphene. Our group [40] suggested that an FeB3 monolayer with a stripe arrangement of Fe atoms is a robust FM metal with a high Curie temperature of 367 K. Zhang et al. [42] predicted the graphene-like FeB6 monolayer is an indirect bandgap semiconductor with a band gap of 1.89 eV. In another study, we predicted a type of stable sandwiched B-Fe-B compound, known as the Fe2B6 monolayer, in which the Curie temperature is as high as 420 K [50]. Recently, we found that the monoatom-thickness FeB12 monolayer, composed of a TM©B8 wheel and B4 cluster within the space group of Pmmm, is a stable AFM metal [52]. Therefore, TM borides provide a playground for studying 2D magnetic materials.
Here, based on density functional theory calculations, we report a new class of 2D AFM TM borides, TMB12 (TM = V, Cr, Mn, and Fe) monolayers composed of TM atoms and B12 icosahedra. Such structures are different from the TMB12 monolayer, with the same chemical formula as we predicted previously [52]. On the basis of the results of lattice dynamic calculations and thermodynamic studies, we show that 2D TMB12 structures are stable AFM semiconductors or metals. The antiferromagnetism mainly arises from the super-exchange interaction between the B-p orbitals and TM-3d orbitals. It is found that the VB12 monolayer and the MnB12 monolayer are AFM metals, while the CrB12 monolayer and the FeB12 monolayer are AFM semiconductors with band gaps of 0.13 eV and 0.35 eV, respectively. In addition, all four TMB12 monolayers have large magnetic anisotropic energy, and three TMB12 (TM = V, Cr, Mn) monolayers display an in-plane easy magnetization axis, while the FeB12 monolayer has an out-of-plane easy magnetization axis. More interestingly, the AFM semiconducting CrB12 monolayer and FeB12 monolayer can be modulated into an FM half metal or an FM metal under biaxial strains, and the magnetic transition temperature and band gap can also be adjusted. Our findings provide a new strategy for designing 2D TM borides with potential applications in electronic and spintronic devices, though such TMB12 monolayers have not yet been synthesized in experiment.
2. Results and Discussions
The top and side views of the TMB12 (TM = V, Cr, Mn, and Fe) monolayer are shown in Figure 1a, which consists of TM atoms and B12 icosahedra, and the TM atoms bind with four nearby B12 icosahedras. The TMB12 monolayers have space groups of C2/m. Moreover, both phases have the potential to be fabricated by using different precursors in different experimental conditions. As summarized in Table 1, the schematic of lattice constants (a) and monoclinic angles (θ) are shown in the top view of TMB12 monolayers in Figure 1a. For TM = V, Cr, Mn, and Fe, the lattice constants are 4.78 Å, 4.78 Å, 4.86 Å, and 4.81 Å, respectively, and the monoclinic angles are in the range of 81.76~83.95°. The TM-B bond lengths for the TMB12s are in the range of 1.97~2.35 Å, and the detailed structure parameters of TMB12 monolayers are listed in Table 1.
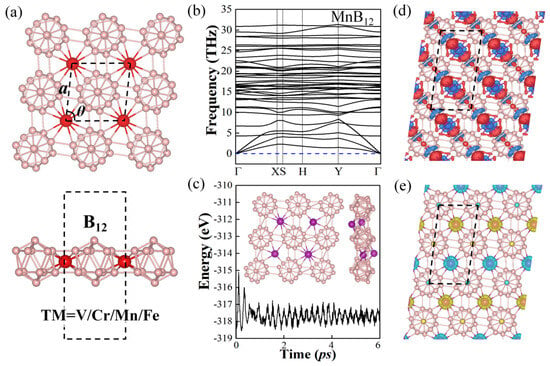
Figure 1.
(a) Top and side views of the TMB12 monolayer; the unit cell is marked by black dotted lines, and red and pink balls represent the TM atoms and B atoms, respectively. (b) Phonon spectrum of the MnB12 monolayer in the whole Brillouin zone. (c) Total energy profiles of the MnB12 monolayer and a snapshot of the MnB12 monolayer at the end of 6 ps with the temperature of 300 K. (d) Charge density difference and (e) spin density of the MnB12 monolayer. Red and blue colors in charge density differences denote electron accumulation and depletion, respectively. Light blue and yellow regions in the spin density plot represent spin-up and spin-down electrons, respectively.

Table 1.
The lattice constant (L, Å), monoclinic angle (θ, degree), TM-B bond length (dTM-B, Å), formation energy (Ef, eV), energy difference between the ground AFM state and the FM state (ΔE = EFM − EAFM, eV), local magnetic moment on TM atoms (LMM, μB), electrons transferred from TM atoms to B atoms (Δe, e), exchange integral (J1, J2, meV), and Néel temperatures (TN, K) for TMB12 monolayers (TM = V, Cr, Mn, and Fe).
To determine the stability of these TMB12 monolayers, phonon spectra and ab initio molecular dynamics (AIMD) calculation curves are calculated. As shown in the phonon dispersion spectra plot in Figure 1b and Figure S1a–c, there are no imaginary frequencies along the high symmetry points path in the whole Brillouin zone, indicating that all the TMB12 monolayers are dynamically stable. In addition, the thermodynamical stabilities of the TMB12 monolayers were evaluated using AIMD simulations. The total energy profiles of the TMB12 monolayer are shown in Figure 1c and Figure S1d–f, and the structures of these TMB12 monolayers at the end of 6 ps under 300 K are shown in the insets. It is clearly shown that all the TMB12 monolayers could retain their main framework, indicating that they are thermodynamically stable at room temperature. In addition, the formation energy () of the TMB12 monolayers are calculated using the following Equation (1):
where , , and are the energies of the TMB12 monolayer, the chemical potential of the B atom in the B12 icosahedron, and the chemical potential of the TM atom in its bulk, respectively, and n is the atom number in the unit cell. The values for TM = V, Cr, Mn, and Fe are −0.68, −0.63, −0.74, and −0.58 eV/atom, respectively, implying that the formation of the TMB12 monolayers is possible and energetically favorable. It is proposed that the TMB12 monolayer may be synthesized by reducing the dimension from bulk to 2D nanosheets [53,54] or by doping the TM atoms in 2D γ-boron film with a certain concentration by the chemical vapor deposition method [55].
The stability of the TMB12 monolayers can be explained by the electron transfer between the TM atoms and B12 icosahedra. The charge density difference (CDD) plots defined as are calculated and plotted in Figure 1d, where , , and are the electron densities of the TMB12 monolayer, the TM atom, and the B12 unit, respectively. It is shown that the red regions are distributed around the bonds between the B12 icosahedra and the TM atoms, as well as the area near the B atoms on top of the B12 icosahedra, while the blue-color regions are mainly around the TM atoms, suggesting that the electrons are depleted from the TM atoms and accumulated on the TM-B bonds and the B atoms of the B12 icosahedra, which indicates that the bonding in such complexes is the coexistence of ionic and covalent bonding. Moreover, the electrons transferred between the B12 icosahedra and the TM atoms are analyzed by calculating the Bader charge (see Table 1). It is found that about 1.05 e, 0.93 e, 0.93 e, and 0.66 e are transferred from the TM atoms to the B atoms at TM = V, Cr, Mn, and Fe, respectively, which is consist with the charge density difference results in Figure 1d.
To ascertain the magnetic ground state of the TMB12 monolayers, four different magnetic configurations, including one FM state and three AFM states, labeled AFM-1, AFM-2, and AFM-3, are considered, as displayed in Figure 2. (i) AFM-1 configuration: the TM atoms with opposite spins are arranged in a stripy distribution (Figure 2b); (ii) AFM-2 configuration: magnetization with up and down directions are in zigzag distribution (Figure 2c); (iii) AFM-3 configuration: two rows of TM with the same spins are in a stripy arrangement (Figure 2d). According to the energies of these magnetic configurations, it is shown that all the TMB12 monolayers favor an AFM ground state, namely, the VB12 monolayer has an AFM-2 ground state, which is 0.016 eV/u.c., 0.001 eV/u.c., and 0.011 eV/u.c. lower than those of FM, AFM-1, and AFM-3 states, respectively. The TMB12 monolayers with TM = Cr, Mn, and Fe have an AFM-1 ground state, which are lower than the FM, AFM-2, and AFM-3 states by about 0.019~0.086 eV/u.c., 0.001~0.046 eV/u.c., and 0.033~0.093 eV/u.c., respectively. Detailed energy information is summarized in Table S1 in SI. The spin density plots of the TMB12 monolayers with different AFM ground states are shown in Figure 1e and Figure S2. The distances of the TM-TM atoms are around 4.78 Å to 4.86 Å, which are much larger than the covalent radius, indicating that the direct exchange interactions are weak. By analyzing the orbital components and the bond angles of the TM-B-TM, it is shown that the antiferromagnetism of the TMB12 monolayers mainly arises from the super-exchange interaction, which comes from the p-d hybridization between the B-p orbitals and the TM-3d orbitals. According to the Goodenough–Kanamori–Anderson (GKA) rule [56,57,58], systems with TM-B-TM angles close to 90° favor an FM magnetic ordering. As shown in Figure S3 in Supplementary Materials, the two TM-B-TM bond angles are around 119.29–122.16° and 125.73–127.61°, which are much larger than 90°; therefore, antiferromagnetic ordering is preferred through a super-exchange interaction.
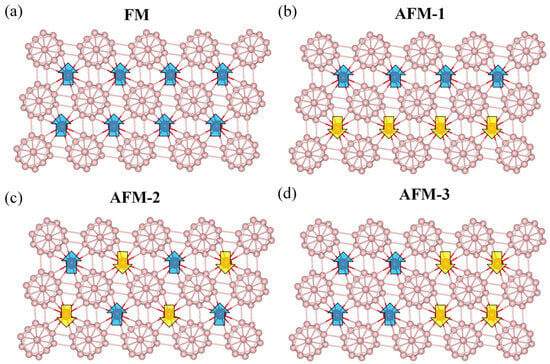
Figure 2.
Different magnetic configurations considered for TMB12 monolayers. (a) FM state, (b) AFM-1 state, (c) AFM-2 state, and (d) AFM-3 state. Blue and yellow arrows are spin-up and spin-down electrons, respectively.
The projected band structures of these TMB12 monolayers are plotted in Figure 3 and Figure S4. It is shown that the 2D VB12 monolayer and the MnB12 monolayer are AFM metals with bands crossing the Fermi level. The according projected density of states (PDOS) are also explored, as shown in Figure S4 in Supplementary Materials. For the VB12 monolayer, the states around the Fermi level are mainly contributed by the B-p and V-dz2 orbitals, while for the MnB12 monolayer, the contributions near the Fermi level are mainly from the B-p orbitals, and the Mn-dyz, dxz, and dxy orbitals also have a slight contribution. The CrB12 monolayer and the FeB12 monolayer are AFM semiconductors with band gaps of 0.13 eV and 0.35 eV, respectively. The projected density of states of the semiconducting CrB12 monolayer and the FeB12 monolayer are plotted in Figure 3b,d. It is indicated that for the CrB12 monolayer, the valence band maximum (VBM) is located in the Γ-X path, which is dominated by B-p orbitals, while the conduction band minimum (CBM) is located in the Γ-X path, which primarily comes from the hybridization of B-p, Cr-dxz, and Cr-dyz orbitals. As for the FeB12 monolayer (Figure 3d), the CBM located at the X/Y point is dominated by the hybridization of the B-p, Fe-dxy, and Fe-dyz orbitals, while the VBM located at the S-P/P-Q path comes from the B-p orbitals. The magnetic moments of these TMB12 monolayers are mainly contributed by the d orbitals of TM atoms, while a few are contributed by p orbitals of the B atoms. The local magnetic moments on the TM atoms are 2.05 μB, 3.18 μB, 3.86 μB, and 2.79 μB for TM = V, Cr, Mn, and Fe, respectively.
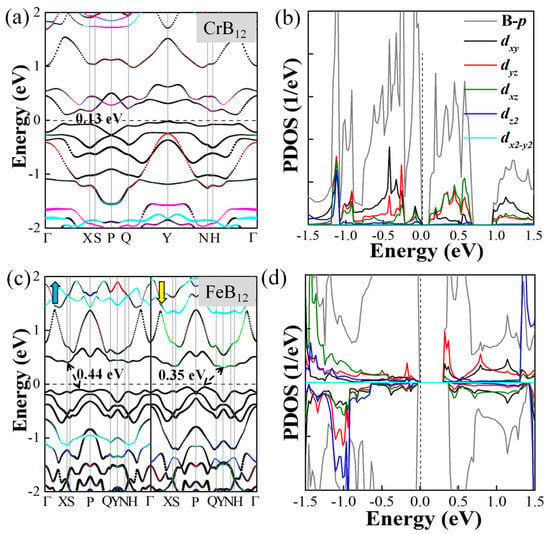
Figure 3.
Projected band structure and PDOS of the semiconducting CrB12 monolayer (a,b) and FeB12 monolayer (c,d), respectively. Black, red, green, blue, cyan, and magenta dotted lines are the B-p, TM-dxy, dyz, dxz, dz2, and dx2-y2 orbitals in the projected band structures, respectively. Blue and yellow arrows represent spin-up and spin-down channels, respectively.
The magnetic anisotropy energy (MAE) is an important parameter of 2D magnets in terms of thermal stability, which is defined as the larger energy difference between the out-of-plane z direction and in-plane x/y directions: MAE = |Ez − Ex/y|. By considering spin–orbit coupling (SOC) effects (the MAE values of the TMB12 monolayers are displayed in Figure 4b) it is shown that the easy magnetization axes of the VB12 monolayer, the CrB12 monolayer, and the MnB12 monolayer are in-plane and along the x direction, and their MAE values are 6.133 meV, 0.157 meV, and 0.054 meV, respectively. As for the FeB12 monolayer, the easy magnetization axis is out-of-plane and along the z direction with an MAE of 0.357 meV, which is highly desired for information storage. Furthermore, Monte Carlo (MC) simulations were performed to calculate the TN with the Hamiltonian based on the 2D Heisenberg model written as Equation (2):
where J1 and J2 are the nearest and the second-nearest exchange coupling parameters as shown in Figure 4a, and Si is the spin vector of TM atom on site i. Two exchange parameters (J1 and J2) are derived from the energy mapping results of different magnetic configurations as listed in Equation (3):
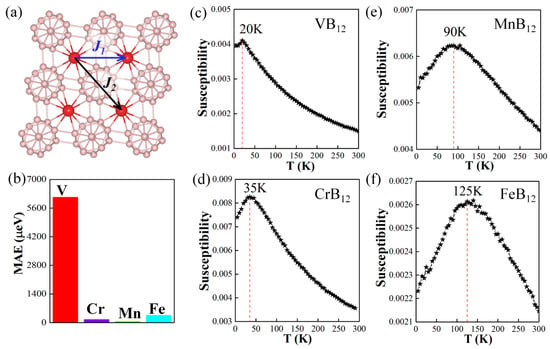
Figure 4.
(a) Schematic of magnetic configuration for estimating the exchange–interaction constants of TMB12 monolayers. J1 and J2 are the nearest and second-nearest exchange parameters, respectively. (b) The magnetic anisotropic energy (MAE) of the TMB12 monolayers. The susceptibility as a function of temperature for the VB12 monolayer (c), the CrB12 monolayer (d), the MnB12 monolayer (e), and the FeB12 monolayer (f).
The exchange parameters (J1 and J2) can be derived with Equation (4):
The calculated J1 and J2 values of the TMB12 monolayers according to the energies of different magnetic configurations are listed in Table 1. It is shown that all the J1 and J2 values are negative, indicating the AFM coupling between the TM atoms. The susceptibility as a function of temperature for TMB12 monolayers are shown in Figure 4c–f. The TNs can be obtained by locating the peak of the susceptibility, which are 20 K, 35 K, 90 K, and 135 K for the VB12 monolayer, the CrB12 monolayer, the MnB12 monolayer, and the FeB12 monolayer, respectively. Such magnetic transition temperatures are comparable with the reported Cr2B12 (145 K) and Mn2B12 (135 K) monolayers [51]. On the other hand, we should state that the magnetic transition temperatures of the predicted systems are much lower than room temperature, which blocks their applications in spintronic devices.
Next, the effects of biaxial strains from −5% to +5% on the electronic and magnetic properties of the semiconducting CrB12 monolayer and the FeB12 monolayer are investigated. The strain intensity is defined as ε = (a − a0)/a0, where a0 and a are the lattice constant before and after imposing biaxial strains. It is proposed that such strains with a uniform strain gradient may be imposed on the TMB12 monolayers by applying a displacement-controlled stretch to the monolayers that can be shaped by focused ion beams (FIB) in experiments. [59] The energy difference (ΔE = EFM − EAFM) between the FM and the lowest-energy AFM state as a function of strain intensity are shown in Figure 5a. It is shown that the CrB12 monolayer and the FeB12 monolayer retain the AFM-1 ground states under biaxial compressive strains, which are transformed to FM ground states when the biaxial tensile strains are up to 3% and 1%, respectively. The band structures of the CrB12 monolayer and the FeB12 monolayer under biaxial strains are shown in Figures S5 and S6 in Supplementary Materials. It is shown that for the CrB12 monolayer, it is turned metallic under tensile strains; that is, it is maintained as an AFM-1 metal under 1% and 2% biaxial tensile strains, but turned to an FM half metal under larger (3~5%) tensile strains with the spin band gap of 0.49 eV, 0.60 eV, and 0.69 eV for ε = 3%, 4%, and 5% (Figure S5c–e in Supplementary Materials), respectively. When exerting biaxial compressive strains, the CrB12 monolayer retains the AFM-1 semiconductor property till −4%, with the band gap decreasing with the increasing of the biaxial compressive strains, as shown in Figure 5b and Figure S5f–i. Under −5% biaxial compressive strain, the CrB12 monolayer is transformed into an AFM metal (Figure S5j in Supplementary Materials). As shown in Figure S6 in Supplementary Materials, the semiconducting FeB12 monolayer transforms into an FM metal under biaxial tensile strain within 4%, and it turns into an FM half metal under 5% tensile strain. When biaxial compressive strains are imposed, it maintains the AFM-1 semiconductor properties, in which the band gap decreases with the increasing of compressive strain as shown in Figure 5b. Moreover, the influence of the magnetic transition temperature of the CrB12 and FeB12 monolayers under biaxial strains is explored. As shown in Figure 5c,d, Figures S7 and S8, the TC of the FM CrB12 monolayer increases with the increasing of the tensile strain from 3% to 5%, and the TN of the AFM CrB12 monolayer increases with the increasing of the compressive strain from −2% to −5%. There is a sharp increase in TN at the −2% compressive strain, which is due to the large variation in J2 as shown in Figure 5e. For the FeB12 monolayer, the TC of the FM FeB12 monolayer decreases with the increasing of the tensile strains, in which the J1 and J2 values are positive. The TN for the AFM semiconductors or metal are oscillating in the range of 75–120 K, which is due to the different changing trends in J1 and J2 as shown in Figure 5f.
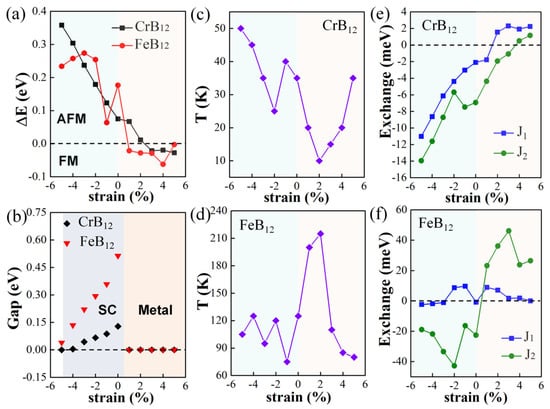
Figure 5.
(a) The energy difference between FM and AFM state, ΔE = EFM − EAFM; (b) Band gap of CrB12 monolayer and FeB12 monolayer under biaxial strains; SC represents semiconductor. (c) The variation in magnetic transition temperature (TC for FM configuration/TN for AFM configuration) under biaxial strains for CrB12 monolayer (c) and FeB12 monolayer (d). The exchange parameters J1 and J2 as a function of biaxial strain intensity for the CrB12 monolayer (e) and FeB12 (f) monolayer.
3. Materials and Methods
All the first-principles calculations were performed within the Vienna Ab-initio Simulation Package (VASP) [60,61] with projector-augmented wave (PAW) potentials [62]. The exchange–correlation interaction is described by the general gradient approximation of the Perdew–Burke–Ernzerholf (PBE) functional [63], where the generalized gradient approximation (GGA) was employed. The energy cutoff for the plane–wave basis set was set to 500 eV, and the vacuum spaces were larger than 15 Å to eliminate the physical interactions caused by periodic boundary conditions. For transition metal atoms V, Cr, Mn, and Fe, a GGA + U method with Ueff = 4.0 eV was adopted to treat the Coulomb and exchange interactions of the 3d-electron according to previous studies [38,51,64,65]. The k mesh was set as 9 × 9 × 1, 5 × 9 × 1, and 5 × 5 × 1 for FM, AFM-1, and AFM-2 geometry optimization, and a denser k-mesh of 27 × 27 × 1, 15 × 27 × 1, and 15 × 15 × 1 was adopted for electronic structure calculations. Conjugated gradient (CG) atomic optimization was performed with a criterion of convergence for energy and atom force set to 10-5 eV and 0.01 eV/Å, respectively. During the optimization, both the cell shape and the position of the atoms was fully relaxed. The Néel temperature (TN) and the Curie temperature (TC) of the TMB12 monolayers were calculated by using the EspinS package, [66] in which 20 × 20 ×1 lattices were adopted in the Monte Carlo (MC) simulations, and the spins randomly rotated in the space. Phonon dispersions were calculated using 2 × 2 × 1 supercells to reduce the lattice translational constraints using the Phonopy code on the basis of DFPT [67] to identify the dynamic stability, with the threshold for the convergence on energy and force selected as 10−8 eV and 10−4 eV/Å. The ab initio molecular dynamics (AIMD) simulations in the NVT ensemble were employed to evaluate the thermal stability using 2 × 2 × 1 supercells with a temperature of 300 K for 6 ps using a Nose–Hoover thermostat method [68].
4. Conclusions
In summary, we predicted a type of 2D transition metal boride, TMB12 (TM = V, Cr, Mn, and Fe) monolayers consisting of transition metal atoms and B12 icosahedras, using first-principles calculations. Our results show that all the TMB12 monolayers are stable antiferromagnets with large magnetic anisotropy, and the Néel temperatures for the TMB12 monolayers range from 20 K to 125 K. Specifically, the CrB12 monolayer and the FeB12 monolayer are antiferromagnetic semiconductors with band gaps of 0.13 eV and 0.35 eV, respectively. In addition, the electronic and magnetic properties of the semiconducting CrB12 monolayer and the FeB12 monolayer could be effectively modulated by exerting biaxial strains due to the variation in exchange parameters. In particular, the FeB12 monolayer is a spin-polarized antiferromagnet with a Néel temperature of 125 K. By imposing tensile strains, the FeB12 monolayer can be altered to be an FM metal with a magnetic transition temperature of up to 210 K. Our findings provide a way to design candidates that are flexible for electronic and spintronic applications.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28247945/s1. Figure S1: Phonon spectrum and AIMD simulations of VB12, CrB12, and FeB12 monolayers; Table S1: The energies of TMB12 monolayers with FM, AFM-1, AFM-2, and AFM-3 configurations; Figure S2: Spin densities of TMB12 monolayers; Figure S3: TM-B-TM bond angles of TMB12 monolayers; Figure S4: Projected band structure and PDOS of metallic VB12 monolayer and MnB12 monolayer; Figure S5: Band structures of CrB12 monolayer under biaxial tensile and compressive strains within 5%; Figure S6: Band structures of FeB12 monolayer under biaxial tensile and compressive strains within 5%; Figure S7: The susceptibility as a function of temperature for CrB12 monolayer under biaxial tensile and compressive strains within 5%; Figure S8: The susceptibility as a function of temperature for FeB12 monolayer under biaxial tensile and compressive strains within 5%.
Author Contributions
Conceptualization and data curation: H.Z.; Formal analysis and writing—original draft: N.G.; Investigation: Z.W.; Validation: Y.X.; Software: X.Z. (Xiangfei Zhu); Validation: S.W.; Formal analysis and supervision: X.Y.; Writing—review and editing: Y.L.; Supervision and project administration: X.Z. (Xiuyun Zhang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (12004098), the Six Talent Peaks Project in Jiangsu Province (XCL-104), Innovation technology platform project (YZ2020268), jointly built by Yangzhou City and Yangzhou University, and the open research fund of Key Laboratory of Quantum Materials and Devices (Southeast University), Ministry of Education.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank the computational resources at Yangzhou University and Hebei Normal University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Awschalom, D.D.; Flatté, M.E. Challenges for semiconductor spintronics. Nat. Phys. 2007, 3, 153–159. [Google Scholar] [CrossRef]
- Ashton, M.; Gluhovic, D.; Sinnott, S.B.; Guo, J.; Stewart, D.A.; Hennig, R.G. Two-dimensional intrinsic half-metals with large spin gaps. Nano Lett. 2017, 17, 5251–5257. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, Q.; Xing, J.; Liu, N.; Guo, Y.; Liu, Z.; Zhao, J. Recent progress on 2D magnets: Fundamental mechanism, structural design, and modification. Appl. Phys. Rev. 2021, 8, 031305. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, B.; Zhang, X.; Yuan, S.; Ma, L.; Wang, J. Magnetic Two-Dimensional Layered Crystals Meet with Ferromagnetic Semiconductors. InfoMat 2020, 2, 639–655. [Google Scholar] [CrossRef]
- Zhong, D.; Seyler, K.L.; Linpeng, X.Y.; Cheng, R.; Sivadas, N.; Huang, B.; Schmidgall, E.; Taniguchi, T.; Watanabe, K.; McGuire, M.A. Van Der Waals Engineering of Ferromagnetic Semiconductor Heterostructures for Spin and Valleytronics. Sci. Adv. 2017, 3, e1603113. [Google Scholar] [CrossRef]
- Han, W. Perspectives for Spintronics in 2D Materials. APL Mater. 2016, 4, 032401. [Google Scholar] [CrossRef]
- Hirohata, A.; Yamada, K.; Nakatani, Y.; Prejbeanu, I.-L.; Dieny, B.; Pirro, P.; Hillebrands, B. Review on Spintronics: Principles and Device Applications. J. Magn. Magn. Mater. 2020, 509, 166711. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, C.; Zhong, J.; Ding, J.; Wang, Z.M.; Liu, Z. Spintronics in Two-Dimensional Materials. Nanomicro Lett. 2020, 12, 93. [Google Scholar] [CrossRef]
- Geim, A.; Novoselov, K. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Meng, L.; Wang, Y.; Zhang, L.; Du, S.; Wu, R.; Li, L.; Zhang, Y.; Li, G.; Zhou, H.; Hofer, W.A.; et al. Buckled Silicene Formation on Ir(111). Nano Lett. 2013, 13, 685–690. [Google Scholar] [CrossRef]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tománek, D.; Ye, P.D. Phosphorene: An Unexplored 2D Semiconductor with a High Hole Mobility. ACS Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef]
- Gong, C.; Li, L.; Li, Z.L.; Ji, H.W.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.Z.; Wang, Y.; et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef]
- Cai, X.; Song, T.; Wilson, N.P.; Clark, G.; He, M.; Zhang, X.; Taniguchi, T.; Watanabe, K.; Yao, W.; Xiao, D.; et al. Atomically thin CrCl3: An in-plane layered antiferromagnetic insulator. Nano Lett. 2019, 19, 3993–3998. [Google Scholar] [CrossRef]
- Zhang, Z.; Shang, J.; Jiang, C.; Rasmita, A.; Gao, W.; Yu, T. Direct photoluminescence probingof ferromagnetism in monolayer two-dimensional CrBr3. Nano Lett. 2019, 19, 3138–3142. [Google Scholar] [CrossRef]
- Li, P.; Wang, C.; Zhang, J.; Chen, S.; Guo, D.; Ji, W.; Zhong, D. Single-layer CrI3 grown by molecular beam epitaxy. Sci. Bull. 2020, 65, 1064–1071. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, B.; Ma, C.; Yang, Z. Bipolar ferromagnetic semiconductors and doping-tuned room-temperature half-metallicity in monolayer MoX3(X=Cl, Br, I): An HSE06 study. Phys. Rev. B 2021, 103, 075433. [Google Scholar] [CrossRef]
- Kulish, V.V.; Huang, W. Single-layer metal halides MX2 (X = Cl, Br, I): Stability and tunable magnetism from first principles and Monte Carlo simulations. J. Mater. Chem. C 2017, 5, 8734–8741. [Google Scholar] [CrossRef]
- Bonilla, M.; Kolekar, S.; Ma, Y.; Diaz, H.C.; Kalappattil, V.; Das, R.; Eggers, T.; Gutierrez, H.R.; Phan, M.-H.; Batzill, M. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat. Nanotechnol. 2018, 13, 289–293. [Google Scholar] [CrossRef]
- Liu, M.; Huang, Y.L.; Gou, J.; Liang, Q.; Chua, R.; Arramel, S.; Duan, L.; Zhang, L.; Cai, X.; Yu, D.; et al. Diverse Structures and Magnetic Properties in Nonlayered Monolayer Chromium Selenide. J. Phys. Chem. Lett. 2021, 12, 7752–7760. [Google Scholar] [CrossRef]
- Fei, Z.; Huang, B.; Malinowski, P.; Wang, W.; Song, T.; Sanchez, J.; Yao, W.; Xiao, D.; Zhu, X.; May, A.F.; et al. Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater. 2018, 17, 778–782. [Google Scholar] [CrossRef]
- Deng, Y.; Yu, Y.; Song, Y.; Zhang, J.; Wang, N.Z.; Sun, Z.; Yi, Y.; Wu, Y.Z.; Wu, S.; Zhu, J.; et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 2018, 563, 94–99. [Google Scholar] [CrossRef]
- Zhang, L.; Song, L.; Dai, H.; Yuan, J.-H.; Wang, M.; Huang, X.; Qiao, L.; Cheng, H.; Wang, X.; Ren, W.; et al. Substrate-modulated ferromagnetism of two-dimensional Fe3GeTe2. Appl. Phys. Lett. 2020, 116, 042402. [Google Scholar] [CrossRef]
- Wang, X.; Du, K.; Liu, Y.Y.F.; Hu, P.; Zhang, J.; Zhang, Q.; Owen, M.H.S.; Lu, X.; Gan, C.K.; Sengupta, P.; et al. Raman spectroscopy of atomically thin two-dimensional magnetic iron phosphorus trisulfifide (FePS3) crystals. 2D Mater. 2016, 3, 031009. [Google Scholar] [CrossRef]
- Kim, K.; Lim, S.Y.; Kim, J.; Lee, J.-U.; Lee, S.; Kim, P.; Park, K.; Son, S.; Park, C.-H.; Park, J.-G.; et al. Antiferromagnetic ordering in van der Waals 2D magnetic material MnPS3 probed by Raman spectroscopy. 2D Mater. 2019, 6, 041001. [Google Scholar] [CrossRef]
- Chen, X.; Qi, J.; Shi, D. Strain-engineering of magnetic coupling in two-dimensional magnetic semiconductor CrSiTe3: Competition of direct exchange interaction and superexchange interaction. Phys. Lett. A 2015, 379, 60. [Google Scholar] [CrossRef]
- Chittari, B.L.; Lee, D.; Banerjee, N.; MacDonald, A.H.; Hwang, E.; Jung, J. Carrier- and strain-tunable intrinsic magnetism in two-dimensional MAX3 transition metal chalcogenides. Phys. Rev. B 2020, 101, 085415. [Google Scholar] [CrossRef]
- Zhuang, H.L.; Xie, Y.; Kent, P.R.C.; Ganesh, P. Computational discovery of ferromagnetic semiconducting single-layer CrSnTe3. Phys. Rev. B 2015, 92, 035407. [Google Scholar] [CrossRef]
- Yu, M.; Liu, X.; Guo, W. Novel two-dimensional ferromagnetic semiconductors: Ga-based transition-metal trichalcogenide monolayers. Phys. Chem. Chem. Phys. 2018, 20, 6374–6382. [Google Scholar] [CrossRef]
- Wu, D.; Zhuo, Z.; Lv, H.; Wu, X. Two-Dimensional Cr2X3S3 (X=Br, I) Janus Semiconductor with Intrinsic Room-Temperature Magnetism. J. Phys. Chem. Lett. 2021, 12, 2905–2911. [Google Scholar] [CrossRef]
- Rizzo, D.J.; McLeod, A.S.; Carnahan, C.; Telford, E.J.; Dismukes, A.H.; Wiscons, R.A.; Dong, Y.; Nuckolls, C.; Dean, C.R.; Pasupathy, A.N.; et al. Visualizing Atomically Layered Magnetism in CrSBr. Adv. Mater. 2022, 34, 2201000. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Y.; Bai, Y.; Shi, P.; Zhang, G.; Zhang, Y.; Liu, C. Origin and regulation of triaxial magnetic anisotropy in the ferromagnetic semiconductor CrSBr monolayer. Nanoscale 2023, 15, 13402–13410. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, Y.; Jia, C.; Hou, L.; Wang, B. Two-dimensional 4f magnetic EuSn2X2 (X=P, As) monolayers: A first-principles study. Appl. Phys. Lett. 2023, 123, 012401. [Google Scholar] [CrossRef]
- Du, W.; Dou, K.; He, Z.; Dai, Y.; Huang, B.; Ma, Y. Spontaneous Magnetic Skyrmions in Single-Layer CrInX3 (X = Te, Se). Nano Lett. 2022, 22, 3440–3446. [Google Scholar] [CrossRef]
- Pang, K.; Xu, X.; Ku, R.; Wei, Y.; Ying, T.; Li, W.; Yang, J.; Li, X.; Jiang, Y. Ferroelectricity and High Curie Temperature in a 2D Janus Magnet. ACS Appl. Mater. Interfaces 2023, 15, 10133–10140. [Google Scholar] [CrossRef]
- Jungwirth, T.; Marti, X.; Wadley, P.; Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 2016, 11, 231–241. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, P.; Jiang, X.; Zhao, J. MBene (MnB): A new type of 2D metallic ferromagnet with high Curie temperature. Nanoscale Horiz. 2018, 3, 335–341. [Google Scholar] [CrossRef]
- Liu, C.; Fu, B.; Yin, H.; Zhang, G.; Dong, C. Strain-tunable magnetism and nodal loops in monolayer MnB. Appl. Phys. Lett. 2020, 117, 103101. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Hou, J.; Du, A.; Chen, Z. Dirac State in the FeB2 Monolayer with Graphene-Like Boron Sheet. Nano Lett. 2016, 16, 6124–6129. [Google Scholar] [CrossRef]
- Yao, X.; Wang, L.; Sun, Y.; Li, X.; Sun, J.; Wang, B.; He, M.; Zhang, X. Two-dimensional transition metal triborides: Monolayers with robust intrinsic magnetism and high spin stability. Phys. Rev. B 2022, 105, 214421. [Google Scholar] [CrossRef]
- Qu, X.; Yang, J.; Wang, Y.; Lv, J.; Chen, Z.; Ma, Y. A two-dimensional TiB4 monolayer exhibits planar octacoordinate Ti. Nanoscale 2017, 9, 17983–17990. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Hou, J.; Tu, K.; Chen, Z. FeBMonolayers: The Graphene-like Material with Hypercoordinate Transition Metal. J. Am. Chem. Soc. 2016, 138, 5644–5651. [Google Scholar] [CrossRef]
- Wang, S.; Khazaei, M.; Wang, J.; Hosono, H. Hypercoordinate two-dimensional transition-metal borides for spintronics and catalyst applications. J. Mater. Chem. C 2021, 9, 9212–9221. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, H.; Wang, C.; Zhang, M.; Geng, Y.; Li, Q.; Su, Z. All Boron Atoms in a ScB12 Monolayer Contribute to the Hydrogen Evolution Reaction. J. Phys. Chem. C 2020, 124, 23221–23229. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Wang, Z.F.; Du, S.X.; Gao, H.-J.; Liu, F. Prediction of a Dirac state in monolayer TiB2. Phys. Rev. B 2014, 90, 161402. [Google Scholar] [CrossRef]
- Lopez-Bezanilla, A. Interplay between p- and d- orbitals yields multiple Dirac states in one- and two-dimensional CrB4. 2D Mater. 2018, 5, 035041. [Google Scholar] [CrossRef]
- Wang, J.; Khazaei, M.; Arai, M.; Umezawa, N.; Tada, T.; Hosono, H. Semimetallic Two-Dimensional TiB12: Improved Stability and Electronic Properties Tunable by Biaxial Strain. Chem. Mater. 2017, 29, 5922–5930. [Google Scholar] [CrossRef]
- Ozdemir, I.; Kadioglu, Y.; Yüksel, Y.; Akıncı, Ü.; Aktürk, O.Ü.; Aktürk, E.; Ciraci, S. Columnar antiferromagnetic order of a MBene monolayer. Phys. Rev. B 2021, 103, 144424. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, L.; Li, X.; Yao, X.; Xu, X.; Guo, T.; He, A.; Wang, B.; Liu, Y.; Zhang, X. TM2B3 monolayers: Intrinsic anti-ferromagnetism and Dirac nodal line semimetal. Appl. Phys. Lett. 2022, 121, 183103. [Google Scholar] [CrossRef]
- Yao, X.; Zhang, X. TM2B6: A newly designed ferromagnetic 2D metal-boride with a high Curie temperature. J. Mater. Chem. C 2020, 8, 14805–14811. [Google Scholar] [CrossRef]
- Yao, X.; Wang, L.; Sun, Y.; Lu, J.; Zhang, X. Designed two dimensional transition metal borides (TM2B12): Robust ferromagnetic half metal and antiferromagnetic semiconductor. Appl. Phys. Lett. 2023, 122, 193103. [Google Scholar] [CrossRef]
- Wu, F.; Yao, X.; Liu, Y.; Zhu, X.; Lu, J.; Zhou, W. and Zhang, X. TMB12: A newly designed 2D transition-metal boride for spintronics and electrochemical catalyst applications. Nanoscale 2023, 15, 2079–2086. [Google Scholar] [CrossRef]
- Puthirath Balan, A.; Radhakrishnan, S.; Woellner, C.F.; Sinha, S.K.; Deng, L.; Reyes, C.D.L.; Rao, B.M.; Paulose, M.; Neupane, R.; Apte, A.; et al. Exfoliation of a non-van der Waals material from iron ore hematite. Nat. Nanotechnol. 2018, 13, 602–609. [Google Scholar] [CrossRef]
- Puthirath Balan, A.; Radhakrishnan, S.; Kumar, R.; Neupane, R.; Sinha, S.K.; Deng, L.; de los Reyes, C.A.; Apte, A.; Rao, B.M.; Paulose, M.; et al. A Non-van der Waals Two-Dimensional Material from Natural Titanium Mineral Ore Ilmenite. Chem. Mater. 2018, 30, 5923–5931. [Google Scholar] [CrossRef]
- Tai, G.; Hu, T.; Zhou, Y.; Wang, X.; Kong, J.; Zeng, T.; You, Y. and Wang, Q. Synthesis of Atomically Thin Boron Films on Copper Foils. Angew. Chem. 2015, 127, 15693–15697. [Google Scholar] [CrossRef]
- Goodenough, J.B. Theory of the Role of Covalence in the Perovskite-Type Manganites [La, M(II)]MnO3. Phys. Rev. 1955, 100, 564–573. [Google Scholar] [CrossRef]
- Kanamori, J. Crystal distortion in magnetic compounds. J. Appl. Phys. 1960, 31, S14–S23. [Google Scholar] [CrossRef]
- Anderson, P.W. New approach to the theory of superexchange interactions. Phys. Rev. 1959, 115, 2–13. [Google Scholar] [CrossRef]
- Cao, K.; Feng, S.; Han, Y.; Gao, L.; Ly, T.H.; Xu, Z. and Lu, Y. Elastic straining of free-standing monolayer graphene. Nat. Commun. 2019, 10, 2284. [Google Scholar]
- Kresse, G.; Furthmuller, J. Effificiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initiomolecular dynamics for openshell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Islam, M.F.; Canali, C.M. Systematics of electronic and magnetic properties in the transition metal doped Sb2Te3 quantum anomalous Hall platform. Phys. Rev. B 2018, 97, 155429. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, J.; Li, R.; Zhang, C.; Zhang, H.; Han, P.; Fan, C. DFT+U predictions: Structural stability, electronic and optical properties, oxidation activity of BiOCl photocatalysts with 3d transition metals doping. J. Mater. Sci. 2018, 53, 4494–4506. [Google Scholar] [CrossRef]
- Rezaei, N.; Alaei, M.; Akbarzadeh, H. ESpinS: A program for classical Monte-Carlo simulations of spin systems. Comput. Mater. Sci. 2022, 202, 110947. [Google Scholar] [CrossRef]
- Baroni, S.; Gironcoli, S.D.; Corso, A.D. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Martyna, G.J.; Klein, M.L.; Tuckerman, M. Nosé-Hoover chains: The canonical ensemble via continuous dynamics. J. Chem. Phys. 1992, 97, 2635–2643. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).