Temperature-Dependent Kinetic Study of the Reactions of Hydrogen Atoms with H2S and C2H4S
Abstract
:1. Introduction
2. Results and Discussion
2.1. Reaction H + H2S
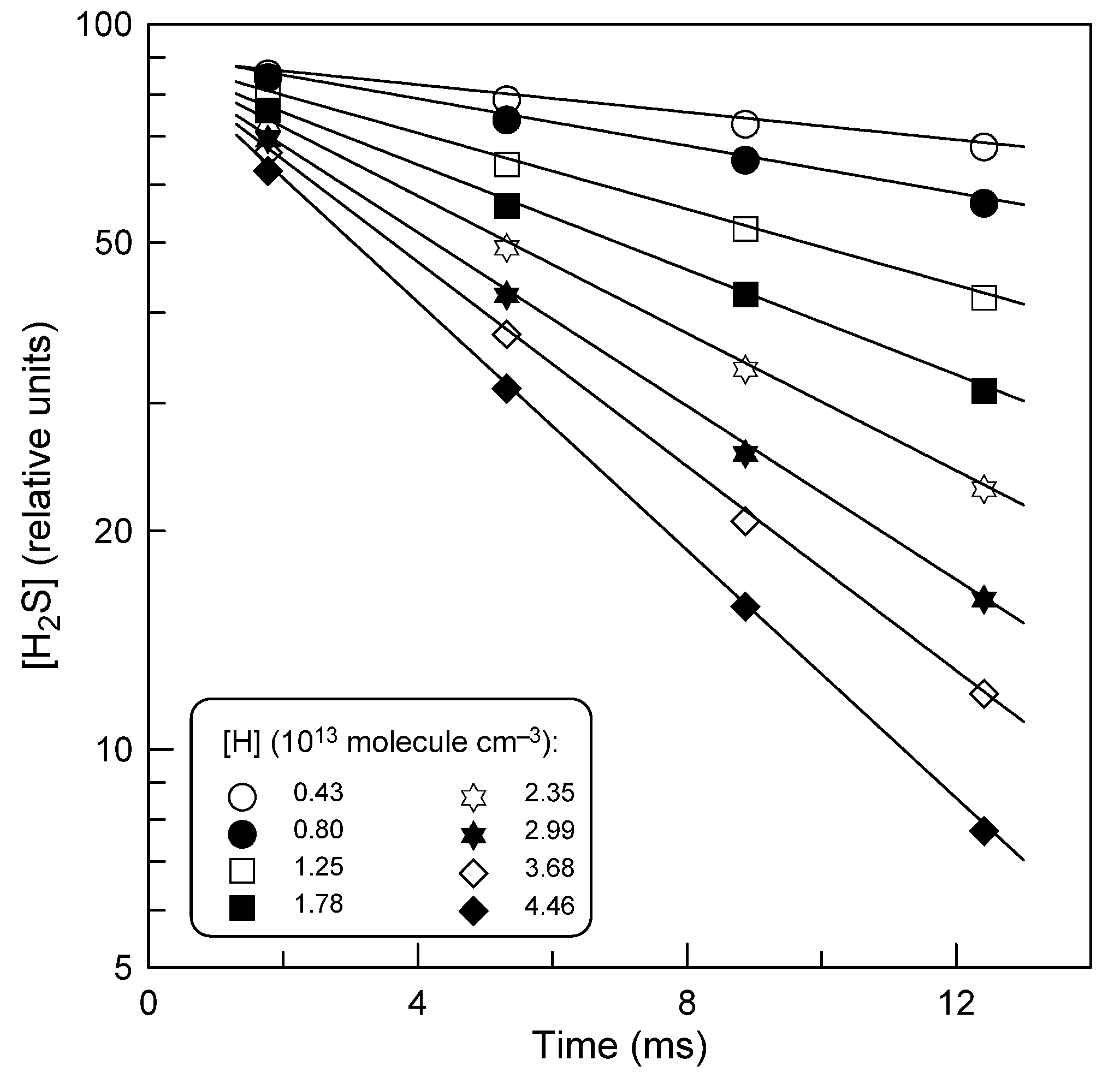
2.1.1. Measurements of the Reaction Rate Constant
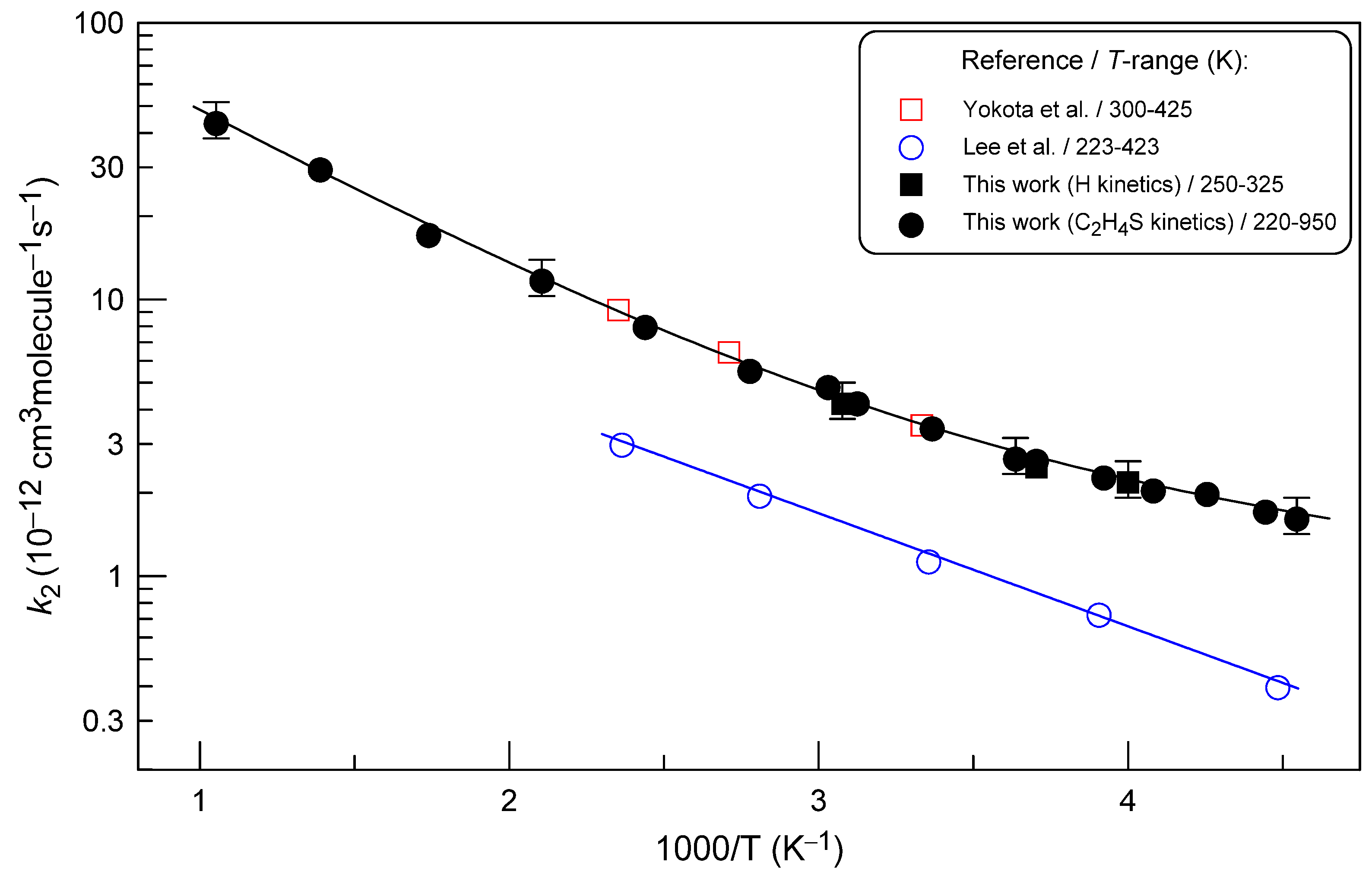
2.1.2. Comparison with Previous Data
2.2. Reaction H + C2H4S
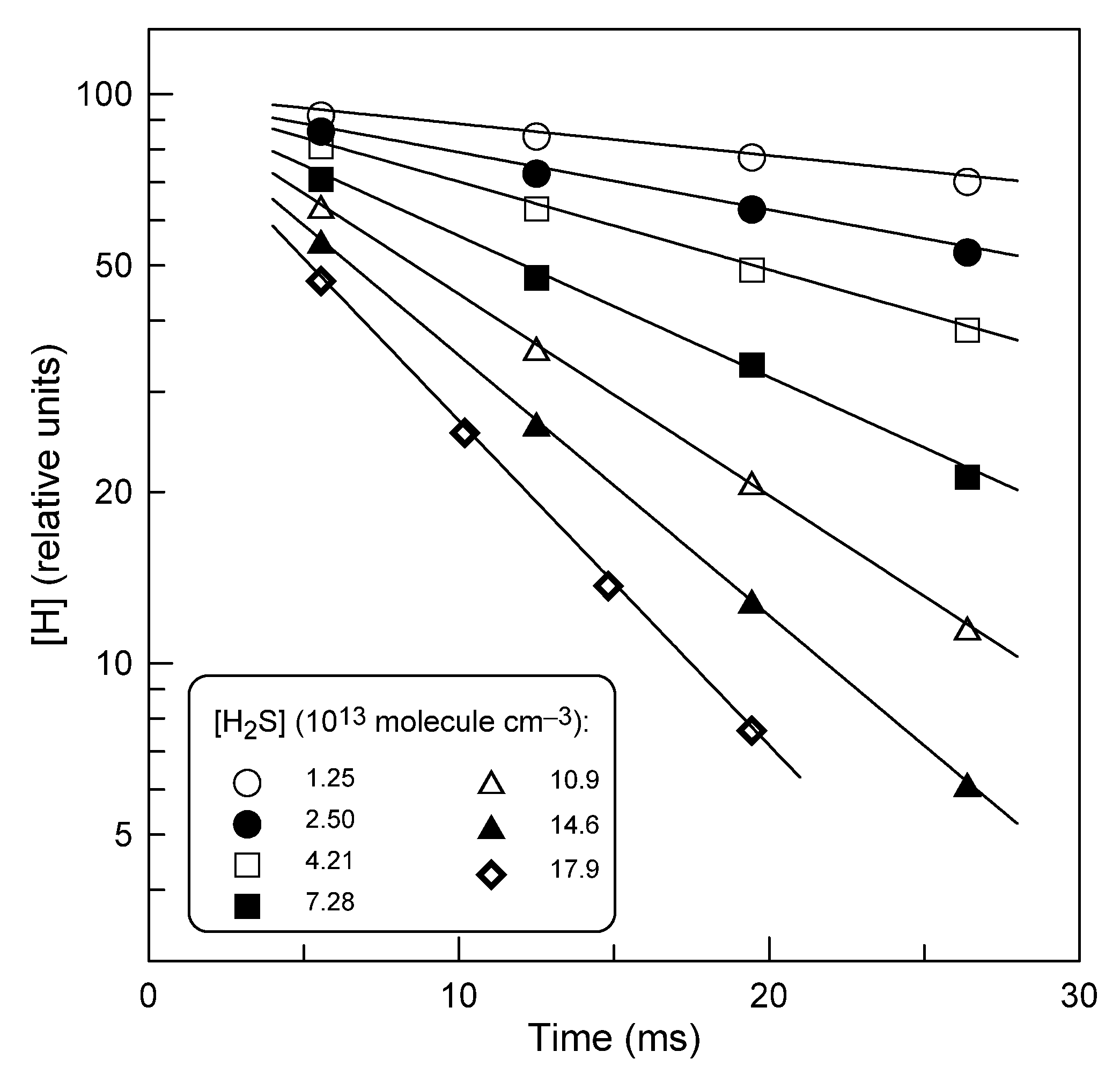
2.2.1. Measurements of the Reaction Rate Constant
2.2.2. Comparison with Previous Data
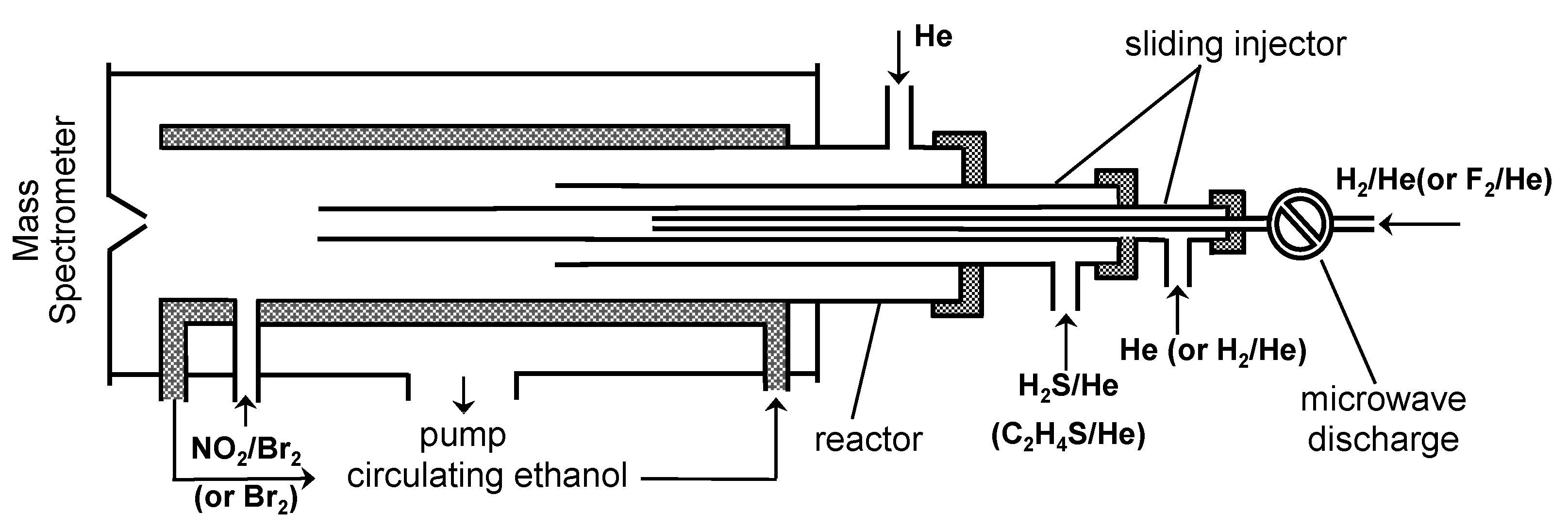
3. Materials and Methods
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sendt, K.; Jazbec, M.; Haynes, B.S. Chemical kinetic modeling of the H/S system: H2S thermolysis and H2 sulfidation. Proc. Combust. Inst. 2002, 29, 2439–2446. [Google Scholar] [CrossRef]
- Qi, J.; Lu, D.; Song, H.; Li, J.; Yang, M. Quantum and quasiclassical dynamics of the multi-channel H + H2S reaction. J. Chem. Phys. 2017, 146, 124303. [Google Scholar] [CrossRef]
- Lamberts, T.; Kästner, J. Tunneling Reaction Kinetics for the Hydrogen Abstraction Reaction H + H2S → H2 + HS in the Interstellar Medium. J. Phys. Chem. A 2017, 121, 9736–9741. [Google Scholar] [CrossRef]
- Cupitt, L.T.; Glass, G.P. Reaction of atomic oxygen with hydrogen sulphide. Trans. Faraday Soc. 1970, 66, 3007–3015. [Google Scholar] [CrossRef]
- Mihelcic, D.; Schindler, R.N. ESR-spektroskopische Untersuchung der Reaktion von atomarem Wasserstoff mit H2S. Ber. Bunsenges. Phys. Chem. 1970, 74, 1280–1288. [Google Scholar] [CrossRef]
- Kurylo, M.J.; Peterson, N.C.; Braun, W. Absolute Rate of the Reaction H+H2S. J. Chem. Phys. 1971, 54, 943–946. [Google Scholar] [CrossRef]
- Rommel, H.; Schiff, H.I. The Reactions of H Atoms with H2S and COS. Int. J. Chem. Kinet. 1972, 4, 547–558. [Google Scholar] [CrossRef]
- Bradley, J.N.; Trueman, S.P.; Whytock, D.A.; Zaleski, T.A. Electron spin resonance study of the reaction of hydrogen atoms with hydrogen sulphide. J. Chem. Soc. Faraday Trans. 1 1973, 69, 416–425. [Google Scholar] [CrossRef]
- Pratt, G.; Rogers, D. Homogeneous isotope exchange reactions. Part 3.—H2S + D2. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1977, 73, 54–61. [Google Scholar] [CrossRef]
- Nicholas, J.E.; Amodio, C.A.; Baker, M.J. Kinetics and mechanism of the decomposition of H2S, CH3SH and (CH3)2S in a radio-frequency pulse discharge. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1979, 75, 1868–1875. [Google Scholar] [CrossRef]
- Husain, D.; Slater, N.K.H. Kinetic study of the reactions of hydrogen and deuterium atoms with HBr and DBr by time-resolved resonance fluorescence. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. Mol. Chem. Phys. 1980, 76, 276–285. [Google Scholar] [CrossRef]
- Clyne, M.A.A.; Ono, Y. Determination of the rate constant of reaction of ground-state CI and H atoms with H2S using resonance fluorescence in a discharge flow. Chem. Phys. Lett. 1983, 94, 597–602. [Google Scholar] [CrossRef]
- Yoshimura, M.; Koshi, M.; Matsui, H.; Kamiya, K.; Umeyama, H. Non-Arrhenius temperature dependence of the rate constant for the H + H2S reaction. Chem. Phys. Lett. 1992, 189, 199–204. [Google Scholar] [CrossRef]
- Woiki, D.; Roth, P. A Shock Tube Study of the Reactions of H Atoms with COS, CS2, and H2S. Isr. J. Chem. 1996, 36, 279–283. [Google Scholar] [CrossRef]
- Peng, J.; Hu, X.; Marshall, P. Experimental and ab Initio Investigations of the Kinetics of the Reaction of H Atoms with H2S. J. Phys. Chem. A 1999, 103, 5307–5311. [Google Scholar] [CrossRef]
- Kurosaki, Y.; Takayanagi, T. Theoretical study of the non-Arrhenius temperature dependence of thermal rate constants for the H+H2S → H2+SH reaction. J. Chem. Phys. 1999, 111, 10529–10536. [Google Scholar] [CrossRef]
- Bedjanian, Y. Rate constant and products of the reaction of O(3P) atoms with thiirane over the temperature range 220–950 K. Int. J. Chem. Kinet. 2022, 54, 552–558. [Google Scholar] [CrossRef]
- Murrells, T.P. Elementary reactions of the SCl radical. Part1.—Rate constants and mechanisms of the reaction Cl + C2H4S → SCl + C2H4, SCl + SCl → products and SCl + Cl2 → SCl2+ Cl. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1988, 84, 67–83. [Google Scholar] [CrossRef]
- Van Roodselaar, A.; Safarik, I.; Strausz, O.P. The reactions of S(3PJ) atoms with thiiranes. Int. J. Chem. Kinet. 1984, 16, 899–907. [Google Scholar] [CrossRef]
- Lee, J.H.; Stief, L.J.; Timmons, R.B. Absolute rate parameters for the reaction of atomic hydrogen with carbonyl sulfide and ethylene episulfide. J. Chem. Phys. 1977, 67, 1705–1709. [Google Scholar] [CrossRef]
- Hynes, A.J.; Wine, P.H. Kinetics and Mechanisms of the Oxidation of Gaseous Sulfur Compounds. In Gas-Phase Combustion Chemistry; Gardiner, W.C., Ed.; Springer: New York, NY, USA, 2000; pp. 343–388. [Google Scholar]
- Tyndall, G.S.; Ravishankara, A.R. Atmospheric oxidation of reduced sulfur species. Int. J. Chem. Kinet. 1991, 23, 483–527. [Google Scholar] [CrossRef]
- Bedjanian, Y. Rate Coefficients of the Reactions of Fluorine Atoms with H2S and SH over the Temperature Range 220–960 K. Molecules 2022, 27, 8365. [Google Scholar] [CrossRef]
- Yokota, T.; Ahmed, M.G.; Safarik, I.; Strausz, O.P.; Gunning, H.E. Reaction of hydrogen atoms with thiirane. J. Phys. Chem. 1975, 79, 1758–1762. [Google Scholar] [CrossRef]
- Kaufman, F. Kinetics of elementary radical reactions in the gas phase. J. Phys. Chem. 1984, 88, 4909–4917. [Google Scholar] [CrossRef]
- Langford, R.B.; Oldershaw, G.A. Flash photolysis of H2S. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1972, 68, 1550–1558. [Google Scholar] [CrossRef]
- Bedjanian, Y. Rate constants for the reactions of F atoms with H2 and D2 over the temperature range 220-960 K. Int. J. Chem. Kinet. 2021, 53, 527–535. [Google Scholar] [CrossRef]
- Su, M.C.; Kumaran, S.S.; Lim, K.P.; Michael, J.V.; Wagner, A.F.; Harding, L.B.; Fang, D.C. Rate Constants, 1100 ≤ T ≤ 2000 K, for H + NO2 → OH + NO Using Two Shock Tube Techniques: Comparison of Theory to Experiment. J. Phys. Chem. A 2002, 106, 8261–8270. [Google Scholar] [CrossRef]
- Bedjanian, Y. Temperature-Dependent Rate Constant for the Reaction of Hydroxyl Radical with 3-Hydroxy-3-methyl-2-butanone. J. Phys. Chem. A 2019, 123, 10446–10453. [Google Scholar] [CrossRef]
- Bedjanian, Y. Rate constant of H atom reaction with Br2 determined between 220 and 950 K. Chem. Phys. Lett. 2023, 825, 140616. [Google Scholar] [CrossRef]





| T (K) | [Excess Reactant] a | k1 b | Reactor Surface c | Method d |
|---|---|---|---|---|
| 220 | 6.51–24.2 | 0.24 ± 0.01 | HW | H kinetics |
| 235 | 4.80–28.8 | 0.26 ± 0.01 | HW | H kinetics |
| 250 | 3.66–28.4 | 0.31 ± 0.01 | HW | H kinetics |
| 270 | 1.60–44.7 | 0.39 ± 0.01 | HW | H kinetics |
| 285 | 0.85–27.8 | 0.49 ± 0.01 | HW | H kinetics |
| 295 | 0.66–4.37 | 0.60 ± 0.01 | Q | H2S kinetics |
| 305 | 1.09–19.7 | 0.59 ± 0.01 | Q | H kinetics |
| 325 | 1.25–20.4 | 0.77 ± 0.02 | HW | H kinetics |
| 330 | 0.46–6.64 | 0.88 ± 0.02 | HW | H2S kinetics |
| 360 | 0.62–5.58 | 1.07 ± 0.02 | Q | H2S kinetics |
| 410 | 0.45–4.60 | 1.58 ± 0.02 | Q | H2S kinetics |
| 475 | 0.57–5.87 | 2.61 ± 0.03 | Q | H2S kinetics |
| 575 | 0.43–4.46 | 4.61 ± 0.08 | Q | H2S kinetics |
| 720 | 0.33–3.31 | 9.96 ± 0.08 | Q | H2S kinetics |
| 950 | 0.18–2.61 | 20.6 ± 0.3 | Q | H2S kinetics |
| T (K) | [Excess Reactant] a | k2 b | Reactor Surface c | Method d |
|---|---|---|---|---|
| 220 | 0.21–9.19 | 1.67 ± 0.04 | HW | C2H4S kinetics |
| 225 | 0.40–8.82 | 1.77 ± 0.03 | HW | C2H4S kinetics |
| 235 | 0.8–7.73 | 2.05 ± 0.04 | HW | C2H4S kinetics |
| 245 | 0.26–7.25 | 2.11 ± 0.03 | HW | C2H4S kinetics |
| 250 | 0.23–3.86 | 2.26 ± 0.06 | HW | H kinetics |
| 255 | 0.45–8.28 | 2.35 ± 0.04 | HW | C2H4S kinetics |
| 270 | 0.24–4.03 | 2.56 ± 0.07 | HW | H kinetics |
| 270 | 0.56–6.44 | 2.7 ± 0.04 | HW | C2H4S kinetics |
| 275 | 0.48–6.73 | 2.75 ± 0.07 | HW | C2H4S kinetics |
| 297 | 0.11–3.84 | 3.54 ± 0.04 | Q | C2H4S kinetics |
| 320 | 0.33–6.03 | 4.36 ± 0.04 | HW | C2H4S kinetics |
| 325 | 0.36–4.86 | 4.35 ± 0.08 | HW | H kinetics |
| 330 | 0.30–4.54 | 4.99 ± 0.06 | HW | C2H4S kinetics |
| 360 | 0.23–3.34 | 5.71 ± 0.06 | Q | C2H4S kinetics |
| 410 | 0.18–2.58 | 8.23 ± 0.07 | Q | C2H4S kinetics |
| 475 | 0.15–2.24 | 12.1 ± 0.1 | Q | C2H4S kinetics |
| 575 | 0.18–1.94 | 17.7 ± 0.1 | Q | C2H4S kinetics |
| 720 | 0.14–1.36 | 30.5 ± 0.2 | Q | C2H4S kinetics |
| 950 | 0.09–1.08 | 44.9 ± 0.1 | Q | C2H4S kinetics |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedjanian, Y. Temperature-Dependent Kinetic Study of the Reactions of Hydrogen Atoms with H2S and C2H4S. Molecules 2023, 28, 7883. https://doi.org/10.3390/molecules28237883
Bedjanian Y. Temperature-Dependent Kinetic Study of the Reactions of Hydrogen Atoms with H2S and C2H4S. Molecules. 2023; 28(23):7883. https://doi.org/10.3390/molecules28237883
Chicago/Turabian StyleBedjanian, Yuri. 2023. "Temperature-Dependent Kinetic Study of the Reactions of Hydrogen Atoms with H2S and C2H4S" Molecules 28, no. 23: 7883. https://doi.org/10.3390/molecules28237883
APA StyleBedjanian, Y. (2023). Temperature-Dependent Kinetic Study of the Reactions of Hydrogen Atoms with H2S and C2H4S. Molecules, 28(23), 7883. https://doi.org/10.3390/molecules28237883







