Abstract
Accurate potential energy curves (PECs) are determined for the twenty-two electronic states of LiRb. In contrast to previous studies, the applied approach relies on the first principle calculations involving correlation among all electrons. The current methodology is founded on the multireference coupled cluster (CC) scheme constructed within the Fock space (FS) formalism, specifically for the (2,0) sector. The FS methodology is established within the framework of the intermediate Hamiltonian formalism and offers an intruder-free, efficient computational scheme. This method has a distinctive feature that, when applied to the doubly ionized system, provides the characteristics of the neutral case. This proves especially beneficial when investigating PECs in situations where a closed-shell molecule dissociates into open-shell fragments, yet its double positive ion forms closed-shell species. In every instance, we successfully computed continuous PECs spanning the entire range of interatomic distances, from the equilibrium to the dissociation limit. Moreover, the spectroscopic characteristic of various electronic states is presented, including relativistic effects. Relativistic corrections included at the third-order Douglas-Kroll level have a non-negligible effect on the accuracy of the determined spectroscopic constants.
1. Introduction
The chemistry and the physics of polar ultracold molecules have been extensively studied in the last decade [1,2,3,4,5]. These types of molecules attract scientists mostly due to their high dipole moment, which induces such phenomena as long-range and anisotropic interactions [6]. An example of a diatomic polar molecule is LiRb, the object of this study. The research finds that the LiRb molecule possesses a dipole moment of around ∼4.2 debye [7] and it has vast potential applications. In 2010, Herrera et al. proposed that the mixture of cold LiRb and LiCs molecules trapped on an optical lattice and controlled using an electric field produces a perfect system for potential applications in quantum simulation, quantum computation, studies of negative refraction of microwave fields, or studies of the formation of wave-vector space crystals of excitons [8]. In 2011, Kuznetsova and her coworkers presented the application of the LiRb molecule as an atom–molecule platform for quantum computing [9]. They discovered that using LiRb, it is possible to encode a qubit in atomic states that allowed an easy initialization, readout, one-qubit operations, and mapping of the qubit state onto a photon for quantum communication. Besides that, LiRb, being a polar molecule composed of alkali metals, can possibly be applied in many fields, e.g., few-body [10] and many-body physics [11], studies of chemical reactions [12], or to expand our knowledge of quantum mechanics itself [13]. These studies have driven us to explore the properties of this molecule more accurately than ever before using the state-of-the-art method [14] described in the Section 3.
The most important experimental works for our study are those concerning potential energy curves (PECs) and/or spectroscopic constants of the LiRb molecule. This consists of the following: two papers by Ivanova et al. in which they used Fourier-transform spectroscopy to evaluate PECs and spectroscopic constants of various states of LiRb [15,16]; the study of Dutta et al. in which they used similar technique [17]; and the studies which were conducted using resonantly enhanced multiphoton ionization spectroscopy [18,19,20,21]. Values obtained in these papers were cited in the Section 2 to evaluate the accuracy of our theoretically obtained data.
In terms of theoretical research, there is a notable number of papers concerning LiRb. These studies may be classified as follows: studies of electric properties [7,22,23,24,25], computations of dispersion coefficients [1,26,27,28,29], calculations of PECs and spectroscopic constants [30,31,32,33,34,35,36,37,38,39,40,41,42,43], and others [44,45,46,47,48,49,50,51]. Among those, the studies of PECs and spectroscopic constants are most relevant in terms of our research.
The current work is focused on the quantum chemical description of the bond-breaking process for LiRb. We have in mind an approach that would be able to provide correct energy values at the dissociation limit as well as an accurate description of the potential energy curves (PECs).
Fundamental information about LiRb can be obtained out of PECs, which allows the evaluation of selected spectroscopic constants of the molecule, e.g., equilibrium distance , adiabatic excitation energy , well depth , etc. The detailed knowledge of PECs in the ground and excited states is crucial in the study of ultracold molecules [52].
A theoretical description is not trivial for alkali metals diatomics using most of the well-established methods. The difficulty comes from the fact that the molecule with a closed-shell character at the equilibrium distance alters into an open-shell system at the dissociation limit. Therefore, the restricted Hartree–Fock scheme (RHF) should not be used for long-range distances in such cases. Usually, the unrestricted Hartree–Fock (UHF) or the restricted open-shell Hartree–Fock (ROHF) methods are used; however, such calculations are often faced with convergence problems of the HF and post-HF solutions. Theoretical chemistry came up with several solutions to this problem, but none of them is ideal. For instance, researchers often use the multireference configuration interaction (MRCI) method, which, in its approximate variants, is not size-extensive. Therefore, they decide to carry out the calculations for valence electrons only, freezing the inner-shells’ electrons, which also affects the accuracy of the results. To overcome this drawback, these electrons are replaced in some studies using the ECP (Effective Core Potential) method, which makes it possible to consider the valence electrons as moving in the potential of atomic cores [36,38,53]. This approximation neglects the subtle effects connected with the correlation of all electrons and, on the other hand, introduces new parameters specific to the considered system to mimic the potential of electrons originating from the inner shells. When discussing interatomic potentials, we should also mention the methods based on the algebraic approaches using the well-known models for interatomic potentials like Morse, Lennard-Jones, or Pöschl–Teller and their usefulness of the characteristic of vibrational spectra [54,55,56,57]. On the other hand, the “method of choice”, frequently applied in the studies of excited states, i.e., EE-EOM-CC (Excitation Energy Equation-of-Motion Coupled Cluster) [58,59,60,61,62], is not size-extensive. This is the major reason that, in the studies of the potential energy curves where the size extensivity plays a prominent role, the latter method is less frequently applied in the calculations of alkali metal dimers [63,64,65].
In our study, we use the Fock space multireference coupled cluster (FS-MRCC) method, which is—on the one hand—size-extensive (an important feature in the PECs calculations) and —on the other—has a built-in capability to provide—by selecting a proper FS sector—correlation corrections for systems with an altered (with respect to the Hartree–Fock (HF) reference) number of electrons. For example, the FS sector produces results pertaining to the system with m electrons added to the HF function. Assuming a neutral HF reference, these results would correspond to the m-tuply negative anion. Smooth and well-behaved PECs are obtained, e.g., in the case of the van der Waals molecules, when the closed shell structure dissociates into the closed shell fragments. This example has been a sort of inspiration when dealing with the problem of the dissociation of alkali metal diatomics. Instead of dissociating the dimer Me (MeMe + Me), we can dissociate the doubly ionized molecule Me according to the following equation:
and we see here that the closed shell structure Me dissociates into closed shell fragments, isoelectronic with noble gas atoms, specifically discussing an alkali metal dimer. So, this scheme allows us to obtain continuous and smooth curves for the reference system. In the next step, the FS-MRCC scheme is employed to solve the FS equations for the valence (2,0) sector, recovering the original neutral structure. Consequently, at the correlated level, we obtain results for the Me molecule.
The state-of-the-art research is documented with many results obtained for the two-valence sector of the Fock space [14,66,67,68]. Such a strategy, applied to the study of the PECs of a large number of electronic states for a series of alkali metal diatomics [66,67,68], provided the results of incomparable accuracy. The results obtained for the Rb dimer (on the basis of the (2,0) sector of Fock space) have already been utilized in the experimental works carried out in ultra-low temperatures [69].
In this study, we present accurately calculated potential energy curves and spectroscopic constants for the 22 lowest-lying electronic states of the LiRb molecule using the FS-CCSD (2,0) (S-Singles, D-Doubles) method in the Intermediate Hamiltonian (IH) formulation [14] to eliminate so-called intruder-state problems [70,71]. Although the structure of the LiRb molecule is similar to that of NaLi, studied in [68], the presence of the heavy Rb atom requires special attention in the choice of the model space and the calculation of the relativistic corrections. The latter effects were included by combining the DK3 (third order Douglas–Kroll) [72] formalism and the IH-FS-CCSD (2,0) scheme [14]. The local version of the IH-FS-CCSD (2,0) program was connected to the GAMESS (General Atomic and Molecular Electronic Structure System) package. This required the development of the necessary software [68].
2. Results and Discussion
All calculations were performed using ACES II [73] ver. 2.7.0 and GAMESS [74] ver. 2021 R2 Patch 1 packages, both supplemented with our own modules in the local version for IH-FS-CCSD(2,0) calculations [14,68]. The spectroscopic constants were computed using 8.0 version of Robert J. LeRoy’s LEVEL program [75]. For the main calculations, we used the uncontracted ANO-RCC [76] basis set with additional diffuse functions, which we called unANO-RCC+. The exponents for the six additional diffuse functions for the lithium are as follows: 0.0027497, 0.0009619 for the s shell; 0.0017173, 0.0006010 for the p shell; and 0.0067528, 0.0023635 for the d shell. Analogously, for the rubidium atom, the exponents for the new diffuse functions are as follows: 0.0012643, 0.0005057, 0.0002023, 0.0000809 for the s shell; 0.0034222, 0.0013689, 0.0005476, 0.0002190 for the p shell; and 0.0727457, 0.0327356, 0.0147310, 0.0066289 for the d shell. We have obtained the exponents using the even-tempered scheme to provide the correct ordering of atomic states. The final size of unANO-RCC+ basis set was 326 basis functions. The spherical harmonic polarization functions were used in all of our calculations and all electrons were correlated.
To evaluate the contribution of relativistic effects in spectroscopic constants of the LiRb molecule, we used the following scheme: we computed potential energy curves and spectroscopic constants of LiRb using Sapporo-QZP-2012-diffuse basis set [77] (167 basis functions), and, in the next step, our calculations were again completed using the scalar relativistic corrections of Douglass–Kroll third order (DK3) [72] and applying the Sapporo-DKH3-QZP-2012-diffuse basis set (also the same number of basis functions), which is the relativistic equivalent of the former basis set. Finally, we calculated the differences between the relativistic and non-relativistic results and these values were added to the constants obtained using the unANO-RCC+ basis set since our previous works show that spectroscopic constants derived from PECs calculated with the family of Sapporo basis sets are not as accurate as those derived from PECs obtained using augmented ANO-RCC basis sets [68,78].
As a reference system for all of the double electron attachment calculations, we used the LiRb cation. The reference function was always RHF. The size of the active space was set to 91 (i.e., 91 lowest virtual orbitals have been selected as active) for IH-FS-CCSD(2,0)/unANO-RCC+ calculations, which resulted in the model space size equal to 8281. For IH-FS-CCSD(2,0)/Sapporo-QZP-2012-diffuse, as well as for IH-FS-CCSD(2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse calculations, the active space size was set to 50 (model space size = 2500).
The dipole moment of the ground state of LiRb was calculated using the numerical Finite Field approach [79]. We used the following equation:
where is the energy of the system in the weak uniform external electric field F.
The value of F was equal to 0.001 a.u. and its vector was aligned with the axis of the molecule. The external electric field perturbation in IH-FS-CCSD(2,0) computations was introduced using ACES II. In order to estimate the contribution of relativistic effects for the dipole moment, we used a similar procedure as in the case of spectroscopic constants, this time using the difference between CCSD/Sapporo-QZP-2012-diffuse and CCSD/Sapporo-DKH3-QZP-2012-diffuse + DK3 results. We used OpenMolcas quantum chemistry software package [80], which allowed us to combine both an external electric field and DK3 scalar relativistic correction.
2.1. Atomic Energies at the Dissociation Limit
The important feature of the IH-FS-CCSD(2,0) method is its size-extensivity. This property enforces that the energies of electronic states of the LiRb molecule should converge at an infinite distance to the sum of atomic values. Table 1 presents computed values in the unANO-RCC+ basis set. The first and the second columns present values of energies of Li and Rb—these were calculated using EA-EOM-CCSD—which is equivalent to the IH-FS-CCSD(1,0) method. The third column presents the sum of those energies, and the fourth column shows the energy in the respective dissociation limit obtained using the IH-FS-CCSD(2,0) method. We can clearly see that the results are equal and our method is strictly size-extensive. Thus, the FS-CC method shows correct separability. This feature is particularly useful in the studies of the dissociation process.

Table 1.
Energies of electronic states at the dissociation limit of the LiRb molecule compared to the atomic energies in the unANO-RCC+ basis set.
2.2. Dipole Moment
The calculated dipole moment of the ground state of the LiRb molecule is presented in Table 2 alongside experimental and theoretical reference values. The LiRb molecule has one of the largest dipole moments among heteronuclear alkali metal dimers, being second only to the species containing cesium [7], and our results comply with this fact. Our value computed using IH-FS-CCSD(2,0) DK3/unANO-RCC+ is very close to the experimental values of Tarnovsky et al. [81] and Stevenson et al. [21]. We can clearly see that the methods based on pseudopotentials usually overestimate the values of the dipole moment of LiRb, and our results are close to the quality of CCSDT [27,40] with significantly smaller computational effort needed to solve the equations.

Table 2.
The dipole moment of the state of the LiRb molecule.
2.3. Potential Energy Curves
Potential energy curves of LiRb were calculated using the IH-FS-CCSD(2,0)/unANO-RCC+ method for the 22 lowest-lying electronic states. These are the states correlating to six dissociation limits: Li(2s) + Rb(5s) – two states (, ), Li(2s) + Rb(5p) – four states (, , , ), Li(2p) + Rb(5s) – four states (, , , ), Li(2s) + Rb(4d) – 6 states (, , , , , ), Li(2s) + Rb(6s) – two states (, ), Li(2s) + Rb(6p) – four states (, , , ). Some molecular states, engaging the p or d atomic levels, are degenerated ( and ).
The computed PECs are shown in Figure 1—we chose separate point types for each symmetry and multiplicity, and states assigned to different dissociation limits have distinct colors. The applied computational method, which uses the closed shell configuration as the reference, has the advantage that the calculations can be completed equally easily for any internuclear distance. The total molecular energies of each state for the various interatomic distances are available in the Supplementary Materials. All of the states are bound, and four of them have double minima, i.e., , , , (see Figure 2), which is in accordance with the results obtained in Ref. [38] via pseudopotential calculations. The energy barriers/positions are 300 cm/4.75 Å, 2314 cm/8.05 Å, 2214 cm/ 6.20 Å, and 3057 cm/8.00 Å, respectively (see Table 3).
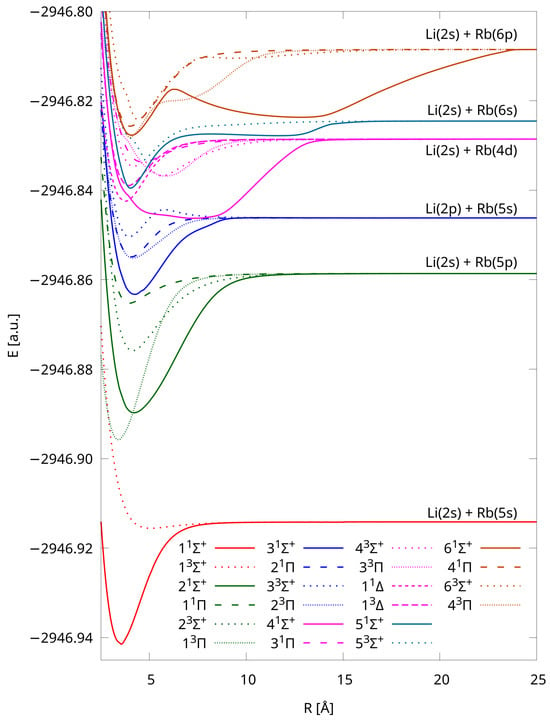
Figure 1.
Potential energy curves of LiRb calculated using the IH-FS-CCSD(2,0)/unANO-RCC+ method for the six lowest dissociation limits.
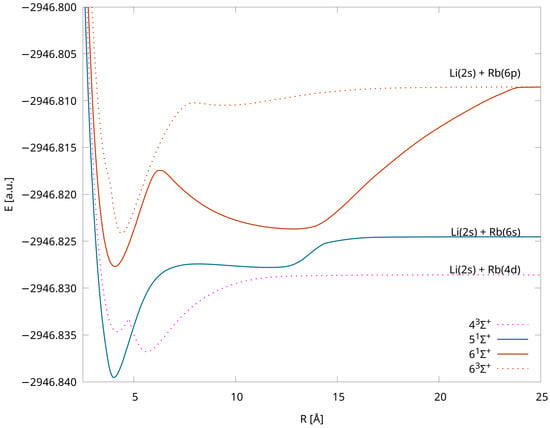
Figure 2.
Potential energy curves for the LiRb molecule with the IH-FS-CCSD (2,0) method for states with double minima in the unANO-RCC+ basis set.

Table 3.
Energy barriers for the states with double minima. IH-FS-CCSD(2,0)/unANO-RCC+.
The higher-lying states have a specific form due to avoided crossing (see Table 4 and Figure 1 and Figure 2).

Table 4.
Avoided crossing positions obtained using IH-FS-CCSD(2,0)/un-ANORCC+ compared with Ref. [38].
We also present Figure 3 in which the comparison with experimental curves of Refs. [15,16] is shown. We were able to compare our theoretical PECs with the experimental ones in two cases: and . We can see the exceptional alignment of our IH-FS-CCSD(2,0) values with the experimental ones. Although the experimental data are accessible only in a limited range, we can see that the respective parts overlap each other very well. This accuracy is also revealed in spectroscopic constants, which are described in the next subsection. In addition, we computed the C coefficient for the ground state and obtained a value of 2457 a.u. comparing well with the experimental one equal to 2550 a.u. [82].
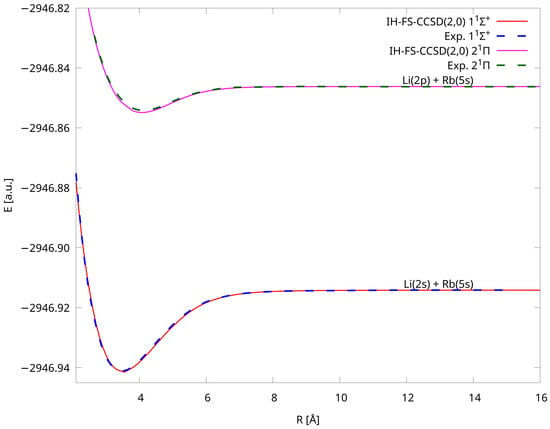
Figure 3.
Comparison of PECs of LiRb for the and states calculated using the IH-FS-CCSD(2,0)/unANO-RCC+ method with experiment (see [15,16] for experimental data).
Finally, just for comparison purposes, we also present PECs calculated using IH-FS-CCSD(2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse (see Figure 4). As we can see, the shapes of the curves are similar to those obtained using a significantly larger unANO-RCC+ basis set (Figure 1).
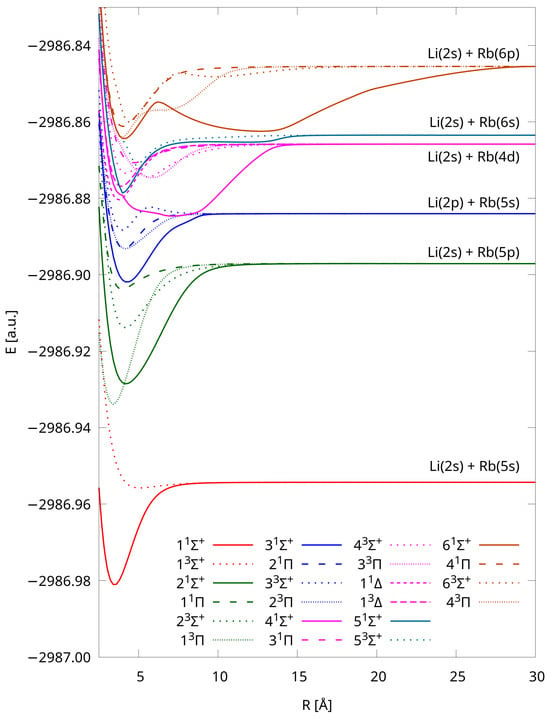
Figure 4.
Potential energy curves of LiRb calculated using the IH-FS-CCSD(2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse method for the six lowest dissociation limits.
2.4. Spectroscopic Constants
The spectroscopic constants of the LiRb molecule are shown in Table 5. These include equilibrium distance , well depth , adiabatic excitation energy , harmonic frequency , anharmonicity constant , and equilibrium rotational constant . The data obtained in the current work include the relativistic contributions, while the pure relativistic corrections are shown in parentheses. In addition to our IH-FS-CCSD(2,0) results, we present values obtained in previous papers for comparison purposes. In order to undertake reliable analysis of our results, we decided to limit the number of cited references to fairly recent and the most relevant theoretical works, i.e., the paper of Berriche et al. in which they use a well-established method based on pseudopotential [38], the two publications of You et al., which apply multireference configuration interaction method (MRCI) [41,42], and the recent article of Kozlov et al. in which they combine effective core potentials with the relativistic variant of FS-CCSD method [43]. Also, we present the experimental values of Refs. [15,16,18,19].

Table 5.
Spectroscopic constants of LiRb. , , e, exe and given in ; given in Å. DK3 relativistic corrections are given in parentheses.
Out of the results cited in the Table 5, we were able to perform a statistically significant mean absolute error (MAE) analysis of experimental values only with the paper by Jendoubi et al. [38]. For , and , our results agree better with experimental values, while for , the results in the cited paper are better. The value of is similar (the difference is about 1.7%). This is the expected behavior—pseudopotential-based methods produce quite accurate results near the equilibrium distance but are not size-extensive, therefore cannot properly reproduce the PECs for the distances far from the minimum, in contrast to our IH-FS-CCSD(2,0) method, which behaves properly in the whole spectrum of interatomic distances. Also, for the case of the ground state of LiRb, our results are closer to the experimental values of [15], with the perfect alignment of the value.
For the ground state, our method provides results more consistent with the multireference configuration interaction (MRCI) method [41,42] than with the method based on pseudopotential [38]. For the other states where MRCI results are available, it is not always the case, i.e., a part of our results is closer to the pseudopotential method. We were also able to compare our results to the relativistic variant of FS-CCSD method by Kozlov et al. [43] for and states. The alignment is exceptionally good with the difference of less than 0.2%, except of the value for the state where the difference is slightly higher but still less than 2%.
We have correctly identified , , , states as having double minima, which we confirmed by comparison with the study of Jendoubi et al. [38]. Generally, the agreement of , , and values with the cited paper is good. The best agreement of can be seen for the singlet and states, in the case of for the state (the difference of 0.4%), and the absolute difference in for the second minimum of state is only 10 cm. The good match in implies the same for the derived values. However, have some exceptions where the differences are larger than expected, i.e., , , and .
Relativistic corrections given in parentheses in the Table 5 are not regular—they fluctuate between states and spectroscopic constants. In some cases, they contribute less than 1% of the value of the given spectroscopic constant (e.g., for or for ), while in others, they contribute more than 50% of the computed value (e.g., 506 vs. 915 cm for of state). Rubidium is an atom where relativistic effects cannot be neglected. Thus, their contribution to the energies of the LiRb dimer should always be included.
3. Methods
Within the single reference (SR) coupled cluster (CC) theory, the wave function is defined via exponential Ansatz [83,84]
where T is a cluster operator defined at the CCSD level as follows:
Operators T, T are responsible for single, double excitations from the reference function . It should be stressed that in our calculations, the reference system is understood as a doubly ionized structure LiRb, and both RHF and CCSD solutions are referred to this reference. The are the second-quantized operators, removing an electron from the occupied level i and placing it on the virtual one a. The amplitudes are the solution of the CC equations obtained by a projection of the operator against excited configurations :
The multireference [85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102] formalism assumes that the configurational space is divided into two subspaces: the model space with the projector operator P and its orthogonal complement defined by the projector Q. The advantage of the FS-MRCC approach lies in the fact that the diagonalization of the Hamiltonian H within full configurational space (size: millions, billions,...) is replaced by the diagonalization of the effective Hamiltonian operator in the model space. The size of the model space is drastically smaller and the diagonalization of the can be carried out in most cases with the standard diagonalization techniques.
The effective Hamiltonian is defined as follows:
where is a wave operator, which, on acting on the model function , generates an exact wave function:
In order to use particle-hole second-quantized operators, the configuration adopted as a Fermi vacuum must be selected. Then, the model determinants can be generated by the action of the particle-hole creation operators within the valence one-particle levels. The K-valence space is defined by indication of the valence electrons and valence unoccupied levels ().
The MR-CC considered here, i.e., formulated in the Fock space (also known as a valence universal), admits the configuration with a variable number of electrons. The FS model is obtained by a distribution of 0,1,2,...,K valence electrons among K valence orbitals. It is obvious that it includes configurations containing 0 valence electrons, i.e., with electrons removed from the system, as well as K valence electrons, i.e., -tuply ionized anion. The valence universality means that i) all model configurations are defined with respect to the same Fermi vacuum; ii) the wave operator is defined identically for all reference determinants.
An important step in the FS approach relates to the selection of the Fermi vacuum, which—on the one hand—defines the reference system for which the one-particle states are obtained (in our approach, the Hartree–Fock solutions) and—on the other—determines the sector structure of the model space. The sector is defined by the number of valence particles and valence holes created with respect to the vacuum, e.g., () sector indicates that the reference configuration contains k valence particles and l valence holes. The (0,0) sector indicates the Fermi vacuum.
The flexibility of the FS approach—indicated already in the Section 1—can be used in all situations where we want to replace the open-shell reference (requiring UHF function) with the closed shell one, conveniently described by the RHF method.
The basic general formula for the MR approach is a Bloch equation of the form
Operating from the left with the P operator, we obtain the expression for the () (the identity has been used) while the projection against the configurations belonging to the orthogonal subspace (represented by the Q operator) generates MR-CC equations. The operator can be expressed as
and the braces indicate that the normal ordering is imposed on the product of operators.
A specificity of the Fock space method lies in the hierarchical structure of the CC solutions. So, when we want to solve the Fock space equations for the given sector, the lower rank sectors solutions must be known. That is why in the current work, since we use the FS-CCSD (2,0) variant, the solutions for the (0,0) and (1,0) sectors are needed. The (0,0) sector corresponds to the single reference solution for the reference system (LiRb ion), and the (1,0) sector is responsible for the electron affinity calculations, and the (2,0) sector is used for double electron affinity ones.
The particular sectors are defined by the configurations belonging to them. So, if the model space contains configurations with a single electron placed on the virtual level, , we have the (1,0) sector; for configurations with two additional electrons placed on the virtual levels, , , we have the (2,0) sector, etc. Note that the convention we adopted here indicates that the indices refer to virtual one-particle levels, and their Greek equivalence refer to active particles, while the refer to inactive particles. Thus, the DEA (double electron attached) states refer to the (2,0) sector. Consequently, only particle active levels belong to the active space and their number determines the size of the active space.
The energy values of the DEA states are obtained by the diagonalization of the effective Hamiltonian within the configurational space:
where the projection operator is defined as
The cluster operators , , and correspond to the sector indicated by the superscripts. As we mentioned before, in order to construct the effective Hamiltonian for the (2,0) sector , the amplitudes from the sectors (1,0) and (0,0) are needed, and the diagonalization of the is performed only within the (2,0) sector. The operator can be constructed by solving the FS-MRCC equations for the (1,0) sector, but the identical result can be obtained by solving the EOM-CC problem set up for the electron affinity (EA). It is known that the Fock space approach at the one-valence level, (1,0) and (0,1), is equivalent to the EOM-CC scheme applied to the EA and IP (Ionization Potentials) cases, respectively. This equivalence means that the eigenvalues in both approaches are identical while the eigenvectors can be obtained from each other by a simple transformation.
A well-known problem that complicates the MR formulations of the coupled cluster theory is the presence of intruder states. They arise when the excited determinants from the orthogonal space (usually low in energy) are close to those belonging to the model space. This may cause numerical instabilities and, consequently, may be a reason for making the MRCC equations divergent.
In order to eliminate convergence problems in the (2,0) sector due to intruder states [70,71], we applied the intermediate Hamiltonian (IH) strategy [98,99,100]. Within IH formalism, we select a part of the orthogonal space, as an intermediate space, , connected with the (projector onto the subspace defined by the operators ). Thus, in this formulation, we have the following subspaces: and projectors: , , with relations:
and wave operators,
with . , operating on the model space , generates determinants belonging to the space, while the operator connects the and subspaces. For the IH-FS-CCSD case, they take the following form:
The eigenvalues of the effective Hamiltonian [99], defined within the FS-CC, are the same as those of the simpler intermediate Hamiltonian operator, i.e., [14]:
This is a matrix representation of in with the part modified by dressing, which is constructed from and the cluster operators S known from the lower sector, i.e., (1,0) (for more details see the paper devoted to the IH-FS-CCSD (2,0) method [14]). The respective matrix to be diagonalized is obtained in the electron-affinity EOM-CC [103,104,105,106] calculations in order to omit convergence problems in the FS one-valence sector. Diagonalization of the operator provides a subset of eigenvalues that are identical to those obtained by diagonalization of the operator. It follows from the above that the diagonalization of the IH matrix can replace the iterative solution of the -based equations. The final advantage of this is the elimination of the intruder state problem from the FS approach. In addition, the (2,0) step scales as (neglecting the limited number of active orbitals). The scaling of the CCSD solution for the ground state is , and the (1,0) part is .
4. Conclusions
The studies of the potential energy curves of diatomic molecules have a well-established place in the quantum chemical literature. The problem is challenging since upon a dissociation of the closed shell structure, usually the open shell fragments are formed, which complicates the calculations at the correlated level.
In this work, we focus on the Fock space realization of the multireference coupled cluster theory, specifically applied to investigate the electronic structure of the LiRb molecule. The central aspect of our approach lies in the Intermediate Hamiltonian formulation, providing a convenient way to circumvent the iterative solution inherent in the standard Bloch equation. Instead, we took advantage of the direct diagonalization of a suitably constructed matrix (’dressed’ , i.e., IH). This methodology eliminates complications associated with intruder states, a persistent hindrance that has restrained the broader adoption of this method over the years.
Promising findings were obtained in the studies of the dissociation of a single bond for LiRb with a solution based on the (2,0) sector of FS as an indirect application of the DEA calculations. Using this scheme, excellent results were obtained in the determination of the spectroscopic constants and PECs for the twenty-two lowest electronic states. Notably, calculations were performed for the first time across the entire range of interatomic distances using the RHF reference function, correlating all 40 electrons. This approach produced smooth and accurate PECs from the equilibrium distance to infinity. The mean absolute error from experimental is equal to 39 cm, while a corresponding value for was 46 cm. Additionally, good agreement with experimental data was observed for , with an average deviation of 13 cm. Thus, the molecular data obtained in this study are well justified and, in the absence of experimental data, may be treated as reference values. This work presents the capability of the IH-FS-CCSD (2,0) method to provide comprehensive characteristics of the investigated molecule without relying on additional approximations.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28227645/s1, Figure S1: Potential energy curves of LiRb calculated using the IH-FS-CCSD(2,0)/unANO-RCC+ method for the six lowest dissociation limits. Energy related to the dissociation limit of the ground state.; Figure S2: Potential energy curves of LiRb calculated using the IH-FS-CCSD(2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse method for the six lowest dissociation limits. Energy related to the dissociation limit of the ground state.; Table S1: Total IH-FS-CCSD (2,0)/unANO-RCC+ energy values (a.u.) for states of LiRb.; Table S2: Total IH-FS-CCSD (2,0)/unANO-RCC+ energy values (a.u.) for states of LiRb.; Table S3: Total IH-FS-CCSD (2,0)/unANO-RCC+ energy values (a.u.) for and states of LiRb.; Table S4: Total IH-FS-CCSD (2,0)/unANO-RCC+ energy values (a.u.) for and states of LiRb.; Table S5: Total IH-FS-CCSD (2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse energy values (a.u.) for states of LiRb.; Table S6: Total IH-FS-CCSD (2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse energy values (a.u.) for states of LiRb.; Table S7: Total IH-FS-CCSD (2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse energy values (a.u.) for and states of LiRb.; Table S8: Total IH-FS-CCSD (2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse energy values (a.u.) for and states of LiRb.; Table S9: Total IH-FS-CCSD (2,0)/unANO-RCC+ energy values (a.u.) (E + 2946.914167 a.u.) for states of LiRb.; Table S10: Total IH-FS-CCSD (2,0)/unANO-RCC+ energy values (a.u.) (E + 2946.914167 a.u.) for states of LiRb.; Table S11: Total IH-FS-CCSD (2,0)/unANO-RCC+ energy values (a.u.) (E + 2946.914167 a.u.) for and states of LiRb.; Table S12: Total IH-FS-CCSD (2,0)/unANO-RCC+ energy values (a.u.) (E + 2946.914167 a.u.) for and states of LiRb.; Table S13: Total IH-FS-CCSD (2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse energy values (a.u.) (E + 2986.954313 a.u.) for states of LiRb.; Table S14: Total IH-FS-CCSD (2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse energy values (a.u.) (E + 2986.954313 a.u.) for states of LiRb.; Table S15: Total IH-FS-CCSD (2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse energy values (a.u.) (E + 2986.954313 a.u.) for and states of LiRb.; Table S16: Total IH-FS-CCSD (2,0) DK3/Sapporo-DKH3-QZP-2012-diffuse energy values (a.u.) (E + 2986.954313 a.u.) for and states of LiRb.
Author Contributions
G.S. carried out theoretical calculations, co-interpretation of the results, preparing all figures and tables, co-editing the manuscript; M.M. conceived the research plan, co-interpreted the results, co-editing the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The research activities co-financed by the funds granted under the Research Excellence Initiative of the University of Silesia in Katowice.
Data Availability Statement
The data that support the findings of this study are available within the article and the supplementary material.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Żuchowski, P.S.; Kosicki, M.; Kodrycka, M.; Soldán, P. Van der Waals coefficients for systems with ultracold polar alkali-metal molecules. Phys. Rev. A 2013, 87, 022706. [Google Scholar] [CrossRef]
- Pazyuk, E.A.; Zaitsevskii, A.V.; Stolyarov, A.V.; Tamanis, M.; Ferber, R. Laser synthesis of ultracold alkali metal dimers: Optimization and control. Russ. Chem. Rev. 2015, 84, 1001–1020. [Google Scholar] [CrossRef]
- Vexiau, R.; Borsalino, D.; Lepers, M.; Orbán, A.; Aymar, M.; Dulieu, O.; Bouloufa-Maafa, N. Dynamic dipole polarizabilities of heteronuclear alkali dimers: Optical response, trapping and control of ultracold molecules. Inv. Rev. Phys. Chem. 2017, 36, 709–750. [Google Scholar] [CrossRef]
- Li, H.; Li, M.; Makrides, C.; Petrov, A.; Kotochigova, S. Universal Scattering of Ultracold Atoms and Molecules in Optical Potentials. Atoms 2019, 7, 36. [Google Scholar] [CrossRef]
- Frye, M.D.; Hutson, J.M. Complexes formed in collisions between ultracold alkali-metal diatomic molecules and atoms. New J. Phys. 2021, 23, 125008. [Google Scholar] [CrossRef]
- Pupillo, G.; Griessner, A.; Micheli, A.; Ortner, M.; Wang, D.W.; Zoller, P. Cold Atoms and Molecules in Self-Assembled Dipolar Lattices. Phys. Rev. Lett. 2008, 100, 050402. [Google Scholar] [CrossRef] [PubMed]
- Aymar, M.; Dulieu, O. Calculation of accurate permanent dipole moments of the lowest 1,3Σ+ states of heteronuclear alkali dimers using extended basis sets. J. Chem. Phys. 2005, 122, 204302. [Google Scholar] [CrossRef] [PubMed]
- Herrera, F.; Litinskaya, M.; Krems, R.V. Tunable disorder in a crystal of cold polar molecules. Phys. Rev. A 2010, 82, 033428. [Google Scholar] [CrossRef]
- Kuznetsova, E.; Yelin, S.F.; Côté, R. An atom-molecule platform for quantum computing. Quantum. Inf. Process. 2011, 10, 821. [Google Scholar] [CrossRef]
- Büchler, H.P.; Micheli, A.; Zoller, P. Three-body interactions with cold polar molecules. Nature Phys 2007, 3, 726–731. [Google Scholar] [CrossRef]
- Cui, Y.; Deng, M.; You, L.; Gao, B.; Tey, M.K. Broad Feshbach resonances in ultracold alkali-metal systems. Phys. Rev. A 2018, 98, 042708. [Google Scholar] [CrossRef]
- Ospelkaus, S.; Ni, K.K.; Wang, D.; de Miranda, M.H.G.; Neyenhuis, B.; Quéméner, G.; Julienne, P.S.; Bohn, J.L.; Jin, D.S.; Ye, J. Quantum-State Controlled Chemical Reactions of Ultracold Potassium-Rubidium Molecules. Science 2010, 327, 853–857. [Google Scholar] [CrossRef] [PubMed]
- Pires, R.; Ulmanis, J.; Häfner, S.; Repp, M.; Arias, A.; Kuhnle, E.D.; Weidemüller, M. Observation of Efimov Resonances in a Mixture with Extreme Mass Imbalance. Phys. Rev. Lett. 2014, 112, 250404. [Google Scholar] [CrossRef] [PubMed]
- Musial, M. Multi-reference Fock space coupled-cluster method in standard an intermediate Hamiltonian formulation for the (2,0) sector. J. Chem. Phys. 2012, 136, 134111. [Google Scholar] [CrossRef] [PubMed]
- Ivanova, M.; Stein, A.; Pashov, A.; Knöckel, H.; Tiemann, E. The X1Σ+ state of LiRb studied by Fourier-transform spectroscopy. J. Chem. Phys. 2011, 134, 024321. [Google Scholar] [CrossRef]
- Ivanova, M.; Stein, A.; Pashov, A.; Knöckel, H.; Tiemann, E. The B1Π and D1Π states of LiRb. J. Chem. Phys. 2013, 138, 094315. [Google Scholar] [CrossRef] [PubMed]
- Dutta, S.; Altaf, A.; Elliott, D.S.; Chen, Y.P. Laser spectroscopy of the X1Σ+ and B1Π states of the LiRb molecule. Chem. Phys. Lett. 2011, 511, 7–11. [Google Scholar] [CrossRef]
- Altaf, A.; Dutta, S.; Lorenz, J.; Pérez-Ríos, J.; Chen, Y.P.; Elliott, D.S. Formation of ultracold 7Li85Rb molecules in the lowest triplet electronic state by photoassociation and their detection by ionization spectroscopy. J. Chem. Phys. 2015, 142, 114310. [Google Scholar] [CrossRef]
- Stevenson, I.C.; Blasing, D.B.; Chen, Y.P.; Elliott, D.S. C1Σ+, A1Σ+, and b3Π0+ states of LiRb. Phys. Rev. A 2016, 94, 062503. [Google Scholar] [CrossRef]
- Stevenson, I.C.; Blasing, D.B.; Altaf, A.; Chen, Y.P.; Elliott, D.S. The d3Π state of LiRb. J. Chem. Phys. 2016, 145, 224301. [Google Scholar] [CrossRef]
- Stevenson, I.C.; Blasing, D.B.; Chen, Y.P.; Elliott, D.S. Production of ultracold ground-state LiRb molecules by photoassociation through a resonantly coupled state. Phys. Rev. A 2016, 94, 062510. [Google Scholar] [CrossRef]
- Urban, M.; Sadlej, A.J. Electronic structure and electric properties of the alkali metal dimers. J. Chem. Phys. 1995, 103, 9692–9704. [Google Scholar] [CrossRef]
- Deiglmayr, J.; Aymar, M.; Wester, R.; Weidemüller, M.; Dulieu, O. Calculations of static dipole polarizabilities of alkali dimers: Prospects for alignment of ultracold molecules. J. Chem. Phys. 2008, 129, 064309. [Google Scholar] [CrossRef]
- Bormotova, E.A.; Kozlov, S.V.; Pazyuk, E.A.; Stolyarov, A.V. Long-range behavior of the transition dipole moments of heteronuclear dimers XY (X, Y = Li, Na, K, Rb) based on ab initio calculations. Phys. Chem. Chem. Phys. 2018, 20, 1889–1896. [Google Scholar] [CrossRef] [PubMed]
- Dyall, K.G.; Tecmer, P.; Sunaga, A. Diffuse Basis Functions for Relativistic s and d Block Gaussian Basis Sets. J. Chem. Theory Comput. 2023, 19, 198–210. [Google Scholar] [CrossRef] [PubMed]
- Bussery, B.; Achkar, Y.; Aubert-Frécon, M. Long-range molecular states dissociating to the three or four lowest asymptotes for the ten heteronuclear diatomic alkali molecules. Chem. Phys. 1987, 116, 319–338. [Google Scholar] [CrossRef]
- Quéméner, G.; Bohn, J.L.; Petrov, A.; Kotochigova, S. Universalities in ultracold reactions of alkali-metal polar molecules. Phys. Rev. A 2011, 84, 062703. [Google Scholar] [CrossRef]
- Byrd, J.N.; Montgomery, J.A.; Côté, R. Long-range forces between polar alkali-metal diatoms aligned by external electric fields. Phys. Rev. A 2012, 86, 032711. [Google Scholar] [CrossRef]
- Olaya, V.; Pérez-Ríos, J.; Herrera, F. C6 coefficients for interacting Rydberg atoms and alkali-metal dimers. Phys. Rev. A 2020, 101, 032705. [Google Scholar] [CrossRef]
- Gáspár, R.; Tamássy-Lentei, I. Molecular pseudopotential calculations III. Acta. Phys. Hung. 1976, 40, 283–291. [Google Scholar] [CrossRef]
- Igel-Mann, G.; Wedig, U.; Fuentealba, P.; Stoll, H. Ground-state properties of alkali dimers XY (X, Y=Li to Cs). J. Chem. Phys. 1986, 84, 5007–5012. [Google Scholar] [CrossRef]
- Korek, M.; Allouche, A.R.; Kobeissi, M.; Chaalan, A.; Dagher, M.; Fakherddin, K.; Aubert-Frécon, M. Theoretical study of the electronic structure of the LiRb and NaRb molecules. Chem. Phys. 2000, 256, 1–6. [Google Scholar] [CrossRef]
- Smirnov, A.D. Calculation of spectroscopic constants for the ground electronic states of CsK, CsLi, and RbLi molecules. J. Struct. Chem. 2007, 48, 21–27. [Google Scholar] [CrossRef]
- Korek, M.; Younes, G.; Al-Shawa, S. Theoretical calculation of the electronic structure of the molecule LiRb including the spin-orbit interaction. J. Mol. Struc. THEOCHEM 2009, 899, 25–31. [Google Scholar] [CrossRef]
- Dardouri, R.; Issa, K.; Oujia, B.; Gadéa, F.X. Theoretical study of the electronic structure of LiX and NaX (X = Rb, Cs) molecules: Electronic Structure of LiX and NaX Molecules. Int. J. Quantum Chem. 2012, 112, 2724–2734. [Google Scholar] [CrossRef]
- Dardouri, R.; Habli, H.; Oujia, B.; Gadéa, F.X. Ab Initio Diabatic energies and dipole moments of the electronic states of RbLi molecule. J. Comput. Chem. 2013, 34, 2091–2099. [Google Scholar] [CrossRef] [PubMed]
- Jendoubi, I.; Berriche, H.; Ben Ouada, H.; Gadéa, F.X. Radial coupling and adiabatic correction for the LiRb molecule. In Advances in the Theory of Quantum Systems in Chemistry and Physics; Hoggan, P., Brändas, E.J., Maruani, J., Piecuch, P., Delgado-Barrio, G., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 405–430. [Google Scholar]
- Jendoubi, I.; Berriche, H.; Ben Ouada, H.; Gadéa, F.X. Structural and Spectroscopic Study of the LiRb Molecule beyond the Born-Oppenheimer Approximation. J. Phys. Chem. A 2012, 116, 2945–2960. [Google Scholar] [CrossRef]
- Bellayouni, S.; Jendoubi, I.; Mabrouk, N.; Berriche, H. Systematic Study of the Electronic Properties and Trends in the LiX (X=Na, K, Rb, Cs and Fr) Molecules. In Advances in Quantum Chemistry; Hoggan, P., Ed.; Academic Press: Cambridge, MA, USA, 2014; Volume 68, pp. 203–238. [Google Scholar]
- Fedorov, D.A.; Derevianko, A.; Varganov, S.A. Accurate potential energy, dipole moment curves, and lifetimes of vibrational states of heteronuclear alkali dimers. J. Chem. Phys. 2014, 140, 184315. [Google Scholar] [CrossRef]
- You, Y.; Yang, C.L.; Wang, M.S.; Ma, X.G.; Liu, W.W.; Wang, L.Z. Analytic functions for potential energy curves, dipole moments, and transition dipole moments of LiRb molecule. Spectrochim. Acta A 2016, 153, 488–495. [Google Scholar] [CrossRef]
- You, Y.; Yang, C.L.; Zhang, Q.Q.; Wang, M.S.; Ma, X.G.; Liu, W.W. Ab initio studies on the spin-forbidden cooling transitions of the LiRb molecule. Phys. Chem. Chem. Phys. 2016, 18, 19838–19846. [Google Scholar] [CrossRef]
- Kozlov, S.V.; Bormotova, E.A.; Medvedev, A.A.; Pazyuk, E.A.; Stolyarov, A.V.; Zaitsevskii, A. A first principles study of the spin-orbit coupling effect in LiM (M = Na, K, Rb, Cs) molecules. Phys. Chem. Chem. Phys. 2020, 22, 2295–2306. [Google Scholar] [CrossRef] [PubMed]
- Benichou, E.; Allouche, A.R.; Antoine, R.; Aubert-Frecon, M.; Bourgoin, M.; Broyer, M.; Dugourd, P.; Hadinger, G.; Rayane, D. Non perturbative approach for a polar and polarizable linear molecule in an inhomogeneous electric field: Application to molecular beam deviation experiments. Eur. Phys. J. D 2000, 10, 233–242. [Google Scholar] [CrossRef][Green Version]
- Ouerdane, H.; Jamieson, M.J. Scattering parameters for cold Li-Rb and Na-Rb collisions derived from variable phase theory. Phys. Rev. A 2004, 70, 022712. [Google Scholar] [CrossRef]
- Pérez-Ríos, J.; Dutta, S.; Chen, Y.P.; Greene, C.H. Quantum defect theory description of weakly bound levels and Feshbach resonances in LiRb. New J. Phys. 2015, 17, 045021. [Google Scholar] [CrossRef]
- Li, X.; Dutta, S. Extracting molecular potentials from incomplete spectroscopic information. Molecular Physics 2015, 113, 3854–3858. [Google Scholar] [CrossRef][Green Version]
- Lutz, J.J.; Hutson, J.M. Deviations from Born-Oppenheimer mass scaling in spectroscopy and ultracold molecular physics. J. Mol. Spectrosc. 2016, 33, 43–56. [Google Scholar] [CrossRef]
- Bormotova, E.A.; Kozlov, S.V.; Pazyuk, E.A.; Stolyarov, A.V.; Skomorowski, W.; Majewska, I.; Moszynski, R. Ab initio and analytical studies of the spin-orbit coupling in heteronuclear alkali-metal dimers AB (A, B = Li, Na, K, Rb) at long ranges. Phys. Rev. A 2019, 99, 012507. [Google Scholar] [CrossRef]
- Bormotova, E.A.; Stolyarov, A.V.; Skripnikov, L.V.; Titov, A.V. Ab initio study of R-dependent behavior of the hyperfine structure parameters for the (1)1,3Σ+ states of LiRb and LiCs. Chem. Phys. Lett. 2020, 760, 137998. [Google Scholar] [CrossRef]
- Bormotova, E.A.; Kozlov, S.V.; Pazyuk, E.A.; Stolyarov, A.V.; Majewska, I.; Moszynski, R. Theoretical study of the Coriolis effect in LiNa, LiK, and LiRb molecules. Phys. Chem. Chem. Phys. 2021, 23, 5187–5198. [Google Scholar] [CrossRef]
- Lamb, H.D.L.; McCann, J.F.; McLaughlin, B.M.; Goold, J.; Wells, N.; Lane, I. Structure and interactions of ultracold Yb ions and Rb atoms. Phys. Rev. A 2012, 86, 022716. [Google Scholar] [CrossRef]
- ElOualhazi, R.; Berriche, H. Electronic Structure and Spectra of the MgLi+ Ionic Molecule. J. Phys. Chem. A 2016, 120, 452–465. [Google Scholar] [CrossRef] [PubMed]
- Hou, X.-W.; Dong, S.-H.; Ma, Z.-Q. Algebraic Model Applied to Vibrations in the Electronic Ground State of NO2*. Commun. Theor. Phys. 1998, 30, 355–360. [Google Scholar]
- Hou, X.-W.; Xie, M.; Dong, S.-H.; Ma, Z.-Q. Overtone Spectra and Intensities of Tetrahedral Molecules in Boson-Realization Models. Ann. Phys. 1998, 263, 340–352. [Google Scholar] [CrossRef][Green Version]
- Frank, A.; Lemus, R.; Iachello, F. Algebraic model for molecular electronic spectra. In Symmetries in Science V; Gruber, B., Biedenharn, L.C., Doebner, H.D., Eds.; Plenum Press: New York, NY, USA, 1991; pp. 173–186. [Google Scholar]
- Lemus, R. Potential Energy Surfaces Using Algebraic Methods Based on Unitary Groups. Adv. Phys. Chem. 2011, 593872. [Google Scholar] [CrossRef]
- Stanton, J.F.; Bartlett, R.J. The equation of motion coupled-cluster method: A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties. J. Chem. Phys. 1993, 98, 7029–7039. [Google Scholar] [CrossRef]
- Kucharski, S.A.; Włoch, M.; Musial, M.; Bartlett, R.J. Coupled-cluster theory for excited electronic states: The full equation-of-motion coupled-cluster single, double, and triple excitation method. J. Chem. Phys. 2001, 115, 8263–8266. [Google Scholar] [CrossRef]
- Kowalski, K.; Piecuch, P. The active-space equation-of-motion coupled-cluster methods for excited electronic states: Full EOMCCSDt. J. Chem. Phys. 2001, 115, 643–651. [Google Scholar] [CrossRef]
- Hirata, S. Higher-order equation-of-motion coupled-cluster methods. J. Chem. Phys. 2004, 121, 51–59. [Google Scholar] [CrossRef]
- Krylov, A.I. Equation-of-Motion Coupled-Cluster Methods for Open-Shell and Electronically Excited Species: The Hitchhiker’s Guide to Fock Space. Annu Rev. Phys. Chem. 2008, 59, 433. [Google Scholar] [CrossRef]
- Bala, R.; Nataraj, H.S.; Abe, M.; Kajita, M. Accurate ab initio calculations of spectroscopic constants and properties of BeLi+. J. Mol. Spec. 2018, 349, 1–9. [Google Scholar] [CrossRef]
- Bala, R.; Nataraj, H.S.; Abe, M.; Kajita, M. Calculations of electronic properties and vibrational parameters of alkaline-earth lithides: MgLi+ and CaLi+. Mol. Phys. 2019, 117, 712–725. [Google Scholar] [CrossRef]
- Musial, M.; Bartlett, R.J. Charge-transfer separability and size-extensivity in the equation-of-motion coupled cluster method: EOM-CCx. J. Chem. Phys. 2011, 134, 034106. [Google Scholar] [CrossRef] [PubMed]
- Musial, M.; Kucharski, S.A. First principle calculations of the potential energy curves for electronic states of the lithium dimer. J. Chem. Theory Comput. 2014, 10, 1200. [Google Scholar] [CrossRef] [PubMed]
- Musial, M.; Bewicz, A.; Kucharski, S.A. Potential energy curves for electronic states of the sodium dimer with multireference coupled cluster calculations. Mol. Phys. 2023, 121, 1–13. [Google Scholar] [CrossRef]
- Musial, M.; Kucharski, S.A.; Bewicz, A.; Skupin, P.; Tomanek, M. Electronic states of NaLi molecule: Benchmark results with Fock space coupled cluster approach. J. Chem. Phys. 2021, 154, 054109. [Google Scholar] [CrossRef]
- Tomza, M.; Goerz, M.H.; Musial, M.; Moszynski, R.; Koch, C.P. Optimized production of ultracold ground-state molecules: Stabilization employing potentials with ion-pair character and strong spin-orbit coupling. Phys. Rev. A 2012, 86, 043424. [Google Scholar] [CrossRef]
- Salomonsen, S.; Lindgren, I. Martensson, A.-M. Numerical Many-Body Perturbation Calculations on Be-like Systems Using a Multi-Configurational Model Space. Phys. Scr. 1980, 21, 351–355. [Google Scholar] [CrossRef]
- Kaldor, U. Intruder states and incomplete model spaces in multireference coupled-cluster theory: The 2p2 states of Be. Phys. Rev. A 1988, 38, 6013–6016. [Google Scholar] [CrossRef]
- Nakajima, T.; Hirao, K. The higher-order Douglas-Kroll transformation. J. Chem. Phys. 2000, 113, 7786–7789. [Google Scholar] [CrossRef]
- Stanton, J.F.; Gauss, J.; Watts, J.D.; Nooijen, M.; Oliphant, N.; Perera, S.A.; Szalay, P.G.; Lauderdale, W.J.; Kucharski, S.A.; Gwaltney, S.R.; et al. Integral Packages Included Are VMOL (Almlof, J.; Taylor, P.); VPROPS (Taylor, P.R.); A Modified Version of ABACUS Integral Derivative Package (Helgaker, T.U.; Jensen, J.J.A.; Olsen, J.; Joergensen, P.; Taylor, P.R.); ACES II Program is a Product of the Quantum Theory Project; University of Florida: Gainesville, FL, USA, 2005. [Google Scholar]
- Barca, G.M.J.; Bertoni, C.; Carrington, L.; Datta, D.; DeSilva, N.; Deustua, J.E.; Fedorov, D.G.; Gour, J.R.; Gunina, A.O.; Guidez, E.; et al. Recent developments in the general atomic and molecular electronic structure system. J. Chem. Phys. 2020, 152, 154102. [Google Scholar] [CrossRef]
- LeRoy, R.J. LEVEL: A computer program for solving the radial Schrödinger equation for bound and quasibound levels. J. Quant. Spectrosc. Ra. 2017, 186, 167–178. [Google Scholar] [CrossRef]
- Roos, B.O.; Veryazov, V.; Widmark, P.O. Relativistic atomic natural orbital type basis sets for the alkaline and alkaline-earth atoms applied to the ground-state potentials for the corresponding dimers. Theor. Chem. Acc. 2004, 111, 345–351. [Google Scholar] [CrossRef]
- Noro, T.; Sekiya, M.; Koga, T. Segmented contracted basis sets for atoms H through Xe: Sapporo-(DK)-nZP sets (n=D, T, Q). Theor. Chem. Acc. 2012, 131, 1124. [Google Scholar] [CrossRef]
- Skupin, P.; Musial, M.; Kucharski, S.A. Potential Energy Curves for the Low-Lying Electronic States of K2+ from ab Initio Calculations with All Electrons Correlated. J. Phys. Chem. A 2017, 121, 1480–1486. [Google Scholar] [CrossRef] [PubMed]
- Kurtz, H.A.; Stewart, J.J.P.; Dieter, K.M. Calculation of the nonlinear optical properties of molecules. J. Comput. Chem. 1990, 11, 82–87. [Google Scholar] [CrossRef]
- Galván, I.F.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef] [PubMed]
- Tarnovsky, V.; Bunimovicz, M.; Vušković, L.; Stumpf, B.; Bederson, B. Measurements of the dc electric dipole polarizabilities of the alkali dimer molecules, homonuclear and heteronuclear. J. Chem. Phys. 1993, 98, 3894–3904. [Google Scholar] [CrossRef]
- Marzok, C.; Deh, B.; Zimmermann, C.; Courteille, W.; Tiemann, E.; Vanne, Y.V.; Saenz, A. Feshbach resonances in an ultracold 7Li and 87Rb mixture. Phys. Rev. A 2009, 79, 012717. [Google Scholar] [CrossRef]
- Čížek, J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 1966, 45, 4256–4266. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musial, M. Coupled-Cluster theory in Quantum Chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Jeziorski, B.; Monkhorst, H.J. Coupled-cluster method for multideterminantal reference states Phys. Rev. A 1981, 24, 1668–1681. [Google Scholar] [CrossRef]
- Jeziorski, B.; Paldus, J. Spin-adapted multireference coupled-cluster approach: Linear approximation for two closed-shell-type reference configurations. J. Chem. Phys. 1988, 88, 5673–5687. [Google Scholar] [CrossRef]
- Meissner, L.; Jankowski, K.; Wasilewski, J.A. A coupled-cluster method for quasidegenerate states. Int. J. Quantum Chem. 1988, 34, 535–557. [Google Scholar] [CrossRef]
- Berkovic, S.; Kaldor, U. Hilbert space coupled-cluster method in an incomplete model space. Chem. Phys. Lett. 1992, 199, 42–46. [Google Scholar] [CrossRef]
- Mukherjee, D.; Moitra, R.K.; Mukhopadhay, A. Applications of a non-perturbative many-body formalism to general open-shell atomic and molecular problems: Calculation of the ground and the lowest π-π* singlet and triplet energies and the first ionization potential of trans-butadiene. Mol. Phys. 1977, 33, 955–969. [Google Scholar] [CrossRef]
- Mukherjee, D. On the hierarchy equations of the wave-operator for open-shell systems. Pramana 1979, 12, 203–225. [Google Scholar] [CrossRef]
- Mukhopadhay, A.; Moitra, R.K.; Mukherjee, D. A non-perturbative open-shell theory for ionisation potential and excitation energies using HF ground state as the vacuum. J. Phys. B 1979, 12, 1–18. [Google Scholar] [CrossRef]
- Lindgren, I. A coupled-cluster approach to the many-body perturbation theory for open-shell systems. Int. J. Quantum Chem. Symp. 1978, 12, 33–58. [Google Scholar] [CrossRef]
- Stolarczyk, L.Z.; Monkhorst, H.J. Coupled-cluster method in Fock space. I. General formalism. Phys. Rev. A 1985, 32, 725–742. [Google Scholar] [CrossRef]
- Jeziorski, B.; Paldus, J. Valence universal exponential ansatz and the cluster structure of multireference configuration interaction wave function. J. Chem. Phys. 1989, 90, 2714–2731. [Google Scholar] [CrossRef]
- Mukherjee, D.; Pal, S. Use of cluster-expansion methods in the open-shell correlation-problem. Adv. Quantum Chem. 1989, 20, 291–373. [Google Scholar]
- Haque, M.A.; Kaldor, U. Open-shell coupled-cluster theory applied to atomic and molecular systems. Chem. Phys. Lett. 1985, 17, 347–351. [Google Scholar] [CrossRef]
- Meissner, L. A Fock-space coupled-cluster method fully utilizing valence universal strategy. J. Chem. Phys. 1995, 103, 8014–8021. [Google Scholar] [CrossRef]
- Meissner, L.; Bartlett, R.J. A Dressing for the matrix elements of the singles and doubles equation-of-motion coupled-cluster method that recovers additive separability of excitation energies. J. Chem. Phys. 1995, 102, 7490–7498. [Google Scholar] [CrossRef]
- Meissner, L. Fock-space coupled-cluster method in the intermediate Hamiltonian formulation: Model with singles and doubles. J. Chem. Phys. 1998, 108, 9227–9235. [Google Scholar] [CrossRef]
- Musial, M.; Bartlett, R.J. Multireference Fock-space coupled-cluster and Equation-of-Motion coupled-cluster theories: The detailed interconnections. J. Chem. Phys. 2008, 129, 134105. [Google Scholar] [CrossRef] [PubMed]
- Lyakh, D.I.; Musial, M.; Lotrich, V.; Bartlett, R.J. Multireference nature of chemistry: The coupled-cluster view. Chem. Rev. 2012, 112, 182–243. [Google Scholar] [CrossRef]
- Oleynichenko, A.V.; Zaitsevskii, A.; Skripnikov, L.V.; Eliav, E. Relativistic Fock Space Coupled Cluster Method for Many-Electron Systems: Non-Perturbative Account for Connected Triple Excitations. Symmetry 2020, 12, 1101. [Google Scholar] [CrossRef]
- Nooijen, M.; Bartlett, R.J. Equation of motion coupled cluster method for electron attachment. J. Chem. Phys. 1995, 102, 3629–3647. [Google Scholar] [CrossRef]
- Musial, M.; Bartlett, R.J. Equation-of-motion coupled cluster method with full inclusion of the connected triple excitations for electron attached states: EA-EOM-CCSDT. J. Chem. Phys. 2003, 119, 1901–1908. [Google Scholar] [CrossRef]
- Kamiya, M.; Hirata, S. Higher-order equation-of-motion coupled-cluster methods for electron attachment. J. Chem. Phys. 2007, 126, 134112. [Google Scholar] [CrossRef]
- Gour, J.R.; Piecuch, P.; Włoch, M. Active-Space Equation-of-Motion Coupled-Cluster Methods for Excited States of Radicals and Other Open-Shell Systems: EA-EOMCCSDt and IP-EOMCCSDt. J. Chem. Phys. 2005, 123, 134113. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).