Spectroscopic and Computational pH Study of NiII and PdII Pyrrole-Imine Chelates with Human Serum Albumin
Abstract
:1. Introduction
2. Results and Discussion
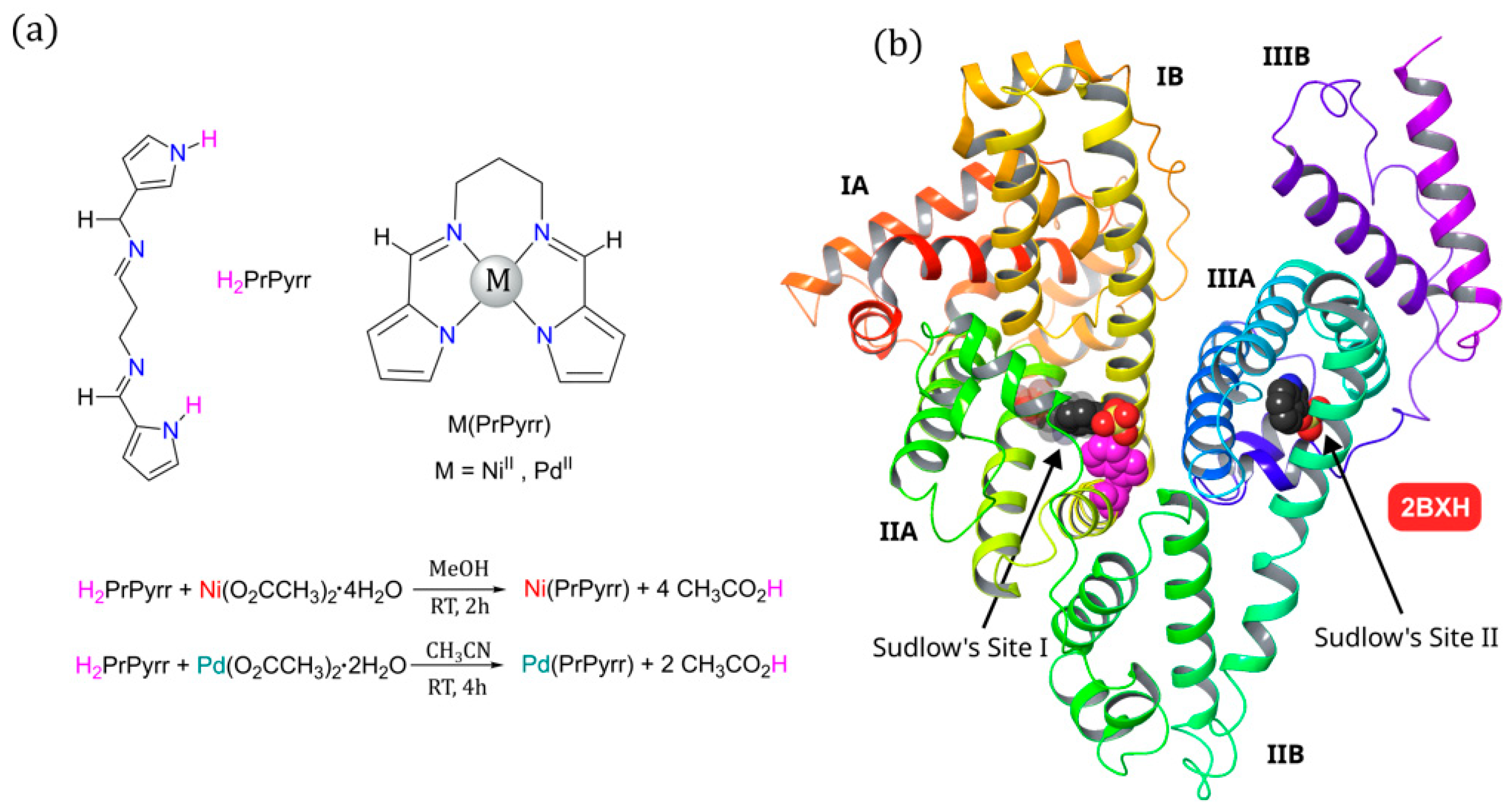
2.1. Metal Chelate Synthesis
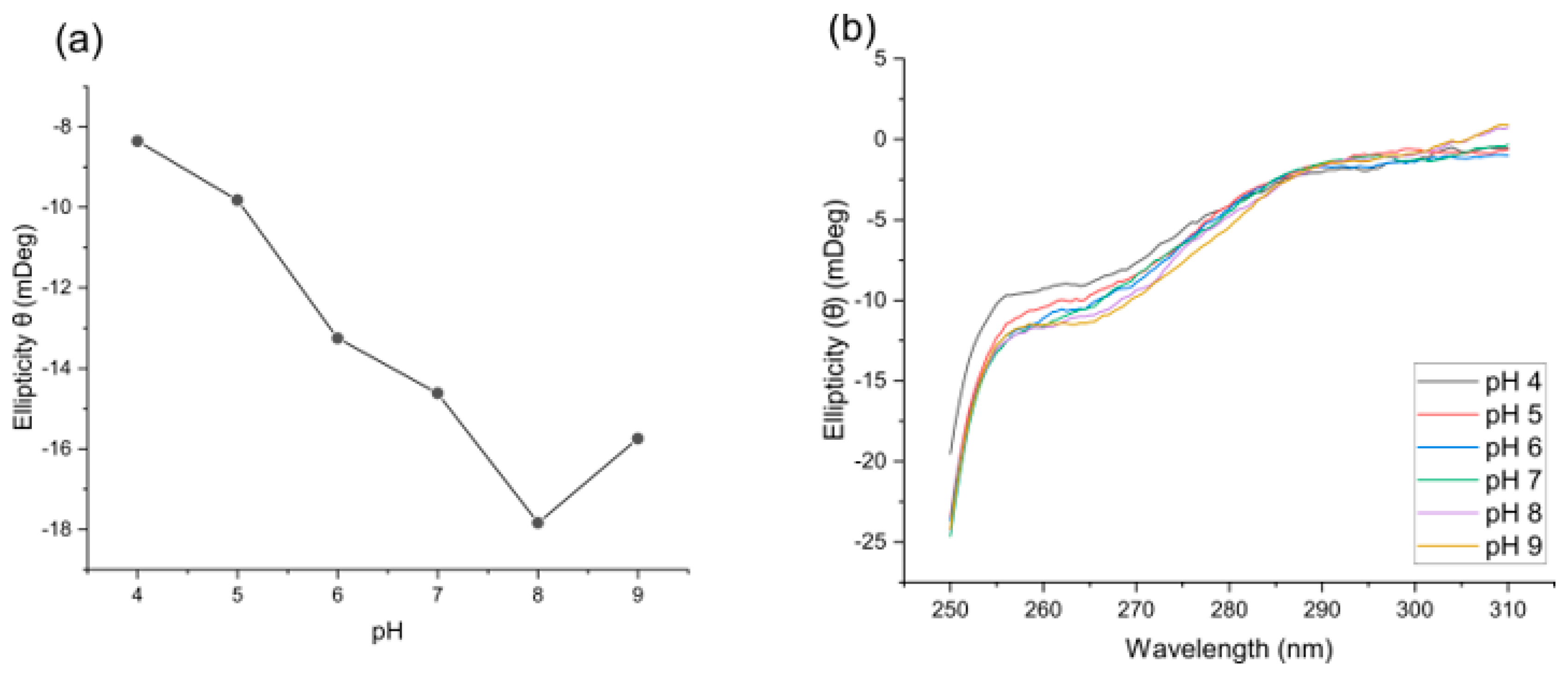
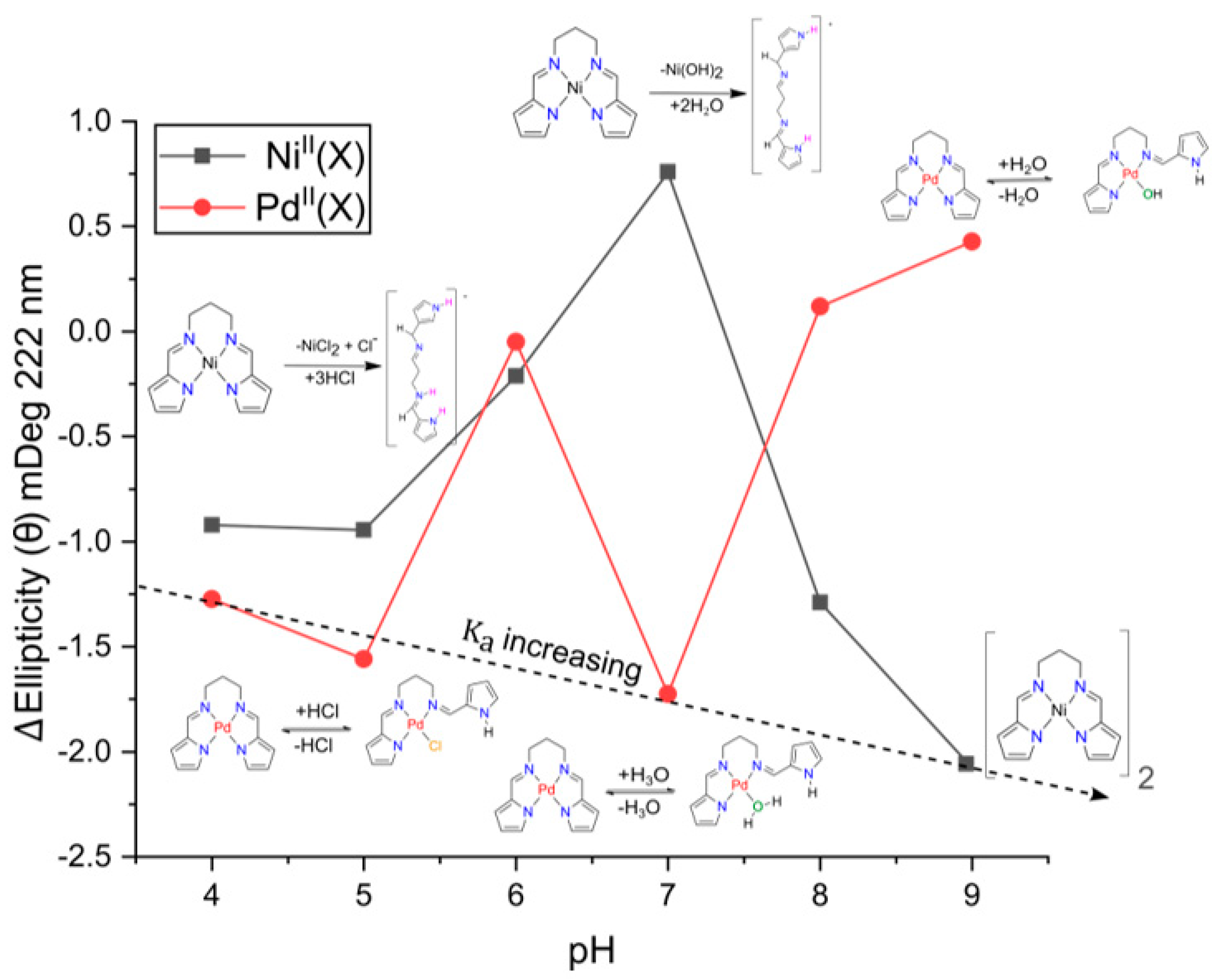
2.2. pH Speciation of Ni(PrPyrr) Species
2.3. Assessing the Binding of the Metal Complex Species to HSA
2.4. Induced Circular Dichroism as a Tool to Investigate the Binding of Small Molecules
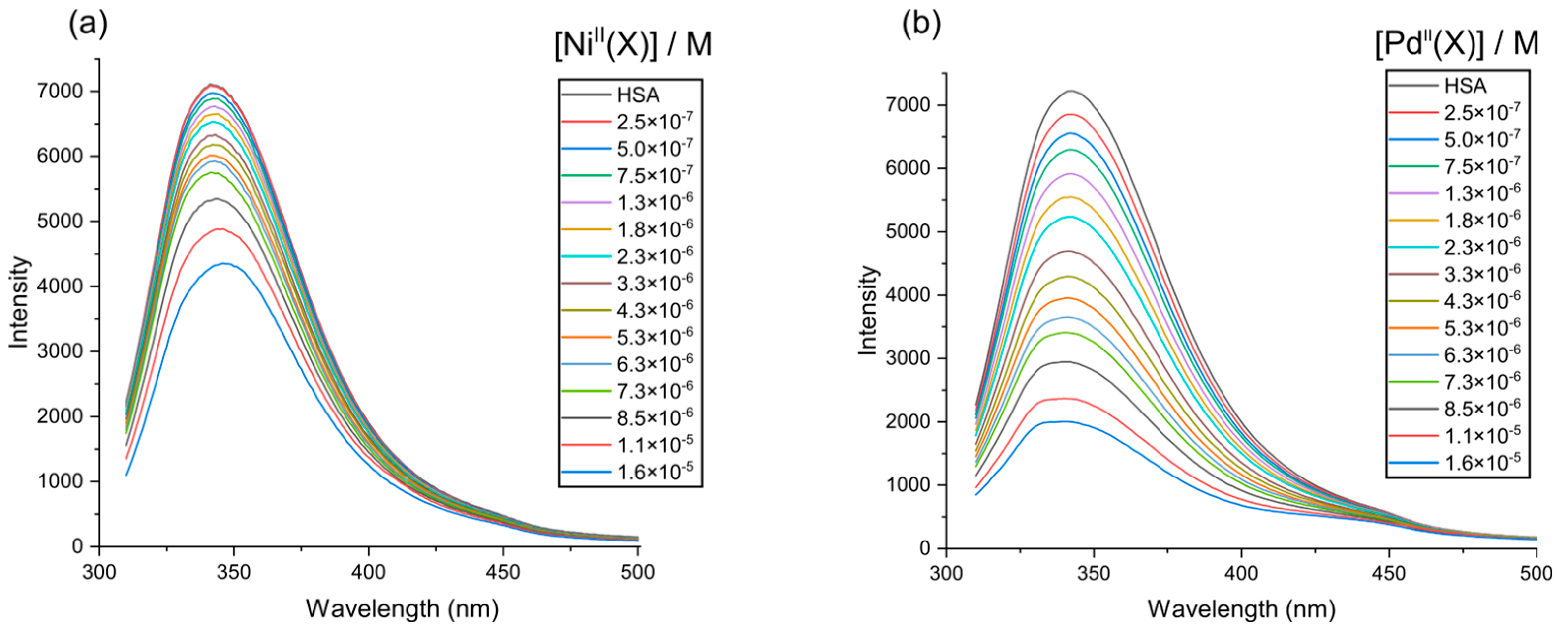
2.5. HSA Fluorescence Quenching by NiII(X) and PdII(X)
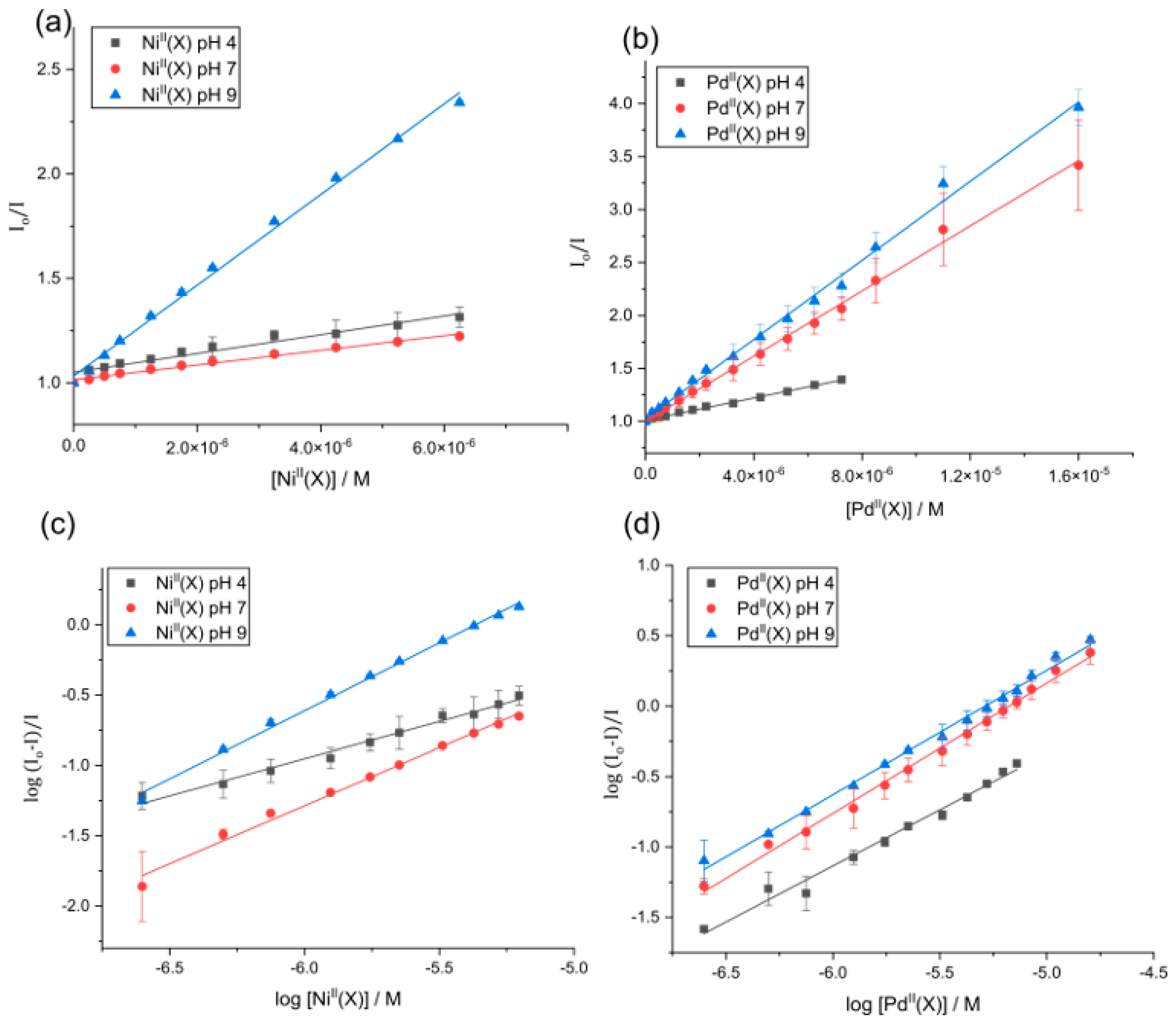
2.6. Fluorescence Quenching Mechanism
2.7. Ligand Binding Equilibrium Constants
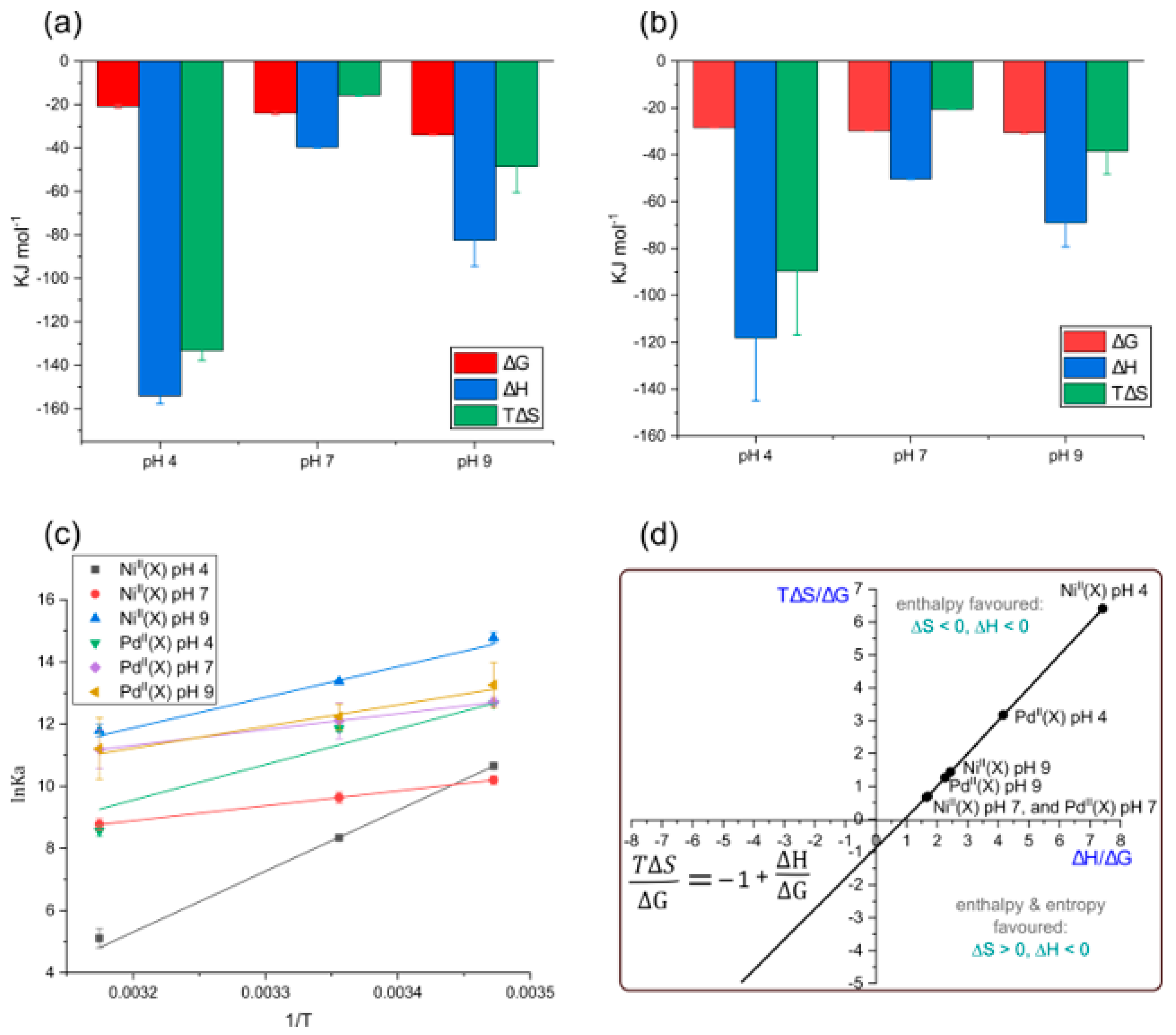
2.8. Thermodynamics of the Ligands Binding by HSA
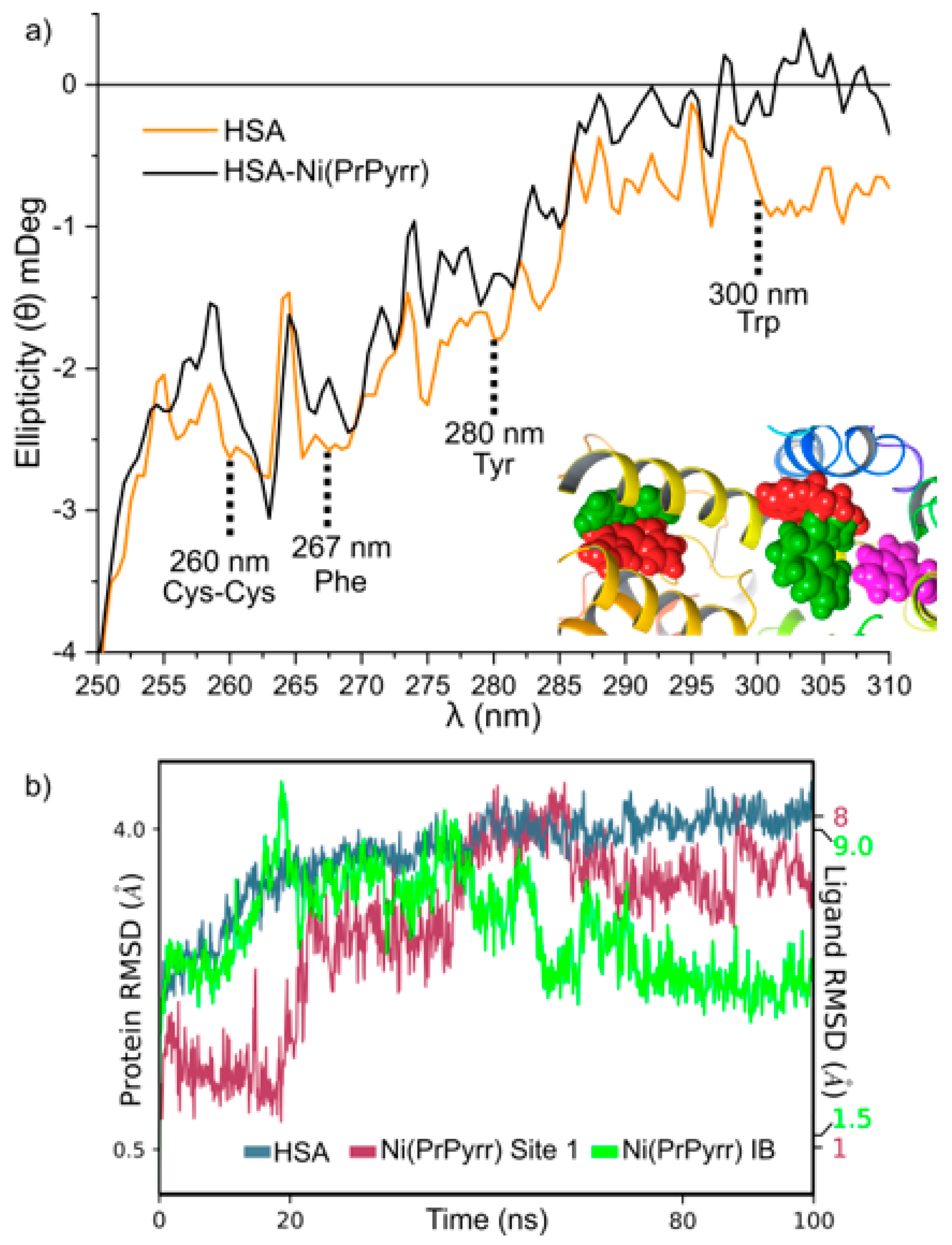
2.9. Ligand and pH-Induced HSA Secondary and Tertiary Structure Changes
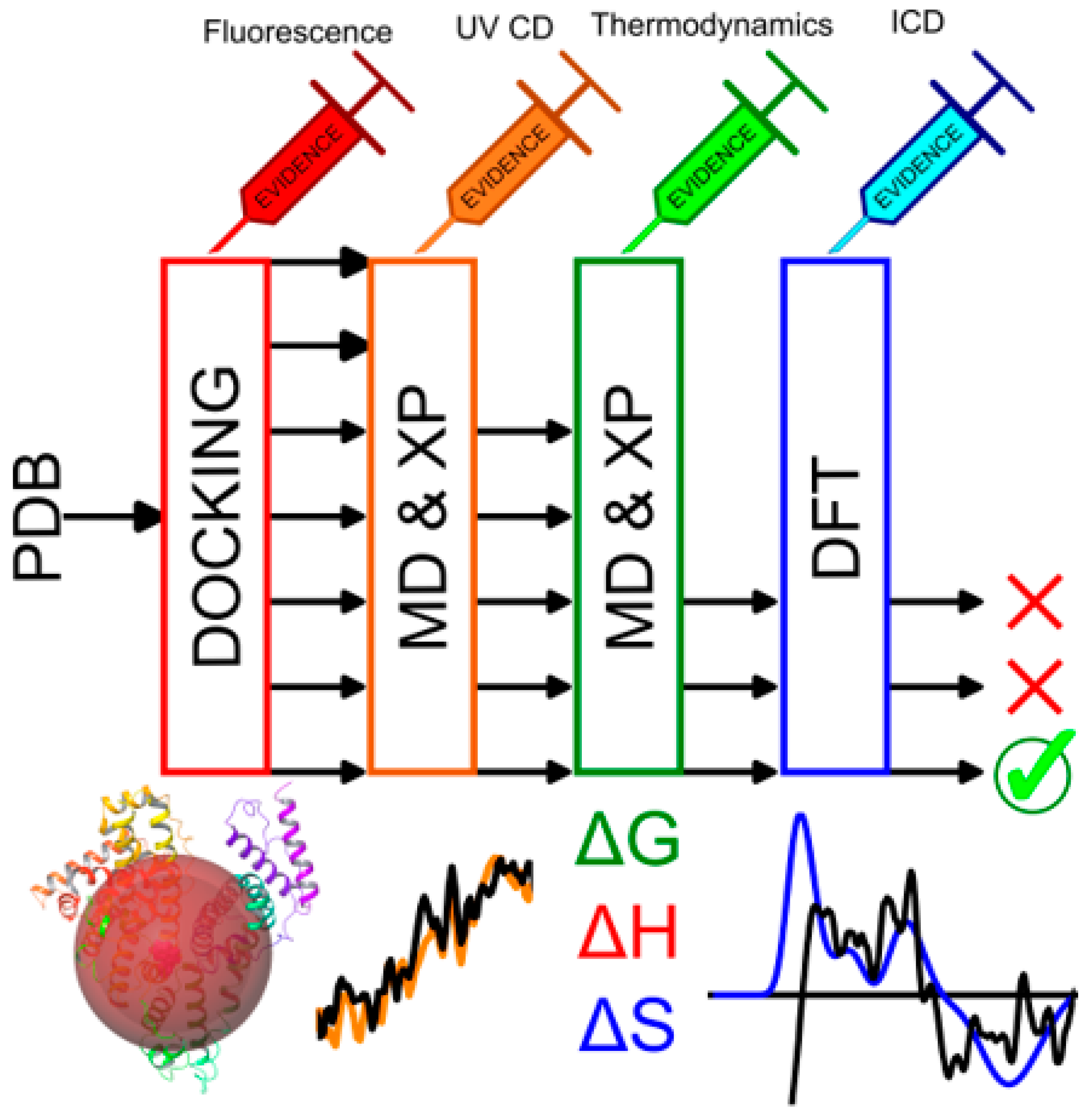
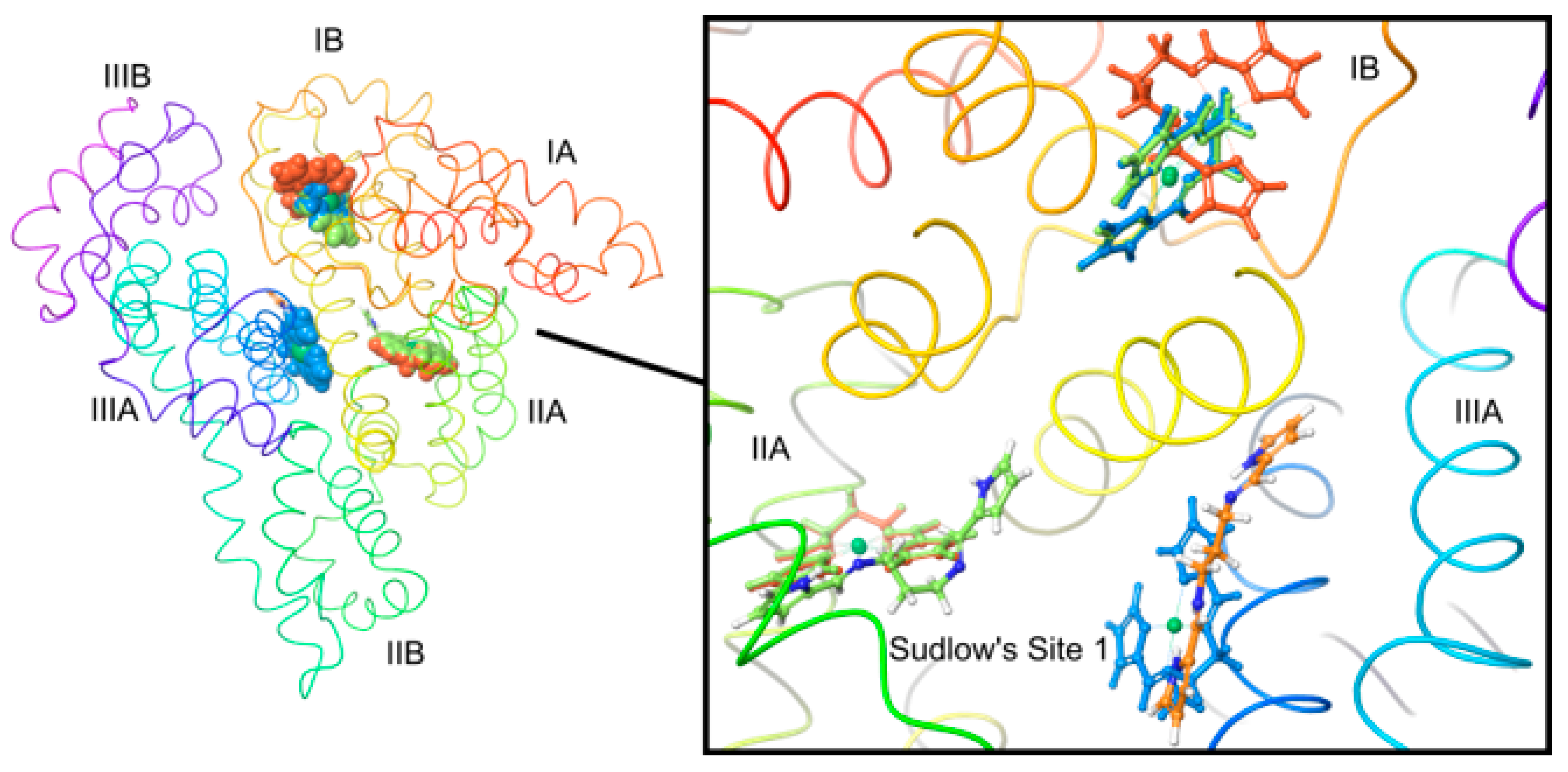
2.10. In Silico Binding Site Determination
3. Materials and Methods
3.1. Experimental Methods
3.2. Instrument Basic Methods
3.3. Compound Synthesis
3.4. Spectroscopic pKa Determinations and Solution Species Characterization
3.5. Fluorescence Spectroscopy
3.6. Circular Dichroism (CD) Spectroscopy
3.7. Density Functional Theory
3.7.1. Ligand Optimization
3.7.2. Ligand TD-DFT
3.7.3. Macromolecular TD-DFT
3.8. Molecular Docking & Dynamics
3.8.1. Ligand Preparation
3.8.2. Protein Preparation
3.8.3. Ligand Docking
3.8.4. Molecular Dynamics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Braun, R.U.; Zeitler, K.; Müller, T.J. A novel one-pot pyrrole synthesis via a coupling-isomerization-stetter-paal-knorr sequence. Org. Lett. 2001, 3, 3297–3300. [Google Scholar] [CrossRef]
- Hewton, C.E.; Kimber, M.C.; Taylor, D.K. A one-pot synthesis of thiophene and pyrrole derivatives from readily accessible 3, 5-dihydro-1, 2-dioxines. Tetrahedron Lett. 2002, 43, 3199–3201. [Google Scholar] [CrossRef]
- Rhine, M.A.; Rodrigues, A.V.; Urbauer, R.J.B.; Urbauer, J.L.; Stemmler, T.L.; Harrop, T.C. Proton-Induced Reactivity of NO− from a {CoNO}8 Complex. J. Am. Chem. Soc. 2014, 136, 12560–12563. [Google Scholar] [CrossRef] [PubMed]
- Brunner, H.; Köllnberger, A.; Zabel, M. Optically active transition metal complexes. Part 133. Preparation, epimerization and crystallization of chiral-at-metal rhodium(III) half-sandwich complexes. Polyhedron 2003, 22, 2639–2646. [Google Scholar] [CrossRef]
- Iverson, C.N.; Carter, C.A.G.; Baker, R.T.; Scollard, J.D.; Labinger, J.A.; Bercaw, J.E. C−H Bond Activation by Unsymmetrical 2-(N-Arylimino)pyrrolide Pt Complexes: Geometric Effects on Reactivity. J. Am. Chem. Soc. 2003, 125, 12674–12675. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.H. Crystallographic determination of stereochemistry for the triclinic and tetragonal modifications of a bis-bidentate metal complex, bis(N-tert-butylpyrrole-2-carbaldimino)copper(II). Inorg. Chem. 1972, 11, 2315–2321. [Google Scholar] [CrossRef]
- Akerman, K.J.; Fagenson, A.M.; Cyril, V.; Taylor, M.; Muller, M.T.; Akerman, M.P.; Munro, O.Q. Gold(III) Macrocycles: Nucleotide-Specific Unconventional Catalytic Inhibitors of Human Topoisomerase I. J. Am. Chem. Soc. 2014, 136, 5670–5682. [Google Scholar] [CrossRef]
- Sookai, S.; Munro, O.Q. Spectroscopic and computational study of the interaction of Pt(II) pyrrole-imine chelates with human serum albumin. Dalton Trans. 2023, 52, 14774–14789. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.H.; Einstein, J.R. Structure of a bis-bidentate metal complex, bis-(N-t-butylpyrrole-2-carbaldimino)nickel(II). Analysis of its configurational disorder in the crystalline state. Acta Crystallogr. B 1972, 28, 2591–2598. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, H.; Shen, F.; Sheng, X.; Peng, A.; Gu, Z.; Ma, H.; Ma, J.S.; Yao, J. Distinct M and P Helical Complexes of H2O and Metal Ions NiII, CuII, and ZnII with Enantiomerically Pure Chiral Bis(pyrrol-2-ylmethyleneamine)cyclohexane Ligands: Crystal Structures and Circular Dichroism Properties. Inorg. Chem. 2007, 46, 3548–3556. [Google Scholar] [CrossRef]
- Bhikraj, S.; Munro, O.Q.; Akerman, M.P. An unusual asymmetric pseudomacrocyclic free base ligand and nickel(II) chelate: X-ray crystallographic and DFT studies. Polyhedron 2017, 124, 22–29. [Google Scholar] [CrossRef]
- Hart, J.S.; Nichol, G.S.; Love, J.B. Directed secondary interactions in transition metal complexes of tripodal pyrrole imine and amide ligands. Dalton Trans. 2012, 41, 5785–5788. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Liu, J.; Li, X.; Li, Y. Synthesis, structure and norbornene polymerization behavior of neutral palladium complexes. Polyhedron 2004, 23, 1619–1627. [Google Scholar] [CrossRef]
- Bhardwaj, V.; Gumber, D.; Abbot, V.; Dhiman, S.; Sharma, P. Pyrrole: A resourceful small molecule in key medicinal hetero-aromatics. RSC Adv. 2015, 5, 15233–15266. [Google Scholar] [CrossRef]
- Brogden, R.N.; Heel, R.C.; Speight, T.M.; Avery, G.S. Tolmetin: A Review of its Pharmacological Properties and Therapeutic Efficacy in Rheumatic Diseases. Drugs 1978, 15, 429–450. [Google Scholar] [CrossRef] [PubMed]
- Atkins, M.; Jones, C.A.; Kirkpatrick, P. Sunitinib maleate. Nat. Rev. Drug Discov. 2006, 5, 279–280. [Google Scholar] [CrossRef]
- Langtry, H.D.; Balfour, J.A. Glimepiride. Drugs 1998, 55, 563–584. [Google Scholar] [CrossRef]
- Hannah, S.; Lynch, V.M.; Gerasimchuk, N.; Magda, D.; Sessler, J.L. Synthesis of a Metal-Free Texaphyrin. Org. Lett. 2001, 3, 3911–3914. [Google Scholar] [CrossRef]
- Patel, H.; Mick, R.; Finlay, J.; Zhu, T.C.; Rickter, E.; Cengel, K.A.; Malkowicz, S.B.; Hahn, S.M.; Busch, T.M. Motexafin Lutetium-Photodynamic Therapy of Prostate Cancer: Short- and Long-Term Effects on Prostate-Specific Antigen. Clin. Cancer Res. 2008, 14, 4869–4876. [Google Scholar] [CrossRef]
- Preihs, C.; Arambula, J.F.; Magda, D.; Jeong, H.; Yoo, D.; Cheon, J.; Siddik, Z.H.; Sessler, J.L. Recent Developments in Texaphyrin Chemistry and Drug Discovery. Inorg. Chem. 2013, 52, 12184–12192. [Google Scholar] [CrossRef]
- Akerman, M.P.; Munro, O.Q.; Mongane, M.; van Staden, J.A.; Rae, W.I.D.; Bester, C.J.; Marjanovic-Painter, B.; Szucs, Z.; Zeevaart, J.R. Biodistribution (as determined by the radiolabelled equivalent) of a gold(III) bis(pyrrolide-imine) Schiff base complex: A potential chemotherapeutic. J. Label. Compd. Radiopharm. 2013, 56, 530–535. [Google Scholar] [CrossRef]
- Biswas, N.; Khanra, S.; Sarkar, A.; Bhattacharjee, S.; Mandal, D.P.; Chaudhuri, A.; Chakraborty, S.; Choudhury, C.R. Cytotoxicity activity, in silico molecular docking, protein- and DNA-binding study of a new Ni(II) Schiff base complex. J. Coord. Chem. 2018, 71, 2740–2766. [Google Scholar] [CrossRef]
- Mbugua, S.N.; Sibuyi, N.R.S.; Njenga, L.W.; Odhiambo, R.A.; Wandiga, S.O.; Meyer, M.; Lalancette, R.A.; Onani, M.O. New Palladium(II) and Platinum(II) Complexes Based on Pyrrole Schiff Bases: Synthesis, Characterization, X-ray Structure, and Anticancer Activity. ACS Omega 2020, 5, 14942–14954. [Google Scholar] [CrossRef] [PubMed]
- Curry, S. Lessons from the crystallographic analysis of small molecule binding to human serum albumin. Drug Metab. Pharmacokinet. 2009, 24, 342–357. [Google Scholar] [CrossRef]
- Quinlan, G.J.; Martin, G.S.; Evans, T.W. Albumin: Biochemical properties and therapeutic potential. Hepatology 2005, 41, 1211–1219. [Google Scholar] [CrossRef]
- Peters, T. All About Albumin: Biochemistry, Genetics, and Medical Applications; Academic Press: Cambridge, MA, USA, 1995; ISBN 978-0-08-052704-8. [Google Scholar]
- Yamasaki, K.; Chuang, V.T.G.; Maruyama, T.; Otagiri, M. Albumin–drug interaction and its clinical implication. Biochim. Biophys. Acta BBA-Gen. Subj. 2013, 1830, 5435–5443. [Google Scholar] [CrossRef] [PubMed]
- Alam, M. Exploration of Binding Affinities of a 3β, 6β-Diacetoxy-5α-cholestan-5-ol with Human Serum Albumin: Insights from Synthesis, Characterization, Crystal Structure, Antioxidant and Molecular Docking. Molecules 2023, 28, 5942. [Google Scholar] [CrossRef]
- Vallianatou, T.; Lambrinidis, G.; Tsantili-Kakoulidou, A. In silico prediction of human serum albumin binding for drug leads. Expert Opin. Drug Discov. 2013, 8, 583–595. [Google Scholar] [CrossRef]
- Hein, K.L.; Kragh-Hansen, U.; Morth, J.P.; Jeppesen, M.D.; Otzen, D.; Møller, J.V.; Nissen, P. Crystallographic analysis reveals a unique lidocaine binding site on human serum albumin. J. Struct. Biol. 2010, 171, 353–360. [Google Scholar] [CrossRef]
- Mao, H.; Hajduk, P.J.; Craig, R.; Bell, R.; Borre, T.; Fesik, S.W. Rational design of diflunisal analogues with reduced affinity for human serum albumin. J. Am. Chem. Soc. 2001, 123, 10429–10435. [Google Scholar] [CrossRef]
- Rabbani, G.; Ahn, S.N. Structure, enzymatic activities, glycation and therapeutic potential of human serum albumin: A natural cargo. Int. J. Biol. Macromol. 2019, 123, 979–990. [Google Scholar] [CrossRef] [PubMed]
- Fogh-Andersen, N.; Bjerrum, P.J.; Siggaard-Andersen, O. Ionic binding, net charge, and Donnan effect of human serum albumin as a function of pH. Clin. Chem. 1993, 39, 48–52. [Google Scholar] [CrossRef] [PubMed]
- Dockal, M.; Carter, D.C.; Ruker, F. Conformational transitions of the three recombinant domains of human serum albumin depending on pH. J. Biol. Chem. 2000, 275, 3042–3050. [Google Scholar] [CrossRef]
- FostER, J.F. Plasma albumin. In The plasma Proteins; Elsevier: Amsterdam, The Netherlands, 1960; pp. 179–239. [Google Scholar]
- Sadler, P.J.; Tucker, A. pH-induced structural transitions of bovine serum albumin: Histidine pKa values and unfolding of the N-terminus during the N to F transition. Eur. J. Biochem. 1993, 212, 811–817. [Google Scholar] [CrossRef] [PubMed]
- Leonard, W.J., Jr.; Vijai, K.K.; Foster, J.F. A structural transformation in bovine and human plasma albumins in alkaline solution as revealed by rotatory dispersion studies. J. Biol. Chem. 1963, 238, 1984–1988. [Google Scholar] [CrossRef]
- Wanwimolruk, S.; Birkett, D.J. The effects of N-B transition of human serum albumin on the specific drug-binding sites. Biochim. Biophys. Acta BBA-Protein Struct. Mol. Enzymol. 1982, 709, 247–255. [Google Scholar] [CrossRef]
- Wilting, J.; Van der Giesen, W.F.; Janssen, L.H.M.; Weideman, M.M.; Otagiri, M.; Perrin, J.H. Effect of albumin conformation on the binding of warfarin to human serum albumin on the hydrogen, calcium and chloride ion concentration as studied by circular dichroism, fluorescence and equilibriam dialysis. J. Biol. Chem. 1980, 255, 3032–3037. [Google Scholar] [CrossRef]
- Wilting, J.; Hart, B.J.; De Gier, J.J. The role of albumin conformation in the binding of diazepam to human serum albumin. Biochim. Biophys. Acta BBA-Protein Struct. 1980, 626, 291–298. [Google Scholar] [CrossRef]
- Fukada, H.; Takahashi, K. Enthalpy and heat capacity changes for the proton dissociation of various buffer components in 0.1 M potassium chloride. Proteins Struct. Funct. Bioinforma. 1998, 33, 159–166. [Google Scholar] [CrossRef]
- Williams, H.D.; Trevaskis, N.L.; Charman, S.A.; Shanker, R.M.; Charman, W.N.; Pouton, C.W.; Porter, C.J. Strategies to address low drug solubility in discovery and development. Pharmacol. Rev. 2013, 65, 315–499. [Google Scholar] [CrossRef]
- Stoll, V.S.; Blanchard, J.S. Buffers: Principles and practice. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 2009; Volume 463, pp. 43–56. [Google Scholar] [CrossRef]
- Ellis, K.J.; Morrison, J.F. [23] Buffers of constant ionic strength for studying pH-dependent processes. In Methods in Enzymology; Elsevier: Amsterdam, The Netherlands, 1982; Volume 87, pp. 405–426. [Google Scholar] [CrossRef]
- Ghuman, J.; Zunszain, P.A.; Petitpas, I.; Bhattacharya, A.A.; Otagiri, M.; Curry, S. Structural Basis of the Drug-binding Specificity of Human Serum Albumin. J. Mol. Biol. 2005, 353, 38–52. [Google Scholar] [CrossRef] [PubMed]
- Bacchi, A.; Carcelli, M.; Gabba, L.; Ianelli, S.; Pelagatti, P.; Pelizzi, G.; Rogolino, D. Syntheses, characterization and X-ray structure of palladium(II) and nickel(II) complexes of tetradentate pyrrole containing ligands. Inorganica Chim. Acta 2003, 342, 229–235. [Google Scholar] [CrossRef]
- Sookai, S.; Munro, O.Q. Complexities of the Interaction of NiII, PdII and PtII Pyrrole-Imine Chelates with Human Serum Albumin. Chem. Eur. 2023, 1, e202300012. [Google Scholar] [CrossRef]
- Rosenfeld, L. Quantenmechanische Theorie der natürlichen optischen Aktivität von Flüssigkeiten und Gasen. Z. Für Phys. 1929, 52, 161–174. [Google Scholar] [CrossRef]
- Allenmark, S. Induced circular dichroism by chiral molecular interaction. Chirality 2003, 15, 409–422. [Google Scholar] [CrossRef] [PubMed]
- Gottarelli, G.; Lena, S.; Masiero, S.; Pieraccini, S.; Spada, G.P. The use of circular dichroism spectroscopy for studying the chiral molecular self-assembly: An overview. Chirality 2008, 20, 471–485. [Google Scholar] [CrossRef]
- Pescitelli, G.; Bari, L.D.; Berova, N. Application of electronic circular dichroism in the study of supramolecular systems. Chem. Soc. Rev. 2014, 43, 5211–5233. [Google Scholar] [CrossRef] [PubMed]
- He, X.M.; Carter, D.C. Atomic structure and chemistry of human serum albumin. Nature 1992, 358, 209–215. [Google Scholar] [CrossRef]
- Ross, P.D.; Subramanian, S. Thermodynamics of protein association reactions: Forces contributing to stability. Biochemistry 1981, 20, 3096–3102. [Google Scholar] [CrossRef]
- Soares, S.; Mateus, N.; de Freitas, V. Interaction of Different Polyphenols with Bovine Serum Albumin (BSA) and Human Salivary α-Amylase (HSA) by Fluorescence Quenching. J. Agric. Food Chem. 2007, 55, 6726–6735. [Google Scholar] [CrossRef]
- Gehlen, M.H. The centenary of the Stern-Volmer equation of fluorescence quenching: From the single line plot to the SV quenching map. J. Photochem. Photobiol. C Photochem. Rev. 2020, 42, 100338. [Google Scholar] [CrossRef]
- Abou-Zied, O.K.; Al-Shihi, O.I.K. Characterization of Subdomain IIA Binding Site of Human Serum Albumin in its Native, Unfolded, and Refolded States Using Small Molecular Probes. J. Am. Chem. Soc. 2008, 130, 10793–10801. [Google Scholar] [CrossRef]
- Callis, P.R. Binding phenomena and fluorescence quenching. I: Descriptive quantum principles of fluorescence quenching using a supermolecule approach. J. Mol. Struct. 2014, 1077, 14–21. [Google Scholar] [CrossRef]
- Yue, Y.; Liu, J.; Yao, M.; Yao, X.; Fan, J.; Ji, H. The investigation of the binding behavior between ethyl maltol and human serum albumin by multi-spectroscopic methods and molecular docking. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2012, 96, 316–323. [Google Scholar] [CrossRef]
- Hussain, A.; AlAjmi, M.F.; Rehman, M.T.; Amir, S.; Husain, F.M.; Alsalme, A.; Siddiqui, M.A.; AlKhedhairy, A.A.; Khan, R.A. Copper(II) complexes as potential anticancer and Nonsteroidal anti-inflammatory agents: In vitro and in vivo studies. Sci. Rep. 2019, 9, 5237. [Google Scholar] [CrossRef]
- Feroz, S.R.; Mohamad, S.B.; Bujang, N.; Malek, S.N.A.; Tayyab, S. Multispectroscopic and Molecular Modeling Approach To Investigate the Interaction of Flavokawain B with Human Serum Albumin. J. Agric. Food Chem. 2012, 60, 5899–5908. [Google Scholar] [CrossRef] [PubMed]
- Divsalar, A.; Bagheri, M.J.; Saboury, A.A.; Mansoori-Torshizi, H.; Amani, M. Investigation on the Interaction of Newly Designed Anticancer Pd(II) Complexes with Different Aliphatic Tails and Human Serum Albumin. J. Phys. Chem. B 2009, 113, 14035–14042. [Google Scholar] [CrossRef] [PubMed]
- Carter, D.C.; Ho, J.X. Structure of serum albumin. Adv. Protein Chem. 1994, 45, 153–203. [Google Scholar]
- Curry, S.; Mandelkow, H.; Brick, P.; Franks, N. Crystal structure of human serum albumin complexed with fatty acid reveals an asymmetric distribution of binding sites. Nat. Struct. Biol. 1998, 5, 827–835. [Google Scholar] [CrossRef]
- Leggio, C.; Galantini, L.; Pavel, N.V. About the albumin structure in solution: Cigar Expanded form versus heart Normal shape. Phys. Chem. Chem. Phys. 2008, 10, 6741–6750. [Google Scholar] [CrossRef]
- Yamasaki, K.; Maruyama, T.; Yoshimoto, K.; Tsutsumi, Y.; Narazaki, R.; Fukuhara, A.; Kragh-Hansen, U.; Otagiri, M. Interactive binding to the two principal ligand binding sites of human serum albumin: Effect of the neutral-to-base transition. Biochim. Biophys. Acta BBA-Protein Struct. Mol. Enzymol. 1999, 1432, 313–323. [Google Scholar] [CrossRef] [PubMed]
- Bos, O.J.M.; Labro, J.F.A.; Fischer, M.J.E.; Wilting, J.; Janssen, L.H.M. The molecular mechanism of the neutral-to-base transition of human serum albumin: Acid/Base titration and proton nuclear magnetic resonance studies on a large peptic and a large tryptic fragment of albumin. J. Biol. Chem. 1989, 264, 953–959. [Google Scholar] [CrossRef] [PubMed]
- Flora, K.; Brennan, J.D.; Baker, G.A.; Doody, M.A.; Bright, F.V. Unfolding of Acrylodan-Labeled Human Serum Albumin Probed by Steady-State and Time-Resolved Fluorescence Methods. Biophys. J. 1998, 75, 1084–1096. [Google Scholar] [CrossRef]
- Helms, M.K.; Petersen, C.E.; Bhagavan, N.V.; Jameson, D.M. Time-resolved fluorescence studies on site-directed mutants of human serum albumin. FEBS Lett. 1997, 408, 67–70. [Google Scholar] [CrossRef]
- Alam, P.; Chaturvedi, S.K.; Anwar, T.; Siddiqi, M.K.; Ajmal, M.R.; Badr, G.; Mahmoud, M.H.; Hasan Khan, R. Biophysical and molecular docking insight into the interaction of cytosine β-D arabinofuranoside with human serum albumin. J. Lumin. 2015, 164, 123–130. [Google Scholar] [CrossRef]
- Ariga, G.G.; Naik, P.N.; Chimatadar, S.A.; Nandibewoor, S.T. Interactions between epinastine and human serum albumin: Investigation by fluorescence, UV–vis, FT–IR, CD, lifetime measurement and molecular docking. J. Mol. Struct. 2017, 1137, 485–494. [Google Scholar] [CrossRef]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: Boston, MA, USA, 2006; ISBN 978-0-387-31278-1. [Google Scholar]
- Li, X.; Wang, S. Study on the interaction of (+)-catechin with human serum albumin using isothermal titration calorimetry and spectroscopic techniques. New J. Chem. 2015, 39, 386–395. [Google Scholar] [CrossRef]
- Du, X.; Li, Y.; Xia, Y.-L.; Ai, S.-M.; Liang, J.; Sang, P.; Ji, X.-L.; Liu, S.-Q. Insights into Protein–Ligand Interactions: Mechanisms, Models, and Methods. Int. J. Mol. Sci. 2016, 17, 144. [Google Scholar] [CrossRef]
- Kelly, S.M.; Jess, T.J.; Price, N.C. How to study proteins by circular dichroism. Biochim. Biophys. Acta BBA-Proteins Proteom. 2005, 1751, 119–139. [Google Scholar] [CrossRef]
- Nikkel, H.J.; Foster, J.F. Reversible sulfhydryl-catalyzed structural alteration of bovine mercaptalbumin. Biochemistry 1971, 10, 4479–4486. [Google Scholar] [CrossRef]
- Sreerama, N.; Woody, R.W. Computation and Analysis of Protein Circular Dichroism Spectra. In Methods in Enzymology; Numerical Computer Methods, Part D; Academic Press: Cambridge, MA, USA, 2004; Volume 383, pp. 318–351. [Google Scholar] [CrossRef]
- Bowers, K.J.; Chow, D.E.; Xu, H.; Dror, R.O.; Eastwood, M.P.; Gregersen, B.A.; Klepeis, J.L.; Kolossvary, I.; Moraes, M.A.; Sacerdoti, F.D.; et al. Scalable Algorithms for Molecular Dynamics Simulations on Commodity Clusters. In Proceedings of the ACM/IEEE SC 2006 Conference (SC’06), Tampa, FL, USA, 11–17 November 2006; IEEE: Piscataway, NJ, USA, 2006; p. 43. [Google Scholar] [CrossRef]
- Friesner, R.A.; Murphy, R.B.; Repasky, M.P.; Frye, L.L.; Greenwood, J.R.; Halgren, T.A.; Sanschagrin, P.C.; Mainz, D.T. Extra Precision Glide: Docking and Scoring Incorporating a Model of Hydrophobic Enclosure for Protein−Ligand Complexes. J. Med. Chem. 2006, 49, 6177–6196. [Google Scholar] [CrossRef]
- Warren, G.L.; Andrews, C.W.; Capelli, A.-M.; Clarke, B.; LaLonde, J.; Lambert, M.H.; Lindvall, M.; Nevins, N.; Semus, S.F.; Senger, S.; et al. A Critical Assessment of Docking Programs and Scoring Functions. J. Med. Chem. 2006, 49, 5912–5931. [Google Scholar] [CrossRef]
- Chung, L.W.; Sameera, W.M.C.; Ramozzi, R.; Page, A.J.; Hatanaka, M.; Petrova, G.P.; Harris, T.V.; Li, X.; Ke, Z.; Liu, F.; et al. The ONIOM Method and Its Applications. Chem. Rev. 2015, 115, 5678–5796. [Google Scholar] [CrossRef]
- Banks, J.L.; Beard, H.S.; Cao, Y.; Cho, A.E.; Damm, W.; Farid, R.; Felts, A.K.; Halgren, T.A.; Mainz, D.T.; Maple, J.R.; et al. Integrated Modeling Program, Applied Chemical Theory (IMPACT). J. Comput. Chem. 2005, 26, 1752–1780. [Google Scholar] [CrossRef]
- Munro, O.Q.; Camp, G.L. Self-recognition in a flexible bis(pyrrole) Schiff base derivative: Formation of a one-dimensional hydrogen-bonded polymer. Acta Crystallogr. C 2003, 59, o672–o675. [Google Scholar] [CrossRef] [PubMed]
- Van de Weert, M.; Stella, L. Fluorescence quenching and ligand binding: A critical discussion of a popular methodology. J. Mol. Struct. 2011, 998, 144–150. [Google Scholar] [CrossRef]
- van de Weert, M. Fluorescence quenching to study protein-ligand binding: Common errors. J. Fluoresc. 2010, 20, 625–629. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Check, C.E.; Faust, T.O.; Bailey, J.M.; Wright, B.J.; Gilbert, T.M.; Sunderlin, L.S. Addition of Polarization and Diffuse Functions to the LANL2DZ Basis Set for P-Block Elements. J. Phys. Chem. A 2001, 105, 8111–8116. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, version 6.0.16; Semichem Inc.: Shawnee Mission, KS, USA, 2016.
- Lipparini, F.; Scalmani, G.; Mennucci, B.; Cancès, E.; Caricato, M.; Frisch, M.J. A variational formulation of the polarizable continuum model. J. Chem. Phys. 2010, 133, 014106. [Google Scholar] [CrossRef] [PubMed]
- Fuentealba, P.; Preuss, H.; Stoll, H.; Von Szentpály, L. A proper account of core-polarization with pseudopotentials: Single valence-electron alkali compounds. Chem. Phys. Lett. 1982, 89, 418–422. [Google Scholar] [CrossRef]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Madhavi Sastry, G.; Adzhigirey, M.; Day, T.; Annabhimoju, R.; Sherman, W. Protein and ligand preparation: Parameters, protocols, and influence on virtual screening enrichments. J. Comput. Aided Mol. Des. 2013, 27, 221–234. [Google Scholar] [CrossRef]
- Shelley, J.C.; Cholleti, A.; Frye, L.L.; Greenwood, J.R.; Timlin, M.R.; Uchimaya, M. Epik: A software program for pK a prediction and protonation state generation for drug-like molecules. J. Comput. Aided Mol. Des. 2007, 21, 681–691. [Google Scholar] [CrossRef]
- Friesner, R.A.; Banks, J.L.; Murphy, R.B.; Halgren, T.A.; Klicic, J.J.; Mainz, D.T.; Repasky, M.P.; Knoll, E.H.; Shelley, M.; Perry, J.K.; et al. Glide: A New Approach for Rapid, Accurate Docking and Scoring. 1. Method and Assessment of Docking Accuracy. J. Med. Chem. 2004, 47, 1739–1749. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Jorgensen, W.L. Convergence of Monte Carlo simulations of liquid water in the NPT ensemble. Chem. Phys. Lett. 1982, 92, 405–410. [Google Scholar] [CrossRef]
- Dong, C.; Ma, S.; Liu, Y. Studies of the interaction between demeclocycline and human serum albumin by multi-spectroscopic and molecular docking methods. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2013, 103, 179–186. [Google Scholar] [CrossRef]
- Wang, G.; Li, X.; Ding, X.; Wang, D.; Yan, C.; Lu, Y. Exploring the mechanism of interaction between 5-(ethoxycarbonyl)-6-methyl-4-(4-methoxyphenyl)-3,4-dihydropyrimidin-2(1H)-one and human serum albumin: Spectroscopic, calorimetric and molecular modeling studies. J. Pharm. Biomed. Anal. 2011, 55, 1223–1226. [Google Scholar] [CrossRef] [PubMed]




| T (K) | Ni(II)X | Pd(II)X | |
|---|---|---|---|
| Log Ka [a] | Log Ka [a] | ||
| pH 4 | 288 | 4.62 (±0.01) | 5.15 (±0.02) |
| 298 | 3.65 (±0.06) | 4.62 (±0.01) | |
| 310 | 2.22 (±0.06) | 3.71 (±0.04) | |
| 288 | 4.43 (±0.03) | 5.55 (±0.04) | |
| pH 7 | 298 | 4.18 (±0.04) | 5.13 (±0.12) |
| 310 | 3.29 (±0.02) | 4.93 (±0.12) | |
| 288 | 6.42 (±0.04) | 5.74 (±0.12) | |
| pH 9 | 298 | 5.81 (±0.01) | 5.31 (±0.10) |
| 310 | 5.12 (±0.04) | 4.97 (±0.06) |
| NiII(X) [a] | PdII(X) [b] | ||||||
|---|---|---|---|---|---|---|---|
| pH | T (K) | ∆G [c] kJ mol−1 | ∆H [c] kJ mol−1 | T∆S [c] kJ mol−1 | ∆G [c] kJ mol−1 | ∆H [c] kJ mol−1 | T∆S [c] kJ mol−1 |
| 288.00 | −25.26 (±0.9) | −31.31 (±0.1) | |||||
| 4.00 | 298.00 | −20.79 (±0.9) | −154 (±3.6) | −133 (±4.5) | −28.30 (±0.1) | −118 (±27) | −89.70 (±11) |
| 310.00 | −15.43 (±0.9) | −24.69 (±0.1) | |||||
| 288.00 | −24.44 (±0.7) | −30.43 (±0.1) | |||||
| 7.00 | 298.00 | −23.91 (±0.7) | −39.70 (±0.3) | −15.79 (±3) | −29.74 (±0.1) | −50.30 (±1) | −20.56 (±0.1) |
| 310.00 | −23.27 (±0.7) | −28.91 (±0.1) | |||||
| 288.00 | −35.46 (±0.1) | −31.75 (±0.4) | |||||
| 9.00 | 298.00 | −33.83 (±0.1) | −82.40 (±12) | −48.57 (±12) | −30.46 (±0.4) | −68.90 (±10) | −38.44 (±10.4) |
| 310.00 | −31.87 (±0.1) | −28.91 (±0.4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sookai, S.; Bracken, M.L.; Nowakowska, M. Spectroscopic and Computational pH Study of NiII and PdII Pyrrole-Imine Chelates with Human Serum Albumin. Molecules 2023, 28, 7466. https://doi.org/10.3390/molecules28227466
Sookai S, Bracken ML, Nowakowska M. Spectroscopic and Computational pH Study of NiII and PdII Pyrrole-Imine Chelates with Human Serum Albumin. Molecules. 2023; 28(22):7466. https://doi.org/10.3390/molecules28227466
Chicago/Turabian StyleSookai, Sheldon, Matthew Lee Bracken, and Monika Nowakowska. 2023. "Spectroscopic and Computational pH Study of NiII and PdII Pyrrole-Imine Chelates with Human Serum Albumin" Molecules 28, no. 22: 7466. https://doi.org/10.3390/molecules28227466
APA StyleSookai, S., Bracken, M. L., & Nowakowska, M. (2023). Spectroscopic and Computational pH Study of NiII and PdII Pyrrole-Imine Chelates with Human Serum Albumin. Molecules, 28(22), 7466. https://doi.org/10.3390/molecules28227466







