Molecular Liquids versus Ionic Liquids: The Interplay between Inter-Molecular and Intra-Molecular Hydrogen Bonding as Seen by Vaporisation Thermodynamics
Abstract
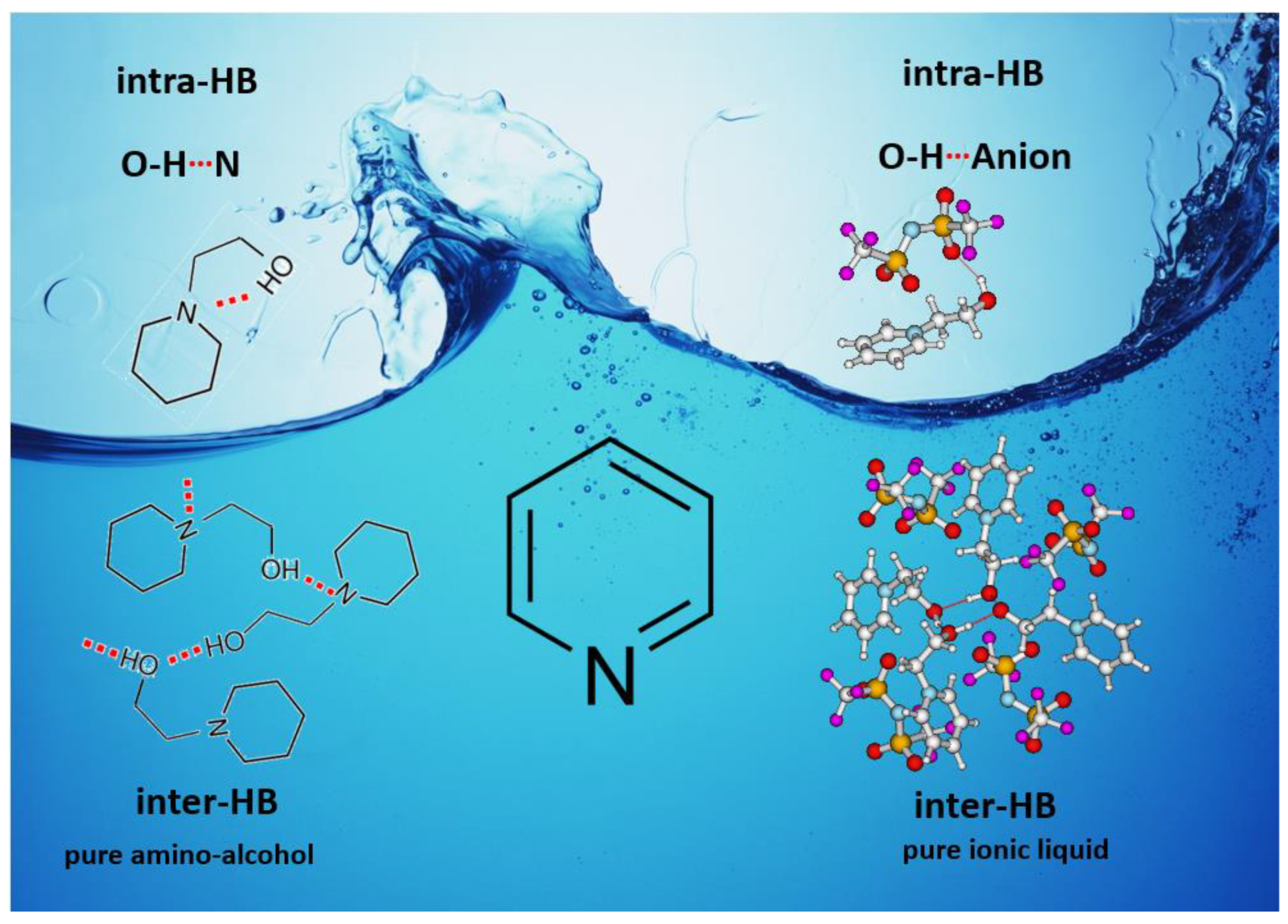
1. Introduction
2. Molecular Liquids: Strength of the Inter-Molecular Hydrogen Bonding
2.1. Series of Hydroxy-Alkyl-Piperidines
2.2. Series of Hydroxy-Alkylbenzenes
2.3. Ionic Liquids: Strength of the Inter-Molecular Hydrogen Bonding
3. Thermodynamic Methods: Strength of the Intra-Molecular Hydrogen Bonding
3.1. Basics of the Group Additivity Concept (“Centerpiece” Approach)
3.2. Intra-HB Strength from Group-Additivity
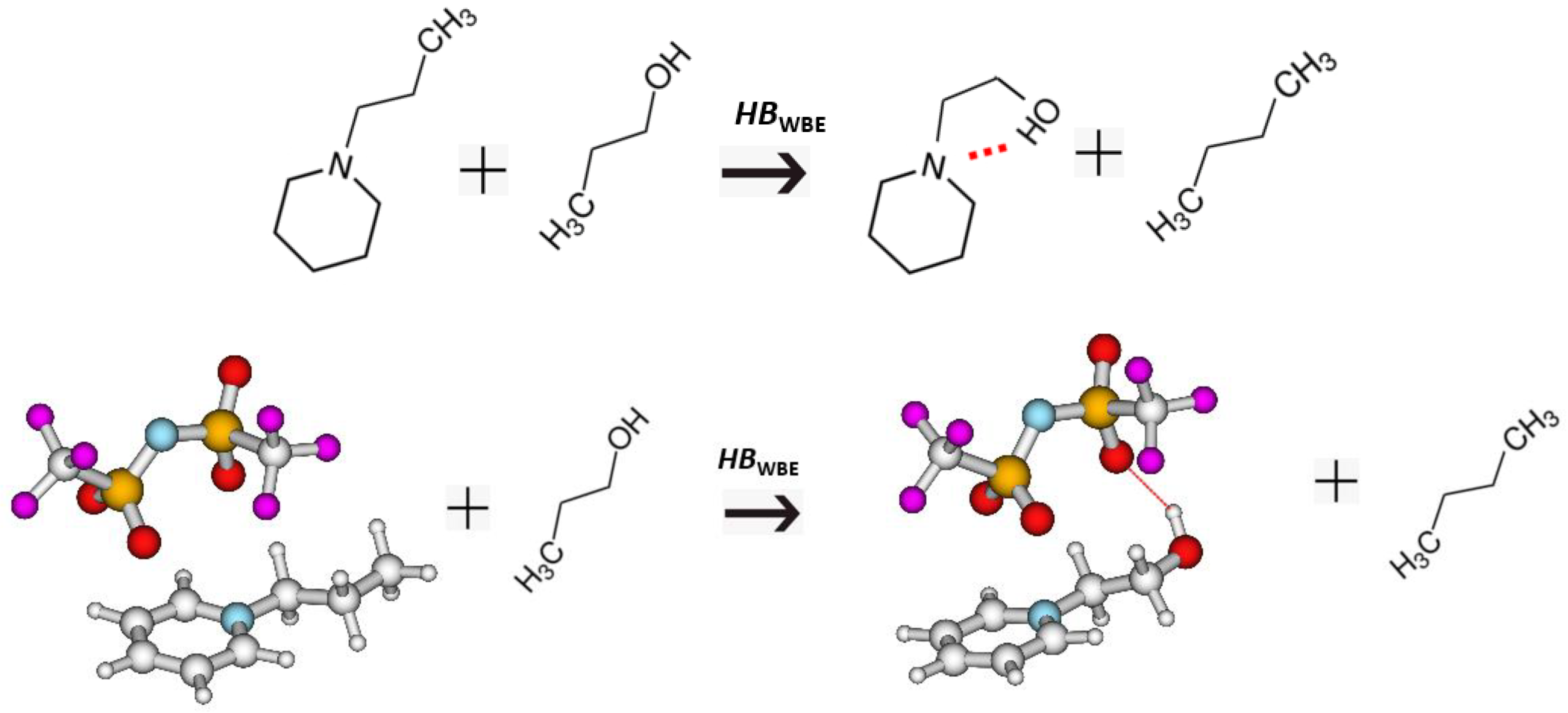
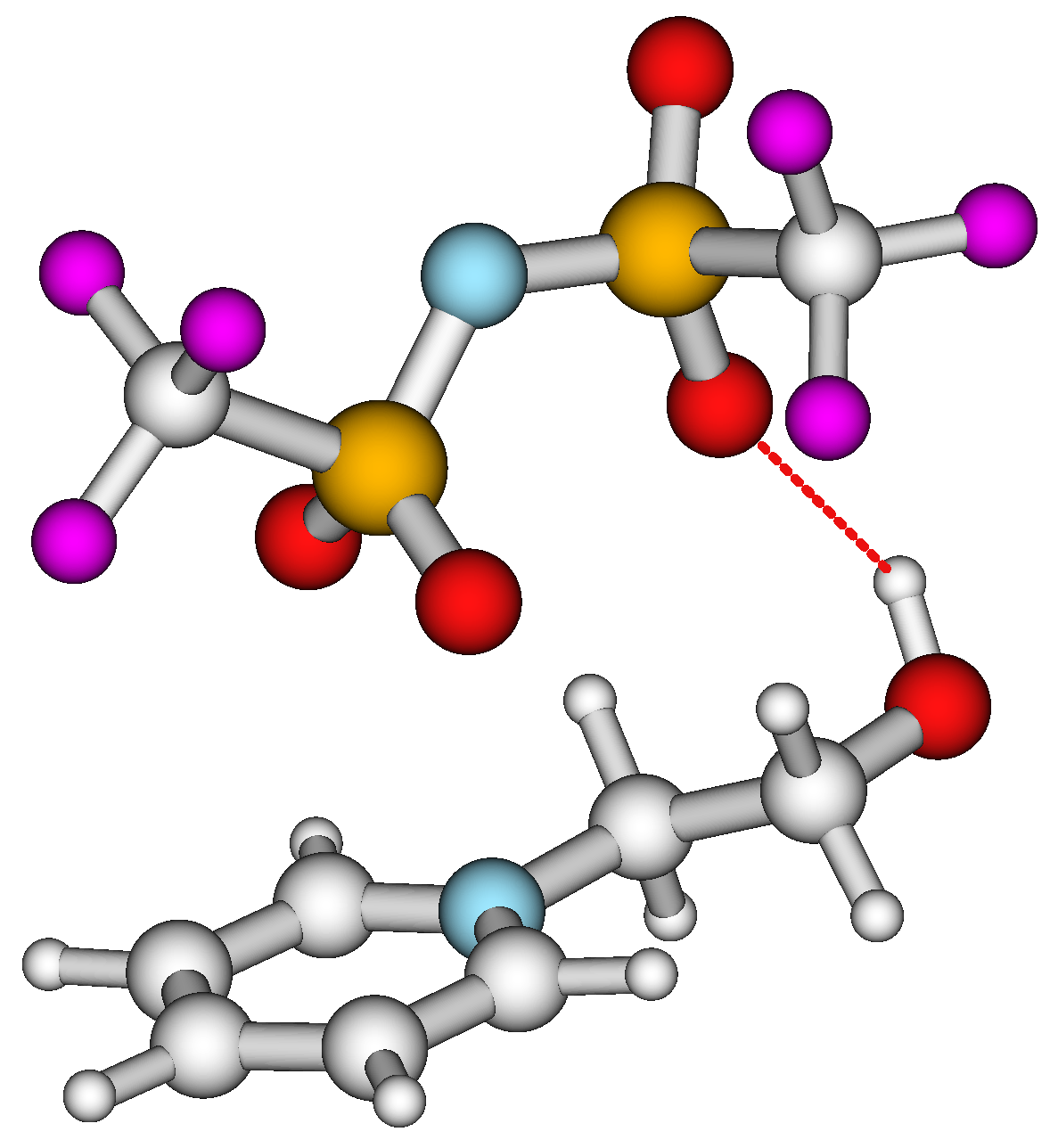
3.3. Intra-HB Strength from Well-Balanced Equations
3.4. Intra-HB Strength in ML and IL Series
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Verevkin, S.P.; Zaitsau, D.H.; Schick, C.; Heym, F. Development of direct and indirect methods for the determination of vaporization enthalpies of extremely low-volatile compounds. In Handbook of Thermal Analysis and Calorimetry; Elsevier: Amsterdam, The Netherlands, 2018; Volume 6, ISBN 9780444640628. [Google Scholar]
- Siewert, R.; Ludwig, R.; Verevkin, S.P. Non-covalent interactions in molecular systems: Thermodynamic evaluation of the hydrogen bond strength in aminoalcohols. Phys. Chem. Chem. Phys. 2021, 23, 25226–25238. [Google Scholar] [CrossRef]
- Siewert, R.; Zherikova, K.V.; Verevkin, S.P. Non-covalent interactions in molecular systems: Thermodynamic evaluation of the hydrogen-bond strength in amino-ethers and amino-alcohols. Chem. Eur. J. 2022, 28, e2022000802022. [Google Scholar] [CrossRef]
- Emel’yanenko, V.N.; Stange, P.; Feder-Kubis, J.; Verevkin, S.P.; Ludwig, R. Dissecting intermolecular interactions in the condensed phase of ibuprofen and related compounds: The specific role and quantification of hydrogen bonding and dispersion forces. Phys. Chem. Chem. Phys. 2020, 22, 4896–4904. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Kondratev, S.O.; Zaitsau, D.H.; Zherikova, K.V.; Ludwig, R. Quantification and understanding of non-covalent interactions in molecular and ionic systems: Dispersion interactions and hydrogen bonding analysed by thermodynamic methods. J. Mol. Liq. 2021, 343, 117547. [Google Scholar] [CrossRef]
- Hunger, L.; Al-Sheakh, L.; Zaitsau, D.H.; Verevkin, S.P.; Appelhagen, A.; Villinger, A.; Ludwig, R. Dissecting noncovalent interactions in carboxyl-functionalized ionic liquids exhibiting double and single hydrogens bonds between ions of like charge. Chem. Eur. J. 2022, 28, e2022009492022. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Ludwig, R.; Verevkin, S.P. Determination of the dispersion forces in the gas phase structures of ionic liquids using exclusively thermodynamic methods. Phys. Chem. Chem. Phys. 2021, 23, 7398–7406. [Google Scholar] [CrossRef]
- Shelepova, E.A.; Paschek, D.; Ludwig, R.; Medvedev, N.N. Comparing the void space and long-range structure of an ionic liquid with a neutral mixture of similar sized molecules. J. Mol. Liq. 2020, 299, 112121. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Neumann, J.; Niemann, T.; Strate, A.; Paschek, D.; Verevkin, S.P.; Ludwig, R. Isolating the role of hydrogen bonding in hydroxyl-functionalized ionic liquids by means of vaporization enthalpies, infrared spectroscopy and molecular dynamics simulations. Phys. Chem. Chem. Phys. 2019, 21, 20308–20314. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Emel´yanenko, V.N.; Stange, P.; Verevkin, S.P.; Ludwig, R. Dissecting the vaporization enthalpies of ionic liquids by exclusively experimental methods: Coulomb interaction, hydrogen bonding, and dispersion forces. Angew. Chem. Int. Ed. 2019, 58, 8589–8592. [Google Scholar] [CrossRef]
- Bonsa, A.-M.; Paschek, D.; Zaitsau, D.H.; Emel´yanenko, V.N.; Verevkin, S.P.; Ludwig, R. The relation between vaporization enthalpies and viscosities: Eyring’s theory applied to selected ionic liquids. ChemPhysChem 2017, 18, 1242–1246. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Emel´yanenko, V.N.; Stange, P.; Schick, C.; Verevkin, S.P.; Ludwig, R. Dispersion and hydrogen bonding rule: Why the vaporization enthalpies of aprotic ionic liquids are significantly larger than those of protic ionic liquids. Angew. Chem. Int. Ed. 2016, 55, 11682–11686. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, R. The effect of dispersion forces on the interaction energies and far infrared spectra of protic ionic liquids. Phys. Chem. Chem. Phys. 2015, 17, 13790–13793. [Google Scholar] [CrossRef]
- Emel´yanenko, V.N.; Boeck, G.; Verevkin, S.P.; Ludwig, R. Volatile times for the very first ionic liquid: Understanding the vapor pressures and enthalpies of vaporization of ethylammonium nitrate. Chem. Eur. J. 2014, 20, 11640–11645. [Google Scholar] [CrossRef] [PubMed]
- Fumino, K.; Wulf, A.; Verevkin, S.P.; Heintz, A.; Ludwig, R. Estimating enthalpies of vaporization of imidazolium-based ionic liquids from far-infrared measurements. ChemPhysChem 2010, 11, 1623–1626. [Google Scholar] [CrossRef] [PubMed]
- Kulikov, D.; Verevkin, S.P.; Heintz, A. Enthalpies of vaporization of a series of aliphatic alcohols: Experimental results and values predicted by the ERAS-model. Fluid Phase Equilib. 2001, 192, 187–207. [Google Scholar] [CrossRef]
- Majer, V.V.; Svoboda, V.V.; Kehiaian, H.V. Enthalpies of Vaporization of Organic Compounds: A Critical Review and Data Compilation; Blackwell Scientific Publications: Oxford, MO, USA, 1985; ISBN 0632015292. [Google Scholar]
- Pimentel, G.C.; McClellan, A.L. Hydrogen Bond; Freeman: San Francisco, CA, USA, 1960. [Google Scholar]
- Jeffrey, G.A.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer: Berlin/Heidelberg, Germany, 1991; ISBN 978-3-540-57903-8. [Google Scholar]
- Verevkin, S.P.; Konnova, M.E.; Zherikova, K.V.; Pimerzin, A.A. Sustainable hydrogen storage: Thermochemistry of amino-alcohols as seminal liquid organic hydrogen carriers. J. Chem. Thermodyn. 2021, 163, 106591. [Google Scholar] [CrossRef]
- Verevkin, S.P. Thermochemistry of amines: Experimental standard molar enthalpies of formation of N-alkylated piperidines. Struct. Chem. 1998, 9, 113–119. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Andreeva, I.V.; Pimerzin, A.A. Evaluation of vaporization thermodynamics of pure amino-alcohols. J. Mol. Liq. 2021, 335, 116568. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Vasiltsova, T.V. Thermochemistry of Benzyl Alcohol: Reaction Equilibria Involving Benzyl Alcohol and tert-Alkyl Ethers. J. Chem. Eng. Data 2004, 49, 1717–1723. [Google Scholar] [CrossRef]
- Emel´yanenko, V.N.; Dabrowska, A.; Hertel, M.O.; Scheuren, H.; Sommer, K. Vapor Pressures, Enthalpies of Vaporization, and Limiting Activity Coefficients in Water at 100 °C of 2-Furanaldehyde, Benzaldehyde, Phenylethanal, and 2-Phenylethanol. J. Chem. Eng. Data 2007, 52, 468–471. [Google Scholar] [CrossRef]
- Verevkin, S.P. Vapour pressures and enthalpies of vaporization of a series of the linear n-alkyl-benzenes. J. Chem. Thermodyn. 2006, 38, 1111–1123. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Zaitsau, D.H.; Emel´yanenko, V.N.; Heintz, A. A new method for the determination of vaporization enthalpies of ionic liquids at low temperatures. J. Phys. Chem. B 2011, 115, 12889–12895. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Zaitsau, D.H.; Emel´yanenko, V.N.; Ralys, R.V.; Yermalayeu, A.V.; Schick, C. Vaporization enthalpies of imidazolium based ionic liquids. A thermogravimetric study of the alkyl chain length dependence. J. Chem. Thermodyn. 2012, 54, 433–437. [Google Scholar] [CrossRef]
- Verevkin, S.P. Imidazolium based ionic liquids: Unbiased recovering of vaporization enthalpies from infinite-dilution activity coefficients. Molecules 2021, 26, 5873. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Zaitsau, D.H.; Ludwig, R. Aprotic ionic liquids: A framework for predicting vaporization thermodynamics. Molecules 2022, 27, 2321. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Yermalayeu, A.V.; Emel´yanenko, V.N.; Schulz, A.; Verevkin, S.P. Thermochemistry of pyridinium based ionic liquids with tetrafluoroborate anion. ZAAC 2017, 643, 87–92. [Google Scholar] [CrossRef]
- Emel´yanenko, V.N.; Verevkin, S.P.; Heintz, A. Pyridinium based ionic liquids. N-Butyl-3-methyl-pyridinium dicyanoamide: Thermochemical measurement and first-principles calculations. Thermochim. Acta 2011, 514, 28–31. [Google Scholar] [CrossRef]
- Krueger, P.J.; Mettee, H.D. Spectroscopic studies of alcohols: VI. Intramolecular hydrogen bonds in ethanolamine and its o- and n-methyl derivatives. Can. J. Chem. 1965, 43, 2970–2977. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Emel´yanenko, V.N.; Diky, V.; Muzny, C.D.; Chirico, R.D.; Frenkel, M. New group-contribution approach to thermochemical properties of organic compounds: Hydrocarbons and oxygen-containing compounds. J. Phys. Chem. Ref. Data 2013, 42, 33102. [Google Scholar] [CrossRef]
- Ducros, M.; Gruson, J.F.; Sannier, H.; Velasco, I. Estimation des enthalpies de vaporisation des composes organiques liquides. Partie 2. Applications aux ethersoxydes, thioalcanes, cetones et amines. Thermochim. Acta 1981, 44, 131–140. [Google Scholar] [CrossRef]
- Verevkin, S.P. Predicting enthalpy of vaporization of Ionic Liquids: A simple rule for a complex property. Angew. Chem. Int. Ed. 2008, 47, 5071–5074. [Google Scholar] [CrossRef]
- Flett, M.S.C. Studies of the band near 3 μ in some hydroxy compounds. Spectrochim. Acta 1957, 10, 21–37. [Google Scholar] [CrossRef]
- Wheeler, S.E.; Houk, K.N.; Schleyer, P.v.R.; Allen, W.D. A hierarchy of homodesmotic reactions for thermochemistry. J. Am. Chem. Soc. 2009, 131, 2547–2560. [Google Scholar] [CrossRef]
- Kulikov, D.; Verevkin, S.P.; Heintz, A. Determination of vapor pressures and vaporization enthalpies of the aliphatic branched C5 and C6 alcohols. J. Chem. Eng. Data 2001, 46, 1593–1600. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Emel´yanenko, V.N. Transpiration method: Vapor pressures and enthalpies of vaporization of some low-boiling esters. Fluid Phase Equilib. 2008, 266, 64–75. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Sazonova, A.Y.; Emel´yanenko, V.N.; Zaitsau, D.H.; Varfolomeev, M.A.; Solomonov, B.N.; Zherikova, K.V. Thermochemistry of halogen-substituted methylbenzenes. J. Chem. Eng. Data 2015, 60, 89–103. [Google Scholar] [CrossRef]
- Emel´yanenko, V.N.; Verevkin, S.P. Benchmark thermodynamic properties of 1,3-propanediol: Comprehensive experimental and theoretical study. J. Chem. Thermodyn. 2015, 85, 111–119. [Google Scholar] [CrossRef]
- Chickos, J.S.; Acree, W.E. Enthalpies of vaporization of organic and organometallic compounds, 1880–2002. J. Phys. Chem. Ref. Data 2003, 32, 519–878. [Google Scholar] [CrossRef]
- Chickos, J.S.; Hosseini, S.; Hesse, D.G.; Liebman, J.F. Heat capacity corrections to a standard state: A comparison of new and some literature methods for organic liquids and solids. Struct. Chem. 1993, 4, 271–278. [Google Scholar] [CrossRef]
- Scifinder. Available online: https://scifinder.cas.org/ (accessed on 29 December 2022).
- Nichols, N.; Wadsö, I. Thermochemistry of solutions of biochemical model compounds 3. Some benzene derivatives in aqueous solution. J. Chem. Thermodyn. 1975, 7, 329–336. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Yermalayeu, A.V.; Emel’yanenko, V.N.; Verevkin, S.P.; Welz-Biermann, U.; Schubert, T. Structure-property relationships in ILs: A study of the alkyl chain length dependence in vaporisation enthalpies of pyridinium based ionic liquids. Sci. China Chem. 2012, 55, 1525–1531. [Google Scholar] [CrossRef]
- Diedrichs, A.; Gmehling, J. Measurement of heat capacities of ionic liquids by differential scanning calorimetry. Fluid Phase Equilib. 2006, 244, 68–77. [Google Scholar] [CrossRef]
- Ahmadi, A.; Haghbakhsh, R.; Raeissi, S.; Hemmati, V. A simple group contribution correlation for the prediction of ionic liquid heat capacities at different temperatures. Fluid Phase Equilib. 2015, 403, 95–103. [Google Scholar] [CrossRef]
- Ribeiro da Silva, M.A.V.; Cabral, J.I.T.A. Standard molar enthalpies of formation of 1-methyl-2-piperidinemethanol, 1-piperidineethanol, and 2-piperidineethanol. J. Chem. Thermodyn. 2006, 38, 1461–1466. [Google Scholar] [CrossRef]
- Lepori, L.; Matteoli, E.; Gianni, P. Vapor pressure and its temperature dependence of 28 organic compounds: Cyclic amines, cyclic ethers, and cyclic and open chain secondary alcohols. J. Chem. Eng. Data 2017, 62, 194–203. [Google Scholar] [CrossRef]
- Zhuravleva, I.L. Evaluation of the polarity and boiling points of nitrogen-containing heterocyclic compounds by gas chromatography. Russ. Chem. Bull. 2000, 49, 325–328. [Google Scholar] [CrossRef]
- Sauerbrey, G. Verwendung von Schwingquarzen zur Wägung dünner Schichten und zur Mikrowägung. Zeitschrift Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Yermalayeu, A.V.; Emel´yanenko, V.N.; Butler, S.; Schubert, T.; Verevkin, S.P. Thermodynamics of imidazolium-based ionic liquids containing PF6 anions. J. Phys. Chem. B 2016, 120, 7949–7957. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Ralys, R.V.; Zaitsau, D.H.; Emel´yanenko, V.N.; Schick, C. Express thermo-gravimetric method for the vaporization enthalpies appraisal for very low volatile molecular and ionic compounds. Thermochim. Acta 2012, 538, 55–62. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Yoo, B.; Afzal, W.; Prausnitz, J.M. Solubility parameters for nine ionic liquids. Ind. Eng. Chem. Res. 2012, 51, 9913–9917. [Google Scholar] [CrossRef]
- Hansen, C.M. 50 Years with solubility parameters—Past and future. Prog. Org. Coat. 2004, 51, 77–84. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics: A Ready-Reference Book of Chemical and Physical Data, 90th ed.; CRC Press: Boca Raton, FL, USA, 2009; ISBN 9781420090840. [Google Scholar]
- Marciniak, A. Activity coefficients at infinite dilution and physicochemical properties for organic solutes and water in the ionic liquid 1-(3-hydroxypropyl)pyridinium bis(trifluoromethylsulfonyl)-amide. J. Chem. Thermodyn. 2011, 43, 1446–1452. [Google Scholar] [CrossRef]
- Marciniak, A. The Hildebrand solubility parameters of ionic liquids—Part 2. Int. J. Mol. Sci. 2011, 12, 3553–3575. [Google Scholar] [CrossRef]
- Domańska, U.; Wlazło, M.; Karpińska, M.; Zawadzki, M. Separation of binary mixtures hexane/hex-1-ene, cyclohexane/cyclohexene and ethylbenzene/styrene based on limiting activity coefficients. J. Chem. Thermodyn. 2017, 110, 227–236. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Zaitsau, D.H.; Emel´yanenko, V.; Yermalayeu, A.V.; Schick, C.; Liu, H.; Maginn, E.J.; Bulut, S.; Krossing, I.; Kalb, R.; et al. Making sense of enthalpy of vaporization trends for ionic liquids: New experimental and simulation data show a simple linear relationship and help reconcile previous data. J. Phys. Chem. B 2013, 117, 6473–6486. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Yermalayeu, A.V.; Pimerzin, A.A.; Verevkin, S.P. Imidazolium based ionic liquids containing methanesulfonate anion: Comprehensive thermodynamic study. Chem. Eng. Res. Des. 2018, 137, 164–173. [Google Scholar] [CrossRef]



| Compound | Compound | HBinter (Equation (1)) | FWb | HBintra (Equation (2)) | ||
|---|---|---|---|---|---|---|
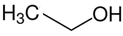 ethanol | 42.5 | 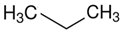 propane | 16.3 | −26.0 | 42.5 | −0.2 |
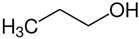 1-propanol | 47.5 | 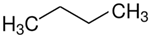 butane | 22.4 | −25.1 | 47.5 | 0.0 |
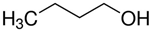 1-butanol | 52.4 |  pentane | 26.8 | −25.6 | 52.5 | −0.1 |
 1-pentanol | 57.0 |  hexane | 31.7 | −25.3 | 57.5 | −0.5 |
| Compound | Compound | HBinter (Equation (1)) | FWc | HBintra (Equation (2)) | HBintra (Equation (3)) | ||
|---|---|---|---|---|---|---|---|
 1-piperidine-ethanol | 58.1 ± 0.4 | 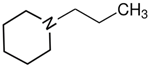 N-propyl-piperidine | 44.9 ± 0.4 | −13.2 | 72.0 | −13.9 | −11.9 |
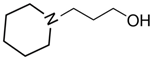 1-piperidine-propanol | 62.1 ± 0.4 | 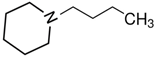 N-butyl-piperidine | 48.9 ± 0.2 | −13.2 | 77.0 | −14.9 | −12.4 |
 1-piperidine-butanol | 70.0 ± 2.6 | 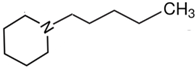 N-pentyl-piperidine | 53.7 ± 1.0 | −16.3 | 82.0 | −12.0 | −9.0 |
 N,N-diEt-2-aminoethanol | 52.6 ± 0.2 [20] | 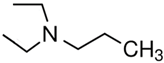 N,N-diEt-propylamine | 39.8 ± 0.2 [17] | −12.8 | 66.2 | −13.6 | −12.3 |
| Compound | Compound | HBinter (Equation (1)) | FWb | HBintra (Equation (2)) | HBintra (Equation (3)) | ||
|---|---|---|---|---|---|---|---|
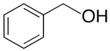 phenyl-methanol | 65.8 ± 0.5 [23] |  ethylbenzene | 42.3 | −23.5 | 68.5 | −2.7 | −2.7 |
 2-phenyl-ethanol | 66.7 ± 0.3 [24] | 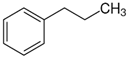 1-propylbenzene | 46.2 | −20.5 | 73.5 | −6.8 | −4.6 |
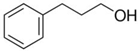 3-phenyl-1-propanol | 75.1 ± 2.4 [Table S4] |  1-butylbenzene | 50.8 | −24.3 | 78.5 | −3.4 | −1.3 |
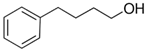 4-phenyl-1-butanol | 80.2 ± 3.0 [Table S4] | 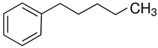 1-pentylbenzene | 55.1 | −25.1 | 73.5 | −3.3 | −0.2 |
| IL | Method | Trange | Tav | |||
|---|---|---|---|---|---|---|
| K | K | kJ·mol−1 | J·mol−1·K−1 | kJ·mol−1 | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| [N-C2OH-Py][NTf2] | TGA | 532–592 | 562 | 125.2 ± 1.1 | 68 | 143.1 ± 3.8 |
| QCM | 379–428 | 403.6 | 134.6 ± 1.0 | 141.8 ± 1.7 | ||
| 142.0 ± 1.6e | ||||||
| [N-C3OH-Py][NTf2] | QCM | 389–436 | 412.5 | 136.8 ± 1.0 | 72 | 145.0 ± 1.9 |
| GC | 298 | 143.6 ± 3.0 f | ||||
| 144.6 ± 1.9e | ||||||
| [N-C4OH-Py][NTf2] | QCM | 359–409 | 382.6 | 143.0 ± 0.8 | 76 | 149.4 ± 1.5 |
| [N-C3OH-Py][DCA] | TGA | 532–592 | 563.7 | 141.6 ± 2.0 | 81 | 163.1 ± 4.7 |
| GC | 298 | 163.9 ± 3.0 g | ||||
| 163.7 ± 2.5e | ||||||
| [N-C3OH-Py][BF4] | TGA | 532–592 | 563.7 | 134.5 ± 2.1 | 67 | 152.3 ± 4.1 |
| [N-C3H7-Py][NTf2] | QCM | 375.1–422.4 | 398.2 | 127.9 ± 0.5 | 66 | 134.5 ± 1.4 |
| [N-C4H9-Py][NTf2] | QCM | 377.6–422.3 | 399.5 | 131.0 ± 0.5 | 70 | 138.0 ± 1.5 |
| [N-C2OH-Py][OMs] | QCM | 394.1–444.2 | 419.1 | 136.0 ± 1.0 | 74 | 145.0 ± 2.1 |
| [N-C3OH-Py][OMs] | QCM | 379.2–451.2 | 412.7 | 136.8 ± 1.0 | 81 | 146.1 ± 2.1 |
| Cation | Cation | HBinter (Equation (1)) | FWb | HBintra (Equation (2)) | HBintra (Equation (3)) | ||
|---|---|---|---|---|---|---|---|
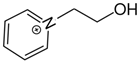 1-(2-hydroxyethyl)pyridinium | 142.0 ± 1.6 | 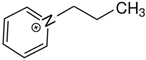 1-propyl-pyridinium | 134.5 ± 1.4 | −7.5 | 162.1 | −20.1 | −17.6 |
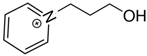 1-(3-hydroxypropyl)pyridinium | 144.6 ± 1.9 | 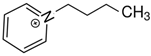 1-butyl-pyridinium | 138.0 ± 1.5 | −6.6 | 165.7 | −21.1 | −19.0 |
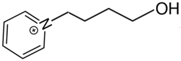 1-(4-hydroxybutyl)pyridinium | 149.4 ± 1.5 | 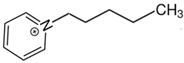 1-pentyl-pyridinium | 141.7 ± 1.8 [29] | −7.7 | 169.3 | −19.9 | −17.6 |
| IL | IL | HBinter (Equation (1)) | HBintra (Equation (3)) | ||
|---|---|---|---|---|---|
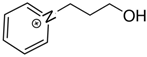 DCA DCA1-(3-hydroxypropyl)pyridinium | 163.7 ± 2.5 | 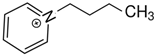 DCA DCA1-propyl-pyridinium | 162.1 ± 4.1 b | −1.6 | −24.0 |
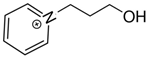 BF4 BF41-(3-hydroxypropyl)pyridinium | 152.3 ± 4.1 | 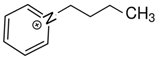 BF4 BF41-butyl-pyridinium | 149.9 ± 2.3 [30] | −2.4 | −23.2 |
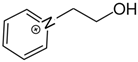 OMs OMs1-(2-hydroxyethyl)pyridinium | 145.0 ± 2.1 | 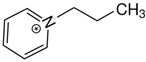 OMs OMs1-propyl-pyridinium | 152.6 ± 2.1 c | 7.6 | −32.7 |
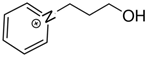 OMs OMs1-(3-hydroxypropyl)pyridinium | 146.1 ± 2.1 | 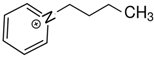 OMs OMs1-butyl-pyridinium | 156.0 ± 2.1 c | 9.9 | −35.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verevkin, S.P.; Zaitsau, D.H.; Ludwig, R. Molecular Liquids versus Ionic Liquids: The Interplay between Inter-Molecular and Intra-Molecular Hydrogen Bonding as Seen by Vaporisation Thermodynamics. Molecules 2023, 28, 539. https://doi.org/10.3390/molecules28020539
Verevkin SP, Zaitsau DH, Ludwig R. Molecular Liquids versus Ionic Liquids: The Interplay between Inter-Molecular and Intra-Molecular Hydrogen Bonding as Seen by Vaporisation Thermodynamics. Molecules. 2023; 28(2):539. https://doi.org/10.3390/molecules28020539
Chicago/Turabian StyleVerevkin, Sergey P., Dzmitry H. Zaitsau, and Ralf Ludwig. 2023. "Molecular Liquids versus Ionic Liquids: The Interplay between Inter-Molecular and Intra-Molecular Hydrogen Bonding as Seen by Vaporisation Thermodynamics" Molecules 28, no. 2: 539. https://doi.org/10.3390/molecules28020539
APA StyleVerevkin, S. P., Zaitsau, D. H., & Ludwig, R. (2023). Molecular Liquids versus Ionic Liquids: The Interplay between Inter-Molecular and Intra-Molecular Hydrogen Bonding as Seen by Vaporisation Thermodynamics. Molecules, 28(2), 539. https://doi.org/10.3390/molecules28020539






