Abstract
Recently, non-fullerene-based organic solar cells (OSCs) have made great breakthroughs, and small structural differences can have dramatic impacts on the power conversion efficiency (PCE). We take ITIC and its isomers as examples to study their effects on the performance of OSCs. ITIC and NFBDT only differed in the side chain position, and they were used as models with the same donor molecule, PBDB-T, to investigate the main reasons for the difference in their performance in terms of theoretical methods. In this work, a detailed comparative analysis of the electronic structure, absorption spectra, open circuit voltage and interfacial parameters of the ITIC and NFBDT systems was performed mainly by combining the density functional theory/time-dependent density functional theory and molecular dynamics simulations. The results showed that the lowest excited state of the ITIC molecule possessed a larger ∆q and more hybrid FE/CT states, and PBDB-T/ITIC had more charge separation paths as well as a larger kCS and smaller kCR. The reason for the performance difference between PBDB-T/ITIC and PBDB-T/NFBDT was elucidated, suggesting that ITIC is a superior acceptor based on a slight modulation of the side chain and providing a guiding direction for the design of superior-performing small molecule acceptor materials.
1. Introduction
As a promising renewable photovoltaic technology, organic solar cells (OSCs) can directly convert sunlight and electricity, with significant advantages such as a low cost, light weight, flexibility, adjustable optical transparency, etc. [1,2,3]. As the best of OSC device architectures so far, the bulk heterojunction (BHJ), which is vital to achieve efficient charge extraction and transport, is composed with a blend of a donor and an acceptor [4]. Due to the rapid development of small molecule acceptors, OSCs have achieved high power conversion efficiencies (PCEs) of [5]. Totally, acceptors are classified into two categories, which are fullerene acceptors (FAs) and non-fullerene acceptors (NFAs). Fullerene has been an efficient acceptor in past decades, but its inherent properties including weak light absorption and limited chemical structural tunability have posed limitations on its further development. Meanwhile, the high cost and poor thermal stability of FA-based OSCs are not conducive to the commercialization progress of OSCs [6]. Compared with FAs, NFAs with stronger and wider absorption, precisely tuned bandgap, crystallization properties and ease of synthesis are regarded as superior materials [7]. Recently, NFAs, which contain the A-D-A and A-DA’D-A structures, have been utilized widely and play a pivotal role in advancing OSC performance [8,9]. For instance, perylene diimide (PDI) dimers of bis-PDI-T-EG linked through thiophene reduced aggregation and resulted in a PCE of 4.03% with the donor of PBDTTT-CT relative to the PDI monomer [10]. The TPH NFA and selenium-annulated TPH-Se with fused PDI monomers were synthesized. In particular, its single-crystal architectures exhibited a propeller-like 3D network that accelerates electron transport, with the PCEs reaching 8.28% and 9.28%, respectively [11]. In 2015, Zhan et al. reported a novel A-D-A 3,9-bis(2-methylene-(3-(1,1-dicyanomethylene)-indanone))-5,5,11, 11-tetrakis (4-hexylphenyl)-dithieno [2,3-d:2′,3′-d′]-s-indaceno [1,2-b:5,6-b′]dithiophene (ITIC) featuring a dithieno [2,3d:2′,3′d′]-sindaceno [1,2b:5,6b′]dithiophene (IDTT) core and an end group of 2-methylene-(3-(1,1-dicyanomethylene) indanone) (IC) [12]. However, based on the limited spectral overlap in absorption, PTB7-Th:ITIC exhibited a PCE of 6.8%. Subsequently, ITIC was blended with the wide-bandgap J71, and the PBDB-T polymer achieved PCEs of 11.41% and 11.21%, respectively [13,14]. In order to enhance the efficiency of OSCs, introducing the electron-donating or electron-withdrawing units in the terminal groups, which can tune the energy level and morphology, were proposed as promising strategies. Hou et al. synthesized IT-M and IT-OM2 with methyl and methoxyl units substituted on the IC terminal group, resulting in an upward shift in the LUMO/HOMO levels. The PCEs of PBDB-T:IT-M and PBDB-T:IT-OM2 reached 12.5% and 11.9%, respectively [15,16]. Furthermore, a four-fluorine atom was introduced to the IC group (named as IT-4F), enhancing the charge transport and intermolecular interactions. A high PCE of 14.7% was achieved based on PTO2:IT-4F, and a higher PCE (15.3%) with another donor, PFBCPZ for IT-4F-based OSCs, was reported [17,18]. Chen and co-workers reported NFBDT with a heptacyclic benzodi(cyclopentadithiophene) (FBDT) core based on BDT, with 2-(2,3-dihydro-3-oxo-1H-inden-1-ylidene) propanedinitrile (INCN) as the terminal group. NFBDT not only has a planar backbone, but also reasonable aggregation at the solid state, and it is an isomer of ITIC with the differences of the side chain position in the donor unit (shown in Figure 1). However, PBDB-T:NFBDT devices showed a PCE of 8.80%, which is lower than PBDB-T:ITIC OSCs (11.21%) [14,19]. Based on extensive experimental data, small differences in the donor unit generate large differences in the PCE, but the intrinsic influences remain ambiguous [20,21,22,23]. Actually, the donor/acceptor (D/A) interface has dominated the charge separation efficiency, which is related with the PCE in OSCs [24].
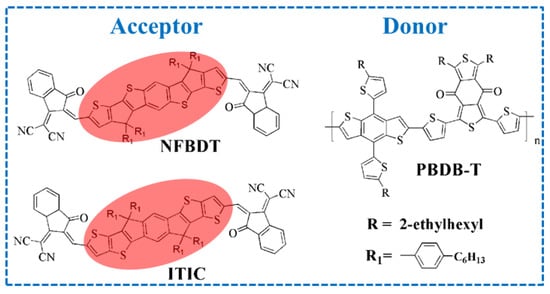
Figure 1.
Chemical structure of donor PBDB-T, acceptor NFBDT and its isomer ITIC, with different donor units marked red.
In this work, molecular dynamics simulations (MD) and the density functional theory/time-dependent density functional theory (DFT/TDDFT) methods were combined to probe factors influencing the performance differences for PBDB-T:ITIC and PBDB-T:NFBDT systems. The geometry optimization, absorption spectra, open-circuit voltage (VOC) and important parameters at the interface were analyzed. The results could provide theoretical guidance for designing efficient acceptor materials.
2. Computational Methods
2.1. MD Simulations
MD simulations were utilized to simulate the PBDB-T/ITIC and PBDB-T/NFBDT BHJ interfaces with general AMBER force field (GAFF) in Gromacs software package [25]. The GAFF with the restricted electrostatic potential (RESP) [26,27] charge was established for all molecules at Hartree–Fock/6-31G (d, p). According to the experiment [19], the best D/A weight ratio was 1:0.8 for two systems. The simulation systems were subjected to initial energy minimization, followed by a 3 ns canonical (NVT) ensemble, incorporating long-range electrostatics using Particle Mesh Ewald (PME) and van der Waals interactions with a cutoff of 0.1 Å. Whole MD simulations were conducted throughout the leap-frog integrator with a time step of 1 fs at 300 k and 1 bar. Additionally, Nosé–Hoover thermostat [28,29] and Parrinello–Rahman barostat [30] were used to control temperature and pressure, respectively. When an equilibration was reached in NVT, the isothermal–isobaric (NPT) ensemble at 300 k and 1 bar for 10 ns were subsequently adopted to simulate interfacial morphologies until the system reached equilibrium. From all potential curves, the PBDB-T/ITIC and PBDB-T/NFBDT reached equilibrium states with minimum energy via NVT and NPT ensemble simulation (Figures S1 and S2). Therefore, the initial geometry structures of D/A interface models with good π-π stacking were extracted from the final cluster models after MD simulation (shown Figure S3), respectively. The selection of these clusters was performed using the quantum mechanical/molecular mechanics (QM/MM) method [31], taking into account the influence of the surrounding environment. The QM part was treated at the B3LYP/6-31G (d, p) level.
2.2. Quantum Chemical Calculations
The optimizations and frontier molecular orbital (FMO) energy levels of ITIC and NFBDT were computed using the B3LYP/6-31G (d, p) [32], which can provide reliable electronic structures for organic small molecules [33,34]. A solvent (chloroform) effect was considered using a polarizable continuum model (PCM) during TD-DFT calculations. The absorption properties were calculated using PBE0/6-31G(d, p) level based on the ground-state geometries, which was consistent with experimental values for ITIC and NFBDT (Figure S4). Furthermore, the CAM-B3LYP function presented good description for estimating the excitation energies in small compounds, and all excited state calculations were evaluated at the CAM-B3LYP/6-31G(d, p) level in the TD-DFT theory [35]. The charge transfer properties were computed using the semi-classical Marcus theory [36]:
where VDA is the transfer integral between the initial and last states, ∆G denotes the Gibbs free energy difference, λ denotes the reorganization energy, T denotes the temperature (generally set as 300 K), and kB and h denote the Boltzmann and Plank constants, respectively. Here, the reorganization energy (λ), which comprises an internal component from intramolecular vibrations λint and an external part affected by the surrounding medium λs, was evaluated using the method from references [37,38,39,40]. In addition, the electronic coupling in the charge separation (CS) process and charge recombination (CR) process [40] were computed via CAM-B3LYP/6-31G(d, p) in the Q-Chem 4.0 software [41] with the Generalized Mulliken–Hush (GMH) method [42]. The absorption spectra and the charge density difference (CDD) maps were visualized via Multiwfn 3.8 code [43]. Additionally, the quantum chemical calculations were performed using the Gaussian 09 program package [44].
3. Results and Discussion
3.1. Properties Related to Ground State
The geometric structures have important impacts on the photoelectric properties. As shown in Figure S5, the optimized side and half side of ITIC and NFBDT show that the bulk of ITIC has good planarity, which is consistent with the results of the experiment. The position of the side chain of NFBDT is closer to the end groups, and the steric hindrance makes the end group twist at a small angle with the donor unit. However, the skeletons of isomers are quite planar with the large steric hindrance of side chains, which is favorable to increase end-group π-π stacking, especially for ITIC. The π-π stacking of the electron-withdrawing end groups in A-D-A acceptors can considerably increase the energy splitting of the singlet state and further obtain a reduction in the ∆EST, which is effective to suppress the triplet recombination channel, finally leading to a high FF for OSCs [45]. Recently, it was proposed that the A-D-A molecules will pre-aggregate via end-group π–π stacking, promoting a greater tendency for molecules to form the horizontal and face-on orientations [46]. Furthermore, both the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are delocalized (Figure 2). Relative to the HOMO orbital, the LUMO orbital is distributed on the terminal benzene rings. Obviously, the electronic structure of the two molecules is similar.
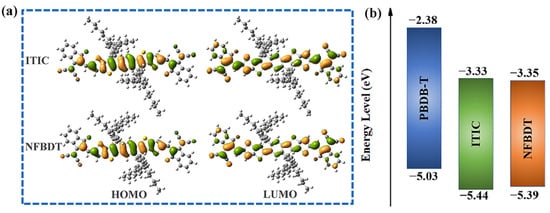
Figure 2.
(a) Frontier molecular orbital (FMO) distributions of ITIC and NFBDT molecules. The green color represents the positive and negative phase, respectively. (b) Energy levels of donors and acceptors.
The energy driving force (ΔE) is provided from the energy offsets of the HOMO level and LUMO level between the donors and acceptors, which is essential to provide excess energy to the charge transfer (CT) state for effective CS. The ΔE > 0.3 eV at the D/A interface will greatly increase the probability of free carriers formed via exciton dissociation [45]. Herein, the computed values of the HOMO and LUMO for PBDB-T, ITIC and NFBDT are −5.03, −5.44 and −5.39 eV and −2.38, −3.33 and −3.35 eV, respectively. ΔELUMO and ΔEHOMO of the PBDB-T/ITIC and PBDB-T/NFBDT systems are 0.95 and 0.97 eV and 0.41 and 0.36 eV (Table S1), respectively, all exceeding 0.3 eV; thus, two systems have sufficient ΔE to achieve efficient exciton dissociation at the D/A interface. In addition, the HOMO and the LUMO are lower lying than PBDB-T; thus, they can receive electrons from PBDB-T or deliver holes to PBDB-T. Meanwhile, the HOMO level of ITIC is lower than NFBDT, which is favorable for hole transport. The reason for the difference in the HOMO and LUMO of NFBDT and ITIC is mainly the differences in the side chain positions of both acceptors.
VOC is one of the important parameters used to measure the PCE of OSCs, which is closely related to the energy level arrangement of the donor and acceptor. Obviously, the lower the HOMO energy level of the donor, the higher the LUMO energy level of the acceptor, and the higher the VOC of the OSCs. Due to the slightly higher LUMO energy level, ITIC has a slightly larger VOC (Table S1). However, the low LUMO levels of the NFAs are conducive to the air-stable electron transmission and the avoidance of electro-chemical oxidation reactions with H2O and O2, which helps to improve the stability of OSCs [47].
3.2. Properties Related to Excited State
The amount of transfer charge (∆q) for the excited states are calculated via Multiwfn 3.8. The excited states in the OSCs can be classified into three categories through the value of ∆q: (1) the Frankel exciton (FE) state, which has a ∆q value between 0 and 0.3 |e|; (2) the CT state, whose ∆q exceeds 0.7 |e|; and (3) the hybrid charge transfer (HCT) state, namely the mixture of two formers, whose ∆q is distributed from 0.3 to 0.7 |e| [47]. In all excited states, the lowest singlet excited state (S1) corresponds to the FE state with the largest oscillation intensity and makes an important contribution to the CS process, and it is calculated as the FE state in this system. Here, only the S0→S1 of the acceptors are calculated, and the ∆q values of the acceptors are 0.646 and 0.615 |e|, which indicates that S1 exhibits HCT properties and facilitates the charge separation. Compared with NFBDT, ITIC has a larger ∆q, indicating that it may have a higher charge separation efficiency.
The degree of overlap between the absorption spectra and the solar absorption range is closely related to the short-circuit current (JSC) of OSCs. As shown in Figure S4, ITIC and NFBDT have two absorption peaks, 423.3 and 660.3 and 459.9 and 685.3 nm, respectively, and the maximum absorption peak of the NFBDT molecule is red-shifted. The maximum absorption peaks of ITIC and NFBDT are mainly obtained from the S0→S1 transition, corresponding to the orbital transition of HOMO→LUMO. Therefore, the absorption spectra of ITIC and NFBDT are substantially identical in terms of the peak position.
3.3. The Charge Separation and Recombination at the D/A Interface
After the active layer materials absorb the incident photons, it is necessary for the excitons to undergo diffusion towards the D/A interfaces and be dissociated into CT states prior to their decay into the ground state (S0). Then, the CT states are simultaneously dissociated into free electrons and hole carriers, which migrate along the A and D domains and are extracted by the cathode and anode, respectively. However, the charge transfer process accompanied by charge recombination, and the competition between the two processes, will result in very different PCEs of OSCs. It was reported that the donor and acceptor arrangement could be face-on, edge-on and slipped in donor/acceptor interfaces, and the face-on interfaces make the largest contribution to the charge transfer [46,48,49]. In this work, the interface models extracted from the final equilibrium system with a face-on style are mainly considered, which normally have good intermolecular π-π stacking (shown in Figure S6). And the strength of the competition is measured by calculating the rates of the interfacial charge transfer and recombination of the dimer to describe the interfacial exciton dissociation process in detail.
3.3.1. The Frenkel Exciton States and CT States
The excited-state properties of the D/A interface including the FE states and CT states is a major factor used to evaluate the D/A separation ability. Generally, the excited states with the largest oscillation strength of all electrons and holes on the D or A are called the FE states (the donor materials in the system are the same; only the FE states of acceptor molecules are considered below). The holes are distributed on the donor, and the electrons on the acceptor are called the CT state. The energy of the lowest CT state (CT1) and the FE are depicted in Figure 3. In addition, the charge separation paths are also summarized in Figure 4, including the separation process paths and recombination process paths. When the energy of the FE state exceeds that of the CT state, path 1 is preferred; path 2 may be taken for the higher CT state, and path 3 may be taken if the CT state has a higher oscillator intensity. The electrons and holes may also undergo recombination back to the ground state, namely path 4. Relative to PBDB-T/NFBDT, PBDB-T/ITIC has a lower energy difference between the FE and CT states and more patterns that the energy of the Frenkel exciton state is higher than that of the CT state (such as style 1, style 3, style 4 and style 8, which are shown in Figure 3a). The results indicate that PBDB-T/ITIC is favorable for the hot exciton mechanism (path 1), while PBDB-T/NFBDT without a higher energy of the FE state than the CT state implies that the photogenerated charge process may be carried out through the IEF mechanism (path 2) or direct excitation (path 3), which may be relatively difficult for the charge separation process. When the FE state has a CT fraction, and the CT state has an FE fraction for PBDB-T/ITIC, it is defined as the hybrid FE/CT state. The excited state of PBDB-T/ITIC has obvious characteristics of a hybrid FE and CT state. The FE/CT state is related to the strong vibration coupling of the system, which can induce the ultrafast CS process and reduce the non-radiated voltage loss [50]. Importantly, due to the incorporation of a degree of FE fraction, it is possible for PBDB-T/ITIC to achieve the direct generation of a CT state via light excitation, carrying out the rapid CS process. Compared to PBDB-T/ITIC, PBDB-T/NFBDT has only one FE/CT state among ten dimers with good π-π stacking. Obviously, PBDB-T/ITIC has obvious FE states with higher energies than the CT state, and a more hybrid FE/CT state, which may be one of the reasons for the higher device performance.
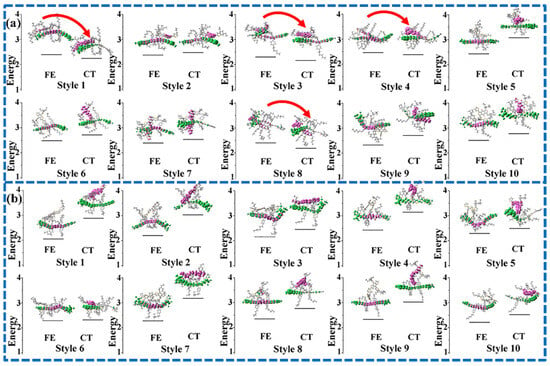
Figure 3.
The excitation energies (eV) of FE and CT states of ten dimers extracted from the final equilibrium system for PBDB-T/ITIC (a) and PBDB-T/NFBDT (b) were calculated at the level of CAM-B3LYP/6-31G (d, p).
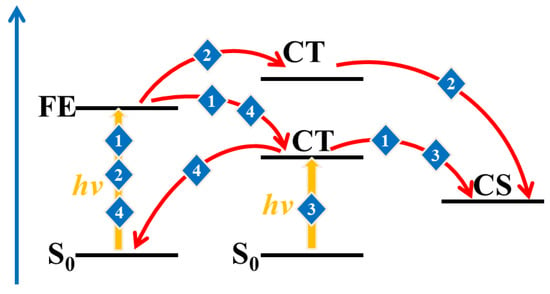
Figure 4.
Possible path diagram for describing the photogenerated charge process (1, 2 and 3 are charge separation paths and 4 is charge recombination path, respectively).
3.3.2. Charge Separation and Recombination Rate
The charge separation or recombination rate will be influenced by the Gibbs free energy difference and λ from the Marcus theory. λ is affected by the change in the geometric structure of the materials and is mainly related to the polarization of the surrounding medium. The values of external reorganization energy only have a little difference due to the same donor and the small geometric change in the acceptor in two systems. Furthermore, both the CS (λCS) and CR (λCR) processes of the PBDB-T/ITIC and PBDB-T/NFBDT interfaces were calculated and are presented in Table 1. The reorganization energy of PBDB-T/NFBDT is higher than PBDB-T/ITIC in both the charge separation and recombination processes. The difference is mainly from the internal reorganization energy, indicating more geometric relaxation of NFBDT during the charge transfer process.

Table 1.
The internal reorganization energy (λi-CS (eV) and λi-CR (eV)), external reorganization energy (λs (eV)), total reorganization energy (λCS (eV) and λCR (eV)) and Gibbs free energy difference (ΔGCS (eV) and ΔGCR (eV)) for the PBDB-T/ITIC and PBDB-T/NFBDT interfacial models.
The ∆GCS and ∆GCR are lower than zero, which is consistent with the exothermic reaction in the charge transfer and recombination processes [51]. PBDB-T/ITIC has a larger absolute value of ∆GCR and a smaller absolute value of ∆GCS, as shown in Table 1, which is related with the higher LUMO energy level of the ITIC molecules. In addition, when the sum of the Gibbs free energy difference and the total reorganization energy is equal to zero, the rate value of the system is the largest. The value of ∆G + λ is less than 0, namely the absolute value of ∆G is higher than λ, and the rate, k, of the system increases with the increased ∆G. It can be seen that the ∆G + λ value of both the CS (−0.383 and −0.368 eV, respectively) and CR (−1.18 and −1.14 eV, respectively) are less than 0 for PBDB-T/ITIC and PBDB-T/NFBDT. The ∆G of PBDB-T/ITIC is −0.954, which is larger than PBDB-T/NFBDT (−0.967 eV), indicating a larger kCS of PBDB-T/ITIC in the CS process. During the CR process, PBDB-T/ITIC has a lower ∆G (−1.701 eV) than PBDB-T/NFBDT (−1.687 eV), and may have a smaller kCR. These results mean that PBDB-T/ITIC may have a higher charge separation rate and a lower charge recombination rate. Electron coupling plays a crucial role in determining the final rate, and an effective charge dissociation requires a large VCS and a small VCR. The electronic coupling values (VCS and VCR) of the extracted interface models are calculated (Table S2). Most of the extracted PBDB-T/ITIC models have larger VCS values than PBDB-T/NFBDT, and the remaining have a smaller difference. A larger VCS value can be found in PBDB-T/ITIC.
Based on the Marcus formula, there is a strong correlation between the rate and the square of the electronic coupling. The scatter plot with the kCS and kCR values of the extracted models as the logarithm of the vertical coordinate and the horizontal coordinate as the name of the dimer are shown in Figure 5. Therefore, the kCS and kCR values of PBDB-T/ITIC and PBDB-T/NFBDT decrease sequentially, and the corresponding VCS and VCR values decrease in the same trend, respectively. Obviously, the kCS values of the PBDB-T/ITIC systems are higher than those of the PBDB-T/NFBDT systems. On the contrary, the distribution of kCR indicates that the values of the PBDB-T/ITIC systems are lower than those of PBDB-T/NFBDT. Compared to PBDB-T/NFBDT, the difference between the kCS and kCR values of PBDB-T/ITIC is larger, which means a larger charge separation and a smaller charge recombination rate, facilitating effective charge separation. The higher kCS and lower kCR of PBDB-T/ITIC demonstrates a greater charge separation efficiency than PBDB-T/NFBDT.
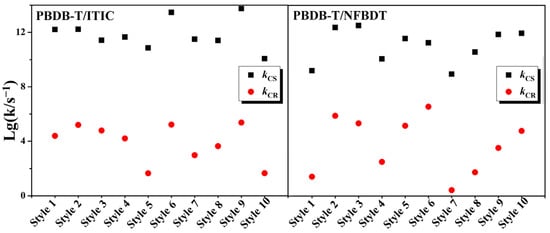
Figure 5.
The distribution of charge separation rate kCS (s−1) and charge recombination rate kCR (s−1) for PBDB-T/ITIC and PBDB-T/NFBDT systems.
4. Conclusions
In summary, the geometric structure, absorption spectrum, VOC, ∆E and interface parameters were concluded and analyzed using DFT methods to find the reason for the performance difference in the two isomers. The geometric structure, absorption spectrum and VOC of the two molecules are similar and have sufficient ∆E values for the dissociation of exciton. However, the lowest excited state of ITIC has a larger ∆q, which may have a positive impact on the charge separation process. By analyzing the main excited states at the interfaces, it was found that the PBDB-T/ITIC interface has a more matching relative position between the FE and CT states, which is conducive to having more separation paths and increasing the efficiency of charge separation. Furthermore, there are more FE/CT states in the PBDB-T/ITIC systems, indicating a rapid charge separation process. Compared with PBDB-T/NFBDT, PBDB-T/ITIC presented a larger kCS and a smaller kCR. The results showed that more FE/CT hybridization states, more charge separation paths and the excellent interface parameters of PBDB-T/ITIC may be the main reasons for its excellent performance. This work contributes to the study of structural differences in the performance of acceptors, and also provides an idea for the design of new materials for OSCs.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/molecules28196968/s1, Computational details, Figure S1: Time–potential curves of PBDB-T/ITIC and PBDB-T/NFBDT in NVT process; Figure S2: Time–potential curves of PBDB-T/ITIC and PBDB-T/NFBDT in NPT process; Figure S3: (a) PBDB-T/ITIC and (b) PBDB-T/NFBDT system via MD simulation; Figure S4: Absorption spectra of ITIC and NFBDT calculated at the PBE0/6-31G(d, p) level; Figure S5: The optimized geometric structures of the side and half side of ITIC and NFBDT molecules, with red as the plane; Figure S6. Typical interface models (the gray and red represent PBDB-T and ITIC/NFBDT, respectively) in PBDB-T/ITIC (a) and PBDB-T/NFBDT (b) systems extracted from MD; Table S1: Computed orbital energy (EHOMO and ELUMO), energy driving force (∆ELUMO and ∆EHOMO), open circuit voltage (VOC) and transferred charge number (∆q) of ITIC and NFDFT; Table S2: Electronic coupling values of charge separation VCS (eV) and charge recombination VCR (eV) of PBDB-T/ITIC and PBDB-T/NFBDT.
Author Contributions
Conceptualization and methodology, S.-Q.H.; validation and writing—original draft preparation, L.-L.W. and Q.-Q.P.; formal analysis, Z.-W.Z., Y.G. and Z.-M.S. All authors have read and agreed to the published version of the manuscript.
Funding
S.-Q.H. gratefully acknowledges the Hubei college students’ innovation and entrepreneurship training programs. Z.-W.Z. gratefully acknowledges the financial support from the National Natural Science Foundation of China (22209042), the Science and Technology Program of Xiangyang, China (2022ABH006084), the Foundation of Educational Commission of Hubei Province (grant number: qdf2022012). Q.-Q.P. gratefully acknowledges the financial support from the Thirteenth Five-Year Program for Science and Technology of the Education Department of Jilin Province (JJKH20230806KJ). The super-computing facilities were provided by the Hefei Advanced Computing Center.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, R.; Jiang, Z.; Yang, C.; Yu, J.; Feng, J.; Adil, M.A.; Deng, D.; Zou, W.; Zhang, J.; Lu, K.; et al. All-small-molecule organic solar cells with over 14% efficiency by optimizing hierarchical morphologies. Nat. Commun. 2019, 10, 5393. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Lv, J.; Yang, K.; He, Y.; Yang, Q.; Chen, H.; Chen, Q.; Liao, Z.; Kan, Z.; Duan, T.; et al. 15.8% efficiency binary all-small-molecule organic solar cells enabled by a selenophene substituted sematic liquid crystalline donor. Energy Environ. Sci. 2021, 14, 5366–5376. [Google Scholar] [CrossRef]
- Markina, A.; Lin, K.H.; Liu, W.; Poelking, C.; Firdaus, Y.; Villalva, D.R.; Khan, J.I.; Paleti SH, K.; Harrison, G.T.; Gorenflot, J.; et al. Chemical Design Rules for Non-Fullerene Acceptors in Organic Solar Cells. Adv. Energy Mater. 2021, 11, 2102363. [Google Scholar] [CrossRef]
- Arredondo, B.; Carlos Pérez-Martínez, J.; Muñoz-Díaz, L.; López-González, M.d.C.; Martín-Martín, D.; del Pozo, G.; Hernández-Balaguera, E.; Romero, B.; Lamminaho, J.; Turkovic, V.; et al. Influence of solvent additive on the performance and aging behavior of non-fullerene organic solar cells. Sol. Energy 2022, 232, 120–127. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, J.; Bi, P.; Ren, J.; Wang, Y.; Yang, Y.; Liu, X.; Zhang, S.; Hou, J. Tandem organic solar cell with 20.2% efficiency. Joule 2022, 6, 171–184. [Google Scholar] [CrossRef]
- Jiang, Z.-Q.; Wang, T.-T.; Wu, F.-P.; Lin, J.-D.; Liao, L.-S. Recent advances in electron acceptors with ladder-type backbone for organic solar cells. J. Mater. Chem. A 2018, 6, 17256–17287. [Google Scholar] [CrossRef]
- Liu, W.; Xu, X.; Yuan, J.; Leclerc, M.; Zou, Y.; Li, Y. Low-bandgap non-fullerene acceptors enabling high-performance organic solar cells. ACS Energy Lett. 2021, 6, 598–608. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, J.; Xu, Z.; Xu, H.; Quan, J.; Deng, J.; Li, Y.; Tong, Y.; Hu, B.; Chen, L. Recent advances of nonfullerene acceptors in organic solar cells. Nano Energy 2022, 103, 107802. [Google Scholar] [CrossRef]
- Zhang, Y.; Lang, Y.; Li, G. Recent advances of non-fullerene organic solar cells: From materials and morphology to devices and applications. Ecomat 2023, 5, e12281. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Z.; Ye, L.; Zhan, C.; Hou, J.; Zhang, S.; Jiang, B.; Zhao, Y.; Huang, J.; Zhang, S.; et al. A potential perylene diimide dimer-based acceptor material for highly efficient solution-processed non-fullerene organic solar cells with 4.03% efficiency. Adv. Mater. 2013, 25, 5791–5797. [Google Scholar] [CrossRef]
- Meng, D.; Fu, H.; Xiao, C.; Meng, X.; Winands, T.; Ma, W.; Wei, W.; Fan, B.; Huo, L.; Doltsinis, N.L.; et al. Three-bladed rylene propellers with three-dimensional network assembly for organic electronics. J. Am. Chem. Soc. 2016, 138, 10184–10190. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Wang, J.; Zhang, Z.-G.; Bai, H.; Li, Y.; Zhu, D.; Zhan, X. An electron acceptor challenging fullerenes for efficient polymer solar cells. Adv. Mater. 2015, 27, 1170–1174. [Google Scholar] [CrossRef] [PubMed]
- Bin, H.; Gao, L.; Zhang, Z.G.; Yang, Y.; Zhang, Y.; Zhang, C.; Chen, S.; Xue, L.; Yang, C.; Xiao, M.; et al. 11.4% Efficiency non-fullerene polymer solar cells with trialkylsilyl substituted 2D-conjugated polymer as donor. Nat. Commun. 2016, 7, 13651. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Qian, D.; Zhang, S.; Li, S.; Inganas, O.; Gao, F.; Hou, J. Fullerene-free polymer solar cells with over 11% efficiency and excellent thermal stability. Adv. Mater. 2016, 28, 4734–4739. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Ye, L.; Zhao, W.; Zhang, S.; Mukherjee, S.; Ade, H.; Hou, J. Energy-level modulation of small-molecule electron acceptors to achieve over 12% efficiency in polymer solar cells. Adv. Mater. 2016, 28, 9423–9429. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Ye, L.; Zhao, W.; Zhang, S.; Ade, H.; Hou, J. Significant influence of the methoxyl substitution position on optoelectronic properties and molecular packing of small-molecule electron acceptors for photovoltaic cells. Adv. Energy Mater. 2017, 7, 1700183. [Google Scholar] [CrossRef]
- Yao, H.; Cui, Y.; Qian, D.; Ponseca, C.S., Jr.; Honarfar, A.; Xu, Y.; Xin, J.; Chen, Z.; Hong, L.; Gao, B.; et al. 14.7% efficiency organic photovoltaic cells enabled by active materials with a large electrostatic potential difference. J. Am. Chem. Soc. 2019, 141, 7743–7750. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Fan, Q.; Xiong, M.; Wang, Q.; Chen, K.; Liu, H.; Gao, M.; Ye, L.; Guo, X.; Fang, J.; et al. Carboxylate substituted pyrazine: A simple and low-cost building block for novel wide bandgap polymer donor enables 15.3% efficiency in organic solar cells. Nano Energy 2021, 82, 105679. [Google Scholar] [CrossRef]
- Kan, B.; Feng, H.; Wan, X.; Liu, F.; Ke, X.; Wang, Y.; Wang, Y.; Zhang, H.; Li, C.; Hou, J.; et al. Small-molecule acceptor based on the heptacyclic benzodi (cyclopentadithiophene) unit for highly efficient nonfullerene organic solar cells. J. Am. Chem. Soc. 2017, 139, 4929–4934. [Google Scholar] [CrossRef]
- Xin, Y.; Zeng, G.; OuYang, J.; Zhao, X.; Yang, X. Enhancing thermal stability of nonfullerene organic solar cells via fluoro-side-chain engineering. J. Mater. Chem. C 2019, 7, 9513–9522. [Google Scholar] [CrossRef]
- Yang, J.; Li, Q.S.; Li, Z.S. End-capped group manipulation of indacenodithienothiophene-based non-fullerene small molecule acceptors for efficient organic solar cells. Nanoscale 2020, 12, 17795–17804. [Google Scholar] [CrossRef] [PubMed]
- Han, G.; Guo, Y.; Ning, L.; Yi, Y. Improving the electron mobility of ITIC by end-group modulation: The role of fluorination and π-extension. Solar RRL 2019, 3, 1800251. [Google Scholar] [CrossRef]
- Fan, Q.; Su, W.; Zhang, M.; Wu, J.; Jiang, Y.; Guo, X.; Liu, F.; Russell, T.P.; Zhang, M.; Li, Y. Synergistic Effects of Side-Chain Engineering and Fluorination on Small Molecule Acceptors to Simultaneously Broaden Spectral Response and Minimize Voltage Loss for 13.8% Efficiency Organic Solar Cells. Solar RRL 2019, 3, 1900169. [Google Scholar] [CrossRef]
- Clarke, T.M.; Durrant, J.R. Charge photogeneration in organic solar cells. Chem. Rev. 2010, 110, 6736–6767. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Fox, T.; Kollman, P.A. Application of the RESP methodology in the parametrization of organic solvents. J. Phys. Chem. B 1998, 102, 8070–8079. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Dapprich, S.; Komáromi, I.; Byun, K.S.; Morokuma, K.; Frisch, M.J. A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. J. Mol. Struct. THEOCHEM 1999, 461, 1–21. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. I. The effect of the exchange-only gradient correction. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Qiu, M.; Zhu, D.; Yan, L.; Wang, N.; Han, L.; Bao, X.; Du, Z.; Niu, Y.; Yang, R. Strategy to manipulate molecular orientation and charge mobility in D–A type conjugated polymer through rational fluorination for improvements of photovoltaic performances. J. Phys. Chem. C 2016, 120, 22757–22765. [Google Scholar] [CrossRef]
- Tang, X.-D.; Liao, Y.; Gao, H.-Z.; Geng, Y.; Su, Z.-M. Theoretical study of the bridging effect on the charge carrier transport properties of cyclooctatetrathiophene and its derivatives. J. Mater. Chem. 2012, 22, 6907–6918. [Google Scholar] [CrossRef]
- Sarkar, R.; Boggio-Pasqua, M.; Loos, P.F.; Jacquemin, D. Benchmarking TD-DFT and wave function methods for oscillator strengths and excited-state dipole moments. J. Chem. Theory Comput. 2021, 17, 1117–1132. [Google Scholar] [CrossRef] [PubMed]
- Marcus, R.A. Electron transfer reactions in chemistry: Theory and experiment (Nobel lecture). Angew. Chem. Int. Ed. 1993, 32, 1111–1121. [Google Scholar] [CrossRef]
- Burquel, A.; Lemaur, V.; Beljonne, D.; Lazzaroni, R.; Cornil, J. Pathways for photoinduced charge separation and recombination at donor−acceptor heterojunctions: The case of oligophenylenevinylene−perylene bisimide complexes. J. Phys. Chem. A 2006, 110, 3447. [Google Scholar] [CrossRef]
- Kavarnos, G.J.; Turro, N.J. Photosensitization by reversible electron transfer: Theories, experimental evidence, and examples. Chem. Rev. 1986, 86, 401–449. [Google Scholar] [CrossRef]
- Lemaur, V.; Steel, M.; Beljonne, D.; Brédas, J.L.; Cornil, J. Photoinduced charge generation and recombination dynamics in model donor/acceptor pairs for organic solar cell applications: A full quantum-chemical treatment. J. Am. Chem. Soc. 2005, 127, 6077–6086. [Google Scholar] [CrossRef]
- Pan, Q.-Q.; Li, S.-B.; Wu, Y.; Zhang, J.; Li, H.-B.; Geng, Y.; Zhang, M.; Su, Z.-M. Theoretical design of three-dimensional non-fullerene acceptor materials based on an arylenediimide unit towards high efficiency organic solar cells. New J. Chem. 2017, 41, 3857–3864. [Google Scholar] [CrossRef]
- Krylov, A.I.; Gill, P.M. Q-Chem: An engine for innovation. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 317–326. [Google Scholar] [CrossRef]
- Voityuk, A.A. Estimation of electronic coupling in π-stacked donor-bridge-acceptor systems: Correction of the two-state model. J. Chem. Phys. 2006, 124, 64505. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; Li, X.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Han, G.; Yi, Y. Molecular insight into efficient charge generation in low-driving-force nonfullerene organic solar cells. Acc. Chemcial Res. 2022, 55, 869–877. [Google Scholar] [CrossRef]
- Zheng, W.; Liu, J.; Guo, Y.; Han, G.; Yi, Y. Regulation of Molecular Orientations of A–D–A Nonfullerene Acceptors for Organic Photovoltaics: The Role of End-Group π–π Stacking. Adv. Funct. Mater. 2022, 32, 2108551. [Google Scholar] [CrossRef]
- Yang, J.; Ding, W.L.; Li, Q.S.; Li, Z.S. Theoretical study of non-fullerene acceptors using end-capped groups with different electron-withdrawing abilities toward efficient organic solar cells. J. Phys. Chem. Lett. 2022, 13, 916–922. [Google Scholar] [CrossRef]
- Han, G.; Hu, T.; Yi, Y. Reducing the singlet− triplet energy gap by end-group π−π stacking toward high-efficiency organic photovoltaics. Adv. Mater. 2020, 32, 2000975. [Google Scholar] [CrossRef]
- Li, M.-Y.; Ren, Y.; Huang, J.-C.; Sui, M.-Y.; Sun, G.-Y.; Su, Z.-M. Charge transfer regulated by domain differences between host and guest donors in ternary organic solar cells. J. Mater. Chem. A 2022, 10, 22477–22487. [Google Scholar] [CrossRef]
- Han, G.; Yi, Y. Local excitation/charge-transfer hybridization simultaneously promotes charge generation and reduces nonradiative voltage loss in nonfullerene organic solar cells. J. Phys. Chem. Lett. 2019, 10, 2911–2918. [Google Scholar] [CrossRef]
- Pan, Q.-Q.; Li, S.-B.; Wu, Y.; Geng, Y.; Zhang, M.; Su, Z.-M. Exploring more effective polymer donors for the famous non-fullerene acceptor ITIC in organic solar cells by increasing electron-withdrawing ability. Org. Electron. 2018, 53, 308–314. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).