Redox-Regulated Magnetic Conversions between Ferro- and Antiferromagnetism in Organic Nitroxide Diradicals
Abstract
:1. Introduction
2. Results and Discussion
2.1. Magnetic Couplings and Molecular Geometries
2.2. Spin Polarization Analysis
2.3. Spin Coupling Channels and Spin Alternation Rule Analysis
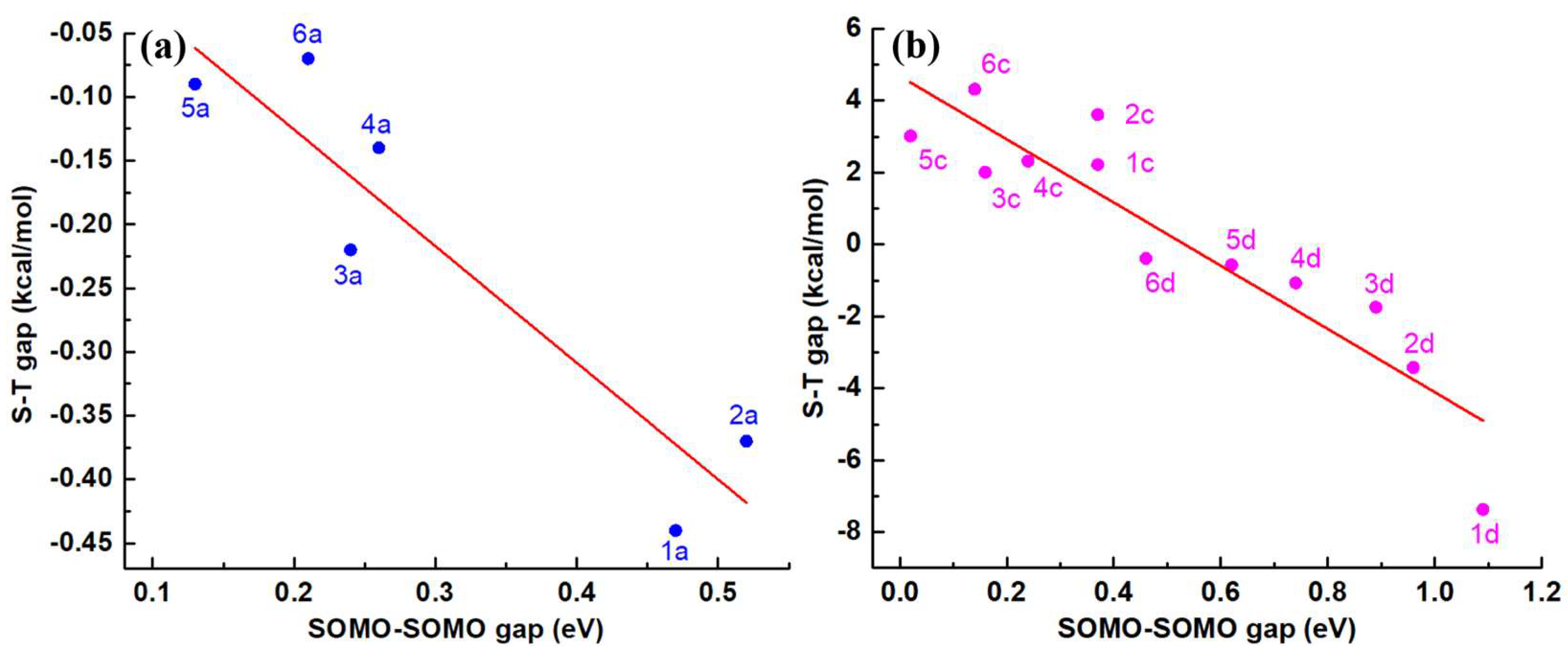
2.4. SOMO Effect and SOMO-SOMO Energy Level Splitting
3. Computational Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Nam, Y.; Cho, D.; Lee, J.Y. Doping Effect on Edge-Terminated Ferromagnetic Graphene Nanoribbons. J. Phys. Chem. C 2016, 120, 11237–11244. [Google Scholar] [CrossRef]
- Ratera, I.; Ruiz-Molina, D.; Vidal-Gancedo, J.; Wurst, K.; Daro, N.; Létard, J.-F.; Rovira, C.; Veciana, J. A New Photomagnetic Molecular System Based on Photoinduced Self-Assembly of Radicals. Angew. Chem. Int. Ed. 2001, 40, 919–922. [Google Scholar] [CrossRef]
- Itkis, M.E.; Chi, X.; Cordes, A.W.; Haddon, R.C. Magneto-Opto-Electronic Bistability in a Phenalenyl-Based Neutral Radical. Science 2002, 296, 1443–1445. [Google Scholar] [CrossRef]
- Prinz, G.A. Magnetoelectronics. Science 1998, 282, 1660–1663. [Google Scholar] [CrossRef]
- Kobayashi, H.; Kobayashi, A.; Cassoux, P. BETS as a Source of Molecular Magnetic Superconductors (BETS = Bis(Ethylenedithio)Tetraselenafulvalene. Chem. Soc. Rev. 2000, 29, 325–333. [Google Scholar] [CrossRef]
- Uji, S.; Shinagawa, H.; Terashima, T.; Yakabe, T.; Terai, Y.; Tokumoto, M.; Kobayashi, A.; Tanaka, H.; Kobayashi, H. Magnetic-Field-Induced Superconductivity in a Two-Dimensional Organic Conductor. Nature 2001, 410, 908–910. [Google Scholar] [CrossRef] [PubMed]
- Abe, M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. [Google Scholar]
- Rajca, A.; Shiraishi, K.; Vale, M.; Han, H.; Rajca, S. Stable Hydrocarbon Diradical, An Analogue of Trimethylenemethane. J. Am. Chem. Soc. 2005, 127, 9014–9020. [Google Scholar] [CrossRef]
- Rajca, A.; Takahashi, M.; Pink, M.; Spagnol, G.; Rajca, S. Conformationally Constrained, Stable, Triplet Ground State (S = 1) Nitroxide Diradicals. Antiferromagnetic Chains of S = 1 Diradicals. J. Am. Chem. Soc. 2007, 129, 10159–10170. [Google Scholar] [CrossRef]
- Gallagher, N.M.; Olankitwanit, A.; Rajca, A. High-Spin Organic Molecules. J. Org. Chem. 2015, 80, 1291–1298. [Google Scholar] [CrossRef]
- Shimizu, D.; Osuka, A. A Benzene-1,3,5-Triaminyl Radical Fused with ZnII-Porphyrins: Remarkable Stability and a High-Spin Quartet Ground State. Angew. Chem. Int. Ed. 2018, 57, 3733–3736. [Google Scholar] [CrossRef]
- Zhang, G.B.; Li, S.H.; Jiang, Y.S. Effects of Substitution on the Singlet-Triplet Energy Splittings and Ground-State Multiplicities of m-Phenylene-Based Diradicals: A Density Functional Theory Study. J. Phys. Chem. A 2003, 107, 5573–5582. [Google Scholar] [CrossRef]
- Ali, M.E.; Datta, S.N. Broken-Symmetry Density Functional Theory Investigation on Bis-Nitronyl Nitroxide Diradicals: Influence of Length and Aromaticity of Couplers. J. Phys. Chem. A 2006, 110, 2776–2784. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, D.; Misra, A. Density Functional Theory Based Study of Magnetic Interaction in Bis-Oxoverdazyl Diradicals Connected by Different Aromatic Couplers. J. Phys. Chem. A 2009, 113, 5470–5475. [Google Scholar] [CrossRef] [PubMed]
- Cho, D.; Ko, K.C.; Lee, J.Y. Organic Magnetic Diradicals (Radical-Coupler-Radical): Standardization of Couplers for Strong Ferromagnetism. J. Phys. Chem. A 2014, 118, 5112–5121. [Google Scholar] [CrossRef]
- Cho, D.; Ko, K.C.; Lee, J.Y. Quantum Chemical Approaches for Controlling and Evaluating Intramolecular Magnetic Interactions in Organic Diradicals. Int. J. Quantum Chem. 2016, 116, 578–597. [Google Scholar] [CrossRef]
- Cui, M.L.; Zhao, Y.; Gao, W.; Cui, X.X.; Zhang, C.Y.; Changzhe Zhang, C.Z.; Meng, Q.T. Theoretical Simulation on Regulating the Magnetic Coupling Properties of Diradical Artificial Bases. J. Phys. Chem. A 2022, 126, 7820–7828. [Google Scholar] [CrossRef]
- Burnea, F.K.B.; Nam, Y.; Lee, J.Y. H-Bonding on Spin Centres Enhances Spin-Spin Coupling for Organic Diradicals. J. Mater. Chem. C 2020, 8, 3402–3408. [Google Scholar] [CrossRef]
- Sato, O.; Tao, J.; Zhang, Y.Z. Control of Magnetic Properties through External Stimuli. Angew. Chem. Int. Ed. 2007, 46, 2152–2187. [Google Scholar] [CrossRef]
- Ratera, I.I.; Veciana, J.J. Playing with Organic Radicals as Building Blocks for Functional Molecular Materials. Chem. Soc. Rev. 2012, 41, 303–349. [Google Scholar] [CrossRef]
- Shultz, D.A.; Fico, R.M.; Lee, H.; Kampf, J.W.; Kirschbaum, K.; Pinkerton, A.A.; Boyle, P.D. Mechanisms of Exchange Modulation in Trimethylenemethane-Type Biradicals: The Roles of Conformation and Spin Density. J. Am. Chem. Soc. 2003, 125, 15426–15432. [Google Scholar] [CrossRef]
- Barone, V.; Boilleau, C.; Cacelli, I.; Ferretti, A.; Prampolini, G. Conformational Effects on the Magnetic Properties of an Organic Diradical: A Computational Study. J. Chem. Theory Comput. 2013, 9, 1958–1963. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.Y.; Luo, Q.; Song, X.F.; Song, X.Y.; Bu, Y.X. Intriguing Diaza Effects on Magnetic Coupling Characteristics in Diaza-Benzo[k]Tetraphene-Bridged Nitroxide Diradicals. Int. J. Quantum Chem. 2018, 118, e25693. [Google Scholar] [CrossRef]
- Wang, Q.; Song, X.Y.; Li, P.; Bu, Y.X. Proton-Transfer Regulated Magnetic Spin Couplings in Nitroxide-Functionalized Porphycene Diradicaloids. J. Phys. Chem. C 2019, 123, 10764–10776. [Google Scholar] [CrossRef]
- Malik, R.; Bu, Y.X. Intramolecular Proton Transfer Modulation of Magnetic Spin Coupling Interaction in Photochromic Azobenzene Derivatives with an Ortho-Site Hydroxyl as a Modulator. J. Phys. Chem. A 2022, 126, 9165–9177. [Google Scholar] [CrossRef]
- Malik, R.; Bu, Y.X. Proton-Transfer Regulated Magnetic Coupling Characteristics in Blatter-Based Diradicals. New J. Chem. 2023, 47, 6903–6915. [Google Scholar] [CrossRef]
- Souto, M.; Guasch, J.; Lloveras, V.; Mayorga, P.; López Navarrete, J.T.; Casado, J.; Ratera, I.; Rovira, C.; Painelli, A.; Veciana, J. Thermomagnetic Molecular System Based on TTF-PTM Radical: Switching the Spin and Charge Delocalization. J. Phys. Chem. Lett. 2013, 4, 2721–2726. [Google Scholar] [CrossRef]
- Ali, E.; Staemmler, V.; Illas, F.; Oppeneer, P.M. Designing the Redox-Driven Switching of Ferro- to Antiferromagnetic Couplings in Organic Diradicals. J. Chem. Theory Comput. 2013, 9, 5216–5220. [Google Scholar] [CrossRef]
- Zhang, F.Y.; Song, X.Y.; Bu, Y.X. Redox-Modulated Magnetic Transformations between Ferro- and Antiferromagnetism in Organic Systems: Rational Design of Magnetic Organic Molecular Switches. J. Phys. Chem. C 2015, 119, 27930–27937. [Google Scholar] [CrossRef]
- Song, M.Y.; Song, X.Y.; Bu, Y.X. Core-Modified Porphyrin Diradicals with a C=C Unit: Redox-Driven Magnetic Switching. J. Phys. Chem. C 2017, 121, 21231–21243. [Google Scholar] [CrossRef]
- Matsuda, K.; Irie, M. A Diarylethene with Two Nitronyl Nitroxides: Photoswitching of Intramolecular Magnetic Interaction. J. Am. Chem. Soc. 2000, 122, 7195–7201. [Google Scholar] [CrossRef]
- Saha, A.; Latif, I.A.; Datta, S.N. Photoswitching Magnetic Crossover in Organic Molecular Systems. J. Phys. Chem. A 2011, 115, 1371–1379. [Google Scholar] [CrossRef] [PubMed]
- Okuno, k.; Shigeta, Y.; Kishi, R.; Nakano, M. Photochromic Switching of Diradical Character: Design of Efficient Nonlinear Optical Switches. J. Phys. Chem. Lett. 2013, 4, 2418–2422. [Google Scholar] [CrossRef]
- Shil, S.; Roy, M.; Misra, A. Role of the Coupler to Design Organic Magnetic Molecules: LUMO Plays an Important Role in Magnetic Exchange. RSC Adv. 2015, 5, 105574–105582. [Google Scholar] [CrossRef]
- Zhang, F.Y.; Feng, Y.W.; Song, X.Y.; Bu, Y.X. Enhancing Magnetic Coupling through Protonation of Benzylideneaniline-Bridged Diradicals and Comparison with Stilbene- and Azobenzene-Based Diradicals. RSC Adv. 2022, 12, 31442–31450. [Google Scholar] [CrossRef]
- Trindle, C.; Datta, S.N. Molecular Orbital Studies on the Spin States of Nitroxide Species: Bis- and Trisnitroxymetaphenylene, 1,1-Bisnitroxyphenylethylene, and 4,6-Dimethoxy-1,3-dialkylnitroxybenzenes. Int. J. Quantum Chem. 1996, 57, 781–799. [Google Scholar] [CrossRef]
- Trindle, C.; Datta, S.N.; Mallik, B. Phenylene Coupling of Methylene Sites. The Spin States of Bis(X-methylene)-p-phenylenes and Bis(chloromethylene)-m-phenylene. J. Am. Chem. Soc. 1997, 119, 12947–12951. [Google Scholar] [CrossRef]
- Borden, W.T.; Davidson, E.R. Effects of Electron Repulsion in Conjugated Hydrocarbon Diradicals. J. Am. Chem. Soc. 1977, 99, 4587–4594. [Google Scholar] [CrossRef]
- Gallagher, N.; Zhang, H.; Junghoefer, T.; Giangrisostomi, E.; Ovsyannikov, R.; Pink, M.; Rajca, S.; Casu, M.B.; Rajca, A. Thermally and Magnetically Robust Triplet Ground State Diradical. J. Am. Chem. Soc. 2019, 141, 4764–4774. [Google Scholar] [CrossRef]
- Baumgarten, M. Chapter 1: High Spin Organic Molecules. In World Scientific Reference on Spin in Organics; Miller, J.S., Ed.; World Scientific: Singapore, 2018; Volume 4, pp. 1–93. [Google Scholar] [CrossRef]
- Tretyakov, E.V.; Ovcharenko, V.I.; Terent’ev, A.O.; Krylov, I.B.; Magdesieva, T.V.; Mazhukin, D.G.; Gritsan, N.P. Conjugated Nitroxides. Russ. Chem. Rev. 2022, 91, RCR5025. [Google Scholar] [CrossRef]
- Bencini, A.; Gatteschi, D.; Totti, F. Density Functional Modeling of Long Range Magnetic Interactions in Binuclear Oxomolybdenum(V) Complexes. J. Phys. Chem. A 1998, 102, 10545–10551. [Google Scholar] [CrossRef]
- Constantinides, C.P.; Koutentis, P.A.; Schatz, J. A DFT Study of the Ground State Multiplicities of Linear vs Angular Polyheteroacenes. J. Am. Chem. Soc. 2004, 126, 16232–16241. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, R.; Zeiss, G.D.; Van Dine, G.W. The Electronic Structure of Methylenes. J. Am. Chem. Soc. 1968, 90, 1485–1499. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Yamaguchi, K.; Takahara, Y.; Fueno, T.; Nasu, K. Ab Initio MO Calculations of Effective Exchange Integrals between Transition-Metal Ions via Oxygen Dianions: Nature of the Copper-Oxygen Bonds and Superconductivity. Jpn. J. Appl. Phys. 1987, 26, L1362–L1364. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Jensen, F.; Dorigo, A.; Houk, K.N. A Spin Correction Procedure for Unrestricted Hartree-Fock and Møller-Plesset Wavefunctions for Singlet Diradicals and Polyradicals. Chem. Phys. Lett. 1988, 149, 537–542. [Google Scholar] [CrossRef]
- Ginsberg, A.P. Magnetic Exchange in Transition Metal Complexes. 12. Calculation of Cluster Exchange Coupling Constants with the Xα-Scattered Wave Method. J. Am. Chem. Soc. 1980, 102, 111–117. [Google Scholar] [CrossRef]
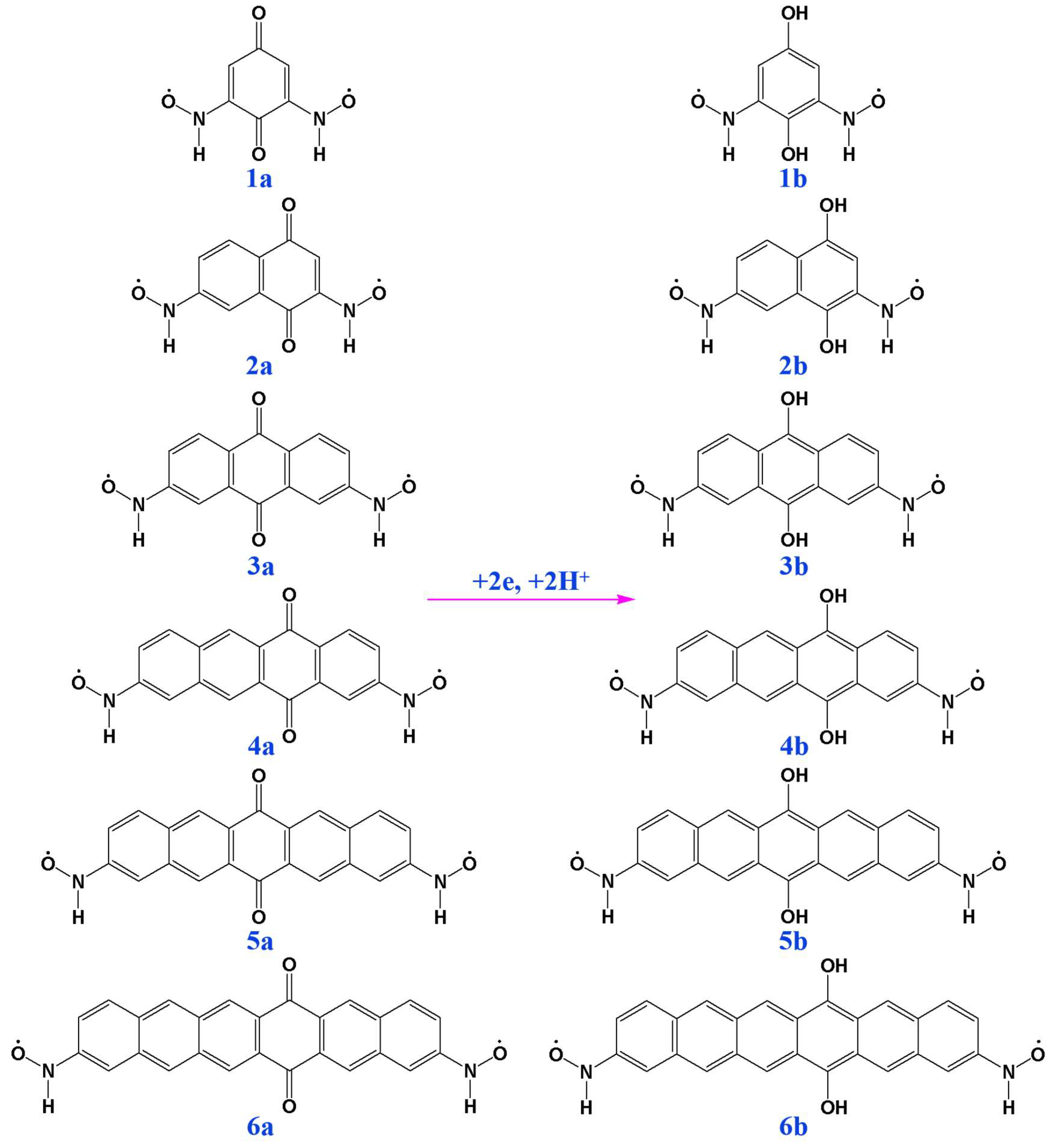
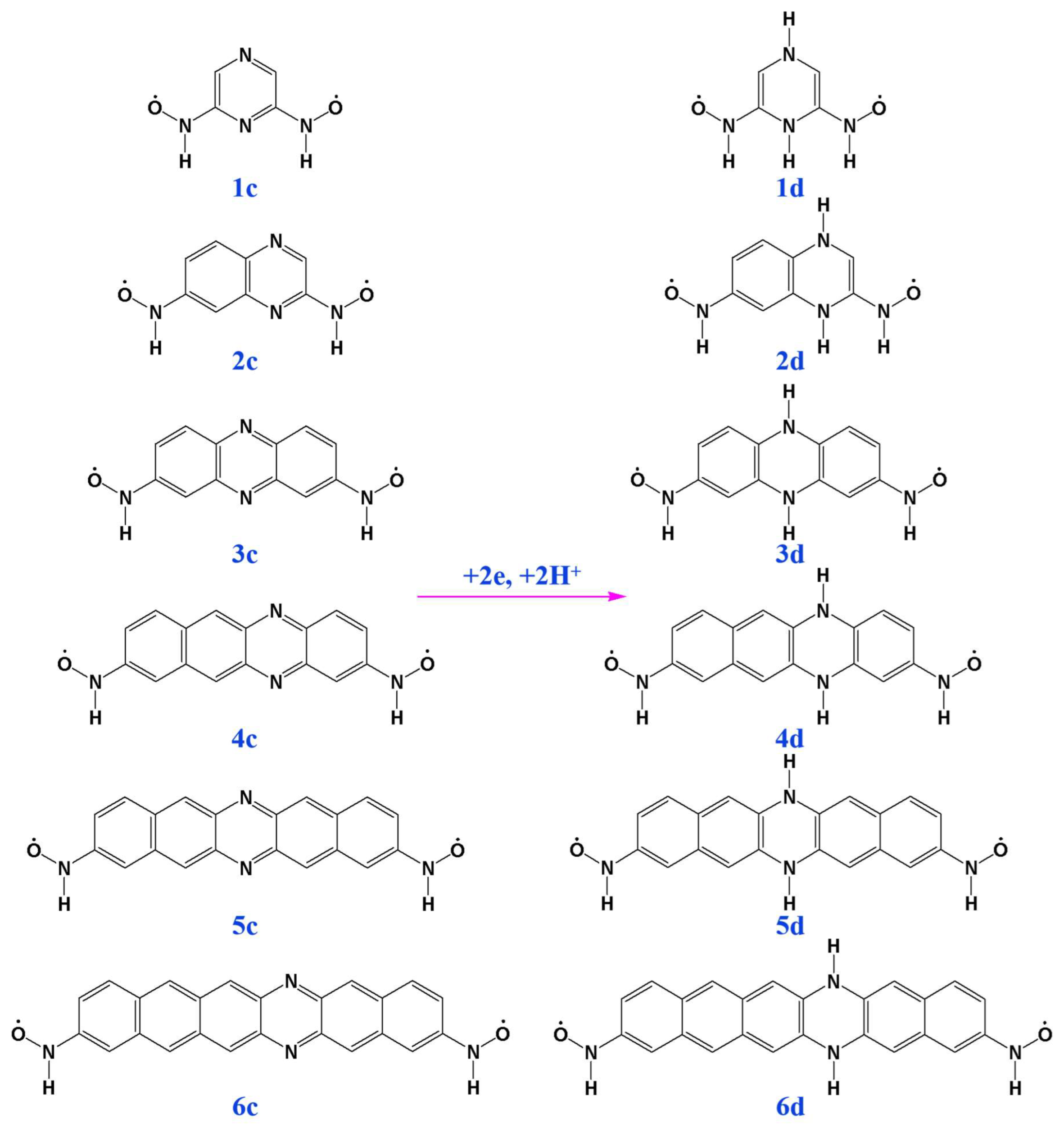
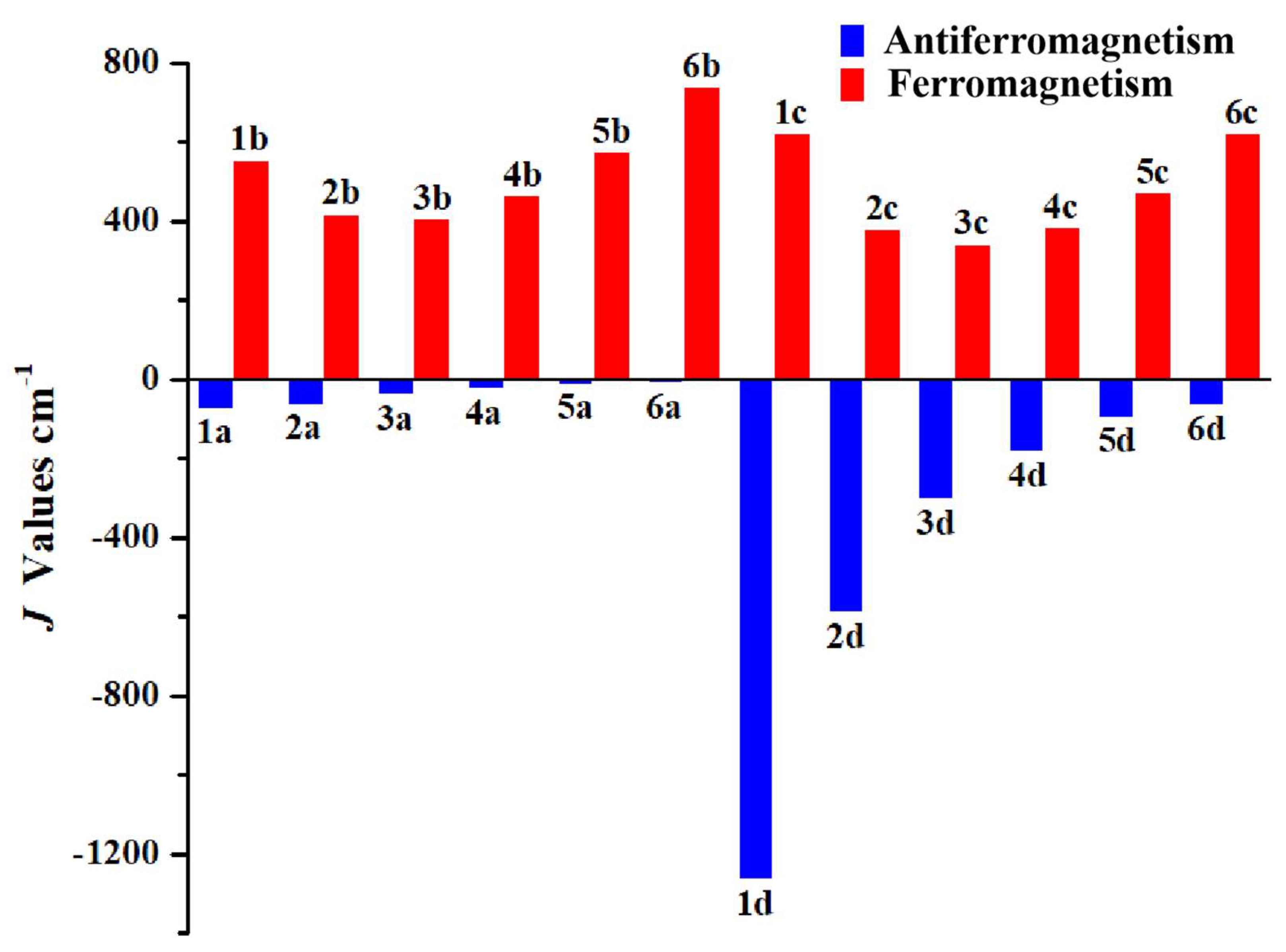

| Species | Average Spin Density Delocalization into Coupler (%) | J | Species | Average Spin Density Delocalization into Coupler (%) | J |
|---|---|---|---|---|---|
| 1a | 25.7 | −74.8 | 1b | 13.8 | 551.6 |
| 2a | 20.1 | −63.4 | 2b | 16 | 417.2 |
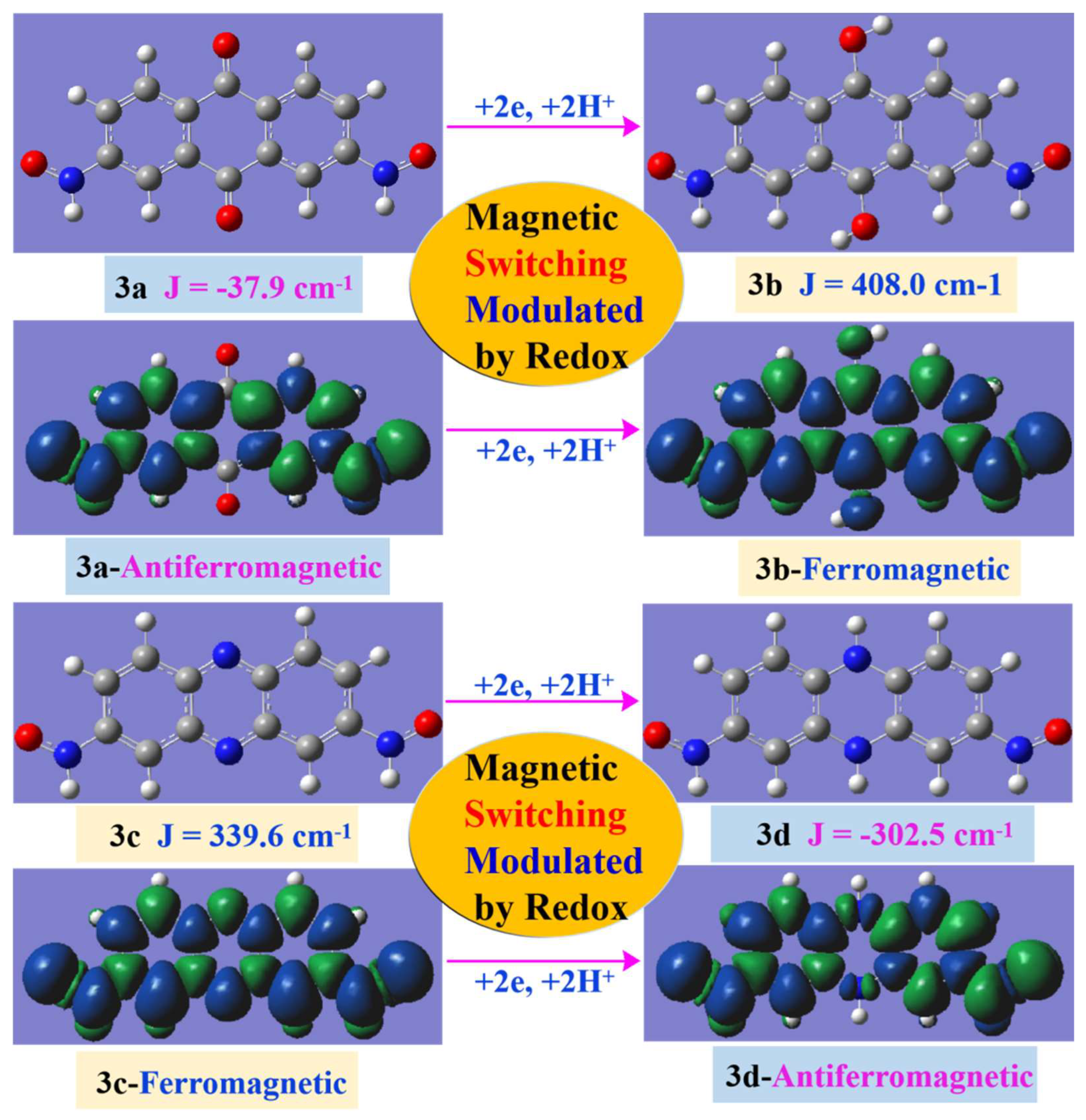
| 3a | 15.1 | −37.9 | 3b | 17.6 | 408 |
| 4a | 15 | −24.3 | 4b | 19.9 | 464.5 |
| 5a | 14.9 | −15.0 | 5b | 21.6 | 576.6 |
| 6a | 15.3 | −11.2 | 6b | 22.5 | 740.7 |
| 1c | 13.6 | 621.7 | 1d | 37 | −1267.5 |
| 2c | 14.7 | 380.9 | 2d | 23.7 | −589.4 |
| 3c | 16.9 | 339.6 | 3d | 17.8 | −302.5 |
| 4c | 19.2 | 383 | 4d | 16.4 | −184.4 |
| 5c | 21.3 | 473.3 | 5d | 15.3 | −98.5 |
| 6c | 22.6 | 621.6 | 6d | 15.1 | −66.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Zhang, Z.; Zhao, Y.; Du, C.; Li, Y.; Gao, J.; Ren, X.; Ma, T.; Li, B.; Bu, Y. Redox-Regulated Magnetic Conversions between Ferro- and Antiferromagnetism in Organic Nitroxide Diradicals. Molecules 2023, 28, 6232. https://doi.org/10.3390/molecules28176232
Zhang F, Zhang Z, Zhao Y, Du C, Li Y, Gao J, Ren X, Ma T, Li B, Bu Y. Redox-Regulated Magnetic Conversions between Ferro- and Antiferromagnetism in Organic Nitroxide Diradicals. Molecules. 2023; 28(17):6232. https://doi.org/10.3390/molecules28176232
Chicago/Turabian StyleZhang, Fengying, Zijun Zhang, Yali Zhao, Chao Du, Yong Li, Jiaqi Gao, Xiaobo Ren, Teng Ma, Boqiong Li, and Yuxiang Bu. 2023. "Redox-Regulated Magnetic Conversions between Ferro- and Antiferromagnetism in Organic Nitroxide Diradicals" Molecules 28, no. 17: 6232. https://doi.org/10.3390/molecules28176232
APA StyleZhang, F., Zhang, Z., Zhao, Y., Du, C., Li, Y., Gao, J., Ren, X., Ma, T., Li, B., & Bu, Y. (2023). Redox-Regulated Magnetic Conversions between Ferro- and Antiferromagnetism in Organic Nitroxide Diradicals. Molecules, 28(17), 6232. https://doi.org/10.3390/molecules28176232







