Abstract
The reaction of N-phenyl iminoborane with benzaldehyde yielding a fused aromatic compound, recently reported by Liu et al., has been studied within the Molecular Electron Density Theory (MEDT). Formation of the fused aromatic compound is a domino process that comprises three consecutive reactions: (i) formation of a weak molecular complex between the reagents; (ii) an intramolecular electrophilic attack of the activated carbonyl carbon of benzaldehyde on the ortho position of the N-phenyl substituent of iminoborane; and (iii) a formal 1,3-hydrogen shift yielding the final fused aromatic compound. The two last steps correspond to a Friedel–Crafts acylation reaction, the product of the second reaction being the tetrahedral intermediate of an electrophilic aromatic substitution reaction. However, the presence of the imino group adjacent to the aromatic ring strongly stabilizes the corresponding intermediate, being the reaction product when the ortho positions are occupied by t-butyl substituents. This domino reaction shows a great similitude with the Brønsted acid catalyzed Povarov reaction. Although N-phenyl iminoborane can experience a formal [2+2] cycloaddition reaction with benzaldehyde, its higher activation Gibbs free energy compared to the intramolecular electrophilic attack of the activated carbonyl carbon of benzaldehyde on the ortho position of the N-phenyl substituent, 6.6 kcal·mol−1, prevents the formation of the formal [2+2] cycloadduct. The present MEDT study provides a different vision of the molecular mechanism of these reactions based on the electron density.
1. Introduction
Iminoboranes are isoelectronic with alkynes yet contain a polar B–N triple bond, which readily undergoes 1,2-addition [1,2] or [2+2] cycloaddition reactions [3,4,5] (see Scheme 1).
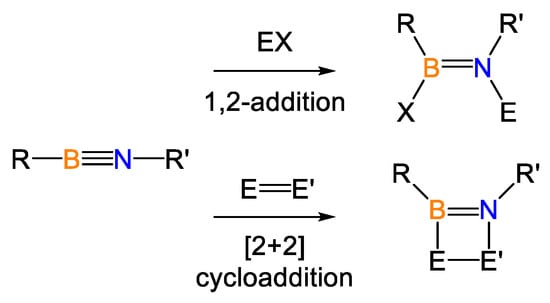
Scheme 1.
Reactions of iminoboranes.
Recently, Liu et al. [6] suggested that BN-substituted π-conjugated systems may be versatile species participating in formal Diels-Alder reactions, given that enynes have been well documented as the diene component for [4+2] cycloaddition reactions with alkenes [7,8,9]. Thus, when B-(N-heterocyclic imine) N-aryl iminoborane 1 was treated with benzaldehyde 2 in toluene at room temperature, the fused bicyclic compound 3 was obtained with a yield of 97% (see Scheme 2) [6]. On the other hand, when the N-aryl iminoborane 1 was treated with CO2, the four-membered heterocyclic 5 was obtained with a yield of 65% (see Scheme 2).
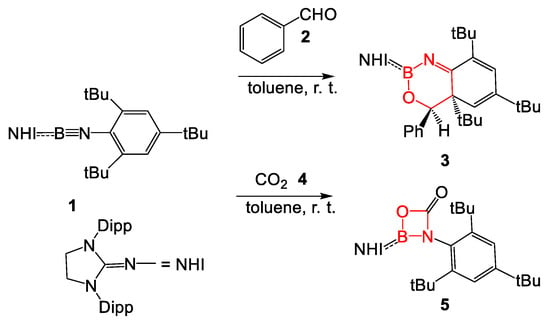
Scheme 2.
Experimental reactions of B-(N-heterocyclic imine) N-aryl iminoborane 1 with benzaldehyde 2 and CO2 4, reported by Liu et al. [6].
Liu et al. theoretically studied the two reactions, suggesting that the formation of fused bicyclic compound 3 takes place by a concerted [4+2] cycloaddition reaction between N-aryl iminoborane 1 and benzaldehyde 2 through a transition state structure (TS) that presented an activation Gibbs free energy of 23.1 kcal·mol−1 [6]. The formal [2+2] cycloaddition of N-aryl iminoborane 1 with benzaldehyde 2 to give an adduct like 5 was also studied. The TS associated with the corresponding formal [2+2] cycloaddition reaction was found to be 9.6 kcal·mol−1 above the TS associated with the formation of fused bicyclic compound 3, explaining the absence of the formal [2+2] cycloadduct.
Interestingly, when N-phenyl iminoborane 6, which has no substitution at the ortho positions of benzene, was treated with benzaldehyde 2, the aromatic compound 7 was obtained with a yield of 97% (see Scheme 3) [6]. Formation of the aromatic compound 7 was explained by a hydrogen shift from the ortho position of the formal [4+2] cycloadduct to the imino nitrogen atom.
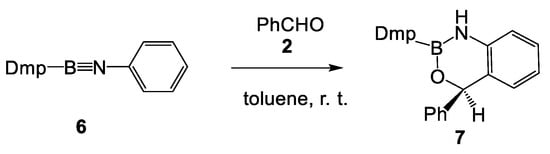
Scheme 3.
Experimental reaction of N-phenyl iminoborane 6 with benzaldehyde 2, reported by Liu et al. [6].
Formation of the aromatic compound 7 can be understood as an intramolecular boron-catalyzed Friedel–Crafts acylation reaction of the N-phenyl iminoborane 6. The presence of alkyl substituents at the ortho positions of the N-aryl iminoborane 1 prevents the elimination of the alkyl group, while the presence of strong electron-releasing amino nitrogen at the aromatic compound strongly stabilizes the tetrahedral intermediate involved in an electrophilic aromatic substitution (SEAr) reaction, thus yielding the non-aromatic compound 3.
The reaction between an N-aryl imine 8 and a nucleophilic ethylene 9 in the presence of a Lewis acid, known as the Povarov reaction [10], has become a powerful tool for the construction of the 1,2,3,4-tetrahydroquinoline (THQ) structure (see Scheme 4). Povarov reactions are domino processes involving two consecutive reactions: (i) a Lewis acid (LA) catalyzed aza-Diels-Alder (A-DA) reaction between an N-aryl imine 8 and a nucleophilic ethylene 9 giving a formal [4+2] cycloadduct 10; and (ii) a subsequent 1,3-hydrogen shift in 10 yielding the final THQ 11, with regeneration of the aromatic ring [11].
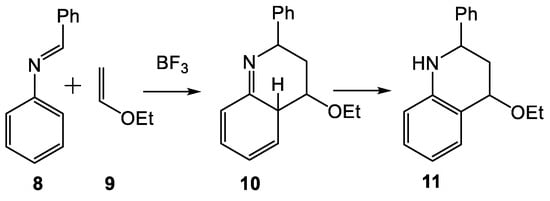
Scheme 4.
Povarov reaction of N-aryl imines with nucleophilic ethylenes.
In 2015, the mechanism of the Brønsted acid-catalyzed Povarov reaction of N-phenyl-C-methoxycarbonyl imine 12 with methylenecyclopropane 13 was investigated [12]. The quick nucleophilic attack of methylenecyclopropane 13 on the carbon atom of protonated imine 14 yields the stabilized carbocation intermediate 15, which experiences a rapid electrophilic attack on the ortho position of the aromatic ring of the N-phenyl imine (see Scheme 5). Finally, a hydrogen abstraction on the tetrahedral cationic intermediate 16 yields the aromatic THQ 17, a formal [4+2] cycloadduct. The mechanism of this Brønsted acid-catalyzed Povarov reaction was explained as a domino process initialized by the formation of a cationic intermediate, which experiences a quick intramolecular Friedel–Crafts alkylation reaction yielding the final THQ 17 [12].
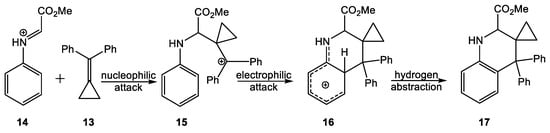
Scheme 5.
Brønsted acid catalyzed Povarov reaction.
A comparative study of the reaction products of iminoboranes 1 and 6 given in Scheme 2 and Scheme 3 with the species theoretically characterized in the study of the Brønsted acid catalyzed Povarov reaction given in Scheme 5 shows a great similitude. The formal [4+2] cycloadduct 17 is obtained using an intramolecular Friedel–Crafts alkylation reaction in the strong electrophilic cation intermediate 15.
In order to provide a new mechanistic interpretation of the reaction of N-aryl iminoborane 1 with benzaldehyde 2, experimentally and theoretically studied by Liu et al. (see Scheme 2) [6], a Molecular Electron Density Theory (MEDT) [13] study of the reaction of model N-phenyl iminoborane 18 with benzaldehyde 2, yielding fused aromatic compound 20 and the formal [2+2] cycloadduct 21, is herein studied. In model N-phenyl iminoborane 18, the Dipp groups of experimental N-phenyl iminoborane 6 were substituted by phenyl groups (see Scheme 6).
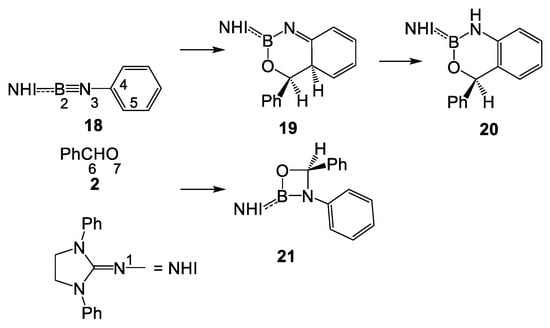
Scheme 6.
Reactions of model N-phenyl iminoborane 18 with benzaldehyde 2, are investigated in the present theoretical study.
2. Results and Discussion
2.1. ELF and AIM Characterization of the Electronic Structure of N-Phenyl Iminoborane 18 and Benzaldehyde 2
The topological analysis of the electron localization function (ELF) [14] permits a quantitative characterization of the electron density distribution in a molecule [15], allowing the establishment of a correlation between its electronic structure and its reactivity. Thus, an ELF topological analysis of the electronic structures of N-phenyl iminoborane 18 and benzaldehyde 2 was performed first. ELF basin attractor positions, together with the most relevant valence basin populations, as well as ELF Lewis-like structures, are shown in Figure 1. Atom numbering is provided in Scheme 6.
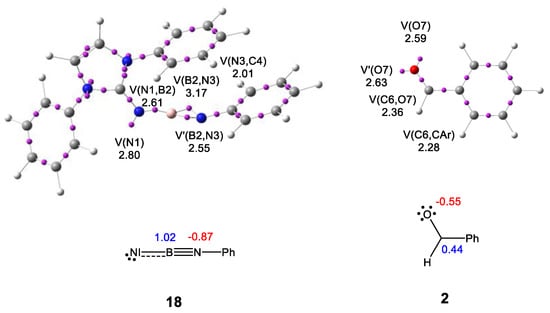
Figure 1.
ωB97X-D/6-311G(d,p) ELF basin attractor positions, populations of the most relevant valence basins, natural atomic charges, and ELF Lewis-like structures of N-phenyl iminoborane 18 and benzaldehyde 2. Valence basin populations and natural atomic charges are given in an average number of electrons, e. Negative charges are colored in red, and positive charges in blue.
ELF topology of the iminoborane moiety of 18 shows the presence of one V(N1) monosynaptic basin, integrating 2.80 e, one V(N1,B2) disynaptic basin, integrating 2.61 e, a pair of disynaptic basins, V(B2,N3) and V′(B2,N3), integrating a total of 5.72 e, and one V(N3,C4) disynaptic basin, integrating 2.01 e. While the two V(B2,N3) and V′(B2,N3) disynaptic basins allow characterizing the B2–N3 bonding region as a B2–N3 triple bond, the V(N1,B2) disynaptic basin allows relating the N1–B2 bonding region to a populated N1–B2 single bond. The V(N1) monosynaptic basin indicates the presence of a non-bonding region at the N1 nitrogen. Finally, the population of the V(N3,C4) disynaptic basin, which is near 2.0 e, permits the relation of the N3–C4 bonding region as an N3–C4 single bond. The presence of the V(N1,B2) and V(B2,N3) disynaptic basins suggests that the B2 boron is covalently bound to the N1 and N3 nitrogens.
The carbonyl C–O bonding region of benzaldehyde 2 is characterized by the presence of one V(C6,O7) disynaptic basin, integrating 2.36 e, and a pair of monosynaptic basins, V(O7) and V′(O7), integrating a total of 5.22 e. The low population of the V(C6,O7) disynaptic basin, which is a consequence of the strong electronegative character of the O7 oxygen, characterizes the C6–O7 bonding region as a C6–O7 single bond.
Finally, a natural population analysis (NPA) [16,17] of the atomic charges of N-phenyl iminoborane 18 indicates that while the B2 boron is positively charged by +1.02 e, the N3 nitrogen is negatively charged by −0.87 e. The NPA of the atomic charges of benzaldehyde 2 indicates that while the carbonyl C6 carbon is positively charged by +0.44 e, the O7 oxygen is negatively charged by −0.55 e.
Interestingly, while the ELF analysis of the electronic structure of N-phenyl iminoborane 18 agrees with the proposed Lewis structures for iminoboranes given in Scheme 1, the NPA gives opposite charges at the boron and nitrogen to those proposed for them on the basis of classic Lewis structures.
In order to further understand the nature of the electronic interactions at the N1–B2 and B2–N3 bonding regions of N-phenyl iminoborane 18, a topological analysis of the electron density in these N–B bonding regions was performed within the Quantum Theory of Atoms in Molecules (QTAIM) [18,19]. The contour line map of the Laplacian ∇2ρ(r) of the electron density of N-phenyl iminoborane 18 is shown in Figure 2, while the QTAIM parameters at the (3, −1) critical points (CPc) CP1 and CP2 associated with the N–B regions are given in Table 1.
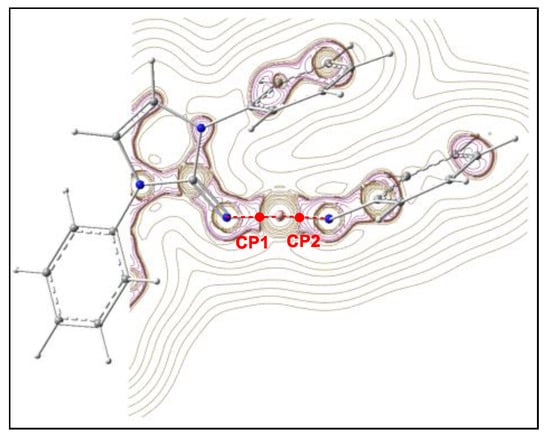
Figure 2.
Representations of the contour line maps of the Laplacian ∇2ρ(r) of the electron density at N-phenyl iminoborane 18. The critical points CP1 and CP2 associated with the N1–B2 and B2–N3 interaction regions, respectively, are colored in red.

Table 1.
QTAIM parameters at the (3, −1) CPs associated with the N1–B2 and B2–N3 interacting regions of N-phenyl iminoborane 18. ρ(r) is given in e·Å−3, ∇2ρ(r) in e·Å−5, and H(r), G(r), and V(r) in hartree·Å−3.
QTAIM analysis of N-phenyl iminoborane 18 provides electron density ρ(r) values higher than 0.22 e·Å−3 for both CP1 and CP2, suggesting covalent interactions [20]. However, both CPs present a high positive Laplacian ∇2ρ(r) value and a negative local energy density H(r), suggesting an intermediate interaction such as highly polar covalent bonds or dative bonds (see Table 1) [20,21,22,23,24]. The H(r)/ρ(r) << 0 and G(r)/ρ(r) > 1 found at CP1 and CP2 are also characteristic of intermediate interactions.
Espinosa [21] proposed a useful criterion to characterize interactions at the CPs using an analysis of the ratio of the potential and kinetic energy densities, |V(r)|/G(r). For non-covalent interactions, |V(r)|/G(r) < 1, partially covalent interactions are characterized by 1 < |V(r)|/G(r) < 2, while covalent interactions show |V(r)|/G(r) > 2. The calculated values of |V(r)|/G(r) at CP1 and CP2 of N-phenyl iminoborane 18 are given in Table 1. The |V(r)|/G(r) values of CP1 and CP2 are lower than 1.68, indicating that these B–N bonding regions present somewhat covalent character, which may well correspond to a dative bond type considering the previous parameters. This suits the common understanding that boron usually participates as an acceptor in chemical bonding with donors such as nitrogen.
Recently, Berski et al. [25] studied the nature of the B–N multiple bonds by using ELF and QTAIM, finding a similar behavior for the B–N triple and single bonds to that found in N-phenyl iminoborane 18. While ELF showed the presence of V(B,N) disynaptic basins integrating ca. 6.4 and 2.0 e, the QTAIM analysis yielded the typical features for shared (∇2ρ(r) < 0) and closed-shell (∇2ρ(r) > 0) interactions. The ELF and natural bond orbital (NBO) topological analyses yielded a similar description for the B–N bonds. Both approaches revealed a significant contribution of the nitrogen atom to the B–N bonding, which is in agreement with a formal dative mechanism of its formation. Consequently, unlike the C–C or N–N covalent bonds, the N→B bonds should be considered as dative bonds [25].
2.2. Study of the Reaction of N-Phenyl Iminoborane 18 with Benzaldehyde 2
The reaction of N-phenyl iminoborane 18 with benzaldehyde 2 yielding aromatic compound 20 is a domino process that comprises three consecutive reactions: (i) formation of a weak molecular complex (MC) resulting from the interactions between the carbonyl O7 oxygen of benzaldehyde 2 and the B2 boron of N-phenyl iminoborane 18; (ii) an intramolecular electrophilic attack of the activated carbonyl C6 carbon of benzaldehyde 2 on the ortho C5 carbon of the phenyl substituent of iminoborane 18 yielding the fused bicyclic compound 19; and finally (iii) a formal 1,3-hydrogen shift from the C5 carbon to the N3 nitrogen regenerating the aromatic ring (see Scheme 7). In the cases of N-aryl iminoboranes having alkyl substituents in the ortho positions, this process is not possible, obtaining compound 19 as the reaction product (see Scheme 2). This domino process can take place along two stereoisomeric reaction paths, named trans and cis, depending on the relative position of the phenyl substituent of benzaldehyde 2 with respect to the ortho hydrogen of the N-phenyl substituent of iminoborane 18 (see Scheme 7). The relative enthalpies and Gibbs free energies are given in Table 2, while complete thermodynamic data are gathered in Table S2 in Supporting Information.
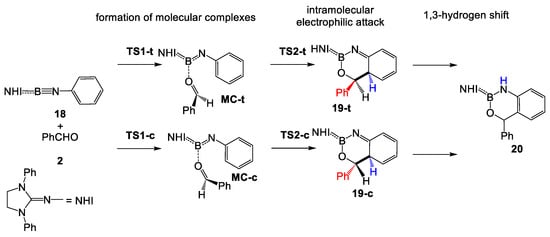
Scheme 7.
Trans and cis stereoisomeric reaction paths associated with the domino reaction of N-phenyl iminoborane 18 with benzaldehyde 2.

Table 2.
ωB97X-D/6-311G(d,p) relative enthalpies and Gibbs free energies (in kcal·mol−1), computed in toluene at 298.15 K, of the stationary points involved in the domino reaction of N-phenyl iminoborane 18 with benzaldehyde 2.
The activation Gibbs free energies associated with the formation of the MCs are 15.8 (TS1-c) and 16.7 (TS1-t) kcal·mol−1, their formation being endergonic by 14.9 (MC-c) and 17.2 (MC-t) kcal·mol−1. The very high endergonic character of these MCs means that they cannot be considered reaction intermediates. Note, however, that the formation of these MCs is necessary for the electrophilic activation of the carbonyl C6 carbon of benzaldehyde 2 for the subsequent electrophilic attack to the phenyl substituent of N-phenyl iminoborane 18.
From these MCs, the subsequent electrophilic attacks of the activated carbonyl C6 carbon of benzaldehyde 2 on the ortho C5 carbon of the phenyl substituent of N-phenyl iminoborane 18 have low activation Gibbs free energies of 6.2 (TS2-c) and 2.6 (TS2-t) kcal·mol−1. From the separated reagents, the formation of the fused bicyclic compounds 19-c and 19-t is exergonic by 6.8 and 4.6 kcal·mol−1, respectively. Finally, a subsequent formal 1,3-hydrogen shift converts the fused bicyclic compounds 19 into the aromatic compound 20. This process is strongly exergonic by 39.4 kcal·mol−1 as a consequence of the regeneration of the aromatic ring of the phenyl substituent. Due to the strain associated with this intramolecular 1,3-hydrogen shift process, it has a very high activation energy [26], and consequently, this tautomerization requires an external acid/base species [27].
Considering the endergonic character of the formation of MCs, the second step, corresponding to the electrophilic attack of the carbonyl C6 carbon of benzaldehyde 2 on the ortho C5 carbon of the phenyl substituent of N-phenyl iminoborane 18, can be considered the rate-determining step (RDS) of this domino processes. If the formation of these fused bicyclic compounds is considered irreversible, trans 19-t will be the product of a kinetic control as TS2-t is 1.8 kcal·mol−1 below TS2-c (see Figure 3). Consequently, the activation Gibbs free energy associated with this domino reaction via TS2-t is 19.8 kcal·mol−1.
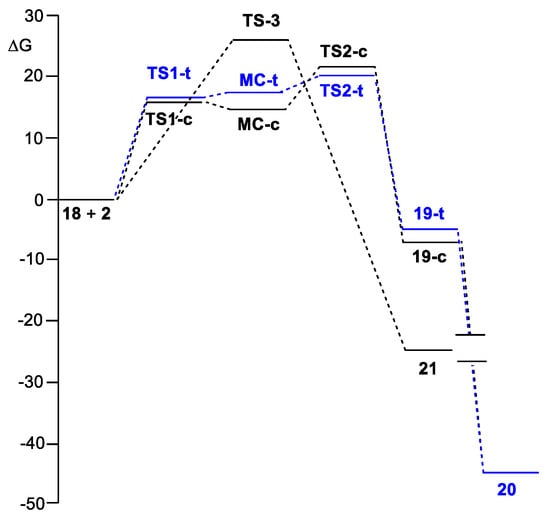
Figure 3.
ωB97X–D/6-311G(d,p) Gibbs free energy profiles, in kcal·mol−1, computed in toluene at 298.15 K, of the competitive reaction paths associated with the domino reaction of N-phenyl iminoborane 18 with benzaldehyde 2. The most favorable trans reaction path yielding the aromatic compound 20 is given in blue.
Liu et al. found that when N-aryl iminoborane 1 was treated with CO2, the four-membered heterocyclic compound 5 was obtained with a yield of 65% (see Scheme 2) [6]. However, the formation of a formal [2+2] cycloadduct 21 between N-aryl iminoborane 1 and formaldehyde 2 was not experimentally observed. Therefore, the two formal [2+2] cycloaddition reactions in N-phenyl iminoborane 18 were studied herein (see Scheme 8). Relative enthalpies and Gibbs free energies are given in Table 2, while complete thermodynamic data are gathered in Table S2 in Supporting Information.
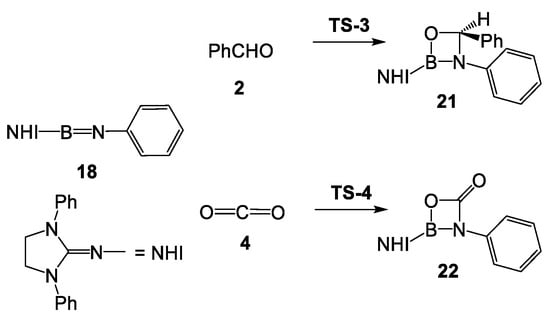
Scheme 8.
Formal [2+2] cycloaddition reaction between N-phenyl iminoborane 18 with benzaldehyde 2 and with CO2 4.
The activation Gibbs free energy associated with the [2+2] addition of CO2 4 to N-phenyl iminoborane 18 via TS-4 is 19.4 kcal·mol−1 (see Table 2), formation of the formal [2+2] cycloadduct 22 being strongly exergonic by 14.1 kcal·mol−1. The activation Gibbs free energy associated with this [2+2] addition is close to that associated with the intramolecular electrophilic attack in MC-t, justifying the experimental observation of cycloadduct 22 (see Table 2). On the other hand, the activation Gibbs free energy associated with the [2+2] addition of benzaldehyde 2 to N-phenyl iminoborane 18 via TS-3 is 26.4 kcal·mol−1, formation of the formal [2+2] cycloadduct 21 being also strongly exergonic by 24.4 kcal·mol−1. Consequently, although the formation of the formal [2+2] cycloadduct 21 is thermodynamically more favorable than the formation of fused bicyclic compounds 19, the former reaction is 6.6 kcal·mol−1 kinetically more unfavorable, thus preventing the formation of the formal [2+2] cycloadduct 21.
The geometries of the TSs involved in the more favorable trans reaction path are given in Figure 4. At the TS related to the formation of MC-t, the B2–O7 distance is 1.736 Å, while this distance at MC-t is 1.629 Å, indicating the very advanced character of TS1-t. At TS2-t, the C5–C6 distance is 2.395 Å. Considering that this distance at MC-t is 2.843 Å, TS2-t can be considered very early, in agreement with the low activation energy associated with TS2-t, 2.6 kcal·mol−1. Finally, at TS-3, associated with the formation of the formal [2+2] cycloadduct 21, the N3–C6 and B2–O7 distances are 1.811 and 2.329 Å, respectively. These distances indicate that it corresponds to a highly asynchronous TS associated with the nucleophilic attack of the N3 nitrogen of N-phenyl iminoborane 18 on the carbonyl C6 carbon atom of benzaldehyde 2.
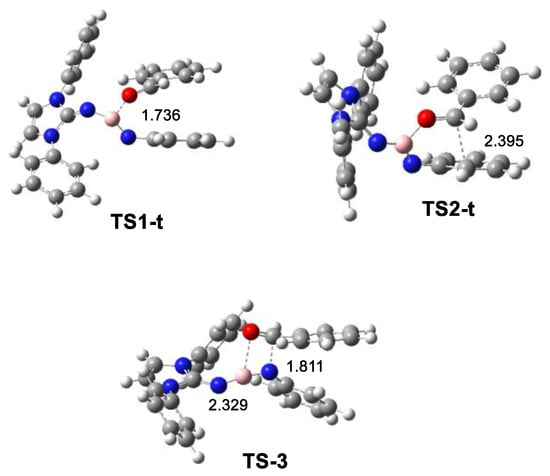
Figure 4.
ωB97X-D/6-311G(d,p) optimized geometries in toluene of the TSs involved in the trans reaction paths and formal [2+2] cycloaddition between N-phenyl iminoborane 18 with benzaldehyde 2.
Finally, the polar character of the [2+2] cycloaddition reactions was evaluated by computing the global electron density transfer (GEDT) [28] at the corresponding TSs. TSs with a GEDT lower than 0.05 e correspond to non-polar processes, while TSs with a GEDT higher than 0.20 e correspond to high-polar processes. The GEDT computed at the two TSs is 0.25 e at TS-3 and 0.27 e at TS-4. These high values account for the high polar character of these formal [2+2] cycloaddition reactions, which can be related to the nucleophilic attack of the imino N3 nitrogen of N-phenyl iminoborane 18 on the carbonyl carbons of benzaldehyde 2 and CO2. In addition, the higher polar character of TS-4 than that of TS-3 accounts for the lower activation enthalpy of the former (see Table 2).
2.3. ELF and QTAIM Analysis of the Stationary Points Associated with the Trans Reaction Path of the Domino Reaction between N-Phenyl Iminoborane 18 and Benzaldehyde 2
In order to reveal the structural changes along the domino reaction between N-phenyl iminoborane 18 and benzaldehyde 2 yielding the aromatic compound 20, an ELF topological analysis of the stationary points in toluene associated with the more favorable trans reaction path was performed. ELF basin attractor positions are shown in Figure 5, while the most relevant ELF valence basin populations are given in Table 3.
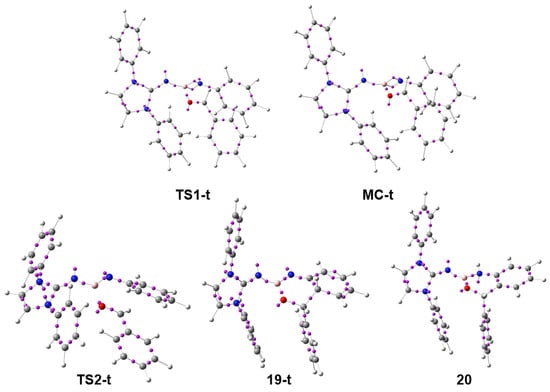
Figure 5.
ωB97X-D/6-311G(d,p) ELF basin attractor positions of the stationary points associated with the trans reaction path of the domino reaction between N-phenyl iminoborane 18 and benzaldehyde 2.

Table 3.
ELF basin populations, in average number of electrons, e, of the stationary points involved in the trans reaction path of the domino reaction between N-phenyl iminoborane 18 and benzaldehyde 2.
Some appealing conclusions can be obtained from the variation of ELF valence basin populations corresponding to the stationary points involved in the trans reaction path: (i) Along the domino reaction, some molecular regions are depopulated while others are populated. Thus, while the N1–B2 is depopulated from 2.74 e at TS1-t to 2.48 e at 20 the N3=C4 bonding region is populated from 2.00 e at TS1-t to 2.75 e at 19-t. At the final aromatic compound 20, the population of the N3–C4 bonding region is 1.91 e. The total population of the non-bonding region of the O7 oxygen decreases from 5.22 e at benzaldehyde 2 to 4.30 e at 20; (ii) the presence of benzaldehyde 2 at MC-t, with the O7 oxygen near the B2 boron, remarkably depopulates the B2–N3 region from 5.72 to 3.15 e, and causes the accumulation of non-bonding electron density at the N3 nitrogen; (iii) the absence of any V(B2,O7) disynaptic basin at MC-t indicates that at this weak MC, there is a non-covalent interaction between the B2 boron and the carbonyl O7 oxygen; and finally, (iv) the bonding changes found in the conversion of 19-t into the aromatic compound 20 via the 1,3-hydrogen shift are a consequence of the strong stabilization of the tetrahedral compound 19-t resulting from the intramolecular electrophilic attack of benzaldehyde 2 on the ortho position of N-phenyl iminoborane 18.
Finally, a QTAIM topological analysis of the electron density ρ(r) at the stationary points MC-t, 19-t, and 20 was performed in order to characterize the nature of the B2–O7 and C5–C6 interactions at these species. The calculated QTAIM parameters at the (3, −1) CPs at these interacting regions, CP1 and CP2, are given in Table 4, while the contour line map of the Laplacian ∇2ρ(r) of the electron density of the final aromatic compound 20 is shown in Figure 6.

Table 4.
AIM parameters, in atomic units a.u., of the (3, −1) CPs at the stationary points MC-t, 19-t, and 20 in the regions associated with the B2–O7 and C5–C6 interacting atoms. ρ(r) is given in e·Å−3, ∇2ρ(r) in e·Å−5, and H(r), G(r), and V(r) in hartree·Å−3.
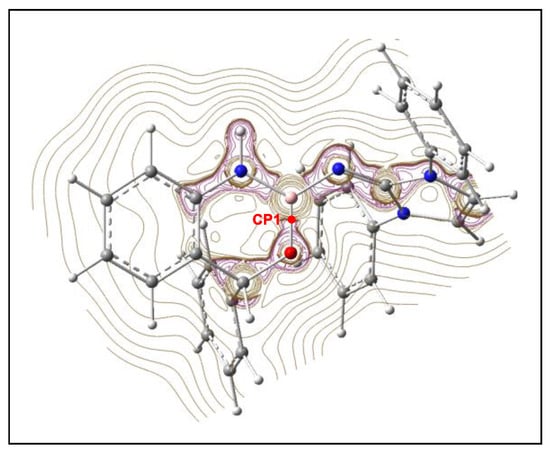
Figure 6.
Representations of the contour line maps of the Laplacian ∇2ρ(r) of the electron density at the aromatic compound 20. The critical point CP1 associated with the B2–O7 interaction region is colored in red.
QTAIM analysis of these species shows very different values of electron density at CP1. While MC-t presents a ρ(r) value of 0.09 e·Å−3, this increases up to 0.19 e·Å−3 at products 19-t and 20. These values suggest an intermediate (dative) B2–O7 interaction at MC-t that increases its covalent character at both 19-t and 20. On the other hand, the value of ca. 0.25 e·Å−3 at CP2 is characteristic of a C5–C6 covalent bond.
At the three compounds, CP1 shows a positive Laplacian ∇2ρ(r) value, indicating the absence of any pure covalent interaction in the B2–O7 bonding region (see Table 4). Conversely, at 19-t and 20, CP2 shows a negative Laplacian ∇2ρ(r) value, indicating the presence of a covalent C5–C6 interaction.
The G(r)/ρ(r) and |V(r)|/G(r) parameters also allow a clear distinction between the two different types of bonds in these species. At the three compounds, G(r)/ρ(r) > 1 at CP1, clearly indicating an intermediate (dative) B2–O7 interaction, while G(r)/ρ(r) < 1 at CP2, featuring the covalent C5–C6 bond at 19-t and 20. On the other hand, the |V(r)|/G(r) values of CP1 at the three compounds are lower than 1.42, indicating that, according the Espinosa criteria [21], the B2–O7 bonding region of these species present a non-covalent interaction with somewhat covalent character, while the corresponding values of CP2 at 19-t and 20, higher than 4.40, indicate a covalent interaction between the C5 and C6 carbons.
The H(r)/ρ(r) indicators are always negative, thus providing no particular discrimination. However, the similar QTAIM parameters at each CP1 and CP2 in both 19-t and 20 indicate no remarkable changes in the B2–O7 and C5–C6 bonding regions along the conversion of 19-t into the aromatic compound 20.
On the other hand, the figure of the contour line map of the Laplacian ∇2ρ(r) of the electron density of the aromatic compound 20 in the plain containing the N1 and N3 nitrogen and the O7 oxygen nuclei shows that these heteroatoms are not covalently bound to the B2 boron (see Figure 6).
Recently, Berski et al. [29] studied the nature of chalcogen B-Ch (Ch = O, S, Se, Te) multiple bonds, finding that the B–O bond presents similar behaviors to the B–N ones. The B–O bond has a high degree of polarity, with a large positive ∇2ρ(r) value. The oxygen quantum atom delivers about 90% of the electron density of the V(B,O) disynaptic basin, indicating that the O→B bond has a high dative character. Thus, it is reasonable that the B–N bonds are also dative bonds, as Figure 6 suggests.
2.4. BET Study of the Molecular Mechanisms of the Electrophilic Attack of Benzaldehyde 2 on the Phenyl Substituent of Imine Borane 18
In order to characterize the bonding changes taking place in the first step of the acylation of imine borane 18 with benzaldehyde 2, a Bonding Evolution Theory (BET) [30] study of the electron density redistribution along the electrophilic attack of the carbonyl C6 carbon of benzaldehyde 2 on the ortho C5 carbon of the phenyl substituent of N-phenyl iminoborane 23, as a reduced model of N-phenyl iminoborane 18, was carried out (see Scheme 9). In N-phenyl iminoborane 23, the two phenyl substituents present in N-phenyl iminoborane 18 were replaced by methyl groups. The topological analysis of the ELF of N-phenyl iminoborane 23 is given in Figure S1 in Supporting Information. The population of the most relevant regions at key structures of the IRC is given in Table 5, while a simplified representation of the mechanism is displayed in Scheme 10. The ELF valence basin attractor positions of the structures involved in the bond formation processes are shown in Figure 7.
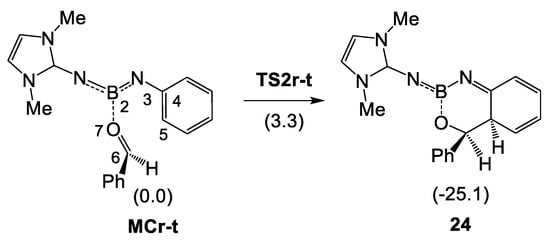
Scheme 9.
Step of the electrophilic attack of the carbonyl C6 carbon on the ortho C5 carbon of the phenyl substituent of N-phenyl iminoborane 23. Relative energies in toluene are given in parentheses in kcal·mol−1.

Table 5.
ELF valence basin populations, relative energies in toluene, and B2–O7 and C5–C6 distances of the most relevant structures along the IRC associated with the electrophilic attack of the carbonyl C6 carbon on the ortho C5 carbon of the phenyl substituent of N-phenyl iminoborane 23. Populations are given in average number of electrons, e, energies in kcal·mol-1, and distances in angstroms, Å.
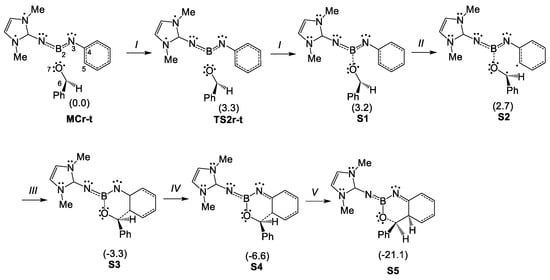
Scheme 10.
Representation of the molecular mechanism of the electrophilic attack of the carbonyl C6 carbon on the ortho C5 carbon of the phenyl substituent of N-phenyl iminoborane 23, by Lewis-like structures based on the topological analysis of the ELF.
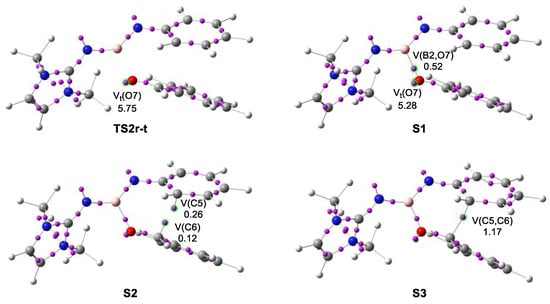
Figure 7.
ELF basin attractor positions of TS2r-t and the structures involved in the formation of the C5–C6 single bond.
The first structure of the IRC corresponds to the molecular complex MCr-t formed between the two interacting frameworks. Similar to MC-t (see Table 3), the B2–N3 bonding region is characterized as an underpopulated double bond integrating 3.03 e, with a non-bonding electron density of 2.66 e at the N3 nitrogen. No conjugation of the B2–N3 bond with the phenyl ring is observed, given that the N3–C4 region presents a population of 2.02 e. On the other hand, the benzaldehyde moiety presents a markedly polarized carbonyl C6–O7 single bond integrating 2.16 e, while the O7 oxygen atom bears a total population of 5.41 e.
The topological analysis of the ELF of TS2r-t shows no significant changes in the electron density distribution with respect to that of MCr-t, which accounts for the low activation energy associated with the electrophilic attack of the carbonyl C6 carbon of the benzaldehyde framework on the ortho C5 carbon of the phenyl substituent of N-phenyl iminoborane one, 3.3 kcal·mol−1. This barrier might be associated with the depopulation of the B2–N3 bonding region by 0.29 e towards the N3 nitrogen and N3–C4 regions and with the depopulation of the C6–O7 bonding region by 0.27 e towards the O7 oxygen. Note that the V(O7) monosynaptic basins have been populated by 0.34 e.
Just after passing TS2r-t, the topological analysis of the ELF suggests that the non-covalent interaction between the carbonyl O7 oxygen and the B2 boron becomes covalent at a B2–O7 distance of ca. 1.59 Å and an initial bonding population of 0.52 e, through the donation of non-bonding electron density of the carbonyl O7 oxygen to the B2 boron (see the new V(B2,O7) disynaptic basin at S1 in Figure 7 and the corresponding Lewis-like structure in Scheme 10). However, QTAIM analysis suggests an intermediate dative-type bond.
At structure S2, the progressive depopulation of the C4–C5 and C6–O7 bonding regions gathers non-bonding electron density at the C5 and C6 carbon atoms, with a population of 0.26 and 0.12 e, respectively, which are associated with two C5 and C6 pseudoradical centers [31] (see the new V(C5) and V(C6) monosynaptic basins in S2 in Figure 7 and the corresponding Lewis-like structure in Scheme 10).
At S3, the C-to-C coupling of these two C5 and C6 pseudoradical centers forms the new C5–C6 single bond at a C–C distance of ca. 2.00 Å, and an initial population of 1.17 e, via the sharing bond formation model [28] (see the V(C5,C6) disynaptic basin at S3 in Figure 7 and the corresponding Lewis-like structure in Scheme 10). At this moment, the C4–C5 bonding region can already be considered a single bond after the continued population along the reaction path, just as the C4–C and C5–C regions of the new hexadiene ring (see the Lewis-like structure of S3 in Scheme 10). Only at the end of the reaction path does the N3–C4 region become an imine partial N–C double bond, in agreement with the expected structure for cycloadduct 24 (see S4 in Scheme 10).
Some appealing conclusions can be drawn from this BET study: (i) formation of the new C5–C6 single bond takes place at a C–C distance of ca. 2.00 Å, following the general sharing model involving C–C multiple bonds [28]; (ii) a delocalized structure in the phenyl ring, such as that in a cationic tetrahedral intermediate characteristic of the first step of SEAr reactions, is not observed. Instead, a localized and well-defined cyclohexadienimine structure is formed as a consequence of the presence of the N2 nitrogen in N-phenyl iminoborane 23. Note that the fused bicyclic compound 24 is 25.1 kcal·mol−1 more stable than 23 (see Scheme 9). This behavior allows explaining the stability of fused bicyclic compound 3 in which the ortho positions of the aromatic ring are substituted by a t-butyl group (see Scheme 2).
2.5. REG-IQA Energy Partitioning Analysis of the Activation Energy
As mentioned above, no significant changes in the bonding pattern are observed at TS2r-t with respect to MCr-t (see both Lewis-like structures in Scheme 10). Thus, the activation energy associated with the electrophilic attack of carbonyl C6 carbon of benzaldehyde 2 on the ortho C5 carbon of the phenyl substituent of N-phenyl iminoborane 23 is only 3.3 kcal·mol−1. Based on variations of ELF valence basin populations, it seems that this low activation barrier is mainly associated with the depopulation of the B2–N3 and C6–O7 bonding regions. However, changes in ELF populations should not be directly related to the energy of the system [32]. Thus, in order to determine the origin of the activation energy, a REG-IQA energy partitioning analysis was carried out (see the theoretical background in Supporting Information for more details on REG-IQA). The ten IQA energy terms with the largest contribution to the barrier, i.e., REG absolute values, are gathered in Table 6, while Pearson correlation coefficients of REG regressions are given in Table S1 in Supporting Information.

Table 6.
Ten largest REGi values corresponding to the IQA partitioning into intra-atomic and interatomic energy terms along the activation IRC path associated with the SEAr reaction between N-phenyl iminoborane 23 and benzaldehyde 2. REGi values of the and contributors to are also included. Relative energies are given in kcal·mol−1.
The REG-IQA analysis shows that the terms participating the most in the activation energy are of an interatomic nature. The terms most contributing towards the barrier, i.e., the most unfavorable energies for the reaction, are Vinter(C6,O7) and Vinter(B2,N3), associated with the interatomic interactions that take place in the C6–O7 and B2–N3 bonding regions as they are depopulated. The REG values of the corresponding and terms indicate that these interatomic interactions are mainly related to classical electrostatic (non-covalent) interactions rather than covalency. Note that, especially in the B2–N3 region, the REG value of Vcl(B2,N3) is almost four times larger than that of Vxc(B2,N3).
On the other hand, the factors most working against the barrier, i.e., the ones that most favor the reaction, are Vinter(B2,O7) and Vinter(N3,C4), associated with the interatomic interactions in the B2–O7 and N3–C4 bonding regions, followed by Vinter(C5,C6), belonging to one of the phenyl ring bonds. While the electrostatic component of Vinter(B2,O7) and Vinter(N3,C4) overcomes the effect of exchange-correlation in decreasing the activation barrier, the favorable role of Vinter(C5,C6) in the barrier is mostly due to exchange-correlation, i.e., covalency.
Consequently, the present REG-IQA study allows concluding that the low activation energy associated with the electrophilic attack of carbonyl C6 carbon on the ortho C5 carbon of the phenyl substituent of N-phenyl iminoborane 23 is mainly associated with the unfavorable electrostatics developed in the B2–N3 and C6–O7 bonding regions as a consequence of their depopulation from MCr-t to TS2r-t.
3. Computational Methods
All calculations were performed using the ωB97X-D [33] functional together with the standard 6-311G(d,p) basis set [34]. The TSs were characterized by the presence of only one imaginary frequency. The Berny method was used in optimizations [35,36]. The intrinsic reaction coordinates (IRC) paths [37] were traced to establish the unique connection between the TSs and the corresponding minima [38,39].
Solvent effects of toluene in the thermodynamic calculations were taken into account by full optimization of the gas-phase structures at the same computational level using the polarizable continuum model (PCM) [40,41] in the framework of the self-consistent reaction field (SCRF) [42,43,44]. Values of ωB97X-D/6-311G(d,p) enthalpies, entropies, and Gibbs free energies in toluene were calculated with standard statistical thermodynamics [34] at room temperature and pressure by PCM frequency calculations at the solvent-optimized structures.
The GEDT [28] values were computed using the equation GEDT(f) = Σqf, where q is the natural charges [16,17] of the atoms belonging to one of the two frameworks (f) at the TS geometries.
The Gaussian 16 suite of programs was used to perform the calculations [45]. ELF [14] analyses of the ωB97X-D/6-311G(d,p) monodeterminantal wavefunctions were performed by using the TopMod [46] package with a cubical grid of step size of 0.1 Bohr. Molecular geometries and ELF basin attractors were visualized by using the GaussView program [47].
A stand-alone script based on the Ramer-Douglas-Peucker algorithm [48,49] was used to find a reduced but still suitable number of structures on which to run the REG-IQA [50] analysis out of the 23 points belonging to the respective activation IRC path; an RMSE value of 0.01 kcal·mol−1 was considered. The IQA analysis [51] was performed with the AIMAll package [52] using the corresponding B3LYP/6-311G(d,p) monodeterminantal wavefunctions. To achieve this, the corresponding TSs were optimized, and the IRCs were obtained at that computational level. Note that the ωB97X-D functional is not available in AIMAll. The REG analysis was carried out via the REG.py program developed by Popelier’s group [53].
4. Conclusions
The reaction of N-phenyl iminoborane 18 with benzaldehyde 2 yielding fused aromatic compound 20, recently reported experimentally and theoretically by Liu et al. [6], has been studied within MEDT at the ωB97X-D/6-311G(d,p) computational level.
Formation of the fused aromatic compound 20 is a domino process that comprises three consecutive reactions: (i) formation of a weak molecular complex MC-t between the N-phenyl iminoborane 18 and benzaldehyde 2; (ii) an intramolecular electrophilic attack of the activated carbonyl carbon of benzaldehyde on the ortho position of the N-phenyl substituent yielding the fused bicyclic compound 19-t; (iii) and a formal 1,3-hydrogen shift yielding the final fused aromatic compound 20. The two last reactions of this domino process correspond to an intramolecular Friedel–Crafts acylation reaction, the fused bicyclic compound 19-t of the second reaction being the tetrahedral intermediate of a SEAr reaction. The presence of the imino N3 nitrogen adjacent to the aromatic ring strongly stabilizes the tetrahedral compound 19-t, being obtained as the reaction product when the ortho positions of the phenyl substituent are occupied by t-butyl groups. This domino reaction shows a great similitude with the mechanism of the Brønsted acid-catalyzed Povarov reactions (see Scheme 11).
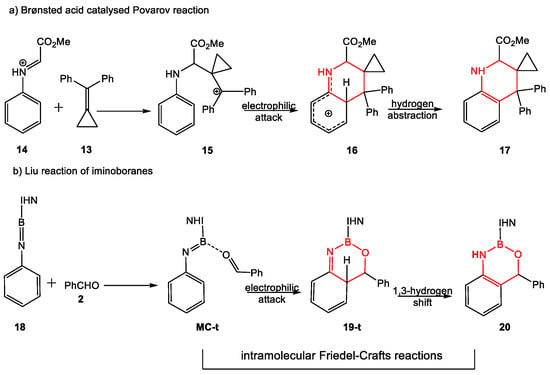
Scheme 11.
Comparative analysis of the domino reactions involved in the Brønsted acid-catalyzed Povarov reaction and the reaction of N-phenyl iminoborane 18 with benzaldehyde 2.
Although N-phenyl iminoborane 18 can experience a formal [2+2] cycloaddition reaction with benzaldehyde 2, the higher activation Gibbs free energy associated with this cycloaddition reaction, 26.4 kcal·mol−1, than that associated with the intramolecular electrophilic attack of the activated carbonyl carbon of benzaldehyde on the ortho position of the N-phenyl substituent, 19.8 kcal·mol−1, prevents the formation of the formal [2+2] cycloadduct 21.
Analysis of the electron density reorganization along the domino reaction of N-phenyl iminoborane 23 with benzaldehyde 2 allows for an explanation of the experimental outcomes. The electron density changes taking place along the electrophilic attack of the carbonyl C6 carbon of benzaldehyde 2 on the ortho position of the phenyl substituent permits a strong stabilization of the product of the electrophilic attach, allowing this compound as the reaction product when the subsequent formal 1,3-hydrogen shift is not possible. ELF and QTAIM analyses of the electron density of the species involved in this domino reaction indicate that the N→B and O→B bonds have a dative nature instead of a covalent one.
The present MEDT study provides a different vision of the molecular mechanism of these reactions to that reported by Liu et al., allowing an interpretation of this domino reaction based on the changes in electron density. The MCs are very unfavorable coordination complexes between the carbonyl oxygen atom of benzaldehyde and the boron of the N-phenyl iminoboranes, while the second reaction of this domino process is the first step of an intramolecular SEAr reaction related to a Friedel–Crafts acylation. In contrast, Liu et al. related TS1-t to the TS of a concerted DA reaction [6].
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28176211/s1, Theoretical background on REG-IQA; Figure S1: ωB97X-D/6-311G(d,p) ELF basin attractor positions, populations of the most relevant valence basins, and natural atomic charges of N-phenyl iminoborane 23; Table S1: Pearson correlation coefficients R of the ten IQA terms with largest REGi values along the activation IRC path associated with the SEAr reaction between N-phenyl iminoborane 23 and benzaldehyde 2; Table S2: ωB97X-D/6-311G(d,p) total electronic energies, enthalpies, entropies, and Gibbs free energies, computed in toluene at 298.15 K, of the stationary points involved in the reactions of N-phenyl iminoborane 18 with benzaldehyde 2 and with CO2 4. ωB97X-D/6-311G(d,p) Cartesian coordinates of the optimized geometries in toluene of the stationary points involved in the reactions of N-phenyl iminoborane 18 with benzaldehyde 2, and with CO2 4, including the single imaginary frequencies for the TSs. References [54,55,56,57] are cited in the supplementary materials.
Author Contributions
Conceptualization, L.R.D. Furthermore, M.R.-G.; methodology, L.R.D. Furthermore, M.R.-G.; investigation, L.R.D., M.J.A. and M.R.-G.; resources, L.R.D., M.J.A. and M.R.-G.; writing—original draft preparation, L.R.D., M.R.-G.; writing—review and editing, L.R.D., M.J.A. and M.R.-G.; supervision, L.R.D.; funding acquisition, L.R.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the Ministry of Science and Innovation (MICINN) of the Spanish Government, project PID2019-110776GB-I00 (AEI/FEDER, UE).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data underlying this study are available in the published article and its supporting information.
Acknowledgments
The Ministry of Science and Innovation (MICINN) of the Spanish Government is acknowledged for financial support through project PID2019-110776GB-I00 (AEI/FEDER, UE).
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Not applicable.
References
- Nöth, H. The Chemistry of Amino Imino Boranes. Angew. Chem. Int. Ed. 1988, 27, 1603–1622. [Google Scholar] [CrossRef]
- Paetzold, P. Iminoboranes. Adv. Inorg. Chem. 1987, 31, 123–170. [Google Scholar]
- Braunschweig, H.; Ewing, W.C.; Geetharani, K.; Schäfer, M. The Reactivities of Iminoboranes with Carbenes: BN Isosteres of Carbene–Alkyne Adducts. Angew. Chem. Int. Ed. 2015, 54, 1662–1665. [Google Scholar] [CrossRef] [PubMed]
- Winner, L.; Bélanger-Chabot, G.; Celik, M.A.; Schäfer, M.; Braunschweig, H. Intriguing migrations in transient iminoborane adducts: Two new pathways to aminoboranes. Chem. Commun. 2018, 54, 9349–9351. [Google Scholar] [CrossRef]
- Winner, L.; Hermann, A.; Bélanger-Chabot, G.; González-Belman, O.F.; Jiménez-Hall, J.O.C.; Kelch, H.; Braunschweig, H. Cleavage of BN triple bonds by main group reagents. Chem. Commun. 2018, 54, 8210–8213. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Zhang, X.; Hu, C.; Chu, H.; Li, Q.; Ruiz, D.A.; Liu, L.L.; Tung, C.-H.; Kong, L. Unveiling Hetero-Enyne Reactivity of Aryliminoboranes: Dearomative Hetero-Diels-Alder-Like Reactions. Angew. Chem. Int. Ed. 2022, 61, e202205814. [Google Scholar] [CrossRef]
- Brückner, R.; Huisgen, R. 2,2-bis(trifluoromethyl)ethylene-1,1-dicarbonitrile and styrenes the concertedness of the [2 + 4] cycloaddition. Tetrahedron Lett. 1990, 31, 7133–7136. [Google Scholar] [CrossRef]
- Brückner, R.; Huisgen, R.; Schmid, J. 2,2-bis(trifluoromethyl)ethylene-1,1-dicarbonitrile and styrenes a dichotomy of cycloaddition pathways. Tetrahedron Lett. 1990, 31, 7129–7132. [Google Scholar] [CrossRef]
- Middleton, W.J. 1,1-Dicyano-2,2-bis(trifluoromethyl)ethylene. J. Org. Chem. 1965, 30, 1402–1407. [Google Scholar] [CrossRef]
- Povarov, L.S. α,β-Unsaturated ethers and their analogues in reactions of diene synthesis. Russ. Chem. Rev. 1967, 36, 656–670. [Google Scholar] [CrossRef]
- Domingo, L.R.; Aurell, M.J.; Sáez, J.A.; Mekelleche, S.M. Understanding the mechanism of the Povarov reaction. A DFT study RSC Adv. 2014, 4, 25268–25278. [Google Scholar] [CrossRef]
- Rios-Gutierrez, M.; Layeb, H.; Domingo, L.R. A DFT Study of the Mechanisms of Bronsted Acid Catalysed Povarov Reactions. Tetrahedron 2015, 71, 9339–9345. [Google Scholar] [CrossRef]
- Domingo, L.R. Molecular electron density theory: A modern view of reactivity in organic chemistry. Molecules 2016, 21, 1319. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular-systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Tang, Y.H.; Tal, Y.; Biegler-König, F.W. Properties of toms and bonds in hydrocarbon molecules. J. Am. Chem. Soc. 1982, 104, 946–952. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, NY, USA, 1994. [Google Scholar]
- Gatti, C. Chemical Bonding in Crystals: New Directions. Z. Krist. 2005, 220, 399–457. [Google Scholar] [CrossRef]
- Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H⋯F–Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
- Silvi, B. The Synaptic Order: A Key Concept to Understand Multicenter Bonding. J. Mol. Struct. 2002, 614, 3–10. [Google Scholar] [CrossRef]
- Grabowski, S.J. What Is the Covalency of Hydrogen Bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef]
- Gervasio, G.; Bianchi, R.; Marabello, D. About the Topological Classification of the Metal-Metal Bond. Chem. Phys. Lett. 2004, 387, 481–484. [Google Scholar] [CrossRef]
- Mierzwa, G.; Gordon, A.J.; Berski, S. The nature of multiple boron-nitrogen bonds studied using electron localization function (ELF), electron density (AIM), and natural bond orbital (NBO) methods. J. Mol. Model. 2020, 26, 136. [Google Scholar] [CrossRef]
- Andrés, J.; Domingo, L.R.; Picher, M.T.; Safont, V.S. Comparative theoretical study of transition structures, barrier heights, and reaction energies for the intramolecular tautomerization in acetaldehyde vinyl alcohol and acetaldimine/vinylamine systems. Int. J. Quant. Chem. 1998, 66, 9–24. [Google Scholar] [CrossRef]
- Emamian, S.R.; Domingo, L.R.; Tayyari, S.F. Tautomerism in pyridazin-3(2H)-one: A theoretical study using implicit/explicit solvation models. J. Mol. Graph. Model. 2014, 49, 47–54. [Google Scholar] [CrossRef]
- Domingo, L.R. A new C-C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef]
- Berski, S.; Latajka, Z.; Gordon, A.J. Theoretical insights and quantitative rediction of the nature of boron–chalcogen (O, S, Se, Te) interactions using the electron density and the electron localisation function (ELF). New J. Chem. 2011, 35, 89–96. [Google Scholar] [CrossRef]
- Krokidis, X.; Noury, S.; Silvi, B. Characterization of Elementary Chemical Processes by Catastrophe Theory. J. Phys. Chem. A 1997, 101, 7277–7282. [Google Scholar] [CrossRef]
- Domingo, L.R.; Sáez, J.A. Understanding the Electronic Reorganization along the Non-polar [3 + 2] cycloaddition reactions of carbonyl ylides. J. Org. Chem. 2011, 76, 373–379. [Google Scholar] [CrossRef]
- Ríos-Gutiérrez, M.; Falcioni, F.; Domingo, L.R.; Popelier, P.L.A. A Combined BET and IQA-REG Study of the Activation Energy of non-polar zw-type [3+2] Cycloaddition Reactions. Phys. Chem. Chem. Phys. 2023, 25, 10853–10865. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Phys. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Hehre, M.J.; Radom, L.; Schleyer, P.V.R.; Pople, J. Ab initio Molecular Orbital Theory; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Schlegel, H.B. Optimization of equilibrium geometries and transition structures. J. Comput. Chem. 1982, 3, 214–218. [Google Scholar] [CrossRef]
- Schlegel, H.B. Modern Electronic Structure Theory; Yarkony, D.R., Ed.; World Scientific Publishing: Singapore, 1994. [Google Scholar]
- Fukui, K. Formulation of the reaction coordinate. J. Phys. Chem. 1970, 74, 4161–4163. [Google Scholar] [CrossRef]
- González, C.; Schlegel, H.B. Reaction path following in mass-weighted internal coordinates. J. Phys. Chem. 1990, 94, 5523–5527. [Google Scholar] [CrossRef]
- González, C.; Schlegel, H.B. Improved algorithms for reaction path following: Higher-order implicit algorithms. J. Chem. Phys. 1991, 95, 5853–5860. [Google Scholar] [CrossRef]
- Tomasi, J.; Persico, M. Molecular interactions in solution: And overview of methods based on continuous distributions of the solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Simkin, B.Y.; Sheikhet, I.I. Quantum Chemical and Statistical Theory of Solutions–Computational Approach; Ellis Horwood: London, UK, 1995. [Google Scholar]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Cances, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M.; Tomasi, J. Geometry optimization of molecular structures in solution by the polarizable continuum model. J. Comput. Chem. 1998, 19, 404–417. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597–604. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, 6th ed.; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartographica 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Ramer, U. An iterative procedure for the polygonal approximation of plane curves. Comput. Graph. Image Process. 1972, 1, 244–256. [Google Scholar] [CrossRef]
- Thacker, J.C.R.; Popelier, P.L.A. The ANANKE relative energy gradient (REG) method to automate IQA analysis over configurational change. Theor. Chem. Acc. 2017, 136, 86. [Google Scholar] [CrossRef]
- Blanco, M.A.; Martín Pendás, A.; Francisco, E. Interacting Quantum Atoms: A Correlated Energy Decomposition Scheme Based on the Quantum Theory of Atoms in Molecules. J. Chem. Theory Comput. 2005, 1, 1096–1109. [Google Scholar] [CrossRef]
- Keith, T.A. AIMAll; Version 19.10.12; TK Gristmill Software: Overland Park, KS, USA, 2019; Available online: aim.tkgristmill.com (accessed on 8 August 2023).
- Falcioni, F.; Duarte Jose, L.; Popelier, L.A.P. REG.py, Version 0.1; Computer Software; 2023. Available online: https://github.com/popelier-group/REG (accessed on 8 August 2023).
- Wilson, A.L.; Popelier, P.L.A. Exponential Relationships Capturing Atomistic Short-Range Repulsion from the Interacting Quantum Atoms (IQA) Method. J. Phys. Chem. A 2016, 120, 9647–9659. [Google Scholar] [CrossRef]
- Popelier, P.L.A.; Kosov, D.S. Atom–atom partitioning of intramolecular and intermolecular Coulomb energy. J. Chem. Phys. 2001, 114, 6539–6547. [Google Scholar] [CrossRef]
- Popelier, P.L.A.; Joubert, L.; Kosov, D.S. Convergence of the Electrostatic Interaction Based on Topological Atoms. J. Phys. Chem. A 2001, 105, 8254–8261. [Google Scholar] [CrossRef]
- Martín Pendás, A.; Francisco, E.M.; Blanco, A.; Gatti, C. Bond Paths as Privileged Exchange Channels. Chem. Eur. J. 2007, 13, 9362–9371. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).