Abstract
Cyclic dipeptides with two intramolecular peptide bonds forming a six-membered 2,5-diketopiperazine ring are gaining significant attention due to their biological and chemical properties. Small changes in the local geometry of such molecules (from cis to trans) can lead to significant structural differences. This work presents the results of a study of cyclo(l-Cys-d-Cys), a dipeptide comprising two cysteine molecules in opposite chiral configurations, with the functional groups situated at both sides of the diketopiperazine ring. X-ray diffraction (XRD) experiment revealed that the molecule crystallises in the P-1 space group, which includes the centre of inversion. The IR and Raman vibrational spectra of the molecule were acquired and interpreted in terms of the potential energy distribution (PED) according to the results of density functional theory (DFT) calculations. The DFT-assisted analysis of energy frameworks for the hydrogen bond network within molecular crystals was performed to support the interpretation of X-ray structural data. The optimisation of the computational model based on three-molecule geometry sections from the crystallographic structure, selected to appropriately reflect the intermolecular interactions responsible for the formation of 1D molecular tapes in cyclo(l-Cys-d-Cys) crystal, allowed for better correspondence between theoretical and experimental vibrational spectra. This work can be considered the first complete structural characterisation of cyclo(l-Cys-d-Cys), complemented via vibrational spectroscopy results with full band assignment aided with the use of the DFT method.
1. Introduction
Cyclic dipeptides containing a six-membered 2,5-diketopiperazine ring are an important family of chemical compounds. Naturally occurring diketopiperazines constitute a class of secondary metabolites that are widespread in numerous living organisms [1], including humans [2]. They were marginalised for a long time, considered only as by-products of protein degradation [3,4]. Cyclic dipeptides have been gaining increasing attention due to their constrained geometry, often resulting in improved stability, binding affinity, and specificity compared with their linear counterparts [5]. In addition, their native ability to bind to a wide range of receptors makes them promising templates for drug development [6,7]. Diverse biological properties of 2,5-diketopiperazine-based cyclic dipeptides include antitumor [8], antimicrobial [9], and neuroprotective activity [10], while in chemical applications, they are used as catalysts [11], building blocks for self-assembling hydrogels [12], and polymers with high melting point [13], among others, as reviewed in [14,15,16,17,18].
Cyclic dipeptide isomers can be classified in terms of the configuration of two side chains of the diketopiperazine ring: cis (composed of two amino acid units of a single L/D configuration, i.e., L-L or D-D) and trans (with alternate L/D chirality). Moreover, the ring can adopt various conformations, which are strongly affected by the properties of amino acids’ side chains. Small substituents tend to form planar structures, such as that of cyclo(Gly-Gly) in a solid state [19], while more bulky residues lead to an out-of-plane conformation, as evidenced by the puckered (twist-boat) structure of the crystalline cyclo(l-Ala-l-Ala) [20] or the less typical flattened chair form, observed, e.g., for cyclo(l-Tyr–l-Pro) [21].
Cyclic dipeptides composed of identical residues are of particular interest, as various conformations and symmetry groups emerge in these molecules. For example, cyclo(d-Ala-l-Ala) exhibits symmetry with its nearly planar diketopiperazine ring and the equivalent positions of the two methyl groups [20], and shows a clear contrast resulting from the chirality change to the abovementioned cyclo(l-Ala-l-Ala) isomer with its puckered ring structure. Strong chirality dependence of the structure was also reported for cyclo(Tyr-Tyr) and was explained by stabilising interactions within the O-H∙∙∙O hydrogen bond [22].
Moreover, a proper choice of the structural motif containing a 2,5-diketopiperazine ring unit allows one to control the type of the supramolecular structure emerging from the self-assembly of individual dipeptide monomers. Depending on the type of hydrogen bond involved, crystallographic studies revealed linear, tape structures for planar cyclo(Gly-Gly) and a few other cyclic dipeptides [23] while a layer-type structure was demonstrated for cyclo(l-His-d-His) [24] and cyclo(d-Ala-l-Ala) [25]. Thus, the stereochemistry of dipeptides has a strong influence on the self-assembly process and the resulting architectures: the LL system favours the formation of 1D molecular chains, while LD promotes 2D layers [26]. The use of a combination of hydrogen bonding and aromatic interactions within the molecular crystals of cyclic homodipeptides composed of phenylglycine enabled a rational design of a new material with exceptional mechanical properties [26]. Control over the conformation through the selection of amino acid side chains is also essential for practical applications of dipeptides with the 2,5-diketopiperazine ring, particularly those demanding high selectivity, such as catalytic activity [27], accessibility of metal ion binding sites [28], and smart drug delivery [6,29,30,31].
To the best of our knowledge, this work is the first to present the exact crystal structure of cyclo(l-Cys-d-Cys) in a solid state and a comprehensive analysis of its vibrational spectra, providing complementary information on intermolecular interactions. The selection of naturally widespread cysteine as a building unit of the 2,5-diketopiperazine ring offers exceptional versatility in the design of such materials, due to the presence of a thiol moiety in addition to typical amino acid N- and O-containing units. This opens the route for, e.g., the thiol–ene click reaction, which proceeds with a high yield under mild conditions [32,33,34,35]. Extraordinary chelating properties toward zinc [36], lead [37], silver, nickel, and numerous other ions [38], further enhanced by the rigidity of the six-membered 2,5-diketopiperazine ring, are also anticipated.
Despite the interest in this family of compounds continuing for more than a century, research on cyclic dipeptides of cysteine is far from exhaustive and still uncovers new issues. A diligent literature review resulted in just a few synthetic protocols for the cyclo(l-Cys-l-Cys) (or cyclo-l-cystine, due to the inevitable creation of intramolecular S-S bond) [39,40,41,42,43,44], as well as several reports of the crystallographic structure [45,46,47] and spectroscopic characterisation, including Raman [48], IR [40,44], nuclear magnetic resonance [49], UV, optical rotatory dispersion, and circular dichroism spectra [50]. Cyclo(l-Cys-l-Cys) was used as an important model for the chiroptical and conformational properties of disulfides [51,52,53]. Gockel et al. concluded that this compound can coordinate zinc(II) ions [54], with binding properties of –SH groups superior to the imidazole ligand in cyclo(l-His-l-His). However, only the binuclear complex (2:2 stoichiometry) was found, suggesting that the localisation of the two thiolate side chains in the ring-shaped molecule was not optimal for the coordination of zinc ions.
Surprisingly, the cyclo(l-Cys-d-Cys) diastereomer seems to have attracted little attention: Our extensive review of the literature yielded only one patent application mentioning this compound [55]. Thus, in this paper, we present a structural description of cyclo(l-Cys-d-Cys) with properties distinctly different than those of the cyclo(l-Cys-l-Cys) due to its trans conformation and centrosymmetry. We followed a standard approach for the comprehensive structural characterisation of cyclic dipeptides comprising the analysis of crystallographic X-ray diffraction data and vibrational spectra, together with theoretical simulations, mostly employing density functional theory (DFT) calculations [56,57,58,59,60,61,62]. Additionally, the use of geometry derived from a crystal, utilising one- or three-molecule models in DFT calculations, enhanced the workflow of vibrational analysis and improved the accuracy of the hydrogen bonding model and its effect on vibrational energies.
The complete determination of the crystal structure, as well as the DFT-aided interpretation of the vibrational (IR and Raman) spectra of cyclo(l-Cys-d-Cys) provided a meaningful contribution to the evaluation of the effect of stereochemistry on tailoring the structure of 2,5-diketopiperazine-based dipeptides toward specific applications.
2. Results and Discussion
2.1. Crystallographic Analysis
The identity of the investigated compound was confirmed via single-crystal X-ray diffraction (XRD) analysis. Cyclo(l-Cys-d-Cys) crystallises in a triclinic P-1 space group with half of the molecule in the asymmetric unit of the crystal lattice (Figure 1). The crystal and structural refinement details are presented in Table S1 (Supplementary Material). The list of bond lengths, valence, and torsion angle values is provided in Tables S2, S3, and S4 of Supplementary Materials, respectively.
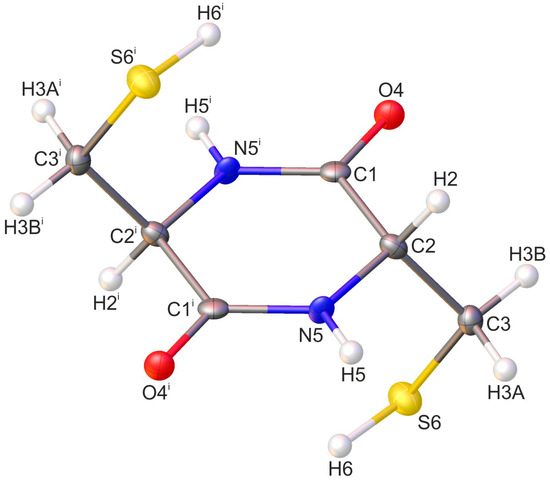
Figure 1.
Molecular structure of cyclo(l-Cys-d-Cys) compound with crystallographic atom numbering (the asymmetric unit of the crystal lattice consists of the part of the molecule with the atoms not labelled with a symmetry code). Hydrogen atoms are in white, oxygen atoms in red, sulfur in yellow, and nitrogen in blue. The same atom numbering was used to present the results of the PED analysis. Displacement ellipsoids are drawn at the 50% probability level. The H-atoms are shown as small spheres of an arbitrary radius. Symmetry code: (i) −x + 1, −y, −z + 1.
The diketopiperazine (DKP) ring is planar, with the atoms of the ring having a standard deviation of 0.003 Å from the mean plane. This planar conformation is similar to that observed in unsubstituted 2,5-diketopiperazine [19,63,64,65] or cyclo(l-Ser-l-Ser) [66]. A more in-depth comparison of the conformation to other cyclic dipeptides is presented in Table 1, which shows that the virtually ideal planarity of the DKP ring is uncommon across cyclic dipeptides, including those constituting amino acids of opposing chirality. The thiol side chains are twisted above and below the ring in such a way that the overall conformation of the cyclo(l-Cys-d-Cys) molecule is S-shaped. The values of the peptide torsional angles ω, φ, and ψ are 0.9(5)°, 0.8(5)°, and 0.8(4)°, respectively.

Table 1.
DKP ring conformation in crystal structures of various cyclic dipeptides. Conformation in italics: assignment contested.
The crystallographic analysis allowed for an understanding of the supramolecular architecture of investigated crystal. In this case, adjacent molecules of cyclo(l-Cys-d-Cys) are held together by a network of the N-H···O (d(D···A) = 2.843(3) Å, <(D-H···A) = 168(3)°) hydrogen bonds in one-dimensional tapes running along the [101] direction (Figure 2a). The hydrogen bonds within these supramolecular assemblies form the R22(8) ring motif (Figure 2a). The presence of similar tapes was reported in the past for other symmetrically substituted diketopiperazines [91]. In the next step, adjacent molecules in neighbouring tapes further interact with themselves via the S-H···O hydrogen bonds (d(D···A) = 3.387(2) Å, <(D-H···A) = 144(2)°) (Table S5 in Supplementary Materials), which results in the appearance of an infinite layer of molecules spreading along the [101] plane (Figure 2b). Such formed layers also interact with each other through the network of bifurcated S···S contacts (d(S···S) = 3.590(2) and 3.556(2) Å) that involve neighbouring molecules from adjoining layers (Figure 2c).
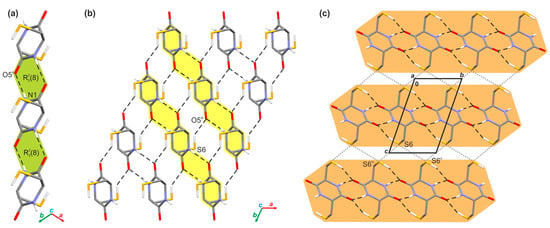
Figure 2.
Supramolecular architecture of the crystal of investigated compound: (a) H-bonded tape of molecules running along [101] direction (the R22(8) motifs are highlighted in green); (b) section of infinite layer built of H-bonded tapes of molecules spreading along [101] plane (single tapes are highlighted in yellow); (c) general view of the layered arrangement of molecules (single layers are highlighted in orange), viewed along the crystallographic a-direction. The hydrogen bonds are represented by the black dashed lines and the S···S contacts by the grey dotted lines. The H-atoms not participating in the above intermolecular interactions were omitted for clarity. Symmetry codes: (ii) x − 1, y − 1, z; (iii) x, −y + 1, z; (iv) −x + 2, −y, −z + 2; (v) −x + 2, −y + 1, −z + 2.
2.2. DFT Studies of the Cyclo(l-Cys-d-Cys) Molecule
2.2.1. Investigation of the Interaction Energy in the Crystal
The analysis of the calculated energy values for respective pairwise interactions (Table S6) shows that the most energetically relevant interactions in the analysed crystal network are the hydrogen bonds. Thus, the total interaction energy values within the pair of molecules engaged in the N−H···O and S−H···O contacts are −71.4 and −40.3 kJ/mol, respectively. In the case of the S−H···O contacts, the value is smaller; however, it cannot be overlooked that the dimer modeling the N−H···O bonding is tied together by two hydrogen bonds. Some differences can be noted, considering the nature of the above contacts. Theoretical calculations reveal that the N−H···O interactions are mostly Coulombic, while in the case of the S−H···O hydrogen bonds, the Coulombic and dispersive contributions are almost the same. Moreover, it can be seen that the intermolecular S···S contacts assisting the hydrogen bonds in the cyclo(l-Cys-d-Cys) crystal are significantly weaker (−6.3 and −3.0 kJ/mol) than the hydrogen bonding interactions. In the case of stronger contact (S6···S6iv; (iv) −x + 2, −y, −z + 2), the Coulombic contribution dominates the dispersive one, while for the weaker one (S6···S6v; (v) −x + 2, −y + 1, −z + 2), the opposite tendency is observed. In addition to the above interactions, the crystal lattice is stabilised via a network of dispersive contacts with total energy values of −19.0, −14.7, and −6.3 kJ/mol, respectively. The strength and nature of individual pairwise interactions within the investigated crystal are additionally shown in the form of energy frameworks (Figure 3).
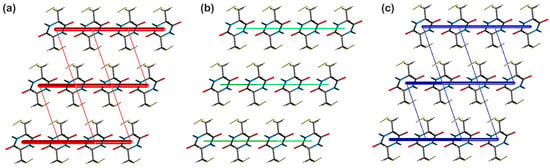
Figure 3.
Energy frameworks of cyclo(l-Cys-d-Cys) representing the (a) electrostatic, (b) dispersive, and (c) total energy viewed along the crystallographic a direction. The tube size is 30 arbitrary units. The radius of the cylinder is proportional to the magnitude of the pairwise interaction energy. Interactions of energy values less than 10 kJ/mol were omitted for clarity.
2.2.2. Optimising the Model of a Single Cyclo(l-Cys-d-Cys) Molecule
The XRD-derived experimental structure of cyclo(l-Cys-d-Cys) was used as a starting point for the optimisation of the computational model of the cyclo(l-Cys-d-Cys) single molecule (see Figure S1 for comparison of optimized theoretically and XRD-originating structure) and, subsequently, its calculated vibrational spectra. However, obtaining a valid computational model that corresponded to a minimum on the energy hypersurface was not straightforward. These problems are identified and described in Section S1.2 of Supplementary Materials. The final valid model that is used and discussed in the results presented here has all harmonic frequencies calculated to be real. This model was obtained by first optimising a system composed of three molecules involved in N-H···O hydrogen bonding at the B3LYP/May-cc-pVDZ level of theory (within the symmetry) and then reoptimising the middle molecule using any of the augmented cc-pVDZ basis sets. The stability of the wave function upon the release of the symmetry constraints was verified. Unless stated otherwise, the results discussed here were obtained using this model at the B3LYP/Aug-cc-pVDZ level of theory.
The three-molecule model in which cyclo(l-Cys-d-Cys) molecules interact via two pairs of the N-H···O hydrogen bonds was flawlessly optimised at the B3LYP/Aug-cc-pVDZ level of theory in symmetry using the positions of atoms derived from the XRD structure (Figure S2a). The model incorporating the S-H···O hydrogen bonds was obtained in the same manner (Figure S2b), but required the addition of Grimme’s D3 empirical dispersion [92] in order to converge into the designated geometry.
2.2.3. Structure of the Optimised Model
The geometry of the optimised structure of a single cyclo(l-Cys-d-Cys) molecule at the B3LYP/Aug-cc-pVDZ level, superimposed on the geometry obtained from the XRD data, is presented in Figure S1, while the calculated basic parameters of the structure are compared with the experimental values in Tables S2–S4. In general, the optimisation process did not alter the geometry significantly, and the model can be considered a reasonable approximation of the cyclo(l-Cys-d-Cys) structure present in the solid state.
Similar conclusions can be drawn for the three-molecule models, visualised in Figure S2. Their structures are closely related to the experimental XRD-derived positions; thus, the intermolecular interactions within them can be expected to follow the experimental system.
The atom positions of all the models are disclosed in Section S2.1. of Supplementary Materials.
2.2.4. Conformational Analysis
To put the molecular geometry from the XRD into a broader context, a complete conformational analysis of the system was also performed. The systematic rotor search implemented in Avogadro yielded nine conformers of cyclo(l-Cys-d-Cys) (denoted Conf1 to Conf9). The atomic coordinates of all conformers are reported in Section S2.2. of Supplementary Materials. All the predicted conformers were reoptimised at the B3LYP/Aug-cc-pVDZ level of theory without empirical dispersion, resulting in eight distinct structures (two different initial conformers converged to one final state), all of which were verified to be at the minimal point of the energy hypersurface using vibrational analysis. The coordinates of the atoms in these models are presented in Section S2.3 of Supplementary Materials.
It was revealed that the conformer evidenced in the experimental solid-state structure of cyclo(l-Cys-d-Cys) was not found through the systematic search performed using Avogadro. Furthermore, this conformation, with the computational methods and procedures used (the single molecule in the gas phase surrounded by vacuum), had significantly higher energy than the supposedly best structure among the optimised conformers. The difference of about 4.00 kJ/mol can be attributed to the intermolecular hydrogen bonding stabilising the structure, which is absent in this model. A detailed comparison of the energy values obtained for the various conformers is presented in Table S7 in Supplementary Materials.
2.3. Vibrational Spectroscopy
The experimental and calculated vibrational (IR and Raman) spectra of cyclo(l-Cys-d-Cys) in the low-, medium-, and high-wavenumber ranges are compared in Figure 4, Figure 5, and Figure 6, respectively. The plots showing the full-range overview of the spectra are shown in Figures S3 and S4 for IR and Raman, respectively. All the results in the figures are presented for the computational gas-phase model of a single cyclo(l-Cys-d-Cys) molecule calculated at the B3LYP/Aug-cc-pVDZ level of theory. The full vibrational assignment based on the PED analysis is shown in Table S8, while the summary of the most prominent experimental bands is presented in Table 2.
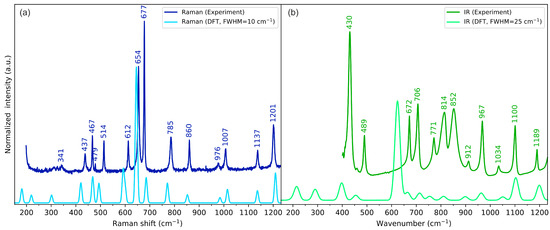
Figure 4.
Experimental (dark-coloured lines) and theoretical (light-coloured lines) (a) Raman and (b) IR spectra of cyclo(l-Cys-d-Cys) in the low-wavenumber range. Theoretical spectra were calculated using a one-molecule in-vacuum model at the B3LYP/Aug-cc-pVDZ level of theory.
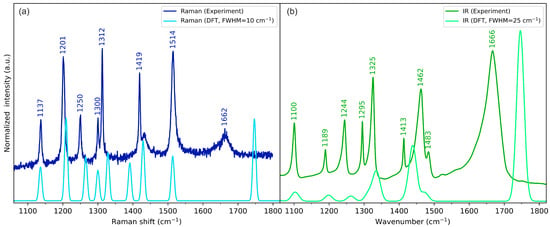
Figure 5.
Experimental (dark-coloured lines) and theoretical (light-coloured lines) (a) Raman and (b) IR spectra of cyclo(l-Cys-d-Cys) in the medium-wavenumber range. Theoretical spectra were calculated using a one-molecule in-vacuum model at the B3LYP/Aug-cc-pVDZ level of theory.
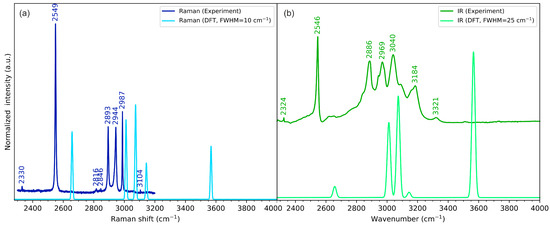
Figure 6.
Experimental (dark-coloured lines) and theoretical (light-coloured lines) (a) Raman and (b) IR spectra of cyclo(l-Cys-d-Cys) in the high-wavenumber range. Theoretical spectra were calculated using a one-molecule in-vacuum model at the B3LYP/Aug-cc-pVDZ level of theory.

Table 2.
Summary of the PED-based assignments of the main bands in the experimental vibrational spectra of solid cyclo(l-Cys-d-Cys).
In general, the single-molecule model is in good agreement with the experimental spectra. The largest discrepancies were observed for bands originating from vibrations of atoms involved in intermolecular interactions, which were not included in the computational model. Such differences are discussed in the following paragraphs in the context of DFT calculations for models comprising three cyclo(l-Cys-d-Cys) molecules.
In our system, the three-molecule model is the simplest one that allows for the computational vibrational analysis of a molecule surrounded by other interacting molecules from both sides, as deduced from XRD analysis. In the assumed model, the vibrations of the interacting groups (e.g., amino group and carbonyl group) can be divided into groups localised on the outer molecules (e.g., for atoms not involved in the hydrogen bonding and thus virtually absent in the solid state) and groups localised on the central molecule and the adjacent groups directly interacting with it. Ultimately, only the vibrations of groups involved in intermolecular interactions are relevant for the assignment of the experimental bands, and only these modes will be generally discussed in more detail.
2.3.1. N-H Stretching Vibrations
According to DFT calculations, in the isolated cyclo(l-Cys-d-Cys) molecule, there are two bands that can be attributed to the νN-H vibrations: symmetric stretching at 3568 cm−1 (active in Raman) and antisymmetric stretching at 3566 cm−1 (active in IR). These vibrations can be assigned to the experimental bands at 3160 cm−1 and 3185 cm−1 in Raman and IR, respectively, in line with the literature assignment for cyclo(l-Met-l-Met) [80]. The energy of these vibrations is obviously vastly overestimated in the computational model, as the single-molecule model does not include hydrogen bonding. The three-molecule model predicts the in-phase stretching vibrations of the N-H groups involved in the hydrogen bonding at 3192 cm−1 (symmetric, Raman-active vibration) and 3194 cm−1 (antisymmetric, IR-active vibration). These DFT-calculated vibrational energies are much closer to the experimental values, proving that hydrogen bonding substantially influences the N-H vibrations. The IR spectrum also includes a very weak signal at 3321 cm−1. Weak bands appearing at similar energy are sometimes assigned to the N-H stretching vibration (e.g., the 3328 cm−1 band of cyclo(Gly-l-Val) [59], the 3327 cm−1 band of cyclo(l-His-l-Phe) [60], 3329 cm−1 band in cyclo(Gly-Leu) [61], or the 3320 cm−1 band of cyclo(l-Ala-l-His) [62]), while other times they are not assigned at all (e.g., the 3328 cm−1 band in cyclo(Gly-Gly), 3322 cm−1 in cyclo(l-Ala-l-Ala), or 3326 cm−1 in cyclo(l-Ala-Gly) [57]). As the cyclo(l-Cys-d-Cys) system is centrosymmetric and thus restricts the normal modes to be active only in either Raman or IR spectra, the number of available normal modes that can be assigned to the experimental bands is even smaller. Thus, for consistency with the symmetry rules, in our assignment, this band is not explicitly assigned to the νN-H normal mode. Instead, we tentatively attribute it to the overtone of the very strong 1667 cm−1 band (see Figure 5). This assignment could be improved by performing the isotopic substitution, which is beyond the scope of this work. At the same time, the reports on the results of such experiments in other cyclic dipeptides are not unequivocal, as the band seems to remain present for cyclo(l-Ala-l-Ala) after an isotopic exchange but disappears for some other dipeptides [57].
Contrary to the DFT predictions, the observed Raman band due to νN-H is very weak (Figure 5); however, this can be again rationalised by considering that the hydrogen atom of the amino group is involved in hydrogen bonding. As the vibrational spectra were collected for the samples in a solid state, the network of molecules can have various local defects that lead to changes in the local intermolecular interactions, affecting the energy of this vibration and, as a result, broadening the peak. The respective IR signal is also broader than others, but its intensity is sufficient to easily resolve it.
2.3.2. C=O Stretching Vibrations
Generally speaking, the carbonyl group stretching vibrations can be analysed in analogy to the N-H group stretching vibrations. The one-molecule model estimated the energy of these vibrations at 1746 cm−1 and 1747 cm−1 (antisymmetric and symmetric vibrations, respectively), but the plausible experimental bands corresponding to these vibrations appear as relatively broad features at 1667 cm−1 and 1664 cm−1 in IR and Raman, respectively (Figure 5). As the crystallographic analysis shows that the DKP ring is planar, these values can expand the systematic analysis of the dependence between the conformation of the ring and the energy of the vibrations provided by Palacin et al. [91]. The IR and Raman spectra of cyclic dipeptides of two different amino acids generally exhibit a doublet resulting from the stretching of two non-equivalent carbonyl groups in the diketopiperazine ring [59,60,62]. The splitting into doublet also appears for some cyclic dipeptides composed of two molecules of the same amino acid with the same chirality (including, e.g., cyclo(l-Asp-l-Asp) [58] and cyclo(Gly-Gly) [93]) due to the presence of more than one molecule in the unit cell, contrary to cyclo(l-Ala-l-Ala) that includes only one molecule in its unit cell [57]. Finally, a previous report on cyclo(d-Ala-l-Ala) shows the group splitting as well, again rationalising it with the occurrence of two molecules in the unit cell [94]. In the case of the compound studied here, the unit cell only contains half of the molecule; thus, no group splitting is observed.
This substantial shift between the energy value of the νC=O vibration calculated for the one-molecule model and the experimental spectra can be a result of the N−H···O hydrogen bonding since the three-molecule model that includes these interactions predicts the bands originating from in-phase carbonyl stretching vibrations at 1702 cm−1 and 1705 cm−1 (antisymmetric and symmetric vibrations, respectively). The PED analysis of the three-molecule model reveals that this mode is highly coupled with the δHNC vibrations, which in turn increase their energy compared with the one-molecule model. This type of coupling was postulated for a variety of cyclic dipeptides and proved using deuteration studies [56]. The more in-depth analysis of these modes is challenging, however, as the decomposition reported using the VEDA4 (v. 4e1) software is limited to vibrations with no less than 10% of energy contribution to a particular mode. As the number of vibrations involved in modes rapidly increases with the number of atoms in the model, only a high-level overview can be reliably provided. Nonetheless, both the energy shift of the DFT-predicted modes and the involvement of the δHNC vibration in the mode itself prove the significance of considering intermolecular interactions for the energy values and interpretation of carbonyl group stretching vibrations.
However, the N−H···O hydrogen bonding can describe only part of the discrepancy between the single-molecule DFT model and the experimental results. The crystal structure and the calculations presented in Section 2.2.1. reveal that the S−H···O hydrogen bonding can also be considered an important intermolecular interaction influencing the energy of the carbonyl group stretching vibration. The three-molecule model (visualised in Figure S2b) developed to address these interactions predicts the νC=O vibrations at the energy of 1720 and 1728 cm−1 (symmetric and antisymmetric vibrations, respectively). Thus, the cumulative effect of all the intermolecular interactions is a decrease in the experimental energy of the stretching vibration.
Furthermore, the Raman band due to carbonyl stretching vibration is again weak and broad, suggesting that there is some variation in intermolecular interactions in the sample, typical of a non-monocrystalline state.
2.3.3. S-H Stretching Vibrations
The S-H stretching vibrations were assigned to the bands at 2547 cm−1 and 2549 cm−1 in IR and Raman, respectively. The one-molecule model again vastly overestimated the energy of these bands, calculating both of them at 2658 cm−1. Again, the discrepancy results from neglecting the intermolecular interactions, as the three-molecule model that includes the S−H···O hydrogen bonding estimated the energy of these vibrations at 2617 cm−1, much closer to the experimental values.
2.3.4. Skeletal Vibrations
The skeletal vibrations of cyclo(l-Cys-d-Cys) are generally reproduced fairly well using the one-molecule model, particularly for atoms that are not considerably involved in intermolecular interactions. Approximate vibrational assignments will be given below, but since these modes are generally delocalised across the molecule, only the results of the PED analysis in Table S8 are able to provide a comprehensive description of the system. Nonetheless, this interpretation can serve as a high-level approximation and a starting point for a more in-depth analysis. In descending energy order, there is a ring deformation mode mainly composed of the in-plane motion of nitrogen atoms: combined N-C stretching and HCN bending. The in-phase and out-of-phase modes relative to the inversion centre were assigned to a weak Raman band at 1300 cm−1 and a strong IR band at 1325 cm−1, respectively (and their DFT-calculated equivalents at 1300 cm−1 and 1335 cm−1, respectively). Subsequently, there are hydrogen wagging vibrations (localised on all the hydrogen atoms except for the thiol groups): one with methylene wagging and methine group hydrogens moving in-phase, which were assigned to the Raman band at 1312 cm−1 and the IR band 1295 cm−1 (calc. 1329 cm−1 and 1313 cm−1, respectively), and one with hydrogens of C-H moving in counterphase, which were assigned to the Raman band at 1250 and the IR band at 1244 cm−1 (calc. 1265 cm−1 and 1262 cm−1, respectively). Next, the carbon–hydrogen twisting vibrations in the methylene group coupled with the in-plane bending of the HCN fragment were attributed to the Raman band at 1201 cm−1 and IR signal at 1190 cm−1 (calc. 1209 cm−1 and 1199 cm−1, respectively). Subsequently, we assigned the N-C stretching vibrations to the Raman peak at 1137 cm−1 and IR peak at 1100 cm−1 (calc. 1136 cm−1 and 1103 cm−1, respectively). The IR signal at 1034 cm−1 and Raman signal at 1007 cm−1 were attributed to Cring-Cmethylene stretching vibrations (calc. 1051 cm−1 and 1014 cm−1, respectively). Following that, the methylene group rocking coupled with CSH bending manifested itself with bands at 976 cm−1 in Raman and 967 cm−1 in IR (calc. 984 cm−1 and 963 cm−1, respectively) for in-phase vibrations and at 814 cm−1 in IR and 785 cm−1 in Raman (calc. 810 cm−1 and 771 cm−1, respectively) for vibrations in counterphase.
Out-of-plane ring deformations were attributed to Raman bands at 862 cm−1 and 679 cm−1 (calc. 852 cm-1 and 685 cm−1, respectively), as well as IR signals at 912 cm−1, 772 cm−1, and 707 cm−1 (calc. 899 cm-1, 754 cm−1, and 713 cm−1, respectively). Notably, in this model, the experimental Raman band at 679 cm−1 (calc. 685 cm−1) exhibited a significantly higher intensity than that predicted with DFT (both with one- and three-molecule models). Moreover, this intensity was not consistent across the sample, showing different relative intensity ratios with respect to the 656 cm−1 signal (lower or higher than 1), depending on the location. Finally, the IR band at 672 cm−1 and the Raman band at 654 cm−1 were assigned to the strongly delocalised S-C and C-C stretching vibrations, coupled with out-of-plane N-H bending (calc. 665 cm−1 and 645 cm−1, respectively), while the 431 cm−1 IR band was assigned to OCN bending (calc. 398 cm−1).
3. Experimental Procedure
3.1. Materials and Methods
Cyclo(l-Cys-d-Cys) (preferred IUPAC name: (3R,6S)-3,6-bis(mercaptomethyl)piperazine-2,5-dione, purity ≥ 95%) was custom-synthesised by Bachem (Bubendorf, Switzerland) and used as received without any purification apart from the crystallisation studies. Acetonitrile (p.a.) was purchased from POCh (Gliwice, Poland). Ultrapure water obtained from a Milli-Q system (Millipore, Burlington, MA, USA) was used throughout all the experiments, and its specific resistivity was controlled at 18.2 MΩ·cm.
3.2. Raman Spectroscopy
The Raman spectra of solid cyclo(l-Cys-d-Cys) were acquired using a LabRAM HR800 (Horiba Jobin Yvon S.A.S., Palaiseau, France) coupled to an Olympus BX41 (Olympus, Tokyo, Japan) confocal microscope. Vibrations were excited at room temperature using a diode-pumped frequency-doubled Nd:YAG laser providing 532 nm radiation (100 mW power at the head, less than 5 mW at the sample). The instrument was configured in the back-scattering mode, and the signal was analysed and collected with 1800 grooves/mm diffraction grating (unless stated otherwise) and a Peltier-cooled (−70 °C) CCD detector (1024 × 256 pixels). The excitation beam was focused on the sample surface using 50× long working distance Olympus objective lenses. The spectrometer was calibrated using the 520 cm−1 Raman band of crystalline silicon. The experimental Raman spectra were baseline-corrected using the LabSpec 5.45.09 software, applying the implemented automatic procedure of the polynomial fitting of the sixth degree.
3.3. IR Spectroscopy
A solid-state sample of cyclo(l-Cys-d-Cys) was studied via Fourier-transform IR spectroscopy using a Nicolet iS50 (Thermo Scientific, Waltham, MA, USA) spectrometer. The spectra were acquired using attenuated total reflectance (single reflection diamond ATR accessory) mode in the 400–4000 cm−1 region. The nominal spectral resolution of the measurement was 2 cm−1.
3.4. Single-Crystal Growth
Single crystals of cyclo(l-Cys-d-Cys) were obtained via slow solvent evaporation from the solution under ambient conditions. About 1 mg of cyclo(l-Cys-d-Cys) was dissolved in 4 mL of an acetonitrile–water 1:1 (v/v) mixture. The solution was left in the fume hood until the solvent evaporated completely. The generated crystals were initially analysed using an Olympus BX41 optical microscope to select a suitable specimen for further crystallographic studies.
3.5. X-ray Diffraction Data Collection and Structural Refinement
A good-quality single crystal of the investigated compound was selected for the X-ray diffraction experiment at T = 100(2) K. The crystal was mounted with paratone-N oil using the MiTeGen micromount. Diffraction data were collected on an Agilent Technologies (Santa Clara, CA, USA) SuperNova Dual Source diffractometer with MoKα radiation (λ = 0.71073 Å) using the CrysAlis PRO software (version 39.46) [95]. The analytical numeric absorption correction using a multifaceted crystal model based on the expressions derived by Clark and Reid was applied [96]. The structural determination procedure was carried out using the SHELX package. The structure was solved with the intrinsic phasing method using the SHELXT program [97], and then successive least-square refinement was carried out based on the full-matrix least-square method on F2 using the SHELXL program [98]. The H atoms linked to the N and S atoms were located on the Fourier difference electron density map and refined to Uiso(H) = 1.2Ueq(N). The remaining H atoms were positioned geometrically with C–H equal to 0.97 and 0.98 Å for methine and methylene, respectively, and constrained to ride on their parent atoms with Uiso(H) = 1.2Ueq(C). The molecular interactions in the crystal of the investigated compound were identified using the PLATON program [99]. Figure for this publication were prepared using Olex2 and Mercury programs [100,101].
3.6. Theoretical Calculations of Pairwise Intermolecular Interaction Energies
The selected energies of pairwise intermolecular interactions in the crystal of investigated compound were calculated using CrystalExplorer 21.5 [102,103]. The wave-function calculations were performed using Becke’s three-parameter functional [104,105] incorporating the non-local correlation as defined by the Lee–Yang–Parr expression [106] (B3LYP) and the 6-31G(d,p) basis set [107,108,109,110,111] along with Grimme’s D2 dispersion corrections [112] using Gaussian16 software (revision C.01) [113]. Single-point calculations were performed for each example of a pair of interacting molecules in the crystal. The obtained CE-B3LYP model energy enabled us to obtain accurate values of electrostatic, polarisation, and repulsion energies and represent energies between interacting molecules as energy frameworks [114].
3.7. DFT Calculations
All calculations were performed using the Gaussian 16 C.01 software suite [113]. Density functional theory was used as a primary model [115,116,117]. B3LYP was used as a functional of choice, as it has been successfully utilised for similar applications in the literature [118,119,120]. Calculations were typically performed with a Dunning-type double-zeta basis set family (cc-pVDZ) [121,122]. The augmentation of the fundamental basis set with diffuse function either on all atoms (Aug-cc-pVDZ) [123] or as described by Truhlar et al. in their calendar basis sets (May-, Jun-, and Jul-cc-pVDZ) [124] was used whenever necessary.
The initial geometry for optimisation processes was developed in one of the following two ways: The first approach involved using conformer generation based on a systematic rotor search as implemented in the Avogadro software (version 1.2.0) [125,126]. In the second approach, the initial geometry was derived from the XRD data. One or three molecules were extracted from the crystallographic structure. The molecules were selected so that they were involved in intermolecular hydrogen bonding, with two pairs of either S−H···O or N−H···O hydrogen bonds. The one-molecule model and the three-molecule model that included the N−H···O hydrogen bonds were optimised without taking into account empirical dispersion, while the three-molecule model that included the S−H···O hydrogen bonds was optimised using Grimme’s D3 empirical dispersion correction [92].
Optimisation was performed for each initial geometry. The energy of harmonic oscillations was calculated for each final geometry [127,128,129], together with the respective theoretical IR intensities and Raman activities. The obtained vibrational energies were not scaled, although in general, it can improve the agreement between calculated and experimental bands [130]. The transformation from Raman activities to excitation-dependent Raman intensities was conducted according to the method described in our earlier studies [131,132]. The relevant calculations were performed using house-made scripts based on the SciPy library [133]. The calculated Raman and IR spectra were prepared using Gaussian-type signals, with FWHM of 10 and 25 cm−1, respectively. For visualisation purposes, the computed spectra were normalised via multiplication with a constant chosen in such a way that the global intensity of the theoretical spectra was similar to the intensity of the experimental spectra.
The assignment of vibrational modes for the selected systems was carried out by means of potential energy distribution (PED) analysis using VEDA4 software (version 4e1) [134,135]. The visualisations of the optimised structures superimposed onto the positions derived from the XRD experiments were prepared using Facio software (version 23.1.5.64) [136].
4. Conclusions
This work describes the crystal structure and vibrational (IR and Raman) spectra in the solid state of a cyclic dipeptide composed of two cysteine molecules of opposing chirality, cyclo(l-Cys-d-Cys). Cyclo(l-Cys-d-Cys) crystallises in the P-1 space group, with half of the molecule in the unit cell. The diketopiperazine ring in the molecule is almost exactly planar, whereas the whole molecule assumes an S-shape in the crystal. Numerous intermolecular interactions can be found within the crystal, among which the N−H···O and S−H···O hydrogen bonds were calculated to be the strongest. The molecules involved in N−H···O hydrogen bonding are arranged into one-dimensional molecular tapes that run along the [101] direction. This type of architecture in a solid is not intuitive, as usually, cyclic LD-type dipeptides favour the formation of 2D layers. Such one-dimensional hydrogen-bonded tapes in the crystalline solid are intriguing materials as a scaffold to further design the structure and molecular properties of solids.
Curiously, the conformation assumed with the cyclo(l-Cys-d-Cys) molecule in the crystal was not found using a standard systematic rotor search procedure for conformer identification.
The atomic positions derived from the XRD experiment were used as an initial geometry for optimisation in the DFT model of cyclo(l-Cys-d-Cys). A model comprising one molecule was used for the assignment of the IR and Raman spectra acquired for the sample in the solid state. A high degree of agreement between the DFT-calculated and the experimental spectra allowed for a comprehensive assignment of the experimental bands to the vibrational normal modes using the potential energy distribution (PED) method. Small energy discrepancies were successfully explained using larger, three-molecule models that included some of the intermolecular interactions identified in the crystal. In general, the DFT models based on the atomic positions from the XRD experiments allowed for a much better agreement between the DFT-calculated and experimental vibrational spectra than the models obtained without this experimental input.
The approach we used elegantly demonstrates that an intelligent design of computational models, based on the skilful use of crystallographic data, allows for better representation of structural features in the condensed phase resulting from the interaction of intra- and intermolecular factors, and thus for improved DFT-assisted assignment of vibrational spectra.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28155902/s1, Table S1. Crystal data and structure refinement for investigated compound: cyclo(L-Cys-D-Cys); Table S2. Bond lengths for investigated compound: cyclo(L-Cys-D-Cys); Table S3. Valence angles for investigated compound: cyclo(L-Cys-D-Cys); Table S4. Torsion angles for investigated compound: cyclo(L-Cys-D-Cys); Table S5. The geometry of hydrogen bonds in the crystal of investigated compound: cyclo(L-Cys-D-Cys); Table S6. The values of the energies (kJ/mol) calculated for selected pairs of adjacent molecules in the crystal of investigated compound: cyclo(L-Cys-D-Cys); Figure S1. Structure of the cyclo(L-Cys-D-Cys) single molecule model optimized at B3LYP/Aug-cc-pVDZ level of theory (green) superimposed onto the structure derived from the XRD experiment in the solid state (red); Figure S2. Structure of the cyclo(L-Cys-D-Cys) three molecules model (green) superimposed onto the structures derived from the XRD experiment in the solid state (red). Molecules are involved in (a) N−H···O, (b) S−H···O hydrogen bonding; Table S7. Energy of the cyclo(L-Cys-D-Cys) conformers optimized at the B3LYP/Aug-cc-pVDZ level of theory; Figure S3. Experimental (dark-colored lines) and theoretical (light-colored lines) IR spectra of cyclo(L-Cys-D-Cys) in the full wavenumber range. Theoretical spectra were calculated using a one-molecule in vacuum model at B3LYP/Aug-cc-pVDZ level of theory; Figure S4. Experimental (dark-colored lines) and theoretical (light-colored lines) Raman spectra of cyclo(L-Cys-D-Cys) in the full wavenumber range. Theoretical spectra were calculated using a one-molecule in vacuum model at B3LYP/Aug-cc-pVDZ level of theory. ‘Diff. grating’ refers to diffraction grating used during Raman measurements; Table S8. PED analysis for the one-molecule model of cyclo(L-Cys-D-Cys) at B3LYP/Aug-cc-pVDZ level of theory; atom coordinates and energies of the computational systems.
Author Contributions
Conceptualization, W.D., K.W. and A.K.; methodology, M.W., D.T. and A.K.; software, M.W.; validation, M.W. and A.K.; formal analysis, M.W., D.T. and S.P.; investigation, M.W., D.T., S.P. and A.K.; resources, K.W. and A.K.; data curation, M.W.; writing—original draft preparation, M.W., D.T., S.P. and A.K.; writing—review and editing, M.W., D.T., A.K. and W.D.; visualization M.W. and D.T.; supervision, A.K., W.D. and K.W.; project administration, A.K.; funding acquisition, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
The experimental part of this work was financed with funds from the National Science Centre of Poland, Grant No. 2018/29/B/ST4/01310 (A.K.).
Data Availability Statement
Data will be made available upon reasonable request.
Acknowledgments
CCDC 2277461 contains the supplementary crystallographic data for this paper. These data can be obtained freely via http://www.ccdc.cam.ac.uk/data_request/cif (accessed on 4 August 2023), by emailing data_request@ccdc.cam.ac.uk, or by contacting directly the Cambridge Crystallographic Data Centre (12 Union Road, Cambridge CB2 1EZ, UK. Fax: +44-1223-336033). This study was carried out at the Biological and Chemical Research Centre, University of Warsaw, established within a project co-financed by the European Union with the European Regional Development Fund under the Operational Programme Innovative Economy, 2007–2013. The collection of X-ray diffraction data was accomplished at the Core Facility for Crystallographic and Biophysical Research to support the development of medicinal products. The “Core Facility for Crystallographic and biophysical research to Support the Development of medicinal products” project was carried out within the TEAM-TECH Core Facility Programme of the Foundation for Polish Science co-financed by the European Union under the European Regional Development Fund. The computational part of the study was supported by the Wroclaw Centre for Networking and Supercomputing (M.W.), Grant No. 321.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ding, G.-Z.; Liu, J.; Wang, J.-M.; Fang, L.; Yu, S.-S. Secondary metabolites from the endophytic fungi Penicillium polonicum and Aspergillus fumigatus. J. Asian Nat. Prod. Res. 2013, 15, 446–452. [Google Scholar] [CrossRef] [PubMed]
- Prasad, C. Cyclo(His-Pro): Its distribution, origin and function in the human. Neurosci. Biobehav. Rev. 1988, 12, 19–22. [Google Scholar] [CrossRef] [PubMed]
- Lautru, S.; Gondry, M.; Genet, R.; Pernodet, J.-L. The Albonoursin Gene Cluster of S. noursei: Biosynthesis of Diketopiperazine Metabolites Independent of Nonribosomal Peptide Synthetases. Chem. Biol. 2002, 9, 1355–1364. [Google Scholar] [CrossRef]
- Prasad, C.; Matsui, T.; Peterkofsky, A. Antagonism of ethanol narcosis by histidyl-proline diketopiperazine. Nature 1977, 268, 142–144. [Google Scholar] [CrossRef] [PubMed]
- Conza, M.; Wennemers, H. Selective binding of two-armed diketopiperazine receptors to side-chain-protected peptides. J. Org. Chem. 2002, 67, 2696–2698. [Google Scholar] [CrossRef]
- Borthwick, A.D.; Liddle, J.; Davies, D.E.; Exall, A.M.; Hamlett, C.; Hickey, D.M.; Mason, A.M.; Smith, I.E.D.; Nerozzi, F.; Peace, S.; et al. Pyridyl-2,5-diketopiperazines as potent, selective, and orally bioavailable oxytocin antagonists: Synthesis, pharmacokinetics, and in vivo potency. J. Med. Chem. 2012, 55, 783–796. [Google Scholar] [CrossRef]
- Deigin, V.; Ksenofontova, O.; Yatskin, O.; Goryacheva, A.; Ignatova, A.; Feofanov, A.; Ivanov, V. Novel platform for the preparation of synthetic orally active peptidomimetics with hemoregulating activity. II. Hemosuppressor activity of 2,5-diketopiperazine-based cyclopeptides. Int. Immunopharmacol. 2020, 81, 106185. [Google Scholar] [CrossRef]
- Bojarska, J.; Mieczkowski, A.; Ziora, Z.M.; Skwarczynski, M.; Toth, I.; Shalash, A.O.; Parang, K.; El-Mowafi, S.A.; Mohammed, E.H.M.; Elnagdy, S.; et al. Cyclic Dipeptides: The Biological and Structural Landscape with Special Focus on the Anti-Cancer Proline-Based Scaffold. Biomolecules 2021, 11, 1515. [Google Scholar] [CrossRef]
- Fdhila, F.; Vázquez, V.; Sánchez, J.L.; Riguera, R. DD-diketopiperazines: Antibiotics active against Vibrio anguillarum isolated from marine bacteria associated with cultures of Pecten maximus. J. Nat. Prod. 2003, 66, 1299–1301. [Google Scholar] [CrossRef]
- Minelli, A.; Bellezza, I.; Grottelli, S.; Pinnen, F.; Brunetti, L.; Vacca, M. Phosphoproteomic analysis of the effect of cyclo-His-Pro dipeptide on PC12 cells. Peptides 2006, 27, 105–113. [Google Scholar] [CrossRef]
- Oku, J.-i.; Inoue, S. Asymmetric cyanohydrin synthesis catalysed by a synthetic cyclic dipeptide. J. Chem. Soc. Chem. Commun. 1981, 5, 229–230. [Google Scholar] [CrossRef]
- You, Y.; Xing, R.; Zou, Q.; Shi, F.; Yan, X. High-tolerance crystalline hydrogels formed from self-assembling cyclic dipeptide. Beilstein J. Nanotechnol. 2019, 10, 1894–1901. [Google Scholar] [CrossRef] [PubMed]
- Akerlund, J.; Harmeier, S.; Pumphrey, J.; Timm, D.C.; Brand, J.I. Diketopiperazine-based polymers from common amino acids. J. Appl. Polym. Sci. 2000, 78, 2213–2218. [Google Scholar] [CrossRef]
- Borthwick, A.D. 2,5-Diketopiperazines: Synthesis, reactions, medicinal chemistry, and bioactive natural products. Chem. Rev. 2012, 112, 3641–3716. [Google Scholar] [CrossRef]
- Bellezza, I.; Peirce, M.J.; Minelli, A. Cyclic dipeptides: From bugs to brain. Trends Mol. Med. 2014, 20, 551–558. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Zhang, X.; Lai, D.; Zhou, L. Structural Diversity and Biological Activities of the Cyclodipeptides from Fungi. Molecules 2017, 22, 2026. [Google Scholar] [CrossRef]
- Zhao, K.; Xing, R.; Yan, X. Cyclic dipeptides: Biological activities and self-assembled materials. Pept. Sci. 2021, 113, 1713. [Google Scholar] [CrossRef]
- Martins, M.B.; Carvalho, I. Diketopiperazines: Biological activity and synthesis. Tetrahedron 2007, 63, 9923–9932. [Google Scholar] [CrossRef]
- Degeilh, R.; Marsh, R.E. A refinement of the crystal structure of diketopiperazine (2,5-piperazinedione). Acta Cryst. 1959, 12, 1007–1014. [Google Scholar] [CrossRef]
- Sletten, E. Conformation of cyclic dipeptides. The crystal and molecular structures of cyclo-d-alanyl-l-alanyl and cyclo-l-alanyl-l-alanyl (3,6-dimethylpiperazine-2,5-dione). J. Am. Chem. Soc. 1970, 92, 172–177. [Google Scholar] [CrossRef]
- Milne, P.J.; Oliver, D.W.; Roos, H.M. Cyclodipeptides: Structure and conformation of cyclo(tyrosyl-prolyl). J. Cryst. Spectr. Res. 1992, 22, 643–649. [Google Scholar] [CrossRef]
- BenNasr, F.; Pérez-Mellor, A.; Alata, I.; Lepere, V.; Jaïdane, N.-E.; Zehnacker, A. Stereochemistry-dependent hydrogen bonds stabilise stacked conformations in jet-cooled cyclic dipeptides: (LD) vs. (LL) cyclo tyrosine-tyrosine. Faraday Discuss. 2018, 212, 399–419. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, J.C.; Whitesides, G.M. Solid-State Structures of Hydrogen-Bonded Tapes Based on Cyclic Secondary Diamides. Chem. Rev. 1994, 94, 2383–2420. [Google Scholar] [CrossRef]
- Benedetti, E.; Bavoso, A.; Blasio, B.; Pavone, V.; Pedone, C.; Paolillo, L.; D’Alagni, M. Structural studies of cyclopeptides: Solid state and solution conformation of cyclo(l-histidyl-d-histidyl). Int. J. Pept. Protein Res. 1988, 31, 220–224. [Google Scholar] [CrossRef]
- Benedetti, E.; Corradini, P.; Pedone, C. Crystal and molecular structure of trans-3,6-dimethyl-2,5-piperazinedione (l-alanyl-d-alanine 2,5-diketopiperazine). J. Phys. Chem. 1969, 73, 2891–2895. [Google Scholar] [CrossRef]
- Avinash, M.B.; Raut, D.; Mishra, M.K.; Ramamurty, U.; Govindaraju, T. Bioinspired Reductionistic Peptide Engineering for Exceptional Mechanical Properties. Sci. Rep. 2015, 5, 16070. [Google Scholar] [CrossRef]
- Kawaguchi, K.; Tanihara, M.; Imanishi, Y. Catalytic Hydrolysis of Charged Carboxylic Acid Active Esters with Cyclic Dipeptides Carrying Hydrophobic and Nucleophilic Groups. Polym. J. 1983, 15, 97–102. [Google Scholar] [CrossRef]
- Gahan, L.R.; Cusack, R.M. Metal complexes of synthetic cyclic peptides. Polyhedron 2018, 153, 1–23. [Google Scholar] [CrossRef]
- Pandurangan, K.; Roy, B.; Rajasekhar, K.; Suseela, Y.V.; Nagendra, P.; Chaturvedi, A.; Satwik, U.R.; Murugan, N.A.; Ramamurty, U.; Govindaraju, T. Molecular Architectonics of Cyclic Dipeptide Amphiphiles and Their Application in Drug Delivery. ACS Appl. Bio Mater. 2020, 3, 3413–3422. [Google Scholar] [CrossRef]
- Feldstein, R.; Glass, J.; Steiner, S.S. Self Assembling Diketopiperazine Drug Delivery System. U.S. Patent US5352461A, 11 May 1992. [Google Scholar]
- Chibh, S.; Mishra, J.; Kour, A.; Chauhan, V.S.; Panda, J.J. Recent advances in the fabrication and bio-medical applications of self-assembled dipeptide nanostructures. Nanomedicine 2021, 16, 139–163. [Google Scholar] [CrossRef]
- Hoyle, C.E.; Lowe, A.B.; Bowman, C.N. Thiol-click chemistry: A multifaceted toolbox for small molecule and polymer synthesis. Chem. Soc. Rev. 2010, 39, 1355–1387. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, X.; Lu, Y.; Hou, M.; Xu, Z.; Li, B. A thiol-responsive and self-immolative podophyllotoxin prodrug for cancer therapy. Tetrahedron Lett. 2021, 71, 153044. [Google Scholar] [CrossRef]
- Nolan, M.D.; Scanlan, E.M. Applications of Thiol-Ene Chemistry for Peptide Science. Front. Chem. 2020, 8, 583272. [Google Scholar] [CrossRef] [PubMed]
- Vanslambrouck, S.; Riva, R.; Ucakar, B.; Préat, V.; Gagliardi, M.; Molin, D.G.M.; Lecomte, P.; Jérôme, C. Thiol-ene Reaction: An Efficient Tool to Design Lipophilic Polyphosphoesters for Drug Delivery Systems. Molecules 2021, 26, 1750. [Google Scholar] [CrossRef]
- Pace, N.J.; Weerapana, E. Zinc-binding cysteines: Diverse functions and structural motifs. Biomolecules 2014, 4, 419–434. [Google Scholar] [CrossRef]
- Li, N.C.; Manning, R.A. Some Metal Complexes of Sulfur-containing Amino Acids. J. Am. Chem. Soc. 1955, 77, 5225–5228. [Google Scholar] [CrossRef]
- Berthon, G. Critical evaluation of the stability constants of metal complexes of amino acids with polar side chains (Technical Report). Pure Appl. Chem. 1995, 67, 1117–1240. [Google Scholar] [CrossRef]
- Greenstein, J.P. Studies Of Multivalent Amino Acids and Peptides: IX. The Synthesis Of l-Cystinyl-I-Cystine. J. Biol. Chem. 1937, 121, 9–17. [Google Scholar] [CrossRef]
- Sakakibara, S.; Tani, H. Synthesis of Polycysteine. Bull. Chem. Soc. Japn. 1956, 29, 85–88. [Google Scholar] [CrossRef]
- Kamber, B. Cystinpeptide aus (S-Acetamidomethyl-cystein)-peptiden durch Oxydation mit Jod: Die Synthese von cyclo-l-Cystin. Helv. Chim. Acta 1971, 54, 927–930. [Google Scholar] [CrossRef]
- Weber, U.; Hartter, P. Synthese und Stabilität von cyclischen Disulfiden des Typs. Hoppe-Seyler Z. Physiol. Chem. 1974, 355, 189–199. [Google Scholar] [CrossRef] [PubMed]
- Pastuszak, J.J.; Chimiak, A. tert-Butyl group as thiol protection in peptide synthesis. J. Org. Chem. 1981, 46, 1868–1873. [Google Scholar] [CrossRef]
- Iannotta, D.; Castellucci, N.; Monari, M.; Tomasini, C. A straightforward synthesis and partial hydrolysis of cysteine-derived 2,5-diketopiperazines. Tetrahedron Lett. 2010, 51, 4558–4559. [Google Scholar] [CrossRef]
- Mez, H.-C. Cyclo-L-cystine acetic acid. Cryst. Struct. Comm. 1974, 3, 657. [Google Scholar]
- Varughese, K.I.; Lu, C.T.; Kartha, G. Crystal structure and conformation of cyclo-L-cystine. Int. J. Pept. Protein Res. 1981, 18, 88–102. [Google Scholar] [CrossRef]
- Lu, C.T.; Kartha, G. The crystal and molecular structure of cyclo-L-cystine. In Proceedings of the Program and Abstracts Summer Meeting, Storrs, CT, USA, 17–22 June 1973; Yannoni, N.F., Frueh, A.J., Eds.; American Crystallographic Association: Buffalo, NY, USA, 1973; p. 188. [Google Scholar]
- van Wart, H.E.; Scheraga, H.A. Raman spectra of cystine-related disulfides. Effect of rotational isomerism about carbon-sulfur bonds on sulfur-sulfur stretching frequencies. J. Phys. Chem. 1976, 80, 1812–1823. [Google Scholar] [CrossRef]
- Schwyzer, R. Hormone-receptor interactions. Synthesis and conformational study of cyclo-L-cystathionine. Helv. Chim. Acta 1976, 59, 2187–2195. [Google Scholar] [CrossRef]
- Donzel, B.; Kamber, B.; Wüthrich, K.; Schwyzer, R. A Chiral Cystine Disulfide Group without Inherent Optical Activity in the Long-Wavelength Region. (1 H- and 13 C-NMR., UV., CD., and ORD. Studies with cyclo—L-cystine). Helv. Chim. Acta 1972, 55, 947–961. [Google Scholar] [CrossRef]
- Jung, G.; Ottnad, M. Temperature-induced change in helicity of the inherently dissymmetrical disulfide group in cyclocystine. Angew. Chem. Int. Ed. Engl. 1974, 13, 818–819. [Google Scholar] [CrossRef]
- Strickland, R.W.; Richardson, F.S. Chiroptical properties of cyclo-L-cystine. J. Chem. Soc. Perkin Trans. 2 1976, 15, 1818–1821. [Google Scholar] [CrossRef]
- Mitra, A.K.; Chandrasekaran, R. Conformational analysis of cyclo (L-cystine). Int. J. Pept. Protein Res. 1977, 10, 235–239. [Google Scholar] [CrossRef]
- Gockel, P.; Vogler, R.; Gelinsky, M.; Meißner, A.; Albrich, H.; Vahrenkamp, H. Zinc complexation of cyclic dipeptides containing cysteine and/or histidine. Inorg. Chim. Acta 2001, 323, 16–22. [Google Scholar] [CrossRef]
- Cook, J.M.; Baker, D.A.; Yin, W.; Johnson, E.M. Cysteine and Cystine Prodrugs to Treat Schizophrenia and Reduce Drug Cravings. U.S. Patent US8173809B2, 13 August 2009. [Google Scholar]
- Mendham, A.P.; Dines, T.J.; Snowden, M.J.; Withnall, R.; Chowdhry, B.Z. IR/Raman spectroscopy and DFT calculations of cyclic di-amino acid peptides. Part III: Comparison of solid state and solution structures of cyclo(L-Ser-L-Ser). J. Raman Spectrosc. 2009, 40, 1508–1520. [Google Scholar] [CrossRef]
- Mendham, A.P.; Dines, T.J.; Snowden, M.J.; Chowdhry, B.Z.; Withnall, R. Vibrational spectroscopy and DFT calculations of di-amino acid cyclic peptides. Part I: Cyclo(Gly-Gly), cyclo(L-Ala-L-Ala) and cyclo(L-Ala-Gly) in the solid state and in aqueous solution. J. Raman Spectrosc. 2009, 40, 1478–1497. [Google Scholar] [CrossRef]
- Mendham, A.P.; Dines, T.J.; Withnall, R.; Mitchell, J.C.; Chowdhry, B.Z. Vibrational spectroscopic studies of the structure of di-amino acid peptides. Part II: Cyclo(L-Asp-L-Asp) in the solid state and in aqueous solution. J. Raman Spectrosc. 2009, 40, 1498–1507. [Google Scholar] [CrossRef]
- Celik, S.; Ozel, A.E.; Akyuz, S.; Kecel, S.; Agaeva, G. Conformational preferences, experimental and theoretical vibrational spectra of cyclo(Gly–Val) dipeptide. J. Mol. Struct. 2011, 993, 341–348. [Google Scholar] [CrossRef]
- Celik, S.; Ozel, A.E.; Kecel, S.; Akyuz, S. Structural and IR and Raman spectral analysis of cyclo(His-Phe) dipeptide. Vib. Spectrosc. 2012, 61, 54–65. [Google Scholar] [CrossRef]
- Celik, S.; Ozel, A.E.; Akyuz, S. Comparative study of antitumor active cyclo(Gly-Leu) dipeptide: A computational and molecular modeling study. Vib. Spectrosc. 2016, 83, 57–69. [Google Scholar] [CrossRef]
- Celik, S.; Yilmaz, G.; Ozel, A.E.; Akyuz, S. Structural and spectral analysis of anticancer active cyclo(Ala-His) dipeptide. J. Biomol. Struct. Dyn. 2022, 40, 660–672. [Google Scholar] [CrossRef]
- Corey, R.B. The Crystal Structure of Diketopiperazine. J. Am. Chem. Soc. 1938, 60, 1598–1604. [Google Scholar] [CrossRef]
- Nonappa; Ahonen, K.; Lahtinen, M.; Kolehmainen, E. Cyclic dipeptides: Catalyst/promoter-free, rapid and environmentally benign cyclization of free amino acids. Green Chem. 2011, 13, 1203. [Google Scholar] [CrossRef]
- Corey, R.B. Interatomic Distances in Proteins and Related Substances. Chem. Rev. 1940, 26, 227–236. [Google Scholar] [CrossRef]
- Gasparri Fava, G.; Ferrari Belicchi, M.; Marchelli, R.; Dossena, A. Synthesis, crystal structure and conformation of the cyclic dipeptide cyclo (-L-seryl-L-seryl-). Acta Crystallogr. B Struct. Sci. 1981, 37, 625–629. [Google Scholar] [CrossRef]
- Mendham, A.P.; Spencer, J.; Chowdhry, B.Z.; Dines, T.J.; Mujahid, M.; Palmer, R.A.; Tizzard, G.J.; Coles, S.J. X-Ray Crystallographic Structure and Absolute Configuration of the Cyclic Di-amino Acid Peptide: Cyclo(l-HomoCySH-l-HomoCySH). J. Chem. Crystallogr. 2011, 41, 1328–1334. [Google Scholar] [CrossRef]
- Ramani, R.; Venkatesan, K.; Marsh, R.E. Crystal structure and conformation of the cyclic dipeptide cyclo-(L-histidyl-L-aspartyl) trihydrate. J. Am. Chem. Soc. 1978, 100, 949–953. [Google Scholar] [CrossRef]
- Bressan, M.; Ettore, R.; Marchiori, F.; Valle, G. Coordination chemistry of peptides: Part II. Crystal structure of cyclo-L-methionylglycine and studies of metal complexation. Int. J. Pept. Protein Res. 1982, 19, 402–407. [Google Scholar] [CrossRef]
- Cotrait, M.; Ptak, M. The crystal structure and conformation of the cyclic dipeptide cyclo (-L-seryl-L-histidyl-) monohydrate. Acta Crystallogr. B Struct. Sci. 1978, 34, 528–532. [Google Scholar] [CrossRef]
- Lin, C.-F.; Webb, L.E. Crystal structures and conformations of the cyclic dipeptides cyclo-(Glycyl-L-tyrosyl) and cyclo-(L-seryl-L-tyrosyl) Monohydrate. J. Am. Chem. Soc. 1973, 95, 6803–6811. [Google Scholar] [CrossRef]
- Sletten, J.; Grundnes, J.; Klæboe, P.; Tørneng, E.; Woldbæk, T.; Strand, T.G.; Sukhoverkhov, V.F. The Structure of a Second Crystallographic Modification of Cyclo-D-alanyl-L-alanyl. Acta Chem. Scand. 1980, 34a, 593–595. [Google Scholar] [CrossRef][Green Version]
- Grant, G.D.; Hunt, A.L.; Milne, P.J.; Roos, H.M.; Joubert, J.A. The structure and conformation of the tryptophanyl diketopiperazines cyclo(Trp-Trp)·C2H6SO and cyclo(Trp-Pro). J. Chem. Crystallogr. 1999, 29, 435–447. [Google Scholar] [CrossRef]
- Görbitz, C.H. Crystal and Molecular Structure of cyclo-L-Aspartyl-L-alanyl (3,6-Dioxo-5-methyl-2-piperazineacetic acid). Acta Chem. Scand. 1987, 41b, 83–86. [Google Scholar] [CrossRef]
- Cotrait, M.; Ptak, M.; Busetta, B.; Heitz, A. Crystal structure and conformation of the cyclic dipeptide cyclo-(L-threonyl-L-histidyl) dihydrate. J. Am. Chem. Soc. 1976, 98, 1073–1076. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, I.; Iwata, T.; Takahashi, N.; Ashida, T.; Tanihara, M. Cyclo- L -leucyl- L -histidyl monohydrate. Acta Crystallogr. B Struct. Sci. 1977, 33, 3902–3904. [Google Scholar] [CrossRef]
- Suguna, K.; Ramakumar, S.; Kopple, K.D. Structure of cyclo(-L-leucyl-L-tyrosyl-) monohydrate, C15H20N2O3·H2O. Acta Crystallogr. C 1984, 40, 2053–2056. [Google Scholar] [CrossRef]
- Budesinsky, M.; Cisarova, I.; Podlaha, J.; Borremans, F.; Martins, J.C.; Waroquier, M.; Pauwels, E. Structures of cyclic dipeptides: An X-ray and computational study of cis- and trans-cyclo(Pip-Phe), cyclo(Pro-Phe) and their N-methyl derivatives. Acta Crystallogr. B Struct. Sci. 2010, 66, 662–677. [Google Scholar] [CrossRef] [PubMed]
- Ramani, R.; Venkatesan, K.; Marsh, R.E.; Hu Kung, W.J. Crystal structure and conformation of the cyclic dipeptide cyclo-L-prolyl-D-phenylalanyl. Acta Crystallogr. B Struct. Sci. 1976, 32, 1051–1056. [Google Scholar] [CrossRef]
- Mendham, A.P.; Potter, B.S.; Palmer, R.A.; Dines, T.J.; Mitchell, J.C.; Withnall, R.; Chowdhry, B.Z. Vibrational spectra and crystal structure of the di-amino acid peptide cyclo(L-Met-L-Met): Comparison of experimental data and DFT calculations. J. Raman Spectrosc. 2010, 41, 148–159. [Google Scholar] [CrossRef]
- Mosetti, V.; Rosetti, B.; Pierri, G.; Bellotto, O.; Adorinni, S.; Bandiera, A.; Adami, G.; Tedesco, C.; Crosera, M.; Magnano, G.C.; et al. Cyclodipeptides: From Their Green Synthesis to Anti-Age Activity. Biomedicines 2022, 10, 2342. [Google Scholar] [CrossRef]
- Valle, G.; Guantieri, V.; Tamburro, A.M. On the molecular and crystal structure of cyclo(l-methionyl-l-methionyl). J. Mol. Struct. 1990, 220, 19–24. [Google Scholar] [CrossRef]
- Mendham, A.P.; Palmer, R.A.; Potter, B.S.; Dines, T.J.; Snowden, M.J.; Withnall, R.; Chowdhry, B.Z. Vibrational spectroscopy and crystal structure analysis of two polymorphs of the di-amino acid peptide cyclo(L-Glu-L-Glu). J. Raman Spectrosc. 2010, 41, 288–302. [Google Scholar] [CrossRef]
- Dreele, R.B. von. The crystal structure of cyclo- L -prolylglycyl: A refinement of high-angle diffraction data. Acta Crystallogr. B Struct. Sci. 1975, 31, 966–970. [Google Scholar] [CrossRef]
- Karle, I.L. Crystal structure and conformation of the cyclic dipeptide cyclo-L-prolyl-L-leucyl. J. Am. Chem. Soc. 1972, 94, 81–84. [Google Scholar] [CrossRef]
- Mazza, F.; Lucente, G.; Pinnen, F.; Zanotti, G. Cyclic dipeptides containing proline. Structure and conformation of cyclo-(-L-Phe-L-Pro-), C14H16N2O2. Acta Crystallogr. C 1984, 40, 1974–1976. [Google Scholar] [CrossRef]
- Palmer, R.A.; Potter, B.S.; Mendham, A.P.; Dines, T.J.; Chowdhry, B.Z. Refined Crystal Structure and Absolute Configuration of the Di-amino Acid Peptide Cyclo(l-Aspartyl-l-Aspartyl): Comparison with the DFT Calculated Structure. J. Chem. Crystallogr. 2010, 40, 608–615. [Google Scholar] [CrossRef]
- Tayhas, G.R.; Palmore; Luo, T.-J.M.; McBride-Wieser, M.T.; Picciotto, E.A.; Reynoso-Paz, C.M. Engineering Crystalline Architecture with Diketopiperazines: An Investigation of the Strength of Hydrogen-Bonded Tapes Based on the Cyclic Dipeptide of (S)-Aspartic Acid. Chem. Mater. 1999, 11, 3315–3328. [Google Scholar] [CrossRef]
- Benedetti, E.; Corradini, P.; Pedone, C. Crystal and molecular structure ofL-cis-3,6-dimethyl-2,5-piperazinedione (L-alanyl-L-alanyl-2,5-diketopiperazine). Biopolymers 1969, 7, 751–764. [Google Scholar] [CrossRef]
- Hong, Y.P.; Lee, S.-H.; Choi, J.-H.; Kashima, A.; Nakamura, G.; Suzuki, T. Crystal Structure and Spectroscopic Properties of Cyclic Dipeptide: A Racemic Mixture of cyclo(ᴅ-Prolyl-ʟ-Tyrosyl) and cyclo(ʟ-Prolyl-ᴅ-Tyrosyl). Bull. Kor. Chem. Soc. 2014, 35, 2299–2303. [Google Scholar] [CrossRef]
- Palacin, S.; Chin, D.N.; Simanek, E.E.; MacDonald, J.C.; Whitesides, G.M.; McBride, M.T.; Palmore, G.T.R. Hydrogen-Bonded Tapes Based on Symmetrically Substituted Diketopiperazines: A Robust Structural Motif for the Engineering of Molecular Solids. J. Am. Chem. Soc. 1997, 119, 11807–11816. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Cheam, T.C.; Krimm, S. Vibrational analysis of crystalline diketopiperazine—I. Raman and i.r. spectra. Spectrochim. Acta A 1984, 40, 481–501. [Google Scholar] [CrossRef]
- Cheam, T.C.; Krimm, S. Vibrational analysis of cyclo(d-Ala-l-Ala) in two crystalline forms. Effect of structure on peptide group and CH modes. Spectrochim. Acta A 1988, 44, 185–208. [Google Scholar] [CrossRef]
- Oxford Diffraction. CrysAlis CCD and CrysAlis RED; Oxford Diffraction Ltd.: Yarnton, UK, 2008. [Google Scholar]
- Clark, R.C.; Reid, J.S. The analytical calculation of absorption in multifaceted crystals. Acta Crystallogr. A Found. Crystallogr. 1995, 51, 887–897. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. A Found. Crystallogr. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. D Biol. Crystallogr. 2009, 65, 148–155. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0—New features for the visualization and investigation of crystal structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
- Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer model energies and energy frameworks: Extension to metal coordination compounds, organic salts, solvates and open-shell systems. IUCrJ 2017, 4, 575–587. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Binkley, J.S.; Gordon, M.S.; DeFrees, D.J.; Pople, J.A. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements. J. Chem. Phys. 1982, 77, 3654–3665. [Google Scholar] [CrossRef]
- Gordon, M.S.; Binkley, J.S.; Pople, J.A.; Pietro, W.J.; Hehre, W.J. Self-consistent molecular-orbital methods. 22. Small split-valence basis sets for second-row elements. J. Am. Chem. Soc. 1982, 104, 2797–2803. [Google Scholar] [CrossRef]
- Hariharan, P.C.; Pople, J.A. The influence of polarization functions on molecular orbital hydrogenation energies. Theoret. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Turner, M.J.; Thomas, S.P.; Shi, M.W.; Jayatilaka, D.; Spackman, M.A. Energy frameworks: Insights into interaction anisotropy and the mechanical properties of molecular crystals. Chem. Commun. 2015, 51, 3735–3738. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Pople, J.A.; Gill, P.M.W.; Johnson, B.G. Kohn—Sham density-functional theory within a finite basis set. Chem. Phys. Lett. 1992, 199, 557–560. [Google Scholar] [CrossRef]
- Su, T.-F.; Huang, R.; Su, Y.-Q.; Zhao, G.-Z.; Wu, D.-Y.; Wang, J.-A.; Gong, C.-R.; Xu, C.-L. Vibrational spectra of guaiacylglycerol-β-guaiacyl ether: Experiment and theory. Spectrochim. Acta A 2015, 139, 456–463. [Google Scholar] [CrossRef]
- Wrzosek, B.; Cukras, J.; Dobrowolski, M.A.; Bukowska, J. Real Chemical States of the 3-Sulfur Derivative of 1,2,4-Triazole in Different Conditions: Complex Experimental and Theoretical Studies. J. Phys. Chem. C 2017, 121, 9282–9295. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Wu, D.-Y.; Tian, Z.-Q. Theoretical Investigation on the Substituent Effect of Halogen Atoms at the C8 Position of Adenine: Relative Stability, Vibrational Frequencies, and Raman Spectra of Tautomers. J. Phys. Chem. A 2016, 120, 4049–4058. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Papajak, E.; Zheng, J.; Xu, X.; Leverentz, H.R.; Truhlar, D.G. Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions. J. Chem. Theory Comput. 2011, 7, 3027–3034. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef]
- Avogadro: An Open-Source Molecular Builder and Visualization Tool. Version 1.2.0. Available online: http://avogadro.cc/ (accessed on 31 July 2023).
- Johnson, B.G.; Fisch, M.J. An implementation of analytic second derivatives of the gradient-corrected density functional energy. J. Chem. Phys. 1994, 100, 7429–7442. [Google Scholar] [CrossRef]
- Johnson, B.G.; Frisch, M.J. Analytic second derivatives of the gradient-corrected density functional energy. Effect of quadrature weight derivatives. Chem. Phys. Let. 1993, 216, 133–140. [Google Scholar] [CrossRef]
- Stratmann, R.E.; Burant, J.C.; Scuseria, G.E.; Frisch, M.J. Improving harmonic vibrational frequencies calculations in density functional theory. J. Chem. Phys. 1997, 106, 10175–10183. [Google Scholar] [CrossRef]
- Su, Y.-Q.; Liu, J.; Huang, R.; Yang, H.-T.; Li, M.-X.; Pang, R.; Zhang, M.; Yang, M.-H.; Su, H.-F.; Devasenathipathy, R.; et al. Plasmon-Mediated Photoelectrochemical Hot-Hole Oxidation Coupling Reactions of Adenine on Nanostructured Silver Electrodes. J. Phys. Chem. Lett. 2023, 14, 5163–5171. [Google Scholar] [CrossRef]
- Królikowska, A.; Cukras, J.; Witkowski, M.; Tymecka, D.; Hernik-Magoń, A.; Misicka, A.; Dzwolak, W. SERS and DFT Study of Noble-Metal-Anchored Cys-Trp/Trp-Cys Dipeptides: Influence of Main-Chain Direction and Terminal Modifications. J. Phys. Chem. C 2020, 124, 7097–7116. [Google Scholar] [CrossRef]
- Witkowski, M.; Królikowska, A.; Cukras, J.; Dzwolak, W. Hidden Dynamics of Noble-metal-bound Thiol Monolayers Revealed by SERS-monitored Entropy-driven Exchange of Cysteine Isotopologues. Appl. Surf. Sci. 2023, 623, 156985. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Jamróz, M.H. Vibrational Energy Distribution Analysis VEDA 4, Warsaw, 2004–2010. Available online: https://smmg.pl/software/veda (accessed on 20 November 2021).
- Jamróz, M.H.; Dobrowolski, J.C.; Brzozowski, R. Vibrational modes of 2,6-, 2,7-, and 2,3-diisopropylnaphthalene. A DFT study. J. Mol. Struct. 2006, 787, 172–183. [Google Scholar] [CrossRef]
- Suenaga, M. Facio 23.1.5. 2021. Available online: https://zzzfelis.sakura.ne.jp/ (accessed on 27 September 2021).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).