Interaction of Macromolecular Chain with Phospholipid Membranes in Solutions: A Dissipative Particle Dynamics Simulation Study
Abstract
1. Introduction
2. Results
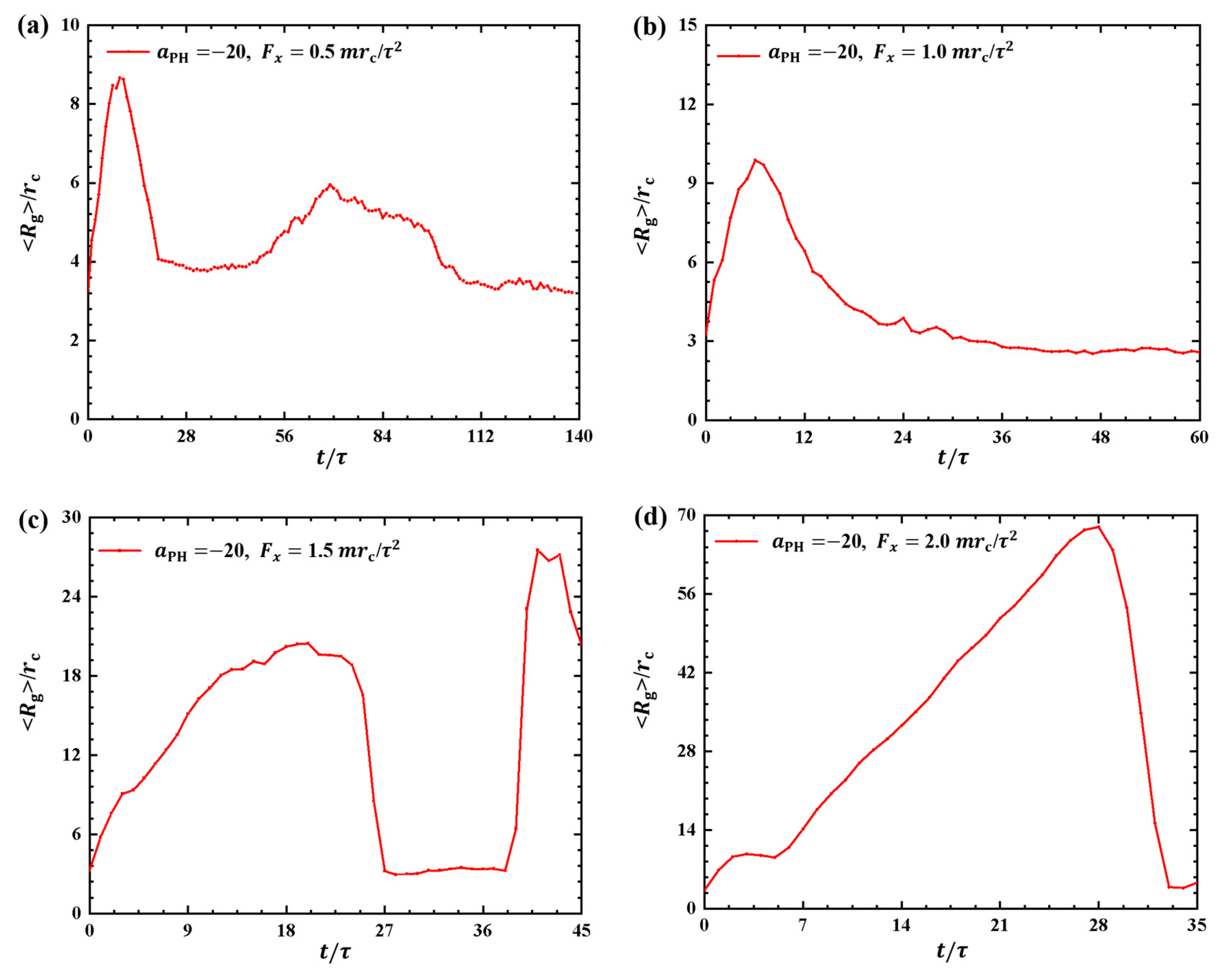
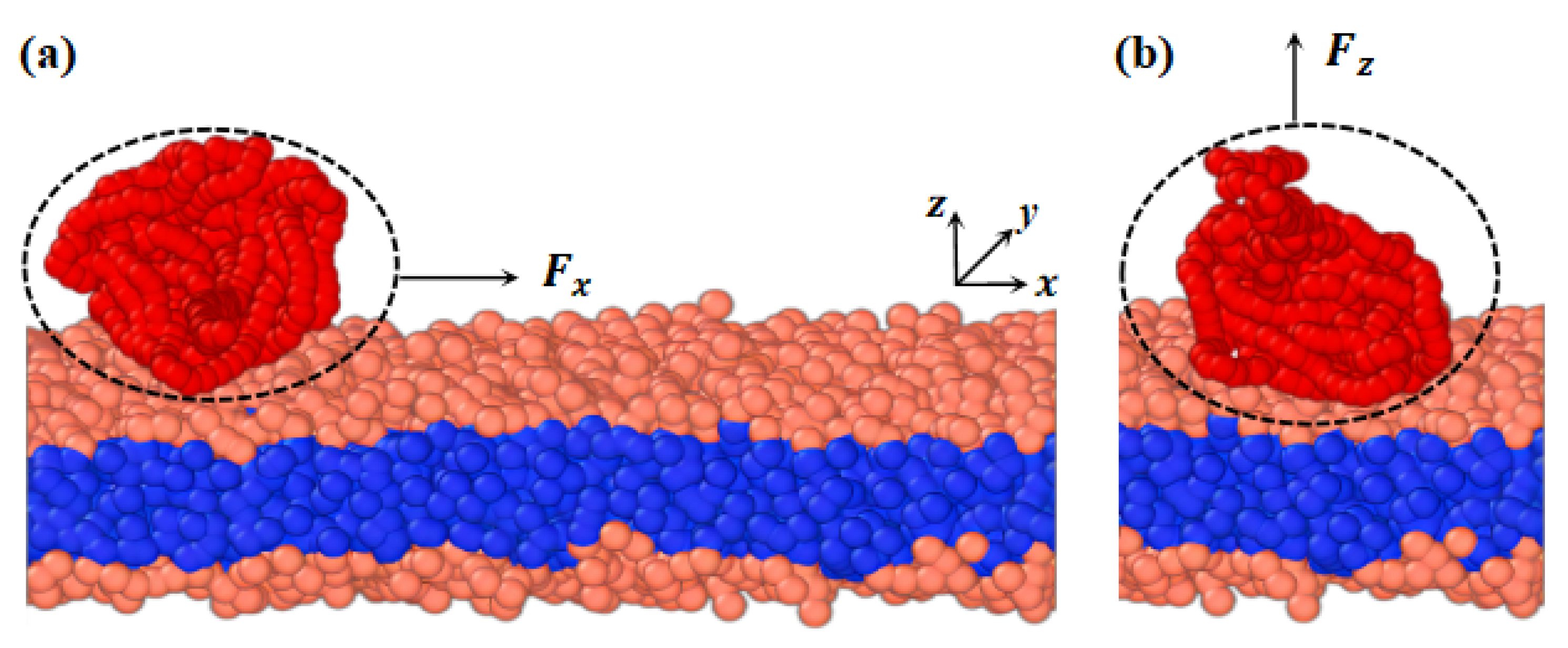
2.1. Pulling Forces along the Direction Parallel to Membrane Surfaces
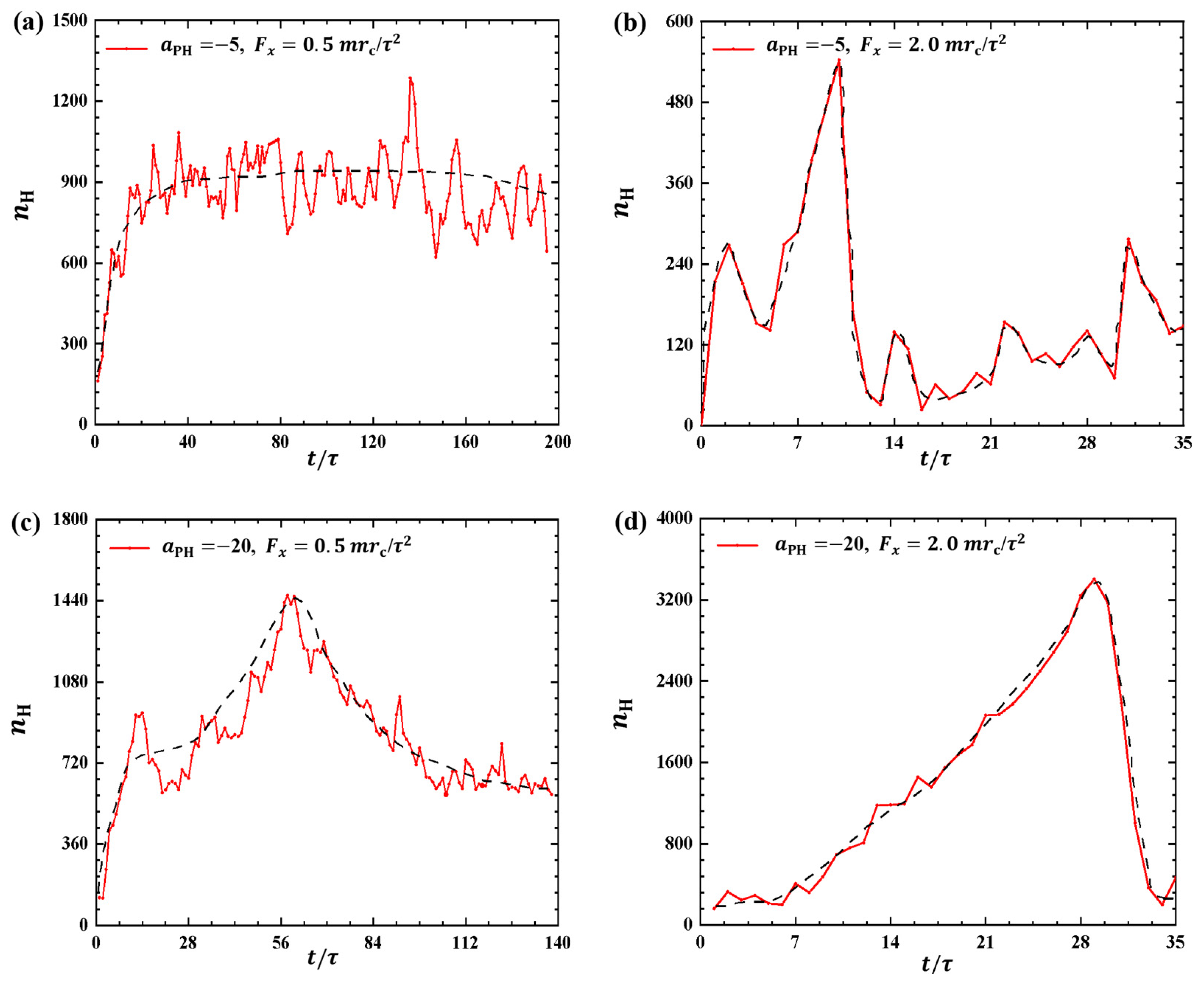
2.1.1. Conformations of Polymer Chains under Weak Adsorption
2.1.2. Conformations of Polymer Chains under Strong Adsorption
2.1.3. Variance of Bead Number in Membrane
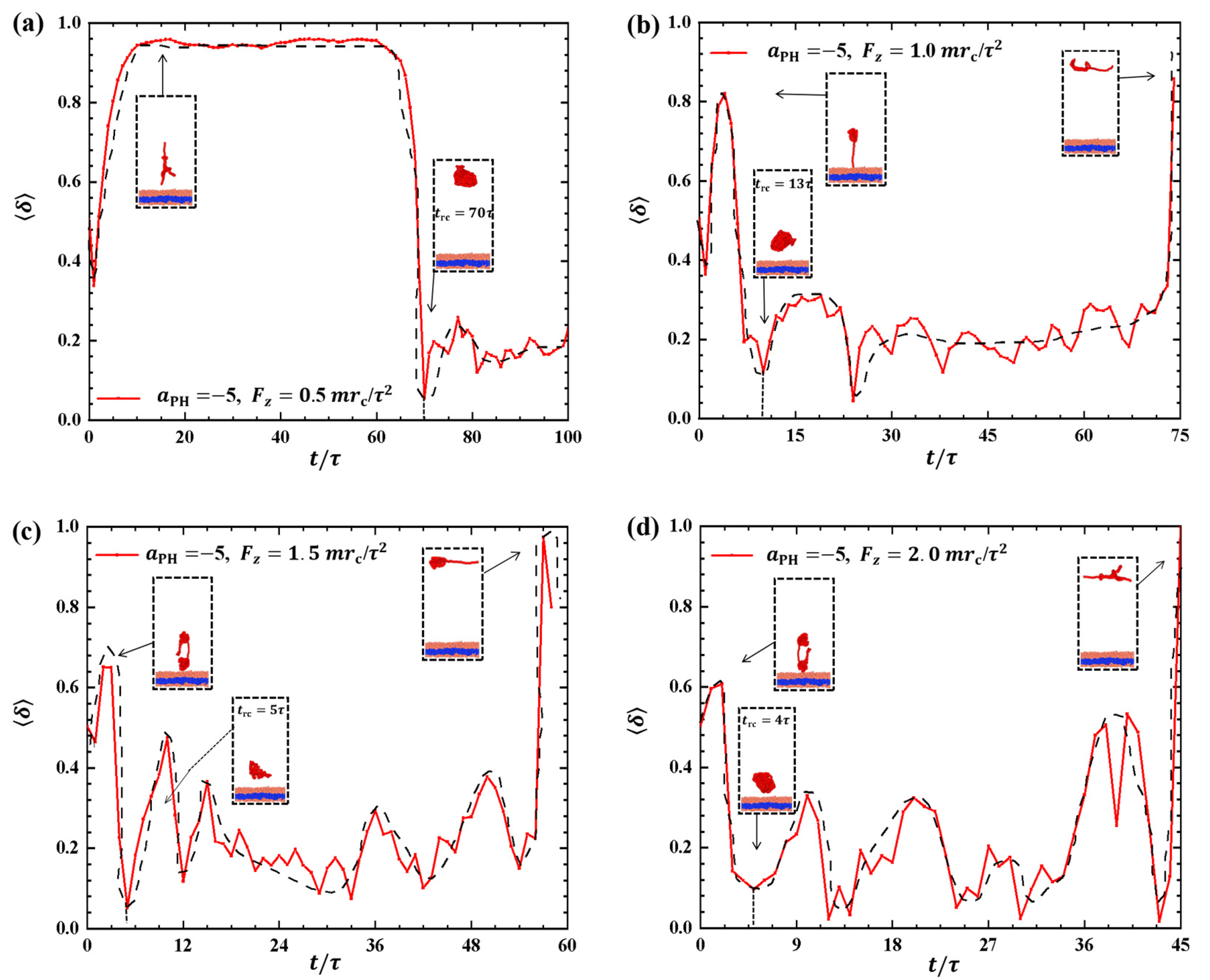
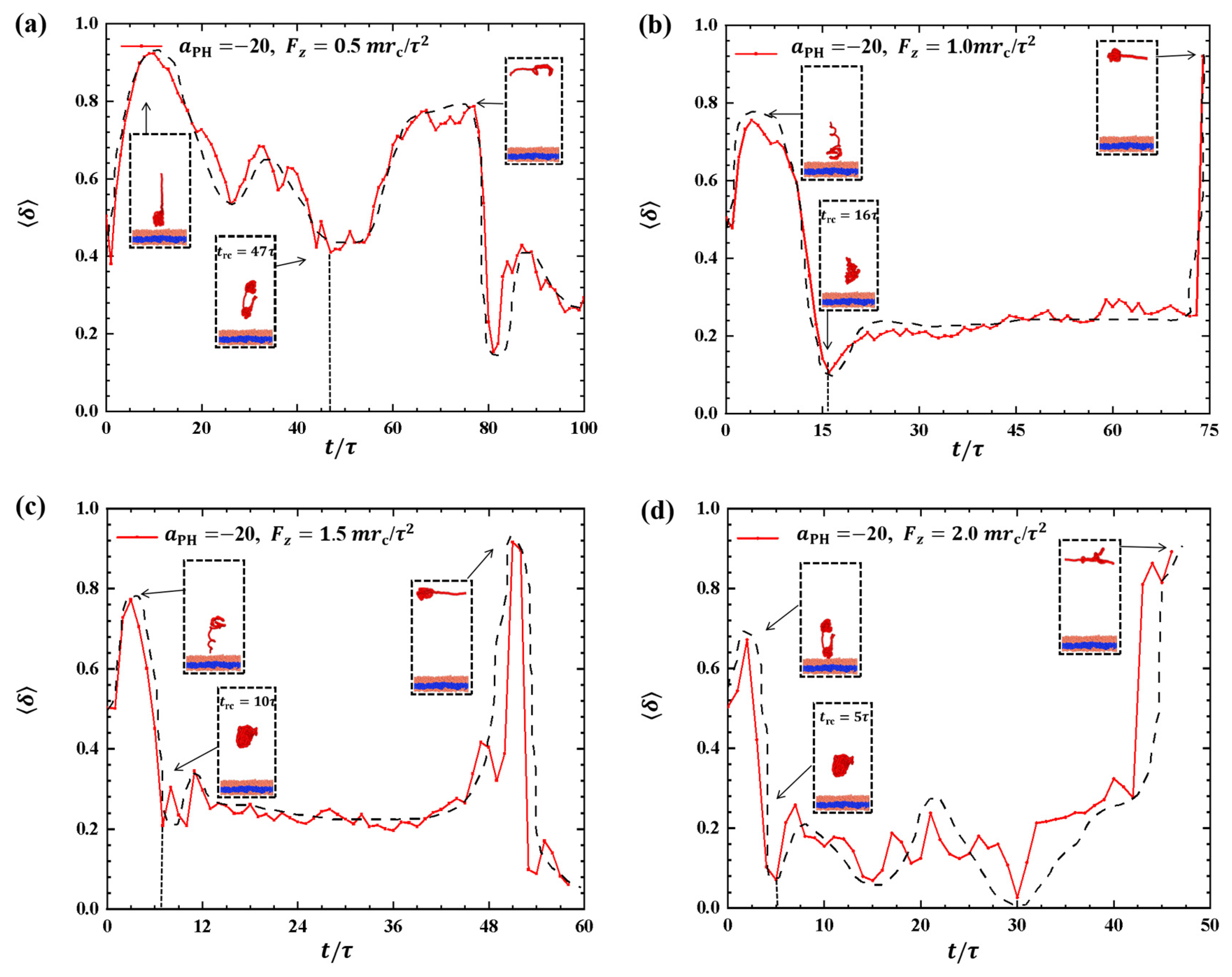
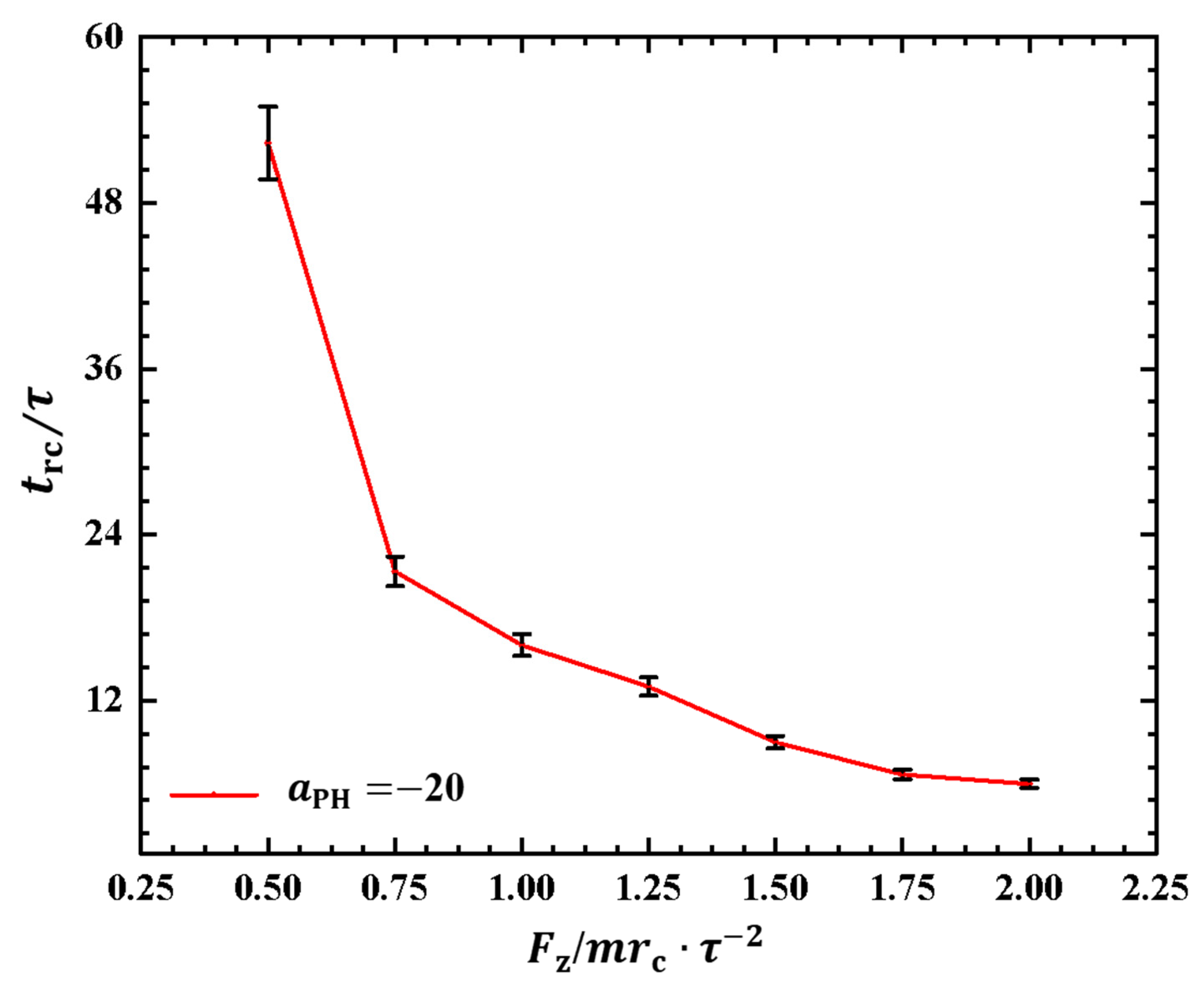
2.2. Pulling Forces Perpendicular to Membrane Surfaces
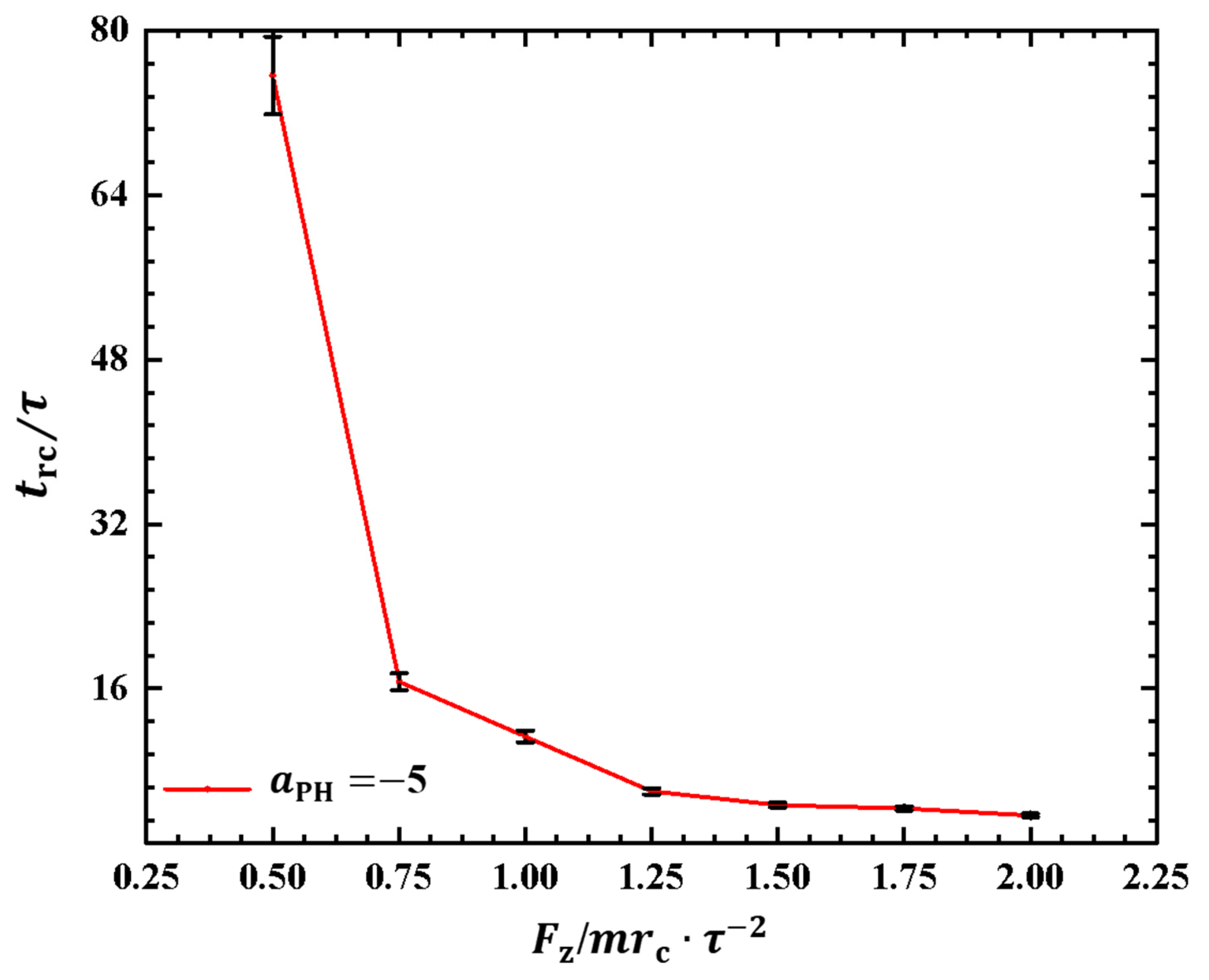
2.2.1. Conformations of Polymer Chains under Weak Adsorption
2.2.2. Conformations of Polymer Chains under Strong Adsorption
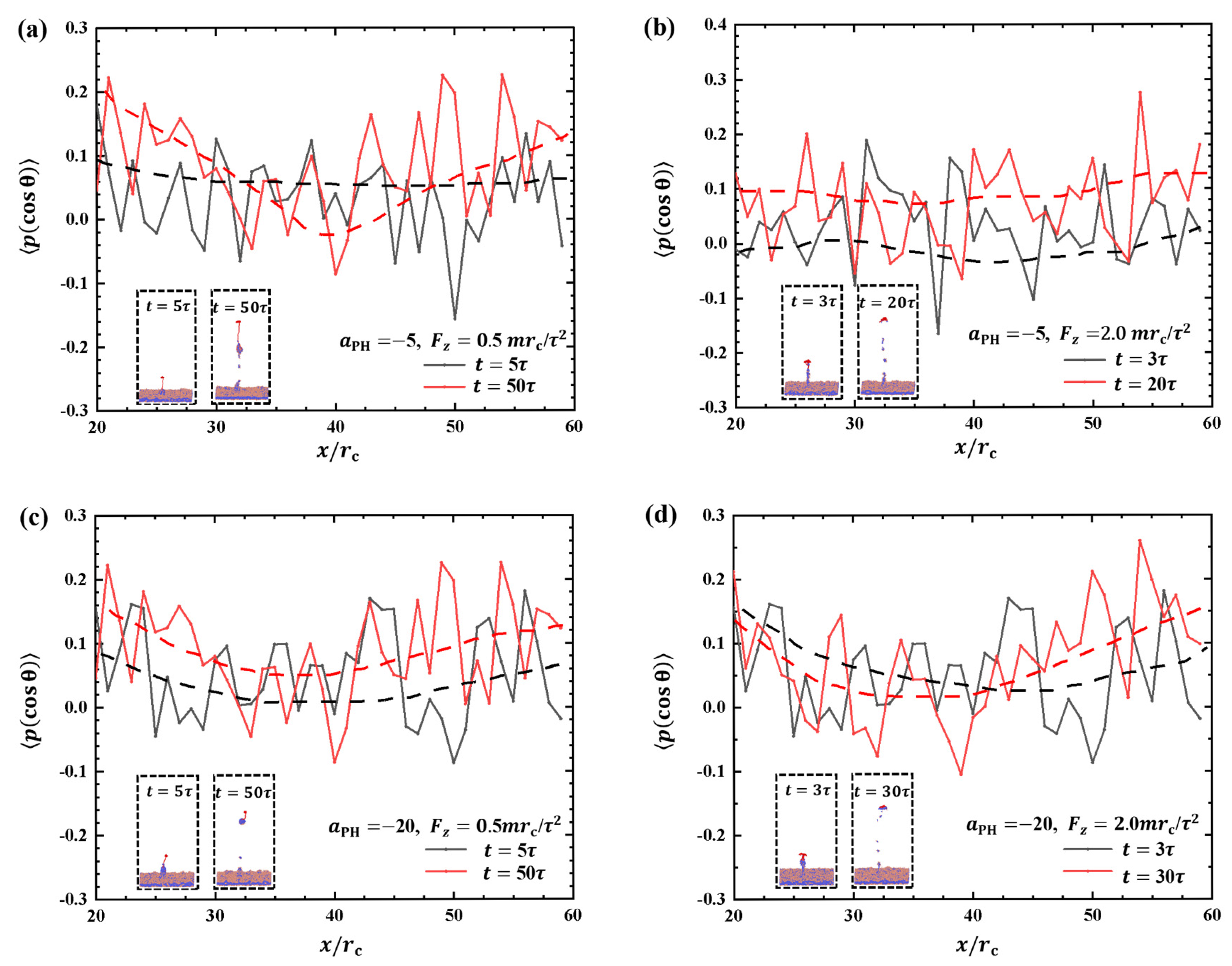
2.2.3. Order Parameters of Phospholipid Molecules
3. Model and Method
3.1. Methodology
3.2. Model
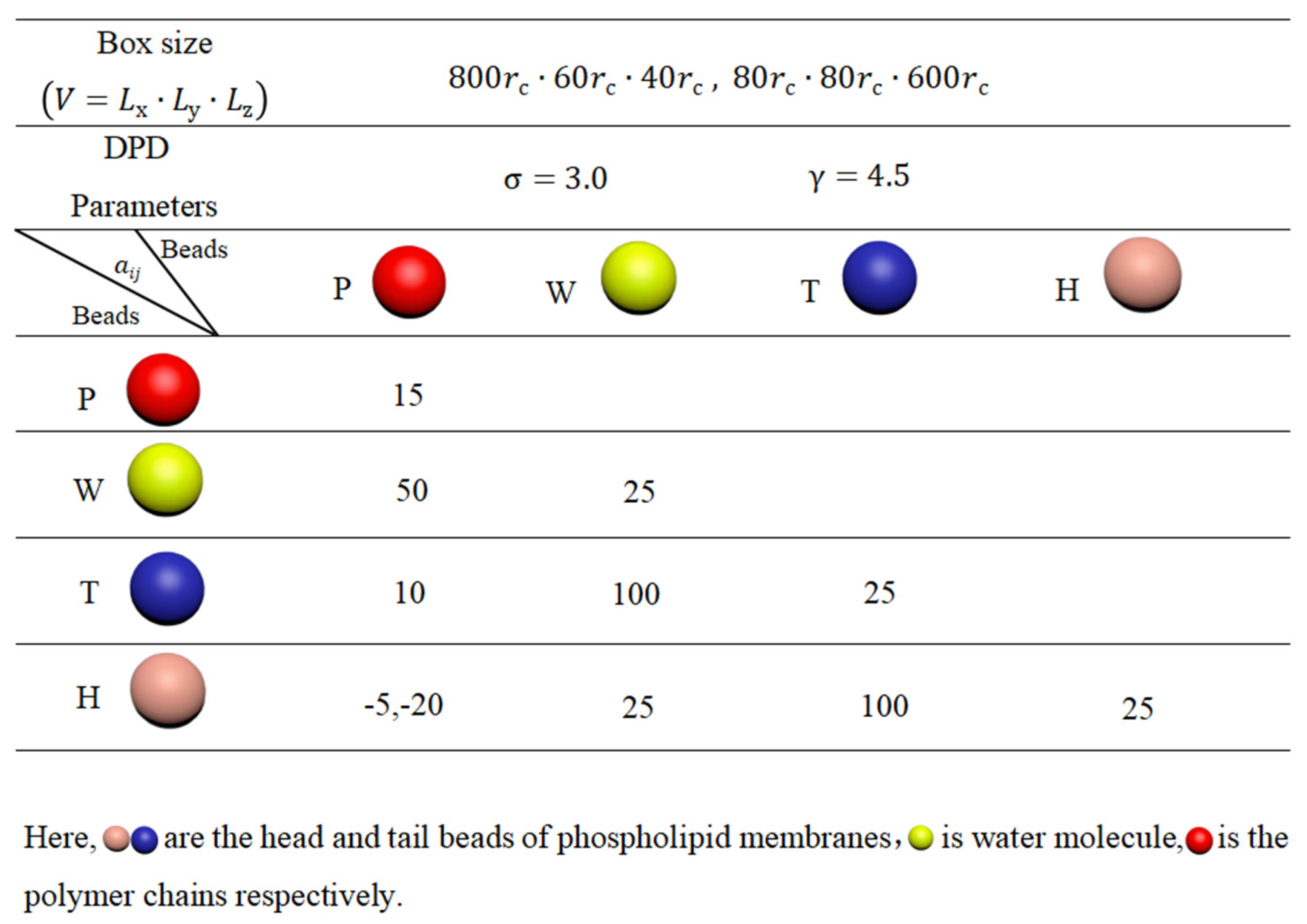
3.3. Simulation Parameters
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kooijmans, S.A.; Vader, P.; van Dommelen, S.M.; van Solinge, W.W.; Schiffelers, R.M. Exosome mimetics: A novel class of drug delivery systems. Int. J. Nanomed. 2012, 7, 1525–1541. [Google Scholar]
- Mancho, A.M.; Small, D.; Wiggins, S.; Pascalutsa, V.; Vanderhaeghen, M.; Yang, S.N.; Kresin, V.Z.; Ovchinnikov, Y.N.; Wolf, S.A. Mesoscopic models of biological membranes. Phys. Rep. 2007, 437, 235. [Google Scholar]
- Arnott, P.M.; Joshi, H.; Aksimentiev, A.; Howorka, S. Dynamic interactions between lipid-tethered DNA and phospholipid membranes. Langmuir 2018, 34, 15084–15092. [Google Scholar] [CrossRef] [PubMed]
- Schulz, M.; Olubummo, A.; Binder, W.H. Beyond the lipid-bilayer: Interaction of polymers and nanoparticles with membranes. Soft Matter 2012, 8, 4849–4864. [Google Scholar] [CrossRef]
- Bunker, A.; Rog, T. Mechanistic understanding from molecular dynamics simulation in pharmaceutical research 1: Drug delivery. Front. Mol. Biosci. 2020, 7, 604770. [Google Scholar] [CrossRef]
- Bunea, A.I.; Harloff-Helleberg, S.; Taboryski, R.; Nielsen, H.M. Membrane interactions in drug delivery: Model cell membranes and orthogonal techniques. Adv. Colloid Interface Sci. 2020, 281, 102177. [Google Scholar] [CrossRef]
- Firestone, M.A.; Wolf, A.C.; Seifert, S. Small-angle X-ray scattering study of the interaction of poly(ethylene oxide)-b-poly(propylene oxide)-b-poly(ethylene oxide) triblock copolymers with lipid bilayers. Biomacromolecules 2003, 4, 1539–1549. [Google Scholar] [CrossRef]
- Lee, B.; Firestone, M.A. Electron density mapping of triblock copolymers associated with model biomembranes: Insights into conformational states and effect on bilayer structure. Biomacromolecules 2008, 9, 1541–1550. [Google Scholar] [CrossRef]
- Wang, J.Y.; Chin, J.; Marks, J.D.; Lee, K.Y.C. Effects of PEO-PPO-PEO triblock copolymers on phospholipid membrane integrity under osmotic stress. Langmuir 2010, 26, 12953–12961. [Google Scholar] [CrossRef]
- Wang, J.Y.; Marks, J.; Lee, K.Y.C. Nature of interactions between PEO-PPO-PEO triblock copolymers and lipid membranes: (I) Effect of polymer hydrophobicity on its ability to protect liposomes from peroxidation. Biomacromolecules 2012, 13, 2616–2623. [Google Scholar] [CrossRef]
- Jurak, M.; Minones, J.J. Interactions of lauryl gallate with phospholipid components of biological membranes. Biochim Biophys Acta 2016, 1858, 1821–1832. [Google Scholar] [CrossRef]
- Banquy, X.; Lee, D.W.; Kristiansen, K.; Gebbie, M.A.; Israelachvili, J.N. Interaction forces between supported lipid bilayers in the presence of PEGylated polymers. Biomacromolecules 2016, 17, 88–97. [Google Scholar] [CrossRef]
- Travkova, O.G.; Moehwald, H.; Brezesinski, G. The interaction of antimicrobial peptides with membranes. Adv. Colloid Interface Sci. 2017, 247, 521–532. [Google Scholar] [CrossRef]
- Zhang, M.H.; Wang, D.Y.; Li, P.P.; Sun, C.; Xu, R.; Geng, Z.M.; Xu, W.M.; Dai, Z.Q. Interaction of Hsp90 with phospholipid model membranes. Biochim Biophys Acta Biomembr 2018, 1860, 611–616. [Google Scholar] [CrossRef]
- Li, P.P.; Wang, J.J.; Zou, Y.; Sun, Z.l.; Zhang, M.H.; Geng, Z.M.; Xu, W.M.; Wang, D.Y. Interaction of Hsp90AA1 with phospholipids stabilizes membranes under stress conditions. Biochim. Biophys. Acta Biomembr. 2019, 1861, 457–465. [Google Scholar] [CrossRef]
- Brodszkij, E.; Hviid, M.J.; Ade, C.; Schattling, P.S.; Burmeister, M.; Szilagyi, S.; Gal, N.; Zhu, C.; Han, X.J.; Städler, B. Interaction of pH-responsive polyanions with phospholipid membranes. Polym. Chem. 2019, 10, 5992–5997. [Google Scholar] [CrossRef]
- Zhang, W.; Coughlin, M.L.; Metzger, J.M.; Hackel, B.J.; Bates, F.S.; Lodge, T.P. Influence of cholesterol and bilayer curvature on the interaction of PPO–PEO block copolymers with liposomes. Langmuir 2019, 35, 7231–7241. [Google Scholar] [CrossRef]
- Zhang, W.J.; Metzger, J.M.; Hackel, B.J.; Bates, F.S.; Lodge, T.P. Influence of the headgroup on the interaction of poly(ethylene oxide)-poly(propylene oxide) block copolymers with lipid bilayers. J. Phys. Chem. B 2020, 124, 2417–2424. [Google Scholar] [CrossRef]
- Kim, M.; Heinrich, F.; Haugstad, G.; Yu, G.C.; Yuan, G.C.; Satija, S.K.; Zhang, W.J.; Seo, H.S.; Metzger, J.M.; Azarin, S.M.; et al. Spatial distribution of PEO–PPO–PEO block copolymer and PEO homopolymer in lipid bilayers. Langmuir 2020, 36, 3393–3403. [Google Scholar] [CrossRef]
- Mainali, L.; O’Brien, W.J.; Timsina, R. Interaction of alpha-crystallin with phospholipid membranes. Curr. Eye Res. 2021, 46, 185–194. [Google Scholar] [CrossRef]
- Starosta, R.; Santos, T.C.; Dinis de Sousa, A.F.; Santos, M.S.; Corvo, M.L.; Tomaz, A.I.; de Almeida, R.F.M. Assessing the role of membrane lipids in the action of ruthenium(III) anticancer compounds. Front. Mol. Biosci. 2022, 9, 1059116. [Google Scholar] [CrossRef] [PubMed]
- Van Zee, N.J.; Peroutka, A.S.; Crabtree, A.; Hillmyer, M.A.; Lodge, T.P. Lipid membrane binding and cell protection efficacy of poly(1,2-butylene oxide)-b-poly(ethylene oxide) copolymers. Biomacromolecules 2022, 23, 1433–1442. [Google Scholar] [CrossRef]
- Ge, Y.K.; Liu, J.J.; Dou, Y.J.; Chen, Z.L.; Li, Z.H.; Yang, K.; Yuan, B.; Kang, Z.H. A real-time and in-situ monitoring of the molecular interactions between drug carrier polymers and a phospholipid membrane. Colloids Surf. B 2022, 209, 112161. [Google Scholar] [CrossRef] [PubMed]
- Hassler, J.F.; Crabtree, A.; Liberman, L.; Bates, F.S.; Hackel, B.J.; Lodge, T.P. Effect of bottlebrush poloxamer architecture on binding to liposomes. Biomacromolecules 2023, 24, 449–461. [Google Scholar] [CrossRef] [PubMed]
- Hezaveh, S.; Samanta, S.; De Nicola, A.; Milano, G.; Roccatano, D. Understanding the interaction of block copolymers with DMPC lipid bilayer using coarse-grained molecular dynamics simulations. J. Phys. Chem. B 2012, 116, 14333–14345. [Google Scholar] [CrossRef]
- Nawaz, S.; Redhead, M.; Mantovani, G.; Alexander, C.; Bosquillon, C.; Carbone, P. Interactions of PEO–PPO–PEO block copolymers with lipid membranes: A computational and experimental study linking membrane lysis with polymer structure. Soft Matter 2012, 8, 6744–6754. [Google Scholar] [CrossRef]
- Rabbel, H.; Werner, M.; Sommer, J.U. Interactions of amphiphilic triblock copolymers with lipid membranes: Modes of interaction and effect on permeability examined by generic monte carlo simulations. Macromolecules 2015, 48, 4724–4732. [Google Scholar] [CrossRef]
- Houang, E.M.; Bates, F.S.; Sham, Y.Y.; Metzger, J.M. All-atom molecular dynamics-based analysis of membrane-stabilizing copolymer interactions with lipid bilayers probed under constant surface tensions. J. Phys. Chem. B 2017, 121, 10657–10664. [Google Scholar] [CrossRef]
- Huang, Y.C.; Liu, Y.C.; Chen, Y.Y.; Song, M.; Huang, M.D.; Xue, J.P.; Liu, L.; Li, J.Y. Probing the interactions of phthalocyanine-based photosensitizers with model phospholipid bilayer by molecular dynamics simulations. J. Porphyr. Phthalocyanines 2018, 22, 764–770. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, X.H.; Ji, Y.Y.; Qiang, X.W.; He, L.L.; Li, S.B. Bottlebrush block polymers in solutions: Self-assembled microstructures and interactions with lipid membranes. Polymer 2018, 140, 304–314. [Google Scholar] [CrossRef]
- Beldowski, P.; Yuvan, S.; Dedinaite, A.; Claesson, P.M.; Poschel, T. Interactions of a short hyaluronan chain with a phospholipid membrane. Colloids Surf. B 2019, 184, 110539. [Google Scholar] [CrossRef]
- Drenscko, M.; Loverde, S.M. Molecular dynamics simulations of the interaction of phospholipid bilayers with polycaprolactone. Mol. Simul. 2019, 45, 859–867. [Google Scholar] [CrossRef]
- Losasso, V.; Hsiao, Y.-W.; Martelli, F.; Winn, M.D.; Crain, J. Modulation of antimicrobial peptide potency in stressed lipid bilayers. Phys. Rev. Lett. 2019, 122, 208103. [Google Scholar] [CrossRef]
- Angelescu, D.G. Structural behavior of amphiphilic polyion complexes interacting with saturated lipid membranes investigated by coarse-grained molecular dynamic simulations. RSC Adv. 2020, 10, 39204–39216. [Google Scholar] [CrossRef]
- Dai, X.Y.; Ji, Y.Y.; Wang, Z.G.; He, L.L.; Wang, X.H.; Li, S.B. Interaction between bottlebrush polymers and phospholipid membranes in solutions. Polymers 2020, 12, 3033. [Google Scholar] [CrossRef]
- Huang, W.W.; Zaburdaev, V. The shape of pinned forced polymer loops. Soft Matter 2019, 15, 1785–1792. [Google Scholar] [CrossRef]
- Zifferer, G.; Preusser, W. Monte carlo simulation studies of the size and shape of ring polymers. Macromol. Theory Simul. 2001, 10, 397–407. [Google Scholar] [CrossRef]
- Nardai, M.M.; Zifferer, G. Concentration dependence of size, shape, and orientation of copolymers, 1 - linear diblock and 4-arm hetero star polymers. Macromol. Theory Simul. 2011, 20, 675–689. [Google Scholar] [CrossRef]
- Vogiatzis, G.G.; Megariotis, G.; Theodorou, D.N. Equation of state based slip spring model for entangled polymer dynamics. Macromolecules 2017, 50, 3004–3029. [Google Scholar] [CrossRef]
- Schroeder, C.M. Single polymer dynamics for molecular rheology. J. Rheol. 2018, 62, 371–403. [Google Scholar] [CrossRef]
- Jehser, M.; Zifferer, G.; Likos, C.N. Scaling and interactions of linear and ring polymer brushes via DPD simulations. Polymers 2019, 11, 541. [Google Scholar] [CrossRef] [PubMed]
- Bagatolli, L.; Kumar, P. Phase behavior of multicomponent membranes: Experimental and computational techniques. Soft Matter 2009, 5, 3234–3248. [Google Scholar] [CrossRef]
- Yevlampieva, N.; Bermeshev, M.; Vezo, O.; Chapala, P.; Il’yasova, Y. Metathesis and additive poly(tricyclononenes) with geminal trimethylsilyl side groups: Chain rigidity, molecular and thin film properties. J. Polym. Res. 2018, 25, 162. [Google Scholar] [CrossRef]
- Yang, X.; Wu, F.; Hu, D.D.; Zhang, S.; Luo, M.B. Simulation of the critical adsorption of semi-flexible polymers*. Chinese Phys. Lett. 2019, 36, 098202. [Google Scholar] [CrossRef]
- Innes-Gold, S.N.; Berezney, J.P.; Saleh, O.A. Single-molecule stretching shows glycosylation sets tension in the hyaluronan-aggrecan bottlebrush. Biophys. J. 2020, 119, 1351–1358. [Google Scholar] [CrossRef]
- Schmidt, K.; Pester, C.W.; Schoberth, H.G.; Zettl, H.; Schindler, K.A.; Böker, A. Electric field induced gyroid-to-cylinder transitions in concentrated diblock copolymer solutions. Macromolecules 2010, 43, 4268. [Google Scholar] [CrossRef]
- Liedel, C.; Pester, C.W.; Ruppel, M.; Urban, V.S.; Boker, A. Beyond orientation: The impact of electric fields on block copolymers. Macromol. Chem. Phys. 2012, 213, 259–269. [Google Scholar] [CrossRef]
- Li, S.B.; Jiang, Y.; Ji, Y.Y.; Wang, X.H. Electric-field-induced sphere-cylinder phase transitions of diblock copolymers. Polymer 2013, 54, 6636–6643. [Google Scholar] [CrossRef]
- Ly, D.Q.; Pinna, M.; Honda, T.; Kawakatsu, T.; Zvelindovsky, A.V.M. Kinetic pathways of sphere-to-cylinder transition in diblock copolymer melt under electric field. J. Chem. Phys. 2013, 138, 074904. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.H.; Ji, Y.Y.; He, L.L.; Li, S.H. Phase diagrams of diblock copolymers in electric fields: A self-consistent field theory study. Phys. Chem. Chem. Phys. 2016, 18, 10309–10319. [Google Scholar] [CrossRef]
- Hatano, I.; Mochizuki, K.; Sumi, T.; Koga, K. Hydrophobic polymer chain in water that undergoes a coil-to-globule transition near room temperature. J. Phys. Chem. B 2016, 120, 12127–12134. [Google Scholar] [CrossRef]
- Hadley, K.R.; McCabe, C. A simulation study of the self-assembly of coarse-grained skin lipids. Soft Matter 2012, 8, 4802–4814. [Google Scholar] [CrossRef][Green Version]
- Skjevik, A.A.; Madej, B.D.; Walker, R.C.; Teigen, K. LIPID11: A modular framework for lipid simulations using amber. J. Phys. Chem. B 2012, 116, 11124–11136. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Xu, R.; Kan, D.; He, X.H. Molecular dynamics simulation of electric-field-induced self-assembly of diblock copolymers. J. Chem. Phys. 2016, 144, 234901. [Google Scholar] [CrossRef]
- Wohlert, J.; den Otter, W.K.; Edholm, O.; Briels, W.J. Free energy of a trans-membrane pore calculated from atomistic molecular dynamics simulations. J. Chem. Phys. 2006, 124, 154905. [Google Scholar] [CrossRef]
- den Otter, W.K. Free energies of stable and metastable pores in lipid membranes under tension. J. Chem. Phys. 2009, 131, 205101. [Google Scholar] [CrossRef]
- Levadny, V.; Tsuboi, T.A.; Belaya, M.; Yamazaki, M. Rate constant of tension-induced pore formation in lipid membranes. Langmuir 2013, 29, 3848–3852. [Google Scholar] [CrossRef]
- Karal, M.A.; Yamazaki, M. Communication: Activation energy of tension-induced pore formation in lipid membranes. J. Chem. Phys. 2015, 143, 081103. [Google Scholar] [CrossRef]
- Espanol, P.; Warren, P.B. Perspective: Dissipative particle dynamics. J. Chem. Phys. 2017, 146, 150901. [Google Scholar] [CrossRef]
- Yang, C.F.; Yuan, C.; Liu, W.Y.; Guo, J.W.; Feng, D.C.; Yin, X.Q.; Lin, W.J.; Shuttleworth, P.S.; Yue, H.B. DPD studies on mixed micelles self-assembled from MPEG-PDEAEMA and MPEG-PCL for controlled doxorubicin release. Colloids Surf. B 2019, 178, 56–65. [Google Scholar] [CrossRef]
- Delgado-Buscalioni, R.; Kremer, K.; Praprotnik, M. Concurrent triple-scale simulation of molecular liquids. J. Chem. Phys. 2008, 128, 114110. [Google Scholar] [CrossRef] [PubMed]
- Moeendarbary, E.; Ng, T.Y.; Zangeneh, M. Dissipative particle dynamics in soft matter and polymeric applications—A review. Int. J. Appl. Mech. 2012, 02, 161–190. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Yang, Y.; Zhu, G.L.; Chen, P.Y.; Huang, Z.H.; Dai, X.B.; Hou, C.L.; Yan, L.T. Simulating transport of soft matter in micro/nano channel flows with dissipative particle dynamics. Adv. Theory Simul. 2018, 2, 1800160. [Google Scholar] [CrossRef]
- Mai-Duy, N.; Phan-Thien, N.; Tran-Cong, T. An improved dissipative particle dynamics scheme. Appl. Math. Model. 2017, 46, 602–617. [Google Scholar] [CrossRef][Green Version]
- Hansen, J.S.; Greenfield, M.L.; Dyre, J.C. Hydrodynamic relaxations in dissipative particle dynamics. J. Chem. Phys. 2018, 148, 1034503. [Google Scholar] [CrossRef]
- Sokhan, V.P.; Todorov, I.T. Dissipative particle dynamics: Dissipative forces from atomistic simulation. Mol. Simul. 2019, 47, 248–256. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Becton, M.; Wang, X.Q. Designing nanoparticle translocation through cell membranes by varying amphiphilic polymer coatings. J. Phys. Chem. B 2015, 119, 3786–3794. [Google Scholar] [CrossRef]
- Ye, T.; Li, Y. A comparative review of smoothed particle hydrodynamics, dissipative particle dynamics and smoothed dissipative particle dynamics. Int. J. Comput. Methods 2018, 15, 1850083. [Google Scholar] [CrossRef]
- Zhu, G.D.; Shang, J.Q.; Wen, W.H.; Li, Y.Y.; Yin, G.Q. Multilamellar spherical micelles of alkali lignin: Dissipative particle dynamics simulations. J. Mol. Model. 2023, 29, 33. [Google Scholar] [CrossRef]
- Sun, L.L.; Pan, F.; Li, S.B. Self-assembly of lipid mixtures in solutions: Structures, dynamics processes and mechanical properties. Membranes 2022, 12, 730. [Google Scholar] [CrossRef]
- Qiang, X.W.; Wang, X.H.; Ji, Y.Y.; Li, S.B.; He, L.L. Liquid-crystal self-assembly of lipid membranes on solutions: A dissipative particle dynamic simulation study. Polymer 2017, 115, 1–11. [Google Scholar] [CrossRef]
- Klein, M.L.; Shinoda, W. Large-scale molecular dynamics simulations of self-assembling systems. Science 2008, 321, 798–800. [Google Scholar] [CrossRef]
- Gao, L.H.; Shillcock, J.; Lipowsky, R. Improved dissipative particle dynamics simulations of lipid bilayers. J. Chem. Phys. 2007, 126, 015101. [Google Scholar] [CrossRef]
- Ruhle, V.; Junghans, C.; Lukyanov, A.; Kremer, K.; Andrienko, D. Versatile object-oriented toolkit for coarse-graining applications. J. Chem. Theory Comput. 2009, 5, 3211–3223. [Google Scholar] [CrossRef]
- Gao, L.H.; Fang, W.H. Semi-bottom-up coarse graining of water based on microscopic simulations. J. Chem. Phys. 2011, 135, 184101. [Google Scholar] [CrossRef]
- Li, Y.; Abberton, B.C.; Kröger, M.; Liu, W.K. Challenges in multiscale modeling of polymer dynamics. Polymers 2013, 5, 751–832. [Google Scholar] [CrossRef]
- Shan, Y.; Wang, X.H.; Ji, Y.Y.; He, L.L.; Li, S.B. Self-assembly of phospholipid molecules in solutions under shear flows: Microstructures and phase diagrams. J. Chem. Phys. 2018, 149, 244901. [Google Scholar] [CrossRef]
- Venturoli, M.; Smit, B.; Sperotto, M.M. Simulation studies of protein-induced bilayer deformations, and lipid-induced protein tilting, on a mesoscopic model for lipid bilayers with embedded proteins. Biophys. J. 2005, 88, 1778–1798. [Google Scholar] [CrossRef]
- Maiti, A.; McGrother, S. Bead-bead interaction parameters in dissipative particle dynamics: Relation to bead-size, solubility parameter, and surface tension. J. Chem. Phys. 2004, 120, 1594–1601. [Google Scholar] [CrossRef]
- Shan, Y.; Qiang, X.W.; Ye, J.Z.; Wang, X.H.; He, L.L.; Li, S.B. Shear-induced microstructures and dynamics processes of phospholipid cylinders in solutions. Sci. Rep. 2019, 9, 15393. [Google Scholar] [CrossRef]
- Shan, Y.; Ji, Y.Y.; Wang, X.H.; He, L.L.; Li, S.B. Predicting asymmetric phospholipid microstructures in solutions. RSC Adv. 2020, 10, 24521–24532. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.Y.; Wang, Z.G.; Ji, Y.Y.; He, L.L.; Wang, X.H.; Li, S.B. Asymmetric lipid membranes under shear flows: A dissipative particle dynamics study. Membranes 2021, 11, 655. [Google Scholar] [CrossRef] [PubMed]
- Li, X.J.; Liu, Y.; Wang, L.; Deng, M.; Liang, H.J. Fusion and fission pathways of vesicles from amphiphilic triblock copolymers: A dissipative particle dynamics simulation study. Phys. Chem. Chem. Phys. 2009, 11, 4051–4059. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.F.; Li, X.J.; Li, Z.H.; Gao, H.J. Surface-structure-regulated penetration of nanoparticles across a cell membrane. Nanoscale 2012, 4, 3768–3775. [Google Scholar] [CrossRef]
- Li, X.; Han, X.; Wang, X.; Chen, Z.; Lu, X. Observing different dynamic behaviors of weakly and strongly adsorbed polystyrene chains at interfaces. Soft Matter 2018, 14, 2762–2766. [Google Scholar] [CrossRef]
- Naderi, A.; Iruthayaraj, J.; Vareikis, A.; Makuška, R.; Claesson, P.M. Surface properties of bottle-brush polyelectrolytes on mica: Effects of side chain and charge densities. Langmuir 2007, 23, 12222–12232. [Google Scholar] [CrossRef]
- Chen, J.H.; Lu, L.Q.; Zhao, H.X.; Yang, Y.; Shu, X.; Ran, Q.P. Conformational properties of comb-shaped polyelectrolytes with negatively charged backbone and neutral side chains studied by a generic coarse-grained bead-and-spring model. Chin. J. Polym. Sci. 2020, 38, 371–381. [Google Scholar] [CrossRef]
- Gore, J.; Bryant, Z.; Nöllmann, M.; Le, M.U.; Cozzarelli, N.R.; Bustamante, C. DNA overwinds when stretched. Nature 2006, 442, 836–839. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Mou, X.; Ji, Y.; Pan, F.; Li, S. Interaction of Macromolecular Chain with Phospholipid Membranes in Solutions: A Dissipative Particle Dynamics Simulation Study. Molecules 2023, 28, 5790. https://doi.org/10.3390/molecules28155790
Wang Y, Mou X, Ji Y, Pan F, Li S. Interaction of Macromolecular Chain with Phospholipid Membranes in Solutions: A Dissipative Particle Dynamics Simulation Study. Molecules. 2023; 28(15):5790. https://doi.org/10.3390/molecules28155790
Chicago/Turabian StyleWang, Yuane, Xuankang Mou, Yongyun Ji, Fan Pan, and Shiben Li. 2023. "Interaction of Macromolecular Chain with Phospholipid Membranes in Solutions: A Dissipative Particle Dynamics Simulation Study" Molecules 28, no. 15: 5790. https://doi.org/10.3390/molecules28155790
APA StyleWang, Y., Mou, X., Ji, Y., Pan, F., & Li, S. (2023). Interaction of Macromolecular Chain with Phospholipid Membranes in Solutions: A Dissipative Particle Dynamics Simulation Study. Molecules, 28(15), 5790. https://doi.org/10.3390/molecules28155790





