Abstract
In this work the rovibrational spectrum of the acetylide anion HCC is investigated using high-level electronic structure methods and variational rovibrational calculations. Using a composite approach the potential energy surface and dipole surface is constructed from explicitly correlated coupled-cluster accounting for corrections due to core-valence correlation, scalar relativistic effects and higher-order excitation effects. Previous approaches for approximating the latter are critically evaluated. Employing the composite potential, accurate spectroscopic parameters determined from variational calculations are presented. In comparison to the few available reference data the present results show excellent agreement with ground state rotational constants within 0.005% of the experimental value. Intensities determined from the variational calculations suggest the bending fundamental transition around 510 cm to be the best target for detection. The rather weak CD stretching fundamental in deuterated isotopologues show a second-order resonance with the state and the consequences are discussed in some detail. The spectroscopic parameters and band intensities provided for a number of vibrational bands in isotopologues of the acetylide anion should facilitate future spectroscopic investigations.
1. Introduction
Many of the ca. 240 molecules which have been detected in the interstellar medium or circumstellar shells [1,2,3,4,5] are highly reactive species such as radicals, carbenes or molecular ions. These can be challenging to study in the laboratory by spectroscopic techniques due to low obtainable concentrations. Therefore, highly accurate predictions of spectroscopic parameters based on ab initio theory are desirable [6,7,8,9,10,11,12]. While about 10% of the astromolecules are cationic species, the number of detected anions amounts to only a quarter of that [5]. See also the work of Millar et al. [13] for reviews on the role of anions in astrophysics. Among the anionic interstellar molecules the class of linear chains of type CH is the most extensive with CH being the first molecular anion to ever be detected in the interstellar medium [14,15,16,17,18,19].
Following the initial detection as a series of unidentified lines (termed B1377) toward IRC + 10216 by Kawaguchi et al. [14] it took more than 10 years until McCarthy and coworkers [15] could record the rotational spectrum of CH in the centimeter- and millimeter-wave bands and unambigously assign the B1377 transition. This lead to an increased effort of detecting more anionic species and the series was extended in the following year through the work of Cernicharo and coworkers [18] observing CH towards IRC + 10216 as well as Brünken et al. [16] and Remijan et al. [17] who independently reported the detection of CH. Quite recently Remijan and coworkers [19] published results as part of their GOTHAM program (GBT Observations of TMC-1: Hunting Aromatic Molecules) describing the identification of CH towards TMC-1 using the Green Bank Telescope.
Despite considerable effort [20,21], the acetylide anion HCC—the smallest member of the series—has not yet been detected in space. This has been ascribed to a reduced rate for the dominant radiative electron attachment path in the fromation of these anions [22,23,24]
Furthermore, spectroscopic information for this system is rather scarce. In 2007 Brünken et al. [25] succeeded in recording the rotational spectrum of HCC produced by discharge through an acetylene/argon mixture in a free space millimeter-wave spectrometer. The five lowest rotational transitions of HCC were observed as well as rotational transitions of the two singly C substituted species. One year later Amano [26] extended the range of observed rotational lines for the main isotopologue up to the transition by the use of a submillimeter-wave spectrometer and extended negative glow discharge. Together these measurements provide accurate vibrational ground state rotational parameters and of MHz and kHz, respectively, where numbers in parentheses indicate one standard deviation to the last significant digits. With regards to the vibrational spectrum of HCC the only reliable available experimental information has been obtained by Ervin and Lineberger [27] from photoelectron spectroscopy of HCC. Through the analysis of hot bands in the HCC() ← HCC() spectrum they determined the bending fundamental frequency to be cm and the CC-stretching fundamental cm.
Given its importance there have been a number of theoretical studies dedicated to the spectroscopy of HCC [28,29,30,31,32,33,34]. A careful investigation was presented by Mladenović et al. [32] who developed an analytic three-dimensional representation of the potential energy surface (PES) based on coupled-cluster calculations with singles, doubles, and perturbative triples CCSD(T) [35]. Variational calculations using that PES yielded band origins of the fundamental vibrational transitions of 511 and 1805 cm for and , respectively, as well as a value of 3211 cm for the CH-stretching fundamental . These results also ruled out claims by Gruebele et al. [36] who reported the observation of the band around 1758.621(3) cm. The experimentally determined band center clearly is at odds with both the theoretical predictions as well as the results of Ervin and Lineberger [27]. By comparison with results obtained for hydrogen cyanide (HCN) at the same level of theory and experiment [37] Mladenović et al. derived recommended equilibrium bond lengths of Å and Å.
In 2009 Huang and Lee presented results for HCC based quartic force fields (QFF) within a composite procedure that combines complete basis set (CBS) limit CCSD(T) results with corrections for missing correlation contributions. Besides core-valence correlation and scalar relativistic effects, emphasis was given to the inclusion of higher-order correlation contributions beyond CCSD(T) which were obtained by forming the difference between averaged coupled-pair functional (ACPF) [38] calculations based on a full-valence complete active space self-consistent field (CASSCF) [39] reference and canonical CCSD(T). The final equilibrium bond lengths were Å and Å. Based on vibrational configuration interaction calculations [40,41,42] Huang and Lee obtained cm, cm, and cm from their best QFF. These results differ quite significantly from previous results [32] by as much as 9 cm for the fundamental vibrational transtions and 0.0014 Å for the CH bond length, the latter thus well outside the estimated error bar of Mladenović and coworkers. Finally, Morgan and Fortenberry [34] also investigated HCC by use of a similar composite QFF scheme [43]. However, their results are somewhat more in line with the work of Mladenović et al. given that no correction for higher-order correlation based on ACPF has been included.
It appears that some of the theoretical results are somewhat questionable. This could be problematic for future spectroscopic studies on HCC since comparison between experiment and theory might not be conclusive. Therefore, this study aims at providing benchmark quality predictions for the rovibrational spectrum of the acetylide anion. To this end, a high-level ab initio composite approach is employed in the construction of a PES. Variational calculations employing the composite PES then provide vibrational band origins with an accuracy of around 1 cm. Combined with an electric dipole moment surface (EDMS) the rovibrational spectrum up to about the first excited CH stretching state ∼3300 cm will be investigated. Finally, comparisons with published composite approaches to HCC will highlight shortcomings of the previous work which should prove valuable for future theoretical investigations not only of the title compound.
2. Methods
2.1. Electronic Structure Calculations
The construction of the PES is based on a well established composite procedure which has been applied to a variety of small polyatomic molecules [44,45,46,47,48,49,50,51,52,53]. The employed contributions closely follow the Feller-Peterson-Dixon partitioning of the energy [54,55,56,57,58,59,60]. Here, the basic contribution is obtained from frozen-core (fc) explicitly correlated coupled-cluster calculations with singles, doubles and (scaled) perturbative triples CCSD(T*)-F12b [61,62,63] together with an aug-cc-pV5Z basis set [64,65]. This level of theory will be abbreviated as F12bs in the following. The auxiliary basis sets, as required for F12-calculations, were AV5Z/OPTRI [66], AV5Z/JKFIT [67], and AV5Z/MP2FIT [68]. As suggested by Peterson et al. [69] a geminal parameter of 1.5 has been used.
The composite procedure adds small corrections to the basic F12bs contribution to incorporate core-core and core-valence correlation (CV), scalar-relativisitic effects (SR), higher-order correlation (HC) beyond CCSD(T), and the diagonal Born-Oppenheimer-Correction (DBOC). In detail these effects are calculated in the following ways:
- CV:
- The CV effects are captured by conventional CCSD(T) calculation and a large (781 contracted Gaussian-type orbitals) aug-cc-pCV6Z basis set [70]. By subtracting the result of frozen-core CCSD(T) from that of an all-electron (ae) calculation the CV contribution is obtained.
- SR:
- Second-order Dogulas-Kroll-Hess calculations [71,72] are employed at the fc-CCSD(T) level to provide SR effects, where difference of calculations with the relativistic Hamiltonian employing a aug-cc-pVQZ-DK basis set [73] and non-relativistic calculations with an aug-cc-pVQZ basis [64,65] yields the contribution to the composite PES.
- HC:
- Three distinct HC contributions are employed. The first, which is termed (Q)–(T), corrects for the fully iterative treatment of triple excitations as well as for a quadruple excitation effect by a perturbative treatment. The second contribution Q–(Q) accounts for the full iterative treatment of quadruples. This partitioning has been shown to be rather efficient since larger basis sets can be used for (Q)–(T) compared to Q–(Q). Finally, the P–Q contribution incorporates pentuple excitation contributions.
- (Q)–(T):
- This contribution employs the fc-CCSDT(Q) method [74] and is obtained as the difference to fc-CCSD(T). The calculations are performed with an aug-cc-pVTZ basis set [64].
- Q–(Q):
- The second HC contribution is obtained by forming the difference of fc-CCSDTQ [75] with respect to fc-CCSDT(Q). The basis is constructed by omiting the highest angular momentum functions in the cc-pVTZ basis [64], i.e., f-functions are omitted for carbon and d-functions for hydrogen.
- P–Q:
- The third HC contribution is obtained from the difference of fc-CCSDTQP [75] and fc-CCSDTQ together with the cc-pVDZ basis [64].
Karton and coworkers demonstrated repeatedly [76,77,78,79] that basis set dependencies of HC effects diminishes with the excitation level. - DBOC:
- All-electron CCSD calculations are employed for the adiabatic DBOC correction [80,81,82] together with a cc-pCVQZ basis [70]. The DBOC calculations were perfomed with the Cfour program [83,84]. Due to the inverse mass dependence this contribution is important for hydrogen containing systems. It is evaluated for 6 possible H/D and C/C combinations, i.e., H/D substitution and single C/C switch, and in turn the inclusion of DBOC leads to 6 different adiabatic PESs for HCC isotopologues.
All electronic structure calculations, unless noted otherwise, have been performed with the Molpro suite of ab initio programs [85,86,87] and an interface to Mrcc by Kállay and coworkers [88,89] for the HC calculations.
The linear reference structure employed for all contributions corresponds to the recommended bond lengths by Botschwina and coworkers [32], i.e., a CH bond length of Å, and a CC bond length of Å. The PES is sampled in the ranges , , and , where the internal coordinates and are simple bond stretches and the angle measures the deviation from linearity. These ranges cover energies up to ∼10,000 cm above the reference along the diagonal cuts of the PES. Each contribution (labeled ) is represented by a least-squares fit to a polynomial form
In Equation (1) the exponent k is even as required by symmetry. The individual fitted contributions are summed up and transformed to the minimum. This procedure yields composite PESs and equilibrium bond lengths and .
The EDMS is developed by combining the F12bs, CV, SR, and HC contributions employed for the PES. This allows the calculation of transition dipole moments and rovibrational line intensities. The EDMS is sampled in the same coordinate range as the PES and the dipole moment vector is obtained by finite field calculations ( a.u.), i.e., for the difference based contributions this involves up to 8 individual calculations. Molecule fixed components of the dipole vector (parallel and perpendicular ) are obtained by locally transforming to the Eckart frame of the main isotopologue HCC. Each component of the individual contributions is then least-squares fit to a polynomial form:
The EDMS of other isotopologues is obtained by transforming the components to the new Eckart frame during the rovibrational calculations.
2.2. Rovibrational Calculations
The acetylide anion is a rather semi-rigid system in the lower spectral region [32]. Therefore, rovibrational calculations based on normal coordinates and the Eckart-Watson isomorphic Hamiltonian [90,91,92,93] are feasible. The two common approaches are based on either second-order vibrational perturbation theory (VPT2) [94,95,96,97] or variational calculations using harmonic oscillator/rigid rotor product basis functions [98,99,100]. One-dimensional harmonic oscillators [101] are used for the two stretching coordinates and 2D isotropic harmonic oscillator functions for the degenerate bending [102]. Both approaches either based on perturbation theory or on the variational principle will be employed and compared in the present work. All (ro)vibrational calculations employ atomic masses [103].
The appeal of VPT2 is that this treatment leads to compact formula for spectroscopic parameters [104,105] and in absence of resonance interactions is easy to apply. To this end, the composite PESs are transformed to a QFF representation
In Equation (3), is the harmonic vibrational frequency. The cubic and quartic force constants are denoted by and , respectively. They are obtained by numerical differentiation of the composite PES with respect to dimensionless normal coordinates . Various (ro)vibrational spectroscopic parameters can then be calculated by standard formulae [104,105,106,107,108], e.g., anharmonicity constants defining vibrational term energies for triatomic linear molecules
or rotation-vibration coupling constants which provide the vibrational dependencies of rotational constants according to
In Equations (4) and (5) is a constant (quantum number independent) contribution to the zero-point vibrational energy (ZPVE) [105,106,107,108], the degeneracy of the respective vibrational mode and the equilibrium rotational constant. The vibrational angular momentum quantum number for the degenerate bending mode is given by ℓ.
The variational calculations are performed with Sebald’s C8vpro program [109] to obtain rovibrational term energies and wavefunctions. To this end, the Hamiltonian up to a total angular momentum quantum number of is diagonalized in a basis of 2360 Wang-symmetrized [110,111] basis functions per K-block, where K is the quantum number for the projection of the total angular momentum unto the molecular axis. For linear triatomic systems the Sayvetz rule [91] requires . In order to reduce the computational costs the maximum value of ℓ was fixed at 8. This “frozen ℓ” approach has been succesfully applied previously even to floppy C [52]. In summary, this basis yields vibrational term energies converged to within 0.1 cm or better for the states of interest.
In the following, vibrational states of HCC are designated by v which collects the label with , , and being the vibrational quantum numbers of the CH-stretching, bending, and CC-stretching, respectively. For states with spectroscopic parameters can be determined by least-squares fitting the variational term energies according to
where is the vibrational term energy and is the rotational constant. The quartic and sextic centrifugal distortion parameters are given by and , respectively. Effects due to ℓ-type doubling and resonance [112,113,114] in states with are accounted for by setting up effective Hamiltonian matrices in conjunction with least-squares fitting to the variational rovibrational term energies. The diagonal and off-diagonal elements are given by [96]
and
respectively. In Equation (8) , , and are the ℓ-type doubling constants.
Line intensities for rovibrational transitions at a temperatur T between initial states with energy and final states with energy are given by
In Equation (9), the first factor contains Planck’s constant h as well as the speed of light c. Boltzmann’s constant is denoted by . Furthermore, g is the statistical weight (accounting for isotopical abundance), the squared transition dipole moment and the total internal partition function.
3. Results and Discussion
3.1. Construction of the PES and EDMS
As a first step in the development of the composite PES, the basis set convergence of the equilibrium bond lengths and and harmonic vibrational frequencies is investigated. Conventional CCSD(T) result with very large basis sets up to AV8Z are provided in Table 1. The AV7Z and AV8Z calculations have been perfomed with Dalton [115,116]. Results for explicitly correlated CCSD(T)-F12b and the triples scaled variant CCSD(T*)-F12b, i.e., the F12bs contribution, are provided as well. The CCSD(T) equilibrium bond lengths show a systematic convergence and the AV8Z are probably within about 0.00005 Å of the CBS limit. That is, no further extrapolation appears to be neccessary. The CCSD(T)-F12b results appear to slightly overshoot the AV8Z calculations. This is remedied by the triples scaling. Such behaviour has been observed previously for similar triatomic systems when using augmented basis sets [52].

Table 1.
Frozen-core CCSD(T) and CCSD(T)-F12b equilibrium bond lengths (in Å) and harmonic vibrational frequencies (in cm) for HCC.
The convergence of the harmonic vibrational frequencies is also graphically displayed in Figure 1. The F12bs results clearly are very close to the CBS limit and somewhat more consistent with the conventional CCSD(T) values than without triples scaling. In summary F12bs provides near-CBS quality results at a significantly reduced computational cost which is important when sampling a PES.
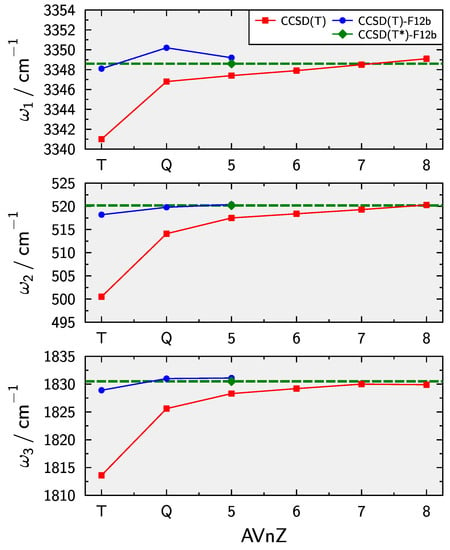
Figure 1.
Convergence of conventional CCSD(T) and explicitly correlated CCSD(T)-F12b harmonic vibrational frequencies for HCC.
The dependence of smaller contributions on the internal coordinates is presented in Figure 2. The dominant contribution for the stretching coordinates (upper panel) and (lower panel) are CV effects. Effects due to HC only show a slight dependence on the CH-stretch whereas they are still significant for and act in the opposite direction of the CV contribution. These trends are in line with what has been observed previously [44,45,46,47,48,49,50,51,52,53]. In case of the bending motion (inset lower panel) it is clear that the inclusion of (Q)–(T) is important with a contribution of about cm at . For comparison the isoelectronic HCS ion [51] yields a slightly larger value of cm.
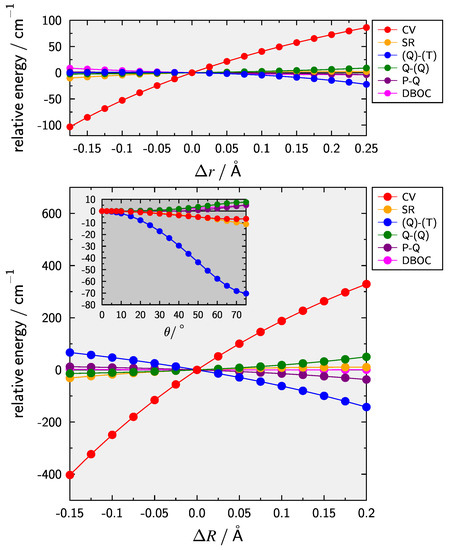
Figure 2.
Dependence of smaller contributions to the HCC composite PES on the internal coordinates (CH-stretch, upper panel), (CC-stretch, lower panel), and (deviation from linearity, inset lower panel). The DBOC contribution is depicted for the main isotopologue.
The impact of the smaller contributions on the equilibrium bond lengths and harmonic vibrational frequencies is presented in Table 2.

Table 2.
Dependence of equilibrium bond lengths (in Å) and harmonic vibrational frequencies (in cm) on the contributions to the composite PES of HCC.
While CV effects dominate the shifts in and , the combination of CV and HC is necessary for the CC-stretching and most importantly for the bending, in line with Figure 2. The total HC correction, i.e., the sum of the present three individual effects, amounts to +0.00007 and +0.00080 Å for and , respectively, as well as , , and cm for , , and , respectively. Comparing the full composite results to the basic F12bs the overall difference is significant for the bond lengths with changes of about and Å. In contrast, for the harmonic vibrational frequencies there is some amount of compensation between the different contributions, e.g., for the bending vibration F12bs and the composite PES differ only by about 1 cm and doesn’t exceed ∼6 cm for stretches. Nevertheless, when aiming at high-accuracy their inclusion is of course mandatory.
It is interesting to compare the composite results to those published earlier [32,33,34] (cf. lower part of Table 2). The results provided by Mladenović et al. are very close despite the fact that their employed theoretical level is only approximately ae-CCSD(T)/ACVQZ. While this is not surprising for the bond lengths which include a further empirical correction based on equivalent calculations for HCN, the harmonic vibrational frequencies provided by Mladenović et al. are within less than 1 cm compared to the present ones. Clearly this is due to fortuitous error compensation between the basis set incompleteness with ACVQZ and missing HC effects. The incompleteness error can be estimated by comparing the ae-CCSD(T)/ACVQZ harmonic frequencies with composite F12bs + CV, the latter of which should provide close to CBS limit. This yields values of , , and cm in almost perfect agreement with the shifts due to the summed HC effects given above. The results of Morgan and Fortenberry [34] can also be compared to the F12bs + CV + SR. At that level of theory the bond lengths are and Å which are larger than the F12bs + CV + SR results by 0.00046 and 0.00168 Å, respectively. Given the formally comparable level of theory this large difference is surprising. Moreover, while both methods yield almost identical results for and the CH-stretching harmonic vibrational frequency differs by 1.9 cm. This may suggest some numerical instabilities in the results of Morgan and Fortenberry since large differences in a bond length usually are associated with changes in the harmonic frequncies that are associated with that bond, i.e., the significant difference of 0.00168 Å in the CC bond length would suggest a larger deviation in the CC stretching which, however, is not observed.
In contrast to the good agreement with the comparatively lower level results of Mladenović et al., the results of Huang and Lee [33] show very large differences despite the fact that they account for similar corrections. Compared to the present composite PES, their and equilibrium bond lengths differ by as much as 0.00172 and 0.00081 Å, respectively and harmonic frequencies by 1.8, 16.5, and 6.0 cm for , and , respectively. As discussed in the introduction Huang and Lee constructed a composite QFF combining CBS extrapolated CCSD(T) results with smaller correction due to CV, SR, and HC effects. The latter were obtained as the difference between CBS-extrapolated ACPF and CCSD(T) calculations (termed 3-pt AC/AVXZ in Ref. [33]). A closer look at Table III in Ref. [33] shows that this way of approximating HC appears to overestimate the effects. For example the harmonic frequencies are shifted by , and cm for , and , respectively. These numbers are significantly different than the present HC effects by factors of about 1.5, 3.5 and 2.2, including a sign change for the CH-stretching contribution.
In order to rule out numerical issues due to the fitting procedure, graphical representations for 1D scans of the ACPF−CCSD(T) difference (including the same 3-pt CBS extrapolation as Huang and Lee [33,117]) along the internal coordinates , , and are provided in Figure 3. Furthermore, to check wether the problems are due to the treatment of dynamical correlation Figure 3 also shows results obtaind with multi-reference configuration interaction with singles and doubles [118,119,120,121,122] including the Davidson correction (MRCI+D) [123,124,125] and averaged quadratic coupled-cluster (AQCC) [126]. Finally, results obtained with explicitly correlated methods [127,128] and an AV5Z basis are also shown. From inspection of Figure 3 it is clear that, while there are subtle differences between ACPF, MRCI+D, and AQCC, none of the methods provides an accurate description of HC effects beyound CCSD(T). These difficulties could indicate that the actual problem is within the the reference used for the multi-reference approaches. It is well known that full-valence CASSCF can lead to problems in providing an appropriate active space. The reader is referred to the works by Veryazov et al. [129] as well as Stein and Reiher [130] for general discussions of this problem. Furthermore, the works of Makhnev et al. [131] on isoelectronic HCN and Schröder et al. [50] on nitrous oxide (NO) have highlighted this issue when constructing high-level ab initio PESs for triatomic systems. In summary, the HC contribution employed by Huang and Lee [33] based on the ACPF-CCSD(T) differenc is not recommended.
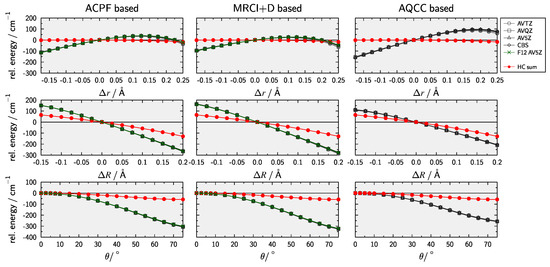
Figure 3.
Comparison of dependencies with respect to HCC internal coordinates for single reference and multi-reference based methods of calculating higher-order correlation contributions.
The final composite PES is constructed from 165 symmetry unique points for F12bs whereas a lower number of points—especially for the 2D and 3D coupling portion of the PES—is required to accurately determine the smaller contributions. These data points are available at GRO.data [132]. The least-squares fit according to Equation (1) employs up to powers of 8 and 10 for the diagonal stretching and bending monomials, respectively. For the 2D and 3D couping terms a total polynomial degree of 6 is found to be sufficient in the target energy regime. The residual error of the F12bs least-squares fit is 0.008 cm and even smaller for the individual contributions. Tables S1 and S2 in the Supplementary Materials provides the coefficients . The polynomial representations of the adiabatic PESs can be found in Table S3 of the Supplementary Materials.
Table 3 presents fc-CCSD(T) and fc-CCSD(T)-F12b results for the equilibrium dipole moment and band intensities of fundamental vibrational transitions for the main isotopologue. The negative sign for the dipole moment indicates the direction of the dipole vector pointing from the terminal C to the H atom, i.e., a polarity according to . Band intensities are obtained within the double harmonic approximation, i.e., harmonic wave function and linear dependency of the dipole moment with respect to normal coordinates. Using the present composite PES defines the harmonic wave function for the squared transition dipole moments. Both and the appear to be converged to within about 0.001 D and 0.2 km/mol or better, respectively, at the fc-CCSD(T)/AV6Z level of theory. The standard CCSD(T)-F12b and its triples scaled variant are very close to each other and match the conventional AV6Z results very well. An interesting observation regarding the stretching fundamentals can be made. While in isoelectronic HCN the CN-stretching band is very weak compared to the CH-stretching [133,134], the situation is reversed for HCC. In both systems the lower of the two streching band intensities results from a compensation effect of the dipole moment derivatives with respect to the (internal) stretching coordinates upon transformation to normal coordinates.

Table 3.
Frozen-core CCSD(T) and CCSD(T)-F12b equilibrium dipole moments (in D) and fundamental band intensities (double harmonic approximation, in km/mol) for HCC.
In Table 4 the numerical influence of the smaller contributions is given. All effects are rather small in absolute numbers which has also been observed previously by Schröder et al. [50] for NO. However, due to the small band intensity of the CH-stretching fundamental the relative change from F12bs (1.77 km/mol) to the composite result (2.27 km/mol) is almost 30%. The effect on the other band intensities is significantly lower. The final EDMS is determined from the same 165 points as employed for the PES. Least-squares fits according to Equation (2) were perfomed with terms up to a total polynomial degree of 5 yielding fitting residuals on the order of about 10 D for the individual contributions.

Table 4.
Dependence of the equilibrium dipole moment (in D) and fundamental band intensities (double harmonic approximation, in km/mol) on the contributions to the composite EDMF of HCC.
The coefficients are provided in Table S4 of the Supplementary Materials and the combined polynomial representation of the HCC EDMS can be found in Table S5.
3.2. Spectroscopic Parameters from VPT2
VPT2 allows a rather compact assessment of the influence of anharmonicity on the rovibrational spectrum due to straightforward formulae to calculate spectroscopic parameters. In turn, using VPT2 allows to take a more detailed look at the influence of smaller contributions. Table 5 presents results for the main isotopologue of HCC.

Table 5.
Dependence of spectroscopic parameters obtained from VPT2 on the contributions to the composite PES of HCC.
The commonly reported VPT2 based spectroscopic parameters and their change upon inclusion of the different effects are quoted. It is clear that the observation made for harmonic frequencies, i.e., a large degree of compensation between the contributions, is more pronounced for anharmonicity constants and subsequently for anharmonic corrections to vibrational transtion frequencies . However, for highly accurate rotational constants the inclusion of higher-order correlation appears to be mandatory. Overall the relative difference between the full composite PES and F12bs amounts to less than 1% on average, with the exception of which due to the very small value shows a large relative shift of more than 50%.
3.3. Results of Variational Calculations
The C8vpro outputs containing the lowest 90 variationally determined eigenvalues of the rovibrational Hamiltonian up to for HCC isotopologues are available from GRO.data [132]. In the following spectroscopic parameters and spectra determined from these calculations will be discussed. The only experimental spectroscopic information available for HCC has been obtained from rotational spectroscopy. Therefore the vibrational ground state is investigated first and Table 6 presents the relevant spectroscopic parameters for selected HCC isotopologues. For comparison the results of Brünken and coworkers [16] as well as Amano [26] are provided. The present theoretical rotational constants obtained from variational calculations agree to within about 0.005% with their experimental counterparts. Interestingly, the obtained from VPT2 of 41,637.8 MHz is even slightly closer to experiment. This changes when looking at the centrifugal distortion parameters. The variational results of 96.871, 92.581, and 90.080 kHz for H12C12C, H13C12C and, H12C13C, deviate from experiment by not more than 0.1%.

Table 6.
Zero-point vibrational energies (ZPVE, in cm) and rotational spectroscopic parameters (in MHz) for the ground vibrational state in istopologues of HCC obtained from variational calculations. Where available experimental results are provided for comparison a.
In contrast, VPT2 yields a value of 94.1 kHz for H12C12C, i.e., a deviation by 2.9% can be observed. As is well known, VPT2 based quartic centrifugal distortion constants for linear molecules do not include contributions from bending vibrations and lack effects due to vibrational averaging [45,135,136,137]. In their determination of the rotational spectroscopic parameters both experimental works [16,26] fixed to a value recommended by Sebald and Botschwina based on the PES reported earlier [32]. Clearly this value is a reasonable choice as the present calculations yield almost the same value based on a much more accurate PES. Finally, the ZPVE of 3078.0 cm calculated variationally for H12C12C is in perfect agreement with the VPT2 result as is expected for such a semi-rigid molecule.
It may appear tempting to use the results for HCC, HCC, and HCC to deduce a semi-experimental equilibrium structure. This is a well established approach [138,139,140,141,142,143,144,145] where the theoretically calculated difference is used to correct experimental ground state rotational parameters to obtain equilibrium values which then can be converted to an equilibrium geometry. However, the absence of data for deuterated isotopologues will make the determination of a semi-experimental questionable. The outlined approach yields values of Å and Å upon combination of the from experiment [25,26] with obtained from variational calculations. While the latter value is in perfect agreement with the ab initio result of 1.24621 Å, the difference of 0.00034 Å obtained for the is significantly larger than what has been observed previously [50,52]. Note that this way of calculating semi-experimental equilibrium structures can be used even for systems with strong rovibrational coupling yielding close agreement to high-level composite ab initio results (see, e.g., Ref. [52]). Nevertheless, considering the close agreement to the from experiment an updated recommended linear equilibrium structure with Å and Å appears to be appropriate, where a conservative error estimate in terms of the last significant digit is given in parentheses.
Calculated spectroscopic parameters for the singly excited states , , and are collected in Table 7. No experimental information is yet available for comparison and therefore these results stand as predictions. Spectroscopic parameters for additional selected rovibrational states in H12C12C are provided in Table S6 of the Supplementary Materials. Based on previous experience with similar molecules [46,47,49,50,51,52] the vibrational term energies are expected to be accurate to within 1 cm and rotational parameters should display the same level of accuracy as observed for the vibrational ground state. Comparing the variational results for in H12C12C with the corresponding composite VPT2 values for in Table 5 almost perfect agreement can be observed as expected for a semi-rigid molecule.

Table 7.
Vibrational term energies (in cm) and rotational spectroscopic parameters (in MHz) for singly excited vibrational states in istopologues of HCC obtained from variational calculations.
The fortuitous error compensation mentioned earlier for the results of Mladenović et al. [32] can also be extended to the anharmonic vibrational term energies. The latter authors obtained values (in cm) of 511.1, 1805.0, and 3211.3 for , , and , respectively, with an ae-CCSD(T) based PES to be compared with the present composite results of 510.1, 1804.5, and 3209.6. In contrast, the rotational parameters calculated by Mladenović et al. [32] are less accurate than the present results which can be traced back to differences in the equilibrium geometry used by these authors in their rovibrational calculations ( Å and Å).
The state of the deuterated isotopologues shows signs of an anharmonic resonance. This can be inferred from the anomalous large values of and by comparing the effective with VPT2 results. The latter values (in MHz) are calculated from the variational calculations to be 284.6, 268.9, and 206.3, for D12C12C, D13C12C, and D12C13C, respectively, to be compared with the VPT2 results of 301.0, 282.2, and 286.2. Note that for H12C12C this analysis yields 299.0 MHz and 295.7 from variational calculations and VPT2, respectively, in good agreement. Upon inspection of the rovibrational wave functions the state is identified as the perturbing state. The energetic situation is graphically depicted in Figure 4. Such a 1-3 Darling-Dennison resonance [107,146,147] can be analyzed in terms of the vibrational term energies by setting up an effective Hamiltonian of the form
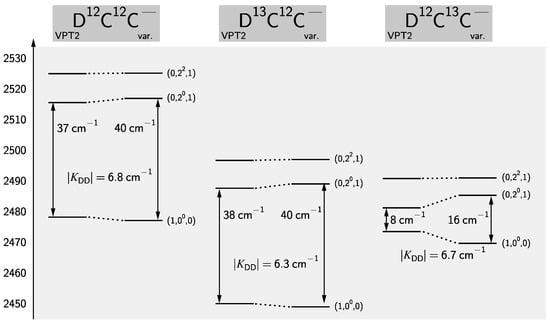
Figure 4.
Energy level scheme of and vibrational states involved in the 1-3 Darling-Dennison resonance in DCC isotopologues.
In Equation (10), are so-called “deperturbed” vibrational term energies and is the Darling-Dennison coupling matrix element. From two perturbed term energies of the and states alone one can not determine the three parameters in the effective Hamiltonian of Equation (10). However, given the excellent agreement between VPT2 and the variational calculations observed for HCC one can fix the to the perturbational results 2478.2, 2449.9, and 2473.4 cm for D12C12C, D13C12C, D12C13C, respectively. This yields values of 2515.7, 2488.0, and 2481.5 cm, to be compared with the VPT2 results of 2515.5, 2487.6, and 2481.2, for D12C12C, D13C12C, D12C13C, respectively, showing good agreement. The coupling constants differ only slightly between the isotopologues (cf. also Figure 4) with an average value of 6.6 cm. For a full analysis, i.e., for a deperturbation of rotational parameters, the effective Hamiltonian from Equation (10) would need to be extended to allow for the simultaneous ℓ-type resonance between and the state with e-parity [51]. However, no attempt in that direction has been undertaken here and therefore the parameters for DCC isotopologues have to be treated as effective parameters.
The ground state dipole moment of HCC is calculated to be −3.100 D very close to the earlier results of Mladenović et al. [32] Comparing and from Table 4 one finds that the vibrational averaging reduces the absolute value by 0.121 D or 4 %. The latter quantity can also be evaluated through 2nd order via the differences . Using the dipole moments from the variational calculations of the vibrational states (3.054 D), (3.014 D), and (3.073 D), one arrives at 0.096 D in good agreement. The remaining difference is probably due to higher-order contributions. In contrast, H/D substitution changes by 11 % (DCC3.431 D) which is predominantly due to the change in the equilibrium dipole moment which has to be considered for charged species. Similar results have been obtained previously for isoelecronic HCS by Schröder and Sebald [51].
Finally, rovibrational line intensities for the fundamental transitions were obtained following Equation (9). At K the total internal partition function amounts to 180.33 for the main isotopologue, based on the present rovibrational calculations. Results for other isotopologues as well as different temperatures are collected in the Supplementary Materials Table S7. Figure 5 compares stick spectra for the fundamental transtions in HCC and DCC. Note that g in Equation (9) has been set to 1 to allow for direct comparison. The band is found to be the most intense fundamental transition followed by the CC-stretching which is weaker by a factor of about 2. These results are in line with the spectra calculated by Mladenovic et al. [32]. In all cases exchanging H for D reduces the intensities.
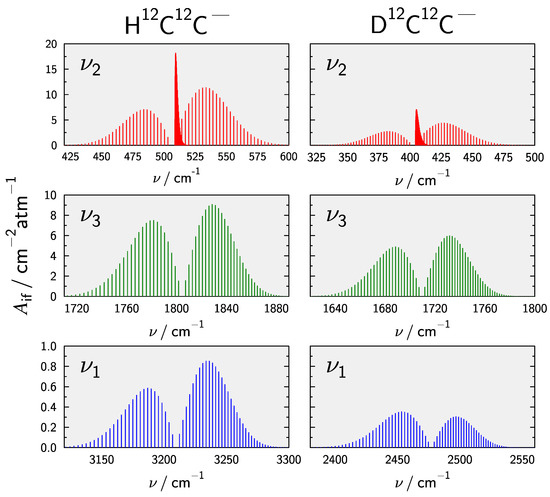
Figure 5.
Comparison of stick spectra for the fundamental rovibrational transitions in HCC and DCCat K. Line intensities are have been calculated using Equation (9) with to facilitate a direct comparison.
An interesting effect can be observed for the band, where upon H/D substitution the intensity ratio of the P- and R-branch reverses. Note that Mladenovic et al. [32] predicted this reversed intensity ratio also for the main isotopologue (cf. Figure 2 of Ref. [32]) but the present calculations based upon a highly accurate PES and EDMS do not reproduce this observation. To understand the intensity pattern a closer look at the squared transition dipole moment is necessary. This quantity can be approximated according to [148]
where is the vibrational transition moment, the Hönl-London factor [149,150], and the Herman-Wallis factor [151]. The latter quantity can be written as
where m is or for P- and R-branch transitions, respectively, and according to Watson [152] the coefficient for a parallel fundamental band within VPT2 is found to be
In Equation (13), indices s and t label stretching and degenerate bending normal modes, respectively. The two terms correspond to two effects responsible for the m-dependence of the effective transition moment; while the first term describes mixing with the rotational spectrum, the second term is due to Coriolis coupling of the stretching with the bending fundamental band. The are rotational derivatives [97], the Coriolis coupling constants and the first derivative of the dipole moment with respect to the dimensionless normal coordinate . With the present PES and EDMS one obtains 0.012 and for coefficient of the band in HCC and DCC, respectively. From the variationally calculated application of Equations (11) and (12) also allows the determination of through least-squares fitting resulting in slightly smaller values of 0.0072 and , in the previous ordering of isotopologues. The change of sign is responsible for the inverted P/R intensity ratio and upon inspection of the contributions to in Equation (13) is due to a change of sign of the dipole moment derivative upon H/D substitution.
It is clear that the most promising target for the detection of HCC will be the bending fundamental. Therefore the spectrum at K in the relevant range is presented in Figure 6. The spectrum includes additional hot bands, i.e., and as well as the same bands for all singly C substituted isotopologues in natural abundance. The spectra of H13C12C and H12C13C are weaker by a factor of 100 in agreement with the reduced abundance of C. Both Q-branches of the bands in the C isotopologues are located inbetween the P- and Q-branch of H12C12C and thus might be possible to detect. Hot bands of H12C12C have slightly larger intensity compared to the other isotopologue bands and should therefor also be observable.
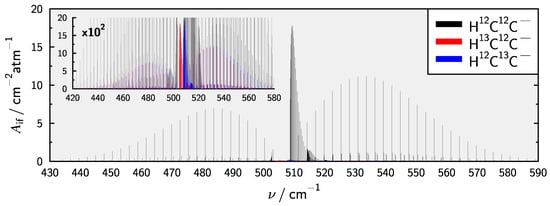
Figure 6.
Calculated stick spectrum in the spectral region of the fundamental for HCC and its C isotopologues at K. Additional hot bands originating from the state and the manifold are also included.
In order to facilitate future experimental work, Table S8 in the Supplementary Materials collects band intensities for a number of overtones, combination bands as well as hot bands in H12C12C. These have been obtained by summing over individual rovibrational lines within a given vibrational transition.
4. Summary
The present work provided a thorough theoretical invesitgation into the rovibrational spectrum of the acetylide anion (HCC) and its isotopologues. An ab initio potential energy surface (PES) and electric dipole moment surface (EDMS) was constructed by a high-level composite procedure within the framework of coupled-cluster theory. Explicitly correlated CCSD(T)-F12b results have been combined with corrections due to core-valence correlation, scalar-relativistic effects, and higher-order correlation (HC). The latter accounted for effects up to pentuple excitation (CCSDTQP) and was found to be necessary to converge the quality of the PES to the target accuracy of 1 cm in the fundamental vibrational transitions. Comparison with previous results based on multi-reference averaged coupled-pair functional (ACPF) calculations have shown the latter as well as other multi-reference based approaches to be significantly lacking in the accurate description of dynamic HC effects.
Variational calculations employing the present PES and EDMS provide spectroscopic parameters for the vibrational ground state as well as the singly excited states. Comparison with the scarce experimental data shows excellent agreement, i.e., the ground state rotational parameters and agree to within 0.005% and 0.1%. For the excited states the present spectroscopic parameters should provide reliable estimates for future experimental spectroscopic investigations. In case of the deuterated species DCC a 1–3 Darling-Dennison resonance between the CD-stretching state and the component of the ℓ-type resonance coupled combination state has been identified. However, due to the rather low intensity of the CD as well as the CH fundamental transition these bands will probably be difficult to detect experimentally. The most promising band (bending) should be observable around 510 cm and is more intens by a factor of 10–20 compared to the band.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28155700/s1, Table S1: Fitted polynomial coefficients of the mass-independent individual contributions to the potential energy surface for HCC; Table S2: Diagonal Born-Oppenheimer correction contributions to the composite potential energy surface for HCC isotopologues; Table S3: Polynomial coefficients of the final adiabatic potential energy surfaces for HCC isotopologues; Table S4: Fitted polynomial coefficients of the individual contributions to the electric dipole moment surface for HCC; Table S5: Polynomial coefficients of the final electric dipole moment surface for HCC; Table S6: Additional spectroscopic parameters for vibrationally excited states in the main isotopologue of HCC; Table S7: Temperature dependant internal partition function values for HCC isotopologues; Table S8: band intensities determined from the variational calculations for the HCC main isotopologue.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)-389479699/GRK2455.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from GRO.data (doi:10.25625/YBLAAU) [132]. This includes the raw ab initio points used in the construction of the composite potential energy surfaces and electric dipole moment surface as well as the outputs of the C8vpro program [109] used for the variational calculations. Within the latter the lowest 90 eigenvalues of the rovibrational Hamiltonian up to in both e and f-parity can be found. Furthermore, a line list for a number of rotational and rovibrational bands in the main isotopologue of HCC has also been deposited with GRO.data. Additional results are included in the article Supplementary Materials (for details see above).
Acknowledgments
Ricardo A. Mata and Peter Sebald are gratefully acknowledged for helpful discussions. Support by the Open Access Publication Funds of the Göttingen University is kindly acknowledged.
Conflicts of Interest
The author declares no conflict of interest.
Sample Availability
Not applicable.
Abbreviations
The following abbreviations are used in this manuscript:
| ae | all-electron |
| fc | frozen core |
| PES | potential energy surface |
| QFF | quartic force field |
| EDMS | electric dipole moment surface |
| CBS | complete basis set |
| CASSCF | complete active space self-consistent field |
| CCSD(T) | coupled-cluster with single, double, and perturbative triple excitations |
| CCSD(T*)-F12b | explicitly correlated coupled-cluster with single, double, and scaled perturbative triple excitations |
| CCSDT(Q) | coupled-cluster with single, double, triple and perturbative quadruple excitations |
| CCSDTQ | coupled-cluster with single, double, triple and quadruple excitations |
| CCSDTQP | coupled-cluster with single, double, triple, quadruple and pentuple excitations |
| ACPF | averaged coupled-pair functional |
| MRCI+D | multi-reference configuration interaction with singles and doubles including the Davidson correction |
| AQCC | averaged quadratic coupled-cluster |
| CV | core-core and core-valence correlation |
| SR | scalar-relativistic effects |
| HC | higher-order correlation |
| (Q)–(T) | difference between fc-CCSDT(Q) and fc-CCSD(T) |
| Q–(Q) | difference between fc-CCSDTQ and fc-CCSDT(Q) |
| P–Q | difference between fc-CCSDTQP and fc-CCSDTQ |
| DBOC | diagonal Born-Oppenheimer correction |
| VPT2 | second-order vibrational perturbation theory |
| ZPVE | zero-point vibrational energy |
References
- Müller, H.S.P.; Thorwirth, S.; Roth, D.A.; Winnewisser, G. The Cologne Database for Molecular Spectroscopy, CDMS. Astron. Astrophys. 2001, 370, L49–L52. [Google Scholar] [CrossRef]
- Müller, H.S.P.; Schlöder, F.; Stutzki, J.; Winnewisser, G. The Cologne Database for Molecular Spectroscopy, CDMS: A useful tool for astronomers and spectroscopists. J. Mol. Struct. 2005, 742, 215–227. [Google Scholar] [CrossRef]
- Endres, C.P.; Schlemmer, S.; Schilke, P.; Stutzki, J.; Müller, H.S.P. The Cologne Database for Molecular Spectroscopy, CDMS, in the Virtual Atomic and Molecular Data Centre, VAMDC. J. Mol. Spectrosc. 2016, 327, 95–104. [Google Scholar] [CrossRef]
- McGuire, B.A. 2018 Census of Interstellar, Circumstellar, Extragalactic, Protoplanetary Disk, and Exoplanetary Molecules. Astrophys. J. Suppl. Ser. 2018, 239, 17. [Google Scholar] [CrossRef]
- McGuire, B.A. 2021 Census of Interstellar, Circumstellar, Extragalactic, Protoplanetary Disk, and Exoplanetary Molecules. Astrophys. J. Suppl. Ser. 2022, 259, 30. [Google Scholar] [CrossRef]
- Fortenberry, R.C. Interstellar Anions: The Role of Quantum Chemistry. J. Phys. Chem. A 2015, 119, 9941–9953. [Google Scholar] [CrossRef]
- Fortenberry, R.C. Quantum astrochemical spectroscopy. Int. J. Quant. Chem. 2017, 117, 81–91. [Google Scholar] [CrossRef]
- Biczysko, M.; Bloino, J.; Puzzarini, C. Computational challenges in Astrochemistry. WIRES Comput. Mol. Sci. 2018, 8, e1349. [Google Scholar] [CrossRef]
- Fortenberry, R.C.; Lee, T.J. Computational vibrational spectroscopy for the detection of molecules in space. In Annual Reports in Computational Chemistry; Dixon, D.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 15, pp. 173–202. [Google Scholar]
- Puzzarini, C.; Bloino, J.; Tasinato, N.; Barone, V. Accuracy and Interpretability: The Devil and the Holy Grail. New Routes across Old Boundaries in Computational Spectroscopy. Chem. Rev. 2019, 119, 8131–8191. [Google Scholar] [CrossRef]
- Puzzarini, C. Grand Challenges in Astrochemistry. Front. Astron. Space Sci. 2020, 7, 8–11. [Google Scholar] [CrossRef]
- Fortenberry, R.C.; Lee, T.J. Vibrational and Rovibrational Spectroscopy Applied to Astrochemistry. In Vibrational Dynamics of Molecules; Bowman, J.M., Ed.; World Scientific Publishing: Singapore, 2022; Chapter 7; pp. 235–295. [Google Scholar]
- Millar, T.J.; Walsh, C.; Field, T.A. Negative Ions in Space. Chem. Rev. 2017, 117, 1765–1795. [Google Scholar] [CrossRef] [PubMed]
- Kawaguchi, K.; Kasai, Y.; Ishikawa, S.I.; Kaifu, N. A Spectral-Line Survey Observation of IRC +10216 between 28 and 50 GHz. Publ. Astron. Soc. Jpn. 1995, 47, 853–876. [Google Scholar]
- McCarthy, M.C.; Gottlieb, C.A.; Gupta, H.; Thaddeus, P. Laboratory and Astronomical Identification of the Negative Molecular Ion C6H−. Astrophys. J. 2006, 652, L141. [Google Scholar] [CrossRef]
- Brünken, S.; Gupta, H.; Gottlieb, C.A.; McCarthy, M.C.; Thaddeus, P. Detection of the Carbon Chain Negative Ion C8H− in TMC-1. Astrophys. J. 2007, 664, L43. [Google Scholar] [CrossRef]
- Remijan, A.J.; Hollis, J.M.; Lovas, F.J.; Cordiner, M.A.; Millar, T.J.; Markwick-Kemper, A.J.; Jewell, P.R. Detection of C8H− and Comparison with C8H toward IRC+10216. Astrophys. J. 2007, 664, L47. [Google Scholar] [CrossRef]
- Cernicharo, J.; Guélin, M.; Agúndez, M.; Kawaguchi, K.; McCarthy, M.; Thaddeus, P. Astronomical detection of C4H−, the second interstellar anion. Astron. Astrophys. 2007, 467, L37–L40. [Google Scholar] [CrossRef]
- Remijan, A.; Scolati, H.N.; Burkhardt, A.M.; Changala, P.B.; Charnley, S.B.; Cooke, I.R.; Cordiner, M.A.; Gupta, H.; Herbst, E.; Lee, K.L.K.; et al. Astronomical Detection of the Interstellar Anion C10H− toward TMC-1 from the GOTHAM Large Program on the Green Bank Telescope. Astrophys. J. Lett. 2023, 944, L45. [Google Scholar] [CrossRef]
- Morisawa, Y.; Hoshina, H.; Kato, Y.; Simizu, Z.; Kuma, S.; Sogoshi, N.; Fushitani, M.; Watanabe, S.; Miyamoto, Y.; Momose, T.; et al. Search for CCH−, NCO−, and NCS− Negative Ions in Molecular Clouds. Publ. Astron. Soc. Jpn. 2005, 57, 325–334. [Google Scholar] [CrossRef]
- Agundez, M.; Cernicharo, J.; Guelin, M.; Gerin, M.; McCarthy, M.C.; Thaddeus, P. Search for anions in molecular sources: C4H− detection in L1527. Astron. Astrophys. 2008, 478, L19–L22. [Google Scholar] [CrossRef]
- Cordiner, M.A.; Millar, T.J.; Walsh, C.; Herbst, E.; Lis, D.C.; Bell, T.A.; Roueff, E. Organic molecular anions in interstellar and circumstellar environments. In Proceedings of the Organic Matter in Space; Kwok, S., Sanford, S., Eds.; Cambridge University Press: Cambridge, UK, 2008; Volume 251, pp. 157–160. [Google Scholar]
- Herbst, E.; Osamura, Y. Calculations on the Formation Rates and Mechanisms for CnH Anions in Interstellar and Circumstellar Media. Astrophys. J. 2008, 679, 1670. [Google Scholar] [CrossRef]
- Lara-Moreno, M.; Stoecklin, T.; Halvick, P. Radiative Electron Attachment and Photodetachment Rate Constants for Linear Carbon Chains. ACS Earth Space Chem. 2019, 3, 1556–1563. [Google Scholar] [CrossRef]
- Brünken, S.; Gottlieb, C.A.; Gupta, H.; McCarthy, M.C.; Thaddeus, P. Laboratory detection of the negative molecular ion CCH−. Astron. Astrophys. 2007, 464, L33–L36. [Google Scholar] [CrossRef]
- Amano, T. Extended negative glow and “hollow anode” discharges for submillimeter-wave observation of CN−, C2H−, and C4H−. J. Chem. Phys. 2008, 129, 244305. [Google Scholar] [CrossRef] [PubMed]
- Ervin, K.M.; Lineberger, W.C. Photoelectron Spectra of C2− and C2H−. J. Phys. Chem. 1991, 95, 1167–1177. [Google Scholar] [CrossRef]
- Lee, T.J.; Schaefer, H.F., III. Systematic study of molecular anions within the self-consistent-field approximation: OH−, CN−, C2H−, NH2−, and CH3−. J. Chem. Phys. 1985, 83, 1784–1794. [Google Scholar] [CrossRef]
- Botschwina, P. Anharmonic potential-energy surfaces, vibrational frequencies and infrared intensities calculated from highly correlated wavefunctions. J. Chem. Soc. Faraday Trans. 2 1988, 84, 1263–1276. [Google Scholar] [CrossRef]
- Botschwina, P. Spectroscopic properties of polyatomic cations and anions from ab initio calculations. In Ion and Cluster-Ion Spectroscopy and Structure; Maier, J.P., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 12, pp. 47–78. [Google Scholar]
- Botschwina, P.; Seeger, S.; Mladenović, M.; Schulz, B.; Horn, M.; Schmatz, S.; Flügge, J.; Oswald, R. Quantum-chemical investigations of small molecular anions. Int. Rev. Phys. Chem. 1995, 14, 169–204. [Google Scholar] [CrossRef]
- Mladenović, M.; Botschwina, P.; Sebald, P.; Carter, S. A theoretical study of the acetylide anion, HCC−. Theor. Chem. Acc. 1998, 100, 134–146. [Google Scholar] [CrossRef]
- Huang, X.; Lee, T.J. Accurate ab initio quartic force fields for NH2− and CCH− and rovibrational spectroscopic constants for their isotopologs. J. Chem. Phys. 2009, 131, 104301. [Google Scholar] [CrossRef]
- Morgan, W.J.; Fortenberry, R.C. Theoretical Rovibronic Treatment of the Σ+ and 2Π states of C2H and the 1Σ+ State of C2H− from Quartic Force Fields. J. Phys. Chem. A 2015, 119, 7013–7025. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Gruebele, M.; Polak, M.; Saykally, R.J. Diode laser velocity modulation spectroscopy of carbanions: The CC stretching vibration of C2H−. J. Chem. Phys. 1987, 87, 1448–1449. [Google Scholar] [CrossRef]
- Carter, S.R.; Mills, I.M.; Handy, N.C. The equilibrium structure of HCN. J. Chem. Phys. 1992, 97, 1606–1607. [Google Scholar] [CrossRef]
- Gdanitz, R.J.; Ahlrichs, R. The averaged coupled-pair functional (ACPF): A size-extensive modification of MR CI(SD). Chem. Phys. Lett. 1988, 143, 413–420. [Google Scholar] [CrossRef]
- Roos, B.O.; Taylor, P.R.; Sigbahn, P.E.M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
- Schwenke, D.W. On the computation of ro-vibrational energy levels of triatomic molecules. Comput. Phys. Commun. 1992, 70, 1–14. [Google Scholar] [CrossRef]
- Carter, S.; Bowman, J.M.; Handy, N.C. Extensions and tests of MULTIMODE: A code to obtain accurate vibration/rotation energies of many-mode molecules. Theor. Chem. Acc. 1998, 100, 191–198. [Google Scholar] [CrossRef]
- Bowman, J.M.; Carter, S.; Huang, X. MULTIMODE: A code to calculate rovibrational energies of polyatomic molecules. Int. Rev. Phys. Chem. 2003, 22, 533–549. [Google Scholar] [CrossRef]
- Fortenberry, R.C.; Huang, X.; Francisco, J.S.; Crawford, T.D.; Lee, T.J. The trans-HOCO radical: Quartic force fields, vibrational frequencies, and spectroscopic constants. J. Chem. Phys. 2011, 135, 134301. [Google Scholar] [CrossRef] [PubMed]
- Sebald, P.; Stein, C.; Oswald, R.; Botschwina, P. Rovibrational States of N3− and CO2 Up to High J: A Theoretical Study Beyond fc-CCSD(T). J. Phys. Chem. A 2013, 117, 13806–13814. [Google Scholar] [CrossRef] [PubMed]
- Botschwina, P.; Stein, C.; Sebald, P.; Schröder, B.; Oswald, R. Strong theoretical support for the assignment of B11244 to l-C3H+. Astrophys. J. 2014, 787, 72. [Google Scholar] [CrossRef]
- Botschwina, P.; Sebald, P.; Schröder, B.; Bargholz, A.; Kawaguchi, K.; Amano, T. Rovibrational states of HBF+ isotopologues: Theory and experiment. J. Mol. Spectrosc. 2014, 302, 3–8. [Google Scholar] [CrossRef]
- Botschwina, P.; Bargholz, A.; Sebald, P.; Schröder, B.; Oswald, R. Theoretical rovibrational spectroscopy of NO2+. J. Mol. Spectrosc. 2015, 311, 12–18. [Google Scholar] [CrossRef]
- Stein, C.; Weser, O.; Schröder, B.; Botschwina, P. High-level theoretical spectroscopic parameters for three ions of astrochemical interest. Mol. Phys. 2015, 113, 2169–2178. [Google Scholar] [CrossRef]
- Schröder, B.; Weser, O.; Sebald, P.; Botschwina, P. Theoretical rovibrational spectroscopy beyond fc-CCSD(T): The cation CNC+. Mol. Phys. 2015, 113, 1914–1923. [Google Scholar] [CrossRef]
- Schröder, B.; Sebald, P.; Stein, C.; Weser, O.; Botschwina, P. Challenging High-Level ab initio Rovibrational Spectroscopy: The Nitrous Oxide Molecule. Z. Phys. Chem. 2015, 229, 1663–1690. [Google Scholar] [CrossRef]
- Schröder, B.; Sebald, P. High-level theoretical rovibrational spectroscopy of HCS+ isotopologues. J. Mol. Spectrosc. 2016, 330, 120–129. [Google Scholar] [CrossRef]
- Schröder, B.; Sebald, P. High-level theoretical rovibrational spectroscopy beyond fc-CCSD(T): The C3 molecule. J. Chem. Phys. 2016, 144, 044307. [Google Scholar] [CrossRef] [PubMed]
- Schröder, B.; Sebald, P. Variational rovibrational calculations for tetra atomic linear molecules using Watson’s isomorphic Hamiltonian: II. The B11244 story retold. J. Mol. Spectrosc. 2022, 386, 111628. [Google Scholar] [CrossRef]
- Feller, D.; Peterson, K.A.; Dixon, D.A. A survey of factors contributing to accurate theoretical predictions of atomization energies and molecular structures. J. Chem. Phys. 2008, 129, 204105. [Google Scholar] [CrossRef] [PubMed]
- Feller, D.; Peterson, K.A.; Dixon, D.A. Refined Theoretical Estimates of the Atomization Energies and Molecular Structures of Selected Small Oxygen Fluorides. J. Phys. Chem. A 2010, 114, 613–623. [Google Scholar] [CrossRef] [PubMed]
- Feller, D.; Peterson, K.A.; Dixon, D.A. Chemical accuracy in ab initio thermochemistry and spectroscopy: Current strategies and future challenges. Theor. Chem. Acc. 2012, 131, 1079. [Google Scholar]
- Feller, D.; Peterson, K.A.; Dixon, D.A. Further benchmarks of a composite, convergent, statistically calibrated coupled-cluster-based approach for thermochemical and spectroscopic studies. Mol. Phys. 2012, 110, 2381–2399. [Google Scholar] [CrossRef]
- Dixon, D.A.; Feller, D.; Peterson, K.A. A Practical Guide to Reliable First Principles Computational Thermochemistry Predictions Across the Periodic Table. In Annual Reports in Computational Chemistry; Wheeler, R.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2012; Volume 8, pp. 1–28. [Google Scholar]
- Feller, D.; Peterson, K.A.; Ruscic, B. Improved accuracy benchmarks of small molecules using correlation consistent basis sets. Theor. Chem. Acc. 2014, 133, 1407. [Google Scholar] [CrossRef]
- Feller, D.; Peterson, K.A.; Dixon, D.A. The Impact of Larger Basis Sets and Explicitly Correlated Coupled Cluster Theory on the Feller–Peterson–Dixon Composite Method. In Annual Reports in Computational Chemistry; Dixon, D.A., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 12, pp. 47–78. [Google Scholar]
- Adler, T.B.; Knizia, G.; Werner, H.J. A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 2007, 127, 221106. [Google Scholar] [CrossRef] [PubMed]
- Knizia, G.; Adler, T.B.; Werner, H.J. Simplified CCSD(T)-F12 methods: Theory and benchmarks. J. Chem. Phys. 2009, 130, 054104. [Google Scholar] [CrossRef]
- Werner, H.; Knizia, G.; Adler, T.B.; Marchetti, O. Benchmark Studies for Explicitly Correlated Perturbation- and Coupled Cluster Theories. Z. Phys. Chem. 2010, 224, 493–511. [Google Scholar] [CrossRef]
- Dunning, T. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Yousaf, K.E.; Peterson, K.A. Optimized complementary auxiliary basis sets for explicitly correlated methods: Auc-cc-pVnZ orbital basis sets. Chem. Phys. Lett. 2009, 476, 303–307. [Google Scholar] [CrossRef]
- Weigend, F. A fully direct RI-HF algorithm: Implementation, optimised auxiliary basis sets, demonstration of accuracy and efficiency. Phys. Chem. Chem. Phys. 2002, 4, 4285–4291. [Google Scholar] [CrossRef]
- Hättig, C. Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations: Core–valence and quintuple-ζ basis sets for H to Ar and QZVPP basis sets for Li to Kr. Phys. Chem. Chem. Phys. 2005, 7, 59–66. [Google Scholar] [CrossRef]
- Peterson, K.A.; Adler, T.B.; Werner, H.J. Systematically convergent basis sets for explicitly correlated wavefunctions: The atoms H, He, B–Ne, and Al–Ar. J. Chem. Phys. 2008, 128, 084102. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys 1995, 103, 4572–4585. [Google Scholar] [CrossRef]
- Douglas, M.; Kroll, N.M. Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. 1974, 82, 89–155. [Google Scholar] [CrossRef]
- Hess, B.A. Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. A 1986, 33, 3742–3748. [Google Scholar] [CrossRef] [PubMed]
- de Jong, W.A.; Harrison, R.J.; Dixon, D.A. Parallel Douglas–Kroll energy and gradients in NWChem: Estimating scalar relativistic effects using Douglas–Kroll contracted basis sets. J. Chem. Phys. 2001, 114, 48–53. [Google Scholar] [CrossRef]
- Bomble, Y.L.; Stanton, J.F.; Kállay, M.; Gauss, J. Coupled-Cluster methods including noniterative corrections for quadriuple excitations. J. Chem. Phys. 2005, 123, 054101. [Google Scholar] [CrossRef]
- Kállay, M.; Surján. Higher excitations in Coupled-Cluster theory. J. Chem. Phys. 2001, 115, 2945–2954. [Google Scholar] [CrossRef]
- Karton, A.; Taylor, P.R.; Martin, J.M.L. Basis set convergence of post-CCSD contributions to molecular atomization energies. J. Chem. Phys. 2007, 127, 064104. [Google Scholar] [CrossRef]
- Karton, A. Post-CCSD(T) contributions to total atomization energies in multireference systems. J. Chem. Phys. 2018, 149, 034102. [Google Scholar] [CrossRef] [PubMed]
- Karton, A. Basis set convergence of high-order coupled cluster methods up to CCSDTQ567 for a highly multireference molecule. Chem. Phys. Lett. 2019, 737, 136810. [Google Scholar] [CrossRef]
- Karton, A. Effective basis set extrapolations for CCSDT, CCSDT(Q), and CCSDTQ correlation energies. J. Chem. Phys. 2020, 153, 024102. [Google Scholar] [CrossRef] [PubMed]
- Handy, N.C.; Yamaguchi, Y.; Schaefer, H.F. The diagonal correction to the Born–Oppenheimer approximation: Its effect on the singlet–triplet splitting of CH2 and other molecular effects. J. Chem. Phys. 1986, 84, 4481–4484. [Google Scholar] [CrossRef]
- Kutzelnigg, W. The adiabatic approximation I. The physical background of the Born-Handy ansatz. Mol. Phys. 1997, 90, 909–916. [Google Scholar] [CrossRef]
- Gauss, J.; Tajti, A.; Kállay, M.; Stanton, J.F.; Szalay, P. Analytic calculation of the diagonal Born-Oppenheimer correction within configuration-interaction and coupled-cluster theory. J. Chem. Phys. 2006, 125, 144111. [Google Scholar] [CrossRef]
- Stanton, J.F.; Gauss, J.; Cheng, L.; Harding, M.E.; Matthews, D.A.; Szalay, P.G. Cfour, Coupled-Cluster Techniques for Computational Chemistry, a Quantum-Chemical Program Package. Available online: http://www.cfour.de (accessed on 21 July 2023).
- Matthews, D.A.; Cheng, L.; Harding, M.E.; Lipparini, F.; Stopkowicz, S.; Jagau, T.C.; Szalay, P.G.; Gauss, J.; Stanton, J.F. Coupled-cluster techniques for computational chemistry: The CFOUR program package. J. Chem. PHys. 2020, 152, 214108. [Google Scholar] [CrossRef] [PubMed]
- Werner, H.J.; Knowles, P.J.; Celani, P.; Györffy, W.; Hesselmann, A.; Kats, D.; Knizia, G.; Köhn, A.; Korona, T.; Kreplin, D.; et al. Molpro 2022.1, A Package of Ab Initio Programs. Available online: https://www.molpro.net (accessed on 21 July 2023).
- Werner, H.J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J.; Manby, F.R.; Black, J.A.; Doll, K.; Heßelmann, A.; Kats, D.; Köhn, A.; Korona, T.; Kreplin, D.A.; et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020, 152, 144107. [Google Scholar] [CrossRef]
- Kállay, M.; Nagy, P.R.; Mester, D.; Gyevi-Nagy, L.; Csóka, J.; Szabó, P.B.; Rolik, Z.; Samu, G.; Csontos, J.; Hégely, B.; et al. Mrcc, A Quantum Chemical Program Suite. Available online: https://www.mrcc.hu (accessed on 21 July 2023).
- Kállay, M.; Nagy, P.R.; Mester, D.; Rolik, Z.; Samu, G.; Csontos, J.; Csóka, J.; Szabó, P.B.; Gyevi-Nagy, L.; Hégely, B.; et al. The MRCC program system: Accurate quantum chemistry from water to proteins. J. Chem. Phys. 2020, 152, 074107. [Google Scholar] [CrossRef]
- Eckart, C. Some Studies Concerning Rotating Axes and Polyatomic Molecules. Phys. Rev. 1935, 47, 552–558. [Google Scholar] [CrossRef]
- Sayvetz, A. The Kinetic Energy of Polyatomic Molecules. J. Chem. Phys. 1939, 7, 383–389. [Google Scholar] [CrossRef]
- Hougen, J.T. Rotational Energy Levels of a Linear Triatomic Molecule in a 2Π Electronic State. J. Chem Phys. 1962, 36, 519–534. [Google Scholar] [CrossRef]
- Watson, J.K.G. The vibration-rotation Hamiltonian of linear molecules. Mol. Phys. 1970, 19, 465–487. [Google Scholar] [CrossRef]
- Nielsen, H.H. The Vibration-rotation Energies of Molecules and their Spectra in the Infra-red. In Handbuch Der Physik; Flügge, S., Ed.; Springer: Berlin/Heidelberg, Germany, 1959; Volume 37, Pt. I, pp. 173–313. [Google Scholar]
- Amat, G.; Nielsen, H.H.; Tarrago, G. Rotation-Vibration of Polyatomic Molecules; Dekker: New York, NY, USA, 1971. [Google Scholar]
- Papoušek, D.; Aliev, M.R. Molecular Vibrational-Rotational Spectra: Theory and Applications of High Resolution Infrared, Microwave and Raman Spectroscopy of Polyatomic Molecules; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Aliev, M.R.; Watson, J.K.G. Higher-order effects in the vibration-rotation spectra of semirigid molecules. In Molecular Spectroscopy: Modern Research; Rao, K.N., Ed.; Academic Press: Cambridge, MA, USA, 1985; pp. 1–67. [Google Scholar]
- Whitehead, R.J.; Handy, N.C. Vari1ational calculation of vibration-rotation energy levels for triatomic molecules. J. Mol. Spectrosc. 1975, 55, 356–373. [Google Scholar] [CrossRef]
- Carney, G.D.; Sprandel, L.L.; Kern, C.W. Variational Approaches to Vibration-Rotation Spectroscopy for Polyatomic Molecules. In Advances in Chemical Physics; Prigogine, I., Rice, S.A., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1978; Volume 37, pp. 305–379. [Google Scholar]
- Bowman, J.M.; Carrington, T.; Meyer, H.D. Variational quantum approaches for computing vibrational energies of polyatomic molecules. Mol. Phys. 2008, 106, 2145–2182. [Google Scholar] [CrossRef]
- Wilson, E.B.; Decius, J.C.; Cross, P.C. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra; Dover Publications: Mineola, NY, USA, 1980. [Google Scholar]
- Shaffer, W.H. Degenerate Modes of Vibration and Perturbations in Polyatomic Molecules. Rev. Mod. Phys. 1944, 16, 245–259. [Google Scholar] [CrossRef]
- Renner, T.; Cohen, E.R.; Cvitas, T.; Frey, J.G.; Holström, B.; Kuchitsu, K.; Marquardt, R.; Mills, I.; Pavese, F.; Quack, M.; et al. Quantities, Units and Symbols in Physical Chemistry; RSC Publishing: London, UK, 2007. [Google Scholar]
- Allen, W.D.; Yamaguchi, Y.; Császár, A.G.; Clabo, D.A.; Remington, R.B.; Schaefer, H.F. A systematic study of molecular vibrational anharmonicity and vibration-rotation interaction by self-consistent-field higher-derivative methods. Linear polyatomic molecules. Chem. Phys. 1990, 145, 427–466. [Google Scholar] [CrossRef]
- Piccardo, M.; Bloino, J.; Barone, V. Generalized vibrational perturbation theory for rotovibrational energies of linear, symmetric and asymmetric tops: Theory, approximations, and automated approaches to deal with medium-to-large molecular systems. Int. J. Quant. Chem. 2015, 115, 948–982. [Google Scholar] [CrossRef] [PubMed]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef]
- Rosnik, A.M.; Polik, W.F. VPT2+K spectroscopic constants and matrix elements of the transformed vibrational Hamiltonian of a polyatomic molecule with resonances using Van Vleck perturbation theory. Mol. Phys. 2014, 112, 261–300. [Google Scholar] [CrossRef]
- Gong, J.Z.; Matthews, D.A.; Changala, P.B.; Stanton, J.F. Fourth-order vibrational perturbation theory with the Watson Hamiltonian: Report of working equations and preliminary results. J. Chem. Phys. 2018, 149, 114102. [Google Scholar] [CrossRef] [PubMed]
- Sebald, P. Ab initio Berechnung spektroskopischer Eigenschaften kleiner linearer Moleküle. In Dissertation; University of Kaiserslautern: Kaiserslautern, Germany, 1990. [Google Scholar]
- Wang, S.C. On the Asymmetrical Top in Quantum Mechanics. Phys. Rev. 1929, 34, 243–252. [Google Scholar] [CrossRef]
- Yamada, K. Effect of Phase Choices in Rovibrational Wavefunctions on the Labeling of K- and l-type Doubling in Molecular Energy Levels. Z. Naturforsch. 1983, 38, 821–834. [Google Scholar] [CrossRef]
- Herzberg, G. l-Type Doubling in Linear Polyatomic Molecules. Rev. Mod. Phys. 1942, 14, 219–223. [Google Scholar] [CrossRef]
- Watson, J.K.G. Higher-order l-doubling of linear molecules. J. Mol. Spectrosc. 1983, 101, 83–93. [Google Scholar] [CrossRef]
- Watson, J.K.G. l-Type doubling: Herzberg versus Nielsen. Can. J. Phys. 2001, 79, 521–532. [Google Scholar] [CrossRef]
- Aidas, K.; Angeli, C.; Bak, K.L.; Bakken, V.; Bast, R.; Boman, L.; Christiansen, O.; Cimiraglia, R.; Coriani, S.; Dahle, P.; et al. The Dalton quantum chemistry program system. WIREs Comput. Mol. Sci. 2014, 4, 269–284. [Google Scholar] [CrossRef] [PubMed]
- Dalton, a Molecular Electronic Structure Program, Release DALTON2013.1 (2013). Available online: http://daltonprogram.org (accessed on 21 July 2023).
- Martin, J.M.L.; Lee, T.J. The atomization energy and proton affinity of NH3. An ab initio calibration study. Chem. Phys. Lett. 1996, 258, 136–143. [Google Scholar] [CrossRef]
- Buenker, R.J.; Peyerimhoff, S.D. CI method for the study of general molecular potentials. Theor. Chim. Acta 1968, 12, 183–199. [Google Scholar] [CrossRef]
- Buenker, R.J.; Peyerimhoff, S.D. Individualized configuration selection in CI calculations with subsequent energy extrapolation. Theor. Chim. Acta. 1974, 35, 33–58. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J. An efficient internally contracted multiconfiguration–reference configuration interaction method. J. Chem. Phys. 1988, 89, 5803–5814. [Google Scholar] [CrossRef]
- Knowles, P.J.; Werner, H.-J. An efficient method for the evaluation of coupling coefficients in configuration interaction calculations. Chem. Phys. Lett. 1988, 145, 514–522. [Google Scholar] [CrossRef]
- Shamasundar, K.R.; Knizia, G.; Werner, H.-J. A new internally contracted multi-reference configuration interaction method. J. Chem. Phys. 2011, 135, 054101. [Google Scholar] [CrossRef]
- Langhoff, S.R.; Davidson, E.R. Configuration interaction calculations on the nitrogen molecule. Int. J. Quant. Chem. 1974, 8, 61–72. [Google Scholar] [CrossRef]
- Davidson, E.R.; Silver, D.W. Size consistency in the dilute helium gas electronic structure. Chem. Phys. Lett. 1977, 52, 403–406. [Google Scholar] [CrossRef]
- Werner, H.-J.; Kállay, M.; Gauss, J. The barrier height of the F+H2 reaction revisited: Coupled-cluster and multireference configuration-interaction benchmark calculations. J. Chem. Phys. 2008, 128, 034305. [Google Scholar] [CrossRef] [PubMed]
- Szalay, P.G.; Bartlett, R.J. Multi-reference averaged quadratic coupled-cluster method: A size-extensive modification of multi-reference CI. Chem. Phys. Lett. 1993, 214, 481–488. [Google Scholar] [CrossRef]
- Shiozaki, T.; Knizia, G.; Werner, H.-J. Explicitly correlated multireference configuration interaction: MRCI-F12. J. Chem. Phys. 2011, 134, 034113. [Google Scholar] [CrossRef]
- Shiozaki, T.; Werner, H.-J. Multireference explicitly correlated F12 theories. Mol. Phys. 2013, 111, 607–630. [Google Scholar] [CrossRef]
- Veryazov, V.; Malmqvist, P.Å.; Roos, B.O. How to select active space for multiconfigurational quantum chemistry? Int. J. Quant. Chem. 2011, 111, 3329–3338. [Google Scholar] [CrossRef]
- Stein, C.J.; Reiher, M. Automated Selection of Active Orbital Spaces. J. Chem. Theory Comput. 2016, 12, 1760–1771. [Google Scholar] [CrossRef]
- Makhnev, V.Y.; Kyuberis, A.A.; Zobov, N.F.; Lodi, L.; Tennyson, J.; Polyansky, O.L. High Accuracy ab initio Calculations of Rotational–Vibrational Levels of the HCN/HNC System. J. Phys. Chem. A 2018, 122, 1326–1343. [Google Scholar] [CrossRef]
- Schröder, B. Replication Data for: Ab initio rovibrational spectroscopy of the acetylide anion. [Data set], GRO.data, V1. J. Mol. Spectrosc. 2023. [Google Scholar] [CrossRef]
- Botschwina, P.; Horn, M.; Matuschewski, M.; Schick, E.; Sebald, P. Hydrogen cyanide: Theory and experiment. J. Mol. Struct. THEOCHEM 1997, 400, 119–137. [Google Scholar] [CrossRef]
- Maki, A.; Quapp, W.; Klee, S.; Mellau, G.C.; Albert, S. The CN Mode of HCN: A Comparative Study of the Variation of the Transition Dipole and Herman-Wallis Constants for Seven Isotopomers and the Influence of Vibration-Rotation Interaction. J. Mol. Spectrosc. 1995, 174, 365–378. [Google Scholar] [CrossRef]
- Botschwina, P. SiCCO and CCCO: Accurate equilibrium structures and spectroscopic constants. J. Mol. Struct. THEOCHEM 2005, 724, 95–98. [Google Scholar] [CrossRef]
- Botschwina, P.; Oswald, R. Carbon chains of type C2n+1N− (n = 2–6): A theoretical study of potential interstellar anions. J. Chem. Phys. 2008, 129, 044305. [Google Scholar] [CrossRef]
- Botschwina, P.; Oswald, R.; Knizia, G.; Werner, H.J. High-level Ab-initio Calculations for Astrochemically Relevant Polyynes (HC2nH), their Isomers (C2nH2) and their Anions (C2nH−). Z. Phys. Chem. 2009, 223, 447–460. [Google Scholar] [CrossRef]
- Pulay, P.; Meyer, W.; Boggs, J.E. Cubic force constants and equilibrium geometry of methane from Hartree-Fock and correlated wavefunctions. J. Chem. Phys. 1978, 68, 5077. [Google Scholar] [CrossRef]
- Domenicano, A.; Hargittai, I. Accurate Molecular Structures: Their Determination and Importance; Oxford University Press: Oxford, UK, 1992; Volume 1. [Google Scholar]
- Bak, K.L.; Gauss, J.; Jørgensen, P.; Olsen, J.; Helgaker, T.; Stanton, J.F. The accurate determination of molecular equilibrium structures. J. Chem. Phys. 2001, 114, 6548. [Google Scholar] [CrossRef]
- Pawłowski, F.; Jørgensen, P.; Olsen, J.; Hegelund, F.; Helgaker, T.; Gauss, J.; Bak, K.L.; Stanton, J.F. Molecular equilibrium structures from experimental rotational constants and calculated vibration–rotation interaction constants. J. Chem. Phys. 2002, 116, 6482–6496. [Google Scholar] [CrossRef]
- Demaison, J. Experimental, semi-experimental and ab initio equilibrium structures. Mol. Phys. 2007, 105, 3109. [Google Scholar] [CrossRef]
- Puzzarini, C.; Stanton, J.F.; Gauss, J. Quantum-chemical calculation of spectroscopic parameters for rotational spectroscopy. Int. Rev. Phys. Chem. 2010, 29, 273–367. [Google Scholar] [CrossRef]
- Piccardo, M.; Penocchio, E.; Puzzarini, C.; Biczysko, M.; Barone, V. Semi-Experimental Equilibrium Structure Determinations by Employing B3LYP/SNSD Anharmonic Force Fields: Validation and Application to Semirigid Organic Molecules. J. Phys. Chem. A 2015, 119, 2058–2082. [Google Scholar] [CrossRef]
- Demaison, J.; Boggs, J.E.; Császár, A.G. Equilibrium Molecular Structures: From Spectroscopy to Quantum Chemistry; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Darling, B.T.; Dennison, D.M. The Water Vapor Molecule. Phys. Rev. 1940, 57, 128–139. [Google Scholar] [CrossRef]
- Martin, J.M.L.; Taylor, P.R. Accurate ab initio quartic force field for trans-HNNH and treatment of resonance polyads. Spectrochim. Acta A 1997, 53, 1039–1050. [Google Scholar] [CrossRef]
- Carter, S.; Senekowitsch, J.; Handy, N.C.; Rosmus, P. Calculations of the ro-vibrational absorption transition probabilities in triatomic molecules. Mol. Phys. 1988, 65, 143–160. [Google Scholar] [CrossRef]
- Hönl, H.; London, F. Über die Intensitäten der Bandenlinien. Z. Physik 1925, 33, 803–809. [Google Scholar] [CrossRef]
- Hansson, A.; Watson, J.K.G. A comment on Hönl-London factors. J. Mol. Spectrosc. 2005, 233, 159–173. [Google Scholar] [CrossRef]
- Herman, R.; Wallis, R.F. Influence of Vibration-Rotation Interaction on Line Intensities in Vibration-Rotation Bands of Diatomic Molecules. J. Chem. Phys. 1955, 23, 637–646. [Google Scholar] [CrossRef]
- Watson, J.K.G. Quadratic Herman-Wallis Factors in the Fundamental Bands of Linear Molecules. J. Mol. Spectrosc. 1987, 125, 428–441. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).