Space Charge Characteristics at the Interface of Laminated Epoxy Resin
Abstract
1. Introduction
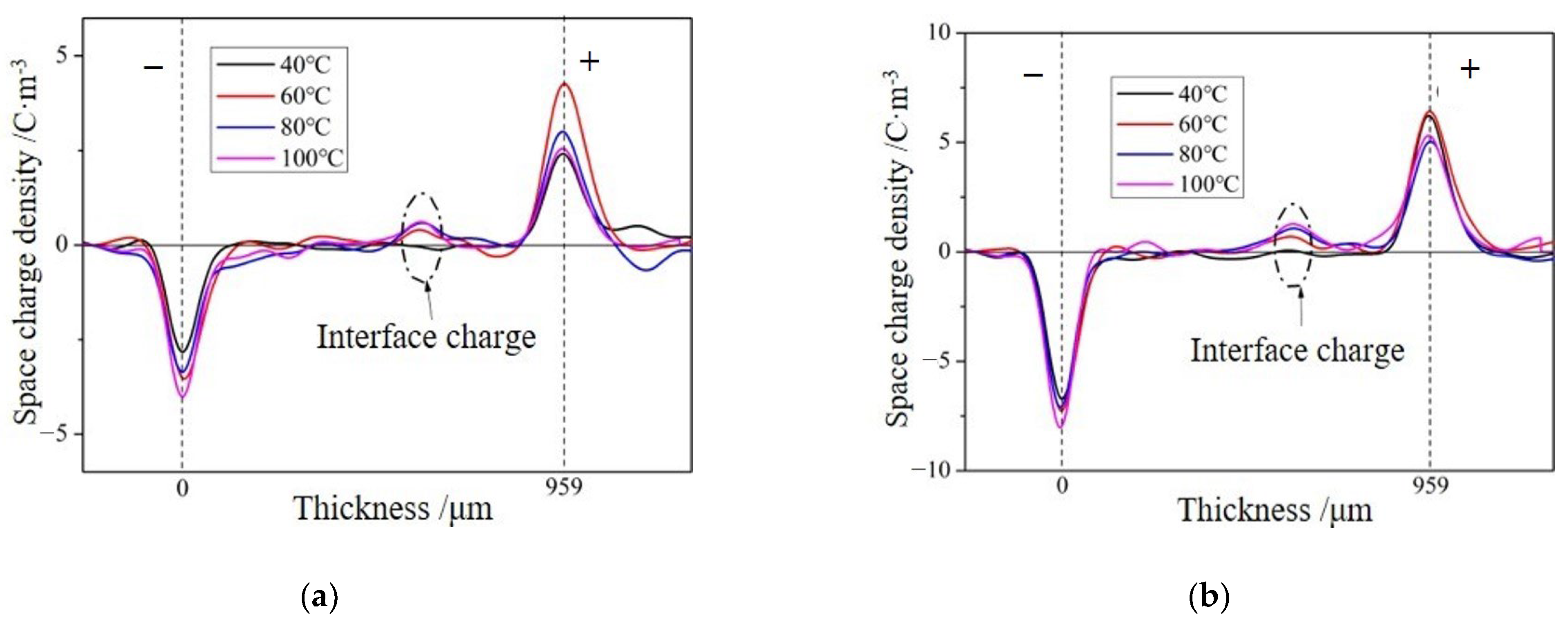
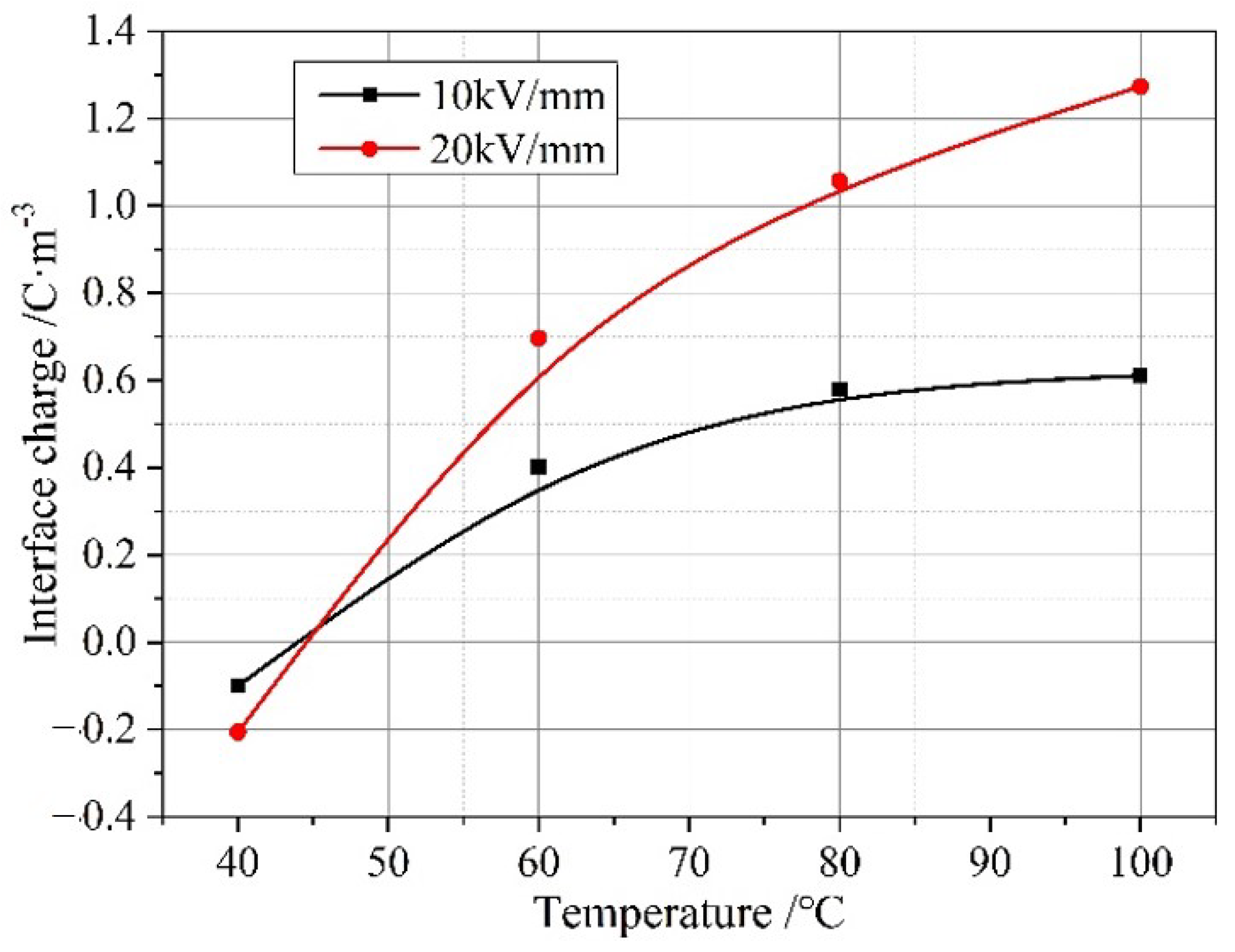
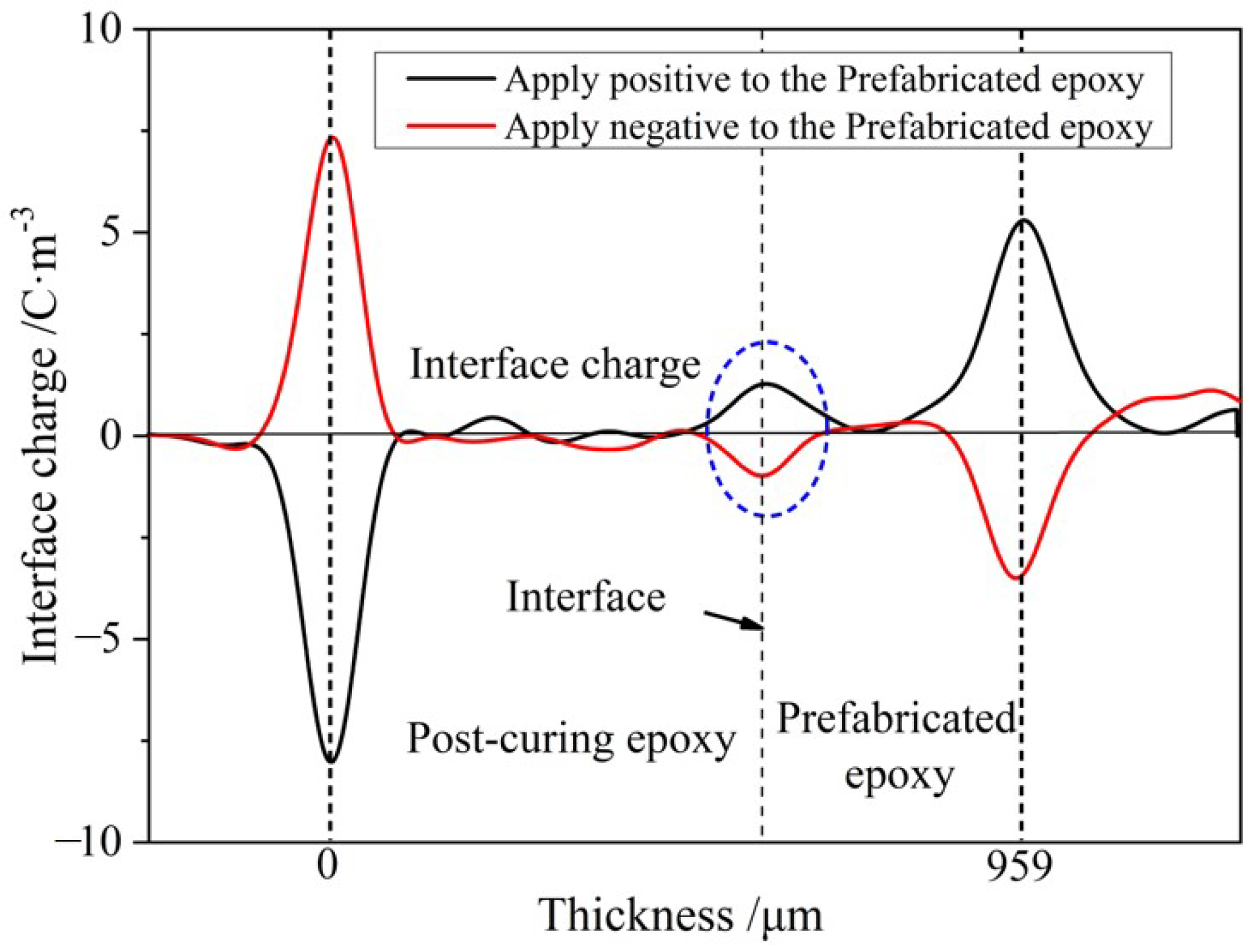
2. Experimental Result
2.1. PEA
2.2. TSDC
3. Analysis and Discussion
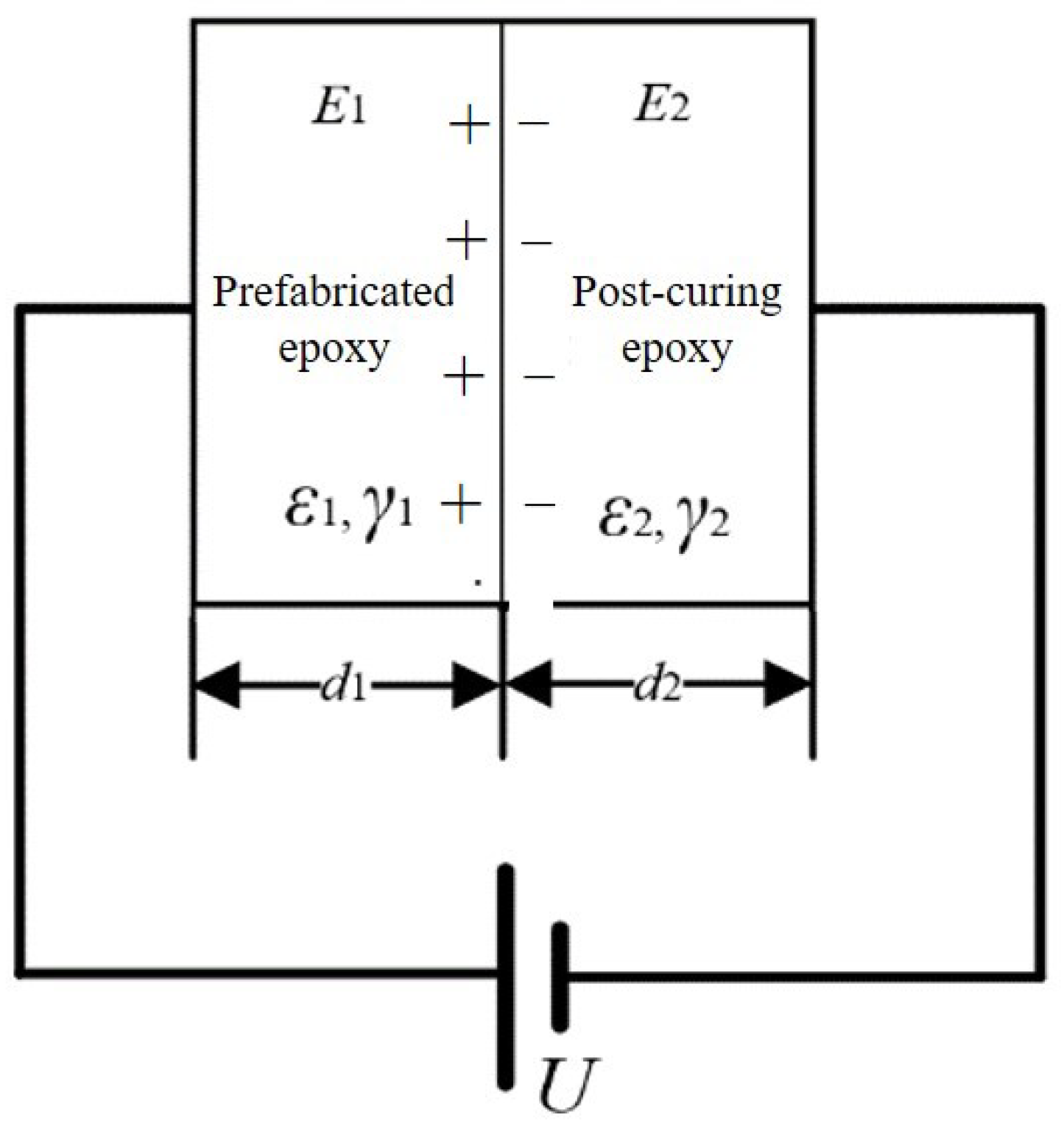
4. Materials and Methods
4.1. Sample Preparation
4.2. PEA
4.3. TSDC
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Saba, N.; Jawaid, M.; Alothman, O.Y.; Paridah, M.; Hassan, A. Recent advances in epoxy resin, natural fiber-reinforced epoxy composites and their applications. J. Reinf. Plast. Compos. 2016, 35, 447–470. [Google Scholar] [CrossRef]
- May, C. Epoxy Resins: Chemistry and Technology; Routledge: London, UK, 2018. [Google Scholar]
- Mohan, P. A critical review: The modification, properties, and applications of epoxy resins. Polym.-Plast. Technol. Eng. 2013, 52, 107–125. [Google Scholar] [CrossRef]
- Hao, Y.; Zheng, Y.; Liu, L.; Yang, L.; Wang, G.; Gao, C.; Zhou, F.; Gong, R. Failure mechanism of three-post insulators in the GIL under radial loads. Eng. Fail. Anal. 2021, 127, 105545. [Google Scholar] [CrossRef]
- Du, B.; Dong, J.; Liang, H.; Kong, X. Polarity reversal and over voltage affecting dischahrge inception of tri-post insulator in ± 800 kV GIL. IEEE Trans. Dielectr. Electr. Insul. 2022, 29, 223–230. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, X.; Peng, Z. 3D Coupled Electromagnetic-Thermal-Fluid Method for Computation ofTemperature Field of Converter Transformer RIP Bushings. Proc. CSEE 2016, 36, 6269–6275. [Google Scholar]
- Chen, M.; Liu, X.; Shao, Y.; Shang, G.; Zhang, Q.; Tang, H.; Liu, L. Degradation characteristics of insulation near aluminium foil edges inside dry-type bushing cores under electrothermal compound stress. High Volt. 2022, 7, 1153–1164. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, G.; Sun, Q.; Chen, C.; Zhang, Z.; Li, H.; Peng, Z. Numerical simulation of the interfacial stress between epoxy resin and metal conductor of power equipment during epoxy curing. High Volt. 2022, 7, 903–915. [Google Scholar] [CrossRef]
- Liu, P.; Xie, Z.; Pang, X.; Xu, T.; Zhang, S.; Morshuis, P.H.F.; Li, H.; Peng, Z. Space Charge Behavior in Epoxy-Based Dielectrics: Progress and Perspective. Adv. Electron. Materials. 2022, 8, 2200259. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, P.; Feng, H.; Zhang, S.; Li, D.; Peng, Z. Space charge dynamics in epoxy resin impregnated crepe paper multilayer under voltage polarity reversal. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 253–260. [Google Scholar] [CrossRef]
- Das, S.; Gupta, N. Effect of ageing on space charge distribution in homogeneous and composite dielectrics. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 541–547. [Google Scholar] [CrossRef]
- Das, S.; Gupta, N. Interfacial charge behaviour at dielectric-dielectric interfaces. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1302–1311. [Google Scholar] [CrossRef]
- Cao, W.; Shen, W.; Wu, K. Study on the properties of space charge and breakdown for epoxy-paper composites. IEEJ Trans. Electr. Electron. Eng. 2015, 10, 364–367. [Google Scholar] [CrossRef]
- Lan, L.; Wu, J.; Wang, Y. Interfacial space charge characteristics of low-density polyethylene/Ethylene propylene rubber bilayer dielectric. Proc. CSEE. 2015, 35, 1266–1272. [Google Scholar]
- Wu, K.; Cheng, C. Interface charges between insulating materials. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 2633–2642. [Google Scholar] [CrossRef]
- Wang, C.; Sun, Q.; Zhao, L.; Jia, J.; Yao, L.; Peng, Z. Mechanical and dielectric strength of laminated epoxy dielectric graded materials. Polymers 2020, 12, 622. [Google Scholar] [CrossRef]
- Rogti, F.; Ferhat, M. Maxwell–Wagner polarization and interfacial charge at the multi-layers of thermoplastic polymers. J. Electrost. 2014, 72, 91–97. [Google Scholar] [CrossRef]
- Ning, X. Study on the Space Charge Characteristics of Epoxy Composite Materials for Ultra High Voltage DC Dry Bushing. Ph.D. Thesis, Xi’an Jiaotong University, Xi’an, China, 2015. [Google Scholar]
- Neagu, R.M.; Neagu, E.R.; Kalogeras, I.M.; Vassilikou-Dova, A. Evaluation of the dielectric parameters from TSDC spectra: Application to polymeric systems. Mater. Res. Innov. 2001, 4, 115–125. [Google Scholar] [CrossRef]
- Wang, W.; Li, S.; Tanaka, Y.; Takada, T. Interfacial charge dynamics of cross-linked polyethylene/ethylene-propylene-diene dual dielectric polymer as revealed by energy band structure. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1755–1762. [Google Scholar] [CrossRef]
- Takada, T.; Tohmine, T.; Tanaka, Y.; Li, J. Space Charge Accumulation in Double-Layer Dielectric Systems—Measurement Methods and Quantum Chemical Calculations. IEEE Electr. Insul. Mag. 2019, 35, 36–46. [Google Scholar] [CrossRef]
- Rogti, F.; Mekhaldi, A.; Laurent, C. Space Charge Behavior at Physical Interfaces in Cross-linked Polyethylene under DC Field. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1478–1485. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, X.; Wu, K.; Chen, X.; Cheng, Y.; Dissado, L.A. Dependence of Charge Accumulation on Sample Thickness in Nano-SiO2 Doped LDPE. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 337–345. [Google Scholar]
- Li, G.; Zhou, X.; Li, X.; Wei, Y.; Hao, C.; Li, S.; Lei, Q. DC breakdown characteristics of XLPE/BNNS nanocomposites considering BN nanosheet concentration, space charge and temperature. High Volt. 2020, 5, 280–286. [Google Scholar] [CrossRef]
- Gun’Ko, V.; Zarko, V.; Goncharuk, E.; Andriyko, L.; Turov, V.; Nychiporuk, Y.; Leboda, R.; Skubiszewska-Zięba, J.; Gabchak, A.; Osovskii, V.; et al. TSDC spectroscopy of relaxational and interfacial phenomena. Adv. Colloid Interface Sci. 2007, 131, 1–89. [Google Scholar] [CrossRef] [PubMed]


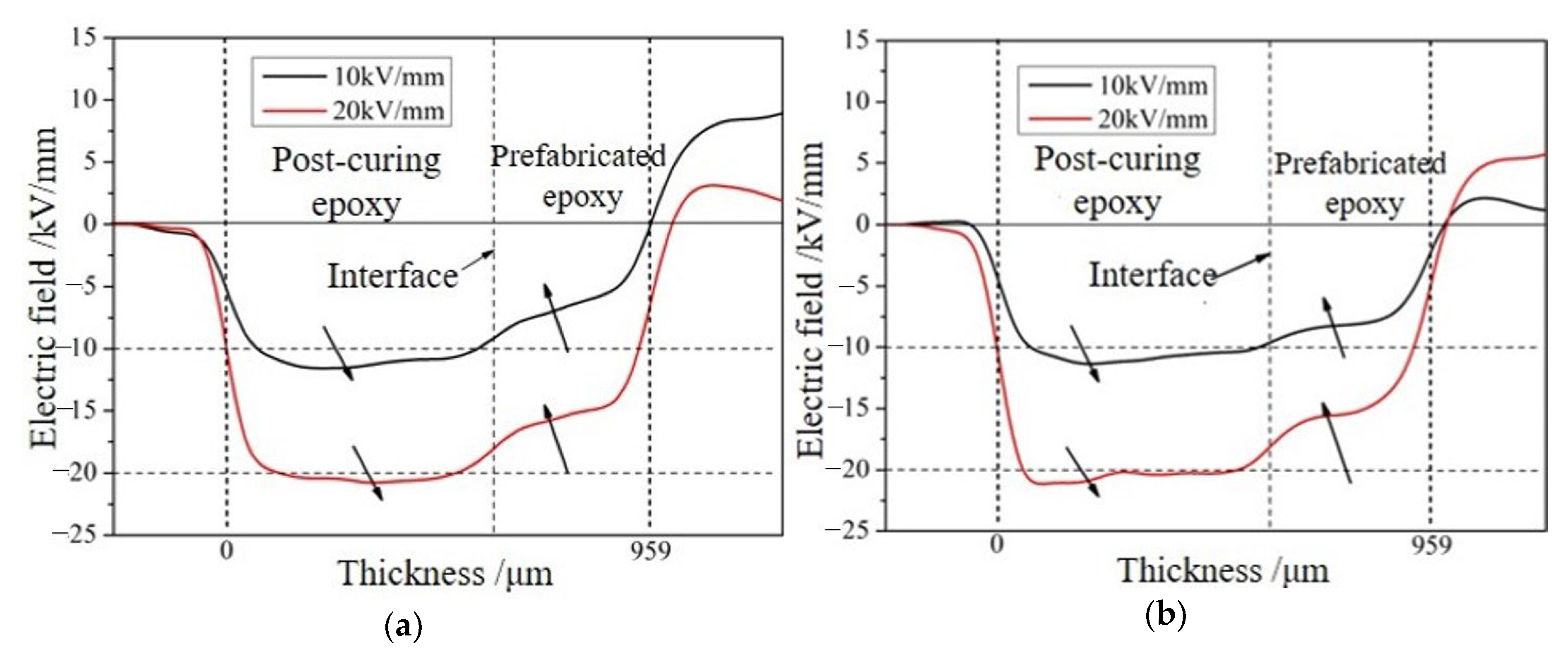
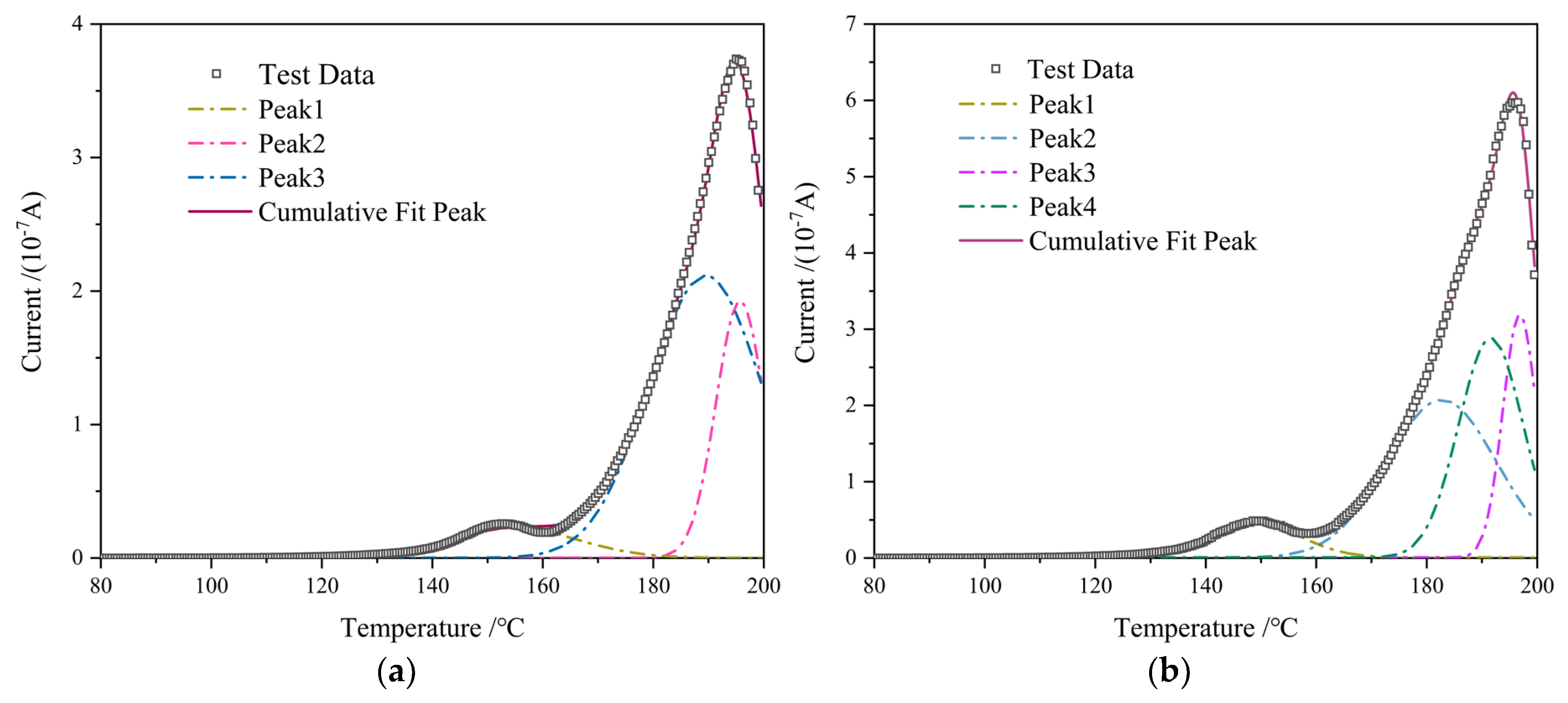
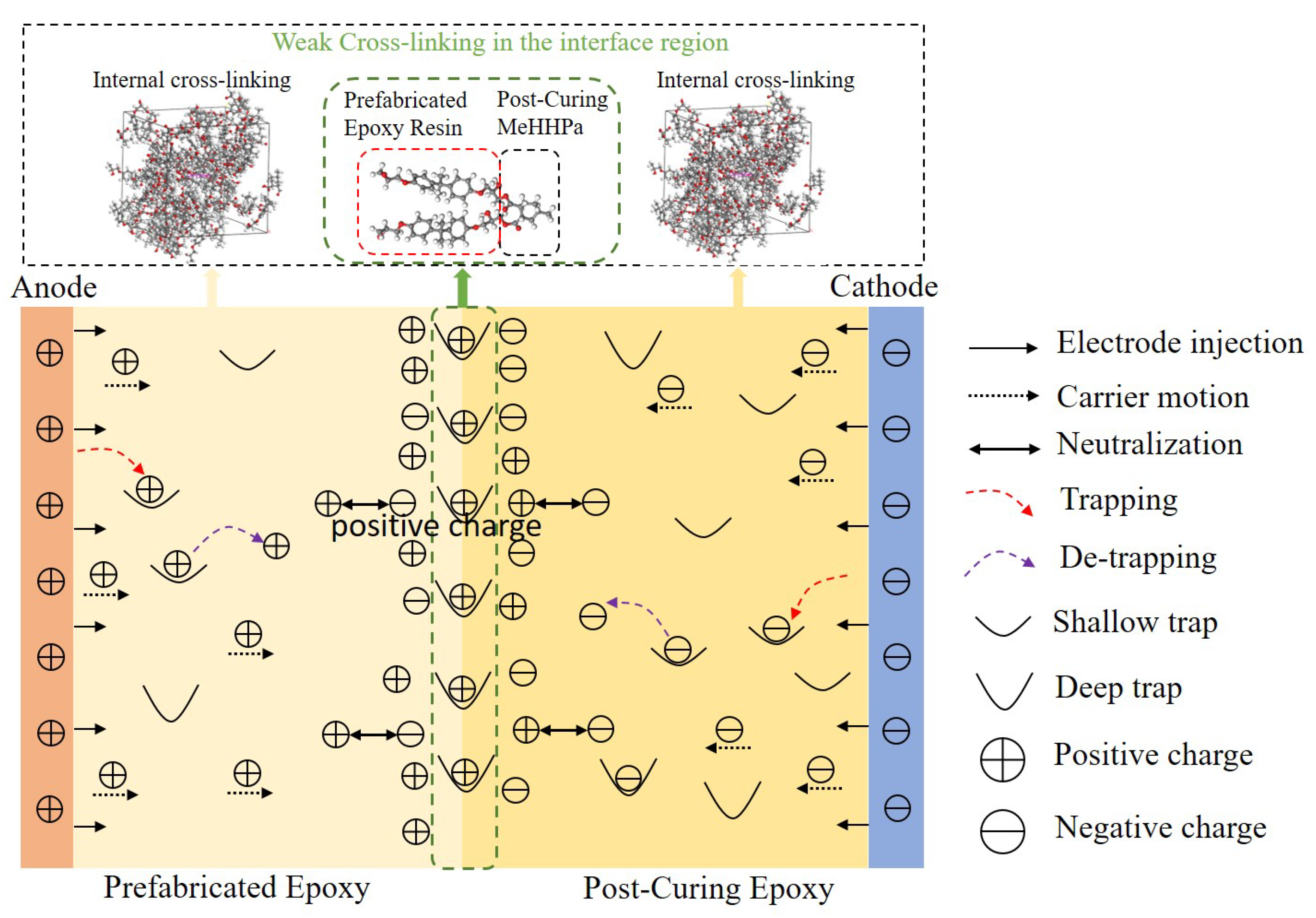

| Temperature/°C | Field Strength Ep/kV·mm−1 | Maximum Field Strength Emax/kV·mm−1 | Field Distortion Factor Fd/% |
|---|---|---|---|
| 80 | 10 | 11.58 | 15.8 |
| 20 | 20.78 | 3.9 | |
| 100 | 10 | 11.36 | 13.6 |
| 20 | 21.15 | 5.8 |
| Peak (Sample) Type | Trap Energy Level (eV) | Trap Charge Quantity (μC) | |
|---|---|---|---|
| Peak 1 | Interface-free specimens | 1.13 | 0.212 |
| Specimens with interface | 0.89 | 0.308 | |
| Peak 2 | Interface-free specimens | 1.27 | 1.515 |
| Specimens with interface | 1.29 | 1.635 | |
| Peak 3 | Interface-free specimens | 2.20 | 0.566 |
| Specimens with interface | 2.31 | 0.659 | |
| Peak 4 | Specimens with interface | 2.06 | 1.279 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Luo, B.; Fu, M.; Jia, L.; Chen, C.; Zhou, G.; Wang, C. Space Charge Characteristics at the Interface of Laminated Epoxy Resin. Molecules 2023, 28, 5537. https://doi.org/10.3390/molecules28145537
Zhang Y, Luo B, Fu M, Jia L, Chen C, Zhou G, Wang C. Space Charge Characteristics at the Interface of Laminated Epoxy Resin. Molecules. 2023; 28(14):5537. https://doi.org/10.3390/molecules28145537
Chicago/Turabian StyleZhang, Yifan, Bing Luo, Mingli Fu, Lei Jia, Chi Chen, Gang Zhou, and Chuang Wang. 2023. "Space Charge Characteristics at the Interface of Laminated Epoxy Resin" Molecules 28, no. 14: 5537. https://doi.org/10.3390/molecules28145537
APA StyleZhang, Y., Luo, B., Fu, M., Jia, L., Chen, C., Zhou, G., & Wang, C. (2023). Space Charge Characteristics at the Interface of Laminated Epoxy Resin. Molecules, 28(14), 5537. https://doi.org/10.3390/molecules28145537






