Abstract
By using molecular dynamics simulation, we investigate the wettability of a surface texturized with a periodic array of hierarchical pillars. By varying the height and spacing of the minor pillars on top of major pillars, we investigate the wetting transition from the Cassie–Baxter (CB) to Wenzel (WZ) states. We uncover the molecular structures and free energies of the transition and meta-stable states existing between the CB and WZ states. The relatively tall and dense minor pillars greatly enhance the hydrophobicity of a pillared surface, in that, the CB-to-WZ transition requires an increased activation energy and the contact angle of a water droplet on such a surface is significantly larger.
1. Introduction
Superhydrophobic surfaces find wide applications including anti-icing [1], anti-frosting [2], water collection [3], oil-water separation [4], drag-reducing [5,6], self-cleaning [7], prevention of corrosion [8,9], solar cells [10,11], and light-emitting diodes [12,13], just to name a few. Over the years, the wettability of a pillared surface has been extensively studied both experimentally [3] and theoretically [14,15,16,17]. Researchers have explored surfaces texturized with pillars that are diverse in shape and size. Surfaces texturized with cylindrical, rectangular, or dome-shaped pillars have been most commonly studied [18,19,20,21,22].
The current consensus view is that a superhydrophobic surface should provide a static contact angle (CA) > 150° for a water droplet deposited on it. Additionally, a sliding angle < 10° and a hysteresis of (advancing and receding) CA < 10° are required for the high mobility of a water droplet on a surface (dynamic hydrophobicity).
Besides CA, another critical information pertaining to the wettability (hydrophobicity) of a pillared surface is whether the gaps between pillars are wetted by a water droplet deposited on top. The wetted and de-wetted states of the inter-pillar gap are, respectively, called the Wenzel (WZ) [23] and Cassie–Baxter (CB) [24] states. Attempts have been made to find out the optimal geometry (shape, size, and spacing of pillars) of a pillared surface, which preferentially provides the CB, instead of WZ state.
It is well known that a natural superhydrophobic surface, such as that of lotus leaf or rose petal, is texturized with an array of pillars with a hierarchical structure; each major pillar is covered by multiple minor pillars smaller in size (Figure 1a). In the case of a surfaced texturized with dual-scale pillars, there can be four distinct wetting states, depending on whether the gaps between the minor and major pillars are wetted or not, giving rise to the CB-CB, CB-WZ, WZ-CB, and WZ-WZ states (Figure 1b).

Figure 1.
(a) Periodic simulation cell of the present surface texturized with hierarchical pillars. The height, width, and interpillar spacing of major pillars are represented by H, W, and S, respectively. On top of each major pillar, we constructed multiple minor pillars of h, w, and s in height, width and interpillar spacing, respectively. (b) Schematic diagram for four distinct wetting states possible for a surface texturized hierarchical pillars: CB-CB, WZ-WZ, CB-WZ, and WZ-CB states.
Experimental and computational efforts have been made to study the superior hydrophobicity of a surface patterned with hierarchical pillars. Yang et al. reported the CA of a water droplet on a flat surface increased from 71.6° to 104° and 145° by fabricating single-scale and dual-scale pillars on the flat surface, respectively [25]. Nikosokhan et al. obtained a CA of 160° by patterning cobalt-based hierarchical pillars on a surface [26]. By using molecular dynamics (MD) simulation, Kwon et al. found that the presence of hierarchical pillars greatly increases the CA from that of a surface texturized with nonhierarchical pillars. Additionally, the mobility of a droplet also enhanced with the hierarchical pillars [27].
In spite of the extensive prior studies on the wettability of a surface texturized with hierarchical pillars, we still poorly understand the metastable state and transition state (TS) existing between the CB and WZ states. The structures and relative stabilities of these intermediate states are quite important to understand the wettability of a pillared surface. The (de)wetting transition can be kinetically trapped in the meta-stable state due to the free energy barrier(s) needed to surmount the TS (s). The molecular details and free energies involved in this activated process are largely unknown.
Previously, we have studied, by using the MD simulation, the CB-to-WZ transition for a surface engraved with dual-scale trenches [28]. However, such a trenched surface differs from a pillared surface that is grooved along two lateral directions crossing each other. Others reported MD simulations for surfaces engraved with hierarchical pillars [14,15,17] but the focus was on the CA of water droplet deposited on such a surface.
Herein, we report on the MD simulation on a surface texturized with hierarchical pillars, which emulates a natural superhydrophobic surface. We uncover the intermediate metastable states and TSs of the CB-to-WZ transition for a surface patterned with hierarchical pillars. By identifying these intermediate states, we estimate the free energy barriers and feasibilities (kinetics) for the wetting and de-wetting transitions. We show that hierarchical pillars exhibit a superior hydrophobicity by making the CB state more stable than the WZ state, and by lowering the free energy barrier for the de-wetting transition. Our results provide fundamental insights into the design of a novel hydrophobic surface utilizing hierarchical pillars.
2. Results and Discussion
We simulated a surface texturized with a periodic array of hierarchical pillars as follows. Out of the face-centered cubic lattice of carbon [29], we engraved four major pillars with a height H and a width W, separated from each other by spacing S (Figure 1a). We simulated major pillars with various heights, Hs (=7.1, 8.9, 10.7, 12.5, 14.3, and 19.6 Å) by fixing S to 23.2 Å and W to 48.2 Å. On top of each major pillar, we constructed multiple minor pillars with a height h and a width w, each of which is separated by an interpillar spacing, s (Figure 1a). An infinite array of hierarchical pillars was emulated by applying the periodic boundary conditions (PBCs) to the simulation cell (Figure 1a).
In the case of a pillar patterned with hierarchical pillars, we fixed H to 14.3 Å and w to 5.35 Å. We examined the effects of varying the relative height of the minor pillars h* defined as h* = h/H. We varied h* as 0.5 and 0.75 by fixing the relative spacing of minor pillars s*, defined as s* = s/S, to 0.23. We also studied both the dense and sparse minor pillars by simulating s* = 0.23 and 0.69, respectively (h* = 0.25 for both cases). The sparse and dense minor pillars provided 9 or 25 minor pillars per major pillar, respectively. For comparison, we also simulated surfaces texturized with nonhierarchical pillars.
We first examine the (CB-to-WZ) wetting transition for a surface texturized with nonhierarchical pillars. By changing H as 8.9, 10.7, 12.5, 14.3, and 19.6 Å with S fixed to 23.2 Å, we investigated how the PMF and water density depend on the filling level F (Figure 2). As shown in the top of Figure 2, two minima of PMF near F = 0 and F = 1 are noticeable, corresponding to the CB and WZ states, respectively. The relative stabilities of CB and WZ states depend on the height of pillars; for the surfaces with relatively short pillars with H = 8.9 and 10.7 Å, the WZ state is more stable than CB state (near F = 0) because the global minimum of PMF curve is found near F = 1. Therefore, the CB state is a metastable state and the interpillar gap is more likely to be filled with water for these short pillars. On the other hand, for the surfaces with relatively tall pillars, H = 12.5, 14.3, and 19.6 Å, the CB state is more stable than the WZ state, signifying that the interpillar gap tends to be de-wetted thermodynamically. In these cases, the CB (WZ) state is stable (metastable).
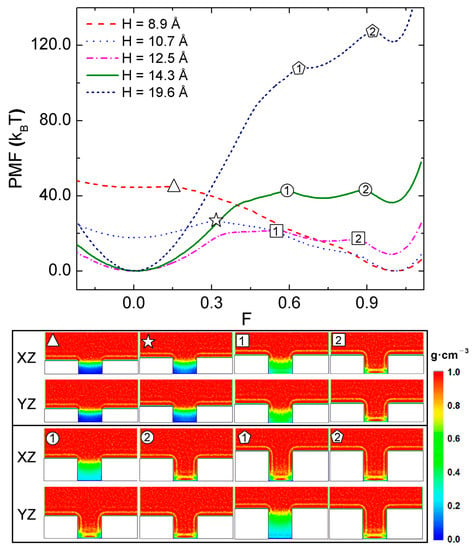
Figure 2.
Free energy profiles of the CB-to-WZ wetting transitions of the surfaces texturized with nonhierarchical pillars. At the top, the PMF is plotted vs. the filling level F for surfaces with pillars with heights Hs of 8.9, 10.7, 12.5, 14.3, and 19.6 Å. The transition states, defined as the maxima in the PMF curves, are marked as symbols. The density profiles of water at the transition states are shown at the bottom, marked as different symbols in the PMF curves. In each panel, two cross sections of the density profile taken along the XZ and YZ planes are drawn as color maps.
We marked the maxima in the PMF curves (Figure 2, top) as different symbols. These maxima correspond to the TSs in the CB-to-WZ transition. The heights of these maxima (measured from the minima on the left) can be regarded as the activation energies of the wetting transitions. As H varies as H = 12.5, 14.3, and 19.6 Å, the activation energy increases 21.641, 42.969, and 127.763 , respectively; as the aspect ratio of pillar increases, the wetting transition to the WZ state becomes increasingly difficult. One can conclude that increasing the aspect ratio of a pillar enhances the stability of the CB state, and therefore the super-hydrophobicity of the present pillared surface. It can be also seen that two TSs exist in the cases of surfaces with relatively tall pillars (H = 12.5, 14.3, and 19.6 Å).
At the bottom of Figure 2, we illustrate the structures of various TSs marked in the PMF curves (Figure 2, top). In each panel, we show two cross sections of the density profile of water taken along the XZ and YZ planes (note the surface normal is along the Z axis). In the cases of relatively tall pillars with H = 14.3, and 19.6 Å, water penetrates into the interpillar gap non-uniformly as the density profiles projected onto the XZ and YZ planes are different; for example, the first TS for H = 14.3 Å has different density profiles taken along the XZ and YZ planes. Along the XZ plane, the liquid water barely penetrates into the interpillar gap, while the water touches the bottom of the interpillar gap along the YZ plane. Similarly, an anisotropic penetration of water is seen in the first TS for H = 19.6 Å. Therefore, two TSs existing between the CB and WZ states originate from the anisotropic penetration of water into the interpillar gap. The first TS corresponds to the penetration along one direction, and the second TS to the penetration along the other direction. The present anisotropic penetration of water was also found the previous study on the wetting transition [30]. Interestingly, in the case of H = 12.5 Å, the TS looks identical along the XZ and YZ planes. Nevertheless, two TSs are found for the CB-to-WZ transition.
We have seen, for nonhierarchical pillars, that increasing the height of pillars makes the CB state more stable than the WZ state, thereby enhancing the activation energy for the CB-to-WZ transition. In this perspective, we investigate the effects of varying h* for surfaces with hierarchical pillars. To do so, we fixed H = 14.3 Å and s* = 0.231 and simulated the cases for h* = 0, 0.5, and 0.75. Figure 3 plots the PMF vs. F and the simulation snapshots of various TSs marked in the PMF curves. For all three PMF curves shown, two TSs exist between the CB and WZ states. This again originates from the fact that water penetrates into the interpillar gap anisotropically. For example, in the first TS of the PMF curve for h* = 0.5, water penetrates halfway down to the bottom of the gap between major pillars along one direction, but nearly touches the bottom in the other direction. One can also see that the degree of penetration into the minor-interpillar gap also differs depending on the direction.
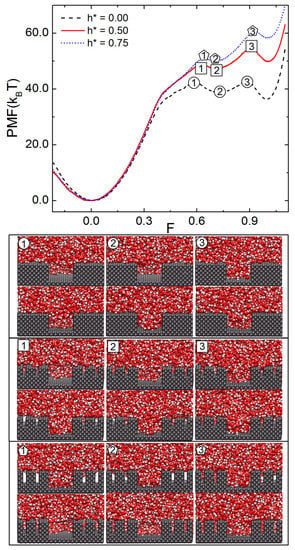
Figure 3.
Free energy profiles for the wetting transitions of surfaces with the hierarchical pillars. The PMF is plotted vs. the filling level F for minor pillars with relative heights, h*s (h* = h/H), of 0.0, 0.5 and 0.75. The representative snapshots of water at the transition states, marked as different symbols in the PMF curves, are shown at the bottom. In all the cases shown here, s* is fixed to 0.231.
The present anisotropic penetration of water is a non-ergodic event on the timescale of the present MD simulation (ns). Statistically, the penetration along the X and Y directions should be identical. Dynamically or kinetically, however, the symmetry of X and Y directions is broken temporarily due to the thermal fluctuation of water. Such a non-ergodicity of molecular dynamics has been often observed in the MD simulation; for example, the velocity distribution of molecules evaporating from a nanodroplet of water did not follow the Maxwell–Boltzmann equation [31]. The diffusivity of a liquid water was found to depend on the initial condition of the MD simulation [32]. It is left as a future work to investigate whether the present nonergodicity persists on a much longer timescale (micro or milliseconds).
The presence of minor pillars greatly affects the wetting properties of the present pillared surface. More specifically, by increasing h* from 0 to 0.5 and 0.75, the WZ state becomes increasingly more unstable than the CB state. The activation energy for the CB-to-WZ transition increases by increasing h*. The free energy barrier of the first TS (measured from the CB state) varies at 42.87 49.41 , and 51.15 , as h* changes from 0, 0.5, and 0.75, respectively. The second activation energy for the transition from the intermediate metastable state to the WZ state (transition from label 2 to label 3 in the PMF curve) varies between 4.27 , 7.65 , and 11.00 , respectively, by changing h* as 0, 0.5, and 0.75. Therefore, as h* increases, the CB-to-WZ transition becomes increasingly difficult.
We now demonstrate how the presence of minor pillars can deteriorate the hydrophobicity of the present pillared surface. Figure 4 illustrates the PMF profiles and various TSs and metastable states simulated by setting s* to 0, 0.23, and 0.69. Here, H is fixed 14.3 Å and h* = 0.25. By increasing s*, the first TS appears at a lower value of F; the first TS is found at F = 0.59, 0.57, and 0.45, respectively, for the cases of s* = 0.0, 0.23, and 0.69. In the case of s* = 0.23, the PMF vs. F curve qualitatively resembles that of the surface with nonhierarchical pillars, s* = 0. Quantitatively, however, the free energy barrier of the first TS decreases from 42.8 to 41.43 by increasing s* from 0 to 0.23. The barrier of the second transition (label 2 to 3) also decreases from 4.27 to 3.50 . With further increasing s* to 0.69, the free energy of the WZ state is significantly lowered, only slightly above that of the CB state. Additionally, the free energy barrier for the first TS noticeably lowers to 23.15 . Additionally, the free energy barrier for the second TS is negligible. The snapshots of the TSs in this case show that water penetrates into the gap between major pillars nearly isotropically. In summary, the presence of hierarchical pillars with sparse minor pillars reduces the hydrophobicity of the present pillared surface. The previous studies also reported that a secondary structure of a pillar can decrease the hydrophobicity of a pillared surface.
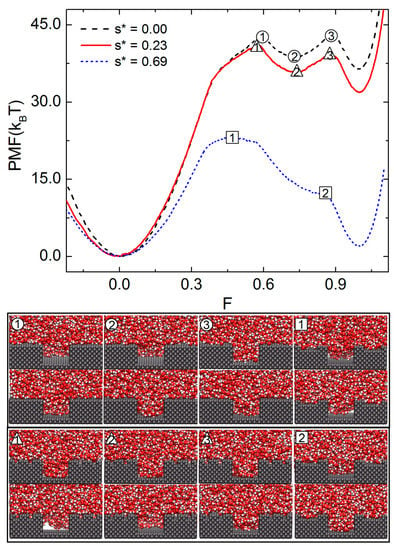
Figure 4.
Free energy profiles for the wetting transitions of surfaces patterned with hierarchical pillars. The PMF is plotted vs. the filling level F for minor pillars s* = 0.0, 0.23 and 0.69. The representative snapshots of water at the transition states, marked as different symbols (numbers in triangles or squares) in the PMF curves, are shown in the bottom. In all three cases, h* is fixed to 0.25.
Above, we have seen that the presence of hierarchical pillars with dense minor pillars increases the hydrophobicity of a surface by destabilizing the WZ state and by increasing the activation energies for the CB-to-WZ transition. To confirm this conclusion, we further check the CAs of water droplets deposited on the flat surface and if the surfaces are texturized with nonhierarchical and hierarchical pillars. In order to eliminate the effects of line tension on the CA, we simulate a large droplet made of 8000 water molecules [33]. As shown in Figure 5, a water droplet composed of 47,940 water molecules (14 nm radius) is deposited on three surfaces described above. By fixing H = 14.3 Å, we simulated a surface with non-hierarchical pillars and a surface with hierarchical pillars of h* = 0.5 and s* = 0.23. The CAs are 111, 118, and 138 degrees, respectively, for the flat surface, the surface with nonhierarchical pillars, and the surface with hierarchical pillars. Therefore, the existence of hierarchical pillars provides the highest CA. Note the water droplet on the hierarchical pillars takes the CB state, while the water droplet penetrates down into the interpillar gap of the nonhierarchical pillars (shown in the middle of Figure 5). This increase in CA by 20° through introducing minor pillars corroborates our conclusion that the existence of hierarchical pillars with dense minor pillars enhances the hydrophobicity of a surface.

Figure 5.
Variation in the CA of a water droplet with changing the texture of a surface. The CAs are shown for the flat surface and the surfaces patterned with nonhierarchical and hierarchical pillars. We set H = 14.3 Å and S = 23.2Å for the pillared surfaces. In the case of the surface with hierarchical pillars, h* = 0.5 and s* = 0.23.
3. Simulation Methods
A macroscopic water droplet resting on top of a pillared surface was simulated as follows. A surface texturized with pillars were carved out from the face-centered cubic lattice of carbon [29] with a lattice space of 3.567 Å. Each pillared surface was covered by a layer of water with a thickness of 40.0 Å (6200 water molecules). In order to prevent the fictitious interaction between water and bottom of the surface, due to the PBCs applied in simulation, we added a 3.0–5.0 nm vacuum slab on top of the water layer. We used the extended-simple-point-charge model (SPC/E) [34] to describe the intermolecular interaction of water. The interaction between water oxygen atoms were modeled by using the Lennard–Jones (LJ) potential, , where and are the well-depth parameters and the size parameters set to 0.6502 kJ mol−1 and 3.166 Å, respectively. The interactions between carbon and water oxygen atoms were also modeled by using the LJ potential with is 0.4389 kJ mol−1 and is 3.190 Å. The long-range Coulomb interactions between point charges were treated with the particle–particle-particle–mesh (PPPM) method [35]. We cut off both the LJ and Coulomb interactions at a distance of 12.0 Å.
The MD trajectories were propagated using the velocity Verlet algorithm [36] with a time step of 2.0 fs. We simulated rigid water molecules by using the SHAKE algorithm [37] and all the carbon atoms were frozen. A 3.0 ns long MD simulation was run in the canonical ensemble (NVT) at 300 K by using the Nosé–Hoover thermostat [38,39]. The final configuration obtained in the NVT MD simulation was used as the initial condition for the subsequent calculation of the potential-of-mean force (PMF) below. MD methods were implemented by using LAMMPS (22Aug2018) software [40].
We calculated the PMF by varying the collective variable D, defined as the height of the center-of-mass of water measured from the bottom of the surface. D is an input parameter controlled in our calculation of PMF, in order to continuously tune the degree of wetting (from that of the CB state to that of the WZ state). In simulating the PMF vs. F, D is restrained to a specific value. By varying D in a series of such restrained MD simulations, F changes from 0 to 1. Using the umbrella sampling [41], we set up D to a target value ranging from 29.0 to 23.8 Å, from 30.4 to 24.4 Å, from 33.2 to 25.4 Å, from 34.4 to 26.4 Å, from 37.6 to 26.8 Å, from 44.0 to 28.2 Å, (with a decrement of 0.2 Å) for H = 7.1 Å, 8.9 Å, 10.7 Å, 12.5 Å,14.3 Å, and 19.6 Å, respectively. For each D in the PMF curve, we ran a 6.0 ns-long NVT simulation at 300K by imposing the harmonic-bias potential with 200.0 kcal/(mol·Å2), which constrains D to a target value. The initial 0.2 ns was discarded for equilibration. The PMF profile was extracted using the weighted histogram analysis method [40,42]. Finally, D was converted to the filling fraction F defined as:
where DCB and DWZ were Ds corresponding to the CB and WZ states, respectively. By construction, F = 0 and 1 for the CB and WZ states, respectively. The CB and WZ states were defined as those located at the local or global minima of the PMF curve. The PMF calculation method described above was implemented by using the LAMMPS combined with the PLUMED package [42].
We further calculated the CA of a water droplet for a selective set of the present pillared surfaces. The water droplet on a pillared surface (Figure 5) was simulated by using a normal MD simulation without restraining D. To do so, a spherical droplet of 47,940 H2O molecules (14.0 nm in diameter) was equilibrated by running an NVT simulation at 300 K for 2.0 ns. The equilibrated droplet was then positioned 1.0 nm above a pillared or flat surface. A 16.0 ns-long NVT simulation was run for the water droplet. The initial 1.0 ns was discarded for equilibration. The CA was calculated by employing the method of Khalkhali et al. [43]: in this method, a convex hull algorithm was used to approximate the liquid–vapor interface of a droplet as a collection of small interconnected triangles. The CA was further obtained from the surface normal vectors of these triangles. This method obviates construction of the density profile of water by means of the three-dimensional binning of molecules, which can be computationally intensive. Additionally, the shape of a liquid droplet does not have to be assumed in this method. The computational efficiency of this method is much better than that of a conventional method, especially for a big droplet. The present large droplet, made of 47,940 water molecules, prevents the line tension effect, which provides an increased CA with decreasing the size of a droplet [33,44].
A pillared surface might contain defects and atomic-scale roughness that should be considered to be modelled more realistically. However, the present ideal geometry without any defects should be a reasonable starting point and should capture the essential features of the wetting transition of a pillared surface. Unlike a typical hydrophilic surface terminated by surface hydroxyls, we modelled a nonpolar carbon surface which should have minimal effects of water dissociation or the electrostatic interaction of water with the surface. Similarly, Walther et al. [45] reported that the electrostatic interaction has a negligible effect on the structure of a liquid water surrounding a carbon nanotube. It is left as a future work to implement the electrostatic water–surface interaction by using sophisticated force fields, such as those reported by Heinz et al. [46] and by Pramanik et al. [47].
4. Conclusions
By using MD simulation, we studied the CB-to-WZ wetting transition for a surface texturized with hierarchical pillars. Various TSs and metastable states existing between the CB and WZ states were found. Owing to the anisotropic penetration of water into the interpillar gap, two distinct TSs existed in the CB-to-WZ transition. The presence of the minor pillars on top of major pillars could increase or decrease the hydrophobicity of a pillared surface. Relatively tall and dense minor pillars greatly enhanced the hydrophobicity of a pillared surface; the CB state became more stable than the WZ state and the activation energy for the CB-to-WZ transition increased. This enhanced hydrophobicity was also confirmed by the increased CA of a water droplet on such a surface. On the other hand, relatively short and sparse minor pillars actually decreased the hydrophobicity of a pillared surface from that of a surface with nonhierarchical pillars. The present findings should be helpful for furthering our understanding of how the presence of hierarchical pillars affects the wettability of a surface.
Author Contributions
Conceptualization, Z.Z. and J.J.; Methodology, Z.Z.; Software, K.K. and S.C.; Validation, K.K. and S.C.; Formal Analysis, Z.Z. and K.K.; Investigation, Z.Z. and K.K.; Resources, K.K. and J.J.; Data Curation, Z.Z. and K.K.; Writing—Original Draft Preparation, K.K.; Writing—Review and Editing, J.J.; Visualization, K.K. and S.C.; Supervision, J.J.; Project Administration, J.J.; Funding Acquisition, J.J. and Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (2021R1A2C1010936), BK21 FOUR Program by Pusan National University Research Grant, 2021 and the National Natural Science Foundation of China grant funded by the China government (No. 22108202).
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Not applicable.
References
- Li, W.; Zhan, Y.; Yu, S. Applications of superhydrophobic coatings in anti-icing: Theory, mechanisms, impact factors, challenges and perspectives. Prog. Org. Coat. 2021, 152, 106117. [Google Scholar] [CrossRef]
- Shen, Y.; Jin, M.; Wu, X.; Tao, J.; Luo, X.; Chen, H.; Lu, Y.; Xie, Y. Understanding the frosting and defrosting mechanism on the superhydrophobic surfaces with hierarchical structures for enhancing anti-frosting performance. Appl. Therm. Eng. 2019, 156, 111–118. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.; Wu, M.; Wei, W. Durable superhydrophobic surface with hierarchical microstructures for efficient water collection. Surf. Coat. Technol. 2021, 419, 127279. [Google Scholar] [CrossRef]
- Rasouli, S.; Rezaei, N.; Hamedi, H.; Zendehboudi, S.; Duan, X. Superhydrophobic and superoleophilic membranes for oil-water separation application: A comprehensive review. Mater. Des. 2021, 204, 109599. [Google Scholar] [CrossRef]
- Sun, P.; Feng, X.; Tian, G.; Zhang, X.; Chu, J. Ultrafast Self-Healing Superhydrophobic Surface for Underwater Drag Reduction. Langmuir 2022, 38, 10875–10885. [Google Scholar] [CrossRef] [PubMed]
- Mollicone, J.-P.; Battista, F.; Gualtieri, P.; Casciola, C.M. Superhydrophobic surfaces to reduce form drag in turbulent separated flows. AIP Adv. 2022, 12, 075003. [Google Scholar] [CrossRef]
- Dalawai, S.P.; Saad Aly, M.A.; Latthe, S.S.; Xing, R.; Sutar, R.S.; Nagappan, S.; Ha, C.-S.; Kumar Sadasivuni, K.; Liu, S. Recent Advances in durability of superhydrophobic self-cleaning technology: A critical review. Prog. Org. Coat. 2020, 138, 105381. [Google Scholar] [CrossRef]
- Vazirinasab, E.; Jafari, R.; Momen, G. Application of superhydrophobic coatings as a corrosion barrier: A review. Surf. Coat. Technol. 2018, 341, 40–56. [Google Scholar] [CrossRef]
- Yang, C.; Cui, S.; Weng, Y.; Wu, Z.; Liu, L.; Ma, Z.; Tian, X.; Fu, R.K.Y.; Chu, P.K.; Wu, Z. Scalable superhydrophobic T-shape micro/nano structured inorganic alumina coatings. Chem. Eng. J. 2021, 409, 128142. [Google Scholar] [CrossRef]
- Cherupurakal, N.; Mozumder, M.S.; Mourad, A.-H.I.; Lalwani, S. Recent advances in superhydrophobic polymers for antireflective self-cleaning solar panels. Renew. Sustain. Energy Rev. 2021, 151, 111538. [Google Scholar] [CrossRef]
- Kim, D.H.; Park, J.-H.; Lee, T.I.; Myoung, J.-M. Superhydrophobic Al-doped ZnO nanorods-based electrically conductive and self-cleanable antireflecting window layer for thin film solar cell. Sol. Energy Mater. Sol. Cells 2016, 150, 65–70. [Google Scholar] [CrossRef]
- Vüllers, F.; Gomard, G.; Preinfalk, J.B.; Klampaftis, E.; Worgull, M.; Richards, B.; Hölscher, H.; Kavalenka, M.N. Bioinspired Superhydrophobic Highly Transmissive Films for Optical Applications. Small 2016, 12, 6144–6152. [Google Scholar] [CrossRef]
- Wang, S.; Wang, H.; Zhang, D.; Dou, Y.; Li, W.; Cao, F.; Yin, L.; Wang, L.; Zhang, Z.-J.; Zhang, J.; et al. Perovskite nanocrystals-polymer composites with a micro/nano structured superhydrophobic surface for stable and efficient white light-emitting diodes. Chem. Eng. J. 2022, 437, 135303. [Google Scholar] [CrossRef]
- Kwon, T.W.; Jang, J.; Ambrosia, M.S.; Ha, M.Y. Molecular dynamics study on the hydrophobicity of a surface patterned with hierarchical nanotextures. Colloids Surf. A Physicochem. Eng. Asp. 2018, 559, 209–217. [Google Scholar] [CrossRef]
- Li, H.; Yan, T. Importance of moderate size of pillars and dual-scale structures for stable superhydrophobic surfaces: A molecular dynamics simulation study. Comput. Mater. Sci. 2020, 175, 109613. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, Y.; Jiang, J.; Zhu, C.; Zuhlke, C.; Alexander, D.; Francisco, J.S.; Zeng, X.C. Multiple Wetting-Dewetting States of a Water Droplet on Dual-Scale Hierarchical Structured Surfaces. JACS Au 2021, 1, 955–966. [Google Scholar] [CrossRef]
- Kwon, T.W.; Jang, J.; Sim, G.H.; Park, S.H.; Ha, M.Y. Wetting Behavior of a Surface with Dual-Scale Structures. Langmuir 2021, 37, 7995–8006. [Google Scholar] [CrossRef]
- Lin, H.-P.; Chen, L.-J. Direct observation of wetting behavior of water drops on single micro-scale roughness surfaces of rose petal effect. J. Colloid Interface Sci. 2021, 603, 539–549. [Google Scholar] [CrossRef]
- Kim, H.; Saha, J.K.; Jang, J. Drying Transition of Water Confined between Hydrophobic Pillars. J. Phys. Chem. C 2012, 116, 19233–19239. [Google Scholar] [CrossRef]
- Giacomello, A.; Meloni, S.; Chinappi, M.; Casciola, C.M. Cassie-Baxter and Wenzel states on a nanostructured surface: Phase diagram, metastabilities, and transition mechanism by atomistic free energy calculations. Langmuir 2012, 28, 10764–10772. [Google Scholar] [CrossRef]
- Cansoy, C.E.; Erbil, H.Y.; Akar, O.; Akin, T. Effect of pattern size and geometry on the use of Cassie–Baxter equation for superhydrophobic surfaces. Colloids Surf. A Physicochem. Eng. Asp. 2011, 386, 116–124. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Bhushan, B. Patterned Nonadhesive Surfaces: Superhydrophobicity and Wetting Regime Transitions. Langmuir 2008, 24, 1525–1533. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, C.; Zheng, N.; Le, D.; Zhou, J. Superhydrophobic Surface Preparation and Wettability Transition of Titanium Alloy with Micro/Nano Hierarchical Texture. Materials 2018, 11, 2210. [Google Scholar] [CrossRef]
- Nikosokhan, R.; Norouzbeigi, R.; Velayi, E. Fabrication of cobalt-based superhydrophobic coating with micro/nano hierarchical structure without additional hydrophobization treatment. Ceram. Int. 2021, 47, 30711–30721. [Google Scholar] [CrossRef]
- Kwon, T.W.; Lee, K.H.; Seo, Y.M.; Jang, J.; Ha, M.Y. Dynamic Wetting Behaviors of Water Droplets on Surfaces with Dual Structures at the Nanoscale. Int. J. Multiph. Flow 2020, 129, 103352. [Google Scholar] [CrossRef]
- Zhang, Z.; Ha, M.Y.; Jang, J. Contrasting water adhesion strengths of hydrophobic surfaces engraved with hierarchical grooves: Lotus leaf and rose petal effects. Nanoscale 2017, 9, 16200–16204. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Kim, H.; Ha, M.Y.; Jang, J. Molecular dynamics study on the wettability of a hydrophobic surface textured with nanoscale pillars. Phys. Chem. Chem. Phys. 2014, 16, 5613–5621. [Google Scholar] [CrossRef] [PubMed]
- Bai, L.; Kim, K.; Ha, M.Y.; Ahn, Y.; Jang, J. Molecular Insights on the Wetting Behavior of a Surface Corrugated with Nanoscale Domed Pillars. Langmuir 2021, 37, 9336–9345. [Google Scholar] [CrossRef]
- Abdoul-Carime, H.; Berthias, F.; Feketeová, L.; Marciante, M.; Calvo, F.; Forquet, V.; Chermette, H.; Farizon, B.; Farizon, M.; Märk, T.D. Velocity of a Molecule Evaporated from a Water Nanodroplet: Maxwell–Boltzmann Statistics versus Non-Ergodic Events. Angew. Chem. Int. Ed. 2015, 54, 14685–14689. [Google Scholar] [CrossRef] [PubMed]
- VandeVondele, J.; Mohamed, F.; Krack, M.; Hutter, J.; Sprik, M.; Parrinello, M. The influence of temperature and density functional models in ab initio molecular dynamics simulation of liquid water. J. Chem. Phys. 2004, 122, 014515. [Google Scholar] [CrossRef]
- Hung, S.W.; Hsiao, P.Y.; Chen, C.P.; Chieng, C.C. Wettability of Graphene-Coated Surface: Free Energy Investigations Using Molecular Dynamics Simulation. J. Phys. Chem. C 2015, 119, 8103–8111. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Crozier, P.S.; Rowley, R.L.; Henderson, D. Molecular-dynamics simulations of ion size effects on the fluid structure of aqueous electrolyte systems between charged model electrodes. J. Chem. Phys. 2001, 114, 7513–7517. [Google Scholar] [CrossRef]
- Tildesley, D.; Allen, M. Computer Simulation of Liquids; Clarendon: Oxford, UK, 1987. [Google Scholar]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A Gen. Phys. 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Tribello, G.A.; Bonomi, M.; Branduardi, D.; Camilloni, C.; Bussi, G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 2014, 185, 604–613. [Google Scholar] [CrossRef]
- Khalkhali, M.; Kazemi, N.; Zhang, H.; Liu, Q. Wetting at the nanoscale: A molecular dynamics study. J. Chem. Phys. 2017, 146, 114704. [Google Scholar] [CrossRef]
- Wang, F.-C.; Zhao, Y.-P. Contact angle hysteresis at the nanoscale: A molecular dynamics simulation study. Colloid Polym. Sci. 2013, 291, 307–315. [Google Scholar] [CrossRef]
- Walther, J.H.; Jaffe, R.; Halicioglu, T.; Koumoutsakos, P. Carbon Nanotubes in Water: Structural Characteristics and Energetics. J. Phys. Chem. B 2001, 105, 9980–9987. [Google Scholar] [CrossRef]
- Heinz, H.; Lin, T.-J.; Kishore Mishra, R.; Emami, F.S. Thermodynamically Consistent Force Fields for the Assembly of Inorganic, Organic, and Biological Nanostructures: The INTERFACE Force Field. Langmuir 2013, 29, 1754–1765. [Google Scholar] [CrossRef] [PubMed]
- Pramanik, C.; Gissinger, J.R.; Kumar, S.; Heinz, H. Carbon Nanotube Dispersion in Solvents and Polymer Solutions: Mechanisms, Assembly, and Preferences. ACS Nano 2017, 11, 12805–12816. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).