Exploring Routes to Enhance the Calculation of Free Energy Differences via Non-Equilibrium Work SQM/MM Switching Simulations Using Hybrid Charge Intermediates between MM and SQM Levels of Theory or Non-Linear Switching Schemes
Abstract
1. Introduction
2. Results
2.1. Overview of Calculated Free Energy Differences and Paths
2.2. Performances of 2 and 5 ps Linear Switching Protocols in Solution
2.3. Performances of Hybrid Charge Intermediates
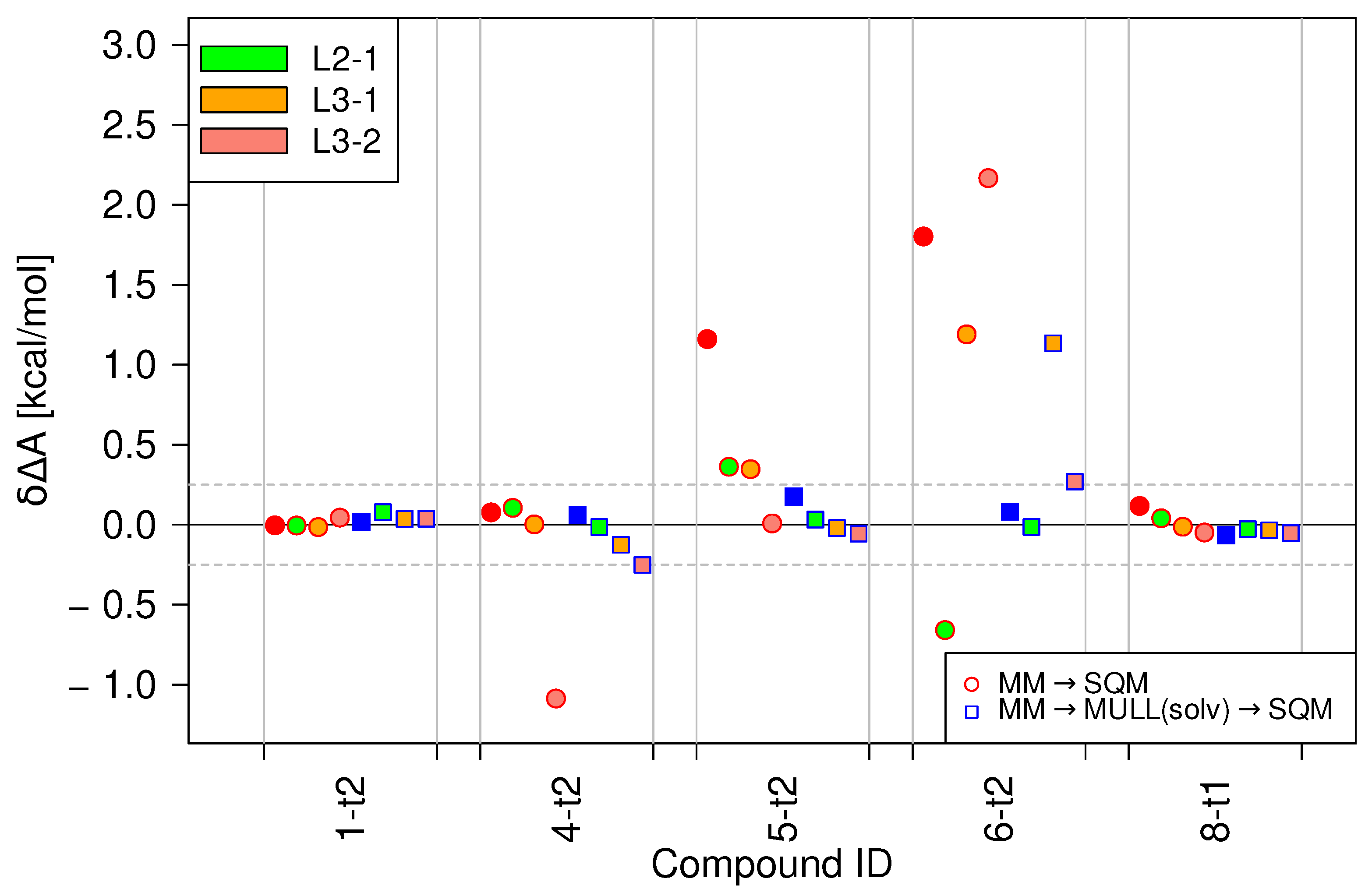
2.4. Performances of Modified Switching Protocols
2.5. A Detailed Analysis of the Factors Affecting Convergence
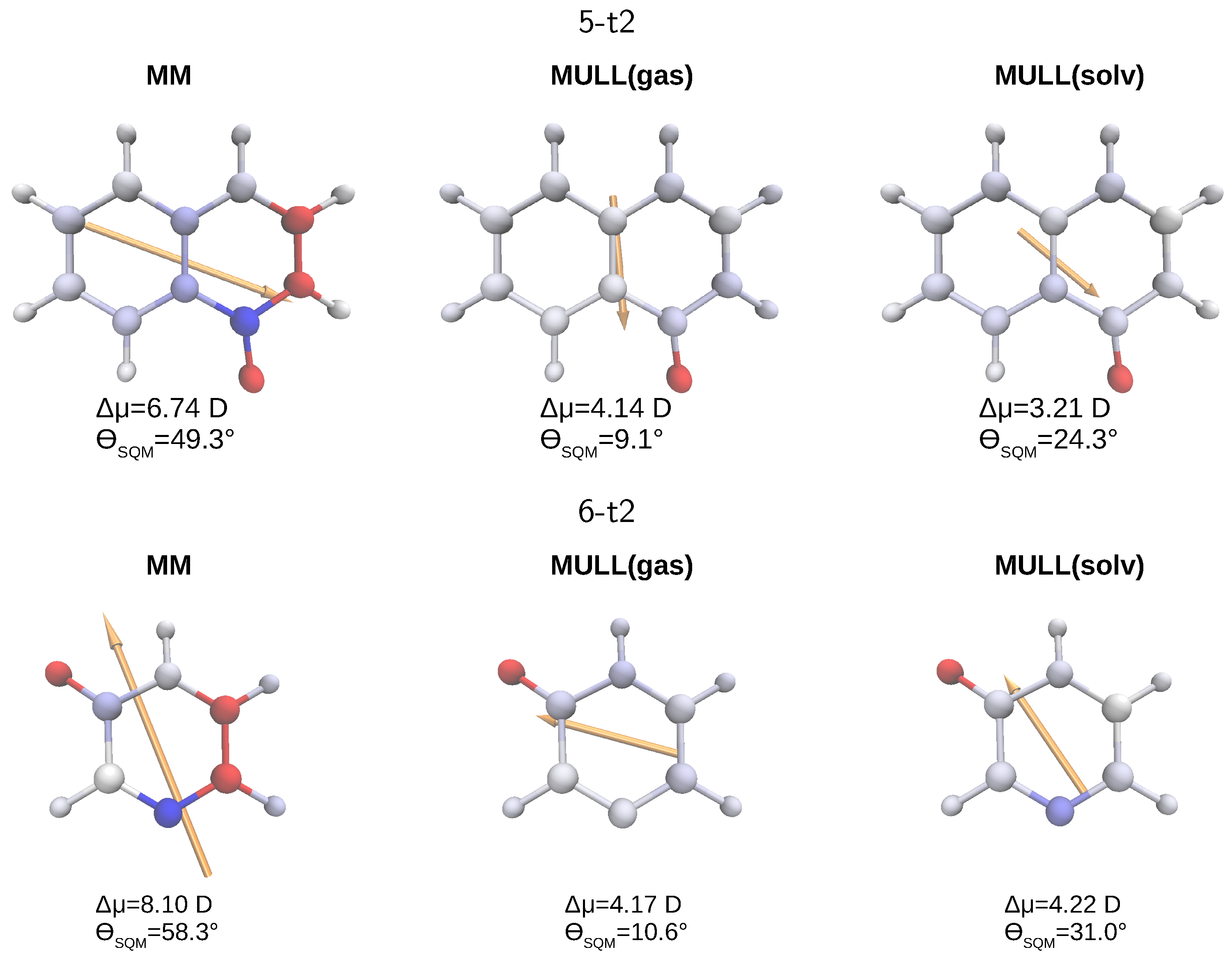
2.5.1. Effects of Charge Distribution on Solute Properties
2.5.2. Effects of Charge Distribution on the First Solvation Shell
2.5.3. Water Reorientation Dynamics
2.5.4. Interplay between Charge Distribution and Conformational Preferences
3. Discussion
4. Materials and Methods
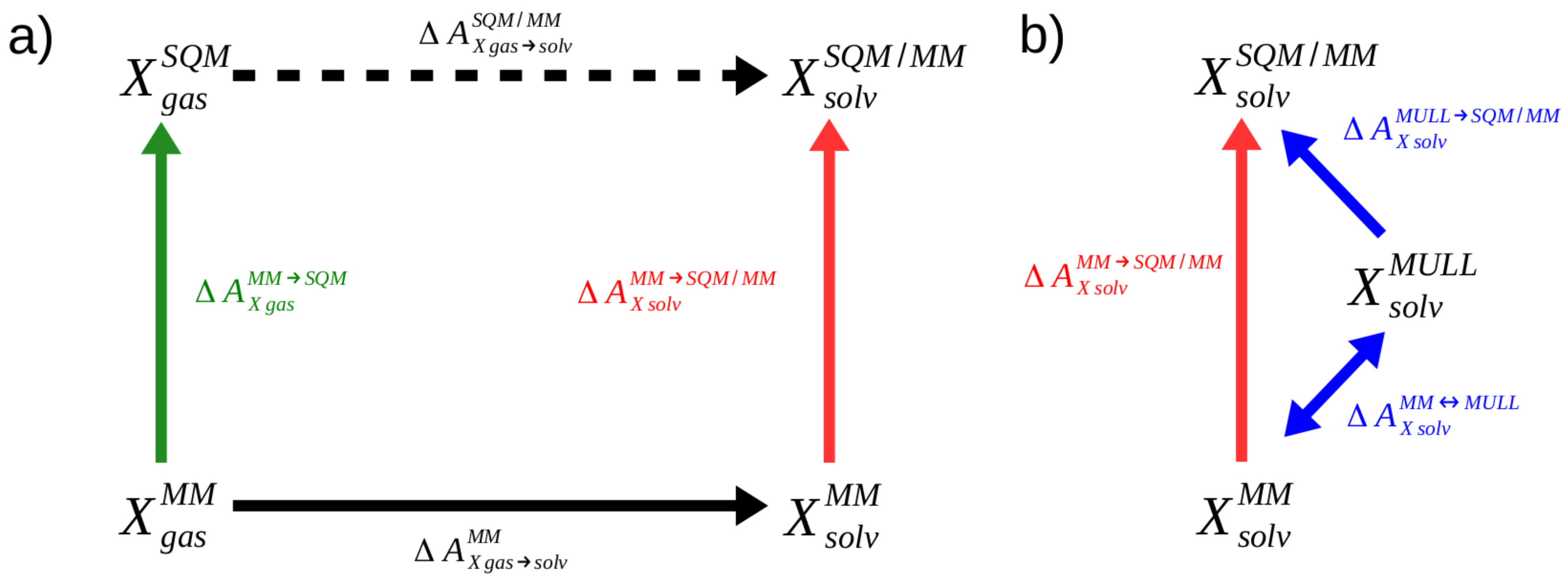
4.1. Computing Free Energy Differences between the Levels of Theory Using NEW Methods
4.2. Choice of Model Systems
4.3. Strategies to Improve the Convergences of NEW Simulations
4.3.1. Hybrid Charge Intermediates
4.3.2. Stepwise Linear Switching Protocols
4.3.3. Analyses Carried Out
Characterizing Charge Distributions
Characterization of the First Solvation Shell
Dynamics of Solvent Reorientation
4.4. Overview of Simulations Carried Out
4.4.1. Simulation Details
Preparation and Initial Equilibration
Force Field-Based Equilibrium Simulations
SQM(/MM) Equilibrium Simulations
4.4.2. Non-Equilibrium Work Simulations
4.4.3. Calculation of :
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MD | Molecular Dynamics |
| MM | Molecular Mechanics |
| (S)QM | (Semi-empirical-)Quantum Mechanics |
| (S)QM/MM | (Semi-empirical-)Quantum Mechanical/ Molecular Mechanical hybrid methods |
| FES | Free energy simulation |
| FEP | Free energy perturbation |
| TI | Thermodynamic integration |
| BAR | Bennett’s acceptance ratio |
| NEW | Non-equilibrium work methods |
| JAR | Jarzynski’s Equation |
| CRO | Crook’s Equation |
References
- Bash, P.A.; Singh, U.C.; Langridge, R.; Kollman, P.A. Free Energy Calculations by Computer Simulation. Science 1987, 236, 564–568. [Google Scholar] [CrossRef]
- Gao, J.; Kuczera, K.; Tidor, B.; Karplus, M. Hidden Thermodynamics of Mutant Proteins: A Molecular Dynamics Analysis. Science 1989, 244, 1069–1072. [Google Scholar] [CrossRef]
- Chodera, J.D.; Mobley, D.L.; Shirts, M.R.; Dixon, R.W.; Branson, K.; Pande, V.S. Alchemical free energy methods for drug discovery: Progress and challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. [Google Scholar] [CrossRef]
- Barros, E.P.; Ries, B.; Böselt, L.; Champion, C.; Riniker, S. Recent developments in multiscale free energy simulations. Curr. Opin. Struct. Biol. 2022, 72, 55–62. [Google Scholar] [CrossRef]
- Mey, A.S.; Allen, B.K.; Macdonald, H.E.B.; Chodera, J.D.; Hahn, D.F.; Kuhn, M.; Michel, J.; Mobley, D.L.; Naden, L.N.; Prasad, S.; et al. Best practices for alchemical free energy calculations [Article v1.0]. Living J. Comput. Mol. Sci. 2020, 2, 18378. [Google Scholar] [CrossRef]
- Schindler, C.E.; Baumann, H.; Blum, A.; Boöse, D.; Buchstaller, H.P.; Burgdorf, L.; Cappel, D.; Chekler, E.; Czodrowski, P.; Dorsch, D.; et al. Large-scale assessment of binding free energy calculations in active drug discovery projects. J. Chem. Inf. Model. 2020, 60, 5457–5474. [Google Scholar] [CrossRef]
- Cournia, Z.; Allen, B.; Sherman, W. Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model. 2017, 57, 2911–2937. [Google Scholar] [CrossRef]
- Limongelli, V. Ligand binding free energy and kinetics calculation in 2020. Comput. Mol. Sci. 2020, 10, e1455. [Google Scholar] [CrossRef]
- Maier, S.; Thapa, B.; Erickson, J.; Raghavachari, K. Comparative assessment of QM-based and MM-based models for prediction of protein–ligand binding affinity trends. Phys. Chem. Chem. Phys. 2022, 24, 14525–14537. [Google Scholar] [CrossRef]
- Yang, W.; Gao, Y.Q.; Cui, Q.; Ma, J.; Karplus, M. The missing link between thermodynamics and structure in F1-ATPase. Proc. Natl. Acad. Sci. USA 2003, 100, 874–879. [Google Scholar] [CrossRef]
- Mulholland, A.J. Chemical accuracy in QM/MM calculations on enzyme-catalysed reactions. Chem. Cent. J. 2007, 1, 19. [Google Scholar] [CrossRef] [PubMed]
- Lev, B.; Roux, B.; Noskov, S.Y. Relative free energies for hydration of monovalent ions from QM and QM/MM simulations. J. Chem. Theory Comput. 2013, 9, 4165–4175. [Google Scholar] [CrossRef] [PubMed]
- Riahi, S.; Roux, B.; Rowley, C.N. QM/MM molecular dynamics simulations of the hydration of Mg (II) and Zn (II) ions. Can. J. Chem. 2013, 91, 552–558. [Google Scholar] [CrossRef]
- Delgado, J.A.; Wineman-Fisher, V.; Pandit, S.; Varma, S. Inclusion of High-Field Target Data in AMOEBA’s Calibration Improves Predictions of Protein–Ion Interactions. J. Chem. Inf. Model. 2022, 62, 4713–4726. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Cui, Q.; Min, D.; Li, H. QM/MM Alchemical Free Energy Simulations: Challenges and Recent Developments. Annu. Rep. Comput. Chem. 2010, 6, 51–62. [Google Scholar] [CrossRef]
- Gao, J. Absolute free energy of solvation from Monte Carlo simulations using combined quantum and molecular mechanical potentials. J. Phys. Chem. 1992, 96, 537–540. [Google Scholar] [CrossRef]
- Luzhkov, V.; Warshel, A. Microscopic models for quantum mechanical calculations of chemical processes in solutions: LD/AMPAC and SCAAS/AMPAC calculations of solvation energies. J. Comput. Chem. 1992, 13, 199–213. [Google Scholar] [CrossRef]
- Cui, Q.; Pal, T.; Xie, L. Biomolecular QM/MM Simulations: What Are Some of the “Burning Issues”? J. Phys. Chem. B 2021, 125, 689–702. [Google Scholar] [CrossRef]
- Hudson, P.S.; Aviat, F.; Meana-Pañeda, R.; Warrensford, L.; Pollard, B.C.; Prasad, S.; Jones, M.R.; Woodcock, H.L.; Brooks, B.R. Obtaining QM/MM binding free energies in the SAMPL8 drugs of abuse challenge: Indirect approaches. J. Comput.-Aided Mol. Des. 2022, 36, 263–277. [Google Scholar] [CrossRef]
- Wang, X.; He, Q.; Sun, Z. BAR-based multi-dimensional nonequilibrium pulling for indirect construction of a QM/MM free energy landscape. Phys. Chem. Chem. Phys. 2019, 21, 6672–6688. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, Z. BAR-Based Multi-Dimensional Nonequilibrium Pulling for Indirect Construction of QM/MM Free Energy Landscapes: Varying the QM Region. Adv. Theory Simula. 2021, 4, 2100185. [Google Scholar] [CrossRef]
- Wang, J.N.; Liu, W.; Li, P.; Mo, Y.; Hu, W.; Zheng, J.; Pan, X.; Shao, Y.; Mei, Y. Accelerated Computation of Free Energy Profile at Ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semiempirical Reference Potential. 4. Adaptive QM/MM. J. Chem. Theory Comput. 2021, 17, 1318–1325. [Google Scholar] [CrossRef] [PubMed]
- Hudson, P.S.; Han, K.; Woodcock, H.L.; Brooks, B.R. Force matching as a stepping stone to QM/MM CB [8] host/guest binding free energies: A SAMPL6 cautionary tale. J. Comput.-Aided Mol. Des. 2018, 32, 983–999. [Google Scholar] [CrossRef] [PubMed]
- König, G.; Pickard, F.C.; Mei, Y.; Brooks, B.R. Predicting hydration free energies with a hybrid QM/MM approach: An evaluation of implicit and explicit solvation models in SAMPL4. J. Comput.-Aided Mol. Des. 2014, 28, 245–257. [Google Scholar] [CrossRef]
- König, G.; Brooks, B.R.; Thiel, W.; York, D.M. On the convergence of multi-scale free energy simulations. Mol. Simul. 2018, 44, 1062–1081. [Google Scholar] [CrossRef]
- König, G.; Brooks, B.R. Predicting binding affinities of host-guest systems in the SAMPL3 blind challenge: The performance of relative free energy calculations. J. Comput.-Aided Mol. Des. 2012, 26, 543–550. [Google Scholar] [CrossRef]
- Zeng, J.; Tao, Y.; Giese, T.J.; York, D.M. Modern semiempirical electronic structure methods and machine learning potentials for drug discovery: Conformers, tautomers, and protonation states. J. Chem. Phys. 2023, 158, 124110. [Google Scholar] [CrossRef]
- Heimdal, J.; Ryde, U. Convergence of QM/MM free-energy perturbations based on molecular-mechanics or semiempirical simulations. Phys. Chem. Chem. Phys. 2012, 14, 12592–12604. [Google Scholar] [CrossRef]
- Giese, T.J.; York, D.M. Development of a robust indirect approach for MM→QM free energy calculations that combines force-matched reference potential and Bennett’s acceptance ratio methods. J. Chem. Theory Comput. 2019, 15, 5543–5562. [Google Scholar] [CrossRef]
- Hudson, P.S.; Woodcock, H.L.; Boresch, S. Use of Nonequilibrium Work Methods to Compute Free Energy Differences Between Molecular Mechanical and Quantum Mechanical Representations of Molecular Systems. J. Phys. Chem. Lett. 2015, 6, 4850–4856. [Google Scholar] [CrossRef]
- Kearns, F.L.; Hudson, P.S.; Woodcock, H.L.; Boresch, S. Computing Converged Free Energy Differences Between Levels of Theory via Nonequilibrium Work Methods: Challenges and Opportunities. J. Comput. Chem. 2017, 38, 1376–1388. [Google Scholar] [CrossRef] [PubMed]
- Boresch, S.; Woodcock, H.L. Convergence of single-step free energy perturbation. Mol. Phys. 2017, 115, 1200–1213. [Google Scholar] [CrossRef]
- Hudson, P.S.; Boresch, S.; Rogers, D.M.; Woodcock, H.L. Accelerating QM/MM Free Energy Computations via Intramolecular Force Matching. J. Chem. Theory Comput. 2018, 14, 6327–6335. [Google Scholar] [CrossRef]
- Kearns, F.L.; Warrensford, L.; Boresch, S.; Woodcock, H.L. The Good, the Bad, and the Ugly: “HiPen”, a New Dataset for Validating (S)QM/MM Free Energy Simulations. Molecules 2019, 24, 681. [Google Scholar] [CrossRef]
- Hudson, P.S.; Woodcock, H.L.; Boresch, S. Use of Interaction Energies in QM/MM Free Energy Simulations. J. Chem. Theory Comput. 2019, 15, 4632–4645. [Google Scholar] [CrossRef]
- Schöller, A.; Kearns, F.; Woodcock, H.L.; Boresch, S. Optimizing the Calculation of Free Energy Differences in Nonequilibrium Work SQM/MM Switching Simulations. J. Phys. Chem. B 2022, 126, 2798–2811. [Google Scholar] [CrossRef]
- Ito, S.; Cui, Q. Multi-level free energy simulation with a staged transformation approach. J. Chem. Phys. 2020, 153, 044115. [Google Scholar] [CrossRef]
- Maroncelli, M.; Fleming, G.R. Computer simulation of the dynamics of aqueous solvation. J. Chem. Phys. 1988, 89, 5044–5069. [Google Scholar] [CrossRef]
- Maroncelli, M. The dynamics of solvation in polar liquids. J. Mol. Liq. 1993, 57, 1–37. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Crooks, G.E. Path-ensemble averages in systems driven far from equilibrium. Phys. Rev. E 2000, 61, 2361. [Google Scholar] [CrossRef]
- Bennett, C.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Marenich, A.V.; Jerome, S.V.; Cramer, C.J.; Truhlar, D.G. Charge Model 5: An Extension of Hirshfeld Population Analysis for the Accurate Description of Molecular Interactions in Gaseous and Condensed Phases. J. Chem. Theory Comput. 2012, 8, 527–541. [Google Scholar] [CrossRef] [PubMed]
- Dellago, C.; Hummer, G. Computing Equilibrium Free Energies Using Non-Equilibrium Molecular Dynamics. Entropy 2014, 16, 41–61. [Google Scholar] [CrossRef]
- Pohorille, A.; Jarzynski, C.; Chipot, C. Good Practices in Free-Energy Calculations. J. Phys. Chem. B 2010, 114, 10235–10253. [Google Scholar] [CrossRef]
- Woodcock, H.L.; Miller, B.T.; Hodoscek, M.; Okur, A.; Larkin, J.D.; Ponder, J.W.; Brooks, B.R. MSCALE: A general utility for multiscale modeling. J. Chem. Theory Comput. 2011, 7, 1208–1219. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L., III; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef]
- Hunter, J.E.; Reinhardt, W.P.; Davis, T.F. A finite-time variational method for determining optimal paths and obtaining bounds on free energy changes from computer simulations. J. Chem. Phys. 1993, 99, 6856–6864. [Google Scholar] [CrossRef]
- Geballe, M.T.; Skillman, A.G.; Nicholls, A.; Guthrie, J.P.; Taylor, P.J. The SAMPL2 Blind Prediction Challenge: Introduction and Overview. J. Comput.-Aided Mol. Des. 2010, 24, 259–279. [Google Scholar] [CrossRef]
- Wahl, O.; Sander, T. Tautobase: An open tautomer database. J. Chem. Inf. Model. 2020, 60, 1085–1089. [Google Scholar] [CrossRef]
- Wieder, M.; Fass, J.; Chodera, J.D. Fitting quantum machine learning potentials to experimental free energy data: Predicting tautomer ratios in solution. Chem. Sci. 2021, 12, 11364–11381. [Google Scholar] [CrossRef] [PubMed]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260. [Google Scholar] [CrossRef]
- Elstner, M. The SCC-DFTB method and its application to biological systems. Theor. Chem. Acc. 2006, 116, 316–325. [Google Scholar] [CrossRef]
- Pearlman, D.A.; Kollman, P.A. The lag between the Hamiltonian and the system configuration in free energy perturbation calculations. J. Chem. Phys. 1989, 91, 7831–7839. [Google Scholar] [CrossRef]
- Hermans, J. Simple analysis of noise and hysteresis in (slow-growth) free energy simulations. J. Phys. Chem. 1991, 95, 9029–9032. [Google Scholar] [CrossRef]
- Jarzynski, C. Rare events and the convergence of exponentially averaged work values. Phys. Rev. E 2006, 73, 046105. [Google Scholar] [CrossRef]
- Heid, E.; Harringer, S.; Schröder, C. The small impact of various partial charge distributions in ground and excited state on the computational Stokes shift of 1-methyl-6-oxyquinolinium betaine in diverse water models. J. Chem. Phys. 2016, 145, 164506. [Google Scholar] [CrossRef]
- Schröder, C.; Heid, E. Computational solvation dynamics: Implementation, application, and validation. In Annual Reports in Computational Chemistry; Elsevier: Amsterdam, The Netherlands, 2020; pp. 93–154. [Google Scholar] [CrossRef]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef]
- Lee, J.; Cheng, X.; Swails, J.M.; Yeom, M.S.; Eastman, P.K.; Lemkul, J.A.; Wei, S.; Buckner, J.; Jeong, J.C.; Qi, Y.; et al. CHARMM-GUI input generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM36 additive force field. J. Chem. Theory Comput. 2016, 12, 405–413. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; MacKerell, A.D., Jr. Automation of the CHARMM General Force Field (CGenFF) I: Bond perception and atom typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Raman, E.P.; MacKerell, A.D., Jr. Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; He, X.; Vanommeslaeghe, K.; MacKerell Jr, A.D. Extension of the CHARMM general force field to sulfonyl-containing compounds and its utility in biomolecular simulations. J. Comput. Chem. 2012, 33, 2451–2468. [Google Scholar] [CrossRef] [PubMed]
- Neria, E.; Fischer, S.; Karplus, M. Simulation of activation free energies in molecular systems. J. Chem. Phys. 1996, 105, 1902. [Google Scholar] [CrossRef]
- Feller, S.E.; Zhang, Y.; Pastor, R.W.; Brooks, B.R. Constant pressure molecular dynamics simulation: The Langevin piston method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Cui, Q.; Elstner, M.; Kaxiras, E.; Frauenheim, T.; Karplus, M. A QM/MM implementation of the self-consistent charge density functional tight binding (SCC-DFTB) method. J. Phys. Chem. B 2001, 105, 569–585. [Google Scholar] [CrossRef]
- Gaus, M.; Goez, A.; Elstner, M. Parametrization and Benchmark of DFTB3 for Organic Molecules. J. Chem. Theory Comput. 2013, 9, 338–354. [Google Scholar] [CrossRef]
- Gaus, M.; Lu, X.; Elstner, M.; Cui, Q. Parameterization of DFTB3/3OB for Sulfur and Phosphorus for Chemical and Biological Applications. J. Chem. Theory Comput. 2014, 10, 1518–1537. [Google Scholar] [CrossRef]
- Lu, X.; Gaus, M.; Elstner, M.; Cui, Q. Parametrization of DFTB3/3OB for Magnesium and Zinc for Chemical and Biological Applications. J. Phys. Chem. B 2015, 119, 1062–1082. [Google Scholar] [CrossRef]
- Kubillus, M.; Kubař, T.; Gaus, M.; Řezáč, J.; Elstner, M. Parameterization of the DFTB3 Method for Br, Ca, Cl, F, I, K, and Na in Organic and Biological Systems. J. Chem. Theory Comput. 2015, 11, 332–342. [Google Scholar] [CrossRef] [PubMed]
- Eastman, P.; Swails, J.; Chodera, J.D.; McGibbon, R.T.; Zhao, Y.; Beauchamp, K.A.; Wang, L.P.; Simmonett, A.C.; Harrigan, M.P.; Stern, C.D.; et al. OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLoS Comput. Biol. 2017, 13, e1005659. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.; Li, P.; Ho, J.; Pu, J.; Mei, Y.; Shao, Y. Accelerated computation of free energy profile at ab initio quantum mechanical/molecular mechanical accuracy via a semi-empirical reference potential. II. Recalibrating semi-empirical parameters with force matching. Phys. Chem. Chem. Phys. 2019, 21, 20595–20605. [Google Scholar] [CrossRef] [PubMed]
- Wood, R.H.; Muhlbauer, W.C.F.; Thompson, P.T. Systematic errors in free energy perturbation calculations due to a finite sample of configuration space: Sample-size hysteresis. J. Phys. Chem. 1991, 95, 6670–6675. [Google Scholar] [CrossRef]
- Wu, D.; Kofke, D.A. Model for small-sample bias of free-energy calculations applied to Gaussian-distributed nonequilibrium work measurements. J. Chem. Phys. 2004, 121, 8742–8747. [Google Scholar] [CrossRef]

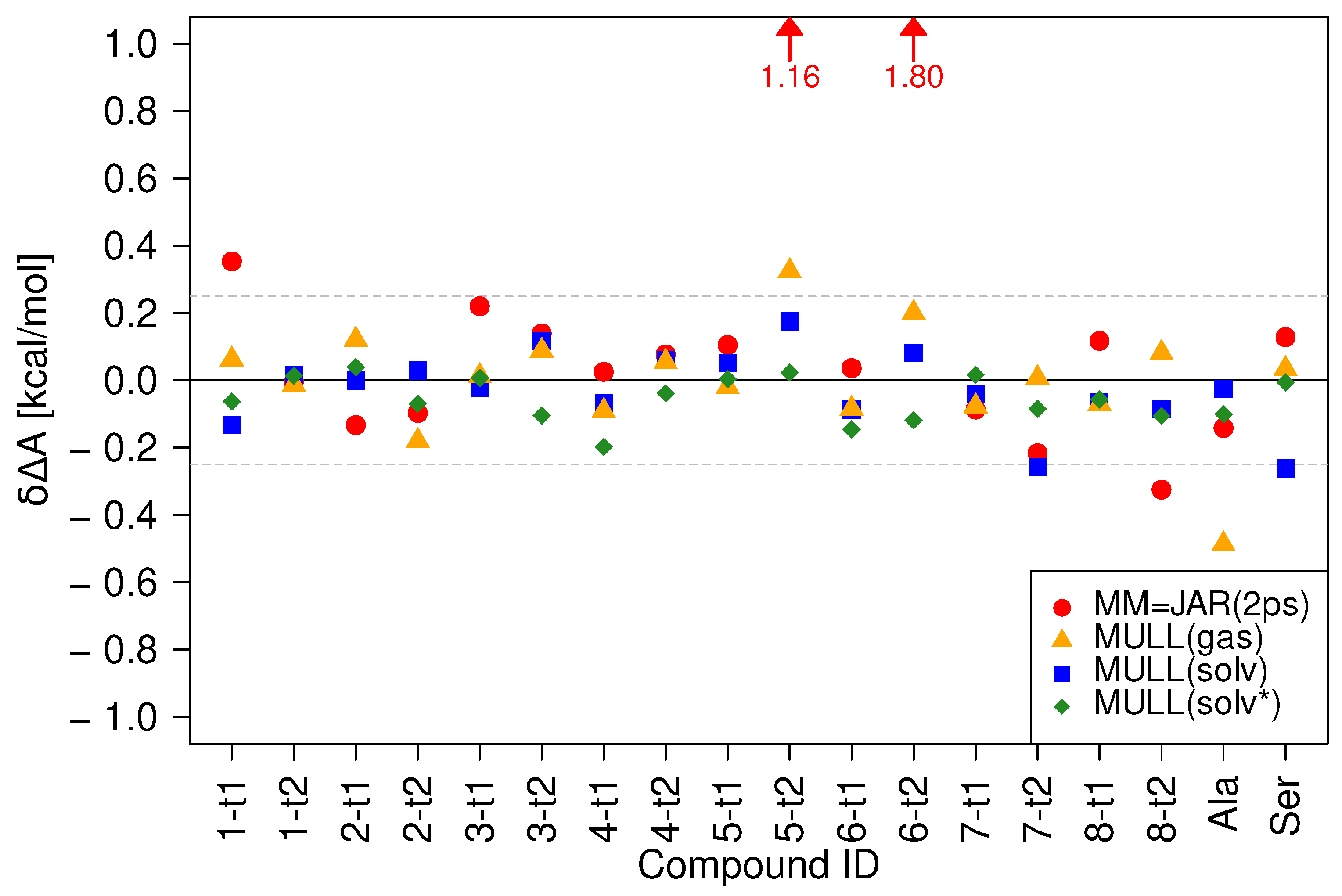
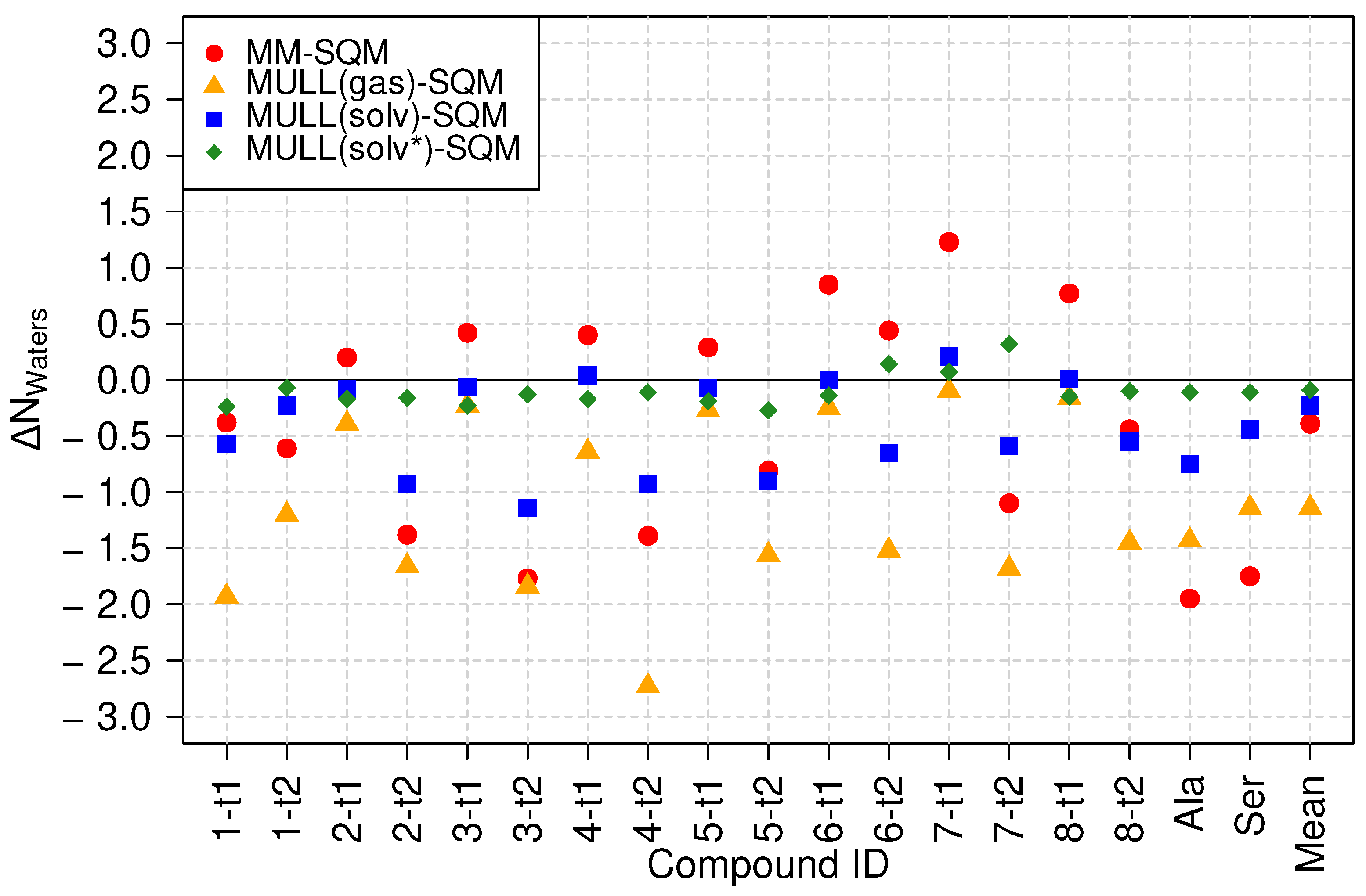


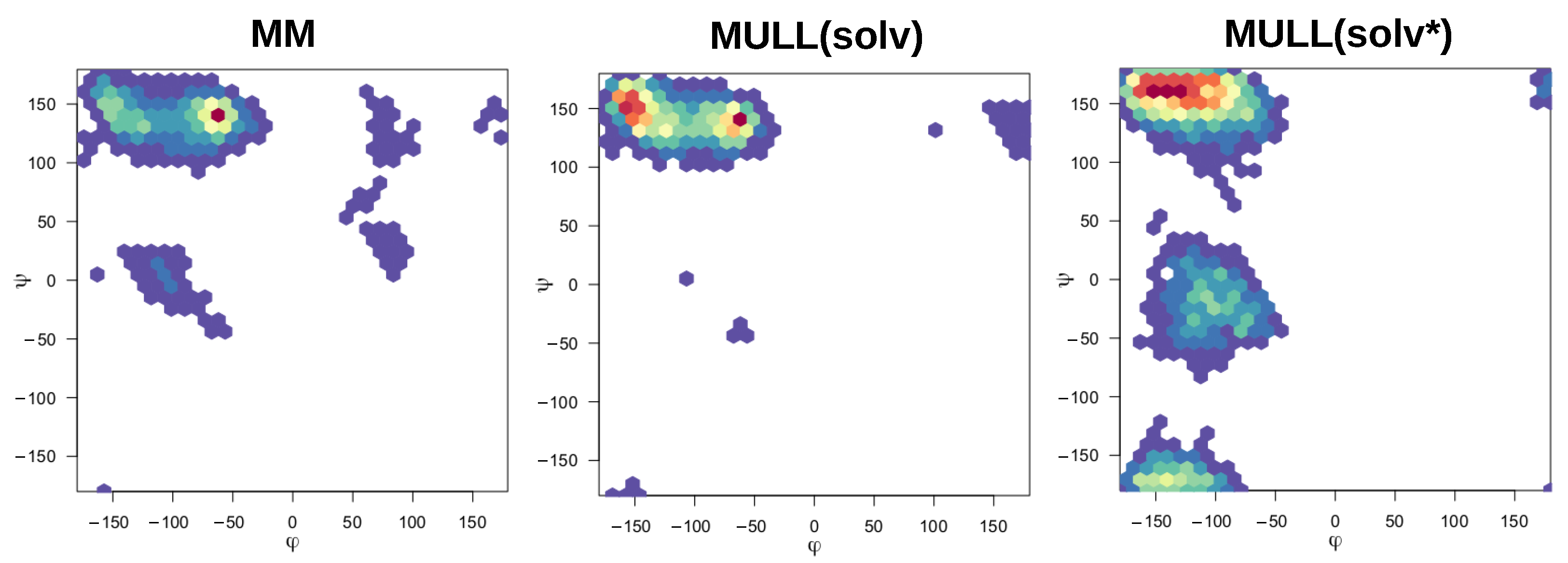
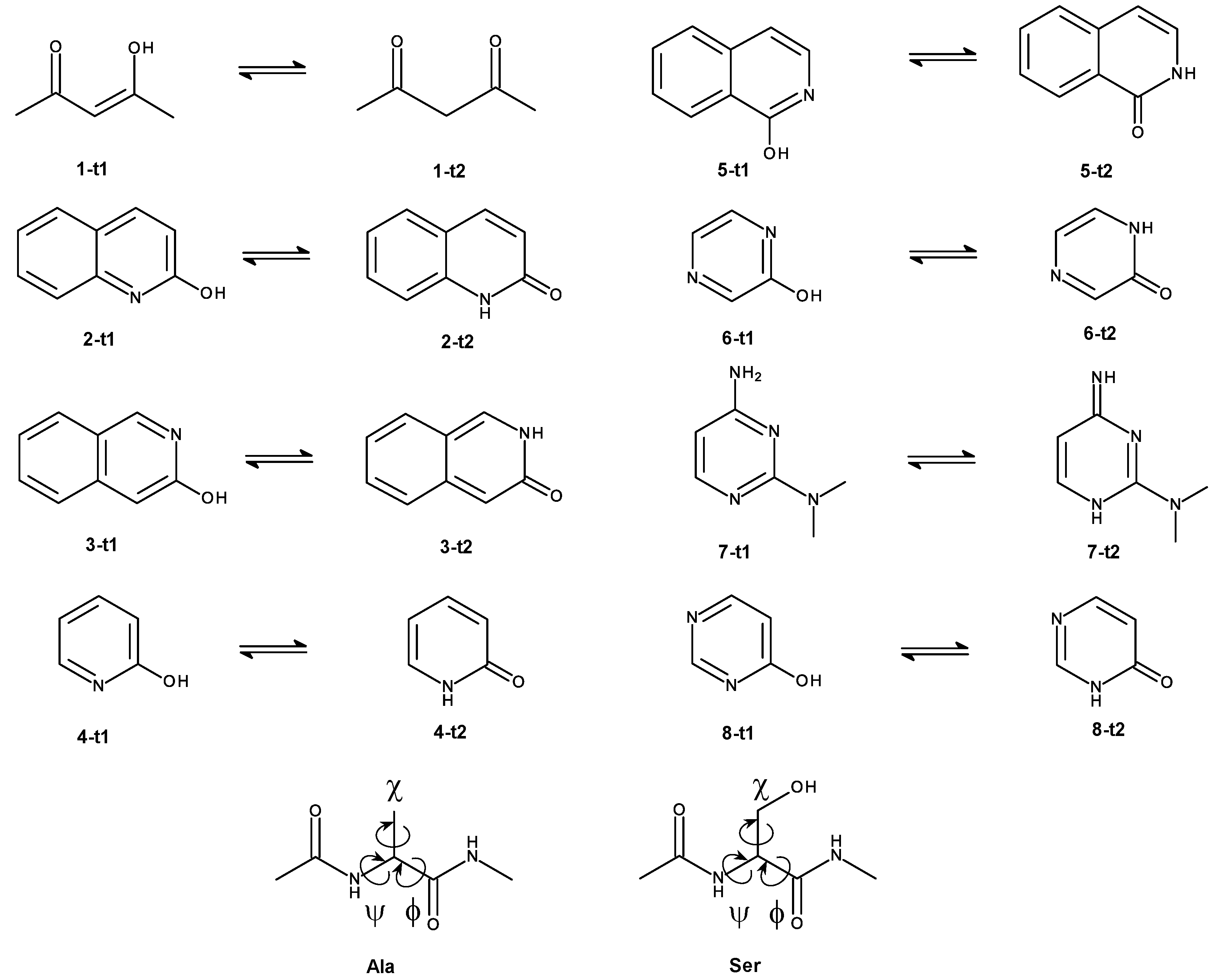
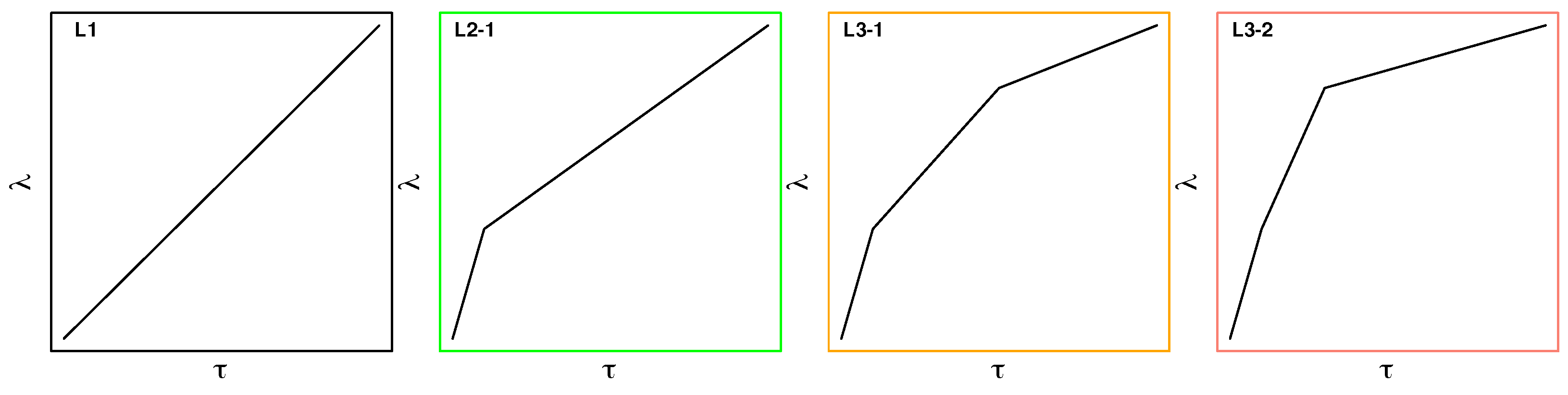
| Pathway | MAD [kcal/mol] | Spread MAD [kcal/mol] | |
|---|---|---|---|
| Min | Max | ||
| MM | 0.29 | 0.01 | 1.80 |
| MULL(gas) | 0.12 | 0.01 | 0.49 |
| MULL(solv) | 0.09 | 0.01 | 0.28 |
| MULL(solv*) | 0.07 | 0.01 | 0.20 |
| Pathway | MAD RMSD | MAD [D] | MAD [°] |
|---|---|---|---|
| MM | 0.14 | 3.38 | 29.8 |
| MULL(gas) | 0.06 | 2.44 | 7.6 |
| MULL(solv) | 0.04 | 1.81 | 16.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schöller, A.; Woodcock, H.L.; Boresch, S. Exploring Routes to Enhance the Calculation of Free Energy Differences via Non-Equilibrium Work SQM/MM Switching Simulations Using Hybrid Charge Intermediates between MM and SQM Levels of Theory or Non-Linear Switching Schemes. Molecules 2023, 28, 4006. https://doi.org/10.3390/molecules28104006
Schöller A, Woodcock HL, Boresch S. Exploring Routes to Enhance the Calculation of Free Energy Differences via Non-Equilibrium Work SQM/MM Switching Simulations Using Hybrid Charge Intermediates between MM and SQM Levels of Theory or Non-Linear Switching Schemes. Molecules. 2023; 28(10):4006. https://doi.org/10.3390/molecules28104006
Chicago/Turabian StyleSchöller, Andreas, H. Lee Woodcock, and Stefan Boresch. 2023. "Exploring Routes to Enhance the Calculation of Free Energy Differences via Non-Equilibrium Work SQM/MM Switching Simulations Using Hybrid Charge Intermediates between MM and SQM Levels of Theory or Non-Linear Switching Schemes" Molecules 28, no. 10: 4006. https://doi.org/10.3390/molecules28104006
APA StyleSchöller, A., Woodcock, H. L., & Boresch, S. (2023). Exploring Routes to Enhance the Calculation of Free Energy Differences via Non-Equilibrium Work SQM/MM Switching Simulations Using Hybrid Charge Intermediates between MM and SQM Levels of Theory or Non-Linear Switching Schemes. Molecules, 28(10), 4006. https://doi.org/10.3390/molecules28104006





