Abstract
In this study, an old concept of anchimeric assistance is viewed from a different angle. Primary cations with two different heteroatomic substituents in the α-position to the cationic carbon atom CHXY–CH2+ (X, Y = Me2N, MeO, Me3Si, Me2P, MeS, MeS, Br) can be stabilized by the migration of either the X or Y group to the cation center. In each case, the migration can be either complete, resulting in the transfer of the migrating group to the adjacent carbon atom and the formation of a secondary carbocation stabilized by the remaining heteroatom, or incomplete, leading to an anchimerically assisted iranium ion. For all combinations of the above groups, these transformations have been studied by theoretical analysis at the MP2/aug-cc-pVTZ level and were shown to occur depending on the ability of anchimeric assistance by X and Y, as well as the conformation of the starting primary carbocation. In the conformers of α-amino cations with the p-orbital, C–N bond and the nitrogen lone pair in one plane, the Me2N group migrates to the cationic center to give aziranium ions. Otherwise, the second heteroatom is shifted to give iminium ions, without or with very slight anchimeric assistance. In the α-methoxy cations, the MeO group can be shifted to the cationic center to give the O-anchimerically assisted ions as local minima, the global minima being the ions anchimerically assisted by another heteroatom. The electropositive silicon tends to migrate towards the cationic center, but with the formation of a π-complex of the Me3Si cation with the C=C bond rather than a Si-anchimerically assisted cation. The phosphorus atom can either fully migrate to the cationic center (X = P, Y = S, Se) or form anchimerically stabilized phosphiranium ions (X = P, Y = O, Si, Br). The order of the anchimeric assistance for the heaviest atoms decreases in the order Se >> S > Br.
1. Introduction
The concept of anchimeric assistance (or acceleration of a reaction due to neighboring group participation) is over 60 years old [1,2]. It has also been termed synartetic acceleration [3,4,5] and, in the chemistry of carbocations, non-vertical stabilization [6,7]. Over the past decades, the concept has been broadened and enriched by new data. In addition to the neighboring aryl or other carbon-centered groups [1,2,3,4,5,6,8,9], the anchimeric assistance by many other juxtaposed atoms and groups has been studied. For illustration, the anchimeric assistance of nitrogen [10,11,12,13], oxygen [14,15], halogens [16,17], and even hydrogen atoms [18] can be mentioned. Well-documented are the abilities of various metals —chromium [19], platinum [20], palladium [21], vanadium [22], and many others—to facilitate different reactions by anchimeric assistance. Well-known is anchimeric assistance in the hydrolysis of yperite and nitrogen yperite [23,24], in which the generated S or N three-membered rings strongly accelerate the reaction, as well as in the reactions of triphenylphosphine with α,β-unsaturated carboxylic acids [24] and bifunctional tertiary phosphines with activated alkenes [25]. The mechanism of anchimeric assistance was also analyzed theoretically at the DFT level [12,26,27,28] and proved experimentally [9,29,30]. Of most relevance to the present work are the studies on anchimeric assistance by silicon- [31,32], phosphorus- [33], sulfur-, and selenium-containing groups [7,13,34,35], which shows a pronounced stabilizing effect on the carbocationic intermediates.
Computational Details
All calculations were performed with full geometry optimization using the MP2/aug-cc-pVTZ method as implemented in Gaussian 09 [36]. Conditionally, cations with incomplete transfer of group X or Y were considered as “iranium” when the C–C–X(Y) angle was less than 100° and as “open” when it was more than 100° and close to the tetrahedral angle of 109.5°. Of course, any “demarcation” between the “iranium” and “open” forms is conditional, but the deviation of this angle from the tetrahedral value of ten to fifty degrees can only be due to attractive interaction between the X or Y group and the adjacent carbocationic center, while a deviation of only several degrees is insignificant and does not imply any notable interaction. Apart from the “iranium” or “open” structure obtained during geometry optimization with the shift of group X, the isomeric cations corresponding to the complete or incomplete transfer of group Y were calculated as local or global minima on the PES. Since the course of optimization depends on the relative orientation of the empty p-orbital on the carbocation center and the C–X bond, as well as the lone pair on heteroatom X, different starting geometries of the primary cations were examined. The total energies of the stationary points optimized as global or local minima were compared. No frequency calculations were performed because of the extremely high computational costs at such a high level of theory.
2. Results and Discussion
In the present paper, the problem of anchimeric assistance is studied from a new perspective, namely, by investigation of the relative ability of different groups attached to the same carbon to stabilize the adjacent primary carbocationic center either by anchimeric assistance via the formation of the X- or Y-type iranium cation or via full migration to this carbon atom, forming linear secondary cations, as shown in Figure 1.
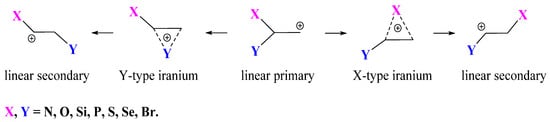
Figure 1.
Stabilization of the primary cation with respect to the iranium cation by anchimeric assistance or to the secondary cation by 1,2-shift of the substituent.
For this, high-level theoretical calculations were performed for all 21 combinations of substituents X and Y, including both global and local minima corresponding to the iranium and linear cations presented in Figure 1. In order to avoid possible isomerization via hydrogen migration from the XH or YH group, all heteroatoms were protected by methyl groups (OMe, SMe, SeMe, NMe2, PMe2, and SiMe3), which allowed for the analysis of “pure” anchimeric assistance or migration of X or Y. Among the issues addressed in this study are the dependence of the type of the migrating group and the degree of its shift towards the carbocationic center on the nature of the migrating and remaining groups X and Y, the reasons for the formation of local (kinetically controlled) and global (thermodynamically controlled) products on the potential energy surface (PES), and the relative effectiveness of anchimeric assistance versus stabilization by direct conjugation with the lone pair of a heteroatom.
The main factors affecting the degree of anchimeric assistance are the covalent radius of the interacting group and its polarizability. The larger the covalent radius, the longer the distance at which the migrating group interacts effectively with the carbocationic center. The larger the polarizability, the easier it is to induce a dipole, and hence the larger the binding energy. The ability of a specific group to stabilize the existing or incipient charge on the adjacent carbon atom is usually estimated by comparing the rates of the reactions of the parent and substituted compounds. By contrast, in the present work, the relative abilities of different groups to stabilize the positive charge are estimated from the relative stabilities of the structures formed by full or incomplete transfer of one of two substituents in the same molecule. This raises four main questions that are answered in this paper: (i) that of which group migrates spontaneously during geometry optimization; (ii) that of which factors are responsible for the migration of a particular group; (iii) that of which stabilization is preferable: anchimeric assistance with the partially shifted group X or direct conjugation with the lone pair on the non-migrating group Y; and (iv) that of the structure of the formed cations (covalently bound iranium ions, anchimerically assisted ions, or π-complexes with practically intact double bonds). The primary cations in Figure 1 are inherently unstable and in all cases are stabilized by group X or Y to either iranium or secondary cations. Below, the transformations of primary cations with all possible combinations of groups X and Y will be considered.
X = NMe2, Y = OMe (1). The neighboring amino group participation may result in the formation of the rearranged products via the formation of the anchimerically assisted aziridinium ion. For example, as applied to our case, the amino group wins the competition with iodine, as proved by the intramolecular ring opening of the preliminarily formed halogen-assisted cation [37]. The result of geometry optimization of cation 1 depends on the relative orientations of the Me–N–Me and N–C–CH2 planes. If they are perpendicular, that is, if the p-orbital and the nitrogen lone pair are eclipsed (lie in the same plane), the aziranium cation 1b is formed; for all other conformations, full migration of the methoxy group is observed, resulting in the iminium cation 1a, as shown in Scheme 1.

Scheme 1.
Iminium 1a versus aziranium 1b cation formation.
No isomeric oxiranium cation analogous to 1b could be located. However, linear oxenium cation 1c was found to be at a local minimum on the PES (Figure 2). The relative energies increased in the order 1a (0) < 1b (10.0) < 1c (28.5 kcal/mol) (see Supplementary Materials).
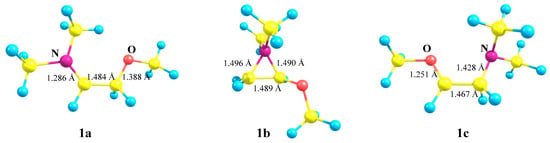
Figure 2.
Optimized geometries of the iminium 1a, aziranium 1b, and oxenium 1c cations.
The geometries of the located minima are given in Figure 2. Strong N and O stabilization of the secondary cations 1a and 1c is evidenced by ~0.14 Å shortening of the N–C+ and O–C+ bonds. In both 1a and 1c, the C–C bond length is close to that of the ordinary bond, suggesting their existence as iminium (1a) or oxenium (1c) cations. The 0.017 Å longer C–C bond in 1a relative to that in 1c is indicative of stronger N versus O stabilization. The lengths of the C–N bonds in 1a and in the almost equilateral triangle of 1b fall in the range of normal ordinary C–N bonds.
Therefore, the relative orientation of the C–N bond and the nitrogen lone pair with respect to the empty p-orbital on the carbocation center in 1 has a strong impact on the migration ability of the NMe2 group.
The Mulliken charge distribution in the aziranium cation 1b is strongly polarized: qN = +0.621, qCH2 = −0.683, and qCH = +0.101, suggesting the covalent nature of the N–CH bond and the electrovalent nature of the N–CH2 bond.
X = NMe2, Y = SiMe3 (2). For the same reasons, optimization of cation 2 gives rise to the iminium cation 2a via the migration of the Me3Si group for all initial conformations except the one that has both the Me2N–C bond and the nitrogen lone pair in the same plane with the cationic p-orbital. In the latter case, aziranium cation 2b was located on the PES as the local minimum lying 20.8 kcal/mol above the global minimum of 2a, Scheme 2.

Scheme 2.
Iminium 2a versus (trimethylsilyl)aziranium 2b cation formation.
The planar structure of the NC3 fragment and the tetrahedral C–C–Si angle of 109° proves the absence of interaction of the silicon atom with the cationic center in 2a. The aziranium triangle in 2b is close to equilateral.
The aziranium cation 2b is polarized more strongly than its methoxy-substituted analogue 1b due to the electron donor effect of the trimethylsilyl group: qN = +0.706, qCH2 = −0.822, and qCH = −0.315. No siliranium cation was found on the PES.
X = NMe2, Y = PMe2 (3). The transformations of cation 3, which has two heteroatoms belonging to the same group of the periodic table (Scheme 3), are completely similar to those of cation 2, except that the energy difference between the global minimum of the iminium cation 3a and the local minimum of the aziranium cation 3b is notably smaller: 16.1 kcal/mol. Apparently, this is due to the practically equal lengths of all three P–C bonds in 3b (Δl~0.01 Å), whereas in its analogue 2b the Si–C bonds with the methyl groups are ~0.06 Å shorter than in the CNC ring carbon atom.

Scheme 3.
Iminium 3a versus (dimethylphosphino)aziranium 3b cation formation.
The planar structure of the NC3 fragment and the nearness to the tetrahedral C–C–P angle of 108° proves the iminium structure of cation 3a and the absence of interaction of the phosphorus atom with the cationic center (l(P–C+) = 2.743 Å).
The aziranium cation 3b is polarized even more strongly than its trimethylsilyl-substituted analogue 2b: qN = +0.762, qCH2 = −0.858, and qCH = 0.302. Note that, unlike 2b, the CH carbon in 3b is charged positively, apparently, due to the higher electronegativity of phosphorus compared to silicon. In line with this, the N–C bond between the oppositely charged atoms in 3b (1.480 Å) is shorter than that between the likely charged ones (1.504 Å). No phosphiranium cation was found on the PES.
X = NMe2, Y = SMe (4). Moving further along the third row of the periodic table (Si → P → S) results in a further decrease in the energy gap between the global 4a (linear iminium cation) and local 4b (aziranium cation) minima on the PES (Scheme 4). As above, the primary cation 4 is optimized to the aziranium cation 4b only for the starting conformation of 4 with the p-orbital, C–N bond and the lone pair on nitrogen lying in one plane. The value of ΔE = 12.1 kcal/mol is minimal in the series of all Me2N-containing carbocations (1)–(6).

Scheme 4.
Iminium 4a versus (methylthio)aziranium 4b cation formation.
Note the appearance of the signs of anchimeric assistance of the sulfur atom in 4a, as evidenced by a smaller C–C–S angle of 101° in 4a as compared to the tetrahedral angles of C–C–Si and C–C–P in 2a and 3a (Figure 3, Figure 4 and Figure 5). The non-covalent C–S distance in 4a is 2.554 Å, which is larger than the covalent bond length but much less than the sum of the van der Waals radii (3.5 Å) [38]. Note, also, the less symmetrical structure of the CNC triangle in 4b, in particular, the larger difference in the angles and, especially, the C–N distances in the ring (0.053 Å).
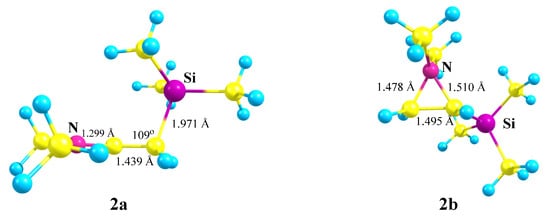
Figure 3.
Optimized geometries of the iminium 2a and aziranium 2b cations.
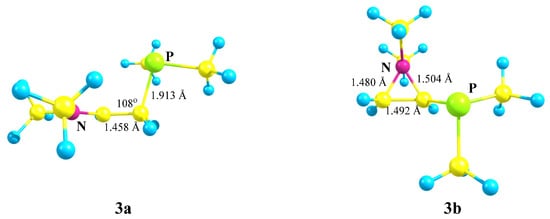
Figure 4.
Optimized geometries of the iminium 3a and aziranium 3b cations.
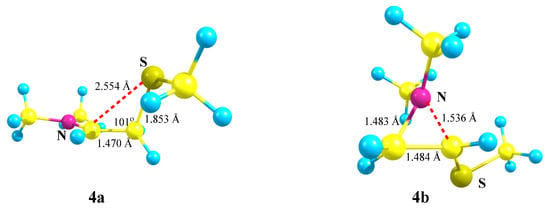
Figure 5.
Iminium cation 4a, with reduced CCS angle and C⋯S distance, and unsymmetrical aziranium cation 4b.
The Mulliken charge on nitrogen and the polarization of the aziranium cation 4b (qN = +0.687, qCH2 = −0.769, and qCH = +0.121) are somewhat higher than those in its oxygen analogue 1b but lower than those in 2b and 3b.
X = NMe2, Y = SeMe (5). Introduction of a heavier chalcogen, selenium, in place of sulfur, has a small effect on the structure and energetics of the corresponding carbocations (Scheme 5, Figure 6). The comparison of the covalent and non-covalent distances and bond angles allows the conclusion that the anchimeric assistance in the aziranium cation 5b must be somewhat stronger than in its analogue 4b. However, the calculated energy difference of 15.0 kcal/mol between 5a and 5b is slightly larger than that between 4a and 4b (12.1 kcal/mol). Apparently, this is due to the more diffuse electron density on the selenium atom that weakens the resonance stabilization of the cationic center by selenium with respect to the sulfur atom.

Scheme 5.
Iminium 5a versus (methyselanyl)aziranium cation 5b formation.
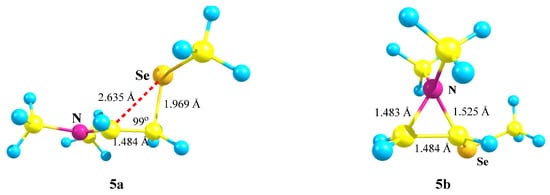
Figure 6.
Immonium cation 5a, with reduced CCSe angle and C⋯Se distance, and unsymmetrical aziranium cation 5b.
A weaker resonance stabilization by the selenium atom can also be clearly seen by comparison of the atomic charges in the aziranium cations 4b (vide supra) and 5b (qN = +0.715, qCH2 = −0.764, and qCH = −0.220). A larger contraction of the S–CH with respect to the S–Me bond in 4b (0.064 Å) compared to that of the Se–CH with respect to the Se–Me bond in 5b (0.053 Å) is fully consistent with the weaker resonance of the SeMe group and explains the negative charge qCH in 5b and its positive value in 4b.
X = NMe2, Y = Br (6). The carbocation 6 potential energy surface profile and the structure of the global and local minima on it (Scheme 6, Figure 7) are very close to those of carbocation 5.

Scheme 6.
Iminium 6a versus bromoaziranium cation 6b formation.
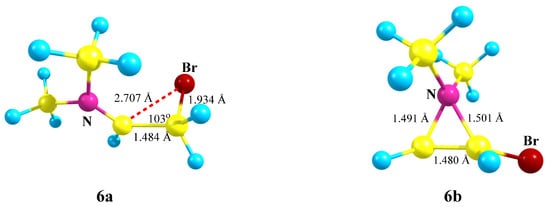
Figure 7.
Br-assisted immonium cation 6a, with reduced C⋯Br distance, and aziranium cation 6b.
The iminium ion 6a lies lower in energy than the aziranium ion 6b by 15.7 kcal/mol, which is very close to the energy gap for their closest analogues 5a and 5b. The charge on the nitrogen atom is the lowest among the above-considered aziranium cations (qN = +0.500). The N–CH2 bond of 1.491 Å is slightly shorter than the N–CHBr bond (1.501 Å), in agreement with a higher electron density for the CH2 carbon (qCH2 = −0.692, qCH = −0.260).
To summarize the results obtained for the amino-containing carbocations (1)–(6), one can conclude that the Me2N group migrates spontaneously towards the carbocationic center to form the corresponding aziranium ions only in the conformers with the p-orbital, C–N bond and the lone pair on the nitrogen lying in one plane. In all other cases, the second heteroatom is shifted towards the carbocationic center to form the corresponding iminium ions [Me2N=CH–CH2Y]+ without (Y = O, SiMe3, PMe2; tetrahedral CCY angle) or with very slight (Y = SMe, SeMe, Br; CCY angle from 99 to 103°) anchimeric assistance. The local minima lie 12–21 kcal/mol above the corresponding global minima.
X = OMe, Y = SiMe3 (7). Let us turn to combinations of oxygen with other heteroatoms. With the most electropositive heteroatom, silicon (χ = 1.74), almost full migration of the trimethylsilyl group occurs during geometry optimization, leading to cation 7a (Scheme 7) for almost all conformations of 7 except the one with the eclipsed MeO–C bond and the p-orbital. In the latter case, the oxiranium ion 7b is formed as a local minimum on the PES.

Scheme 7.
Oxenium 5a versus (trimethysilyl)oxiranium cation 7b formation.
The C–C–Si angle in 7a is slightly less than the tetrahedral angle (104°, Figure 8), and the non-covalent distance C⋯Si is large (2.745 Å) but still less than the sum of the vdW radii (3.8 Å). The C–C bond length in 7a of 1.397 Å is in between those of the double and ordinary bonds, but 0.04 Å shorter than in the nitrogen analogue 2a (1.439 Å, Figure 3), indicating a weaker conjugation of the OMe versus the NMe2 group. In the oxiranium ion 7b, the C–C distance is much longer and is close to that for the ordinary bond, indicating strong anchimeric assistance by oxygen. However, ion 7b corresponds to a local minimum on the PES lying as much as 35.2 kcal/mol above the global minimum 7a in energy. This is the maximum difference between the two minima on the PESs of all the studied structures. The much larger value of ΔE for the 7a/7b pair than for the 2a/2b pair could be due to the lower stability of the oxiranium 7b relative to the aziranium ion 2b. Geometrically, it is represented by a slightly shorter C–C bond in 7b as compared with that in 2b (1.471 versus 1.495 Å) and a larger sum for the two C–O bonds in 7b as compared with the two C–N bonds in 2b (3.025 versus 2.988 Å, Figure 3 and Figure 8). However, these effects, which are themselves moderate, should be further reduced by a stronger conjugation in the iminium 2a than in the oxenium ion 7a. A more probable reason for a large difference (ΔΔE = 14.4 kcal/mol) between the global and local minima is that iminium ions 2a and 7a have principally different electronic structures. While in the aziranium ion 2b the positive charge is localized on the Me2N group (mostly on nitrogen), in the oxiranium ion 7b it is concentrated on the carbon fragment CHCH2 (summed with hydrogens), the OMe group bearing negative charge (−0.063 on OMe, −0.409 on oxygen).
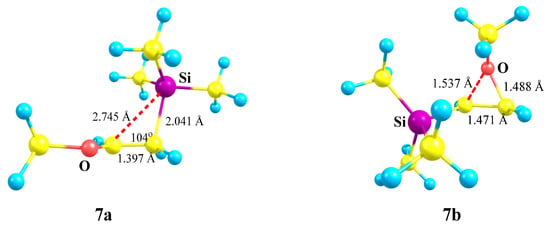
Figure 8.
The structures of the oxenium 7a and oxiranium 7b cations.
X = OMe, Y = PMe2 (8). The transition from silicon to its closest neighbor, phosphorus, changes the situation dramatically. Even in the most favorable migration conformation for the OMe group in carbocation 8, only the dimethylphosphino group is shifted towards the cationic center and stops at the formation of the anchimerically stabilized phosphiranium cation 8a (Scheme 8).

Scheme 8.
Formation of phosphiranium cation 8a and no spontaneous optimization to the oxiranium cation 8b.
The isomeric oxiranium cation 8b was also located on the PES, but only starting with the “preorganized COC triangle”. Note that, unlike all the above-considered structures, no minima on the PES corresponding to open linear cations could be found. The phosphiranium 8a and oxiranium 8b cations look similar, but there is one principal geometrical difference: the C–C bond lengths in the almost isosceles triangle in 8a coincide with that of normal ordinary C–C bonds (1.545 Å), whereas in the COC ring in 8b (1.465 Å) the lengths are intermediate between those of the C–C and C=C bonds (Figure 9). The charge density distribution is also radically different. The charge on phosphorus qP in 8a is equal to +1.041, which allows it to be considered as a true phosphiranium ion, whereas in 8b it is −0.399, the largest positive charge of +0.929 (summed with hydrogens) being located on the ring carbon bonded anchimerically with oxygen (qC = 0.287). Therefore, electronically, cation 8b is similar to 7b, except for the fact that the charges on the ring carbons in the latter are reduced due to the electron-donating effect of the trimethylsilyl group. For the same reasons as discussed for 7b, the oxiranium cation 8b lies high above (28.4 kcal/mol) the phosphiranum cation 8a.
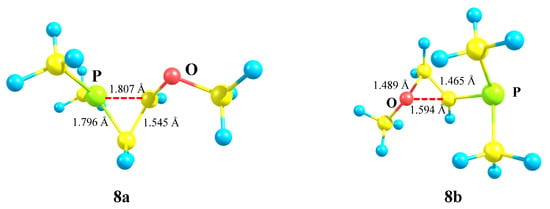
Figure 9.
P-stabilized 8a and O-stabilized 8b anchimerically assisted cations.
X = OMe, Y = SMe (9). No oxiranium cation 9b could be localized on the PES of cation 9. Even in the conformation with the eclipsed MeO–C bond and p-orbital, the MeS group shifts towards the cationic center to form the anchimerically stabilized cation 9a (Scheme 9), which is the global minimum. Moreover, the “preorganized” oxiranium structure 9b suffers the COC ring opening during optimization, resulting in practically linear S-stabilized cation 9c (Figure 10), which lies 17.0 kcal/mol above the global minimum 9a.
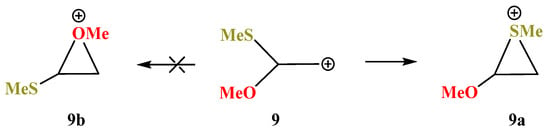
Scheme 9.
Formation of thiiranium cation 9a and no spontaneous optimization to the oxiranium cation 9b.
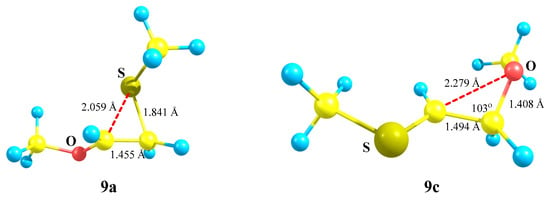
Figure 10.
Strong anchimeric assistance in the thiiranium cation 9a and its absence in the linear cation 9c.
Thiiranium cation 9a has a slightly asymmetrical ring, suggesting a substantial interaction with the sulfur atom, whereas in 9c the interaction of the cationic center with oxygen is insignificant. It follows from a large non-bonded C⋯O distance of 2.279 Å and the C–C–O angle in 9c being only slightly different from the tetrahedral bond angle (Figure 10).
Noteworthy is the difference in the atomic charges: in the thiiranium cation 9a, the C–C bond is strongly polarized in the direction from the OCH to the CH2S group, the value of Δq = qCH − qCH2 being 0.716, and there is a zero charge on the sulfur atom. In the less stable isomeric cation 9c, the direction of the C–C bond polarization is the same but the degree of polarization is much smaller (Δq = 0.298), and the sulfur atom is positively charged (qS = 0.085). The charge on oxygen is the same (qO = −0.573).
X = OMe, Y = SeMe (10). Selenium, the heavier analogue of sulfur, wins even more in competition with oxygen, Scheme 10; the seleniranium cation 10a is 22.1 kcal mol more stable than the isomeric 10c. As in the case of 9, neither conformation of cation 10 can be optimized to the oxiranium cation 10b, which, being taken as the starting point, is optimized to the linear cation 10c with the C–C–Se angle even closer to the tetrahedral than in its analogue 9c.
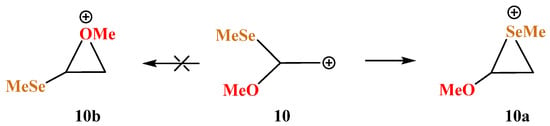
Scheme 10.
Formation of seleniranium cation 10a and no spontaneous optimization to the oxiranium cation 10b.
Cation 10a in Figure 11 is geometrically very similar to 9a in Figure 10. However, a stronger anchimeric stabilization in 10a becomes evident from the analysis of atomic charges in the two structures. While the electron donation from the sulfur atom estimated as Δq(9c–9a) is as low as 0.084, the same effect calculated as Δq(10b–10a) is about three times as large as that, being 0.238, in spite of a slightly larger non-bonded C⋯Se distance and a C–C–Se bond angle. Apparently, this is also due to a more diffuse electron density on the selenium atom, as in the case of cations 5 (vide supra).
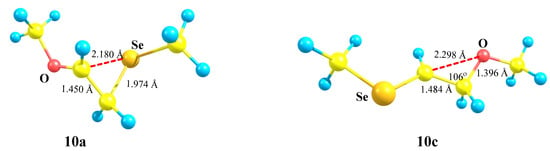
Figure 11.
Strong anchimeric assistance in seleniranium cation 10a and its absence in cation 10c.
The C–C bond in both 10a and 10c is polarized in the same direction as in cation 9, but the values of Δq are substantially larger: 0.850 in 10a and 0.658 in 10c. The electron density on selenium is much lower than in the corresponding sulfur analogues: qSe = 0.192 in 10a versus qS = 0 in 9a and qSe = 0.430 in 10c versus qS = 0.298 in 9c.
X = OMe, Y = Br (11). Cation 11 behaves similarly to its analogues 9 and 10. The trend of distortion of the most stable Y-stabilized iranium cation and the increase in the energy gap between the global (Y-stabilized) and local (O-stabilized) cations is maintained in going to the heaviest member of the O-containing cations in the series Y = S, Se, Br (Scheme 11, Figure 12).
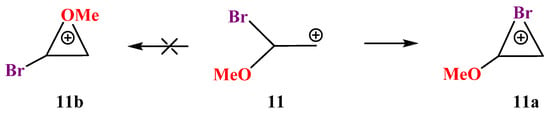
Scheme 11.
Formation of the (methoxy)bromiranium cation 11a and no spontaneous optimization to the bromooxiranium cation 11b.
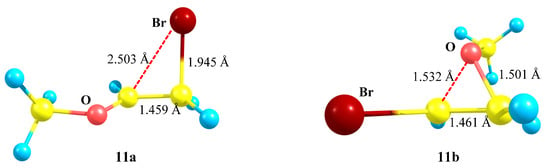
Figure 12.
Anchimeric stabilization in the bromiranium 11a and oxiranium 11b cations.
Cation 11a in Figure 12 is more asymmetric than all its analogues in the series of O-containing cations, except for cation 7a in Figure 8, which was, apparently, due to the presence of the most electropositive SiMe3 group in 7a.
Therefore, similar to the amino-containing carbocations (1)–(6), no spontaneous migration of the MeO group to the carbocationic center occurs in carbocations (7)–(11). However, a partial or complete shift of the MeO group gives rise to the formation of local minima corresponding to the O-anchimerically assisted cations lying 17.0–35.2 kcal/mol above the Y-anchimerically assisted global minima. Moreover, the oxiranium cations are well-known species whose involvement, e.g., in the deoxyfluorination reaction of fluorocarbohydrates, has been shown and reinforced by DFT calculations [39,40]. A remarkable feature of the oxygen-containing cations (7b)–(11b) is that they can be divided into two types, depending on the C–C–O angle, and have drastically different electronic distributions in the C–C–O fragment as well as different energy gaps between the a and c isomers. The former group includes O,S and O,Se cations 9c and 10c, which have C–C–O angles close to tetrahedral angles (103 and 106°) and the lowest values for ΔE (17.0 and 22.1 kcal/mol). The C–C bonds in 9c and 10c are polarized in the direction from oxygen, as shown in Figure 13. The second group includes O,Si, O,P, and O,Br cations 7b, 8b, and 11b, which have C–C–O angles of 63, 65, and 60°, respectively, and larger ΔE values equal to 35.2, 28.4, and 24.3 kcal/mol, respectively. The C–C bonds in them are polarized towards the carbon bearing the covalently bound oxygen atom, Figure 13.
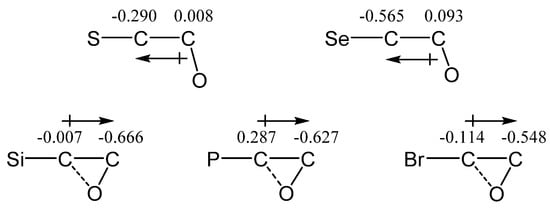
Figure 13.
C–C bond polarization in the O,Y carbocations (Y = Si, P, S, Se, Br).
The oppositely directed polarization in the two types of cations can be explained by substantial binding of the oxygen atom with the second heteroatom-bearing carbon in cations 7b, 8b, and 11b.
X = SiMe3, Y = PMe2 (12). Cation 12 contains in one molecule a silicon and phosphorus atoms, which are the least electronegative among the studied analogues, both being more electropositive than carbon (χSi = 1.8, χP = 2.1, and χC = 2.5). In the case of 12, as in a number of the above-considered cations containing a group capable of the formation of iranium structures, the P-anchimerically stabilized cation 12b is formed only if the starting conformation has the Me2P–C and p-orbital eclipsed. Otherwise, the geometry optimization results in the migration of the more electropositive (and hence less capable of anchimeric assistance) Me3Si group, Scheme 12.

Scheme 12.
Competitive formation of siliranium 12a and phosphiranium 12b cations.
However, the phosphiranium cation 12b is the global minimum on the PES lying 20.8 kcal/mol below the local minimum of the siliranium cation 12a, and thus phosphorus wins in the competition with silicon. The C–P and C–C bond lengths in the isosceles CPC triangle in 12b are practically equal to those of ordinary C–P and C–C bonds, proving that it is a true phosphiranium ion (Figure 14). As for cation 12a, judging from the strongly elongated C–Si bonds and the C–C bond length close to that in alkenes, it is rather a π-complex of the Me3Si cation with dimethyl(vinyl)phosphine. This is independently proved by a notably larger charge on the Me3Si group in 12a (qMe3Si = +0.531) than in 12b (qMe3Si = +0.281).
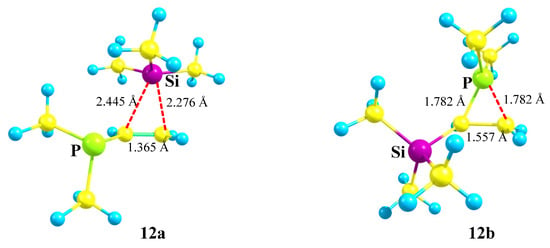
Figure 14.
A π-complex of the Me3Si cation with the C=C bond 12a and symmetric phosphiranium cation 12b.
X = SiMe3, Y = Sme (13). Interesting results were obtained for the Si,S-containing cations 13. The same secondary 1-(methylthio)-2-(trimethylsilyl)ethanium cation 13a is formed by geometry optimization of either the primary 2-(methylthio)-2-(trimethylsilyl)ethanium cation 13 or the secondary 2-(methylthio)-1-(trimethylsilyl)ethanium cation 13b, Scheme 13, and 13a is the global minimum on the PES. The transformation 13 → 13a occurs by migration of the Me3Si group to the cationic center, whereas the 13b → 13a conversion is the result of the sigmatropic rearrangement with 1,2-hydride shift.

Scheme 13.
Formation of the same cation 13a from the primary cation 13 and the secondary cation 13b.
The S-anchimerically stabilized cation 13c is a local minimum on the PES formed only from the most favorable conformation of 13 with the MeS and p-orbital lying in one plane. Notably, the anchimerically stabilized cation 13c is 2.82 kcal/mol less stable than the linear cation 13a. The structures of both minima are shown in Figure 15.
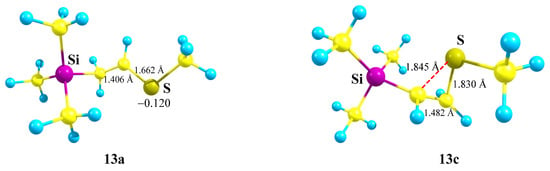
Figure 15.
1-Methylthio-2-(trimethylsilyl)ethanium cation 13a (global minimum) and thiiranium cation 13c (local minimum).
The Si–C–C angle in 13a (105°) is close to the tetrahedral angle; the S–C–C angle (124°) is close to trigonal. The structure of cation 13a is close to perpendicular; the Si–C–C–S dihedral angle is 96°. The CCS triangle in 13c is close to isosceles, the lengths of the two C–S bonds evidencing strong anchimeric stabilization by sulfur, which is also proved by the positive charge qS = +0.144 in 13c, in contrast to the negative value of qS = −0.120 in 13a.
X = SiMe3, Y = SeMe (14). The situation changes when the sulfur atom in cation 13 is replaced by its heavier analogue, selenium, in cation 14. As in the case of Si,S-containing cations, no Si-stabilized cation is formed, even in the form of a π-complex, but the Me3Si group migrates to the cationic center to form linear cation 14a, Scheme 14.

Scheme 14.
Formation of linear cation 14a and anchimerically assisted seleniranium cation 14b.
As in the case of Si,S-containing cation 13c, the selenium anchimerically stabilized cation 14b was located on the PES by optimization of the conformation of 14 most appropriate for the shift of the MeSe group to the cationic center. Remarkably, the seleniranium cation 14b corresponds to the global minimum, although it lies only 0.9 kcal/mol lower in energy than 14a. The structures of the isomeric cations 14a and 14b are shown in Figure 16. Note the much shorter C–C bond in 14a compared to that in 14b, indicating a weaker stabilization of the former cationic species, which, probably, is responsible for the energetic preference of the latter.
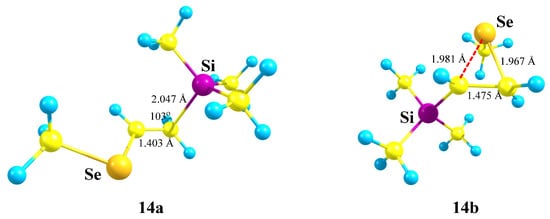
Figure 16.
Linear (14a, local minimum) and Se-anchimerically stabilized (14b, global minimum) Si,Se cations.
The inverse energy order of the linear and anchimerically assisted 14 cations with respect to the corresponding Si,S-containing 13 analogues is in agreement with the stronger anchimeric assistance of the selenium atom as compared to that of the sulfur atom.
X = SiMe3, Y = Br (15). Similar to the examples above, cation 15 can be stabilized by either the Si atom in the form of a π-complex of the trimethylsilyl cation with the double bond in vinyl bromide or by the Br atom in the form of a bromiranium cation formed from the conformation most appropriate for the bromine shift to the cationic center, Scheme 15.

Scheme 15.
Competitive formation of π-complex 15a of the trimethylsilyl group with vinyl bromide and the bromiranium cation 15b.
The structure of π-complex 15a (Figure 17) is very similar to that of the Si,P-containing cation 12a (Figure 14). A drastic difference between the two is that π-complex 15a is 12.2 kcal/mol more stable than the bromiranium cation 15b, whereas π-complex 12a is much less stable than the isomeric phosphiranium ion 12b (vide supra).
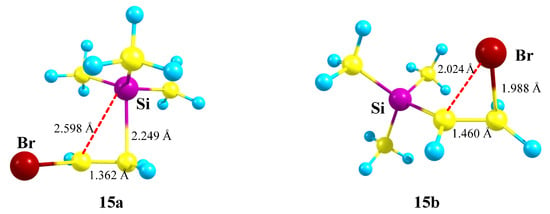
Figure 17.
Siliranium 15a (global minimum) and bromiranium 15b (local minimum) cations.
The most reasonable explanation for this difference is that stabilization of the phosphiranium ion 12b is much stronger than that of the bromiranium ion 15b, as evidenced by a much longer C–C bond in 12b (1.557 Å) as compared with 15b (1.460 Å). This, in turn, is due to the well-known tendency of phosphorus to form tetracoordinated species, along with the much less pronounced ability of bromine to expand its coordination number to 2, although bromiranium (bromonium) ions have been known for many years [41,42,43,44] and have been the subject of experimental studies [45].
Note that the higher stability of cation 15a cannot be assigned to anchimeric assistance by the silicon atom since it has long C⋯Si bonds of 2.25–2.60 Å, a short C–C bond of 1.362 Å, and, as its analogue 12a, is in fact a π-complex of the Me3Si cation with vinyl bromide. However, stabilization via the formation of a siliranium cation was proposed in the literature [46]. Thus, its formation via the migration of the ButPh2Si group in N-tosylazetidines, leading to the corresponding pyrrolidines, was reported [47]. Notably, the silyl group formation was shown to be non-concerted with the C–N bond cleavage, which is in accordance with our conclusion regarding a π-complex rather than a real Si-anchimerically assisted structure of the “siliranium” ion (vide supra) [47].
X = PMe2, Y = SMe (16). The phosphorus atom can either fully migrate to the adjacent carbocationic center (N,P cation 3a, Scheme 3) or form anchimerically stabilized phosphiranium ions (O,P and Si,P cations 8a and 12b, Scheme 8 and Scheme 12). The optimization of the conformation of cation 16 with the eclipsed Me2P–C bond and p-orbital results in full migration of the Me2P group and formation of the open cation 16a, Scheme 16, Figure 18. The same procedure for the conformation with the eclipsed MeS–C bond and p-orbital gives rise to the thiiranium cation 16b lying 2.3 kcal/mol lower in energy than 16a, and so the MeS group wins over Me2P in anchimerical assistance.

Scheme 16.
Competitive formation of linear cation 16a versus thiiranium cation 16b.
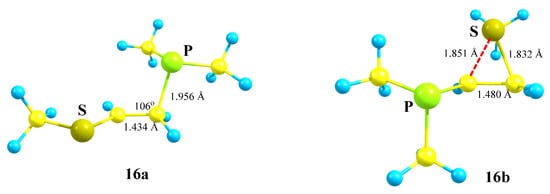
Figure 18.
1-Methylthio-2-(dimethylphosphino)ethan-1-ium 16a and thiiranium 16b cations.
Note the opposite charges on the phosphorus and sulfur atoms in 16a and 16b: in the former, the phosphorus atom is charged positively (qP = 0.089) and the sulfur atom negatively (qS = −0.040), whereas in 16b the ratio is vice versa (qP = −0.336, qS = 0.002). The lower electron densities on phosphorous in 16a and on sulfur in 16b are, respectively, due to hyperconjugation with the PMe2 group and the anchimeric assistance by the MeS group.
X = PMe2, Y = SeMe (17). The structures and relative energies of the isomeric cations (Scheme 17, Figure 19) change only slightly in going to the heavier chalcogen, selenium, except that the energy difference between the anchimerically assisted seleniranium ion 17b and the open 1-methylseleno-2-(dimethylphosphino)ethan-1-ium cation 17a increases to 8.2 kcal/mol, indicating a greater energy gain in the case of selenium as compared to sulfur.

Scheme 17.
Competitive formation of linear cation 17a versus seleniranium cation 17b.
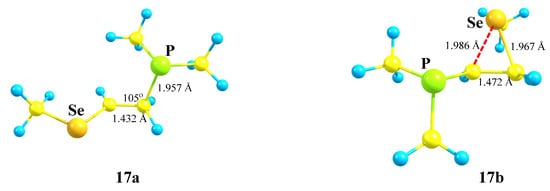
Figure 19.
1-Methylseleno-2-(dimethylphosphino)ethan-1-ium 17a and seleniranium 17b cations.
As in the P,S cations 16a and 16b, the phosphorus atom is charged positively in 17a (qP = 0.107) and negatively in 17b (qP = −0.378). The selenium atom is charged positively in both cations, but the electron density on it in 17b is lower (ΔqSe = 0.316 − 0.242 = 0.074), due to the anchimeric assistance being stronger than that of the MeS group.
X = PMe2, Y = Br (18). Unlike cations 16 and 17, in which the PMe2 group fully migrates to the cationic center and in which no phosphiranium ion could be located on the PES, the geometry optimization of cation 18 in the conformation with the eclipsed Me2P–C bond and the p-orbital gives rise to phosphiranium ion 18c as the global minimum. Unlike all other cases, two more local minima, bromiranium ion 18a and linear ion 18b, were found on the PES, Scheme 18.

Scheme 18.
Global minimum of phosphiranium cation 18c and successive formation of bromiranium 18a and linear 18b cations.
The phosphiranium ion 18c is energetically most favorable; the next favorable is the open cation 18b, lying 8.2 kcal/mol above 18c; and the least stable is bromiranium ion 18a, lying high above 18c, by 28.9 kcal/mol.
The phosphiranium ion 18c is practically symmetrical (Figure 20), and the length of the C–C bond in it falls in the range typical for ordinary bonds. The positive charge in 18c is located on the phosphorus atom (qP = +1.026), and its structure is very similar to the O,P- and Si,P-containing cations 8a and 12b shown in Figure 9 and Figure 14. The values for qP in cation 18b are even larger (qP = +1.075), which may seem strange, but this is explained by the much shorter P–CH bond (1.647 Å) and a negative charge on the adjacent CH carbon (qC = −0.628), indicating its dipolar structure: P+–C−. The P–CH bonds in 18a and 18c are significantly longer (1.853 and 1.795 and 1.802 Å, respectively). The charges on bromine qBr in 18b and 18c are slightly negative (−0.04), whereas in 18a the charge is expectedly positive (+0.144).
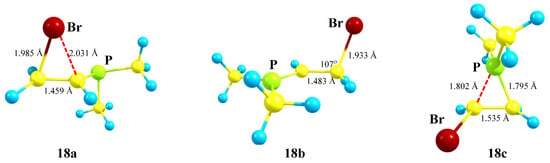
Figure 20.
High-lying intermediate cation 18a, linear cation with full migration of bromine 18b, and phosphiranium ion 18c (global minimum).
1-Methyl-1-phenylphosphonium triflate salt was synthesized at the end of the last century and its X-ray crystal structure was determined [48]. It contains a weakly coordinated triflate counterion and hence an almost “free” phosphiranium cation, which is structurally close to those determined in the present work. Thus, the phosphiranium ring in it is isosceles and the length of the C–P bonds is 1.76 Å (cf. Figure 9, Figure 14 and Figure 20).
X = SMe, Y = SeMe (19). Of particular interest is the rivalry between the sulfur and selenium atoms in cation 19. The intermediacy of thiiranium and seleniranium ions has been confirmed by extensive studies of the chalcogenofunctionalization reactions of alkenes by Denmark et al. [49,50,51,52]. One can assume that selenium, as a more polarizable atom capable of stronger anchimeric assistance [7,13,35,53], would preferably migrate to the cationic center to form the corresponding seleniranium cation. However, the migration of a particular group X is determined by the orientation of the C–X bond with respect to the empty p-orbital on the carbocation center: either SMe or SeMe migrates, provided that it is eclipsed with the p-orbital (Scheme 19).
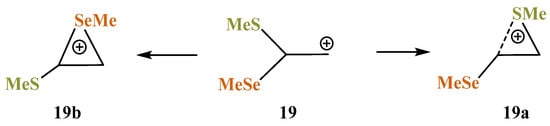
Scheme 19.
Competition between the formation of thiiranium 19a and seleniranium 19b cations.
The isomeric seleniranum cation 19b expectedly turned out to be the global minimum, lying 5.2 kcal/mol below 19a. The structures of the two anchimerically assisted chalcogeniranium cations are presented in Figure 21.
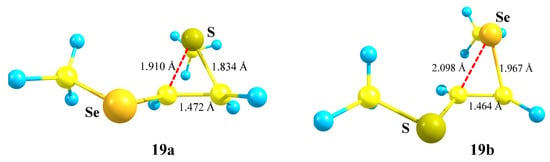
Figure 21.
Thiiranium 19a and seleniranium cation 19b.
The chalcogen atoms in the onium rings are expectedly positively charged (qS = +0.167 in 19a, qSe = +0.328 in 19b) but bear the opposite charge, not being involved in anchimeric assistance (qS = −0.284 in 19b, qSe = +0.054 in 19a).
X = SMe, Y = Br (20) and X = SeMe, Y = Br (21). The formation and transformations of haliranium ions were summarized in an excellent review covering the literature published up to 2014 [54]. Later, the use of haliranium ions as efficient halogenating agents via halogen olefin-to-olefin transfer was reported [55,56]. For Y = Br, in the presence of most electronegative second heteroatoms N and O, the geometry optimization results in the migration of the bromine atom (Scheme 6 and Scheme 11, Figure 7 and Figure 12) to give the most stable cations. The migration of bromine was also observed in the P,Br-containing cation 18 (Scheme 18), although the formed open cation 18a was only a local minimum. For the most electropositive silicon atom, the Me3Si group migrated during optimization, the bromiranium ion 15b (Figure 16) being also a local minimum on the PES. Therefore, the combination of bromine with sulfur and selenium, as the elements with intermediate electronegativity and different polarizability, is of particular interest. In the conformations of cations 20 and 21 with the X–C and p-orbital eclipsed, the corresponding chalcogeniranium ions 20b and 21b are formed. In all other cases, the shift of bromine was observed with the formation of bromiranium ions 20a and 21a (Scheme 20).
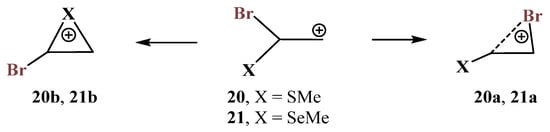
Scheme 20.
Competitive formation of bromiranium 20a and 21a versus chalcogeniranium 20b and 21b cations.
The chalcogeniranium ions 20b and 21b are the global minima, the isomeric bromiranium ions 20a and 21a being less stable by 1.1 and 8.2 kcal/mol, respectively. Expectedly, the energy difference is notably larger in the case of selenium, clearly demonstrating its higher anchimeric stabilization. Both bromiranium ions are highly asymmetric and have very similar structures, Figure 22. Interestingly, the positive charge on sulfur in the thiiranium ion 20b (qS = +0.222) is larger than that in the isomeric bromiranium ion 20a (qS = +0.114), whereas that on selenium in the seleniranium ion 21b (qSe = +0.388) is smaller than that in 21a (qSe = +0.498).
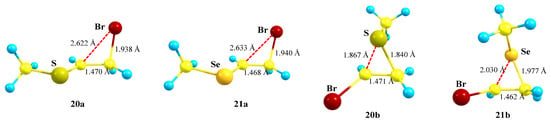
Figure 22.
The structures of bromiranium 20a and 21a and chalcogeniranium 20b and 21b cations.
In order to give a compact overview, the results are summarized below in Table 1.

Table 1.
MP2/aug-cc-pVTZ optimized geometries (°, Å) and total atomic charges on X (qX) for the X-anchimerically assisted cations.
Note that, among most electropositive substituents Y in the X-stabilized three-membered ring, Y = PMe2 and especially Y = SiMe3 attenuate the demands of anchimeric assistance and decrease the total positive charge on X (qX). It is incorrect to compare the charges on the substituents with different electronegativities, but for those with practically the same electronegativity, SMe and SeMe, the values of qX for X = Se, which are larger by ~0.1–0.2 (depending on Y), provide a semi-quantitative estimation of their anchimeric assistance abilities.
3. Conclusions
The routes of rearrangement and the structures and relative energies of the inherently unstable primary carbocations with two different heteroatoms in the molecule CHXY–CH2+ (X, Y = Me2N, MeO, Me3Si, Me2P, MeS, MeS, Br) were analyzed theoretically at the MP2/aug-cc-pVTZ level. Depending on the ability to stabilize an adjacent carbocationic center either by direct conjugation or via anchimeric assistance by a heteroatom and the relative orientation of the C–X and C–Y bonds with respect to the empty p-orbital on the cationic center, the complete migration or a partial shift of either X or Y or a sigmatropic 1,2-hydride shift may take place. The Me2N group is shifted to the cationic center to give aziranium ions only in the conformers with the p-orbital, C–N bond and the nitrogen lone pair lying in one plane. In other cases, the second heteroatom migrates to form the corresponding iminium ions lying 12–21 kcal/mol below the local minima. The MeO group can be partly shifted to the cationic center to give the O-anchimerically assisted cations or undergo full migration to form the oxenium cations lying 17.0–35.2 kcal/mol lower in energy. The group least capable of anchimeric assistance, Me3Si, either fully migrates to the cationic center, resulting in the linear secondary cations, or suffers a partial shift to form loose π-complexes of Me3Si+ with the C=C bond rather than anchimerically assisted siliranium ions, as proved by the charges on silicon and the structures of the corresponding complexes with dimethyl(vinyl)phosphine or vinyl bromide. Phosphorus in combination with chalcogens fully migrates to the cationic center to form linear cations, which, however, lie above the isomeric chalconiranium anchimerically assisted ions. Phosphorus loses to sulfur and especially selenium in the stabilization of the corresponding iranium cations. On the potential energy surface of the P,Br-containing cation, a third local minimum of the high-lying bromiranium ion can be located. For the S,Se-containing cation, as anticipated, the seleniranium cation is the global minimum on the PES. The S,Br and Se,Br cations, depending on the starting conformation, give upon optimization either the corresponding chalcogeniranium ions, as global minima, or bromiranium ions, lying, respectively, 1.1 and 8.2 kcal/mol higher in energy.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28010038/s1, Structures, Cartesian coordinates and energies of all calculated species.
Funding
The research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Streitwieser, A. Solvolytic displacement reactions at saturated carbon atoms. Chem. Rev. 1956, 56, 571–752. [Google Scholar] [CrossRef]
- Vandenheuvel, W.J.A., III; Wallis, E.S. An investigation of anchimeric assistance in certain homoallylic alcohols. J. Org. Chem. 1962, 56, 1233–1237. [Google Scholar] [CrossRef]
- Ingold, C.K. Structure and Mechanism in Organic Chemistry, 2nd ed.; Cornell University Press: Ithaca, NY, USA, 1953; 1266p. [Google Scholar]
- Brown, F.; Hughes, E.B.; Ingold, C.K.; Smith, J.F. Wagner changes, synartetic acceleration and synartetic ions. Nature 1951, 168, 65–67. [Google Scholar] [CrossRef]
- Winstein, S.; Trifan, D. Neighboring carbon and hydrogen. XI. Solvolysis of exo-norbornyl p-bromobenzenesulfonate. J. Am. Chem. Soc. 1952, 74, 1154–1160. [Google Scholar] [CrossRef]
- Grossel, M.C. Carbonium ions. In Organic Reaction Mechanisms. 1978: An Annual Survey Covering the Literature Dated December 1977 through November 1978; Knipe, A., Watts, W., Eds.; Wiley: Hoboken, NJ, USA, 1980; Chapter 8; pp. 313–342. [Google Scholar]
- White, J.M.; Lambert, J.B.; Spiniello, M.; Jones, S.A.; Gable, R.W. Vertical and nonvertical participation by sulfur, selenium, and tellurium. Chem. Eur. J. 2002, 8, 2799–2811. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Bentley, T.W.; Koch, W.; Kos, A.J.; Schwarz, H. Structures and energies of isomeric cyclopentenyl cations. Resolution of the question of anchimeric assistance in cyclopenten-4-yl solvolysis. J. Am. Chem. Soc. 1987, 109, 6953–6957. [Google Scholar] [CrossRef]
- Crestoni, M.E.; Fornarini, S.; Lentini, M.; Speranza, M. Hydride-transfer reactions in the gas phase. 2. Anchimeric assistance in the H– transfer from 1,1-dimethylcyclopentane to alkyl cations. J. Phys. Chem. 1996, 100, 8285–8294. [Google Scholar] [CrossRef]
- Subramaniam, G. Theoretical study of nitrogen-nitrogen bond cleavage in 1,2-diaza compounds: Evidence of anchimeric assistance leading to azaphenonium ion. J. Org. Chem. 1993, 58, 1730–1733. [Google Scholar] [CrossRef]
- Easton, C.J.; Merrett, M.C. Anchimeric assistance in hydrogen atom transfer reactions on the side chains of amino acid derivatives. J. Am. Chem. Soc. 1996, 118, 3035–3036. [Google Scholar] [CrossRef]
- Calvaresi, M.; Rinaldi, S.; Arcelli, A.; Garavelli, M. Computational DFT investigation of vicinal amide group anchimeric assistance in ether cleavage. J. Org. Chem. 2008, 73, 2066–2073. [Google Scholar] [CrossRef]
- Accurso, A.A.; Cho, S.-H.; Amin, A.; Potapov, V.A.; Amosova, S.V.; Finn, M.G. Thia-, aza-, and selena[3.3.1]bicyclononane dichlorides: Rates vs. internal nucleophile in anchimeric assistance. J. Org. Chem. 2011, 76, 4392–4395. [Google Scholar] [CrossRef] [PubMed]
- Herdewijn, P.A.M. Anchimeric assistance of a ′O-carbonyl function for inversion of configuration at the 3′-carbon atom of 2′-deoxyadenosine. Synthesis of 3′-azido-2′,3′-dideoxyadenosine and 3′-azido-2′,3′-dideoxyinosine. J. Org. Chem. 1988, 53, 5050–5053. [Google Scholar] [CrossRef]
- Nyquist, H.L.; Davenport, D.A.; Han, P.Y.; Shih, J.G.; Speechl, T.G. Solvolysis of the sulfonate esters of 1-(4,6-dimethyl-s-triazin-2-yl)-2-propanol and 4-(4,6-dimethyl-s-triazin-2-yl)-2-butanol involving a special salt effect and anchimeric assistance. J. Org. Chem. 1992, 57, 1449–1456. [Google Scholar] [CrossRef]
- Shemet, A.; David Sarlah, D.; Carreira, E.M. Stereochemical studies of the opening of chloro vinyl epoxides: Cyclic chloronium ions as intermediates. Org. Lett. 2015, 17, 1878–1881. [Google Scholar] [CrossRef]
- Pavlović, R.Z.; Border, S.E.; Gallucci, J.; Badjić, J.D. Stereo- and regioselective halogenation of norbornenes directed by neighboring group participation. Tetrahedron Lett. 2016, 57, 5584–5587. [Google Scholar] [CrossRef]
- Fǎrcaşiu, D.; Leu, R. Theoretical studies of carbocations in ion pairs. 8. Search for anchimeric assistance in the ionization of 2-butyl cation precursors. J. Phys. Chem. A 2008, 112, 2955–2961. [Google Scholar] [PubMed]
- Traylor, T.G.; Goldberg, M.J. Neighboring group participation in organometallic chemistry: Anchimeric assistance in catalyzed arene exchange reactions of (diarylalkane)tricarbonylchromium complexes. Organometallics 1987, 6, 2531–2536. [Google Scholar] [CrossRef]
- Argazzi, R.; Bergamini, P.; Costa, E.; Gee, V.; Hogg, J.K.; Martín, A.; Orpen, A.G.; Pringle, P.G. Anchimeric assistance by platinum(II) in the epimerizations of [PtX(CHXSiMe3)(R,R-chiraphos)]. Organometallics 1996, 15, 5591–5597. [Google Scholar] [CrossRef]
- Aranyos, A.; Szabó, K.J.; Bäckvall, J.-E. Palladium-catalyzed 1,4-acetoxy-trifluoroacetoxylation and 1,4-alkoxy-trifluoroacetoxylation of cyclic 1,3-dienes. Scope and mechanism. J. Org. Chem. 1998, 63, 2523–2529. [Google Scholar] [CrossRef]
- Bühl, M. Theory predicts anchimeric assistance in olefin polymerization with imidovanadium(V) model catalysts. Organometallics 1999, 18, 4894–4896. [Google Scholar] [CrossRef]
- Annatelli, M.; Trapasso, G.; Salaris, C.; Salata, C.; Castellano, S.; Aricò, F. Mustard carbonate analogues as sustainable reagents for the aminoalkylation of phenols. Eur. J. Org. Chem. 2021, 2021, 3459–3464. [Google Scholar] [CrossRef]
- Salin, A.V.; Fatkhutdinov, A.R.; Il’in, A.V.; Galkin, V.I. Effect of anchimeric assistance in the reaction of triphenylphosphine with α,β-unsaturated carboxylic acids. Int. J. Chem. Kinet. 2014, 14, 206–215. [Google Scholar] [CrossRef]
- Salin, A.V.; Fatkhutdinov, A.R.; Il’in, A.V.; Shamsutdinova, F.G. Effect of anchimeric assistance in addition reaction of bifunctional tertiary phosphines to electron deficient alkenes. Int. J. Chem. Kinet. 2016, 48, 161–168. [Google Scholar] [CrossRef]
- Buck, H. An adjusted model for simple 1,2-dyotropic reactions. Ab Initio MO and VB considerations. Open J. Phys. Chem. 2013, 3, 119–125. [Google Scholar] [CrossRef][Green Version]
- Luiggi, M.; Mora, J.R.; Loroño, M.; Marquez, E.; Lezama, J.; Cordova, T.; Chuchani, G. Theoretical calculations on the gas-phase thermal decomposition kinetics of selected thiomethyl chloroalkanes: A new insight of the mechanism. Comput. Theor. Chem. 2014, 1027, 165–172. [Google Scholar] [CrossRef]
- Fjellaksel, R.; Dugalic, D.; Demissie, T.B.; Riss, P.J.; Hjelstuen, O.-K.; Sundset, R.; Hansen, J.H. An acylation-Finkelstein approach to radioiodination of bioactives: The role of amide group anchimeric assistance. J. Phys. Org. Chem. 2018, 31, 29–40. [Google Scholar] [CrossRef]
- Shvily, R.; Müller, T.; Apeloig, Y.; Mandelbaum, A. Direct evidence for anchimeric assistance in alcohol elimination from gas-phase MH+ ions of 1,4-dialkoxycyclohexanes under chemical ionisation. Experiment and theory. J. Chem. Soc. Perkin Trans. 1997, 1221–1234. [Google Scholar] [CrossRef]
- Amosova, S.V.; Shagun, V.A.; Makhaeva, N.A.; Novokshonova, I.A.; Potapov, V.A. Quantum chemical and experimental studies of an unprecedented reaction pathway of nucleophilic substitution of 2-bromomethyl-1,3-thiaselenole with 1,3-benzothiazole-2-thiol proceeding stepwise at three different centers of seleniranium intermediates. Molecules 2021, 26, 6685. [Google Scholar] [CrossRef]
- Conlin, R.T.; Kwak, Y.W. Kinetics of the thermal isomerization of (trimethylsilyl)cyclopropane. Evidence for anchimeric assistance. Organometallics 1986, 5, 1205–1207. [Google Scholar] [CrossRef]
- Ayoko, A.; Eaborn, C. Anchimeric assistance by and migration of the vinyl group in reactions of sterically hindered organosilicon compounds of the type (Me3Si)2C(SiMe2CH=CH2)(SiR2X). J. Chem. Soc. Perkin Trans. 2 1987, 1047–1058. [Google Scholar] [CrossRef]
- Lambert, J.B.; Zhao, Y. β-Effect of phosphorus functionalities. J. Am. Chem. Soc. 1996, 118, 3156–3167. [Google Scholar] [CrossRef]
- Eaborn, C.; Kowalewska, A.; Smith, J.D.; Stańczyk, W.A. Anchimeric assistance by γ-substituents Z, Z=MeO, PhO, MeS or PhS, in reactions of the bromides (Me3Si)2(ZMe2Si)CSiMe2Br with AgBF4. J. Organomet. Chem. 2001, 640, 29–36. [Google Scholar] [CrossRef]
- Harris, B.L.; White, J.M. Modes of neighbouring group participation by the methyl selenyl substituent in β-methylselenylmethyl-substituted 1-phenylethyl carbenium ions. Molecules 2013, 18, 11705–11711. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09, Rev. A.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Krow, G.R.; Gandla, D.; Guo, W.; Centafont, R.A.; Lin, G.; DeBrosse, C.; Sonnet, P.E.; Ross, C.W.; Ramjit, H.G.; Carroll, P.J.; et al. Neighboring group participation in the additions of iodonium and bromonium ions to N-alkoxycarbonyl-2-azabicyclo[2.2.n]alk-5-enes (n = 1,2). J. Org. Chem. 2008, 73, 2114–2121. [Google Scholar] [PubMed]
- Bondi, A. van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Lainé, D.; Denavit, V.; Lessard, O.; Carrier, L.; Fecteau, C.-É.; Johnson, P.A.; Giguère, D. Fluorine effect in nucleophilic fluorination at C4 of 1,6-anhydro-2,3-dideoxy-2,3-difluoro-β-D-hexopyranose. Beilstein J. Org. Chem. 2020, 16, 2880–2887. [Google Scholar] [CrossRef]
- Quiquempoix, L.; Wang, Z.; Graton, J.; Latchem, P.G.; Light, M.; Le Questel, J.-Y.; Linclau, B.J. Synthesis of 2,3,4-Trideoxy-2,3,4-trifluoroglucose. Org. Chem. 2019, 84, 5899–5906. [Google Scholar]
- Poirier, R.A.; Demaré, G.R.; Yates, K.; Csizmadia, I.G. Stabilities of isomeric bromonium ions C2H4Br+. J. Molec. Struct. 1983, 94, 137–141. [Google Scholar]
- Ruasse, M.F. Bromonium ions or β-bromocarbocations in olefin bromination. A kinetic approach to product selectivities. Acc. Chem. Res. 1990, 23, 87–93. [Google Scholar] [CrossRef]
- Cossi, M.; Persico, M.; Tomasi, J. Aspects of electrophilic bromination of alkenes in solution. Theoretical calculation of atomic charges in bromonium ions. J. Am. Chem. Soc. 1994, 116, 5373–5378. [Google Scholar] [CrossRef]
- Balaji, P.V.; Chandrasekaran, S. Stereoselective anti-Markovnikov geminal diamination and dioxygenation of vinylarenes mediated by the bromonium ion. Eur. J. Org. Chem. 2016, 2016, 2547–2554. [Google Scholar] [CrossRef]
- Slebocka-Tilk, H.; Ball, R.G.; Brown, R.S. The question of reversible formation of bromonium ions during the course of electrophilic bromination of olefins. 2. The crystal and molecular structure of the bromonium ion of adamantylideneadamantane. J. Am. Chem. Soc. 1985, 107, 4504–4508. [Google Scholar] [CrossRef]
- Agrawal, D.; Yadav, V.K. Silylmethyl-substituted cyclopropyl and other strained ring systems: Cycloaddition with dipolarophiles. Chem. Commun. 2008, 6471–6488. [Google Scholar] [CrossRef] [PubMed]
- Narhe, B.D.; Sriramurthy, V.; Yadav, V.K. A smooth rearrangement of N-p-toluenesulfonyl 2-tert-butyldiphenylsilylmethylsubstituted azetidines into N-p-toluenesulfonyl 3-tert-butyldiphenylsilyl-substituted pyrrolidines. Org. Biomol. Chem. 2012, 10, 4390–4399. [Google Scholar] [CrossRef] [PubMed]
- Hockless, D.C.R.; McDonald, M.A.; Pabel, M.; Wild, S.B. 1-Methyl-1-phenylphosphiranium triflate: Synthesis, structure and reactivity. Chem. Commun. 1995, 257–258. [Google Scholar] [CrossRef]
- Denmark, S.E.; Collins, W.R. Lewis base activation of Lewis acids: Development of a Lewis base catalyzed selenolactonization. Org. Lett. 2007, 9, 3801–3804. [Google Scholar] [CrossRef]
- Denmark, S.E.; Kalyani, D.; Collins, W.R. Preparative and mechanistic studies toward the rational development of catalytic, enantioselective selenoetherification reactions. J. Am. Chem. Soc. 2010, 132, 15752–15765. [Google Scholar] [CrossRef]
- Denmark, S.E.; Collins, W.R.; Cullen, M.D. Observation of direct sulfenium and selenenium group transfer from thiiranium and seleniranium ions to alkenes. J. Am. Chem. Soc. 2009, 131, 3490–3492. [Google Scholar] [CrossRef]
- Denmark, S.E.; Vogler, T. Synthesis and reactivity of enantiomerically enriched thiiranium ions. Chem. Eur. J. 2009, 15, 11737–11745. [Google Scholar] [CrossRef]
- Potapov, V.A.; Amosova, S.V.; Abramova, E.V.; Musalov, M.V.; Lyssenko, K.A.; Finn, M.G. 2,6-Dihalo-9-selenabicyclo[3.3.1]nonanes and their complexes with selenium dihalides: Synthesis and structural characterization. New J. Chem. 2015, 39, 8055–8059. [Google Scholar] [CrossRef]
- Cresswell, A.J.; Eey, S.T.-C.; Denmark, S.E. Catalytic, stereoselective dihalogenation of alkenes: Challenges and opportunities. Angew. Chem. Int. Ed. 2015, 54, 15642–15682. [Google Scholar] [CrossRef] [PubMed]
- Ascheberg, C.; Bock, J.; Buß, F.; Mück-Lichtenfeld, C.; Daniliuc, C.G.; Bergander, K.; Dielmann, F.; Hennecke, U. Stable bromiranium ions with weakly-coordinating counterions as efficient electrophilic brominating agents. Chem. Eur. J. 2017, 23, 11578–11586. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Nakatsuji, H.; Okumura, Y.; Yao, L.; Ishihara, K. Chiral enantioselective halooxy- and haloazacyclizations induced by amidophosphate catalysts and halo-Lewis acids. J. Am. Chem. Soc. 2018, 140, 6039–6043. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).