Hybrid Classification/Regression Approach to QSAR Modeling of Stoichiometric Antiradical Capacity Assays’ Endpoints
Abstract
:1. Introduction
2. Data and Methods
2.1. Data Selection and Curation
2.2. Geometry Optimization and Electronic Parameters Calculations
2.3. Descriptor Calculations and Statistics
3. Results and Discussion
3.1. Calculation and Analysis of Electronic Parameters
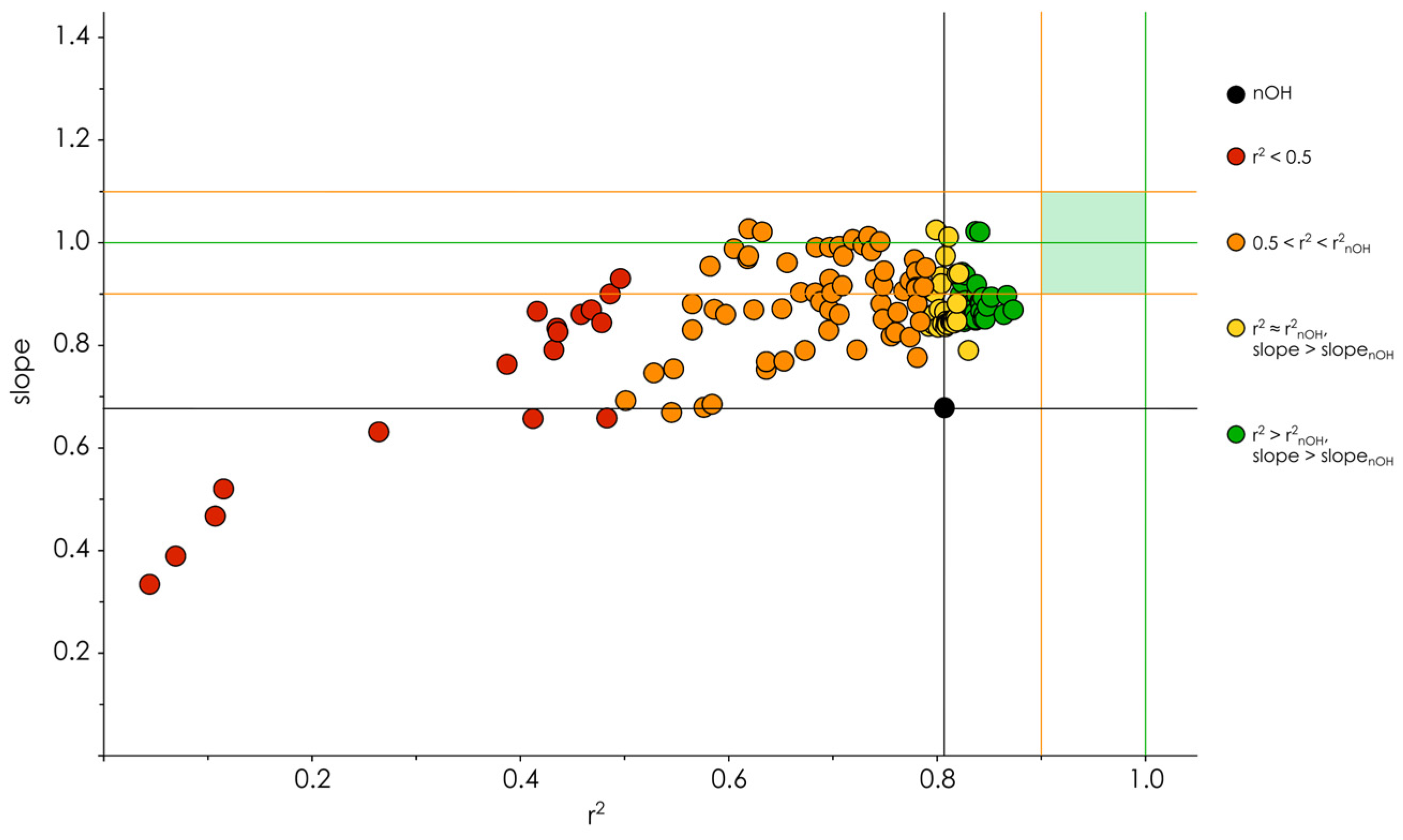
3.2. Hydroxyl Group Classification and Regression Model Construction
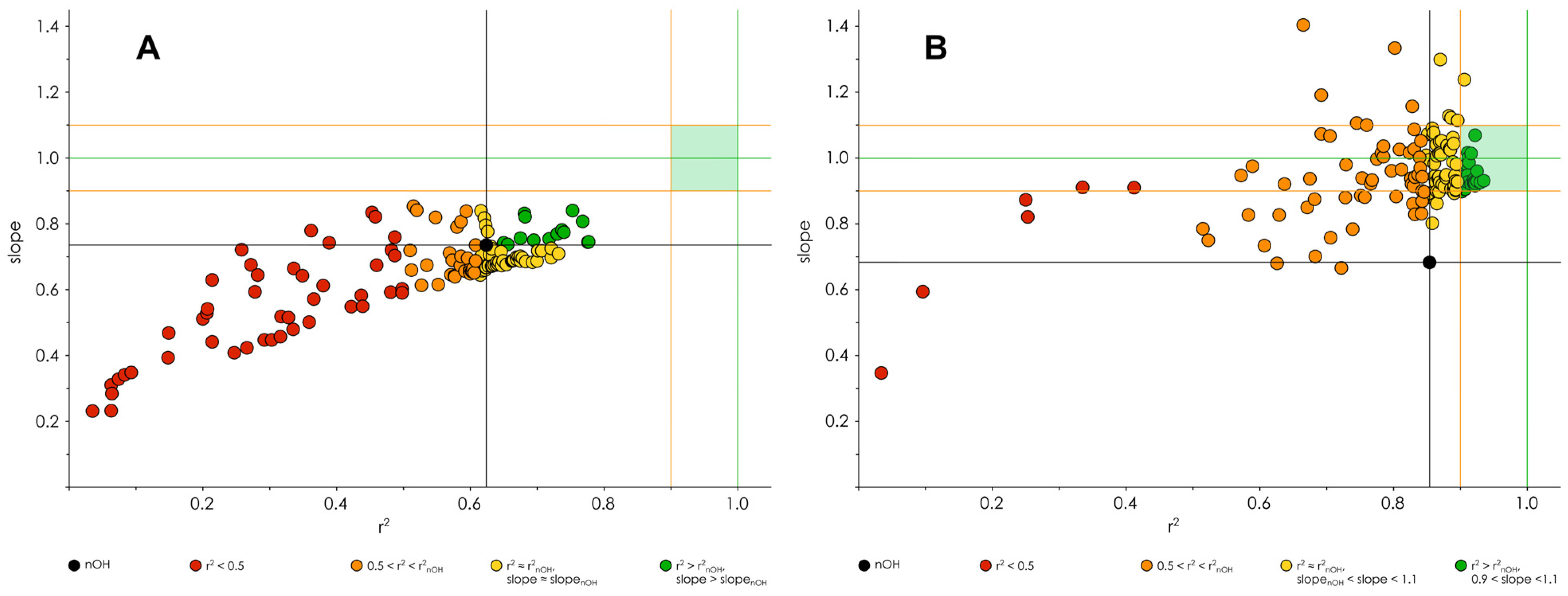
3.3. Optimization of the Classification/Regression Models
3.4. Testing of Classification/Regression Modeling on Less Chemically Diverse Datasets
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sies, H. Oxidative Stress: A Concept in Redox Biology and Medicine. Redox Biol. 2015, 4, 180–183. [Google Scholar] [CrossRef] [Green Version]
- Valko, M.; Leibfritz, D.; Moncol, J.; Cronin, M.T.D.; Mazur, M.; Telser, J. Free Radicals and Antioxidants in Normal Physiological Functions and Human Disease. Int. J. Biochem. Cell Biol. 2007, 39, 44–84. [Google Scholar] [CrossRef]
- Denisov, E.T.; Afanas’ev, I.B. Oxidation and Antioxidants in Organic Chemistry and Biology; Taylor & Francis: Boca Raton, FL, USA, 2005; ISBN 978-0-8247-5356-6. [Google Scholar]
- Sies, H. Polyphenols and Health: Update and Perspectives. Arch. Biochem. Biophys. 2010, 501, 2–5. [Google Scholar] [CrossRef]
- Leopoldini, M.; Russo, N.; Toscano, M. The Molecular Basis of Working Mechanism of Natural Polyphenolic Antioxidants. Food Chem. 2011, 125, 288–306. [Google Scholar] [CrossRef]
- Foti, M.; Piattelli, M.; Baratta, M.T.; Ruberto, G. Flavonoids, Coumarins, and Cinnamic Acids as Antioxidants in a Micellar System. Structure−Activity Relationship. J. Agric. Food Chem. 1996, 44, 497–501. [Google Scholar] [CrossRef]
- Burda, S.; Oleszek, W. Antioxidant and Antiradical Activities of Flavonoids. J. Agric. Food Chem. 2001, 49, 2774–2779. [Google Scholar] [CrossRef]
- Karadag, A.; Ozcelik, B.; Saner, S. Review of Methods to Determine Antioxidant Capacities. Food Anal. Methods 2009, 2, 41–60. [Google Scholar] [CrossRef]
- Foti, M.C. Use and Abuse of the DPPH• Radical. J. Agric. Food Chem. 2015, 63, 8765–8776. [Google Scholar] [CrossRef]
- Firuzi, O.; Lacanna, A.; Petrucci, R.; Marrosu, G.; Saso, L. Evaluation of the Antioxidant Activity of Flavonoids by “Ferric Reducing Antioxidant Power” Assay and Cyclic Voltammetry. Biochim. Biophys. Acta 2005, 1721, 174–184. [Google Scholar] [CrossRef]
- Franke, R.; Gruska, A. General Introduction to QSAR. In Quantitative Structure-Activity Relationship (QSAR) Models of Mutagens and Carcinogens; Benigni, R., Ed.; CRC Press: Boca Raton, FL, USA, 2003; pp. 1–41. [Google Scholar]
- Rice-Evans, C.; Miller, N.; Paganga, G. Structure-Antioxidant Activity Relationships of Flavonoids and Phenolic Acids. Free Radic. Biol. Med. 1996, 20, 933–956. [Google Scholar] [CrossRef]
- van Acker, S.A.; de Groot, M.J.; van den Berg, D.-J.; Tromp, M.N.; Donné-Op den Kelder, G.; van der Vijgh, W.J.; Bast, A. A Quantum Chemical Explanation of the Antioxidant Activity of Flavonoids. Chem. Res. Toxicol. 1996, 9, 1305–1312. [Google Scholar] [CrossRef]
- Amić, D.; Davidović-Amić, D.; Bešlo, D.; Rastija, V.; Lučić, B.; Trinajstić, N. SAR and QSAR of the Antioxidant Activity of Flavonoids. Curr. Med. Chem. 2007, 14, 827–845. [Google Scholar] [CrossRef] [PubMed]
- Alov, P.; Tsakovska, I.; Pajeva, I. Computational Studies of Free Radical-Scavenging Properties of Phenolic Compounds. Curr. Top. Med. Chem. 2015, 15, 85–104. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.-Z.; Sun, M.; Xing, J.; Luo, Q.; Corke, H. Structure-Radical Scavenging Activity Relationships of Phenolic Compounds from Traditional Chinese Medicinal Plants. Life Sci. 2006, 78, 2872–2888. [Google Scholar] [CrossRef] [PubMed]
- Filipović, M.; Marković, Z.; Đorović, J.; Marković, J.D.; Lučić, B.; Amić, D. QSAR of the Free Radical Scavenging Potency of Selected Hydroxybenzoic Acids and Simple Phenolics. C. R. Chim. 2015, 18, 492–498. [Google Scholar] [CrossRef]
- Amić, D.; Lučić, B. Reliability of Bond Dissociation Enthalpy Calculated by the PM6 Method and Experimental TEAC Values in Antiradical QSAR of Flavonoids. Bioorg. Med. Chem. 2010, 18, 28–35. [Google Scholar] [CrossRef]
- Lien, E.; Ren, S.; Bui, H.; Wang, R. Quantitative Structure-Activity Relationship Analysis of Phenolic Antioxidants. Free Radic. Biol. Med. 1999, 26, 285–294. [Google Scholar] [CrossRef]
- Marković, Z.; Filipović, M.; Manojlović, N.; Amić, A.; Jeremić, S.; Milenković, D. QSAR of the Free Radical Scavenging Potency of Selected Hydroxyanthraquinones. Chem. Pap. 2018, 72, 2785–2793. [Google Scholar] [CrossRef]
- Rackova, L.; Firakova, S.; Kostalova, D.; Stefek, M.; Sturdik, E.; Majekova, M. Oxidation of Liposomal Membrane Suppressed by Flavonoids: Quantitative Structure-Activity Relationship. Bioorg. Med. Chem. 2005, 13, 6477–6484. [Google Scholar] [CrossRef]
- Hotta, H.; Nagano, S.; Ueda, M.; Tsujino, Y.; Koyama, J.; Osakai, T. Higher Radical Scavenging Activities of Polyphenolic Antioxidants Can Be Ascribed to Chemical Reactions Following Their Oxidation. Biochim. Biophys. Acta-Gen. Subj. 2002, 1572, 123–132. [Google Scholar] [CrossRef]
- Nakao, K.; Shimizu, R.; Kubota, H.; Yasuhara, M.; Hashimura, Y.; Suzuki, T.; Fujita, T.; Ohmizu, H. Quantitative Structure-Activity Analyses of Novel Hydroxyphenylurea Derivatives as Antioxidants. Bioorg. Med. Chem. 1998, 6, 849–868. [Google Scholar] [CrossRef]
- Yamagami, C.; Motohashi, N.; Emoto, T.; Hamasaki, A.; Tanahashi, T.; Nagakura, N.; Takeuchi, Y. Quantitative Structure–Activity Relationship Analyses of Antioxidant and Free Radical Scavenging Activities for Hydroxybenzalacetones. Bioorg. Med. Chem. Lett. 2004, 14, 5629–5633. [Google Scholar] [CrossRef] [PubMed]
- Pratt, D.A.; DiLabio, G.A.; Valgimigli, L.; Pedulli, G.F.; Ingold, K.U. Substituent Effects on the Bond Dissociation Enthalpies of Aromatic Amines. J. Am. Chem. Soc. 2002, 124, 11085–11092. [Google Scholar] [CrossRef] [PubMed]
- Zavitsas, A.A.; Rogers, D.W.; Matsunaga, N. Shortcomings of Basing Radical Stabilization Energies on Bond Dissociation Energies of Alkyl Groups to Hydrogen. J. Org. Chem. 2010, 75, 5697–5700. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Zheng, Y.; An, L.; Zhang, L.; Qian, Y.; Yu, D.; Gong, X.; Liu, Y. A Theoretical Study of the Structure–Radical Scavenging Activity of Hydroxychalcones. Comput. Theor. Chem. 2012, 982, 74–83. [Google Scholar] [CrossRef]
- Nikolic, K.M. Theoretical Study of Phenolic Antioxidants Properties in Reaction with Oxygen-Centered Radicals. J. Mol. Struct. Theor. Chem. 2006, 774, 95–105. [Google Scholar] [CrossRef]
- Miličević, A.; Miletić, G.I.; Novak Jovanović, I. Electrochemical Oxidation of Flavonoids: PM6 and DFT for Elucidating Electronic Changes and Modelling Oxidation Potential (Part II). J. Mol. Liq. 2019, 295, 111730. [Google Scholar] [CrossRef]
- Todorova, T.Z.; Traykov, M.G.; Tadjer, A.V.; Velkov, Z.A. Structure of Flavones and Flavonols. Part I: Role of Substituents on the Planarity of the System. Comput. Theor. Chem. 2013, 1017, 85–90. [Google Scholar] [CrossRef]
- Lin, L.; Zhu, J. Antiaromaticity-Promoted Radical Stability in α-Methyl Heterocyclics. J. Org. Chem. 2021, 86, 15558–15567. [Google Scholar] [CrossRef]
- Jeremić, S.; Radenković, S.; Filipović, M.; Antić, M.; Amić, A.; Marković, Z. Importance of Hydrogen Bonding and Aromaticity Indices in QSAR Modeling of the Antioxidative Capacity of Selected (Poly)Phenolic Antioxidants. J. Mol. Graph. Model. 2017, 72, 240–245. [Google Scholar] [CrossRef]
- Arts, M.J.T.J.; Dallinga, J.S.; Voss, H.P.; Haenen, G.R.M.M.; Bast, A. A Critical Appraisal of the Use of the Antioxidant Capacity (TEAC) Assay in Defining Optimal Antioxidant Structures. Food Chem. 2003, 80, 409–414. [Google Scholar] [CrossRef]
- Haenen, G.R.M.M.; Arts, M.J.T.J.; Bast, A.; Coleman, M.D. Structure and Activity in Assessing Antioxidant Activity in Vitro and in Vivo A Critical Appraisal Illustrated with the Flavonoids. Environ. Toxicol. Pharmacol. 2006, 21, 191–198. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B.; et al. PubChem in 2021: New Data Content and Improved Web Interfaces. Nucleic Acids Res. 2021, 49, D1388–D1395. [Google Scholar] [CrossRef] [PubMed]
- Pence, H.E.; Williams, A. ChemSpider: An Online Chemical Information Resource. J. Chem. Educ. 2010, 87, 1123–1124. [Google Scholar] [CrossRef]
- NCI/CADD Chemical Identifier Resolver. Available online: https://cactus.nci.nih.gov/chemical/structure (accessed on 19 May 2021).
- Chemical Computing Group Inc. Molecular Operating Environment (MOE); Chemical Computing Group Inc.: Montreal, QC, Canada, 2016. [Google Scholar]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An Open Chemical Toolbox. J. Chem. Inform. 2011, 3, 33. [Google Scholar] [CrossRef] [Green Version]
- Obara, H.; Onodera, J. Structure of Carthamin. Chem. Lett. 1979, 8, 201–204. [Google Scholar] [CrossRef]
- Kim, J.-B.; Paik, Y.-S. Stability of Carthamin from Carthamus Tinctorius in Aqueous Solution: PH and Temperature Effects. Arch. Pharm. Res. 1997, 20, 643–646. [Google Scholar] [CrossRef]
- Labute, P. LowModeMD—Implicit Low-Mode Velocity Filtering Applied to Conformational Search of Macrocycles and Protein Loops. J. Chem. Inf. Model. 2010, 50, 792–800. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of Parameters for Semiempirical Methods VI: More Modifications to the NDDO Approximations and Re-Optimization of Parameters. J. Mol. Model. 2013, 19, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Stewart, J.J.P. MOPAC 2016; Stewart Computational Chemistry: Colorado Springs, CO, USA, 2016. [Google Scholar]
- Löwdin, P.-O. On the Nonorthogonality Problem. In Advances in Quantum Chemistry; Elsevier: Amsterdam, The Netherlands, 1970; Volume 5, pp. 185–199. ISBN 978-0-12-034805-3. [Google Scholar]
- Klein, E.; Rimarčík, J.; Lukeš, V. DFT/B3LYP Study of the O–H Bond Dissociation Enthalpies and Proton Affinities of Para-and Meta-Substituted Phenols in Water and Benzene. Acta Chim. Slovaca 2009, 2, 37–51. [Google Scholar]
- Rimarčík, J.; Lukeš, V.; Klein, E.; Ilčin, M. Study of the Solvent Effect on the Enthalpies of Homolytic and Heterolytic N–H Bond Cleavage in p-Phenylenediamine and Tetracyano-p-Phenylenediamine. J. Mol. Struct. Theor. Chem. 2010, 952, 25–30. [Google Scholar] [CrossRef]
- Wall, L. The PERL Programming Language; Prentice Hall Software Series; Prentice Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- Vedernikova, I.; Tollenaere, J.P.; Haemers, A. Quantum Mechanical Evaluation of the Anodic Oxidation of Phenolic Compounds. J. Phys. Org. Chem. 1999, 12, 144–150. [Google Scholar] [CrossRef]
- Alov, P.; Tsakovska, I.; Pajeva, I. Quantitative Structure-Property Relationship Modelling of Antiradical Properties of Natural Polyphenols Using EVA Vector Descriptor Approach. Comptes Rendus de L’Acade’mie Bulgare des Sciences 2016, 69, 1145–1152. [Google Scholar]
- Foti, M.C.; Daquino, C.; Mackie, I.D.; DiLabio, G.A.; Ingold, K.U. Reaction of Phenols with the 2,2-Diphenyl-1-Picrylhydrazyl Radical. Kinetics and DFT Calculations Applied to Determine ArO-H Bond Dissociation Enthalpies and Reaction Mechanism. J. Org. Chem. 2008, 73, 9270–9282. [Google Scholar] [CrossRef] [PubMed]
- Galano, A.; Alvarez-Idaboy, J.R. A Computational Methodology for Accurate Predictions of Rate Constants in Solution: Application to the Assessment of Primary Antioxidant Activity. J. Comput. Chem. 2013, 34, 2430–2445. [Google Scholar] [CrossRef] [PubMed]
- Apak, R.; Capanoglu, E.; Shahidi, F. (Eds.) Measurement of Antioxidant Activity & Capacity: Recent Trends and Applications; Functional Food Science and Technology; Wiley-Blackwell: Hoboken, NJ, USA, 2017; ISBN 978-1-119-13538-8. [Google Scholar]
- Klein, E.; Lukeš, V. DFT/B3LYP Study of the Substituent Effect on the Reaction Enthalpies of the Individual Steps of Single Electron Transfer−Proton Transfer and Sequential Proton Loss Electron Transfer Mechanisms of Phenols Antioxidant Action. J. Phys. Chem. A 2006, 110, 12312–12320. [Google Scholar] [CrossRef] [PubMed]
- Litwinienko, G.; Ingold, K.U. Solvent Effects on the Rates and Mechanisms of Reaction of Phenols with Free Radicals. Acc. Chem. Res. 2007, 40, 222–230. [Google Scholar] [CrossRef]
- Ellis, G.P. Chromenes, Chromanones, and Chromones—Introduction. In Chemistry of Heterocyclic Compounds: A Series of Monographs; Ellis, G.P., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; ISBN 978-0-470-18701-2. [Google Scholar]
- Migliavacca, E.; Carrupt, P.-A.; Testa, B. Theoretical Parameters to Characterize Antioxidants. Part 1. The Case of Vitamin E and Analogs. HCA 1997, 80, 1613–1626. [Google Scholar] [CrossRef]
- Wright, J.S.; Johnson, E.R.; DiLabio, G.A. Predicting the Activity of Phenolic Antioxidants: Theoretical Method, Analysis of Substituent Effects, and Application to Major Families of Antioxidants. J. Am. Chem. Soc. 2001, 123, 1173–1183. [Google Scholar] [CrossRef]
- Wijtmans, M.; Pratt, D.A.; Valgimigli, L.; DiLabio, G.A.; Pedulli, G.F.; Porter, N.A. 6-Amino-3-Pyridinols: Towards Diffusion-Controlled Chain-Breaking Antioxidants. Angew. Chem. Int. Ed. 2003, 42, 4370–4373. [Google Scholar] [CrossRef]
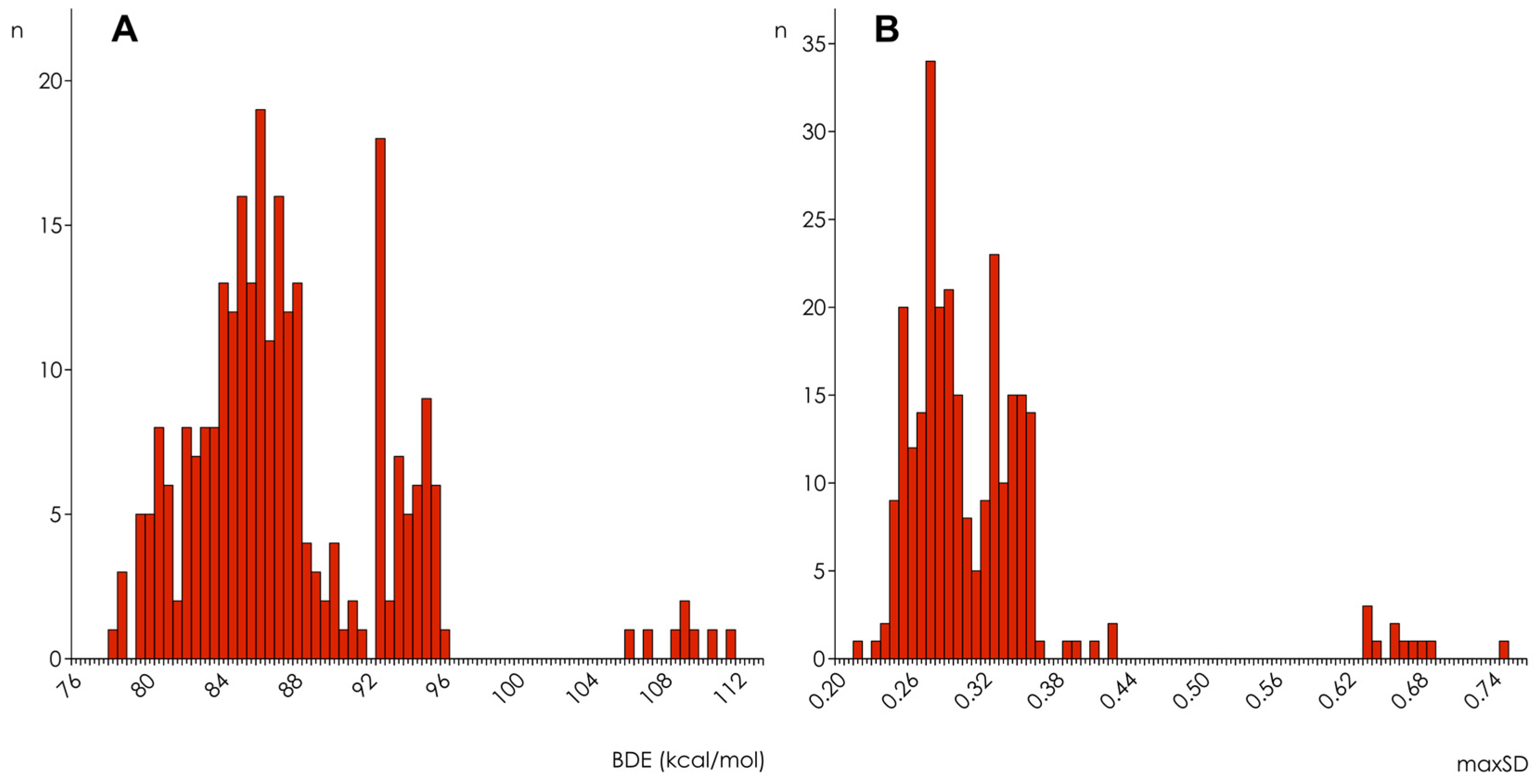
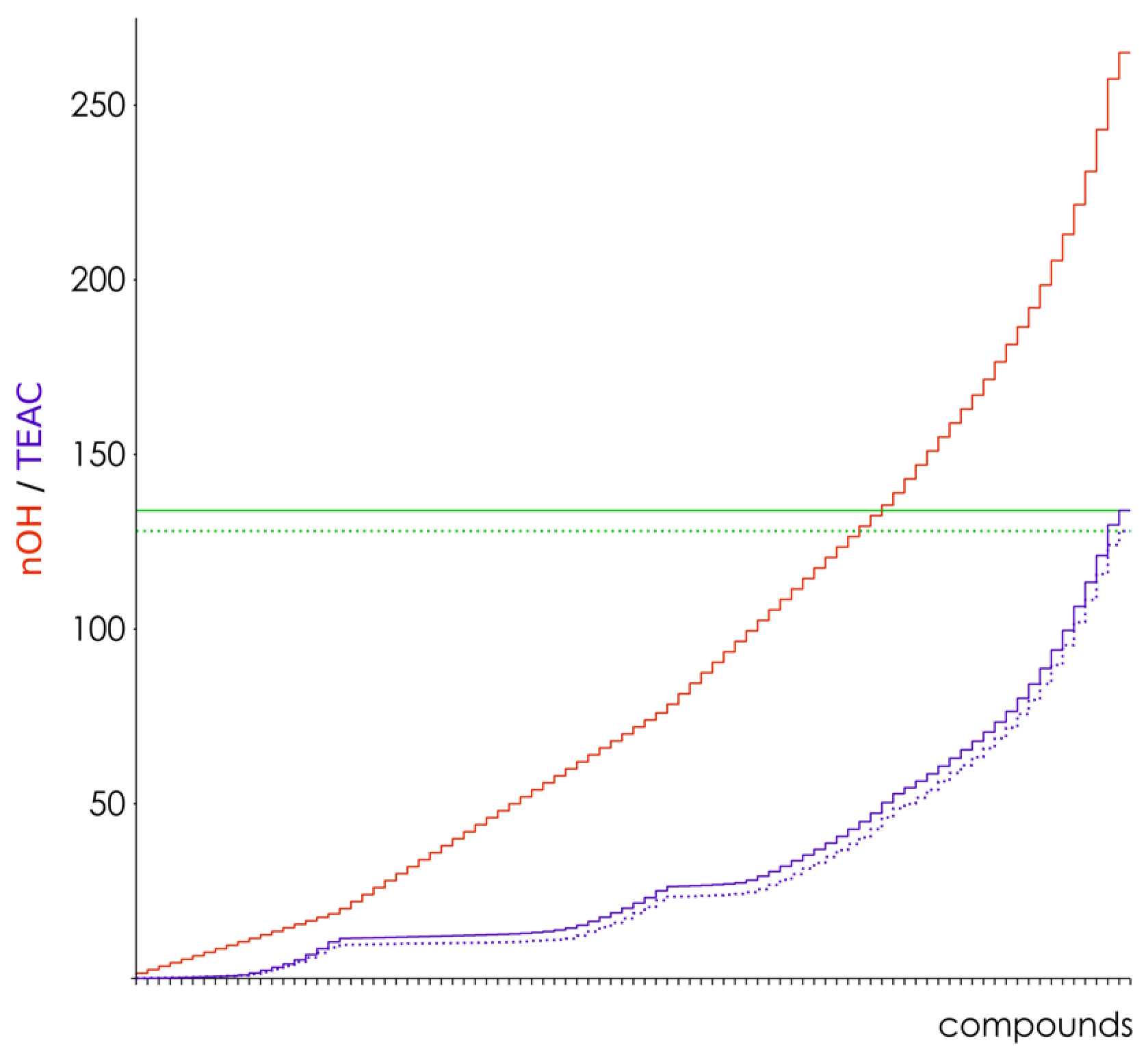
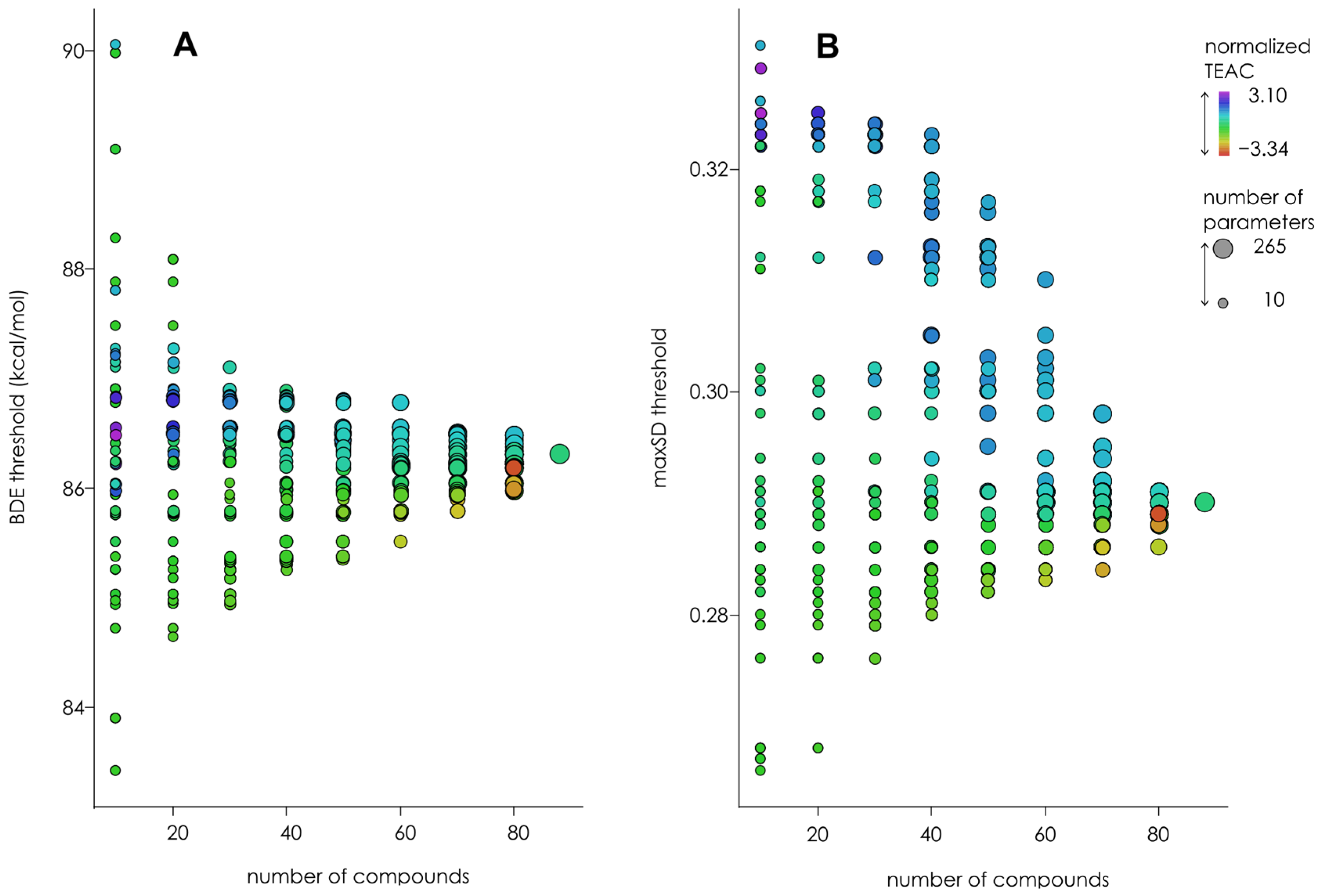

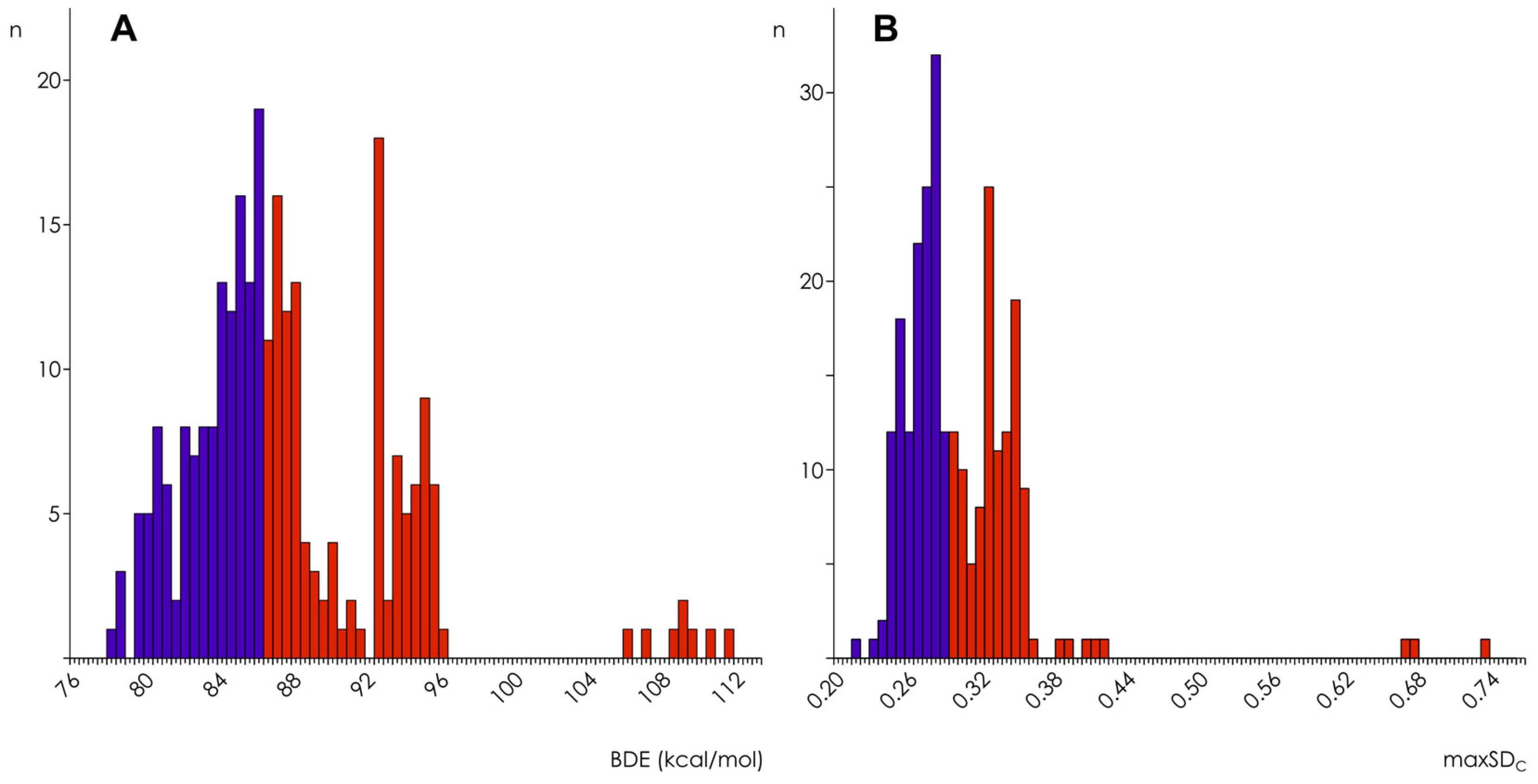
| Hamiltonian | Parameter | Thresholds | |||
|---|---|---|---|---|---|
| Vacuum | COSMO | ||||
| ABTS●+ | DPPH● | ABTS●+ | DPPH● | ||
| AM1 | BDE | 86.2 | 86.0 | 82.6 | 82.0 |
| maxSDC | 0.286 | 0.283 | 0.278 | 0.274 | |
| BDE × maxSDC | 25.5 | 25.2 | 23.8 | 22.7 | |
| PM6 | BDE | 84.8 | 84.3 | 80.8 | 80.2 |
| maxSDC | 0.315 | 0.313 | 0.303 | 0.300 | |
| BDE × maxSDC | 28.0 | 27.5 | 24.5 | 24.0 | |
| PM7 | BDE | 85.8 | 85.2 | 82.4 | 82.0 |
| maxSDC | 0.296 | 0.294 | 0.298 | 0.292 | |
| BDE × maxSDC | 27.1 | 26.5 | 25.1 | 24.5 | |
| RM1 | BDE | 83.8 | 83.5 | 79.2 | 79.1 |
| maxSDC | 0.299 | 0.296 | 0.291 | 0.290 | |
| BDE × maxSDC | 25.7 | 25.7 | 24.3 | 24.1 | |
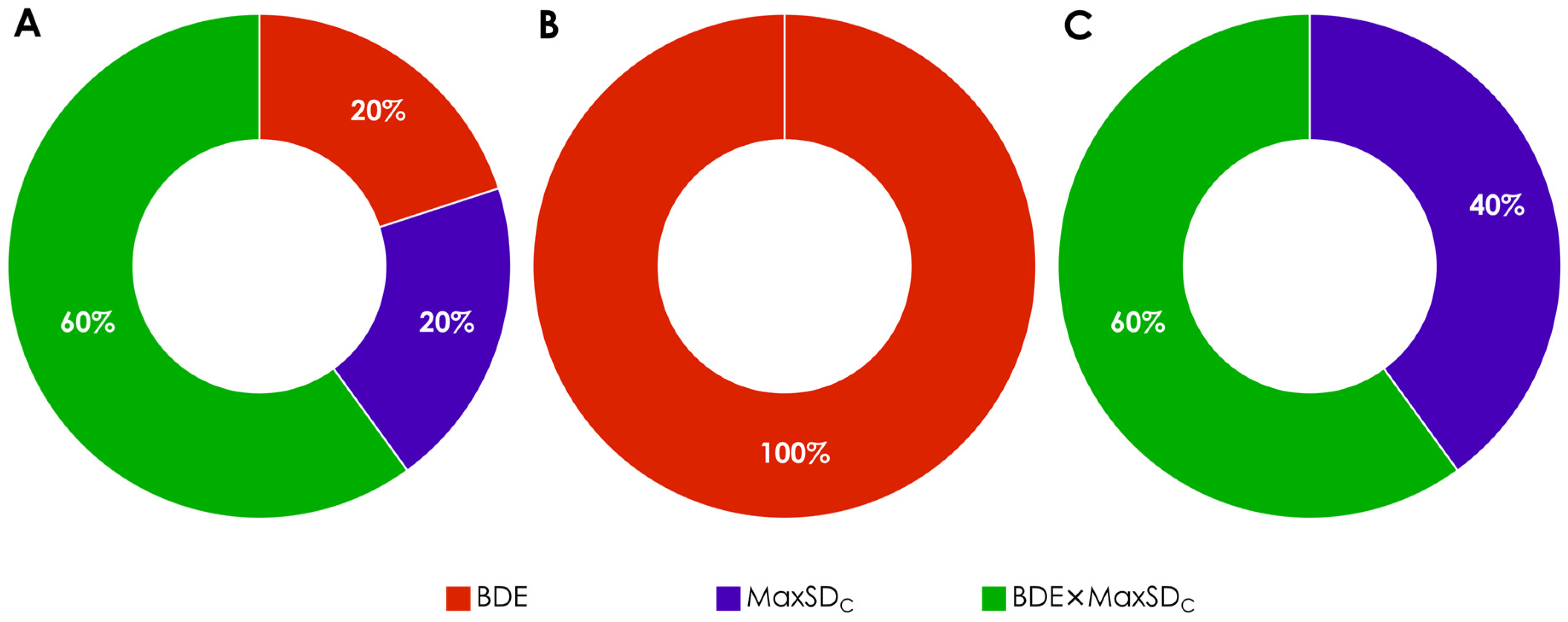
| Assay | Simulation Type | Classification Parameter | Model (n = 88) |
|---|---|---|---|
| ABTS●+ | PM6, vacuum | BDE × PA | TEAC = 0.206 + 0.871 × nOHactive r2 = 0.887, q2LOO = 0.875 |
| – | – | TEAC = −0.562 + 0.692 × nOHtotal r2 = 0.817, q2LOO = 0.802 | |
| DPPH● | RM1, vacuum | BDE × maxSDC × PA | TEAC = 0.206 + 0.859 × nOHactive r2 = 0.864, q2LOO = 0.860 |
| – | – | TEAC = −0.582 + 0.677 × nOHtotal r2 = 0.807, q2LOO = 0.792 |
| Assay | Simulation Type | Classification Parameter | Model (n = 48) |
|---|---|---|---|
| ABTS●+ | PM6, vacuum | BDE × PA | TEAC = 0.220 + 0.809 × nOHactive r2 = 0.813, q2LOO = 0.755 |
| – | – | TEAC = −0.677 + 0.803 × nOHtotal r2 = 0.649, q2LOO = 0.545 | |
| DPPH● | PM6, vacuum | BDE × PA | TEAC = 0.257 + 0.746 × nOHactive r2 = 0.777, q2LOO = 0.769 |
| – | – | TEAC = −0.622 + 0.736 × nOHtotal r2 = 0.624, q2LOO = 0.539 |
| Assay | Simulation Type | Classification Parameter | Model (n = 40) |
|---|---|---|---|
| ABTS●+ | AM1, COSMO | maxSDC × IP | TEAC = 0.100 + 0.954 × nOHactive r2 = 0.950, q2LOO = 0.948 |
| – | – | TEAC = −0.734 + 0.697 × nOHtotal r2 = 0.876, q2LOO = 0.855 | |
| DPPH● | AM1, COSMO | maxSDC × IP | TEAC = 0.154 + 0.932 × nOHactive r2 = 0.935, q2LOO = 0.925 |
| – | – | TEAC = −0.718 + 0.684 × nOHtotal r2 = 0.854, q2LOO = 0.829 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alov, P.; Tsakovska, I.; Pajeva, I. Hybrid Classification/Regression Approach to QSAR Modeling of Stoichiometric Antiradical Capacity Assays’ Endpoints. Molecules 2022, 27, 2084. https://doi.org/10.3390/molecules27072084
Alov P, Tsakovska I, Pajeva I. Hybrid Classification/Regression Approach to QSAR Modeling of Stoichiometric Antiradical Capacity Assays’ Endpoints. Molecules. 2022; 27(7):2084. https://doi.org/10.3390/molecules27072084
Chicago/Turabian StyleAlov, Petko, Ivanka Tsakovska, and Ilza Pajeva. 2022. "Hybrid Classification/Regression Approach to QSAR Modeling of Stoichiometric Antiradical Capacity Assays’ Endpoints" Molecules 27, no. 7: 2084. https://doi.org/10.3390/molecules27072084
APA StyleAlov, P., Tsakovska, I., & Pajeva, I. (2022). Hybrid Classification/Regression Approach to QSAR Modeling of Stoichiometric Antiradical Capacity Assays’ Endpoints. Molecules, 27(7), 2084. https://doi.org/10.3390/molecules27072084






