Machine Learning for Evaluating the Cytotoxicity of Mixtures of Nano-TiO2 and Heavy Metals: QSAR Model Apply Random Forest Algorithm after Clustering Analysis
Abstract
:1. Introduction
2. Results and Discussion
2.1. Experimental Results
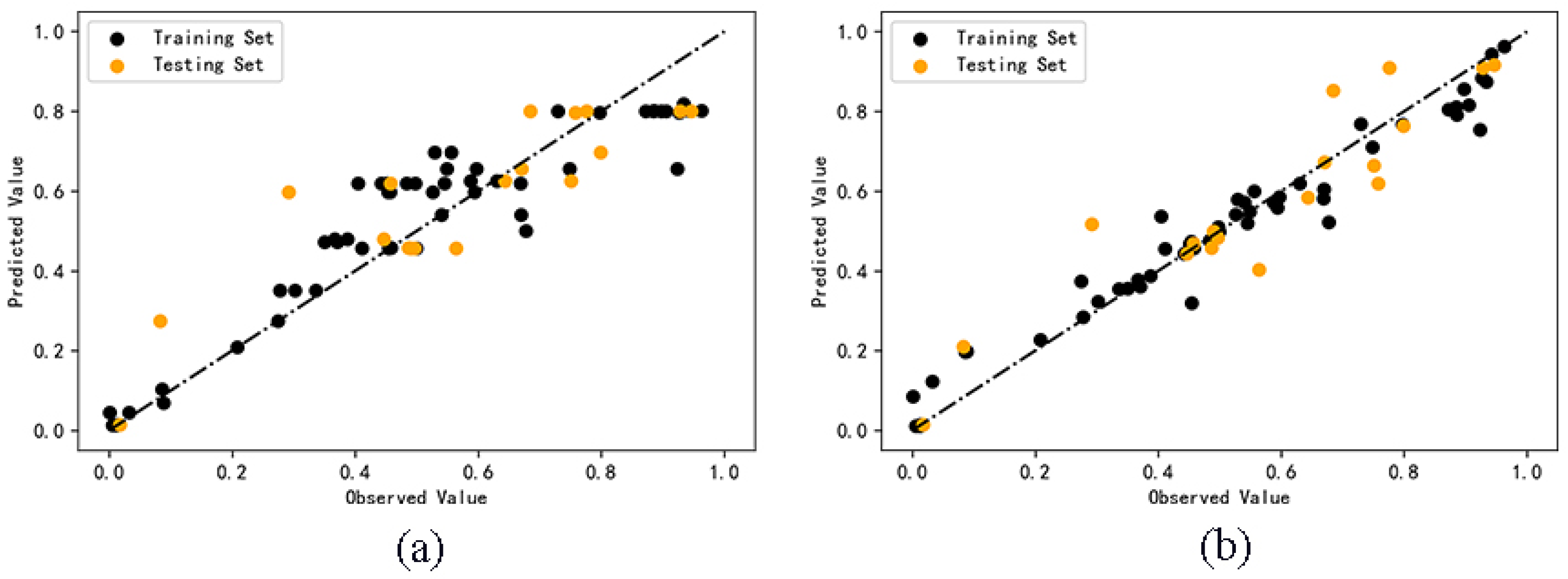
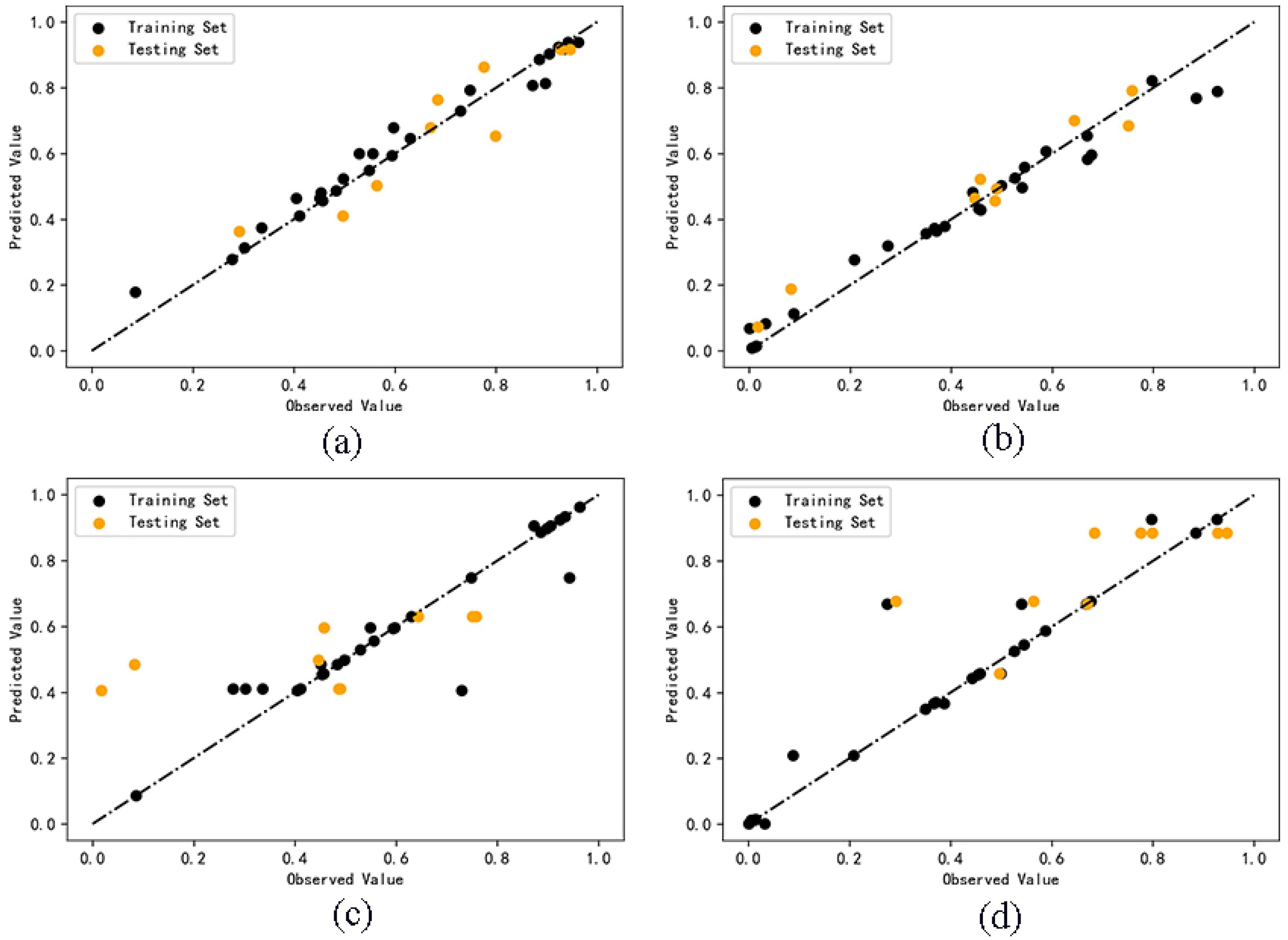
2.2. QSAR Model Calculation Results
2.3. Model Validation Results
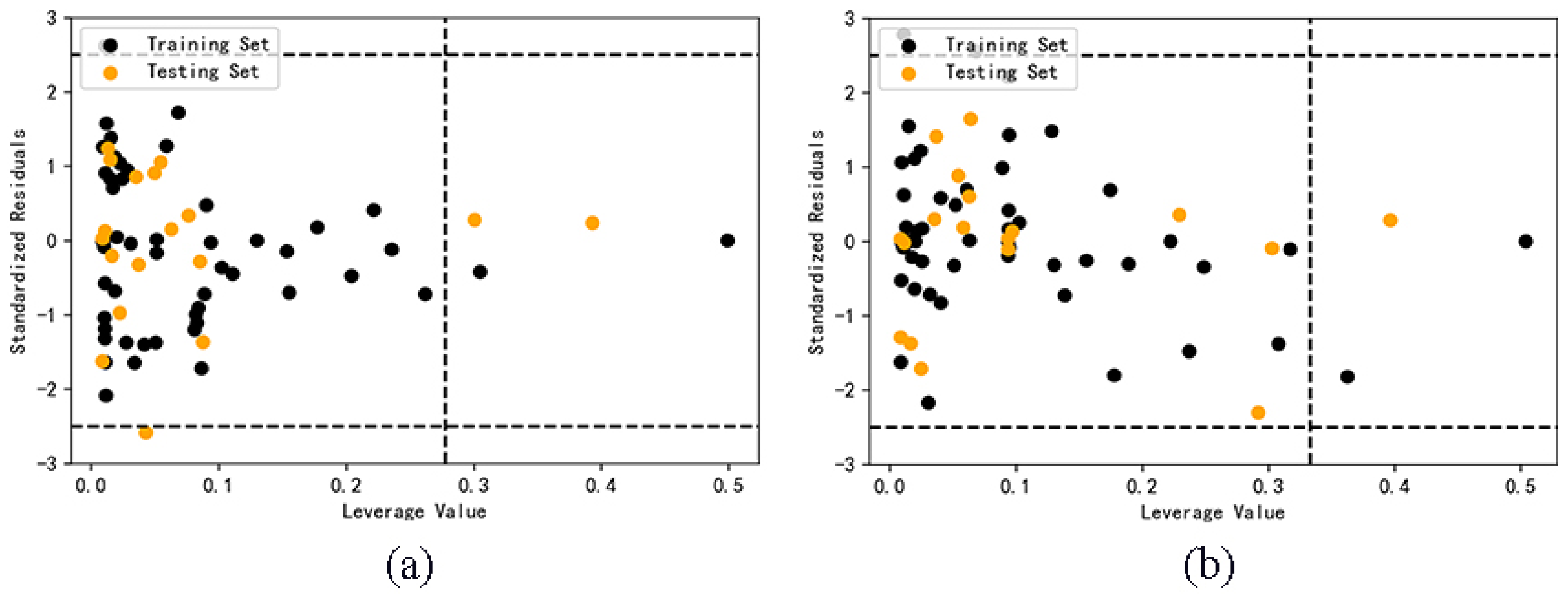
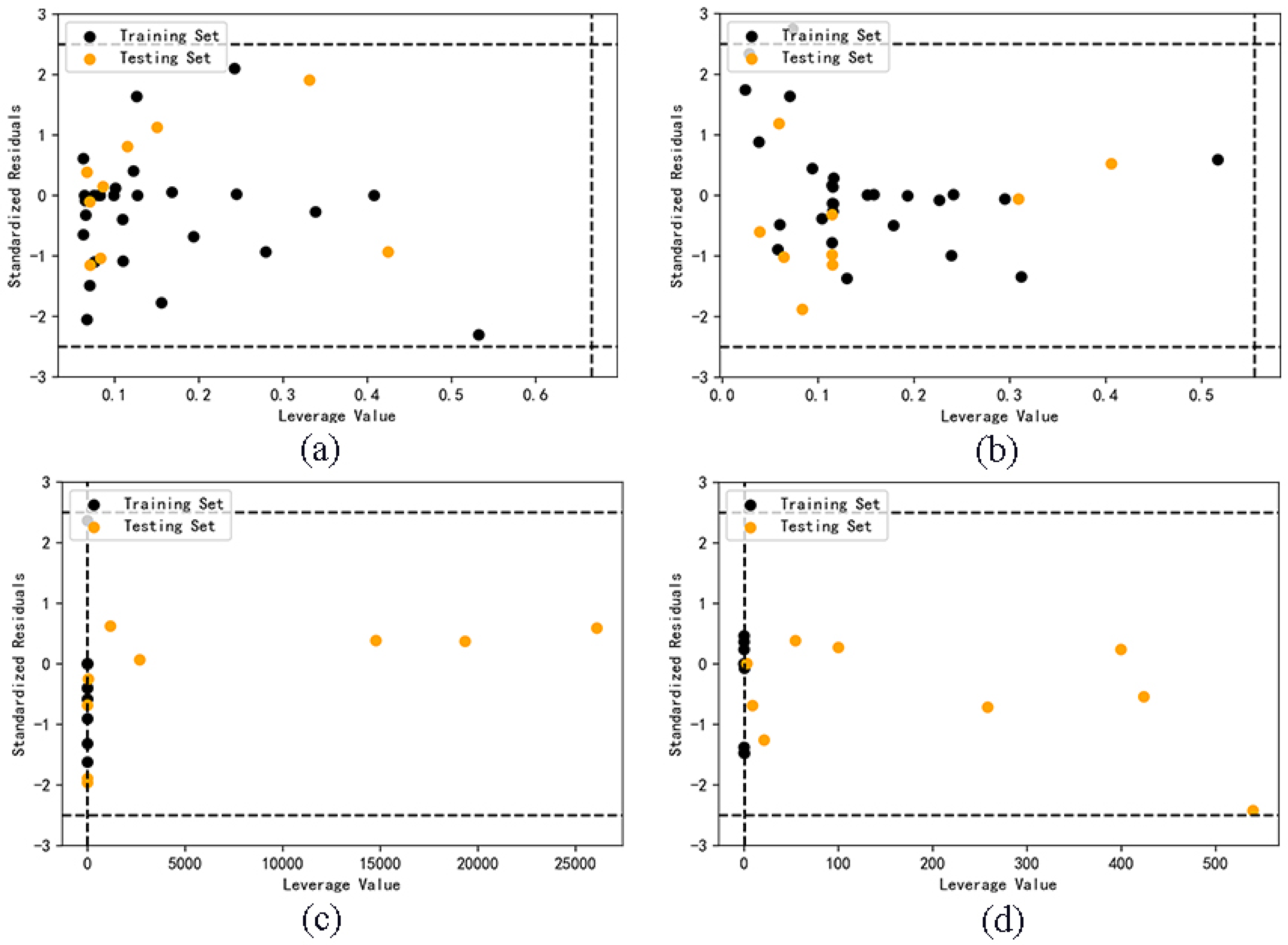
2.4. Application domain analysis
2.5. Research Results of the Toxicity Mechanisms
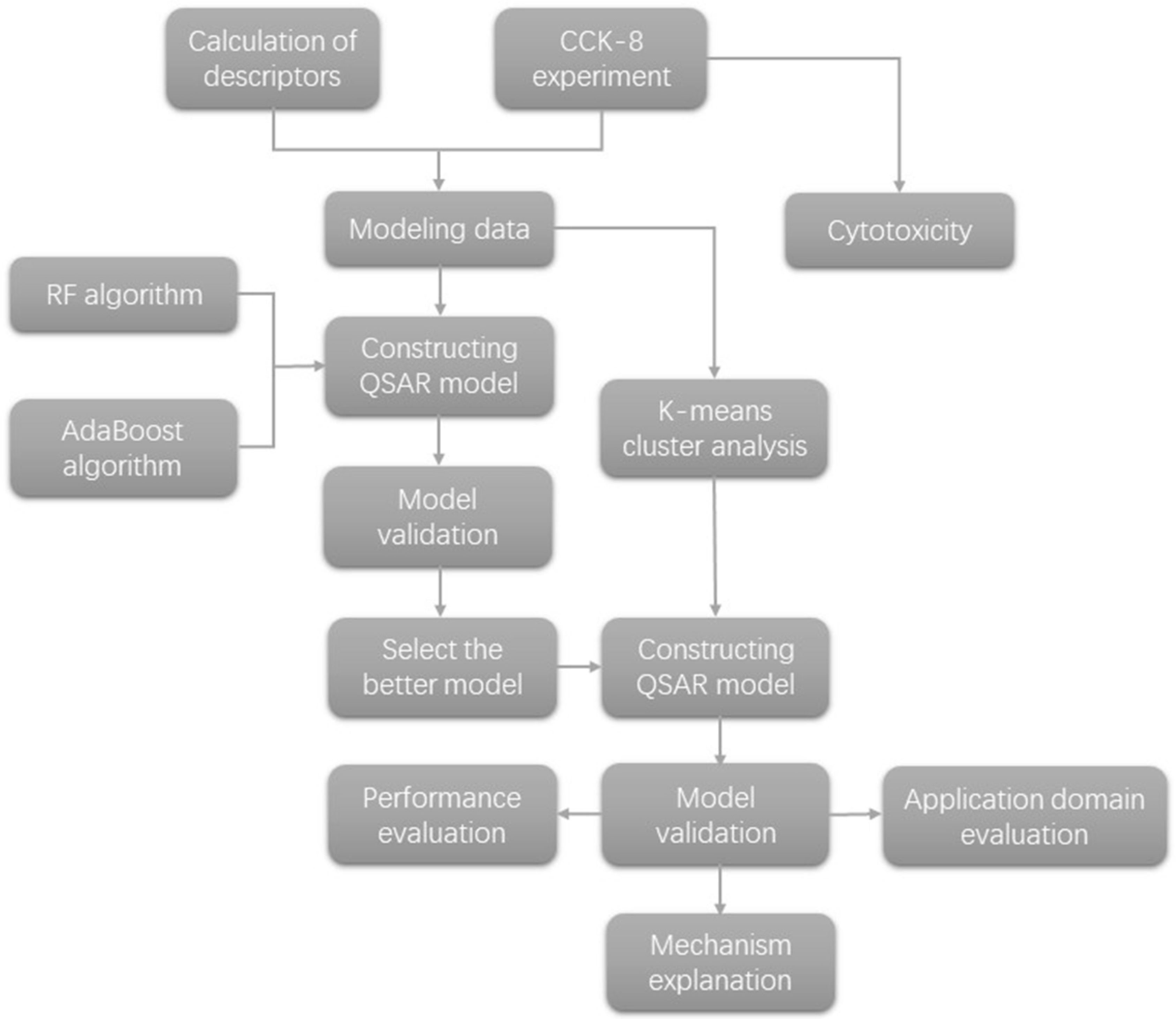
3. Materials and Methods
3.1. Cell Experiments
3.2. Research on the QSAR Model
3.2.1. Selection and Calculation of Descriptors
3.2.2. Classification of Mixture Types
3.2.3. Data Set Division
3.2.4. Algorithm Application
3.2.5. Model Validation
3.2.6. Application Domain of the Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sharifi, S.; Behzadi, S.; Laurent, S.; Forrest, M.L.; Stroeve, P.; Mahmoudi, M. Toxicity of Nanomaterials. Chem. Soc. Rev. 2012, 41, 2323–2343. [Google Scholar] [CrossRef] [PubMed]
- Roy, J.; Roy, K. Assessment of Toxicity of Metal Oxide and Hydroxide Nanoparticles Using the QSAR Modeling Approach. Environ. Sci. Nano 2021, 8, 3395–3407. [Google Scholar] [CrossRef]
- Qi, Y.; Xiang, B.; Zhang, J. Effect of Titanium Dioxide (TiO2) with Different Crystal Forms and Surface Modifications on Cooling Property and Surface Wettability of Cool Roofing Materials. Sol. Energy Mater. Sol. Cells 2017, 172, 34–43. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Z.R.; Fu, X.; Xu, Y.J. TiO2-Graphene Nanocomposites for Gas-Phase Photocatalytic Degradation of Volatile Aromatic Pollutant: Is TiO2-Graphene Truly Different from Other TiO2-Carbon Composite Materials? ACS Nano 2010, 4, 7303–7314. [Google Scholar] [CrossRef]
- Dastjerdi, R.; Montazer, M. A Review on the Application of Inorganic Nano-Structured Materials in the Modification of Textiles: Focus on Anti-Microbial Properties. Colloids Surf. B Biointerfaces 2010, 4, 7303–7314. [Google Scholar] [CrossRef]
- Chong, M.N.; Tneu, Z.Y.; Poh, P.E.; Jin, B.; Aryal, R. Synthesis, Characterisation and Application of TiO2-Zeolite Nanocomposites for the Advanced Treatment of Industrial Dye Wastewater. J. Taiwan Inst. Chem. Eng. 2015, 50, 288–296. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, G.; Wang, Y.; Zhao, Y.; Su, H.; Tan, T. Preparation of Chitosan-TiO2 Composite Film with Efficient Antimicrobial Activities under Visible Light for Food Packaging Applications. Carbohydr. Polym. 2017, 169, 101–107. [Google Scholar] [CrossRef]
- Sabzi, M.; Mirabedini, S.M.; Zohuriaan-Mehr, J.; Atai, M. Surface Modification of TiO2 Nano-Particles with Silane Coupling Agent and Investigation of Its Effect on the Properties of Polyurethane Composite Coating. Prog. Org. Coat. 2009, 65, 222–228. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, Q.; Yu, J.; Liu, B. Development of Multifunctional Photoactive Self-Cleaning Glasses. J. Non-Cryst. Solids 2008, 354, 1424–1430. [Google Scholar] [CrossRef]
- Gupta, A.K.; Gupta, M. Synthesis and Surface Engineering of Iron Oxide Nanoparticles for Biomedical Applications. Biomaterials 2005, 354, 1424–1430. [Google Scholar] [CrossRef]
- Aruoja, V.; Dubourguier, H.C.; Kasemets, K.; Kahru, A. Toxicity of Nanoparticles of CuO, ZnO and TiO2 to Microalgae Pseudokirchneriella Subcapitata. Sci. Total Environ. 2009, 354, 1424–1430. [Google Scholar] [CrossRef] [PubMed]
- Buglak, A.A.; Zherdev, A.V.; Dzantiev, B.B. Nano-(Q)SAR for Cytotoxicity Prediction of Engineered Nanomaterials. Molecules 2019, 24, 4537. [Google Scholar] [CrossRef] [PubMed]
- Zukal, J.; Pikula, J.; Bandouchova, H. Bats as Bioindicators of Heavy Metal Pollution: History and Prospect. Mamm. Biol. 2015, 80, 220–227. [Google Scholar] [CrossRef]
- Jacob, J.M.; Karthik, C.; Saratale, R.G.; Kumar, S.S.; Prabakar, D.; Kadirvelu, K.; Pugazhendhi, A. Biological Approaches to Tackle Heavy Metal Pollution: A Survey of Literature. J. Environ. Manag. 2018, 217, 56–70. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.Z.N.; Wan Salleh, W.N.; Ismail, A.F.; Yusof, N.; Mohd Yusop, M.Z.; Aziz, F. Adsorptive Removal of Heavy Metal Ions Using Graphene-Based Nanomaterials: Toxicity, Roles of Functional Groups and Mechanisms. Chemosphere 2020, 248, 126008. [Google Scholar] [CrossRef]
- Ahmadi, S.; Toropova, A.P.; Toropov, A.A. Correlation Intensity Index: Mathematical Modeling of Cytotoxicity of Metal Oxide Nanoparticles. Nanotoxicology 2020, 14, 1118–1126. [Google Scholar] [CrossRef]
- Manganelli, S.; Leone, C.; Toropov, A.A.; Toropova, A.P.; Benfenati, E. QSAR Model for Predicting Cell Viability of Human Embryonic Kidney Cells Exposed to SiO2 Nanoparticles. Chemosphere 2016, 144, 1118–1126. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, J.; Huang, Y.; Zhou, Q.; Zhang, X.; Zhang, S. Toxicity of Ionic Liquids: Database and Prediction via Quantitative Structure-Activity Relationship Method. J. Hazard. Mater. 2014, 278, 320–329. [Google Scholar] [CrossRef]
- Muratov, E.N.; Bajorath, J.; Sheridan, R.P.; Tetko, I.V.; Filimonov, D.; Poroikov, V.; Oprea, T.I.; Baskin, I.I.; Varnek, A.; Roitberg, A.; et al. Correction: QSAR without Borders. Chem. Soc. Rev. 2020, 49, 3716. [Google Scholar] [CrossRef]
- Chatterjee, M.; Banerjee, A.; De, P.; Gajewicz-Skretna, A.; Roy, K. A Novel Quantitative Read-across Tool Designed Purposefully to Fill the Existing Gaps in Nanosafety Data. Environ. Sci. Nano 2022, 9, 189–203. [Google Scholar] [CrossRef]
- Jiao, Z.; Hu, P.; Xu, H.; Wang, Q. Machine Learning and Deep Learning in Chemical Health and Safety: A Systematic Review of Techniques and Applications. J. Chem. Health Saf. 2020, 27, 316–334. [Google Scholar] [CrossRef]
- Roy, J.; Roy, K. Modeling and Mechanistic Understanding of Cytotoxicity of Metal Oxide Nanoparticles (MeOxNPs) to Escherichia Coli: Categorization and Data Gap Filling for Untested Metal Oxides. Nanotoxicology 2022, 16, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Pathakoti, K.; Tchounwou, P.B.; Leszczynska, D.; Leszczynski, J. Evaluating the Cytotoxicity of a Large Pool of Metal Oxide Nanoparticles to Escherichia Coli: Mechanistic Understanding through In Vitro and In Silico Studies. Chemosphere 2021, 264, 128428. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Gajewicz, A.; Puzyn, T.; Roy, K.; Leszczynski, J. Periodic Table-Based Descriptors to Encode Cytotoxicity Profile of Metal Oxide Nanoparticles: A Mechanistic QSTR Approach. Ecotoxicol. Environ. Saf. 2014, 107, 162–169. [Google Scholar] [CrossRef] [PubMed]
- Marković, Z.; Filipović, M.; Manojlović, N.; Amić, A.; Jeremić, S.; Milenković, D. QSAR of the Free Radical Scavenging Potency of Selected Hydroxyanthraquinones. Chem. Pap. 2018, 72, 2785–2793. [Google Scholar] [CrossRef]
- Luan, F.; Tang, L.; Zhang, L.; Zhang, S.; Monteagudo, M.C.; Cordeiro, M.N.D.S. A Further Development of the QNAR Model to Predict the Cellular Uptake of Nanoparticles by Pancreatic Cancer Cells. Food Chem. Toxicol. 2018, 112, 571–580. [Google Scholar] [CrossRef]
- Roy, J.; Ojha, P.K.; Roy, K. Risk Assessment of Heterogeneous TiO2-Based Engineered Nanoparticles (NPs): A QSTR Approach Using Simple Periodic Table Based Descriptors. Nanotoxicology 2019, 13, 701–716. [Google Scholar] [CrossRef]
- Fereidoonnezhad, M.; Faghih, Z.; Mojaddami, A.; Rezaei, Z.; Sakhteman, A. A Comparative QSAR Analysis, Molecular Docking and PLIF Studies of Some N-Arylphenyl-2,2- Dichloroacetamide Analogues as Anticancer Agents. Iran. J. Pharm. Res. 2017, 16, 981–998. [Google Scholar] [CrossRef]
- Sifonte, E.P.; Castro-Smirnov, F.A.; Jimenez, A.A.S.; Diez, H.R.G.; Martínez, F.G. Quantum Mechanics Descriptors in a Nano-QSAR Model to Predict Metal Oxide Nanoparticles Toxicity in Human Keratinous Cells. J. Nanoparticle Res. 2021, 23, 161. [Google Scholar] [CrossRef]
- Cao, J.; Pan, Y.; Jiang, Y.; Qi, R.; Yuan, B.; Jia, Z.; Jiang, J.; Wang, Q. Computer-Aided Nanotoxicology: Risk Assessment of Metal Oxide Nanoparticlesvianano-QSAR. Green Chem. 2020, 22, 3512–3521. [Google Scholar] [CrossRef]
- Jain, N.; Jhunthra, S.; Garg, H.; Gupta, V.; Mohan, S.; Ahmadian, A.; Salahshour, S.; Ferrara, M. Prediction Modelling of COVID Using Machine Learning Methods from B-Cell Dataset. Results Phys. 2021, 21, 103813. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, J.B.O. Machine Learning Methods in Chemoinformatics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 468–481. [Google Scholar] [CrossRef] [PubMed]
- Livingston, F. Implementation of Breiman’s Random Forest Machine Learning Algorithm. Mach. Learn. J. Pap. 2005, 1–13. [Google Scholar]
- Louppe, G. Understanding Random Forests; Cornell University Library: Ithaca, NY, USA, 2014. [Google Scholar]
- Hajjem, A.; Bellavance, F.; Larocque, D. Mixed-Effects Random Forest for Clustered Data. J. Stat. Comput. Simul. 2014, 84, 1313–1328. [Google Scholar] [CrossRef]
- Donges, N. The Random Forest Algorithm. Towards Data Sci. 2018, 22. [Google Scholar]
- Cheng, L.; Chen, X.; De Vos, J.; Lai, X.; Witlox, F. Applying a Random Forest Method Approach to Model Travel Mode Choice Behavior. Travel Behav. Soc. 2019, 14, 1–10. [Google Scholar] [CrossRef]
- Osisanwo, F.Y.; Akinsola, J.E.T.; Awodele, O.; Hinmikaiye, J.O.; Olakanmi, O.; Akinjobi, J. Supervised Machine Learning Algorithms: Classification and Comparison. IJCTT 2017, 48, 128–138. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Tenenhaus, M.; Vinzi, V.E.; Chatelin, Y.M.; Lauro, C. PLS Path Modeling. Comput. Stat. Data Anal. 2005, 48, 159–205. [Google Scholar] [CrossRef]
- Lučić, B.; Batista, J.; Bojović, V.; Lovrić, M.; Kržić, A.S.; Bešlo, D.; Nadramija, D.; Vikić-Topić, D. Estimation of Random Accuracy and Its Use in Validation of Predictive Quality of Classification Models within Predictive Challenges. Croat. Chem. Acta 2019, 92, 379–391. [Google Scholar] [CrossRef]
- Golbraikh, A.; Tropsha, A. Beware of Q2! J. Mol. Graph. Model. 2002, 20, 269–276. [Google Scholar] [CrossRef]
- Rücker, C.; Rücker, G.; Meringer, M. Y-Randomization and Its Variants in QSPR/QSAR. J. Chem. Inf. Model. 2007, 47, 2345–2357. [Google Scholar] [CrossRef] [PubMed]
- Tropsha, A.; Gramatica, P.; Gombar, V.K. The Importance of Being Earnest: Validation Is the Absolute Essential for Successful Application and Interpretation of QSPR Models. QSAR Comb. Sci. 2003, 22, 67–77. [Google Scholar] [CrossRef]
- Schüürmann, G.; Ebert, R.U.; Chen, J.; Wang, B.; Kühne, R. External Validation and Prediction Employing the Predictive Squared Correlation Coefficient - Test Set Activity Mean vs Training Set Activity Mean. J. Chem. Inf. Model. 2008, 48, 2140–2145. [Google Scholar] [CrossRef]
- Consonni, V.; Ballabio, D.; Todeschini, R. Comments on the Definition of the Q2 Parameter for QSAR Validation. J. Chem. Inf. Model. 2009, 1669–1678. [Google Scholar] [CrossRef]
- Chirico, N.; Gramatica, P. Real External Predictivity of QSAR Models: How to Evaluate It? Comparison of Different Validation Criteria and Proposal of Using the Concordance Correlation Coefficient. J. Chem. Inf. Model. 2011, 51, 2320–2335. [Google Scholar] [CrossRef]
- Yuan, B.; Wang, P.; Sang, L.; Gong, J.; Pan, Y.; Hu, Y. QNAR Modeling of Cytotoxicity of Mixing Nano-TiO2 and Heavy Metals. Ecotoxicol. Environ. Saf. 2021, 208, 111634. [Google Scholar] [CrossRef]
- Khan, S.T.; Ahmad, J.; Ahamed, M.; Musarrat, J.; Al-Khedhairy, A.A. Zinc Oxide and Titanium Dioxide Nanoparticles Induce Oxidative Stress, Inhibit Growth, and Attenuate Biofilm Formation Activity of Streptococcus Mitis. J. Biol. Inorg. Chem. 2016, 21, 295–303. [Google Scholar] [CrossRef]
- Boulangier, J.; Gobrecht, D.; Decin, L.; De Koter, A.; Yates, J. Developing a Self-Consistent AGB Wind Model–II. Non-Classical, Non-Equilibrium Polymer Nucleation in a Chemical Mixture. Mon. Not. R. Astron. Soc. 2019, 489, 4890–4911. [Google Scholar] [CrossRef]
- Przybyla, J.; Kile, M.; Smit, E. Description of Exposure Profiles for Seven Environmental Chemicals in a US Population Using Recursive Partition Mixture Modeling (RPMM). J. Expo. Sci. Environ. Epidemiol. 2019, 29, 61–70. [Google Scholar] [CrossRef]
- Udhayakala, P.; Rajendiran, T.V.; Gunasekaran, S. Quantum Chemical Investigations on Some Quinoxaline Derivatives as Effective Corrosion Inhibitors for Mild Steel. Pharm. Lett. 2012, 4, 1285–1298. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Rev. C.01; Gaussian Inc.: Wallingford, UK, 2016. [Google Scholar]
- Abendroth, J.A.; Blankenship, E.E.; Martin, A.R.; Roeth, F.W. Joint Action Analysis Utilizing Concentration Addition and Independent Action Models. Weed Technol. 2011, 25, 436–446. [Google Scholar] [CrossRef]
- Gafourian, T.; Safari, A.; Adibkia, K.; Parviz, F.; Nokhodchi, A. A Drug Release Study from Hydroxypropylmethylcellulose (HPMC) Matrices Using QSPR Modeling. J. Pharm. Sci. 2007, 96, 3334–3351. [Google Scholar] [CrossRef] [PubMed]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A Comparison of Random Forest and Its Gini Importance with Standard Chemometric Methods for the Feature Selection and Classification of Spectral Data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef] [PubMed]
- Zakariah, M. Classification of Large Datasets Using Random Forest Algorithm in Various Applications: Survey. Int. J. Eng. Innov. Technol. (IJEIT) 2014, 4, 189–198. [Google Scholar]
- Schröder, W.; Holy, M.; Pesch, R.; Ilyin, I.; Harmens, H.; Gebhardt, H. Monitoring the Bioaccumulation of Metals and Nitrogen as Part of the Long-Term Integrated Environmental Monitoring in Baden-Württemberg. Umweltwiss. Schadst.-Forsch. 2010, 22, 721–735. [Google Scholar] [CrossRef]
- Altman, N.; Krzywinski, M. Ensemble Methods: Bagging and Random Forests. Nat. Methods 2017, 14, 933–934. [Google Scholar] [CrossRef]
- Alexander, D.L.J.; Tropsha, A.; Winkler, D.A. Beware of R2: Simple, Unambiguous Assessment of the Prediction Accuracy of QSAR and QSPR Models. J. Chem Inf. Model. 2015, 55, 1316–1322. [Google Scholar] [CrossRef]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Problems in RMSE-Based Wave Model Validations. Ocean Model. 2013, 72, 53–58. [Google Scholar] [CrossRef]
- Cedeño, W.; Agrafiotis, D.K. Using Particle Swarms for the Development of QSAR Models Based on K-Nearest Neighbor and Kernel Regression. J. Comput. Aided Mol. Des. 2003, 72, 53–58. [Google Scholar] [CrossRef]
| Serial Number | CdCl2 (μmol/L) | ZnCl2 (μmol/L) | CuSO4 (μmol/L) | NiCl2 (μmol/L) | Pb(NO3)2 (μmol/L) | MnCl2 (μmol/L) | SbCl3 (μmol/L) | CoCl2 (μmol/L) |
|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 60 | 30 | 100 | 100 | 100 | 5 | 10 |
| 2 | 20 | 90 | 60 | 200 | 200 | 200 | 10 | 20 |
| 3 | 30 | 120 | 90 | 300 | 300 | 300 | 15 | 30 |
| 4 | 40 | 150 | 120 | 400 | 400 | 400 | 20 | 40 |
| 5 | 50 | 180 | 150 | 500 | 500 | 500 | 25 | 50 |
| 6 | 60 | 210 | 180 | 600 | 600 | 600 | 30 | 60 |
| 7 | 70 | 240 | 210 | 700 | 700 | 700 | 35 | 70 |
| 8 | 80 | 270 | 240 | 800 | 800 | 800 | 40 | 80 |
| 9 | 90 | 300 | 270 | 900 | 900 | 900 | 45 | 90 |
| Descriptor | AdaBoost | RF | Model A | Model B |
|---|---|---|---|---|
| Highest orbital energy | ||||
| Lowest orbital energy | 0.15 | 0.39 | ||
| Ionization potentials | 0.10 | |||
| Electron affinity | 0.14 | 0.07 | ||
| Absolute electronegativity | 0.16 | 0.25 | ||
| Absolute hardness | 0.25 | 0.20 | 0.22 | 0.22 |
| Molecular energy | 0.11 | 0.14 | 0.31 | |
| Adsorption energy | 0.49 | 0.40 | 0.16 | 0.21 |
| Model Parameters | AdaBoost | RF | Model A | Model B | Model C | Model D |
|---|---|---|---|---|---|---|
| Training set samples | 54 | 54 | 27 | 27 | 27 | 27 |
| Test set samples | 18 | 18 | 9 | 9 | 9 | 9 |
| N estimators | 8 | 4 | 4 | 9 | 1 | 1 |
| Random state | 93 | 35 | 95 | 83 | 19 | 79 |
| R2 (train) | 0.86 | 0.95 | 0.97 | 0.97 | 0.88 | 0.90 |
| R2 (test) | 0.78 | 0.85 | 0.85 | 0.95 | 0.31 | 0.35 |
| RMSE (train) | 0.10 | 0.06 | 0.04 | 0.05 | 0.08 | 0.09 |
| RMSE (test) | 0.12 | 0.10 | 0.08 | 0.06 | 0.20 | 0.16 |
| 0.69 | 0.70 | 0.73 | 0.81 | −0.06 | 0.64 | |
| −0.20 | −0.44 | −0.45 | −0.47 | −0.86 | −0.79 | |
| −0.25 | −0.45 | −0.49 | −0.50 | −1.01 | −1.03 | |
| 0.79 | 0.86 | 0.87 | 0.95 | 0.50 | 0.79 | |
| 0.78 | 0.85 | 0.85 | 0.95 | 0.31 | 0.35 | |
| 0.37 | 0.57 | 0.61 | 0.85 | −0.51 | 0.36 | |
| CCC | 0.87 | 0.92 | 0.93 | 0.97 | 0.43 | 0.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sang, L.; Wang, Y.; Zong, C.; Wang, P.; Zhang, H.; Guo, D.; Yuan, B.; Pan, Y. Machine Learning for Evaluating the Cytotoxicity of Mixtures of Nano-TiO2 and Heavy Metals: QSAR Model Apply Random Forest Algorithm after Clustering Analysis. Molecules 2022, 27, 6125. https://doi.org/10.3390/molecules27186125
Sang L, Wang Y, Zong C, Wang P, Zhang H, Guo D, Yuan B, Pan Y. Machine Learning for Evaluating the Cytotoxicity of Mixtures of Nano-TiO2 and Heavy Metals: QSAR Model Apply Random Forest Algorithm after Clustering Analysis. Molecules. 2022; 27(18):6125. https://doi.org/10.3390/molecules27186125
Chicago/Turabian StyleSang, Leqi, Yunlin Wang, Cheng Zong, Pengfei Wang, Huazhong Zhang, Dan Guo, Beilei Yuan, and Yong Pan. 2022. "Machine Learning for Evaluating the Cytotoxicity of Mixtures of Nano-TiO2 and Heavy Metals: QSAR Model Apply Random Forest Algorithm after Clustering Analysis" Molecules 27, no. 18: 6125. https://doi.org/10.3390/molecules27186125
APA StyleSang, L., Wang, Y., Zong, C., Wang, P., Zhang, H., Guo, D., Yuan, B., & Pan, Y. (2022). Machine Learning for Evaluating the Cytotoxicity of Mixtures of Nano-TiO2 and Heavy Metals: QSAR Model Apply Random Forest Algorithm after Clustering Analysis. Molecules, 27(18), 6125. https://doi.org/10.3390/molecules27186125








