Continuum Electronic States: The Tiresia Code
Abstract
1. Introduction
2. The Tiresia Program
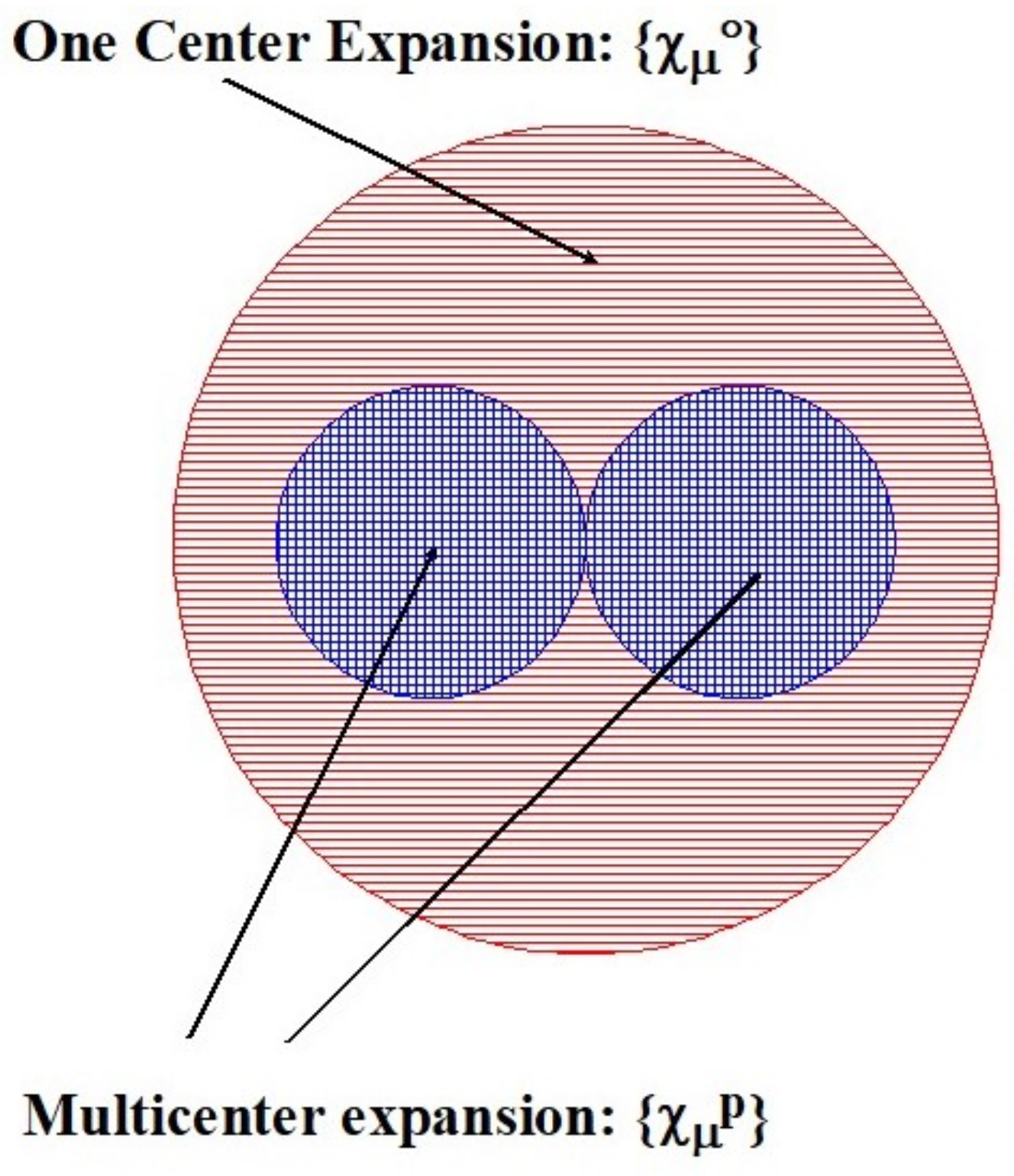
2.1. The Basis Set
2.2. The Galerkin Approach
2.3. The Many Electron Wavefunction
2.3.1. The Static Exchange Approach
2.3.2. The TDDFT Approach
2.3.3. The Correlated Single Channel Approach
3. Multiphoton and Strong Field Processes
- 1.
- Calculation of , which is and depends on the particular excitation mechanism considered.
- 2.
- Calculation of or equivalently , which is independent of the former, as eigenvector of the molecular hamiltonian already considered.
- 1.
- In the multiphoton domain, generally the lowest order perturbation theory is employedvalid for a single photon field, and non-resonant intermediate states, but can be easily generalized, and can be evaluated recursively.
- 2.
- For nonperturbative fields a standard approach is now the solution of the time dependent Schrödinger equation (TDSE)with a time dependent hamiltonian which includes the external field.
4. Ab Initio Developments
5. Applications
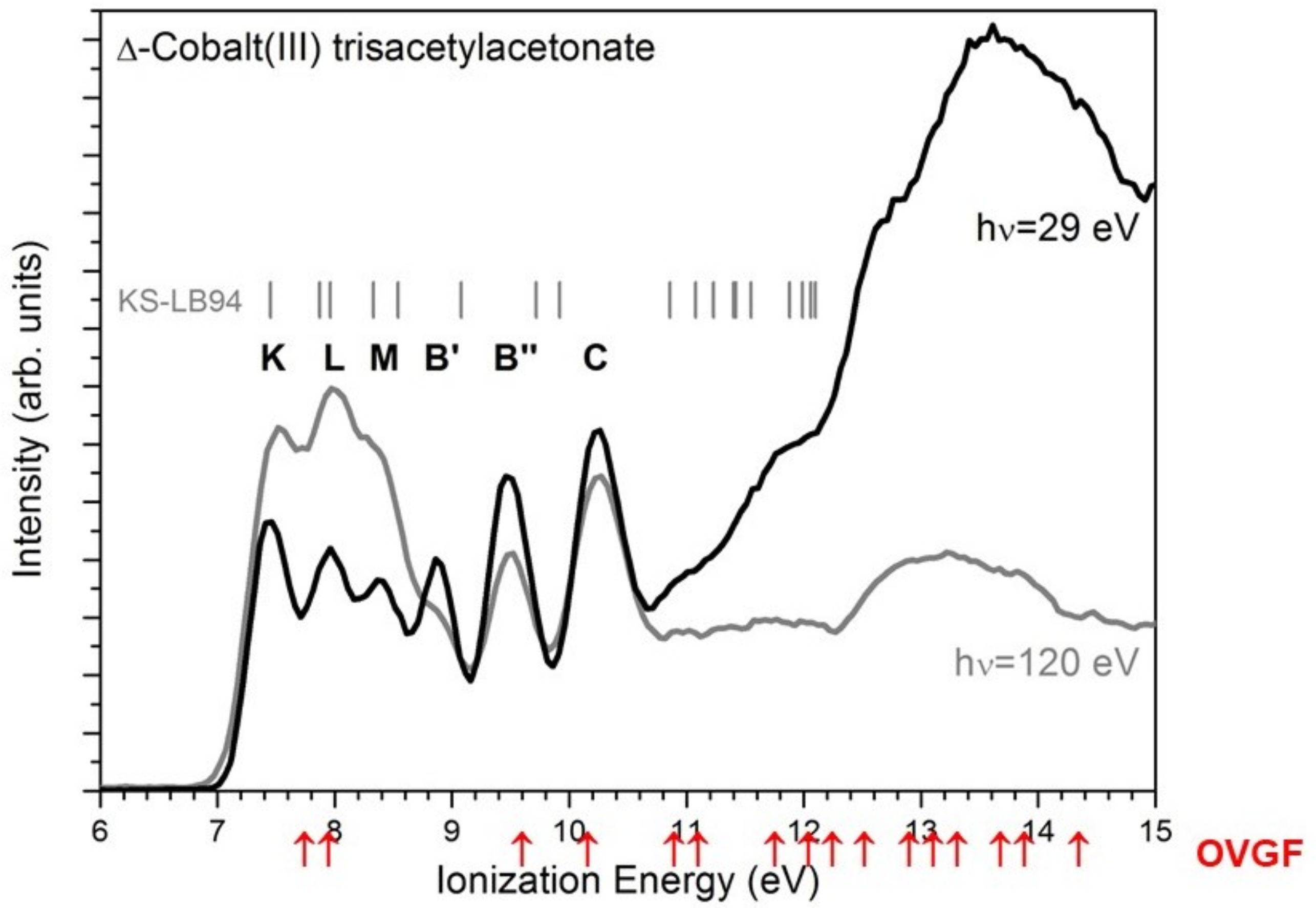
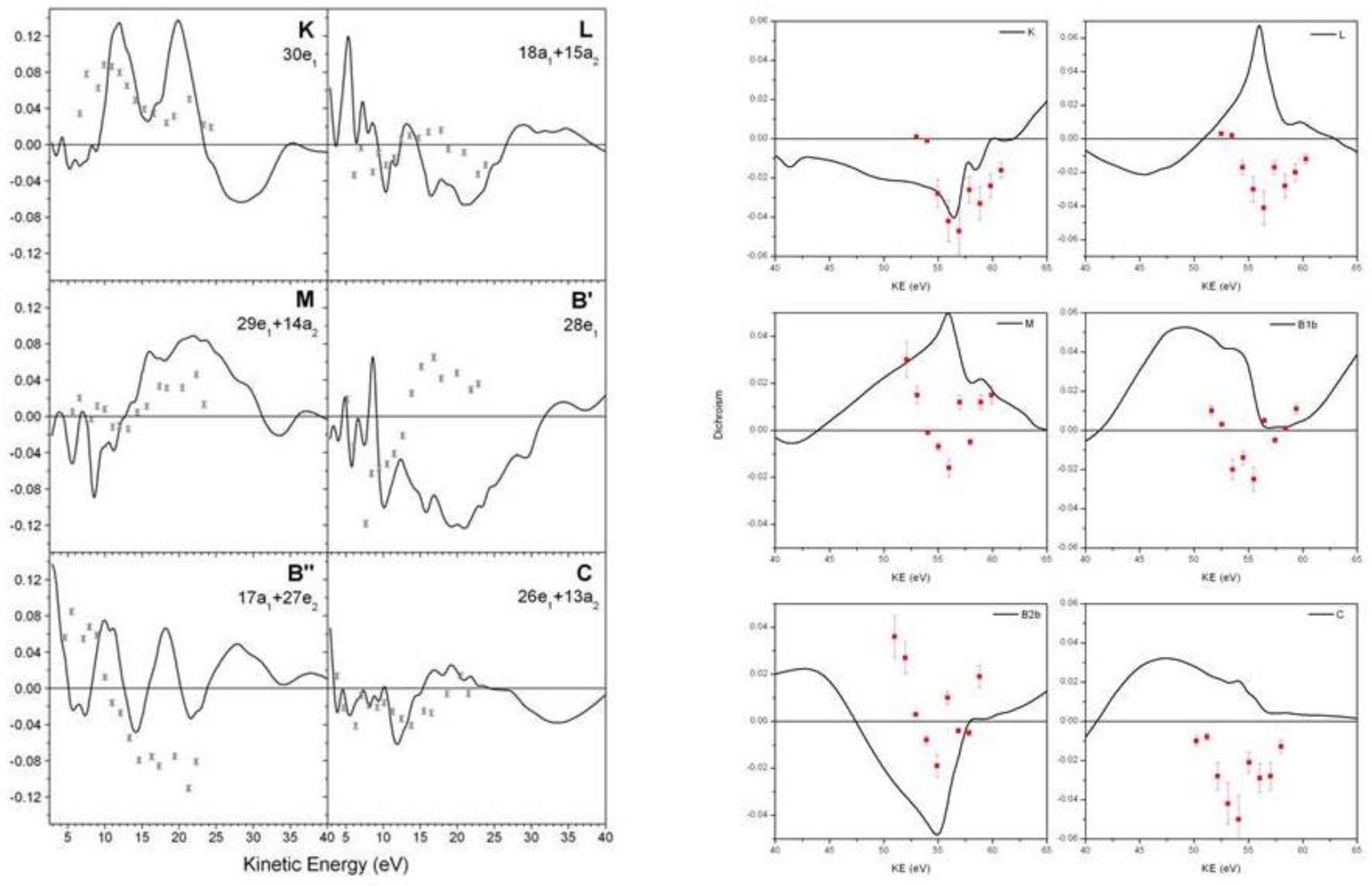
5.1. Molecular Photoionization
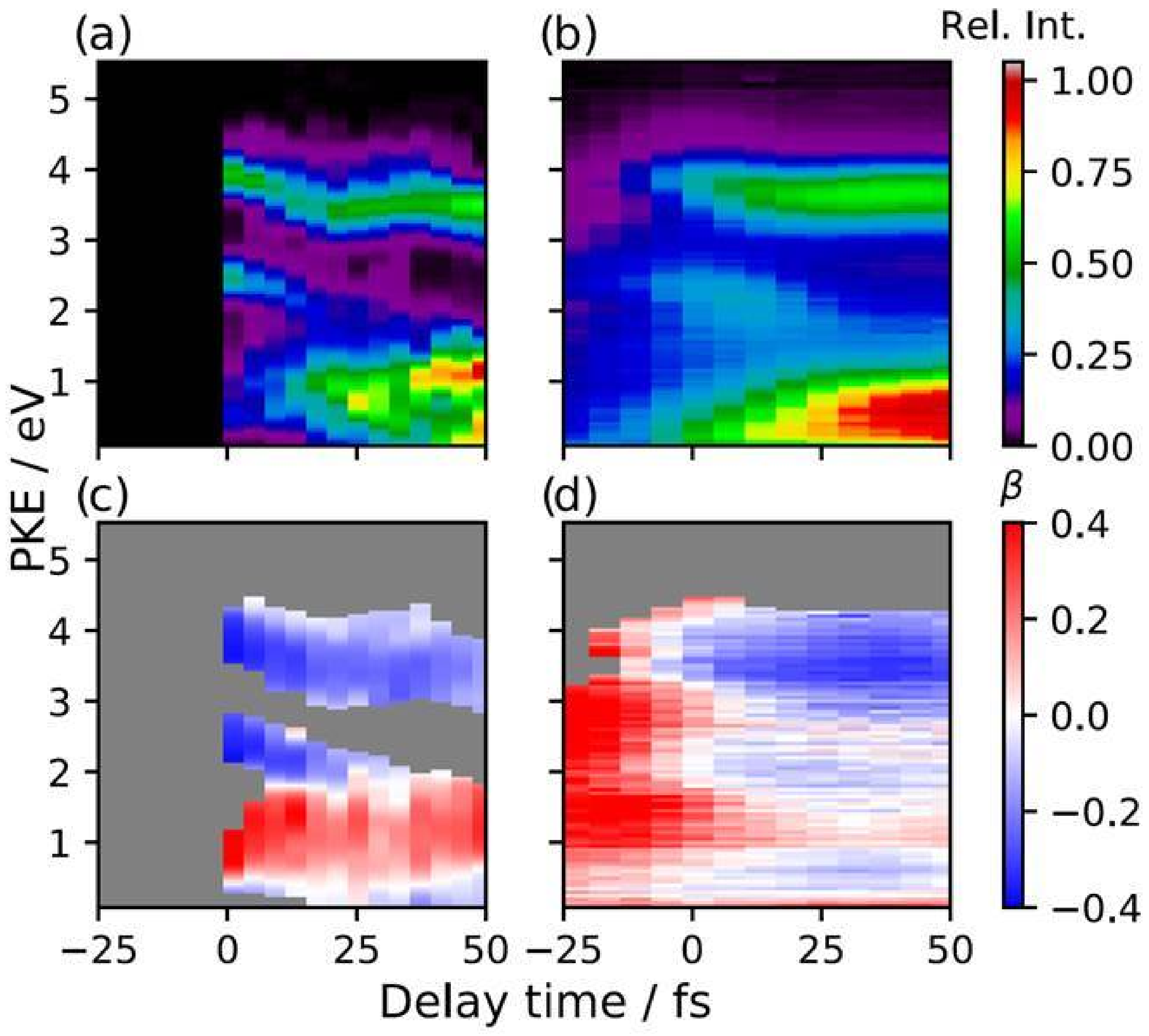
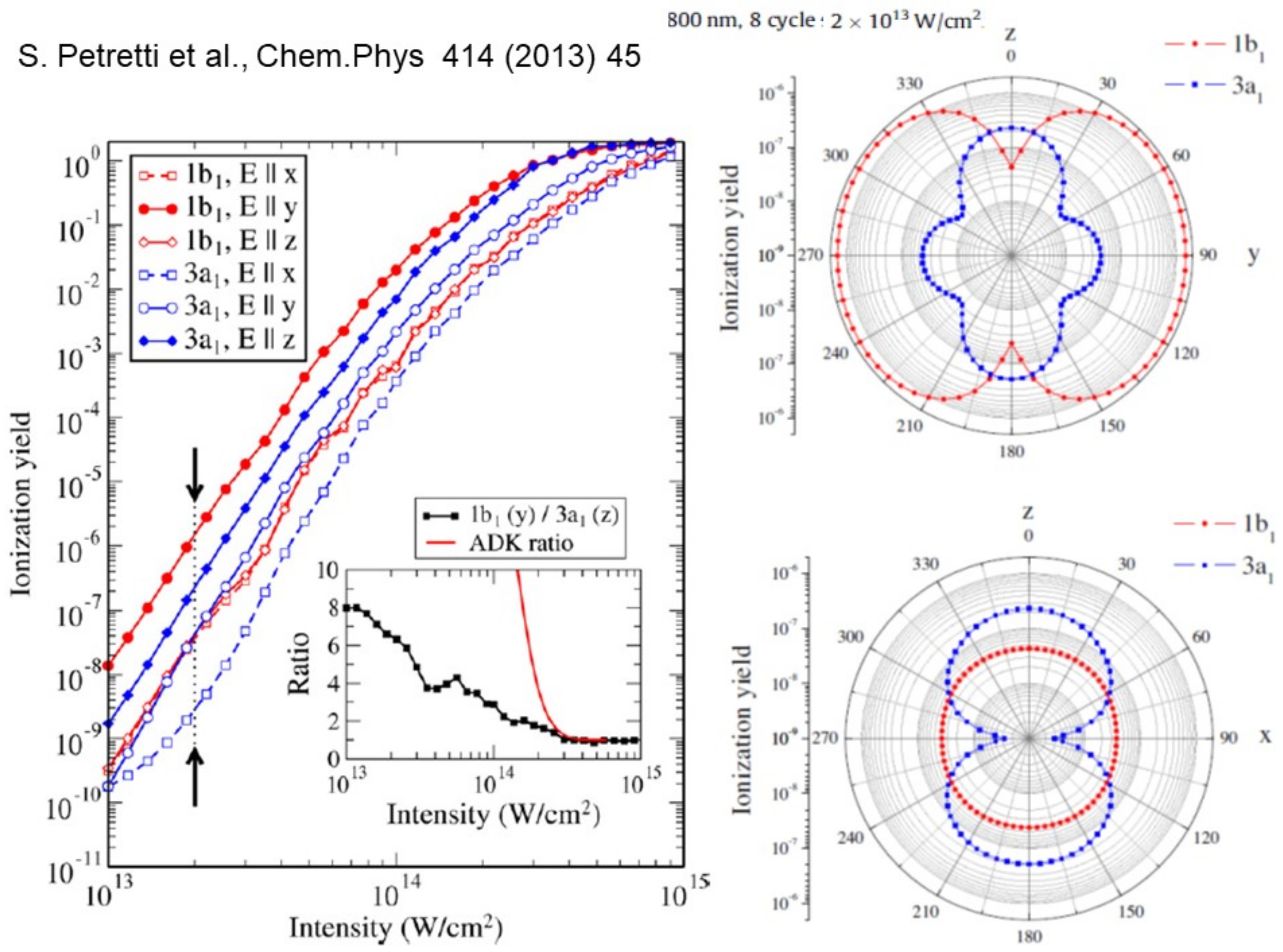
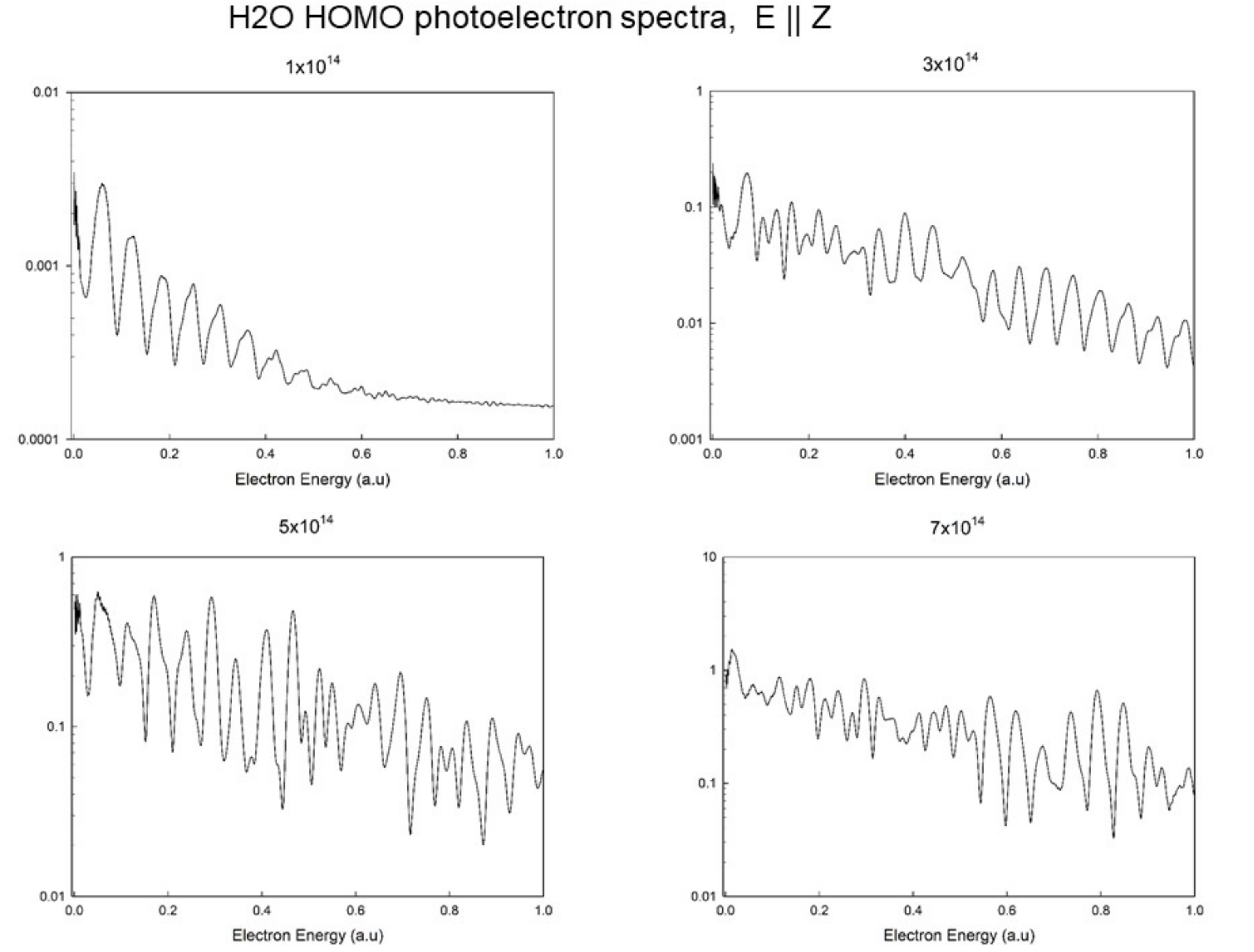
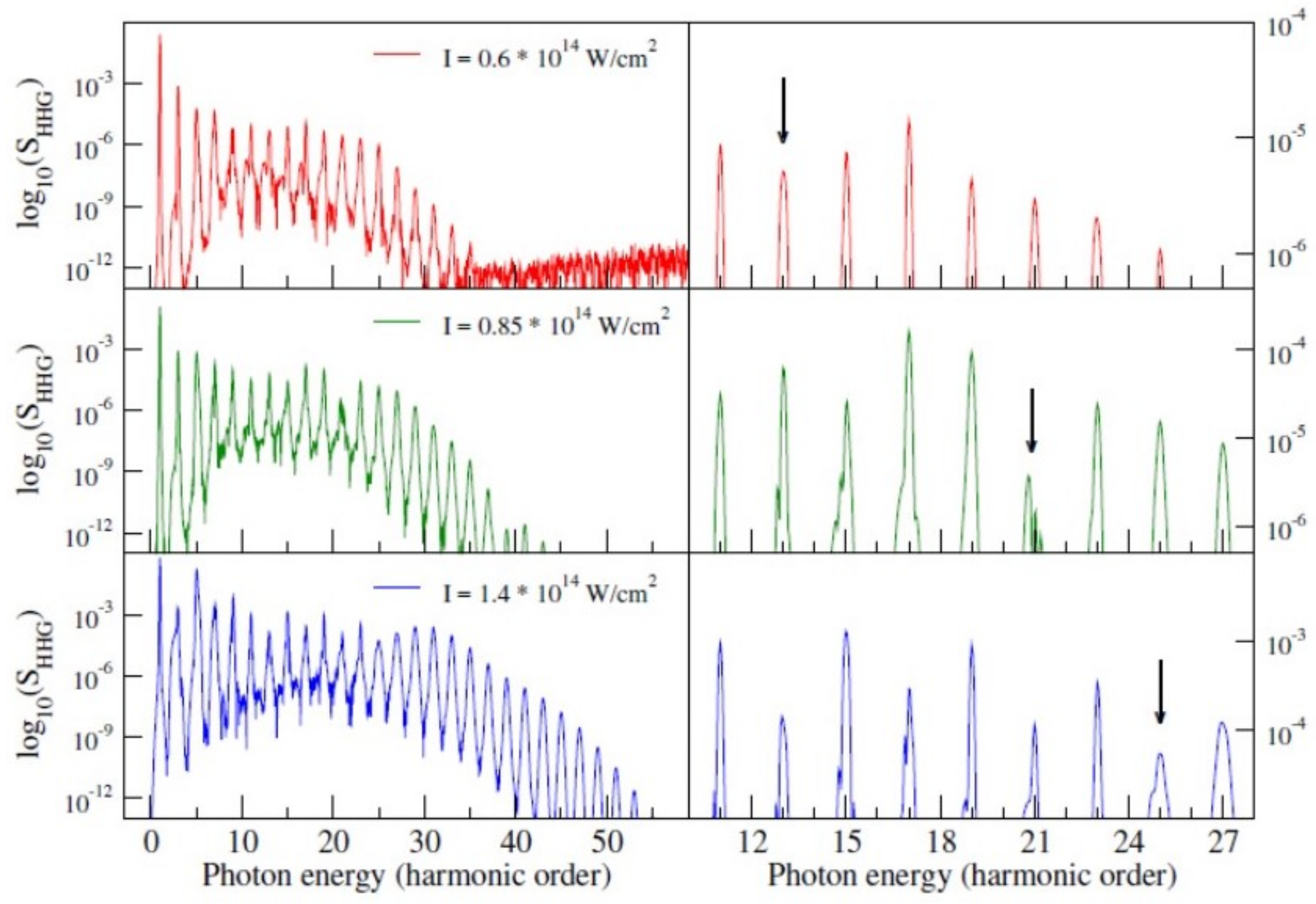
5.2. Strong Field and Ultrafast Processes
6. Conclusions
- A dense set within a finite range (a sphere) of arbitrary length. It can approach completeness and therefore converge to the required solutions.
- A complete control of the overlap matrix, hence numerical linear independence and stability.
- Accurate solutions of homogeneous and inhomogeneous equations within the range, with proper boundary conditions, which are easily implemented.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Ueda, K.; Sokell, E.; Schippers, S.; Aumayr, F.; Sadeghpour, H.; Burgdörfer, J.; Lemell, C.; Tong, X.M.; Pfeifer, T.; Calegari, F.; et al. Roadmap on photonic, electronic and atomic collision physics: I. Light–matter interaction. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 171001. [Google Scholar] [CrossRef]
- Lucchese, R.R.; Raseev, G.; McKoy, V. Studies of differential and total photoionization cross sections. of molecular nitrogen. Phys. Rev. A 1982, 25, 2572. [Google Scholar] [CrossRef]
- Demekhin, P.V.; Ehresmann, A.; Sukhorukov, V.L. Single center method: A computational tool for ionization and electronic excitation studies of molecules. J. Chem. Phys. 2011, 134, 024113. [Google Scholar] [CrossRef]
- Dill, D.; Dehmer, J.L. Electron-molecule scattering and molecular photoionization using the multiple scattering method. J. Chem. Phys. 1974, 61, 692. [Google Scholar] [CrossRef]
- Son, S.K.; Chu, S.I. Theoretical study of orientation-dependent multiphoton ionization of polyatomic molecules in intense ultrashort laser fields: A new time-dependent Voronoi-cell finite difference method. Chem. Phys. 2009, 366, 91. [Google Scholar] [CrossRef]
- Sawada, R.; Sato, T.; Ishikawa, K.L. Implementation of the multiconfiguration time-dependent Hatree-Fock method for general molecules on a multiresolution Cartesian grid. Phys. Rev. A 2016, 93, 023434. [Google Scholar] [CrossRef]
- Majety, V.P.; Zielinski, A.; Scrinzi, A. Photoionization of few electron systems: A hybrid coupled channels approach. New J. Phys. 2015, 17, 063002. [Google Scholar] [CrossRef]
- Toffoli, D.; Stener, M.; Fronzoni, G.; Decleva, P. Convergenge of the Multicenter B-spline DFT approach for the continuum. Chem. Phys. 2002, 276, 25. [Google Scholar] [CrossRef]
- Masin, Z.; Benda, J.; Gorfinkiel, J.D.; Harvey, A.G.; Tennyson, J. UKRmol+: A suite for modelling electronic processes in molecules interacting with electrons, positrons and photons using the R-matrix method. Comput. Phys. Commun. 2020, 249, 107092. [Google Scholar] [CrossRef]
- Marante, C.; Klinker, M.; Corral, I.; Gonzalez-Vazquez, J.; Argenti, L.; Martin, F. Hybrid-Basis Close-Coupling Interface to Quantum Chemistry Packages for the Treatment of Ionization Problems. J. Chem. Theory Comput. 2017, 13, 499. [Google Scholar] [CrossRef]
- Burke, P.G. R-Matrix Theory of Atomic Collisions; Springer: New York, NY, USA, 2011. [Google Scholar]
- de Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978. [Google Scholar]
- Bachau, H.; Cormier, E.; Decleva, P.; Hansen, J.E.; Martin, F. Applications of B-splines in Atomic and Molecular Physics. Rep. Prog. Phys. 2001, 64, 1815. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Idrees, M. Spline algorithms for continuum functions. Comput. Phys. 1989, 3, 53. [Google Scholar] [CrossRef]
- Brosolo, M.; Decleva, P. Variational approach to continuum orbitals in a spline basis: An application to H+2 photoionization. Chem. Phys. 1992, 159, 185. [Google Scholar] [CrossRef]
- Brosolo, M.; Decleva, P.; Lisini, A. Continuum wavefunctions calculations with least-squares schemes in a B-splines basis. Comput. Phys. Comm. 1992, 71, 207. [Google Scholar] [CrossRef]
- Stener, M.; Fronzoni, G.; Decleva, P. Time-dependent density-functional theory for molecular photoionization with noniterative algorithm and multicenter B-spline basis set: CS2 and C6H6 case studies. J. Chem. Phys. 2005, 122, 234301. [Google Scholar] [CrossRef] [PubMed]
- Arneberg, R.; Muller, J.; Manne, R. Configuration Interaction Calculations of Satellite Structure In Photoelectron Spectra of H2O. Chem. Phys. 1982, 64, 249. [Google Scholar] [CrossRef]
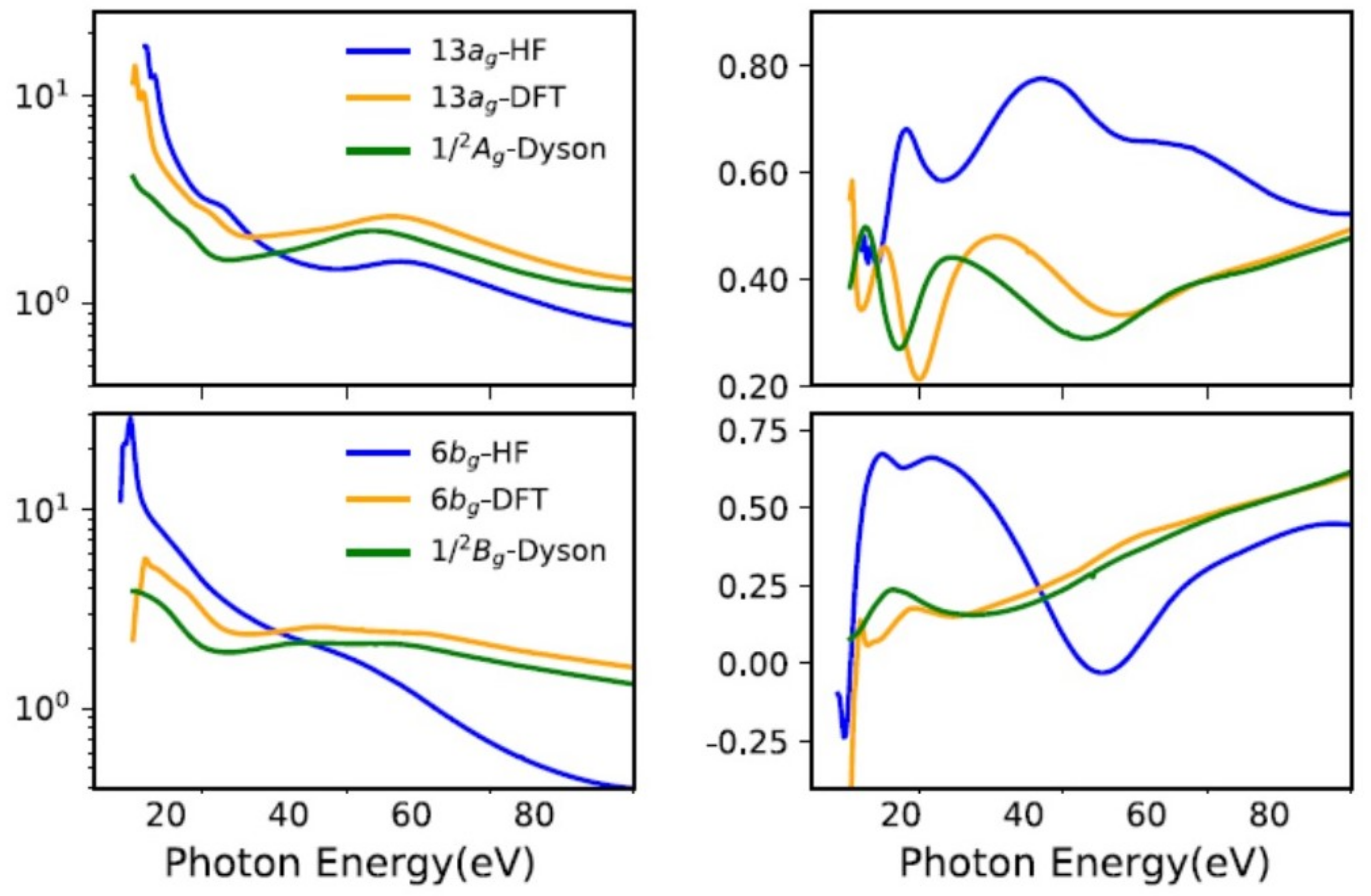
- Moitra, T.; Ponzi, A.; Koch, H.; Coriani, S.; Decleva, P. Accurate Description of Photoionization Dynamical Parameters. J. Phys. Chem. Lett. 2020, 11, 5330–5337. [Google Scholar] [CrossRef]
- Moitra, T.; Coriani, S.; Decleva, P. Capturing Correlation Effects on Photoionization Dynamics. J. Chem. Theory Comput. 2021, 17, 5064. [Google Scholar] [CrossRef]
- van Leeuwen, R.; Baerends, E.J. Exchange-correlation potential with correct asymptotic behavior. Phys. Rev. A 1994, 49, 2421. [Google Scholar] [CrossRef]
- Stener, M.; Furlan, S.; Decleva, P. Density functional calculations of photoionization with an exchange-correlation potential with the correct asymptotic behaviour. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 1081. [Google Scholar] [CrossRef]
- Slater, J.C. Statistical Exchange-Correlation in the Self-Consistent Field. Adv. Quantum Chem. 1972, 6, 1. [Google Scholar]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200. [Google Scholar] [CrossRef]
- Cormier, E.; Lambropoulos, P. Above-threshold ionization spectrum of hydrogen using B-spline functions. J. Phys. B At. Mol. Opt. Phys. 1997, 30, 77. [Google Scholar] [CrossRef]
- Tao, L.; Scrinzi, A. Photoelectron momentum spectra from minimal volumes: The time-dependent surface flux method. New J. Phys. 2012, 14, 013021. [Google Scholar] [CrossRef]
- Toffoli, D.; Decleva, P. Density Functional Theory for Molecular Multiphoton Ionization in the Perturbative Regime. J. Chem. Phys. 2012, 137, 134103. [Google Scholar] [CrossRef] [PubMed]
- Toffoli, D.; Decleva, P. A Multichannel least-squares B-spline approach to molecular photoionization. Theory, implementation and applications within the configuration-interaction singles approximation. J. Chem. Theory Comput. 2016, 12, 4996. [Google Scholar] [CrossRef]
- Decleva, P.; Lisini, A.; Venuti, M. Multichannel continuum states by least squares approach in spline basis. Application to He and H- photoionization. J. Phys. B At. Mol. Opt. Phys. 1994, 27, 4867. [Google Scholar] [CrossRef]
- Qiu, Y.; Fischer, C.F. Integration by Cell Algorithm for Slater Integrals in a Spline Basis. J. Comput. Phys. 1999, 156, 257. [Google Scholar] [CrossRef]
- Toffoli, D.; (DSCF, Universita’ di Trieste, Trieste, Italy); Decleva, P.; (Istituto Officina dei Materiali IOM-CNR, Trieste, Italy). Manuscript in preparation, to be submitted.
- Ruberti, M. Restricted Correlation Space B-Spline ADC Approach to Molecular Ionization: Theory and Applications to Total Photoionization Cross Sections. J. Chem. Theory Comput. 2019, 15, 3635. [Google Scholar] [CrossRef]
- Grell, G.; Bokarev, S.I. Multi-reference protocol for (auto)ionization spectra: Application to molecules. J. Chem. Phys. 2020, 152, 074108. [Google Scholar] [CrossRef]
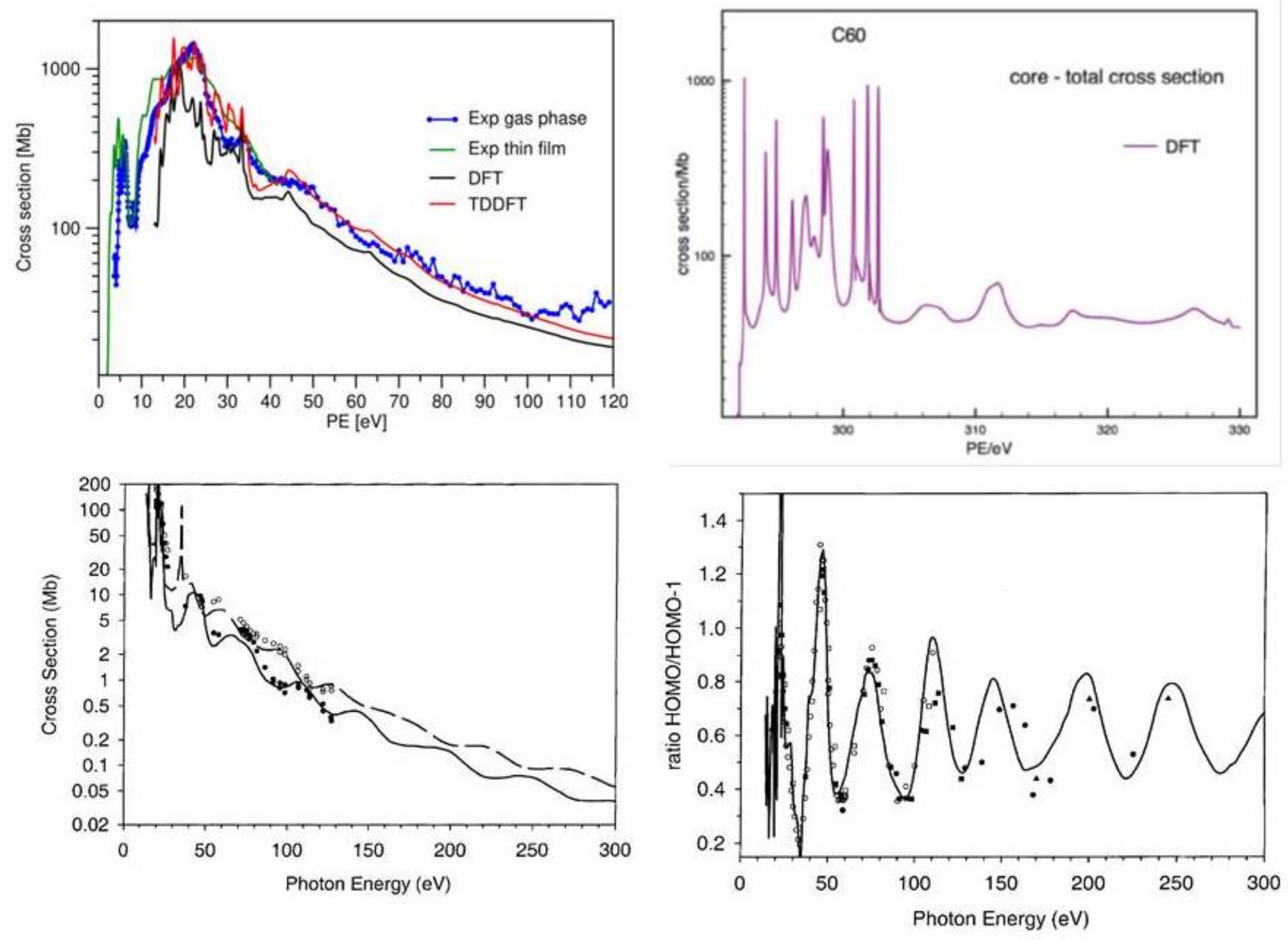
- Venuti, M.; Stener, M.; De Alti, G.; Decleva, P. Photoionization of C60 by large scale one-centre density functional explicit continuum wave-function. J. Chem. Phys. 1999, 111, 4589. [Google Scholar] [CrossRef]
- Colavita, P.; De Alti, G.; Decleva, P.; Fronzoni, G.; Stener, M. Theoretical Study of the Valence and Core Photoemission Spectra of C60. Phys. Chem. Chem. Phys. 2001, 3, 4481. [Google Scholar] [CrossRef][Green Version]
- Ponzi, A.; Manson, S.T.; Decleva, P. Photoionization of C60: Effects of Correlation on cross sections and angular distributions of Valence Subshells. J. Phys. Chem. A 2020, 124, 108. [Google Scholar] [CrossRef] [PubMed]
- Ponzi, A.; (Department of Physical Chemistry, Ruđer Bošković Institute, Zagreb, Croatia); Manson, S.T.; (Department of Physics and Astronomy, Georgia State University, Atlanta, GA, USA); Decleva, P.; (Istituto Officina dei Materiali IOM-CNR, Trieste, Italy). Manuscript in preparation, to be submitted.
- Decleva, P.; Fronzoni, G.; Furlan, S.; Stener, M. High energy oscillations in the photoionization partial cross section of C60. Chem. Phys. Lett. 2001, 348, 363. [Google Scholar] [CrossRef]
- Canton, S.E.; Plesiat, E.; Bozek, J.D.; Rude, B.S.; Decleva, P.; Martin, F. Direct observation of Cohen-Fano interferences in vibrationally resolved valence-shell photoionization spectra of H2, N2 and CO. Proc. Natl. Acad. Sci. USA 2011, 108, 7302. [Google Scholar] [CrossRef]
- Plesiat, E.; Argenti, L.; Miron, C.; Kukk, E.; Ueda, K.; Decleva, P.; Martin, F. Vibrationally resolved photoelectron spectroscopy of CH4: Studying electron diffraction from within. Phys. Rev. A 2012, 85, 023409. [Google Scholar]
- Argenti, L.; Thomas, T.D.; Plésiat, E.; Liu, X.J.; Miron, C.; Lischke, T.; Prümper, G.; Sakai, K.; Ouchi, T.; Püttner, R.; et al. Double-slit experiment with a polyatomic molecule: Vibrationally-resolved C 1s photoelectron spectra of acetylene. New J. Phys. 2012, 14, 033012. [Google Scholar] [CrossRef]
- Kushawaha, R.K.; Patanen, M.; Guillemin, R.; Journel, L.; Miron, C.; Simon, M.; Piancastelli, M.N.; Decleva, P. From double-slit interference to structural information in simple hydrocarbons. Proc. Natl. Acad. Sci. USA 2013, 110, 15201. [Google Scholar] [CrossRef]
- Toffoli, D.; Decleva, P. Strong Oscillations in the nondipole corrections to the photoelectron angular distributions from C60. Phys. Rev. A 2010, 81, 061201. [Google Scholar] [CrossRef]
- Cederbaum, L.S.; Domcke, W. Theoretical Aspects Of Ionization Potentials and Photoelectron Spectroscopy: A Green’s Function Approach. Adv. Chem. Phys. 1977, 36, 205. [Google Scholar]
- Cederbaum, L.S.; Domcke, W.; Schirmer, J.; Von Niessen, W. Correlation Effects in The Ionization of Molecules: Breakdown of the Molecular Orbital Picture. Adv. Chem. Phys. 1986, 65, 115. [Google Scholar]
- Kuleff, A.I.; Cederbaum, L.S. Ultrafast Correlation-Driven Electron Dynamics. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 124002. [Google Scholar] [CrossRef]
- Nicholson, R.J.; McCarthy, I.E.; Weyrich, W. Dyson orbitals from electron momentum spectroscopy. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 3873. [Google Scholar] [CrossRef]
- Stranges, S.; Turchini, S.; Alagia, M.; Alberti, G.; Contini, G.; Decleva, P.; Fronzoni, G.; Stener, M.; Zema, N.; Prosperi, T. Valence Photoionization Dynamics in Circular Dichroism of Chiral Free Molecules: The Methyl-Oxirane. J. Chem. Phys. 2005, 122, 244303. [Google Scholar] [CrossRef] [PubMed]
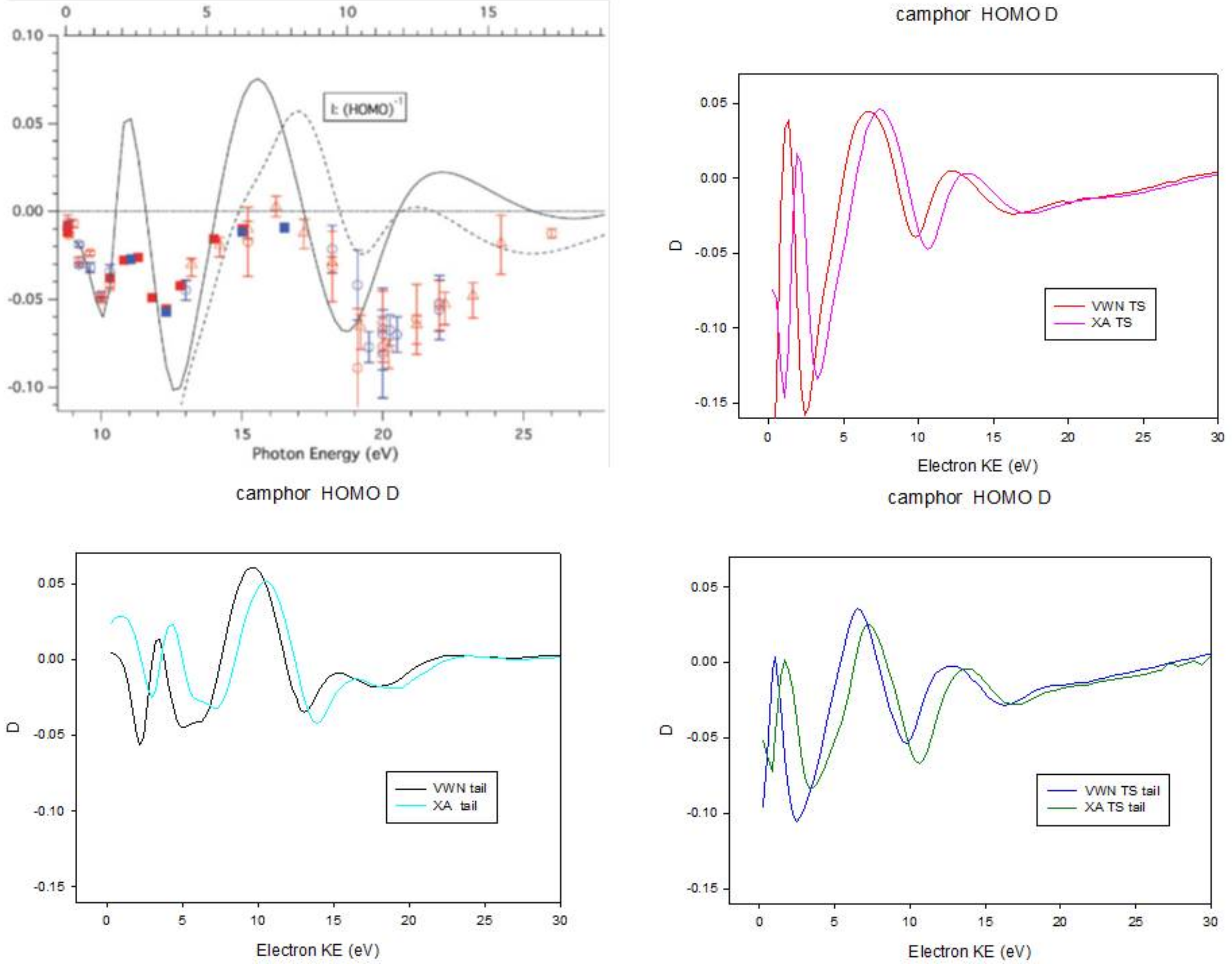
- Nahon, L.; Nag, L.; Garcia, G.A.; Myrgorodska, I.; Meierhenrich, U.; Beaulieu, S.; Wanie, V.; Blanchet, V.; Geneaux, R.; Powis, I. Determination of accurate electron chiral asymmetries in fenchone and camphor in the VUV range: Sensitivity to isomerism and enantiomeric purity. Phys. Chem. Chem. Phys. 2016, 18, 12696. [Google Scholar] [CrossRef] [PubMed]
- Catone, D.; Stener, M.; Decleva, P.; Contini, G.; Zema, N.; Prosperi, T.; Feyer, V.; Prince, K.C.; Turchini, S. Resonant circular dichroism of chiral metal-organic complex. Phys. Rev. Lett. 2012, 108, 083001. [Google Scholar] [CrossRef] [PubMed]
- Catone, D.; Turchini, S.; Stener, M.; Decleva, P.; Contini, G.; Prosperi, T.; Feyer, V.; Prince, K.C.; Zema, N. Photoelectron Spectroscopy and Circular Dichroism of a Chiral Metal-organic Complex. Rend. Fis. Acc. Lincei 2013, 24, 269. [Google Scholar] [CrossRef]
- Pitesa, T.; Sapunar, M.; Ponzi, A.; Gelin, M.F.; Doslic, N.; Decleva, P. A combined surface-hopping, Dyson orbital and B-spline approach for the computation of time-resolved photoelectron spectroscopy signals: The internal conversion in pyrazine. J. Chem. Theory Comput. 2021, 17, 5098. [Google Scholar] [CrossRef]
- Plesiat, E.; Lara-Astiaso, M.; Decleva, P.; Palacios, A.; Martin, F. Real-time determination of ultrafast charge dynamics in tetrafluoromethane from attosecond pump-probe photoelectron spectroscopy. Chem. Eur. J. 2018, 24, 12061. [Google Scholar] [CrossRef]
- Nandi, S.; Plesiat, E.; Zhong, S.; Palacios, A.; Busto, D.; Isinger, M.; Neoricic, L.; Arnold, C.L.; Squibb, R.J.; Feifel, R.; et al. Attosecond timing of electron emission from a molecular shape resonance. Sci. Adv. 2020, 6, eaba7762. [Google Scholar] [CrossRef]
- Petretti, S.; Vanne, Y.V.; Saenz, A.; Castro, A.; Decleva, P. Alignment-Dependent Ionization of N2, O2, and CO2 in Intense Laser Fields. Phys. Rev. Lett. 2010, 104, 223001. [Google Scholar] [CrossRef] [PubMed]
- Petretti, S.; Saenz, A.; Castro, A.; Decleva, P. Water Molecules in Ultrashort Intense Laser Fields. Chem. Phys. 2013, 414, 45. [Google Scholar] [CrossRef]
- Benda, J.; Gorfinkiel, J.D.; Mašín, Z.; Armstrong, G.S.; Brown, A.C.; Clarke, D.D.; van der Hart, H.W.; Wragg, J. Perturbative and nonperturbative photoionization of H2 and H2O using the molecular R-matrix-with-time method. Phys. Rev. A 2020, 102, 052826. [Google Scholar] [CrossRef]
- Ruberti, M.; Decleva, P.; Averbukh, V. Multi-channel dynamics and correlation-driven inter-channel couplings in high harmonic generation spectra of aligned CO2 molecule: Ab initio Time Dependent B-spline ADC ab initio analysis. Phys. Chem. Chem. Phys. 2018, 20, 8311. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Decleva, P.; Stener, M.; Toffoli, D. Continuum Electronic States: The Tiresia Code. Molecules 2022, 27, 2026. https://doi.org/10.3390/molecules27062026
Decleva P, Stener M, Toffoli D. Continuum Electronic States: The Tiresia Code. Molecules. 2022; 27(6):2026. https://doi.org/10.3390/molecules27062026
Chicago/Turabian StyleDecleva, Piero, Mauro Stener, and Daniele Toffoli. 2022. "Continuum Electronic States: The Tiresia Code" Molecules 27, no. 6: 2026. https://doi.org/10.3390/molecules27062026
APA StyleDecleva, P., Stener, M., & Toffoli, D. (2022). Continuum Electronic States: The Tiresia Code. Molecules, 27(6), 2026. https://doi.org/10.3390/molecules27062026





